割平面法求解整数规划问题实验报告
割平面法Gommoy

割平面法Gommoy算法步骤:① 求解原整数规划对应的线性规划 min f (x )=cx , .⎩⎨⎧≥≤为整数xi x b A t s x .0.,设最优解为x*。
② 如果最优解的分量均为整数,则x *为原整数规划的最优解:否则任选一个x *中不是整数的分量,设其对应的基变量为x p ,, 定义包含这个基变量的切割约束方程∑=+jcom j ij b x r p x ,其中x j 为非基变量。
③ 令][b b b ],[r com com com ij ij ij r r -=-=,其中[]为高斯函数符号,表示不大于某数的最大整数. 将切割约束方程变换为∑∑-=-+jj ij j j ijp x r x r x com com b ][b ][,由于10,1r 0<≤<≤com ij b ,所以有∑-j ij com x r b 〈1,因为自变量为整数,则∑-j ij com x r b 也为整数,所以进一步有∑-j ij com x r b 〈=0.④ 将切割方程加入约束方程中,用对偶单纯算法求解线性规划⎪⎪⎩⎪⎪⎨⎧≥≤-≤=∑00b b Ax .,)(min com x x r t s cx x f j j ij ,转 。
算法MATLAB 实现代码:function [intx ,intf ]=Gomory(A,c ,b ,base )%约束矩阵:A ;%目标函数系数向量:c%约束右端向量:b%初始基向量base%目标函数取最小化时的自变量值:x%目标函数的最小值:minfsz=size(A);nVia=sz(2);n=sz(1);xx=1:nVia;if length(base)~=ndisp(’基变量的个数要与约束矩阵的行数相等!');mx=NaN;mf=NaN;return;endM=0;sigma=—[transpose(c) zeros(1,(nVia—length(c)))];xb=b;while 1[maxs,ind]=max(sigma);if maxs〈=0vr=find(c~=0,1,’last');for l=1:vrele=find(base==l,1);if(isempty(ele))mx(l)=0;elsemx(l)=xb(ele);endendif max(abs(round(mx)—mx))<1.0e—7intx=mx;intf=mx*c;return;elsesz=size(A);sr=sz(1);sc=sz(2);[max_x,index_x]=max(ads(round(mx)—mx)); [isB,num]=find(index_x==base);fi=xb(num)-floor(xb(num));for i=1:(index_x—1)Atmp(1,i)=A(num,i)-floor(A(num,i));endfor i=(infex_x+1):scAtmp(1,i)=A(num,i)-floor(A(num,i));end%构建对单纯形法的初始表格Atmp(1,index_x)=0;A=[A zeros(sr,1);-Atmp(1,:) 1];xb=[xb;-fi];base=[base sc+1];sigma=[sigma 0];%对偶单纯形法迭代过程while 1if(xb)>=0if max(abs(round(xb)—xb))<1。
割平面法

《线性规划》课程设计题目:割平面法及其数值实现院系:数理科学与工程学院应用数学系专业:数学与应用数学姓名学号:*** 1********* 1********* 1********* 1******指导教师:***日期:2015 年 6 月11 日整数规划与线性规划有着密不可分的关系,它的一些基本算法的设计都是从相应的线性规划的最优解出发的。
整数规划问题与我们的实际生活有着密切的联系,如合成下料问题、建厂问题、背包问题、投资决策问题、旅行商问题、生产顺序表问题等都是求解整数模型中的著名问题。
所以要想掌握生活中这些解决问题的方法,研究整数规划是必然的路径。
用于解决整数规划的方法主要有割平面法,分支定界法,小规模0-1规划问题的解法,指派问题和匈牙利法。
本文重要对整数规划中经常用的割平面法加以介绍及使用Matlab 软件对其数值实现。
割平面法从线性规划问题着手,在利用单纯型法的时候,当约束矩阵中出现分数,给出一种"化分为整"的方法。
然后在割平面方法来解决整数线性规划的理论基础上,把"化分为整"的方法进行到底,直到求解出最有整数解。
关键词:最优化;整数规划;割平面法;数值实现;最优解;Matlab软件。
AbstractThe integer programming are closely related to the linear programming. Some of the basic algorithms of the former are designed from the optimal solution of the corresponding linear programming. What’s more, our daily life has a close relationship with it as well, such as synthesis problem, plant problem, knapsack problem, investment decision problem, traveling salesman problem and production sequence table problems. They are famous questions in solving integer model. So, to study the integer programming is the inevitable way to master the methods of solving these problems in life. The methods used in solving the integer programming include cutting plane method, branch and bound method, and solving the problem of small-scale 0-1 programming, assignment problem and Hungarian method. In this paper, we introduce the cutting plane method and use Matlab to get its numerical implementation in the integer programming.Cutting plane method, giving us a "integrated" method when we meet the constraint matrix scores in the use of simplex method, starts from the linear programming problem. Then, based on the theory of cutting plane method to solve the integer linear programming, we use “integrated” method until the most integer solution is solved.Keywords:Optimization; Integer programming; Cutting plane method; Numerical implementation; Optimal solution; Matlab software.第一章问题描述 (2)1.1 整数规划问题概述 (2)1.2 整数规划的基本定理 (2)第二章求解整数规划问题的割平面法 (3)2.1 基本思想 (3)2.2 算法步骤 (3)2.3 算法流程图 (5)第三章数值实验 (6)3.1算例 (6)3.2 数值实现 (7)总结 (8)参考文献……………………………………………………………………………附录…………………………………………………………………………………第一章 问题描述1.1 整数规划问题概述规划中的变量(全部或部分)限制为整数,称为整数规划简称为IP 问题。
运筹学__割平面法

x1
1 0 0 0 x1 1 0 0 0
x2
0 1 0 0 x2 0 1 0 0
x3
1/6 1/4 -1/4 -1/4 x3 0 0 1 0
x4
-1/6 1/4 -1/4 -1/4 x4 -1/3 0 1 0
s1
0 0 1 0 s1 2/3 1 -4 -1
CB
0 1 0
XB
x1 x2 x3
b
2/3 1 2
1 1 1 ( x 3 x4 ) 0 2 4 4
1 1 1 x3 x4 s1 4 4 2
Cj CB 0 1 0 σj XB x1 x2 s1 b 1 3/2 -1/2 -3/2 0 x1 1 0 0 0 1 x2 0 1 0 0 0 x3 1/6 1/4 -1/4 -1/4 0 x4 -1/6 1/4 -1/4 -1/4 0 s1 0 0 1 0
CB
0 1 0
XB
x1 x2 x3
b
2/3 1 2
x1
1 0 0
x2
0 1 0
x3
0 0 1
x4
-1/3 0 1
s1
2/3 1 -4
σj
-1
0
0
0
0
-1
CB 0
XB x1
b 2/3
x1 1
x2 0
x3 0
x4 -1/3
s1 2/3
1
0
x2
x3
1
2
0
0
1
0
0
1
0
1
1
-4
σj -1 0 0 0 0 -1 此时,X1 =(2/3, 1), Z=1,仍不是整数解。继续以x1为源行生成割 2 2 2 平面,其条件为:
割平面法 运筹学整数规划

整数规划(Integer Programming)
分类:1. 纯整数线性规划(Pure Integer Linear Programming) 2. 混合整数线性规划(Mixed Integer Linear Programming) 3. 0-1型整数线性规划(Zero-One Integer Linear Programming)
割平面解法(Cutting Plane Approach) 第三节 割平面解法
割平面法是1958年美国学者R. E. Gomory提出的。 基本思想是:先不考虑变量的取整数约束,求解相应的线性规 划,然后不断增加线性约束条件(即割平面),将原可行域割掉不 含整数可行解的一部分,最终得到一个具有整数坐标顶点的可行域, 而该顶点恰好是原整数规划问题的最优解。 例:求解
Z=40x1+90x2 LP-1 9x1+7x2=56 7x1+20x2=70 LP-2
第二步:分枝与定界过程。 • 将其中一个非整数变量的解,比如x1, 进行分枝,即 x1≤ 4.81 =4, x1≥ 4.81 =5 并分别加入LP问题的约束条件中, 得两个子LP规划问题LP-1, LP-2, 分 别求解此两个子线性规划问题, 其最优解分别是 LP-1: x1=4, x2=2.1, Z1=349 LP-2: x1=5, x2=1.57, Z2=341
二、具体步骤(以例子说明)
max Z = 40 x 1 + 90 x 2 9 x 1 + 7 x 2 ≤ 56 7 x + 20 x ≤ 70 1 2 x1 , x 2 ≥ 0 x 1 , x 2取整数
s .t
解:
第一步:先不考虑整数约束条件,求解相应的线性规划问题,得最 优解和最优值如下 x1=4.81, x2=1.82, Z=356 此解不满足整数解条件。定出整数规划问题目标函数的上下界。上 界为 Z=356;用观察法可知x1=0,x2=0是可行解,从而其整数规划问题目 标函数的下界应为0,即 0≤ Z* ≤356
实验四:整数规划

实验四:整数规划一、实验目的:整数规划问题建模及软件求解。
二、实验要求:1.掌握一般整数规划、0-1整数规划问题、指派问题的建模;2.了解求解整数规划问题的方法:分支定界法、割平面法、隐枚举法、匈牙利法;3.学会用matlab 、 lingo 软件求解整数规划问题。
三、实验内容:1、求解下列整数规划问题:⎪⎪⎩⎪⎪⎨⎧≥≤+≤++=.,0,30561652..max 2121212121为整数x x x x x x x x t s x x z(1)给出lingo 原始代码;(2)求解结果粘贴。
(1)model :max =x1+x2;2*x1+5*x2<=16;6*x1+5*x2<=30;@gin (x1);@gin (x2);end(2)Global optimal solution found.Objective value: 5.000000Objective bound: 5.000000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X1 5.000000 -1.000000 X2 0.000000 -1.000000Row Slack or Surplus Dual Price 1 5.000000 1.000000 2 6.000000 0.000000 3 0.000000 0.0000002、求解下列0-1整数规划问题:⎪⎩⎪⎨⎧==≤+-+-≤--+-+-+-=.5,4,3,2,1,100242645723..4352max 543215432154321i x x x x x x x x x x x t s x x x x x z i或 (1)给出matlab 、lingo 原始代码;(2)求解结果粘贴。
(1)Lingomodel :max =2*x1-x2+5*x3-3*x4+4*x5;3*x1-2*x2+7*x3-5*x4-4*x5<=6;x1-x2+2*x3-4*x4+2*x5<=0;@bin (x1);@bin (x2);@bin (x3);@bin (x4);@bin (x5);!sets: A/1..5/x @(for(A:@bin(x)));end(2)Global optimal solution found.Objective value: 7.000000Objective bound: 7.000000Infeasibilities: 0.000000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost X1 1.000000 -2.000000X2 1.000000 1.000000X3 1.000000 -5.000000X4 1.000000 3.000000X5 1.000000 -4.000000Row Slack or Surplus Dual Price1 7.000000 1.0000002 7.000000 0.0000003 0.000000 0.000000(1)matlabf=[-2 1 -5 3 -4];A=[3 -2 7 -5 -4;1 -2 2 -4 2];b=[6 0];[x,z]=bintprog(f,A,b)z=-z(2)>> exOptimization terminated.x =11111z =-7z =73、(指派问题)现有A,B,C,D,E 5个人,挑选其中4个人去完成4项工作。
割平面法求解整数规划问题实验报告

运筹学与最优化MATLAB 编程实验报告割平面法求解整数规划问题一、 引言:通过对MATLAB 实践设计的学习,学会使用MATLAB 解决现实生活中的问题。
该设计是在MATLAB 程序设计语言的基础上,对实际问题建立数学模型并设计程序,使用割平面法解决一个整数规划问题。
经实验,该算法可成功运行并求解出最优整数解。
二、 算法说明:割平面法有许多种类型,本次设计的原理是依据Gomory 的割平面法。
Gomory 割平面法首先求解非整数约束的线性规划,再选择一个不是整数的基变量,定义新的约束,增加到原来的约束中,新的约束缩小了可行域,但是保留了原问题的全部整数可行解。
算法具体设计步骤如下:1、首先,求解原整数规划对应的线性规划,*)(min x c x f =⎩⎨⎧≥≤0..x bAx t s ,设最优解为x*。
2、如果最优解的分量均为整数,则x*为原整数规划的最优解;否则任选一个x*中不为整数的分量,设其对应的基变量为x p ,定义包含这个基变量的切割约束方程con jj ij p b x r x =+∑,其中x p 为非基变量。
3、令][ij ij ij r r r -=,][con con con b b b -=,其中[]为高斯函数符号,表示不大于某数的最大整数。
将切割约束方程变换为∑∑-=-+jjij con con jj ij p x r b b x r x ][][,由于0<ij r <1,0<con b <1,所以有1<-∑jj ij con x r b ,因为自变量为整数,则∑-jj ij con x r b 也为整数,所以进一步有0≤-∑jj ij con x r b 。
4、将切割方程加入约束方程中,用对偶单纯形法求解线性规划⎪⎪⎩⎪⎪⎨⎧≥≤-≤=∑00..,*)(min x x r b b Ax t s x c x f j j ij con ,然后在转入步骤2进行求解,直到求出最优整数解停止迭代。
整数规划的割平面法计算流程与举例

整数规划的割平面法计算流程与举例下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!整数规划的割平面法计算流程与举例在整数规划问题中,割平面法是一种有效的求解方法。
割平面法_精品文档

从而
fi-ΣfijXj≤0
⑸
取⑸式作为切割方程。因为任何整数可行解都满足这个方程,所以 把它加到原问题的约束中,它能够对原可行域进行切割,而不会切 割掉整数解。
例3 用割平面法求解
maxZ=x1+x2 -x1+x2≤1 3xx1,1x+2x≥20≤,4 整数
解:将问题标准化得
maxZ=x1+x2
⑴
-x1+x2=1
1
D B(1,1)
x3 =1+x1-x2 x4=4 -3x1-x2 代入切割方程 得
-1 0
3x1+x2=4
3(1+x1-x2)+(4-3x1-x2)≥3
1
x1
即 x2≤1,将此切割方程 加入原约 束中,就等于切掉原可行域得
A1B部分,如图。 显然在A1B区域不含整数解点,对原可行域切割的结果是产生了一
下面讨论切割方程的求法。
设与整数规划相对应的线性规划最优解中基变量XBi=(B-1b)i不 是整数,将最优单纯形表中该基变量对应的行还原成约束方程,即
XBi +ΣaijXj=(B-1b)i
⑴
将(B-1b)i,aij都分解成整数与非负真分数之和的形式,即
(B-1b)i=Ni+fi 其中0< fi <1 ⑵
aij=Nij+fij
其中0≤ fij <1 ⑶
这里Ni、Nij是整数,将⑵、 ⑶代入⑴,得
XBi +Σ(Nij+fij)Xj=Ni+fi
即
XBi +ΣNijXj-Ni=fi-ΣfijXj
⑷
当诸Xi都是整数时, ⑷式左端是整数,所以右端亦应是整数,但右
求解整数规划实验报告

求解整数规划实验报告1. 引言整数规划是运筹学领域的重要分支,广泛应用于实际问题中。
本实验旨在研究和探索整数规划的求解方法,并通过实验验证算法的有效性和效率。
2. 实验目的本实验的主要目的如下:1. 了解整数规划的概念和基本原理;2. 学习并掌握整数规划的求解算法;3. 探索整数规划的应用实例,并进行模型构建;4. 运用求解工具求解整数规划模型,并进行结果分析。
3. 实验过程3.1 整数规划的概念和基本原理整数规划是指决策变量为整数的线性规划问题。
与线性规划相比,整数规划在模型的约束条件中要求决策变量为整数。
3.2 整数规划的求解算法常见的整数规划求解算法有分支定界法、割平面法等。
本实验主要采用分支定界法进行求解。
分支定界法是一种基于深度优先搜索的算法,其核心思想是通过不断分割问题的可行域,将整数规划问题转化为一系列子问题,以便找到最优解。
3.3 模型构建与求解工具选择本实验选择了某航空公司飞机调度问题作为研究对象。
在该问题中,需要确定飞机的起飞和降落时间以及机组成员的配备情况,以最小化总飞行成本为目标。
采用Python作为实验的编程语言,并使用PuLP库进行整数规划模型的构建和求解。
3.4 计算实验及结果分析首先,根据问题描述构建了完整的整数规划模型,并利用PuLP库求解得到最优解。
然后,通过对比不同约束条件下的模型求解结果,分析影响结果的关键因素。
最后,对实验结果进行总结,并提出改进措施和优化建议。
4. 实验结果与分析通过对某航空公司飞机调度问题的求解,得到了最优的飞行计划和配备方案,有效降低了航空公司的飞行成本。
同时,通过对比不同约束条件下的模型求解结果,发现起飞时间和降落时间的限制对最终成本的影响较大。
因此,建议航空公司在制定飞行计划时,合理安排飞机的起飞和降落时间,以减少不必要的成本。
5. 总结与展望本实验通过对整数规划的研究和实践,深入理解了整数规划的概念、原理和求解方法。
同时,通过实验还发现了整数规划在实际问题中的应用价值,并掌握了使用PuLP库求解整数规划模型的方法。
gomory割平面法原理及应用

gomory割平面法原理及应用标题:Gomory割平面法:原理及应用引言:在运筹学领域,Gomory割平面法是一种强大的整数规划求解方法,它通过引入一系列割平面来逐步逼近最优解。
本文将深入探讨Gomory割平面法的原理和应用,解释其工作原理以及在实际问题中的应用场景。
对于理解和应用这一方法,本文将从简到繁、由浅入深地进行解释。
一、Gomory割平面法原理1.1 整数规划问题简介在介绍Gomory割平面法之前,我们首先了解整数规划问题。
整数规划是线性规划的一种扩展形式,其中变量被限制为取整数值。
我们将探讨整数规划问题的基本概念、约束条件以及目标函数。
1.2 割平面的引入割平面是指在整数规划问题中,通过添加一系列附加约束来限制解的空间。
这些约束通常是线性的,并且通过改进松弛线性规划问题的解来逼近整数解。
1.3 Gomory割平面法的基本思想Gomory割平面法通过将松弛线性规划问题求解为一个整数规划问题,然后应用割平面的思想逐步逼近最优整数解。
本节将详细介绍Gomory割平面法的基本思想和具体步骤。
二、Gomory割平面法应用案例在本节中,我们将通过一个实际案例来展示Gomory割平面法的应用。
假设我们有一个生产计划问题,需要确定如何分配资源以最大化利润并满足资源的限制条件。
我们将逐步应用Gomory割平面法来解决这个问题,并解释每一步的具体操作。
三、Gomory割平面法的优缺点在实际应用中,我们需要综合考虑Gomory割平面法的优点和局限性。
本节将讨论Gomory割平面法的优缺点,并帮助读者在实践中做出合理的选择。
四、总结与回顾通过本文的学习,我们了解了Gomory割平面法的原理和应用。
这种方法通过引入割平面,可以逐步逼近整数规划问题的最优解。
我们探讨了Gomory割平面法的基本思想、具体步骤以及应用案例,希望读者能够对该方法有更深入、全面的理解和应用。
观点和理解:Gomory割平面法作为整数规划领域中的重要方法,具有以下观点和理解:1. Gomory割平面法通过引入割平面,可以在保证最优解的情况下进一步限制解的空间,提高整数规划问题的求解效率。
整数规划中的割平面法和分枝定界法的研究

研究的主要内容:
1.引言
2.Gomory割平面法
2.1割平面法的基本思想
2.2割平面法步骤
3.分枝定界法
.1分枝定界法的基本思想
.2分枝定界法步骤
4.割平面法和分枝定界法比较
5.一种新型割平面法
6.分枝定界法在最优化问题中的应用
结束语
预期目标:
熟练掌握两种算法,了解各自算法的优点与缺点;会建立整数规划模型,并合理应用算法和计算机解决问题。
and Complexity[M].NewJersey:Prentice-Hall,1982
[3]许志国,马仲蕃.整数规划初步[M].沈阳:辽宁教育出版社,1990
[4]赵玮,王荫清.随机运筹学[M].北京:高等教育出版社,1993
[5]张香云.线性规划[M].浙江:浙江大学出版社,2009
[6]张雅琴,王希云.分枝定界法在最优化问题中的应用[J].经济技术协作信息,2007.17(17):83
三、拟采用的研究方法、步骤
1.研究方法:
主要采用文献资料法对大量文献进行分析,以使对研究课题的研究现状、背
景意义有深刻的理解。
运用描述性研究法研究两种算法的优劣、在模型中的应用等。
2.研究步骤
(1)选定课题:根据对所学专业知识熟练与理解程度评估,选择了自己较为容易
研究的课题。
(2)收集资料:根据所选课题收集大量相关的材料。首先将有关运筹学中整数规划
的内容进行收集、归纳;再则去校图书馆查阅相关的资料,借阅有
关的书籍以及习题讲解;最后利用电脑在网上查阅更多的资料来丰
富论文研究内容。
(3)整合资料:将所收集的资料进行整合,则优而不泛用。
(4)确定题目:在整理好所需资料,大致的方向有所掌握后再确定论文的题目,好
实验报告——整数规划1

6 0.000000 0.000000
7 0.000000 0.000000
解得,最大目标函数值为300,最优解为x1=100,x2=0,x3=0。也就是说生产100台小容器可得最大利润300万元。
例2:已知
项目A:从第一年到第四年每年年初需要投资,并于次年末回收本利115%,但要求第一年投资最低金额为4万元,第二、三、四年不限;
项目B:第三年初需要投资,到第五年末能回收本利128%,但规定最低投资金额为3万元,最高金额为5万元;
项目C:第二年初需要投资,到第五年末能回收本利140%,但规定其投资额或为2万元或为4万元或为6万元或为8万元。
项目D:五年内每年初可购买公债,于当年末归还,并加利息6%,此项投资金额不限。
该部门现有资金10万元,问它应如何确定给这些项目的每年投资额,使到第五年末拥有的资金本利总额为最大?
Bx3B
Cx2C
D x1D x2D x3D x4Dx5D
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等)(接上页):
maxz= 1.15x4A+ 1.40x2C+ 1.28x3B+ 1.06x5D
s.t.x1A+x1D= 100000;
x2A+x2C+x2D= 1.06x1D;
x3A+x3B+x3D= 1.15x1A+ 1.06x2D;
x3<=M*y3;
@GIN(x1);@GIN(x2);@GIN(x3);
@BIN(y1);@BIN(y2);@BIN(y3);
end
(转下页)
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等)(接上页):
第五章整数规划报告

2. 用观察法找问题ILP的一个整数可行解,求得其目标函 数值,并记作 Z ,以Z*表示ILP的最优目标函数值,则
Z Z* Z
分支,如松弛问题有一个最优解xj为非整数值bj,则可以构造两个 分支。 xj≤[bj] xj≥[bj]+1 定界,以每个后继问题为一分支表明求解的结果。
2018/10/15
8
1.整数线性规划(ILP)的类型
整数线性规划的一般形式: Max (min) z=CX AX≤(≥,=)b X ≥0 X中部分或全部为整数 X为0或1
纯ILP: Xj全为整数
混合ILP:部分Xj为整数
0-1 ILP:Xj为0或1
2018/10/15 浙江科技学院经济管理学院管工系 9
2.整数线性规划(ILP)实例
1.割平面法
割平面束构造:
设具有最大真分数部分的非整分量所在行为:
x i a ik x k bi
将该约束方程所在系数和常数分解为整数N和正
真分数f之和,即:
x i ( N ik f ik ) x k N bi f bi
则该约束方程等价于:
f ik xk
2018/10/15
-4/5 0 -6/5 0 -1/5 0 0 0 5/4 -1
1 1 0
X1 x3 δj
0 -4/5 1
X2 16/5
0 -3/2 1 -5/4
由上面结果构造割平面束
4 4 x5 5 5
2018/10/15
δj
0
0
0
0
0 -1/4
X * (0,4,2,0,1,0)T
浙江科技学院经济管理学院管工系
第章 整数规划(割平面法)

割平面法求解整数规划问题:Max Z=3x1+2x22x1+3x2≤144x1+2x2≤18x1,x2≥0,且为整数解:首先,将原问题的数学模型标准化,这里标准化有两层含义:(1)将不等式转化为等式约束,(2)将整数规划中所有非整数系数全部转化为整数,以便于构造切割平面。
从而有:Max Z=3x1+2x22x1+3x2+x3=142x1+x2+x4=9x1,x2≥0,且为整数利用单纯形法求解,得到最优单纯形表,见表1:表1最优解为:x1=13/4, x2=5/2, Z=59/4根据上表,写出非整数规划的约束方程,如:x2+1/2x3-1/2x4=5/2 (1)将该方程中所有变量的系数及右端常数项均改写成“整数与非负真分数之和”的形式,即:(1+0)x2+(0+1/2)x3+(-1+1/2)x4=2+1/2把整数及带有整数系数的变量移到方程左边,分数及带有分数系数的变量称到方程右边,得:x2 - x4-2 =1/2-(1/2x3+1/2x4) (2)由于原数学模型已经“标准化”,因此,在整数最优解中,x2和x4也必须取整数值,所以(2)式左端必为整数或零,因而其右端也必须是整数。
又因为x3,x4≥0,所以必有:1/2-(1/2x3+1/2x4)<1由于(2)式右端必为整数,于是有:1/2-(1/2x3+1/2x4)≤0 (3)或x3+x4≥1 (4)这就是考虑整数约束的一个割平面约束方程,它是用非基变量表示的,如果用基变量来表示割平面约束方程,则有:2x1+2x2≤11 (5)从图1中可以看出,(5)式所表示的割平面约束仅割去线性规划可行域中不包含整数可行解的部分区域,使点E(3.5,2)成为可行域的一个极点。
图1在(3)式中加入松弛变量x5,得:-1/2x3-1/2x4+x5=-1/2 (6)将(6)式增添到问题的约束条件中,得到新的整数规划问题:Max Z=3x1+2x22x1+3x2+x3=142x1+x2+x4=9-1/2x3-1/2x4+x5=-1/2x i 0,且为整数,i=1,2,…,5该问题的求解可以在表1中加入(6)式,然后运用对偶单纯形法求出最优解。
运筹学试验:整数规划
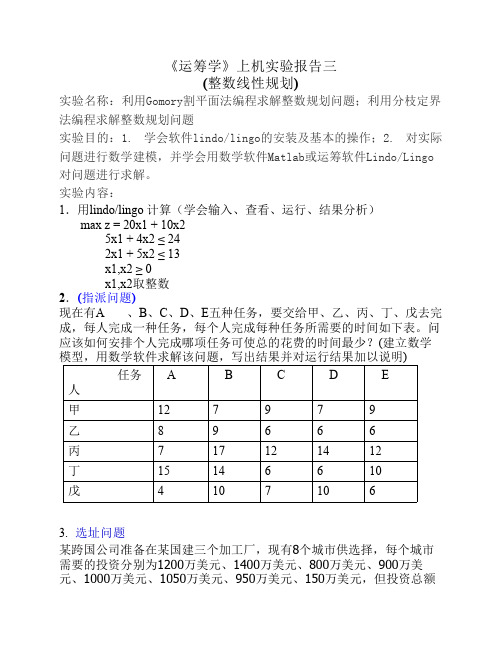
《运筹学》上机实验报告三(整数线性规划)实验名称:利用Gomory割平面法编程求解整数规划问题;利用分枝定界法编程求解整数规划问题实验目的:1. 学会软件lindo/lingo的安装及基本的操作;2. 对实际问题进行数学建模,并学会用数学软件Matlab或运筹软件Lindo/Lingo 对问题进行求解。
实验内容:1.用lindo/lingo 计算(学会输入、查看、运行、结果分析)max z = 20x1 + 10x25x1 + 4x2 ≤ 242x1 + 5x2 ≤ 13x1,x2 ≥ 0x1,x2取整数2.(指派问题)现在有A 、B、C、D、E五种任务,要交给甲、乙、丙、丁、戊去完成,每人完成一种任务,每个人完成每种任务所需要的时间如下表。
问应该如何安排个人完成哪项任务可使总的花费的时间最少?(建立数学模型,用数学软件求解该问题,写出结果并对运行结果加以说明)A B C D E任务人甲127979乙89666丙717121412丁15146610戊41071063.选址问题某跨国公司准备在某国建三个加工厂,现有8个城市供选择,每个城市需要的投资分别为1200万美元、1400万美元、800万美元、900万美元、1000万美元、1050万美元、950万美元、150万美元,但投资总额不能超过3400万美元,形成生产能力分别为100万台、120万台、80万台、85万台、95万台、100万台、90万台、130万台,由于需求的原因,要求:城市1和城市3最多选1个,城市3、城市4、城市5最多选两个,城市6和城市7最少选1个,问选择哪些城市建厂,才能使总的生产能力最大?(建立数学模型,用数学软件求解该问题,写出结果并对运行结果加以说明)整数变量定义LinDo一般整数变量:GIN <Variable>0-1整数变量: INT <Variable>LinGo一般整数变量: @GIN( variable_name);0-1整数变量:@BIN( variable_name);例如(1)Lindo运算程序max 3 x1+5 x2+4 x3subject to2 x1+3 x2<=15002 x2+4 x3<=8003 x1+2 x2 +5 x3<=2000endgin x1gin x3(2) max z = 3x1 - 2x2 + 5x3x1 + 2x2 - x3 ≤ 2x1 + 4x2 + x3 ≤ 4x1 + x2 ≤ 34x2 + x3 < 6x1,x2,x3 = 0或1lingo程序:max =3*x1 – 2*x2 + 5*x3;x1 + 2*x2 - x3 <= 2;x1 + 4*x2 + x3 <= 4;x1 + x2 <= 3 ; 4*x2 + x3< 6; @bin(x1);@bin(x2);@bin(x3);。
割平面方法

割平面方法我折腾了好久割平面方法,总算找到点门道。
说实话这割平面方法,我一开始也是瞎摸索。
我当时就听人说这个方法在某些优化问题里特别有用,但是我一开始真的是一头雾水。
我最初的尝试就是看书上那一堆理论,全是密密麻麻的数学符号和公式,什么线性规划啦,整数规划啦,和这个割平面联系在一起就感觉特别复杂。
就好比你要走进一个到处都是门,但你不知道哪个门能通到你想去的地方的大迷宫。
我顺着一条路,按照书上说的,先把问题转化成标准的线性规划形式,这就像是把一堆乱七八糟的积木先按照形状和颜色分类,以为这样能简单点。
然后我就卡在找割平面方程这儿了。
书上的例子看起来简单,可我一自己做,不是找错约束条件,就是算错系数。
有一次我拿到一个整数规划的小例子,是关于分配资源的,要使得某种效益最大化。
我觉得我前面步骤都对,可算出来的结果完全不对,我检查半天才发现是忘记考虑一个重要的隐含约束条件了。
后来我就想了个笨办法,把每一步都写得特别细,就像小学生做数学题那种详细步骤。
慢慢地,我就开始找到感觉了。
我发现找割平面方程的这个过程就像是给一个大蛋糕切一刀,但这一刀怎么切特别有讲究,得按照已有的条件和规则来切,不能乱切一气。
如果切得不好,这个平面就不能把我们不需要的那些非整数解部分“割”掉。
在实际操作里,我还试过从最简单的整数规划问题开始找规律。
比如说那种变量少,约束条件也简单的。
就像你一开始学骑自行车,先从平地上骑,而不是直接上那种高难度的斜坡弯道。
这样慢慢积累经验后,再去处理那些更复杂的问题。
我还不确定这个方法在特别大规模、特别复杂的整数规划问题里是不是通用。
但我感觉只要扎实地按照这些步骤走,多从简单的例子里找经验,在处理不是超大规模的问题时应该是够用的。
反正就是多练多总结错误,这割平面方法总会越来越熟的。
再说说这割平面的思路,其实就是逐步加一些线性的约束,把可行域一点点变小,但同时又得保证原来的整数解还在这个缩小后的可行域里,就像你把一个大包围圈慢慢缩小到只包含你想要抓的那些猎物,这些猎物就是我们要求的整数最优解。
整数规划问题(割平面-分枝定界算例)

x1 3.25;
x2 2.5
分枝定界法思路
第二步:分枝与定界 在x1=3.25;x2=2.5 中,任选一变量的解X2=2.5 , 可将其分为 x2≤2;x2≥3(去掉小数部分),则有:
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x1 , x2 0
(3.5, 2); z 14.5
X1可分为x1≤3;x1≥4,则有:
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x 3 1 x1 , x2 0 (3, 2); z 13
逻辑变量在建立数学模型中的作用
y1 y2 ... ym
中m-k不起作用
(2)割平面法思路
max Z 3 x1 2 x2 2 x1 3 x2 14 s.t. x1 0.5 x2 4.5 x , x 0 且取整数 1 2
第一步:将约束条件决策变量的系数化为整数,用单纯形法求 解出最终单纯形表 找一个分数部
(3)分支定界法
max Z 3 x1 2 x2 2 x1 3 x2 14 s.t. x1 0.5 x2 4.5 x , x 0束,求解。
max Z 3x1 2 x2 2 x1 3x2 14 s.t. x1 0.5 x2 4.5 x , x 0 1 2
max Z 3x1 2 x2 2 x1 3x2 14 x 0.5 x 4.5 1 2 s.t. x2 2 x 4 1 x1 , x2 0
(4, 1);
割平面法例题及讲解

割平面法例题及讲解割平面法是一种求解整数线性规划问题的有效方法。
以下是使用割平面法求解整数线性规划问题的步骤和例题:首先,让我们简要介绍一下割平面法的概念。
割平面法的基本思想是在原始可行域的基础上,通过添加割平面来缩小可行域,直到找到整数最优解。
割平面是通过考察非整数最优解的某一分量,并构造一个线性约束条件来得到的。
接下来,我们通过一个具体的例题来演示割平面法的应用。
例题:目标函数:最大化 Z = 3x1 + 4x2约束条件:1. x1 + x2 <= 42. x1 + 2x2 <= 63. x1, x2 属于整数集合首先,我们不考虑整数约束,使用单纯形法求解线性规划问题。
得到最优解为:x1 = 2, x2 = 1, Z = 11。
这个解不是整数解,因此我们需要使用割平面法来找到整数最优解。
观察最优解的x1分量为2,它不是整数。
我们可以根据x1的取值构造一个割平面:x1 >= 3。
这意味着我们可以添加一个线性约束条件来限制x1的值大于等于3。
现在,我们再次使用单纯形法求解线性规划问题,同时考虑新添加的割平面。
得到新的最优解为:x1 = 3, x2 = 1, Z = 14。
这个解是整数解,满足问题的整数约束条件。
通过上述步骤,我们成功地使用割平面法找到了整数最优解。
总结:割平面法是一种求解整数线性规划问题的有效方法。
它通过在原始可行域上添加割平面来缩小可行域,直到找到整数最优解。
在应用割平面法时,需要注意选择正确的变量和对应的线性约束条件来构造割平面。
此外,在使用单纯形法求解线性规划问题时,需要注意处理变量的取值范围和整数约束条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学与最优化MATLAB 编程实验报告割平面法求解整数规划问题一、 引言:通过对MATLAB 实践设计的学习,学会使用MATLAB 解决现实生活中的问题。
该设计是在MATLAB 程序设计语言的基础上,对实际问题建立数学模型并设计程序,使用割平面法解决一个整数规划问题。
经实验,该算法可成功运行并求解出最优整数解。
二、 算法说明:割平面法有许多种类型,本次设计的原理是依据Gomory 的割平面法。
Gomory 割平面法首先求解非整数约束的线性规划,再选择一个不是整数的基变量,定义新的约束,增加到原来的约束中,新的约束缩小了可行域,但是保留了原问题的全部整数可行解。
算法具体设计步骤如下:1、首先,求解原整数规划对应的线性规划,*)(min x c x f =⎩⎨⎧≥≤0..x bAx t s ,设最优解为x*。
2、如果最优解的分量均为整数,则x*为原整数规划的最优解;否则任选一个x*中不为整数的分量,设其对应的基变量为x p ,定义包含这个基变量的切割约束方程con jj ij p b x r x =+∑,其中x p 为非基变量。
3、令][ij ij ij r r r -=,][con con con b b b -=,其中[]为高斯函数符号,表示不大于某数的最大整数。
将切割约束方程变换为∑∑-=-+jjij con con jj ij p x r b b x r x ][][,由于0<ij r <1,0<con b <1,所以有1<-∑jj ij con x r b ,因为自变量为整数,则∑-jj ij con x r b 也为整数,所以进一步有0≤-∑jj ij con x r b 。
4、将切割方程加入约束方程中,用对偶单纯形法求解线性规划⎪⎪⎩⎪⎪⎨⎧≥≤-≤=∑00..,*)(min x x r b b Ax t s x c x f j j ij con ,然后在转入步骤2进行求解,直到求出最优整数解停止迭代。
三、 程序实现:程序设计流程图如图1,具体设计代码(见附录)。
图1四、 算例分析:已知AM 工厂是一个拥有四个车间的玩具生产厂商,该厂商今年新设计出A 、B 、C、D 、E 、F 六种玩具模型,根据以前的生产情况及市场调查预测,得知生产每单位产品所需的工时、每个车间在一季度的工时上限以及产品的预测价格,如下表所示。
问:每种设计产品在这个季度各应生产多少,才能使AM 工厂这个季度的生产总值达到最大?1、问题分析并建立模型:由题意可知这是一个求解产量使产值最大的整数规划问题。
根据上述问题和已知数据,可以假设每种产品在这个季度各应生产产量分别为:x 1、x 2、x 3、x 4、x 5、x 6,则有以下线性方程组maxZ=20x 1+14x 2+16x 3+36x 4+32x 5+30x 6⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤+≤+≤+≤+++++6,,1i ,090008.003.010005.002.070005.002.085003.003.003.001.001.001.0..635241654321 且为整数,i x x x x x x x x x x x x x t s 2、实验步骤:首先引入松弛变量x 7、x 8、x 9 、x 10,使其化为标准型 minZ=-20x 1-14x 2-16x 3-36x 4-32x 5-30x 6⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=++=++=++=++++++10,,1i ,090008.003.010005.002.070005.002.085003.003.003.001.001.001.0..10639528417654321 且为整数,i x x x x x x x x x x x x x x x x x t s其次从标准型可表示出约束系数矩阵、右端项常数矩阵、目标系数矩阵分别为A 、b 、c 。
然后调用DividePlane 函数,使用割平面法进行求解。
在MATLAB的命令窗口输入一下命令:>> A=[0.01 0.01 0.01 0.03 0.03 0.03 1 0 0 0;0.02 0 0 0.050 0 0 1 0 0;0 0.02 0 0 0.05 0 0 0 1 0;0 0 0.03 0 0 0.08 0 0 01];>> c=[-20;-14;-16;-36;-32;-30];>> b=[850;700;100;900];>> [intx,intf]=DividePlane(A,c,b,[7 8 9 10])3、实验结果及分析:intx =35000 5000 30000 0 0 0intf =-1250000实验结果求出的目标函数值是化为标准型的最小值,则转化为原问题的目标函数值应取相反数,所以从实验结果可知:生产各种产品的产量分别应为为,生产A 35000、生产B 5000、生产C 30000、生产D 、E、F均为0,此时的季度产值为最大即1250000元。
该结果是可信的,故通过该实例说明该程序能够运用于实际,用来解决实际生活中求解整数规划的问题。
五、结束语:Matlab是个很强大的软件,提供了大量的函数来处理各种数学、工程、运筹等的问题,并且含有处理二维、三维图形的功能,使用matlab能够解决许多实际生活中的问题。
通过这个学期的学习,仅是了解了matlab的部分函数功能和简单的GUI界面设计,掌握了一些基本的程序编写技能,同时,在老师的指导下简单了解了使用LinGo和Excel解决线性和非线性规划问题的求解方法,收获相当丰富,同时认识到要学好matlab仍然需要一个长期的过程。
六、参考文献:[1] 龚纯,王正林.精通MATLAB最优化计算.北京:电子工业出版社,2009[2]吴祈宗,郑志勇,邓伟等.运筹学与最优化MATLAB编程.北京:机械工业出版社,2009[3]邓成梁.运筹学的原理和方法(第二版).武汉:华中科技大学出版社,2002七、附录:function [intx,intf] = DividePlane(A,c,b,baseVector)%功能:用割平面法求解整数规划%调用格式:[intx,intf]=DividePlane(A,c,b,baseVector)%其中,A:约束矩阵;% c:目标函数系数向量;% b:约束右端向量;% baseVector:初始基向量;% intx:目标函数取最小值时的自变量值;% intf:目标函数的最小值;sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;if length(baseVector) ~= ndisp('基变量的个数要与约束矩阵的行数相等!');mx = NaN;mf = NaN;return;endM = 0;sigma = -[transpose(c) zeros(1,(nVia-length(c)))];xb = b;%首先用单纯形法求出最优解while 1[maxs,ind] = max(sigma);%--------------------用单纯形法求最优解--------------------------------------if maxs <= 0 %当检验数均小于0时,求得最优解。
vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if(isempty(ele))mx(l) = 0;elsemx(l)=xb(ele);endendif max(abs(round(mx) - mx))<1.0e-7 %判断最优解是否为整数解,如果是整数解。
intx = mx;intf = mx*c;return;else%如果最优解不是整数解时,构建切割方程sz = size(A);sr = sz(1);sc = sz(2);[max_x, index_x] = max(abs(round(mx) - mx));[isB, num] = find(index_x == baseVector);fi = xb(num) - floor(xb(num));for i=1:(index_x-1)Atmp(1,i) = A(num,i) - floor(A(num,i));endfor i=(index_x+1):scAtmp(1,i) = A(num,i) - floor(A(num,i));endAtmp(1,index_x) = 0; %构建对偶单纯形法的初始表格A = [A zeros(sr,1);-Atmp(1,:) 1];xb = [xb;-fi];baseVector = [baseVector sc+1];sigma = [sigma 0];%-------------------对偶单纯形法的迭代过程----------------------while 1%----------------------------------------------------------if xb >= 0 %判断如果右端向量均大于0,求得最优解if max(abs(round(xb) - xb))<1.0e-7 %如果用对偶单纯形法求得了整数解,则返回最优整数解vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if(isempty(ele))mx_1(l) = 0;elsemx_1(l)=xb(ele);endendintx = mx_1;intf = mx_1*c;return;else%如果对偶单纯形法求得的最优解不是整数解,继续添加切割方程 sz = size(A);sr = sz(1);sc = sz(2);[max_x, index_x] = max(abs(round(mx_1) - mx_1));[isB, num] = find(index_x == baseVector);fi = xb(num) - floor(xb(num));for i=1:(index_x-1)Atmp(1,i) = A(num,i) - floor(A(num,i));endfor i=(index_x+1):scAtmp(1,i) = A(num,i) - floor(A(num,i));endAtmp(1,index_x) = 0; %下一次对偶单纯形迭代的初始表格A = [A zeros(sr,1);-Atmp(1,:) 1];xb = [xb;-fi];baseVector = [baseVector sc+1];sigma = [sigma 0];continue;endelse%如果右端向量不全大于0,则进行对偶单纯形法的换基变量过程 minb_1 = inf;chagB_1 = inf;sA = size(A);[br,idb] = min(xb);for j=1:sA(2)if A(idb,j)<0bm = sigma(j)/A(idb,j);if bm<minb_1minb_1 = bm;chagB_1 = j;endendendsigma = sigma -A(idb,:)*minb_1;xb(idb) = xb(idb)/A(idb,chagB_1);A(idb,:) = A(idb,:)/A(idb,chagB_1);for i =1:sA(1)if i ~= idbxb(i) = xb(i)-A(i,chagB_1)*xb(idb);A(i,:) = A(i,:) - A(i,chagB_1)*A(idb,:);endendbaseVector(idb) = chagB_1;end%------------------------------------------------------------end%--------------------对偶单纯形法的迭代过程--------------------- endelse%如果检验数有不小于0的,则进行单纯形算法的迭代过程minb = inf;chagB = inf;for j=1:nif A(j,ind)>0bz = xb(j)/A(j,ind);if bz<minbminb = bz;chagB = j;endendendsigma = sigma -A(chagB,:)*maxs/A(chagB,ind);xb(chagB) = xb(chagB)/A(chagB,ind);A(chagB,:) = A(chagB,:)/A(chagB,ind);for i =1:nif i ~= chagBxb(i) = xb(i)-A(i,ind)*xb(chagB);A(i,:) = A(i,:) - A(i,ind)*A(chagB,:);endendbaseVector(chagB) = ind;endM = M + 1;if (M == 1000000)disp('找不到最优解!');mx = NaN;minf = NaN;return;endend。
