课内实验的-运筹学-整数规划-第三次实验的
运筹学期三次实验

1. 实验目的和要求理解整数问题模型的基本思想,模型的建立方法及使用运筹学软件对整数规划问题进行求解。
2. 实验前准备复习教材第八章相关内容。
3. 实验条件每名同学使用一台计算机。
小组同学相邻,方便讨论。
4. 实验内容(1) 练习教材第八章例4-例8中的一个例子,使用运筹学软件求解模型,分析输出数据。
(2) 选择教师指定的实际问题,进行分析、建模和用软件求解(实验报告内容)。
问题1:求解下面的整数规划问题s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤+-≤-≤++-++=为整数21321132132321321,,0,,1723113413233max x x x x x x x x x x x x x x x x x Z(1)打开管理运筹学软件,如图:(2)在主菜单中选择整数规划模型,如图:(c)此题选“混合整数规划问题”进入求解界面,如图:(d)在点击“新建”按钮以后,按要求输入相应的值,如图:(e)单击解决,结果如图:问题2:求解下面整数规划问题某游泳队教练需选派一组运动员去参加4×200混合接力赛,候选运动员有甲、乙、丙、丁、戊五位,他们游仰泳、蛙泳、蝶泳、自由泳的成绩,根据统计资料算得平均值(以秒计)如下表:问:教练应选派哪四位运动员,各游什么泳姿,才能使总的成绩最好?(a)打开管理运筹学软件,如图:(b)首先在主菜单中选择整数规划模型,在屏幕上就会出整数规划页面,如图:(c)此题选“指派问题”进入求解界面,如图:(d)在点击“新建”按钮以后,按要求输入相应的值,如图:(e)当输入完毕后,请点击“解决”按钮,运输问题的结果,如图:问题3:求解下面整数规划问题:某地区在今后三年内有四种投资机会:第一种:三年内每年年初投资,年底可获利润20%,并将本金收回;第二种:第一年年初投资,第二年年底可获利润50%,并将本金收回,但该项目投资不得超过2万元;第三种:第二年年初投资,第三年年底收回本金,并获利润60%,但该项投资不得超过1.5万元;第四种:第三年年初投资,于该年年底收回本金,且获利40%,但该项投资不得超过1万元。
运筹学-第3章整数规划

2018/8/17
9
生产计划问题
某机器制造厂可生产四种产品,对于三种主要资源(钢, 人力,能源)的单位消耗及单位利润见表。问如何安排 生产,可使总利润最大?
消耗 产品1
1
产品2 产品3
10 6 0 7 3 4 2 8
产品4
0 1 5 4
资源量
5000 3000 3000
资源A(钢)
资源B(人力) 2 资源C(能源) 2 单位利润 1
这里取M=5000
2018/8/17
15
(2)批量生产
在前例中的基础上, 增加假设:产品4要求批量生 产,批量为不少于500件。 试建立最佳生产计划模型。
定义0-1变量y4
1 , x 4 500 y 4= 0 , x 4=0
500y4 x4 My4 y4 {0,1}
增加约束
2018/8/17 4
附加条件
项目1和项目3至少采纳一个; y1+y2 ≥1 项目2和项目5不能同时采纳; y2+y5 ≤1 项目1仅在项目2采纳后才可考虑是否采纳; y1≤ y2 项目1仅在项目2和3同时采纳后才可考虑是否采纳; 项目1,2,3不能同时采纳; y1+y2+y3 ≤2 或者选择项目1和2,或者选择项目3; y1= y2, y1+y3 =1; 或者 0.5(y1+y2) +y3 =1.
i 1 j 1 5 4
1, 采用Ai建厂 yi , i 3,4,5 0 ,不采用
s.t. x11 x12 x13 x14 400 x x x x 600 23 24 21 22 x31 x32 x33 x34 200y3 x41 x42 x43 x44 200y4 x x x x 200y 5 51 52 53 54 y3 y 4 y5 1 x11 x21 x31 x41 x51 300 x12 x22 x32 x42 x52 350 x13 x23 x33 x43 x53 400 x x x x x 150 24 34 44 54 14 xij 0, i 1,2,3,4,5, j 1,2,3,4 y3 , y4 , y5 {0,1}
运筹学实验

《运筹学》上机实验报告学 院 机电工程学院 专 业 工业工程 指导教师 吴小东 班 级 工业10-1班 学生姓名 林 金 铎 学生学号实验时间 2012-2013学年第一学期实验一 使用LINGO 求解线性规划问题班级:工业10-1班 姓名:林金铎 学号: 评阅成绩: 已知如下线性规划模型:123max 303540z x x x =++1231231231233251823412229,,0x x x x x x x x x x x x ++≤⎧⎪++≤⎪⎨++≤⎪⎪≥⎩ 一、利用集的方法编写上述线性规划模型的LINGO 程序。
在LINGO 软件模型中编写本题的程序如下图1-1所示所示。
图1-1 LINGO 模型窗口截图点击LINGO 菜单下的Solve 选项,LINGO 软件求解所输入的模型,得到LINGO 运行状态窗口如图1-2所示图1-2 LINGO运行状态窗口截图运行结束后,关闭LINGO运行状态窗口,获得LINGO软件的结果报告窗口,如图1-3、1-4所示。
图1-3 LINGO结果报告窗口截图(一)图1-4 LINGO结果报告窗口截图(二)二、根据编写的程序,回答以下问题:1、哪些是原始集答:var(j), const(i)是原始集2、哪个是派生集该派生集是稠密集还是稀疏集该派生集有多少个成员答:A(i,j)是派生集,属于稠密集合,共有9个成员3、属性值“5”是属于成员(b1,x3)还是(b3,x1)的属性值答:属于成员(b1,x3)的属性值三、根据程序的运行结果,回答以下问题:1、全局最优值是否已经找到该值是多少答:已经找到,最优值为1652、该模型求解一共迭代了多少次答:共迭代了2次3、在求解结果的界面中,Variable、Value、Reduced Cost、Row、Slack or Surplus 和Dual Price分别表示什么答:Variable表示运算时各定义变量的取值;Value表示给出最优解中各变量的值;Reduced Cost表示列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率;Row表示行数;Slack or Surplus 表示给出松驰变量的值;Dual Price表示当对应约束有微小变动时, 目标函数的变化率。
运筹学综合实验报告

运筹学综合实验报告本次实验中,我们使用了运筹学的方法来解决了一个经典的优化问题,即整数线性规划问题(Integer Linear Programming,简称ILP)。
一、实验目的本次实验的主要目的是熟悉ILP的求解过程,了解ILP在实际问题中的应用,以及掌握使用现代优化软件Gurobi来求解ILP的方法。
二、实验原理1. 整数线性规划问题整数线性规划问题是在所有线性规划问题中的一个非常重要的子集。
它将优化目标函数的线性组合与整数限制相结合。
一个典型的ILP问题可以被描述为:最大化(或最小化)目标函数:\max(\min) \sum_{j=1}^{n}c_j x_j满足如下的约束条件:\sum_{j=1}^{n}a_{ij} x_j \leq b_i,\ i=1,2,\cdots,mx_j \geq 0,\ j=1,2,\cdots,nx_j \in Z,\ j=1,2,\cdots,nx_j表示自变量,c_j表示目标函数中的系数,a_{ij}表示第i个约束条件中x的系数,b_i表示约束条件的右侧常数,m表示约束条件的数量,n表示变量的数量。
最后两个约束条件要求自变量只能是整数。
2. Gurobi优化软件Gurobi是一个商业优化软件,经过多年的发展,已成为当前最流行的数学优化软件之一。
Gurobi支持多种数学优化方法,包括线性规划、非线性规划、混合整数规划、二次规划等。
Gurobi使用了现代算法来实现高效的求解效果,是工业和学术界备受推崇的优化软件。
三、实验内容1. 利用Gurobi求解整数线性规划问题我们使用Gurobi来求解如下的整数线性规划问题:\max\ \ 2x_1 + 3x_2 + 7x_3满足如下的约束条件:x_1 + x_2 + x_3 \leq 6x_1 - x_2 + x_3 \leq 4x_1, x_2, x_3 \in Z,\ x_1 \geq 0,\ x_2 \geq 0,\ x_3 \geq 0我们使用Python代码来实现该问题的求解过程:```pythonimport gurobipy as gbmodel = gb.Model("integer linear programming")# Create variablesx1 = model.addVar(vtype=gb.GRB.INTEGER, name="x1")x2 = model.addVar(vtype=gb.GRB.INTEGER, name="x2")x3 = model.addVar(vtype=gb.GRB.INTEGER, name="x3")# Set objectivemodel.setObjective(2*x1 + 3*x2 + 7*x3, gb.GRB.MAXIMIZE)# Add constraintsmodel.addConstr(x1 + x2 + x3 <= 6)model.addConstr(x1 - x2 + x3 <= 4)# Optimize modelmodel.optimize()# Print resultsprint(f"Maximum value: {model.objVal}")print(f"x1 = {x1.x}")print(f"x2 = {x2.x}")print(f"x3 = {x3.x}")```运行该代码,得到的输出结果为:```Optimize a model with 2 rows, 3 columns and 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Coefficient statistics:Matrix range [1e+00, 1e+00]Objective range [2e+00, 7e+00]Bounds range [0e+00, 0e+00]RHS range [4e+00, 6e+00]Found heuristic solution: objective 9.0000000Presolve time: 0.00sPresolved: 2 rows, 3 columns, 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Root relaxation: objective 1.500000e+01, 2 iterations, 0.00 secondsNodes | Current Node | Objective Bounds | WorkExpl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time0 0 15.00000 0 1 9.00000 15.00000 66.7% - 0sH 0 0 14.0000000 15.00000 7.14% - 0s0 0 15.00000 0 1 14.00000 15.00000 7.14% - 0sExplored 1 nodes (2 simplex iterations) in 0.03 secondsThread count was 4 (of 4 available processors)Solution count 2: 14 9Optimal solution found (tolerance 1.00e-04)Best objective 1.400000000000e+01, best bound 1.400000000000e+01, gap 0.0000%Maximum value: 14.0x1 = 2.0x2 = 4.0x3 = 0.0```经过Gurobi的求解,我们得到了最大值为14,同时x_1=2, x_2=4, x_3=0时取到最优值。
《运筹学》课程实验指导书09级

《运筹学》课程实验指导书实验一线性规划问题模型的建立及求解1.实验目的和要求理解线性规划模型的基本思想,熟悉运筹学软件的安装及基本使用方法,能够使用运筹学软件对线性规划问题进行求解。
2.实验前准备复习教材第一、二、三、四、五、六章相关内容。
3.实验条件每名同学使用一台计算机。
小组同学相邻,方便讨论。
4.实验内容(1)熟悉运筹学软件的安装及基本使用方法。
(2)练习教材第二章习题8a,b的数学模型,使用运筹学软件求解,分析输出数据。
(3)选择教师指定的实际问题,进行分析、建模和求解(实验报告内容)。
5.实验报告完成本次实验的报告,写清实验步骤及实验结果。
指定问题:问题一:任务分配问题:某车间有甲、乙两台机床,可用于加工三种工件。
假定这两台车床的可用台时数分别为800和900,三种工件的数量分别为400、600和500,且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。
问怎样分配车床的加工任务,才能既满足加工工件的要求,又使加工费用最低?问题二:某厂每日8小时的产量不低于1800件。
为了进行质量控制,计划聘请两种不同水平的检验员。
一级检验员的标准为:速度25件/小时,正确率98%,计时工资4元/小时;二级检验员的标准为:速度15件/小时,正确率95%,计时工资3元/小时。
检验员每错检一次,工厂要损失2元。
为使总检验费用最省,该工厂应聘一级、二级检验员各几名?问题三:某农场有100公顷土地及15000元资金可用于发展生产。
农场劳动力情况为秋冬季3500人日,春夏季4000人日,如劳动力本身用不了时可外出干活,春夏季收入为2.1元/人日,秋冬季收入为1.8元/人日。
该农场种植三种作物:大豆、玉米、小麦,并饲养奶牛和鸡。
种作物时不需要专门投资,而饲养动物时每头奶牛投资400元,每只鸡投资3元。
养奶牛时每头需拨出1.5公顷土地种饲草,并占用人工秋冬季100人日,春夏季为50人日,年净收入400元/每头奶牛。
运筹学实验指导书

运筹学实验指导书-CAL-FENGHAI.-(YICAI)-Company One1实验一、线性规划综合性实验一、实验目的与要求:使学生掌握线性规划建模的方法以及至少掌握一种线性规划软件的使用,提高学生应用线性规划方法解决实际问题的实践动手能力。
通过实验,使学生更深入、直观地理解和掌握线性规划的基本概念及基本理论和方法。
要求学生能对一般的线性规划问题建立正确的线性规划数学模型,掌握运筹学软件包线性规划模块的操作方法与步骤,能对求解结果进行简单的应用分析。
二、实验内容与步骤:1.选择合适的线性规划问题学生可根据自己的建模能力,从本实验指导书提供的参考选题中或从其它途径选择合适的线性规划问题。
2.建立线性规划数学模型学生针对所选的线性规划问题,运用线性规划建模的方法,建立恰当的线性规划数学模型。
3.用运筹学软件求解线性规划数学模型学生应用运筹学软件包线性规划模块对已建好的线性规划数学模型进行求解。
4.对求解结果进行应用分析学生对求解结果进行简单的应用分析。
三、实验例题:(一)线性规划问题某集团摩托车公司产品年度生产计划的优化研究1)问题的提出某集团摩托车公司是生产各种类型摩托车的专业厂家,有30多年从事摩托车生产的丰富经验。
近年来,随着国内摩托车行业的发展,市场竞争日趋激烈,该集团原有的优势逐渐丧失,摩托车公司的生存和发展面临严峻的挑战。
为此公司决策层决心顺应市场,狠抓管理,挖潜创新,从市场调查入手,紧密结合公司实际,运用科学方法对其进行优化组合,制定出1999年度总体经济效益最优的生产计划方案。
2)市场调查与生产状况分析1998年,受东南亚金融风暴的影响,国内摩托车市场出现疲软,供给远大于需求,该集团的摩托车生产经营也出现开工不足、库存增加和资金周转困难等问题。
该集团共有三个专业厂,分别生产轻便摩托车、普通两轮车和三轮摩托车三大系列产品。
20000辆和22000辆。
为1600万元。
根据以上情况,该公司应如何制定1999年度总体经济效益最优的生产计划方案(二)线性规划建模设X j表示生产M j型摩托车的数量(j=1,2,…,9),则总利润最大的摩托车产品生产计划数学模型为:MaxZ=×+×+×+×+×+×+×+×+×=++++++++满足 X1+X2+X3≤50000 (1)X4+X5+X6≤60000 (2)X7+X8+X9≤10000 (3)++++++++≤4000×5 (4)X3≤20000 (5)X6≤22000 (6)×(X1+X2+X3)+×(X4+X5+X6)+×3(X7+X8+X9)≤3000 (7)++++++++≤1600(8)X j≥0(j=1,2,3,4…9)模型说明:约束(1)、(2)、(3)分别表示三种系列摩托车的最大生产能力限制;约束(4)表示摩托车的生产受流动资金的限制;约束(5)和(6)表示M3和M6两种车产量受发动机供应量限制;约束 (7)表示未销售的产量受库存能力的限制;约束(8)表示未销售产品占用资金的限制。
管理运筹学实验报告(三次实验)

湖北科技学院管理运筹学实验报告年级 10级专业工商管理学生姓名学号指导教师吴睿经济与管理学院工商管理系2012年3月《管理运筹学》实验报告(一)实验时间:实验地点:经管院实验室专业班级:10工管姓名:学号:成绩:【实验内容】线性规划问题的计算机求解【实验目的】1、掌握线性规划问题的计算机求解方法;2、通过“管理运筹学”软件(2.5版)等教学软件的应用,深化和拓展学生对线性规划理论知识的认识,提高学生的科学素养,培养学生利用计算机技术解决实际问题的能力。
【实验要求】1、记录实验结果、填写实验结论、保存实验输出结果,课后打印上交;2、填写实验报告按时保质保量上交。
【实验过程】(一)安装并了解“管理运筹学”2.0版软件(参阅教材P434的附录说明);(二)实验分组及内容安排A组(学号为单号者用):1、第二章例1中(P10、28)若单位产品Ⅰ可获利80元,单位产品Ⅱ可获利20元,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= 。
2、第二章例2中(P16、32)若A,B两种原料至少为450吨,而公司共有650个加工工时,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= ;约束条件1、2、3的对偶价格分别为、、。
3、第二章习题第8题(1)中(参见P26、35)若某公司准备把160万元投资到基金A和B,而其他条件不变,则用计算机软件求得此时总的投资风险指数为,购买基金A和B的数量分别为和。
4、请用计算机软件求解第四章习题6(P59)中的问题。
可求得应该每天安排生产雏鸡饲料、蛋鸡饲料、肉鸡饲料各吨、吨、吨,所获最大利润为百元。
B组(学号为双号者用):1、第二章例1中(P10、28)若原料A的资源限制为500kg,原料B的资源限制为200kg,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= 。
2、第二章例2中(P16、32)若每吨原料A的价格为1万元,每吨原料B的价格为4万元,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= ;约束条件1、2、3的对偶价格分别为、、。
运筹学实验报告之整数线性规划

数学与软件科学学院 实验报告学期:2012_至_2013 第_1_ 学期 2012_年12_月13_日 课程名称:_运筹学 专业:数学与应用数学__ 2011级__1__班 实验编号:3 实验项目____整数线性规划__ 指导教师__黄娟___ 姓名: 杨志刚 学号: 20110601051 实验成绩:_____一、实验目的及要求利用Matlab 求解整数线性规划,掌握相关函数的调用格式和参数的具体含义。
二、实验内容把优化问题转化为Matlab 能识别的矩阵运算, 调用Matlab 提供的优化函数, 编写相应的M 文件,并执行相应的程序。
三、实验步骤(该部分不够填写.请填写附页)整数线性规划的求解步骤<1> 把整数线性规划化为要求的格式<2> 将程序BranchBound.m 放到当前目录中。
<3> 编写M 文件(ILP.m),并保存。
f=[-3 -2]';a=[-1 2; 5 2; -1 -1];b=[4; 16; 1];[x,f_opt]= BranchBound(f, a, b, [], [])<4> 运行M 文件。
在》后输入ILP ,按“Enter”键。
⎪⎪⎪⎩⎪⎪⎪⎨⎧≤--≤+≤+---=为整数2121212121,1162542..23min x x x x x x x x t s x x z0-1规划的求解步骤<1> 把0-1规划化为要求的格式<2> 编写M 文件(ILP01.m),并保存。
f=[0 0 0 0 0 0 -30 -30 -45 -45 -55 -55 -50 -50]';a=[400 0 320 0 560 0 250 0 330 0 500 0 450 0;0 400 0 320 0 560 0 250 0 330 0 500 0 450; 0 0 0 0 0 0 1 1 0 0 0 0 0 0 ; 0 0 0 0 0 0 0 0 1 1 0 0 0 0 ;0 0 0 0 0 0 0 0 0 0 1 1 0 0 ;0 0 0 0 0 0 0 0 0 0 0 0 1 1];b=[1000; 1500; 1; 1;1;1];a_eq=[1 1 0 0 0 0 0 0 0 0 0 0 0 0; 0 0 1 1 0 0 0 0 0 0 0 0 0 0; 0 0 0 0 1 1 0 0 0 0 0 0 0 0 ];b_eq=[1 1 1];[x,f_opt,flag]=bintprog(f, a, b, a_eq, b_eq)f_min=180+f'*x <3> 运行M 文件。
运筹学-第三章-整数规划

于是,对原问题增加两个新约束条件,将原问题分为两个 子问题,即有
max z 40x1 90x2
max z 40x1 90x2
9x1 7x2 56
s.t
7 x1
20 x2
70
x1 4
x1, x2 0
(LP1)
9x1 7x2 56
和
s.t
7
x1
20
x2
70
(LP2)
x1 5
表 3.1
货物 体积(米 3/箱) 重量(百公斤/箱) 利润(百元/箱)
甲
5
2
20
乙
4
5
10
托运限制 24 米 3
13 百公斤
解: 设x1,x2 分别为甲、乙两种货物的托运箱数,则数 学模型可以表示为:
max z 20x1 10x2
5x1 4x2 24 2x1 5x2 13 x1, x2 0, x1, x2整数
其中,目标函数表示追求最大的卫星实验价值;第1,2个约
束条件表示体积和重量的限制;第3-5个约束条件表示特定的卫
星装载要求,该问题的决策变量是0-1整数变量。
3.2.3隐枚举法 从上面两个例子可以看出,此类型问题是整数规划中的特
殊情形,其中决策变量 xi 的取值只能为0或1,此时变量 xi 称 为0-1变量,这类问题被称为0-1整数规划。对于 xi 的取值的 0-1约束,可以转化成下述整数约束条件:xi 1, xi 0, xi Z
目前对于整数规划问题的求解主要有两种方法:分支 定解法和割平面法。本章仅介绍分枝定界法,该方法在上 世纪60年代由Land Doig和Dakin等人提出,其具有灵活 且便于计算机求解的优点,所以现在已成为解决整数规划 问题的重要方法。下面通过例子说明分支定界方法的算法 思想和步骤。
《运筹学》实验报告

《运筹学》实验报告专业:工商管理专业班级:11-2班姓名:胡坤学号:3指导老师:雷莹前言第十一周、十二周,我们在雷莹老师的指导下,用计算机进行了有关运筹学的一系列实验。
本实验报告即是对这次试验的反馈。
本这次试验是为了帮助我们顺利完成有关《运筹学》课程内容的学习。
在先期,雷老师带领我们进行了《运筹学》理论课程的学习,不仅使我们了解和掌握了运筹学的相关知识,而且让我们认识到运筹学的现实意义,认识到现代社会数学与人们生产、生活之间的紧密联系和对人们生产、生活的巨大促进作用。
然而,与此同时,现代社会同时是一个计算机时代,我们只拥有理论知识还不够,必须把理论知识和计算技术结合起来,这样才能进一步提高生产力。
我相信这也是老师要求我们做这次试验的目的和初衷。
在实验中,我们主要是利用WinQSB软件进行相关试验,根据实验指导书中详细给出的各个实验的基本步骤和内容,独立完成各项实验。
本次实验中共包含4个实验,分别是线性规划实验、运输问题实验、整数规划实验,以及网络优化实验。
每个实验均与理论课中讲解的内容相对应。
部分实验内容用于使我们了解WinQSB软件的基本操作,而其它实验内容要求我们能够根据给出的问题,进行分析、建模和求解。
通过完成各项实验任务,使我们得以巩固已有的理论课程学习内容,为将来进一步的学习和实际应用打下基础。
线性规划实验通过对以下问题的分析,建立线性规划模型,并求解:某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。
已知产品的规格要求,产品单价,每天能供应的原材料数量及原材料单价分别见下表1和2。
该厂应如何安排生产,使利润收入为最大表1表2实验报告要求(1)写出自己独立完成的实验内容,对需要建模的问题,给出问题的具体模型;(2)给出利用WinQSB软件得出的实验结果;(3)提交对实验结果的初步分析,给出自己的见解;实验过程:一、建立模型设Ac 是A 产品中用c 材料,同理得出Ap 、Ah 、Bc 、Bp 、Bh 、Dc 、Dp 、Dh⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧≤++≤++≤++≤++≥++≤++≥++++++++++++++++=60Dh Bh Ah 100Dp Bp Ap 100Dc Bc Ac 5.0Bh Bp Bc Bp 25.0Bh Bp Bc Bc 25.0Ah Ap Ac Ap 5.0Ah Ap Ac Ac Dh Bh Ah 35-Dp Bp Ap 25-Dc Bc Ac 65-Dh Dp Dc 25Bh Bp Bc 35)(50 max )()()()()(H P C A A A z二、求解过程三、实验分析实验结果表明,在题目的要求下,该工厂只能生产A产品才能盈利,并且在使用c材料100个单位、p材料50个单位、h材料50个单位时,即生产200个单位的A产品时,才能获得最大利润,最大利润为500。
运筹学实训实验报告

一、实验背景运筹学是一门应用数学的分支,它运用数学模型和算法来解决各种优化问题。
随着现代科技的发展,运筹学在各个领域的应用越来越广泛,如生产管理、物流运输、资源分配等。
为了提高学生运用运筹学知识解决实际问题的能力,我们开展了运筹学实训实验。
二、实验目的1. 熟悉运筹学的基本概念和常用方法;2. 掌握线性规划、整数规划、运输问题、目标规划等运筹学模型;3. 学会运用计算机软件解决实际问题;4. 培养学生的团队合作精神和创新意识。
三、实验内容本次实验主要包括以下内容:1. 线性规划:以生产计划问题为例,建立数学模型,并运用Excel规划求解器求解最优解。
2. 整数规划:以人员排班问题为例,建立数学模型,并运用Lingo软件求解最优解。
3. 运输问题:以物流配送问题为例,建立数学模型,并运用Lingo软件求解最优解。
4. 目标规划:以投资组合问题为例,建立数学模型,并运用Lingo软件求解最优解。
四、实验步骤1. 线性规划实验(1)问题分析:某企业需要生产甲、乙两种产品,已知生产甲、乙两种产品所需的原料、劳动力及设备等资源消耗量,以及产品的售价和利润。
(2)模型建立:根据问题分析,建立线性规划模型,目标函数为最大化利润,约束条件为资源消耗量不超过限制。
(3)求解:运用Excel规划求解器求解最优解。
2. 整数规划实验(1)问题分析:某公司需要安排员工值班,要求每天至少有3名员工值班,且员工值班时间不能超过一周。
(2)模型建立:根据问题分析,建立整数规划模型,目标函数为最小化员工值班成本,约束条件为员工值班时间不超过限制。
(3)求解:运用Lingo软件求解最优解。
3. 运输问题实验(1)问题分析:某物流公司需要将货物从A、B两个仓库运送到C、D两个销售点,已知各仓库的货物量、各销售点的需求量以及运输成本。
(2)模型建立:根据问题分析,建立运输问题模型,目标函数为最小化运输成本,约束条件为各仓库的货物量不超过需求量。
运筹学第三章 整数规划PPT课件

(一)
问题(1)
X1=2, x2=2.67
Z=83.3
x2≤2
x2≥3
问题(0) X1=2.5, x2=2.5
问题(0)的原问题 的目标函数值
上界为:Z^=87.5 下界为:Z=0
Z=87.5
x1≤2
x1≥3
(二)
问题(2)的原问题 的目标函数值
上界为:Z^=80 下界为:Z=75
问题(2)
X1=3, x2=1.75
20
1 11/14 4 2/7 0
检验数zj-cj
0
0
1 11/14 4 2/7 0
15
x1 2
1
0
0
20
x2 2 2/3 0
1
0
0
x5 2 1/3 0
0
1
zj
15
20
0
检验数zj-cj
0
0
0
27.11.2020
问题1求解的单纯形表
《整数规划》
0 1/3
-1 1/3 6 2/3
6 2/3
1 - 1/3 -4 2/3 8 1/3
原问题的松弛问题
max Z 15 x1 20 x 2
6 x1 4 x 2 25
x
1
3x2
10
x 1 0 , x 2 0
注:此松弛问题的最优目标值为原整数规划问题目标值的上界
原问题目标值的上界为Z^=87.5 下界可定为Z=0
27.11.2020
《整数规划》
10
CB 0 0
cj
问题(5)的原问题 的目标函数值 上界为:Z^=72.5 下界为:
问题(6) 无可行解
25
运筹学试验:整数规划
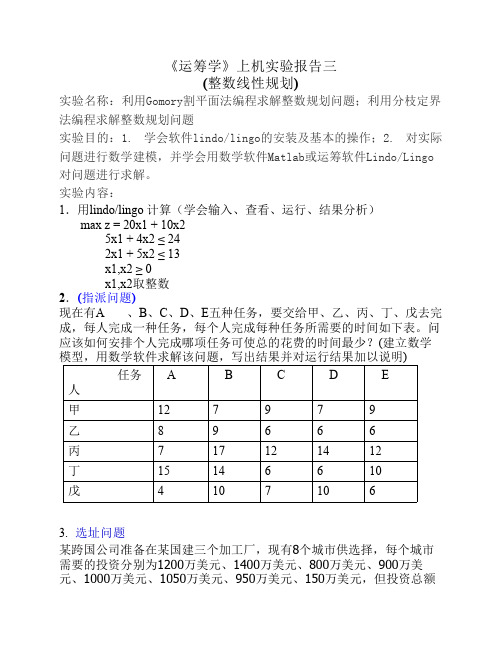
《运筹学》上机实验报告三(整数线性规划)实验名称:利用Gomory割平面法编程求解整数规划问题;利用分枝定界法编程求解整数规划问题实验目的:1. 学会软件lindo/lingo的安装及基本的操作;2. 对实际问题进行数学建模,并学会用数学软件Matlab或运筹软件Lindo/Lingo 对问题进行求解。
实验内容:1.用lindo/lingo 计算(学会输入、查看、运行、结果分析)max z = 20x1 + 10x25x1 + 4x2 ≤ 242x1 + 5x2 ≤ 13x1,x2 ≥ 0x1,x2取整数2.(指派问题)现在有A 、B、C、D、E五种任务,要交给甲、乙、丙、丁、戊去完成,每人完成一种任务,每个人完成每种任务所需要的时间如下表。
问应该如何安排个人完成哪项任务可使总的花费的时间最少?(建立数学模型,用数学软件求解该问题,写出结果并对运行结果加以说明)A B C D E任务人甲127979乙89666丙717121412丁15146610戊41071063.选址问题某跨国公司准备在某国建三个加工厂,现有8个城市供选择,每个城市需要的投资分别为1200万美元、1400万美元、800万美元、900万美元、1000万美元、1050万美元、950万美元、150万美元,但投资总额不能超过3400万美元,形成生产能力分别为100万台、120万台、80万台、85万台、95万台、100万台、90万台、130万台,由于需求的原因,要求:城市1和城市3最多选1个,城市3、城市4、城市5最多选两个,城市6和城市7最少选1个,问选择哪些城市建厂,才能使总的生产能力最大?(建立数学模型,用数学软件求解该问题,写出结果并对运行结果加以说明)整数变量定义LinDo一般整数变量:GIN <Variable>0-1整数变量: INT <Variable>LinGo一般整数变量: @GIN( variable_name);0-1整数变量:@BIN( variable_name);例如(1)Lindo运算程序max 3 x1+5 x2+4 x3subject to2 x1+3 x2<=15002 x2+4 x3<=8003 x1+2 x2 +5 x3<=2000endgin x1gin x3(2) max z = 3x1 - 2x2 + 5x3x1 + 2x2 - x3 ≤ 2x1 + 4x2 + x3 ≤ 4x1 + x2 ≤ 34x2 + x3 < 6x1,x2,x3 = 0或1lingo程序:max =3*x1 – 2*x2 + 5*x3;x1 + 2*x2 - x3 <= 2;x1 + 4*x2 + x3 <= 4;x1 + x2 <= 3 ; 4*x2 + x3< 6; @bin(x1);@bin(x2);@bin(x3);。
运筹学实验报告
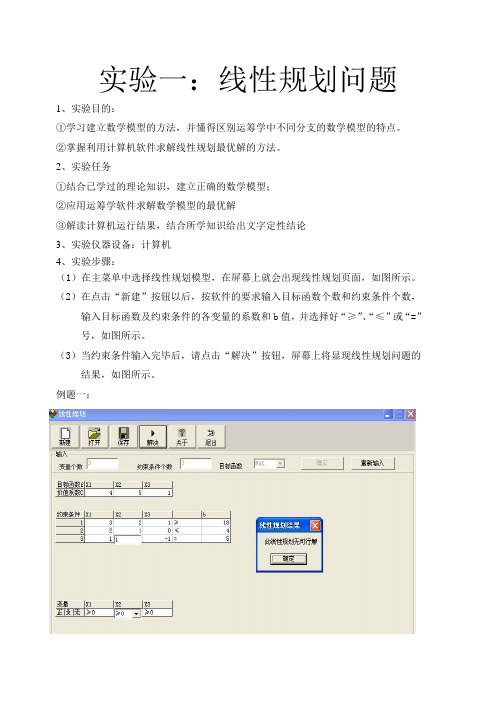
实验一:线性规划问题1、实验目的:①学习建立数学模型的方法,并懂得区别运筹学中不同分支的数学模型的特点。
②掌握利用计算机软件求解线性规划最优解的方法。
2、实验任务①结合已学过的理论知识,建立正确的数学模型;②应用运筹学软件求解数学模型的最优解③解读计算机运行结果,结合所学知识给出文字定性结论3、实验仪器设备:计算机4、实验步骤:(1)在主菜单中选择线性规划模型,在屏幕上就会出现线性规划页面,如图所示。
(2)在点击“新建”按钮以后,按软件的要求输入目标函数个数和约束条件个数,输入目标函数及约束条件的各变量的系数和b值,并选择好“≥”、“≤”或“=”号,如图所示。
(3)当约束条件输入完毕后,请点击“解决”按钮,屏幕上将显现线性规划问题的结果,如图所示。
例题一:例题二:例题三:例题四:例题五5、试验体会或心得运筹学是一门实用的学科,学习运筹学,结合生活实际运用运筹学,我们可以将资源最大化利用。
学习理论的目的就是为了解决实际问题。
线性规划的理论对我们的实际生活指导意义很大。
当我们遇到一个问题,需要认真考察该问题。
如果它适合线性规划的条件,那么我们就利用线性规划的理论解决该问题。
线性规划指的是在资源有限的条件下,为达到预期目标最优,而寻找资源消耗最少的方案。
其数学模型有目标函数和约束条件组成。
一个问题要满足一下条件时才能归结为线性规划的模型:⑴要求解的问题的目标能用效益指标度量大小,并能用线性函数描述目标的要求;⑵为达到这个目标存在很多种方案;⑶要到达的目标是在一定约束条件下实现的,这些条件可以用线性等式或者不等式描述。
所以,通过这次实验,不仅对运筹学的有关知识有了进一步的掌握,同时对在自己的计算机操作水准也有了很大的提高。
这次实验让我懂得了运筹学在电脑的应用,让我对运输与数学相结合的应用理解更深了。
实验二:整数规划与运输问题1、实验目的:①学习建立数学模型的方法,并懂得区别运筹学中不同分支的数学模型的特点。
运筹学-第3次实验内容(信计专业)打印

《运筹学》实验3一、实验名称:熟悉LINDO 软件的灵敏度分析功能,进一步理解分枝定界法的思想。
二、实验目的:熟悉LINDO 软件的灵敏度分析功能,会用LINDO 软件进行灵敏度分析。
掌握进用分枝定界法求解整数线性规划问题。
三、实验内容通过求解一个具体线性规划问题,学会使用LINDO 软件的灵敏度分析功能,包括目标函数的系数、右端常数项的灵敏度分析。
用分枝定界法求解一具体整数线性规划。
四、实验步骤1、示例:求解线性规划⎪⎩⎪⎨⎧≥≤+≤++=,0x ,x 135x 2x 244x 5x s.t.10x 20x z max 21212121,并进行灵敏度分析则在LINDO 的模型窗口中输入如下代码:max 20 x1+10 x2S .T .5 x1+4 x2<=242 x1+5 x2<=13END点击运行图标,屏幕上出现 DO RANGE (SENSITIVITY) ANALYSIS? 是(Y ) 否(N )回答是后,屏幕上出现运行结果:LP OPTIMUM FOUND AT STEP 1OBJECTIVE FUNCTION VALUE (目标函数值)1) 96.00000VARIABLE (变量) VALUE (值) REDUCED COST(影子价格或最优单纯表中的检验数) X1 4.800000 0.000000 X2 0.000000 6.000000ROW SLACK OR SURPLUS DUAL PRICES(行) (松驰变量或剩余变量) (检验数,对偶问题的解)2) 0.000000 4.0000003) 3.400000 0.000000NO. ITERATIONS= 1RANGES IN WHICH THE BASIS IS UNCHANGED:(保持最优基不变量的取值范围)OBJ COEFFICIENT RANGES (价值系数的变化范围) VARIABLE CURRENT ALLOWABLE ALLOWABLE(变量) COEF INCREASE DECREASE(当前系数) (允许增加量) (允许减少量) X1 20.000000 INFINITY 7.500000X2 10.000000 6.000000 INFINITYRIGHTHAND SIDE RANGES (右端常量范围)ROW CURRENT ALLOWABLE ALLOWABLE(行) RHS INCREASE DECREASE(当前值) (允许增加量) (允许减少量) 2 24.000000 8.500000 24.000000 3 13.000000 INFINITY 3.400000结论:C1=20,C1在(12.5,+∞)内原最优解不变,但最优值是要变的C2=10,C2在(-∞,16)内原最优解,最优值都是不变的B1=24,, b1在(0,32.5)内原最优基不变,但最优解和最优值是要变的 B2=10,, b2在(9.6, ∞)内原最优基不变,但最优解和最优值是要变的点击菜单栏中的Reports,然后再点击Tableau,再运行以上程序可得如下最优单纯表:ROW (BASIS) X1 X2 SLK 2 SLK 31 ART 0.000 6.000 4.000 0.000 96.0002 X1 1.000 0.800 0.200 0.000 4.8003 SLK 3 0.000 3.400 -0.400 1.000 3.400五、实验题目1、求解线性规划:,⎪⎩⎪⎨⎧≥≤+≥++=0x ,x 82x x 125x 2x s.t.2x x z max 21212121并价值系数、右端常量进行灵敏度分析。
课内实验-运筹学-整数规划-第三次 实验

在西区由A4,A5两个点中至少选一个;
在南区由A6,A7两个点中至少选一个;
在北区由A8,A9,A10三个点中至少选两个。
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
投资额
100
120
150
80
70
90
80
140
160
180
利润
36
40
50
22
20
30
25
48
课内实验报告
课 程 名:运筹学
*******
专 业:电子商务
学 号:
姓 名:
2012 /2013 学年 第 2 学期
南京邮电大学 经济与管理学院
《 运筹学 》课程实验第 3 次实验报告
实验内容及基本要求:
实验项目名称:整数规划实验
实验类型:验证
每组人数:1
实验内容及要求:
内容:整数规划建模与求解
要求:能够写出求解模型、运用软件进行求解并对求解结果进行分析
我们应该好好学习运筹学这门科学,为以后进入社会打下良好的基础,是自己的工作效率达到最大化。
成绩评定:
该生对待本次实验的态度□认真□良好□一般□比较差。
本次实验的过程情况□很好□较好□一般□比较差
对实验结果的分析□很好□良好□一般□比较差
文档书写符合规范程度□很好□良好□一般□比较差
综合意见:
成绩
指导教师签名
58
61
Aj各点的设备投资及每年可获利润由于地点不同都是不一样的,预测情况见表所示(单位:万元)。但投资总额不能超过720万元,问应选择哪几个销售点,可使年利润为最大?
运筹学实验答案

运筹学实验报告册(适用于经济管理类专业)学号:姓名:专业:实验三整数规划一、实验目的熟悉Excel软件,掌握整数规划问题的Excel求解。
二、实验要求掌握整数规划问题的特殊性,以及分支定界法和线性规划单纯形法的区别。
三、实验原理及内容建立整数规划问题模型后,在Excel界面中输入数据,进行求解。
熟悉整数规划问题模型的建立过程,掌握数据整理与Excel整数规划求解的操作步骤;整数规划问题模型的建立,数据的输入与求解是最基础的要求。
本节实验要求完成以下内容:1、整数规划问题模型的建立;2、Excel界面内数据的输入;3、利用Excel规划求解进行整数规划问题模型的求解。
四、实验步骤及结论分析1、某公司拟用集装箱托运甲、乙两种货物,这两种货物每件的体积、重量,可获利润以及托运所受限制如表所示:解:设托运甲货物X1件,托运乙货物X2件目标:max 2X1 + 3X2约束条件:X1 <= 4195X1 + 273X2 <= 13654X1 + 40 X2 <=140X1 ,X2 为整数。
一:数据输入与处理:目标 2 3 0约束一195 273 0 <= 1365约束二 4 40 0 <= 140约束三 1 0 0 <= 4变量X1 X2二:利用“工具”中的“规划求解”进行求解,结果如下: 目标 2 3 14 约束一 195 273 1326 <= 1365 约束二 4 40 96 <= 140 约束三 1 0 4 <= 4 变量 4 2 X1 X22、求解下面的混合整数规划问题:为整数31321332132321321,,0,,,1,323,234,4233max x x x x x x x x x x x x x x x x x z ≥≤≤+-≤-≤++-++=一:数据输入与处理: 目标 3 1 3 0约束一 -1 2 1 0 <= 4约束二 0 4 -3 0 <= 2 约束三 1 -3 2 0 <= 3 约束三 0 0 1 0 <= 1变量 X1 X2 X3二:利用“工具”中的“规划求解”进行求解,结果如下: 目标 3 1 3 16.25约束一 -1 2 1 -0.5 <= 4 约束二 0 4 -3 2 <= 2 约束三 1 -3 2 2.25 <= 3 约束三 0 0 1 1 <= 1变量 4 1.25 1 X1 X2 X3。
整数规划实验报告心得

整数规划实验报告心得引言整数规划是运筹学中一种重要的优化方法,它在决策问题中有着广泛的应用。
在整数规划实验中,我们通过数学模型的建立和求解来解决实际问题。
本次实验我们使用了MATLAB软件,通过调用优化工具箱中的整数规划函数,对一个具体的问题进行了求解。
实验内容本次实验主要任务是解决一个生产调度问题。
在一个工厂中,有n种原料,每种原料的供应量和价格都不同,而产品的生产需要用到这些原料。
研究目的是确定每种原料的需求量,以最小化总成本,并满足产品的需求。
实验步骤1. 问题分析与建模:首先,我们需要对问题进行分析,并建立数学模型。
在这个问题中,我们需要确定每种原料的需求量,所以我们可以将原料的需求量作为决策变量。
而最小化成本是我们的目标,所以我们可以将成本作为目标函数。
同时,由于原料的需求量必须是整数,我们可以将问题转化为整数规划问题。
2. 模型求解:然后,我们使用MATLAB软件来求解整数规划模型。
首先,我们需要将模型转化为标准形式,并进行线性规划求解。
然后,我们通过整数规划函数来求解整数规划模型。
3. 结果分析:最后,我们对求解结果进行分析。
通过对原料需求量的分析,我们可以评估生产成本的优劣。
同时,我们还可以通过敏感性分析,来评估模型的稳定性和可靠性。
心得体会通过本次实验,我对整数规划方法有了更深入的理解。
整数规划是一种非常实用的优化方法,广泛应用于生产调度、资源分配、路径规划等问题中。
在实验中,我学会了如何将实际问题转化为整数规划模型,并通过MATLAB软件来求解模型。
通过对实验结果的分析,我更直观地了解了整数规划方法在实际问题中的应用效果。
在实验过程中,我还遇到了一些困难。
首先是模型建立的难度,问题分析和建模是整个求解过程的关键。
如果模型建立不准确,就会导致求解结果的不准确。
其次是模型求解的复杂性,整数规划问题求解难度较大,需要运用一些优化方法和工具进行求解。
最后是结果分析的复杂性,结果分析需要对求解结果和敏感性分析进行综合判断,需要一定的经验和专业知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
投资额
100
120
150
80
70
90
80
140
160
180
利润
36
40
50
22
20
30
25
48
58
61
Aj各点的设备投资及每年可获利润由于地点不同都是不一样的,预测情况见表所示 (单位:万元)。但投资总额不能超过720万元,问应选择哪几个销售点,可使年利润为最大?
实验结果:(附后)
实验背景:
某公司计划在市区的东、西、南、北四区建立销售中心,拟议中有10个位置 Aj(j=1,2,3,…,10)可供选择,考虑到各地区居民的消费水平及居民居住密集度,规定:
在东区由A1, A2,A3三个点至多选择两个;
在西区由A4, A5两个点中至少选一个;
在南区由A6, A7两个点中至少选一个;
课内实验报告
课 程 名:运 筹 学
任课教师:邢光军
专 业:电子商务
学 号:ቤተ መጻሕፍቲ ባይዱ
姓 名:
2012 /2013 学年 第 2 学期
南京邮电大学 经济与管理学院
《 运筹学 》课程实验第 3 次实验报告
实验内容及基本要求:
实验项目名称:整数规划实验
实验类型:验证
每组人数:1
实验内容及要求:
内容:整数规划建模与求解
建立模型:
设10个销售位置分别为Xj(j=1……10),建立0—1整数规划数学模型如下:
目标函数:max Z=36X1+40X2+50X3+22X4+20X5+30X6+25X7+48X8+58X9+61X10
s.t:
100X1+120X2+150X3+80X4+70X5+90X6+80X7+140X8+160X9+180X10<=720
我们应该好好学习运筹学这门科学,为以后进入社会打下良好的基础,是自己的工作效率达到最大化。
成绩评定:
该生对待本次实验的态度 □认真 □良好 □一般 □比较差。
本次实验的过程情况 □很好 □较好 □一般 □比较差
对实验结果的分析 □很好 □良好 □一般 □比较差
文档书写符合规范程度 □很好 □良好 □一般 □比较差
要求:能够写出求解模型、运用软件进行求解并对求解结果进行分析
实验考核办法:
实验结束要求写出实验报告。实验报告的形式可以包括以下3点:
1.问题的分析与建立模型,阐明建立模型的过程。
2.计算过程,包括采用什么算法,使用什么软件以及计算详细过程和结果。
3.结果分析,将结果返回到实际问题进行分析、讨论、评价和推广。
综合意见:
成绩
指导教师签名
邢光军
日期
X1+X2+X3<=2
X4+X5>=1
X6+X7>=1
X8+X9+X19>=2
Xj=0或1(j=1……10)
Xj=1 表示项目被选中(j=1……10)
决策变量Xj=
Xj=0 表示项目没有被选中(j=1……10)
规划求解:
(1)在excel表格中输入数据后,工具→加载宏,工具→规划求解
(2)添加约束方程等,规划求解
(3)规划求解结果如下:
当X1=1,X2=0,X3=1,X4=0,X5=1,X6=1,X7=0,X8=1,X9=1,X10=0时,该规划取得最优解,最优解为Z=242
实验总结:
线性规划包括很多种形式,因此不同的问题都可以采用线性规划的方法进行解决,对现实生活中的排产、安排工人等生产活动具有重要作用。
通过线性规划可以很方便的解决生产中的问题,可以节约成本、运费以及工人工资,是企业利用最少的资源、最简便的方法,达到最理想的效果,获得最大利润。
本题目采用了0—1整数线性规划,对企业的生产安排进行了合理的规划,达到是利润最大化的目的,即在当X1=1, X2=0, X3=1, X4=0 , X5=1, X6=1, X7=0, X8=1, X9=1, X10=0时,该规划取得最大利润,最大利润为Z=242
