电路第4章习题电路定理
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
电路原理 第4章 常用的电路定理

U ad ' U s = I5' I5
Us 6 因此 I 5 = I5 '= × 1 = 0.05 A U ad ' 120
需要注意 注意的是,应用叠加 叠加定理和齐次 齐次定 注意 叠加 齐次 理时,当激励的参考方向反向 反向时,相当于激 反向 励变为原来的-1倍。 - 倍 4.2 替代定理 已知电路中第k条支路的电压uk和电流ik, 那么无论该条支路是由何种元件构成的,它 都可以用电压等于uk的理想电压源或电流等 于ik的理想电流源去替代,替代之后,电路 中其他支路的电压和电流均不变。
得原电路的戴维南等效电路 得原电路的戴维南等效电路 由全电路欧姆定律可得: 由全电路欧姆定律可得:
24Ω
A
I5 16Ω
+ _ 2V
B
电路如图示, 例题 电路如图示,求UR 。 将待求支路断开
(1) 求开路电压 OC 求开路电压U UOC=6I1+3I1 I1=9÷ (6+3)=1A UOC=9V +
解:这个电路是由电阻的串、并联组成,可 以用等效电路的分析方法进行计算,但是 用齐次定理计算会更方便。 先设I5支路电流为I5’=1A, 则:
U cd ' = (15 + 15) I 5' = 30V
4
所以, I
U cd ' 30 '= = = 1A 30 30
I3 ' = I 4 '+I5 ' = 1+1 = 2A
例4.1-1 图4.1-2(a)所示电路,试用叠加 定理求3Ω电阻上的电压U及功率。
8Ω 2Ω (a) 8Ω 2Ω (c) 图4.1-2 例4.1-1图 3A 6Ω + 3Ω U’’ - 3A 6Ω (d) 3A 6Ω + 3Ω U - 8Ω 2Ω (b) 8Ω 2Ω - 3Ω U’’ + 6Ω + 3Ω U’ -
电路第4章习题集电路定理教程文件

电路第4章习题集电路定理第4章电路定理4-1XX 简单题4-2XX 叠加定理4-3XX 戴维宁定理4-201、试用叠加定理计算下图所示电路中US2=2V时,电压U4的大小。
若US1的大小不变,要使U4=0,则US2应等于多少?答案 U4=-0.4V, Us2=1.2V4-202、电路如图所示。
(1)用叠加定理求各支路电流;(2)求电压源发出的功率。
答案 I1=-50mA, I2=15mA, I3=60mA (2)电压源发出的功率为:P=25I1=-1.25W4-204、4-205、求题3-22图示电路的电压U和电流I。
+-2I110V+-3A-+ U4Ω6Ω9ΩI1题3-22图I例4-4 用叠加定理求图4-5(a)电路中电压u。
图4-5解:画出独立电压源u S和独立电流源i S单独作用的电路,如图(b)和(c)所示。
由此分别求得u’和u”,然后根据叠加定理将u’和u”相加得到电压u4-206、例4-1 利用叠加定理求图(a )所示电路中的电压U 。
(a ) (b) (c)解:首先画出分电路图如图(b)、(c)所示。
当12V 电压源作用时,应用分压原理有:V 43912)1(-=⨯-=U 当3A 电流源作用时,应用分流公式得:V 633636)2(=⨯+⨯=U 则所求电压:V 264=+-=U4-207、例4-2利用叠加定理求图(a )所示电路中的电压u 和电流i 。
(a ) (b) (c)解:首先画出分电路图如图(b)、(c)所示。
当 10V 电源作用时:)12/()210()1()1(+-=i i 解得:A i 2)1(=,V i i i u 6321)1()1()1()1(==+⨯=当5A 电源作用时,由左边回路的KVL :02)5(12)2()2()2(=++⨯+i i i 解得:A i 1)2(-=,V i u 22)2()2(=-= 所以: V u u u 8)2()1(=+= A i i i 1)2()1(=+=注意:受控源始终保留在分电路中。
大学电路习题第4章
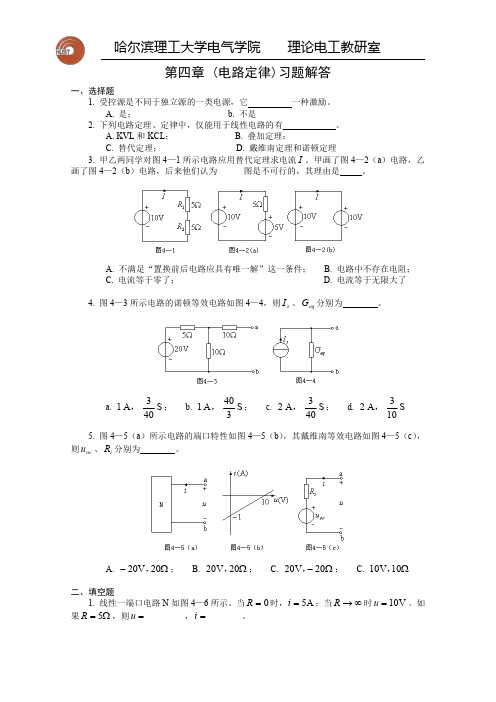
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源,它一种激励。
A.是; b.不是2.下列电路定理、定律中,仅能用于线性电路的有。
A.KVL 和KCL ; B.叠加定理;C.替代定理; D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。
甲画了图4—2(a )电路,乙画了图4—2(b )电路,后来他们认为图是不可行的,其理由是。
A.不满足“置换前后电路应具有唯一解”这一条件;B.电路中不存在电阻;C.电流等于零了;D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4,则s I 、eq G 分别为。
a.S 403A 1,;b.S 340A 1,;c.S 403A 2,;d.S 103A 2,5.图4—5(a )所示电路的端口特性如图4—5(b ),其戴维南等效电路如图4—5(c ),则oc u 、i R 分别为。
A.Ω-20V 20,;B.Ω20V 20,;C.Ω-20V 20,; C.Ω10V 10,二、填空题1.线性一端口电路N 如图4—6所示。
当0=R 时,A 5=i ;当∞→R 时V 10=u 。
如果Ω=5R ,则=u ,=i 。
2.图4—7所示电路中,N 为线性电路,且Ω=10R 。
当0=s u ,0=s i 时,V 5=u ;当A 2=s i ,0=s u 时,V 8=u ;当0=s i ,V 10=s u 时,V 6=u 。
那么,当A 6=s i ,V 4=s u 时,=i 。
3.图4—8(a )所示电路的戴维南等效电路如图4—8(b ),那么=s U ,=eq R 。
4.图4—9(a )所示电路的戴维南等效电路如图4—9(b ),则=s U ,=eq R 。
5.在图4—10(a )所示的电路中,i u 1024-=(i 的单位用安培时,u 的单位为伏特),其戴维南等效电路如图4—10(b ),则=s u ,=0R 。
三、计算题1.用叠加定理计算图4—11所示电路中的u 。
第四章 电路定理

2、电路中含有受控源。
R1 R2 R3 R4 R2 R3
即: R1 R3 R2 R4
求uoc 时,就是含受控源的线性电路分析问题; 求Re q 时,将独立源置零、受控源保留,用外加激励法。
1 uS R1 R2
i1
i2
R2 iS R1 R2
R1 iS R1 R2
u2 R2i2
R1 R2 iS R1 R2
i1 i1 i1,
u2 u2 u2
二,使用叠加定理的注意事项: • • • 叠加定理只适用于线性电路; 分解电路时,除独立电源以外的所有元件及连线不予更动; 电路中所有电压电流的参考方向不变;
示线性电阻电路,用叠加定理求得:
10 2 i1 (t ) A 2.5e t A (2.5 1.25e t )A 22 22 10 2 i 2 (t ) A 2.5e t A (2.5 1.25e t )A 22 22
§4-3 戴维南定理和诺顿定理 一、问题的引入: 1、对于一个无源线性一端口: 2、对于一个含独立源的线性一端口:
思考一下:如果上图中,不止一个电源激励,还有另外一个激励时, 如何分析? 结论:当两个电源激励同时增大K倍时,所有支路的响应也相 应增大K倍。 (这一点可以很方便的用叠加定理加以证明。) 2、齐性定理的推广: 在线性电路中,如果所有激励同时均增大K倍,则所有响 应也相应增大K倍。
再思考:如果线性电路中有两个电源激励,不同时增大同一倍数, 一个增大K1倍,而另一个增大K2倍,则响应会如何变化? 请看下图电路:
•
• •
独立电压源置零,用短路线取代(支路作短路处理) ;
邱关源《电路》第五版 第四章 电路定理

1 + u 1
-
任何一个有源一端口网络,对外电路来说,可 以用一个电流源和电阻相并的组合来等效代替。电
1 R0=Req + + u uS =uOC 1
i
外 电 路
u uS R0i
uS uoc
R0 Req
§4-3 戴维宁定理和诺顿定理
3. 举例
【例1】电路如图,求通过电阻R3的电流I3 。
I3
4
R3 5
8
a Uoc
b 8
2
2
4 2
2 I1
+
40V
+
40V
10
+
-
2.25A 1
A 1.5A 1
B
1 0.5A 1A
US
+ Us D 4.5A 1 6
0.75A
6.75V
U AD 6 4.5V
U BC 2 3V
U 0 =2V
C 1 B 1
A 3A
+ 13.5V
1.5A
1A
2A
Us
-
6
U AD 6 9V
U BC 2 6V
U 0 =4V
iS1
+
R3
uS3
R3 iS1
中,任一支路电流
(或支路电压)都是
i iR1 R4 R2 R2 R1
i R1
R1
uS2
+ -
=
R4 i R 2 R2电路各个独立电源单
独作用时在该支路产
+
i R1
R1
R4 i R 2 R2
iR1
生的电流(或电压)
Chapter4电路定理

a
c
a
R1 Rab R2 i3i3 R3
R5
+ ++
uS1 uab uS2
R4RRcd6
– ––
b
b
d
例2 求图示电路的等效发电机。
解:
iSc
40 20
40 40
60 20
3
1A
Req 20 // 40 // 20
1
1 1
1
8
20 40 20
20Ω
40Ω
20Ω 3A
+
25V
20
U
-
-
用结点电压法
o
1'
uao
1 5
1 20
1 4
25 5
3
U 4
uao
16
U 2
由 I uao U
4
U 32 8I
+ 8 I +1
4A
32V
-
U
-
1'
I +1
8 U
-
1'
i
ia
a +
Req
+
uoc=Reqisc
Nu
+
-b
uoc
-
u isc -
3.定理的应用
(1)开路电压uoc和短路电流iSc的计算
戴维宁等效电路中电压源电压等于将外电路断开时的开 路电压uoc,电压源方向与所求开路电压方向有关。诺顿等效 电路中电流源电流等于将外电路短路时的短路电流iSc,电流源 方向与所求短路电流的方向有关。计算uoc、 iSc的方法视电路 形式选择前面学过的任意方法,使易于计算。
电路理论第4章-电路定理

本章主要内容
一、叠加定理
四、戴维南定理和诺顿定理 五、最大功率传输定理
第四章、电路定理
一、叠加定理
几个概念 (1)线性电阻:电阻的伏安特性曲线为线性。
R为常数,符合u=iR 。
(2)激励:独立电源又称为激励,由于它的存在, 电路中能够产生电流或电压。
(3)响应:由激励在电路中产生电流或电压称 为响应。
(3)、有源二端网络:二端网络中含有电源。
有源二端网络:
第四章、电路定理 四、戴维南定理和诺顿定理 说明有源一端口网络,其对外的最简等效电路是一
个电压源与电阻的串联.
等效
第四章、电路定理
四、戴维南定理和诺顿定理
1. 戴维宁定理
任何一个线性含源一端口网络,对外电路来说,
总可以用一个电压源和电阻的串联组合来等效置
+-+-UUoocc
66
66
bb 10V
44
+–
+ Req Uoc
–
Ia Rx b
①求开路电压
Uoc = U1 - U2 = -104/(4+6)+10 6/(4+6) = 6-4=2V
②求等效电阻Req
Req=4//6+6//4=4.8
③ Rx =1.2时,
I= Uoc /(Req + Rx) =0.333A
u(2) (6i(2) 6) (21) 8V u u(1) u(2) 9 8 17V
3A
+ - 6 i (2)
+ u(1)
6 3
1
- 6V
+
3+u(2) - +
12V -
1 2A
电路理论4电路定理

2V 3
R1 图(a) R2 b
I3
a
Us1
rI3
+
Eo
求 等效内阻(求短路电流),图(c):
I0 I3 I1 I2,
I1
US1 R1
1A ,
I2
rI3 R2
1 I3 2
0.5I3 2
I3 1 0.5I3 , I3 3 A
I0
2 3
A
,
R0
E0 I0
1
R1图(b +
R1
Is
R2
Uoc
I1
图(b)
_ b
2)求等效内阻,方法1:外加电压源,图(c):
I2
US R2
US 3
I1
2I2 US R1
2I2 US
1 3
U
S
2 I0 I2 I1 3 US
R0
US I0
3 2
2I2
a
I2 Io
R1
R2
I1 图(c)
Us
b
2)求等效内阻方法2:直接求等效电阻
4.1.2 叠加定理 (Superposition Theorem) 定理内容:
在任一线性电路中,任一支路电流(或电压)都等于电路中各个独立电源单 独作用于网络时,在该支路产生的电流(或电压)的叠加(代数和)。
定理特点:
将多电源电路转化为单电源电路进行计算。
例1:
R1
i2
+
Us
R2
-
两个独立源分别单独作用
若替代后电路仍具有唯一解,则整个电路的各支路电压和电流保持不变。
例子:
i
u=3V
i=1A +
《电路原理导论》第四章习题解答
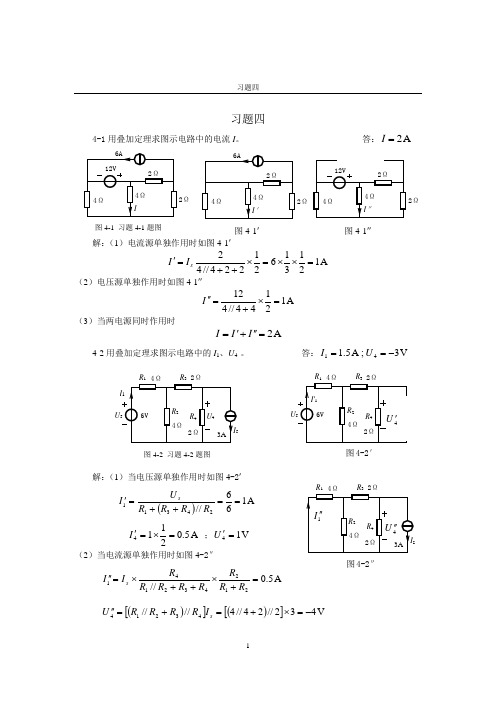
习题四习题四4-1用叠加定理求图示电路中的电流I 。
答:A 2=I解:(1)电流源单独作用时如图4-1′A 12131621224//42=⨯⨯=⨯++='sI I(2)电压源单独作用时如图4-1″A 12144//412=⨯+=''I(3)当两电源同时作用时A 2=''+'=I I I4-2用叠加定理求图示电路中的I 1、U 4 。
答:V 3;A 5.141-==U I解:(1)当电压源单独作用时如图4-2′()A 166//24311==++='R R R R U I sA 5.02114=⨯='I ;V 14='U (2)当电流源单独作用时如图4-2″A 5.0//212432141=+⨯++⨯=''R R R R R R R R I I s()[]()[]V 432//24//4////43214-=⨯+=+=''s I R R R R U 图4-1 习题4-1题图图4-2 习题4-2题图2Ω图4-1′ 2Ω图4-1″图4-2′图4-2″习题四(3)当两电源同时作用时A 5.15.01111=+=''+'=I I I V 341444-=-=''+'=U U U 4-3利用叠加定理求图4-3电路中的电压U 。
答:V 6=U解:(1)当电压源单独作用时如图4-3′V 11516=+⋅='U (2)当电流源单独作用时如图4-3″A 51556=+⨯=''I ,V 551=⨯=''U (3)当两电源同时作用时V 651=+=''+'=U U U4-4利用叠加定理求图示电路的电压U ab 。
答:V 9=ab U解:(1)当电流源单独作用时如图4-4′V 5.46241866186A 3-=⨯-=Ω⨯+⨯-='abU (2)当电压源单独作用时如图4-4″A 875.12.1936181218121236==+⨯+=''us I习题四V 5.1312875.15312181218=⨯⨯=Ω⨯''+=''usabI U (3)当两电源同时作用时V 95.135.4=+-=''+'=ab abab U U U 4-5图4-5电路中已知Ω=11R ,Ω=22R ,Ω=33RΩ=44R ,Ω=55R ,V 6=s U ,A 7=s I ,试用叠加定理求电路中的I 。
电路分析习题解答(第四章)
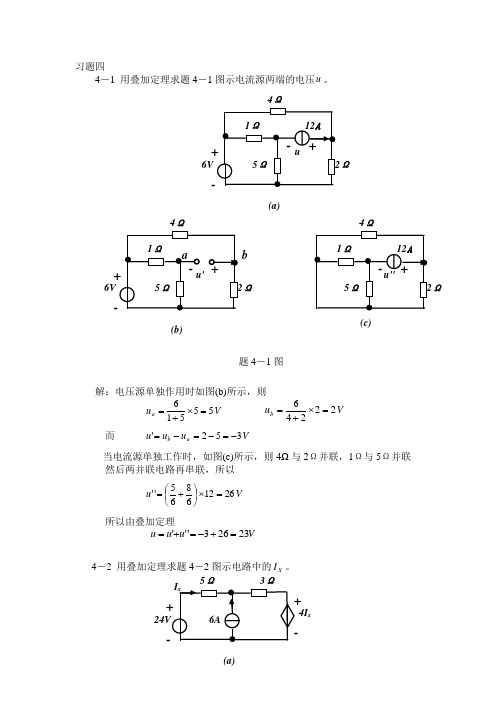
习题四4-1 用叠加定理求题4-1图示电流源两端的电压u 。
解:电压源单独作用时如图(b)所示,则V u a 55516=⨯+= V u b 22246=⨯+=而 V u u u a b 352'-=-=-=当电流源单独工作时,如图(c)所示,则4Ω与2Ω并联,1Ω与5Ω并联然后两并联电路再串联,所以V u 26126865''=⨯⎪⎭⎫⎝⎛+=所以由叠加定理V u u u 23263'''=+-=+=4-2 用叠加定理求题4-2图示电路中的X I 。
题4-1图 6V 4Ω Ω (b)b (c) 4Ω Ω5Ω 3Ω (a)4I x6V 4Ω Ω (a)解:电压源单独作用时的电路如图(b) 所示,则()24435''=++x x I I 解得 A I x 2'=电流源单独作用时的电路如图(c)所示,图中虚线为网孔电流,则 ()0''4''63''5=+++x x x I I I 解得 A I x 5.1''-= 所以 A I I I x x x 5.05.12'''=-=+=4-3 用叠加定理求题4-3图示电路中的独立电压源和独立电流源发出的功率。
5Ω 3Ω '(b) 4I 'x 4I ''x5Ω 3Ω I ''x(c) 题4-2图 题4-3图 2A 4Ω (a) 2V2A 4Ω 2i'(b) + - i''14Ω (c) u''1 2V解:电流源单独作用时的电路如图(b) 所示,则A i 2'1= 0'=i则 V i i u 824''1'1=-=电压源单独作用时的电路如图(b) 所示,则A i 5.042''1-=-= A i i 5.0''1''=-=则 V i u 122''''1=-=所以由叠加定理 A i i i 5.15.02''1'11=-=+=V u u u 918''1'11=+=+=可得电压源和电流源的功率分别为W i P V 3212-=-= W u P A 18212==4-4 题4-4图示电路中,R N 为电阻网络,由两个电流源供电。
电路第4章

4-1 叠加定理 示电路求电压U和电流I 一、引例 图示电路求电压U和电流I。
R1
Us
R2
Is
=
U s / R1 + I s U= 1 1 ( + ) R1 R2
+
R2 R2R 1 U= Us + Is =U′ +U′ ′ R + R2 R + R2 1 1
⊥
U s R 2 + R1 R 2 I s = R1 + R 2
三、应用举例: 应用举例:
求图示电路中的U 求图示电路中的 S和R。 。 解: I=2A U=28v US
US=43.6v 利用替代定理, 有 利用替代定理
U1 = 28−20×0.6−6
=10v I1=0.4A + IR=0.6-0.4=0.2A ∴ R=50Ω. Ω 28V I1 + U1 9 IR
R0 =
不除源
3、含受控源单口有源网络不一定同时存在两种等效电源; 、含受控源单口有源网络不一定同时存在两种等效电源; 4、含源单口网络与外电路应无耦合; 受控源及控制量均在线 、含源单口网络与外电路应无耦合;
性含源网络内部
5、含源单口网络应为线性网络; 、含源单口网络应为线性网络; 6、等效参数计算。 、等效参数计算。
ϕ
⊥
1、10V电压源单独作用时: 、 电压源单独作用时: 电压源单独作用时
10 − 2I ′ I′ = 2 +1
ϕ
I ′ = 2A
3 I′′ = − A 5
2、3A电流源单独作用时,有 、 电流源单独作用时, 电流源单独作用时 ′ 3+ 2I′ /1 ϕ ϕ=
电路定理

I
I
3
4V 10A
2 3
5A
5
20V 5
4V
2
20V
(a)
(b)
【解】 (1) 电压源单独作用时,电路如图(b)所示
(2) 10A电流源单独作用,电路如图(c)所示
I
3 10A
2
5
(c)
(3) 5A电流源单独作用,电路如图(d)所示
I 3
2 5A 5
(d)
由叠加定理得
4.1.2 齐性定理
定理内容:在线性电阻电路中,当所有激励都 增大或缩小k倍时,响应也同样增大或缩小k倍。
11 / /1
1 0.5
由KCL和VAR得
(2) 求
,电路如图(c)所示。
1
1
I0
1
U 1
U0
0.5U
(c)
(3) 求电流 ,电路如图(d)所示。
I
15
2
3
2 3
(d)
由分流公式
4.2.3 最大功率传递定理
一个线性含源单口电路,当所接负载不同时, 一端口电路传输给负载的功率就不同。
讨论:负载为何值时,能从电路获取最大功率, 及最大功率的值是多少。
u1iˆ1 u2iˆ2 uˆ1i1 uˆ2i2
u2is uˆ1is
iˆ1 0
+
uˆ1 NR
-
iˆ2
+
is
uˆ 2
-
iˆ1 0 iˆ2 is
可得: uˆ1 u2
形式3
i1
+
i2
iˆ1 0
iˆ2
+
+
+
is
(电路分析)常用电路定理 习题和答案解析

习题和习题答案第 4 章必做习题习题 4-1 电路如图题 4.1 所示,求 6 Ω电阻吸收的功率。
习题 4-2 电路如图题 4.2 所示,试用叠加定理求电流 I 。
习题 4-3 电路如图题 4.3 所示,用戴维南定理计算 5 Ω电阻吸收的功率。
习题 4-4 电路如图题 4.4 所示,求 a 、 b 两端的诺顿等效电路。
习题 4-5 电路如图题 4.5 所示,用戴维南定理求电流 I 。
习题 4-6 电路如图题 4.6 所示,试问电阻 R 为何值时获得最大功率?并求最大功率。
第 4 章选做习题选做题 4-1 电路如图题 4.1 所示, N 是线性电阻网络,三个独立源 uS1 、uS2 和 iS 同时对 N 激励时,测得电流 i= 12A ;若将电压源 uS2 短路时,测得电流 i= 20A ;若将电压源 uS1 短路时,测得电流 i= - 5A 。
试问:将电流源 iS 和电压源 uS2 同时反向,而电压源 uS1 保持不变,电流 i 为多少?选做题 4-2 图题 4.2 所示电路中,已知 Uab=0 ,试用替代定理求电阻 R 。
选做题 4-3 电路如图题 4.3 所示,求 a 、 b 两端的戴维南等效电路。
选做题 4-4 图题 4.4 所示电路中, RL 可调,问 RL 为何值时获得最大功率?最大功率是多少?选做题 4-5 图题 4.17 所示电路中, Ns 是线性含源二端网络,电流表 A 和电压表 V 均是理想的,当开关 S 处于位置 1 时,电流表的读数为 2A ,当开关S 处于位置 2 时,电压表的读数为 4V ,求开关 S 处于位置 3 时, 5 Ω电阻吸收的功率。
选做题 4-6 求图题 4.6 所示电路中,电阻 R 获得最大功率时的电流 I 。
第 4 章必做习题精解习题 4-1解:为了求6 Ω电阻吸收的功率,就要先求出流过 6 Ω电阻的电流。
下面,用叠加定理计算电流 I 。
图题 4.1 电路中有两个独立源共同激励。
电路第4章习题集电路定理

第4章电路定理4-1XX 简单题4-2XX 叠加定理4-3XX 戴维宁定理4-201、试用叠加定理计算下图所示电路中US2=2V时,电压U4的大小。
若US1的大小不变,要使U4=0,则US2应等于多少?答案U4=-0.4V, Us2=1.2V4-202、电路如图所示。
(1)用叠加定理求各支路电流;(2)求电压源发出的功率。
答案I1=-50mA, I2=15mA, I3=60mA (2)电压源发出的功率为:P=25I1=-1.25W4-204、4-205、求题3-22图示电路的电压U 和电流I 。
+-2I 110V+ -3A -+ U 4Ω 6Ω9Ω I 1题3-22图I例4-4 用叠加定理求图4-5(a)电路中电压u 。
图4-5解:画出独立电压源u S 和独立电流源i S 单独作用的电路,如图(b)和(c)所示。
由此分别求得u ’和u ”,然后根据叠加定理将u ’和u ”相加得到电压uS4242"S 424' i R R RR u u R R R u +=+=)(S 2S 424"'i R u R R R u u u ++=+=4-206、例4-1 利用叠加定理求图(a )所示电路中的电压U 。
(a ) (b) (c)解:首先画出分电路图如图(b)、(c)所示。
当12V 电压源作用时,应用分压原理有:V 43912)1(-=⨯-=U 当3A 电流源作用时,应用分流公式得:V 633636)2(=⨯+⨯=U 则所求电压:V 264=+-=U4-207、例4-2利用叠加定理求图(a )所示电路中的电压u 和电流i 。
(a ) (b) (c)解:首先画出分电路图如图(b)、(c)所示。
当 10V 电源作用时:)12/()210()1()1(+-=i i解得:A i2)1(=,V i i i u 6321)1()1()1()1(==+⨯=当5A 电源作用时,由左边回路的KVL :02)5(12)2()2()2(=++⨯+i i i解得:A i1)2(-=,V i u 22)2()2(=-=所以: V u u u 8)2()1(=+=A i ii 1)2()1(=+=注意:受控源始终保留在分电路中。
第四章 电路定理习题

+ -
15V
解:求开路电压Uoc: 由于开路,I=0, 故有
U o c 1 0 0 .5 m ( 4 k 6 k )
外加电压求输入电阻 Req: 由除源等效电路,有
u 6 k ( i i ) 4 k i (6 6 4 ) k i (6 1 0 ) k i
由最大功率传 输定理可知 R=Ro =8 Pm =50W
R
+
40V
-
-
+ U -
8
60Ω Ro UOC
+ +
30Ω 80Ω 80Ω 100V -
例13:(1)求电阻R为多少时可获最大功率?
6I
PL (2)求此最大功率为多少?并求电源的效率. η = P s
+ + R U I 3Ω + 3V 6Ω
U Req + OC-
40 10 I A 75 3
3Ω
I
5Ω
画出戴维宁等效电路,并接入待求支路求响应。
-
-
40V
-
40V
+
-
+
40V
Req
6Ω
8Ω
10Ω
2Ω
3)含受控源电路分析
例10:图示电路,用戴维宁定理求电流I2。 解: 移去待求支路,有
(6 k 4 k ) I 4 k 10 m 2 kI
例14:(1)若在2-2’端接2电阻,则U1 = 3V, I2 = 1A (2)若2-2’端开路,则U1 = 5V 。试求2-2’以左电路 的戴维宁等效电路。其中N为纯电阻电路。
1 2
1
∧
2
《电路原理》第四章 电路定理

u
(2)
2i
(2)
2 (1) 2V
受控源始终 保留 2 5A + 1 u(2) + (2) 2i - -
u 6 2 8V
2
i 2 (1) 1A
1 u(1)+i (2) + (1) 2i - - +
i(1) + 画出分 10V 电路图 -
+
2A
1A
5
+
U0C
– b (1) 求开路电压Uoc
Req + Uoc –
5 15V
+
b
20 10 I 0.5 A 20
U oc 0.5 10 10 15V
(2) 求等效电阻Req
Req 10 // 10 5
定理的证明 ia
N
电 流 源 置 零 ' 则 替代
a N N' a + u' – b + u – b a i
端口 N中s
''
+
N0 Req
+ u'' – b a + u – b
i
u uoc u Req i ' '' uu u uoc Req i
i Req + Uoc –
N'
2 求戴维宁等效电路的一般步骤与方法
(1) 开路电压Uoc 的计算 戴维宁等效电路中电压源电压等于将外电路断开时的开 路电压Uoc,电压源方向与所求开路电压方向有关。计算 Uoc的方法视电路形式选择前面学过的任意方法,使易于计 算。 (2)等效电阻的计算 等效电阻为将一端口网络内部独立电源全部置零(电压源 短路,电流源开路)后,所得无源一端口网络的输入电阻。 常用下列方法计算:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章电路定理练习题
4-209、
4-2用叠加定理求题4-2图示电路中的I1。
I1
5Ω
3Ω
+
24V
6A
+
4I1
-
-
4-2
解:
I
/
1
5Ω3Ω
I
//
1
5Ω
3Ω
+
24V
+
4I
/ቤተ መጻሕፍቲ ባይዱ
1
6A
+
4I
//
1
--
-
解:(53)I14I124
I12A
5I13(6I1)4I10
I11.5A
I1I1I10.5A
4-210、用叠加定理求题4-3图示电路中的独立电压源和独立电流源发出的
4-208、
例4-4封装好的电路如图,已知下列实验数据:当uV
s1,is1A时,响应i2A,当
us1,is2A时,响应i1A,求:us3V,is5A时的电流i。
V
解:根据叠加定理,有:ik1isk2us
代入实验数据,得:
k
1
2k
1
k
2
k
2
2
1
解得:
k
1
k
2
1
1
因此:iisus352A
本例给出了研究激励和响应关系的实验方法。
功率。
答案I1=-50mA,I2=15mA,I3=60mA(2)电压源发出的功率为:P=25I1=-1.25W
4-204、
1
第四章电路定理练习题
4-205、求题3-22图示电路的电压U和电流I。
I
69
+
10V
-
3A
+U
-
I1
+
2I1
-
4
题3-22图
例4-4用叠加定理求图4-5(a)电路中电压u。
图4-5
第四章电路定理练习题
第4章电路定理
4-1XX简单题
4-2XX叠加定理
4-3XX戴维宁定理
4-201、试用叠加定理计算下图所示电路中US2=2V时,电压U4的大小。若
US1的大小不变,要使U4=0,则US2应等于多少?
答案U4=-0.4V,Us2=1.2V
4-202、电路如图所示。(1)用叠加定理求各支路电流;(2)求电压源发出的
功率。
4Ω
+
i
2V
2A2i4Ω
+-
-
题4-3图
4
第四章电路定理练习题
4-211、4-1用叠加定理求题4-1图示电流源两端的电压u。
4Ω
1Ω12A
+
6V
-+
u
5Ω2Ω
-
题4-1图
4-301、
答案
4-302、
答案I=0.75A
4-303、
5
第四章电路定理练习题
答案
4-304、
答案
4-305、
6
第四章电路定理练习题
解:画出独立电压源uS和独立电流源iS单独作用的电路,如图(b)和(c)所示。由此分别
求得u’和u”,然后根据叠加定理将u’和u”相加得到电压u
RRR
'4"24iuuu
SS
RRRR
2424
u
'
u
"
u
R
4
R
2
R
4
(uSR2iS)
4-206、例4-1利用叠加定理求图(a)所示电路中的电压U。
(a)(b)(c)
当10V电源作用时:i(1)(102i(1))/(21)
解得:i(1)2A,u(1)1i(1)2i(1)3i(1)6V
当5A电源作用时,由左边回路的KVL:2i(2)1(5i(2))2i(2)0
解得:i(2)1A,u(2)2i(2)2V
所以:uu(1)u(2)8V
i(1)(2)1
iiA
注意:受控源始终保留在分电路中。
答案
4-306、
答案
4-307、
7
解:首先画出分电路图如图(b)、(c)所示。
12(1)
当12V电压源作用时,应用分压原理有:34V
U
9
63(2)
当3A电流源作用时,应用分流公式得:36V
U
63
则所求电压:U462V
2
第四章电路定理练习题
4-207、
例4-2利用叠加定理求图(a)所示电路中的电压u和电流i。
(a)(b)(c)
解:首先画出分电路图如图(b)、(c)所示。
