数学建模作业题目
大学生数学建模练习题

大学生数学建模练习题一、线性规划问题假设你是一家制造公司的经理,公司生产两种产品A和B。
生产一个产品A需要3小时的机器时间和2小时的人工时间,产品B需要2小时的机器时间和4小时的人工时间。
公司每天有24小时的机器时间和40小时的人工时间可用。
如果产品A的销售价格是50元,产品B是80元,如何安排生产计划以最大化利润?二、排队论问题一家银行有3个服务窗口,平均每天接待200名顾客。
每名顾客的平均服务时间是5分钟。
假设顾客到达银行是随机的,服从泊松分布,服务时间服从指数分布。
请计算银行的平均排队长度和顾客的平均等待时间。
三、库存管理问题一家零售商销售一种季节性产品,该产品的需求量在一年中波动很大。
产品的成本是每个20元,存储成本是每个每年2元,缺货成本是每个10元。
如果零售商希望在一年内保持至少95%的服务水平,应该如何确定最优的订货量和订货频率?四、网络流问题在一个供水系统中,有四个水库和五个城市。
水库1和2可以向城市A 供水,水库2和3可以向城市B供水,水库3和4可以向城市C和D供水。
每个水库的供水能力不同,每个城市的需求也不同。
如果需要确保所有城市的需求都得到满足,如何确定最优的供水方案?五、预测问题给定一个公司过去5年的季度销售额数据,使用时间序列分析方法预测下个季度的销售额。
请考虑季节性因素和趋势,并给出预测的置信区间。
六、优化问题一个农场主有一块矩形土地,打算围成一个矩形的牧场。
如果围栏的总长度是固定的,比如400米,如何确定牧场的长和宽,使得牧场的面积最大?七、多目标决策问题一家公司需要在多个项目中做出选择,每个项目都有不同的预期收益、风险和实施时间。
如果公司需要在风险和收益之间做出权衡,并且希望项目尽快完成,如何使用多目标决策方法来选择最合适的项目组合?通过解决这些练习题,大学生可以加深对数学建模的理解,提高分析和解决实际问题的能力。
希望这些练习题能够帮助学生在数学建模的道路上更进一步。
数学建模题目及答案

09级数模试题1. 把四只脚的连线呈长方形的椅子往不平的地面上一放,通常只有三只脚着地,放不稳,然后稍微挪动几次,就可以使四只脚同时着地,放稳了。
试作合理的假设并建立数学模型说明这个现象。
(15分)解:对于此题,如果不用任何假设很难证明,结果很可能是否定的。
因此对这个问题我们假设 :(1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言,方桌的腿是足够长的(4)方桌的腿只要有一点接触地面就算着地。
那么,总可以让桌子的三条腿是同时接触到地面。
现在,我们来证明:如果上述假设条件成立,那么答案是肯定的。
以长方桌的中心为坐标原点作直角坐标系如图所示,方桌的四条腿分别在A 、B 、C 、D 处,A 、B,C 、D的初始位置在与x 轴平行,再假设有一条在x 轴上的线ab,则ab 也与A 、B ,C 、D 平行。
当方桌绕中心0旋转时,对角线 ab 与x 轴的夹角记为θ。
容易看出,当四条腿尚未全部着地时,腿到地面的距离是不确定的。
为消除这一不确定性,令 ()f θ为A 、B 离地距离之和,()g θ为C 、D 离地距离之和,它们的值由θ唯一确定。
由假设(1),()f θ,()g θ均为θ的连续函数。
又由假设(3),三条腿总能同时着地, 故()f θ()g θ=0必成立(∀θ)。
不妨设(0)0f =,(0)0g >g (若(0)g 也为0,则初始时刻已四条腿着地,不必再旋转),于是问题归结为:已知()f θ,()g θ均为θ的连续函数,(0)0f =,(0)0g >且对任意θ有00()()0f g θθ=,求证存在某一0θ,使00()()0f g θθ=。
证明:当θ=π时,AB 与CD 互换位置,故()0f π>,()0g π=。
作()()()h f g θθθ=-,显然,()h θ也是θ的连续函数,(0)(0)(0)0h f g =-<而()()()0h f g πππ=->,由连续函数的取零值定理,存在0θ,00θπ<<,使得0()0h θ=,即00()()f g θθ=。
2023年全国数学建模题目

2023年全国数学建模题目
一、优化模型
题目:全球能源分配优化问题
问题描述:全球各国对能源的需求不断增长,而能源资源有限。
为了实现可持续发展,需要优化全球能源分配,确保各国都能获得适量的能源供应。
请运用优化模型和方法,设计一个全球能源分配方案,以满足各国能源需求,并尽量减少能源浪费和环境污染。
二、统计分析
题目:社交媒体用户行为分析
问题描述:社交媒体平台上积累了大量用户数据,包括用户发布的内容、关注对象、互动情况等。
请运用统计分析方法,分析社交媒体用户的偏好、行为模式和社交网络结构,为相关企业提供营销策略建议。
三、机器学习
题目:基于机器学习的文本分类问题
问题描述:文本数据包括各种主题,如政治、经济、文化等。
请运用机器学习算法,对给定的文本数据进行分类,并评估分类效果。
同时,请探讨如何提高分类准确率和泛化能力。
四、预测模型
题目:商品价格预测问题
问题描述:商品价格受到多种因素的影响,如市场需求、生产成本、政策因素等。
请运用预测模型和方法,预测未来一段时间内某种商品的价格走势,为投资者和企业提供决策依据。
五、决策分析
题目:企业投资决策问题
问题描述:企业需要在多个项目中做出投资决策,以实现利润最大化。
请运用决策分析方法,评估各项目的风险和收益,为企业制定最优投资策略。
六、系统动力学
题目:城市交通拥堵问题研究
问题描述:城市交通拥堵是一个复杂的问题,涉及多个因素之间的相互作用。
请运用系统动力学方法,建立城市交通拥堵问题的动力学模型,分析各因素之间的因果关系和动态变化规律,提出缓解交通拥堵的策略建议。
小学数学建模练习题

小学数学建模练习题在小学数学教学中,数学建模是一种培养学生综合应用数学解决实际问题的能力的有效方法。
通过数学建模,学生可以运用所学的数学知识和技能,将数学运用到生活实际中,培养他们的创新思维和问题解决能力。
为了提高学生的数学建模能力,以下是一些小学数学建模练习题,供大家练习和思考。
题目一:小明放风筝小明想放风筝,他站在一个长方形草坪的一角,正北方向有一面墙,南边是一条宽为10米的小溪,他希望风筝飞向墙上方,但是又不希望风筝落入小溪中。
现在假设整个草坪的长和宽分别是100米和50米,请问小明站在哪个位置放风筝比较好呢?题目二:水果销售某水果店的负责人想要通过一些促销活动提高水果的销量。
经过分析,他发现在夏季,顾客特别喜欢购买西瓜和橙子。
为了促进销售,他决定对这两种水果进行优惠。
西瓜的售价为每斤2元,而橙子的售价为每斤1元。
他希望考虑到顾客的购买力和需求情况,从而设置一个合理的促销策略,使得总销售额最大化。
请帮助他确定西瓜和橙子的最佳促销比例。
题目三:花坛设计小学的花坛设计已经老旧不堪,学校决定对花坛进行翻新。
花坛的形状为一个等腰梯形,底边长为4米,上底边长为2米,高为3米。
学校希望设计一个新的花坛,使得花坛内尽可能多地摆放花朵。
已知每平方米花坛能够容纳8朵花,请计算这个新花坛最多可以摆放多少朵花。
题目四:学校跑步比赛学校要举办一场跑步比赛,共有4个年级的学生参加,每个年级的学生人数分别为100人、150人、120人和80人,比赛规则是每个年级选择3名参赛选手代表该年级参加比赛。
为了公平起见,学校希望每个年级参加比赛的总成绩最好的选手之和尽可能接近。
请帮助学校确定每个年级的3名代表选手。
题目五:果园采摘小明去果园采摘水果,他发现果园里有苹果、橘子和桃子,他看到的苹果数是橘子数的2倍,橘子数又是桃子数的3倍。
小明准备采摘苹果和橘子,但是由于时间有限,他只能采摘400个水果,请问他应该采摘多少个苹果和多少个橘子才能使得采摘的水果总重量最大?以上是五道小学数学建模练习题,通过这些练习题,学生可以锻炼他们的数学思维和解决问题的能力。
简单数学建模100例

“学”以致用-----简单数学建模应用问题100例数学教学过程中学习了一个数学公式后,需要做大量的应用题,通过训练来加深理解所学公式。
但是在生活中又有多少实际问题是可以直接套用公式的呢?理想状态下的公式直接运用,在生产及生活中的实例是少之又少。
为此学生总感到学了数学没有什么实际用处,所以对学习数学少有兴趣。
数学建模的引入对培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径,让中职学生从中体会到数学是来源于生活并应用于生活的.数学建模是一种思维方式,它是一个动态的过程,通过此过程可以将一个实际的问题,经过模型准备、模型假设、模型构成、模型解析、模型检验与应用等五个具体步骤,转变为可以用数学方法(公式)来解决的,在理想状态下的数学问题,上述的整个流程统称为数学建模如果想解决某个实际问题(也许它和数学没有直接的关系),可以按下面流程对问题进行数学建模。
一.模型准备先了解该问题的实际背景和建模目的,尽量弄清要建模的问题属于哪一类学科的问题,可能需要用到哪些知识,然后学习或复习有关的知识,为接下来的数学建模做准备.由于人们所掌握的专业知识是有限的,而实际问题往往是多样和复杂的,模型准备对做好数学建模问题是非常重要的.二.模型假设有了模型准备的基础,要想把实际问题变为数学问题还要对其进行必要合理的简化和假设.明确了建模目的又掌握了相关资料,再去除一些次要因素.以主要矛盾为主来对该实际问题进行适当的简化并提出一些合理的假设。
模型假设不太可能一蹴而就,可以在模型的不断修改中得到逐步完善.三.模型构成在模型假设的基础上,选择适当的数学工具并根据已知的知识和搜集的信息来描述变量之间的关系或其他数学结构(如数学公式、定理、算法等).做模型构成时可以使用各种各样的数学理论和方法,但要注意的是在保证精度的条件下尽量用简单的数学方法是建模时要遵循的一个原则.四.模型解析在模型构成中建立的数学模型可以采用解方程、推理、图解、计算机模拟、定理证明等各种传统的和现代的数学方法对其进行求解,其中有些可以借助于计算机软件来做这些工作。
数学建模例题和答案

数学建模例题和答案
题目:
一个汽车公司拥有两个工厂,分别生产两种型号的汽车,A型和B型,每种型号的汽车都有一定的销售价格。
现在,该公司需要在两个工厂中生产A型和B型汽车,使得总收入最大。
答案:
1、建立数学模型
设A型汽车在第一个工厂生产的数量为x,在第二个工厂生产的数量为y,A型汽车的销售价格为a,B型汽车的销售价格为b,则该公司的总收入可以表示为:
总收入=ax+by
2、确定目标函数
由于题目要求使得总收入最大,因此可以将总收入作为目标函数,即:
最大化Z=ax+by
3、确定约束条件
由于两个工厂的生产能力有限,因此可以设置约束条件:
x+y≤M,其中M为两个工厂的总生产能力
4、求解
将上述模型转化为标准的数学规划模型:
最大化Z=ax+by
s.t. x+y≤M
x≥0,y≥0
由于该模型是一个线性规划模型,可以使用数学软件进行求解,得到最优解:
x=M,y=0
即在第一个工厂生产M件A型汽车,在第二个工厂不生产B型汽车,此时该公司的总收入最大,为Ma。
数学建模竞赛题目

数学建模竞赛题目
以下是某数学建模竞赛的部分题目,仅供参考:
1. 你是一位体育用品商店的经理,想要预测下个月篮球鞋的销售量。
你将如何利用历史销售数据和其他相关信息来建立预测模型?
2. 你是一位城市规划师,需要设计一个公共交通系统,以满足市民的出行需求。
你将如何利用数学模型来优化公交线路和站点设置?
3. 你是一位环保组织成员,想要评估某地区生态保护项目的成效。
你将如何利用数学模型来量化评估该项目的环境影响?
4. 你是一位投资经理,需要为你的客户制定一个投资组合方案。
你将如何利用数学模型来优化投资组合,以实现客户的投资目标?
5. 你是一位医生,想要预测某疾病患者的康复时间。
你将如何利用医学数据和数学模型来建立预测模型?
请注意,以上题目仅为示例,具体的数学建模题目可能因竞赛而异。
数学建模作业---优化模型

P104页,复习题题目:考虑以下“食谱问题":某学校为学生提供营养套餐,希望以最小的费用来满足学生对基本营养的需求按照营养学家的建设,一个人一天要对蛋白质,维生素A和钙的需求如下:50g蛋白质、4000IU维生素A和1000mg的钙,我们只考虑以不食物构成的食谱:苹果,香蕉,胡萝卜,枣汁和鸡蛋,其营养含量见下表。
制定食谱,确定每种食物的用量,以最小费用满足营养学家建议的营养需求,并考虑:(1)对维生素A的需求增加一个单位时是否需要改变食谱?成本增加多少?如果对蛋白质的需求增加1g呢?如果对钙的需求增加1mg呢?(2)胡萝卜的价格增加Ⅰ角时,是否需要改变食谱?成本增加多少?问题分析:(1)此优化问题的目标是使花费最小.(2)所做的决策是选择各种食物的用量,即用多少苹果,香蕉,胡萝卜,枣汁,鸡蛋来制定食谱。
(3)决策所受限制条件:最少应摄入的蛋白质、维生素和钙的含量(4)设置决策变量:用x1表示苹果的个数、x2表示香蕉的个数、x3表示胡萝卜的个数、x4表示枣汁的杯数量、x5表示鸡蛋的个数(5)x1个苹果花费10·x1角x2个香蕉花费15·x2角x3个胡萝卜花费5·x3角x4杯枣汁花费60·x4角x5个鸡蛋花费8·x5角目标函数为总花费金额:z=10·x1+15·x2+5·x3+60·x4+8·x5 (角)(6)约束条件为:最少摄入蛋白质的含量:0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥50最少摄入维生素A的含量:73x1+96x2+20253x3+890x4+279x5≥4000最少摄入钙的含量:10x1+15x2+5x3+60x4+8x5≥1000非负约束:x 1,x 2,x 3,x 4,x 5≥0优化模型:minz =10x 1+15x 2+5x 3+60x 4+8x 5s.t. 0.3x 1+1.2x 2+0.7x 3+3.5x 4+5.5x 5≥5073x 1+96x 2+20253x 3+890x 4+279x 5≥4000 9.6x 1+7x 2+19x 3+57x 4+22x 5≥1000 x 1,x 2,x 3,x 4,x 5≥0由线性规划模型的定义,容易得到线性规划的性质:1. 比例性 每个决策变量的对目标函数的“贡献”与该决策变量的取值成正比;每个决策变量对每个约束条件右端项的“贡献”,与该决策变量的取值成正比.2. 可加性 各个决策变量对目标函数的“贡献”,与其他决策变量的取值无关;各个决策变量对每个约束条件右端项的“贡献”,与其他决策变量的取值无关.3. 连续性 每个决策变量的取值是连续的. 考察本题,实际上隐含下面的假设 :1.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个(杯)的花费是与各自的用量无关的常数;苹果、香蕉、胡萝卜、枣汁、鸡蛋每个(杯)所包含的蛋白质、维生素、钙的含量是与各自的用量无关的常数.(线性规划性质1—比例性)2.购买苹果、香蕉、胡萝卜、枣汁、鸡蛋每个(杯)的花费是与它们相互间用量无关的常数;苹果、香蕉、胡萝卜、枣汁、鸡蛋每个(杯)所包含的蛋白质、维生素A 、钙的含量是与它们相互间的用量无关的常数. (线性规划性质2—可加性)3. 购买苹果、香蕉、胡萝卜、枣汁、鸡蛋的数量都是实数. (线性规划性质3—连续性) 模型求解:(决策变量是5维的,不适用图解法求解模型)软件求解:线性规划模型:min z=10x1+15x2+5x3+60x4+8x5s.t. 0.3x1+1.2x2+0.7x3+3.5x4+5.5x5≥5073x1+96x2+20253x3+890x4+279x5≥40009.6x1+7x2+19x3+57x4+22x5≥1000x1,x2,x3,x4,x5≥0模型全局最优解:(Global optimal solution)x1=0x2=0x3=49.38272x4=0x5=2.805836z的最优值为269.3603角用LINGO 软件求解,得到如下输出:结果分析:1. 3个约束条件的右端项可视为3种资源:蛋白质含量、维生素A 含量、钙含量.LINGO 的输出项Row Slack or Surplus ,给出了3种资源在最优解下的剩余.2.目标函数可视为“支出(成本)”,紧约束的“资源”增加1单位时,“支出”的增加由LINGO 的输出项 Dual Price 给出。
数学建模大作业题目

(1) 用起泡法对10个数由小到大排序. 即将相邻两个数比较,将小的调到前头. (10个数字自己选择,方法要一般)(2)有一个45⨯矩阵,编程求出其绝对值最大值及其所处的位置. (用abs 函数求绝对值)(3)编程求201!n n =∑ ( 分别用for 和while 循环)(4)一球从100米高度自由落下,每次落地后反跳回原高度的一半,再落下. 求它在第10次落地时,共经过多少米?第10次反弹有多高? (5)有一函数2(,)sin 2f x y x xy y =++,写一程序,输入自变量的值,输出函数值,并画出其图像,加上图例和注释. (区间自理) (6) 建立一个脚本M 文件将向量a,b 的值互换。
(7) 某商场对顾客所购买的商品实行打折销售,标准如下(商品价格用price 来表示): price<200 没有折扣; 200≤price<500 3%折扣; 500≤price<1000 5%折扣; 1000≤price<2500 8%折扣; 2500≤price<5000 10%折扣;5000≤price 14%折扣;输入所售商品的价格,求其实际销售价格。
(用input 函数) (8) 已知y ,22221111123y n=++++,当n=100时,求y 的值。
(9)画出分段函数2221y 1 122 1 2x x x x x x x ⎧<⎪=-≤<⎨⎪-+≥⎩的图像,并求分段函数在任意几点的函数值。
(用hold on 函数)(10) 给定5阶方阵,求方阵的行列式、特征值、迹、上三角元素的和。
(11) 输入40个数字,按照从小到大的顺序排列输出。
(12) 把当前窗口分成四个区域,在每个区域中分别用不同的颜色和线形画sin ;tan y x y x==,x y e =和31y x x =++的图像。
(区间自理)(13) 对于,AXB YA B==,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,,求解X,Y ;(14) 如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,242679836B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求1122,*,.*,,,,T A B A B A B AB A B A A ---。
数学建模作业线性规划

数学建模(第 1 次作业)题目:线性规划工厂生产摘要:某工厂用三种原材料,,c,p,h混合调配出三种不同规格的产品A,B,D。
已知产品的规格要求,产品单价,每天能提供的原材料数量及原材料单价,分别见表1和表2.该厂应该如何安排,使得利润收入最大?Table: 1.产品规格要求与单价表假设一:每天没有原材料损耗假设二:生产的产品都能卖出去假设三:市场价格恒定(利润恒定)假设四:工厂能有效完成工程任务量正文:设产品A,B,D的每日产量分别为X1,X2,X3。
其中A产品需要原材料为X11,X12,X13。
产品B为X21,X22,X23。
产品D为X31,X32,X33。
厂家利润为Z元。
由上图所给表格1与表格2,给出利润表达式Zmax=50X1+35X2+25X3-(X11+X21+X31)*65-(X12+X22+X32)*25-(X13+X23+X33)*35由A,B,D,原材料生产要求给出限制条件X11≥50%X1X12≤25%X1X21≥25%X2X22≤50%X2X11+X21+X31≤100X12+X22+X32≤100X13+X23+X33≤60X1=X11+X12+X13X2=X21+X22+X23X3=X31+X32+X33X1,X2,X3,X11,X12,X13,X21,X22,X23,X31,X32,X33≥0由上述限制推出:-X11+1/2*X1≤0X12-1/4*X1≤0-X21+1/4*X2≤0X22-1/2*X2≤0X11+X21+X31≤100X12+X22+X32≤100X13+X23+X33≤60X1-(X11+X12+X13)=0X2-(X21+X22+X23)=0X3-(X31+X32+X33)=OX1,X2,X3,X11,X12,X13,X21,X22,X23,X31,X32,X33≥0将上述方程通过编程然后输入matlabe,得出答案-6.1000e+03编程输出结果截图程序:c=[50,35,25,-65,-25,-35,-65,-25,-35,-65,-25,-35];A=[1/2,0,0,-1,0,0,0,0,0,0,0,0;-1/4,0,0,0,1,0,0,0,0,0,0,0;0,1/4,0,0,0, 0,-1,0,0,0,0,0;0,-1/2,0,0,0,0,0,1,0,0,0,0;0,0,0,1,0,0,1,0,0,1,0,0;0,0 ,0,0,1,0,0,1,0,0,1,0;0,0,0,0,0,1,0,0,1,0,0,1];b=[0;0;0;0;100;100;60];Aeq=[1,0,0,-1,-1,-1,0,0,0,0,0,0;0,1,0,0,0,0,-1,-1,-1,0,0,0;0,0,1,0,0, 0,0,0,-1,-1,-1,0];beq=[0;0;0];vlb=[0;0;0;0;0;0;0;0;0;0;0;0];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)注:采用小四宋体、单位行距。
初中数学建模题目

初中数学建模题目一、代数方程建模1. 小明每天早上7点上学,他以每分钟70米的速度走到学校,需要30分钟。
请问小明家离学校的距离是多少?2. 一个化肥厂生产化肥,每生产一吨需要耗电40度。
如果电费每度为0.6元,那么生产100吨化肥需要多少电费?二、几何图形建模1. 一个矩形花园的长是15米,宽是8米。
要在花园四周种上花边,花边的总长度是多少?2. 一个三角形ABC的三边长分别为3、4、5厘米,求三角形的面积?三、概率统计建模1. 一盒子里有红球和白球共10个,其中红球有6个。
如果随机从盒子里摸出一个球,那么摸到红球的概率是多少?2. 小华在数学考试中得了85分,全班平均分是90分。
求小华的分数高于全班平均分的概率?四、函数关系建模1. 小明从家里出发去公园,走了1小时后,他走了3公里。
如果他的速度保持不变,请问他还需要多少时间才能到达公园?2. 一个水库的水位高度与降雨量有关,当降雨量为50毫米时,水位会上升5米。
求水库的水位高度与降雨量的函数关系。
五、三角函数建模1. 一个摩天轮的高度为40米,直径为50米。
当摩天轮转过一圈时,求最顶端点到地面的高度?2. 一个登山队要从山脚爬到山顶,已知山的斜度为60度,登山队爬了300米后,他们还有多远才能到达山顶?六、数列建模1. 一个自然数列的前两项分别为1和2,以后各项都是其前面各项的和。
求这个数列的第10项是多少?2. 一个商场销售某商品,每件商品的进价为8元,售价为10元。
每天售出50件,求一个月(30天)后,商场能赚多少钱?七、线性规划建模1. 某地计划建设一个生态公园,需要种上一些树木。
已知种一棵树需要花费100元,而生态公园的总预算是5000元。
问在满足预算限制的条件下,最多能种多少棵树?2. 某公司生产两种产品:产品A的单价为20元,利润率为20%;产品B的单价为15元,利润率为15%。
公司现有资金20万元,问应如何安排两种产品的生产量,才能使公司获得最大利润?。
数学建模c题 2023

数学建模c题 2023
2023年数学建模竞赛C题是:
题目:太空电梯
太空电梯是一种设想中的巨型建筑,其主体是一条长长的缆绳,一端固定在地球上,另一端固定在地球同步轨道的平衡物(如大质量卫星)上。
太空电梯作为运输通道,可实现人员和物资的低成本、快速运输。
问题:
1. 假设地球同步轨道的平衡物是一个质量为M = 5 × 10^5 kg 的静止卫星,地球质量为× 10^24 kg,半径为 6371 km,计算该平衡物离地面的高度。
2. 假设一根缆绳的长度为 L = 10^6 km,单位质量为 800 kg/m^3,总质量为M = 8 × 10^10 kg,计算该缆绳的直径。
3. 假设太空电梯的缆绳由纳米纤维制成,纳米纤维的杨氏模量为100 GPa,密度为× 10^4 kg/m^3,纳米纤维直径为 5 nm,纳米纤维的长度分布服从 Rician 分布,平均长度为 500 km,求纳米纤维的临界长度分布和平均
强度。
4. 考虑太空电梯的运行安全,应确保电梯在受到扰动时不会发生整体崩溃。
若太空电梯的缆绳受到质量为 m = 10^4 kg 的小物体的冲击,为了保证电梯的安全运行,求该物体冲击缆绳的速度最大值。
5. 基于以上分析和计算,给出太空电梯的设计方案和潜在风险。
数学建模题目及答案

09级数模试题1. 把四只脚的连线呈长方形的椅子往不平的地面上一放,通常只有三只脚着地,放不稳,然后稍微挪动几次,就可以使四只脚同时着地,放稳了。
试作合理的假设并建立数学模型说明这个现象。
(15分)解:对于此题,如果不用任何假设很难证明,结果很可能是否定的。
因此对这个问题我们假设 : (1)地面为连续曲面(2)长方形桌的四条腿长度相同(3)相对于地面的弯曲程度而言,方桌的腿是足够长的 (4)方桌的腿只要有一点接触地面就算着地。
那么,总可以让桌子的三条腿是同时接触到地面。
现在,我们来证明:如果上述假设条件成立,那么答案是肯定的。
以长方桌的中心为坐标原点作直角坐标系如图所示,方桌的四条腿分别在A、B、C、D 处,A、B,C、D的初始位置在与x 轴平行,再假设有一条在x 轴上的线ab,则ab 也与A、B,C、D 平行。
当方桌绕中心0旋转时,对角线 ab 与x 轴的夹角记为θ。
容易看出,当四条腿尚未全部着地时,腿到地面的距离是不确定的。
为消除这一不确定性,令()f θ为A、B 离地距离之和,()g θ为C、D 离地距离之和,它们的值由θ唯一确定。
由假设(1),()f θ,()g θ均为θ的连续函数。
又由假设(3),三条腿总能同时着地, 故()f θ()g θ=0必成立(∀θ)。
不妨设(0)0f =,(0)0g >g (若(0)g 也为0,则初始时刻已四条腿着地,不必再旋转),于是问题归结为: 已知()f θ,()g θ均为θ的连续函数,(0)0f =,(0)0g >且对任意θ有00()()0f g θθ=,求证存在某一0θ,使00()()0f g θθ=。
证明:当θ=π时,AB 与CD 互换位置,故()0f π>,()0g π=。
作()()()h f g θθθ=−,显然,()h θ也是θ的连续函数,(0)(0)(0)0h f g =−<而()()()0h f g πππ=−>,由连续函数的取零值定理,存在0θ,00θπ<<,使得0()0h θ=,即00()()f g θθ=。
数学建模练习题
数学建模练习题数学建模习题题⽬11. 在超市购物时你注意到⼤包装商品⽐⼩包装商品便宜这种现象了吗。
⽐如洁银⽛膏50g装的每⽀元,120g装的每⽀元,⼆者单位重量的价格⽐是:1.试⽤⽐例⽅法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由⽣产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正⽐,有的与表⾯积成正⽐,还有与w⽆关的因素。
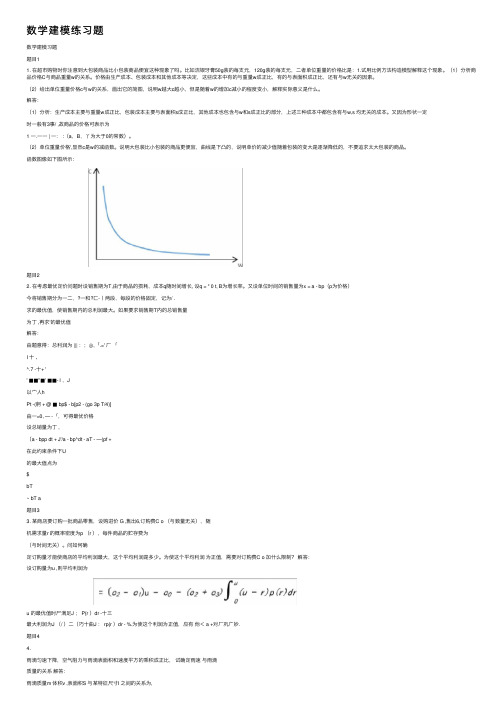
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越⼤c越⼩,但是随着w的增加c减⼩的程度变⼩,解释实际意义是什么。
解答:(1)分析:⽣产成本主要与重量w成正⽐,包装成本主要与表⾯积s成正⽐,其他成本也包含与w和s成正⽐的部分,上述三种成本中都包含有与w,s 均⽆关的成本。
⼜因为形状⼀定时⼀般有3事/ ,故商品的价格可表⽰为1 ⼀.⼀⼀ | ⼀: :(a,B,丫为⼤于0的常数)。
(2)单位重量价格',显然c是w的减函数。
说明⼤包装⽐⼩包装的商品更便宜,曲线是下凸的,说明单价的减少值随着包装的变⼤是逐渐降低的,不要追求太⼤包装的商品。
函数图像如下图所⽰:题⽬22. 在考虑最优定价问题时设销售期为T,由于商品的损耗,成本q随时间增长, 设q = * 0 t, B为增长率。
⼜设单位时间的销售量为x = a - bp(p为价格)今将销售期分为⼀⼆,?⼀和?⼕-⼁两段,每段的价格固定,记为/ .求的最优值,使销售期内的总利润最⼤。
如果要求销售期T内的总销售量为丁 ,再求'的最优值解答:由题意得:总利润为 ||| :;◎,「.=' ⼚「I ⼗、^.7 -⼗+ '' ■■''■' ■■- l ,J以⼧⼈hPt -(舸 + @ ■ bp$ - b[p2 - (go 3p T/4)]由⼀=0, — -「,可得最优价格设总销量为丁 ,〔a - bpp dt + J'/a - bp^dt - aT - —(pf +在此约束条件下U的最⼤值点为$bT~ bT a题⽬33. 某商店要订购⼀批商品零售,设购进价 G ,售出6,订购费C o (与数量⽆关),随机需求量r 的概率密度为p (r ),每件商品的贮存费为(与时间⽆关)。
数学建模试题(带答案)大全

(14 分)
得分
四、(满分 10 分) 雨滴的速度 v 与空气密度 、粘滞系数 和重力加速度 g 有关,其中粘
滞系数的量纲[ ]= L1MT 1 1,用量纲分析方法给出速度 v 的表达式.
解:设 v , , , g 的关系为 f ( v , , , g ) =0.其量纲表达式为
[ v ]=LM0T-1,
学分 5 4 4
4
数据结构
3
5
应用统计
4
6
计算机模拟 3
7
计算机编程 2
8
预测理论
2
9
数学实验
3
所属类别 数学 数学 数学;运筹学
数学;计算机 数学;运筹学
计算机;运筹学 计算机 运筹学 运筹学;计算机
先修课要求
微积分;线性代 数 计算机编程 微积分;线性代 数 计算机编程
应用统计 微积分;线性代 数
由 U 0, U 0 可得到最优价格:
p1
p2
1
T
1
3T
p1 2b [a b(q0
)] 4
P2 2b [a b(q0 4 )]
前期销售量
T、(2 a
0
bp1
)dt
后期销售量
T
T /2 (a p2 )dt
总销售量
Q0
=
aT
bT 2
(
p1
p2 )
在销售量约束条件下 U 的最大值点为
~p1
a b
Q0 bT
T 8
,
P~2
a b
Q0 bT
T 8
7. (1)雨水淋遍全身, s 2(ab bc ac) 2*(1.5*0.5 0.5*0.2 1.5*0.2) 2.2m2
数学建模13道题

数学建模13道题数学建模是数学中的一个分支,它是指将现实世界中的问题抽象成数学模型,并用数学方法来解决这些问题。
数学建模题一般包含数学模型的建立,问题的分析和求解等几个方面。
下面介绍13道数学建模题,希望读者可以从中得到启发。
题目一:如何预测股票价格?这是一个经典的数学建模题。
股票价格是由多种因素决定的,如市场供求关系、经济政策等。
数学建模者需要考虑这些因素,并根据历史数据建立合适的模型来预测未来的股票价格。
题目二:如何优化物流配送?对于物流配送问题,数学建模者需要考虑到多种因素,如配送距离、时间、运输工具等。
通过建立运输成本函数,制定合适的配送策略,可以实现物流配送的优化。
题目三:如何求解最优化问题?在最优化问题中,数学建模者需要考虑多种因素,如成本、效率、质量等。
通过建立目标函数、限制条件等方程,可以求得最优解。
题目四:如何优化网络布局?网络布局优化是一个复杂的问题。
数学建模者需要考虑到多种因素,如节点距离、带宽、延迟等。
通过建立合适的模型,可以制定出最优的网络布局方案。
题目五:如何预测自然灾害?自然灾害是不能预测的,但数学建模可以通过历史数据、气象预报等多种信息来建立模型,以预测未来可能发生的自然灾害,提前做好应对措施。
题目六:如何优化生产流程?生产流程优化需要考虑多种因素,如成本、效率、质量等。
数学建模者可以通过建立合适的模型,分析生产流程的瓶颈和优化空间,从而实现生产流程的优化。
题目七:如何优化城市规划?城市规划优化需要考虑多种因素,如人口密度、交通拥堵、环境保护等。
数学建模者可以通过建立合适的模型,预测城市未来的发展趋势,制定出最优的城市规划方案。
题目八:如何提高学生的学习成绩?学生的学习成绩受多种因素影响,如个人能力、学习环境、教学质量等。
数学建模者可以建立合适的模型,帮助学生发现自己的学习问题,并制定出最优的学习策略。
题目九:如何优化教学质量?教学质量优化需要考虑多种因素,如教师水平、教材质量等。
全国数学建模大赛题目

全国数学建模大赛题目
题目一:城市交通优化方案
某城市的交通状况日益拥堵,为了解决交通问题,需要制定一个交通优化方案。
假设该城市的道路网络呈现网状结构,拥有多个交叉口和道路,每个交叉口都有多个入口和出口道路。
现在需要你们设计一个算法,以找到最优的交通优化方案,使得城市的车辆数最小化,同时满足交通流量平衡和道路容量约束。
题目二:无人机配送路径规划
某公司使用无人机进行货物配送,无人机需要从指定的起点出发,依次经过多个目标点进行货物的投放,最后返回起点。
每个目标点有不同的货物量和不同的时间窗限制。
现在需要你们设计一个路径规划算法,以最小化无人机在配送过程中的总飞行距离,同时满足货物量和时间窗的要求。
题目三:自然灾害预测与应急响应
某地区常常受到洪水的威胁,为了及时应对洪水灾害,需要建立一个洪水预测和应急响应系统。
现有该地区多个监测站点,能够实时测量水位、降雨量等数据,并预测洪水的发生时间和范围。
现在需要你们设计一个预测模型,以准确预测洪水的发生时间和范围,并制定相应的应急响应措施,以最大程度地减少洪灾对人民生命和财产的威胁。
题目四:物流中心选址与配送路径规划
某公司计划在某区域新建一个物流中心,以提高货物配送的效率。
现在需要你们选取一个最佳的物流中心位置,并设计一个配送路径规划算法,以最小化货物配送的总距离和成本。
同时,
由于该区域存在不同的道路类型和限制条件,需要考虑不同道路类型的通行能力和限制,以确保货物配送的顺利进行。
简单的数学建模题目

简单的数学建模题目一、问题的提出假设我们有一个简单的金融问题:一家银行按照每天的存款利率给客户支付利息,这个利率是存款金额的1%。
客户每天会收到他们存款的利息,但是他们也可能会提取他们的存款。
如果一个客户决定提取他们的存款,他们将只能提取存款的本金,而不能提取利息。
假设一个客户存入1000元,并且决定在接下来的5天内每天提取100元。
我们要计算在5天后,这个客户在银行还有多少钱。
二、建立数学模型1、定义变量:假设客户最初存入的金额为 P元,每天提取的金额为 D元,经过的天数为 N天。
2、建立数学方程:根据题目,我们可以建立以下方程:P - N × D =最终余额这是因为客户每天都会提取D元的金额,并且总存款是P元。
N天后,他们将剩下P - N × D元。
3、填入已知数值:根据题目,P = 1000元,D = 100元,N = 5天。
所以方程变为:1000 - 5 × 100 =最终余额三、执行计算我们可以直接计算这个方程。
1000元减去5天的提取金额(5 × 100元)等于最终的余额。
计算结果为:最终余额 = 500元所以,5天后,客户在银行还有500元。
四、整合答案通过这个简单的数学模型,我们可以清楚地解释这个问题,并且计算出最终的余额。
这个模型还可以应用于其他类似的金融问题,例如不同的存款利率、不同的提取规则等等。
数学建模题目及答案数学建模100题数学建模是应用数学方法和计算机技术,对实际问题进行抽象和概括,建立数学模型的过程。
它是连接数学理论与实际问题的桥梁,能帮助我们更好地理解世界,解决现实问题。
以下是一百个数学建模题目及答案,供大家参考。
题目一:简单的线性回归模型给定一组一元线性回归的数据,解释数据之间的关系,并预测新的数据点的结果。
答案:我们通过最小二乘法拟合一条直线来描述数据之间的关系。
然后,我们使用这条直线来预测新的数据点。
题目二:逻辑回归模型给定一组二元分类的数据,用逻辑回归模型预测新的数据点的类别。
数学建模典型例题

典型例题1.报童每天订购的报纸,每卖出一份赢利a 元,如果卖不出去并将报纸退回发行单位,将赔本b 元.每天买报人数不定,报童订报份数如超过实际需要,就要受到供过于求的损失;反之,要受到供不应求的损失.设P (m )是售出m 份报纸的概率,试确定合理的订报份数,使报童的期望损失最小.解:设报童每天订购Q 份报纸,则其收益函数为⎩⎨⎧>≤--=Q m am Qm b m Q am m y ,,)()( 利润的期望为∑∑∞+==+-+=1)()(])[()]([Q m Qm m aQP m P bQ m b a m y E比较各个m 的)]([m y E 值,使其最大者即为所求.若m 的取值过多,可将)]([m y E 当成m 的连续函数或借鉴连续函数求极值的方法令0d )]([d =mm y E .2.血友病也是一种遗传疾病,得这种病的人由于体内没有能力生产血凝块因子而不能使出血停止.很有意思的是,虽然男人及女人都会得这种病,但只有女人才有通过遗传传递这种缺损的能力.若已知某时刻的男人和女人的比例为1:1.2,试建立一个预测这种遗传疾病逐代扩散的数学模型. 解:假设有α%的人患有血友病,并假设下一代与上一代虽人数可能不等,但所生男女比例一样.基于这样一个假设,不妨设下一代男女与上一代相同,设初始第一代男女分别占总人数的比例占总人数的比例为 a 0,b 0,由题设,a 0:b 0=1:1.2.注意到只有女人遗传血友病,由此,第一代将有%210αb 个女人及%210αb 个男人有血友病,血友病占总人数的百分比为 %2.22.1%0001αα=+=b a b c同理,第二代将有%21210αb ⋅个女人及%21210αb ⋅个男人有血友病,血友病占总人数的百分比为 %2.22.121%210002αα⋅=+=b a b c依次类推,第n 代将有%)21(0αb n个女人及%)21(0αb n个男人有血友病,血友病占总人数的百分比为%2.22.1)21(%)21(10001αα⋅=+=--n n n b a b c令∞→n ,则0→n c .3.某石油公司必须就下一个打井位置作出决定.如果打出来的井什么也没有(既无油也无天然气),则投资费用(打井费用)全部赔掉.如果打出来的是气井,则可以说是部分成功,如果打出来的是油井,则是完全成功.由于结果的不确定性,更由于做某种测试(取样)只能得到不完全的信息,因而作出决定是困难的.试建立一个数学模型,使公司的预期收益最大 解:设 B 1——预测是油井,B 2——预测是气井,B 3——预测是无油气井. 由于做取样只能得到不完全的信息,因此根据取样结果,计算出在B 1,B 2,B 3分别发生的条件下,B 1,B 2,B 3发生的概率.然后利用贝叶斯公式,计算出实际是油井、气井和废井情况下,而预测是B 1,B 2,B 3之一的概率值,若给出各种情况下的费用,计算出各个期望值即可.下面画出决策树(如图3).图34 假设有一笔1000万元的资金于依次三年年初分别用于工程A 和B 的投资.每年初如果投资工程A ,则年末以0.4的概率回收本利2000万元或以0.6的概率分文不收;如果投资工程B ,则年末以0.1的概率回收2000万元或以0.9的概率回收1000万元.假定每年只允许投资一次,每次只投1000万元;试确定第3年末期望资金总数为最大的投资策略.解: 建立决策树(如图4).0 2000 0 2000 10002000 4000 4000 3000图4在投资A 的决策树中,第一年投资A ,第二年投资B ,第三年投资B 的期望值最大. 在投资B 的决策树中(只在A 的决策树中②节点中的0.4,0.6分别换成0.1,0.9即可),可算得第一年投资B ,第二年投资B ,第三年投资B 的期望值是两个决策树中的最大者.5.某工程队承担一座桥梁的施工任务.由于施工地区夏季多雨,需停工三个月.在停工期间该工程队可将施工机械搬走或留在原处.如搬走,需搬运费1800元.如留原处,一种方案是花500元筑一护堤,防止河水上涨发生高水位的侵袭.若不筑护堤,发生高水位侵袭时将损失10000元.如下暴雨发生洪水时,则不管是否筑护堤,施工机械留在原处都将受到60000元的损失.据历史资料,该地区夏季高水位的发生率是25%,洪水的发生率是2%.试用决策树法分析该施工队要不要把施工机械搬走及要不要筑护堤?解:建立决策树模型如图5.图5 使用期望值法计算过程见图6.-1800 -500-60500-10000 -60000-1800 -500 -60500-10000-60000图6最优决策为:不必搬走机械,但要筑一个护堤,期望损失1335元.。
数学建模大作业题目

A 题:图书馆购书计划的制定现代化图书馆馆藏图书,主要目的不是为了收藏而是为了使用。
除了国家图书馆等特大型的图书馆以外,一般图书馆都有特定的服务群体,办馆宗旨就是要尽量好地为这些特定群体服务,提高馆藏资源的利用率、读者文献信息需求的满足率以及对图书馆服务功能的满意率。
图书馆每年用于购书的经费是有限的,如何合理分配使用,以便使有限的购书经费最大限度地发挥其特定的经济效益是图书馆工作的重要环节之一。
以学校图书馆为例,要实现办馆效益,必须做到入藏文献合乎本校教师、学生(有时也兼顾社会)的需求,使图书馆藏书结构(学科结构、文种结构、文献类型结构等)满足本校教学科研的要求,以求藏书体系与本校专业设置相适应。
所购图书要能够真实地反映读者的实际需要,使读者结构和藏书结构尽量吻合,以便减少读者借不到图书的现象,即降低读者被借的比率、增加满足率。
文献只有在流通中才能传播信息,产生效益。
文献资料得不到利用,购置文献资料所耗费的资金就体现不出其价值。
因此,图书馆在增加藏书规模的同时,要千方百计地把文献提供给读者,以增加图书的出借次数、出借时间以及在借图书的数量等,力求使有限的价值投入获得最大的办馆效益。
设某普通高校现有十个系:计算机科学与技术系,在校学生960 人,信息科学与工程系,在校学生900 人,信息与计算科学系,在校学生280 人,生物与制药工程系,在校学生1500 人,机电工程系,在校学生1440 人,建筑工程系,在校生960 人,外语系,在校学生720 人,法律系,在校学生460 人,新闻系,在校学生642 人,经济与管理系,在校学生2400 人。
此外,该校目前还有“药物分子设计及生物化工”和“土木建筑工程”2 个重点学科;“外国语言学及应用语言学”重点扶植学科以及“计算机科学与技术”、“市场营销”2 个重点专业。
该校图书馆每学年都要投入大量资金购置图书,图书覆盖全院各学科专业、具有较完整的中外文文献资源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模作业题目
1、深圳杯数学建模夏令营题目(3)
A题计划生育政策调整对人口数量、结构及其影响的研究
B题基因组组装
C题垃圾焚烧厂的经济补偿问题
2、吉林省第五届数学建模竞赛试题(2)
E题汽车租赁调度问题
F题:阶梯电价的效用分析
3、西北工业大学校数模竞赛试题(2)
A题西安市经开区公共自行车服务系统设计
B题食品价格变动分析
4、浙江大学城市学院第八届数学建模竞赛题目(2)
A题:外汇交易策略算法设计
B题:雾霾时空分布研究
5、井冈山大学第七届“井冈杯”数学建模竞赛试题(2)A题:课表编排问题
B题:客房预定的价格和数量问题
6、第十一届五一数学建模联赛(原苏北) (1)
B题:能源总量控制问题
7、第七届华中数学建模邀请赛赛题发布(2)
A题:加速度检测仪数据校正
B题:互联网搜索引擎的排名与设计
8、第十六届华东杯大学生数学建模邀请赛试题(3)
A电力网络
出租车打车模式的现状和未来
污水排放问题
9、南京信息工程大学第八届数学建模竞赛赛题(2)
A 污染气体的传播扩散
B 乳腺癌病因分析
10、北京交通大学数学建模校赛赛题(1)
电梯运输策略问题
11、武汉科技大学(2)
A题:装配线平衡问题的随机算例生成
B题:研究生研究水平的成因分析
12、广州六校数学建模联赛题目(2)
A题:中国GDP是否超过美国
B题:反服贸团体游行的人数
13、同济大学数学建模竞赛本科组赛题(2)
A题经济金三角
C题基因重排
14、甘肃农业大学第十届数学建模竞赛试题(1)
B题石油资源的开发与储备
15江西理工大学数学建模竞赛题目(1)
高层建筑火灾中的烟雾扩散建模与仿真
以上为2014年各校试题。
从以上题目或者自行收集2014各高校的数学建模比赛试题(与我院数学建模选拔赛相同的不算,自己收集以上题目的信息)中选一作一篇不少于15页的论文。
论文格式如下
●论文用白色A4纸单面打印;上下左右各留出至少2.5厘米的页边距;从上
面装订。
●论文第一页为搜索的高校姓名与学号、班级。
●论文题目和摘要写在论文第二页上,从第三页开始是论文题目内容与论文正
文。
●论文从第二页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从
“1”开始连续编号。
●论文题目用三号黑体字、一级标题用四号黑体字,并居中;二级、三级标题
用小四号黑体字,左端对齐(不居中)。
论文中其他汉字一律采用小四号宋体字,行距用单倍行距,打印时应尽量避免彩色打印。
●论文应该思路清晰,表达简洁(正文尽量控制在20页以内,附录页数不限)。
●引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的
参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
参考文献按正文中的引用次序列出,其中书籍的表述方式为:
[编号] 作者,书名,出版地:出版社,出版年。
参考文献中期刊杂志论文的表述方式为:
[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
参考文献中网上资源的表述方式为:
[编号] 作者,资源标题,网址,访问时间(年月日)。
数学公式必须用word自带的公式编辑器,不得用mathtype。
请于6月23日之前交打印稿作业。
电子稿发送格式
主题:数学建模附件:第一个同学的学号.rar
2011级数学建模作业
选择作业的题目是:
选择作业的学校是:
参赛队员信息:
班级学号姓名
队员1
队员2
队员3
日期:年月日
题目:
摘要。
