常微分方程数值解及其Matlab实现
重要:MATLAB常微分方程(组)数值解法

Matlab常微分方程求解问题分类
边值问题:
初值问题:
• 定解附加条件在自变量 的一端
• 一般形式为: y' f (x, y)
y(a)
y0
• 初值问题的数值解法一 般采用步进法,如 Runge-Kutta法
➢ 在自变量两端均给定附加 条件
y' f (x, y)
➢ 一般形式:y(a)y1, y(b)y2
1.根据常微分方程要求的求解精度与速度要求
求解初值问题:
y
'
y
2x y
y ( 0 ) 1
(0x1)
比较ode45和ode23的求解精度和速度
ode45和ode23的比较-1
function xODE clear all clc
format long
y0 = 1; [x1,y1] = ode45(@f,[0,1],y0); [x2,y2] = ode23(@f,[0,1],y0); plot(x1,y1,'k-',x2,y2,'b--') xlabel('x') ylabel('y')
rD = k(3)*C(2)-k(5)*C(4);
rE = k(4)*C(3)+k(5)*C(4);
% Mass balances dCdt = [rA; rB; rC; rD; rE];
三个串联的CSTR等温反应器(例4-3)
function IsothermCSTRs clear all clc CA0 = 1.8; % kmol/m^3 CA10 = 0.4; % kmol/m^3 CA20 = 0.2; % kmol/m^3 CA30 = 0.1; % kmol/m^3 k = 0.5; % 1/min tau = 2; stoptime = 2.9; % min [t,y] = ode45(@Equations,[0 stoptime],[CA10 CA20 CA30],[],k,CA0,tau); disp(' Results:') disp(' t CA1 CA2 CA3') disp([t,y]) plot(t,y(:,1),'k--',t,y(:,2),'b:',t,y(:,3),'r-') legend('CA_1','CA_2','CA_3') xlabel('Time (min)') ylabel('Concentration') % -----------------------------------------------------------------function dydt = Equations(t,y,k,CA0,tau) CA1 = y(1); CA2 = y(2); CA3 = y(3); dCA1dt = (CA0-CA1)/tau - k*CA1; dCA2dt = (CA1-CA2)/tau - k*CA2; dCA3dt = (CA2-CA3)/tau - k*CA3; dydt = [dCA1dt; dCA2dt; dCA3dt];
matlab 二阶常微分方程数值求解函数

matlab 二阶常微分方程数值求解函数【最新版】目录1.Matlab 二阶常微分方程数值求解函数概述2.二阶常微分方程的一般形式3.Matlab 中用于数值求解二阶常微分方程的函数4.数值求解的步骤5.结论正文Matlab 二阶常微分方程数值求解函数概述二阶常微分方程是指具有以下形式的微分方程:a * y"" + b * y" + c * y = f(x)。
其中,a、b、c 为常数,y 是函数,x 是自变量,f(x) 是已知函数。
求解这类微分方程对于许多实际问题具有重要意义,如物理、生物学、经济学等领域。
Matlab 作为一种广泛应用于科学计算的语言,提供了丰富的函数库用于数值求解二阶常微分方程。
二阶常微分方程的一般形式在 Matlab 中,二阶常微分方程的一般形式可以表示为:y"" + p(x) * y" + q(x) * y = r(x)其中,p(x)、q(x) 和 r(x) 是已知函数,y 是待求解的函数。
Matlab 中用于数值求解二阶常微分方程的函数Matlab 提供了多个函数用于数值求解二阶常微分方程,如 ode45、ode23、ode113 等。
这些函数的用法及参数如下:- ode45:该函数是四阶龙格库塔法(RK45)的实现,适用于大多数情况。
其用法为:解 = ode45(函数句柄,[a, b], [c, d], e, [f, g])其中,函数句柄是一个函数句柄,它接受自变量 x 和时间 t 作为参数,并返回因变量 y。
a 和 b 分别是函数 y 的第一个和第二个导数。
c 和 d 分别是函数 y 的第三个和第四个导数。
e 是初始条件。
f 和g 是边界条件。
- ode23:该函数是二阶龙格库塔法(RK23)的实现,适用于某些特殊情况。
其用法与 ode45 类似。
- ode113:该函数是十一阶龙格库塔法(RK113)的实现,适用于要求高精度解的情况。
matlab常微分方程的数值解法实验报告

实验四常微分方程的数值解法 指令:[t,y]=ode23(‘fun ’,tspan,yo) 2/3阶龙格库塔方法 [t,y]=ode45(‘fun ’,tspan,yo) 4/5阶龙格库塔方法 [t,y]=ode113(‘fun ’,tspan,yo) 高阶微分方程数值方法其中fun 是定义函数的文件名。
该函数fun 必须以为dx 输出量,以t,y 为输入量。
tspan=[t0 tfina]表示积分的起始值和终止值。
yo 是初始状态列向量。
考虑到初始条件有00d , (0)0,d d , (0)0.d SSI S S tI SI I I I tββμ⎧=-=>⎪⎪⎨⎪=-=≥⎪⎩ (5.24) 这就是Kermack 与McKendrick 的SIR 仓室模型. 方程(5.24)无法求出()S t 和()I t 的解析解.我们先做数值计算。
Matlab 代码为:function dy=rigid(t,y) dy=zeros(2,1); a=1; b=0.3;dy(1)=a*y(1).*y(2)-b*y(1); dy(2)=-a*y(1).*y(2);ts=0:.5:50; x0=[0.02,0.98];[T,Y]=ode45('rigid',ts,x0); %plot(T,Y(:,1),'-',T,Y(:,2),'*') plot(Y(:,2),Y(:,1),'b--') xlabel('s') ylabel('i')任务:1 画出i (t ),2分析各参数的影响例57:求解两点边值问题:0)5(,0)1(,32==='-''y y x y y x 。
(注意:相应的数值解法比较复杂)。
y=dsolve('x*D2y-3*Dy=x^2','y(1)=0,y(5)=0','x') ↙ y =-1/3*x^3+125/468+31/468*x^4例:用数值积分的方法求解下列微分方程 π21''2t y y -=+设初始时间t0=0;终止时间tf=3*pi ;初始条件0|',0|00====x x y y 。
MATLAB常微分方程的数值解法

MATLAB常微分⽅程的数值解法MATLAB常微分⽅程的数值解法⼀、实验⽬的科学技术中常常要求解常微分⽅程的定解问题,所谓数值解法就是求未知函数在⼀系列离散点处的近似值。
⼆、实验原理三、实验程序1. 尤拉公式程序四、实验内容选⼀可求解的常微分⽅程的定解问题,分别⽤以上1, 4两种⽅法求出未知函数在节点处的近似值,并对所求结果与分析解的(数值或图形)结果进⾏⽐较。
五、解答1. 程序求解初值问题取n=10源程序:euler23.m:function [A1,A2,B1,B2,C1,C2]=euler23(a,b,n,y0)%欧拉法解⼀阶常微分⽅程%初始条件y0h = (b-a)/n; %步长h%区域的左边界a%区域的右边界bx = a:h:b;m=length(x);%前向欧拉法y = y0;for i=2:my(i)=y(i-1)+h*oula(x(i-1),y(i-1));A1(i)=x(i);A2(i)=y(i);endplot(x,y,'r-');hold on;%改进欧拉法y = y0;for i=2:my(i)=y(i-1)+h/2*( oula(x(i-1),y(i-1))+oula(x(i),y(i-1))+h*(oula(x(i-1),x(i-1))));B1(i)=x(i);B2(i)=y(i);endplot(x,y,'m-');hold on;%欧拉两步公式y=y0;y(2)=y(1)+h*oula(x(1),y(1));for i=2:m-1y(i+1)=y(i-1)+2*h*oula(x(i),y(i));C1(i)=x(i);C2(i)=y(i);endplot(x,y,'b-');hold on;%精确解⽤作图xx = x;f = dsolve('Dy=-3*y+8*x-7','y(0)=1','x');%求出解析解y = subs(f,xx); %将xx代⼊解析解,得到解析解对应的数值plot(xx,y,'k--');legend('前向欧拉法','改进欧拉法','欧拉两步法','解析解');oula.m:function f=oula(x,y)f=-3*y+8*x-7;2. 运算结果A1,A2为前向欧拉法在节点处的近似值,B1,B2为改进的欧拉法在节点处的近似值,C1,C2为欧拉公式法在节点处的近似值。
MATLAB应用第8章 常微分方程的数值求解
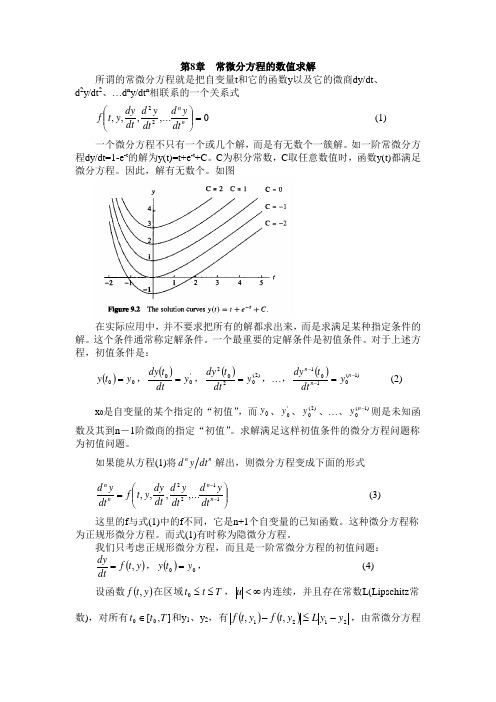
第8章 常微分方程的数值求解所谓的常微分方程就是把自变量t 和它的函数y 以及它的微商dy/dt 、d 2y/dt 2、…d n y/dt n 相联系的一个关系式0,...,,,22=⎪⎪⎭⎫ ⎝⎛n n dt y d dt y d dt dy y t f (1) 一个微分方程不只有一个或几个解,而是有无数个一簇解。
如一阶常微分方程dy/dt=1-e -t 的解为y(t)=t+e -t +C 。
C 为积分常数,C 取任意数值时,函数y(t)都满足微分方程。
因此,解有无数个。
如图在实际应用中,并不要求把所有的解都求出来,而是求满足某种指定条件的解。
这个条件通常称定解条件。
一个最重要的定解条件是初值条件。
对于上述方程,初值条件是:()00y t y =,()'00y dt t dy =,())2(0202y dt t dy =,…,())1(0101---=n n n y dt t dy (2) x 0是自变量的某个指定的“初值”,而0y 、'0y 、)2(0y 、…、)1(0-n y 则是未知函数及其到n -1阶微商的指定“初值”。
求解满足这样初值条件的微分方程问题称为初值问题。
如果能从方程(1)将n n dt y d 解出,则微分方程变成下面的形式⎪⎪⎭⎫ ⎝⎛=--1122,...,,,n n n n dt y d dt y d dt dy y t f dt y d (3) 这里的f 与式(1)中的f 不同,它是n+1个自变量的已知函数。
这种微分方程称为正规形微分方程。
而式(1)有时称为隐微分方程。
我们只考虑正规形微分方程,而且是一阶常微分方程的初值问题: ()y t f dtdy,=,()00y t y =, (4) 设函数()y t f ,在区域T t t ≤≤0,∞<u 内连续,并且存在常数L(Lipschitz 常数),对所有],[00T t t ∈和y 1、y 2,有()()2121,,y y L y t f y t f -≤-,由常微分方程理论得知,初值问题(4)在区间[t 0, T]有唯一解,且连续可微。
常微分方程数值解及其Matlab实现

高振荡微分方程是指其解具有高振荡性的一类微分方程,在分子动力学、天体力学、量子化学以及原子物理等方面有着广泛的应用。因此,研究其 数值解法具有重要意义。然而对于高振荡微分方程,一般的数值解法难以给出好的计算结果。
设计数值计算格式的一个基本想法是数值解法保持原问题的基本特征。对于Hamilton方程,Hamilton函数(通常表示能量)为守恒量。按照上述原则 ,数值解法也应较好地保持这一性质。
万方数据
一b一
科技信息
博士·专家论坛
在儿=y(_)前提下,将岛,心作泰勒屉开,则
尼。=/(%,%) ☆:=,(%+自,此+胁:,)=,(%,")+妩+^墨‘+o(^2)
=y’(_)+咖”(“)+D(^2) 以+.=n+矗(y’(‘)+y’(矗)+砂”(%))/2+D(旷)
:,(矗)+吵-(矗)+嬖y”(‘)+。(矿)
— 万8一 方数据
常微分方程数值解及其Matlab实现
作者: 作者单位: 刊名:
英文刊名: 年,卷(期): 被引用次数:
武瑞婵, 邓黎 武瑞婵(襄樊学院数学系), 邓黎(华东交通大学)
科技信息(学术版) SCIENCE & TECHNOLOGY INFORMATION 2007,""(35) 1次
儿“=以+(向+2乞+2岛+缸)/6 屯=可(吒,此) 如=矿(%+五/2,咒+矗/2) 尼3=矿(■+厅/2,虬+屯/2) 尼4=矽(矗+厶,蚝+乜)
本文讨论主要以改进尤拉法(3)和标准四阶龙格库塔法(4)为例。 2利用_at Iab求解一阶方程初值问题¨1 2.1利用内嵌程序直接得到结果 一阶微分方程仞值问题的求解在liatlab中有非常简便易求的方法.而且由于Matlab中内嵌的微分方程初值问题的求解 方法足变步长的龙格库塔法,故而求解结果值得信赖.
matlab_常微分方程数值解法

dt 2
简朴问题可以求得解析解,多数实际问题靠数值求解 。
第4页
一阶常微分方程(ODE )初值问题 : ODE :Ordinary Differential Equation
dy
f
(x,
y)
dx
x0 x xn
y(x0 ) y0
数值解法就是求y(x)在某些分立旳节点 xn 上旳近似值 yn,用以近似y(xn)
x0
y0
x1 f y(x), x dx
x0
x2 f y(x), x dx
x1
y(x1) f y(x1), x1 h
第17页
同样,在[x0,xn+1] ,积分采用矩形近似,得:
y(xn1) y0
f xn1
x0
y(x), x dx
y(xn ) f y(xn ), xn h
yn y(xn )
第5页
2、欧拉近似办法
2.1 简朴欧拉(L.Euler, 1707-1783)办法。
dy
dx
f
(y, x)
y(x0 ) y0
欧拉数值算法就是由初值通过递推求解,递推求解
就是从初值开始,后一种函数值由前一种函数值得到。核 心是构造递推公式。
y0 y1 y2 yn
第6页
i 1,2,...
第36页
没有一种算法可以有效地解决所有旳 ODE 问题,因此 MATLAB 提供了多种ODE函数。
函数 ODE类
特点
阐明
型
ode45
非刚性 单步法;4,5 阶 R-K 措施;合计 大部分场合旳首选措施
截断误差为 (△x)3
ode23
非刚性 单步法;2,3 阶 R-K 措施;合计 使用于精度较低旳情形
matlab数值求解常微分方程快速方法

MATLAB是一种用于科学计算和工程应用的高级编程语言和交互式环境。
它在数学建模、模拟和分析等方面有着广泛的应用。
在MATLAB 中,常微分方程的数值求解是一个常见的应用场景。
在实际工程问题中,通常需要对常微分方程进行数值求解来模拟系统的动态行为。
本文将介绍MATLAB中对常微分方程进行数值求解的快速方法。
1. 基本概念在MATLAB中,可以使用ode45函数来对常微分方程进行数值求解。
ode45是一种常用的Runge-Kutta法,它可以自适应地选取步长,并且具有较高的数值精度。
使用ode45函数可以方便地对各种类型的常微分方程进行求解,包括一阶、高阶、常系数和变系数的微分方程。
2. 函数调用要使用ode45函数进行常微分方程的数值求解,需要按照以下格式进行函数调用:[t, y] = ode45(odefun, tspan, y0)其中,odefun表示用于描述微分方程的函数,tspan表示求解的时间跨度,y0表示初值条件,t和y分别表示求解得到的时间序列和对应的解向量。
3. 示例演示为了更好地理解如何使用ode45函数进行常微分方程的数值求解,下面我们以一个具体的例子来进行演示。
考虑如下的一阶常微分方程:dy/dt = -2*y其中,y(0) = 1。
我们可以编写一个描述微分方程的函数odefun:function dydt = odefun(t, y)dydt = -2*y;按照上述的函数调用格式,使用ode45函数进行求解:tspan = [0 10];y0 = 1;[t, y] = ode45(odefun, tspan, y0);绘制出解曲线:plot(t, y);4. 高级用法除了基本的函数调用方式外,MATLAB中还提供了更多高级的方法来对常微分方程进行数值求解。
可以通过设定选项参数来控制数值求解的精度和稳定性,并且还可以对刚性微分方程进行求解。
5. 性能优化在实际工程应用中,常常需要对大规模的常微分方程进行数值求解。
常微分方程数值解与matlab

其中,r a / v
d 2 - S0 2
令: dx p, dy
d 2 x dp 2 dy dy
dy dp r 2 y 1 p p ( d 2 S 2 ) S0 0 2 2 d S 0
dy dp r 2 y 1 p p (20) 0
当 y 0 时,
x ,缉私艇不可能追赶上走私船。
dx 1 20 r y r dy 2 y 20 x(20) 0
(b)用MATLAB软件求解析解
MATLAB软件5.3以上版本提供的解常微分方程解析解的指令是 Dsolve, 完整的调用格式是: dsolve('eqn1','eqn2', ...) 其中‘eqn1’,‘eqn2’, ...是输入宗量,包括三部分: 微分方程、初始 条件、指定变量,若不指定变量,则默认小写字母t为独立变量.书P-69 微分方程的书写格式规定:当y是因变量时,用“Dny”表示y的n阶导数. 例 求微分方程
a 2) r 1 , v 1 20r r 1 r r 1 r x 20 (1 r ) y 20 (1 r ) y 2 1 r2
当 y 0 时,
x
缉私艇不可能追赶上走私船。
1 1 2 3) r 1 , x 2 20ln y 40 y
M(x,y)
d
S0
追赶方向可用方向余弦表示为:%两点形成的向量的方向余弦
cosk
S0 at xk (S0 at xk )2 ( yk )2
yk (S0 at x)2 ( yk )2
用MATLAB求解微分方程

1. 微分方程的解析解
求微分方程(组)的解析解命令:
dsolve(‘方程1’, ‘方程2’,…‘方程n’, ‘初始条件’, ‘自变量’)
结 果:u = tan(t-c)
解 输入命令:dsolve('Du=1+u^2','t')
STEP2
STEP1
解 输入命令: y=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
导弹追踪问题
设位于坐标原点的甲舰向位于x轴上点A(1, 0)处的乙舰发射导弹,导弹头始终对准乙舰.如果乙舰以最大的速度v0(是常数)沿平行于y轴的直线行驶,导弹的速度是5v0,求导弹运行的曲线方程.又乙舰行驶多远时,导弹将它击中? 解法一(解析法)
由(1),(2)消去t整理得模型:
解法二(数值解)
结 果 为:x = (c1-c2+c3+c2e -3t-c3e-3t)e2t y = -c1e-4t+c2e-4t+c2e-3t-c3e-3t+c1-c2+c3)e2t z = (-c1e-4t+c2e-4t+c1-c2+c3)e2t
2、取t0=0,tf=12,输入命令: [T,Y]=ode45('rigid',[0 12],[0 1 1]); plot(T,Y(:,1),'-',T,Y(:,2),'*',T,Y(:,3),'+')
3、结果如图
图中,y1的图形为实线,y2的图形为“*”线,y3的图形为“+”线.
第六章 MATLAB教程常微分方程的数值解

0
-1
-2
-3
0
5
10
15
20
25
30
35
40
45
50
例3 x′ = y, y′ = 0.2 y sin t
(1)转化方程。
H=[0,100] t = 0, x = 0, y = 2
(2)建立文件,设文件名为dzdt03.m。 function dz=f(t,z) a=-0.2;
1.5 2
dz(1)=z(2);
(3)调用求解。 H=[0.1,30];z0=[0;0;0]; [t,z]=ode45('dzdt01',H,z0); plot(t,z(:,1),'m-')
1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2.5 x 10
5
plot(t,z(:,1),'m-')
0
5
10
15
20
25
30
例2 y′′ c(1 y 2 ) y′ + y = 0 H=[0,50] t = 0, y = 2, y′ = 1
30 20 10 0
dz(3)=c*z(2)-z(3)-z(1)*z(2); dz=[dz(1);dz(2);dz(3)]; (3)调用求解。
-10 -20 -30 20 10 60 0 -10 -20 -20 0 40 20
H=[0,80];z0=[0;0;0.222/10^15]; [t,z]=ode23('dzdt05',H,z0); plot3(z(:,1),z(:,2),z(:,3),'m-')
第六章 常微分方程的数值解
常见的近似数值求解方法有欧拉 折线法、阿当姆斯法、龙格-库塔 法与吉尔法。 不受方程类型的限制,可以求任 何形状常微分方程的特解,但求 出的解只能是数值的解函数。
常微分方程初值问题的数值求解及MATLAB实现

要】 本文主要讨论 了数值 求解常微 分方程初值 问题的 R ne K t 方 法和 A a s . g— ua u t dm 方法以及 MA L B 实现 , TA 并且给 出两个例 子 , 借
助 Maa 求解 . db 将数值结果用 图形直观的表示 。 增强 了文章 的可读性和直观性. 【 关键词】 常微 分方程初值 问题 ; 数值解 ; f Maa l b
1 常微分方程初值 问题 的数值解法
常微分方程初值问题的数值解法一般分 为两大类 . 即单步法和多 步法 . 所谓单步法是 指这类 方法在计算 ‰。 时只用 到前一步的 ‰这个 算法 的代表是 R n e K t 法 . u g— u a 法关于初值是稳 定 的, u g— ut a R ne K t 方 t 每 步的步长可 以独立选取 . 四阶显式 R n e K t 方法是求解普通 常 u g— u a t 微分 方程初值 问题 的重要方法 . 隐式 R ne K t 方法 是求解 刚性 而 u g— ut a 常微 分方 程初值 问题的重要方法 . 所谓多步法是指在计算 时, 除了 用到前一步 的值 之外, 还要用到 y p 12 … ,, > ) 一(= , , k O 的值, 这个算 法的代表就是 A a s d 方法. m 1 龙格一库塔方法( _ . 1 R K方法1 R K方法通过计算不 同点上 的函数值 。 这些函数值作线性组 — 并对 合, 造近似公式 , 构 利用待定系数 法确定近似 精度, 它是非线性 高阶单 步法 . 事实上,u g — u a 以看作在 ( , + 上取若干条 积分曲线 的 R neK t 可 t ) 若干个点 的切线斜率, 再进行一次( 或多次) 算术( 或NC ) Z 平均后产生 的 新斜率, 再按这个斜率从 ( ,m出发, £ y) 以直线带曲线 向前推进一步 的过
常微分方程数值解及其MATLAB实现

常微分方程数值解及其MATLAB实现常微分方程是数学中的一个重要分支,研究的是含有导数或微分的方程。
由于常微分方程往往难以求得精确解,因此数值解方法成为研究常微分方程的重要手段之一、本文将介绍常微分方程的数值解方法,并给出MATLAB实现。
首先介绍欧拉法,该方法是最简单的一种数值解法。
对于形如y'=f(x,y)的一阶常微分方程,将自变量x的范围分割为若干小区间,设步长为h。
在每个区间内,通过近似斜率来估计下一个点的函数值。
具体的递推关系式为:y_{n+1}=y_n+h*f(x_n,y_n)其中,y_n表示第n个解,x_n表示第n个点,f(x,y)表示一阶常微分方程右侧的函数。
下面给出欧拉法的MATLAB实现代码:function y = euler_method(f, x_range, y0, h)x = x_range(1):h:x_range(2);y = zeros(size(x));y(1)=y0;for i = 1:length(x)-1y(i+1)=y(i)+h*f(x(i),y(i));endend使用该函数只需提供函数句柄f,自变量范围x_range,初始条件y0和步长h即可。
函数返回数值解y。
改进欧拉法是对欧拉法的一种改进,通过使用函数连续两个点的斜率来估计下一个点的函数值。
具体的递推关系式为:y_{n+1}=y_n+h/2*[f(x_n,y_n)+f(x_{n+1},y_n+h*f(x_n,y_n))]下面给出改进欧拉法的MATLAB实现代码:function y = improved_euler_method(f, x_range, y0, h)x = x_range(1):h:x_range(2);y = zeros(size(x));y(1)=y0;for i = 1:length(x)-1k1=f(x(i),y(i));k2=f(x(i+1),y(i)+h*k1);y(i+1)=y(i)+h/2*(k1+k2);endend四阶龙格-库塔法是一种更精确的数值解法,通过使用函数四个点的斜率来估计下一个点的函数值。
常微分方程数值求解 MATLAB 求解

dsolve 举例
例:[x,y]=dsolve('Dx+5*x=0', 'Dy-3*y=0', ...
'x(0)=1', 'y(0)=1', 't') sol = dsolve('Dx+5*x=0', 'Dy-3*y=0', ...
'x(0)=1', 'y(0)=1', 't') 这里返回的 sol 是一个 结构类型 的数据 sol.x % 查看解函数 x(t) sol.y % 查看解函数 y(t)
常微分方程数值求解
—— MATLAB 求解
Matlab 解初值问题函数
用 Maltab自带函数 解初值问题
求解析解:dsolve
求数值解:
ode45、ode23、 ode113、ode23t、ode15s、 ode23s、ode23tb
2
符号求解
符号求解
dsolve
3
dsolve 求解析解
如果省略自变量,则默认自变量为 t
dsolve('Dy=2*x','x'); % dy/dx = 2x
dsolve('Dy=2*x');
% dy/dt = 2x
若找不到解析解,则提出警告,并返回空解。
5
dsolve 的使用
使用符号方程
导数:diff,如 diff(y),diff(y,2) 等号:== 必须声明应变量与自变量!
求解析解:dsolve
y=dsolve('eq1','eq2', ... ,'cond1','cond2', ... ,'v')
常微分方程的数值解的matlab命令实现方法

常微分方程的数值解的matlab命令实现方法常微分方程的数值解在 MATLAB 中可以通过 ode 函数或 dsolve 函数进行求解。
其中,ode 函数可以求解一阶常微分方程,而 dsolve 函数可以求解二阶及以上的常微分方程。
下面是具体的实现方法:1. 一阶常微分方程的求解对于一阶常微分方程,可以使用 ode 函数求解。
假设我们要求解的常微分方程为:dx/dt = f(x, t)可以使用以下命令进行求解:y0 = [a, 0]; % 初值条件tspan = [0, 20]; % 时间区间[t, y] = ode45(@(t, y) odefun(t, y, a), tspan, y0); % 求解其中,odefun 函数用于定义常微分方程的解,它是一个自定义函数,其形式可以为:dy/dt = f(t, y)其中,dy 是 y 的求导,f(t, y) 是常微分方程的系数矩阵。
在 MATLAB 中,可以使用 dy[] 函数来计算 y 的求导,例如:dy = dy[](t, y);最后,使用 ode45 函数求解常微分方程的解,其中 tspan 是时间区间,y0 是初值条件。
2. 二阶常微分方程的求解对于二阶常微分方程,可以使用 dsolve 函数求解。
假设我们要求解的二阶常微分方程为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0可以使用以下命令进行求解:syms t pqr;y0 = [a1, a2, a3]; % 初值条件[t, y] = dsolve(@(t, y) dy0(t, y), t, y0); % 求解其中,dy0 函数用于定义二阶常微分方程的解,其形式可以为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0其中,d2y/dt2 是 y 的二阶求导,其它项是 y 的求导。
在 MATLAB 中,可以使用 dy0[] 函数来计算 y 的二阶求导。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高振荡微分方程是指其解具有高振荡性的一类微分方程,在分子动力学、天体力学、量子化学以及原子物理等方面有着广泛的应用。因此,研究其 数值解法具有重要意义。然而对于高振荡微分方程,一般的数值解法难以给出好的计算结果。
设计数值计算格式的一个基本想法是数值解法保持原问题的基本特征。对于Hamilton方程,Hamilton函数(通常表示能量)为守恒量。按照上述原则 ,数值解法也应较好地保持这一性质。
j或+·2虬+6(¨一2_7")
(3)
ln+,=虬+Ⅱ(¨一2矗/%)+(只+。一2矗/只+.)],2
定理改进尤拉法的精度是二阶的. 证明对(3)作如下变形
f%+。=%+向(^十如)/2 {毛=厂(_,儿) . 【屯=厂(‰。M+饨)
基金项目,目孪自燕科学基仝啊目膏助(批准号。70371063) 作者简介-武瑞蝉,士,讲师。主薹研宽期碱为复杂康垃、并行计算午
2.2根据数值解法的思想编程实现
对于一阶微分方程的初值问题
』y’一砂2(o≤x≤5)
(6)
、
7
ly(o)=2
运用改进尤拉法和四阶龙格库塔法求解程序如下:
(”改进尤拉法
建立如下H文件:
一
Ⅱ=O:
6=5:
月=120:
M=0:
y"=2;
矗=(6一日)/一; 向,,=l:以 yp=”一h’xH+yn’y% xn=Ⅺl十k
科技信息
博士·专家论坛
常微分方程数值积及其Matlab实坝
襄类学院数学系 武瑞蝉华东交通大学 邓黎
[摘要]本文对常豢分方程初值问道竹薮值解法作1进一步探讨,并运用Manab对其中较难以求解的疫进尤拉法和 四阶龙格库塔法进行编程实现,程序简洁、直观,求并速度快,方法实用性较强. [关键词]擞分方程数值解法M“lBb
2.期刊论文 阳莺.YANG Ying 应用Matlab辅助微分方程数值解法教学 -桂林电子科技大学学报2007,27(4)
灵活运用Matlab软件中的一些科学计算的工具箱能对微分方程数值解法这门课程的教学起到很好的辅助作用.通过带有点源奇性的泊松方程为例,阐 述了利用Matlab中的"pdetool"工具箱来实现有限元方法求解这一偏微分方程的具体步骤.实例表明,利用Matlab软件中的工具箱来辅助微分方程数值解法 教学,有助于学生进一步深入学习算法,也有益于教师在课堂有限的时间内,传授更为丰富的知识和提供更多的信息.
本文介绍了Hamilton方程的性质、辛几何算法、对称方法、Magnus展开和Neumann展开方法。在Magnus展开和Neumann展开方法中,迭代都起着重要 作用,我们考虑了利用迭代法构造高振荡微分方程的数值解法。对于基于迭代的数值解法,以FPU问题为例进行了数值实验,实验显示,该方法可给出较 好的数值结果。
1一阶微分方程初值问题的数值解法 对于一阶方程的初值问题
』-y:2f(x,y)(口≤x≤6)
ly(xo)2%
从理沦上说,只要函数,(x,y)适当光滑,譬如关于,满足李氏条件
厂(x,y)一厂(x,歹)l≤三Iy一歹
就可以保证初值问题(1)的解y=y(x)存在且惟一.
求解问题(1)的数值解法又可称之为差分方法,因为常用的数值解法,如尤拉法,改进尤拉挂,龙格厍培珐等等本质上 均是将导数化为差商来做近似。
万方数据
一b一
科技信息
博士·专家论坛
在儿=y(_)前提下,将岛,心作泰勒屉开,则
尼。=/(%,%) ☆:=,(%+自,此+胁:,)=,(%,")+妩+^墨‘+o(^2)
=y’(_)+咖”(“)+D(^2) 以+.=n+矗(y’(‘)+y’(矗)+砂”(%))/2+D(旷)
:,(矗)+吵-(矗)+嬖y”(‘)+。(矿)
£盯d
当迭代次数盯=20时获得计算结果:Jw=O.07692668513821,比运用改进尤拉法迭代120步的效果都要好得多; 而尚迭代次数胛=120时,迭代结果J啊=O.07692307941295基本已达到精确解.
3结果分析 对问题(5)的求解简单方便,但难于体现求解的具体思想;对于问题(6)的求解运用编程实现,从实验角度来帮助理解 理论知识,不仅可以深入掌握求解方法的思想,而且还可以提高实践动手能力.对于数学教学的改进有很大帮助。 闷题(6)中,初值问题的糟确解为.”玎=O.07692307…,改进尤拉法在迭代到120步时误差还较大.迭代到5000步 时误差较小,但与精确解仍有出入,而且从迭代过程来看,迭代次数门越大.收敛速度越慢,效果不很显著.而四阶龙格库 塔法迭代20步的结果远远好于改进尤拉法选代120步的结果,当它迭代到120步时已跟精确解非常接近。故而龙格库塔法不 仅得到的解比改进尤拉法准确得多,而且收敛速度非常快,确实足一种很好的算法。但惟一的不足是计算量大,这一对矛盾很 难解决。
参考文献 【1】王能超.数值分析简明教程.北京:高等教育出版社,2003.97一124 【2】崔国华.计算方法.武汉:华中科技大学出版社,1996.89—119 【3】华中理工大学数学系.计算方法.北京:高等教育出版社,1999.105—126 【4】李庆扬,王能超,易太义.数值分析.武汉:华中理工大学出版社,1987.102—291 15l苏全明,阮洗勇.卧TL^B6.1实用指南.北京:电于工业出版社,2002.337—343 16】桂现才,刁群.解线性方程组的Matlab浩.湛江师范学院学报,2003,24(6):14~18
— 万8一 方数据
常微分方程数值解及其Matlab实现
作者: 作者单位: 刊名:
英文刊名: 年,卷(期): 被引用次数:
武瑞婵, 邓黎 武瑞婵(襄樊学院数学系), 邓黎(华东交通大学)
科技信息(学术版) SCIENCE & TECHNOLOGY INFORMATION 2007,""(35) 1次
O.4000 1t3416
O.6000 1.4832
O.8000 1.6125
1.OOOO J.7321
此结果与四阶龙格库塔法求解结果相同,比改进尤拉法求解结果要精确得多.运用内建函数直接求解最大的优点是简洁 方便,只要依照函数调用格式调用即可,但是对于理解数值解法的思想没有太大帮助,故而要体现数值解法的具体思想,可以 通过编写程序来实现.
常微分方程的求解是现代科学研究和工程技术中经常遇到的实际问题,然而,从实际问题中建立出来的微分方程往往具有 非常复杂的形式,有些解析式难以计算,有些则根本不能用解析式来表达,所以利用数值解法“1。求解实际问题就显得非常重 要。本文在总结常微分方程数值解法的基础上给出了Matlab“1求解常微分方程的多种方法.并对其中较为复杂的改进尤拉法和 四阶龙格库塔法给出了Matlab程序.
4.期刊论文 张宏伟 注重培养研究能力的《微分方程数值解法》课程教学研究与实践 -大学数学2006,22(6)
论述了注重培养研究能力的教学的重要性,数学专业基础课教学在研究能力培养中的作用,在《微分方程数值解法》课程教学中的体会,以及关于《微 分方程数值解法》课程教学进一步改进的探讨.
5.学位论文 李晓红 常微分方程数值解法及其应用 2008
本文系统地介绍了Hamilton方程的性质、辛几何算法及对称、组合、分裂数值方法。主要讨论了形如(x)+Ω2x=g(x)(g(x)=-аU/аx)的一类高 振荡微分方程。此类方程可以写成Hamilton方程,相应的Hamilton函数为守恒量。FPU问题可以表示成该类方程的形式。针对这类方程,本文给出了两个 新的对称数值格式。以FPU问题为例进行了数值实验,实验结果显示,这两个解法具有较好的能量保守性。
对于微分方程{y:i,(墨y)o≤x≤6),直接利用Matlab语言中的内建函数。‘I。23或。如45,按照调用格式 Iy【卅2%
[x,y】=o出45(’厂:x,虬)即可求出最终结果.其中,指函数名或所建立的M文件的文件名.x为已知的离散节点向量,
J七为初值a 例如:求解一阶微分方程初值问题:I.2x源自M=0:y聆=2;
厅=(6一d)/门; 南,f=1:”
女1.一^+M+"+"; M=M+矗/2: ^2=一^+xH+t朋+≈l/2)+(yH+t1/2);
.
女3=-厅’M+(”+t2/2)+("+t2/2);
xn=xn+h}2:
t4=·^4朋+("+☆3)+("+女3); "="+(≈l+2+^2+2+后3+女4)/6
参考文献(6条) 1.王能超 数值分析简明教程 2003 2.崔国华 计算方法 1996 3.华中理工大学数学系 计算方法 1999 4.李庆扬.王能超.易大义 数值分析 1987 5.苏金明.阮沈勇 MATLAB6.1实用指南 2002
6.桂现才.刁群 解线性方程组的Matlab法[期刊论文]-湛江师范学院学报 2003(06)
弦=彬·^+(x"+即+”); "=(即+妒)/2=
.
P胛d
选代次数,?=120时求解结果;Jw=0.07694733409450#若
仰=O.07692309052101.
(2)标准四阶龙格库塔法 对于上述初值问题建立如下M文件:
Ⅳ=5000时,求解结果
万方数据
一,——
科技信总
博士·专家论坛
口=O: 6=5: 胛=20:
微分方程初值问题模型是数学建模竞赛中常见的一类数学模型。对于一些简单而典型的微分方程模型,譬如线性方程、某些特殊的一阶非线性方程 等是可以设法求出其解析解的,并有理论上的结果可资利用。但在数学建模中碰到的常微分方程初值问题模型,通常很难,甚至根本无法求出其解析解 ,而只能求其近似解。因此,研究其数值方法,以便快速求得数值解有其重大意义。针对于此,本文对常微分方程初值问题模型现有的数值解法问题进 行了综述研究。主要讨论了针对多种常微分方程模型中数值解法精度比较而言的,某些常用的数值解法:即欧拉法,向后欧拉法,θ—法,改进欧拉法 ,龙格库塔方法,阿达姆斯外插公式与内插公式等。并通过追溯数值解法的历史,利用数值解法的事例,总结了各类数值解法的优、缺点,为在数学建 模及数学建模竞赛中寻求满足各种精度要求的合理算法提供借鉴。文章最后,结合常见的较为典型的运用微分方程模型数值解法的实例,诸如耐用消费 新产品的销售规律模型、司机饮酒驾车防避模型的数值解法等,探讨了上述数值算法在实际建模问题中的应用。
