自动控制原理结构图及等效变换ppt课件
合集下载
自动控制原理教学ppt

前馈校正
在系统的输入端引入一个前馈环节, 根据输入信号的特性对系统进行补 偿,以提高系统的跟踪精度和抗干 扰能力。
复合校正方法
串联复合校正
将串联超前、串联滞后和串联滞 后-超前等校正方法结合起来, 设计一个复合的串联校正环节, 以实现更复杂的系统性能要求。
反馈复合校正
将局部反馈、全局反馈和前馈等 校正方法结合起来,设计一个复 合的反馈校正环节,以实现更全
自适应控制系统概述
简要介绍自适应控制系统的基本原理、结构和特点,为后续内容 做铺垫。
自适应控制方法
详细介绍自适应控制方法,如模型参考自适应控制、自校正控制等, 及其在自动控制领域中的应用实例。
自适应控制算法
阐述自适应控制算法的实现过程,包括参数估计、控制器设计等关 键技术。
鲁棒控制理论应用
鲁棒控制系统概述
自动控制应用领域
工业领域
自动控制广泛应用于工业领域,如自 动化生产线、工业机器人、智能制造 等。
01
02
航空航天领域
自动控制是航空航天技术的重要组成 部分,如飞行器的自动驾驶仪、导弹 的制导系统等。
03
交通运输领域
自动控制也应用于交通运输领域,如 智能交通系统、自动驾驶汽车等。
其他领域
此外,自动控制还应用于农业、医疗、 环保等领域,如农业自动化、医疗机 器人、环境监测与治理等。
提高系统的稳态精度。
串联滞后-超前校正
03
结合超前和滞后校正的优点,设计一个既有超前又有滞后的校
正环节,以同时改善系统的动态性能和稳态精度。
反馈校正方法
局部反馈校正
在系统的某个局部引入反馈环节, 以改善该局部的性能,而不影响 系统的其他部分。
全局反馈校正
在系统的输入端引入一个前馈环节, 根据输入信号的特性对系统进行补 偿,以提高系统的跟踪精度和抗干 扰能力。
复合校正方法
串联复合校正
将串联超前、串联滞后和串联滞 后-超前等校正方法结合起来, 设计一个复合的串联校正环节, 以实现更复杂的系统性能要求。
反馈复合校正
将局部反馈、全局反馈和前馈等 校正方法结合起来,设计一个复 合的反馈校正环节,以实现更全
自适应控制系统概述
简要介绍自适应控制系统的基本原理、结构和特点,为后续内容 做铺垫。
自适应控制方法
详细介绍自适应控制方法,如模型参考自适应控制、自校正控制等, 及其在自动控制领域中的应用实例。
自适应控制算法
阐述自适应控制算法的实现过程,包括参数估计、控制器设计等关 键技术。
鲁棒控制理论应用
鲁棒控制系统概述
自动控制应用领域
工业领域
自动控制广泛应用于工业领域,如自 动化生产线、工业机器人、智能制造 等。
01
02
航空航天领域
自动控制是航空航天技术的重要组成 部分,如飞行器的自动驾驶仪、导弹 的制导系统等。
03
交通运输领域
自动控制也应用于交通运输领域,如 智能交通系统、自动驾驶汽车等。
其他领域
此外,自动控制还应用于农业、医疗、 环保等领域,如农业自动化、医疗机 器人、环境监测与治理等。
提高系统的稳态精度。
串联滞后-超前校正
03
结合超前和滞后校正的优点,设计一个既有超前又有滞后的校
正环节,以同时改善系统的动态性能和稳态精度。
反馈校正方法
局部反馈校正
在系统的某个局部引入反馈环节, 以改善该局部的性能,而不影响 系统的其他部分。
全局反馈校正
等效变换自动控制原理课件

等效变换自动控制原理课 件
本课件介绍了等效变换自动控制原理的基本概念和原理,探讨了等效变换在 自动控制中的广泛应用,并讨论了等效变换的优点和局限性。
通过数学方法和计算过程的详细说明,结合实例分析,帮助大家全面理解等 效变换在自动控制中的重要性。
最后,通过总结和结论,我们对等效变换自动控制原理进行了进一步的讨论 和思考。
等效变换在自动控制中的应用
等效变换在自动控制中有着广泛的应用,包括系统建模、系统分析和控制器设计等方面。 通过将系统转化为等效模型,可以更好地理解系统的动态特性、稳定性和性能。 等效变换还可以用于解决多变量系统的控制问题,提高系统的控制效果和鲁棒性。
等效变换的优点和局限性
优点
等效变换可以简化系统分析和设计过程,提高 工程效率。
等效变换的概念和原理
等效变换是一种在自动控制中广泛使用的数学方法,通过将复杂的系统转化 为等效的简化模型,简化了分析和设计过程。
等效变换的原理是通过变换系统的输入和输出,将系统转化为具有特定特性 的等效模型,从而更好地理解和控制系统的行为。
等效变换的概念和原理对于自动控制工程师和研究人员来说是非常重要的基 础知识。
等效变换实例分析
1
步骤 2
2
通过等效变换方法,将机械振动系统转
化为等效的电路模型。
3
步骤 1
选择一个复杂的系统,例如一个机械振 动系统。
步骤 3
分析和设计电路模型的控制器,以实现 对振动系统的良好控制。
总结和结论
通过本课件的学习,我们深入了解了等效变换自动控制原理的基本概念、原理和应用。 我们了解了等效变换的优点和局限性,并学会了使用数学方法和计算过程进行等效变换的分析和设计。 通过实例分析,我们进一步理解了等效变换在自动控制中的重要性和实际应用。 希望这些知识能够对大家在自动控制领域的学习和工作有所帮助。
本课件介绍了等效变换自动控制原理的基本概念和原理,探讨了等效变换在 自动控制中的广泛应用,并讨论了等效变换的优点和局限性。
通过数学方法和计算过程的详细说明,结合实例分析,帮助大家全面理解等 效变换在自动控制中的重要性。
最后,通过总结和结论,我们对等效变换自动控制原理进行了进一步的讨论 和思考。
等效变换在自动控制中的应用
等效变换在自动控制中有着广泛的应用,包括系统建模、系统分析和控制器设计等方面。 通过将系统转化为等效模型,可以更好地理解系统的动态特性、稳定性和性能。 等效变换还可以用于解决多变量系统的控制问题,提高系统的控制效果和鲁棒性。
等效变换的优点和局限性
优点
等效变换可以简化系统分析和设计过程,提高 工程效率。
等效变换的概念和原理
等效变换是一种在自动控制中广泛使用的数学方法,通过将复杂的系统转化 为等效的简化模型,简化了分析和设计过程。
等效变换的原理是通过变换系统的输入和输出,将系统转化为具有特定特性 的等效模型,从而更好地理解和控制系统的行为。
等效变换的概念和原理对于自动控制工程师和研究人员来说是非常重要的基 础知识。
等效变换实例分析
1
步骤 2
2
通过等效变换方法,将机械振动系统转
化为等效的电路模型。
3
步骤 1
选择一个复杂的系统,例如一个机械振 动系统。
步骤 3
分析和设计电路模型的控制器,以实现 对振动系统的良好控制。
总结和结论
通过本课件的学习,我们深入了解了等效变换自动控制原理的基本概念、原理和应用。 我们了解了等效变换的优点和局限性,并学会了使用数学方法和计算过程进行等效变换的分析和设计。 通过实例分析,我们进一步理解了等效变换在自动控制中的重要性和实际应用。 希望这些知识能够对大家在自动控制领域的学习和工作有所帮助。
(自动控制原理)2.4控制系统的结构图及其等效变换

实例二:复杂控制系统的等效变换
总结词
通过等效变换简化复杂控制系统的结构图,便于分析。
详细描述
以一个包含多个回路和元件的液压控制系统为例,介绍如何 通过等效变换简化其结构图。通过合并、化简等步骤,将复 杂的结构图简化为易于分析的形式,以便更好地理解系统的 工作原理和控制性能。
实例三:实际应用中的控制系统等效变换
控制系统的性能指标
总结词
控制系统的性能指标是用来评估控制系统性能优劣的一系列参数。常见的性能指标包括稳定性、快速 性、准确性等。
详细描述
稳定性是指控制系统在受到扰动后能够恢复到原来的平衡状态的能力。快速性是指控制系统对于输入 信号的响应速度。准确性是指控制系统对于输入信号的跟踪精度。这些性能指标可以通过数学分析和 实验测试等方法进行评估。
不断调整和完善结 构图,确保其准确 反映系统的工作原 理。
结构图的基本元件及其作用
控制器
根据设定值与实际值的偏差, 计算出控制量并输出给执行器。
被控对象
需要被控制的设备或系统,如 温度、压力、流量等。
传感器
用于检测被控对象的参数变化, 并将检测到的信号转换为电信 号或数字信号输出。
执行器
根据控制器输出的控制量,驱 动被控对象进行相应的动作或 调节。
课程背景
自动控制原理是自动化专业的一门核心课程,主要介绍控制系统的基本原理、分 析和设计方法。
本节内容是该课程的重要章节之一,通过学习结构图及其等效变换,学生可以深 入理解控制系统的组成和动态行为,为后续章节的学习打下基础。
02 控制系统的基本概念
控制系统的定义
总结词
控制系统的定义是指通过一定的控制装置,对被控对象施加控制作用,从而使 被控对象的输出量按照预期的规律变化的过程。
自动控制原理2.4 结构图及其等效变换1.4 结构图及其等效变换

u R1
i1
u R1 R1
ur
i2
C
duR1 dt
uc iR2 (i1 i2 )R2
R1
R2
uc
结构图(续)
第二章 数学模型
U R1 (s) U r (s) U c (s) 1
I1 (s) R1 U R1 (s)
I 2 (s) CSU R1 (s) I(s) I1(s) I2(s) U c (s) R2 I (s)
-
(s)
Kf
三、结构图的等效变换:
第二章 数学模型
建立结构图的目的是求系统传递函数,对系统性能
进行分析。所以对于复杂的结构图就需要进行运算
和变换,设法将其化为一个等效的方框,其中的数
学表达式即为总传递函数。这一步骤相当于对方程
消元。
R
C
G
总传递函数
等效原则:
变换前后,输入输出总的数学关系应保持不变
Uc (s)
则
1
U ( s)
I(s)) 1
I(s)
R
R
及U c (s)
1 Cs
I(s)
(3)
I(s)
1 Uc (s) Cs
结构图(续)
第二章 数学模型
1.定义:由具有一定函数关系组成的、并标明信号 传递方向的系统方框图称为动态结构图。
2.组成:4个基本单元。
①信号线:带箭头的直线,表示信号传递的方向,
线上标注信号所对应的变量,信号传递
具有单向性。 X
②引出点:信号引出或测量的位置,从同一信号线
《自动控制原理》课件

集成化:智能控制技术将更加集 成化,能够实现多种控制技术的 融合和应用。
添加标题
添加标题
添加标题
添加标题
网络化:智能控制技术将更加网 络化,能够实现远程控制和信息 共享。
绿色化:智能控制技术将更加绿 色化,能够实现节能减排和环保 要求。
控制系统的网络化与信息化融合
网络化控制:通过互联网实现远程控制和监控
现代控制理论设计方法
状态空间法:通过建立状态空间模型,进行系统分析和设计 频率响应法:通过分析系统的频率响应特性,进行系统分析和设计 极点配置法:通过配置系统的极点,进行系统分析和设计 线性矩阵不等式法:通过求解线性矩阵不等式,进行系统分析和设计
最优控制理论设计方法
基本概念:最优控制、状态方程、控制方程等 设计步骤:建立模型、求解最优控制问题、设计控制器等 控制策略:线性二次型最优控制、非线性最优控制等 应用领域:航空航天、机器人、汽车电子等
动态性能指标
稳定性:系统在受到扰动后能否恢复到平衡状态 快速性:系统在受到扰动后恢复到平衡状态的速度 准确性:系统在受到扰动后恢复到平衡状态的精度 稳定性:系统在受到扰动后能否保持稳定状态
抗干扰性能指标
稳定性:系统在受到干扰后能够 恢复到原来的状态
准确性:系统在受到干扰后能够 保持原有的精度和准确性
信息化控制:利用大数据、云计算等技术实现智能化控制
融合趋势:网络化与信息化的融合将成为未来控制系统的发展方向 应用领域:工业自动化、智能家居、智能交通等领域都将受益于网络化与 信息化的融合
控制系统的模块化与集成化发展
模块化:将复杂的控制系统分解为多个模块,每个模块负责特定的功能,便于设计和维护 集成化:将多个模块集成为一个整体,提高系统的性能和可靠性 发展趋势:模块化和集成化是未来控制系统发展的重要方向 应用领域:广泛应用于工业自动化、智能家居、智能交通等领域
自动控制原理02结构图及其等效变换

e)
R( s )
G 1 G 2 G3G 4 C (s) 1 G 1 G 2 G3G 4 G 2 G3 H 1 G3G 4 H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统
N (s)
R( s )
E ( s)
G1 (s)
结构图。
2.3.2 结构图的建立
例2-7 RLC电路网络的结构图
解: U (s) U (s) U (s) U (s) i R L 0
U R ( s) RI ( s)
U L ( s) LsI ( s)
{
I ( s)
U i ( s) U 0 ( s ) U R ( s ) U L ( s )
C 传输到 ( s)
单位反馈: H ( s) 1 开环传递函数:
G( s) H ( s)
2.3.3 结构图的等效变换和简化
(4)比较点的移动
R1 (s)
G(s)
R2 ( s )
a)
C (s)
R2 ( s )
R1 (s)
G(s)
C (s)
1/ G(s)
b)
R1 (s)
R2 ( s )
a)
G(s)
C (s) G(s) ( s) R( s) 1 G ( s) H ( s )
2.3.3 结构图的等效变换和简化
反馈连接中的术语:
R( s)
E (s)
G (s)
H (s)
C (s)
B( s)
前向通道:信号从 R( 传输到 s) 反馈通道:信号从
的通道 C ( s) 的通道 R( s )
R(s)
R( s )
G 1 G 2 G3G 4 C (s) 1 G 1 G 2 G3G 4 G 2 G3 H 1 G3G 4 H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统
N (s)
R( s )
E ( s)
G1 (s)
结构图。
2.3.2 结构图的建立
例2-7 RLC电路网络的结构图
解: U (s) U (s) U (s) U (s) i R L 0
U R ( s) RI ( s)
U L ( s) LsI ( s)
{
I ( s)
U i ( s) U 0 ( s ) U R ( s ) U L ( s )
C 传输到 ( s)
单位反馈: H ( s) 1 开环传递函数:
G( s) H ( s)
2.3.3 结构图的等效变换和简化
(4)比较点的移动
R1 (s)
G(s)
R2 ( s )
a)
C (s)
R2 ( s )
R1 (s)
G(s)
C (s)
1/ G(s)
b)
R1 (s)
R2 ( s )
a)
G(s)
C (s) G(s) ( s) R( s) 1 G ( s) H ( s )
2.3.3 结构图的等效变换和简化
反馈连接中的术语:
R( s)
E (s)
G (s)
H (s)
C (s)
B( s)
前向通道:信号从 R( 传输到 s) 反馈通道:信号从
的通道 C ( s) 的通道 R( s )
R(s)
自动控制原理课件ppt

G3(s)
G2(s)
H3(s)
E(S)
R(s)
G1(s)
H1(s)
H2(s)
C(s)
P2= - G3G2H3
△2= 1
P2△2=
梅逊公式求E(s)
P1= –G2H3
△1= 1
N(s)
G1(s)
H1(s)
H2(s)
C(s)
G3(s)
G2(s)
H3(s)
R(s)
E(S)
四个单独回路,两个回路互不接触
e
A
100%
一阶系统时域分析
无零点的一阶系统 Φ(s)=
Ts+1
k
, T
时间常数
(画图时取k=1,T=0.5)
单 位 脉 冲 响 应
k(t)=
T
1
e-
T
t
k(0)=
T
1
K’(0)=
T
1
2
单位阶跃响应
h(t)=1-e-t/T
h’(0)=1/T
h(T)=0.632h(∞)
h(3T)=0.95h(∞)
h(2T)=0.865h(∞)
第一章 自动控制的一般概念
1-1 自动控制的基本原理与方式 1-2 自动控制系统示例 1-3 自动控制系统的分类 1-4 对自动控制系统的基本要求
飞机示意图
给定电位器
反馈电位器
给定装置
放大器
舵机
飞机
反馈电位器
垂直陀螺仪
θ0
θc
扰动
俯仰角控制系统方块图
飞机方块图
液位控制系统
控制器
自动控制原理课件ppt
课件3 ~6为第一章的内容。制作目的是节省画图时间,便于教师讲解。 课件6要强调串联并联反馈的特征,在此之前要交待相邻综合点与相邻引出点的等效变换。 课件7中的省略号部分是反过来说,如‘合并的综合点可以分开’等。最后一条特别要讲清楚,这是最容易出错的地方! 课件10先要讲清H1和H3的双重作用,再讲分解就很自然了。 课件11 、12 、13是直接在结构图上应用梅逊公式,制作者认为没必要将结构图变为信号流图后再用梅逊公式求传递函数。
自动控制原理胡寿松(课堂PPT)

G2(s)G4(s)
G3(s)H(s) G4(s)H(s)
C(s) G5 (s)
3
R(s) G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s )
C(s) G5 (s)
G 3 ( s ) G 4 ( s ) H ( s )
4
R(s)
1
G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s ) 1G3(s)G4(s)H(s)
函数确定。 r (t )
1 e(t) 1/ s
1
c(t)
1
22
信号流图常用的名词术语
➢源节点(输入节点):只有信号输出支路的节点。
➢阱节点(输出节点):只有信号输入支路的节点。
C(s) G5 (s)
5
C R ( (s s) ) G 1 1 (s G )G 3 3 (( ss )) G G 4 2 (( ss ))H G 4 (( ss ))G 5(s) 6
21
• 信号流图的组成及性质
信号流图是以点和有向线段,描述系统的组成、结构、信号传 递关系的图形。它完全表述了一个系统。
C(s)
1G2(s)G3(s)H2(s) G4(s)
H3(s)/G2(s) H1(s)
G2(s)G3(s)G4(s) 1G2(s)G3(s)H2(s)
C(s)
H3(s)/G2(s) H1(s)
G1(s)
G 2(s)G 3(s)G 4(s)
C(s)
1G 2(s)G 3(s)H 2(s)G 3(s)G 4(s)H 3(s)
1
§2-3 控制系统的结构图与信号流图
1.系统结构图的组成和绘制 2.结构图的等效变换和简化 3.信号流图的组成和性质 4.信号流图的绘制 5.梅逊增益公式 6.闭环系统的传递函数
G3(s)H(s) G4(s)H(s)
C(s) G5 (s)
3
R(s) G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s )
C(s) G5 (s)
G 3 ( s ) G 4 ( s ) H ( s )
4
R(s)
1
G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s ) 1G3(s)G4(s)H(s)
函数确定。 r (t )
1 e(t) 1/ s
1
c(t)
1
22
信号流图常用的名词术语
➢源节点(输入节点):只有信号输出支路的节点。
➢阱节点(输出节点):只有信号输入支路的节点。
C(s) G5 (s)
5
C R ( (s s) ) G 1 1 (s G )G 3 3 (( ss )) G G 4 2 (( ss ))H G 4 (( ss ))G 5(s) 6
21
• 信号流图的组成及性质
信号流图是以点和有向线段,描述系统的组成、结构、信号传 递关系的图形。它完全表述了一个系统。
C(s)
1G2(s)G3(s)H2(s) G4(s)
H3(s)/G2(s) H1(s)
G2(s)G3(s)G4(s) 1G2(s)G3(s)H2(s)
C(s)
H3(s)/G2(s) H1(s)
G1(s)
G 2(s)G 3(s)G 4(s)
C(s)
1G 2(s)G 3(s)H 2(s)G 3(s)G 4(s)H 3(s)
1
§2-3 控制系统的结构图与信号流图
1.系统结构图的组成和绘制 2.结构图的等效变换和简化 3.信号流图的组成和性质 4.信号流图的绘制 5.梅逊增益公式 6.闭环系统的传递函数
自动控制原理02结构图及其等效变换课件

G1 (s)
N (s)
G2 (s)
C (s)
B(s) H (s)
(1)R(s)作用下的系统闭环传递函数
此时, N(s) 0
R(s) E(s)
G1 (s)
B(s)
G2 (s) C1(s)
(s) C1(s) R(s)
H (s)
C1
(s)
(s)R(s)
1
G1 (s)G2 (s) G1 (s)G2 (s)H
d)
2.3.3 结构图的等效变换和简化
例2-9 R(s)
G2G3G4
C(s)
G1
1 G2G3H1 G3G4H 2
e)
R(s)
G1G2G3G4
C(s)
1G1G2G3G4 G2G3H1 G3G4H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统 的结构图:
R(s) E(s)
I (s)
1 Ls U L (s)
U0
(s)
1 Cs
I (s)
Ui (s)
UL (s) UR (s)
Uo (s)
a)
UR (s) 1/ R I (s)
b)
UL (s) 1/ Ls I (s)
c)
I (s) 1 / Cs U o (s)
d)
2.3.2 结构图的建立
例2-7 按照信号的流向将以上各个环节连接起来。就构成了 系统的动态结构图。
(6)多个比较点与引出点的交换与合并
R(s)
C(s)
G(s)
B1(s) B2(s) a)
R(s)
C(s)
G(s) R(s)
R(s)
N (s)
G2 (s)
C (s)
B(s) H (s)
(1)R(s)作用下的系统闭环传递函数
此时, N(s) 0
R(s) E(s)
G1 (s)
B(s)
G2 (s) C1(s)
(s) C1(s) R(s)
H (s)
C1
(s)
(s)R(s)
1
G1 (s)G2 (s) G1 (s)G2 (s)H
d)
2.3.3 结构图的等效变换和简化
例2-9 R(s)
G2G3G4
C(s)
G1
1 G2G3H1 G3G4H 2
e)
R(s)
G1G2G3G4
C(s)
1G1G2G3G4 G2G3H1 G3G4H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统 的结构图:
R(s) E(s)
I (s)
1 Ls U L (s)
U0
(s)
1 Cs
I (s)
Ui (s)
UL (s) UR (s)
Uo (s)
a)
UR (s) 1/ R I (s)
b)
UL (s) 1/ Ls I (s)
c)
I (s) 1 / Cs U o (s)
d)
2.3.2 结构图的建立
例2-7 按照信号的流向将以上各个环节连接起来。就构成了 系统的动态结构图。
(6)多个比较点与引出点的交换与合并
R(s)
C(s)
G(s)
B1(s) B2(s) a)
R(s)
C(s)
G(s) R(s)
R(s)
自动控制原理课件ppt

控制目标。
传感器
检测系统的状态或参数,并将 检测结果转换为电信号传输给
控制器。
调节机构
根据控制器的指令调整系统的 参数或结构,以实现系统的稳
定和性能优化。
02
控制系统基本概念
系统稳定性
01Biblioteka 0203稳定性的定义
一个控制系统在受到扰动 后能够回到原始状态的能 力。
稳定性的分类
根据系统响应的不同,可 以分为渐近稳定、指数稳 定和不稳定三种类型。
闭环控制系统
系统的输出反馈到输入端,通过反馈 控制提高控制精度。
03
控制系统的数学模型
传递函数
定义
传递函数是描述线性定常系统动 态特性的数学模型,它反映了系 统输出与输入之间的函数关系。
形式
传递函数通常表示为有理分式的 形式,即 G(s) = num(s)/den(s) ,其中 s 是复变量,num(s) 是 分子多项式,den(s) 是分母多项
参数优化
根据系统性能指标,调整控制器的参数,以实现更好的控制效果 。
结构优化
对控制系统结构进行调整,以提高系统的稳定性和动态性能。
鲁棒性优化
提高系统对不确定性和干扰的抵抗能力,保证系统在各种情况下 都能稳定运行。
控制系统的调试与测试
硬件调试
对控制系统的硬件部分进行调试,确保硬件设备正常工作 。
软件调试
自动控制的应用
工业自动化
航空航天
交通运输
智能家居
自动化生产线、机器人 、自动化仪表等。
飞行器控制、卫星轨道 控制等。
自动驾驶车辆、列车控 制等。
智能家电、智能照明等 。
自动控制系统的组成
01
02
03
传感器
检测系统的状态或参数,并将 检测结果转换为电信号传输给
控制器。
调节机构
根据控制器的指令调整系统的 参数或结构,以实现系统的稳
定和性能优化。
02
控制系统基本概念
系统稳定性
01Biblioteka 0203稳定性的定义
一个控制系统在受到扰动 后能够回到原始状态的能 力。
稳定性的分类
根据系统响应的不同,可 以分为渐近稳定、指数稳 定和不稳定三种类型。
闭环控制系统
系统的输出反馈到输入端,通过反馈 控制提高控制精度。
03
控制系统的数学模型
传递函数
定义
传递函数是描述线性定常系统动 态特性的数学模型,它反映了系 统输出与输入之间的函数关系。
形式
传递函数通常表示为有理分式的 形式,即 G(s) = num(s)/den(s) ,其中 s 是复变量,num(s) 是 分子多项式,den(s) 是分母多项
参数优化
根据系统性能指标,调整控制器的参数,以实现更好的控制效果 。
结构优化
对控制系统结构进行调整,以提高系统的稳定性和动态性能。
鲁棒性优化
提高系统对不确定性和干扰的抵抗能力,保证系统在各种情况下 都能稳定运行。
控制系统的调试与测试
硬件调试
对控制系统的硬件部分进行调试,确保硬件设备正常工作 。
软件调试
自动控制的应用
工业自动化
航空航天
交通运输
智能家居
自动化生产线、机器人 、自动化仪表等。
飞行器控制、卫星轨道 控制等。
自动驾驶车辆、列车控 制等。
智能家电、智能照明等 。
自动控制系统的组成
01
02
03
等效变换自动控制原理课件
G3 G4 / G2
C(s) +
R(s) -
(c) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
17
R(s) -
(c) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
R(s) -
1/ G1
G1G2 1 G1G2
G3 G4 / G2
C(s)
(d)
18
2、变换前后有关前向通道中各方框传递 函数的乘积应保持不变。
15
例2-11 试化简如图所示系统结构图,求出 传递函数Φ(s)=C(s)/R(s)。
R(s)
-
(a)
-
G1
C(s)
G2
G3
+
G4
R(s) -
(b) -
1/ G1 G1 G2
G3 G4 / G2
C(s) +
16
R(s) -
(b) -
1/ G1 G1 G2
G(s)
C(s) R(s)
G1(s)G2 (s)
结论:环节串联的等效 传递函数等于各串联连
n
G(s) Gi (s)
i1
(n为相串联 的环节数)
接传递函数的乘积。
1
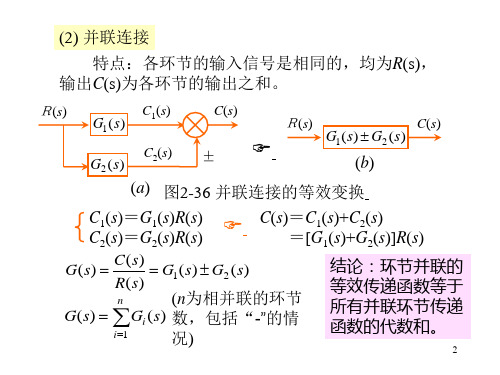
(2) 并联连接
特点:各环节的输入信号是相同的,均为R(s), 输出C(s)为各环节的输出之和。
R(s)
G1(s) C1(s) G2 (s) C2(s)
R(s) -
(a)
G1
+
H1
C(s)
G2 H2
R(s) -
(b)
C(s)
G1
G2
H1
+
H1 H2
自动控制原理课件ppt

03
非线性控制系统
非线性控制系统的特点
非线性特性
01
非线性控制系统的输出与输入之间存在非线性关系,
如放大器、继电器等。
复杂的动力学行为
02 非线性控制系统具有复杂的动力学行为,如混沌、分
叉、稳定和不稳定等。
参数变化范围广
03
非线性控制系统的参数变化范围很广,如电阻、电容
、电感等。
非线性控制系统的数学模型
线性控制系统的性能指标与评价
性能指标
衡量一个控制系统性能的好坏,需要使用一些性能指标,如响应时间、超调量、稳态误差等。
性能分析
通过分析系统的性能指标,可以评价一个控制系统的优劣。例如,响应时间短、超调量小、稳态误差小的系统性能较 好。
系统优化
根据性能分析的结果,可以对控制系统进行优化设计,提高控制系统的性能指标。例如,可以通过调整 控制器的参数,减小超调量;或者通过改变系统的结构,减小稳态误差。
。
采样控制系统的数学模型
描述函数法
描述函数法是一种分析采样控制系统的常用方法,通过将连续时间 函数离散化,用差分方程来描述系统的动态特性。
z变换法
z变换法是一种将离散时间信号变换为复平面上的函数的方法,可 用于分析采样控制系统的稳定性和性能。
状态空间法
状态空间法是一种基于系统状态变量的方法,可以用于分析复杂的采 样控制系统。
航空航天领域中的应用
总结词
高精度、高可靠性、高安全性
详细描述
自动控制原理在航空航天领域中的应用至关重要。例如 ,在飞机系统中,通过使用自动控制原理,可以实现飞 机的自动驾驶和自动着陆等功能,从而提高飞行的精度 和安全性。在火箭和卫星中,通过使用自动控制原理, 可以实现推进系统的精确控制和姿态调整等功能,从而 保证火箭和卫星能够准确地进行轨道变换和定点着陆。
自动控制原理课件2-2

3 典型环节传递函数 4、传递 函数计算举例
本节计划内容:控制系统方框图及等效变换
1、控制系统的方框图 (1)控制系统方框图/方块图/动态结构图/框图的 基本概念与组成; 1)函数方块 2)信号流线 3)相加点 4)分支点 (2)控制系统方框图的绘制方法; (3)控制系统方框图的绘制举例;
2、控制系统方框图的等效变换规则 (1)串联环节的简化 (2)并联环节的简化 (3)反馈回路的简化 (4)相加点和分支点的移动 1)相加点前移 2)相加点之间的移动 3)分支点后移 4)相邻分支点之间的移动
重点:绘制方框图并求传递函数;方框图的变换与化简 难点:方框图的变换与化简。
• 被控信号c(t)对控制信号r(t)的闭环传递函数:
若 f(t)=0,则系统的被控制信号的拉氏变换C(s)与控制信号的拉 氏变换R(s)之比,称之为被控制信号c(t)对于控制信号r(t)的闭环 传递函数,记作Фr(s)(或 Ф(s) )。
整理得:
对于单位反馈系统有:
• 被控制信号对于干扰信号的闭环传递函数
解:(1)根据电路定理列出方程,写出对应的拉氏 变换,也可直接画出该电路的运算电路图如图(b);
(2)根据输出量——中间量——输入量列出4个含s 的代数式;
(3)根据上述四个表达式,画出各个表达式的框图, 再根据信号的流向将各方框依次连接起来;
2、控制系统方框图的等效变换规则 目的:为了从一个闭环控制系统方便的得到其对应的闭 环传递函数,通常需要对方块图进行等效变换;
chap2:控制系统数学模型
本节计划内容:控制系统方框图及等效变换
建立自动控制系统传递函数数学模型的方法(复习) (1)传递函数的定义和性质 1)定义 2)性质 (2)传递函数的极点和零点对输出的影响 (3)典型环节及其传递函数 1)比例环节 2)惯性环节 3)微分环节 4)积分环节 5)振荡环节 6)纯时间延时环节 (4)传递函数计算举例
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[定义]:表示变量之间数学关系的方块图称为动态结构图或结 构图。
[例]:结构: X(t) 放大器 结Y(构t) 图:
X(s)
Y(s)
G(s)=K
微分方程:y(t)=kx(t)
若已知系统的组成和各部分的传递函数,则可以画出各个部 分的结构图并连成整个系统的结构图。
Tuesday, June 02, 2020 NhomakorabeaK2
(s
1)
ua (s) u2 (s)
K3
u1(s) K2(s 1) u2 (s)
u2 (s)K3 ua (s)
Tuesday, June 02, 2020
3
反馈环节:
u f (s) (s)
K
f
(s)
Kf
u f (s)
电动机环节: 返回例2-6
(Tms 1)(s) Kuua (s) KmMc (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
X (s)
X 3 (s)
G(s)
X (s)
X 3 (s)
G(s)
X 2 (s)
X 2 (s)
所以,一般情况下,相加点向相加点移动,分支点向分支
点移动。
Tuesday, June 02, 2020
12
结构图的化简, 应注意以下两点:
Tuesday, June 02, 2020
10
信号相加点和分支点的移动和互换
分支点从环节的输出端移到输入端:
X1(s) G(s) Y (s) Y (s)
X1(s) G(s) Y (s) N(s) Y (s)
N(s) ? X1(s)G(s) Y(s), X1(s)N(s) Y(s),N(s) G(s)
Tuesday, June 02, 2020
X1(s) G(s) X2(s) N(s)
N(s) G(s)
Y (s)
8
信号相加点的移动和互换
把相加点从环节的输出端移到输入端:
X1(s) G(s) X 2 (s)
Y (s)
X1(s)
X2(s) N(s)
G(s) Y (s)
N(s) ? Y (s) X1(s)G(s) X 2(s), Y (s) X1(s)G(s) X 2(s)N(s)G(s), N(s) 1
Mc (s)
Km Tms 1
Ua (s)
Ku Tms 1
- (s)
将上面几部分按照逻辑连接起来,形成下页所示的完 整结构图。
Tuesday, June 02, 2020
4
结构图的基本概念
M c (s) Km (Tas 1)
TaTms Tms 1
ug (s)
ue (s)
K1
u1(s) K2(s 1) u2 (s)
1. 化简的关键是解除环路与环路的交叉,或形成大环套小环的 形式.
2. 解除交叉连接的有效方法是移动相加点或分支点.
Tuesday, June 02, 2020
13
结构图等效变换例子||例2-11
[例2-11]利用结构图等效变换讨论两级RC串联电路的传递函数。
R1
R2
ui
i1
i, u
C1i2 C2
[类型]:①环节的合并; --串联 --并联 --反馈连接
②信号分支点或相加点的移动。
Tuesday, June 02, 2020
6
环节的合并
(一)环节的合并:有串联、并联和反馈三种形式。
环节的串联:
X (s) G1(s) …
Y (s) Gn (s)
环节的并联:
G1 ( s )
X (s)
Y (s)
G(s)
Y (s) X (s)
n i 1
Gi (s)
反馈联接:
X (s) E(s) G(s) Y (s)
Gn (s)
Y (s) E(s)G(s)
H (s)
Y (s) n
G(s) X (s) i1 Gi (s)
E(s) X (s) H (s)Y (s), G(s) Y(s) G(s)
K3
ua (s)
Ku TaTms Tms 1
u f (s)
Kf
- (s)
在结构图中,不仅能反映系统的组成和信号流向,还能表 示信号传递过程中的数学关系。系统结构图也是系统的数学模 型,是复域的数学模型。
Tuesday, June 02, 2020
5
结构图的等效变换
二、结构图的等效变换:
[定义]:在结构图上进行数学方程的代数运算。 [原则]:变换前后环节的数学关系保持不变。
[解]:不能把左图简单地看成两个
i2
uo
RC电路的串联,有负载效应。根据 电路定理,有以下式子:
[ui (s) u(s)]
1 R1
I1(s)
I1(s) I (s) I2(s)
[注意]:
相临的信号相加点位置可以互换;见下例
X1(s)
X2(s)
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
Tuesday, June 02, 2020
11
信号相加点和分支点的移动和互换
同一信号的分支点位置可以互换:见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
G(s)
Tuesday, June 02, 2020
9
信号分支点的移动和互换
②信号分支点的移动: 分支点从环节的输入端移到输出端
X1(s) G(s) Y (s)
X1(s)
X1(s) G(s)
Y (s)
N(s) X1(s)
N(s) ? 1
X1(s)G(s)N (s) X1(s), N (s) G(s)
2
结构图的基本概念
[例2-10]求例2-5所示的速度控制统的结 构图。各部分传递函数见例2-6.
比较环节:
ue (s) ug (s) u f (s)
ug (s) ue (s) u f (s)
运放Ⅰ:
u1 ( s) ue (s)
K1,
ue (s) K1 u1(s)
运放Ⅱ:
功放环节:
u2 (s) u1(s)
Tuesday, June 02, 2020
X (s) 1 G(s)H (s) 7
信号相加点的移动
(二)信号相加点和分支点的移动和互换:
如果上述三种连接交叉在一起而无法化简,则要考虑移动某 些信号的相加点和分支点。 ①信号相加点的移动:
把相加点从环节的输入端移到输出端
X1(s) X2(s)
G(s) Y (s)
第三节 结构图及其等效变换
Tuesday, June 02, 2020
1
结构图的基本概念
一、结构图的基本概念:
我们可以用方块图表示系统的组成和信号流向。在引入传 递函数后,可以把环节的传递函数标在方块图的方块里,并把 输入量和输出量用拉氏变换表示。这时Y(s)=G(s)X(s)的关系可 以在结构图中体现出来。
