运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论
合集下载
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第3章
第2节 改进单纯形法
由此得到新的基
B2 P 1 ,P 4 ,P 2 1 P 4 1 0
主元素
1 B2 E2 B11
0 1 1 2 4 E2 4 1 0 0 0 0 0 1 0 1 / 2 1 4 1 0 0 1 0 0 0 1 0 0 1/ 4 0 1 0 1 / 2 2 1/ 4
清华大学出版社
19
第2节 改进单纯形法
而后以第2列的
(1) a22
为主元素，进行变换
(1) 12 (1) 22
a / a (1) 1 / a22 (1) P2 2 (2) (1) (1) am 2 / a22
20
清华大学出版社
第2节 改进单纯形法
二 线性规划与目标规划
第 1 章
第2章
第3章 第4章
线性规划与单纯形法 对偶理论与灵敏度分析 运输问题 目标规划
1
清华大学出版社
第3章 对偶理论和灵敏度分析
第1节
单纯形法的矩阵描述 第2节 改进单纯形法 第3节 对偶问题的提出 第4节 线性规划的对偶理论 第5节 对偶问题的经济解释——影子价格 第6节 对偶单纯形法 第7节 灵敏度分析 第8节* 参数线性规划
12
清华大学出版社
第1节 单纯形法的矩阵描述
单纯形表中的数据
基变量 非基变量 等式右边
XB
系数矩阵
XN B 1N1
1
Xs B 1
1
RHS B 1b CB B b
13
检验数
B B 1 0
1
C N1 C B B N 1 C B B
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论课件PPT
❖ 在运筹学中除常用的数学方法以外，还引入 一些非数学方法和理论。
❖ 美国运筹学家沙旦(T.L.Saaty)，在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考，它适用于解决那种结构 明确的系统以及战术和技术性问题，而对于 结构不明确的，有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
（例如投入产出方法）。在当时这些先遣者中，越民义先
生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、
徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
2021/3/10
2
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学，至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是：“为决策机构在对其控 制下业务活动进行决策时，提供以数量化为 基础的科学方法。”
❖ 以上过程应反复进行。
2021/3/10
6
第4节 运筹学的模型
模型有三种基本形式： ❖ ①形象模型； ❖ ②模拟模型； ❖ ③符号或数学模型。
2021/3/10
7
构模的方法和思路有以下五种：
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
2021/3/10
12
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化，使用高深的数学工具，而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
运筹学钱颂迪答案
运筹学钱颂迪答案【篇一： 803 运筹学】class=txt>运筹学考试大纲一、考试性质运筹学是我校航空运输管理学院硕士生入学考试的综合考试科目之一，它是我校为招收交通运输规划与管理学科硕士研究生而实施的水平考试，其评价标准是普通高等院校优秀本科毕业生能够达到的及格以上水平，以保证被录取者较好地掌握了必备的专业基础知识。
本门课程主要考试内容包括：线性规划及其对偶理论、运输问题、目标规划、整数规划、动态规划、图与网络分析，注重考察考生是否已经掌握运筹学最基本的理论知识与方法。
二、考试形式与试卷结构1.答卷方式：闭卷、笔试2.答卷时间： 180 分钟3.题型比例：满分 150 分，基本概念 20% ，计算及证明题 80%三、考查要点1.线性规划及对偶理论：单纯形法，改进单纯形法。
线性规划的对偶理论，对偶单纯形法，灵敏度分析；2.运输问题：运输问题的数学模型；用表上作业法求解运输问题；产销不平衡的运输问题及其求解方法；3.目标规划：目标规划的数学模型，目标规划的图解法与单纯形法；4.整数规划：0－1 型整数规划，分支定界解法，割平面解法，指派问题；5.动态规划：动态规划的基本概念和基本方法，动态规划的最优性原理与最优性定理，动态规划与静态规划的关系，动态规划的应用；6.图与网络分析：图与树的基本概念，最短路问题，网络最大流问题，最小费用最大流问题，中国邮路问题，网络计划。
四、主要参考书目1、郭耀煌，李军 .运筹学原理与方法. 成都：西南交通大学出版社，2004 ；2 、钱颂迪主编. 运筹学（修订版）. 北京：清华大学出版社，1991 。
【篇二：运筹学大纲(13 、 14 级使用)2014.9 】（理论课程）开课系（部）：数理教研部课程编号：380020 、 381703课程类型：专业必修课或学科必修课总学时： 48 或 32学分：3或2适用专业：信息管理与信息系统、投资学、工业工程、工程管理、经济统计学、物流管理开课学期： 3 或 4 或 5先修课程：高等数学、线性代数一、课程简述本课程是以经济活动方面的问题以及解决这类问题的原理和方法作为研究的对象，把经济活动中的问题归结为对应的某种数学模型，运用数学知识等工具求得最合理的工作方案。
运筹学(一)ppt课件
2x3 4 3x3 6
x1 0, x2 0, x3取值无约束
解： z令 z,x1 x1,x3x3 x3 ,其x中 3 ， x3 0， 同时引入 x4和 松剩 弛余 变 x5,标 变 量准 量形式
m z x 1 a 2 x 2 x 3 x 3 3 x 3 0 x 4 0 x 5
案、措施，是问题中要确定的未知量。
2.目标函数:指问题要达到的目的要求，表示为 决策变量的函数。
3.约束条件:指决策变量取值时受到的各种可用 资源的限制，表示为含决策变量的等式或不等 式。
最新版的一般表示形式：
m ax (mm in ) 或 f ( xm ) a cz 1 x 1 c 1 cx x 21 i x 2 c 2 n x 2 ( cn x ) n c n x n
( 4 )无可行解。
目标函数为max z=3x1+x2，约束条件为
x 1 x 2 2 ; 最x 新1 版整 理ppt 2 x 2 6
库存管理。存储论应用于多种物资库存量的管理，确定某些设备的合 理的能力或容量以及适当的库存方式和库存量
运输问题。用运筹学中运输问题的方法，可以确定最小成本的运输线 路、物资的调拨、运输工具的调度以及建厂地址的选择。
人事管理。可以用运筹学方法对人员的需求和获得情况进行预测；确 定合适需要的人员编制；用指派问题对人员合理分配；用层次分析法 等方法来确定一个人才评价体系等。
数为0；
（4）第i 个约束为 型，在不等式左边减去一 个非负的变量，称为剩余变量；同时令该变量在目
标函数中的系数为0；
（5）若 ，x令0 xx
（6）若 无x约束，令 x，x其中x，
x,x0
例3：将下述线性规划模型化为标准形式：
运筹学的主要内容及如何学好运筹学
运筹学的主要内容及如何学好运筹学
兰天 sky 收集整理 davidluocq@
第一章 概述
运筹学是一门研究如何有效地组织和管理人机系统的科学。由于它同 管理科学的紧密联系，研究解决实际问题时的系统优化思想，以及从提出 问题、分析建模、求解到方案实施的一整套严密科学方法，使它在培养提 高管理人才的素质上起到重要作用。运筹学已成为经济管理类专业普遍外 设的一门重要专业基础课。随着国内运筹学教学形势的发展，对教学内容 的要求也在不断提高。我们认为，应当根据我国社会主义市场经济的需要， 将运筹学的最新理论相应用成果及时充实到教材守去，并进一步研究如何 满足 21 世纪运筹学教学的要求。
克。现有五种饲料，搭配使用，饲料成分如下表：
例题 2 建模
设抓取饲料 I x1kg;饲料 II x2kg;饲料 III x3kg……
目标函数：最省钱 minZ=2x1+7x2+4x3+9x4+5x5
约束条件：3x2+2x2+x3+6x4+18x5 ≥700
营养要求： x1+0.5x2+0.2x3+2x4+0.5x5 ≥30 0.5x1+x2+0.2x3+2x4+0.8x5 =200
在认真听课的同时，学习或复习时要掌握以下三个重要环节： (1)、认真阅读教材和参考资料，以指定教材为主，同时参考其他有关书 籍。一般每一本运筹学教材都有自己的特点，但是基本原理、概念都是一 致的。注意主从，参考资料会帮助你开阔思路，使学习深入。但是，把时 间过多放在参考资料上，会导致思路分散，不利于学好。 (2)、要在理解了基本概念和理论的基础上研究例题。注意例题是为了帮 助你理解概念、理论的。作业练习的主要作用也是这样，它同时还有让你 自己检查自己学习的作用。因此，做题要有信心，要独立完成，不要怕出 错。因为，整个课程是一个整体，各节内容有内在联系，只要学到一定程 度，知识融会贯通起来，你做题的正 确性自己就有判断。 (3)、要学会做学习小结。每一节或一章学完后，必须学会用精炼的语言 来概括该书所学内容。这样，你才能够从 较高的角度来看问题，更深刻 的理解有关知识和内容，这就称为“把书读薄"。若能够结合自己参考大量 文献后的深入理解，把相关知识从更深入、广泛的角度进行论述，则称之 为"把书读厚"。
兰天 sky 收集整理 davidluocq@
第一章 概述
运筹学是一门研究如何有效地组织和管理人机系统的科学。由于它同 管理科学的紧密联系，研究解决实际问题时的系统优化思想，以及从提出 问题、分析建模、求解到方案实施的一整套严密科学方法，使它在培养提 高管理人才的素质上起到重要作用。运筹学已成为经济管理类专业普遍外 设的一门重要专业基础课。随着国内运筹学教学形势的发展，对教学内容 的要求也在不断提高。我们认为，应当根据我国社会主义市场经济的需要， 将运筹学的最新理论相应用成果及时充实到教材守去，并进一步研究如何 满足 21 世纪运筹学教学的要求。
克。现有五种饲料，搭配使用，饲料成分如下表：
例题 2 建模
设抓取饲料 I x1kg;饲料 II x2kg;饲料 III x3kg……
目标函数：最省钱 minZ=2x1+7x2+4x3+9x4+5x5
约束条件：3x2+2x2+x3+6x4+18x5 ≥700
营养要求： x1+0.5x2+0.2x3+2x4+0.5x5 ≥30 0.5x1+x2+0.2x3+2x4+0.8x5 =200
在认真听课的同时，学习或复习时要掌握以下三个重要环节： (1)、认真阅读教材和参考资料，以指定教材为主，同时参考其他有关书 籍。一般每一本运筹学教材都有自己的特点，但是基本原理、概念都是一 致的。注意主从，参考资料会帮助你开阔思路，使学习深入。但是，把时 间过多放在参考资料上，会导致思路分散，不利于学好。 (2)、要在理解了基本概念和理论的基础上研究例题。注意例题是为了帮 助你理解概念、理论的。作业练习的主要作用也是这样，它同时还有让你 自己检查自己学习的作用。因此，做题要有信心，要独立完成，不要怕出 错。因为，整个课程是一个整体，各节内容有内在联系，只要学到一定程 度，知识融会贯通起来，你做题的正 确性自己就有判断。 (3)、要学会做学习小结。每一节或一章学完后，必须学会用精炼的语言 来概括该书所学内容。这样，你才能够从 较高的角度来看问题，更深刻 的理解有关知识和内容，这就称为“把书读薄"。若能够结合自己参考大量 文献后的深入理解，把相关知识从更深入、广泛的角度进行论述，则称之 为"把书读厚"。
运筹学第4版本科版
1.1运筹学的简史
线性规划是由丹捷格(G.B.Dantzig)在1947年发表的 成果。所解决的问题是美国制定空军军事规划时提 出的，并提出了求解线性规划问题的单纯形法。
而早在1939年苏联学者康托洛维奇 (Л.В.Канторович)在解决工业生产组织和计划问 题时，已提出了类似线性规划的模型，并给出了 “解乘数法”的求解方法。由于当时未被领导重视， 直到1960年康托洛维奇再次发表了《最佳资源利用 的经济计算》一书后，才受到国内外的一致重视。 为此康托洛维奇得到了诺贝尔奖。
(1) 提出和形成问题。即要弄清问题的目标，可能的约束，问题的可控变量 以及有关参数，搜集有关资料；
(2) 建立模型。即把问题中可控变量、参数和目标与约束之间的关系用一 定的模型表示出来；
(3) 求解。用各种手段(主要是数学方法，也可用其他方法)将模型求解。解 可以是最优解、次优解、满意解。复杂模型的求解需用计算机，解的精度 要求可由决策者提出；
19
举例：问题的提出
例 2 靠近某河流有两个化工厂 (见图1-1)，流经第一化工厂的河 流流量为每天500万立方米，在
两个工厂之间有一条流量为每天
200万立方米的支流。
图1-1
化工厂1每天排放含有某种有害物质的工业污水2万立方米，化工厂2每天 排放的工业污水为1.4万立方米。从化工厂1排出的污水流到化工厂2前， 有20%可自然净化。根据环保要求，河流中工业污水的含量应不大于 0.2%。因此两个工厂都需处理一部分工业污水。化工厂1处理污水的成本 是1000元/万立方米,化工厂2处理污水的成本是800元/万立方米。问:
清华大学出版社
25
解的概念变化
相应的一些概念和方法都应有所变化，如将过分理想 化的“最优解”换成“满意解”。过去把求得的“解 ”看作精确的、不能变的凝固的东西，而现在要以“ 易变性”的理念看待所得的“解”以适应系统的不断 变化 。
运筹学第四版·清华大学出版社·运筹学教材组·1绪论
一 运筹学简史
（2）产生
运筹学作为一门系统的科学，产生的背景为第二 次世界大战。主要用于解决如何在与德军的对抗 中最大限度地杀伤敌人，减少损失。 “运作研究(Operational Research)小组”:解决复杂 的战略和战术问题。例如：
1. 如何合理运用雷达有效地对付德军德空袭； 2. 对商船如何进行编队护航，使船队遭受德国潜艇 攻击时损失最少； 3. 在各种情况下如何调整反潜深水炸弹的爆炸深度， 才能增加对德国潜艇的杀伤力等。
典型战例
不列颠之战
究竟保持多大比例的飞机在巡逻才能持久作战呢？OR 小组的专家纷纷研究这个问题，这个问题最后被生物学家 康顿解决了。他根据计算生物平均寿命的方法，运用飞机 飞行时间、维修时间、空战特点和飞机被落击伤状况等数 据，得出的结论是：只要保持 35% 的飞机在飞行状态，就 能使全部飞机的飞行战斗时间最多。这一研究成果为取得 不列颠之战的胜利作出了贡献。
运筹学的学科地位
运筹学
基础理论
应用理论
应用技术
1 1 1 1 1 1
在数学学科中的地位 在系统科学中的地位 在管理科学中的地位 与经济学的关系 与工程科学的关系
运筹数学 系统工程 管理与运筹学 问题与方法 方法与应用 核心算法与工具
与计算机科学的关系
四 运筹学的应用
1.市场营销: 广告预算、媒介选择、定价、产品开 发与销售计划制定等;
1.囚徒困境问题
两个小偷甲和乙联手作案，因私入民宅被警方
抓住但未获证据。警方将两人分别置于两间房间分
开审讯，政策是若一人招供但另一人未招，则招者
立即被释放，未招者判入狱10年；若二人都招，
则两人各判刑8年；若两人都不招，则未获证据但 因私入民宅各拘留1年。
运筹学第四版·清华大学出版社·运筹学教材组·1绪论
• 4、决策论：研究决策者如何有效进行决策的理论 与方法，根据信息和评价标准用数量方法寻找或 选取最优决策方案的科学。
运筹学的学科地位
运筹学
基础理论
应用理论
应用技术
1 在数学学科中的地位 1 在系统科学中的地位 1 在管理科学中的地位 1 与经济学的关系 1 与工程科学的关系 1 与计算机科学的关系
二运筹学的性质和特点专业文档?引入数学方法解决实际问题定性与定量方法结合?系统与整体性从全局考察问题?应用性源于实践为了实践服务于实践?交叉学科涉及经济管理数学工程和系统等多学科?开放性不断产生新的问题和学科分支?多分支问题的复杂和多样性22运筹学的特点二运筹学的性质和特点专业文档线性规划数学规划非线性规划整数规划动态规划运筹学多目标规划双层规划组合优化最优计数问题图论与网络优化排序问题统筹图随机优化对策论排队论库存论决策论可靠性分析三运筹学的内容系统仿真专业文档1排队论
1942年美国和加拿大也都相继成立运筹学小组。这些小组 在确定扩建舰队规模、开展反潜艇战侦察和组织有效对敌轰 炸等方面作了大量研究，为取得反法西斯战争的胜利及运筹 学有关分支的建立作出了贡献。
典型战例
不列颠之战
1941年，希特勒为了实施在英伦三岛登陆的计划，命 令德国空军轮番对英国进行狂轰滥炸。当时英国皇家空军 以一比七的数量劣势迎战，为此需要尽可能地保持飞机处 于飞行状态。于是，空军司令部规定保持70%的飞机在天上 巡逻。但是，英军很快发现要保持这么高的飞行比例有困 难，因为飞机的被击落的、有需要维修的，飞行员也有伤 亡。这一决策的后果是在空中飞行的飞机数量越来越少。
四 运筹学的应用
6.人事管理: 对人员的需求和使用的预测，确定 人员编制、人员合理分配，建立人才评价体系等; 7.财务和会计: 预测、贷款、成本分析、定价、 证券管理、现金管理等;
运筹学的学科地位
运筹学
基础理论
应用理论
应用技术
1 在数学学科中的地位 1 在系统科学中的地位 1 在管理科学中的地位 1 与经济学的关系 1 与工程科学的关系 1 与计算机科学的关系
二运筹学的性质和特点专业文档?引入数学方法解决实际问题定性与定量方法结合?系统与整体性从全局考察问题?应用性源于实践为了实践服务于实践?交叉学科涉及经济管理数学工程和系统等多学科?开放性不断产生新的问题和学科分支?多分支问题的复杂和多样性22运筹学的特点二运筹学的性质和特点专业文档线性规划数学规划非线性规划整数规划动态规划运筹学多目标规划双层规划组合优化最优计数问题图论与网络优化排序问题统筹图随机优化对策论排队论库存论决策论可靠性分析三运筹学的内容系统仿真专业文档1排队论
1942年美国和加拿大也都相继成立运筹学小组。这些小组 在确定扩建舰队规模、开展反潜艇战侦察和组织有效对敌轰 炸等方面作了大量研究，为取得反法西斯战争的胜利及运筹 学有关分支的建立作出了贡献。
典型战例
不列颠之战
1941年，希特勒为了实施在英伦三岛登陆的计划，命 令德国空军轮番对英国进行狂轰滥炸。当时英国皇家空军 以一比七的数量劣势迎战，为此需要尽可能地保持飞机处 于飞行状态。于是，空军司令部规定保持70%的飞机在天上 巡逻。但是，英军很快发现要保持这么高的飞行比例有困 难，因为飞机的被击落的、有需要维修的，飞行员也有伤 亡。这一决策的后果是在空中飞行的飞机数量越来越少。
四 运筹学的应用
6.人事管理: 对人员的需求和使用的预测，确定 人员编制、人员合理分配，建立人才评价体系等; 7.财务和会计: 预测、贷款、成本分析、定价、 证券管理、现金管理等;
清华大学运筹学完整
②
Q3
③
Q2(4,2)
①
4 Q1
*
x1
*
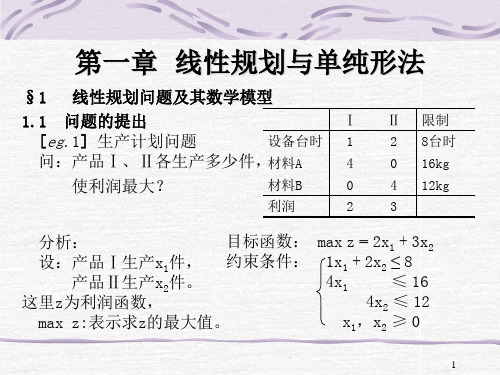
∴由此求得最优解：x1* = 4 x2* = 2 最大值：max z = z* = 2x1 + 3x2 = 14(元)
6
讨论： (1)唯一最优解 max z = z*时，解唯一，如上例。
(2)无穷多最优解
[eg.4] 对eg.1，若目标函数
②
x2
Q4
Q3(2,3)
化工厂1处理污水x1万m3, 化工厂2处理污水x2万m3。 200万m3
1.4万m3 800元/万m3
min z = 1000x1 + 800x2
(2 - x1)/500 ≤ 2/1000
[(1 - 0.2)(2 - x1) + 1.4 - x2]/(500 + 200) ≤ 2/1000
x1 ≤ 2
2、定理2 线性规划的基可行解对应于可行域的顶点。
3、定理3 若线性规划有解，则一定存在基可行解 为最优解。
20
§3 单纯形法 基本思路：从可行域的一个顶点到另一个顶点迭代求最优解。
3.1 初始基可行解的确定
1、松弛基（松弛变量对应的B）
[eg.8]max z = x1 + 3x2
x1 + 2x2 ≤ 3
(2)不等式(≤，≥) 对于“≤”情况：在“≤”左边加上一个松弛变量（非
负），变为等式； 对于“≥”情况：在“≥”左边减去一个剩余变量（非
负），变为等式。 注意：松弛变量、剩余变量在目标函数中的价值系数为0。
(3)无约束变量 令xk = xk’ - xk”，xk’,xk” ≥ 0，代入即可。
13
[eg.7]将下述问题化为标准型
(NEW)运筹学教材编写组《运筹学》(第4版)笔记和课后习题(含考研真题)详解
线性规划问题的共同特征：
（1）每一个问题都用一组决策变量
表示某一方案，这组
决策变量的某一确定值就代表一个具体方案。一般这些变量的取值是非
负且连续的。
（2）存在有关的数据，如资源拥有量、消耗资源定额、创造新价值 量等，同决策变量构成互不矛盾的约束条件，这些约束条件可以用一组 线性等式或线性不等式来表示。
1.2 课后习题详解
本章无课后习题。
1.3 考研真题详解
本章只是对本课程的一个简单介绍，不是考试重点，所以基本上没 有学校的考研试题涉及到本章内容，因此，读者可以简单了解，不必作 为复习重点，本部分也就没有可选用的考研真题。Leabharlann 第2章 线性规划与目标规划
2.1 复习笔记
1．线性规划模型的概念及其一般形式
目 录
第1章 运筹学概论 1.1 复习笔记 1.2 课后习题详解 1.3 考研真题详解
第2章 线性规划与目标规划 2.1 复习笔记 2.2 课后习题详解 2.3 考研真题详解
第3章 对偶理论与灵敏度分析 3.1 复习笔记 3.2 课后习题详解 3.3 考研真题详解
第4章 运输问题 4.1 复习笔记 4.2 课后习题详解
2．线性规划问题的标准型及标准化 （1）线性规划的标准型
或
（2-4） （2-5） 线性规划的标准型要求：目标函数是Max型；约束条件是等式约 束；决策变量非负。 （2）线性规划的标准化方法
① 若要求目标函数实现最小化，即
，则只需将目标函数最
小化变换为求目标函数最大化，即令 ，于是得到
第13章 排队论
13.1 复习笔记 13.2 课后习题详解 13.3 考研真题详解 第14章 存储论 14.1 复习笔记 14.2 课后习题详解 14.3 考研真题详解 第15章 对策论基础 15.1 复习笔记 15.2 课后习题详解 15.3 考研真题详解 第16章 单目标决策 16.1 复习笔记 16.2 课后习题详解 16.3 考研真题详解 第17章 多目标决策 17.1 复习笔记
管理运筹学(第四版)PPT全套课件
我国古代有很多关于运筹学思想方法的典故。
➢ 齐王赛马
➢ 丁渭修皇宫
➢ 沈括运军粮
第一章
绪论
运筹学的产生和发展
运筹学作为一门新兴的学科是在第二次世界大战期
间才出现的。
第一章
绪论
运筹学的产生和发展
英美成立了“运作研究”（Operation Research）
小组，解决了许多复杂的战略和战术问题。
➢ 有效保护从美国到英国的商船补给运输线；
2
2
B
无限制
1
3
总资源需求
（A+B）需求≥350吨
时间限制（小时）
600
试问在满足生产需要的前提下，在公司加工能力的范围
内，如何购买 A，B 两种原料，使得购进成本最低？
§2
图解法
建立模型：
目标函数：min = 21 + 32
约束条件：1 + 2 ≥350
1 ≥ 125
2x1 + 2 ≤ 600
集团CRHG
惠普
戴尔Dell
效果
收入2-4%年增长率，增加1600
万美元
商业转型中的决策分析
2002-2012年电子商务业务翻3番
价值链渠道转型
系统解决方案和服务占收入1/3和
利润的50%
§3
运筹学在工商管理中的应用
组织
配对捐赠联盟
美国能源局
应用
优化匹配
拯救了220个生命
水力发电量优化
根据风电和太阳能电源数量调整
0
1
50
100
250kg
目标函数：max z = 50 + 100
约束条件： + ≤ 300
➢ 齐王赛马
➢ 丁渭修皇宫
➢ 沈括运军粮
第一章
绪论
运筹学的产生和发展
运筹学作为一门新兴的学科是在第二次世界大战期
间才出现的。
第一章
绪论
运筹学的产生和发展
英美成立了“运作研究”（Operation Research）
小组，解决了许多复杂的战略和战术问题。
➢ 有效保护从美国到英国的商船补给运输线；
2
2
B
无限制
1
3
总资源需求
（A+B）需求≥350吨
时间限制（小时）
600
试问在满足生产需要的前提下，在公司加工能力的范围
内，如何购买 A，B 两种原料，使得购进成本最低？
§2
图解法
建立模型：
目标函数：min = 21 + 32
约束条件：1 + 2 ≥350
1 ≥ 125
2x1 + 2 ≤ 600
集团CRHG
惠普
戴尔Dell
效果
收入2-4%年增长率，增加1600
万美元
商业转型中的决策分析
2002-2012年电子商务业务翻3番
价值链渠道转型
系统解决方案和服务占收入1/3和
利润的50%
§3
运筹学在工商管理中的应用
组织
配对捐赠联盟
美国能源局
应用
优化匹配
拯救了220个生命
水力发电量优化
根据风电和太阳能电源数量调整
0
1
50
100
250kg
目标函数：max z = 50 + 100
约束条件： + ≤ 300
运筹学-第一讲
本课程的特点及学习方法
先修课：高等数学，概率论与数理统计、线性代数 特点： 应用数学、交叉科学
系统整体优化 模型方法的应用，以定量研究为主，定性研 究为辅 （运筹学、博弈论、计量经济学）
学习方法建议： 数学建模能力的培养+模型求解能力的训练
运筹学的应用
运筹学在工商管理、工程管理、物流管理中的应用涉及 几个方面：
4：在分析研究问题的基础上，建立数学模型描来述所研 究的问题，求解并检验该模型，从而得出最优解，用于 指导现实问题的决策。（补充）
真实系统
系统分析 问题描述
数据准备
模型建立 与修改
模型求解 与检验
结果分析与 实施
运筹学简述
运筹学的历史（略） 1：运筹学思想的出现可以追溯到很早—“田忌赛 马”、孙子兵法等都体现了博弈论的思想 2：第二次世界大战期间—— 美、英等国家的作 战研究小组解决作战中所遇到的许多错综复杂的 战略、战术问题而对运筹学做了进一步的研究。 3：1947年，丹齐格在研究美国空军配置时，提 出了求解线性规划问题的单纯型法（里程碑式的发现
运筹学-第一讲.ppt
教材、参考书及刊物
选用教材 《运筹学》 运筹学教材编写组 清华大学出版社
参考教材 《运筹学教程》胡运权主编 第四版 清华大学出版社
刊物 《Management science》 《Interfaces》 《European Journal of Operations Research》 《运筹与管理》
本课程授课方式与考核
1：讲授为主，结合课堂习题作业
2：开卷考试
学科总成绩
平时成绩 （30％）
期末成绩 （70％）
课堂考勤 （100％）
点名5次
运筹学第四版·清华大学出版社·运筹学教材组·1绪论共43页
运筹学第四版·清华大学出版社·运筹学教 材组·1绪论
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
60、人民的幸福是至高无个的法。— —西塞 罗
ቤተ መጻሕፍቲ ባይዱ 谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
60、人民的幸福是至高无个的法。— —西塞 罗
ቤተ መጻሕፍቲ ባይዱ 谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第章
27
清华大学出版社
2.1.4 线性规划问题的解概念
❖ 1.可行解 ❖ 2.基 ❖ 3.基可行解 ❖ 4.可行基
28
清华大学出版社
2.1.4 线性规划问题的解的概 念
1. 可行解
❖ 定义
满足约束条件(1-5)、(1-6)式的解X=(x1,x2，…，xn)T， 称为线性规划问题的可行解，其中使目标函数达到最 大值的可行解称为最优解。
21
清华大学出版社
2.1.3 线性规划问题的标准型式
线性规划问题的几种表示形式
用向量形式表示的标准形式线性规划
M
'' 1
:目标函数：max
z
CX
n
约束条件： j1 Pj x j
b
x
j
0,
j 1,2,,n
C c1 ,c2 ,,cn ;
x1
a1 j
b1 Xx2 ; NhomakorabeaPj
a2
j
若约束条件为“≤”型不等式，则可在不等式左端加入非负松弛变 量，把原“≤”型不等式变为等式约束； 若约束条件为“≥”型不等式，则可在不等式左端减去一个非负剩 余变量(也称松弛变量)，把不等式约束条件变为等式约束。 (3) 若存在取值无约束的变量xk,可令
xk xk' xk" xk' , xk" 0
2.1.3 线性规划问题的标准型式
M1 : 目标函数：max z c1x1 c2 x2 cn xn
a11x1 a12 x2 约束条件：a21x1 a22 x2
a1n xn b1 a2n xn b2
am1x1 am2 x2 amn xn bm
x1, x2 , , xn 0
2024版运筹学第四版清华大学出版社pdf
社2024pdfcontents •绪论•线性规划•整数规划•动态规划•图与网络分析•存储论•排队论目录01绪论运筹学的起源与发展起源运筹学起源于20世纪30年代，最初是应用在军事领域，旨在研究和解决军事策略和资源分配问题。
发展随着计算机技术的飞速发展和数学理论的不断完善，运筹学逐渐从军事领域扩展到经济、管理、工程等各个领域，并形成了完整的学科体系。
运筹学的定义与特点定义运筹学是一门应用数学、计算机科学和经济学等多学科交叉的综合性学科，旨在通过数学建模、优化算法和计算机技术等方法，对复杂系统进行优化决策。
特点运筹学具有多学科交叉性、广泛应用性、理论性与实践性相结合等特点。
它注重定量分析和实证研究，强调优化决策和系统效率。
经济领域运筹学在经济管理、市场预测、投资决策等方面有广泛应用，如生产计划、库存管理、物流运输等。
社会领域运筹学在社会服务、城市规划、医疗卫生等方面也有应用，如交通规划、教育资源分配等。
工程领域运筹学在工程设计、施工计划、质量控制等方面提供优化方法和技术支持。
军事领域运筹学在军事战略制定、作战计划优化、后勤资源分配等方面发挥重要作用。
运筹学的应用领域02线性规划线性规划问题的数学模型目标函数线性规划问题中需要优化的目标，通常表示为决策变量的线性函数。
约束条件限制决策变量取值的条件，通常表示为决策变量的线性不等式或等式。
决策变量线性规划问题中需要确定的未知量，通常表示为向量形式。
可行域满足所有约束条件的决策变量取值范围所构成的区域。
最优解使目标函数达到最优值的决策变量取值点。
目标函数等值线目标函数取不同值时对应的决策变量取值点所连成的曲线。
线性规划问题的图解法满足所有约束条件且基变量取非负值的决策变量取值点。
初始基可行解通过不断更换基变量和非基变量，使目标函数值不断改善的过程。
迭代过程判断当前基可行解是否为最优解的方法，通常通过计算检验数来实现。
最优性检验单纯形法如何合理安排生产计划以最小化成本或最大化利润。
运筹学第一章第1-5节(新)a
第六节
如何学习运筹学课程
1.学习运筹学一定要注重理论联系实际，紧密 结合工商企业的实际管理工作和问题。 掌握运筹学的基本概念、基本理论和基本 的计算技术后，要把重点放在如何把管理中的 决策问题定量化、模型化，然后借助计算机技 术去求得需要的答案。（软件） 2.在学习过程中，应该多向自己提问，如一个 方法的实质是什么，为什么这样做，怎么做等。
解：设A厂每天处理的污水量为x1万立方米 ,B 厂每天处理的污水量为x2万立方米。 因此在A厂到B厂之间应有： （2- x1)/500 ≤ 2/1000 河流经过B厂之后有： [0.8(2 - x1 )+(1.4 - x2 )]/700 ≤ 2/1000 每个工厂的最大排放量为：x1≤2，x2≤1.4 目标函数为两厂用于污水处理的总费用： z=1000x1+800x2
C c1 , c2
(1.3a) (1.3b) (1.3c)
a1 j x1 b1 a2 j x2 b2 . . . X ; Pj ( j 1,2,..., n); b . . . . . . x b a n m mj
绪
论
第一节 运筹学（Operations Research或OR） 及其发展简史
运筹学的定义： 1.英国运筹学会 运筹学是运用科学的方法来解决工业、 商业、民政和国防等部门有关人力、机器、 物资、资金等大系统的指挥和管理中出现的 复杂问题的一种方法，其目的是帮助主管人 员科学地对方针和行动进行决策。
线性规划问题数学模型的一般形式： 求目标函数： max(或min) z=c1x1 +c2x2 +…+ cnxn (1.1a) 满足约束条件： s.t. a11x1+ a12x2 +…+ a1nxn ≤ (=或≥ ） b1 a21x1+ a22x2 +…+ a2nxn ≤ (=或≥ ） b2 (1.1b) . . . . . . am1x1+ am2x2 +…+ amnxn ≤ (=或≥ ）bm x1 ,x2 , …, xn ≥0 (1.1c)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
8
.
模型的一般数学形式可用下列表达式描述：
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中：xi——可控变量；
yj——已知参数；
ζk——随机因素。
9
.
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
.
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。 ❖ 第二次世界大战后，20世纪发展概况。 ❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西
方引入我国，并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍，使运筹数学的很多分支很快跟上当时的国际水平
❖ 1959年，运筹学部门在中国科学院数学研究所成立，力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室，当时的主要研究方向为排队论、非线性规划和 图论，还有人专门研究运输理论、动态规划和经济分析 （例如投入产出方法）。在当时这些先遣者中，越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (5) 宽容原则。解决问题的思路要宽，方法要多，而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡，关系的平衡。
4
.
第3节 运筹学的工作步骤
❖ (1) 提出和形成问题。即要弄清问题的目标，可 能的约束，问题的可控变量以及有关参数，搜集 有关资料；
❖ (2) 建立模型。即把问题中可控变量、参数和目 标与约束之间的关系用一定的模型表示出来；
这种方法不追求严格最优，具有启发式 思路。
16
.
❖ 美国运筹学家沙旦(T.L.Saaty)，在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考，它适用于解决那种结构 明确的系统以及战术和技术性问题，而对于 结构不明确的，有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
3
.
前英国运筹学学会会长托姆林森提出六条原则
❖ (1) 合伙原则。是指运筹学工作者要和各方面人，尤 其是同实际部门工作者合作。
❖ (2) 催化原则。在多学科共同解决某问题时，要引导 人们改变一些常规的看法。
❖ (3) 互相渗透原则。要求多部门彼此渗透地考虑问题， 而不是只局限于本部门。
❖ (4) 独立原则。在研究问题时，不应受某人或某部门 的特殊政策所左右，应独立从事工作。
❖ (3) 求解。用各种手段(主要是数学方法，也可 用其他方法)将模型求解。解可以是最优解、次 优解、满意解。复杂模型的求解需用计算机，解 的精度要求可由决策者提出；
5
.
第3节 运筹学的工作步骤
❖ (4) 解的检验。首先检查求解步骤和程序有无 错误，然后检查解是否反映现实问题；
❖ (5) 解的控制。通过控制解的变化过程决定对 解是否要作一定的改变；
❖ (6) 解的实施。是指将解用到实际中必须考虑 到实施的问题，如向实际部门讲清解的用法， 在实施中可能产生的问题和修改。
❖ 以上过程应反复进行。
6
.
第4节 运筹学的模型
模型有三种基本形式： ❖ ①形象模型； ❖ ②模拟模型； ❖ ③符号或数学模型。
7
.
构模的方法和思路有以下五种：
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
10
.
第5节 运筹学的应用
❖ (8) 工程的优化设计 ❖ (9) 计算机和信息系统 ❖ (10) 城市管理 ❖ (11)军事 ❖ (12)其他
11
.
第6节 运筹学的展望
美国前运筹学会主席邦特(S.Bonder)认为， 运筹学应在三个领域发展：
❖ 运筹学应用 ❖ 运筹科学 2
.
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学，至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是：“为决策机构在对其控 制下业务活动进行决策时，提供以数量化为 基础的科学方法。”
❖ 另一定义是：“运筹学是一门应用科学，它 广泛应用现有的科学技术知识和数学方法， 解决实际中提出的专门问题，为决策者选择 最优决策提供定量依据。”
14
.
解的概念变化
❖ 相应的一些概念和方法都应有所变化， 如将过分理想化的“最优解”换成“满 意解”。过去把求得的“解”看作精确 的、不能变的凝固的东西，而现在要以 “易变性”的理念看待所得的“解”以 适应系统的不断变化 。
15
.
两个很重要的趋势
❖ 一个趋势是软运筹学崛起。 ❖ 一个趋势是与优化有关的，即软计算。
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化，使用高深的数学工具，而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
13
.
非数学的方法和理论引入运筹学
❖ 在运筹学中除常用的数学方法以外，还引入 一些非数学方法和理论。
.
模型的一般数学形式可用下列表达式描述：
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中：xi——可控变量；
yj——已知参数；
ζk——随机因素。
9
.
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
.
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。 ❖ 第二次世界大战后，20世纪发展概况。 ❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西
方引入我国，并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍，使运筹数学的很多分支很快跟上当时的国际水平
❖ 1959年，运筹学部门在中国科学院数学研究所成立，力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室，当时的主要研究方向为排队论、非线性规划和 图论，还有人专门研究运输理论、动态规划和经济分析 （例如投入产出方法）。在当时这些先遣者中，越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (5) 宽容原则。解决问题的思路要宽，方法要多，而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡，关系的平衡。
4
.
第3节 运筹学的工作步骤
❖ (1) 提出和形成问题。即要弄清问题的目标，可 能的约束，问题的可控变量以及有关参数，搜集 有关资料；
❖ (2) 建立模型。即把问题中可控变量、参数和目 标与约束之间的关系用一定的模型表示出来；
这种方法不追求严格最优，具有启发式 思路。
16
.
❖ 美国运筹学家沙旦(T.L.Saaty)，在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考，它适用于解决那种结构 明确的系统以及战术和技术性问题，而对于 结构不明确的，有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
3
.
前英国运筹学学会会长托姆林森提出六条原则
❖ (1) 合伙原则。是指运筹学工作者要和各方面人，尤 其是同实际部门工作者合作。
❖ (2) 催化原则。在多学科共同解决某问题时，要引导 人们改变一些常规的看法。
❖ (3) 互相渗透原则。要求多部门彼此渗透地考虑问题， 而不是只局限于本部门。
❖ (4) 独立原则。在研究问题时，不应受某人或某部门 的特殊政策所左右，应独立从事工作。
❖ (3) 求解。用各种手段(主要是数学方法，也可 用其他方法)将模型求解。解可以是最优解、次 优解、满意解。复杂模型的求解需用计算机，解 的精度要求可由决策者提出；
5
.
第3节 运筹学的工作步骤
❖ (4) 解的检验。首先检查求解步骤和程序有无 错误，然后检查解是否反映现实问题；
❖ (5) 解的控制。通过控制解的变化过程决定对 解是否要作一定的改变；
❖ (6) 解的实施。是指将解用到实际中必须考虑 到实施的问题，如向实际部门讲清解的用法， 在实施中可能产生的问题和修改。
❖ 以上过程应反复进行。
6
.
第4节 运筹学的模型
模型有三种基本形式： ❖ ①形象模型； ❖ ②模拟模型； ❖ ③符号或数学模型。
7
.
构模的方法和思路有以下五种：
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
10
.
第5节 运筹学的应用
❖ (8) 工程的优化设计 ❖ (9) 计算机和信息系统 ❖ (10) 城市管理 ❖ (11)军事 ❖ (12)其他
11
.
第6节 运筹学的展望
美国前运筹学会主席邦特(S.Bonder)认为， 运筹学应在三个领域发展：
❖ 运筹学应用 ❖ 运筹科学 2
.
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学，至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是：“为决策机构在对其控 制下业务活动进行决策时，提供以数量化为 基础的科学方法。”
❖ 另一定义是：“运筹学是一门应用科学，它 广泛应用现有的科学技术知识和数学方法， 解决实际中提出的专门问题，为决策者选择 最优决策提供定量依据。”
14
.
解的概念变化
❖ 相应的一些概念和方法都应有所变化， 如将过分理想化的“最优解”换成“满 意解”。过去把求得的“解”看作精确 的、不能变的凝固的东西，而现在要以 “易变性”的理念看待所得的“解”以 适应系统的不断变化 。
15
.
两个很重要的趋势
❖ 一个趋势是软运筹学崛起。 ❖ 一个趋势是与优化有关的，即软计算。
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化，使用高深的数学工具，而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
13
.
非数学的方法和理论引入运筹学
❖ 在运筹学中除常用的数学方法以外，还引入 一些非数学方法和理论。