运筹学第四版清华大学出版社运筹学教材编写组第1章 绪论课件
合集下载
18010_清华大学运筹学课件(完整课件)

29
存储论的应用举例
要点一
物资库存管理
在制造业、零售业等领域中,物资库 存管理是一个重要环节。通过应用存 储论的相关模型和策略,可以制定合 理的库存计划和控制策略,降低库存 成本并提高客户服务水平。
要点二
供应链优化
在供应链管理中,存储论可以帮助企 业优化供应链的运作效率。通过协调 供应链各个环节的库存水平和运输计 划,可以减少资源浪费并提高整体供 应链的竞争力。
20
05
图与网络分析
2024/1/25
21
图与网络的基本概念
图与网络定义
由节点和边构成的数学结构, 用于描述对象之间的关系。
有向图与无向图
根据边的方向性分类的图。
2024/1/25
连通性
图中任意两点间都存在路径的 性质。
子图与生成子图
部分节点和边构成的图,及其 与原图的关系。
22
最短路问题
最短路问题的定义
Edmonds-Karp算法
在容量网络中寻找从源点到汇 点的最大可行流。
存在增广路是流非最大的充分 必要条件。
通过不断寻找增广路来增大流 的值,直至达到最大流。
对Ford-Fulkerson算法的改进 ,使用BFS寻找增广路,保证 时间复杂度为多项式级。
2024/1/25
24
最小费用流问题
2024/1/25
清华大学运筹学课件(完整课件)
2024/1/25
1
目 录
2024/1/25
• 绪论 • 线性规划 • 整数规划 • 动态规划 • 图与网络分析 • 存储论 • 排队论 • 对策论基础
2
01
绪论
2024/1/25
3
运筹学的定义与发展
存储论的应用举例
要点一
物资库存管理
在制造业、零售业等领域中,物资库 存管理是一个重要环节。通过应用存 储论的相关模型和策略,可以制定合 理的库存计划和控制策略,降低库存 成本并提高客户服务水平。
要点二
供应链优化
在供应链管理中,存储论可以帮助企 业优化供应链的运作效率。通过协调 供应链各个环节的库存水平和运输计 划,可以减少资源浪费并提高整体供 应链的竞争力。
20
05
图与网络分析
2024/1/25
21
图与网络的基本概念
图与网络定义
由节点和边构成的数学结构, 用于描述对象之间的关系。
有向图与无向图
根据边的方向性分类的图。
2024/1/25
连通性
图中任意两点间都存在路径的 性质。
子图与生成子图
部分节点和边构成的图,及其 与原图的关系。
22
最短路问题
最短路问题的定义
Edmonds-Karp算法
在容量网络中寻找从源点到汇 点的最大可行流。
存在增广路是流非最大的充分 必要条件。
通过不断寻找增广路来增大流 的值,直至达到最大流。
对Ford-Fulkerson算法的改进 ,使用BFS寻找增广路,保证 时间复杂度为多项式级。
2024/1/25
24
最小费用流问题
2024/1/25
清华大学运筹学课件(完整课件)
2024/1/25
1
目 录
2024/1/25
• 绪论 • 线性规划 • 整数规划 • 动态规划 • 图与网络分析 • 存储论 • 排队论 • 对策论基础
2
01
绪论
2024/1/25
3
运筹学的定义与发展
运筹学 绪论PPT课件

No Image
●英1938年成立防空委员会,H.G.铁寨为主席 (历史上第一个运筹学小组)
当时正处在二战前夕,德国有一支强大的 空军,英国是一个岛国,国内任何一地点离海 岸线不超过一百公里,这段距离,德国飞机只 需飞十七分钟。英国要在十七分钟内完成预警、 起飞、爬高、拦击等动作,很难。
事。
No Image
(2)运筹学的发展阶段
运筹学的发展大致经历四个阶段:
① 萌芽阶段 (1915年~30年代)
上世纪初,一些数学方法逐渐应用于经营管理中, 如:
边际分析、盈亏平衡分析、经济批量模型等。 ●边际分析:包括边际成本分析、边际利润分析。
边际成本:增加单位产量所增加的成本。 边际利润:增加单位产量所增加的利润。
No Image
围魏救赵(齐国,孙宾提出直接攻 打魏都大梁)
赤壁之战(三国,诸葛,周俞,曹 操)
No Image
丁渭主持皇宫的修复(北宋,皇宫因火焚毁) 北宋真宗年间,皇城失火,宫殿烧毁,大臣丁谓主持了皇宫修复工
程。他采用了一套综合施工方案: ①先在需要重建的大道上就近取土烧砖; ②在取土后的深沟中引水,形成人工河,再由此水路运入建筑材料,
现代运筹学涵盖了一切领域的管理与优化问题,称为 Management Science
运筹学是研究人能够控制的、需要做出决策的、并且能用数学模型表达、 分析和优化的系统、是一系列用于提高系统有效性的分析工具(主要是 指数学模型)的集合,是人或组织进行合理决策的科学工具。
2.运筹学的发展简史
(1)朴素的运筹学思想
雷达的有效使用:
No Image
1938年,英国为解决空袭的早期 预警,作好反侵略战争准备,积极 进行“雷达”的研究。但随着雷达 性能的改善和配置数量的增多,出 现了来自不同雷达站的信息以及雷 达站同整个防空作战系统的协调配 合问题。为此,在1938年7月,波 德塞(Bawdsey)雷达站的负责人 罗伊(A.P.Rowe)提出立即进行 整个防空作战系统运行的研究,以 使军事领导人学会使用雷达定位敌 方飞机。
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论课件PPT

❖ 在运筹学中除常用的数学方法以外,还引入 一些非数学方法和理论。
❖ 美国运筹学家沙旦(T.L.Saaty),在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考,它适用于解决那种结构 明确的系统以及战术和技术性问题,而对于 结构不明确的,有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
(例如投入产出方法)。在当时这些先遣者中,越民义先
生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、
徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
2021/3/10
2
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学,至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是:“为决策机构在对其控 制下业务活动进行决策时,提供以数量化为 基础的科学方法。”
❖ 以上过程应反复进行。
2021/3/10
6
第4节 运筹学的模型
模型有三种基本形式: ❖ ①形象模型; ❖ ②模拟模型; ❖ ③符号或数学模型。
2021/3/10
7
构模的方法和思路有以下五种:
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
2021/3/10
12
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化,使用高深的数学工具,而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
运筹学(一)ppt课件

2x3 4 3x3 6
x1 0, x2 0, x3取值无约束
解: z令 z,x1 x1,x3x3 x3 ,其x中 3 , x3 0, 同时引入 x4和 松剩 弛余 变 x5,标 变 量准 量形式
m z x 1 a 2 x 2 x 3 x 3 3 x 3 0 x 4 0 x 5
案、措施,是问题中要确定的未知量。
2.目标函数:指问题要达到的目的要求,表示为 决策变量的函数。
3.约束条件:指决策变量取值时受到的各种可用 资源的限制,表示为含决策变量的等式或不等 式。
最新版的一般表示形式:
m ax (mm in ) 或 f ( xm ) a cz 1 x 1 c 1 cx x 21 i x 2 c 2 n x 2 ( cn x ) n c n x n
( 4 )无可行解。
目标函数为max z=3x1+x2,约束条件为
x 1 x 2 2 ; 最x 新1 版整 理ppt 2 x 2 6
库存管理。存储论应用于多种物资库存量的管理,确定某些设备的合 理的能力或容量以及适当的库存方式和库存量
运输问题。用运筹学中运输问题的方法,可以确定最小成本的运输线 路、物资的调拨、运输工具的调度以及建厂地址的选择。
人事管理。可以用运筹学方法对人员的需求和获得情况进行预测;确 定合适需要的人员编制;用指派问题对人员合理分配;用层次分析法 等方法来确定一个人才评价体系等。
数为0;
(4)第i 个约束为 型,在不等式左边减去一 个非负的变量,称为剩余变量;同时令该变量在目
标函数中的系数为0;
(5)若 ,x令0 xx
(6)若 无x约束,令 x,x其中x,
x,x0
例3:将下述线性规划模型化为标准形式:
清华大学运筹学课件(完整课件)
2、定理2
线性规划的基可行解对应于可行域的顶点。
3、定理3 若线性规划有解,则一定存在基可行解 为最优解。
20
§3 单纯形法 基本思路:从可行域的一个顶点到另一个顶点迭代求最优解。
3.1 初始基可行解的确定 1、松弛基(松弛变量对应的B) max z = x1 + 3x2 + 0x3 + 0x4 [eg.8]max z = x1 + 3x2 x1 + 2x2 + x3 =3 x1 + 2x2 ≤ 3 化标准型 2x1 + 3x2 + x4 = 4 2x1 + 3x2 ≤ 4 x1,x2,x3,x4 ≥ 0 x1,x2 ≥ 0
O(0,0)
Q3(2,3)
Q5(4,3) Q2(4,2)
Q1(4,0)
6、可行基 基可行解对应的B为可行基。
基可行解 非可行解
可行解
基解
17
§2 线性规划问题的几何意义 2.1 基本概念 1、凸集:设K为En(n维欧式空间)的一点集,X(1)∈K,X(2)∈K。 若α X(1)+(1-α )X(2)∈K,则称K为凸集。(0<α <1)
15
4、基解:取B = (p1,p2,·,pm) · · a11,·,a1m x1 · · a1m+1,·,a1n xm+1 · · b1 ┆ ┆ ┆ + ┆ ┆ ┆ =┆ am1,·,amm xm · · amm+1,·,amn xn · · bm ↑ ↑ ↑ ↑ 基 基变量 非基 非基变量 令 xm+1 = · = xn = 0 (非基变量为0) · · 则 BXB = b 1 (0) (0) (0) T ∴
运筹学第4版本科版

1.1运筹学的简史
线性规划是由丹捷格(G.B.Dantzig)在1947年发表的 成果。所解决的问题是美国制定空军军事规划时提 出的,并提出了求解线性规划问题的单纯形法。
而早在1939年苏联学者康托洛维奇 (Л.В.Канторович)在解决工业生产组织和计划问 题时,已提出了类似线性规划的模型,并给出了 “解乘数法”的求解方法。由于当时未被领导重视, 直到1960年康托洛维奇再次发表了《最佳资源利用 的经济计算》一书后,才受到国内外的一致重视。 为此康托洛维奇得到了诺贝尔奖。
(1) 提出和形成问题。即要弄清问题的目标,可能的约束,问题的可控变量 以及有关参数,搜集有关资料;
(2) 建立模型。即把问题中可控变量、参数和目标与约束之间的关系用一 定的模型表示出来;
(3) 求解。用各种手段(主要是数学方法,也可用其他方法)将模型求解。解 可以是最优解、次优解、满意解。复杂模型的求解需用计算机,解的精度 要求可由决策者提出;
19
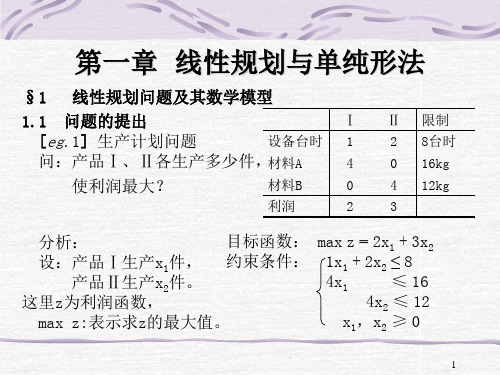
举例:问题的提出
例 2 靠近某河流有两个化工厂 (见图1-1),流经第一化工厂的河 流流量为每天500万立方米,在
两个工厂之间有一条流量为每天
200万立方米的支流。
图1-1
化工厂1每天排放含有某种有害物质的工业污水2万立方米,化工厂2每天 排放的工业污水为1.4万立方米。从化工厂1排出的污水流到化工厂2前, 有20%可自然净化。根据环保要求,河流中工业污水的含量应不大于 0.2%。因此两个工厂都需处理一部分工业污水。化工厂1处理污水的成本 是1000元/万立方米,化工厂2处理污水的成本是800元/万立方米。问:
清华大学出版社
25
解的概念变化
相应的一些概念和方法都应有所变化,如将过分理想 化的“最优解”换成“满意解”。过去把求得的“解 ”看作精确的、不能变的凝固的东西,而现在要以“ 易变性”的理念看待所得的“解”以适应系统的不断 变化 。
运筹学第四版·清华大学出版社·运筹学教材组·1绪论

一 运筹学简史
(2)产生
运筹学作为一门系统的科学,产生的背景为第二 次世界大战。主要用于解决如何在与德军的对抗 中最大限度地杀伤敌人,减少损失。 “运作研究(Operational Research)小组”:解决复杂 的战略和战术问题。例如:
1. 如何合理运用雷达有效地对付德军德空袭; 2. 对商船如何进行编队护航,使船队遭受德国潜艇 攻击时损失最少; 3. 在各种情况下如何调整反潜深水炸弹的爆炸深度, 才能增加对德国潜艇的杀伤力等。
典型战例
不列颠之战
究竟保持多大比例的飞机在巡逻才能持久作战呢?OR 小组的专家纷纷研究这个问题,这个问题最后被生物学家 康顿解决了。他根据计算生物平均寿命的方法,运用飞机 飞行时间、维修时间、空战特点和飞机被落击伤状况等数 据,得出的结论是:只要保持 35% 的飞机在飞行状态,就 能使全部飞机的飞行战斗时间最多。这一研究成果为取得 不列颠之战的胜利作出了贡献。
运筹学的学科地位
运筹学
基础理论
应用理论
应用技术
1 1 1 1 1 1
在数学学科中的地位 在系统科学中的地位 在管理科学中的地位 与经济学的关系 与工程科学的关系
运筹数学 系统工程 管理与运筹学 问题与方法 方法与应用 核心算法与工具
与计算机科学的关系
四 运筹学的应用
1.市场营销: 广告预算、媒介选择、定价、产品开 发与销售计划制定等;
1.囚徒困境问题
两个小偷甲和乙联手作案,因私入民宅被警方
抓住但未获证据。警方将两人分别置于两间房间分
开审讯,政策是若一人招供但另一人未招,则招者
立即被释放,未招者判入狱10年;若二人都招,
则两人各判刑8年;若两人都不招,则未获证据但 因私入民宅各拘留1年。
运筹学(第四版)清华大学出版社《运筹学》教材编写组-第1章 绪论

8
.
模型的一般数学形式可用下列表达式描述:
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中:xi——可控变量;
yj——已知参数;
ζk——随机因素。
9
.
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
.
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。 ❖ 第二次世界大战后,20世纪发展概况。 ❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西
方引入我国,并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍,使运筹数学的很多分支很快跟上当时的国际水平
❖ 1959年,运筹学部门在中国科学院数学研究所成立,力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室,当时的主要研究方向为排队论、非线性规划和 图论,还有人专门研究运输理论、动态规划和经济分析 (例如投入产出方法)。在当时这些先遣者中,越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (5) 宽容原则。解决问题的思路要宽,方法要多,而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡,关系的平衡。
.
模型的一般数学形式可用下列表达式描述:
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中:xi——可控变量;
yj——已知参数;
ζk——随机因素。
9
.
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
.
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。 ❖ 第二次世界大战后,20世纪发展概况。 ❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西
方引入我国,并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍,使运筹数学的很多分支很快跟上当时的国际水平
❖ 1959年,运筹学部门在中国科学院数学研究所成立,力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室,当时的主要研究方向为排队论、非线性规划和 图论,还有人专门研究运输理论、动态规划和经济分析 (例如投入产出方法)。在当时这些先遣者中,越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (5) 宽容原则。解决问题的思路要宽,方法要多,而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡,关系的平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
❖ 在运筹学中除常用的数学方法以外,还引入 一些非数学方法和理论。
❖ 美国运筹学家沙旦(T.L.Saaty),在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考,它适用于解决那种结构 明确的系统以及战术和技术性问题,而对于 结构不明确的,有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
3
运筹学第四版清华大学出版社
前英国运筹学学会会长托姆林森提出六条原则
❖ (1) 合伙原则。是指运筹学工作者要和各方面人,尤 其是同实际部门工作者合作。
❖ (2) 催化原则。在多学科共同解决某问题时,要引导 人们改变一些常规的看法。
❖ (3) 互相渗透原则。要求多部门彼此渗透地考虑问题, 而不是只局限于本部门。
2
运筹学第四版清华大学出版社
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学,至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是:“为决策机构在对其控 制下业务活动进行决策时,提供以数量化为 基础的科学方法。”
❖ 另一定义是:“运筹学是一门应用科学,它 广泛应用现有的科学技术知识和数学方法, 解决实际中提出的专门问题,为决策者选择 最优决策提供定量依据。”
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
运筹学第四版清华大学出版社
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。
❖ 第二次世界大战后,20世纪发展概况。
❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西 方引入我国,并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍,使运筹数学的很多分支很快跟上当时的国际水平
10
运பைடு நூலகம்学第四版清华大学出版社
第5节 运筹学的应用
❖ (8) 工程的优化设计 ❖ (9) 计算机和信息系统 ❖ (10) 城市管理 ❖ (11)军事 ❖ (12)其他
11
运筹学第四版清华大学出版社
第6节 运筹学的展望
美国前运筹学会主席邦特(S.Bonder)认为, 运筹学应在三个领域发展:
❖ 运筹学应用 ❖ 运筹科学 ❖ 运筹数学。
8
运筹学第四版清华大学出版社
模型的一般数学形式可用下列表达式描述:
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中:xi——可控变量;
yj——已知参数;
ζk——随机因素。
9
运筹学第四版清华大学出版社
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
❖ 1959年,运筹学部门在中国科学院数学研究所成立,力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室,当时的主要研究方向为排队论、非线性规划和 图论,还有人专门研究运输理论、动态规划和经济分析 (例如投入产出方法)。在当时这些先遣者中,越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (4) 独立原则。在研究问题时,不应受某人或某部门 的特殊政策所左右,应独立从事工作。
❖ (5) 宽容原则。解决问题的思路要宽,方法要多,而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡,关系的平衡。
4
运筹学第四版清华大学出版社
第3节 运筹学的工作步骤
❖ (1) 提出和形成问题。即要弄清问题的目标,可 能的约束,问题的可控变量以及有关参数,搜集 有关资料;
6
运筹学第四版清华大学出版社
第4节 运筹学的模型
模型有三种基本形式: ❖ ①形象模型; ❖ ②模拟模型; ❖ ③符号或数学模型。
7
运筹学第四版清华大学出版社
构模的方法和思路有以下五种:
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
❖ (2) 建立模型。即把问题中可控变量、参数和目 标与约束之间的关系用一定的模型表示出来;
❖ (3) 求解。用各种手段(主要是数学方法,也可 用其他方法)将模型求解。解可以是最优解、次 优解、满意解。复杂模型的求解需用计算机,解 的精度要求可由决策者提出;
5
运筹学第四版清华大学出版社
第3节 运筹学的工作步骤
14
运筹学第四版清华大学出版社
解的概念变化
❖ 相应的一些概念和方法都应有所变化, 如将过分理想化的“最优解”换成“满 意解”。过去把求得的“解”看作精确 的、不能变的凝固的东西,而现在要以 “易变性”的理念看待所得的“解”以 适应系统的不断变化 。
15
运筹学第四版清华大学出版社
两个很重要的趋势
❖ 一个趋势是软运筹学崛起。 ❖ 一个趋势是与优化有关的,即软计算。
❖ (4) 解的检验。首先检查求解步骤和程序有无 错误,然后检查解是否反映现实问题;
❖ (5) 解的控制。通过控制解的变化过程决定对 解是否要作一定的改变;
❖ (6) 解的实施。是指将解用到实际中必须考虑 到实施的问题,如向实际部门讲清解的用法, 在实施中可能产生的问题和修改。
❖ 以上过程应反复进行。
这种方法不追求严格最优,具有启发式 思路。
16
运筹学第四版清华大学出版社
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
运筹学第四版清华大学出版社运筹学教材编写组第1章 绪论
12
运筹学第四版清华大学出版社
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化,使用高深的数学工具,而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
13
运筹学第四版清华大学出版社
非数学的方法和理论引入运筹学
❖ 美国运筹学家沙旦(T.L.Saaty),在20世纪70 年代末提出了层次分析法(AHP)。
❖ 切克兰特(P.B.Checkland)把传统的运筹学方 法称为硬系统思考,它适用于解决那种结构 明确的系统以及战术和技术性问题,而对于 结构不明确的,有人参与活动的系统就不太 胜任了。这就应采用软系统思考方法。
3
运筹学第四版清华大学出版社
前英国运筹学学会会长托姆林森提出六条原则
❖ (1) 合伙原则。是指运筹学工作者要和各方面人,尤 其是同实际部门工作者合作。
❖ (2) 催化原则。在多学科共同解决某问题时,要引导 人们改变一些常规的看法。
❖ (3) 互相渗透原则。要求多部门彼此渗透地考虑问题, 而不是只局限于本部门。
2
运筹学第四版清华大学出版社
第2节 运筹学的性质和特点
❖ 运筹学是一门应用科学,至今还没有统一且 确切的定义。
❖ 莫斯(P.M.Morse)和金博尔(G.E.Kimball)曾对 运筹学下的定义是:“为决策机构在对其控 制下业务活动进行决策时,提供以数量化为 基础的科学方法。”
❖ 另一定义是:“运筹学是一门应用科学,它 广泛应用现有的科学技术知识和数学方法, 解决实际中提出的专门问题,为决策者选择 最优决策提供定量依据。”
一、绪论
第1节 运筹学的简史 第2节 运筹学的性质和特点 第3节 运筹学的工作步骤 第4节 运筹学的模型 第5节 运筹学的应用 第6节 运筹学的展望
1
运筹学第四版清华大学出版社
第1节 运筹学的简史
❖ 运筹学作为科学名字出现在20世纪30年代末。
❖ 第二次世界大战后,20世纪发展概况。
❖ 在20世纪50年代中期钱学森、许国志等教授将运筹学由西 方引入我国,并结合我国的特点在国内推广应用。在此期 间以华罗庚教授为首的一大批数学家加入到运筹学的研究 队伍,使运筹数学的很多分支很快跟上当时的国际水平
10
运பைடு நூலகம்学第四版清华大学出版社
第5节 运筹学的应用
❖ (8) 工程的优化设计 ❖ (9) 计算机和信息系统 ❖ (10) 城市管理 ❖ (11)军事 ❖ (12)其他
11
运筹学第四版清华大学出版社
第6节 运筹学的展望
美国前运筹学会主席邦特(S.Bonder)认为, 运筹学应在三个领域发展:
❖ 运筹学应用 ❖ 运筹科学 ❖ 运筹数学。
8
运筹学第四版清华大学出版社
模型的一般数学形式可用下列表达式描述:
❖ 目标的评价准则 U=f(xi,yj,ξk)
❖ 约束条件
g(xi,yj,ξk)≥0
❖ 其中:xi——可控变量;
yj——已知参数;
ζk——随机因素。
9
运筹学第四版清华大学出版社
第5节 运筹学的应用
❖ (1) 市场销售 ❖ (2) 生产计划 ❖ (3) 库存管理 ❖ (4) 运输问题 ❖ (5) 财政和会计 ❖ (6) 人事管理 ❖ (7) 设备维修、更新和可靠性、项目选择和评价
❖ 1959年,运筹学部门在中国科学院数学研究所成立,力学 所小组与数学所的小组于1960年合并成为数学研究所的一 个研究室,当时的主要研究方向为排队论、非线性规划和 图论,还有人专门研究运输理论、动态规划和经济分析 (例如投入产出方法)。在当时这些先遣者中,越民义先 生、刘源张院士、朱永津教授、桂湘云教授、陈锡康教授、 徐光煇教授、韩继业教授、李秉全教授、郭绍僖教授等。
❖ (4) 独立原则。在研究问题时,不应受某人或某部门 的特殊政策所左右,应独立从事工作。
❖ (5) 宽容原则。解决问题的思路要宽,方法要多,而 不是局限于某种特定的方法。
❖ (6) 平衡原则。要考虑各种矛盾的平衡,关系的平衡。
4
运筹学第四版清华大学出版社
第3节 运筹学的工作步骤
❖ (1) 提出和形成问题。即要弄清问题的目标,可 能的约束,问题的可控变量以及有关参数,搜集 有关资料;
6
运筹学第四版清华大学出版社
第4节 运筹学的模型
模型有三种基本形式: ❖ ①形象模型; ❖ ②模拟模型; ❖ ③符号或数学模型。
7
运筹学第四版清华大学出版社
构模的方法和思路有以下五种:
❖ (1) 直接分析法 ❖ (2) 类比法 ❖ (3) 数据分析法 ❖ (4) 试验分析法 ❖ (5) 想定(构想)法(scenario)
❖ (2) 建立模型。即把问题中可控变量、参数和目 标与约束之间的关系用一定的模型表示出来;
❖ (3) 求解。用各种手段(主要是数学方法,也可 用其他方法)将模型求解。解可以是最优解、次 优解、满意解。复杂模型的求解需用计算机,解 的精度要求可由决策者提出;
5
运筹学第四版清华大学出版社
第3节 运筹学的工作步骤
14
运筹学第四版清华大学出版社
解的概念变化
❖ 相应的一些概念和方法都应有所变化, 如将过分理想化的“最优解”换成“满 意解”。过去把求得的“解”看作精确 的、不能变的凝固的东西,而现在要以 “易变性”的理念看待所得的“解”以 适应系统的不断变化 。
15
运筹学第四版清华大学出版社
两个很重要的趋势
❖ 一个趋势是软运筹学崛起。 ❖ 一个趋势是与优化有关的,即软计算。
❖ (4) 解的检验。首先检查求解步骤和程序有无 错误,然后检查解是否反映现实问题;
❖ (5) 解的控制。通过控制解的变化过程决定对 解是否要作一定的改变;
❖ (6) 解的实施。是指将解用到实际中必须考虑 到实施的问题,如向实际部门讲清解的用法, 在实施中可能产生的问题和修改。
❖ 以上过程应反复进行。
这种方法不追求严格最优,具有启发式 思路。
16
运筹学第四版清华大学出版社
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
运筹学第四版清华大学出版社运筹学教材编写组第1章 绪论
12
运筹学第四版清华大学出版社
近几年来出现一种新的批评
❖ 指出有些人只迷恋于数学模型的精巧、 复杂化,使用高深的数学工具,而不善 于处理面临大量新的不易解决的实际问 题。现代运筹学工作者面临的大量新问 题是经济、技术、社会、生态和政治等 因素交叉在一起的复杂系统。
13
运筹学第四版清华大学出版社
非数学的方法和理论引入运筹学
