天线方向图仿真
相控阵雷达天线方向图仿真研究

2008 年第 1 期 中国雷达 China Radar
37
图 3 d/λ = 0. 5 时的天线方向图 图 4 d/λ = 1 时的天线方向图
参考文献
[ 1 ] 张社欣 ,李文臣 ,郭新海. 密度加权相控阵天线方向图仿真 [J ] . 舰船电子对抗 ,2006 ,29 (4)
(ψ- φ) 。按等比级数求和并运用尤拉公式 ,式(1) 化简为
E (θ)
=
E
si n [
N 2
(ψ -
φ)
]
ej[
N2
1
(ψ-
φ)
]
si n [
1 2
(ψ -
φ)
]
由式 (1) 容易看出 ,当φ = ψ时 , 各分量同相相加 , 场强
幅值最大 ,其值为
| E(θ) | max = N E
场强幅值最大时的归一化方向性函数为
φ = 0 时 , 也就是各阵元等幅同相馈电时 , 由式 (2) 可 知 ,若θ = 0 ,有 F(θ) = 1 ,即方向图最大值在阵列法线 方向 。当φ ≠0 时 , 则方向图最大值方向 (波束指向) 就 要偏移 ,偏移角θ0 由移相器相移量φ决定 。θ0 =θ时 ,应 有 F(θ0 ) = 1 ,由式 (2) 可知应满足
位为基准 ,则
N- 1
∑ E(θ) = E ejk (ψ-φ)
(1)
k=0
式中 :ψ = λ2πd sinθ———由于波程差引起的相邻阵元辐
射场的相位差 ; φ———相邻阵元激励电流相位差 ; kψ———波程差引起的 Ek 对 E0 的相位引前 ; kφ———激励电流相位差引起的 Ek 对 E0 的相位迟后。 任一阵元辐射场与前一阵元辐射场之间的相位差为
双极天线方向图仿真实验报告(B5)

(1)垂直平面
=00的xOz平面即为双极天线的垂直平面。将=00代入式6,可得双极天线垂直平面的方向函数为:
(1-7)
可见,臂长l对垂直平面的方向性没有影响。
(2)水平平面
根据水平平面的定义,仰角为一个常量c,所以,双极天线水平平面的方向函数为:
以振子中心为原点,忽略振子损耗,则细对称振子的电流分布为:
(1-2)
(3)对称振子的辐射场及方向函数
已知对称振子的电流分布后,将电基本振子的远区电场表达式沿对称振子进行积分,就可以得到对称振子的远区电场表达式。
图1双极天线及其坐标
建立上图的坐标系,即可得到对称振子的辐射场表达式:
(1-3)
根据方向函数的定义,对称振子的方向函数如下:
双极天线可以理解成架设在地面上的对称振子,因此,研究双级天线的性质(这里主要指方向性)可以分两步进行。
(1)电基本振子的远区辐射场
如果对称振子的电流分布已知,则由电基本振子的远区辐射场表达式沿对称振子几分,就可以得到对称振子的辐射场表达式。
电基本振子的远区(满足kr>>1,即 )辐射场表达式如下:
(1-1)
式中:
I——电基本振子的电流;
l——电基本振子的长度;
r——远区中一点到电基本振子的距离。
根据远区辐射场的性质可知,Eθ和Hφ的比值为常数(称为媒质的波阻抗),所以,在研究天线的辐射场时,只需要讨论其中的一个量即可。通常总是采用电场强度作为分析的主体。
(2)对称振子的电流分布
如果将细对称振子看成是末端开路的传输线张开形成,则细对称振子的电流分布与末端开路线上的电流分布相似,即非常接近于正弦驻波分布。
天线线列阵方向图
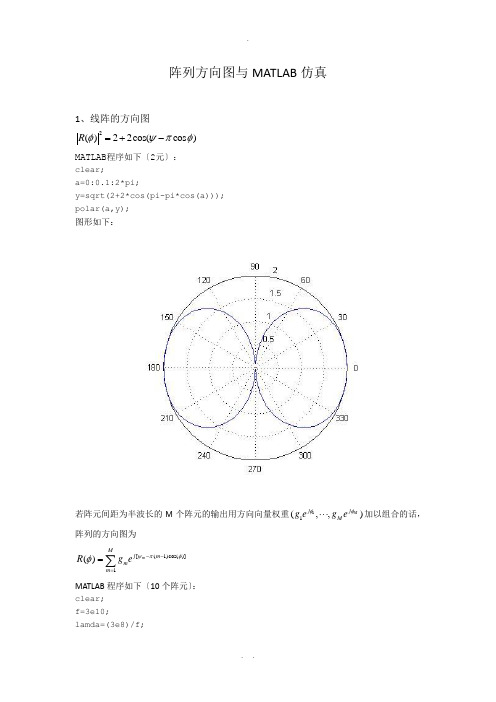
阵列方向图与MATLAB 仿真1、线阵的方向图2()22cos(cos )R φψπφ=+-MATLAB 程序如下〔2元〕:clear;a=0:0.1:2*pi;y=sqrt(2+2*cos(pi-pi*cos(a)));polar(a,y); 图形如下:若阵元间距为半波长的M 个阵元的输出用方向向量权重11(,,)M j j M g eg e φφ⋅⋅⋅加以组合的话,阵列的方向图为 [(1)cos()]1()m Mj m m m R g e ψπφφ--==∑MATLAB 程序如下〔10个阵元〕:clear;f=3e10;lamda=(3e8)/f;beta=2.*pi/lamda;n=10;t=0:0.01:2*pi;d=lamda/4;W=beta.*d.*cos(t);z1=((n/2).*W)-n/2*beta* d;z2=((1/2).*W)-1/2*beta* d;F1=sin(z1)./(n.*sin(z2));iK1=abs(F1) ;polar(t,K1);方向图如下:2、圆阵方向图程序如下:clc;clear all;close all;M = 16; % 行阵元数k = 0.8090; % k = r/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值m = [0 : M-1];w = exp(-j*2*pi*k*cos(2*pi*m'/M-DOA_theta*pi/180)*cos(DOA_fi*pi/180));% w = exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)+sin(2*pi*m'/M)*si n(DOA_fi*pi/180))); % 竖直放置% w = chebwin(M, 20) .* w; % 行加切比雪夫权% 绘制水平面放置的均匀圆阵的方向图theta = linspace(0,180,360);fi = linspace(0,90,180);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)a = exp(-j*2*pi*k*cos(2*pi*m'/M-theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180));%a=exp(-j*2*pi*k*(cos(2*pi*m'/M)*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)+sin(2*pi*m'/ M)*sin(fi(i_fi)*pi/180))); % 竖直放置Y(i_theta,i_fi) = w'*a;endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);% Y = (Y+20) .* ((Y+20)>0) - 20; % 切图Z = Y + 20;Z = Z .* (Z > 0);Y = Z - 20;figure; mesh(fi, theta, Y); view([66, 33]);title('水平放置时的均匀圆阵方向图');% title('竖面放置时的均匀圆阵方向图'); % 竖直放置axis([0 90 0 180 -20 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角/(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:3、平面阵方向图:clc;clear all;close all;Row_N = 16; % 行阵元数Col_N = 16; % 列阵元数k = 0.5; % k = d/lambdaDOA_theta = 90; % 方位角DOA_fi = 0; % 俯仰角% 形成方位角为theta,俯仰角位fi的波束的权值Row_n = [0 : Row_N-1]; Col_n = [0 : Col_N-1];W_Row = exp(-j*2*pi*k*Row_n'*cos(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_theta*pi/180)*cos(DOA_fi*pi/180)); % W_Col = exp(-j*2*pi*k*Col_n'*sin(DOA_fi*pi/180)); % 竖直放置W_Row = chebwin(Row_N, 20) .* W_Row; % 行加切比雪夫权W_Col = chebwin(Col_N, 30) .* W_Col; % 列加切比雪夫权W = kron(W_Row, W_Col); % 合成的权值N*N x 1% 绘制水平面放置的平面阵的方向图theta = linspace(0,180,180);fi = linspace(0,90,90);for i_theta = 1 : length(theta)for i_fi = 1 : length(fi)row_temp = exp(-j*2*pi*k*Row_n'*cos(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 行导向矢量N x 1col_temp = exp(-j*2*pi*k*Col_n'*sin(theta(i_theta)*pi/180)*cos(fi(i_fi)*pi/180)); % 列导向矢量N x 1% col_temp = exp(-j*2*pi*k*Col_n'*sin(fi(i_fi)*pi/180)); % 竖直放置Y(i_theta,i_fi) = W'*kron(row_temp, col_temp); % 合成的导向矢量N*N x 1 endendY= abs(Y); Y = Y/max(max(Y));Y = 20*log10(Y);Y = (Y+60) .* ((Y+60)>0) - 60; % 切图% Z = Y + 60;% Z = Z .* (Z > 0);% Y = Z - 60;figure; mesh(fi, theta, Y); view([66, 33]);title('水平面放置时的面阵方向图');axis([0 90 0 180 -60 0]);xlabel('俯仰角/(\circ)'); ylabel('方位角(\circ)'); zlabel('P/dB');figure; contour(fi, theta, Y);方向图如下:4、CAPON方法波束形成MATLAB程序如下〔阵元16,信号源3,快拍数1024〕:clear alli=sqrt(-1);j=i;M=16;%均匀线阵列数目P=3;%信号源数目f0=10;f1=50;f2=100;%信号频率nn=1024;%快拍数angle1=-15;angle2=15;angle3=30;%the signal angleth=[angle1;angle2;angle3]';SN1=10;SN2=10;SN3=10;%信噪比sn=[SN1;SN2;SN3];degrad=pi/180;tt=0:.001:1024;x0=exp(-j*2*pi*f0*tt);%3个信号x0、x1、x2x1=exp(-j*2*pi*f1*tt); %x2=exp(-j*2*pi*f2*tt); %t=1:nn;S=[x0(t);x1(t);x2(t)];nr=randn(M,nn);ni=randn(M,nn);u=nr+j*ni;%复高斯白噪声Ps=S*S'./nn;%信号能量ps=diag(Ps);refp=2*10.^(sn/10);tmp=sqrt(refp./ps);S2=diag(tmp)*S;%加入噪声tmp=-j*pi*sin(th*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A=exp(a2);X=A*S2+.1*u;%接收到的信号Rxx=X*X'./nn;%相关矩阵invRxx=inv(Rxx);%搜寻信号th2=[-90:90]';tmp=-j*pi*sin(th2'*degrad);tmp2=[0:M-1]';a2=tmp2*tmp;A2=exp(a2);den=A2'*invRxx*A2;doa=1./den;semilogy(th2,doa,'r');title('spectrum'); xlabel('angle'); ylabel('spectrum'); axis([-90 90 1e1 1e5]); grid;。
平面相控阵天线方向图测量中的栅瓣问题仿真与分析研究

(1)
其中 f (θ , ϕ ) 称为单元天线的方向函数,即元因子,虽然天线阵中各个阵元之间存在互耦, 每个天线元的电流分布必然受到其他天线元的影响, 靠近边缘的阵元所受的影响与阵中心所 受的影响必然不同,不过,这些影响都比较小,通常认为阵中所有天线元具有相同的方向函 数,即 f (θ , ϕ ) = 1 。 F (θ , ϕ ) 称为阵因子,它与阵中各天线元的位置、激励电流幅度和相位 有关。因此,在阵列天线中,方向性主要由阵因子来决定。在平面相控阵天线中,有:
ϕ
2
3
...
N-1
N
y
x
dx
dy
图 1 矩形平面相控阵天线
N −1
对于 xoz 平面, ϕ = 0 ,于是 f ay (θ , ϕ = 0) =
M −1
∑Ae
n n =0
jnα y
为常数,平面阵因子为
f a (θ , 0) = ∑ Am e jm ( kd x sinθ +α x ) = f ax (θ )
�
(c) d x = d y = 2.5λ
图 2 扫描角度为 ±20 时 8 × 8 均匀激励面阵波束扫描方向图 由仿真结果图 2 可知,在阵元间距 d x = d y = 0.5λ、1.5λ、2.5λ 的情况下,通过控制 扫描角度,可以清晰地看到在 ±20 扫描范围内,波束唯一并且指向目标方向,并没有出现 栅瓣。 在 其 余 条 件 不 变 化 的 情 况 下 , 扩 大 扫 描 范 围 , 控 制 电 扫 描 为
1
的幅度为 I n ,步进相位为 α y ,从而形成矩形栅格的平面阵。其中第 (m, n ) 号阵元的电流幅 度为 I mn 。根据方向图乘积定理,天线阵的方向函数 D (θ , ϕ ) 可以表示成单元天线的方向函 数 f (θ , ϕ ) 和阵因子 F (θ , ϕ ) 的乘积:
基于Matlab的阵列天线方向图仿真

赋形的性能受阵列天线[4]的类型及相关参数的影响, 可通过阵列天线的方向图进行直观展现,因此,对阵 列天线的方向图进行仿真研究具有重要的现实意义。
Matlab 能够将数值分析、矩阵计算、科学数据可 视化以及系统建模和仿真等诸多强大的功能都集成在 一个易于使用的视窗环境中,是计算机仿真实验中非 常实用的一种工具。使用 Matlab 对不同类型的天线阵 列的方向图进行仿真研究,首先建立 3 种类型的天线 阵——直线阵、圆阵及平面阵的数学模型并推导各自 的阵因子表达式,之后通过仿真,对比分析阵元数、 波长、阵元间距等参数对不同类型的阵列天线方向图 的影响。
收稿日期: 2019-12-10 基金项目: 重庆市教育教学改革重大项目(171014);重庆邮电大
学教育教学改革019-06);重庆邮电大学 大学生科研训练计划项目(A2018-56) 作者简介: 张承畅(1975—),男,湖北利川,博士,副教授、高 级实验师,研究方向为软件无线电、实验教学改革。 E-mail: zhangcc@
影响,仿真结果表明:直线阵、平面阵的性能与阵元数、阵元间距呈正相关,与波长呈负相关;圆阵的性能
与阵元数呈正相关,而与圆阵半径和波长的关系并不是线性的。
关键词:天线阵列;方向图;Matlab
中图分类号:TN710-45
文献标识码:A
文章编号:1002-4956(2020)08-0062-06
Directional diagram of array antenna based on Matlab
Abstract: The mathematical models of linear arrays antenna, circular arrays and planar arrays are constructed, and the corresponding array factor expressions are derived. The simulation research on three kinds of array antenna directional diagrams are carried out with Matlab. Through a comparative study of the influence of the number of elements, wavelength, spacing and other parameters on the different types of array antenna directional diagrams, the simulation results show that the performance of linear array and plane array is positively correlated with the number of array elements and the spacing of array elements, and negatively correlated with the wavelength. The performance of circular array is positively correlated with the number of array elements, but not linearly correlated with the radius and wavelength of circular array. Key words: antenna array; directional diagram; Matlab
天线方向图
5
图 Theta面方向图:E-theata分量,phi=0,44,92°
6
八木天线的方向图
7
8
板状天线 9ຫໍສະໝຸດ Sidelobes (low gain)
Main Lobe (High gain)
10
11
12
13
l 可以增加第二个频率的微带天线,半球形方向图,厚度增加约4mm。
l 天线形式:微带天线
l 极化:垂直线极化(E-syt)
l 3dB波束宽度:水平面( =90°)70°,垂直面( =90°)110°
2
图 立体方向图
3
4
图 Phi面方向图:Etheta分量,theta=20,30,40,50,60,70,80,90°
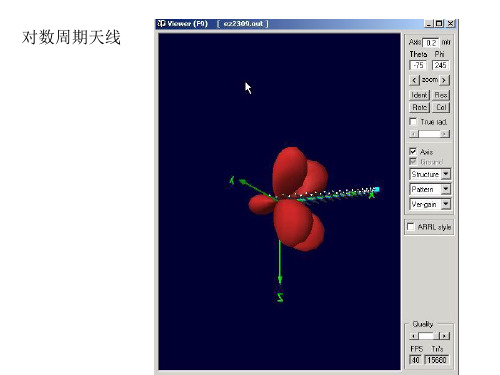
对数周期天线
1
仿真模型(从上到下:辐射片、介质、安装面、插座。介质芯片尺 寸:直径80mm×厚5mm;仿真的安装面尺寸:直径90mm)
l “葫芦形”方向图。 最大辐射方向:+Y,-Y轴方向,适用于需要覆盖狭长空间的场合
l 体积小:相当于普通微带天线的尺寸
l 相对带宽:约5.5%(VSWR<1.5), 13%(VSWR<2)
手把手教你天线设计——用MATLAB仿真天线方向图

手把手教你天线设计——用MATLAB仿真天线方向图吴正琳天线是一种变换器,它把传输线上传播的导行波,变换成在无界媒介(通常是自由空间)中传播的电磁波,或者进行相反的变换。
在无线电设备中用来发射或接收电磁波的部件。
无线电通信、广播、电视、雷达、导航、电子对抗、遥感、射电天文等工程系统,凡是利用电磁波来传递信息的,都依靠天线来进行工作。
此外,在用电磁波传送能量方面,非信号的能量辐射也需要天线。
一般天线都具有可逆性,即同一副天线既可用作发射天线,也可用作接收天线。
同一天线作为发射或接收的基本特性参数是相同的。
这就是天线的互易定理。
天线的基本单元就是单元天线。
1、单元天线对称振子是一种经典的、迄今为止使用最广泛的天线,单个半波对称振子可简单地单独立地使用或用作为抛物面天线的馈源,也可采用多个半波对称振子组成天线阵。
两臂长度相等的振子叫做对称振子。
每臂长度为四分之一波长、全长为二分之一波长的振子,称半波对称振子。
对称振子是一种经典的、迄今为止使用最广泛的天线,单个半波对称振子可简单地单独立地使用或用作为抛物面天线的馈源,也可采用多个半波对称振子组成天线阵。
两臂长度相等的振子叫做对称振子。
每臂长度为四分之一波长、全长为二分之一波长的振子,称半波对称振子。
1.1用MATLAB画半波振子天线方向图主要是说明一下以下几点:1、在Matlab中的极坐标画图的方法:polar(theta,rho,LineSpec);theta:极坐标坐标系0-2*pirho:满足极坐标的方程LineSpec:画出线的颜色2、在方向图的过程中如果rho不用abs(f),在polar中只能画出正值。
也就是说这时的方向图只剩下一半。
3、半波振子天线方向图归一化方程:Matlab程序:clear alllam=1000;%波长k=2*pi./lam;L=lam/4;%天线臂长theta=0:pi/100:2*pi;f1=1./(1-cos(k*L));f2=(cos(k*L*cos(theta))-cos(k*L))./sin(theta);rho=f1*f2;polar(theta,abs(rho),'b');%极坐标系画图2、线性阵列天线2.1方向图乘积定理阵中第i 个天线单元在远区产生的电场强度为:2(,)ij i i i i ie E K If r πλθϕ-=式中,i K 为第i 个天线单元辐射场强的比例常数,i r 为第i 个天线单元至观察点的距离,(,)i f θϕ为第i 个天线单元的方向图函数,i I 为第i 个天线单元的激励电流,可以表示成为:Bji i i I a e φ-∆=式中,i a 为幅度加权系数,B φ∆为等间距线阵中,相邻单元之间的馈电相位差,亦称阵内相移值。
天线方向图仿真

阵列天线方向图MATLAB 仿真一.实验要求1.运用MATLA仿真16单元阵列天线的方向图。
2.变换9和d观察曲线变化。
二.实验原理1.阵列天线:阵列天线是一类由不少于两个天线单元规则或随机排列并通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整,这就使阵列天线具有各种不同的功能,这些功能是单个天线无法实现的。
2.方向图原理:对于单元数很多的天线阵,用解析方法计算阵的总方向图相当繁杂。
假如一个多元天线阵能分解为几个相同的子阵,则可利用方向图相乘原理比较简单地求出天线阵的总方向图。
一个可分解的多元天线阵的方向图,等于子阵的方向图乘上以子阵为单元天线阵的方向图。
这就是方向图相乘原理。
一个复杂的天线阵可考虑多次分解,即先分解成大的子阵,这些子阵再分解为较小的子阵,直至得到单元数很少的简单子阵为止,然后再利用方向图相乘原理求得阵的总方向图。
这种情况适应于单元是无方向性的条件,当单元以相同的取向排列并自身具有非均匀辐射的方向图时,则天线阵的总方向图应等于单元的方向图乘以阵的方向图。
三、仿真结果16单元天线方向图,9 =0°, d=2/入16单元天线方向图,0 =0°, d= X16单元天线方向图,0 =20 °, d=2/ Xradian16 单元天线方向图,9 =20°, d=X结果分析:经过仿真结果实现了16单元天线方向图,并分别在d=2/入时在9 =0。
9 =20°方向形成波束。
在d= X时,通过对比d=2/入时的曲线可以发现随着阵元之间间隔的增加,方向图衰减越快,主次瓣的差距越大,次瓣衰减越快,效果越好。
四、源代码1.clear;theta=-pi/2:0.01:pi/2;lamda=0.03;d=lamda/2;n1=16; beta=2*pi*d*sin(theta)/lamda; z11=(n1/2)*beta;z21=(1/2)*beta; f1=sin(z11)./(n1*sin(z21));F1=abs(f1); figure(1); plot(theta,F1, 'b' ); xlabel( 'theta/radian' ); ylabel( 'amplitude' ); legend( 'n=16' );2.clear;theta=-pi/2:0.01:pi/2; lamda=0.03;d=lamda;n1=16; beta=2*pi*d*sin(theta)/lamda; z11=(n1/2)*beta;z21=(1/2)*beta; f1=sin(z11)./(n1*sin(z21));F1=abs(f1); figure(1); plot(theta,F1, 'b' ); xlabel( 'theta/radian' ); ylabel( 'amplitude' ); legend( 'n=16' );3.clear;theta=-pi/2:0.01:pi/2; lamda=0.03;d=lamda/2;n1=16; beta=2*pi*d*(sin(theta)-pi/9)/lamda; z11=(n1/2)*beta;z21=(1/2)*beta; f1=sin(z11)./(n1*sin(z21));F1=abs(f1); figure(1); plot(theta,F1, 'b' ); xlabel( 'theta/radian' ); ylabel( 'amplitude' ); legend( 'n=16' );4.clear;theta=-pi/2:0.01:pi/2;lamda=0.03;d=lamda;n1=16; beta=2*pi*d*(sin(theta)-pi/9)/lamda; z11=(n1/2)*beta;z21=(1/2)*beta; f1=sin(z11)./(n1*sin(z21));F1=abs(f1); figure(1);plot(theta,F1, 'b' );xlabel( 'theta/radian' ); ylabel( 'amplitude' ); legend( 'n=16' );。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阵列天线方向图MATLAB仿真
一.实验要求
1.运用MATLAB仿真16单元阵列天线的方向图。
2.变换θ和d观察曲线变化。
二.实验原理
1.阵列天线:阵列天线是一类由不少于两个天线单元规则或随机排列并
通过适当激励获得预定辐射特性的特殊天线。
阵列天线的辐射电磁场是组成该天线阵各单元辐射场的总和—矢量和由于各单元的位置和馈电电流的振幅和相位均可以独立调整,这就使阵列天线具有各种不同的功能,这些功能是单个天线无法实现的。
2.方向图原理:对于单元数很多的天线阵,用解析方法计算阵的总方向图相当繁杂。
假如一个多元天线阵能分解为几个相同的子阵,则可利用方向图相乘原理比较简单地求出天线阵的总方向图。
一个可分解的多元天线阵的方向图,等于子阵的方向图乘上以子阵为单元天线阵的方向图。
这就是方向图相乘原理。
一个复杂的天线阵可考虑多次分解,即先分解成大的子阵,这些子阵再分解为较小的子阵,直至得到单元数很少的简单子阵为止,然后再利用方向图相乘原理求得阵的总方向图。
这种情况适应于单元是无方向性的条件,当单元以相同的取向排列并自身具有非均匀辐射的方向图时,则天线阵的总方向图应等于单元的方向图乘以阵的方向图。
三、仿真结果
16单元天线方向图,θ=0°,d=2/λ
16单元天线方向图,θ=0°,d=λ
16单元天线方向图,θ=20°,d=2/λ
16单元天线方向图,θ=20°,d=λ
结果分析:
经过仿真结果实现了16单元天线方向图,并分别在d=2/λ时在θ=0°,θ=20°方向形成波束。
在d=λ时,通过对比d=2/λ时的曲线可以发现随着阵元之间间隔的增加,方向图衰减越快,主次瓣的差距越大,次瓣衰减越快,效果越好。
四、源代码
1. clear;
theta=-pi/2:0.01:pi/2;
lamda=0.03;
d=lamda/2;
n1=16;
beta=2*pi*d*sin(theta)/lamda; z11=(n1/2)*beta;
z21=(1/2)*beta;
f1=sin(z11)./(n1*sin(z21));
F1=abs(f1); figure(1);
plot(theta,F1,'b');
xlabel('theta/radian');
ylabel('amplitude');
legend('n=16');
2. clear;
theta=-pi/2:0.01:pi/2;
lamda=0.03;
d=lamda;
n1=16;
beta=2*pi*d*sin(theta)/lamda; z11=(n1/2)*beta;
z21=(1/2)*beta;
f1=sin(z11)./(n1*sin(z21));
F1=abs(f1); figure(1);
plot(theta,F1,'b');
xlabel('theta/radian');
ylabel('amplitude');
legend('n=16');
3. clear;
theta=-pi/2:0.01:pi/2;
lamda=0.03;
d=lamda/2;
n1=16;
beta=2*pi*d*(sin(theta)-pi/9)/lamda; z11=(n1/2)*beta;
z21=(1/2)*beta;
f1=sin(z11)./(n1*sin(z21));
F1=abs(f1); figure(1);
plot(theta,F1,'b');
xlabel('theta/radian');
ylabel('amplitude');
legend('n=16');
4. clear;
theta=-pi/2:0.01:pi/2;
lamda=0.03;
d=lamda;
n1=16;
beta=2*pi*d*(sin(theta)-pi/9)/lamda; z11=(n1/2)*beta;
z21=(1/2)*beta;
f1=sin(z11)./(n1*sin(z21));
F1=abs(f1); figure(1);
plot(theta,F1,'b');
xlabel('theta/radian'); ylabel('amplitude'); legend('n=16');。
