量子化学厦门大学理论化学研究中心整理.ppt
• 价键理论 Valence Bond Theory, VB • 密度泛函
Density Functional Theory, DFT
计算方法
• 分子力学: MM • 半经验方法: MNDO、CNDO … • 从 头 计 算 方 法 (ab initio methods): HF 、
post-SCF ( MP2、CI、CCSD、CASSCF…) • 密度泛函理论: DFT • 量子力学与分子力学结合: QM/MM；ּ ּ ּ
介
量子化学
• 第一章Schrödinger 方程
– 1.1 量子化学概论 – 1.2 量子力学发展简况 – 1.3 Schroedinger 方程 – 1.4 复数 (Complex number)
1.1 量子化学概论
•
量子化学的建立
• 量子力学 (矩阵力学与波动力学）建立 1923-27年。
• 1927年Heitler和London 用量子力学研 究氢分子，提出了共价键的理论基础。
|z| = r = (x2 + y2)1/2
tan = y/x
x = rcos, y = rsin
y
r x
如上图所示，z可表示为
z = rcos + irsin = rei ei = cos + isin
z的复共轭 z* = x – iy = re-i zz* = x2 + y2 = r2 = |z|2
xp ħ / 2
(1.2)
1. 3 Schrödinger 方程
(1) 含时Schroedinger方程 The Time-Dependent Schroedinger
Equation （单粒子、一维情况：m，x）
一维Schroedinger方程
(x,t)
2
2(x,t) V (x,t)(x,t)
dt
2 2m
f
(t)
d 2 (x)
dx2
V (x) (x)
f
(t)
i
1 f (t)
df (t) dt
2 1
2m (x)
d 2 (x)
dx2
V (x)
(1.5)
显然，上式两边应等于一个常数：E. 即
df (t) iE dt f (t)
f (t) eiEt /
2 2m
d
2 (x)
dx2
V
(h = 6.6 10-27 erg .sec) (2) 光电效应 H. Hertz, 1888; J. J. Thomson, 1896 观测
到了光电子与入射光的频率，光电流与光强度的关系。 1905 年Einstein 光子学说：
Ephoton ＝ h ; h = W + 1/2 mv2
(3) 原子的线状光谱及其规律
i t
2m x2
(1.3)
其 中 : ħ = h/2π; (x,t) 为 波 函 数 (wave
function / state function), 描述体系的状态(量子态), |(x,t)|2dx表示t时刻, 在x－x + dx 间找到粒子 的几率，即，量子力学基本假设I (Postulate I)； V(x, t) 为体系的位能函数。
• 4《量子有机化学》，朱永，韩世纲，朱平仇，上海 科学技术出版社，1983.
• 5 《群论在化学中的应用》，F. A. Cotton, 科学出版社， 1987.
6《量子化学》，唐敖庆等，科学出版社，1982.
7 Modern Quantum Chemistry-Introduction to Advanced Electronic Structure Theory, A. Szabo, N. S. Ostlund.
(1.8)
由 |ψ|2 给出的几率密度不随时间变化；具有 这一性质的态为定态 （stationary state），(1.6) 式为定态Schroedinger方程。通过求解(1.6)式的 薛定谔方程，可得确定体系满足边界条件的状 态波函数ψ与允许的能量 E，以及相关的物理 量。
通常，波函数ψ应满足标准化条件： a) 连续性；b) 单值；c) 平方可积。
1913年Bohr量子论，提出了原子量子能级、轨道的概念。
Quantization of energy; Orbital (stationary state); = E/h, ...
1923 年 de Broglie 关系式：
=h/mv = h/p
(1.1）
1927年Heisenberg测不准原理：
量子化学 (Quantum Chemistry)
量子化学是用量子力学原理研究原子、 分子和晶体的电子层结构、化学键理论、 分子间作用力、化学反应理论、各种光 谱、波谱和电子能谱的理论, 以及无机和 有机化合物、生物大分子和各种功能材 料的结构和性能关系的科学.
理论形式
• 分子轨道理论 Molecular Orbital Theory, MO
(2) 定态Schroedinger方程
The Time-Independent Schroedinger Equation
假定： V与时间无关，且
(x,t) = f(t) (x)
(1.4)
( x, t ) t
df (t dt
)
(
x),
2(x, x2
t
)
f
d 2 (x)
(t) dx2
i
df (t) (x)
量化学与其它学科的交叉
• 物理化学: 计算热分子的力学 性质、动力学性质、光谱性 质、固体的化学成键性质等. －量子电化学；量子反应动 力学；…
• 有机化学: 预测异构体的相对 稳定性、反应中间体性质、 反应机理与谱学性质 (NMR, ESR…) 等。 ―量子有机化学.
分析化学: 实验光谱的解析等.
(1.9) (1.10)
(1.11)
例子：解方程 n = 1.
由(1.10)式， 当 = 0，2, 4, …, 2k 时，有 1 = ei2k = ei2k/n , k = 0, 1, 2,…, n-1 (1.12)
薛定谔方程的三维形式
2 2m
(
2 x2
2 y2
2 z2
)
(x,
y,
z)
V
(x,
y,
z)
(x,
y,
z)
E (x, y, z)
1.4 复数 (Complex number)
复数的定义: z = x + iy, 其中 x、y为实数，x和 y分别称为复数z的实部 和虚部。记为 x = Re(z); y = Im(z). 复数 的模与相角为
8 Methods of Electronic Structure Theory, H. F. Schaefer III.
9《量子力学》，曾谨言，科学出版社，1984.
10 The Principles of Quantum Mechanics, Dirac (1958，有中译本).
P. Q. M.
无机化学: 过渡金属化合物的成 键的性质的解析等。
―量子无机化学.
生物化学: 活性中心结构、结 构环境效应、酶与底物相互 作用等。―量子生物化学.
随着计算量子化学方法与计算 机科学的发展, 本世纪可望在 复杂体系的精确量子化学计 算研究方面取得较大进展.
1.2 量子力学发展简况
经典力学的困难? (1) 黑体辐射 １９００年Max Planck量子论：ε ＝ h
11 《线性代数》/《微分方程》
量子化学
• 第一章 Schrödinger 方程 • 第二章 简单量子力学体系 • 第三章 矩阵与算符 • 第四章 角动量与自旋 • 第五章 原子结构 • 第六章 分子的对称性与对称群
• 第七章 简单分子轨道理论 • 第八章 共轭分子的结构与性能 • 第九章 自洽场分子轨道法简介 • 第十章 配位场理论 • 第十一章 分子光谱学原理 • 第十二章 现代计算量子化学计算方法与应用简
量子化学
H E
厦门大学
参考书目
• 1 Quantum Chemistry, Ira N. Levine.Fifth Edition, 2000
• 2 《量子化学》-基本原理和从头计算法(上，中，下) 徐光宪、黎乐民，科学出版社，2001.
• 3 《量子化学基础》，刘若庄等编，科学出版社， 1983.
( x)
(x)
E
(x)
(1.6)
d
2 (x)
dx2
8 2m
2
[E
V
( x)]
(x)
0
式中m为单个粒子的质量；E与V有相同的 量纲，为体系的能量。
体系总的波函数为
(x, t) eiEt / (x) (1.7)
几率密度 (probability density)
||2 = * = |ψ|2 =ψ*ψ
Density Functional Theory, DFT
计算方法
• 分子力学: MM • 半经验方法: MNDO、CNDO … • 从 头 计 算 方 法 (ab initio methods): HF 、
post-SCF ( MP2、CI、CCSD、CASSCF…) • 密度泛函理论: DFT • 量子力学与分子力学结合: QM/MM；ּ ּ ּ
介
量子化学
• 第一章Schrödinger 方程
– 1.1 量子化学概论 – 1.2 量子力学发展简况 – 1.3 Schroedinger 方程 – 1.4 复数 (Complex number)
1.1 量子化学概论
•
量子化学的建立
• 量子力学 (矩阵力学与波动力学）建立 1923-27年。
• 1927年Heitler和London 用量子力学研 究氢分子，提出了共价键的理论基础。
|z| = r = (x2 + y2)1/2
tan = y/x
x = rcos, y = rsin
y
r x
如上图所示，z可表示为
z = rcos + irsin = rei ei = cos + isin
z的复共轭 z* = x – iy = re-i zz* = x2 + y2 = r2 = |z|2
xp ħ / 2
(1.2)
1. 3 Schrödinger 方程
(1) 含时Schroedinger方程 The Time-Dependent Schroedinger
Equation （单粒子、一维情况：m，x）
一维Schroedinger方程
(x,t)
2
2(x,t) V (x,t)(x,t)
dt
2 2m
f
(t)
d 2 (x)
dx2
V (x) (x)
f
(t)
i
1 f (t)
df (t) dt
2 1
2m (x)
d 2 (x)
dx2
V (x)
(1.5)
显然，上式两边应等于一个常数：E. 即
df (t) iE dt f (t)
f (t) eiEt /
2 2m
d
2 (x)
dx2
V
(h = 6.6 10-27 erg .sec) (2) 光电效应 H. Hertz, 1888; J. J. Thomson, 1896 观测
到了光电子与入射光的频率，光电流与光强度的关系。 1905 年Einstein 光子学说：
Ephoton ＝ h ; h = W + 1/2 mv2
(3) 原子的线状光谱及其规律
i t
2m x2
(1.3)
其 中 : ħ = h/2π; (x,t) 为 波 函 数 (wave
function / state function), 描述体系的状态(量子态), |(x,t)|2dx表示t时刻, 在x－x + dx 间找到粒子 的几率，即，量子力学基本假设I (Postulate I)； V(x, t) 为体系的位能函数。
• 4《量子有机化学》，朱永，韩世纲，朱平仇，上海 科学技术出版社，1983.
• 5 《群论在化学中的应用》，F. A. Cotton, 科学出版社， 1987.
6《量子化学》，唐敖庆等，科学出版社，1982.
7 Modern Quantum Chemistry-Introduction to Advanced Electronic Structure Theory, A. Szabo, N. S. Ostlund.
(1.8)
由 |ψ|2 给出的几率密度不随时间变化；具有 这一性质的态为定态 （stationary state），(1.6) 式为定态Schroedinger方程。通过求解(1.6)式的 薛定谔方程，可得确定体系满足边界条件的状 态波函数ψ与允许的能量 E，以及相关的物理 量。
通常，波函数ψ应满足标准化条件： a) 连续性；b) 单值；c) 平方可积。
1913年Bohr量子论，提出了原子量子能级、轨道的概念。
Quantization of energy; Orbital (stationary state); = E/h, ...
1923 年 de Broglie 关系式：
=h/mv = h/p
(1.1）
1927年Heisenberg测不准原理：
量子化学 (Quantum Chemistry)
量子化学是用量子力学原理研究原子、 分子和晶体的电子层结构、化学键理论、 分子间作用力、化学反应理论、各种光 谱、波谱和电子能谱的理论, 以及无机和 有机化合物、生物大分子和各种功能材 料的结构和性能关系的科学.
理论形式
• 分子轨道理论 Molecular Orbital Theory, MO
(2) 定态Schroedinger方程
The Time-Independent Schroedinger Equation
假定： V与时间无关，且
(x,t) = f(t) (x)
(1.4)
( x, t ) t
df (t dt
)
(
x),
2(x, x2
t
)
f
d 2 (x)
(t) dx2
i
df (t) (x)
量化学与其它学科的交叉
• 物理化学: 计算热分子的力学 性质、动力学性质、光谱性 质、固体的化学成键性质等. －量子电化学；量子反应动 力学；…
• 有机化学: 预测异构体的相对 稳定性、反应中间体性质、 反应机理与谱学性质 (NMR, ESR…) 等。 ―量子有机化学.
分析化学: 实验光谱的解析等.
(1.9) (1.10)
(1.11)
例子：解方程 n = 1.
由(1.10)式， 当 = 0，2, 4, …, 2k 时，有 1 = ei2k = ei2k/n , k = 0, 1, 2,…, n-1 (1.12)
薛定谔方程的三维形式
2 2m
(
2 x2
2 y2
2 z2
)
(x,
y,
z)
V
(x,
y,
z)
(x,
y,
z)
E (x, y, z)
1.4 复数 (Complex number)
复数的定义: z = x + iy, 其中 x、y为实数，x和 y分别称为复数z的实部 和虚部。记为 x = Re(z); y = Im(z). 复数 的模与相角为
8 Methods of Electronic Structure Theory, H. F. Schaefer III.
9《量子力学》，曾谨言，科学出版社，1984.
10 The Principles of Quantum Mechanics, Dirac (1958，有中译本).
P. Q. M.
无机化学: 过渡金属化合物的成 键的性质的解析等。
―量子无机化学.
生物化学: 活性中心结构、结 构环境效应、酶与底物相互 作用等。―量子生物化学.
随着计算量子化学方法与计算 机科学的发展, 本世纪可望在 复杂体系的精确量子化学计 算研究方面取得较大进展.
1.2 量子力学发展简况
经典力学的困难? (1) 黑体辐射 １９００年Max Planck量子论：ε ＝ h
11 《线性代数》/《微分方程》
量子化学
• 第一章 Schrödinger 方程 • 第二章 简单量子力学体系 • 第三章 矩阵与算符 • 第四章 角动量与自旋 • 第五章 原子结构 • 第六章 分子的对称性与对称群
• 第七章 简单分子轨道理论 • 第八章 共轭分子的结构与性能 • 第九章 自洽场分子轨道法简介 • 第十章 配位场理论 • 第十一章 分子光谱学原理 • 第十二章 现代计算量子化学计算方法与应用简
量子化学
H E
厦门大学
参考书目
• 1 Quantum Chemistry, Ira N. Levine.Fifth Edition, 2000
• 2 《量子化学》-基本原理和从头计算法(上，中，下) 徐光宪、黎乐民，科学出版社，2001.
• 3 《量子化学基础》，刘若庄等编，科学出版社， 1983.
( x)
(x)
E
(x)
(1.6)
d
2 (x)
dx2
8 2m
2
[E
V
( x)]
(x)
0
式中m为单个粒子的质量；E与V有相同的 量纲，为体系的能量。
体系总的波函数为
(x, t) eiEt / (x) (1.7)
几率密度 (probability density)
||2 = * = |ψ|2 =ψ*ψ
合集下载
化合物的量子化学性质和反应机制
化合物的量子化学性质和反应机制一、量子化学基本概念1.量子力学：研究微观粒子（如原子、分子、离子等）运动规律的学科。
2.波函数：描述微观粒子状态的数学函数，代表粒子在空间某一点出现的概率。
3.薛定谔方程：量子力学的基本方程，描述微观粒子在势能场中的运动。
4.能量本征态：系统可能的能量状态，对应于波函数的特定值。
5.分子轨道理论：研究分子中电子运动规律的理论，包括分子轨道的构建、填充和跃迁。
二、化合物的量子化学性质1.分子轨道对称性：分子轨道关于某个轴或平面对称的性质，影响分子的化学键合和反应性。
2.分子轨道能量：分子轨道的能量级别，决定分子的稳定性和化学反应活性。
3.电负性：描述原子吸引电子能力的物理量，影响化合物中电子分布和化学键性质。
4.分子极性：分子中正负电荷中心不重合导致的极性，影响分子的物理和化学性质。
5.化学键：原子间通过共享或转移电子而形成的相互作用，包括共价键、离子键和金属键等。
三、化学反应的量子化学机制1.反应物和产物：化学反应中参与转化的物质，其分子结构和能量状态发生变化。
2.过渡状态：化学反应过程中能量最高的状态，是反应物转化为产物的必经之路。
3.活化能：使反应物转化为过渡状态所需的能量，影响反应速率。
4.催化剂：参与反应但在反应结束后不消耗的物质，通过降低活化能加速反应速率。
5.电子转移：化学反应中电子从一个物质转移到另一个物质的过程，涉及氧化还原反应。
四、量子化学在化合物研究中的应用1.分子模拟：利用量子化学方法模拟分子结构和性质，预测化学反应结果。
2.化学键理论：分析化学键的类型、长度和强度，解释化合物的稳定性和反应性。
3.光谱学：研究分子在吸收、发射或散射光过程中产生的光谱现象，揭示分子结构和化学环境。
4.量子化学计算：利用计算机算法和软件，计算分子结构和性质，为实验研究和应用提供理论依据。
五、化合物量子化学性质与反应机制的关系1.分子结构与性质：分子结构决定其性质，量子化学方法可用于预测和解释分子性质。
量子化学和计算化学简介PPT课件
Ψ=Φ, 只有一个 Slater 行列式
未考虑电子相关 !
• Post Hartree – Fock 计算
CI, PT, CC
CI 及各种近似
Full CI
0 ca i ia ca ij biaj b ca ij b kiacjb k c
i,a
i,j
i,j,k
a,b
a,b,c
Dim
c
1
求解Schrödinger 方程, 必需:
1. 做近似 2. 有适当的计算工具 3. 有计算程序
主要近似
1. 非相对论近似 2. Born-Oppenheimer 近似 3. Hartree-Fock 近似
独立粒子模型, “轨道”
4. 代数近似 (LCAO) ············
模型 Hamiltonian
- McGraw-Hill Encyclopedia of Chemistry, 1993
理论化学
量子化学 + 统计热力学
1927年, Heitler-London 发表 一篇处理H2分子的论文： W. Heitler and F. London,
Z. Physik, 44, 455 (1927)
从Hubbard model, 排除双占据, 得到
H ti kE ik Ji k 2 S iS k1 2n in k
Heisenberg Model
在 t-J 模型中,令第一项为零, ni=nj=1,
HJi k2SiSk 12
对Ψ(波函数)的近似
对于 ab initio 计算
• Hartree – Fock 计算
理论化学 和
计算化学
什么是理论化学 ?
1893 Nernst 以 “理论化学”
未考虑电子相关 !
• Post Hartree – Fock 计算
CI, PT, CC
CI 及各种近似
Full CI
0 ca i ia ca ij biaj b ca ij b kiacjb k c
i,a
i,j
i,j,k
a,b
a,b,c
Dim
c
1
求解Schrödinger 方程, 必需:
1. 做近似 2. 有适当的计算工具 3. 有计算程序
主要近似
1. 非相对论近似 2. Born-Oppenheimer 近似 3. Hartree-Fock 近似
独立粒子模型, “轨道”
4. 代数近似 (LCAO) ············
模型 Hamiltonian
- McGraw-Hill Encyclopedia of Chemistry, 1993
理论化学
量子化学 + 统计热力学
1927年, Heitler-London 发表 一篇处理H2分子的论文： W. Heitler and F. London,
Z. Physik, 44, 455 (1927)
从Hubbard model, 排除双占据, 得到
H ti kE ik Ji k 2 S iS k1 2n in k
Heisenberg Model
在 t-J 模型中,令第一项为零, ni=nj=1,
HJi k2SiSk 12
对Ψ(波函数)的近似
对于 ab initio 计算
• Hartree – Fock 计算
理论化学 和
计算化学
什么是理论化学 ?
1893 Nernst 以 “理论化学”
量子化学第一章 厦门大学
05
量子化学的未来发展与挑战
量子化学的发展趋势和前沿领域
量子计算的应用
01
随着量子计算技术的不断发展，量子化学在药物研发、材料设
计等领域的应用前景将更加广阔。
人工智能与量子化学的结合
02
利用人工智能技术对量子化学数据进行处理和分析，有助于加
速新材料的发现和优化。
实验与理论的深度融合
03
实验技术和理论模拟的紧密结合将为量子化学研究提供更精确
量子化学第一章 厦门大学
目录
• 量子化学简介 • 厦门大学量子化学研究概况 • 量子化学的基本理论 • 厦门大学在量子化学领域的贡献 • 量子化学的未来发展与挑战
01
量子化学简介
量子化学的发展历程
1920年代
量子力学的发展为量子化学的 诞生奠定了基础。
1930年代
早期量子化学研究主要集中在 氢原子和类氢离子的电子结构 和光谱。
建立量子化学理论体系
厦门大学在量子化学理论方面做出了重要贡献，通过深入 研究量子力学和化学键理论，建立了完善的量子化学理论 体系，为后续的理论研究奠定了基础。
发展密度泛函理论
厦门大学的学者在密度泛函理论方面取得了重要突破，推 动了量子化学计算方法的进步，提高了计算效率和准确性。
探索化学反应机理
厦门大学在化学反应机理的探索方面取得了显著成果，通 过理论计算和模拟，深入揭示了化学反应的微观过程和机 制。
和深入的见解。
量子化学面临的挑战和问题
1 2
量子计算机的规模和可扩展性
目前量子计算机的规模较小，限制了量子化学应 用的发展。
算法效率和精度
提高量子化学算法的效率和精度是当前面临的重 要挑战。
3
《量子化学》课件 (1)
CHAPTER 6- Basis Sets
9
1
,
n,
l,
m;
r,
,
Nr
e Y n1 r l,m
,
❖ r, and are spherical coordinates.
❖ Yl,m - the angular momentum part (function describing "shape").
Computational Chemistry and Molecular Modeling – Principles and applications
CHAPTER 6- Basis Sets
8
❖ Basis Function,
BF N er
❖ Where N -is the normalization constant,α orbital exponent and r- the radius in angstroms.
1d
Computational Chemistry and Molecular Modeling – Principles and applications
CHAPTER 6- Basis Sets
18
Let the functions be represented by STOs.
1
12
0.5
CHAPTER 6- Basis Sets
19
❖
Similarly
1
0
1
r12
CHAPTER 6- Basis Sets
2
➢ Truncation errors ➢ Basis set super position error ➢ Chemical Hamiltonian approach ➢ Counterpoise method ➢ Interaction energy of ion water cluster ➢ List of common available basis sets. ➢ The internet resources for generating basis
量子化学群论基础PPT培训课件
分子的振动与群论
总结词
群论在分子的振动分析中也有重要应用，通过群论可以描述分子的振动模式和频率，进而研究分子的 热力学和反应动力学性质。
详细描述
分子的振动是指分子内部运动模式的总称，包括伸缩振动、弯曲振动、摇摆振动等。群论可以描述分 子的振动模式和频率，将分子振动分类，进而研究分子的热力学和反应动力学性质。此外，群论还可 以用于研究分子的振动光谱和红外光谱等实验现象。
到表示的不可约性。
无限群的表示
03
无限群的表示可以通过函数来表示，通过傅里叶变换可以得到
函数的展开式和表示的不可约性。
03
量子化学中的群论应用
分子对称性与群论
总结词
分子对称性是群论在量子化学中应用的重要领域之一，通过群论可以描述分子的对称性质和对称操作，进而研究 分子的结构和性质。
详细描述
分子对称性是指分子在空间中的对称性质，包括对称面、对称轴、对称中心等。群论是研究对称性的数学工具， 通过群论可以描述分子的对称操作和对称元素，将分子对称性分类，进而研究分子的电子结构和化学键等性质。
分子光谱的解析
分子光谱的解析是群论在量子化学中应用的一个重要方面，通 过群论可以确定分子光谱的能级和光谱项，从而解析出分子的
结构和性质。
群表示理论
群表示的定义
01
群表示是将群元素与线性空间中的向量对应起来的一种方法，
通过群的表示可以研究群的性质和结构。
有限群的表示
02
有限群的表示可以通过矩阵来表示，通过计算矩阵的迹可以得
量子化学群论基础ppt培训课件
目录
• 量子化学简介 • 群论基础 • 量子化学中的群论应用 • 分子光谱与群论 • 量子化学中的群论计算方法 • 总结与展望
量子化学课件--第五章 谐振子
若 x=0 ， 则 表 明 a0=0 。
其一阶导数：
y(x) a1 2a2 x 3a3x2 ... nan xn1 n1
x=0，则表明a1=0。同理取n阶导数，并使得x=0，则
给出an=0。
[(n 2)(n 1)an2 c2an ]xn 0
n0
(n 2)(n 1)an2 c2an 0
2v 2mE2 0
2mE2 (2v 1)2vm1
E (v 1)hv, v 0,1,2,... 2
（能量量子化，使得一个级数在有限项后中断）
原递推关系式变为：
cn2
2 (n v)
(n 1)(n 2)
cn
为了去掉通解中的另一个无穷级数，必须使任意常数乘
之后等于零。从而剩下一波函数为 ex2 / 2 乘以只含x的
bj x j c j x j (bj c j )x j
j0
j0
j0
类似于上式，我们想要每个和中的求和极限相同以及
x的幂次相同，需要将幂级数展开等式左边的第一项
的求和指标作一变换，令n=k+2，
n(n 1)an xn2 (k 2)(k 1)ak2 xk
n2
k 0
why？
n(n 1)an xn2
n0
n0,2,4
n1,3,5
y
A
(1)k
c2k x2k
B
(1)
k
c x 2k 1 2k 1
k 0
(2k )! k0
(2k 1)!
上式中的两个级数是对于cos(cx)与sin(cx)的Taylor级 数，与下式一致：
y Acos(cx) Bsin(cx)
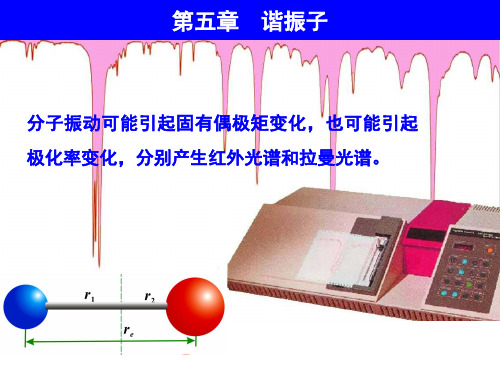
5.2 一维谐振子
在自然界中一维谐振子广泛存在，任何体系在平衡 位置附近的小振动，如分子的振动、晶格的振动、原子 和表面振动以及辐射场的振动等都可以分解成若干彼此 独立的简谐振动。
量子化学计算方法 ppt课件
(PID号由top命令可得，受权限限制)
(7)renice－调整某个进程优先级，格式为：renice 级别 PID号
(级别202为0/120/2~7 19整数，数值越大优先级越低) renice 19 79
21
(8) cat－显示文件内容，格式为：cat 文件名 (9) grep－一般用于从某个或多个文件中搜索某串字符，
(2).对Windows平台：
直接运行setup.exe，其余步骤按提示操作即可；也可将其它 机
器上将已安装好的G03直接拷贝到本机，但需设置运行环境。
对Linux平台：
a.若G03是经过压缩过的(文件结尾为gz)，用gunzip命令解压：
例如： gunzip g03.linux.tar.gz
b.若G03是打包的(文件结尾为tar)，用tar命令将其释放：
辑(该文件内容为默认情况下，计算所花费的内存及硬盘大小)
2020/12/27
12
b.编写或打开g03输入文件
点击RUN，并给定输出 文件名后开始运行
2020/12/27
13
c.g03运行过程的控制：
不要随意点击！
最上行按钮的功能从左至右依次为： 开始运行g03；暂停进程；运行至下一模块(link)时暂停进程； 重新启动进程；清除进程(停止运算)；编辑批作业；运行完 当前任务后，暂停批作业；停止批作业的运算；观看计算结 果；打开文本编辑器；
save the change and quit: :wq
quite without saving : :q!
page down: Ctrl+d page up: Ctrl+u
go to file end: shift+g
《量子化学》PPT课件
Cn 群：只有一条n次旋转轴Cn .
R2 R2
R2
R1
R1
R1
R2
R1
C 群 ppt课件2
14
C3群
C3通过分子中pp心t课件且垂直于荧光屏
15
Cnh群 :
除有一条n次旋转轴Cn外，还有与之垂直的一个镜面σh .
C2h群: 反式二氯乙烯
C2h群: N2F2
C2垂直于荧光屏, σh 在荧光屏上
ppt课件
16
C3h 群
R
R
C3垂直于荧光屏,
σh
在荧光屏上 ppt课件
R
17
Cnv群：
除有一条n次旋转轴Cn外，还有与之相包含的n个镜面σv
C2v群：臭氧
C2v 群：菲
C2与两个σv 的取向参见H2O分子
ppt课件
19
C3v ：NF3
ppt课件
C3v ：CHCl3
（1）旋转轴与旋转操作
分子中若存在一条轴线，绕此轴旋转一定角度能使 分子复原，就称此轴为旋转轴, 符号为Cn . 旋转可以实际 进行，为真操作；相应地，旋转轴也称为真轴.
H2O2中的C2
(旋转轴上的椭圆形为C2的图形符号。类似地，正三角 形、正方p形pt课、件正六边形分别是C3、C4和C6的图形符号3）
Y
X
从正四面体的每个顶点到对
ppt课件
面的正三角形中点有一条C3 穿过, 所以共有4条C3,可作出 8个C3对称操作。
32
Td 群:
沿着每一条C3去看, 看到的是这样:
沿着每一条C2去看,
ppt课件
27
D3d : 乙烷交错型
ppt课件
D4d ：单质硫
量子化学学习课件
Aeib / e ib2 / Aeib /
eib2 / 1
精品
(4.19) (4.20)
由 ，ei cos i sin 1 有 = 2m
m = 0, 1, 2, …
即 2b / 2m
b m, m 0,1,2,...
(4.30) (4.31)
精品
本征函数：
Sl,m
(
)
(2l
2
1)
(l (l
| |
m m
|)!1/ |)!
2
Pl|m|
(cos
)
(4.32)
(Pauling & Wilson, Introduction to Quantum Mechanics, McGraw-Hill, New York, 1935)
(4.21)
(4.18)式可写成
T ( ) Aeim m = 0, 1, 2, … (4.22)
角动量z分量的本征值是量子化的。
精品
令 F(r,,) = R(r) Y(,) = R(r) S() T() (4.23)
由归一化条件有
2
| F2 (r,,) | r2 sin drdd 1 0 00
px
p
y
3 sin cos 4 3 sin sin 4
3x
4 r
3y
4 r
精品
Y2,1
15 sin cos exp(2i) 8
Y2,1
d xz
d
yz
15 sin cos cos 4 15 sin cos sin 4
eib2 / 1
精品
(4.19) (4.20)
由 ，ei cos i sin 1 有 = 2m
m = 0, 1, 2, …
即 2b / 2m
b m, m 0,1,2,...
(4.30) (4.31)
精品
本征函数：
Sl,m
(
)
(2l
2
1)
(l (l
| |
m m
|)!1/ |)!
2
Pl|m|
(cos
)
(4.32)
(Pauling & Wilson, Introduction to Quantum Mechanics, McGraw-Hill, New York, 1935)
(4.21)
(4.18)式可写成
T ( ) Aeim m = 0, 1, 2, … (4.22)
角动量z分量的本征值是量子化的。
精品
令 F(r,,) = R(r) Y(,) = R(r) S() T() (4.23)
由归一化条件有
2
| F2 (r,,) | r2 sin drdd 1 0 00
px
p
y
3 sin cos 4 3 sin sin 4
3x
4 r
3y
4 r
精品
Y2,1
15 sin cos exp(2i) 8
Y2,1
d xz
d
yz
15 sin cos cos 4 15 sin cos sin 4
量子化学 PPT
是量子化学家目前面临的挑战之一。
三、量子化学中的三个基本近似
非相对论近似
电子在原子核附近运动但又不被原子核俘获，必须保持很高的运动速 度。根据相对论，此时电子的质量 μ不是一个常数，而是由电子运动速度
v 、光速c 和电子静止质量μ0 决定的 ：
μ
μ0 v 1 c
2
非相对论近似忽略这一相对论效应，认为电子质量μ＝μ0
量子化学可分基础研究和应用研究两大类，基础研究主要是
寻求量子化学中的自身规律，建立量子化学的多体方法和计算方
法等，多体方法包括化学键理论、密度矩阵理论和传播子理论， 以及多级微扰理论、群论和图论在量子化学中的应用等。应用研
究是利用量子化学方法处理化学问题，用量子化学的结果解释化
学现象。
量子化学的研究结果在其他化学分支学科的直接应用，导致
该方程中把电子的质量视为其静止质量，这仅在非相对论条件下
成立，故称为非相对论近似。
Born-Oppenheimer 近似
因为原子核的质量远大于电子的质量，而电子的运动速度比原子核的 运动速度快的多，使得对原子核的每一微小运动，电子都能很快建立起适 应于原子核位置变化后的力场的新的平衡，因此可以近似认为电子是在固 定不动的核势场中运动，这种近似称为Born-Oppenheimer近似，又称为 固定核近似。光谱学实验表明，体系中原子核运动的光谱和电子运动的光 谱可以分离，所以这种近似是合理的。固定核近似下的电子运动方程为:
（1 ）测不准原理是具有波动性的微观粒子的特有运动规律，是
波粒二象性的反映。
（2）测不准关系只说明同时精确测定微观粒子的位置和动量是不 可能的，但不排除在特定条件下非常精确测量某些个别物理量的可 能性。