(完整版)切线的判定与性质、切线长定理练习题
圆的切线的性质和判定-练习题-含答案.doc

D.不能确定的切线的性质与判定副标题 题号 * 总分 得分一、选择题(本大题共2小题,共6.0分)1.己知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为() A.相离 B.相切 C.相交 D.无法确定【答案】C 【解析】解:半径r = 5,圆心到直线的距离d=3,v 5 > 3, BPr > d,二直线和圆相交,故选C.由直线和圆的位置关系:r>d,可知:直线和圆相交.本题考查了直线和圆的位置关系,判断的依据是半径和直线到圆心的距离的大小关系: 设。
的半径为厂,圆心。
到直线/的距离为丈 ①直线/和0。
相交②直线 /和。
相切od=r ;③直线/和。
0相离^d>r.2. 在中,zC= 90°, BC=3cm, AC=4cm,以点 C 为圆心,以2.5cm 为半径画圆,则。
C 与直线AB 的位置关系是() A,相交 B.相切 C.相离 【答案】A 【解析】解:过C 作CD LAB 于。
,如图所示: A ABC 中,L.C — 90, AC= 4, BC = 3, ・・・AB =、泌=5,7 A ABC^Jm=^-ACxBC=预8x CD, 2 2・•. 3 X 4 = 5 CD ,CD= 2.4<2.5, 即』< r, .••以2.5为半径的。
C 与直线AB 的关系是相交; 故选A.过C 作CD LAB 于C,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出 d<r,根据直线和圆的位置关系即可得出结论.本题考查了直线和圆的位置关系,用到的知识点是勾股定理,三角形的面积公式;解此 题的关键是能正确作出辅助线,并进一步求出CO 的长,注意:直线和圆的位置关系有: 相离,相切,相交.二、填空题(本大题共3小题,共9.0分)3, 如图,已知。
是MBC 的内切圆,切点为。
、E 、 尸,如果AE=2, CD= 1, BF= 3,则内切圆的半 径『= .BD【答案】1【解析】解:・.・。
3.7 切线长定理(练习)(解析版)

第三章 圆第七节 切线长定理精选练习一、单选题1.(2021·北京九年级专题练习)如图,PA ,PB 为⊙O 的两条切线,点A ,B 是切点,OP 交⊙O 于点C ,交弦AB 于点D .下列结论中错误的是( )A .PA =PBB .AD =BDC .OP ⊥ABD .∠PAB =∠APB【答案】D【分析】利用切线长定理、等腰三角形的性质即可得出答案.【详解】解:由切线长定理可得:∠APO =∠BPO ,PA =PB ,从而AB ⊥OP ,AD =BD .因此A .B .C 都正确.无法得出∠PAB =∠APB ,可知:D 是错误的.综上可知:只有D 是错误的.故选:D .【点睛】本题考查了切线长定理、等腰三角形的性质,关键是利用切线长定理、等腰三角形的性质解答.2.(2021·全国九年级课时练习)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PA =AO ,PD 与⊙O 相切于点D ,BC ⊥AB 交PD 的延长线于点C ,若⊙O 的半径为1,则BC的长是( )A .1.5B .2CD 【答案】D【分析】连接OD ,根据切线的性质求出∠ODP =90°,根据勾股定理求出PD ,证明BC 是⊙O 的切线,根据切线长定理得出C D =BC ,再根据勾股定理求出BC 即可.【详解】连接OD ,如图所示∵PC 切⊙O 于D ∴∠ODP =90°∵⊙O 的半径为1,PA =AO ,AB 是⊙O 的直径 ∴PO =1+1=2,PB =1+1+1=3,OD =1∴由勾股定理得:PD ==∵BC ⊥AB ,AB 过O ∴BC 切⊙O 于B ∵PC 切⊙O 于D ∴CD =BC设CD =CB =x 在Rt △PBC 中,由勾股定理得:PC 2=PB 2+BC 2即222)3x x +=+ 解得:x 即BC故选:D【点睛】本题考查了切线的性质和判定,及切线长定理,切线的性质定理为:圆的切线垂直于过切点的半径,切线长定理为:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.同时考查了利用勾股定理解直角三角形.3.(2021·湖北武汉市·九年级一模)如图,经过A 、C 两点的⊙O 与△ABC 的边BC 相切,与边AB 交于点D ,若∠AD C =105°,BC =CD =3,则AD 的值为( )A .B .CD 【答案】A【分析】连接OC 、OD ,作OE AB ^于点E .易求出75CBD CDB Ð=Ð=°,30BCD Ð=°.再由切线的性质,即可求出60OCD Ð=°,即三角形OCD 为等边三角形.得出结论60ODC Ð=°,3OC OD CD ===.从而即可求出45ADO Ð=°,即三角形OED 为等腰直角三角形,由此即可求出DE 的长,最后根据垂径定理即可求出AD 的长.【详解】如图,连接OC 、OD ,作OE AB ^于点E .∵BC CD =,∴CBD CDB Ð=Ð,∵105ADC Ð=°,∴75CBD CDB Ð=Ð=°,∴18027530BCD Ð=°-´°=°.由题意可知OC BC ^,即90OCB Ð=°,∴903060OCD OCB BCD Ð=Ð-Ð=°-°=°,∵OD =OC ,∴三角形OCD 为等边三角形.∴60ODC Ð=°,3OC OD CD ===.∴1056045ADO ADC ODC Ð=Ð-Ð=°-°=°,∴三角形OED 为等腰直角三角形,∴3DE ===∴22AD DE ===故选:A .本题考查切线的性质,等腰三角形的性质,三角形外角的性质,等腰直角三角形与等边三角形的判定和性质以及垂径定理,综合性强.正确的连接辅助线是解答本题的关键.4.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB//CD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )A.5cm B.10cm C.745cm D.625cm【答案】C【分析】连接OF,利用切线性质和切线长定理可证明BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,再根据平行线的性质证得∠BOC=90°,进而由勾股定理求得BC长,根据三角形的面积公式求得OF,进而可求得四边形的周长.【详解】解:连接OF,∵直线AB,BC,CD分别与⊙O相切于E,F,G,∴BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBF+∠OCF=90°,即∠BOC=90°,∴在Rt△BOC中,OB=3cm,OC=4cm,由勾股定理得:BC==,由1122OB OC BC OF××=××得:OF=341255´=cm,∴OE=OG=OF= 125cm,∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×125+2×5=745cm,【点睛】本题考查切线的性质、切线长定理、平行线的性质、勾股定理、三角形的面积公式,熟练掌握切线长定理的运用,证得∠BOC =90°和利用等面积法求出OF 是解答的关键.5.(2021·山西吕梁市·九年级月考)如图,四边形ABCD 内接于⊙O ,AB =BC .AT 是⊙O 的切线,∠BAT =55°,则∠D 等于( )A .110°B .115°C .120°D .125°【答案】A【分析】连接AC ,OA ,OB ,先结合切线的性质以及圆的性质求得ACB BAT Ð=Ð,再结合等腰三角形的性质以及圆的内接四边形的性质求得2D ACB Ð=Ð即可.【详解】如图所示,连接AC ,OA ,OB ,则()11802AOB OBA OAB =°-ÐÐÐ=,∵2AOB ACB Ð=Ð,∴90ACB OAB =°-ÐÐ,∴90ACB OAB Ð=°-Ð,∵AT 是⊙O 的切线,∴90BAT OAB Ð=°-Ð,∴55ACB BAT Ð=Ð=°,∵AB BC =,∴1802ABC ACB Ð=°-Ð,根据圆的内接四边形可得:180D ABC Ð=°-Ð,∴2110D ACB Ð=Ð=°,故选:A .【点睛】本题考查圆的综合问题,理解圆的切线的性质以及内接四边形的性质是解题关键.6.(2021·浙江九年级专题练习)如图,⊙O 的弦AB =8,M 是弦AB 上的动点,若OM 的最小值是3,则⊙O 的半径是( )A .4B .5C .6D .7【答案】B【分析】过O 点作OH ⊥AB 于H ,连接OA ,如图,根据垂径定理得到AH =BH =4,利用垂线段最短得到OH =3,然后利用勾股定理计算出OA 即可.【详解】解:过O 点作OH ⊥AB 于H ,连接OA ,如图,∵OH ⊥AB ,∴AH =BH =12AB =12×8=4,∵OM 的最小值是3,∴OH =3,在Rt △OAH 中,OA =5,即⊙O 的半径是5.故选:B .【点睛】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.7.(2020·聊城市茌平区实验中学九年级月考)如图,P 为O 外一点,PA 、PB 分别切O 于点A 、B ,CD 切O 于点E 且分别交PA 、PB 于点C ,D ,若PA =4,则△PCD 的周长为( )A .5B .7C .8D .10【答案】C【分析】根据切线长定理求解即可【详解】解:∵PA 、PB 分别切O 于点A 、B ,CD 切O 于点E ,PA=4,∴PA=PB=4,AC=CE ,BD=DE ,∴△PCD 的周长为PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=4+4=8,故选:C .【点睛】本题考查切线长定理,熟练掌握切线长定理及其应用是解答的关键.8.(2021·北京九年级专题练习)如图,ABC D 的内切圆O e 与A B ,BC ,CA 分别相切于点D ,E ,F ,且2AD =,ABC D 的周长为14,则BC 的长为( )A .3B .4C .5D .6【答案】C 【分析】根据切线长定理得到AF =AD =2,BD =BE ,CE =CF ,由△ABC 的周长为14,可求BC 的长.【详解】解:O Qe 与A B ,BC ,CA 分别相切于点D ,E ,F2AF AD \==,BD BE =,CE CF =,ABC D Q 的周长为14,14AD AF BE BD CE CF \+++++=2()10BE CE \+=5BC \=故选:C .【点睛】本题考查了三角形的内切圆与内心,切线长定理,熟练掌握切线长定理是解题的关键.二、填空题9.如图,PA 、PB 、CD 是⊙O 的切线,A 、B 、E 是切点,CD 分别交PA 、PB 于C 、D 两点,若∠COD =70°,则∠AP B =_______.【答案】40°【分析】先利用切线长定理,得出∠BDO =∠CDO ,∠ACO =∠DCO ,再利用三角形内角和求出∠CDO +∠DCO 后得到∠BDC+∠A CD 的值,最后利用三角形外角的性质得到关于∠P 的方程,解方程即可得出答案.【详解】解:∵PA 、PB 、CD 是⊙O 的切线,∴∠BDO =∠CDO ,∠ACO =∠DCO ,∵∠COD =70°,∴∠CDO +∠DCO =180°-70°=110°,∴∠BDC +∠ACD =2(∠CDO +∠DCO )=2 ×110°=220°,∵∠BDC =∠DCP +∠P ,∠ACD =∠CDP +∠P ,∴∠DCP +∠P +∠CDP +∠P =220°,即180°+∠P =220°,∴∠P =40°,即∠APB =40°,故答案为:40°.【点睛】本题综合考查了圆的切线长定理、三角形的内角和定理、三角形外角的性质等,解决本题的关键是要牢记各定理与性质的内容,能灵活运用它们进行不同的角之间的转化,考查了学生推理分析的能力.10.(2021·浙江九年级其他模拟)如图,已知AD 是BAC Ð的平分线,以线段AB 为直径作圆,交BAC Ð和角平分线于C ,D 两点.过D 向AC 作垂线DE 垂足为点E .若24DE CE ==,则直径AB =_______.【答案】10【分析】连接CD 、OD 、OC 、BD ,运用勾股定理求得CD 的长,再证明DE 是圆O 的切线,运用全等三角形的判定与性质以及余角的性质得出∠CDE =∠BAD ,易得BD =CD ,然后再根据正切函数求得AD ,最后根据勾股定理解答即可.【详解】解:如图:连接CD 、OD 、OC 、BD∵AE ⊥DE , 24DE CE ==∴CD =∵OA =OD∴∠OAD =∠ODA∴∠BOD =∠OAD +∠ODA = 2∠OAD∵∠ODA =∠OAD∴∠EAD =∠ODA∴OD //AE∴OD ⊥DE ,即DE 是圆O 的切线∴∠CDE +∠ODC =90°∵AB是直径∴∠BAD+∠B=90°在△BOD和△DOC中OC=OB,DO=DO,BD=CD ∴△BOD≌△DOC∴∠ODC=∠OBD∴∠CDE=∠BAD∵∠BAD=∠DAC∴∠COD=∠BOD∴BD=CD=∵tan∠BAD=BDAD= tan∠CDE=12CEDE=,∴AD=∴AB10=.故填10.【点睛】本题主要考查了三角形的性质、圆的切线的判定与性质、勾股定理、三角函数等知识点,灵活应用相关知识成为解答本题的关键.11.(2020·湖北孝感市·九年级月考)如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=108°,则∠B+∠D=_____.【答案】216°【分析】连接AB,根据切线得出PA=PB,求出∠PBA=∠PAB=36°,根据圆内接四边形的对角互补得出∠D+∠CBA=180°,再求出答案即可.【详解】解:连接AB,∵PA、PB是⊙O的切线,A、B为切点,∴PA=PB,∴∠PAB=∠PBA,∵∠APB=108°,∴∠PBA=∠PAB=12×(180°﹣∠APB)=36°,∵A、D、C、B四点共圆,∴∠D+∠CBA=180°,∴∠PBC+∠D=∠PBA+∠CBA+∠D=36°+180°=216°,故答案为:216°.【点睛】本题考查了切线长定理,圆周角定理,等腰三角形的性质,三角形内角和定理,圆内接四边形等知识点,能综合运用知识点进行推理和计算是解此题的关键.12.(2021·河北石家庄市·石家庄外国语学校九年级月考)已知△ABC中,⊙I为△ABC的内切圆,切点为H,若B C=6,AC=8,AB=10,则点A到圆上的最近距离等于_____.-【答案】2【分析】连接IA,IA与⊙I半径的差即为点A到圆上的最近距离,只需求出IA和⊙I半径即可得答案.【详解】解:连接IA,设AC、BC分别切⊙I于E、D,连接IE、ID,如图:∵BC=6,AC=8,AB=10,∴BC2+AC2=AB2∴∠C=90°∵⊙I为△ABC的内切圆,∴∠IEC=∠IDC=90°,IE=ID,∴四边形IDCE是正方形,设它的边长是x,则IE=EC=CD=ID=IH=x,∴AE=8﹣x,BD=6﹣x,由切线长定理可得:AH=8﹣x,BH=6﹣x,而AH+BH=10,∴8﹣x+6﹣x=10,解得x=2,∴AH=6,IH=2,∴IA,∴点A到圆上的最近距离为﹣2,故答案为:﹣2.【点睛】本题考查勾股定理、切线长定理、三角形的内切圆等知识,是重要考点,难度较易,掌握相关知识是解题关键.三、解答题13.(2021·浙江温州市·九年级一模)如图,点C ,D 在以AB 为直径的半圆O 上, AD BC=,切线DE 交AC 的延长线于点E ,连接OC .(1)求证:∠ACO =∠ECD .(2)若∠CDE =45°,DE =4,求直径AB 的长.【答案】(1)证明见详解;(2)【分析】(1)由 AD BC=,可得∠A =∠B ,内接四边形可得出∠ECD=∠B ,进而得出∠ACO =∠ECD ;(2))连接OD ,由切线的性质可得出∠ODE =90°,进而得出∠CDO =∠DCO=45°,再根据已知条件计算出∠E=∠ECD ,得到CD=DE =4,再利用勾股定理求出半径,进而得出答案;【详解】(1)证明:∵ AD BC=,∴∠A =∠B ;∵ABDC 是内接四边形∴∠ECD=∠B∴∠ECD=∠A∵AO =CO ;∴∠ACO =∠A∴∠ACO =∠ECD(2)连接OD∵DE 是圆的切线∴∠ODE =90°,∵∠CDE =45°,OC=OD∴∠CDO =∠DCO =45°,∴∠COD =90°,∵ AD BC=,∴ AC DC=,∴∠AOC =∠DOB=45°,∴AO =OC ,∴∠ACO =∠A=1804567.52°-°=° ;∵∠DCO =45°,∴∠ECD =180°-45°-67.5°=67.5°,∵∠E=180°-∠CDE -∠ECD =180°-45°-67.5°=67.5°,∴∠E=∠ECD∴CD=DE =4,∵∠COD =90°,∴222CD OC OD =+∴2216OC OD +=,即28OC =∴OC= 故⊙O 的半径为∴直径AB 的长,【点睛】本题属于圆综合题,考查了圆周角定理,内接四边形,切线性质定理,等腰三角形的判定与性质,勾股定理等知识,熟练掌握性质及定理是解决本题的关键.14.(2021·江苏无锡市·九年级期中)如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,与BA 的延长线交于点D ,DE ⊥P O 交PO 延长线于点E ,连接PB ,∠EDB =∠EPB .(1)求证:PB 是⊙O 的切线.(2)若PB =3,tan ∠PDB =34,求⊙O 的半径.【答案】(1)见解析;(2)32【分析】(1)根据三角形的内角和定理可证E PBO Ð=Ð,然后根据垂直定义可得90E Ð=°,从而得出半径CB PB ^,根据切线的判定定理即可证出结论;(2)连接OC ,根据题意求出45BD PD ==,,再结合切线长定理得到3PC =,2CD =,从而设O e 的半径是r ,利用勾股定理求解即可.【详解】(1),EDB EPB DOE POB Ð=ÐÐ=ÐQ ,E PBO \Ð=Ð,DE PO ^Q ,90E \Ð=°,90PBO \Ð=°,\半径CB PB ^,PB \是O e 的切线.(2)如图,连接OC ,33tan 904PB PDB PBD =Ð=Ð=°Q ,,tan 45BD PB PDB PD \=Ð===g ,.PB Q 和PC 是O e 的切线,3PC PB \==,2CD PD PC \=-=,设O e 的半径是r ,则4OD DB OB r =-=-,PD Q 切O e 于点C ,OC PD \^,222CD OC OD \+=,()22224r r \+=-,32r \=.【点睛】本题考查圆的综合问题,理解切线的判定与性质定理以及正切函数的定义是解题关键.15.(2021·天津九年级学业考试)已知AB 为O e 的直径,点C ,D 为O e 上的两点,AD 的延长线于BC 的延长线交于点P ,连接CD ,30CAB Ð=°.(Ⅰ)如图①,若 2=CBCD ,4AB =,求AD 的长;(Ⅱ)如图②,过点C 作O e 的切线交AP 于点M ,若6CD AD ==,求CM 的长.【答案】(1)AD =;(2)CM = .【分析】(1)根据弧、圆周角之间的关系可求得∠BAD =45°,连接BD ,可得△ABD 为等腰直角三角形,求解即可;(2)根据弦、圆心角之间关系、等边对等角以及三角形外角的性质可求得∠PDM =60°,OC //AP ,再根据切线的性质定理易得△CDM 为直角三角形,解直角三角形即可.【详解】解:(1)∵ 2=CBCD ,30CAB Ð=°,∴1152CAD CAB Ð=Ð=°,∴∠BAD =45°,连接BD ,∵AB 为直径,∴∠BDA =90°,∴cos45AD AB =×°=(2)连接OD 、OC ,∵30CAB Ð=°,∴∠COB =60°,∠AOC =120°,∵6CD AD ==,∴∠AOD =∠COD =60°,∴∠ACD =∠CAD =30°,∠BAP =∠CAD +∠CAB =60°=∠COB ,∴OC //AP ,∠CDP =∠ACD +∠CAD =60°,∵CM 为O e 的切线,∴∠OCM =90°,∴∠AMC =180°-∠OCM =90°,在Rt △CDM 中,sin 60CM CD =×°=.【点睛】本题考查切线的性质定理,等腰三角形等边对等角,弧、圆心角、圆周角、弦之间的关系,解直角三角形.正确作出辅助线是解题关键.。
【单点训练】切线长定理

【单点训练】切线长定理【单点训练】切线长定理一、选择题(共15小题)1.(2011•台湾)如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确()2.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,0C=8cm,则BE+CG的长等于()3.如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么的值等于().C D4.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为()5.(2001•嘉兴)已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,C D..C.7.(2000•金华)如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于()8.(2007•大连)如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()9.(2004•云南)如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()10.如图,PA、PB是⊙O的两条切线,A、B为切点,连接OP交AB于点C,连接OA、OB,则图中等腰三角形、直角三角形的个数分别为()11.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()12.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是()13.(2008•凉山州)如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P 的度数为()14.(2005•杭州)如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()15.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积()二、填空题(共15小题)(除非特别说明,请填准确值)16.PA、PB是⊙O的切线,切点是A、B,∠APB=50°,过A作⊙O直径AC,连接CB,则∠PBC=_________.17.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为_________cm.18.一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是_________cm(结果保留根号).19.如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=68°,则∠PAE+∠PBE的度数为_________.20.如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=10cm,则△PDE的周长为_________.21.如图,PA、PB是⊙O的切线,A、B是切点,已知∠P=60°,OA=3,那么AB的长为_________.22.如图,在Rt△ABC中,∠C=90°,BC=5,⊙O与Rt△ABC的三边AB、BC、AC分相切于点D、E、F,若⊙O 的半径r=2,则Rt△ABC的周长为_________.23.圆外切四边形ABCD中,AB=a,BC=b,CD=c,则AD=_________.24.(1999•辽宁)如图,PA、PB分别切⊙O于A、B.PA=5,在劣弧上取点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长等于_________.25.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E,若AB=CD=2,则CE=_________.26.(1999•昆明)已知:如图,圆外切等腰梯形的中位线长为12cm,则梯形的周长=_________cm.27.半径分别是3cm和2cm的两圆的圆心距为13cm,则一条内公切线的长度是_________.28.如图,PA、PB分别切⊙O于A、B,∠APB=50°,则∠AOP=_________度.29.(2009•庆阳)如图,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB= _________度.30.如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为_________ cm.【单点训练】切线长定理参考答案与试题解析一、选择题(共15小题)1.(2011•台湾)如图中,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点.若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确()2.如图,直线AB、CD、BC分别与⊙O相切于E、F、G,且AB∥CD,若OB=6cm,0C=8cm,则BE+CG的长等于()OBC=∠OCB==103.如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么的值等于().C D=CN==4.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为()5.(2001•嘉兴)已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,C D.AP==4.C.,AD=AF+DF=2+x=,即等腰梯形的腰长为7.(2000•金华)如图,圆外切等腰梯形ABCD的中位线EF=15cm,那么等腰梯形ABCD的周长等于()8.(2007•大连)如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()9.(2004•云南)如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()10.如图,PA、PB是⊙O的两条切线,A、B为切点,连接OP交AB于点C,连接OA、OB,则图中等腰三角形、直角三角形的个数分别为()11.如图所示,PA,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()12.如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是()13.(2008•凉山州)如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P 的度数为()14.(2005•杭州)如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()15.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积()二、填空题(共15小题)(除非特别说明,请填准确值)16.PA、PB是⊙O的切线,切点是A、B,∠APB=50°,过A作⊙O直径AC,连接CB,则∠PBC=155°.OBC=∠17.已知⊙O与△ABC的三边AB、BC、AC分别相切于点D、E、F,如果BC边的长为10cm,AD的长为4cm,那么△ABC的周长为28cmcm.18.一位小朋友在不打滑的平面轨道上滚动一个半径为5cm的圆环,当滚到与坡面BC开始相切时停止.其AB=40cm,BC与水平面的夹角为60°.其圆心所经过的路线长是40﹣cm(结果保留根号).,19.如图,PA、PB、CD分别切⊙O于A、B、E,CD交PA、PB于C、D两点,若∠P=68°,则∠PAE+∠PBE的度数为56°.AEB=20.如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=10cm,则△PDE的周长为20cm.21.如图,PA、PB是⊙O的切线,A、B是切点,已知∠P=60°,OA=3,那么AB的长为3.AB×,AB=2AC=322.如图,在Rt△ABC中,∠C=90°,BC=5,⊙O与Rt△ABC的三边AB、BC、AC分相切于点D、E、F,若⊙O 的半径r=2,则Rt△ABC的周长为30.23.圆外切四边形ABCD中,AB=a,BC=b,CD=c,则AD=a+b﹣c.24.(1999•辽宁)如图,PA、PB分别切⊙O于A、B.PA=5,在劣弧上取点C,过C作⊙O的切线,分别交PA,PB于D,E,则△PDE的周长等于10.25.如图,AB是⊙O的直径,C是AB延长线上的一点,CD是⊙O的切线,D为切点,过点B作⊙O的切线交CD于点E,若AB=CD=2,则CE=.,=,=CE=故答案为26.(1999•昆明)已知:如图,圆外切等腰梯形的中位线长为12cm,则梯形的周长=48cm.27.半径分别是3cm和2cm的两圆的圆心距为13cm,则一条内公切线的长度是12cm.==12cm28.如图,PA、PB分别切⊙O于A、B,∠APB=50°,则∠AOP=65度.APO=29.(2009•庆阳)如图,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB= 60度.30.如图:PA、PB切⊙O于A、B,过点C的切线交PA、PB于D、E,PA=8cm,则△PDE的周长为16cm.。
圆的切线的性质与判定-练习题 含答案

圆的切线的性质与判定副标题一、选择题(本大题共2小题,共6.0分)1.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为A. 相离B. 相切C. 相交D. 无法确定【答案】C【解析】解:半径,圆心到直线的距离,,即,直线和圆相交,故选C.由直线和圆的位置关系:,可知:直线和圆相交.本题考查了直线和圆的位置关系,判断的依据是半径和直线到圆心的距离的大小关系:设的半径为r,圆心O到直线l的距离为d,直线l和相交;直线l和相切;直线l和相离.2.在中,,,,以点C为圆心,以为半径画圆,则与直线AB的位置关系是A. 相交B. 相切C. 相离D. 不能确定【答案】A【解析】解:过C作于D,如图所示:在中,,,,,的面积,,,即,以为半径的与直线AB的关系是相交;故选A.过C作于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出,根据直线和圆的位置关系即可得出结论.本题考查了直线和圆的位置关系,用到的知识点是勾股定理,三角形的面积公式;解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.二、填空题(本大题共3小题,共9.0分)3.如图,已知是的内切圆,切点为D、E、F,如果,,,则内切圆的半径______ .【答案】1【解析】解:是的内切圆,切点为D、E、F,,,,,,,,,,,,,是直角三角形,内切圆的半径,故答案为1.根据切线长定理得出,,,进而得出是直角三角形,再利用直角三角形内切圆半径求法得出内切圆半径即可.此题主要考查了切线长定理以及直角三角形内切圆半径求法,根据切线长定理得出是直角三角形是解题关键.4.如图,AD、AE、CB均为的切线,D,E,F分别是切点,,则的周长为______ .【答案】16【解析】解:、AE、CB均为的切线,D,E,F分别是切点,,,,的周长,的周长,,的周长为16.根据切线长定理得:,,,再由的周长代入可求得结论.本题主要考查了切线长定理,熟练掌握从圆外一点引圆的两条切线,它们的切线长相等;此题运用线段间的等量代换将周长转化为一条线段长的2倍,得出结论.5.如图,PA、PB是的切线,A、B是切点,已知,,那么AB的长为______.【答案】【解析】解:过点O作于点C,,、PB是的切线,,,,是等边三角形,,,在中,,,.故答案为:.首先过点O作于点C,由垂径定理可得:,又由PA、PB是的切线,由切线长定理可得,由,即可得是等边三角形,继而可求得,则可求得AC的长,继而求得答案.此题考查了切线长定理、垂径定理、等边三角形的判定与性质以及三角函数的定义此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.三、解答题(本大题共3小题,共24.0分)6.如图,AB为直径,C为上一点,点D是的中点,于E,于F.判断DE与的位置关系,并证明你的结论;若,求AC的长度.【答案】解:与相切.证明:连接OD、AD,点D是的中点,,,,,,,,,与相切.连接BC交OD于H,延长DF交于G,由垂径定理可得:,,,,弦心距,是直径,,,是的中位线,.【解析】先连接OD、AD,根据点D是的中点,得出,进而根据内错角相等,判定,最后根据,得出DE与相切;先连接BC交OD于H,延长DF交于G,根据垂径定理推导可得,再根据AB是直径,推出OH是的中位线,进而得到AC的长是OH长的2倍.本题主要考查了直线与圆的位置关系,在判定一条直线为圆的切线时,当已知条件中明确指出直线与圆有公共点时,通常连接过该公共点的半径,证明该半径垂直于这条直线本题也可以根据与相似,求得AC的长.7.如图,AB为的直径,C为上一点,AD与过点C的切线互相垂直,垂足为点D,AD交于点E,连接CE,CB.求证:;若,,求AE的长.【答案】证明:连接OC,是的切线,.,,.又,,,;解:是直径,,,,.,,∽,,即,,.在直角中,,.【解析】连接OC,利用切线的性质和已知条件推知,根据平行线的性质和等角对等边证得结论;,通过相似三角形∽的对应边成比例求得,在直角中,由勾股定理得到,故AE.本题考查了切线的性质,勾股定理,相似三角形的判定与性质,解题时,注意辅助线的作法.8.如图,AB为的直径,C是上一点,过点C的直线交AB的延长线于点D,,垂足为E,F是AE与的交点,AC平分.求证:DE是的切线;若,,求图中阴影部分的面积.【答案】证明:连接OC,,,平分,,,,,,,,,点C在圆O上,OC为圆O的半径,是圆O的切线;解:在中,,,,在中,,,,,,,,,,,,阴影部分的面积为.【解析】连接OC,先证明,进而得到,于是得到,进而证明DE是的切线;分别求出的面积和扇形OBC的面积,利用即可得到答案.本题主要考查了切线的判定以及扇形的面积计算,解的关键是证明,解的关键是求出扇形OBC的面积,此题难度一般.。
课题:切线的性质与判定及切线长定理专题

切线的性质与判定、切线长定理专题班级:姓名:1、切线的性质例1:(1)AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C;连接BC,若∠P=40°,则∠B等于 . (2).如图,在矩形ABCD中,AB=6,AD=10,AD,AB,BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,且点为N,则DM的长为()A. B.8 C. D.2(1)(2)练习:1、如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=115°,过D点的切线PD与射线BA交于点P,则∠ADP的度数为;2.如图,AB是⊙的直径,CD是∠ACB的平分线交⊙O于点D,过D作⊙O的切线交CB的延长线于点E.若AB=4,∠E=75°,则CD的长为;3.如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a>0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为,则a的值是()A. B. C. D.(1)(2)(3)4.如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=:2.当⊙O与边BC所在的直线与相切时,则AB的长是.5.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值() A.5 B.4 C.4.75 D.4.82、切线的判定例2:(1)如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D 为圆心,DB长为半径作⊙D,AB=10,EB=6.(1)求证:AC是⊙D的切线;(2)求线段AC的长.(2)如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C 作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长度.练习:1.已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.(1)判断⊙O与BC的位置关系,并说明理由;(2)若CE=2,求⊙O的半径r.3、切线长定理例3:(P102,第11题)若AB、BC、CD分别与⊙O相切于E、F、G 三点,且AB∥CD,BO=6,CO=8.(1)求∠BOC的度数;(2)求BC的长;(3)求半径OF的长;(4)E、O、G共线吗?说明理由.(5)连接G、F,求证OB∥FG(6)连接EF 、GF 分别交OB 于P ,交OC 于Q,求证:四边形OPFQ 为矩形.(7)若延长CO 交⊙O 于点M ,过点M 作MN ∥OB 交CD 于点N ,求MN 的长.变式1.如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC=90°,AB=12cm ,AD=8cm ,BC=22cm ,AB 为⊙O 的直径,动点P 从点A 开始沿AD 边向点D 以1cm/s 的速度运动,动点Q 从点C 开始沿CB 边向点B 以2cm/s 的速度运动.P 、Q 分别从点A 、C 同时出发,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t (s ).(1)当t 为何值时,四边形PQCD 为平行四边形?(2)当t 为何值时,PQ 与⊙O 相切?变式2.如图,四边形ABCD 中,AD 平行BC ,∠ABC=90°,AD=2,AB=6,以AB 为直径的半⊙O 切CD 于点E ,F 为弧BE 上一动点,过F 点的直线MN 为半⊙O 的切线,MN 交BC 于M ,交CD 于N ,则△MCN 的周长为( )A .9B .10C .3D .2(变式2) (变式3) (变式4) (变式5) 变式3.如图,正方形ABCD 边长为4cm ,以正方形的一边BC 为直径在正方形ABCD 内作半圆,过A 作半圆的切线,与半圆相切于F 点,与DC 相交于E 点,则△ADE 的面积( )A .12B .24C .8D .6变式4.如图,PA 、PB 、分别切⊙O 于A 、B 两点,∠P=40°,则∠C 的度数为 ;变式5.如图,PA 、PB 、CD 分别切⊙O 于A 、B 、E ,CD 交PA 、PB 于C 、D 两点,若∠P=40°,则∠PAE+∠PBE 的度数为PQ变式6.如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.B.3 C.3 D.(变式6) (例4)4、动态问题例4:如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时运动时间是 s.练习:1.如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,则l沿OC所在直线平移后与⊙O相切,则平移的距离是 cm.(1题) (2题)2.如图,∠AOB=60°,点M是射线OB上的点,OM=4,以点M为圆心,2cm为半径作圆.若OA绕点O按逆时针方向旋转,当OA和⊙M相切时,OA旋转的角度是.变式:如2题图,已知∠AOB=60°,M为OB边上一点,以M为圆心、2cm为半径作⊙M.若⊙M在OB边上运动,则当OM= cm时,⊙M与OA相切.3.如图,P为正比例函数y=x图象上的一个动点,⊙P的半径为3,设点P的坐标为(x,y).则⊙P与直线x=2相切时点P的坐标为.4.如图,已知⊙P的半径为2,圆心P在抛物线y=﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为.。
中考真题;切线的判定与性质(答案详解)

中考复习:切线的判定与性质知识考点:1、掌握切线的判定及其性质的综合运用,在涉及切线问题时,常连结过切点的半径,切线的判定常用以下两种方法:一是连半径证垂直,二是作垂线证半径。
2、掌握切线长定理的灵活运用,掌握三角形和多边形的内切圆,三角形的内心。
精典例题:【例1】如图,AC 为⊙O 的直径,B 是⊙O 外一点,AB 交⊙O 于E 点,过E 点作⊙O 的切线,交BC 于D 点,DE =DC ,作EF ⊥AC 于F 点,交AD 于M 点。
(1)求证:BC 是⊙O 的切线;(2)EM =FM 。
:【例2】如图,△ABC 中,AB =AC ,O 是BC 的中点,以O 为圆心的圆与AB 相切于点D 。
求证:AC 是⊙O 的切线。
》【例3】如图,已知AB 是⊙O 的直径,BC 为⊙O 的切线,切点为B ,OC 平行于弦AD ,OA =r 。
<(1)求证:CD 是⊙O 的切线; (2)求OC AD ⋅的值;(3)若AD +OC =r 29,求CD 的长。
•例1图321MFOEDCB A例2图 EO D C B A •例3图321OD C BA探索与创新:【问题一】如图,以正方形ABCD 的边AB 为直径,在正方形内部作半圆,圆心为O ,CG 切半圆于E ,交AD 于F ,交BA 的延长线于G ,GA =8。
(1)求∠G 的余弦值;!(2)求AE 的长。
【问题二】如图,已知△ABC 中,AC =BC ,∠CAB =α(定值),⊙O 的圆心O 在AB 上,并分别与AC 、BC 相切于点P 、Q 。
,(1)求∠POQ ;(2)设D 是CA 延长线上的一个动点,DE 与⊙O 相切于点M ,点E 在CB 的延长线上,试判断∠DOE 的大小是否保持不变,并说明理由。
(|•问题一图 G F E O DCB A 问题二图NQ P EO DC BA答案精典例题:【例1】如图,AC 为⊙O 的直径,B 是⊙O 外一点,AB 交⊙O 于E 点,过E 点作⊙O 的切线,交BC 于D 点,DE =DC ,作EF ⊥AC 于F 点,交AD 于M 点。
2.5.3切线长定理

(4)垂直关系: OA⊥AP,OB⊥BP,AB⊥OP
课后作业: 课本P75-76习题2.5第5.6.11题
处事,如线段,有始有终; 求知,如射线,只有起点……
感谢倾听,再见!
AP
O. C
B
Q
1.切线长定义: 从圆外一点引圆的切线,这个点与切点
间的线段的长称为切线长。
2.切线长定理: 从圆外一点可以引圆的两条切线,它们
的切线长相等。这一点和圆心的连线平分这 两条切线的夹角。
3.(1)线段的相等关系: OA=OB,PA=PB,AC=BC
(2)角的相等关系: ∠1=∠2 ∠AOP=∠BOP ∠OAP=∠OBP=90O
PA = PB ∠OPA=∠OPB
反思:切线长定理为证明线段相等、角相 等提供新的方法
1、如图,AB、AC切⊙O于B、C两点,连接AO,则下列
说法正确的是( C )
A.∠BAC=60°
B.OB=AC,OC=AB
C.AB=AC,∠BAO=∠CAO
2、如图,AB、AC切⊙O于B、C两点,连接AO,
若OC=6,OA=10,则切线长AB=( C )
切线长定义: 经过圆外一点作圆的切线,这点和切点之间的线段 的长,叫做这点到圆的切线长。
A
比一比
O·
P
切线与切线长是一
B
回事吗?它们有什
么区别与联系呢?
切 线: 是直线,不可以度量; 切线长: 是线段,可以度量。
A
。
P
O
B
几何语言: PA、PB分别切⊙O于A、B
切线长定理 :从圆外 一点可以引圆的两条 切线,它们的切线长 相等,这一点和圆心 的连线平分两条切线 的夹角。
初三数学中考专项练习 切线长定理—知识讲解(基础)

切线长定理—知识讲解(基础)【学习目标】1.了解切线长定义;理解切线的判定和性质;理解三角形的内切圆及内心的定义;2.掌握切线长定理;利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线的判定定理和性质定理1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.要点诠释:切线的判定方法:(1)定义:直线和圆有唯一公共点时,这条直线就是圆的切线;(2)定理:和圆心的距离等于半径的直线是圆的切线;(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点,二是直线与过交点的半径垂直,缺一不可).2.切线的性质定理:圆的切线垂直于过切点的半径.要点诠释:切线的性质:(1)切线和圆只有一个公共点;(2)切线和圆心的距离等于圆的半径;(3)切线垂直于过切点的半径;(4)经过圆心垂直于切线的直线必过切点;(5)经过切点垂直于切线的直线必过圆心.要点二、切线长定理1.切线长:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.要点诠释:切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释:切线长定理包含两个结论:线段相等和角相等.3.圆外切四边形的性质:圆外切四边形的两组对边之和相等.要点三、三角形的内切圆1.三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆.2.三角形的内心:三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心. 要点诠释:(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S 为三角形的面积,P 为三角形的周长,r 为内切圆的半径).【典型例题】类型一、切线长定理1.如图,PA 、PB 、DE 分别切⊙O 于A 、B 、C ,⊙O 的半径长为6 cm ,PO =10 cm ,求△PDE 的周长.【答案与解析】连结OA ,则OA ⊥AP .在Rt △POA 中,PA =22OA OP -=22610-=8(cm ). 由切线长定理,得EA =EC ,CD =BD ,PA =PB , ∴ △PDE 的周长为PE +DE +PD =PE +EC +DC +PD ,=PE +EA +PD +DB =PA +PB =16(cm ).【总结升华】本题考查切线长定理、切线的性质、勾股定理.注意:在有关圆的切线长的计算中,往往利用切线长定理进行线段的转换.2.(2015•柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,∠DAE=∠ABE,边CD与⊙O相交于点E,连接AE,BE.(1)求证:AB=AC;(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.【思路点拨】(1)根据圆周角定理证明∠ABC=∠ACB,得到答案;(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.【答案与解析】证明:(1)∵∠ABE=∠DAE,又∠EAC=∠EBC,∴∠DAC=∠ABC,∵AD∥BC,∴∠DAC=∠ACB,∴∠ABC=∠ACB,∴AB=AC;(2)作AF⊥CD于F,∵四边形ABCE是圆内接四边形,∴∠ABC=∠AEF,又∠ABC=∠ACB,∴∠AEF=∠ACB,又∠AEB=∠ACB,∴∠AEH=∠AEF,在△AEH和△AEF中,,∴△AEH≌△AEF,∴EH=EF,∴CE+EH=CF,在△ABH和△ACF中,,∴△ABH≌△ACF,∴BH=CF=CE+EH.【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.举一反三:【变式】(2015•青海)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.(1)求证:AM=AC;(2)若AC=3,求MC的长.【答案】(1)证明:连接OA,∵AM是⊙O的切线,∴∠OAM=90°,∵∠B=60°,∴∠AOC=120°,∵OA=OC,∴∠OCA=∠OAC=30°,∴∠AOM=60°,∴∠M=30°,∴∠OCA=∠M,∴AM=AC;(2)作AG⊥CM于G,∵∠OCA=30°,AC=3,∴AG=,由勾股定理的,CG=,则MC=2CG=3.类型二、三角形的内切圆3.已知:如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.【答案与解析】设内切圆与三角形的三边AB 、AC 、BC 分别交于D 、E 、F , 连接OE 、 OF 、OD 、AO 、BO 、CO.∴△ABC=△AO B +△AO C +△BO C=12r(a+b+c). 【总结升华】考虑把△ABC 的面积分割成3个以圆的半径为高的三角形面积的和,从而求出△ABC 的面积. 举一反三:【变式】已知如图,△ABC 中,∠C=90°,BC=4,AC=3,求△ABC 的内切圆⊙O 的半径r.【答案】连结OA 、OB 、OC ,∵△ABC 中,∠C=90°,BC=4,AC=3,∴AB=5. 则S △AOB +S △COB +S △AOC =S △ABC ,即11115+4+3=34=12222r r r r ⨯⨯⨯⨯⨯,类型三、与相切有关的计算与证明4.如图,平行四边形ABCD 中,以A 为圆心,AB 为半径的圆交AD 于F ,交BC 于G ,延长BA 交圆于E .(1)若ED 与⊙A 相切,试判断GD 与⊙A 的位置关系,并证明你的结论; (2)在(1)的条件不变的情况下,若GC =CD =5,求AD 的长.G FEDCBA【答案与解析】(1)结论:GD 与O 相切证明:连接AG ∵点G 、E 在圆上, ∴AG AE =∵四边形ABCD 是平行四边形, ∴AD BC ∥ ∴123B ∠=∠∠=∠,∵AB AG =,∴3B ∠=∠,∴12∠=∠654321F EDA在AED ∆和AGD ∆12AE AG AD AD =⎧⎪∠=∠⎨⎪=⎩∴AED AGD ∆∆≌,∴AED AGD ∠=∠ ∵ED 与A 相切∴90AED ∠=︒,∴90AGD ∠=︒ ∴AG DG ⊥∴GD 与A 相切(2)∵5GC CD ==,四边形ABCD 是平行四边形 ∴AB DC =,45∠=∠,5AB AG ==∵AD BC ∥,∴46∠=∠,∴1562B ∠=∠=∠∴226∠=∠ ,∴630∠=︒ ∴10AD =.【总结升华】本题虽然是圆和平行四边形的位置关系问题,但是依然考察的是如何将所有条件放在最基本的三角形中求解的能力.判断出DG 与圆相切不难,难点在于如何证明.第二问则不难,重点在于如何利用角度的倍分关系来判断直角三角形中的特殊角度,从而求解.。
切线的性质与判定练习题及答案

切线的性质与判定练习题及答案1. 已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是A.相切 B.相离C.相离或相切D.相切或相交2.如图,AB与⊙O切于点B,AO=6cm,AB=4cm,则⊙O 的半径为A.B.C.D3.如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,?2cm?为半径作⊙M,?当OM=______cm时,⊙M 与OA相切.4.如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于A.0°B.50°C.0° D.70°5.如图,⊙O的半径为2,点A的坐标为,直线 AB为⊙O的切线,B为切点,则B点的坐标为.A. B. C.5556.如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线,两切线相交于点P,则∠BPC=°。
7.如图,?ABC的一边AB是⊙O的直径,请你添加一个条件,使BC 是⊙O的切线,你所添加的条件为 .A30.8.如图,已知AD为?o的直径,B为AD延长线上一点,BC与?o 切于C点,求证:BD=CD;△AOC≌△CDB.9、如图,AB是⊙O的直径,∠B=45°,AB=AC。
求证:AC是⊙O的切线。
10.已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.求∠BAC的度数;求证:AD=CD.11.如图,AB为⊙O的直径,C为⊙O上一点,AD的过C点的直线互相垂直,垂足为D,且AC平分∠DAB.求证:DC为⊙O的切线;若⊙O的半径为3,AD=4,求AC的长.12.如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.求证:BC平分∠PDB;若PA=6,PC=6,求BD的长.切线的性质与判定练习题1. 如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°.直线BD是否与⊙O相切?为什么?连接CD,若CD=5,求的长.2.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.求证:PA是⊙O的切线;若PD=,求⊙O的直径.3.在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.求证:AC与⊙O相切.若BC=6,AB=12,求⊙O的面积.A4.如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30,D为弧BC 的?中点.求证:AB=BC求证:四边形BOCD是菱形.. C5.如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.AC与CD相等吗?问什么?若AC=2,AO=,求OD的长度.6.如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.判断AF与⊙O的位置关系并说明理由;若⊙O的半径为4,AF=3,求AC的长.7.如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE 的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE 交BA的延长线于点G.求证:CG是⊙O的切线.若∠EAB=30°,CF=2,求GA的长.8.如图,△ABC中,?ACB?90,D是边AB上一点,且?A?2?DCB.E是BC边上的一点,以EC为直径的?O经过点D。
《切线长定理—知识讲解 》同步 2022人教九年级上册专练

切线长定理—知识讲解(基础)【学习目标】1.了解切线长定义;理解切线的判定和性质;理解三角形的内切圆及内心的定义;2.掌握切线长定理;利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线的判定定理和性质定理1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.要点诠释:切线的判定方法:(1)定义:直线和圆有唯一公共点时,这条直线就是圆的切线;(2)定理:和圆心的距离等于半径的直线是圆的切线;(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点,二是直线与过交点的半径垂直,缺一不可).2.切线的性质定理:圆的切线垂直于过切点的半径.要点诠释:切线的性质:(1)切线和圆只有一个公共点;(2)切线和圆心的距离等于圆的半径;(3)切线垂直于过切点的半径;(4)经过圆心垂直于切线的直线必过切点;(5)经过切点垂直于切线的直线必过圆心.要点二、切线长定理1.切线长:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.要点诠释:切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释:切线长定理包含两个结论:线段相等和角相等.3.圆外切四边形的性质:圆外切四边形的两组对边之和相等.要点三、三角形的内切圆1.三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆.2.三角形的内心:三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心. 要点诠释:(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即(S 为三角形的面积,P 为三角形的周长,r 为内切圆的半径).(3) 三角形的外心与内心的区别:名称 确定方法 图形性质外心(三角形外接圆的圆心)三角形三边中垂线的交点(1)OA=OB=OC ;(2)外心不一定在三角形内部内心(三角形内切圆的圆心)三角形三条角平分线的交点(1)到三角形三边距离相等;(2)OA 、OB 、OC 分别平分 ∠BAC 、∠ABC 、∠ACB ; (3)内心在三角形内部.【典型例题】类型一、切线长定理1.如图,PA 、PB 、DE 分别切⊙O 于A 、B 、C ,⊙O 的半径长为6 cm ,PO =10 cm ,求△PDE 的周长.【答案与解析】连结OA ,则OA ⊥AP .在Rt △POA 中,PA =22OA OP -=22610-=8(cm ). 由切线长定理,得EA =EC ,CD =BD ,PA =PB , ∴ △PDE 的周长为PE +DE +PD =PE +EC +DC +PD ,=PE +EA +PD +DB =PA +PB =16(cm ).【总结升华】本题考查切线长定理、切线的性质、勾股定理.注意:在有关圆的切线长的计算中,往往利用切线长定理进行线段的转换.2.(2020•柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.(1)求证:AB=AC;(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.【思路点拨】(1)根据弦切角定理和圆周角定理证明∠ABC=∠ACB,得到答案;(2)作AF⊥CD于F,证明△AEH≌△AEF,得到EH=EF,根据△ABH≌△ACF,得到答案.【答案与解析】证明:(1)∵AD与△ABC的外接圆⊙O恰好相切于点A,∴∠ABE=∠DAE,又∠EAC=∠EBC,∴∠DAC=∠ABC,∵AD∥BC,∴∠DAC=∠ACB,∴∠ABC=∠ACB,∴AB=AC;(2)作AF⊥CD于F,∵四边形ABCE是圆内接四边形,∴∠ABC=∠AEF,又∠ABC=∠ACB,∴∠AEF=∠ACB,又∠AEB=∠ACB,∴∠AEH=∠AEF,在△AEH和△AEF中,,∴△AEH≌△AEF,∴EH=EF,∴CE+EH=CF,在△ABH和△ACF中,,∴△ABH≌△ACF,∴BH=CF=CE+EH.【总结升华】本题考查的是切线的性质和平行四边形的性质以及全等三角形的判定和性质,运用性质证明相关的三角形全等是解题的关键,注意圆周角定理和圆内接四边形的性质的运用.举一反三:【变式】(2020•青海)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.(1)求证:AM=AC;(2)若AC=3,求MC的长.【答案】(1)证明:连接OA,∵AM是⊙O的切线,∴∠OAM=90°,∵∠B=60°,∴∠AOC=120°,∵OA=OC,∴∠OCA=∠OAC=30°,∴∠AOM=60°,∴∠M=30°,∴∠OCA=∠M,∴AM=AC;(2)作AG⊥CM于G,∵∠OCA=30°,AC=3,∴AG=,由勾股定理的,CG=,则MC=2CG=3.类型二、三角形的内切圆3.已知:如图,△ABC的三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.【答案与解析】设内切圆与三角形的三边AB 、AC 、BC 分别交于D 、E 、F , 连接OE 、 OF 、OD 、AO 、BO 、CO.∴△ABC=△AO B +△AO C +△BO C=12r(a+b+c). 【总结升华】考虑把△ABC 的面积分割成3个以圆的半径为高的三角形面积的和,从而求出△ABC 的面积. 举一反三:【变式】已知如图,△ABC 中,∠C=90°,BC=4,AC=3,求△ABC 的内切圆⊙O 的半径r.【答案】连结OA 、OB 、OC ,∵△ABC 中,∠C=90°,BC=4,AC=3,∴AB=5. 则S △AOB +S △COB +S △AOC =S △ABC ,即11115+4+3=34=12222r r r r ⨯⨯⨯⨯⨯,类型三、与相切有关的计算与证明4.如图,平行四边形ABCD 中,以A 为圆心,AB 为半径的圆交AD 于F ,交BC 于G ,延长BA 交圆于E .(1)若ED 与⊙A 相切,试判断GD 与⊙A 的位置关系,并证明你的结论; (2)在(1)的条件不变的情况下,若GC =CD =5,求AD 的长.G FEDCBA【答案与解析】(1)结论:GD 与O 相切证明:连接AG ∵点G 、E 在圆上, ∴AG AE =∵四边形ABCD 是平行四边形, ∴AD BC ∥ ∴123B ∠=∠∠=∠,∵AB AG =,∴3B ∠=∠,∴12∠=∠1F E在AED ∆和AGD ∆12AE AG AD AD =⎧⎪∠=∠⎨⎪=⎩∴AED AGD ∆∆≌,∴AED AGD ∠=∠ ∵ED 与A 相切∴90AED ∠=︒,∴90AGD ∠=︒ ∴AG DG ⊥∴GD 与A 相切(2)∵5GC CD ==,四边形ABCD 是平行四边形 ∴AB DC =,45∠=∠,5AB AG ==∵AD BC ∥,∴46∠=∠,∴1562B ∠=∠=∠∴226∠=∠ ,∴630∠=︒ ∴10AD =.【总结升华】本题虽然是圆和平行四边形的位置关系问题,但是依然考察的是如何将所有条件放在最基本的三角形中求解的能力.判断出DG 与圆相切不难,难点在于如何证明.第二问则不难,重点在于如何利用角度的倍分关系来判断直角三角形中的特殊角度,从而求解.《圆》全章复习与巩固—巩固练习(提高)【巩固练习】一、选择题1.如图所示,AB 、AC 为⊙O 的切线,B 和C 是切点,延长OB 到D ,使BD =OB ,连接AD .如果∠DAC =78°,那么∠ADO 等于( ).A .70°B .64°C .62°D .51°2.在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ,S 射向地面的光束呈圆锥形,其轴截面SAB 的顶角为120°(如图所示),则光源离地面的垂直高度SO 为( ). A .54m B...第1题图第2题图第3题图第4题图3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心、AD的长为半径作半圆,则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是( ).A. B. C. D.5.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为( )A.12.5寸 B.13寸 C.25寸D.26寸6.(2020•贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是()A.0 B.1 C.2 D.37.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为( ).A.80° B.100° C.80°或100° D.160°或200°8.如图所示,AB、AC与⊙O分别相切于B、C两点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是( ).A.65° B.115° C.65°或115° D.130°或50°二、填空题 9.如下左图,是的内接三角形,,点P 在上移动(点P 不与点A 、C 重合),则的变化范围是__ ________.第9题图 第10题图10.如图所示,EB 、EC 是⊙O 是两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,那么∠A 的度数是________________. 11.已知⊙O 1与⊙O 2的半径1r 、2r 分别是方程2680x x -+= 的两实根,若⊙O 1与⊙O 2的圆心距d =5.则⊙O 1与⊙O 2的位置关系是 __ __ .12.(2020•巴彦淖尔)如图,AB 为⊙O 的直径,AB=AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC ;③AE=2EC ;④劣弧是劣弧的2倍;⑤AE=BC ,其中正确的序号是 .13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______ ________. 14.已知正方形ABCD 外接圆的直径为2a ,截去四个角成一正八边形,则这个正八边形EFGHIJLK 的边长为____ ____,面积为_____ ___.15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形,分别以它们的各顶点为圆心,以l 为半径画弧与两邻边相交,得到3条弧,4条弧,……(1)图(1)中3条弧的弧长的和为___ _____,图(2)中4条弧的弧长的和为_____ ___; (2)求图(m)中n 条弧的弧长的和为____ ____(用n 表示).16.如图所示,蒙古包可以近似地看做由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为9πm 2,高为3.5m ,外围高4 m 的蒙古包,至少要____ ____m 2的毛毡.三、解答题17. 如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD.18.(2020•南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类似的思想提出了如下命题:③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:(1)请你从①②③三个命题中选择一个进行证明;(2)请你继续完成下面的探索;①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.【答案与解析】一、选择题1.【答案】B;【解析】由AB为⊙O的切线,则AB⊥OD.又BD=OB,则AB垂直平分OD,AO=AD,∠DAB=∠BAO.由AB、AC为⊙O的切线,则∠CAO=∠BAO=∠DAB.所以,∠DAB=∠DAC=26°.∠ADO=90°-26°=64°.本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.2.【答案】C;【解析】圆锥的高、底面半径与母线组成直角三角形.由题意,SO⊥AB于O,∴∠SOA=∠SOB=90°.又SA=SB,∠ASB=120°,∴∠SAB=∠SBA=180120302=°-?°,设SO=x m,则AS=2x m.∵ AO=27,由勾股定理,得(2x)2-x2=272,解得93x=.3.【答案】A.;【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系.∵矩形ABCD中,AB=2BC,AB=8cm,∴ AD=BC=4cm,∠DAF=90°,,,又AF=AD=4cm,∴,∴.4.【答案】A;【解析】OM最长是半径5;最短是OM⊥AB时,此时OM=3,故选A.5.【答案】D;【解析】因为直径CD垂直于弦AB,所以可通过连接OA(或OB),求出半径即可.根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”,知(寸),在Rt△AOE中,,即,解得OA=13,进而求得CD=26(寸).故选D.6.【答案】B.【解析】设OP与⊙O交于点N,连结MN,OQ,如图,∵OP=4,ON=2,∴N是OP的中点,∵M为PQ的中点,∴MN为△POQ的中位线,∴MN=OQ=×2=1,∴点M在以N为圆心,1为半径的圆上,当点M在ON上时,OM最小,最小值为1,∴线段OM的最小值为1.故选B.7.【答案】C;【解析】圆周角的顶点在劣弧上时,圆周角为5136010092⨯⨯=°°;圆周角的顶点在优弧上时,圆周角为413608092⨯⨯=°°.注意分情况讨论.8.【答案】C;【解析】连接OC、OB,则∠BOC=360°-90°-90°-50°=130°.点P在优弧上时,∠BPC=12∠BOC=65°;点P在劣弧上时,∠BPC=180°-65°=115°.主要应用了切线的性质定理、圆周角定理和多边形内角和定理.二、填空题9.【答案】; 10.【答案】99°;【解析】由EB=EC ,∠E=46°知,∠ECB= 67°,从而∠BCD=180°-67°-32°=81°, 在⊙O 中,∠BCD 与∠A 互补,所以∠A=180°-81°=99°. 11.【答案】相交;【解析】求出方程2680x x -+= 的两实根1r 、2r 分别是4、2,则1r -2r <d <1r +2r ,所以两圆相交.12.【答案】①②④;【解析】连接AD ,AB 是直径,则AD ⊥BC ,又∵△ABC 是等腰三角形,故点D 是BC 的中点,即BD=CD ,故②正确; ∵AD 是∠BAC 的平分线,由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;∵∠ABE=90°﹣∠EBC ﹣∠BAD=45°=2∠CAD ,故④正确; ∵∠EBC=22.5°,2EC ≠BE ,AE=BE ,∴AE ≠2CE ,③不正确; ∵AE=BE ,BE 是直角边,BC 是斜边,肯定不等,故⑤错误. 综上所述,正确的结论是:①②④.13.【答案】7或3;【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,即另一圆半径为7或3.14.【答案】21)a ; 2(222)a ;【解析】正方形ABCD 外接圆的直径就是它的对角线,由此求得正方形边长为a .如图所示,设正八边形的边长为x .在Rt △AEL 中,LE =x ,AE =AL =2x ,∴ 22x x a +=,21)x a =,即正八边形的边长为21)a .222224[(21)](222)AEL S S S a x a a a =-=-=-=△正方形正八边形.15.【答案】(1)π; 2π; (2)(n-2)π;【解析】∵ n 边形内角和为(n-2)180°,前n 条弧的弧长的和为(2)1801(2)3602n n -=-个以某定点为圆心,以1为半径的圆周长,∴ n 条弧的弧长的和为121(2)(2)2n n ππ⨯⨯-=-.本题还有其他解法,比如:设各个扇形的圆心角依次为1α,2α,…,n α, 则12(2)180n n ααα+++=-…°,∴ n 条弧长的和为1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-.16.【答案】720π;【解析】∵ S =πr 2,∴ 9π=πr 2,∴ r =3.∴ h 1=4,∴ 2215l h r =+=,∴ 223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱,2036720S ππ=⨯=总.所求面积包括圆锥的侧面积和圆柱的侧面积,不包括底面积.三、解答题17.【答案与解析】(1)连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ,∴OF 垂直平分BC∴BF FC =∴AF 平分∠BAC .(2)由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ∴∠1+∠4=∠2+∠3A DO 1234A BCDEO 12∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18.【答案与解析】 证明:(1)∵四边形ABCD 是⊙O 的内接四边形, ∴∠A+∠BCD=180°, ∵∠DCE+∠BCD=180°, ∴∠A=∠DCE , ∵DC=DE ,∴∠DCE=∠AEB , ∴∠A=∠AEB ;(2)∵∠A=∠AEB , ∴△ABE 是等腰三角形, ∵EO ⊥CD , ∴CF=DF ,∴EO 是CD 的垂直平分线, ∴ED=EC , ∵DC=DE , ∴DC=DE=EC ,∴△DCE 是等边三角形, ∴∠AEB=60°,∴△ABE 是等边三角形.19.【答案与解析】解:∵公共弦AB =120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=.20. 【答案与解析】(1)如选命题①.证明:在图(1)中,∵∠BON=60°,∴∠1+∠2=60°.∵∠3+∠2=60°,∴∠1=∠3.又∵ BC=CA,∠BCM=∠CAN=60°,∴△BCM≌△CAN,∴ BM=CM.如选命题②.证明:在图(2)中,∵∠BON=90°,∴∠1+∠2=90°.∵∠3+∠2=90°,∴∠1=∠3.又∵ BC=CD,∠BCM=∠CDN=90°,∴△BCM≌△CDN,∴ BM=CN.如选命题③.证明:在图(3)中,∵∠BON=108°,∴∠1+∠2=108°.∵∠2+∠3=108°,∴∠1=∠3.又∵ BC=CD,∠BCM=∠CDN=108°,∴△BCM≌△CDN,∴ BM=CN.(2)①答:当∠BON=(2)180nn°时结论BM=CN成立.②答:当∠BON=108°时.BM=CN还成立.证明:如图(4),连接BD、CE在△BCD和△CDE中,∵ BC=CD,∠BCD=∠CDE=108°,CD=DE,∴△BCD≌△CDE.∴ BD=CE,∠BDC=∠CED,∠DBC=∠ECD.∵∠CDE=∠DEN=108°,∴∠BDM=∠CEM.∵∠OBC+∠OCB=108°,∠OCB+∠OCD=108°.∴∠MBC=∠NCD.又∵∠DBC=∠ECD=36°,∴∠DBM=∠ECM.∴△BDM≌△CEN,∴ BM=CN.。
切线长定理

O。
C
D
P
A
OP ⊥ AB, 且BC = AC
若已知圆的三条切线呢?
A
圆 O 为 ∆ ABC 的内切圆, 圆心 O 为 ∆ ABC 的内心
右边的图形中有相等的线段是吗? 线段是吗? AF=AE BF=BD CD=CE
B
F . O D
E C
内心O在哪? 内心O在哪?
角平分线的交点
看 谁 做 得 快 比 一 比
已知:在△ABC中,BC=14,AC=9, AB=13,它的内切圆分别和BC、AC、AB 切于点D、E、F,求AF、BD和CE的长。
x
课堂练习
• 完成课本98页练 完成课本98 98页练 习题1,2 习题1,2
问题:请找出三角形 问题:请找出三角形ABC的内心 的内心
解: B
内心 o
·
A
C
是三角形角平分线的 是三角形角平分线的 角平分线 交点
所以, 即为三角形ABC 的内心 所以,点O即为三角形 即为三角形
通过这节课的复习,你有什么收获或体会? 关于切线长定理,你还有什么不明白的问题? 关于切线长定理,你还有什么不明白的问题? 会找三角形的内心吗? 会找三角形的内心吗?
必做题: 教材 教材P102第5题, 必做题:1.教材 第 题 2.画一三角形,并找出它的内心 画一三角形, 画一三角形 选做题 3.如图,P是⊙o外的一点,PA、PB分别与⊙o相切于 如图, 如图 ⊙o外的一点,PA、PB分别与⊙o相切于 外的一点 分别与⊙o 是弧AB上的任意一点,过点C AB上的任意一点 点A、B,C是弧AB上的任意一点,过点C的切线分别叫 PA、PB于点 于点D、E PA、PB于点D、E (1)若PA=4,求△PDE的周长 PA=4 PDE的周长 (2)若∠P=40°,求∠DOE的度数 P=40° 40 DOE的度数 A D P C E B . o
三角形内切圆切线长定理切线判定性质

三角形内切圆、切线长定理、切线的判定、性质例 如图,△ABC 的内心为I ,外心为O ,且∠BIC=115°,求∠BOC 的度数.例 已知,在Rt △ABC 中,∠C=90°,AB=5,AC=4,求直角三角形内切圆的半径的长.例 (陕西省,2001)如图,点I 是△ABC 的内心,AI 的延长线交边BC 于D ,交△ABC 的外接圆于点E .(1)求证:IE=BE ; (2)若IE=4,AE=8,求DE 的长.例 如图,Rt △ABC 中,∠C=90°,BC=5,⊙O 内切Rt △ABC 的三边AB 、BC 、CA 于D 、E 、F ,半径r=2.求△ABC 的周长.例 (上海市,2001)如图,Rt △ABC 中,∠B=90°,∠A 的平分线交BC 于点D ,E 为AB 上的一点,DE=DC ,以D 为圆心,DB 为半径作⊙D .求证:(1)AC 是⊙D 的切线; (2)AB+EB=AC .A BCDEI ABE3. 如图,︒=∠50APB ,PA ,PB ,DE 都为⊙O 的切线,则DOE ∠为()例 (大连市,l 999)阅读:“如图△ABC 内接于⊙O ,∠CAE=∠B . 求证:AE 与⊙O 相切于点A .如图,已知△ABC 内接于⊙O .P 是CB 延长线上一点,连结AP .且PA 2=PB ·PC . 求证:PA 是⊙O 的切线.例 (西宁,1999)已知:如图,Rt △ABC 中,∠C=90°,以AB 为直径的⊙O 交斜边AB 于E ,OD ∥AB . 求证:(1)ED 是⊙O 的切线;(2)2 DE 2=BE ·OD例 (北京市西城区试题,2002)已知:AB 为⊙O 的直径,P 为AB 延长线上的一个动点,过点P 作⊙O 的切线,设切点为C.(1)当点P 在AB 延长线上的位置如图1所示时,连结AC ,作APC ∠的平分线,交AC 于点D ,请你测量出CDP ∠的度数;AB CEOFABCOPAB CDE O(2)当点P 在AB 延长线上的位置如图2和图3所示时,连结AC ,请你分别在这两个图中用尺规作APC ∠的平分线(不写做法,保留作图痕迹),设此角平分线交AC 于点D ,然后在这两个图中分别测量出CDP ∠的度数;猜想:CDP ∠的度数是否随点P 在AB 延长线上的位置的变化而变化?请对你的猜想加以证明.例 如图,已知⊙O 中,AB 为直径,过B 点作⊙O 的切线,连线CO ,若OC AD //交⊙O 于D .求证:CD 是⊙O 的切线.例 如图,以ABC ∆Rt 的一条直角边AB 为直径作圆斜边BC 于E ,F 是AC 的中点,求证:EF 是圆的切线.例 如图,AB 是⊙O 的直径,CD 是⊙O 的切线,C 为切点,AD 交⊙O 于点E ,AC AB AD ,5,4==平分BDA ∠.(1)求证:CD AD ⊥.(2)求AC .。
切线的性质和判定

切线的性质和判定练习一.解答题(共11小题)1.(2018•宿迁)如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A 作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.(1)求证:PC是⊙O的切线;(2)若∠ABC=60°,AB=10,求线段CF的长.2.(2018•常德)如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.(1)求证:EA是⊙O的切线;(2)求证:BD=CF.3.(2018•官渡区二模)如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.(1)求证:DE是⊙O的切线;(2)若AD=l,BC=4,求直径AB的长.4.(2018•洪泽区一模)如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC 是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.5.(2018•淅川县二模)如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.(1)直接写出ED和EC的数量关系:;(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;(3)填空:当BC=时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是.6.(2018•东河区二模)已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.(1)求证:OF⊥CE(2)求证:EF是⊙O的切线;(3)若⊙O的半径为3,∠EAC=60°,求AD的长.7.(2018•海淀区二模)如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB 于点M,过点D作DE⊥CA交CA的延长线于点E.(1)连接AD,则∠OAD=°;(2)求证:DE与⊙O相切;(3)点F在上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.8.(2018•朝阳区二模)AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB 的延长线相交于点D,CA=CD.(1)连接BC,求证:BC=OB;(2)E是中点,连接CE,BE,若BE=2,求CE的长.9.(2018•苏州)如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC与AB相交于点G,连接OC.(1)求证:CD=CE;(2)若AE=GE,求证:△CEO是等腰直角三角形.10.(2017•黄石)如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC 的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.11.(2018•长沙)如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE ∥AD,CE交BA的延长线于点E,BC=8,AD=3.(1)求CE的长;(2)求证:△ABC为等腰三角形.(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.切线的性质和判定参考答案与试题解析一.解答题(共11小题)1.(2018•宿迁)如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A 作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.(1)求证:PC是⊙O的切线;(2)若∠ABC=60°,AB=10,求线段CF的长.【分析】(1)连接OC,可以证得△OAP≌△OCP,利用全等三角形的对应角相等,以及切线的性质定理可以得到:∠OCP=90°,即OC⊥PC,即可证得;(2)先证△OBC是等边三角形得∠COB=60°,再由(1)中所证切线可得∠OCF=90°,结合半径OC=5可得答案.【解答】解:(1)连接OC,∵OD⊥AC,OD经过圆心O,∴AD=CD,∴PA=PC,在△OAP和△OCP中,∵,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP∵PA是半⊙O的切线,∴∠OAP=90°.∴∠OCP=90°,即OC⊥PC∴PC是⊙O的切线.(2)∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∴∠COB=60°,∵AB=10,∴OC=5,由(1)知∠OCF=90°,∴CF=OCtan∠COB=5.【点评】本题考查了切线的性质定理以及判定定理,以及直角三角形三角函数的应用,证明圆的切线的问题常用的思路是根据切线的判定定理转化成证明垂直的问题.2.(2018•常德)如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.(1)求证:EA是⊙O的切线;(2)求证:BD=CF.【分析】(1)根据等边三角形的性质可得:∠OAC=30°,∠BCA=60°,证明∠OAE=90°,可得:AE是⊙O的切线;(2)先根据等边三角形性质得:AB=AC,∠BAC=∠ABC=60°,由四点共圆的性质得:∠ADF=∠ABC=60°,得△ADF是等边三角形,证明△BAD≌△CAF,可得结论.【解答】证明:(1)连接OD,∵⊙O是等边三角形ABC的外接圆,∴∠OAC=30°,∠BCA=60°,∵AE∥BC,∴∠EAC=∠BCA=60°,∴∠OAE=∠OAC+∠EAC=30°+60°=90°,∴AE是⊙O的切线;(2)∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ABC=60°,∵A、B、C、D四点共圆,∴∠ADF=∠ABC=60°,∵AD=DF,∴△ADF是等边三角形,∴AD=AF,∠DAF=60°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAF=∠CAF,在△BAD和△CAF中,∵,∴△BAD≌△CAF,∴BD=CF.【点评】本题考查了全等三角形的性质和判定,等边三角形及外接圆,四点共圆等知识点的综合运用,属于基础题,熟练掌握等边三角形的性质是关键.3.(2018•官渡区二模)如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,连接OD,过点B作BE∥OD交⊙O于点E,连接DE并延长交BN于点C.(1)求证:DE是⊙O的切线;(2)若AD=l,BC=4,求直径AB的长.【分析】(1)求出∠AOD=∠EOD,根据全等三角形的判定和性质推出∠DEO=∠DAO,根据切线的判定得出即可;(2)根据矩形的性质和判定得出AB=DH,AD=BH=1,根据切线长定理求出DC,根据勾股定理求出DH即可.【解答】(1)证明:连接OE,∵OA=OE=OB,∴∠OBE=∠PEB,∵OD∥BE,∴∠AOD=∠OBE,∠OEB=∠DOE,∴∠AOD=∠EOD,在△AOD和△EOD中∴△AOD≌△EOD,∴∠OAD=∠OED,∵AM是⊙O的切线,∴∠OAD=90°,∴∠OED=90°,即OE⊥DE,∵OE为⊙O半径,∴DE是⊙O的切线;(2)解:过D作DH⊥BC于H,∵AM和BN是⊙O的两条切线,∴∠DAB=∠ABH=∠DHB=90°,∴四边形ABHD是矩形,∴AB=DH,AD=BH,∵AD=l,BC=4,∴BH=1,CH=4﹣1=3,∵AM和BN是⊙O的两条切线,DE切⊙O于E,AD=1,BC=4,∴DE=AD=1,BC=CE=4,∴DC=1+4=5,在Rt△DHC中,由勾股定理得:DH===4,即AB=4.【点评】本题考查了切线的性质和判定、全等三角形的性质和判定、等腰三角形的性质、勾股定理、矩形的性质和判定、切线长定理等知识点,能综合运用知识点进行推理和计算是解此题的关键.4.(2018•洪泽区一模)如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC 是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.(1)求证:DC是⊙O的切线;(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.【分析】(1)连接DO,如图,利用平行线的性质和等腰三角形的性质证明∠COD=∠COB.则根据“SAS”可判断△COD≌△COB,所以∠CDO=∠CBO.再根据切线的性质得∠CBO=90°,则∠CDO=90°,然后根据切线的判定定理得到结论;(2)先利用∠OCB=∠OCD=30°得到∠DCB=60°,则∠E=30°,再根据含30度的直角三角形三边的关系计算出DE=4,DC=OD=4,然后根据三角形面积公式计算.【解答】(1)证明:连接DO,如图,∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD,又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB.在△COD和△COB中∴△COD≌△COB(SAS),∴∠CDO=∠CBO.∵BC是⊙O的切线,∴∠CBO=90°,∴∠CDO=90°,∴OD⊥CE,又∵点D在⊙O上,∴CD是⊙O的切线;(2)解:由(1)可知∠OCB=∠OCD=30°,∴∠DCB=60°,又BC⊥BE,∴∠E=30°,在Rt△ODE中,∵tan∠E=,∴DE==4,同理DC=OD=4,=•OD•CE=×4×8=16.∴S△OCE【点评】本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线";有切线时,常常“遇到切点连圆心得半径”.也考查了解直角三角形.5.(2018•淅川县二模)如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.(1)直接写出ED和EC的数量关系:ED=EC;(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;(3)填空:当BC=2时,四边形AOED是平行四边形,同时以点O、D、E、C 为顶点的四边形是正方形.【分析】(1)连结CD,如图,由圆周角定理得到∠ADC=90°,然后根据直角三角形斜边上的中线直线得到DE=CE=BE;(2)连结OD,如图,利用切线性质得∠2+∠4=90°,再利用等腰三角形的性质得∠1=∠2,∠3=∠4,所以∠1+∠3=∠2+∠4=90°,于是根据切线的判定定理可判断DE 是⊙O的切线;(3)要判断四边形AOED是平行四边形,则DE=OA=1,所以BC=2,当BC=2时,△ACB为等腰直角三角形,则∠B=45°,又可判断△BCD为等腰直角三角形,于是得到DE⊥BC,DE=BC=1,所以四边形AOED是平行四边形;然后利用OD=OC=CE=DE=1,∠OCE=90°可判断四边形OCED为正方形.【解答】解:(1)连结CD,如图,∵AC是⊙O的直径,∴∠ADC=90°,∵E是BC的中点,∴DE=CE=BE;(2)DE是⊙O的切线.理由如下:连结OD,如图,∵BC为切线,∴OC⊥BC,∴∠OCB=90°,即∠2+∠4=90°,∵OC=OD,ED=EC,∴∠1=∠2,∠3=∠4,∴∠1+∠3=∠2+∠4=90°,即∠ODB=90°,∴OD⊥DE,∴DE是⊙O的切线;(3)当BC=2时,∵CA=CB=2,∴△ACB为等腰直角三角形,∴∠B=45°,∴△BCD为等腰直角三角形,∴DE⊥BC,DE=BC=1,∵OA=DE=1,AO∥DE,∴四边形AOED是平行四边形;∵OD=OC=CE=DE=1,∠OCE=90°,∴四边形OCED为正方形.故答案为ED=EC;2,正方形.【点评】本题考查了切线的判断与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.常见的辅助线为:判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;有切线时,常常“遇到切点连圆心得半径”.解决(3)小题的关键是熟练掌握平行四边形和正方形的判定方法.6.(2018•东河区二模)已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB 于点E,连接EO并延长交BC的延长线于点D,作OF∥AB交BC于点F,连接EF.(1)求证:OF⊥CE(2)求证:EF是⊙O的切线;(3)若⊙O的半径为3,∠EAC=60°,求AD的长.【分析】(1)由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,(2)得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.(3)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.【解答】证明:(1)如图,连接CE,∵AC是⊙O的直径,∴CE⊥AE,∵OF∥AB,∴OF⊥CE(2)∵OF⊥CE∴OF所在直线垂直平分CE,∴FC=FE,OE=OC,∴∠FEC=∠FCE,∠OEC=∠OCE,∵∠ACB=90°,即:∠OCE+∠FCE=90°,∴∠OEC+∠FEC=90°,即:∠FEO=90°,∴FE为⊙O的切线;(3)如图,∵⊙O的半径为3,∴AO=CO=EO=3,∵∠EAC=60°,OA=OE,∴∠EOA=60°∴∠COD=∠EOA=60°,∵在Rt△OCD中,∠COD=60°,OC=3,∴CD=3,∵在Rt△ACD中,∠ACD=90°,CD=3,AC=6,∴AD=3.【点评】本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,熟练掌握定理是解题的关键.7.(2018•海淀区二模)如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB 于点M,过点D作DE⊥CA交CA的延长线于点E.(1)连接AD,则∠OAD=60°;(2)求证:DE与⊙O相切;(3)点F在上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.【分析】(1)由CD⊥AB和M是OA的中点,利用三角函数可以得到∠DOM=60°,进而得到△OAD是等边三角形,∠OAD=60°.(2)只需证明DE⊥OD.便可以得到DE与⊙O相切.(3)利用圆的综合知识,可以证明,∠CND=90°,∠CFN=60°,根据特殊角的三角函数值可以得到FN的数值.【解答】解:(1)如图1,连接OD,AD∵AB是⊙O的直径,CD⊥AB∴AB垂直平分CD∵M是OA的中点,∴OM=OA=OD∴cos∠DOM==∴∠DOM=60°又:OA=OD∴△OAD是等边三角形∴∠OAD=60°故答案为:60°(2)∵CD⊥AB,AB是⊙O的直径,∴CM=MD.∵M是OA的中点,∴AM=MO.又∵∠AMC=∠DMO,∴△AMC≌△OMD.∴∠ACM=∠ODM.∴CA∥OD.∵DE⊥CA,∴∠E=90°.∴∠ODE=180°﹣∠E=90°.∴DE⊥OD.∴DE与⊙O相切.(3)如图2,连接CF,CN,∵OA⊥CD于M,∴M是CD中点.∴NC=ND.∵∠CDF=45°,∴∠NCD=∠NDC=45°.∴∠CND=90°.∴∠CNF=90°.由(1)可知∠AOD=60°.∴.在Rt△CDE中,∠E=90°,∠ECD=30°,DE=3,∴.在Rt△CND中,∠CND=90°,∠CDN=45°,CD=6,∴.由(1)知∠CAD=2∠OAD=120°,∴∠CFD=180°﹣∠CAD=60°.在Rt△CNF中,∠CNF=90°,∠CFN=60°,,∴.【点评】本题考查圆的综合运用,特别是垂径定理、切线的判定要求较高,同时对于特殊角的三角函数值的运用有所考察,需要学生能具有较强的推理和运算能力.8.(2018•朝阳区二模)AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB 的延长线相交于点D,CA=CD.(1)连接BC,求证:BC=OB;(2)E是中点,连接CE,BE,若BE=2,求CE的长.【分析】(1)连接OC,根据圆周角定理、切线的性质得到∠ACO=∠DCB,根据CA=CD得到∠CAD=∠D,证明∠COB=∠CBO,根据等角对等边证明;(2)连接AE,过点B作BF⊥CE于点F,根据勾股定理计算即可.【解答】(1)证明:连接OC.∵AB为⊙O直径,∴∠ACB=90°,∵CD为⊙O切线∴∠OCD=90°,∴∠ACO=∠DCB=90°﹣∠OCB,∵CA=CD,∴∠CAD=∠D.∴∠COB=∠CBO.∴OC=BC.∴OB=BC;(2)解:连接AE,过点B作BF⊥CE于点F.∵E是AB中点,∴=,∴AE=BE=2.∵AB为⊙O直径,∴∠AEB=90°.∴∠ECB=∠BAE=45°,.∴.∴CF=BF=1.∴.∴.【点评】本题考查的是切线的性质、圆周角定理、勾股定理,掌握圆的切线垂直于经过切点的半径是解题的关键.9.(2018•苏州)如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC 与AB相交于点G,连接OC.(1)求证:CD=CE;(2)若AE=GE,求证:△CEO是等腰直角三角形.【分析】(1)连接AC,根据切线的性质和已知得:AD∥OC,得∠DAC=∠ACO,根据AAS证明△CDA≌△CEA(AAS),可得结论;(2)介绍两种证法:证法一:根据△CDA≌△CEA,得∠DCA=∠ECA,由等腰三角形三线合一得:∠F=∠ACE=∠DCA=∠ECG,在直角三角形中得:∠F=∠DCA=∠ACE=∠ECG=22.5°,可得结论;证法二:设∠F=x,则∠AOC=2∠F=2x,根据平角的定义得:∠DAC+∠EAC+∠OAF=180°,则3x+3x+2x=180,可得结论.【解答】证明:(1)连接AC,∵CD是⊙O的切线,∴OC⊥CD,∵AD⊥CD,∴∠DCO=∠D=90°,∴AD∥OC,∴∠DAC=∠ACO,∵OC=OA,∴∠CAO=∠ACO,∴∠DAC=∠CAO,∵CE⊥AB,∴∠CEA=90°,在△CDA和△CEA中,∵,∴△CDA≌△CEA(AAS),∴CD=CE;(2)证法一:连接BC,∵△CDA≌△CEA,∴∠DCA=∠ECA,∵CE⊥AG,AE=EG,∴CA=CG,∴∠ECA=∠ECG,∵AB是⊙O的直径,∴∠ACB=90°,∵CE⊥AB,∴∠ACE=∠B,∵∠B=∠F,∴∠F=∠ACE=∠DCA=∠ECG,∵∠D=90°,∴∠DCF+∠F=90°,∴∠F=∠DCA=∠ACE=∠ECG=22.5°,∴∠AOC=2∠F=45°,∴△CEO是等腰直角三角形;证法二:设∠F=x,则∠AOC=2∠F=2x,∵AD∥OC,∴∠OAF=∠AOC=2x,∴∠CGA=∠OAF+∠F=3x,∵CE⊥AG,AE=EG,∴CA=CG,∴∠EAC=∠CGA,∵CE⊥AG,AE=EG,∴CA=CG,∴∠EAC=∠CGA,∴∠DAC=∠EAC=∠CGA=3x,∵∠DAC+∠EAC+∠OAF=180°,∴3x+3x+2x=180,x=22。
圆切线习题

圆的切线的判定与性质。
【知识点精析】1. 直线与圆有三种位置关系,其中直线与圆只有唯一的公共点,叫直线与圆相切,这个公共点叫切点。
这条直线叫圆的切线。
2. 圆的切线的判定与性质:(1)判定:经过半径外端并且垂直于这条半径的直线是圆的切线。
如图所示:OA是⊙O半径,直线BC经过点A且垂直于OA,则直线BC与⊙O相切,A为切点。
三角形的内切圆:与三角形三边都相切的圆叫三角形的内切圆三角形内切圆的圆心叫三角形的内心三角形的内心到三角形三边的距离相等三角形的内心是三角形三角平分线的交点【解题方法指导】例1. 已知如图:C为⊙O上一点,DA交⊙O于B,∠DCB=∠CAB。
求证:DC为⊙O 的切线。
A例2. 已知如图:在Rt△ABC中,∠C=90°,点C在AC上,CD为⊙O直径,⊙O切AB于E,若BC=5,AC=12,求⊙O的半径。
AIB C6. 如果半径分别为10cm和8cm的两圆相交,公共弦长12cm,且两圆的圆心在公共弦两旁,则圆心距为()cmA. 241B. 827+C.252D.32777. 两圆的半径之比为2:3,当两圆内切时,圆心距是4cm ,当两圆外切时圆心距为( ) A. 20cm B. 14cm C. 11cm D. 5cm8. ⊙O 1和⊙O 2的半径之比为R :r=4:3,当O 1O 2=21cm 时,两圆外切,当两圆内切时,O 1O 2的长度为( ) A. O O cm3< B. 321cm O O cm << 是____________。
18. 若正多边形的内角和是720°,则这个多边形是正____________边形。
19. 已知正多边形的中心角为120°,边长为3,则其半径长为____________。
20. 若正三角形和正六边形的面积相等,则它们的边长之比为____________。
直线与圆的位置关系及切线的判定与性质(知识解读+真题演练+课后巩固)(原卷版)
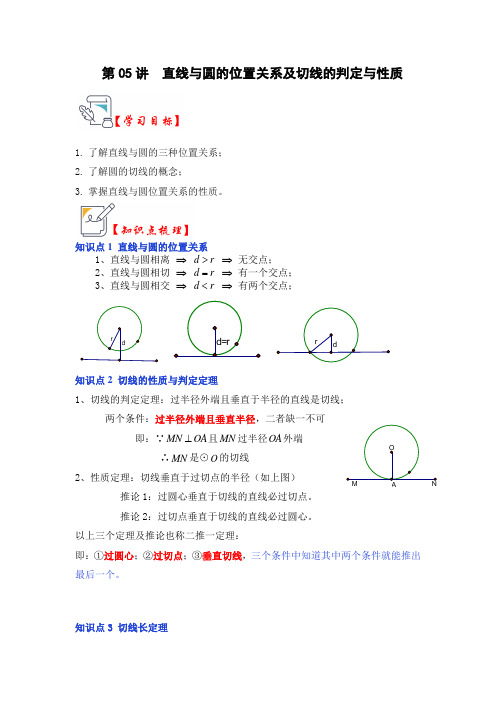
第05讲 直线与圆的位置关系及切线的判定与性质1. 了解直线与圆的三种位置关系;2. 了解圆的切线的概念;3. 掌握直线与圆位置关系的性质。
知识点1 直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点;2、直线与圆相切 ⇒ d r = ⇒ 有一个交点;3、直线与圆相交 ⇒ d r < ⇒ 有两个交点;知识点2 切线的性质与判定定理1、切线的判定定理:过半径外端且垂直于半径的直线是切线;两个条件:过半径外端且垂直半径,二者缺一不可即:∵MN OA ⊥且MN 过半径OA 外端∴MN 是⊙O 的切线2、性质定理:切线垂直于过切点的半径(如上图)推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
知识点3 切线长定理切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵PA 、PB 是的两条切线 ∴PA PB =;PO 平分BPA ∠知识点4 三角形的内切圆和内心1、三角形的内切圆 与三角形的各边都相切的圆叫做三角形的内切圆。
2、三角形的内心三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心。
注意:内切圆及有关计算。
(1)三角形内切圆的圆心是三个内角平分线的交点,它到三边的距离相等。
(2)△ABC 中,∠C=90°,AC=b ,BC=a ,AB=c ,则内切圆的半径r=2c b a -+ 。
(3)S △ABC =)(21c b a r ++,其中a ,b ,c 是边长,r 是内切圆的半径。
(4)弦切角:角的顶点在圆周上,角的一边是圆的切线,另一边是圆的弦。
如图,BC 切⊙O 于点B ,AB 为弦,∠ABC 叫弦切角,∠ABC=∠D 。
C【题型1 直线与圆的位置关系的判定】【典例1】(2023•滨江区二模)已知⊙O 的直径为4,圆心O 到直线l 的距离为2,则直线l 与⊙O ( )A .相交B .相切C .相离D .无法确定【变式1-1】(2022秋•江汉区校级期末)已知⊙O 半径为4cm ,若直线上一点P 与圆心O 距离为4cm ,那么直线与圆的位置关系是( )A .相离B .相切C .相交D .无法确定【变式1-2】(2022秋•洪山区校级期末)圆的半径是6.5cm ,如果圆心与直线上某一点的距离是6.5cm ,那么该直线和圆的位置关系是( )A .相离B .相切C .相交D .相交或相切P BAO B O A D【变式1-3】(2022秋•江夏区校级期末)已知⊙O的半径等于5,圆心O到直线l的距离为4,那么直线l与⊙O的公共点的个数是()A.0B.1C.2D.无法确定【题型2利用切线的性质求有关的角度/边长的运算】【典例2】(2023•西湖区校级二模)如图,菱形OABC的顶点A,B,C在⊙O 上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD 的长为()A.2B.4C.D.【变式2-1】(2023•西湖区校级二模)如图,菱形OABC的顶点A,B,C在⊙O 上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为2,则BD 的长为()A.2B.4C.D.【变式2-2】(2023•九龙坡区模拟)如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=30°,OA=2,则BD的长为()A.2B.2C.3D.3【变式2-3】(2023•沙坪坝区校级模拟)如图,在△ABC中,∠A=30°,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,连接BD.若BD平分∠ABC,,则线段AB的长是()A.B.C.3D.6【典例3】(2023•鹿城区校级模拟)如图,在△ABC中,D是AC上一点,以AD为直径的半圆O恰好切CB于点B.连接BD,若∠CBD=21°,则∠C 的度数为()A.42°B.45°C.46°D.48°【变式3-1】(2023•重庆)如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC,若∠ACD=50°,则∠BAC的度数为()A.30°B.40°C.50°D.60°【变式3-2】(2023•浙江二模)如图,AC与⊙O相切于点A,B为⊙O上一点,BC经过圆心O,若∠B=25°,则∠C的大小等于()A.20°B.40°C.25°D.50°【变式3-3】(2023•泰安三模)如图,AB是⊙O的直径,C、D是⊙O上的点,∠E=40°,过点C作⊙O的切线交AB的延长线于点E,则∠CDB等于()A.25°B.30°C.35°D.40°【题型3切线的判定】【典例4】(2023•东莞市校级模拟)如图,∠AOB=60°,以OB为半径的⊙O 交OA于点C,且OC=CA,求证:AB是⊙O的切线.【变式4-1】(新疆期末)如图,在Rt△ABC中,∠BAC=90°以AB为直径的⊙O与BC相交于点E.在AC上取一点D,使得DE=AD.求证:DE是⊙O的切线.【变式4-2】(昭通期末)如图,AD,BD是⊙O的弦,AD⊥BD,且BD=2AD =8,点C是BD的延长线上的一点,CD=2,求证:AC是⊙O的切线.【变式4-3】(大名县期末)如图,AB是⊙O的直径,点F在⊙O上,∠BAF的平分线AE交⊙O于点E,过点E作ED⊥AF,交AF的延长线于点D,延长DE、AB相交于点C.求证:CD是⊙O的切线.【题型4 切线的性质与判定的综合运用】【典例5】(2023•牧野区校级三模)如图,四边形ABCD内接于⊙O,BD是⊙O 的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)已知AE=4cm,CD=6cm,求⊙O的半径.【变式5-1】(2023•广西)如图,PO平分∠APD,P A与⊙O相切于点A,延长AO交PD于点C,过点O作OB⊥PD,垂足为B.(1)求证:PB是⊙O的切线;(2)若⊙O的半径为4,OC=5,求P A的长.【变式5-2】(2023•金寨县校级模拟)如图,AB是⊙O的直径,CD=CB,AC,BD相交于点E,过点C作CF∥BD,CF与AB的延长线相交于点F,连接AD.(1)求证:CF是⊙O的切线;(2)若AB=10,BC=6,求AD的长.【变式5-3】(2023•德庆县二模)如图,Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的圆交边AC于点D,交边AB于点E,且BC=BE.(1)求证:AB是⊙O的切线.(2)若AE=24,BE=15,求⊙O的半径.【题型5 利用切线长定理的性质求线段长度或周长】【典例6】(2022秋•金东区期末)如图,⊙O是△ABC的内切圆,点D、E分别为边AB、AC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是()A.7B.8C.9D.16【变式6-1】(2022秋•凤台县期末)如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.12cm B.7cmC.6cm D.随直线MN的变化而变化【变式6-2】(2022秋•林州市期中)如图,P A,PB分别切⊙O于点A,B,CD 切⊙O于点E,且分别交P A,PB于点C,D,若P A=6,则△PCD的周长为()A.5B.7C.12D.10【变式6-3】2022秋•潮州期末)如图,P为⊙O外一点,P A、PB分别切⊙O于点A、B,CD切⊙O于点E,分别交P A、PB于点C、D,若P A=8,则△PCD 的周长为()A.8B.12C.16D.20【题型6 三角形的内切圆与内心】【典例7-1】(2023•炎陵县模拟)如图,已知圆O是△ABC的内切圆,且∠A =70°,则∠BOC的度数是()A.140°B.135°C.125°D.110°【典例7-2】(2023•泗阳县一模)《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是“今有直角三角形,勾(短直角边)长为八步,股(长直角边)长为十五步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径长是()A.3步B.5步C.6步D.8步【变式7-1】(2023•娄底一模)如图,△ABC的内切圆圆O与AB,BC,CA分别相切于点D,E,F,若∠DEF=53°,则∠A的度数是()A.36°B.53°C.74°D.128°【变式7-2】(2022秋•丰宁县校级期末)如图,△ABC,AC=3,BC=4,∠C =90°,⊙O为△ABC的内切圆,与三边的切点分别为D、E、F,则⊙O的面积为()(结果保留π)A.πB.2πC.3πD.4π【变式7-3】(2022秋•南开区校级期末)如图,⊙O是△ABC的内切圆,切点分别为D,E,F,且∠A=90°,BC=10,CA=8,则⊙O的半径是()A.1B.C.2D.21.(2023•眉山)如图,AB切⊙O于点B,连结OA交⊙O于点C,BD∥OA交⊙O于点D,连结CD,若∠OCD=25°,则∠A的度数为()A.25°B.35°C.40°D.45°2.(2023•重庆)如图,AB为⊙O的直径,直线CD与⊙O相切于点C,连接AC,若∠ACD=50°,则∠BAC的度数为()A.30°B.40°C.50°D.60°3.(2022•河池)如图,AB是⊙O的直径,P A与⊙O相切于点A,∠ABC=25°,OC的延长线交P A于点P,则∠P的度数是()A.25°B.35°C.40°D.50°4.(2023•滨州)如图,P A,PB分别与⊙O相切于A,B两点,且∠APB=56°,若点C是⊙O上异于点A,B的一点,则∠ACB的大小为.5.(2023•岳阳)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.以点C为圆心,r为半径作圆,当所作的圆与斜边AB所在的直线相切时,r的值为.6.(2023•浙江)如图,点A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,点D在上.已知∠A=50°,则∠D的度数是.7.(2023•金华)如图,点A在第一象限内,⊙A与x轴相切于点B,与y轴相交于点C,D,连结AB,过点A作AH⊥CD于点H.(1)求证:四边形ABOH为矩形.(2)已知⊙A的半径为4,OB=,求弦CD的长.8.(2022•宁夏)如图,以线段AB为直径作⊙O,交射线AC于点C,AD平分∠CAB交⊙O于点D,过点D作直线DE⊥AC于点E,交AB的延长线于点F.连接BD并延长交AC于点M.(1)求证:直线DE是⊙O的切线;(2)求证:AB=AM;(3)若ME=1,∠F=30°,求BF的长.9.(2022•郴州)如图,在△ABC中,AB=AC.以AB为直径的⊙O与线段BC 交于点D,过点D作DE⊥AC,垂足为E,ED的延长线与AB的延长线交于点P.(1)求证:直线PE是⊙O的切线;(2)若⊙O的半径为6,∠P=30°,求CE的长.1.(2022秋•江夏区校级期末)已知⊙O的半径等于5,圆心O到直线l的距离为4,那么直线l与⊙O的公共点的个数是()A.0B.1C.2D.无法确定2.(2022秋•广阳区校级期末)如图,在△ABC中,AB=AC=5,BC=8,以A 为圆心作一个半径为3的圆,下列结论中正确的是()A.点B在⊙A内B.直线BC与⊙A相离C.点C在⊙A上D.直线BC与⊙A相切3.(2023•绿园区校级模拟)将一个含有30°的直角三角板按如图所示的位置摆放,一个顶点O与⊙O的圆心重合,一条直角边AB与⊙O相切,切点为B.将△OAB绕点B按顺时针方向旋转得到△O′A′B,使点O′落在⊙O上,边A′B交线段AO于点C.则∠OCB为()A.60°B.65°C.85°D.90°4.(2023•船营区一模)如图,AB是⊙O的直径,C为⊙O上一点,过点C的切线与AB的延长线交于点P,若AC=PC,则∠P的度数是()A.15°B.20°C.30°D.45°5.(2023•越秀区校级二模)如图,在Rt△ABC中,∠C=90°,AC=6,BC =8,则△ABC的内切圆的半径r是()A.2B.3C.4D.无法判断6.(2022秋•聊城期末)如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为()A.100°B.160°C.80°D.130°7.(2023•婺城区模拟)如图,△ABC是一张周长为18cm的三角形纸片,BC =5cm,⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.13cm B.8cmC.6.5cm D.随直线MN的变化而变化8.(2022秋•南沙区校级期末)如图,四边形ABCD是⊙O的外切四边形,且AB=8,CD=15,则四边形ABCD的周长为.9.(2022•南安市一模)如图,P A、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于.10.(2022秋•越秀区校级期末)如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且∠CDE=∠BAC.求证:DE是⊙O的切线.11.(2022秋•魏都区校级期末)如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC边于点D,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.求证:EF是⊙O的切线.12.(2022•东明县一模)已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,(1)求证:DE是⊙O的切线.(2)当BC=10,AD=4时,求⊙O的半径.13.(2023•零陵区模拟)如图,在△ABC中,∠C=90°,点E在AC边上,BE平分∠ABC,DE⊥BE交AB于D,⊙O是△BDE的外接圆.(1)求证:AC是⊙O的切线;(2)若AD=2,AE=4,求⊙O的半径长.14.(2023•新抚区模拟)如图,AC为⊙O的直径,CB是⊙O的切线,CB>AC,D为AB的中点,E在BC上,CE<BE,连接DE,DE=BC.(1)求证:DE为⊙O的切线;(2)若CE=2,EB=8,求⊙O的半径.。
与切线有关的定理
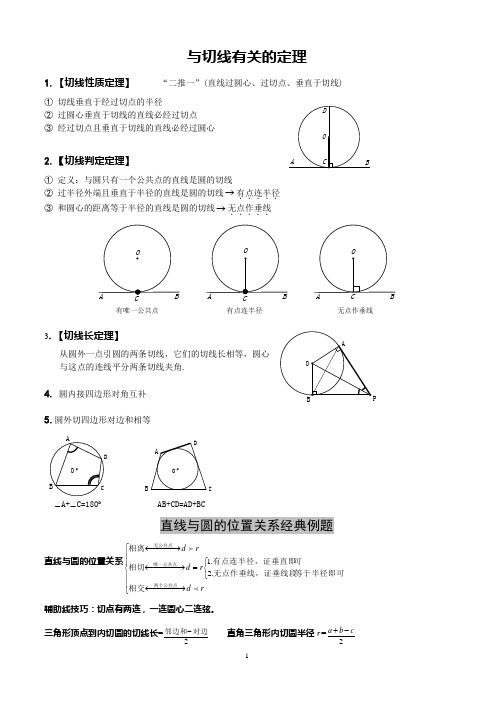
1.【切线性质定理】“二推一”(直线过圆心、过切点、垂直于切线)
①切线垂直于经过切点的半径
②过圆心垂直于切线的直线必经过切点
③经过切点且垂直于切线的直线必经过圆心
2.【切线判定定理】
①定义:与圆只有一个公共点的直线是圆的切线
②过半径外端且垂直于半径的直线是圆的切线 有点连半径
③和圆心的距离等于半径的直线是圆的切线 无点作垂线
(1)求证: ;
(2)若 ,求 的长.
4.如图,已知⊙O是△ABC的外接圆,AB为直径,若PA⊥AB,PO过AC的中点M,求证:PC是⊙O的切线.
5.如图,在 中, , 平分 交 于点 ,点 在 边上且 .
(1)判断直线 与 外接圆的位置关系,并说明理由;
(2)若 ,求 的长.
6.已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
15.已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若 ,则BD的长为()
A. B. C. D.
16.如图, 是 的直径, 是 的切线,点 在 上, , 则 的长为()
A. B. C. D.
17.如图,直线AB切⊙O于C点,D是⊙O上一点,∠EDC=30º,弦EF∥AB,连结OC交EF于H点,连结CF,且CF=2,则HE的长为_________.
解答题
1.已知:如图, 为 的直径, 交 于点 , 交 于点 .
(1)求 的度数;
(2)求证: .
2.如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.
(1)∠E=度;
(2)写出图中现有的一对不全等的相似三角形,并说明理由;
切线长定理

2、叙述角平线的性质与判定
性质:角平线上的点到这个角的两边的距离相等。 判定:到这个角的两边距离相等的点在这个角的平分线上。
3、下图中△ABC与圆O的关系?
△ABC是圆O的内接三角形;
A
圆O是△ABC的外接圆
圆心O点叫△ABC的外心
B
O
李明在一家木料厂上班,工作之余想对厂 里的三角形废料进行加工:裁下一块圆形用 料,且使圆的面积最大。 下图是他的几种设计,请同学们帮他确定一 下。
A
A
B
O
B
O
C
C
三角形外接圆
C
三角形内切圆 切线长定理
C
. o
A B B
. o
A
外接圆圆心:三角形三边 垂直平分线的交点。
外接圆的半径:交点到三 角形任意一个定点的距离。
内切圆圆心:三角形三个 内角平分线的交点。 内切圆的半径:交点到三 角形任意一边的垂直距离。
切线长定理 例2:如图,四边形ABCD的边AB、BC、CD 、DA和 ⊙O分 别相切于点E、F、G、H,试探究这个四边形ABCD的两组 对边的和有什么数量关系?并说明你的正确性。 A E O B F C H AB+CD=AD+BC D G
.
切线长定理 例3: 如图AB是⊙O的直径,C为圆上任意一点,过C 的切线分别与过A、B两点的切线交于P、Q, (1)求证:PO⊥OQ A P (2)已知AP=1cm,BQ=9cm,求⊙O的半径 1 C 思路: 由PA、PQ、BQ为切线 O 1 1 可得 ∠1= APC ∠2= BQC 2
.
2
切线长定理:从圆外一点可以引圆的两条切线,它 们的切线长相等,这一点和圆心的连线平分两条切 线的夹角。
切线长定理,切线的性质和判定
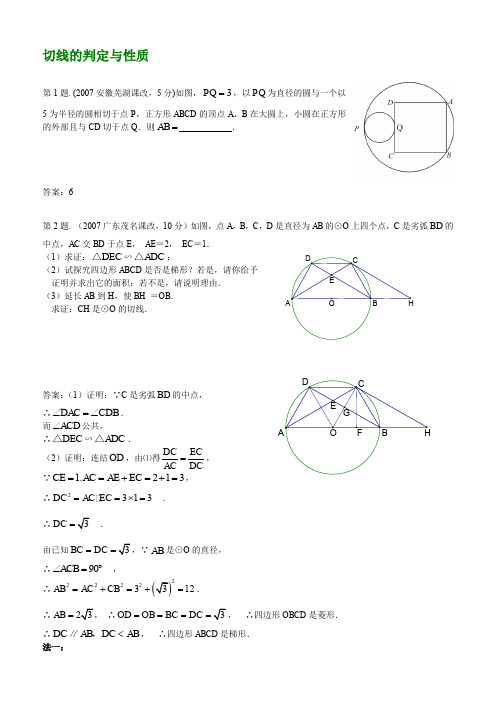
切线的判定与性质第1题. (2007安徽芜湖课改,5分)如图,3PQ =,以PQ 为直径的圆与一个以5为半径的圆相切于点P ,正方形ABCD 的顶点A 、B 在大圆上,小圆在正方形的外部且与CD 切于点Q .则AB = .答案:6第2题. (2007广东茂名课改,10分)如图,点A ,B ,C ,D 是直径为AB 的⊙O 上四个点,C 是劣弧BD 的中点,AC 交BD 于点E , AE =2, EC =1. (1)求证:DEC △∽ADC △;(2)试探究四边形ABCD 是否是梯形?若是,请你给予 证明并求出它的面积;若不是,请说明理由. (3)延长AB 到H ,使BH =OB . 求证:CH 是⊙O 的切线.答案:(1)证明:∵C 是劣弧BD 的中点, ∴DAC CDB ∠=∠. 而ACD ∠公共,∴DEC △∽ADC △.(2)证明:连结OD ,由⑴得DC ECAC DC=, ∵ 1.213CE AC AE EC ==+=+=,∴2313DC AC EC ==⨯= .∴DC = .由已知BC DC ==AB 是⊙O 的直径, ∴90ACB ∠=︒ ,∴22222312AB AC CB =+=+=.∴AB =∴OD OB BC DC ====, ∴四边形OBCD 是菱形. ∴DC AB DC AB <∥,, ∴四边形ABCD 是梯形. 法一:过C 作CF 垂直AB 于F ,连结OC ,则OB BC OC ===∴60OBC ∠=︒.∴sin 60CFBC︒=,3sin 602CF BC =︒==,∴()(113222ABCD S CF AB DC ⨯梯形=+= 法二:(接上证得四边形ABCD 是梯形)又DC AB ∥ ∴AD BC =,连结OC ,则AOD △,DOC △和OBC △ 6分∴AOD △≌DOC △≌OBC △,∴233AOD ABCD S S △梯形== (3)证明:连结OC 交BD 于G 由(2)得四边形OBCD 是菱形, ∴OC BD ⊥且OG GC =.又已知OB =BH , ∴BG CH ∥.∴90OCH OGB ∠=∠=︒ , ∴CH 是⊙O 的切线.第3题. (2007福建三明课改,12分)如图①,②,在平面直角坐标系xOy 中,点A 的坐标为(4,0),以点A 为圆心,4为半径的圆与x 轴交于O ,B 两点,OC 为弦,60AOC ∠=,P 是x 轴上的一动点,连结CP . (1)求OAC ∠的度数;(2分) (2)如图①,当CP 与A 相切时,求PO 的长;(3分) (3)如图②,当点P 在直径OB 上时,CP 的延长线与A 相交于点Q ,问PO 为何值时,OCQ △是等腰三角形?(7分)答案:解:(1)∵60AOC ∠=,AO AC =, ∴AOC △是等边三角形. ∴60OAC ∠=. (2)∵CP 与A 相切,∴90ACP ∠=. ∴9030APC OAC ∠=-∠=.又∵A (4,0),∴4AC AO ==.∴28PA AC ==. ∴844PO PA OA =-=-=.(3)①过点C 作1CP OB ⊥,垂足为1P ,延长1CP 交A 于1Q ,∵OA 是半径, ∴1OC OQ =,∴1OC OQ =, ∴1OCQ △是等腰三角形.又∵AOC △是等边三角形,∴112PO OA ==2 . ②解法一:过A 作AD OC ⊥,垂足为D ,延长DA 交A 于2Q ,2CQ 与x 轴交于2P ,∵A 是圆心, ∴2DQ 是OC 的垂直平分线. ∴22CQ OQ =. ∴2OCQ △是等腰三角形, 过点2Q 作2Q E x ⊥轴于E ,在2Rt AQ E △中,∵21302Q AE OAD OAC ∠=∠=∠=,∴22122Q E AQ AE ===,2Q 的坐标(4+2-). 在1Rt COP △中,∵1260POAOC =∠=,,∴1CP =C 点坐标(2,). 设直线2CQ 的关系式为:y kx b =+,则有2(42k b k b ⎧-=++⎪⎨+⎪⎩,.解得:12k b =-⎧⎪⎨=+⎪⎩,∴2y x =-++. 当0y =时,2x =+∴22P O =+.解法二: 过A 作AD OC ⊥,垂足为D ,延长DA 交A 于2Q ,2CQ 与x 轴交于2P ,∵A 是圆心, ∴2DQ 是OC 的垂直平分线. ∴22CQ OQ =. ∴2OCQ △是等腰三角形.∵60OAC ∠=,∴21302OQ C OAC ∠=∠=.∵2DQ 平分22,OQ C AC AQ ∠=,∴2215ACQ AQ C ∠=∠=. ∵AOC △是等边三角形,1CP OA ⊥, ∴11302PCA ACO ∠=∠=.∴1212301545PCP PCA ACQ ∠=∠+∠=+=. ∴12CPP △是等腰直角三角形.∴121PP CP ==∴21122P O PO PP =+=+第4题. (2007福建厦门课改,12分)已知:如图,PA PB ,是O 的切线,A B ,是切点,连结OA ,OB ,OP , (1)若60AOP ∠=,求OPB ∠的度数;(2)过O 作OC ,OD 分别交AP BP ,于C D ,两点, ①若COP DOP ∠=∠,求证:AC BD =;②连结CD ,设P C D △的周长为l ,若2l A P =,判断直线CD 与O 的位置关系,并说明理由.答案:(1)解:PA PB ,是O 的切线,A B ,是切点,90OAP ∴∠=.60AOP ∠=,30OPA ∴∠=. 30OPB OPA ∴∠=∠=.(2)①证明:COP DOP ∠=∠,CPO DPO ∠=∠,PO PO =, OCP ODP ∴△≌△. CP DP ∴=.PA PB ,是O 的切线,PA PB ∴=. AC BD ∴=.②证明:连结CD .2l AP =,PA PB =, CD AC BD ∴=+.OA OB =,且90OAC OBD ∠=∠=.∴将OAC △绕点O 逆时针旋转,使点A 与B 重合.记点C 的对称点为1C ,1AC BC ∴=,1OC OC =.90OAC OBD ∠=∠=, ∴点1C 在PB 的延长线上.1OC OC =,1DC DC =,OD OD =, 1OC D OCD ∴△≌△.∴过O 作OE CD ⊥,E 是垂足.即OE 是点O 到直线CD 的距离, 11122C D OB CD OE ∴⨯⨯=⨯⨯.P1COB OE ∴=.∴直线CD 与O 相切.第5题. (2007甘肃兰州课改,5分)在Rt ABC △中,90ACB =∠,30CAB =∠,用两种方法把它分成两个三角形,且要求一个三角形是等腰三角形.答案:可参考的作法有:(1)作AC 的中线交AB 于D ,连接CD ,得等腰DAC △; (2)作B ∠的平分线交AC 于D ,得等腰DAB △;(3)作BA 上截取BD BC =,连接CD ,得等腰BCD △; (4)作AB 上截取AD AC =,连接CD ,得等腰ACD △. (每个作图2分,共4分,答语1分.其它作法正确均可得分.)第6题. (2007甘肃白银3市非课改,4分)如图,已知AB 、AC 分别是⊙O 的直径和切线,BC 交⊙O 于D ,AB =8,AC =6,则AD = .答案:4.8第7题. (2007甘肃白银3市非课改,12分)如图,AB 是⊙O 的弦,OA OC ⊥交AB 于点C ,过点B 的直线交OC 的延长线于点E ,当BE CE =时,直线BE 与⊙O 有怎样的位置关系?并证明你的结论.答案:解:BE 与⊙O 相切. 证明:如图,连接OB . ∵ BE CE =,∴ 312∠=∠=∠. ∵ OA OC ⊥,∴ ︒=∠+∠903A . ∴ ︒=∠+∠902A . 又∵ OB OA =,∴ A OBC ∠=∠.∴ 290OBC ∠+∠=︒.即 ︒=∠90OBE . ∴ BE 与⊙O 相切.第8题. (2007广东河池非课改,10分)如图1,已知正方形ABCD的边长为M 是AD 的中点,P 是线段MD 上的一动点(P 不与M ,D 重合),以AB 为直径作⊙O ,过点P 作⊙O 的切线交BC 于点F ,切点为E .(1)除正方形ABCD 的四边和⊙O 中的半径外,图中还有哪些相等的线段(不能添加字母和辅助线)? (2)求四边形CDPF 的周长;(3)延长CD ,FP 相交于点G ,如图2所示. 是否存在点P ,使BF FG CF OF =?如果存在,试求此时AP 的长;如果不存在,请说明理由.答案:解:(1)FB =FE ,PE =P A(2)四边形CDPF 的周长为FC +CD +DP +PE +EF =FC +CD +DP +P A +BF=BF +FC +CD +DP +P A =BC +CD +DA =3=(3)存在. 若BF FG CF OF =,则BF CFOF FG=∵ cos ∠OFB =BF OF ,cos ∠GFC =CFFG∴ ∠OFB =∠GFC又 ∵ ∠OFB =∠OFE∴ ∠OFE =∠OFB =∠GFC=60 ∴ 在Rt OFB △中 FE =FB =tan 60OB=1∴ 在Rt GFC △中CG =()tan tan 60231tan 6063CF GFC CF ∠==-=- ∴ 6DG CG CD =-=-·M ·AFCO PEDB 图1·P DOGEM FB AC图2∴ tan tan 30233DP DG PGD DG =∠==-∴ ()33AP AD DP =-==第9题. (2007广西南宁课改,3分)如图,AB AC ,是圆的两条弦,AD 是圆的一条直径,且AD 平分BAC ∠,下列结论中不.一定正确....的是( ) A .AB DB =B .BD CD =C .BC AD ⊥ D .B C ∠=∠答案:A第10题. (2007广西南宁课改,10分)如图,在平面直角坐标系中,A B ,两点的坐标分别为(20)(80)A B -,,,,以AB 为直径的半圆P 与y 轴交于点M ,以AB 为一边作正方形ABCD .(1)求C M ,两点的坐标;(2)连接CM ,试判断直线CM 是否与P 相切?说明你的理由;(3)在x 轴上是否存在一点Q ,使得QMC △的周长最小?若存在,求出点Q 的坐标;若不存在,请说明理由.答案:解:(1)(20)(80)A B -,,,,四边形ABCD10AB BC CD AD P ∴====,的半径为5 (810)C , 连接5PM PM =,,在Rt PMO △中,4OM === (04)M ∴,(2)方法一:直线CM 是OP 的切线.证明:连接PC CM,如图12(1),B DCA在Rt EMC △中,10CM === C M C B ∴=又PM PB CP CP ==, C P M C P B ∴△≌△ 90CMP CBP CM ∴∠=∠=,是P 的切线方法二:直线CM 是P 的切线 证明:连接PC 如图12(1),在Rt PBC △中,22222510125P C P B B C =+=+=在Rt MEC △中2222286100C M C E M E ∴=+=+= 222P C C M P M ∴=+P M C ∴△是直角三角形,即90PMC ∠= ∴直线CM 与P 相切方法三:直线CM 是P 的切线证明:连接MB PM ,如图12(2),在Rt EMC △中,10CM == CM CB CBM CMB ∴=∴∠=∠PM PB PBM PMB ∴=∴∠=∠90PMB CMB PBM CBM ∴∠+∠=∠+∠=即PM MC ⊥CM ∴是P 的切线.(3)方法一:作M 点关于x 轴的对称点M ',则(04)M '-,,连接M C ',与x 轴交于点Q ,此时QM QC+的和最小,因为MC 为定值,所以QMC △的周长最小M O Q ME C ''△∽△ 4168147O Q M O O Q OQ EC M E '∴===',,1607Q ⎛⎫∴⎪⎝⎭, 方法二:作M 点关于x 轴的对称点M ',则(04)M '-,,连接M C ',与x 轴交于点Q ,此时QM QC+的和最小,因为MC 为定值,所以QMC △的周长最小. 设直线M C '的解析式为y kx b =+把(04)M '-,和(810)C ,分别代入得40108b k b -=+⎧⎨=+⎩,解得744k b ⎧=⎪⎨⎪=-⎩744y x ∴=-,当0y =时,167x = 1607Q ⎛⎫∴⎪⎝⎭, 10分第11题. (2007广西玉林课改,8分)如图1,A 是直角边长等于a 的等腰直角三角形,B 是直径为a 的圆.圆2是选择基本图形A B ,用尺规画出的图案:22π4a S a =-阴影.(1)请你以图1的图形为基本图形,按给定图形的大小设计画一个新图案.....,还要选择恰当的图形部分涂上阴影,并直接写出其面积(尺规作图,不写作法,保留痕迹,作直角三角形时可使用三角板).(2)请你写出一句在解答本题的过程中体会最深且与数学有关的话.答案:解:(1)正确画出图形 3分 涂上阴影并写出阴影面积 6分 答案不唯一,参考举例:(2)写出与要求相符的话 8分答案不唯一,参考举例:①这两个图形的关系很密切,能组合设计出许多美丽的图案来装点我们的生活;②运用圆的半径可作出等腰直角三角形三边的中点;③作数学图形需要一丝不苟,否则会产生误差影响图案的美观,图2B2π16S a =- 2π8S a =- 2π8S a =-2π4S a =-22π16a S a =- 2π4a S = 2S a =第12题. 如图,某机械传动装置在静止状态时,连杆PA 与点A 运动所形成的O 交于B 点,现测得4cm PB =,5cm AB =.O 的半径 4.5cm R =,此时P 点到圆心O 的距离是 cm .答案:7.5第13题. (2007海南课改,2分)如图,⊙B 的半径为4cm , 60=∠MBN ,点A ,C 分别是射线BM ,BN 上的动点,且直线BN AC ⊥.当AC 平移到与⊙B 相切时,AB 的长度是( )A .8cmB .6cmC .4cmD .2cm答案:A第14题. (2007河北课改,2分)如图,EB 为半圆O 的直径,点A 在EB 的延长线上,AD 切半圆O 于点D ,BC ⊥AD 于点C ,AB =2,半圆O 的半径为2,则BC 的长为( )A .2B .1C .1.5D .0.5 答案:B第15题. (2007山东临沂课改,3分)如图,在ABC △中,2AB =,1AC =,以AB 为直径的圆与AC 相切,与边BC 交于点D ,则AD 的长为()ABCD答案:A第16题. (2007河南课改,3分)如图,PA PB ,切O于点A B ,,点C 是O 上一点,且65ACB ∠=,则P ∠=度. 答案:5090C ∠=,第17题. (2007湖北荆门课改,8分)在Rt ACB △中,3AC =,4BC =,D E ,分别是边AB ,AC 的中点.O 过点D E ,且与AB相切于点D ,求O 的半径r .PMCAN B CDBAADCOEB答案:解:连接OD OE ,.过O 作OF ED ⊥,垂足为F .DE 是ABC △的中位线,12DE BC ∴ ∥.90AED C ∴∠=∠=. 又4BC =,2DE ∴=,1FD =. AB 切O 于D ,OD AB ∴⊥.90A ADE ODE ADE ∠+∠=∠+∠=,A ODE ∴∠=∠.Rt Rt ABC DOF ∴△∽△. OD FD AB AC ∴=,即153r =. 53r ∴=.即O 的半径为53.第18题. (2007湖北十堰课改,8分)如图,PA 是O 的切线,切点是A ,过点A 作AH OP ⊥于点H ,交O 于点B .求证:PB 是O 的切线.答案:连结OA OB ,,(图略)PA ∵是O 的切线,90OAP ∠=∴°,OA OB AB OP =⊥∵,,AOP BOP ∠=∠∴, 又OA OB OP OP ==∵,,()AOP BOP SAS ∴△≌△,90OBP OAP ∠=∠=∴°, PB ∴是O 的切线.说明:本题也可根据垂径定理得AH BH =,通过证明AOH BOH △≌△,得AOP BOP ∠=∠.第19题. (2007湖北襄樊非课改,11分)如图-(1),ABC △内接于O ,点P 是ABC △的内切圆的圆心,AP 交边BC 于点D ,交O 于点E ,经过点E 作O 的切线分别交AB AC ,延长线于点F G ,. (1)求证:BC FG ∥;(2)探究:PE 与DE 和AE 之间的关系; (3)当图-(1)中的FE AB =时,如图-(2),若3FB =,2CG =,求AG 的长.ACOEBFP答案:(1)证明:连结BE .点P 是ABC △的内心,12∴∠=∠. 而FG 切O 于E . ∴14∠=∠. 又23∠=∠,34∴∠=∠,BC FG ∴∥. (2)连结BP , 则56∠=∠.1563BPE ∠=∠+∠=∠+∠, ∴BPE PBE ∠=∠,BE PE ∴=. 在ABE △和BDE △中,13∠=∠,BED AEB ∠=∠, ABE BDE ∴△∽△中, BE DE AE BE∴=.2BE AE DE ∴=,2PE AE DE ∴=. (3)2()FE FB FA FB FB AB ==+,而FE AB =,23(3)AB AB ∴=+,设AB x =,则2390x x --=.解之得x =AB ∴=(取正值). 由(1),在AFG △中,BC FG ∥,AB ACBF CG∴=.213AB CG AC BF ∴===+.3AG AC CG ∴=+=+第20题. (2007湖北宜昌课改,7分)如图,某建筑工地上一钢管的横截面是圆环形.王师傅将直尺边缘紧靠内圆,直尺与外圆交于点A B ,(AB 与内圆相切于点C ,其中点A 在直尺的零刻度处).请观察图形,写出线段AB 的长(精确到1cm ),并根据得到的数据计算该钢管的横截面积.(结果用含π的式子表示)EO B A BC 200 10 20 30 40 cm答案:解:24cm AB =; 连接OC OA ,,AB 与内圆相切与点C ,OC AB ∴⊥ 12cm AC BC ∴==∴横截面积为:2222()AO OC AO OC π-π=π-在Rt ACO △中,222AO OC AC -=∴横截面积2AC =π2144(cm )=π(注:读数不按要求精确读数错误扣1分;最后结果中无单位扣1分)第21题. (2007湖南永州课改,10分)AB 是O 的直径,D 是O 上一动点,延长AD 到C 使CD AD =,连结BC BD ,.(1)证明:当D 点与A 点不重合时,总有AB BC =. (2)设O 的半径为2,AD x =,BD y =,用含x 的式子表示y .(3)BC 与O 是否有可能相切?若不可能相切,则说明理由;若能相切,则指出x 为何值时相切.答案:(1)AB 为O 直径,BD AC ∴⊥ 又DC AD =BD ∴是AC 的垂直平分线 A B A C ∴=(2)在Rt ABD △中,222BD AB AD =- 2224y x ∴=-即y = (3)BC 与O 有可能相切当BC 与O 相切时,BC AB ⊥A B B C=,45A ∴∠=2x AB ∴==第22题. (2007吉林课改,2分)如图,AB 为O 的切线,B 为切点.若30A ∠=,6AO =,则OB =.答案:3第23题. (2007江苏常州课改,2分)如图,在ABC △中,10AB =,8AC =,6BC =,经过点C 且与边AB 相切的动圆与CA CB ,分别相交于点P Q ,,则线段PQ 长度的最小值是( ) A .4.75B .4.8C .5D.答案:B第24题. (2007江苏南京课改,2分)如图,在平面直角坐标系中,点P 在第一象限,P 与x 轴相切于点Q ,与y 轴交于(02)M ,,(08)N ,两点,则点P 的坐标是( ) A.(53),B.(35),C.(54),D.(45),答案:D第25题. (2007江苏无锡课改,6分)如图,AB 是O 的直径,PA 切O于A ,OP 交O 于C ,连BC .若30P ∠=,求B ∠的度数.答案:解:PA 切O 于A AB ,是O 的直径,90PAO ∴∠=.30P ∠=,60AOP ∴∠=.1302B AOP ∴∠=∠=.第26题. (2007辽宁大连课改,3分)如图,AB AC ,是O 的两条切线,B C ,是切点,若70A ∠=,则BOC ∠的度数为( )A .130B .120C .110D .100PBAC答案:C第27题. (2007江苏扬州课改,4分)如图,AB 是O 的直径,点D 在AB 的延长线上,过点D 作O 的切线,切点为C ,若25A =∠,则D =∠______.答案:40°第28题. (2007内蒙鄂尔多斯课改,3分)如图,以O 为圆心的两个同心圆中,大圆的弦AB 切小圆于P ,如果4cm AB =,则图中阴影部分的面积为 2cm (结果用π表示).答案:4π第29题. (2007内蒙呼和浩特课改,3分)如图,以点O 为圆心的两个同心圆中,大圆的弦AB 是小圆的切线,点P 为切点,且4AB =,2OP =,连结OA 交小圆于点E ,则扇形OEP 的面积为( ) A.1π4B.1π3C.1π2D.1π8答案:C第30题. (2007山东日照课改,3分)如图,AC ⊥BC 于点C ,BC =a ,CA =b ,AB =c ,⊙O 与直线AB 、 BC 、CA 都相切,则⊙O 的半径等于 . 答案:2a b c -+第31题. (2007山东潍坊课改,3分)如图,以O 为圆心的两个同心圆中,大圆的弦AB 是小圆的切线.若大圆半径为10cm ,小圆半径为6cm ,则弦AB 的长为 .答案:16cm第32题. (2007四川德阳课改,7分)如图,已知AB 是O 的直径,AC 是弦,CD 切O 于点C ,交AB的延长线于点D ,120ACD =∠,10BD =. (1)求证:CA CD =; (2)求O 的半径.答案:解:(1)连结OC .DC 切O 于点C ,90OCD ∴∠=.AA又120ACD ∠=,ACO ACD OCD ∴∠=∠-∠1209030=-=.OC OA =,30A ACO ∴∠=∠=60COD ∴∠=.30D ∴∠=, CA DC ∴=.(2)sin OC OC OB D OD OB BD OB BD ∠===++,1sin sin 302D ∠==, 1102OB OB ∴=+.解得10OB =.即O 的半径为10第33题. (2007四川绵阳课改,12分)如图,AB 是⊙O 的直径,∠BAC = 60︒,P 是OB 上一点,过P 作AB 的垂线与AC 的延长线交于点Q ,过点C 的切线CD 交PQ 于D ,连结OC . (1)求证:△CDQ 是等腰三角形;(2)如果△CDQ ≌△COB ,求BP :PO 的值.答案:(1)由已知得∠ACB = 90︒,∠ABC = 30︒, ∴ ∠Q = 30︒,∠BCO = ∠ABC = 30︒. ∵ CD 是⊙O 的切线,CO 是半径, ∴ CD ⊥CO ,∴ ∠DCQ =∠BCO = 30︒,∴ ∠DCQ =∠Q ,故△CDQ 是等腰三角形.(2)设⊙O 的半径为1,则AB = 2,OC = 1,AC = AB ∕2 = 1,BC =3. ∵ 等腰三角形CDQ 与等腰三角形COB 全等,∴ CQ = BC =3. 于是 AQ = AC + CQ = 1 +3,进而 AP = AQ ∕2 =(1 +3)∕2, ∴ BP = AB -AP = 2-(1 +3)∕2 =(3-3)∕2, PO = AP -AO =(1 +3)∕2-1 =(3-1)∕2, ∴ BP :PO =3.A第34题. (2007浙江金华课改,10分)如图,AB 是O 的切线,A 为切点,AC 是O 的弦,过O 作OH AC ⊥于点H .若2OH =,12AB =,13BO =. 求:(1)O 的半径; (2)sin OAC ∠的值;(3)弦AC 的长(结果保留两个有效数字).答案:解:(1)AB 是O 的切线,∴90OAB ∠=,222AO OB AB ∴=-,5OA ∴=.(2)OH AC ⊥,90OHA ∴∠=,2sin 5OH OAC OA ∴∠==. (3)OH AC ⊥,222AH AO OH ∴=-,AH CH =,225421AH ∴=-=,AH ∴=29.2AC AH ∴==.第35题. (2007浙江丽水课改,12分)如图,⊙O 的直径AB =6cm ,P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC . (1) 若CPA ∠=30°,求PC 的长;(2)若点P 在AB 的延长线上运动,CPA ∠的平分线交AC 于点M ,你认为∠CMP 的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP 的值.答案:解:(1)连接OC ,PC 是⊙O 的切线,∴∠OCP=Rt ∠.∵CPA ∠=30°,OC=2AB=3, ∴03tan 30PC=,即PC= (2)∠CMP 的大小不发生变化.∵PM 是∠CP A 的平分线, ∴∠CPM =∠MP A .∵OA =OC ,∴∠A =∠ACO .在△APC 中,∵∠A +∠ACP +∠CP A =180°,∴2∠A +2∠MP A =90°,∠A +∠MP A =45°. ∴∠CMP =∠A +∠MP A =45°. 即∠CMP 的大小不发生变化.第36题. (2007 浙江宁波课改,3分)如图,AB 切⊙O 于点B ,AB =4 cm ,AO =6 cm ,则⊙O 的半径为 cm .答案:第37题. (2007浙江绍兴课改,5分)如图,P A 切⊙AB 于点A ,该圆的半径为3,P AB =5,则P A 的长等于 .答案:4第38题. (2007甘肃庆阳课改,9分)如图EB 是O 的直径,A 是BE 的延长线上一点,过A 作O 的切线AC ,切点为D ,过B 作O 的切线BC ,交AC 于点C ,若6EB BC ==,求:AD AE ,的长.答案:解:设AE x =,连结OD ,则90ADO ∠=° 又90ABC ∠=∵°,A A ∠=∠ ADO ABC ∴△∽△AD ODAB BC=31662AD x ==+,62x AD +=又2(6)AD x x =+∵ 2(6)(6)4x x x +=+∴即:24120x x +-= 26x x ==-∴,(舍)即:2AE =,4AD ==第39题. (2007江苏盐城课改,3分)如图,O 的半径为5,PA 切O 于点A ,30APO ∠=°,则切线长PA 为 .(结果保留根号)答案:第40题. (2007湖北孝感课改,3分)如图,AM 、AN 分别切⊙O 于M 、N 两点,点B 在⊙O 上,且∠MBN =70°,则A ∠= .答案:40°第41题. (2007湖南益阳课改,4分)如图,直线AB 切O 于点C ,OAC OBC ∠=∠, 则下列结论错误的是( )A .OC 是ABO △中AB 边上的高 B .OC 所在直线是ABO △的对称轴 C .OC 是AOB ∠的平分线D .AC BC >答案:D第42题. (2007四川资阳,9分)如图-1,在等边△ABC 中,AD ⊥BC 于点D ,一个直径与AD 相等的圆与BC 相切于点E 、与AB 相切于点F ,连接EF . ⑴ 判断EF 与AC 的位置关系(不必说明理由);⑵ 如图-2,过E 作BC 的垂线,交圆于G ,连接AG . 判断四边形ADEG 的形状,并说明理由; ⑶ 确定圆心O 的位置,并说明理由.答案:解:⑴ EF ∥AC . ⑵ 四边形ADEG 为矩形 .理由:∵EG ⊥BC ,E 为切点,∴EG 为直径,∴EG =AD .又∵AD ⊥BC ,EG ⊥BC ,∴AD ∥EG ,即四边形ADEG 为矩形 . ⑶ 圆心O 就是AC 与EG 的交点 .理由:连接FG ,由⑵可知EG 为直径,∴ FG ⊥EF , 又由⑴可知,EF ∥AC ,∴AC ⊥FG ,又∵四边形ADEG 为矩形,∴EG ⊥AG ,则AG 是已知圆的切线 . 而AB 也是已知圆的切线,则AF =AG ,∴ AC 是FG 的垂直平分线,故AC 必过圆心, 因此,圆心O 就是AC 与EG 的交点 . 说明:也可据△AGO ≌△AFO 进行说理 .图-1 图-2第43题. (2007湖南邵阳课改,3分)如图(六)是一张电脑光盘的表面,两个圆的圆心都是点O ,大圆的弦AB 所在直线是小圆的切线,切点为C .已知大圆的半径为5cm ,小圆的半径为1cm ,则弦AB 的长度为 cm .答案:第44题. (2007内蒙包头非课改,10分)如图,已知AB 是O 的直径,AC 为弦,且平分BAD ∠,AD CD ⊥,垂足为D .(1)求证:CD 是O 的切线;(5分)(2)若O 的直径为4,3AD =,试求BAC ∠的度数.(5分)答案:(1)证明:连接OC ,AC 平分BAD ∠,12∴∠=∠, 又OA OC =,13∴∠=∠, 23∴∠=∠,OC AD ∴∥, 又AD CD ⊥,OC CD ∴⊥,又OC 是O 的半径,CD ∴是O 的切线. (2)解:连接BC ,AB 是O 的直径,90ACB ∴∠=,90ACB ADC ∴∠=∠=,又12∠=∠, ACB ADC ∴△∽△, AC AB AD AC∴=,即2AC AB AD =,由43AB AD ==,,得212AC =,AC =在Rt ACB △中,cos 142AC AB ∠===, 30BAC ∴∠=.A第45题. (2007新疆课改,8分)如图,O 的直径6AB =,D 为O 上一点,30BAD ∠=,过D 点的切线交AB 的延长线于点C .求:(1)C ∠的度数.(2)阴影部分的面积.(精确到0.01)答案:解:(1)OA OD =,30ADO BAD ∴∠=∠=CD 切O 于D ,OD CD ∴⊥,即90ODC ∠=3090120ADC ADO ODC ∴∠=∠+∠=+=1801801203030C BAD ADC ∴∠=-∠-∠=--=(2)DOC ∠是AOD △的外角,260DOC DAO ∴∠=∠=在Rt COD △中,tan 6033CD OD ==113222COD S OD CD ==⨯⨯=△22π60π33π3603602BODn R S ⨯===扇形3π 3.082COD BOD S S S ∴=-=-≈△阴影扇形.。
切线长定理

问题2:经过圆外一点P, 如何作已知⊙O的切线?
探索活动?
2.如何过⊙O外一点P作⊙O的切线?这 样的切线能作几条?
O
.P
实践操作:
用尺规作图:过⊙O外一点做⊙O的切 线
A
O O ·
P
B
切 线 长 A 的 切线长定理: 定 O P 题设:从圆外一点引圆 义 的两条切线 B 结论:①切线长相等, 以 ②圆心和这一点的连线平分两条切线的夹角 及 几何表述: PA = PB 定 PA、PB分别切⊙O于A、B ∠OPA=∠OPB 理
C D B
P
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP (4)写出图中所有的相似三角形 △AOC∽ △BOC∽ △AOP∽△BOP∽ △ACP∽BCP (5)写出图中所有的等腰三角形 △ABP △AOB (6)若PA=4、PD=2,求半径OA
知 识 整 合
反思:在解决有关 圆的切线长的问题 时,往往需要我们 构建基本图形。
• • • • • • • •
填空: (1)经过( 半径的外端 )且 (垂直于这条半径 ) 的直线是圆的切线。 (2)圆的切线的性质:圆的切线( 垂直于 )经 过切点的(半径 )。 (3)切线的三种判定方法: 根据直线与圆的( 交点 )个数; 根据d与 r的( 大小 )关系; 根据直线与圆的一条半径的( 位置 )关系。
切线的性质有哪些: 1、切线和圆只有一个公共点; 2、圆心到切线的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。
问题1:经过平面上一个已知点,作已 知圆的切线会有怎样的情形?
A
P· · O P· · O P· · O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切线的判定与性质、切线长定理
1. 如图,AB为O O的直径,CE切O O于点C, CD丄AB ,
D
为垂足,AB = 12 cm,Z B =30°,则/ ECB = _____________ , CD = _______________ 。
2. 如图,CA为O O的切线,切点为A。
点B在O O上,如果/ CAB = 55°,那么/ AOB
等于_____________ 。
圆心的距离等于半径的直线是切线;④过圆直径的端点,垂直于该直径的直线的是切线。
其中正确命题有()
A .①②
B .②③
C .③④
D .①④
5. 如图,AB、AC与O O相切与B、C,Z A = 50°,点P是圆上异于B、C的一动点,则
Z BPC的度数是__________________ 。
6. 如图,已知△ ABC的内切圆O O与各边相切于点D、E、F,则点O是厶DEF的
()
A •三条中线的交点
B •三条高的交点
C.三条角平分线的交点D •三条边的垂直平分线的交点
7. 如图,O O 分别与△ ABC 的边BC、CA、AB 相切于D、E、F,Z A = 80°,则Z EDF
3. 如图,P是O O外一点, PA、PB分别和O O相切于点A、B,C是AB上任意一点,过
4.
C作O O的切线分别交PA、
(2)若厶PDE的周长为
PB 于点D、E,
(1)则PA长为
若PA=12,
(3)若/ P=40°,则/ DOE=
则厶PDE的周长为____ ;
度。
(2题图)
F列说法:①与圆有公共点的直线是圆的切线;
(3题图)
②垂直与圆的半径的直线是切线;③与
12
,
(5题图)
8. 点O是厶ABC的内心,
9. 已知:Rt △ ABC 中,
为_______________ 。
(6题图)
Z BAO = 200,Z AOC = 1300,
Z C = 900, AC = 4 , BC =
(7题图)
则Z ACB = _______________。
3 ,则△ ABC内切圆的半径
10. 若直角三角形斜边长为 10 cm,其内切圆半径为 2 cm,则它的周长为 ____________ 。
11. 如图,BA 与O O 相切于B , OA 与O O 相交于E ,若AB =
5 , EA = 1,则O O 的半
14. 如果两圆的半径分别为 6cm 和4cm,圆心距为8cm ,那么这两个圆的位置关系是 (
)
A.外离
B.外切
C.相交
D.内切
15. 若已知Rt △ ABC 中,斜边为26cm ,内切圆的半径为4cm ,那么它的两条直角边的长分 别为
()cm
A 、 7、 27
B 、 8、 26
C 、 16、 18
D 、 24、 104
16. 已知两圆的半径分别是方程
x 2 3x 2 0的两根,圆心距为 3,则两圆的位置关系是
17. 两圆半径分别为5cm 和4cm ,公共弦长为6cm ,则两圆的圆心距等于(
)cm 。
A. 4
7 B. 4 .7 C. 4 .7 或 4 .7 D. . 41
18. 从圆外一点向半径为
9的圆作切线,已知切线长为
18, ?从这点到圆的最短距离为
( )• A . 9.3 B . 9 3
1 C . 9.5 1 D . 9
19. 如图,AB 为O O 的直径,BC 是圆的切线,切点为 是O O
的切线。
径为 _________ 。
12. 如图,在△ ABC 中, 13. 如图,△ ABC △ ABC 是( A.等腰三角形;
I 是内心,/ BIC = 130°, 的内切圆O O 与各边相切于点
)
B.等边三角形;
则/ A 的度数是 ___________ 。
D 、E 、F ,若/ FOD = Z EOD = 135°,则
C •直角三角形
D.等腰直角三角形;
B , O
C 平行于弦A
D ,求证:DC (11题
图) (12题图) A
(13题图) A
20. 已知,如图,AB为O O的直径,O O过BC的中点D,且DE丄AC,求证:DE是O O 的切线。
21. 点P是O O的弦CB延长线上的一点,点A在O O上,且/ PCA = Z BAP,求证:PA
是O O的切线。
22. 如图,在Rt A ABC中,/ ACB = 90°,以BC边为直径的O O交AB于点D,连结OD 并延长交
CA的延长线于点E,过点D作DF丄OE交EC于点F。
(1)说明:AF = CF;
3
(2)若ED = 4, sinE = -,求CE 的长。
5
23. 如图,PA、PB 分别切O O 于A、B,O O 的半径为.3,/ APB = 60°,求PO、PA、PB
的长。
24. 如图,△ ABC 中,/ C= 90°, BD 平分/ ABC 并交AC 于D, DE 丄BD 交AB 于E,
作厶BDE的外接圆O O, (1)试说明:AC与O O相切;(2)若AD = 4, AE = 2,求O O的半径。
25. 如图,等腰三角形ABC中,AC=BC=6 , AB=8,以BC为直径作O O交AB于点D,交
AC于点G , DF丄AC,垂足为F,交CB的延长线于点E。
(1)求证:直线EF是O O的切线;
(2)求sin/ E的值。
