内切球和外接球例题之欧阳光明创编
高考数学中的内切球和外接球问题(附习题)-精选.pdf

一、 有关外接球的问题
如果一个多面体的各个顶点都在同一个球面上, 那么称这个多面
体是球的内接多面体,这个球称为多面体的外接球 . 有关多面体外接
球的问题, 是立体几何的一个重点, 也是高考考查的一个热点 . 考查
学生的空间想象能力以及化归能力 .研究多面体的外接球问题,既要
学习 .
五 .确定球心位置法
例 5 在矩形 ABCD 中, AB 4, BC 3,沿 AC 将矩形 ABCD 折成一
个直二面角 B AC D ,则四面体 ABCD 的外接球的体积为
125
A. 12
125
B. 9
125
C. 6
125
D. 3
D
A
O
C
图4 B
解 设矩形对角线的交点为 O ,则由矩形对角线互相平分,可知
例 2 一个正方体的各顶点均在同一球的球面上,若该正方体的
表面积为 24 ,则该球的体积为 ______________.4 3 . 2、求长方体的外接球的有关问题
例 3 一个长方体的各顶点均在同一球面上, 且一个顶点上的三条
棱长分别为 1,2,3 ,则此球的表面积为
.14 .
例 4、已知各顶点都在一个球面上的正四棱柱高为 4,
只是希望能有个人,在我说没事的时候,知道我不是真的没事;能有个人,在我强颜欢笑的时候,知道我不是真的开心。 ——张小娴
OA OB OC OD .∴点 O 到四面体的四个顶点 A、B、C、D 的距离相
等,即点 O 为四面体的外接球的球心,如图 2 所示 .∴外接球的半径
5 R OA
V 球 4 R3 125
2 .故
3
6 .选 C.
多面体与球的内切和外接常见类型归纳之欧阳与创编

多面体与球的内切和外接常见类型归纳在平常教学中,立体几何的多面体与球的位置关系,是培养学生的立体感,空间想象能力的好教材。
可是学生在两个几何体的组合后,往往感到无从下手。
针对这种情况,笔者把日常教学中有关这方面的习题加以总结和归类如下:一.正四面体与球如图所示,设正四面体的棱长为a ,r 为内切球的半径,R 为外接球的半径。
则高SE=32a,斜高SD=43a ,OE=r=SE-SO ,又SD=BD,BD=SE-OE,则在 r=a 126。
R=SO=OB=a 46 特征分析:1. 由于正四面体是一个中心对成图形,所以它的内切球与外接球的球心为同一个。
CB2. R=3r. r=a 126 R=a 46。
此结论可以记忆。
例题一。
1、一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( ) 分析:借助结论,R=a 46=462=23,所以S=42R π=3π。
2、球的内接正四面体又有一个内切球,则大球与小球的表面积之比是( ) 分析:借助R=3r ,答案为9:1。
二、特殊三棱锥与球 四个面都是直角三角形的三棱锥。
SA AB BC ABC ABC ⊥⊥为直角三角形,面, 因为SA ⊥AC ,SB ⊥BC ,球心落在SC 的中点处。
所以R=2SC 。
三.正方体与球。
1.正方体的外接球即正方体的8个定点都在球面上。
关键找出截面图:ABCD 为正方体的体对角面。
C设正方体的边长为a ,则AB=2a ,BD=2R ,AD=a ,R=23a 。
C2. 正方体的内切球。
(1)与正方体的各面相 切。
如图:ABCD 为正方 体的平行侧面的正方形。
R=2a(2)与正方体的各棱相切。
如图:大圆是正方形ABCD 的外接圆。
AB=CD=a , R=22a 。
3. 在正方体以一个顶点为交点的三条棱组成的三棱锥,特征是:三棱锥的三条侧棱互相垂直且相等,它的外接球可把三棱锥补形成正方体的外接球,再求解。
例题:1。
2024年高考数学二轮专题06 一网打尽外接球与内切球问题(精讲精练)(解析版)

专题06 一网打尽外接球与内切球问题【命题规律】纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见,此部分是重点也是一个难点,属于中等难度.【核心考点目录】核心考点一:正方体、长方体外接球核心考点二:正四面体外接球核心考点三:对棱相等的三棱锥外接球核心考点四:直棱柱外接球核心考点五:直棱锥外接球核心考点六:正棱锥与侧棱相等模型核心考点七:侧棱为外接球直径模型核心考点八:共斜边拼接模型核心考点九:垂面模型核心考点十:二面角模型核心考点十一:坐标法核心考点十二:圆锥圆柱圆台模型核心考点十三:锥体内切球核心考点十四:棱切球【真题回归】1.(2022·全国·高考真题(文))已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( )A .13B .12C D 【答案】C【解析】[方法一]:【最优解】基本不等式设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α,则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅=(当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为22r 又设四棱锥的高为h,则22r h1+=,2123O ABCDV r h-=⋅⋅=≤=当且仅当222r h=即h.故选:C[方法二]:统一变量+基本不等式由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a,底面所在圆的半径为r,则r=,所以该四棱锥的高h,13V a===(当且仅当22142a a=-,即243a=时,等号成立)所以该四棱锥的体积最大时,其高h===故选:C.[方法三]:利用导数求最值由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a,底面所在圆的半径为r,则r=,所以该四棱锥的高h,13V a=,令2(02)a t t=<<,V=()322t tft=-,则()2322tf t t-'=,43t<<,()0f t'>,单调递增,423t<<,()0f t'<,单调递减,所以当43t=时,V最大,此时h=故选:C.【整体点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解;方法二:消元,实现变量统一,再利用基本不等式求最值;方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.2.(2021·全国·高考真题(理))已知A,B,C是半径为1的球O的球面上的三个点,且,1AC BC AC BC⊥==,则三棱锥O ABC-的体积为()A B C D 【答案】A【解析】,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC 1,设O 到平面ABC 的距离为d ,则d ==所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯=故选:A.3.(2022·全国·高考真题)已知正三棱台的高为1,上、下底面边长分别为面上,则该球的表面积为( )A .100πB .128πC .144πD .192π【答案】A【解析】设正三棱台上下底面所在圆面的半径12,r r ,所以1222r r ==123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d =2d =,故121d d -=或121d d +=1=,解得225R =符合题意,所以球的表面积为24π100πS R ==.故选:A .4.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤,则该正四棱锥体积的取值范围是( )A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27]【答案】C【解析】∵球的体积为36π,所以球的半径3R =,[方法一]:导数法设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l <≤时,0V '<,所以当l =时,正四棱锥的体积V 取最大值,最大值为643,又3l =时,274V =,l =814V =,所以正四棱锥的体积V 的最小值为274,所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.[方法二]:基本不等式法由方法一故所以()()()3221224211646122(333333h h h V a h h h h h h h ⎡⎤-++==-=-⨯⨯=⎢⎥⎣⎦…当且仅当4h =取到),当32h =时,得a 22min 11327;3324V a h ==⨯=当l =39322h =+=,a ⇒,正四棱锥体积221119816433243V a h ==⨯=<,故该正四棱锥体积的取值范围是2764[,].435.(2020·全国·高考真题(理))已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A .64πB .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A6.(2020·全国·高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 【答案】C 【解析】设球O 的半径为R ,则2416R ππ=,解得:2R =.设ABC 外接圆半径为r ,边长为a ,ABC212a ∴,解得:3a =,2233r ∴===∴球心O 到平面ABC 的距离1d ===.故选:C.【方法技巧与总结】1、补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.(2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.(3)正四面体-P ABC 可以补形为正方体且正方体的棱长=a ,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1 图2 图3 图4【核心考点】核心考点一:正方体、长方体外接球【规律方法】1、正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.2、长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.【典型例题】例1.(2023·全国·高三专题练习)已知正方体外接球的体积是323π,那么正方体的体对角线等于( )A B .4C D 【答案】B【解析】正方体外接球的直径即为正方体的体对角线,设外接球的半径为R ,则343233V R ππ==,解得2R =,所以正方体的体对角线等于24R =;故选:B例2.(2022·陕西西安·模拟预测(文))长方体的过一个顶点的三条棱长分别是2,4,4,则该长方体外接球的表面积为( )A .9πB .18πC .36πD .48π【答案】C【解析】长方体外接球直径263R R ===⇒=,所以该长方体外接球的表面积2244336S R πππ==⋅=故选:C.例3.(2022·贵州黔南·高三开学考试(理))自2015年以来,贵阳市着力建设“千园之城”,构建贴近生活、服务群众的生态公园体系,着力将“城市中的公园”升级为“公园中的城市”.截至目前,贵阳市公园数量累计达到1025个.下图为贵阳市某公园供游人休息的石凳,它可以看做是一个正方体截去八个一样的四面体得到的,如果被截正方体的的棱长为,则石凳所对应几何体的外接球的表面积为________2cm .【答案】1600π【解析】设正方体的中心为O ,E 为棱的中点,连接1111,,,A D B C A C B D ,则O 为矩形11A DCB 的对角线的交点,则1112022OE B C ==⨯=,同理,O 到其余各棱的中点的距离也为20,故石凳所对应几何体的外接球的半径为20,其表面积为224π201m 600πc ⋅=,故答案为:1600π核心考点二:正四面体外接球【规律方法】如图,设正四面体ABCD 的的棱长为a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为==R ,即正四面体外接球半径为=R .【典型例题】例4.(2022·黑龙江·哈九中模拟预测(理))已知正四面体P ABC -外接球O 表面积为54π,则该正四面体棱长为______;若M 为平面ABC 内一动点,且PM = ,则AM 最小值为______.【答案】 6 -【解析】设该正四面体棱长为a ,过点P 作PD ⊥面ABC ,则点D 为ABC 的重心,则AD =,PD =,又正四面体P ABC -外接球O 表面积为54π,则2454R ππ= ,则R =,即PO AO = 又222AO AD OD =+,则222)=+,解得:6a =;又M 为平面ABC 内一动点,且PM =,则DM ===,即点M 的轨迹为以D 为圆心,又AD =则由点与圆的位置关系可得AM最小值为:-故答案为:6;例5.(2022·江苏南京·高三开学考试)已知一个正四面体的棱长为2,则其外接球与以其一个顶点为球心,1为半径的球面所形成的交线的长度为___________.【解析】设外接球半径为r ,外接球球心到底面的距离为h ,则2243h r r h +==+,所以r =两球相交形成形成的图形为圆,如图,在PDO △中,cos DPO ∠==sin DPO ∠=在1PDO △中,1sin DO PD DOP =∠=所以交线长度为2π=例6.(2022·福建·福州三中模拟预测)表面积为)A.B.12πC.8πD.【答案】B【解析】设正四面体的棱长为a24⨯=a=该正四面体的外接球与棱长为2的正方体的外接球的半径相等,2412Sππ=⨯=.故选:B.核心考点三:对棱相等的三棱锥外接球【规律方法】四面体ABCD中,==AB CD m,==AC BD n,==AD BC t,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为,,a b c,则222222222⎧+=⎪+=⎨⎪+=⎩b c ma c na b t,三式相加可得222++=a b c222,2++m n t 而显然四面体和长方体有相同的外接球,设外接球半径为R,则22224+=+a b c R,所以=R.【典型例题】例7.(2022·全国·高三专题练习)在四面体ABCD中,2==AC BD,AD BC==AB CD==其外接球的表面积为___________.【答案】8π【解析】如图所示,将该四面体补成长方体,设该长方体的长、宽、高分别为a,b,c,则2,===解得2222224,5,7,a b b c c a ⎧+=⎪+=⎨⎪+=⎩所以2228a b c ++==,,其外接球的表面积为248ππ⨯=.故答案为:8π.例8.(2022·全国·高三专题练习)已知四面体ABCD中,AB CD ==BC AD ==AC BD =,若该四面体的各个顶点都在同一球面上,则此球的表面积为( )A .42πB .43πC .14πD .16π【答案】C设长方体的长、宽、高分为,,,x y z 所以2222225,10,13,x y x z z y ⎧+=⎪+=⎨⎪+=⎩∴∴,∴此球的表面积为144144ππ⋅=.故选:C .例9.(2020·全国·模拟预测(文))在三棱锥A BCD -中,若2AB CD ==,3AD BC ==,4AC BD ==,其外接球的表面积为( )A .27πB .29πC .294πD .292π【答案】D【解析】三棱锥A BCD -中,∵2AB CD ==,3AD BC ==,4AC BD ==,显然这六条棱长恰为长方体的六个面的面对角线的长,设此长方体的长、宽、高依次为a 、b 、c ,其对角线的长恰为外接球的直径,如图所示.则有2222224916a b b c a c ⎧+=⎪+=⎨⎪+=⎩,则222292a b c ++=,易知长方体的体对角线长为2R =22942S R ππ==球面积.故选:D核心考点四:直棱柱外接球【规律方法】如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O 1是∆ABC 的外心,则1⊥OO 平面ABC ;第二步:算出小圆1O 的半径1=AO r ,111122==OO AA h (1=AA h 也是圆柱的高);第三步:勾股定理:22211=+OA O A O O ⇒222(2=+hR r ⇒=R R【典型例题】例10.(2022·河南新乡·一模(理))已知正三棱柱的侧棱长为l ,底面边长为a ,若该正三棱柱的外接球体积为32π3,当la +最大时,该正三棱柱的体积为( )A B C D 【答案】B【解析】因为正三棱柱外接球的体积为3432ππ33R =,所以2R =,设球心为O ,底面外接圆圆心为O ',由正三棱锥可得12OO l '=,底面外接圆半径r =,图3-1图3-2图3-3所以由勾股定理得22443l a +=,设l a m +=,当直线l a m +=与曲线22443l a +=相切时,m 最大,联立方程组22443l a m l a +=⎧⎪⎨+=⎪⎩得22763480a ma m -+-=,由Δ0=,得m =或-(舍去),此时a =l所以正三棱柱的体积2V l ==故选:B例11.(2022·湖南岳阳·高三阶段练习)已知直三棱柱111ABC A B C -中,12,AB AA BC ===,当该三棱柱体积最大时,其外接球的体积为( )AB .323πCD【答案】C【解析】因为三棱柱111ABC A B C -为直三棱柱,所以,1AA ⊥平面ABC所以,要使三棱柱的体积最大,则ABC 面积最大,因为1sin 2ABC S BC AC ACB =⋅⋅∠△,令AC x=因为BC =,所以2sin ABC S x ACB ⋅∠ ,在ABC中,222cos 2AC BC AB ACB AC BC +-∠==⋅所以,224224416(1)43216sin 11212x x x ACB x x --+-∠=-=,所以,()22422424123384()sin 34434ABCx x x Sx ACB --+-+-=⋅∠=⋅=≤ ,所以,当24x =,即2AC =时,2()ABC S 取得最大值3,所以,当2AC =时,ABC SABC为等腰三角形,2,AB AC BC ===所以,()22244121cos ,0,22222AB AC BC BAC BAC AB AC π+-+-∠===-∠∈⋅⨯⨯,所以23BAC π∠=,所以,由正弦定理得ABC 外接圆的半径r42r==,即2r =,所以,直三棱柱111ABC A B C -外接球的半径222152AA R r ⎛⎫=+= ⎪⎝⎭,即R =所以,直三棱柱111ABC A B C -外接球的体积为343R π=.故选:C例12.(2021·四川泸州·二模(文))直六棱柱的底面是正六边形,其体积是,则该六棱柱的外接球的表面积的最小值是( )A .4πB .8πC .12πD .24π【答案】C【解析】设正六边形的边长为a,则底面面积为226S ==,设(0)AC x x =>,则正六棱柱的体积为2V Sh x =⨯=解得24xa =,即24a x=,又由该六棱柱的外接球的直径为2BC r ==所以该六棱柱的外接球的表面积为:2222164(4)(),(0)S r x a x x xπππ'==+=+>,令()216(0)f x x x x =+>,则()2162f x x x'=-,令()0f x '=,解得2x =,当02x <<时,()0f x '<,()f x 单调递减;当2x >时,()0f x '<,()f x 单调递增,所以当2x =时,()f x 取得最小值12,所以该六棱柱的外接球的表面积的最小值为12π.故选:C.核心考点五:直棱锥外接球【规律方法】如图,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将∆ABC A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为∆ABC 的外心,所以1⊥OO 平面ABC ,算出小圆1O 的半径1=O D r (三角形的外接圆直径算法:利用正弦定理,得2sin sin sin ===a b c r A B C ),112=OO PA ;第三步:利用勾股定理求三棱锥的外接球半径:①222(2)(2)=+R PA r⇔2=R ②2221=+R r OO⇔=R .【典型例题】例13.(2022·内蒙古鄂尔多斯·高三期中(文))三棱锥-P ABC 中,PA ⊥平面ABC ,ABC 为直角三角形,AB BC ⊥,1AB BC ==,2PA =,则三棱锥-P ABC 的外接球的表面积为( )A .2πB .3πC .4πD .6π【答案】D【解析】由于三棱锥-P ABC 中,PA ⊥平面ABC ,AB BC ⊥,1AB BC ==,2PA =故将该三棱锥置于一个长方体中,如下图所示:则体对角线PC 即为外接球的直径,所以2=故三棱锥-P ABC 的外接球表面积为246S R ππ==.故选:D例14.(2022·福建·宁德市民族中学高三期中)已知三棱锥P -ABC 中,PA ⊥底面ABC ,PA =AB =AC =2,∠BAC =120°,则三棱锥P -ABC 的外接球的表面积为( )A .12πB .16πC .20πD .24π【答案】C【解析】将三棱锥还原成直三棱柱,则三棱柱的外接球即为球O ,,D D '为上下底面的外心,O 为DD '的中点,AD 为底面外接圆的半径,由余弦定理得BC ==由正弦定理得24AD ==,由1,2OD AD ==,得AO =所以球O 的表面积为2420S r ππ==.故选:C例15.(2021·四川成都·高三开学考试(文))已知在三棱锥-P ABC 中,侧棱PA ⊥平面ABC ,3PA =,1AB =,BC =,2AC =,则三棱锥-P ABC 外接球的表面积为( )A .13πB .12πC .9πD .8π【答案】A【解析】因为PA ⊥平面ABC ,,AC BC ⊂平面ABC ,故,PA AC PA BC ⊥⊥,而1AB =,BC =,2AC =,则222AB BC AC +=,所以AB BC ⊥,又PA AB A = ,,PA AB ⊂平面PAB ,故BC ⊥平面PAB ,PB ⊂平面PAB ,所以BC PB ⊥,所以,PAC PBC △△都是以PC 为斜边的直角三角形,故取PC 中点O ,连接OA,OB ,则OA OB OP OC ===,即O 为三棱锥-P ABC外接球的球心,3,2,PA AC PC ==∴= ,故三棱锥-P ABC故三棱锥-P ABC外接球的表面积为24π13π⨯=,故选:A核心考点六:正棱锥与侧棱相等模型【规律方法】1、正棱锥外接球半径:=R .2、侧棱相等模型:如图,P 的射影是∆ABC 的外心⇔三棱锥-P ABC 的三条侧棱相等⇔三棱锥-P ABC 的底面∆ABC 在圆锥的底上,顶点P点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取∆ABC 的外心1O ,则1,,P O O 三点共线;第二步:先算出小圆1O 的半径1=AO r ,再算出棱锥的高1=PO h (也是圆锥的高);第三步:勾股定理:22211=+OA O A O O ⇒222()=-+R h R r ,解出222+=r h R h.【典型例题】例16.(2022·江西·金溪一中高三阶段练习(文))在正三棱锥S -ABC 中,23ASB BSC π∠+∠=,△ABC 的边长为2,则该正三棱锥外接球的表面积为______.【答案】6π【解析】2π3ASB BSC ∠+∠=,正三棱锥中ASB BSC ∠=∠,所以π3ASB BSC ∠=∠=,侧面是正三角形,则正三棱锥S ABC -为正四面体.将正四面体补成正方体(正四面体的四个顶点S ,A ,B ,C 均为正方体的顶点),,则其外接球的半径R =,所以该正三棱锥外接球的表面积为24π6πS R ==.故答案为:6π.例17.(2022·全国·高三专题练习)已知正三棱锥S ABC -,其外接球球O 的半径为R ,则该正三棱锥S ABC -的体积的最大值为__________.3【解析】如图,设正三棱锥S ABC -的高=SH h ,则由射影定理可得2=⋅HA SH HM ,2(2)∴=-HA h R h ,图5-12(2)∴==-△ABC S AB R h,21(2)3-∴=⋅=-△S ABC ABC V S h Rh (2)22=⋅⋅-≤h h Rh 33(2)223⎡⎤++-⎢⎥=⎢⎥⎢⎥⎣⎦h h R h ,当(2)2=-h R h ,即43h R =时,()3max-=S ABC V .例18.(2022·全国·高三专题练习)已知正三棱锥S ABC -的棱长为6.则该正三棱锥外接球的表面积为_______.【答案】2432π【解析】如图,∵正三棱锥S ABC -中,顶点S 在底面的射影为D ,该正三棱锥外接球的球心设为O ,因为底面边长为6,所以23AD ==∴高SD ===.由球心O 到四个顶点的距离相等,在直角三角形AOD 中,AO R =,DO SD OS R =-=,由222AO AD OD =+,得2212)R R =+,R =,∴外接球的表面积为:224342R ππ⋅⋅=.故答案为:2432π.例19.(2022·全国·高三专题练习)三棱锥-P ABC 且,1,PA PB PC AB AC BC =====则三棱锥外接球的表面积为____________.【答案】254π【解析】三棱锥-P ABC 中,取BC 中点D ,连PD ,连AD 并延长至O 1,使DO 1=AD ,连接BO 1,CO 1,PO 1,如图:于是得四边形1ABO C 为平行四边形,而1AB AC ==,1ABO C 是菱形,在ABC 中,BC =2221cos 22AB AC BC BAC AB AC +-∠==-⋅,即120BAC ∠= ,则160ABO ∠= ,1ABO △是正三角形,1111O A O B O C ===,于是得O 1是ABC 外接圆圆心,因PA PB PC ==,D 为BC 中点,则PD ⊥BC ,又AO 1⊥BC ,1PD AO D ⋂=,1,PD AO ⊂平面1PAO ,从而有BC ⊥平面1PAO ,1PO BC ⊥,同理1PO AC ⊥,而AC BC C = ,从而得1PO ⊥平面ABC ,由球的截面小圆性质知,三棱锥-P ABC 外接球球心O 在直线1PO 上,又1sin1202ABC S AB AC =⋅= 113P ABC ABC V PO S -=⋅= 12PO =,设球O 的半径为R ,则OB OP R ==,1|2|OO R =-,1Rt OO B △中,22211O B O O OB +=,即221(2)R R +-=,解得54R =,则球O 的表面积为22544S R ππ==,所以三棱锥外接球的表面积为254π.故答案为:254π例20.(2022·全国·高三专题练习)在三棱锥-P ABC 中,1====PA PC AB AC ,=PB BC ,则三棱锥-P ABC 的外接球的表面积为___________.【答案】73π【解析】在ABC 中,1AB AC ==,BC =所以222AB AC BC +=,所以AB AC ⊥,在PAB 中,1AB PA ==,PB =所以222AB PA PB +=,所以AB PA ⊥.又PA AC A = ,PA ,AC ⊂平面PAC ,所以AB ⊥平面PAC ,在PAC △中,1PA PC AC ===,所以PAC △的外接圆半径为112sin 3π⋅=不妨设PAC △的外接圆圆心为Q ,三棱锥-P ABC 的外接球球心为O连接,,OA OB OQ ,由于OA OB =,故O 在线段AB 的垂直平分线上,即1122OQ AB ==故三棱锥-P ABC 的外接球半径R OA ===外接球的表面积为2743R ππ=.故答案为:73π核心考点七:侧棱为外接球直径模型【规律方法】找球心,然后作底面的垂线,构造直角三角形.【典型例题】例21.(2022·河南河南·一模(文))三棱锥D ABC -的外接球的表面积为8,BD π是该球的直径,,22AC BC AB BC ⊥==,则三棱锥 D ABC -的体积为_____.【解析】如图,设球的半径为r ,由已知得248r ππ=,解得r =BD =,又由AC BC ⊥,所以,取AB 中点H ,H 为ABC 所在外接圆的圆心,故OH ⊥平面ABC ,又因为12OH AD ,所以,AD ⊥平面ABC ,得到AD AB ⊥,在ABD △中,2AD ==由22AB BC ==,AC BC ⊥,得到AC ==所以,12ABC S AC BC =⋅=△,所以,13D ABC ABC V AD S -=⋅=△例22.(2022·河南·一模(理))三棱锥D ABC -的外接球的表面积为20π,AD 是该球的直径,ABC 是边长为D ABC -的体积为______.【答案】【解析】设三棱锥D ABC -的外接球的球心为O ,半径为R ,则24π20πR =,解得R =设ABC 的外接圆圆心为1O ,半径为r ,则122sin BC r BAC ==∠,连接11,O A O O ,∵22211O A O O OA +=,即1=,则点D 到平面ABC 的距离为2,∴三棱锥D ABC -的体积11232V =⨯⨯=故答案为:例23.(2021·全国·高三专题练习(文))已知三棱锥P ﹣ABC 中,AB BC ==AC =2,PA 为其外接球___________.【答案】16π【解析】由题意可得ABC 为等腰直角三角形,AB BC ⊥,同时PA 为其外接球的一条直径,则,PBA PCA ∠∠都是直角,设球心为O ,取AC 的中点为M ,则OM ⊥平面ABC ,因为//OM PC ,则PC ⊥平面ABC ,则1132V =⨯⨯2PC =PC =,由勾股定理得4PA =,则外接球的半径为2,表面积为16.π故答案为:16π核心考点八:共斜边拼接模型【规律方法】如图,在四面体ABCD 中,⊥AB AD ,⊥CB CD ,此四面体可以看成是由两个共斜边的直角三角形拼接而形成的,BD 为公共的斜边,故以“共斜边拼接模型”命名之.设点O 为公共斜边BD 的中点,根据直角三角形斜边中线等于斜边的一半的结论可知,===OA OC OB OD ,即点O 到A ,B ,C ,D 四点的距离相等,故点O 就是四面体ABCD 外接球的球心,公共的斜边BD 就是外接球的一条直径.【典型例题】例24.在矩形ABCD 中,==4,3AB BC ,沿AC 将矩形ABCD 折成一个直二面角--B AC D ,则四面体ABCD 的外接球的体积为()A .π12512B .π1259C .π1256D .π1253【答案】C【解析】设矩形对角线的交点为O ,则由矩形对角线互相平分,可知===OA OB OC OD .∴点O 到四面体的四个顶点、、、A B C D 的距离相等,即点O 为四面体的外接球的球心,如图2所示.∴外接球的半径==52R OA .故ππ==球3412536V R .选C .例25.三棱锥-P ABC 中,平面⊥PAC 平面ABC , =2AC ,⊥PA PC ,⊥AB BC ,则三棱锥-P ABC 的外接球的半径为图 2A【答案】1【解析】AC 是公共的斜边,AC 的中点是球心O ,球半径为=1R .例26.在平行四边形ABCD 中,满足2AB AD AB = ,2224AB BD =- ,若将其沿BD 折成直二面角A BD C --,则三棱锥A BCD -的外接球的表面积为( )A .16πB .8πC .4πD .2π【答案】C【解析】平行四边形ABCD 中,2AB AD AB = ,∴0AB BD = ,AB BD ∴⊥,沿BD 折成直二面角A BD C --,平面ABD ⊥平面BDC三棱锥A BCD -的外接球的直径为AC ,22222224AC AB BD CD AB BD ∴=++=+=∴外接球的半径为1,故表面积是4π.故选:C .核心考点九:垂面模型【规律方法】如图1所示为四面体-P ABC ,已知平面⊥PAB 平面ABC ,其外接球问题的步骤如下:(1)找出△PAB 和△ABC 的外接圆圆心,分别记为1O 和2O .(2)分别过1O 和2O 作平面PAB 和平面ABC 的垂线,其交点为球心,记为O .(3)过1O 作AB 的垂线,垂足记为D ,连接2O D ,则2⊥O D AB .(4)在四棱锥12-A DO OO 中,AD 垂直于平面12DO OO ,如图2所示,底面四边形12DO OO 的四个顶点共圆且OD 为该圆的直径.图1图2【典型例题】例27.(2022·全国·高三专题练习)三棱锥-P ABC 中,平面PAC ⊥平面ABC , 2AC =,PA PC ⊥,AB BC ⊥,则三棱锥-P ABC 的外接球的半径为______【答案】1【解析】因为PA PC ⊥,AB BC ⊥,故AC 是公共的斜边,AC 的中点是球心O ,球半径为12AC R ==.故答案为:1例28.(2022·安徽马鞍山·一模(文))三棱锥-P ABC 中,PAC △与ABC 均为边长为平面PAC ⊥平面ABC ,则该三棱锥的外接球的表面积为________.【答案】20π【解析】等边三角形PAC 、等边三角形ABC 的高为πsin 33⨯==,等边三角形PAC 、等边三角形ABC 的外接圆半径为2323⨯=,设12,O O 分别是等边三角形PAC 、等边三角形ABC 的中心,设O 是三棱锥-P ABC 的外接球的球心,R 是外接球的半径,则2222215R OA ==+=,所以外接球的表面积为24π20πR =.故答案为:20π例29.(2022·全国·高三专题练习)三棱锥-P ABC 中,PAC △是边长为2AB BC ==,平面PAC ⊥平面ABC ,则该三棱锥的外接球的体积为______【解析】等边三角形PAC 的高为πsin 33⨯==,等边三角形PAC 的外接圆半径为222sin 6π=三角形ABC 2=,设12,O O 分别是等边三角形PAC 、等边三角形ABC 的中心,设O 是三棱锥-P ABC 的外接球的球心,R 是外接球的半径,则2222215R OA R ==+=⇒=,所以外接球的体积为34π3R =例30.(2021·全国·高三专题练习)已知在三棱锥-P ABC 中, 90,4,30BAC AB AC APC ︒︒∠===∠=,平面PAC ⊥平面ABC ,则三棱锥-P ABC 外接球的表面积为__________.【答案】80π【解析】如图12,O O 分别为,ABC PAC 的外心.由90BAC ∠=︒,即1O 为BC 中点,取AC 的中点,H 则1O H AC ⊥,又面PAC ⊥面ABC ,面PAC 面ABC AC =,1O H ⊂面ABC ,即1O H ⊥面,PAC 设球心为O ,则2OO ⊥平面,PAC ∴12//O H OO ,又2O H AC ⊥,2O H ⊂面PAC ,面PAC 面ABC AC =,面PAC ⊥面ABC ,∴2O H ⊥平面ABC ,又1OO ⊥平面ABC .∴12//OO O H ,即四边形12OO HO 为矩形. 由正弦定理知:228sin AC O P APC==∠,即24O P =,∴若外接球半径为R ,则2222216420R O P OO =+=+=,∴2480S R ππ==.故答案为:80π.核心考点十:二面角模型【规律方法】如图1所示为四面体-P ABC ,已知二面角--P AB C 大小为α,其外接球问题的步骤如下:(1)找出△PAB 和△ABC 的外接圆圆心,分别记为1O 和2O .(2)分别过1O 和2O 作平面PAB 和平面ABC 的垂线,其交点为球心,记为O .(3)过1O 作AB 的垂线,垂足记为D ,连接2O D ,则2⊥O D AB .(4)在四棱锥12-A DO OO 中,AD 垂直于平面12DO OO ,如图2所示,底面四边形12DO OO 的四个顶点共圆且OD 为该圆的直径.【典型例题】例31.(2022·贵州·模拟预测(理))如图,在三棱锥A BCD -中,ABC 是边长为AD CD ==D AC B --的余弦值为23,则三棱锥A BCD -外接球的表面积为______.【答案】84π5【解析】如图1,取AC 中点E ,连接BE ,DE ,ABC 与ACD 为等边三角形,则,BE AC DE AC ⊥⊥,,,BE DE E BE DE =⊂ 平面BDE ,故AC ⊥平面BDE ,故二面角D AC B --的平面角为DEB ∠,又AC ⊂平面ABC ,所以平面BDE ⊥平面ABC ,平面BDE ⋂平面ABC BE =,过D 作DH BE ⊥于H ,DH ⊂平面BDE ,所以DH ⊥平面ABC ,由题意得2cos 3DEB ∠=,3DE BE ===,∴2323EH =⨯=,则DH ==,设ABC 外接圆圆心为2O ,则2O 在BE 上,半径为2BO ,过2O 作平面ABC 的垂线l ,则三棱锥A BCD -外接球的球心一定在直线l 上.∵21122sin 2AC BO B =⨯==,∴221,1EO O H =∴=,过D 作BE 的平行线交l 于点F ,则21FD O H ==,∵D ,B 在球面上,外接球球心可能在三棱锥内也可能在三棱锥外,取截面如图2,3,设外接球球心O ,半径R ,令2OO x =,则2FO FO x =±,2FO DH ==∴22222222FO FD R OO BO R⎧+=⎪⎨+=⎪⎩,当2FO FO x =+时,化简得64,x +==当2FO FO x =-时,化简得64,x -==得2215R =,∴284π4π5S R ==,故答案为:84π5.例32.(2022·江西赣州·高三阶段练习(文))已知菱形ABCD 的边长为2,且60DAB ∠=︒,沿BD 把ABD △折起,得到三棱锥A BCD '-,且二面角A BD C '--的平面角为120︒,则三棱锥A BCD '-的外接球的表面积为___________.【答案】283π【解析】取BD 的中点H ,连接A H ',CH ,因为ABCD 为菱形,所以A H BD '⊥,CH BD ⊥,故A HC '∠为二面角A BD C '--的平面角,则120A HC '∠=︒,由题意可知A BD '△,BCD △为正三角形,则外接球球心位于过A BD '△,BCD △的中心且和它们所在面垂直的直线上,故分别取A BD '△,BCD △的重心为1G ,2G ,过点1G ,2G 分别作两个平面的垂线,交于点O ,点O 即为三棱锥的外接球的球心,由题意可知A BD BCD '≅△△,球心到面A BD '和面BCD 的距离相等,即12OG OG =,连接OD ,OH ,则1260OHG OHG ∠=∠=︒,菱形ABCD 的边长为2,∴1123HG ==,1cos 60HG OH ===︒,∴2222713OD OH HD =+=+=,即三棱锥A BCD '-的外接球的半径273=,所以其外接球的表面积为27284433R πππ=⨯=.故答案为:283π例33.(2022·江苏·南京市金陵中学河西分校高三阶段练习)在三棱锥A BCD -中,△BCD 是边长为3的正三角形,且AD =,AB =A BD C --的大小为3π,则此三棱锥外接球的体积为________.【解析】根据题意,222AD BD AB +=,所以AD BD ⊥,取BD 中点为E ,AB 中点M ,则//ME AD ,12ME AD ==ME DB ⊥,BCD 是正三角形,CE DB ⊥,MEC ∠是二面角A ﹣BD ﹣C 的平面角,60MEC ∠=︒,90ADB ∠=︒,M 是ADB 的外心,设N 是DBC 的外心,设过M 与平面ABD 垂直的直线与过N 垂直于平面BCD 的直线交于点O ,则O 是三棱锥A DBC -外接球球心,3CN BN ===,EN =,又EM ,由于平面MNO 与MEO 同时垂直于BD ,所以M E N O 、、、共面,在四边形MENO 中,由60MEC ∠=︒,EN =ME 090OME ONE ∠=∠= ,可得:12ON =,外接球半径为r OB ====体积为343V π=⨯=.例34.(2022·广东汕头·高三阶段练习)在边长为2的菱形ABCD 中,BD =将菱形ABCD 沿对角线AC 对折,使二面角B AC D --的余弦值为13,则所得三棱锥A BCD -的外接球的表面积为___________.【答案】6π【解析】依题意在边长为2的菱形ABCD 中,BD =60ABC ADC ︒∠=∠=,如下图所示,易知ABC 和ACD 都是等边三角形,取AC 的中点N ,则DN AC ⊥,BN AC ⊥.DN BN N = ,,DN BN ⊂平面BND ,所以AC ⊥平面BND ,所以BND ∠是二面角B AC D --的平面角,过点B 作BO DN ⊥交DN 于点O ,由AC ⊥平面BND ,BO ⊂平面BND ,所以AC BO ⊥,DN AC N = ,,DN AC ⊂平面ACD ,所以BO ⊥平面ACD .因为在 BDN 中,BN DN ==所以22212cos 332343BD BN DN BN DN BND =+-⋅⋅∠=+-⨯⨯=,则2BD =.故三棱锥A BCD -为正四面体,由BO ⊥平面ACD ,所以O 为底面ACD 的重心,所以23OD DN ==13ON DN ==则BO ==设外接球的半径为R ,则()222R OD BO R =+-,解得R =.因此,三棱锥A BCD -的外接球的表面积为22446R πππ=⨯=.故答案为:6π.核心考点十一:坐标法【规律方法】对于一般多面体的外接球,可以建立空间直角坐标系,设球心坐标为(,,)O x y z ,利用球心到各顶点的距离相等建立方程组,解出球心坐标,从而得到球的半径长.坐标的引入,使外接球问题的求解从繁琐的定理推论中解脱出来,转化为向量的计算,大大降低了解题的难度.【典型例题】例35.(2022·黑龙江·大庆实验中学模拟预测)直角ABC 中2,1AB BC ==,D 是斜边AC 上的一动点,沿BD 将ABD △翻折到A BD 'V ,使二面角A BD C '--为直二面角,当线段A C '的长度最小时,四面体A BCD'的外接球的表面积为( )A .134πB .215πC .133πD .143π【答案】D【解析】解:根据题意,图1的直角三角形沿BD 将ABD △翻折到A BD 'V 使二面角A BD C '--为直二面角,所以,过点'A 作A H BD '⊥交BD 延长线于H ,过点C 作CM BD ⊥交BD 于M ,再作//,//NH CM CN MH ,使得CN 与HN 交于点N ,所以,由二面角A BD C '--为直二面角可得'CM A H ⊥,设ABD θ∠=,即B A D θ'∠=,则2CBD πθ∠=-,因为2,1AB BC ==,所以'2,1A B BC ==,所以,在'Rt A BH 中,'2sin 2cos A H BH θ,θ==,在Rt BCM △中,cos sin sin cos 22BM CM ππθθ,θθ⎛⎫⎛⎫=-==-= ⎪ ⎪⎝⎭⎝⎭,所以2cos sin MH BH BM θθ=-=-,所以A C '==≥当且仅当22=πθ,即4πθ=时等号成立,此时,'A H BH ==BM CM ==MH =,在图1中,由于4πθ=,即BD 为角B 的角平分线,所以2AD AB DC BC ==,即AD =,所以'A D =,所以,DH =,由题知,',,HA HB HN 两两垂直,故以H 为坐标原点,以',,HB HN HA的方向为正方向建立空间直角坐标系,则()',,,A BC D ⎫⎫⎪⎪⎪⎪⎭⎭,所以,设四面体A BCD '的外接球的球心为(),,O x y z ,则',,AOOB OB OC OC OD ===,。
(完整版)高考数学中的内切球和外接球问题.

(完整版)高考数学中的内切球和外接球问题.高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.考查学生的空间想象能力以及化归能力.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.一、直接法(公式法)1、求正方体的外接球的有关问题例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .例2一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为______________.2、求长方体的外接球的有关问题例3一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为.例4已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().A. 16πB. 20πC. 24πD. 32π3.求多面体的外接球的有关问题例5一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为8 9,底面周长为3,则这个球的体积为 .解设正六棱柱的底面边长为x ,高为h ,则有==h x x 24368936==213x h ∴正六棱柱的底面圆的半径21=r ,球心到底面的距离23=d .∴外接球的半径22d r R +=. 体积:334R V π=. 小结本题是运用公式222d r R +=求球的半径的,该公式是求球的半径的常用公式.二、构造法(补形法) 1、构造正方体例5 若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是_______________.例3 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 .故其外接球的表面积ππ942==r S .小结:一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为c b a ,,,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222c b a R ++=. 出现“墙角”结构利用补形知识,联系长方体。
(完整版)高考外接球内切球专题练习

高考外接球与内接球专题练习(1)正方体,长方体外接球1. 如图所示,已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,长为2的线段MN 的一个端点M 在棱DD 1上运动,另一端点N 在正方形ABCD 内运动,则MN 的中点的轨迹的面积为( )A. 4πB. 2πC. πD. 2π 2. 正方体的内切球与其外接球的体积之比为( ) A. 1:3 B. 1:3 C. 1:33 D. 1:93. 长方体ABCD ﹣A 1B 1C 1D 1的8个顶点在同一个球面上,且AB=2,AD=3,AA 1=1, 则该球的表面积为( )A. 4πB. 8πC. 16πD. 32π4. 底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一球面上,则该球的体积为A. 323π B. 4π C. 2π D. 43π 5. 已知正三棱锥P ﹣ABC ,点P ,A ,B ,C 都在半径为3的球面上,若P A ,PB ,PC 两两垂直,则球心到截面ABC 的距离为 _________ .6. 在三棱椎A ﹣BCD 中,侧棱AB ,AC ,AD 两两垂直,△ABC ,△ACD ,△ADB 的 面积分别为22,32,62,则该三棱椎外接球的表面积为( ) A. 2π B. 6π C. 46π D. 24π7. 设A 、B 、C 、D 是半径为2的球面上的四点,且满足AB ⊥AC 、AD ⊥AC 、AB ⊥AD , 则S △ABC +S △ABD +S △ACD 的最大值为( )A. 4B. 8C. 12D. 168. 四面体ABCD 中,已知AB=CD=29,AC=BD=34,AD=BC=37,则四面体的 外接球的表面积为( )A. 25πB. 45πC. 50πD. 100π9. 如图,在三棱锥S ﹣ABC 中,M 、N 分别是棱SC 、BC 的中点,且MN ⊥AM ,若AB=22,则此正三棱锥外接球的体积是A. 12πB. 43πC. 433π D. 123π 10. 已知三棱锥P ABC -的顶点都在同一个球面上(球O ),且2,6PA PB PC ===, 当三棱锥P ABC -的三个侧面的面积之和最大时,该三棱锥的体积与球O 的体积的比值为( )A. 316πB. 38πC. 116πD. 18π (2)直棱柱外接球11. 已知三棱柱ABC ﹣A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC , AA 1=12,则球O 的半径为A. 3172B. 210C. 132D. 310 12. 设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面 积为( )A. 2a πB. 273a πC. 2113a π D. 25a π 13. 直三棱柱ABC ﹣A 1B 1C 1的各顶点都在同一球面上,若AB=AC=AA 1=2,∠BAC=120°, 则此球的表面积等于_________ .14. 三棱锥S ﹣ABC 的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB ⊥BC ,又SA=AB=BC=1,则球O 的表面积为( )A. 32πB. 32π C. 3π D. 12π 15. 已知球O 的面上四点A 、B 、C 、D ,DA ⊥平面ABC ,AB ⊥BC ,DA=AB=BC=3, 则球O 的体积等于 _________ .(3)正棱锥外接球16. 棱长均相等的四面体ABCD 的外接球半径为1,则该四面体的棱长为___________17. 如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB=60°,E 为AB的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B重合于点P ,则P ﹣DCE 三棱锥的外接球的体积为( )A. 4327πB. 62π C. 68π D. 624π 18. 已知三棱锥P ABC -的所有顶点都在表面积为28916π的球面上,底面ABC 是边长为 3的等边三角形,则三棱锥P ABC -体积的最大值为__________19. 正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积 为( )A. 814π B. 16π C. 9π D. 274π 20. 已知正三棱锥P ﹣ABC 的顶点均在球O 上,且P A=PB=PC=25,AB=BC=CA=23, 则球O 的表面积为( )A. 25πB. 1256πC. 52π D. 20π21. 在球O 的表面上有A 、B 、C 三个点,且3AOB BOC COA π∠=∠=∠=,△ABC 的外接圆半径为2,那么这个球的表面积为( ) A. 48π B. 36π C. 24π D. 12π 22. 半径为2的半球内有一内接正六棱锥P ﹣ABCDEF ,则此正六棱锥的侧面积是 ____.23. 表面积为23的正八面体的各个顶点都在同一个球面上,则此球的体积为( )A. 23πB. 3π C. 23π D. 223π 24. 正四棱锥P ﹣ABCD 底面的四个顶点A 、B 、C 、D 在球O 的同一个大圆上,点P 在球面 上,如果163P ABCD V -=,则求O 的表面积为( ) A. 4π B. 8π C. 12π D. 16π(4)棱锥外接球25. 已知A ,B ,C ,D 在同一个球面上,AB ⊥平面BCD ,BC ⊥CD ,若AB=6,213AC =, AD=8,则此球的体积是 _________ .26. 在矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B ﹣AC ﹣D , 则四面体ABCD 的外接球的体积为( )A. 12512πB. 1259πC. 1256πD. 1253π 27. 点A ,B ,C ,D 在同一个球的球面上,AB=BC=2,AC=22,若四面体ABCD 体积 的最大值为43,则该球的表面积为( ) A. 163π B. 8π C. 9π D. 12π 28. 四棱锥S ﹣ABCD 的底面ABCD 是正方形,侧面SAB 是以AB 为斜边的等腰直角三角 形,且侧面SAB ⊥底面ABCD ,若AB=23,则此四棱锥的外接球的表面积为( )A. 14πB. 18πC. 20πD. 24π29. 三棱锥S ﹣ABC 的四个顶点都在球面上,SA 是球的直径,AC ⊥AB ,BC=SB=SC=2, 则该球的表面积为( )A. 4πB. 6πC. 9πD. 12π30. 已知四棱锥V ﹣ABCD 的顶点都在同一球面上,底面ABCD 为矩形,AC∩BD=G ,VG ⊥平面ABCD ,AB=3,AD=3,VG=3,则该球的体积为( )A. 36πB. 9πC. 123πD. 43π(5)内接球31. 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )A. 1B. 2C. 3D. 432. 在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6,8AB BC ==,13AA =,则V 的最大值为A. 4πB. 92πC. 6πD. 323π 33. 已知球O 与棱长为4的正四面体的各棱相切,则球O 的体积为( ) A. 823π B. 833π C. 863π D. 1623π 34. 把一个皮球放入一个由8根长均为20的铁丝接成的四棱锥形骨架内,使皮球的表面 与8根铁丝都有接触点(皮球不变形),则皮球的半径为( )A. 103B. 10C. 102D. 3035. 棱长为23的正四面体内切一球,然后在正四面体和该球形成的空隙处各放入一个小 球,则这些球的最大半径为( )A. 2B. 22C. 24D. 2636. 如图,在四面体ABCD 中,截面AEF 经过四面体的内切球球心O ,且与BC ,DC 分别截于E 、F ,如果截面将四面体分成体积相等的两部分,设四棱锥A ﹣BEFD 与三棱锥A ﹣EFC的表面积分别是S 1,S 2,则必有( )A. S 1<S 2B. S 1>S 2C. S 1=S 2D. S 1,S 2的大小关系不能确定(6)球的截面问题37. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为,则此球的体 积为( )A. 6πB. 43πC. 46πD. 63π38. 已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O 的直径,且SC=2,则此棱锥的体积为( )A. 26B. 36C. 23D. 2239. 高为2的四棱锥S ﹣ABCD 的底面是边长为1的正方形,点S ,A ,B ,C ,D 均在半 径为1的同一球面上,则底面ABCD 的中心与顶点S 之间的距离为( )A. 102B. 232+C. 32D. 240. 已知三棱锥S ﹣ABC 的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,AC =,则球的体积与三棱锥体积之比是( )A. πB. 2πC. 3πD. 4π41. 在半径为13的球面上有A ,B ,C 三点,AB=6,BC=8,CA=10,则(1)球心到平面ABC 的距离为 _________ ;(2)过A ,B 两点的大圆面与平面ABC 所成二面角为(锐角)的正切值为 ____.42. 设A 、B 、C 、D 是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到 该平面的距离是球半径的一半,则球的体积是( )A. B. C. D.43. 已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2, 则球面面积是( ) A. 169π B. 83π C. 4π D. 649π 44. 已知OA 为球O 的半径,过OA 的中点M 且垂直于OA 的平面截球面得到圆M . 若圆M 的面积为3π,则球O 的表面积等于 _________ .45. 三棱锥P ﹣ABC 的各顶点都在一半径为R 的球面上,球心O 在AB 上,且有P A=PB=PC , 底面△ABC 中∠ABC=60°,则球与三棱锥的体积之比是 _________ .46. 已知H 是球O 的直径AB 上一点,:1:2AH HB =,AB ⊥平面α,H 为垂足,α截 球O 所得截面的面积为π,则球O 的表面积为__________(7)旋转体的外接内切47. 半径为4的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面 积之差是 _________ .48. 将4个半径都是R 的球体完全装入底面半径是2R 的圆柱形桶中,则桶的最小高度 是 _________ .1. D ;2. C ;3. B ;4. D ;5. 3; 6. B ; 7. B ; 8. C ; 9. B ;10. A ; 11. C ; 12. B ; 13. 20π; 14. C ; 15. 92π; 16. ;17. C ; 19. A ; 20. A ; 21. A ; 22. ; 23. A ; 24. D ; 25. 2563π; 26. C ; 27. C ; 28. D ; 29. B ; 30. D ; 31. B ; 32. B ; 33. A ; 34. B ; 35. C ; 36. C ; 37. B ; 38. A ; 39. A ; 40. D ;41. 12;3;42. A;43. D;44. 16π;45.3;46.92π47. 30π;48.(2R+;。
第29讲 外接球与内切球问题(解析版)

第29讲 外接球与内切球问题参考答案与试题解析一.选择题(共20小题)1.(2021春•润州区校级期末)若棱长为面积为( ) A .12πB .24πC .36πD .144π【解答】解:正方体外接球的球心在体对角线的中点,设半径为R ,则22(2)3R =⨯, 即2424R =,所以球的表面积为2424R ππ=. 故选:B .2.(2021•泉州二模)如图是一个由6个正方形和8个正三角形围成的十四面体,其所有顶点都在球O 的球面上,若十四面体的棱长为1,则球O 的表面积为( )A .2πB .4πC .6πD .8π【解答】解:根据图形可知,该十四面体是由一个正方体切去八个角得到的,如图所示,十四面体的外接球球心与正方体的外接球球心相同,建立空间直角坐标系, 该十四面体的棱长为1,∴∴该正方体的外接球球心坐标为O ,设十四面体上一点D ,则2D ,故十四面体的外接球的半径为1R OD ===, ∴球O 的表面积为244R ππ=.故选:B .3.(2021•三模拟)如图,已知一底面半径为1,体积为π的圆锥内接于球O (其中球心O 在圆锥内),则球O 的表面积为( )A .1009π B .209π C .203π D .503π 【解答】解:设圆锥的底面圆心为1O ,连接1SO ,1O B ,OB 21113V SO ππ=⨯⨯=锥,13SO ∴=,设球O 的半径为R ,则22(3)1R R -+=,解得53R =, 所以球O 的表面积2251004499S R πππ==⨯=. 故选:A .4.(2021•甲卷)已知A ,B ,C 是半径为1的球O 的球面上的三个点,且AC BC ⊥,1AC BC ==,则三棱锥O ABC -的体积为( )A B C D 【解答】解:因为AC BC ⊥,1AC BC ==,所以底面ABC 为等腰直角三角形,所以ABC ∆所在的截面圆的圆心1O 为斜边AB 的中点, 所以1OO ⊥平面ABC ,在Rt ABC ∆中,AB =12AO =,在1Rt AOO ∆中,1OO ==故三棱锥O ABC -的体积为111111332ABC V S OO ∆=⋅⋅=⨯⨯⨯=. 故选:A .5.(2021春•让胡路区校级期末)一块边长为10cm 的正方形铁片如图所示,将它的阴影部分截下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,则这个正四棱锥的外接球的表面积( )A .2894π B .28916π C .28948π D .28964π 【解答】解:根据题意,可知正四棱锥的底面边长为6,斜高为5,(如图) 从而可得正四棱锥的高4h OE ==,底面ABCD 外接圆r =∴正四棱锥的外接球的半径R解得174R =,可得外接球的表面积228944S R ππ==. 故选:A .6.(2021•晋中三模)在正四棱锥P ABCD -中,已知2PA AB ==,O 为底面ABCD 的中心,以点O PCD 的交线长度为( )A B C D 【解答】解:取CD 的中点E ,则有OE CD ⊥,PE CD ⊥,因为2PA AB ==,所以1OE =,PE =,则OP =PCD ∆为正三角形,球心O 在平面PCD 上的投影M 即为PCD ∆的中心,则OP OE OM PE ⋅=,球的半径OF ,在Rt OMF ∆中,则截面圆的半径MF ==在正三角形PCD 中,以点M 分,圆心角都为90︒,故球的球面与侧面PCD 的交线长度为截面圆周长的14,所以该球的球面与侧面PCD 的交线长度为124MF π⨯⨯=.故选:A .7.(2021•河南模拟)如图,正方形ABCD 与正方形ACEF 所在的平面互相垂直,1AB =,点A ,B ,C ,D ,E ,F 在同一个球面上,则该球的体积是( )A B .43π C D .323π【解答】解:如图,连接BD ,交AC 与G ,则AG GC =, 连接AE 、CF ,设AECF O =,则AO OE =,连接OG ,则//OG CE ,OG AC ∴⊥,平面ACEF ⊥平面ABCD ,平面ACEF ⋂平面ABCD AC =, OG ∴⊥平面ABCD ,则OA OC OB OD OE OF =====,即O 为点A ,B ,C ,D ,E ,F 所在球的球心,半径11122R AE ===. ∴所求球的体积是344133ππ⨯=.故选:B .8.在半径为R 的球内放入5个球,其中有4个球大小相等,两两相外切且均与大球相内切,另一个小球与这四个球均相外切,则这个小球半径为( )A .(3R -B .(4R -C .(5R -D .(6R -【解答】解:由已知中四个半径都是r 的球中的三个放在桌面上,使它两两外切, 然后在它们上面放上第四个球,使它与前三个都相切, 连接四个球的球心,得到一个棱长为2r 的正四面体若这四个球之间有一个小球和这四个球都外切,则这个小球的半径为11)r r =-,另有一个更大的球与这四个球都内切,更大球的1)R r =+.1(5r R∴=-=-,故选:C.9.(2021春•三明期中)在三棱锥P ABC-中,4PA PB BC===,8AC=,AB BC⊥.平面PAB⊥平面ABC,若球O是三棱锥P ABC-的外接球,则球O的表面积为() A.25πB.60πC.72πD.80π【解答】解:三棱锥P ABC-中,若球O是三棱锥P ABC-的外接球,如图所示:在平面PAB中,过点P作PD AB⊥于点D,由于平面PAB⊥平面ABC,故PD⊥平面ABC,所以PD BC⊥,由于AB BC⊥.故BC⊥平面ABP,所以BC AB⊥.由于4PA PB BC===,8AC=,故AB=,所以AD DB==,进一步求出2PD=,设PAB∆的中心为E,设PE x=,利用222(2)x x+-=,解得4x=,所以该三角形的中心在三角形的外部,即2DE=,由于三角形ABC为直角三角形,点H为AC的中点,所以4BH=,过点H作OH⊥平面ABC,所以OA=即外接球的半径为故2480S ππ=⋅⋅=球. 故选:D .10.(2021•白山三模)如图,正四棱锥P ABCD -的每个顶点都在球M 的球面上,侧面PAB 是等边三角形.若半球O 的球心为四棱锥的底面中心,且半球与四个侧面均相切,则半球O 的体积与球M 的体积的比值为( )ABCD【解答】解:如图,连接PO ,BD ,取CD 的中点E ,连接PE ,OE ,过O 作OH PE ⊥于H ,可知PO ⊥底面ABCD ,设4AB =,则BD ==,12BO BD ==,PO ==设球M 的半径为R ,半球O 的半径为r,则R =r OH =, 在等边三角形PCD中,求得PE = 由Rt PHO Rt POE ∆∆∽,可得r OH OE R PO PE ===故33314123()423O Mr V r V R R ππ⨯==⨯=半球球. 故选:D .11.(2021•鼓楼区校级模拟)已知矩形ABCD ,1AB =,2AD =,点E 为BC 边的中点将ABE ∆沿AE 翻折,得到四棱锥B AECD -,且平面BAE ⊥平面AECD ,则四面体B ECD -的外接球的表面积为( )A .72πB .4πC .92πD .5π【解答】解:如图所示,取AE ,DE 中点分别为G ,H ,连结BG , 作HI BG =,且//HI BG , 设外接球球心为O ,半径为r ,由平面BAE ⊥平面AECD ,易知BG ⊥平面AECD ,则有IH ⊥平面DEC ,且易知球心O 在IH 上,四边形BGIH 为矩形,设OH t =,则有2221)12r t t =+=-+,解得t =,所以1r =, 此时点I 与点O 重合,外接球表面积为4π. 故选:B .12.桌面上放着3个半径为1的球,两两相切,在它们上方的空间里放入一个球使其顶点(最高处)恰好和3个球的顶点在同一个平面上,该球的半径为( )A B C .13D 【解答】解:问题转化为摆放在桌面上的三个半径为1的球两两相切,在桌面与三球之间的空间中再摆入一个小球与三球和桌面都相切,设三个半径为1的球的球心分别为1O ,2O ,3O ,与桌面三个切点分别为A ,B ,C ,如下图所示:则三棱柱123ABC O O O -,是一个底面边长为2,高为1的正三棱柱,则小球球心O 在底面ABC 上的投影必为ABC ∆的中心H , 设小球半径为R ,在AOH ∆中,1AO R =+,AH =则OH 又1R OH +=,解得13R =, 故选:C .13.(2021•龙岩模拟)如图,在棱长为10的正方体内放入两个半径不相等的球1O ,2O ,这两个球相外切,且球1O 与正方体共顶点A 的三个面相切,球2O 与正方体共顶点1B 的三个面相切,则球2O 的半径最大时,球2O 的体积是( )A .100πB .5003π C .300π D .【解答】解:由题意,棱长为10的正方体,当球2O 的半径最大时,即是正方体内切球的时候,可得球2O 半径5r =,那么球2O 的体积3450033V r ππ==.故选:B .14.(2021•桂林三模)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器注水,当球面恰好接触水面时测得水深为6cm ,如不计容器的厚度,则球的表面积为( )A .100πB .5003πC .50πD .200π【解答】解:设正方体上底面所在平面截球得小圆M , 则圆心M 为正方体上底面正方形的中心.如图.设球的半径为R ,根据题意得球心到上底面的距离等于(2)R cm -, 而圆M 的半径为4,由球的截面圆性质,得222(2)4R R =-+, 解得:5R =.∴球的表面积为245100ππ=.故选:A .15.(2021•聊城一模)阿基米德是古希腊伟大的数学家、物理学家、天文学家,是静态力学和流体静力学的奠基人,和高斯、牛顿并列为世界三大数学家,他在不知道球体积公式的情况下得出了圆柱容球定理,即圆柱内切球(与圆柱的两底面及侧面都相切的球)的体积等于圆柱体积的三分之二.那么,圆柱内切球的表面积与该圆柱表面积的比为( ) A .12B .13C .23D .34【解答】解:设球的半径为R , 则圆柱的底面半径为R ,高为2R ,则圆柱的表面积为222226S R R R R πππ=+⋅=, 球的表面积为24S R π=球.∴圆柱内切球的表面积与该圆柱表面积的比为224263R R ππ=.故选:C .16.(2021•5月份模拟)已知三棱锥P ABC -的四个顶点在球O 的球面上,2PA PC BC ===,4AB =,120APC ∠=︒,平面PAC ⊥平面ABC ,则球O 的体积为( )A .B C D .【解答】解:因为2PA PC ==,120APC ∠=︒,可知AC = 又4AB =,2BC =,所以222AB BC AC =+,故BC AC ⊥, 取AC 的中点D ,则1PD =,PD AC ⊥,又平面PAC ⊥平面ABC ,且平面PAC ⋂平面ABC AC =, 所以PD ⊥平面ABC ,设PAC ∆的外接圆的圆心为1O ,则1O 在PD 的延长线上,因为2PA PC ==,120APC ∠=︒, 所以112PO AO AP ===,所以11DO =, 设2O 为ABC ∆的外接圆的圆心, 则2O 为AB 的中点,21DO =,连结1OO ,2OO ,由球的性质可知,2OO ⊥平面ABC , 所以12//DO OO ,22OO DO ⊥, 同理可得,12//OO DO ,11OO DO ⊥, 所以四边形12OO DO 为正方形,所以球O 的半径为2222222125R OO AO =+=+=,所以R =,则球O 的体积为343O V R π==球故选:C .17.(2021•广西模拟)已知三棱锥P ABC -的四个顶点在球O 的球面上,PA ⊥平面ABC ,2PA AB BC ===,PB 与平面PAC 所成的角为30︒,则球O 的表面积为( )A .6πB .12πC .16πD .48π【解答】解:如图,由PA ⊥平面ABC ,得平面PAC ⊥平面ABC ,取AC 中点H ,连接BH ,PH ,则BH AC ⊥,可得BH ⊥平面PAC , 则30BPH ∠=︒,2PA AB ==,PB ∴=,得BH ,求得AH HC =H 为底面三角形ABC的外心,过H 作HO ⊥底面ABC ,且1(2HO PA O =在球内部),则O 为三棱锥P ABC -的外接球的球心,可得222213R OA ==+=.∴球O 的表面积为244312R πππ=⨯=.故选:B .18.(2021•厦门模拟)如图,在四棱锥P ABCD -的平面展开图中,四边形ABCD 是边长为2的正方形,ADE ∆是以AD 为斜边的等腰直角三角形,90HDC FAB ∠=∠=︒,则四棱锥P ABCD -外接球的球心到面PBC 的距离为( )A B C D 【解答】解:由平面图形还原原四棱锥如图,该四棱锥底面ABCD 为正方形,边长为2,侧面PAD ⊥底面ABCD ,PA PD =,则PB PC =.取AD 的中点G ,则G 为Rt APD ∆的外心,连接AC 、BD ,相交于O ,则OG ⊥平面PAD , 可得OA OB OC OD OP ====,即O 为四棱锥P ABCD -的外接球的球心, 延长GO 交BC 于E ,则E 为BC 的中点,连接PE ,在Rt PGE ∆中,有1PG =,PE =设O 到PE 的距离为h ,则h PGOE PE =,即PG OE h PE ⋅===.则四棱锥P ABCD -外接球的球心到面PBC . 故选:C .19.(2021•江苏模拟)在三棱锥P ABC -中,ABC ∆是边长为2的正三角形,PA PB PC ==,E ,F 分别是PA ,AB 的中点,且CE EF ⊥,则三棱锥P ABC -接球的表面积为( )A .6πB .12πC .24πD .36π【解答】解:在三棱锥P ABC -中,ABC ∆是边长为2的正三角形,PA PB PC ==,E ,F 分别是PA ,AB 的中点,且CE EF ⊥,所以PB AC ⊥,EF 为PAB ∆中位线,//EF PB ∴又EF CE ⊥,PB CE ∴⊥,CEAC C =,AC ,CE ⊂平面PACPB ∴⊥平面PAC ,PB PA ∴⊥,且PB PC ⊥则PA ,PB ,PC 两两垂直 如图将P ABC -补成一个正方体 2AB AC BC ===∴PA PB PC ===外接球半径r =,246S r ππ==, 故选:A .20.(2021春•扬中市校级期末)已知三棱锥A BCD -的所有顶点都在球O 的球面上,且AB ⊥平面BCD ,AB =4AC AD ==,CD =,则球O 的表面积为( ) A .20π B .18πC .36πD .24π【解答】解:如图,AB ⊥平面BCD ,BC 、BD ⊂平面BCD ,AB BC ∴⊥,AB BD ⊥,2AB =,4AC AD ==,2BC BD ∴===,又CD =,222BC BD CD ∴+=,即BC BD ⊥,取CD 中点G ,则G 为BCD ∆的外心,设球O 的半径为R ,三角形BCD 的外接圆半径为r ,则12r CD ==,R ==∴球O 的表面积为2420S R ππ==.故选:A .二.填空题(共18小题)21.(2021•蚌埠模拟)有四个半径为1的小球,球1O ,球2O ,球3O 放置在水平桌面上,第四个小球4O 放在这三个小球的上方,且四个小球两两外切.在四个小球之间有一个小球O ,与这四个小球均外切.则球O 的半径为 1 . 【解答】解:将四个球的球心两两连线,可得出棱长为2的正四面体1234O O O O ,正四面体1234O O O O 的外接球球心即为球心O ,如图所示,设点4O 在底面123O O O 的射影点为M ,则球心O 在线段4O M 上,设正四面体1234O O O O 的外接球半径为r ,由正弦定理可知,正△123O O O的外接圆半径为322sin3O M π=,而4O M ==,由题意可得,22243()O M r O M r -+=,即224)3r r -+=,解得r =,∴4OM O M r =-=, ∴球O的半径为1+.故答案为:1+.22.(2021•榆林一模)已知直三棱柱111ABC A B C -的各顶点都在同一球面上,若1AB AC ==,12AA =,120BAC ∠=︒,则此球的表面积等于 8π .【解答】解:设直三棱柱111ABC A B C -的上下底面的三角形的外接圆的圆心分别是点P ,M , 设ABC ∆的外接圆半径为r ,直三棱柱111ABC A B C -的外接球的半径为R ,如图所示:,∴直三棱柱111ABC A B C -的外接球的球心O 为线段PM 的中点,在ABC ∆中,1AB AC ==,120BAC ∠=︒,∴由余弦定理得:22201cos12022AB AC BC AB AC +-==-,∴BC =∴由正弦定理得:022sin120BCr ==,1r ∴=, ∴在Rt OMC ∆中,OC R =,1112OM AA ==,1MC r ==, 222112R ∴=+=,∴直三棱柱111ABC A B C -的外接球的表面积为:248R ππ=,故答案为:8π.23.(2021•安徽模拟)已知球O 是圆锥1PO 的外接球,圆锥1PO 的母线长是底面半径的3倍,且球O 的表面积为818π,则圆锥1PO 的侧面积为 3π . 【解答】解:设1O B r =,球O 的半径为R ,则3PB r =,由球O 的表面积为28148R ππ=,得28132R =.在Rt △1OO B 中,2221()R PO R r =-+,即222)R R r =-+,解得1r =, 故圆锥1PO 的侧面积为3r PB ππ⋅=. 故答案为:3π.24.(2021秋•唐山期末)已知一个圆锥内接于球O (圆锥的底面圆周及顶点均在同一球面上),圆锥的高是底面半径的3倍,圆锥的侧面积为,则球O 的表面积为 100π . 【解答】解:设圆锥的底面半径O B r '=,则3SO r '=,SB SA ∴===,圆锥的侧面积为r π=⋅, 解得3r =.∴圆锥的高为9,设球的半径为R , 9OO R ∴'=-,由勾股定理得:222(9)R r R -+=, 解得5R =,∴球O 的表面积为:24100R ππ⋅=.故答案为:100π.25.(2021春•青羊区校级期末)已知边长为ABCD 中,60BAD ∠=︒,沿对角边BD 折成二面角A BD C --为120︒的四面体ABCD ,则四面体的外接球的表面积为28π .【解答】解:如图,设两三角形外心分别为2O ,3O ,球心为O ,BD 中点为1O , 由题意知1120AO C ∠=︒,12OO ∴=,3OO =∴球半径OC =∴四面体的外接球的表面积为2428S ππ=⨯=.故答案为:28π.26.(2021•沈阳三模)在四面体ABCD 中,BCD ∆是边长为2的等边三角形,ABD ∆是以BD 为斜边的等腰直角三角形,平面ABD ⊥平面ABC ,则四面体ABCD 的外接球的表面积为 6π .【解答】解:ABD ∆是以BD 为斜边的等腰直角三角形,AB AD ∴⊥,又平面ABD ⊥平面ABC ,平面ABD ⋂平面ABC AB =, DA ∴⊥平面ABC ,则DA AC ⊥,可得DA 、AB 、AC 两两相互垂直,且2DA AB AC ==== 以A 为顶点,以AB 、AC 、AD 为过A 点的三条棱构造正方体, 可得四面体ABCD 外接球的半径R =,∴四面体ABCD 的外接球的表面积为22446R πππ=⨯=. 故答案为:6π.27.(2021春•包河区校级期中)把四个半径分别为9,9,9,19的小球同时放入一个大球中,使四个小球两两外切并均与大球内切,则大球的半径为 572. 【解答】解:如图,设三个半径为9的球的球心分别为A 、B 、C ,半径为19的球的球心为D ,连接AB 、BC 、AC 、AD 、BD 、CD , 则D 在平面ABC 上的射影为底面正三角形ABC 的外心G ,可得BG =三棱锥D ABC -为正三棱锥,侧棱28DB =,则26DG ==. 再设大球的球心为O ,由对称性可得,O 在线段DG 上, 要使大球与四个小球都内切, 则199OD OB +=+,设OB x =,则OG ,26OD DG OG ∴=-=则26199x =+,解得392x =. ∴大球的半径为39579922x +=+=. 故答案为:572.28.把半径为r 的四个小球全部放入一个大球内,则大球半径的最小值为 (1r + . 【解答】解:当四个小球彼此相外切,与大球内切时,大球半径的最小, 如图所示:四个小球,三个在下,一个在上,四个球心连线成正四面体, 该正四面体的边长为2r ,,,∴大球半径最小为:(1r +,故答案为:(1r +29.(2021•饶阳县校级模拟)如图,在三棱柱111ABC A B C -中,11114A B AC ==,S 为棱11B C 上一点,且90ASC ∠=︒,AB ⊥平面ACS ,则三棱锥S ABC -的外接球的表面积为 32π .【解答】解:如图,取BC 的中点D ,连接AD ,SD .AB ⊥平面ACS ,AC ,SC ⊂平面ACS ,AB SC ∴⊥,AB AC ⊥,90ASC ∠=︒,SC AS ∴⊥,又AB AS A =,AB ,AS ⊂平面ABS ,SC ∴⊥平面ABS ,SC BS ∴⊥,则SD BD CD AD ===,得D 为三棱锥S ABC -的外接球的球心.114AB AC A B ===,∴BC =∴三棱锥S ABC -的外接球的表面积为224()4322BC πππ⋅=⨯=. 故答案为:32π.30.(2021•普陀区模拟)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的表面积为 2π .【解答】解:设内切球的半径为r ,则利用轴截面,根据等面积可得112(332)22r ⨯⨯++,r ∴=, ∴该圆锥内切球的表面积为214422r πππ=⨯=, 故答案为:2π.31.(2021•奉贤区校级二模)已知ABC ∆的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则球O 的体积为 323π;O 到平面ABC 的距离为 .【解答】解:由题意可知图形如图:ABC ∆的等边三角形,2AB =3AB BC AC ∴===,可得:1233AO == 球O 的表面积为16π, 外接球的半径为:R ; 所以2416R ππ=,解得2R =,∴球O 的体积为:343233R ππ⋅=,所以O 到平面ABC 1=. 故答案为:323π,1.32.(2021•渝水区校级模拟)阿基米德多面体,也称为半正多面体,是指至少由两种类型的正多边形为面构成的凸多面体.如图,从正四面体的4个顶点处截去4个相同的正四面体,若得到的几何体是由正三角形与正六边形构成的阿基米德多面体,且该阿基米德多面体的表面积为112π.【解答】解:设阿基米德多面体的棱长为a 22446⨯+⨯=1a =,显然正四面体的棱长为3,且正四面体与半正多面体的外接球的球心相同,设为O .如图:3BC =,则BG ==23BF BG ===AF ∴设OA OB R ==,则OF AF R R =-,在直角三角形OBF 中,222OB BF OF =+,即223)R R =+,解得R =,∴在直角三角形AFB 中cos AF BAF AB ∠==∴在三角形EAO 中,cos cos EAO BAF ∠=∠, 由余弦定理得,22222222cos 22216OE AE AO AE AO EAO =+-⨯⨯∠=+-⨯⨯=,OE ∴.所以这个半正多面体的外接球的半径为.则该阿基米德多面体外接球的表面积为2114()42ππ⨯=故答案为:112π.33.(2021•泰州模拟)由两种或三种正多边形面组成的凸多面体称作阿基米德多面体.将一个棱长为12的正四面体截去4个小正四面体后可以得到一个由正三角形和正六边形构成的阿基米德八面体,则该阿基米德八面体的外接球的表面积为 88π .【解答】解:如图,截去4个小正四面体后得到一个由正三角形和正六边形构成的阿基米德八面体, 可知阿基米德八面体的所有棱长都相等,等于原正四面体棱长的13,为11243⨯=,原正四面体外接球的球心,就是阿基米德八面体的外接球的球心,设球心为O ,半径为R ,一个正六边形的中心为G ,则OG 与正六边形所在平面垂直, OG 的长度为原正四面体内切球的半径,由等体积法可知,OG 等于原正四面体高的14,即1144OG ==⨯4GA =,22261622OA OG GA ∴=+=+=,则该阿基米德八面体的外接球的表面积为2442288R πππ=⨯=. 故答案为:88π.34.(2021•潍坊三模)阿基米德在他的著作《论圆和圆柱》中,证明了数学史上著名的圆柱容球定理:圆柱的内切球(与圆柱的两底面及侧面都相切的球)的体积与圆柱的体积之比等于它们的表面积之比.可证明该定理推广到圆锥容球也正确,即圆锥的内切球(与圆锥的底面及侧面都相切的球)的体积与圆锥体积之比等于它们的表面积之比,则该比值的最大值为 12.【解答】解:设圆锥去的底面半径为r ,母线长为l ,圆锥内切球半径为R ,作出圆锥的轴截面如图所示,设OBC θ∠=,由于tan R r θ=,则tan R r θ=, OD AB ⊥,OE BC ⊥, DBE DOE π∴∠+∠=,又AOD DOE π∠+∠=, 2AOD DBE θ∴∠=∠=, tan2AD R θ∴=,22tan 2tan Rl r AD BD r AD r R θθ∴+=++=+=+, 则圆锥表面积为1()S r l r π=+,圆锥内切球表面积为224S R π=, ∴所求比值为22221242(1)2tan 2()tan 1tan S R tan tan R R R S tan πθθπθθθθ==-+-, 令2tan 0t θ=>,则2212(1)22S t t t t S =-=-+, 当12t =时,21S S 取得最大值为12.故答案为:12. 35.(2021秋•怀化期末)矩形ABCD 中,4AB =,3BC =,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为 1256π . 【解答】解:由题意知,球心到四个顶点的距离相等, 所以球心在对角线AC 上,且其半径为AC 长度的一半, 则345125()326V ππ=⨯=球.故答案为:1256π.36.(2021•闵行区校级模拟)在棱长为2的正方体1111ABCD A B C D -,M ,N ,Q ,P 分别为棱11A B ,11B C ,1BB ,1CC 的中点,三棱锥M PQN -的顶点在同一个球面上,则该球的表面积为 8π .【解答】解:三棱锥M PQN -的顶点在同一个球面上, 由点P 为棱1CC 的中点,可得底面PQN ∆是等腰直角三角形, 那么底面PQN ∆的外接圆半径1r =,设球心到PQN ∆的外接圆的圆心的距离为d ,球半径R ,则2221()R MB d =-+,① 222d r R +=,②联立①②解得R .∴该球的表面积248S R ππ==.故答案为:8π.37.(2021•聊城三模)在棱长为2的正方体1111ABCD A B C D -中,M ,N ,Q 分别为棱11A B ,11B C ,1BB 的中点,点P 为棱1CC 上的动点,则P MNQ V -的最大值为12,若点P 为棱1CC 的中点,三棱锥M PQN -的顶点在同一个球面上,则该球的表面积为 . 【解答】解:由三棱锥P MNQ V -的体积:113NQP MB V S h =⨯,因为1MB 是定值,只需NQP S 最大值即可,当P 在C 点时,可得底面NQP 的面积最大,即32NQP S =. 那么1113113322NQP MB V S h =⨯=⨯⨯=;三棱锥M PQN -的顶点在同一个球面上,由点P 为棱1CC 的中点,可得底面PQN ∆是等腰直角三角形, 那么底面PQN ∆的外接圆半径1r =, 设球心到圆心的距离为d ,球半径R则2221()R MB d =-+⋯⋯① 222d r R +=⋯⋯②根据①②解得R ;∴该球的表面积248S R ππ==.故答案为12;8π.38.(2021•河东区二模)已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC ∆是边长为2正三角形,E ,F 分别是PA ,AB 的中点,90CEF ∠=︒,则球O 的体.【解答】解:如图,由PA PB PC ==,ABC ∆是边长为2的正三角形,可知三棱锥P ABC -为正三棱锥,则顶点P 在底面的射影O 为底面三角形的中心,连接BO 并延长,交AC 于G , 则AC BG ⊥,又PO AC ⊥,POBG O =,可得AC ⊥平面PBG ,则PB AC ⊥,E ,F 分别是PA ,AB 的中点,//EF PB ∴,又90CEF ∠=︒,即EF CE ⊥,PB CE ∴⊥,得PB ⊥平面PAC ,∴正三棱锥P ABC -的三条侧棱两两互相垂直,把三棱锥补形为正方体,则正方体外接球即为三棱锥的外接球,其直径,2R =O 的体积为343V R π=..。
专题11 多面体的外接球和内切球(教师版)-2024年高考二级结论速解技巧
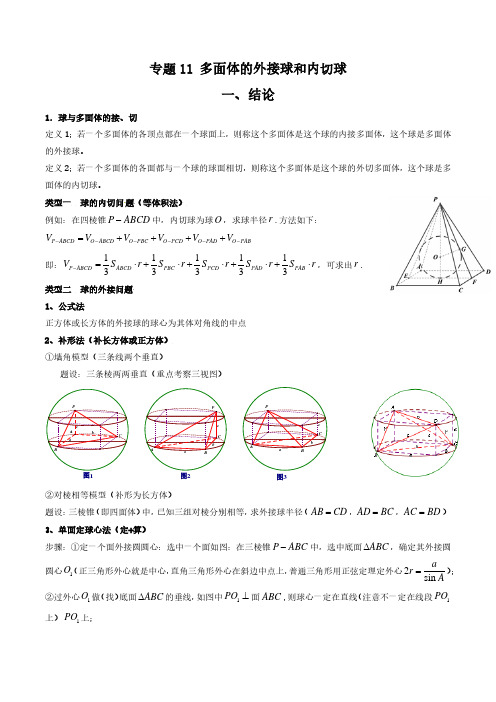
O2
O
A
③分别过 O1 做面 ABC 的垂线,和 O2 做面 PAB 的垂线,两垂线交点即为外接球球心
H
O1
B
C
O.
二、典型例题
例题 1.(2023 春·湖南湘潭·高二统考期末)棱长为 1 的正方体的外接球的表面积为(
)
A. 3π 4
B. 3π
C.12π
D.16π
【答案】B
【详解】解:易知,正方体的体对角线是其外接球的直径,设外接球的半径为 R ,
∠BAC = 120° , A=B A=C A=P 2 ,则该四面体的外接球的表面积为(
)
A.12π
B.16π
C.18π
D. 20π
【答案】D
【详解】因为 PA ⊥ AB , PA ⊥ AC ,= AB AC A, AB, AC ⊂ 平面 ABC ,
所以 PA ⊥ 平面 ABC .
设底面 ABC 的外心为 G ,外接球的球心为 O ,则 OG ⊥ 平面 ABC ,所以 PA// OG . 设 D 为 PA 的中点,
所以O=C O=D OA ,即 O 为该三棱锥的外接球的球心, CD = 4 2
由正弦定理可知, 4= 2 2= R, R 4 6 ,
sin 60°
3
故该三棱锥的外接球的表面积为 S =4π R2 =4π × 16× 2 = 128π .
3
3
故选:C
2.(2023·湖南·模拟预测)在三棱锥 A − BCD 中, AB ⊥ 平面 BCD, BC ⊥ CD,CD = 2AB = 2BC = 4 ,则三
π
.
【反思】本例属于对棱相等模型,可补形为长方体,再借助长方体模型,求外接球半径.
经典三类球:外接球、内切球、棱切球(解析版)

经典三类球:外接球、内切球、棱切球1【考点预测】考点一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.2.长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.(2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA2,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1图2图3图4考点二:正四面体外接球如图,设正四面体ABCD 的的棱长为a ,将其放入正方体中,则正方体的棱长为22a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为R =22a ⋅32=64a ,即正四面体外接球半径为R =64a .考点三:对棱相等的三棱锥外接球四面体ABCD 中,AB =CD =m ,AC =BD =n ,AD =BC =t ,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为a ,b ,c ,则b 2+c 2=m 2a 2+c 2=n 2a 2+b 2=t2,三式相加可得a 2+b 2+c 2=m 2+n 2+t 22,而显然四面体和长方体有相同的外接球,设外接球半径为R ,则a 2+b 2+c 2=4R 2,所以R =m 2+n 2+t 28.直棱柱外接球如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O 的位置,O 1是ΔABC 的外心,则OO 1⊥平面ABC ;第二步:算出小圆O 1的半径AO 1=r ,OO 1=12AA 1=12h (AA 1=h 也是圆柱的高);第三步:勾股定理:OA 2=O 1A 2+O 1O 2⇒R 2=h 22+r 2⇒R =r 2+h 2 2,解出R考点五:直棱锥外接球如图,PA ⊥平面ABC ,求外接球半径.解题步骤:第一步:将ΔABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:O 1为ΔABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理,得a sin A=b sin B =c sin C =2r ),OO 1=12PA ;第三步:利用勾股定理求三棱锥的外接球半径:①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;②R 2=r 2+OO 12⇔R =r 2+OO 12.考点六:正棱锥外接球正棱锥外接球半径:R=r2+h22h.垂面模型如图1所示为四面体P-ABC,已知平面PAB⊥平面ABC,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.图1图2考点八:锥体内切球方法:等体积法,即R=3V体积S表面积考点九:棱切球方法:找切点,找球心,构造直角三角形1【典型例题】1(2023春·天津宁河·高一校考期末)在三棱锥P-ABC中,AP=2,AB=3,PA⊥面ABC,且在△ABC中,C=60°,则该三棱锥外接球的表面积为()B.8πC.10πD.12πA.20π3【答案】B【解析】根据题意得出图形如右图:O为球心,N为底面△ABC截面圆的圆心,ON⊥面ABC,∵在三棱锥P-ABC中,AP=2,AB=3,PA⊥面ABC,且在△ABC中,C=60°=2r,解得r=1,∴根据正弦定理得出:3sin60°∵PA⊥面ABC,∴PA⎳ON,∵PA=2,AN=1,ON=d,∴OA=OP=R,∴根据等腰三角形得出:12+d2=(2-d)2+12,解得d=1,∴R=1+1=2∴三棱锥的外接球的表面积为4πR2=8π.故选:B.2(2023·辽宁沈阳·高一东北育才学校校考阶段练习)在正三棱锥S-ABC中,外接球的表面积为36π,M,N分别是SC,BC的中点,且MN⊥AM,则此三棱锥侧棱SA=()A.1B.2C.3D.23【答案】D【解析】取AC的中点E,连结BE、SE,∵三棱锥S-ABC正棱锥,∴SA=SC,BA=BC.又∵E为AC的中点,∴SE⊥AC且BE⊥AC∵SE、BE是平面SBE内的相交直线,∴AC⊥平面SBE,又SB在平面SBE内可得SB⊥AC又∵MN是△SBC的中位线,∴MN∥SB,可得MN⊥AC又∵MN ⊥AM ,又AM ,AC 是平面SAC 内的相交直线,∴MN ⊥平面SAC ,结合MN ∥SB ,可得SB ⊥平面SAC 又∵三棱锥S -ABC 是正三棱锥,∴∠ASB =∠BSC =∠ASC =90°,因此将此三棱锥补成正方体,则它们有相同的外接球,设球的半径为R ,可得4πR 2=36π,解得R =3,∴SA 2+SA 2+SA 2=2R =6,解之得SA =23故选:D3(2023春·河南南阳·高一校联考期末)《九章算术》是我国古代著名的数学著作,书中记载有几何体“刍甍”.现有一个刍甍如图所示,底面ABCD 为正方形,EF ∥平面ABCD ,四边形ABFE ,CDEF为两个全等的等腰梯形,EF =12AB =2,AE =23则该刍甍的外接球的体积为()A.642π3B.3πC.643π3D.642π【答案】A【解析】取AD ,BC 中点N ,M ,正方形ABCD 中心O ,EF 中点O 2,连接EN ,MN ,FM ,OO 2,如图,依题意,OO2⊥平面ABCD,EF⎳AB⎳MN,点O是MN的中点,MN=AB=4,等腰△AED中,AD⊥EN,EN=AE2-AN2=22,同理FM=22,因此,等腰梯形EFMN的高OO2=EN2-MN-EF22=7,由几何体的结构特征知,刍甍的外接球球心O1在直线OO2上,连O1E,O1A,OA,正方形ABCD外接圆半径OA= 22,则有O1A2=OA2+OO21O1E2=O2E2+O2O21,而O1A=O1E,O2E=12EF=1,当点O1在线段O2O的延长线(含点O)时,视OO1为非负数,若点O1在线段O2O(不含点O)上,视OO1为负数,即有O2O1=O2O+OO1=7+OO1,即(22)2+OO21=1+(7+OO1)2,解得OO1=0,因此刍甍的外接球球心为O,半径为OA=22,所以刍甍的外接球的体积为4π3×223=642π3.故选:A.4(2023·高一课时练习)已知圆台的上下底面半径分别为1和2,侧面积为35π,则该圆台的外接球半径为()A.1055B.654C.1854D.1054【答案】B【解析】设圆台的高和母线分别为h,l,球心到圆台上底面的距离为x,根据圆台的侧面积公式可得π1+2l=35π⇒l=5,因此圆台的高h=l2-2-12=2,当球心在圆台内部时,则12+x2=22+h-x2,解得x=74,故此时外接球半径为1+x2=65 16=65 4,当球心在圆台外部时,则12+x2=22+x-h2,x>h,解得x=74不符合要求,舍去,故球半径为65 4故选:B5(2023·高一课时练习)已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为()A.4πB.42πC.82πD.8π【答案】D【解析】如图,圆锥与内切球的轴截面图,点O为球心,内切球的半径为r,D,E为切点,设OD=OE=r,即BE=BD=2由条件可知,AB=422+22=6,△ADO中,AO2=AD2+DO2,即42-r2=6-22+r2,解得:r=2,所以圆锥内切球的表面积S=4πr2=8π.故选:D6(2023·高一课时练习)一个正四棱柱的每个顶点都在球O的球面上,且该四棱柱的底面面积为3,高为10,则球O的体积为()A.16πB.32π3C.10π D.28π3【答案】B【解析】设该正四棱柱的底面边长为a,高为h,则a2=3,h=10,解得a=3,所以该正四棱柱的体对角线为球O的直径,设球O的半径为R,所以,2R=a2+a2+h2=3+3+10=4,即R=2,所以,球O的体积为4π3×23=32π3.故选:B7(2023·高一课时练习)正八面体是每个面都是正三角形的八面体.如图所示,若此正八面体的棱长为2,则它的内切球的表面积为()A.423π B.8327π C.83π D.163π【答案】C【解析】以内切球的球心为顶点、正八面体的八个面为底面,可将正八面体分为8个全等的正三棱锥,设内切球的半径为r ,则8V 三棱锥=V 正八面体=2V 正四棱锥,且正四棱锥的高为图中CO ,易得CO =2,即:8×13×12×2×2×32 ⋅r =2×13×2×2 ×2解得:r =63,所以,内切球的表面积为8π3.故选:C .8(2023·高一课时练习)已知A ,B ,C 三点均在球O 的表面上,AB =BC =CA =2,且球心O 到平面ABC 的距离等于球半径的13,则下列结论正确的为()A.球O 的外切正方体的棱长为6B.球O 的表面积为8πC.球O 的内接正方体的棱长为3D.球O 的半径为32【答案】A【解析】设球O 的半径为R ,△ABC 的外接圆半径为r ,则r =233,因为球心O 到平面ABC 的距离等于球O 半径的13,所以R 2-19R 2=43,得R 2=32,即R =62,故D 错误;球O 的外切正方体的棱长b 满足b =2R =6,故A 正确;所以球O 的表面积S =4πR 2=4π×32=6π,故B 错误;球O 的内接正方体的棱长a 满足3a =2R =6,即a =2,故C 错误.故选:A .9(2023·河南开封·开封高中校考模拟预测)已知某棱长为22的正四面体的各条棱都与同一球面相切,则该球与此正四面体的体积之比为()A.π2B.π3C.3π3D.2π2【答案】A【解析】如图,正方体ABCD -A 1B 1C 1D 1中,棱长为2,所以,四面体A 1BDC 1是棱长为22的正四面体,当正四面体的各条棱都与同一球面相切时,该球为正方体的内切球,半径为1,所以,该球的体积为4π3,因为正四面体的体积为8-4×13×12×2×2×2=8-163=83,所以,该球与此正四面体的体积之比为4π383=π2.故选:A10(2023·高一课时练习)正四面体ABCD 的棱长为a ,O 是棱AB 的中点,以O 为球心的球面与平面BCD 的交线和CD 相切,则球O 的体积是()A.16πa 3B.26πa 3 C.36πa 3 D.23πa 3【答案】D【解析】设点A 在平面BCD 内的射影为点E ,则E 为△BCD 的中心,取CD 的中点M ,连接BM ,则E ∈BM ,取线段BE 的中点F ,连接OF ,因为O 、F 分别为AB 、BE 的中点,则OF ⎳AE 且OF =12AE ,因为AE ⊥平面BCD ,则OF ⊥平面BCD ,因为BE ⊂平面BCD ,则AE ⊥BE ,正△BCD的外接圆半径为BE=a2sinπ3=33a,∴AE=AB2-BE2=63a,所以,OF=12AE=66a,易知球O被平面BCD所截的截面圆圆心为点F,且BF=EF=EM,故FM=BE=33a,因为△BCD为等边三角形,M为CD的中点,则BM⊥CD,因为以O为球心的球面与平面BCD的交线和CD相切,则切点为点M,则球O的半径为OM=OF2+FM2=22a,因此,球O的体积是V=43π×22a3=23πa3.故选:D.11(2023·高一课时练习)已知直三棱柱ABC-A1B1C1的底面为直角三角形,如图所示,∠BAC= 90°,AB=1,AC=2,AA1=3,则四面体A-A1BC的体积为,四棱锥A1-BCC1B1的外接球的表面积为.【答案】 1 14π【解析】由题意可得S△ABC=12×AB⋅AC=12×2×1=1,且h=AA1,则V A-A1BC=13S△ABC⋅h=13×1×3=1因为△ABC 外接圆的圆心即为BC 中点,设为O ,△A 1B 1C 1外接圆的圆心即为B 1C 1中点,设为O 1,则OO 1的中点到六个顶点的距离相等,则OO 1的中点M 为外接球的球心,即CM 为半径,OC =12BC =12AC 2+AB 2=52,OM =12AA 1 =32所以CM =OC 2+OM 2=54+94=142,即外接球的表面积为4πR 2=4π×144=14π故答案为:1,14π2【过关测试】一、单选题1(2023·高一课时练习)若正四面体的表面积为83,则其外接球的体积为()A.43πB.12πC.86πD.323π【答案】A【解析】设正四面体的棱长为a ,由题意可知:4×34a 2=83,解得:a =22,所以正四面体的棱长为22,将正四面体补成一个正方体,则正方体的棱长为2,正方体的体对角线长为23,因为正四面体的外接球的直径为正方体的体对角线长,所以外接球半径R =3,则外接球的体积为V =43πR 3=43π,故选:A .2(2023·陕西渭南·高一统考期末)在直三棱柱ABC -A 1B 1C 1中,AB =BC =2,AA 1=22,∠ABC =π2,则此三棱柱外接球的表面积为()A.4πB.8πC.16πD.24π【答案】C 【解析】因为AB=BC=2,∠ABC=π2,所以△ABC为等腰直角三角形,将直三棱柱ABC-A1B1C1补全为如图长方体ABCD-A1B1C1D1,则长方体的外接球即直三棱柱的外接球,因为AB=BC=2,AA1=22,所以外接球直径2R=AC1=22+22+222=4,所以外接球半径R=2,表面积S=4πR2=16π.故选:C.3(2023春·河北衡水·高一校考阶段练习)在正四棱锥P-ABCD中,AB=4,PA=26,则平面PAB截四棱锥P-ABCD外接球的截面面积是()A.65π5B.36π5C.12πD.36π【答案】B【解析】如图,作PO ⊥平面ABCD,垂足为O ,则O 是正方形ABCD外接圆的圆心,从而正四棱锥P-ABCD外接球的球心O在PO 上,取棱AB的中点E,连接O D,O E,OD,PE,作OH⊥PE,垂足为H.由题中数据可得O D=22,O E=2,PE=25,O P=4,设四棱锥P-ABCD外接球的半径为R,则R2=O D2+O O2=OP2=O P-O O2,即R2=8+O O2=4-O O2,解得R=3.由题意易证△OPH∽△EPO ,则PHO P=OPPE,故PH=65 5.故所求截面圆的面积是π⋅PH2=36π5.故选:B4(2023春·山西太原·高一校考阶段练习)在三棱锥P -ABC 中,PA =PB =PC =3,侧棱PA与底面ABC 所成的角为60°,则该三棱锥外接球的体积为()A.πB.π3C.4πD.4π3【答案】D【解析】设点P 在平面ABC 内的射影点为E ,如下图所示:由线面角的定义可知,直线PA 与底面ABC 所成的角为∠PAE =60°,所以,PE =3sin60°=32,AE =3cos60°=32,因为PE ⊥平面ABC ,BE 、CE ⊂平面ABC ,∴PE ⊥BE ,PE ⊥CE ,∴BE =PB 2-PE 2=32=PC 2-PE 2=CE ,所以,△ABC 的外接圆圆心为点E ,且其外接圆半径为32,所以,三棱锥P -ABC 的外接球球心O 在直线PE 上,设球O 的半径为r ,由几何关系可得OE 2+AE 2=OA 2,即32-r 2+322=r 2,解得r =1,因此,三棱锥P -ABC 外接球的体积为V =43πr 3=43π.故选:D .5(2023春·河南鹤壁·高一河南省浚县第一中学校考阶段练习)已知三棱锥P -ABC 的四个顶点均在同一个球面上,底面ABC 满足BA =BC =6,∠ABC =π2,若该三棱锥体积的最大值为3,则其外接球的体积为()A.323π B.32π C.16π D.823π【答案】A【解析】在△ABC中,BA=BC=6,∠ABC=π2,因此三棱锥P-ABC的外接球被平面ABC截得的截面小圆圆心是AC的中点O1,令三棱锥P-ABC的外接球球心为O,则OO1⊥平面ABC,而S△ABC=12AB⋅BC=3,O1A=3,因三棱锥P-ABC体积的最大值为3,则三棱锥P-ABC底面ABC上的高最大,设此最大高为h,由13×3h=3得h=3,要三棱锥P-ABC的体积最大,当且仅当球O上的点P到平面ABC的距离最大,则点P在线段O1O的延长线上,设球O半径为R,则有(h-R)2+O1A2=R2,即(3-R)2+(3)2=R2,解得R=2,所以三棱锥P-ABC的外接球体积为V=43πR3=323π.故选:A6(2023·高一课时练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD 是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【解析】因PA⊥平面ABCD,AB⊂平面ABCD,AD⊂平面ABCD,则PA⊥AB,PA⊥AD,又因四边形ABCD为矩形,则AB⊥AD.则阳马的外接球与以PA,AB,AD为长宽高的长方体的外接球相同.又PA=5,AB=3,AD=BC=4.则外接球的直径为长方体体对角线,故外接球半径为:R=PA2+AB2+AD22=32+42+522=522,则外接球的表面积为:S=4πR2=4π⋅504=50π.故选:B7(2023·吉林·高一吉林一中校考阶段练习)如图,在△ABC中,AB=25,BC=210,AC=213,D ,E ,F 分别为三边中点,将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π【答案】C【解析】由题意可知,PE =DF =10,PF =DE =13,PD =EF =5,即三棱锥P -DEF 的对棱相等,先将该三棱锥补充成长方体,如图所示:设FH =x ,HD =y ,HP =z ,则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13,所以x 2+y 2+z 2=14,于是三棱锥P -DEF 的外接球直径为14,半径为142,所以该三棱锥外接球的表面积为:4π⋅142 2=14π.故选:C .8(2023·高一课时练习)如图,在等腰梯形ABCD 中,AB =2DC =2,∠DAB =60°,E 为AB 中点.将ΔADE 与ΔBEC 分别沿ED 、EC 折起,使A 、B 重合于点P ,则三棱锥P -DCE 的外接球的体积为()A.43π27B.6π2C.6π8D.6π24【答案】C【解析】易证所得三棱锥为正四面体,它的棱长为1,故其外接球与棱长为22的正方体的外接球一直,又正方体外接球半径为R=12+12+122=64故外接球的体积为43π633=68π故选C.9(2023·高一课时练习)边长为1的正四面体内切球的体积为()A.6π8B.212C.π6D.6π216【答案】D【解析】将棱长为1的正四面体ABCD补成正方体AECF-GBHD,则该正方体的棱长为22,V A-BCD=223-4V B-ACE=24-4×13×12×22 3=212,设正四面体ABCD的内切球半径为r,正四面体ABCD每个面的面积均为34×12=34,由等体积法可得V A-BCD=212=13r S△ABC+S△ACD+S△ABD+S△BCD=33r,解得r=612,因此,该正四面体的内切球的体积为V=43π×6123=6216π.故选:D.10(2023·高一课时练习)已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SAC⊥平面SBC,SA=AC,SB=BC,球O的体积为36π,则三棱锥S-ABC的体积为()A.9B.18C.27D.36【答案】A【解析】如图,三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径O为SC中点,SA=AC,SB=BC∴AO⊥SC,BO⊥SC,∵平面SAC⊥平面SBC,平面SAC∩平面SBC=SC,BO⊂平面SBC,∴BO⊥平面SCA,设BO=r,由球O的体积为36π,可得43πr3=36π,∴r=3,则V S-ABC=V B-SCA=13S△SCA⋅BO=13×12×2r×r×r=13r3=9,∴三棱锥S-ABC的体积为9,故选∶A.11(2023·高一课时练习)如下图是一个正八面体,其每一个面都是正三角形,六个顶点都在球O 的球面上,则球O与正八面体的体积之比是()A.πB.4π3C.3π2D.2π【答案】A【解析】由题意得正方形ABCD的中心O即为外接球球心,设AB=a,则R=OA=22a,球O的体积为V1=43π×22a3=2π3a3,而h=OE=22a,故正八面体的体积V2=2×13×a2×22a=23a3,得V1V2=π,故选:A12(2023·高一课时练习)已知三棱柱ABC-A1B1C1所有的顶点都在球O的球面上,球O的体积是500π3,∠ABC =60°,AC =43,则AA 1=()A.3B.6C.4D.8【答案】B【解析】设球O 的半径为R ,△ABC 外接圆的半径为r ,则43πR 3=500π3,解得R =5,因为∠ABC =60°,AC =43,由正弦定理得,△ABC 外接圆的半径r =432sin60°=4,则AA 1=2R 2-r 2=2×3=6.故选:B二、多选题13(2023春·湖北襄阳·高一襄阳四中校考阶段练习)如图,线段AB 为圆O 的直径,点E ,F 在圆O 上,EF ⎳AB ,矩形ABCD 所在平面和圆O 所在平面垂直,且AB =2,EF =AD =1,则下列说法正确的是()A.OF ⎳平面BCEB.BF ⊥平面ADFC.三棱锥C -BEF 外接球的体积为5πD.三棱锥C -BEF 外接球的表面积为5π【答案】ABD【解析】选项A :由EF ⎳AB ,AB =2,EF =1,可得EF // OB 则四边形OBEF 为平行四边形,则OF ⎳BE又OF ⊄平面BCE ,BE ⊂平面BCE ,则OF ⎳平面BCE .判断正确;选项B :连接BF ,线段AB 为圆O 的直径,则BF ⊥AF 由平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =AB AD ⊂平面ABCD ,AD ⊥AB ,则AD ⊥平面ABEF则AD ⊥BF ,又AF ∩AD =A ,AF ⊂平面ADF ,AD ⊂平面ADF 则BF ⊥平面ADF .判断正确;选项C :取CD 中点H ,连接OH由平面ABCD ⊥平面ABEF ,平面ABCD ∩平面ABEF =ABOH ⊥AB ,OH ⊂平面ABEF ,可得OH ⊥平面ABEF又点E ,F ,B 在圆O 上,则三棱锥C -BEF 外接球球心在直线OH 上,由OH ⎳BC ,OH ⊄平面BCE ,BC ⊂平面BCE可得OH ⎳平面BCE ,则三棱锥C -BEF 外接球球心到平面BCE 的距离为点O 到平面BCE 的距离由BC ⊥平面ABEF ,BC ⊂平面BCE ,可得平面BCE ⊥平面ABEF ,则点O 到平面BCE 的距离即点O 到直线BE 的距离,又点O 到直线BE 的距离为32,则三棱锥C -BEF 外接球球心到平面BCE 的距离为32在△BCE 中,BC ⊥BE ,BC =BE =1,则CE =2,则△BCE 外接圆半径为22则三棱锥C -BEF 外接球的半径R =22 2+32 2=52则三棱锥C -BEF 外接球的体积为43π⋅52 3=556π.判断错误;选项D :由三棱锥C -BEF 外接球的半径R =52则三棱锥C -BEF 外接球的表面积为4πR 2=4π⋅522=5π.判断正确.故选:ABD14(2023春·江苏无锡·高一江苏省江阴市第一中学校考阶段练习)我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相切的称为棱切球,设下列“等长正棱柱(锥)”的棱长都为1,则下列说法中正确的有()A.正方体的棱切球的半径为2B.正四面体的棱切球的表面积为π2C.等长正六棱柱的棱切球的体积为4π3D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为7π12【答案】BCD 【解析】正方体的棱切球的直径为正方体的面对角线,正方体的棱切球的半径为面对角线的一半,即为22,选项A 错误;如图,四面体ABCD 为棱长为1的正四面体,把正四面体ABCD 放到正方体中,则正方体的棱长即为正四面体的棱切球的直径,所以正四面体的棱切球的半径为24,即正四面体的棱切球的表面积为π2,选项B 正确;如图,等长正六棱柱的棱切球的直径为AB ,即直径为2,半径为1,所以等长正六棱柱的棱切球的体积为4π3,选项C 正确;由棱切球的定义可知,棱切球被每一个面所截,截面为该面的内切圆,则等长正四棱锥的底面内切圆的面积为π×12 2=π4,每个侧面正三角形的内切圆的半径为正三角形高的13,即36,所以四个侧面正三角形的内切圆的面积为4×π×36 2=π3,所以等长正四棱锥的棱切球被棱锥5个面截得的截面面积之和为π4+π3=7π12,选项D 正确.故选:BCD .15(2023春·湖南邵阳·高一湖南省邵东市第三中学校考期中)已知正方体ABCD -A 1B 1C 1D 1的各棱长均为2,下列结论正确的是()A.该正方体外接球的直径为23B.该正方体内切球的表面积为4πC.若球O 与正方体的各棱相切,则该球的半径为2D.该正方体外接球的体积为43【答案】ABC【解析】若正方体的棱长为2,则:①若球为正方体的外接球,则外接球直径等于正方体体对角线,即2R =22+22+22=23,故A 正确,外接球体积为43πR 3=43π,故D 错误;②若球为正方体的内切球,则内切球半径为棱长的一半,故R =1,球的表面积为4πR 2=4π,故B 正确;③若球与正方体的各棱相切,则球的直径等于正方形对角线长,即R =22+22=22,球的半径为R =2,故C 正确.故本题选:ABC .三、填空题16(2023春·陕西汉中·高一校考期中)已知球O 是四棱锥P -ABCD 的外接球,四边形ABCD 是边长为1的正方形,点P 在球面上运动且PA =2,则当四棱锥P -ABCD 的体积最大时,球O 的表面积是.【答案】6π【解析】设PA 与平面ABCD 夹角为θ,则四棱锥P -ABCD 的体积为V =13S ABCD ⋅h =13×1×h =13×PA ×sin θ=23sin θ,当sin θ=1时,四棱锥P -ABCD 的体积最大,即θ=90°,此时PA ⊥平面ABCD ,将四棱锥P -ABCD 补成一个正四棱柱,如图所示,此时四棱锥P -ABCD 和该正四棱柱有相同的外接球O ,设球O 的半径为R ,则2R =PC =12+12+22=6,可得R =62,所以球O 的表面积为S =4πR 2=4π×622=6π.故答案为:6π17(2023·高一课时练习)、已知正方体外接球的体积是323π,那么正方体的棱长等于【答案】433【解析】设正方体的棱长为a ,则外接球的半径为3a 2,外接球的体积V =4π3R 3=4π3×3a 2 3=3πa 32=32π3,解得a =433,即正方体的棱长等于433.18(2023春·浙江宁波·高一余姚中学校考阶段练习)已知某圆锥的内切球的体积为32π3,则该圆锥的表面积的最小值为.【答案】32π【解析】设圆锥的内切球半径为r ,则43πr 3=32π3,解得r =2,设圆锥顶点为A ,底面圆周上一点为B ,底面圆心为C ,内切球球心为D ,内切球切母线AB 于E ,底面半径BC =R >2,∠BDC =θ,则tan θ=R 2,又∠ADE =π-2θ,由已知△BDE ,△BDC 为直角三角形,又DC =DE ,BD =BD ,所以△BDE ≅△BDC ,所以BE =BC =R ,∠BDE =∠BDC =θ,所以∠ADE =π-2θ,故AB=BE +AE =R +2tan π-2θ =R -2tan2θ,又tan2θ=2tan θ1-tan 2θ=R 1-R 24=4R 4-R 2,故AB =R -8R 4-R 2=R R 2+4 R 2-4,故该圆锥的表面积为S =πR 2R 2+4 R 2-4+πR 2=2πR 4R 2-4,令t =R 2-4>0,则S =2π(t +4)2t =2πt +16t +8 ≥2π2t ×16t +8 =32π,当且仅当t =16t,即t =4,R =22时取等号.故答案为:32π.19(2023·高一课时练习)如果圆柱、圆锥的底面直径和高都等于一个球的直径,则圆柱、球、圆锥的体积的比是.【答案】3:2:1【解析】设球的半径为r ,则球的体积为V 球=43πr 3,圆柱的体积为V 圆柱=πr 2⋅2r =2πr 3,圆锥的体积为V 圆锥=13πr 2⋅2r =2πr 33,因此,V 圆柱:V 球:V 圆锥=2:43:23=3:2:1.故答案为:3:2:1.20(2023·高一课时练习)已知A 、B 、C 是球面上三点,且AB =AC =4,∠BAC =90°,若球心O 到平面ABC 的距离为22,则该球表面积为.【答案】64π【解析】因为AB =AC =4,∠BAC =90°,所以BC 为平面ABC 截球所得小圆的直径,如图,设小圆的半径为r ,得2r =AB 2+AC 2=42,解得r =22,又球心O 到平面ABC 的距离d =22,根据球的截面圆性质,得球的半径R =r 2+d 2=4,所以球的表面积为S =4πR 2=64π.故答案为:64π.21(2023春·河南商丘·高一商丘市第一高级中学校考期中)已知正三棱锥S -ABC ,SA =SB =SC =23,AB =3,球O 与三棱锥S -ABC 的所有棱相切,则球O 的表面积为.【答案】(19-83)π【解析】取等边△ABC 的中心E ,连接SE ,则SE ⊥平面ABC ,连接AE 并延长,交BC 于点D ,则D 为BC 中点,且AD ⊥BC ,在SE 上找到棱切球的球心O ,连接OD ,则OD 即为棱切球的半径,过点O 作OF ⊥SA 于点F ,则OF 也是棱切球的半径,设OD =OF =R ,因为SA =SB =SC =23,AB =3,所以求得AD =332,AE =3,DE =32,由勾股定理得:SE =12-3=3,且∠ASE =30°,设OE =h ,OD =OE 2+ED 2=h 2+34,SO =3-h ,OF =123-h ,由题意得:h 2+34=123-h ,解得:h =3-1或-1-3,当h=3-1时,R2=h2+34=194-23,此时球O的表面积为(19-83)π;当棱切球的半径最大时,切点为A,B,C,由于∠ASE=30°,SA=SB=SC=23,可求得最大半径R=23tan30°=2,而当h=-3-1时,R2=h2+34=194+23>4,显然不成立,故h=-3-1舍去,综上:球O的表面积为(19-83)π故答案为:(19-83)π22(2023春·山东德州·高一德州市第一中学校考阶段练习)边长为2的正四面体内有一个球,当球与正四面体的棱均相切时,球的体积为.【答案】2 3π【解析】结合正四面体的性质:球心在正四面体的体高上,且为外接球的球心,如下图:取球心O,若OD⊥PA,则OD即为球的半径,而O 为底面中心,∴PO ⊥面ABC,若E为BC中点,则AE=PE=3,∴PO =263,PO=62,AO=233,由Rt△PDO∼Rt△PO A,则POPA=ODAO,故OD=22,∴球的体积为43π⋅OD3=23π.故答案为:23π23(2023春·广东江门·高一江门市培英高级中学校考期中)已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是.【答案】8π【解析】过正方体的对角面作截面如图,故球的半径r=2,∴其表面积S=4π×(2)2=8π.故答案为:8π.24(2023春·江苏苏州·高一江苏省苏州实验中学校考阶段练习)一个球被平面截下的一部分叫做球缺,截面叫做球缺的底面,垂直于截面的直径被截下的线段长叫做球缺的高,球缺的体积公式为V =π3(3R-h)h2,其中R为球的半径,h为球缺的高.若一球与一棱长为2的正方体的各棱均相切,则该球与正方体的公共部分的体积为.【答案】10-162 3π【解析】由题可得该球与正方体的公共部分球去掉6个球缺,则球的半径为R=22+222=2,球缺高h=2-1,则一个球缺的体积为π332-2-12-12=π342-5,则该球与正方体的公共部分的体积为4π3×23-6×π342-5=10-1623π.故答案为:10-162 3π.四、解答题25(2023·全国·高一专题练习)已知球与正四面体的六条棱都相切,求球与正四面体的体积之比.【解析】如图,设正四面体棱长为a,球半径为R,取AB的中点为E,CD中点F,连接AF,BF,EF,则AF=BF=32a,∴EF⊥AB,同理EF⊥CD,∴EF是AB,CD的公垂线,则EF的长是AB,CD的距离,EF=AF2-AE2=34a2-14a2=22a,又由球与正四面体的六棱都相切,得EF是该球的直径,即2R=22a,∴R3=232a3,V 球=43πR3=43π⋅232a3=224πa3,又V正四面体=13×S×h=13×12×a×a×sin60°×63a=212a3,故V球V正四面体=π226(2023·高一课时练习)有三个球,已知球O1内切于正方体,球O2与这个正方体各棱都相切,球O3过这个正方体的各个顶点,求球O1、球O2、球O3的表面积之比.【解析】设正方体的棱长为a.①球O1为正方体的内切球,球心O1是正方体的中心,切点是正方体六个面的中心,经过四个切点及球心作截面,如图1所示,设球O1的半径为r1,表面积为S1,则2r1=a,r1=a2,所以S1=4πr21=πa2.②球O2与正方体各棱的切点为各棱的中点,过正方体的两个相对面的面对角线作截面,如图2所示,设球O2的半径为r2,表面积为S2,则2r2=2a,r2=22a,所以S2=4πr22=2πa2.③球O3过正方体的各个顶点,即正方体的各个顶点都在球面上,过正方体的体对角线作截面,如图3所示,设球O3的半径为r3,表面积为S3,则2r3=3a,r3=32a,所以S3=4πr23=3πa2.故这三个球的表面积之比S1:S2:S3=πa2:2πa2:3πa2=1:2:3.图1 图2 图3。
高考数学中的内切球和外接球问题附习题.docx

高考数学中的内切球和外接球问题一、有关外接球的问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球 . 有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点 . 考查学生的空间想象能力以及化归能力 .研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用 .一、直接法 (公式法 )1、求正方体的外接球的有关问题例 1 若棱长为 3 的正方体的顶点都在同一球面上,则该球的表面积为 ______________ .27.例 2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 ______________.4 3.2、求长方体的外接球的有关问题例 3 一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为.14.例 4、已知各顶点都在一个球面上的正四棱柱高为4,体积为 16,则这个球的表面积为().A.16B.20C.24D.32C.3.求多面体的外接球的有关问题例 5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知9该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为 8,底面周长为3,则这个球的体积为.解设正六棱柱的底面边长为x,高为h,则有6x 3,x 1 ,93 x26 2 h,h.843r132,球心到底面的距离d∴正六棱柱的底面圆的半径2.∴22V球4 外接球的半径Rr d 1. 3.小结 本题是运用公式 R 2r2d 2求球的半径的,该公式是求球的半径的常用公式 .二、构造法 (补形法 )1、构造正方体例 5 若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是 _______________.9.例 3 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是.故其外接球的表面积S4R29.小结一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a、b、c,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径 .设其外接球的半径为R,则有 2Ra2b2c2.出现“墙角”结构利用补形知识,联系长方体。
内切球与外接球习题讲义教师版(完整资料).doc

【最新整理,下载后即可编辑】立体几何中的“内切”与“外接”问题的探究1 球与柱体规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题. 1.1 球与正方体如图1所示,正方体1111D C B A ABCD -,设正方体的棱长为a ,G H F E ,,,为棱的中点,O 为球的球心。
常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFHG 和其内切圆,则2ar OJ ==;二是与正方体各棱相切的球,截面图为正方形EFHG 和其外接圆,则a R OG 22==; 三是球为正方体的外接球,截面图为长方形11A ACC 和其外接圆,则23'1aR O A ==.通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题 。
例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( ) A .22B .1C .212+D .21.2 球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径22222l a b c R ++==例 2 在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为( )A.10π3B.4πC.8π3D.7π31.3球与正棱柱球与一般的正棱柱的组合体,常以外接形态居多。
下面以正三棱柱为例,介绍本类题目的解法——构造直角三角形法。
外接球与内切球九大模型(解析版)

空间几何体的外接球与内切球九大模型模型一墙角模型【方法总结】墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a2+b2+c2.),秒杀公式:R2=a2+b2+c24.可求出球的半径从而解决问题.有以下四种类型:【例题选讲】[例](1)已知三棱锥A-BCD的四个顶点A,B,C,D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=3,BC=2,CD=5,则球O的表面积为()A.12πB.7πC.9πD.8π答案A解析由AC⊥平面BCD,BC⊥CD知三棱锥A-BCD可构造以AC,BC,CD为三条棱的长方体,设球O的半径为R,则有(2R)2=AC2+BC2+CD2=3+4+5=12,所以S球=4πR2=12π,故选A.(2)若三棱锥ABCS-的三条侧棱两两垂直,且2=SA,4==SCSB,则该三棱锥的外接球半径为().A.3B.6C.36D.9答案A解析616164)2(2=++=R,3=R,故选A.(3)已知S,A,B,C,是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=2,则球O的表面积等于().A.4πB.3πC.2πD.π答案解析由已知,222211(2)2R=++=,244S Rπ∴==球π.(4)在正三棱锥S-ABC中,M,N分别是棱SC,BC的中点,且AM MN⊥,若侧棱SA=S-ABC外接球的表面积是________.答案π36解析 MNAM⊥,MNSB//,∴SBAM⊥, SBAC⊥,∴⊥SB平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,222(2)(2R ∴=+2+36=,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(5)(2019全国Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为().A .68πB .64πC .6πD .6π答案D 解析解法一:, PA PB PC ABC == △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥ 平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===P ABC ∴-为正方体的一部分,2R =,即344π2338R V R π=∴==⨯=,故选D .解法二:设2PA PB PC x ===,, E F 分别为, PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=,又90CEF ∠=︒,1 2CE AE PA x ∴===,AEC △中,由余弦定理可得()2243cos 22x x EAC x+--∠=⨯⨯作PD AC ⊥于D ,PA PC = ,D ∴为AC 的中点,cos E ∠12AD AC PA x==,2243142x x x x +-+∴=,221212 2x x x ∴+=∴==,,PA PB PC ∴===,又2AB BC AC ===,, , PA PB PC ∴两两垂直,2R ∴==,R ∴=,34433V R ππ∴==⨯8=,故选D .(6)已知二面角α-l -β的大小为π3,点P ∈α,点P 在β内的正投影为点A ,过点A 作AB ⊥l ,垂足为点B ,点C ∈l ,BC =22,PA =23,点D ∈β,且四边形ABCD 满足∠BCD +∠DAB =π.若四面体PACD 的四个顶点都在同一球面上,则该球的体积为________.答案86π解析∵∠BCD +∠DAB =π,∴A ,B ,C ,D 四点共圆,直径为AC ,∵PA ⊥平面β,AB ⊥l ,∴易得PB ⊥l ,即∠PBA 为二面角α-l -β的平面角,即∠PBA =π3,∵PA =23,∴BA =2,∵BC =22,∴AC=23.设球的半径为R ,则23-R 2-(3)2=R 2-(3)2,∴R =6,V =4π3(6)3=86π.模型二对棱相等模型【方法总结】对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长,即2R =(长方体的长、宽、高分别为a 、b 、c ).秒杀公式:R 2=x 2+y 2+z 28(三棱锥的三组对棱长分别为x 、y 、z ).可求出球的半径从而解决问题.【例题选讲】[例](1)正四面体的各条棱长都为,则该正面体外接球的体积为________.答案解析这是特殊情况,但也是对棱相等的模式,放入长方体中,32=R ,23=R ,ππ2383334=⋅=V .(2)在三棱锥A -BCD 中,AB =CD =2,AD =BC =3,AC =BD =4,则三棱锥BCD A -外接球的表面积为__.答案292π解析构造长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S .(3)在三棱锥A -BCD 中,AB =CD =6,AC =BD =AD =BC =5,则该三棱锥的外接球的体积为____.答案6解析依题意得,该三棱锥的三组对棱分别相等,因此可将该三棱锥补形成一个长方体,设该长方体的长、宽、高分别为a 、b 、c ,且其外接球的半径为R ,2+b 2=62,2+c 2=52,2+a 2=52,得a 2+b 2+c 2=43,即(2R )2=a 2+b 2+c 2=43,易知2R =,即为该三棱锥的外接球的半径,所以该三棱锥的外接球的表面积为3436R π=.(4)在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +,则该正四面体的外接球的体积是()A B .6πC D .32π答案A解析将侧面ABC ∆和ACD ∆展成平面图形,如图所示:设正四面体的棱长为a ,则BP PE +的最小值为2BE ==,2a ∴=.在正四面体A BCD -的边长为2,外接球的半径42R ==,外接球的体积343V R π==.(5)已知三棱锥A BCD -,三组对棱两两相等,且1AB CD ==,AD BC ==,若三棱锥A BCD -的外接球表面积为92π.则AC =________.答案解析将四面体A BCD -放置于长方体中, 四面体A BCD -的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A BCD -的外接球,1AB CD == ,AD BC ==,且三组对棱两两相等,∴设AC BD x ==,得长方体的对角线长为=,可得外接球的直径2R =以R =, 三棱锥A BCD -的外接球表面积为92π,2942R ππ∴=,解得4R =,324=,解之得x =AC BD ==模型三汉堡模型【方法总结】汉堡模型是直棱柱的外接球、圆柱的外接球模型,用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点.一般情况下只作出一个面的垂线,然后设出球心用算术方法或代数方法即可解决问题.有时也作出两条垂线,交点即为球心.)解决.以直三棱柱为例,模型如下图,由对称性可知球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)(2013辽宁)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上.若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为().A .3172B .210C .132D .310答案C 解析如图所示,由球心作平面ABC 的垂线,则垂足为BC 的中点M .又AM =12BC =52,OM =12AA 1=6,所以球O 的半径R =OA =522+62=132.另解过C 点作AB 的平行线,过B 点作AC 的平行线,交点为D ,同理过C 1作A 1B 1的平行线,过B 1作A 1C 1的平行线,交点为D 1,连接DD 1,则ABCD -A 1B 1C 1D 1恰好成为球的一个内接长方体,故球的半径r 132=.故选C .(2)设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为().A .2a πB .273a πC .2113a πD .237a π答案B 解析222222274312a a R OB OE BE a ==+=+=,22743S a a ππ∴==.故选B .(3)(2009全国Ⅰ)直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上,若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积等于().A .10πB .20πC .30πD .40π答案B解析如图,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.故选B .(4)已知圆柱的高为2,底面半径为3,若该圆柱的两个底面的圆周都在同一个球面上,则这个球的表面积等于()A .4πB .16π3C .32π3D .16π答案D解析由题意知圆柱的中心O 为这个球的球心,于是,球的半径r =OB =OA 2+AB 2=12+(3)2=2.故这个球的表面积S =4πr 2=16π.故选D .(5)若一个圆柱的表面积为12π,则该圆柱的外接球的表面积的最小值为()A .12)π-B .C .3)πD .16π答案A解析设圆柱的底面半径为r ,高为h ,则22212r rh πππ+=,则6h r r=-.设该圆柱的外接球的半径为R ,则22222221659()()333244h R r r r r r r =+=+-=+--=- ,当且仅当22594r r =,即4365r =时,等号成立.故该圆柱的外接球的表面积的最小值为43)12)ππ-=.模型四垂面模型【方法总结】垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球,由对称性可知球心O 的位置是△CBD的外心O 1与△AB 2D 2的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=2h ,2224h R r ∴=+.【例题选讲】[例](1)已知在三棱锥S -ABC 中,SA ⊥平面ABC ,且∠ACB =30°,AC =2AB =23,SA =1.则该三棱锥的外接球的体积为()A .13813πB .13πC .136πD .13136π答案D解析∵∠ACB =30°,AC =2AB =23,∴△ABC 是以AC 为斜边的直角三角形,其外接圆半径r =AC2=3,则三棱锥外接球即为以△ABC 为底面,以SA 为高的三棱柱的外接球,∴三棱锥外接球的半径R 满足R =132,故三棱锥外接球的体积V =43πR 3=13136π.故选D .第(1)小题图第(2)小题图1第(2)小题图2(2)三棱锥P -ABC 中,平面PAC ⊥平面ABC ,AB ⊥AC ,PA =PC =AC =2,AB =4,则三棱锥P -ABC 的外接球的表面积为()A .23πB .234πC .64πD .643π答案D解析如图1,设O 为三棱锥外接球的球心,O 1为正△PAC 的中心,则OO 1=12AB =2.2AO 1=2sinπ3=433,AO 1=233,R 2=OA 2=O 1A 2+O 1O 2=43+4=163,故几何体外接球的表面积S =4πR 2=643.另解:如图2,设O ′为正△PAC 的中心,D 为Rt △ABC 斜边的中点,H 为AC 中点.由平面PAC ⊥平面ABC ,则O ′H ⊥平面ABC .作O ′O ∥HD ,OD ∥O ′H ,则交点O 为三棱锥外接球的球心,连接OP ,又O ′P =23=23×32×2=233,OO ′=DH =12AB =2.∴R 2=OP 2=O ′P 2+O ′O 2=43+4=163.故几何体外接球的表面积S =4πR 2=643π.(3)在三棱锥S -ABC 中,侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25,则该三棱锥的外接球的表面积为()A .643πB .256πC .4363πD .2048327π答案B解析由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为r ,则△ABC 的外接圆直径2r =ACsin ∠ABC =732,∴r =73,又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.(4)在三棱锥P -ABC 中,已知PA ⊥底面ABC ,∠BAC =120˚,PA =AB =AC =2,若该三棱锥的顶点都在同一个球面上,则该球的表面积为()A .103πB .18πC .20πD .93π答案C解析如图1,先由余弦定理求出BC =23,再由正弦定理求出r =AO 1=2,外接球的直径R =12+22=5,所以该球的表面积为4πR 2=20π.第(3)小题图第(4)小题图1第(4)小题图2另解如图2,该三棱锥为图中正六棱柱内的三棱锥P -ABC ,PA =AB =AC =2,所以该三棱锥的外接球即该六棱柱的外接球,所以外接球的直径2R =42+22=25⇒R =5,所以该球的表面积为4πR 2=20π.(5)在三棱锥P ABC -中,PA ⊥平面ABC ,120BAC ∠=︒,2AC =,1AB =,设D 为BC 中点,且直线PD与平面ABC 所成角的余弦值为5,则该三棱锥外接球的表面积为________.答案373π解析在ABC ∆中,120BAC ∠=︒,2AC =,1AB =,由余弦定理得:22BC AC =+22cos AB AC BC BAC -⋅⋅∠,即22221221cos1207BC =+-⨯⨯⨯︒=,解得:BC =.设ABC ∆的外接圆半径为r ,由正弦定理得2sin BC r BAC ===∠解得:r ==;且222cos 2AB BC AC ABC AB BC +-∠==,又D 为BC 中点,在ABD ∆中,122BD BC ==,1AB =,cos 7ABD ∠=.由余弦定理得:2222cos AD AB BD AB BD ABD =+-∠ ,即:22231()212274AD =+-⨯⨯=,解得2AD =.又因为PA ⊥平面ABC ,所以PDA ∠为直线PD 与平面ABC 所成角,由cos 5PDA ∠=,得sin 5PDA ∠=,tan 2PDA ∠=,所以在Rt PAD ∆中,tan 22PA AD PDA =∠== .设三棱锥P ABC -的外接球半径为R ,所以R =,三棱锥P ABC -外接球表面积为23743S R ππ==.模型五切瓜模型【方法总结】切瓜模型是有一侧面垂直底面的棱锥型,常见的是两个互相垂直的面都是特殊三角形且平面ABC ⊥平面BCD ,如类型Ⅰ,△ABC 与△BCD 都是直角三角形,类型Ⅱ,△ABC 是等边三角形,△BCD 是直角三角形,类型Ⅲ,△ABC 与△BCD 都是等边三角形,解决方法是分别过△ABC 与△BCD 的外心作该三角形所在平面的垂线,交点O 即为球心.类型Ⅳ,△ABC 与△BCD 都一般三角形,解决方法是过△BCD 的外心O 1作该三角形所在平面的垂线,用代数方法即可解决问题.设三棱锥A -BCD 的高为h ,外接球的半径为R ,球心为O .△BCD 的外心为O 1,O 1到BD 的距离为d ,O 与O 1的距离为m 2=r 2+m 2,2=d 2+(h -m )2,解得R .可用秒杀公式:R 2=r 12+r 22-l 24(其中r 1、r 2为两个面的外接圆的半径,l 为两个面的交线的长)【例题选讲】[例](1)已知在三棱锥P -ABC 中,V P ABC =433,∠APC =π4,∠BPC =π3,PA ⊥AC ,PB ⊥BC ,且平面PAC ⊥平面PBC ,那么三棱锥P -ABC 外接球的体积为________.答案32π3解析如图,取PC 的中点O ,连接AO ,BO ,设PC =2R ,则OA =OB=OC =OP =R ,∴O 是三棱锥P -ABC 外接球的球心,易知,PB =R ,BC =3R ,∵∠APC =π4,PA ⊥AC ,O 为PC 的中点,∴AO ⊥PC ,又平面PAC ⊥平面PBC ,且平面PAC ∩平面PBC =PC ,∴AO ⊥平面PBC ,∴V P ABC =V A PBC =13×12×PB ×BC ×AO =13×12×R ×3R ×R=433,解得R =2,∴三棱锥P -ABC 外接球的体积V =43πR 3=32π3.(2)如图,已知平面四边形ABCD 满足AB =AD =2,∠A =60˚,∠C =90˚,将△ABD 沿对角线BD 翻折,使平面ABD ⊥平面CBD ,则四面体ABCD 外接球的体积为__.答案323π27解析在四面体ABCD 中,∵AB =AD =2,∠BAD =60˚,∴△ABD为正三角形,设BD 的中点为M ,连接AM ,则AM ⊥BD ,又平面ABD ⊥平面CBD ,平面ABD ∩平面CBD =BD ,∴AM ⊥平面CBD .∵△CBD 为直角三角形,∴其外接圆的圆心是斜边BD 的中点M ,由球的性质知,四面体ABCD 外接球的球心必在线段AM 上,又△ABD 为正三角形,∴球心是△ABD 的中心,则外接球的半径为23×2×32=233,∴四面体ABCD 外接球的体积为43×π×(233)3=323π27.(3)已知三棱锥A -BCD 中,△ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角,则三棱锥A -BCD 的外接球的表面积为()A .10π3B .5πC .6πD .20π3答案D解析如图,取BD 中点M ,连接AM ,CM ,取△ABD ,△CBD 的中心即AM ,CM 的三等分点P ,Q ,过P 作平面ABD 的垂线,过Q 作平面CBD 的垂线,两垂线相交于点O ,则点O 为外接球的球心,如图,其中OQ =33,CQ =233,连接OC ,则外接球的半径R =OC =153,表面积为4πR 2=20π3,故选D .(4)已知ABC ∆是以BC 为斜边的直角三角形,P 为平面ABC 外一点,且平面PBC ⊥平面ABC ,3BC =,PB =PC =,则三棱锥P ABC -外接球的表面积为________.答案10π解析由题意知BC 的中点O 为ABC ∆外接圆的圆心,且平面PBC ⊥平面ABC ,过O 作面ABC 的垂线l ,则垂线l 一定在面ABC 内.根据球的性质,球心一定在垂线l 上, 球心1O 一定在平面PBC 内,且球心1O 也是PBC ∆外接圆的圆心.在PBC ∆中,由余弦定理得222cos 22PB BC PC PBC PB BC +-∠==,sin 2PBC ∴∠=,由正弦定理得:2sin PCR PBC=∠,解得2R =,∴三棱锥的外接球的表面积2410R ππ==.(5)已知等腰直角三角形ABC 中,AB =AC =2,D ,E 分别为AB ,AC 的中点,沿DE 将△ABC 折成直二面角(如图),则四棱锥A -DECB 的外接球的表面积为________.答案10π解析取DE 的中点M ,BC 的中点N ,连接MN (图略),由题意知,MN ⊥平面ADE ,因为△ADE是等腰直角三角形,所以△ADE 的外接圆的圆心是点M ,四棱锥A -DECB 的外接球的球心在直线MN 上,又等腰梯形DECB 的外接圆的圆心在MN 上,所以四棱锥A -DECB 的外接球的球心就是等腰梯形DECB 的外接圆的圆心.连接BE ,易知△BEC 是钝角三角形,所以等腰梯形DECB 的外接圆的圆心在等腰梯形DECB 的外部.设四棱锥A -DECB 的外接球的半径为R ,球心到BC 的距离为d 2=d 2+(2)2,2=(d +222+(22)2,解得R 2=52,故四棱锥A -DECB 的外接球的表面积S =4πR 2=10π.模型六斗笠模型【方法总结】圆锥、顶点在底面的射影是底面外心的棱锥.秒杀公式:R =h 2+r 22h(其中h 为几何体的高,r 为几何体的底面半径或底面外接圆的圆心)【例题选讲】[例](1)一个圆锥恰有三条母线两两夹角为60︒,若该圆锥的侧面积为,则该圆锥外接球的表面积为________.答案272π解析设60ASB BSC CSA ∠=∠=∠=︒,则SA SB SC AB AC BC =====.设AB x =,则底面圆的直径为2sin 60x r ==︒,该圆锥的侧面积为12x π=,解得3x =,高OS =.r ∴=.设圆锥外接球的半径为R ,所以222)R r R -+=,解得R =,则外接球的表面积为22742R ππ=.(2)(2020·全国Ⅰ)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的表面积为()A .64πB .48πC .36πD .32π答案A解析设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin 60°=2r ,∴AB =2r sin 60°=23.∴OO 1=AB =23.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r2=4,∴球O 的表面积S =4πR 2=64π.故选A .(3)在三棱锥P ABC -中,PA PB =26, 4PC AC AB ====,且AC AB ⊥,则该三棱锥外接球的表面积为________.答案36π解析设顶点P 在底面中的射影为1O ,由于PA PB PC ==,所以111O A O B O C ==,即点1O 是底面ABC ∆的外心,又AC AB ⊥,所以1O 为BC 的中点,因为PA PB = 4PC AC AB ====,所以11 4BC AO PO ===,设外接球的球心为O ,半径为R ,则O 必在1PO 上,=-14O O R ,在∆1Rt O OA中,()(2224R R -+=,解得3R =,所以22436S R ππ==.(4)正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为()A .81π4B .16πC .9πD .27π4答案A解析如图所示,设球半径为R ,底面中心为O ′且球心为O ,∵正四棱锥P ABCD 中AB =2,∴AO ′=2,∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.(5)如图所示,在正四棱锥P -ABCD 中,底面ABCD 是边长为4的正方形,E ,F 分别是AB ,CD 的中点,cos ∠PEF =22,若A ,B ,C ,D ,P 在同一球面上,则此球的体积为________.答案36π解析由题意,得底面ABCD 是边长为4的正方形,cos ∠PEF =22,故高PO 1为2.易知正四棱锥P -ABCD 的外接球的球心在它的高PO 1上,记球心为O ,则AO 1=22,PO =AO =R ,PO 1=2,OO 1=2-R 或OO 1=R -2(此时O 在PO 1的延长线上),在直角△AO 1O 中,R 2=AO 21+OO 21=(22)2+(2-R )2,解得R =3,所以球的体积为V =43πR 3=4π3×33=36π.(6)在三棱锥P ABC -中,2PA PB PC ===,1AB AC ==,3BC =棱锥外接球的体积为()A .43πB .823πC .3πD .323π答案A解析由PA PB PC ===P 作PG ⊥平面ABC ,垂足为G ,则G 为三角形ABC 的外心,在ABC ∆中,由1AB AC ==,BC =,可得120BAC ∠=︒,则由正弦定理可得:2AG =,即1AG =.1PG ∴==.取PA 中点H ,作HO PA ⊥交PG 于O ,则O 为该三棱锥外接球的球心.由PHO PGA ∆∆∽,可得PH PG PO PA =,则211PH PA PO PG === .可知O 与G 重合,即该棱锥外接球半径为1.∴该三棱锥外接球的体积为43π.模型七已知球心或球半径模型【例题选讲】[例](1)(2017·全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.答案36π解析如图,连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点,∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB ,平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB ,设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ABC =V A SBC =13×S △SBC ×AO =13×SC ×AO ,即9=13×R ×R ,解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.(2)已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,则球O 的体积为________.答案32π3解析设A 到平面BCD 的距离为h ,∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90˚,∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.(3)(2012全国Ⅰ)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为()A .26B .36C .23D .22答案A解析由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34,高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26.故选A .(4)(2020·新高考全国Ⅰ)已知直四棱柱ABCD -A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以D 1为球心,5为半径的球面与侧面BCC 1B 1的交线长为________.答案2π2解析如图,设B 1C1的中点为E ,球面与棱BB 1,CC 1的交点分别为P ,Q ,连接DB ,D 1B 1,D 1P ,D 1E ,EP ,EQ ,由∠BAD =60°,AB =AD ,知△ABD 为等边三角形,∴D 1B 1=DB =2,∴△D 1B 1C 1为等边三角形,则D 1E =3且D 1E ⊥平面BCC 1B 1,∴E 为球面截侧面BCC 1B 1所得截面圆的圆心,设截面圆的半径为r ,则r =R 2球-D 1E 2=5-3=2.又由题意可得EP =EQ =2,∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ .又D 1P =5,∴B 1P =D 1P 2-D 1B 21=1,同理C 1Q =1,∴P ,Q 分别为BB 1,CC 1的中点,∴∠PEQ =π2,知 PQ的长为π2×2=2π2,即交线长为2π2.(5)三棱锥S -ABC 的底面各棱长均为3,其外接球半径为2,则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A .2+3B .2-3C .3D .2答案C 解析如图,设三棱锥S -ABC 底面三角形ABC 的外心为G ,三棱锥外接球的球心为O ,要使三棱锥S -ABC 的体积最大,则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为OS +OG =2+1=3.故选C .模型八最值模型【方法总结】最值问题的解法有两种方法:一种是几何法,即在运动变化过程中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.【例题选讲】[例](1)已知三棱锥P -ABC 的顶点P ,A ,B ,C 在球O 的球面上,△ABC 是边长为3的等边三角形,如果球O 的表面积为36π,那么P 到平面ABC 距离的最大值为________.答案3+22解析依题意,边长是3的等边△ABC 的外接圆半径r =12·3sin 60°=1.∵球O 的表面积为36π=4πR 2,∴球O 的半径R =3,∴球心O 到平面ABC 的距离d =R 2-r 2=22,∴球面上的点P 到平面ABC 距离的最大值为R +d =3+22.(2)在四面体ABCD 中,AB =1,BC =CD =3,AC =2,当四面体ABCD 的体积最大时,其外接球的表面积为()A .2πB .3πC .6πD .8π答案C 解析∵AB =1,BC =3,AC =2,由勾股定理可得AB 2+AC 2=BC 2,所以△ABC 是以BC 为斜边的直角三角形,且该三角形的外接圆直径为BC =3,当CD ⊥平面ABC 时,四面体ABCD 的体积取最大值,此时,其外接球的直径为2R =BC 2+CD 2=6,因此,四面体ABCD 的外接球的表面积为4πR 2=π×(2R )2=6π.故选C .(3)已知四棱锥S -ABCD 的所有顶点在同一球面上,底面ABCD 是正方形且球心O 在此平面内,当四棱锥的体积取得最大值时,其表面积等于16+163,则球O 的体积等于()A .42π3B .162π3C .322π3D .642π3答案D解析由题意得,当四棱锥的体积取得最大值时,该四棱锥为正四棱锥.因为该四棱锥的表面积等于16+163,设球O 的半径为R ,则AC =2R ,SO =R ,如图,所以该四棱锥的底面边长AB =2R ,则有(2R )2+4×12×2R ×16+163,解得R =22,所以球O 的体积是43πR 3=6423π.故选D .(4)三棱锥A -BCD 内接于半径为5的球O 中,AB =CD =4,则三棱锥A -BCD 的体积的最大值为()A .43B .83C .163D .323答案C解析如图,过CD 作平面ECD ,使AB ⊥平面ECD ,交AB 于点E ,设点E 到CD 的距离为EF ,当球心在EF 上时,EF 最大,此时E ,F 分别为AB ,CD 的中点,且球心O 为EF 的中点,所以EF =2,所以V max =13×12×4×2×4=163,故选C .(5)已知正四棱柱的顶点在同一个球面上,且球的表面积为12π,当正四棱柱的体积最大时,正四棱柱的高为_.答案8解析设正四棱柱的底面边长为a ,高为h ,球的半径为r ,由题意知4πr 2=12π,所以r 2=3,又2a 2+h 2=(2r )2=12,所以a 2=6-h 22,所以正四棱柱的体积V =a 2h ,则V ′=6-32h 2,由V ′>0,得0<h <2,由V ′<0,得h >2,所以当h =2时,正四棱柱的体积最大,V max =8.模型九内切球模型【方法总结】以三棱锥P -ABC 为例,求其内切球的半径.方法:等体积法,三棱锥P -ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和;第一步:先求出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -P AB +V O -P AC +V O -PBC ⇒V P -ABC =13S △ABC ·r +13S △P AB ·r +13S △P AC ·r +13S △r =13S △ABC +S △P AB +S △P AC +S △PBC )·r ;第三步:解出r =3V P -ABC S O -ABC +S O -P AB +S O -P AC +S O -PBC =3VS 表.秒杀公式(万能公式):r =3VS 表【例题选讲】[例](1)已知一个三棱锥的所有棱长均为2,则该三棱锥的内切球的体积为________.答案354π解析由题意可知,该三棱锥为正四面体,如图所示.AE =AB ·sin 60°=62,AO =23AE =63,DO =AD 2-AO 2=233,三棱锥的体积V D ABC =13S △ABC ·DO =13,设内切球的半径为r ,则V D ABC =13r (S △ABC +S △ABD +S △BCD +S △ACD )=13,r =36,V 内切球=43πr 3=354π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为________.答案23π解析圆锥内半径最大的球即为圆锥的内切球,设其半径为r .作出圆锥的轴截面PAB ,如图所示,则△PAB 的内切圆为圆锥的内切球的大圆.在△PAB 中,PA =PB =3,D 为AB 的中点,AB =2,E 为切点,则PD =22,△PEO ∽△PDB ,故PO PB =OEDB ,即22-r 3=r 1,解得r =22,故内切球的体积为43π223=23π.(3)阿基米德(公元前287年~公元前212年)是古希腊伟大的哲学家、数学家和物理学家,他和高斯、牛顿并列被称为世界三大数学家.据说,他自己觉得最为满意的一个数学发现就是“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”.他特别喜欢这个结论.要求后人在他的墓碑上刻着一个圆柱容器里放了一个球,如图,该球顶天立地,四周碰边.若表面积为54π的圆柱的底面直径与高都等于球的直径,则该球的体积为()A .4πB .16πC .36πD .64π3答案C解析设该圆柱的底面半径为R ,则圆柱的高为2R ,则圆柱的表面积S =S 底+S 侧=2×πR 2+2·π·R ·2R =54π,解得R 2=9,即R =3.∴圆柱的体积为V =πR 2×2R =54π,∴该圆柱的内切球的体积为23×54π=36π.故选C .(4)已知三棱锥P -ABC 的三条侧棱PA ,PB ,PC 两两互相垂直,且PA =PB =PC =2,则三棱锥P -ABC 的外接球与内切球的半径比为________.答案33+32解析以PA ,PB ,PC 为过同一顶点的三条棱,作长方体,由PA =PB =PC =2,可知此长方体即为正方体.设外接球的半径为R ,则R =4+4+42=3,设内切球的半径为r ,则内切球的球心到四个面的距离均为r ,由13(S △ACP +S △APB+S △PCB +S △ABC )·r =13·S △PCB ·AP ,解得r =23+3,所以Rr =323+3=33+32.(5)正四面体的外接球和内切球上各有一个动点P 、Q ,若线段PQ ,则这个四面体的棱长为________.答案4解析设这个四面体的棱长为a ,则它的外接球与内切球的球心重合,且半径R =外,r =内,依题意得4123a a +=,4a ∴=.。
-北师版圆解答题之欧阳治创编

圆解答题与证明题综合练习1.在△ABC 中,∠C =90°,AC =6cm ,BC =8cm ,扇形ODF 与BC 边相切,切点是E ,若FO ⊥AB 于点O .求扇形ODF 的半径.2.如图,OA=OB ,AB 交⊙O 于点C 、D ,AC 与BD 是否相等?为什么?3.(本题满分12分)如图,I 是△ABC 的内心,∠BAC 的平分线与△ABC 的外接圆相交于点D 。
BD 与ID 相等吗?为什么?(12)4.如图,AB 是⊙O 的直径,C 是⊙O 上一点,AC 平分∠BAD ;AD ⊥ CD ,垂足为D .(1)求证:CD 是⊙O 的切线(2)若⊙O 的直径为5,CD =2.求AC 的长 . ABODE F5.已知:如图,AB是⊙O的一条弦,点C为的中点,CD是⊙O的直径,过C点的直线l 交AB所在直线于点E,交⊙O于点F。
(1)判定图中CEB∠的数量关系,并写出∠与FDC结论;(2)将直线l绕C点旋转(与CD不重合),在旋转过程中,E点、F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明。
如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点 D.已知:AB cm=824=, CD cm6.求作此残片所在的圆(不写作法,保留作图痕迹)7.求(1)中所作圆的半径已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.8.求证: BC是⊙O的切线;9.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.10.圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
11.(本题满分8分)尺规作图(保留作图痕迹,不写作法)某地要修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等.(1)若三所公寓A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置;(2)若∠BAC=66º,则∠BPC=º.12.如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.(1)求证:直线DE是⊙O的切线;(2)当AB=5,AC=8时,求cosE的值.13.又PE⊥CB 于E ,若BC=10,且CE∶EB=3∶2,求AB 的长.二、解答题如图,AB 是⊙O 的一条弦,OD ⊥AB ,垂足为C ,交⊙O 于点D ,点E 在⊙O 上.14.(1)若52AOD ∠=,求DEB ∠的度数;15.(2)若3OC =,5OA =,求AB 的长.16.如图,已知CD 是⊙O 的直径,点A 为CD 延长线上一点,BC=AB ,∠CAB=30°.(1)求证:AB 是⊙O 的切线;(2)若⊙O 的半径为2,求弧BD 的长17.如图,Rt △ABC 中,∠ABC =90°,以AB 为直径的⊙O 交AC 于点D ,E 是BC 的中点,连接DE 、OE .(1)判断DE 与⊙O 的位置关系并说明理由; EB CA O(2)求证:OEBC⋅=2CD25,DE=2,求AD的长.(3)若tanC=218.(6分)如图,已知AB是⊙O的直径,点C,D在⊙O上.(1)若∠CAB=30°,求∠ADC的度数;(2)若弦AC=阴影部分弓高为6,求弓形的面积;19.(2011•陕西)如图,在△ABC中,∠B=60°,⊙O是△ABC外接圆,过点A作⊙O的切线,交CO的延长线于P点,CP交⊙O 于D(1)求证:AP=AC;(2)若AC=3,求PC的长.20.如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC 的交点为E.(1)求∠BOD的度数及点O到BD的距离;(2)若DE=2BE,求cos OED∠的值.21.如图,⊙O的直径AB为10,弦BC为6,D、E分别为∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.(1)求AC、AD的长;(2)试判断直线PC与⊙O的位置关系,并说明理由;(3)直接写出CD的长为____________.如图,以AB为直径的⊙O经过点C,D是AB 延长线上一点,且DC=AC,∠CAB=30°22.试判断CD所在的直线与⊙O的位置关系,并说明理由23.若AB=2,求阴影部分的面积24.已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,(1)请画出四边形ABCD的外接圆,并标明圆心M的位置;(2)这个圆中弦BC所对的圆周角的度数是。
立体几何之内切球与外接球习题讲义教师版资料

圆梦教育中心 立体几何中的“内切”与“外接”问题的探究 1 球与柱体规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题. 1.1球与正方体如图1所示,正方体1111D C B A ABCD -,设正方体的棱长为a ,G H F E ,,,为棱的中点,O 为球的球心。
常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFHG 和其内切圆,则2a r OJ ==;二是与正方体各棱相切的球,截面图为正方形EFHG 和其外接圆,则a R OG 22==; 三是球为正方体的外接球,截面图为长方形11A ACC 和其外接圆,则23'1a R O A ==. 通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题 。
例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )A.2B .1 C.12+D1.2球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径22l R ==例 2 在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为( ) A.10π3 B.4π C.8π3 D.7π31.3球与正棱柱球与一般的正棱柱的组合体,常以外接形态居多。
下面以正三棱柱为例,介绍本类题目的解法——构造直角三角形法。
内切球和外接球例题之欧阳道创编

欧阳道创编 2021.03.06高考数学中的内切球和外接球问题一、直接法(公式法)1、求正方体的外接球的有关问题 例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .27π.例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为______________..2、求长方体的外接球的有关问题 例3 (2007年天津高考题)一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为 .14π.例4、(2006年全国卷I )已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( ).C.A.16πB.20πC.24πD.32π3.求多面体的外接球的有关问题 例5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9 8,底面周长为3,则这个球的体积为 .解设正六棱柱的底面边长为x,高为h,则有263,1,296,8xxx hh=⎧⎧=⎪⎪∴⎨⎨=⎪⎪=⎩⎩∴正六棱柱的底面圆的半径12 r=,球心到底面的距离d=.∴外接球的半径1R==.43Vπ∴=球.二、构造法(补形法)1、构造正方体例5 (2008年福建高考题)若三棱锥则其外接球的表面积是_______________.9π解据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成一个棱是三棱锥的外接球.设其外接球的半径为R,则有()222229R=++=.∴294R=.故其外接球的表面积249S Rππ==.小结一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R,则有欧阳道创编 2021.03.062222R a b c=++.出现“墙角”结构利用补形知识,联系长方体。
2025重难点突破之外接球与内切球问题 教师版

外接球与内切球问题模拟精练一、选择题:(每小题5分,在每小题给出的选项中,只有一项是符合题目要求的.)1.(2024·江西·一模)在体积为12的三棱锥A -BCD 中,AC ⊥AD ,BC ⊥BD ,平面ACD ⊥平面BCD ,∠ACD =π3,∠BCD =π4,若点A ,B ,C ,D 都在球O 的表面上,则球O 的表面积为()A.12πB.16πC.32πD.48π【答案】D 【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题、面面垂直证线面垂直【详解】如图,取CD 的中点O ,连接AO ,BO ,因为AC ⊥AD ,BC ⊥BD ,所以OA =OB =OC =OD ,因此点O 就是球心,又∠BCD =π4,故△BCD 是等腰直角三角形,所以OB ⊥CD .因为平面ACD ⊥平面BCD ,平面ACD ∩平面BCD =CD ,所以OB ⊥平面ACD .设球O 半径为R ,则OB =R ,AC =R ,又∠ACD =π3,则AD =3R ,所以三棱锥A -BCD 的体积V =13S △ACD ⋅OB =13×12×AC ⋅AD ⋅OB =36R 3=12,所以R =23,所以球O 的表面积为4πR 2=48π.故选:D .2.(2024·湖北·模拟预测)已知三棱锥P -ABC 的四个顶点都在球O 的球面上,P A =PB =PC =4,AB =BC =2,AC =23,则球O 的表面积为()A.64π3B.40π3C.27π4D.21π2【答案】A 【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题【详解】如图:在△ABC 中,AB =BC =2,AC =23,由余弦定理:cos ∠ABC =BA 2+BC 2-AB 22BA ⋅BC=4+4-128=-12,所以∠ABC =120°,所以△ABC 外接圆半径为AC 2sin ∠ABC =233=2,即QB =2.在直角三角形PQB 中,BQ =2,BP =4,所以QP =2 3.设棱锥P -ABC 外接球半径为R ,在直角三角形OQB 中,23-R 2+22=R 2,解得:R =433.所以球O 的表面积为:S =4πR 2=4π×163=64π3.故选:A3.(2024·福建·模拟预测)已知正四棱台下底面边长为42,若内切球的体积为323π,则其外接球表面积是()A.49πB.56πC.65πD.130π【答案】C 【难度】0.65【知识点】球的截面的性质及计算、球的体积的有关计算、球的表面积的有关计算、多面体与球体内切外接问题【详解】正四棱台ABCD -A 1B 1C 1D 1下底面边长AB =42,设其内接球半径为r ,则4π3r 3=323π,解得r=2,取AB ,CD ,A 1B 1,C 1D 1的中点E ,F ,E 1,F 1,则四边形EFF 1E 1内切圆是正四棱台内接球的截面大圆,则四边形EFF 1E 1是等腰梯形,EE 1=12(EF +E 1F 1),而EE 21=12(EF -E 1F 1) 2+(2r )2,12(EF +E 1F 1) 2=12(EF -E 1F 1)2+(2r )2,整理得EF ⋅E 1F 1=16,而EF =42,则E 1F 1=22,设O 为正四棱台ABCD -A 1B 1C 1D 1外接球球心,R 为该球半径,则OC =OC 1=R ,令M ,N 分别为正四棱台ABCD -A 1B 1C 1D 1上下底面的中心,则MC 1=2,NC =4,MN =4,OM =OC 21-MC 21=R 2-4,ON =OC 2-NC 2=R 2-16,当球心O 在线段MN 时,R 2-4+R 2-16=4,解得R 2=654,球O 的表面积为S =4πR 2=65π;当球心O 在线段MN 的延长线时,R 2-4-R 2-16=4,无解,所以所求外接球表面积是65π.故选:C4.(2024·陕西宝鸡·三模)△ABC 与△ABD 都是边长为2的正三角形,沿公共边AB 折叠成60°的二面角,若点A ,B ,C ,D 在同一球O 的球面上,则球O 的表面积为()A.139π B.208π9C.529π D.112π3【答案】C 【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题【详解】解:由题,设正△ABC 与△ABD 的中心分别为N ,M ,根据外接球的性质有OM ⊥平面ABD ,ON ⊥平面ABC ,又二面角D -AB -C 的大小为60°,故∠DEC =60°,又正△ABC 与△ABD 的边长均为2,故DE =CE =3,故EM =EN =13ED =33,∵OE =OE ,∠OME =∠ONE ,∴Rt △MEO ≌Rt △NEO ,故∠MEO =∠NEO =30°,故OE =ME cos30°=23,又EB =1,故球O 的半径OB =12+23 2=133,故球O的表面积为S=4π×1332=52π9.故选:C.5.(2024·山西太原·二模)已知圆锥的顶点为P,底面圆的直径AB=23,tan∠APB=3,则该圆锥内切球的体积为()A.43π27B.43π9C.4π3D.4π【答案】C【难度】0.85【知识点】球的体积的有关计算、多面体与球体内切外接问题【详解】由圆锥的性质易知△P AB为以P为顶点的等腰三角形,又tan∠APB=3,所以∠APB=π3,则△P AB为正三角形,边长为23,如图所示,作出圆锥及其内切球的轴截面,设AB、AP中点分别为C、E,内切球球心为O,由正三角形内心的性质易知OC=OE=12PO=13PC=13×AP2-AC2=13×12-3=1即内切球球半径为1,所以体积V=4 3π.故选:C6.(2024·全国·二模)已知圆锥的轴截面是底角为θ的等腰三角形,圆锥的底面半径为a,圆锥内有一个内接圆柱,则圆柱体积的最大值为()A.a2tanθB.πa33tan2θ C.2πa39tanθ D.4πa327tanθ【答案】D【难度】0.4【知识点】由导数求函数的最值(不含参)、柱体体积的有关计算【详解】如图,圆锥的轴截面是底角为θ的等腰三角形SAB ,圆锥的底面半径为OA =OB =a ,则圆锥的高为SO =a tan θ,设圆锥内接圆柱CDEF 的底面半径为OC =OD =r ,高为DE =h ,由△SHE ∼△SOB 可得,r a =a tan θ-ha tan θ,解得h =(a -r )tan θ,则圆柱的体积为:V =πr 2h =πr 2(a -r )tan θ=-πtan θ⋅r 3+πa tan θ⋅r 2,r ∈(0,a )V =πr 2a -3r tan θ,由V =0,得r =2a 3,当0<r <2a 3时,V >0,则V 在0,2a3上单调递增;当2a 3<r <a 时,V <0,则V 在2a 3,a 上单调递减.故当r =2a 3时,V max =π×2a 3 2a -2a 3 tan θ=427πa 3tan θ.故选:D .【点睛】思路点睛:本题主要考查利用导数解决圆锥体积的最值问题,属于难题.解题思路是,借助于轴截面中的相似三角形,将圆锥的体积用底面半径r 的解析式表示,再运用函数求导求出其最大值.7.(2024·浙江·模拟预测)已知边长为6的正方体与一个球相交,球与正方体的每个面所在平面的交线都为一个面积为16π的圆,则该球的表面积为()A.96πB.100πC.125πD.204π【答案】B 【难度】0.85【知识点】球的截面的性质及计算、球的表面积的有关计算、多面体与球体内切外接问题【详解】由对称性,球心与正方体重心重合,且每个面的交线半径为4.连球心与任意面中心,则连线长为3,且连线垂直该面,再连交线圆上一点与球心(即为球半径),由勾股定理得球的半径为5,则表面积为4π⋅52=100π.故选:B .8.(2024·河南濮阳·模拟预测)某圆锥的侧面展开图是面积为3π,圆心角为2π3的扇形,则该圆锥的轴截面的面积为()A.92B.42C.22D.2【答案】C 【难度】0.85【知识点】圆锥中截面的有关计算、圆锥表面积的有关计算【详解】设圆锥的底面半径为r ,母线长为l ,因为圆锥的侧面展开图是面积为3π,圆心角为2π3的扇形,所以12×2π3×l 2=3π,解得l =3,因为2πr =2π3×l ,所以2πr =2π3×3,得r =1,所以圆锥的高为h =l 2-r 2=9-1=22,所以圆锥的轴截面的面积是12∙2r ∙h =12×2×22=22,故选:C .9.(2024·青海·二模)如图,已知在四棱锥P -ABCD 中,底面四边形ABCD 为等腰梯形,BC ⎳AD ,PD =2AD =4BC =4,底面积为334,PD ⊥AD 且PB =19,则四棱锥P -ABCD 外接球的表面积为()A.9πB.123πC.39πD.20π【答案】D 【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题、证明线面垂直【详解】取AD 的中点为F ,因为AD =2BC =2,等腰梯形ABCD 的面积为334,所以梯形的高为2×3342+1=32,所以cos ∠BAD =32,则∠BAD =π3,所以∠ADC =π3,连接BF 、CF ,所以△ABF 、△DCF 为等边三角形,点F 为梯形ABCD 外接圆的圆心,连接BD ,在△BCD 中,根据余弦定理得cos 2π3=BC 2+CD 2-BD 22BC ⋅CD,即12+12-BD 22×1×1=-12,解得BD =3.因为PB =19,PD =4,所以PD 2+BD 2=PB 2,所以PD ⊥BD .因为PD ⊥AD ,AD ∩BD =D ,AD ,BD ⊂平面ABCD ,所以PD ⊥平面ABCD ,过AD 的中点F 作FO ⎳PD 交P A 于点O ,则FO ⊥平面ABCD ,且O 为P A 的中点,所以点O 为Rt △P AD 外接圆圆心,所以O 为四棱锥P -ABCD 外接球球心,所以外接球半径为12P A =12PD 2+AD 2=5,故表面积S =4π×5 2=20π.故选:D10.(2024·浙江·模拟预测)清代的苏州府被称为天下粮仓,大批量的粮食要从苏州府运送到全国各地.为了核准粮食的数量,苏州府制作了“小嘴大肚”的官斛用以计算粮食的多少,五斗为一斛,而一只官斛的容量恰好为一斛,其形状近似于正四棱台,上口为正方形,内边长为25cm ,下底也为正方形,内边长为50cm ,斛内高36cm ,那么一斗米的体积大约为立方厘米?()A.10500B.12500C.31500D.52500【答案】A 【难度】0.85【知识点】台体体积的有关计算【详解】一斛米的体积为V =13S 上+S 下+S 上S 下 h =13×252+502+25×50 ×36=52500cm 3 ,因为五斗为一斛,所以一斗米的体积为V5=10500cm 3 ,故选:A .11.(2024·江苏无锡·模拟预测)蒙古包是我国蒙古族牧民居住的房子,适于牧业生产和游牧生活.如图所示的蒙古包由圆柱和圆锥组合而成,其中圆柱的高为2m ,底面半径为4m ,O 是圆柱下底面的圆心.若圆锥的侧面与以O 为球心,半径为4m 的球相切,则圆锥的侧面积为()A.85πm 2B.165πm 2C.20πm 2D.40πm 2【答案】C【难度】0.65【知识点】圆锥表面积的有关计算、多面体与球体内切外接问题【详解】设PO 1=h ,P A =l (h 为圆锥高,l 为圆锥母线长)OM ⊥P A ,∵以O 为球心,半径为4的球与圆锥侧面相切,则OM =4,在△POA 中,S △POA =12h +2 ⋅4=12⋅4l ,可得h +2=l ,且h 2+16=l 2,则(l -2)2+16=l 2,解得l =5,所以圆锥的侧面积为S 侧=πrl =π×4×5=20πm 2 .故选:C .12.(2024·云南大理·模拟预测)六氟化硫,化学式为SF 6,在常压下是一种无色、无臭、无毒、不燃的稳定气体,有良好的绝缘性,在电器工业方面具有广泛用途.六氟化硫分子结构为正八面体结构(正八面体每个面都是正三角形,可以看作是将两个棱长均相等的正四棱锥将底面粘接在一起的几何体).如图所示,正八面体E -ABCD -F 的棱长为a ,此八面体的外接球与内切球的体积之比为()A.33B.23C.32D.22【答案】A 【难度】0.65【知识点】球的体积的有关计算、多面体与球体内切外接问题【详解】正八面体E -ABCD -F 的棱长为a ,连接AC ∩EF =O ,由四边形ABCD 为正方形,得AC 2=BC 2+AB 2=2a 2=EC 2+AE 2,则四边形AECF 亦为正方形,即点O 到各顶点距离相等,于是此八面体的外接球球心为O ,半径为R =2a 22=2a 2,此八面体的表面积为S =8S △ABE =8×34a 2=23a 2,设此八面体的内切球半径为r ,由V E -ABCD -F =2V E -ABCD ,得13Sr =2×13×a 2×2a 2,即23a 2r =2a 3,解得r =66a ,所以此八面体的外接球与内切球的体积之比为Rr3=2a 266a3=3 3.故选:A【点睛】结论点睛:一个多面体的表面积为S ,如果这个多面体有半径为r 的内切球,则此多面体的体积V 满足:V =13Sr .13.(2024·天津北辰·三模)中国载人航天技术发展日新月异.目前,世界上只有3个国家能够独立开展载人航天活动.从神话“嫦娥奔月”到古代“万户飞天”,从诗词“九天揽月”到壁画“仕女飞天”⋯⋯千百年来,中国人以不同的方式表达着对未知领域的探索与创新.如图,可视为类似火箭整流罩的一个容器,其内部可以看成由一个圆锥和一个圆柱组合而成的几何体.圆柱和圆锥的底面半径均为2,圆柱的高为6,圆锥的高为4.若将其内部注入液体,已知液面高度为7,则该容器中液体的体积为()A.325π12B.76π3C.215π9D.325π16【答案】A 【难度】0.85【知识点】锥体体积的有关计算、台体体积的有关计算【详解】由题意可知:容器中液体分为:下半部分为圆柱,上半部分为圆台,取轴截面,如图所示,O 1,O 2,O 3分别为AB ,CD ,EF 的中点,可知:AB ∥CD ∥EF ,且O 1B =O 2C =2,O 1O 2=6,O 2P =4,O 2O 3=1,O 3P =3,可得O 3F O 2C =O 3P O 2P=34,即O 3F =32,所以该容器中液体的体积为π×22×6+13π×22+π×32 2+π×22×π×32 2×1=325π12.故选:A .14.(2024·湖北武汉·二模)房屋建造时经常需要把长方体砖头进行不同角度的切割,以契合实际需要.已知长方体的规格为24cm ×11cm ×5cm ,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到12cm ×11cm ×5cm ,24cm ×112cm ×5cm ,24cm ×11cm ×52cm 三种不同规格的长方体.按照上述方式对第1次所截得的长方体进行第2次截取,再对第2次所截得的长方体进行第3次截取,则共可得到体积为165cm 3的不同规格长方体的个数为()A.8B.11C.12D.10【答案】D 【难度】0.65【知识点】柱体体积的有关计算【详解】解:由题意知,长方体的规格为24×11×5=1320,现从长方体的某一棱的中点处作垂直于该棱的截面,截取1次后共可以得到三种规模长方体为:12×11×5,24×112×5,24×11×52,体积为660,一共3种;按照上述方式对第1次所截得的3种长方体进行第2次截取,得到的体积为330的不同规格长方体有:6×11×5,12×112×5,12×11×52,24×114×5,24×112×52,24×11×54,一共6种;再对第2次所截得的6种长方体进行第3次截取,则共可得到体积为165的不同规格长方体有:3×11×5,6×112×5,6×11×52,12×114×5,12×112×52,12×11×54,24×118×5,24×114×52,24×112×54,24×11×58,一共10种.故选:D .二、多选题:(每小题6分,在每小题给出的选项中,只有一项或者多项是符合题目要求的.)15.(2024·山东·模拟预测)四面体ABCD 中,AC =BC =AB =6,CD =10,BD =8,四面体ABCD 外接球的表面积记为S ,则()A.当四面体ABCD 体积最大时,S =112πB.AD ⊥BCC.当AD =6时,S =129611π D.S 可以是400π【答案】ACD 【难度】0.4【知识点】球的表面积的有关计算、多面体与球体内切外接问题、证明线面垂直、线面垂直证明线线垂直【详解】设四面体ABCD 外接球的球心为O ,半径为R ,O 点在平面BCD 内的投影是△BCD 的外心O 1,由CD 2=BC 2+BD 2,△BCD 为直角三角形,外心O 1是CD 边的中点,当四面体ABCD 体积最大时,有平面ABC ⊥平面BCD ,设平面ABC 的外心为O 2,E 为BC 中点,连接OO 2,AE ,O 1E ,则OO 2⊥平面ABC ,由AC =BC =AB =6,则AE =33,AO 2=23,EO 2=3,平面ABC ⊥平面BCD ,平面ABC ∩平面BCD =BC ,AE ⊂平面ABC ,AE ⊥BC ,则AE ⊥平面BCD ,又OO 1⊥平面BCD ,则有OO 1⎳AE ,Rt △BCD 中,BD ⊥BC ,又BD ⎳O 1E ,则O 1E ⊥BC ,同理可得O 1E ⊥平面ABC ,O 1E ⎳OO 2,所以四边形O 1EO 2O 为矩形,OO 1=EO 2=3,Rt △ODO 1中,由OD 2=O 1O 2+O 1D 2,得R =32+52=27,此时S =4πR 2=112π,A 选项正确;假设AD ⊥BC ,由BD ⊥BC ,BD ∩AD =D ,所以BC ⊥平面ABD ,AB ⊂平面ABD ,所以BC ⊥AB ,与AC =BC =AB =6矛盾,所以假设不成立,B 错误;当AD =6时,AC =AD =AB ,则A 点在平面BCD 内的投影是△BCD 的外心O 1,AO 1⊥平面BCD ,OO 1⊥平面BCD ,A ,O ,O 1三点共线,Rt △ADO 1中,AO 1=AD 2-O 1D 2=62-52=11,Rt △ODO 1中,由OD 2=O 1O 2+O 1D 2,得R 2=R -11 2+52,解得R =181111,此时S =4πR 2=129611π,C 选项正确;当OB =OC =OD =10时,OO 12=OD 2-O 1D 2=102-52=75,OE 2=OO 12+O 1E 2=75+42=91,则OA 2=OO 22+AO 22=OE 2-EO 22+AO 22=91-32+23 2=100,即OA =10,四面体ABCD 外接球的半径R =10成立,此时S =400π,D 选项正确.故选:ACD .16.(2024·广东佛山·模拟预测)如图,几何体的底面是边长为6的正方形A 1B 1C 1D 1,AA 1⊥底面A 1B 1C 1D 1,AB ∥A 1B 1,AA 1=AB =3,BC =AD =λA 1D 1,λ∈0,1 ,则()A.当λ=0时,该几何体的体积为45B.当λ=13时,该几何体为台体C.当λ=12时,在该几何体内放置一个表面积为S 的球,则S 的最大值为9πD.当点B 1到直线DD 1距离最大时,则λ=1【答案】ACD 【难度】0.4【知识点】棱台的结构特征和分类、多面体与球体内切外接问题、求组合体的体积、点到直线距离的向量求法【详解】若λ≠0,即BC =AD =λA 1D 1 ≠0,可知ABCD 为矩形,对于选项A :当λ=0时,即BC =AD =0,取A 1B 1,C 1D 1的中点E ,F ,连接BE ,EF ,BF ,如图所示:因为AA 1⊥底面A 1B 1C 1D 1,A 1B 1⊂底面A 1B 1C 1D 1,则AA 1⊥A 1B 1,且A 1B 1C 1D 1为正方形,则A 1D 1⊥A 1B 1,AA 1∩A 1D 1=A 1,AA 1,A 1D 1⊂平面AA 1D 1,可得A 1B 1⊥平面AA 1D 1,又因为AB =A 1E ,AB ∥A 1E ,可知AA 1EB 为平行四边形,则BE ∥AA 1,可知AA 1D 1-BEF 为直三棱柱,BE ⊥底面A 1B 1C 1D 1,所以该几何体的体积为V =V AA 1D 1-BEF +V B -EB 1C 1F =12×3×6×3+13×3×3×6=45,故A 正确;对于选项B :当λ=13时,即BC =AD =13A 1D 1 ,可知AB A 1B 1=12≠AD A 1D 1=13,所以该几何体不为台体,故B 错误;对于选项C :当λ=12时,即BC =AD =12A 1D 1 ,则AB A 1B 1=AD A 1D 1=12,所以该几何体为台体,如图所示,E ,O 1,G 为相应边的中点,则ABCD -A 1EO 1G 为正方形,因为AA 1⊥底面A 1B 1C 1D 1,且AA 1=3,可知所求球的半径R ≤12AA 1=32,且正方形ABCD -A 1EO 1G 的内切球的半径即为12AA 1=32,所以最大球的半径R =32,即S 的最大值为4πR 2=9π,故C 正确;对于选项D :以A 1为坐标原点,A 1B 1,A 1D 1,A 1A 分别为x ,y ,z 轴,建立空间直角坐标系,则B 16,0,0 ,D 10,6,0 ,D 0,6λ,3 ,可得D 1B 1 =6,-6,0 ,D 1D =0,6λ-6,3 ,则点B 1到直线DD 1距离为d λ =D 1B 1 2-D 1B 1 ⋅D 1DD 1D 2=72-144λ-1 24λ-1 2+1=36+364λ-1 2+1,可知d λ 在0,1 内单调递增,所以当点B 1到直线DD 1距离最大时,则λ=1,故D 正确;故选:ACD .【点睛】方法点睛:多面体与球切、接问题的求解方法(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题求解;(2)正方体的内切球的直径为正方体的棱长;(3)球和正方体的棱相切时,球的直径为正方体的面对角线长;(4)利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.17.(23-24高一下·福建福州·期末)某圆锥的底面半径为3,母线长为4,则下列关于此圆锥的说法正确的是()A.圆锥的侧面展开图的圆心角为3π2B.圆锥的体积为97πC.过圆锥的两条母线作截面的面积最大值为8D.圆锥轴截面的面积为37【答案】ACD 【难度】0.65【知识点】三角形面积公式及其应用、余弦定理解三角形、圆锥中截面的有关计算、锥体体积的有关计算【详解】对于A ,设圆锥的侧面展开图的圆心角为α,则4α=2π×3,所以α=3π2,所以A 正确,对于B ,圆锥的底面半径为3,母线长为4,所以圆锥的高为h =42-32=7,所以圆锥的体积为13Sh =13×π×32×7=37π,所以B 错误,对于C ,设圆锥的两条母线的夹角为θ,则过这两条母线所作截面的面积为12×4×4sin θ=8sin θ,因为过圆锥母线的截面中,轴截面三角形对应的θ最大,此时cos θ=42+42-622×4×4=-18<0,所以θ最大是钝角,所以当θ=π2时,截面的面积最大,最大值为8,所以C 正确,对于D ,圆锥轴截面的面积为12×6×7=37,所以D 正确.故选:ACD18.(2024·湖南·三模)如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,点P 是正方体的上底面A 1B 1C 1D 1内(不含边界)的动点,点Q 是棱BC 的中点,则以下命题正确的是()A.三棱锥Q -PCD 的体积是定值B.存在点P ,使得PQ 与AA 1所成的角为60°C.直线PQ 与平面A 1ADD 1所成角的正弦值的取值范围为0,22D.若PD 1=PQ ,则P 的轨迹的长度为354【答案】ACD 【难度】0.85【知识点】锥体体积的有关计算、异面直线夹角的向量求法、线面角的向量求法【详解】对于A ,三棱锥Q -PCD 的体积等于三棱锥P -QCD 的体积,V 三棱锥P -QCD =13S △QCD ×AA 1=13×12×2×1×2=23是定值,A 正确;以A 1为坐标原点,A 1B 1,A 1D 1,AA 1分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,则Q (2,1,-2),设P (x ,y ,0)(0<x <2,0<y <2),则QP=(x -2,y -1,2)对于B ,AA 1=(0,0,2),使得PQ 与AA 1所成的角α满足:cos α=QP ⋅AA 1 QP ⋅AA 1 =2×2x -2 2+y -1 2+4×2,因为0<x <2,0<y <2,故0<x -2 2+y -1 2<5,故cos α∈23,1,而cos60°=12∉23,1 ,B 错误;对于C ,平面A 1ADD 1的法向量n=(1,0,0),所以直线PQ 与平面A 1ADD 1所成角β的正弦值为:sin β=x -2(x -2)2+(y -1)2+4,因为0<x <2,0<y <2,故-2<x -2<0故x -2 (x -2)2+5<x -2 (x -2)2+(y -1)2+4≤x -2(x -2)2+4,而x -2 (x -2)2+5=11+5(x -2)2∈0,23 ,x -2 (x -2)2+4=11+4(x -2)2∈0,22,故0<x -2(x -2)2+(y -1)2+4<22即sin β的取值范围为0,22,C 正确;对于D ,D 1(0,2,0),D 1P=(x ,y -2,0),由PD 1=PQ ,可得x 2+(y -2)2=(x -2)2+(y -1)2+4,化简可得4x -2y -5=0,在xA 1y 平面内,令x =0,得y =32,令y =0,得x =54,则P 的轨迹的长度为2-54 2+32 2=354,D 正确;故选:ACD .三、填空题:(每小题5分,把答案填在答题卡中的横线上.)19.(2025·广东·模拟预测)已知球O 是某圆锥内可放入的最大的球,其半径为该圆锥底面半径的一半,则该圆锥的体积与球O 的体积之比为.【答案】83/223【难度】0.85【知识点】圆锥中截面的有关计算、锥体体积的有关计算、球的体积的有关计算【详解】球O 是某圆锥内可放入的最大的球,则该球为圆锥的内切球,截面如图所示:设球O 的半径为r ,则圆锥底面半径为2r ,可得在△ABC 中,AD ⊥BC ,OF ⊥AC ,CD =CF =2r ,设AE =x ,由勾股定理得AF =AO 2-OF 2=x +r2-r 2=x 2+2rx ,AD 2+CD 2=AC 2,即x +2r 2+2r 2=x 2+2rx +2r 2,化简得3x 2+4rx -4r 2=0,即3x -2r x +2r =0,∵x >0,则x =23r ,即AE =23r ,则圆锥体积为13π2r 22r 3+2r =32πr 39,球O 的体积为4πr 33,所以圆锥的体积与球O 的体积之比为32πr 394πr 33=83.故答案为:83.20.(2023·江苏连云港·模拟预测)已知正四面体ABCD 的棱长为6,点E ,F 满足BC =λBE ,BD =λBF,用过A ,E ,F 三点的平面截正四面体ABCD 的外接球O ,当λ∈[1,3]时,截面的面积的取值范围为.【答案】12π,272π【难度】0.4【知识点】球的截面的性质及计算、锥体体积的有关计算、多面体与球体内切外接问题【详解】过点A 作AO 1⊥平面BCD ,则点O 1在中线DM 上,且DO 1=2O 1M ,球心O 在AO 1上,连接AM ,OD ,因为正四面体ABCD 的棱长为6,所以DM =6sin π3=33,DO 1=23DM =23,由勾股定理得AO 1=AD 2-O 1D 2=26,设外接球O 的半径为R ,设OA =OD =R ,则OO 1=26-R ,由勾股定理得O 1O 2+O 1D 2=OD 2,即26-R 2+12=R 2,解得R =362,λ=32时,E ,O 1,F 三点共线,此时过A ,E ,F 三点的平面过球心O ,此时截面面积最大,截面面积为πR 2=272π;当λ=1或λ=3时,此时球心O 到截面的距离较大,当λ=1时,过A ,E ,F 三点的平面即为平面ACD ,由对称性可知,此时球心O 到平面ACD 的距离等于到平面BCD 的距离,即OO 1=26-R =62,当λ=3时,BE =BF =2,连接BO 1,交EF 于点K ,则O 1B =O 1D =23,由于△BEF 为等边三角形,故BK =BF sin60°=3,则O 1K =O 1B -BK =3,故O 1E =O 1F =2,S △O 1EF =12O 1E ⋅O 1F sin60°=3,由勾股定理得AK =O 1A 2+O 1K 2=33,S △AEF =12EF ⋅AK =33,设点O 1到平面AEF 的距离为h ,则13S △AEF ⋅h =13S △O 1EF ⋅O 1A ,即13×33⋅h =13×3×26,解得h =263,由于O 1A =43OA ,故点O 到平面AEF 的距离为34h =62,故λ=1与λ=3时,点O 到平面AEF 的距离相等,均为62,故平面AEF 截正四面体ABCD 的外接球的半径为R 2-622=23,则截面面积为π23 2=12π,综上,截面的面积的取值范围为12π,272π.故答案为:12π,272π【点睛】方法点睛:解决与球有关的内切或外接的问题时,解题的关键是确定球心的位置.对于外切的问题要注意球心到各个面的距离相等且都为球半径;对于球的内接几何体的问题,注意球心到各个顶点的距离相等,解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形,利用勾股定理求得球的半径21.(2024·陕西铜川·三模)榫卯结构是中国古代建筑文化的瑰宝,在连接部分通过紧密的拼接,使得整个结构能够承受大量的重量,并且具有较高的抗震能力.这其中木楔子的运用,使得榫卯配合的牢度得到最大化满足,木楔子是一种简单的机械工具,是用于填充器物的空隙使其牢固的木橛、木片等.如图为一个木楔子的直观图,其中四边形ABCD 是边长为2的正方形,且△ADE ,△BCF 均为正三角形,EF ∥CD ,EF =4,则该木楔子的外接球的表面积为.【答案】16π【难度】0.4【知识点】球的表面积的有关计算、多面体与球体内切外接问题【详解】如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH ,则EG =4-22=1,故AG =AE 2-EG 2=22-12= 3.取AD 的中点O ,连接GO ,又AG =GD ,∴GO ⊥AD ,则GO =AG 2-AD 22= 2.由对称性易知,过正方形ABCD 的中心O 1且垂直于平面ABCD 的直线必过线段EF 的中点O 2,且所求外接球的球心O 在这条直线上,如图.设球O 的半径为R ,则R 2=OO 21+AO 21,且R 2=OO 22+EO 22,从而OO 21=OO 22+2,即OO 1+OO 2 OO 1-OO 2 =2,当点O 在线段O 1O 2内(包括端点)时,有OO 1+OO 2=GO =2,可得OO 1-OO 2=2,从而OO 1=2,即球心O 在线段EF 的中点,其半径R =2.当点O 在线段O 1O 2外时,O 1O 2=2,2+OO 2 2=OO 22+2,解得OO 2=0(舍).故所求外接球的表面积为4πR 2=16π.故答案为:16π.【点睛】关键点点睛:本题考查球的切接问题,关键在于根据几何体的对称性,通过直观想象明确外接球的球心位置,结合正方形ABCD 的外接圆半径求解可得.22.(2024·辽宁·模拟预测)在三棱锥P -ABC 中,P A =PB =PC =2,∠BP A =∠BPC =60°,∠APC =90°,若该三棱锥内有一球O 与三棱锥各面均相切,则球O 的半径为.【答案】22-6【难度】0.4【知识点】多面体与球体内切外接问题、证明线面垂直【详解】取AC中点E,连接PE,BE,设三棱锥P-ABC的内切球的球心为O,半径为r,在三棱锥P-ABC中,由P A=PB=PC=2,∠BP A=∠BPC=60°,知△P AB,△PBC为等边三角形,则AB=BC=2,又∠APC=90°,则在Rt△APC中,AC=AP2+CP2=22,又AB2+BC2=AC2,则∠ABC=90°,因此,在等腰直角三角形△P AC和等腰直角三角形△ABC中,点E为AC中点,可得PE=BE=12AC=2,又PB=2,则PE2+BE2=PB2,即PE⊥BE,又PE⊥AC,BE∩AC=E,BE,AC⊂平面ABC,则PE⊥平面ABC,即PE为三棱锥P-ABC的高,则三棱锥P-ABC的体积为:V=13S△ABC⋅PE=13×12×2×2×2=223,又三棱锥P-ABC的体积可看作为三棱锥O-ABC,三棱锥O-PBC,三棱锥O-P AC,三棱锥O-P AB的体积之和,由S△ABC=S△P AC=12×2×2=2,S△PBC=S△P AB=12×2×2sin60°=3,则V=13S△ABC⋅r+13S△PBC⋅r+13S△P AC⋅r+13S△P AB⋅r=13S△ABC+S△PBC+S△P AC+S△P AB⋅r=1 34+23⋅r,因此可得223=134+23⋅r,解得r=22-6,故答案为:22- 6.23.(2024·湖南邵阳·三模)在四面体ABCD中,△ABD是边长为42的等边三角形,BC⊥CD,BC=CD,AC=43,点E在棱BD上,且BD=4BE,过点E作四面体ABCD的外接球O的截面,则所得截面圆的面积最小值与球O的表面积之比为.【答案】18/1:8【难度】0.65【知识点】球的截面的性质及计算、球的表面积的有关计算、多面体与球体内切外接问题【分析】先根据勾股定理逆定理得到BC⊥AB,CD⊥AD,再根据直角三角形中线性质找出外接球的球心,再结合球的截面距离分析,要所得的截面圆中面积最小,只需截面圆半径最小,只需球心到截面的距离d最大即可.【详解】由题意知,AB =AD =42,BC =CD =4,AC =43,由勾股定理可知,BC 2+AB 2=AC 2,CD 2+AD 2=AC 2,所以BC ⊥AB ,CD ⊥AD ,取AC 的中点O ,所以OB =OC =OD =OA ,所以四面体ABCD 的外接球O 在斜边AC 的中点处,四面体ABCD 的外接球O 的半径R =12AC =23,根据题意可知,过点E 作球O 的截面,若要所得的截面圆中面积最小,只需截面圆半径最小,设球O 到截面的距离d ,只需球心到截面的距离d 最大即可,而当且仅当OE 与截面垂直时,球心到截面的距离d 最大,即d max =OE ,取BD 的中点F ,EF =14BD =2,易知△OBD 为等腰三角形,OF =OB 2-BF 2=12-8=2,所以OE 2=OF 2+EF 2=22+22=6,所以截面圆的半径为r =R 2-OE 2=12-6=6,所以截面圆的面积为S 1=π6 2=6π,球O 的表面积为S 2=4π23 2=48π,所得截面圆的面积最小值与球O 的表面积之比为6π:48π=1:8故答案为:18.24.(2024·安徽芜湖·模拟预测)在△ABC 中,AB =BC =3,AC =2,将△ABC 沿AC 旋转,当点B 到达点B 的位置时,平面B AC ⊥平面BAC ,则三棱锥B -ABC 外接球表面积为.【答案】5π【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题【详解】如图所示,面AB C 内作B M ⊥AC ,因为AB =B C ,所以M 为AC 的中点,因为平面B AC ⊥平面BAC ,且平面B AC ∩平面BAC =AC ,且B M ⊂平面B AC ,所以B M ⊥平面BAC ,又BM ⊂平面BAC ,所以B M ⊥BM ,由题意知AC =2,可得AM =1,且BM =B M =AB 2-AM 2=2,所以BB =2,对棱相等的三棱锥B -ABC 可放置在边长分别为a ,b ,c 的长方体中,可得a 2+b 2=3,a 2+c 2=3,b 2+c 2=4,设三棱锥B -ABC 外接球的半径为R ,可得2R =a 2+b 2+c 2,故外接球表面积为S =4πR 2=π(2R )2=πa 2+b 2+c 2 =5π.故答案为:5π.25.(2024·吉林·模拟预测)清初著名数学家孔林宗曾提出一种“蒺藜形多面体”,其可由两个正交的全等正四面体组合而成(每一个四面体的各个面都过另一个四面体的三条共点的棱的中点).如图,若正四面体棱长为2,则该组合体的表面积为;该组合体的外接球体积与两正交四面体公共部分的内切球体积的比值为.【答案】6327【难度】0.65【知识点】求组合多面体的表面积、多面体与球体内切外接问题【分析】该组合体一共有24个面,每一个面都是全等的边长为1的等边三角形,则可求出其表面积;该组合体的外接球也是任意一个正四面体的外接球,可用一个正四面体来看,求出外接球半径为R ,两正交四面体公共部分一共有8个面,且每一个面都是全等的边长为1的等边三角形,则中间部分的体积为223-4×212=23,设其内切球半径为r ,由13×23r =23,求出r ,即可得到体积的比值.【详解】该组合体一共有24个面,每一个面都是全等的边长为1的等边三角形,则其表面积为24×12×1×1×sin π3=63;该组合体的外接球也是任意一个正四面体的外接球,可用一个正四面体来看,E 是△BCD 的中心,F 是球心,则2DE cos π6=DC ,则DE =233,AE =22-2332=263,设外接球半径为R,则AF=DF=R,又AF+EF=AE,DF2=EF2+DE2,解得R=6 2 ,两正交四面体公共部分一共有8个面,且每一个面都是全等的边长为1的等边三角形,则其表面积为8×12×1×1×sinπ3=23,大正四面体的体积为13×12×2×2×sinπ3×263=223,则每个小正四面体的体积为223×123=212,则中间部分的体积为223-4×212=23,设其内切球半径为r,则中间部分的体积也可表示为13×23r=23,解得r=66,故外接球和内切球体积之比为Rr3=27故答案为:63;27.26.(2024·内蒙古鄂尔多斯·二模)如图,平面四边形ADBC中,AB⊥BC,AB=3,BC=23,△ABD为等边三角形,现将△ABD沿AB翻折,使点D移动至点P,且PB⊥BC,则三棱锥P-ABC的外接球的表面积为.【答案】16π【难度】0.65【知识点】球的表面积的有关计算、多面体与球体内切外接问题【详解】因为AB⊥BC,PB⊥BC,AB∩PB=B,AB,PB⊂平面P AB,所以BC⊥平面P AB,将三棱锥P-ABC补形为如图所示的直三棱柱,则它们的外接球相同,外接球的球心O在棱柱上下底面三角形的外心连线上,令△P AB的外心为E,由△ABD为等边三角形,AB=3,得BE=23×32×3=1,因为OE=12BC=3,所以在Rt△OBE中,OB=OE2+BE2=(3)2+12=2,。
立体几何之内切球与外接球习题讲义教师版之欧阳音创编

圆梦教育中心立体几何中的“内切”与“外接”问题的探究1 球与柱体规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题.1.1 球与正方体如图1所示,正方体1111D C B A ABCD -,设正方体的棱长为a ,G H F E ,,,为棱的中点,O 为球的球心。
常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFHG 和其内切圆,则2a r OJ ==; 二是与正方体各棱相切的球,截面图为正方形EFHG 和其外接圆,则a R OG 22==;三是球为正方体的外接球,截面图为长方形11A ACC 和其外接圆,则23'1a R O A ==. 通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题 。
例 1 棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( )A .2 B .1 C .12+D 1.2 球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一定存在内切球.设长方体的棱长为,,,a b c 其体对角线为l .当球为长方体的外接球时,截面图为长方体的对角面和其外接圆,和正方体的外接球的道理是一样的,故球的半径2l R ==例 2 在长、宽、高分别为2,2,4的长方体内有一个半径为1的球,任意摆动此长方体,则球经过的空间部分的体积为( )A.10π3B.4πC.8π3D.7π31.3 球与正棱柱球与一般的正棱柱的组合体,常以外接形态居多。
下面以正三棱柱为例,介绍本类题目的解法——构造直角三角形法。
解决几何体的外接球与内切球之欧阳文创编

解决几何体的外接球与内切球,就这6个题型!一、外接球的问题简单多面体外接球问题是立体几何中的难点和重要的考点,此类问题实质是解决球的半径尺或确定球心0的位置问题,其中球心的确定是关键.(一)由球的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.结论4:正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.(二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法.途径1:正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.(三)由性质确定球心利用球心O与截面圆圆心O1的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质,确定球心.二、内切球问题若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不重合。
4、基本方法:构造三角形利用相似比和勾股定理。
5、体积分割是求内切球半径的通用做法。
内切球和外接球常见解法

1球与柱体1.1球与正方体如图1所示,正方体朋CD-J VGD I ,i 殳正方体的棱长为a, E,F,H,G 为按的中点,O 为球的球心.常见组合方式有三类:一是球 为正方体的内切球,截面图为正方® EFGH 和其內切圆,则 pJ|=r=|;二是与正方体各樓相切的球,截面图为正方形防GM 和其外接圆,贝'J|G<?| = ^=^a ;三是球为正方体的外接球,截面图为 长方形£C4C 】和其外接圆,则|40|二尺二.通过这三种类型可以2棱长为1的正方体ABCD-A^C^的8个顶点都在球O 的表面上,棱4人,的中点,则直线EF 被球0截得的线段长为( ) A —B. 1C. 1 + —D. ^2A. 2 21.2球与长方体长方体各顶点可在一个球面上,故长方体存在外切球.但是不一泄存在内切球•设长方体 的棱长为u,b 、c,其体对角线为/.当球为长方体的外接球时,截面图为长方体的对角而和英 外接圆,和正方体的外接球的道理是一样的,故球的半径匚2 2例2在长、宽、髙分別为2, 2, 4的长方体内有一个半径为1的球,任意摆动此长方体, 则球经过的空间部分的体积为()10n 8n 7HA.二-B.4nC.— D —内切与外接E, F 分别是1.3球与正棱柱域与一股的正棱柱的组合体,常以外接形态居多•下面以正三棱柱为例,介绍本粪题目的解法构造直隼三角形法.设正三棱柱ABC-A^C^的高为/底面边长为s如图2所示,D和耳分别为上下底面的中心•根据几何体的特埶球心必落在高DD]的中点0 ,足借助直角三角形HOD的勾股定理,可例3正四棱柱ABCD-^Cp,的各顶点都在半径为/?的球而上,则正四棱柱的侧面积有最_____ 值,为 _______2球与锥体规则的锥体,如正四而体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表而积等相关问题.2.1球与正四面体正四而体作为一个规则的几何阪它既存在外接球’也存在內切球,芥且两心合一,利用这点可顺利解决球的半径与正四面体的棱长的关系.如图4,设正四而体血U的棱长为s內切球半径为厂,夕卜接球的半径为乩取血的中点为D,E^S在底面的射彫,连接CD, ED, SE为正四面体的高•在截面三角形SDC,作一个与边劝和DC相切,圆心在高附上的国「即为內切球的裁面.因为正四面体本身的对称性可知,外接球和内切球的球心同为O.此时, CQ=Q^=R f OE=r ,= =迟 a,贝U 有R + r = */—«> R2— i'2 = \CE「二■,解得:R =V3 1 1 3 4 12例4将半径都为1的四个钢球完全装入形状为正四而体的容器里.这个正四而体的髙的最小值为()还"迹°•込迹B.2+3 3 3 32. 2球与三条侧梭互相垂直的三梭锥法,即把三裱雑彳卜形成正方作或者畏方体.常见两种形式:—是三棱谁的三条侧棱互相垂直并且相等,则可以补形为一个正方体,它的外摻球的球心就是三械锥的外接球的球心.如图5,三樓锥4 -卫场的外接球的球心和正方摩ABCD -£耳C]D]的外接球的球心重合.设AA1=a, 则R = 匕二是如果三棱谁的三条侧棱互相垂直并且不相等,则可以补形2为一个长方体,它的外接球的球心就是三棱锥的外接璘的球2 2 2 2心.左2 =乞皆十匚丄 Q为长方体的体对角线长).4 4例5在正三棱锥S-ABC中,M、/V分別是棱SC、BC的中点,且4M丄MAC若侧棱SA = 2馅侧正三棱锥S-ABC外接球的表而积是___________ 2.3球与正棱锥球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球而上,根拯截而图的特点,可以构造直角三角形进行求解.二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个而相切,球心到四个而的距离相等,都为球半径R.这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体枳. 例6在三棱锥P-ABC中,PA=PB=PC=^Z侧棱PA与底而ABC所成的角为60° ,则该三棱)锥外接球的体积为(n4兀A. 7TB.—C. 4 兀D. ----------3 3接球的球心,则y 例7矩形ABCD中,AB = ^BC = 3.沿AC将矩形ABCD折成一个直二而角B-AC-D,则四而体ABCD的外接球的体积是()125 125 125 125A. ---兀B.——兀C.——龙D. ------ 7t12 9 6 33球与球对多个小球结合在一起,组合成复杂的几何体问题,要求有丰富的空间想彖能力,解决本类问题需掌握恰当的处理手段,如准确确立各个小球的球心的位宜关系,或者巧借截面图等方法.将空间问题转化平而问题求解.例7任半径为R的球内放入大小相等的4个小球,则小球半径r的最大值为(4球与几何体的各条棱相切球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位置为目的,然后通过构造直角三角形进行转换和求解.例:与正四而体各棱都相切的球的半径为棱的一半:.例8把一个皮球放入如图10所示的由8根长均为20 cm的铁丝接成的四樓锥形骨架內,使皮球的表面与S根铁丝都有接触点,则皮球的半径为( )A. 10 V5 cmB. 10 cmC・ lCiJJcm D. 30cin。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学中的内切球和外接球
问题
欧阳光明(2021.03.07)
一、直接法(公式法)
1、求正方体的外接球的有关问题
例1若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为______________ .27π.
例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为
______________..
2、求长方体的外接球的有关问题
例3 (2007年天津高考题)一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为 .14π.
例4、(2006年全国卷I)已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为().C.
A.16π
B.20π
C.24π
D.32π
3.求多面体的外接球的有关问题
例5. 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为
9
8,底面周长为3,则这个球的体积为 .
解设正六棱柱的底面边长为x,高为h
,则有2
63,1
,
2
9
6,
8
x
x
x h
h
=
⎧⎧
=
⎪⎪
∴
⎨⎨
=⨯
⎪⎪=
⎩
⎩∴正六棱柱的底面圆的半径1
2
r=
,球心到底面的距离
d=
.∴外接球的半径
*欧阳光明*创编 2021.03.07
*欧阳光明*创编 2021.03.07
22
1R r d =+=.
43V π∴=
球.
二、构造法(补形法) 1、构造正方体
例5 (2008年福建高考题)若三棱锥的三条
侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是_______________.9π
解 据题意可知,该三棱锥的三条侧棱两两垂
直,∴把这个三棱锥可以补成一个棱长为3的正
方体,于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ,则有
()
()()()
2
2
2
2
23339
R =
++=.∴29
4R =
.故其外接球
的表面积2
49S R ππ==.
小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个
三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有222
2R a b c =
++.出现“墙角”结构
利用补形知识,联系长方体。
【例题】:在四面体
中,共顶点的三条棱两两垂直,其长度分别为
,若该四面体
的四个顶点在一个球面上,求这个球的表面积。
解:因为:长方体外接球的直径为长方体的
体对角线长所以:四面体外接球的直径为
的长即:
所以
球的表面积为
例 6.2,四个顶点在同一球面上,则此球的表面积为( )
A.3π
B.4π
C.33π
D.6π
解析:一般解法,需设出球心,作出高线,
构造直角三角形,再计算球的半径.在此,由于所有棱长都相等,我们联想只有正方体中有这么多相等的线段,所以构造一个正方体,再寻找棱长
相等的四面体,四面体A BDE
-
满足条件,即
AB=AD=AE=BD=DE BE
==
棱长为1
A.
例7.在等腰梯形ABCD中,AB=2DC=2,
DAB=60
∠,E为AB的中点,将ADE
∆与BEC
∆分布沿ED、EC向上折起,使A B
、重合于点P,则三棱锥P-DCE的外接球的体积为().
A.
B.
C.
D.
解析:因为AE=EB=DC=1,
DAB=CBE=DEA=60
∠∠∠,所以
AE=EB=BC=DC=DE=CE=1
AD=,即三棱锥P-DCE为正
四面体,至此,这与例6就完全相同了,故选C.
例8 .已知球O的面上四点A、B、C、D,
DA ABC
⊥平面,AB BC
⊥
,O
的体积等于 .
解析:本题同样用一般方法时,需要找出球
心,求出球的半径.而利用长方体模型很快便可找
到球的直径,由于DA ABC
⊥平面,AB BC
⊥,联想
长方体中的相应线段关系,构造长方体,又因为
CD长
即为外接球的直径,利用直角三角形解出CD=3.故
球O的体积等于
9
2
π
.
2、构造长方体
例9.已知点A、B、C、D在同一个球面上,
*欧阳光明*创编 2021.03.07
*欧阳光明*创编 2021.03.07
B BCD A ⊥平面,B
C DC ⊥
,若6,AB =,
则球的体积是.
解析:首先可联想到例8,构造下面的长方体,于是AD 为球的直径,O 为球心,OB=OC=4为半径,要求B 、C 两点间的球面距离,只要求出
BOC ∠即可,在Rt ABC ∆中,求出=4BC ,所以
C=60
BO ∠,故
B 、
C 两点间的球面距离是4
3π
.
三.多面体几何性质法
例1 0.已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是
A.16π
B.20π
C.24π
D.32π 解 设正四棱柱的底面边长为x ,外接球的半
径为R ,则有2
416x =,解得2x =.
∴
2R R ==∴= .∴这个球的表面积是
2
424R ππ=.选C.小结 本题是运用“正四
棱柱的体对角线的长等于其外接球的直径”这一性质来求解的.
四.寻求轴截面圆半径法
例11.正四棱锥S ABCD -的底面边长和各侧棱长
,点S A B C D 、、、、都在同一球面上,则此球的体积为 .
解 设正四棱锥的底面中心为1O ,外接球的球心为O ,如图1所示.∴由球的截面的性质,可
得1OO ABCD ⊥平面.
又1SO ABCD ⊥平面,∴球心O 必在1SO 所在的直线上.
∴ASC ∆的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球的半径.在ASC ∆中,
由2SA SC AC ===,得222
SA SC AC +=.∴
C
D
A
B S
O 1图3
*欧阳光明*创编 2021.03.07
ASC AC ∆∆是以为斜边的Rt .∴
12AC
=是外接圆的半径,也是外接球的半径.故
43V π=
球.
五 .确定球心位置法
例11.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体
ABCD 的外接球的体积为
A.12512π
B.1259π
C.1256π
D.125
3π
解 设矩形对角线的交点为O ,则由矩形对角线互相平分,可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,∴外接球的半径
5
2R OA ==
.
故
3412536V R ππ
==球.选C.
【例题】:已知三棱锥的四个顶点都在球的球面上,
且,,,
,求球的
体积。
解:且,,,, 因为
所
以知所以
所以可得图形
为:
在
中斜边为
,在
中斜边为
,取斜边的中点,在中
,
在
中
所以在几何体中
,即为该四面体的外接球的球
心,
,所以该外接球的体积为。
