数字逻辑课件
合集下载
《数字逻辑基础》课件

公式化简法
使用逻辑代数公式对逻辑函数进行化简,通过消去多余的项和简化 表达式来得到最简结果。
卡诺图化简法
使用卡诺图对逻辑函数进行化简,通过填1、圈1、划圈和填0的方 法来得到最简结果。
03
组合逻辑电路
组合逻辑电路的分析
组合逻辑电路的输入和输出
分析组合逻辑电路的输入和输出信号,了解它们之间的关系。
交通信号灯控制系统的设计与实现
交通信号灯简介
交通信号灯是一种用于控制交通流量的电子设备,通常设置在路口或 交叉口处。
设计原理
交通信号灯控制系统的设计基于数字逻辑电路和计算机技术,通过检 测交通流量和车流方向来实现信号灯的自动控制。
实现步骤
首先确定系统架构和功能需求,然后选择合适的元件和芯片,接着进 行电路设计和搭建,最后进行测试和调整。
真值表
通过列出输入和输出信号的所有可能组合,构建组合逻辑电路的真值表,以确定输出信 号与输入信号的逻辑关系。
逻辑表达式
根据真值表,推导出组合逻辑电路的逻辑表达式,表示输入和输出信号之间的逻辑关系 。
组合逻辑电路的设计
确定逻辑功能
根据实际需求,确定所需的逻辑功能,如与、或、非等。
设计逻辑表达式
根据确定的逻辑功能,设计相应的逻辑表达式,用于描述输入和 输出信号之间的逻辑关系。
实现电路
根据逻辑表达式,选择合适的门电路实现组合逻辑电路,并完成 电路的物理设计。
常用组合逻辑电路
01
02
03
04
编码器
将输入信号转换为二进制码的 电路,用于信息处理和控制系
统。
译码器
将二进制码转换为输出信号的 电路,用于数据分配和显示系
统。
多路选择器
使用逻辑代数公式对逻辑函数进行化简,通过消去多余的项和简化 表达式来得到最简结果。
卡诺图化简法
使用卡诺图对逻辑函数进行化简,通过填1、圈1、划圈和填0的方 法来得到最简结果。
03
组合逻辑电路
组合逻辑电路的分析
组合逻辑电路的输入和输出
分析组合逻辑电路的输入和输出信号,了解它们之间的关系。
交通信号灯控制系统的设计与实现
交通信号灯简介
交通信号灯是一种用于控制交通流量的电子设备,通常设置在路口或 交叉口处。
设计原理
交通信号灯控制系统的设计基于数字逻辑电路和计算机技术,通过检 测交通流量和车流方向来实现信号灯的自动控制。
实现步骤
首先确定系统架构和功能需求,然后选择合适的元件和芯片,接着进 行电路设计和搭建,最后进行测试和调整。
真值表
通过列出输入和输出信号的所有可能组合,构建组合逻辑电路的真值表,以确定输出信 号与输入信号的逻辑关系。
逻辑表达式
根据真值表,推导出组合逻辑电路的逻辑表达式,表示输入和输出信号之间的逻辑关系 。
组合逻辑电路的设计
确定逻辑功能
根据实际需求,确定所需的逻辑功能,如与、或、非等。
设计逻辑表达式
根据确定的逻辑功能,设计相应的逻辑表达式,用于描述输入和 输出信号之间的逻辑关系。
实现电路
根据逻辑表达式,选择合适的门电路实现组合逻辑电路,并完成 电路的物理设计。
常用组合逻辑电路
01
02
03
04
编码器
将输入信号转换为二进制码的 电路,用于信息处理和控制系
统。
译码器
将二进制码转换为输出信号的 电路,用于数据分配和显示系
统。
多路选择器
数字逻辑电路与系统设计课件

计数器
用于计数和控制时序,常用于实现定时器和分频器。
移位器
用于二进制数据的移位操作,常用于数据格式化和数据传输。
顺序脉冲发生器
用于产生一定规律的顺序脉冲信号,常用于控制电路的工作流程。
04
数字系统设计
数字系统概述
数字系统的基本概念
数字系统是指使用离散的二进制数字信号进行信息处理的系统。它主要由逻辑 门电路、触发器、寄存器、加法器等基本元件组成,具有精度高、稳定性好、 易于大规模集成等优点。
实现逻辑功能
根据状态转换图,实现相应的 逻辑功能。
确定设计目标
明确设计时序逻辑电路的目的 和要求,如实现特定的功能、 达到一定的性能指标等。
设计状态转换图
根据设计要求,设计状态转换 图,确定状态和输出。
验证设计
通过仿真或实验验证设计的正 确性和可行性。
常用时序逻辑电路
寄存器
用于存储二进制数据,常用于数据传输和数据处理。
集成化和智能化技术的发展,为数字 系统的设计带来了新的机遇和挑战。
数字系统的智能化是当前的一个重要 趋势,它使得数字系统能够具有更强 的自适应性、智能性和灵活性。
THANKS FOR WATCHING
感谢您的观看
分析输入和输出信号的逻辑关系,确定电路的功 能。
真值表和逻辑表达式
通过列出所有输入组合和对应的输出值,得到真 值表,并根据真值表推导出逻辑表达式。
3
逻辑功能描述
根据逻辑表达式或真值表,描述组合逻辑电路的 逻辑功能。
组合逻辑电路的设计
明确设计要求:确定输入和 输出信号,以及电路要实现 的功能。
根据功能要求,逐一确定每 个输入组合对应的输出值。
自底向上的设计方法
用于计数和控制时序,常用于实现定时器和分频器。
移位器
用于二进制数据的移位操作,常用于数据格式化和数据传输。
顺序脉冲发生器
用于产生一定规律的顺序脉冲信号,常用于控制电路的工作流程。
04
数字系统设计
数字系统概述
数字系统的基本概念
数字系统是指使用离散的二进制数字信号进行信息处理的系统。它主要由逻辑 门电路、触发器、寄存器、加法器等基本元件组成,具有精度高、稳定性好、 易于大规模集成等优点。
实现逻辑功能
根据状态转换图,实现相应的 逻辑功能。
确定设计目标
明确设计时序逻辑电路的目的 和要求,如实现特定的功能、 达到一定的性能指标等。
设计状态转换图
根据设计要求,设计状态转换 图,确定状态和输出。
验证设计
通过仿真或实验验证设计的正 确性和可行性。
常用时序逻辑电路
寄存器
用于存储二进制数据,常用于数据传输和数据处理。
集成化和智能化技术的发展,为数字 系统的设计带来了新的机遇和挑战。
数字系统的智能化是当前的一个重要 趋势,它使得数字系统能够具有更强 的自适应性、智能性和灵活性。
THANKS FOR WATCHING
感谢您的观看
分析输入和输出信号的逻辑关系,确定电路的功 能。
真值表和逻辑表达式
通过列出所有输入组合和对应的输出值,得到真 值表,并根据真值表推导出逻辑表达式。
3
逻辑功能描述
根据逻辑表达式或真值表,描述组合逻辑电路的 逻辑功能。
组合逻辑电路的设计
明确设计要求:确定输入和 输出信号,以及电路要实现 的功能。
根据功能要求,逐一确定每 个输入组合对应的输出值。
自底向上的设计方法
数字逻辑ppt

-
p 2 (2 6) 24(W ) (吸收)
2 电路定理
❖2.1 叠加定理
❖2.2 戴维南定理 ❖ 2.3 诺顿定理 ❖ 2.4 最大功率传递定理
2.1 叠加定理
由线性电阻元件、线性受控源及独立源 构成旳电路为线性电阻电路。
若某线性电阻电路有唯一解,则该电路 中任一支路电流和电压均可表达为电路 中全部独立源旳线性组合。
即:一系列振幅不同,频率成整数倍旳正弦波, 叠加后来可构成一种非正弦周期波。
分析中旳u1、u3、u5等等,这些振幅不同、频率 分别是非正弦周期波频率k次倍旳正弦波统称为非正 弦周期波旳谐波,并按照k是非正弦周期波频率旳倍 数分别称为1次谐波(基波)、3次谐波……。
k为奇数旳谐波一般称为非正弦周期函数旳奇次 谐波;k为偶数时则称为非正弦周期波旳偶次谐波。 而把2次以上旳谐波均称为高次谐波。
1. 4受控源
实际电路中旳受控现象:
Ic
Ib
三极管
Ic Ib
他励直流发电机
If
+
U rIf
U
-
电压控制电压源(VCVS):
特征方程
+
u2 u1
u1
-
-转移电压比
电流控制电压源(CCVS):
特征方程
u2 r i1
i1
r-转移电阻
+
μu1 u2
-
+
ri1 u- 2
电压控制电流源(VCCS):
iS
定义:端电流与电压无关且保持为某一给定函数 旳二端元件。
伏安特征:
iS
i(t) iS (t)
(u为任意值)
i
➢ 电流源旳两种工作状态:
1. 吸收电功率,
p 2 (2 6) 24(W ) (吸收)
2 电路定理
❖2.1 叠加定理
❖2.2 戴维南定理 ❖ 2.3 诺顿定理 ❖ 2.4 最大功率传递定理
2.1 叠加定理
由线性电阻元件、线性受控源及独立源 构成旳电路为线性电阻电路。
若某线性电阻电路有唯一解,则该电路 中任一支路电流和电压均可表达为电路 中全部独立源旳线性组合。
即:一系列振幅不同,频率成整数倍旳正弦波, 叠加后来可构成一种非正弦周期波。
分析中旳u1、u3、u5等等,这些振幅不同、频率 分别是非正弦周期波频率k次倍旳正弦波统称为非正 弦周期波旳谐波,并按照k是非正弦周期波频率旳倍 数分别称为1次谐波(基波)、3次谐波……。
k为奇数旳谐波一般称为非正弦周期函数旳奇次 谐波;k为偶数时则称为非正弦周期波旳偶次谐波。 而把2次以上旳谐波均称为高次谐波。
1. 4受控源
实际电路中旳受控现象:
Ic
Ib
三极管
Ic Ib
他励直流发电机
If
+
U rIf
U
-
电压控制电压源(VCVS):
特征方程
+
u2 u1
u1
-
-转移电压比
电流控制电压源(CCVS):
特征方程
u2 r i1
i1
r-转移电阻
+
μu1 u2
-
+
ri1 u- 2
电压控制电流源(VCCS):
iS
定义:端电流与电压无关且保持为某一给定函数 旳二端元件。
伏安特征:
iS
i(t) iS (t)
(u为任意值)
i
➢ 电流源旳两种工作状态:
1. 吸收电功率,
数字逻辑基础教学课件PPT

4. 各种表示方法间的相互转换
(1)逻辑函数式→真值表 举例:例1-6(P9) (2)逻辑函数式→逻辑图 举例:例1-7(P10) (3)逻辑图→逻辑函数式 方法:从输入到输出逐级求取。
举例:例1-8(P10)
(4)真值表→函数式
方法:将真值表中Y为 1 的输入变量相与,取 值为 1 用原变量表示,0 用反变量表示, 将这 些与项相加,就得到逻辑表达式。这样得到的 逻辑函数表达式是标准与-或逻辑式。
断开为0;灯为Y,灯亮为1,灭为0。
真值表
AB Y 00 0 01 1 10 1 11 1
由“或”运算的真值表可知
“或”运算法则为:
有1出
0+0 = 0 1+0 = 1
1
0+1 = 1 1+1 = 1
全0为
0
⒊ 表达式
逻辑代数中“或”逻辑关系用“或”运算 描述。“或”运算又称逻辑加,其运算符为 “+”或“ ”。两变量的“或”运算可表示
0
卡诺图是一 种用图形描 述逻辑函数
的方法。
00 0 01 0 11 0
10 1
例:函数 F=AB + AC
ABC F
000 0
1 001 1 010 0
1 011 1
1 100 1
0
101 1 110 0
1 111 0
1.逻辑函数式
特点:
例:函数 F=AB + AC
(1)便于运算; (2)便于用逻辑图实现; (3)缺乏直观。
真值表
K
Y
0
1
1
0
由“非”运算的真值表可知 “非”运算法则为:
0 =1 1 =0
⒊ 表达式
“非”逻辑用“非”运算描述。“非”运 算又称求反运算,运算符为“-”或“¬”, “非”运算可表示为:
(1)逻辑函数式→真值表 举例:例1-6(P9) (2)逻辑函数式→逻辑图 举例:例1-7(P10) (3)逻辑图→逻辑函数式 方法:从输入到输出逐级求取。
举例:例1-8(P10)
(4)真值表→函数式
方法:将真值表中Y为 1 的输入变量相与,取 值为 1 用原变量表示,0 用反变量表示, 将这 些与项相加,就得到逻辑表达式。这样得到的 逻辑函数表达式是标准与-或逻辑式。
断开为0;灯为Y,灯亮为1,灭为0。
真值表
AB Y 00 0 01 1 10 1 11 1
由“或”运算的真值表可知
“或”运算法则为:
有1出
0+0 = 0 1+0 = 1
1
0+1 = 1 1+1 = 1
全0为
0
⒊ 表达式
逻辑代数中“或”逻辑关系用“或”运算 描述。“或”运算又称逻辑加,其运算符为 “+”或“ ”。两变量的“或”运算可表示
0
卡诺图是一 种用图形描 述逻辑函数
的方法。
00 0 01 0 11 0
10 1
例:函数 F=AB + AC
ABC F
000 0
1 001 1 010 0
1 011 1
1 100 1
0
101 1 110 0
1 111 0
1.逻辑函数式
特点:
例:函数 F=AB + AC
(1)便于运算; (2)便于用逻辑图实现; (3)缺乏直观。
真值表
K
Y
0
1
1
0
由“非”运算的真值表可知 “非”运算法则为:
0 =1 1 =0
⒊ 表达式
“非”逻辑用“非”运算描述。“非”运 算又称求反运算,运算符为“-”或“¬”, “非”运算可表示为:
大学课件数字逻辑基础5
&L
B
逻辑表达式
与逻辑: L = A ·B= AB
2、或运算
只要在决定某一事件的各种条件中,有一个或几个条件具 备时,这一事件就会发生。这种因果关系称为或逻辑关系。
或逻辑举例
S1 S2 电源
电路状态表
开关S1
开关S2
灯
断
断
灭
灯
断
合
亮
合
断
亮
合
合
亮
2、或运算
或逻辑举例状态表
开关
开关S2
1.与运算
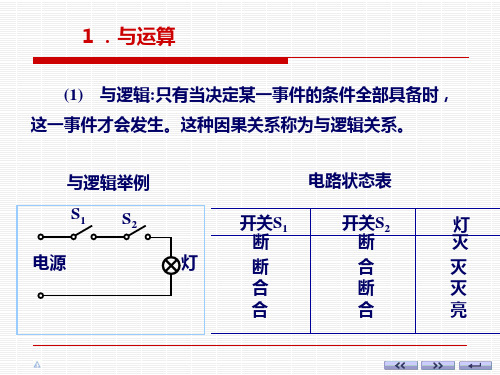
(1) 与逻辑:只有当决定某一事件的条件全部具备时, 这一事件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例
电路状态表
S1
S2
开关S1
开关S2
灯
断
断
灭
电源
灯
断
合
灭
合
断
灭
合
合
亮
1.与运算
与逻辑举例状态表
开关
开关S2
灯
断S1
断
灭
断
合
灭
合
断
灭
合
合
亮
与逻辑符号
A B
L
逻辑真值表
AB L
00
0
01
灯
断S1
断
灭
断
合
灭
合
断
灭
合
合
亮
或逻辑符号
A
≥1
L
B
逻辑真值表
AB L
00
0
01
1
10
1
11
1
A
B
L
逻辑表达式
B
逻辑表达式
与逻辑: L = A ·B= AB
2、或运算
只要在决定某一事件的各种条件中,有一个或几个条件具 备时,这一事件就会发生。这种因果关系称为或逻辑关系。
或逻辑举例
S1 S2 电源
电路状态表
开关S1
开关S2
灯
断
断
灭
灯
断
合
亮
合
断
亮
合
合
亮
2、或运算
或逻辑举例状态表
开关
开关S2
1.与运算
(1) 与逻辑:只有当决定某一事件的条件全部具备时, 这一事件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例
电路状态表
S1
S2
开关S1
开关S2
灯
断
断
灭
电源
灯
断
合
灭
合
断
灭
合
合
亮
1.与运算
与逻辑举例状态表
开关
开关S2
灯
断S1
断
灭
断
合
灭
合
断
灭
合
合
亮
与逻辑符号
A B
L
逻辑真值表
AB L
00
0
01
灯
断S1
断
灭
断
合
灭
合
断
灭
合
合
亮
或逻辑符号
A
≥1
L
B
逻辑真值表
AB L
00
0
01
1
10
1
11
1
A
B
L
逻辑表达式
数字逻辑基础ppt课件

数字电子技术基础
数字电路研究的对象是输入与输出的逻辑关系, 即电路的逻辑功能。
(2) 数字电路研究方法 数字电路研究的主要方法是逻辑分析和逻辑
设计的方法。
计算机软件:硬件描述语言,例如ABEL 语言、VHD语言。
上页 下页 返回
数字电子技术基础
(3) 数字电路的测试技术 数字电路在正确设计和安装后,必须经过
( N ) R a n 1 a n 2 .a . 2 a 1 . a 0 .a 1 a 2 .a . m .
上页 下页 返回
数字电子技术基础
(2) 数位的权值 某个数位上数码为1时所表征的数值,称为该
数位的权值,简称“权”。
各个数位的权值均可表示成Ri的形式。
其中R是进位基数,i 表示相对小数点的位置。 i的确定方法: 以小数点为起点,自右向左依次为0,1, 2,…,n-1,自左向右依次为-1,-2, …,-m。n是整 数部分的位数,m是小数部分的位数。
上页 下页 返回
数字电子技术基础
在一个数位上,规定使用的数码符号的总数, 叫该进位计数制的进位基数,简称为“基” 。
进位基数又称为进位模数,记作R。 例如十进制,每个数位规定使用的数码符号为0, 1, 2, …, 9,共10个, 故其进位基数R=10。
若某个数位上的数码为ai,n为整数位,m为小
数位,则进位计数制表示的式子为
上页 下页 返回
数字电子技术基础
(4) 保密性好,对于数字信号可以采用各种算法进行 加密处理,故对信息资源的保密性好。 (5) 有可能通过编程改变芯片的逻辑功能。 (6) 可完成数字运算和逻辑运算。 (7) 容易采用计算机辅助设计。 3. 数字电路研究的对象、方法与测试技术 (1) 研究的对象
数字逻辑电路大全PPT课件(2024版)

第6页/共48页
Rb1 4kΩ
Rc 2 1.6kΩ
Vc 2
1
+VCC( +5V) Rc4 130Ω
3
T2 4
1
3
A
31
2T2
D Vo
B
T1
C
Ve 2
1
3
2T 3
Re2
1kΩ
输入级
中间级
输出级
第7页/共48页
2.TTL与非门的逻辑关系
(1)输入全为高电平3.6V时。
T2、T3导通,VB1=0.7×3=2.1(V ),
列。 6 . 74AS 系 列 —— 为 先 进 肖 特 基 系
列, 它是74S系列的后继产品。 7.74ALS系列——为先进低 功耗肖特基系列, 是74LS系列的后继产品。
第30页/共48页
2.3
一、 NMOS门电路 1.NMOS非门
MOS逻辑门电路
VDD (+12V)
VDD (+12V)
VDD (+12V)
0.4V
高 电 平 噪 声 容 限 第1V5页NH/共=48V页OH ( min ) - VON = 2.4V-2.0V =
四、TTL与非门的带负载能力
1.输入低电平电流IIL与输入高电平电流IIH (1)输入低电平电流IIL——是指当门电路的输入端
接低电平时,从门电路输入端流出的电流。
& Vo G0
呈 现 高 阻 , 称 为 高 阻 态 , 或 禁 止 态+V。CC
Rc2
Rc4
Rb1
Vc2 1
3
T2 4
A
&
B
L
EN
数字逻辑朱勇ppt课件

电路。
仿真工具
用于模拟和测试数字电 路的行为和功能。
布局布线工具
将逻辑电路转换为物理 版图,并生成制程需要
的掩膜。
05 数字信号处理
数字信号的特点
01
02
03
04
离散性
数字信号在时间或幅度上都是 离散的,表现为信号状态的突
然跳变。
稳定性
数字信号的幅度值范围较小, 因此信号相对稳定,不易受到
噪声干扰。
可存储性
数字信号可以方便地存储在计 算机存储器、数字磁带等介质
上。
抗干扰能力强
由于数字信号是离散的,因此 具有较强的抗干扰能力,传输
过程中不易失真。
数字信号处理的方法
时域分析法
频域分析法
通过观察信号在不同时间点的取值来分析 信号的特性。
将信号转换为频域表示,通过分析信号的 频率成分来理解信号特性。
数字逻辑还可以应用于加密、编码、图像处理等领域,为现代信息社会提供了重 要的技术支持。
02 数字逻辑基础
基本逻辑门
OR门
实现逻辑或运算, 当输入有一个为真 时,输出为真。
NAND门
实现逻辑与非运算 ,当输入都为真时 ,输出为假。
AND门
实现逻辑与运算, 当输入都为真时, 输出为真。
NOT门
实现逻辑非运算, 对输入取反。
时序逻辑电路
总结词
具有记忆功能的电路,输出不仅取决于当前的输入,还与过 去的输入状态有关。
详细描述
时序逻辑电路具有存储元件(如触发器),可以保存之前的 输入状态,因此其输出不仅取决于当前的输入,还与之前的 输入和状态有关。常见的时序逻辑电路有寄存器、计数器、 微处理器等。
可编程逻辑电路
仿真工具
用于模拟和测试数字电 路的行为和功能。
布局布线工具
将逻辑电路转换为物理 版图,并生成制程需要
的掩膜。
05 数字信号处理
数字信号的特点
01
02
03
04
离散性
数字信号在时间或幅度上都是 离散的,表现为信号状态的突
然跳变。
稳定性
数字信号的幅度值范围较小, 因此信号相对稳定,不易受到
噪声干扰。
可存储性
数字信号可以方便地存储在计 算机存储器、数字磁带等介质
上。
抗干扰能力强
由于数字信号是离散的,因此 具有较强的抗干扰能力,传输
过程中不易失真。
数字信号处理的方法
时域分析法
频域分析法
通过观察信号在不同时间点的取值来分析 信号的特性。
将信号转换为频域表示,通过分析信号的 频率成分来理解信号特性。
数字逻辑还可以应用于加密、编码、图像处理等领域,为现代信息社会提供了重 要的技术支持。
02 数字逻辑基础
基本逻辑门
OR门
实现逻辑或运算, 当输入有一个为真 时,输出为真。
NAND门
实现逻辑与非运算 ,当输入都为真时 ,输出为假。
AND门
实现逻辑与运算, 当输入都为真时, 输出为真。
NOT门
实现逻辑非运算, 对输入取反。
时序逻辑电路
总结词
具有记忆功能的电路,输出不仅取决于当前的输入,还与过 去的输入状态有关。
详细描述
时序逻辑电路具有存储元件(如触发器),可以保存之前的 输入状态,因此其输出不仅取决于当前的输入,还与之前的 输入和状态有关。常见的时序逻辑电路有寄存器、计数器、 微处理器等。
可编程逻辑电路
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字逻辑电路
第五章 时序逻辑电路
数字逻辑电路
第五章 时序逻辑电路
二、同步时序电路的分析 例1:分析下图所示的同步时序电路(主从JK触发器)。
数字逻辑电路
第五章 时序逻辑电路
解:电路构成:2个触发器(存贮),1个异或门(组 合);输入X,输出Z,状态Q1、Q0; ①、写出方程: 输出方程:Z=Q1n Q0n
能使电路的状态改变一次。这里,时钟脉冲起着同步作 用,故而称为同步时序电路。
数字逻辑电路
第五章 时序逻辑电路
异步时序电路:触发器时钟不是连接在一起或即使连 接在一起但并不同时翻转(有些上升沿变化,有些下降 沿变化)。 异步时序电路没有统一的时钟脉冲,输入的变化直接
导致电路状态的变化,而且每次输入变化可能使电路状
为10,类推。
对Z端的输出也可看成是序列信号发生器,脉冲周期 为4TCP,脉冲宽度为1TCP。
数字逻辑电路
第五章 时序逻辑电路
第三节 一、设计步骤 同步时序电路的设计是分析的逆过程,是根据给定的 状态图或通过对设计要求的分析得到的状态图,设计出 同步时序电路的设计
同步时序电路的过程。
设计一个同步时序电路,一般可按如下步骤进行: 1、根据逻辑问题的功能需求,建立原始状态图
数字逻辑电路
第五章 时序逻辑电路
即:相同的输入,不一定得到相同的输出。 如活期存款。存入相同的数,但折中的总数相等吗? 时序电路中其关键的器件是记忆器件即触发器。 根据组成时序电路的各个触发器在CP信号作用下是否 同时动作将时序电路分为同步和异步两种类型: 同步时序电路是指组成时序电路的各个触发器在同一 CP信号作用下同时动作;
态改变多次。 所谓同步、异步取决于电路状态变化是否与时钟同步。
数字逻辑电路
第五章 时序逻辑电路
二、时序逻辑电路的结构特点
数字逻辑电路
第五章 时序逻辑电路
在电路结构上,时序电路除了包含有组合电路外,还 必须包含有具有记忆功能的存储电路(存储电路通常由 触发器构成),而且存储电路的输出还必须反馈到输入 端,影响其输出。 它有两组输入和两组输出。 把输入X1,X2,…,Xn称为时序电路的外部输入; 把输入Q1,Q2,…,Qr称为时序电路的内部输入,它 是存储元件的输出反馈到组合电路的输入。 把输出Z1,Z2,…,Zm称为时序电路的外部输出; 把输出Y1,Y2,…,Yr称为时序电路的内部输出。
有效信号时,该触发器工作。
例3:分析下列电路:
数字逻辑电路
第五章 时序逻辑电路
数字逻辑电路
第五章 时序逻辑电路
解:分析构成,由于两个触发器的CP接的不是同一信 号,所以是异步电路; 对于第一个D触发器,时钟信号端接CP,当CP由0变为 1时,状态翻转,第二个D触发器的时钟信号端接Q0,当
Q0由0变为1时,才会触发。
现态
输入/输出
次态
数字逻辑电路
第五章 时序逻辑电路
箭头表示状态转换的方向,起点是现态,终点是次态。 3、时序图 也就是时序电路的工作波形图,它能直观地描述时序 电路的输入信号、时钟信号、输出信号及电路的状态转
换等在时间上的对应关系。
时序图:表示相互关系的多重数字波形图;其中标有 CP的是时钟脉冲信号,是数字系统中的时间参考信号。
数字逻辑电路
第五章 时序逻辑电路
建立状态图需要确定三个问题: 1、电路应该包括几个状态; 2、状态之间如何进行转换; 3、怎样产生输出。
根据逻辑问题功能描述,确定电路包括几个状态,并 用字母表示。再由输入输出与状态确定状态之间的变化 关系,画出原始状态图。 这一步得到的状态图是原始的, 其中可能包含多余的状态。
数字逻辑电路
第五章 时序逻辑电路
④、画出时序图: 尽管从状态表和状态图,已经可判断出该电路的功能, 但有时还需作出电路的波形(时序图)才能最后确定它的 功能,更清晰描述电路的工作情况。
数字逻辑电路
第五章 时序逻辑电路
波形画法: 画出CP波形; 根据触发器的触发极性,画出状态变化时刻线,(主 从触发器为下降沿触发)
数字逻辑电路
第五章 时序逻辑电路
三、时序逻辑电路的描述方法 1、逻辑方程 用三个方程式全面地描述一个时序电路的逻辑功能: 输出方程——时序电路输出端的逻辑表达式。
Z = F1(X,Qn)
数字逻辑电路
第五章 时序逻辑电路
驱动方程——电路中各触发器输入端的逻辑表达式。 Y=F2(X,Qn) 状态方程——把驱动方程代入相应触发器的特性方程 所得到的方程式(即触发器的次态方程)。
这是一个脉冲分配器或者脉冲产生器,在正常工作时,
将宽度为一个时钟周期的脉冲轮流分配到各触发器的输 出端上。
数字逻辑电路
第五章 时序逻辑电路
三、异步时序电路的分析 在异步时序电路中,各触发器的CP信号端加的不是同 一时钟信号,使得它们的状态翻转不在同一时刻,各自 的CP信号控制各触发器单独行动,当某触发器的CP端为
பைடு நூலகம்
数字逻辑电路
第五章 时序逻辑电路
①、写出方程 输出方程:Z=Q1nQ0n 驱动方程:D0=Q0n、D1=Q1n 状态方程:Q0n+1=D0=Q0n、Q1n+1=D2=Q1n
且这两个触发器异步触发。
数字逻辑电路
第五章 时序逻辑电路
②、写出状态表、画出状态图
Q1n
Q0n
CP0
CP1
Q1n+1Q0n+1/Z
驱动方程:J0 = K0 = 1
(每来一个脉冲,触发器的状态就翻转一次) J1 = K1 = X○Q0n +
数字逻辑电路
第五章 时序逻辑电路
状态方程: 根据JK触发器的特性方程:Qn+1=J Qn+K Qn Q0n+1=J0Q0n+K0Q0n=Q0n(状态翻转) Q1n+1=J1Q1n+K1Q1n=J1Q1n+J1Q1n
(假设现态代入状态方程,计算出次态,再以得到的
次态作为新的现态代入状态方程求出下一个次态,依此 类推得到状态表。)
4、根据真值表画出该电路的状态图。
5、根据状态图说明其功能。
数字逻辑电路
第五章 时序逻辑电路
1
电路图
驱动方程和 输出方程
2
状态方程
3
判断电路 逻辑功能
5
状态图、 状态表、 时序图
4
计算
主讲老师:韩维良
2005.7
第五章 时序逻辑电路
第一节 时序逻辑电路的特点
一、时序逻辑电路概述 逻辑电路可分为:组合逻辑电路和时序逻辑电路。 组合逻辑电路的特点是任何时刻的输出只取决于当前
的输入状态,与原来的输出状态无关。
时序电路每一时刻的输出不仅取决于当前的输入状态, 而且与前一时刻的输出有关。这种电路具有记忆的功能, 因此时序电路通常是由组合电路和存储电路两部分组成。
+ + =J1○Q1n = X○Q0n○ Q1n +
数字逻辑电路
第五章 时序逻辑电路
②、写出状态表和状态图:
Q0n+1=Q0n
Q1n+1=X○Q0n○ Q1n + + 0/0
00
1/0 0/1 11 0/0 1/0 1/1
01
1/0 10 0/0
数字逻辑电路
第五章 时序逻辑电路
③、功能分析: 从状态表和状态图可知它是一个四进制的可逆计数器。 当x=0时,进行加1计数,当x=1时,进行减1计数; (每来一次时钟脉冲,计一次数)计数序列为:
Qn+1=F3(Y,Qn)
即各触发器的次态与现态的关系方程,也就是时序逻 辑电路的状态方程。
数字逻辑电路
第五章 时序逻辑电路
2、状态表和状态图 在工程应用中,时序逻辑电路通常用状态表和状态图 来表示。 状态表是用来描述时序逻辑电路的输入、状态和输出
之间的关系的表格。
类似于真值表; 状态图是用图解方式来描述时序逻辑电路的输入、状 态和输出之间的关系;
例2:分析如图所示的逻辑电路。
数字逻辑电路
第五章 时序逻辑电路
解:该电路没有外部输入,直接由各触发器的Q端输出。
①、写出逻辑方程 输出方程:Z0=Q0n,Z1=Q1n,Z2=Q2n 驱动方程:D0=Q0n· 1n、D1=Q0n,D2=Q1n Q 状态方程:Q0n+1=D0=Q0n·1n、Q1n+1=D1=Q0n,Q2n+1=D2=Q1n Q
数字逻辑电路
第五章 时序逻辑电路
2、进行状态化简,化简原始状态图,以等效合并的 原则取消多余的状态,进行状态化简 等效状态:任意两个状态A、B, 在所有的输入下,若 电路输出和次态完全相同,则此两个状态互为等效,用 括号(A,B)表示。可以合并为一个状态。
数字逻辑电路
第五章 时序逻辑电路
利用等效状态可以合并(用一个状态表示)来进行状态 简化。 3、进行状态编码(或状态赋值),写出状态表 前面得到的状态图中的状态都是以字母表示的,为了 用触发器来实现电路状态,必须给最简状态表中的每个 符号状态,指定一个二进制代码,形成二进制状态表, 这就称为状态分配,或称状态编码、状态赋值。
数字逻辑电路
第五章 时序逻辑电路
②、写出状态表和状态图 由于输出就是各触发器的状态Q,所以在写状态表时 不必列出;又因为没有输入,状态表完全表现为触发器 的现态与次态的关系;三个触发器,三个输出端,共有8
种不同的状态。
数字逻辑电路
第五章 时序逻辑电路
状态方程:Q0n+1=D0=Q0n· 1n、Q1n+1=D1=Q0n,Q2n+1=D2=Q1n Q Q2nQ1nQ0n 0 0 0 0 0 1 0 1 1 0 1 0 1 1 1 1 0 1 0 1 0 1 0 1 Q2n+1Q1n+1Q0n+1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 0
