数字逻辑课件第十章
合集下载
高中教育数字逻辑基础新精品PPT课件

例1-3
(218)10 =( 1101?1010 )2
第1章 数字逻辑基础
19
• 十进制小数转换为二进制小数
乘2取整法:乘2取整,先整为高 N10=N2=2-1×b-1+2-2×b-2+…+2-m×b-m
例1-4 (0.6875)10 =( 0.1?011 )2
思考:(218.6875) 10=( ? )2 (11011010.1011)2
11
第1章 数字逻辑基础
重点内容,熟练掌握
• 数制与编码 • 逻辑代数基础 • 逻辑函数的描述方法 • 逻辑函数的化简
第1章 数字逻辑基础
12
1.2 数制与编码
一、 数制 Number System
数制 :人类表示数值大小的各种方法的统称。
1、数的表示方法:
位置记数法 :NR=(rn-1rn-2…r1r0.r-1r-2…r-m)R
• 学科基础核心课 • 承前启后
先修课程:电路分析基础 模拟电子电路
后续课程: 数字通信、微机原理 计算机硬件技术基础
第1章 数字逻辑基础
8
学习要求
• 课前预习,适当自学 • 认真听课,做好笔记,积极思考问题 • 课后复习,完成作业 • 重视实验,理论联系实际
第1章 数字逻辑基础
9
十一五国家教级材规划教材
X反= (00001101)2
Y反= (11110010)2
第1章 数字逻辑基础
24
3、补码表示法
• 符号位:+用0表示,–用1表示。
• 数值位:正数不变,负数按位取反、末位加1 。
• n位二进制补码可表示十进制数范围:
–(2n-1)~ +(2n-1–1)
(218)10 =( 1101?1010 )2
第1章 数字逻辑基础
19
• 十进制小数转换为二进制小数
乘2取整法:乘2取整,先整为高 N10=N2=2-1×b-1+2-2×b-2+…+2-m×b-m
例1-4 (0.6875)10 =( 0.1?011 )2
思考:(218.6875) 10=( ? )2 (11011010.1011)2
11
第1章 数字逻辑基础
重点内容,熟练掌握
• 数制与编码 • 逻辑代数基础 • 逻辑函数的描述方法 • 逻辑函数的化简
第1章 数字逻辑基础
12
1.2 数制与编码
一、 数制 Number System
数制 :人类表示数值大小的各种方法的统称。
1、数的表示方法:
位置记数法 :NR=(rn-1rn-2…r1r0.r-1r-2…r-m)R
• 学科基础核心课 • 承前启后
先修课程:电路分析基础 模拟电子电路
后续课程: 数字通信、微机原理 计算机硬件技术基础
第1章 数字逻辑基础
8
学习要求
• 课前预习,适当自学 • 认真听课,做好笔记,积极思考问题 • 课后复习,完成作业 • 重视实验,理论联系实际
第1章 数字逻辑基础
9
十一五国家教级材规划教材
X反= (00001101)2
Y反= (11110010)2
第1章 数字逻辑基础
24
3、补码表示法
• 符号位:+用0表示,–用1表示。
• 数值位:正数不变,负数按位取反、末位加1 。
• n位二进制补码可表示十进制数范围:
–(2n-1)~ +(2n-1–1)
《数字逻辑基础》课件

公式化简法
使用逻辑代数公式对逻辑函数进行化简,通过消去多余的项和简化 表达式来得到最简结果。
卡诺图化简法
使用卡诺图对逻辑函数进行化简,通过填1、圈1、划圈和填0的方 法来得到最简结果。
03
组合逻辑电路
组合逻辑电路的分析
组合逻辑电路的输入和输出
分析组合逻辑电路的输入和输出信号,了解它们之间的关系。
交通信号灯控制系统的设计与实现
交通信号灯简介
交通信号灯是一种用于控制交通流量的电子设备,通常设置在路口或 交叉口处。
设计原理
交通信号灯控制系统的设计基于数字逻辑电路和计算机技术,通过检 测交通流量和车流方向来实现信号灯的自动控制。
实现步骤
首先确定系统架构和功能需求,然后选择合适的元件和芯片,接着进 行电路设计和搭建,最后进行测试和调整。
真值表
通过列出输入和输出信号的所有可能组合,构建组合逻辑电路的真值表,以确定输出信 号与输入信号的逻辑关系。
逻辑表达式
根据真值表,推导出组合逻辑电路的逻辑表达式,表示输入和输出信号之间的逻辑关系 。
组合逻辑电路的设计
确定逻辑功能
根据实际需求,确定所需的逻辑功能,如与、或、非等。
设计逻辑表达式
根据确定的逻辑功能,设计相应的逻辑表达式,用于描述输入和 输出信号之间的逻辑关系。
实现电路
根据逻辑表达式,选择合适的门电路实现组合逻辑电路,并完成 电路的物理设计。
常用组合逻辑电路
01
02
03
04
编码器
将输入信号转换为二进制码的 电路,用于信息处理和控制系
统。
译码器
将二进制码转换为输出信号的 电路,用于数据分配和显示系
统。
多路选择器
使用逻辑代数公式对逻辑函数进行化简,通过消去多余的项和简化 表达式来得到最简结果。
卡诺图化简法
使用卡诺图对逻辑函数进行化简,通过填1、圈1、划圈和填0的方 法来得到最简结果。
03
组合逻辑电路
组合逻辑电路的分析
组合逻辑电路的输入和输出
分析组合逻辑电路的输入和输出信号,了解它们之间的关系。
交通信号灯控制系统的设计与实现
交通信号灯简介
交通信号灯是一种用于控制交通流量的电子设备,通常设置在路口或 交叉口处。
设计原理
交通信号灯控制系统的设计基于数字逻辑电路和计算机技术,通过检 测交通流量和车流方向来实现信号灯的自动控制。
实现步骤
首先确定系统架构和功能需求,然后选择合适的元件和芯片,接着进 行电路设计和搭建,最后进行测试和调整。
真值表
通过列出输入和输出信号的所有可能组合,构建组合逻辑电路的真值表,以确定输出信 号与输入信号的逻辑关系。
逻辑表达式
根据真值表,推导出组合逻辑电路的逻辑表达式,表示输入和输出信号之间的逻辑关系 。
组合逻辑电路的设计
确定逻辑功能
根据实际需求,确定所需的逻辑功能,如与、或、非等。
设计逻辑表达式
根据确定的逻辑功能,设计相应的逻辑表达式,用于描述输入和 输出信号之间的逻辑关系。
实现电路
根据逻辑表达式,选择合适的门电路实现组合逻辑电路,并完成 电路的物理设计。
常用组合逻辑电路
01
02
03
04
编码器
将输入信号转换为二进制码的 电路,用于信息处理和控制系
统。
译码器
将二进制码转换为输出信号的 电路,用于数据分配和显示系
统。
多路选择器
数字逻辑基础教学课件PPT

4. 各种表示方法间的相互转换
(1)逻辑函数式→真值表 举例:例1-6(P9) (2)逻辑函数式→逻辑图 举例:例1-7(P10) (3)逻辑图→逻辑函数式 方法:从输入到输出逐级求取。
举例:例1-8(P10)
(4)真值表→函数式
方法:将真值表中Y为 1 的输入变量相与,取 值为 1 用原变量表示,0 用反变量表示, 将这 些与项相加,就得到逻辑表达式。这样得到的 逻辑函数表达式是标准与-或逻辑式。
断开为0;灯为Y,灯亮为1,灭为0。
真值表
AB Y 00 0 01 1 10 1 11 1
由“或”运算的真值表可知
“或”运算法则为:
有1出
0+0 = 0 1+0 = 1
1
0+1 = 1 1+1 = 1
全0为
0
⒊ 表达式
逻辑代数中“或”逻辑关系用“或”运算 描述。“或”运算又称逻辑加,其运算符为 “+”或“ ”。两变量的“或”运算可表示
0
卡诺图是一 种用图形描 述逻辑函数
的方法。
00 0 01 0 11 0
10 1
例:函数 F=AB + AC
ABC F
000 0
1 001 1 010 0
1 011 1
1 100 1
0
101 1 110 0
1 111 0
1.逻辑函数式
特点:
例:函数 F=AB + AC
(1)便于运算; (2)便于用逻辑图实现; (3)缺乏直观。
真值表
K
Y
0
1
1
0
由“非”运算的真值表可知 “非”运算法则为:
0 =1 1 =0
⒊ 表达式
“非”逻辑用“非”运算描述。“非”运 算又称求反运算,运算符为“-”或“¬”, “非”运算可表示为:
(1)逻辑函数式→真值表 举例:例1-6(P9) (2)逻辑函数式→逻辑图 举例:例1-7(P10) (3)逻辑图→逻辑函数式 方法:从输入到输出逐级求取。
举例:例1-8(P10)
(4)真值表→函数式
方法:将真值表中Y为 1 的输入变量相与,取 值为 1 用原变量表示,0 用反变量表示, 将这 些与项相加,就得到逻辑表达式。这样得到的 逻辑函数表达式是标准与-或逻辑式。
断开为0;灯为Y,灯亮为1,灭为0。
真值表
AB Y 00 0 01 1 10 1 11 1
由“或”运算的真值表可知
“或”运算法则为:
有1出
0+0 = 0 1+0 = 1
1
0+1 = 1 1+1 = 1
全0为
0
⒊ 表达式
逻辑代数中“或”逻辑关系用“或”运算 描述。“或”运算又称逻辑加,其运算符为 “+”或“ ”。两变量的“或”运算可表示
0
卡诺图是一 种用图形描 述逻辑函数
的方法。
00 0 01 0 11 0
10 1
例:函数 F=AB + AC
ABC F
000 0
1 001 1 010 0
1 011 1
1 100 1
0
101 1 110 0
1 111 0
1.逻辑函数式
特点:
例:函数 F=AB + AC
(1)便于运算; (2)便于用逻辑图实现; (3)缺乏直观。
真值表
K
Y
0
1
1
0
由“非”运算的真值表可知 “非”运算法则为:
0 =1 1 =0
⒊ 表达式
“非”逻辑用“非”运算描述。“非”运 算又称求反运算,运算符为“-”或“¬”, “非”运算可表示为:
(精选)《数字逻辑》PPT课件

=(5.25)10
各数位的权是2的幂
二进制数只有0和1两个数码,它的每一位都可以用电子元件 来实现,且运算规则简单,相应的运算电路也容易实现。
运算 规则
加法规则:0+0=0,0+1=1,1+0=1,1+1=10
乘法规则:0·0=0, 0·1=0 ,1·0=0,1·1=1
13
3、八进制
数码为:0~7;基数是8。
零,则每组二进制数便是一位八进制数。(三位聚一位) 0 0 1 1 0 1 0 1 0 . 0 1 0 = (152.2)8
(2)八进制数转换为二进制数:将每位八进制数用3位二进
制数表示。(一位变三位)
(374.26)8 = 011 111 100 . 010 110
17
2、二进制数与十六进制数的相互转换
运算规律:逢八进一,即:7+1=10。
八进制数的权展开式:
如:(207.04)10= 2×82 +0×81+7×80+0×8-1+4 ×8-2 =(135.0625)10
4、十六进制
各数位的权是8的幂
数码为:0~9、A~F;基数是16。 运算规律:逢十六进一,即:F+1=10。 十六进制数的权展开式: 如:(D8.A)2= 13×161 +8×160+10 ×16-1=(216.625)10
8
本节小结 数字信号的数值相对于时间的变 化过程是跳变的、间断性的。对数 字信号进行传输、处理的电子线路 称为数字电路。模拟信号通过模数 转换后变成数字信号,即可用数字 电路进行传输、处理。
9
1. 2 数制与编码
1.2.1 数制 1.2.2 不同数制间的转换 1.2.3 二进制代码
退出
10
1.2.1 数制
各数位的权是2的幂
二进制数只有0和1两个数码,它的每一位都可以用电子元件 来实现,且运算规则简单,相应的运算电路也容易实现。
运算 规则
加法规则:0+0=0,0+1=1,1+0=1,1+1=10
乘法规则:0·0=0, 0·1=0 ,1·0=0,1·1=1
13
3、八进制
数码为:0~7;基数是8。
零,则每组二进制数便是一位八进制数。(三位聚一位) 0 0 1 1 0 1 0 1 0 . 0 1 0 = (152.2)8
(2)八进制数转换为二进制数:将每位八进制数用3位二进
制数表示。(一位变三位)
(374.26)8 = 011 111 100 . 010 110
17
2、二进制数与十六进制数的相互转换
运算规律:逢八进一,即:7+1=10。
八进制数的权展开式:
如:(207.04)10= 2×82 +0×81+7×80+0×8-1+4 ×8-2 =(135.0625)10
4、十六进制
各数位的权是8的幂
数码为:0~9、A~F;基数是16。 运算规律:逢十六进一,即:F+1=10。 十六进制数的权展开式: 如:(D8.A)2= 13×161 +8×160+10 ×16-1=(216.625)10
8
本节小结 数字信号的数值相对于时间的变 化过程是跳变的、间断性的。对数 字信号进行传输、处理的电子线路 称为数字电路。模拟信号通过模数 转换后变成数字信号,即可用数字 电路进行传输、处理。
9
1. 2 数制与编码
1.2.1 数制 1.2.2 不同数制间的转换 1.2.3 二进制代码
退出
10
1.2.1 数制
《数字逻辑基础》课件

《数字逻Hale Waihona Puke 基础》课件CONTENTS
• 数字逻辑概述 • 数字逻辑基础概念 • 组合逻辑电路 • 时序逻辑电路 • 数字逻辑电路的实现
01
数字逻辑概述
数字逻辑的定义
01
数字逻辑是研究数字电路和数字 系统设计的理论基础,它涉及到 逻辑代数、逻辑门电路、组合逻 辑和时序逻辑等方面的知识。
02
数字逻辑是计算机科学和电子工 程学科的重要分支,为数字系统 的设计和分析提供了基本的理论 和方法。
详细描述
布尔代数是逻辑代数的一个分支,它研究的是逻辑变量和逻辑运算的规律。布尔代数包括基本的逻辑 运算,如与、或、非等,以及一些复合运算,如异或、同或等。布尔代数在数字电路设计中有广泛应 用。
逻辑函数的表示方法
总结词
逻辑函数是指一种特定的函数,它将输 入的逻辑值映射到输出的逻辑值。
VS
详细描述
逻辑函数是指一种特定的函数,它将输入 的逻辑值映射到输出的逻辑值。在数字电 路中,逻辑函数通常用真值表、逻辑表达 式、波形图等形式来表示。理解逻辑函数 的表示方法对于数字电路设计和分析非常 重要。
数字逻辑电路的测试与验证
测试目的
确保电路功能正确、性能稳定。
测试方法
采用仿真测试和实际测试两种方法。
验证手段
逻辑仿真、时序仿真和布局布线仿真等。
谢谢您的聆听
THANKS
逻辑门电路
总结词
逻辑门电路是实现逻辑运算的电路,它是数字电路的基本单 元。
详细描述
逻辑门电路是实现逻辑运算的电路,它是数字电路的基本单 元。常见的逻辑门电路有与门、或门、非门等。这些门电路 可以实现基本的逻辑运算,并能够组合起来实现更复杂的逻 辑功能。
• 数字逻辑概述 • 数字逻辑基础概念 • 组合逻辑电路 • 时序逻辑电路 • 数字逻辑电路的实现
01
数字逻辑概述
数字逻辑的定义
01
数字逻辑是研究数字电路和数字 系统设计的理论基础,它涉及到 逻辑代数、逻辑门电路、组合逻 辑和时序逻辑等方面的知识。
02
数字逻辑是计算机科学和电子工 程学科的重要分支,为数字系统 的设计和分析提供了基本的理论 和方法。
详细描述
布尔代数是逻辑代数的一个分支,它研究的是逻辑变量和逻辑运算的规律。布尔代数包括基本的逻辑 运算,如与、或、非等,以及一些复合运算,如异或、同或等。布尔代数在数字电路设计中有广泛应 用。
逻辑函数的表示方法
总结词
逻辑函数是指一种特定的函数,它将输 入的逻辑值映射到输出的逻辑值。
VS
详细描述
逻辑函数是指一种特定的函数,它将输入 的逻辑值映射到输出的逻辑值。在数字电 路中,逻辑函数通常用真值表、逻辑表达 式、波形图等形式来表示。理解逻辑函数 的表示方法对于数字电路设计和分析非常 重要。
数字逻辑电路的测试与验证
测试目的
确保电路功能正确、性能稳定。
测试方法
采用仿真测试和实际测试两种方法。
验证手段
逻辑仿真、时序仿真和布局布线仿真等。
谢谢您的聆听
THANKS
逻辑门电路
总结词
逻辑门电路是实现逻辑运算的电路,它是数字电路的基本单 元。
详细描述
逻辑门电路是实现逻辑运算的电路,它是数字电路的基本单 元。常见的逻辑门电路有与门、或门、非门等。这些门电路 可以实现基本的逻辑运算,并能够组合起来实现更复杂的逻 辑功能。
数字逻辑概论PPT课件

第二步:列出真值表
列出真值表
第三步:从真值表写出逻辑表达式(标准与或式) (最小项表达式)
取L为1时的A、B、 C与运算组合,然后进 行或运算。A为1时取A, A为0时取A,B、C类同。
L ABC ABC ABC ABC
AB AC BC
第四步:画出逻辑符号图
L AB AC BC 第五步:画出波形图
一、逻辑代数
•逻辑代数与普通代数: 与普通代数不同,逻辑代数中的变量只
有0和1两个可取值,它们分别用来表示完 全两个对立的逻辑状态。
二、自然界中三种基本逻辑关系
1、与逻辑关系:决定某一事物结果的所有
条件同时具备,结果才会发生。这一因果关系 称与逻辑关系
2、或逻辑关系:决定某一事物结果的诸条
例:已知某逻辑函数表达式为 L A B AB,试画出其逻辑图
A
1
&
B
1
≥1 L
A L
&
B
4. 波形图表示方法
用输入端在不同逻辑信号作用下所对应的输出信号的波形 图,表示电路的逻辑关系。
真值表
AB
A
L
1 00 1
00 01 10 11
1B
0
0L
1
11 0 0 010 1 t1 t2 t3 t4
件只要有一个条件具备,结果就会发生。这一 因果关系称或逻辑关系
3、非逻辑关系:决定某一事物结果的某一
条件具备,结果就不发生。这一因果关系称非 逻辑关系
1.与运算
只有当决定某一事件的条件全部具备时,这一事 件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例
电路状态表
S1
S2
列出真值表
第三步:从真值表写出逻辑表达式(标准与或式) (最小项表达式)
取L为1时的A、B、 C与运算组合,然后进 行或运算。A为1时取A, A为0时取A,B、C类同。
L ABC ABC ABC ABC
AB AC BC
第四步:画出逻辑符号图
L AB AC BC 第五步:画出波形图
一、逻辑代数
•逻辑代数与普通代数: 与普通代数不同,逻辑代数中的变量只
有0和1两个可取值,它们分别用来表示完 全两个对立的逻辑状态。
二、自然界中三种基本逻辑关系
1、与逻辑关系:决定某一事物结果的所有
条件同时具备,结果才会发生。这一因果关系 称与逻辑关系
2、或逻辑关系:决定某一事物结果的诸条
例:已知某逻辑函数表达式为 L A B AB,试画出其逻辑图
A
1
&
B
1
≥1 L
A L
&
B
4. 波形图表示方法
用输入端在不同逻辑信号作用下所对应的输出信号的波形 图,表示电路的逻辑关系。
真值表
AB
A
L
1 00 1
00 01 10 11
1B
0
0L
1
11 0 0 010 1 t1 t2 t3 t4
件只要有一个条件具备,结果就会发生。这一 因果关系称或逻辑关系
3、非逻辑关系:决定某一事物结果的某一
条件具备,结果就不发生。这一因果关系称非 逻辑关系
1.与运算
只有当决定某一事件的条件全部具备时,这一事 件才会发生。这种因果关系称为与逻辑关系。
与逻辑举例
电路状态表
S1
S2
计算机组成原理数字逻辑PPT课件

逻辑图、时序波形图、状态转换图等。
(1-9)
§ 1.2 逻辑代数的三种基本运算
• 逻辑代数首先是由英国数学家乔治·布尔 (George Boole)[1815~1864年]奠定的,因此 又称为布尔代数;布尔代数的二值性质应用于 两态元件组成的数字电路(开关电路)尤为适合, 自从布尔代数用于开关数字电路之后,又被称 为开关代数。所以逻辑代数、布尔代数、开关 代数都是指同一概念。
§ 1.1 数字电路的基础知识
– 数字量和ቤተ መጻሕፍቲ ባይዱ拟量
– 模拟量: 可以在一定范围内取任意实数值的物理量, 如:温度、压力、距离和时间等。 – 数字量: 在时间上和数量上都是离散的物理量, 如:自动生产线上的零件记录量,台阶的阶数
– 数字信号和模拟信号
– 模拟信号:表示模拟量的电信号,如:热电 偶的电压信号,温度变化时,电压随之改变
–模拟电路: 处理模拟信号的电路,如:运算放大器 在模拟电路中,晶体管一般工作在放大 状态。
(1-5)
数字信号: 数字信号 产品数量的统计。 数字表盘的读数。 数字电路信号: u
t
(1-6)
模拟电路与数字电路的区别
1. 工作任务不同:
模拟电路研究的是输出与输入信号之间的大小、 相位、失真等方面的关系;数字电路主要研究的 是输出与输入间的逻辑关系(因果关系)。
(1-41)
• 3)最小项编号
其下为标了i为表最达小方项便的,编人号们。通编常号用的m方i表法示是最:小最项小,项 中的原变量取1,反变量取0,则最小项取值为一 组二进制数,其对应的十进制数便为该最小项的 编号。如三变量最小项 ABC对应的变量取值为100, 它对应的十进制数为4,因此,最小项ABC 的编号 为m4。其余最小项的编号以此类推。 • 值得注意的是,在规定n变量最小项的编号时,对 变其量中的隐排含列了顺A是序最是高重位要,的而。C例是如最,低把位A这BC一记排作列m顺4。 序。三变量全体最小项的编号如表1.10所列。
(1-9)
§ 1.2 逻辑代数的三种基本运算
• 逻辑代数首先是由英国数学家乔治·布尔 (George Boole)[1815~1864年]奠定的,因此 又称为布尔代数;布尔代数的二值性质应用于 两态元件组成的数字电路(开关电路)尤为适合, 自从布尔代数用于开关数字电路之后,又被称 为开关代数。所以逻辑代数、布尔代数、开关 代数都是指同一概念。
§ 1.1 数字电路的基础知识
– 数字量和ቤተ መጻሕፍቲ ባይዱ拟量
– 模拟量: 可以在一定范围内取任意实数值的物理量, 如:温度、压力、距离和时间等。 – 数字量: 在时间上和数量上都是离散的物理量, 如:自动生产线上的零件记录量,台阶的阶数
– 数字信号和模拟信号
– 模拟信号:表示模拟量的电信号,如:热电 偶的电压信号,温度变化时,电压随之改变
–模拟电路: 处理模拟信号的电路,如:运算放大器 在模拟电路中,晶体管一般工作在放大 状态。
(1-5)
数字信号: 数字信号 产品数量的统计。 数字表盘的读数。 数字电路信号: u
t
(1-6)
模拟电路与数字电路的区别
1. 工作任务不同:
模拟电路研究的是输出与输入信号之间的大小、 相位、失真等方面的关系;数字电路主要研究的 是输出与输入间的逻辑关系(因果关系)。
(1-41)
• 3)最小项编号
其下为标了i为表最达小方项便的,编人号们。通编常号用的m方i表法示是最:小最项小,项 中的原变量取1,反变量取0,则最小项取值为一 组二进制数,其对应的十进制数便为该最小项的 编号。如三变量最小项 ABC对应的变量取值为100, 它对应的十进制数为4,因此,最小项ABC 的编号 为m4。其余最小项的编号以此类推。 • 值得注意的是,在规定n变量最小项的编号时,对 变其量中的隐排含列了顺A是序最是高重位要,的而。C例是如最,低把位A这BC一记排作列m顺4。 序。三变量全体最小项的编号如表1.10所列。
《数字逻辑详解》课件
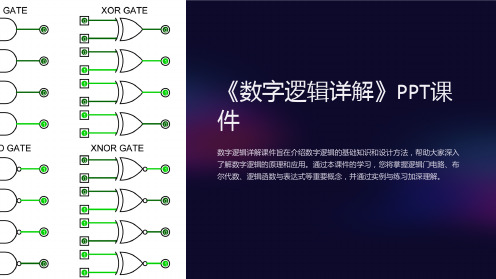
了解布尔函数的定义和特性,学习如何将逻辑表达式转化为真值表。
3
简化布尔表达式
掌握使用布尔代数进行逻辑表达式简化的方法和技巧。
逻辑函数与逻辑表达式
逻辑函数
介绍逻辑函数的概念和表示 方法,学习如何将逻辑函数 转化为逻辑表达式。
逻辑表达式
了解逻辑表达式的结构和常 见的逻辑运算符,学习如何 构建和简化逻辑表达式。
逻辑门
介绍常用逻辑门的基本原理和电路符号,展示它们 在数字电路中的应用。
数字电路
了解数字电路的组成和工作原理,包括组合逻辑电 路和时序逻辑电路。
进制编码
介绍常见的进制编码方式,如BCD码和格雷码,并 学习它们的转换方法。
布尔代数
1
布尔运算
学习布尔代数的基本运算,包括与、或、非等逻辑运算。
2
布尔函数
多输出函数
学习如何处理多输出函数, 掌握多输出函数的最小化方 法。
数字逻辑设计方法
1
时序逻辑设计
2
了解时序逻辑电路的设计原理和方法,
学习如何使用触发器构建时序逻辑功能。
3
组合逻辑设计
介绍组合逻辑电路的设计流程和方法, 学习如何使用逻辑门设计逻辑功能。
状态机设计
学习状态机的基本概念和设计流程,掌 握状态转换图和状态表的建立方法。
结语与总结
数字逻辑详解课件对数字逻辑的基础概念、逻辑门电路、布尔代数等进行了全面的介绍和讲解。希望通过本课 件的学习,能够帮助大家更好地理解和应用数字逻辑,为日后的学习和工作打下坚实的基础。
实例与练习
数字电路实例
通过实际电路示例,展示数字逻辑在计算机和电子 设备中的应用。
逻辑表达式练习
提供一些逻辑表达式练习题,帮助学生巩固所学知 识和提升运算能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
UDD 1
2 3
UDD
uC
+
∞ A
UA
-
≥1
1
1
uO
2 3
UDD
Q ≥1
uO
UDD 0
+
∞ B
UB
-
≥1 Q
T1
T2
V
( a)
( b)
图10.4.2 自由多谐电路
0 t
t
数字逻辑
逻辑器件
10.4.2 工作原理
自由多谐振荡器不具有稳态,只具有两个 暂稳态,暂稳态的时间长短由电路的定时元件 确定,电路工作就在两个暂稳态之间来回转换, 具体工作过程如下:
uC
1 C
t 0
iCdt
I0 t C
I0为恒定电流。其工作波形如图7.3.3(b)所示。实 际中为了防止负载对定时电路影响,uC输出常常通 过射极输出器输出。
逻辑器件
数字逻辑
外接电阻R的范围为2kΩ~20MΩ, 定时电容C为100pF~1000μF,因此其 单稳态电路的延迟时间TW可由几微秒到 几小时。精度可达0.1%。当然还可以增 大R、C值使延时增大,但将导致精度变
逻辑器件
数字逻辑
C
K
+
K
①
②
R U 0
(a)
R C<<K T
R +
C U 0
-
RC<< TK
(b)
RC>>T K
图10.1.1 RC暂态电路波形
逻辑器件
数字逻辑
惰性电路产生的暂态过程,对一 阶问题而言,可用三要素法来描述,获 得电压或电流随时间变化的方程,该方 程是脉冲波形计算的重要依据。三要素 或即起始值X(0+)、趋向值X(∞)和时间常数 τ,若三要素已知,则得方程
放电管V导通,定时电容C两端电压uC=0。工
作期:外界触发信号uI加进来,要求为负脉冲 且平低,U电A平为应低电平,使uO比13 为U 较D高D 器电输平出,U且B为放高电电管
截止,电源UDD通过定时电阻R对定时电容充
电,这是一个暂态问题,只要写出三要素即可。
uC (0 ) 0
uC
(
)
U
பைடு நூலகம்
DD
RC
数字逻辑
逻辑器件
10.3.1 电路组成
图10.3.1(a)是用CC7555构成的单 稳态电路,图10.3.1(b)是其工作波形。 图中R、C为外接定时元件,输入触发信 号uI加至低触发 T R 端,由OUT端给出 输出信号,控制端CO不用时一般均通 过0.01μF接地,以防干扰。
逻辑器件
数字逻辑
(5 )
R
(2 )
+∞ -B
UB
≥1
TR
≥1
1
OU T
1
( 3)
USS 1
8 UDD
TR 2
7D
OUT 3
6 TH
R 4
CO 5
( b)
R
D V
(7 )
(1 )
USS
( a)
图10.2.1 CC7555集成定时电路
数字逻辑
逻辑器件
1.分压器
由3个5kΩ电阻组成,它为两个比
较器提供基准电平。如5脚悬空,则比较
U
DD
R C ln 3
1 .1R C
逻辑器件
数字逻辑
显然改变定时元件R或C即可改变延 迟时间TW;通过改变比较器的参考电压也 可改变TW。一般是在5脚CO端外接电源或 电阻即可改变比较器A、B的参考电压。
为了使电路能正常工作,要求外加触 发脉冲的宽度τCP小于TW。且负脉冲的数 值号u一I和定触要发低电于路之13 间U D加D 一。微为分此电常路在,输如入图信
uO=0,放电管导通,电容通过放电管很快放电,
进入恢复期。由于外界触发脉冲加进来,电路
uO由低电平变为高电平到再次变为低电平这段
时间就是暂稳态时间,其暂稳态时间TW计算
如下:
逻辑器件
数字逻辑
TW
RC
ln uC ( ) uC (0 ) uC ( ) uC (TW )
RC
ln
U
U
DD
DD
0
2 3
USS-0.5V≤UI≤UDD+0.5V
555定时电路除了CMOS型之外,还有 TTL型如5G555(NE555),它的工作原理与 CC7555没有本质区别,但其驱动电流可达 200mA。
数字逻辑
逻辑器件
10.3 单稳态电路
单稳态触发器只有一个稳定状态和 一个暂稳态,在外界触发脉冲的作用下, 电路从稳态翻转到暂态,然后在暂稳态停 留一段时间TW后又自动返回到稳态,并 在输出端产生一个宽度为TW的矩形脉冲。 TW只与电路本身的参数有关,而与触发 脉冲无关。通常把TW称为脉冲宽度。
uC (0 ) 0
uC
(
)
U
DD
( R 1 R 2 ) C
逻辑器件
数字逻辑
放电管V导通时,电容C通过电阻 R2和放电管放电,电路进入第二暂稳态 期,放电过程为
放
u u
C C
(0 ) ( )
2 3 0
U
DD
R 2C
逻辑器件
数字逻辑
由于比较器A、B的存在,电容器不可能
放电至0。当电容放电时,UA=UB=0,RS触发
UDD
uI
R
1
+ -
∞ A
UA
≥1
1
Q ≥1
1
uo
1 3
UDD
2 3
UDD
UDD
0.01μF
uI
1 3
UDD
C
+ -
∞ A
UB
≥1 Q
V
( a)
uC TW
uO
( b)
图10.3.1 CC7555构成的单稳态触发器
数字逻辑
逻辑器件
10.3.2 工作原理
静止期:触发信号uI处于高电平,电路
处于稳态,根据555工作原理知道uO为低电平,
数字逻辑
逻辑器件
图10.1.1(b)组成积分电路,当 RC<<TK时,在电容上可得矩形波;而 RC>>TK时,在电容上又可得线性扫描的 波形。由上可看出脉冲形成电路的组成应 有两大部分,惰性电路和开关。开关是用 来破坏稳态,使惰性电路产生暂态的。开 关可用不同的电子器件来完成,如可用运 算放大器,可用分立器件晶体三极管或场 效应管,也可以用逻辑门。目前用得较多 的是555定时电路。
10.3.2所示。
逻辑器件
Rp uI
Cp
数字逻辑
UD D
R
84
7
6
uO
3
2
C
15
0.01 μF
图10.3.2 具有微分环节的单稳态电路
数字逻辑
逻辑器件
恢复期:当放电管V导通时,定时电容C 通过放电管迅速放电,即进入恢复期,恢复到 静止期状态。恢复期TR由下式决定
TR=(3~5)rd·C 其中rd为放电管导通时呈现的电阻,一般 R>>rd,所以恢复期很短。 利用单稳态触发器我们也可以获得线性锯 齿波。由上述工作原理和输出波形可看出,在 电容C两端可得到按指数规律上升的电压,为 获得线性锯齿波,只要对电容C恒流充电即可。 故用恒流源代替R即可组成线性锯齿波电路。
逻辑器件
UDD u1
84
Re
Rb2
7
uI
2
V
6
3 uo
uC
uC
Rb1
C 15
0.01μF
uO
(a )
数字逻辑
(b )
图10.3.3 线性锯齿波电路
逻辑器件
数字逻辑
图10.3.3为线性锯齿波电路,其中晶体三
极管V及电阻Re、Rb1、Rb2组成恒流源,给
定时电容提供恒定的充电电流。电容两端电压
随时间线性增长
低。单稳态电路的主要应用是定时、延 时(对输入uI的下降沿而言)和波形变换。
逻辑器件
数字逻辑
10.4 多谐振荡器
多谐振荡器是一种无稳态电路,它在 接通电源后,不需要外加触发信号,电路 状态能够自动地不断变换,产生矩形波的 输出。由于矩形波中的谐波分量很多,因 此又常称为多谐振荡器。
在数字电路中,为了定量地描述多谐 振荡器所产生的矩形脉冲波形的特性,经 常使用如图10.4.1所示的几个指标,即
数字逻辑
逻辑器件
10.4.1 电路组成
图10.4.2(a)给出用CC7555构成的 多谐振荡器。由图可见,除将高电平触 发端TH和低电平触发端 T R 短接外,在 放电回路中还串接一个电阻R2。电路中 R1、R2、C均是定时元件。图10.4.2(b) 为工作波形。
逻辑器件
数字逻辑
R1 R2
uC C
数字逻辑
上升时间tr:脉冲前沿从0.1Um上 升到0.9Um所需的时间。
下降时间tf:脉冲后沿从0.9Um下降 到0.1Um所需的时间。
利用上述指标,就可以把一个矩形 脉冲的基本特性大体上表示清楚了。
逻辑器件
tr 0.9Um 0.5Um
数字逻辑
tf Um
0.1Um
TW T
图10.4.1 描述矩形脉冲特性的指 标
t
X(t) X()[X(0)X()]e
t ln X()X(0)
X()X(t)
逻辑器件
数字逻辑
10.2 555定时电路
555定时电路是目前应用十分广泛
的一种器件,本章仅介绍它在脉冲形成方 面的基本电路。555定时电路有TTL集成 定时电路和CMOS集成定时电路,功能完 全一样,不同之处是前者驱动能力大于后 者,我们以CMOS集成定时器CC7555为 例进行介绍。
