数字逻辑第二章
数字逻辑课件——门电路概述

其中,i为流过二极管的电流;u为加到二极
管两端的电压;UT
kT q
k为玻耳兹曼常数,T为热力学温度,q为电子电荷, 在常温下(即结温为27℃,T = 300K),VT ≈26mV; IS为反相饱和电流。
它和二极管的材料、工艺和尺寸有关,但对每只二 极管而言,它是一个定值。
9
i
二极管的特性也可用图 2-1-4的伏安特性曲线描 述。
5
2.1.2 半导体器件的开关特性
▪ 1. 半导体二极管的开关特性
因为半导体二极管具有单向导
电性,即外加正电压时导通,
+VCC
外加反电压时截止,所以它相
当于一个受外加电压极性控制
D
R
的开关,
uI
uO
S
如果用它取代图2-1-1中的S, 图2-1-3 二极管开关电路 就得到了图2-1-3所示的二极
管开关电路。
•以图2-1-10为例,设图中MOS管为
N沟道增强型,它的开启电压为UTN , 则当uI = uGS < UTN时,MOS管工作
在截止区,D-S之间没有形成导电 沟道,沟道间电阻为109~1010Ω, 呈高阻状态,因此D-S间的状态就
像开关断开一样。
图2-1-10 MOS管的 开关电路
20
当uI = uGS > UTN时,且uGD > UTN,则
当uI ≤ 0时,uBE ≤ 0,三极管工
作在截止区,其工作特点是基极电
流iB ≈ 0,集电极电流iC = ICE
≈ 0,因此三极管的集-射极之间 相当于一个断开的开关。
输出电压为uo = UOH ≈ VCC 。
图2-1-7 双极型三 极管开关电路
16
数字逻辑与计算机组成原理:第二章 数据的表示与运算

第二章 数据的表示与运算
第一节 数的表示
一、无符号数和有符号数
1、无符号数:
没有符号的数,寄存器中的每一位都可用 来存放数据
机器字长为n位,无符号数的表示范围 为0~2n-1
反映无符号数的表示范围
8位 16 位
0 ~ 255 0 ~ 65535
有两种常用的无符号表示法: ◆ 非负数码:表示0或一个正数
(1) 定义
整数
0,x
2n > x ≥ 0
[x]反 = ( 2n+1 – 1) + x 0 ≥ x > 2n(mod 2n+1 1)
x 为真值
n 为整数的位数
如 x = +1101
x = 1101
[x]反 = 0,1101
[x]反 = (24+1 1) 1101 = 11111 1101
用 逗号 将符号位
= 1,0010
和数值部分隔开
小数 x
[x]反 = ( 2 – 2-n) + x
1>x≥ 0 0 ≥ x > 1(mod 2 2-n)
x 为真值 n 为小数的位数
如 x = + 0.1101
x = 0.1010
[x]反 = 0.1101
[x]反 = (2 2-4) 0.1010
= 1.1111 0.1010
有符号小数: +0.1011,在机器中表示为
-0.1011,在机器中表示为
第一节 数的表示
一、无符号数和有符号数 2、有符号数
有符号整数: +1101,机器中表示为
-1101, 机器中表示为
第一节 数的表示
一、无符号数和有符号数
数字逻辑第二章课后答案

2-1
2-2
均可以作为反相器使用。
与非门:
或非门:
异或门:
2-3 1
Y V
CMOS 与非门的一个输入端通过电阻接地,相当于该输入端输入低电平,输出Y1是高电平。
2Y V
CMOS 或非门的一个输入端通过电阻接高电平与直接接高电平是一样的,输出Y2是低电平。
V 3
Y V 低电平有效的三态门的使能端EN 接高电平,则Y3为高阻态。
4
Y V
与或非门的一个与门输入全为高电平,则输出Y4是低电平。
2-4
E D C B A Y ⋅⋅⋅⋅=1 E D C B A Y ++++=2
))((3F E D C B A Y ++++=
F E D C B A Y ⋅⋅+⋅⋅=4 2-5
当1=EN ,T1`和T2截止,Y=Z (高阻)。
当0=EN ,T1`导通,A A Y ==。
2-7
(1)忽略所有门电路的传输延迟时间,除去开始的一小段时间,与非门的两个输入端总有一个是低电平,输出一直为高电平。
(2)考虑每个门都有传输延迟时间。
假设1级门的传输延迟时间为tpd ,则与非门的两个输入端的输入信号变化实际上并不是同时的。
信号A 经过两级门的传输延迟,比信号B 要晚2tpd 时间到达与非门的输入端。
因此,将出现,在短暂时间里,两个输入端的输入信号都是高电平的情况,输出电压波形出现毛刺。
大学计算机原理--数字逻辑课件--第二章组合逻辑剖析

A B C
F
A B C
F ABBC C A
方法二:对F两次求反
F ABBC C A
ABBC C A
ABBC C A
( A B C )(A B C) ——F的“或-与”表达 式
逻辑函数的“与非”门实
现A
1 11
F=ABCD+ABCD
1 1 1 1D
C 11
1
11 11
F=ABCD+ABCD =ABCD•ABCD
B
ABCD
F
ABCD
例:采用或非门实现F A B BC C A
方法一:对F两次求对偶
F (A B )(B C )(C A ) ABC ABC
F ABC ABC
A B C F C’
A
A
0 0 0 0 00
0 2 1 6 41
0
21 6
4
1 0 0 1 1 1 C 11 3 71 5 C 11 3 1 71 5
2 0 1 0 11
B
B
3 0 1 1 01
F
C’
4 1 0 0 10
5 1 0 1 00
F=ABC+ABC+ABC+ABC
6 1 1 0 00 7 1 1 1 11
每个学生总计要获得10个以上学分才能通过本学期 考试。要求写出反映学生是否通过本学期考试的逻 辑函数。
设 A、B、C、D 分别为四门课,“1” 表示通过此门
课通过,“0” 表示不通过;F 为“1”时表示本学期
考试通过,“0”为没通过。
A
F=AB+AC+BCD
0 1 3
C2
数字逻辑第2章-逻辑代数

例如:
Y AB CDE
Y A B C D E
Y AB C
Y ( A B )(C D E)
(B A) B
证明:由于(A B ) (A B) (A B A) B
A (B B)
A 1
1
而且(A B ) (A B) A B A A B B
00
0 所以,根据公理 5的唯一性可得到:
A B A B
A A
定理6:反演律
A B A B
A B A B
定理7:还原律
A B A B A ( A B ) ( A B ) A
定理8:冗余律
AB A C BC AB A C
( A B)(A C)(B C) ( A B)(A C)
A B B A 交换律: A B B A
公理2
( A B) C A ( B C ) 结合律: ( A B) C A ( B C )
公理3
公理4
A (B C) A B A C 分配律: A B C ( A B) ( A C )*
判断两个逻辑函数是否相等,通常有两种方法。
①列出输入变量所有可能的取值组合,并按逻 辑运算法则计算出各种输入取值下两个逻辑 函数的相应值,然后进行比较。
②用逻辑代数的公理、定律和规则进行证明。
2.2 逻辑代数的基本定理和重要规则
数字逻辑课后答案第二章
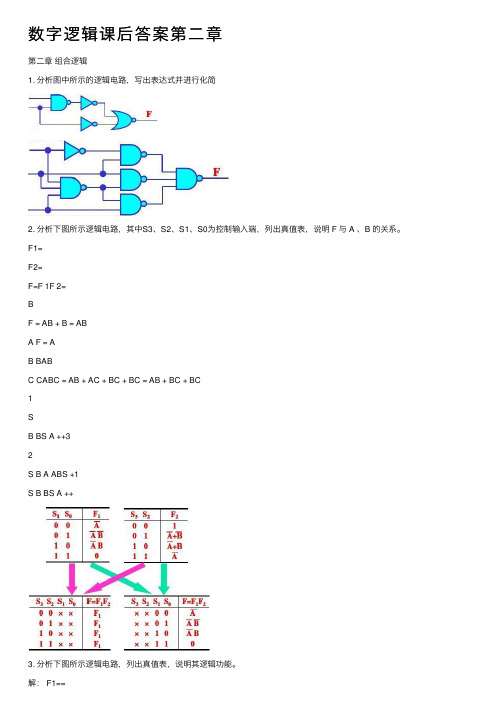
数字逻辑课后答案第⼆章第⼆章组合逻辑1. 分析图中所⽰的逻辑电路,写出表达式并进⾏化简2. 分析下图所⽰逻辑电路,其中S3、S2、S1、S0为控制输⼊端,列出真值表,说明 F 与 A 、B 的关系。
F1=F2=F=F 1F 2=BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC1SB BS A ++32S B A ABS +1S B BS A ++3. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能。
解: F1==真值表如下:当B ≠C 时, F1=A 当B=C=1时, F1=A 当B=C=0时, F1=0裁判判决电路,A 为主裁判,在A 同意的前提下,只要有⼀位副裁判(B ,C )同意,成绩就有效。
F2=真值表如下:CB BC A C AB C B A +++ABCC B A ABC C B A C B A +⊕=++)(A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111AC BC AB C A C B B A ++=++当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2 = 1 。
4.图所⽰为数据总线上的⼀种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=只有当变量A0~A15全为0时,F = 1;否则,F = 0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所⽰逻辑电路,列出真值表,说明其逻辑功能解:因此,这是⼀个四选⼀的选择器。
6. 下图所⽰为两种⼗进制数代码转换器,输⼊为余三码,输出为什么代码?解:A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1000011111514131211109876543210A A A A A A A A A A A A A A A A +++301201101001X A A X A A X A A X A A F +++=这是⼀个余三码⾄8421 BCD 码转换的电路7. 下图是⼀个受 M 控制的4位⼆进制码和格雷码的相互转换电路。
数字逻辑

第二章逻辑代数基础逻辑代数是描述、设计数字系统的重要工具,是由逻辑学发展而来的。
逻辑学是研究逻辑思维和推理规律的一门学科。
19世纪中布尔(Boole)创立了布尔代数,即用代数形式来描述、研究逻辑学问题。
二十世纪初香农(Shannon)把布尔代数应用于继电器构成的开关电路,称为开关代数。
目前逻辑门是数字系统的基础,因此把开关代数又称为逻辑代数。
2.1 逻辑代数的基本概念2.1.1 逻辑变量与逻辑函数逻辑代数有两个逻辑常量:逻辑0和逻辑1。
不同于普通代数中的0和1,逻辑0和逻辑1不具有数量的概念,而是两个对立的状态。
数字系统中可用电平值或元件状态表示逻辑0和逻辑1。
逻辑变量是一个符号,它可以取值逻辑0或逻辑1。
逻辑代数中,若某逻辑变量F 的取值唯一地由一组变量A 1, A 2, …, A n 的取值确定,则称这样的逻辑关系为逻辑函数关系,可表示为:F = f ( A 1, A 2, …, A n )其中,称逻辑变量F 为逻辑因变量或输出变量,多用于描述数字系统的输出状态;变量组A 1, A 2, …, A n 称为逻辑自变量或输入变量,常用于描述数字系统的输入状态。
与普通代数中的函数不同,逻辑函数中的变量仅能取离散值逻辑0、逻辑1,逻辑函数中的运算可分解为与、或、非这三种逻辑运算。
逻辑函数相同的概念为,若有逻辑函数F 1= f 1( A 1, A 2, …, A n )F 2= f 2( A 1, A 2, …, A n )且对于A 1, A 2, …, A n 的所有取值组,F 1 、F 2的取值都相同,则认为逻辑函数F 1 、F 2相同。
2.1.2 逻辑运算逻辑代数中有“与”、“或”、“非”三种逻辑运算。
1. “与”运算若决定某事件发生的多个条件同时满足时,该事件才能发生,称这样的逻辑关系为“与”逻辑。
逻辑代数中用“与”运算描述“与”逻辑,其运算符为“·”或“∧”。
“与”运算式可表示为:F = A ·B或F = A∧B“与”运算也称为逻辑乘。
数字逻辑 第2章课件

For outputs: logic 1 is light on logic 0 is light off. NOT uses a switch such that: logic 1 is switch open logic 0 is switch closed
Switches in series => AND
Normally-closed switch => NOT
2013-5-13
11
Boolean Algebra
An algebraic structure, L={K, +, •, -, 0, 1} defined on a set of logical variables, constant 0 and 1, and three binary operators (denoted +, ·and ) that satisfies the following axioms:
2013-5-13
7
Logic Gate Symbols and Behavior
Logic gates have special symbols:
Waveform behavior in time
2013-5-13
8
Gate Delay
In actual physical gates, if one or more input changes causes the output to change, the output change does not occur instantaneously. The delay between an input change(s) and the resulting output change is the gate delay denoted by tG:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用对偶规则可以简化等式的证明。
例:试证 A+BC=(A+B)(A+C) 令: F1=A+BC F2=(A+B)(A+C)
求两个函数的对偶:
F1`=A(B+C)=AB+AC F2`=AB+AC
可知:F1`= F2`
所以F1=F2 得证
28
四、展开规则
一个多变量函数F=f(X1,X2,· · · Xn),可以将其中 任意一个变量,例如X1分离出来,并展开成:
9
F
定义:一个事件的成立与否有许多条件,只要 其中一个或几个条件成立,事件便成立,这样 的逻辑关系被称逻辑加(或)。 即:F=f(A,B)=A∨B=A+B
实现逻辑加的电路称或门。
或门的逻辑符号为: A B + F A B ≥1 F A B 美国符号 10 F
曾用符号
国标符号
3、非运算 若定义开关闭合为1,E 断开为0。灯亮为1, 灯灭为0。 真值表 A F 0 1 1 0
反演规则是摩根律的推广。摩根律与反演互证 例3: F AB B( A C ) 按反演规则可直接写出:
F ( A B)( B AC )
25
若用摩根律则先对原函数两边取非,得:
F AB B( A C )
AB B( A C )
( A B)(B A C )
+
F
F=AB+CD
&
A B C D
&
≥1
F
A B C D
F
32
F A B AB AB 同或 F A B AB A B
异或
异或门的逻辑符号:
A B
F
A B
A
=1
F
B 美国符号
F
曾用符号
国标符号
同或门的逻辑符号:
A B F A B
=1
F
A B
F
曾用符号
国标符号
美国符号
A A
A A
使用反演规则时,应注意保持原函数式中的运算 符号的优先顺序不变。另外不属于单个变量上的 反号应保持不变。 24
例1: F A B(C DE )
例2:F AB C
F A[ B C ( D E )]
F AB C (直接去掉反号)
F ( A B) C A B C AB C
13
二、逻辑函数的相等
设有F1=f1(A1A2……An)、F2=f2(A1A2……An)如 果对应A1A2……An的任一组取值,F1和F2的值都 相等,则称F1和F2相等。计为F1=F2 。 判断两个逻辑表达式是否相等的方法有: 1、列表法(真值表) 2、利用逻辑代数的公理、定理和规则证明。
14
2.1.3 逻辑函数的表示方法
A+(B+C)=(A+B)+C=(A+C)+B 五、分配律
A(B+C)=AB+AC
A+BC=(A+B)· (A+C) 加法的分配律 证:右式=AA+AC+AB+BC=A+AC+AB+BC =A(1+C+B)+BC=A+BC=左式
18
六、摩根律
AB A B
A B A B
证:用真值表法证明 AB A B
R
A F
功能表 A F
断 亮 闭 灭
11
定义:一个事件的成立取决于条件的否定,即 事件与事件的成立条件之间构成矛盾,这样的 逻辑关系称逻辑反(非)。 函数式为:F=A 。
完成逻辑反运算的电路称非门。
非门的逻辑符号为: A F=A
A
1
F=A
A 美国符号
F=A
曾用符号
国标符号
12
2.1.2逻辑函数及逻辑函数间的相等
1 A=A A A=0 A A=1
0 A=A A A=1 A A=0
35
(3) 交换律 A B=B A (4) 结合律 A B=B A
A (B C)=(A B) C A (B C)=(A B) C (5) 分配律
A(B C)=AB AC 证: 右式=ABAC+ABAC=AB(A+C)+AC(A+B) 36 =ABC+ABC=A(B C)=左式
F f ( X 1 , X 2 , X n )
X 1 f (0, X 2 X n ) X 1 f (1, X 2 X n ) [ X 1 f (0, X 2 X n )][ X 1 f (1, X 2 X n )
上述算式之正确性的验证只要令X1=0或1分别代 入便知。 用以化简某个变量出现次数较多的情况 29
一、真值表 主要用于直观的观察变量和函数之间的关系 * 二、逻辑函数表达式 主要用于获得逻辑电路图 * 三、卡诺图 主要用于逻辑函数化简 四、时序图、时间图 主要用于工作波形图 *
15
2.2 逻辑代数的基本定理和规律
2.2.1 逻辑代数的基本定理
一、公理
00 0 0 1 0 1 0 0 1 1 1 0 1
3
反码与补码运算小结
1 符号位必须对齐
2 简单判断结果是否溢出,适当调整 符号位置 例1: -100 + (-10)
例2: -0.010 - 0.110
4
第二章
逻辑代数基础
2.1 逻辑代数的基本概念
2.2 逻辑代数的基本定理和规律 2.3 逻辑函数表达式的形式与变换 2.4 逻辑函数的化简
5
2.1.1 三种基本运算
二、逻辑代数的三个基本运算
1、与运算 若定义开关闭合为1,断开 为0。灯亮为1,灯灭为0。 E
A
B F
真值表 A B F
0 0 1 1 0 1 0 1 0 0 0 1
A 断 断 闭 闭
功能表 B F 断 灭 闭 灭 断 灭 闭 亮7
定义:某个事件受若干个条件影响,若所有的 条件都齐备,该事件才能成立,这样的逻辑关 系被称为逻辑乘(与)。
即 F=f(A,B)=A∧B=A· B=AB
实现逻辑乘的逻辑电路称为与门。
与门的逻辑符号为: A B
F
A B
& 国标符号
F
A B 美国符号
8
F
曾用符号
2、或运算
若定义开关闭合为1,断 开为0。灯亮为1,灯灭 为0。 真值表 A 0 0 1 1 B 0 1 0 1 F 0 1 1 1 E
A
B 功能表 A B F 断 断 闭 闭 断 闭 断 闭 灭 亮 亮 亮
22
以此推广得到摩根律的一般形式:
ABCD A B C D
A B C D A B C D
23
二、反演规则
即由 F ( A, B, C ) 求反函数 F ( A, B, C ) 0 1 1 0 + +
( A B) ( A B) A
冗余律 添加律
AB AB A
AB AC BC AB AC ( A B) ( A C ) ( B C ) ( A B) ( A C )
在两个乘积项中,若有一个变量是互反的,那 么由这两个乘积项中的其它变量组成的新的乘 积项就是多余的,可以消去。 20
33
异或和同或的真值表如下:
A B 0 0 1 1 0 1 0 1 A B A B 0 1 1 0 1 0 0 1
结论:偶数个变量的异或和同或是互反的,奇 数个变量的异或和同或是相同的。
34
异或和同或的基本运算公式
(1) 1 0=0 1=1 0 0=0 1 1=0 (2) 0 A=A 0 1=1 0=0 1 1=1 0 0=1 1 A=A
有数据溢出错误 6位二进制(63 ~ -63)
2
习题7: 分别用二进制反码补码完成运算-54-30
N1 = - 54 , N1 = - 0110110 N2 = - 30 , N2 = - 0011110 反码 11001001 + 11100001 110101010 1 10101011 补码 11001010 + 11100010 10101100
第一章 知识点回顾
1
2 3
计数进位制 与 数制转换(2,8,16,10)
带符号数的代码表示 原码、反码、补码的运算
4
BCD码:二进制码编写的十进制码 (8421, 2421,余三码等) 格雷码、奇偶校验码
1
习题7: 分别用二进制反码补码完成运算-54-30
N1 = - 54 , N1 = - 110110 N2 = - 30 , N2 = - 11110 反码 1001001 + 1100001 10101010 1 0101011 补码 1001010 + 1100010 0101100
A B A B A B A B A B
0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0
19
七、其他常用公式
吸收律: A AB A 消去律:A AB A B 其它:
A ( A B) A A ( A B) A B
证明: 左式 AB AC [ BCD E (G H )] BC
AB AC BC [1 D E (G H )]
AB AC BC
AB AC = 右式
21
2.2.2 重要规则
一、代入规则 任何一个含有变量A的逻辑等式,如果将所有出 现A的位置都代之以同一个逻辑函数F,则等式仍 然成立。 例:对摩根律 AB A B 令 B BC 代入式中 则:A( BC ) A BC A B C
