同底数幂的除法1
8.3同底数幂的除法(1)

则mn=
学生回答
由学生自己先做(或互相讨论),然后回答,若有答不全的,教师(或其他学生)补充.
学生板演
作业
第62页第1(1)(2)(3)(4)(5)、4题
板书设计
复习例1板演
………………
………………
……例2……
………………
………………
教学后记
n个
(m-n)个n个
( a﹒a﹒﹒﹒﹒a) (a﹒a﹒﹒﹒﹒a)
=
a﹒a﹒﹒﹒﹒a
n个
= am-n
所以am÷an= am-n(a≠0 , m、n是正整数,且m>n)
学生口述:同底数幂相除,底数不变,指数相减。
3.例题解析P58
例1:题略
说明:(1)直接运用法则。
(2)负数的奇次幂仍是负数。
(3)与其它法则的综合。
(4)可把除式中t2的2改为m-1呢?
4.练一练P58
(1)学生板演,教师讲评。
(2)学生口答,说明原因。
(3)解答本节开始时提出的问题。
用计算器计算科学计数法表示。
7.9×103×3600 2.844×107
1.0×103×1000 1.0×106
= 2.844×10或28.44(倍)
小结:本课讲了同底数幂相除的除法法则,要求同学们一定明确法则的由来,然后再利用此法则进行有关运算。
教学素材:
A组题:
(1)(a3.a2)3÷(-a22·x2=
(3)若xm= 2 , xn= 5 ,
则xm+n= , xm-n=
(4)已知A·x2n+1= x3nx≠0
那么A=
(5)(ab)12÷[(ab)4÷(ab)3]2=
人教版同底数幂的除法1

2m-3n
m
n
的值??
综合练习2:
1、若4 8
m
m 1
2 的值为512,
m
则m的值为? 2、计算: (1)( a b) (a b)
7 4 2n
(2)a (a )
2
2 n 1
a (a)
测验:
8 2
(1) x x
5
(2) (a) (a)
2、a
2 m 1
2m n
a
m n 1 14 8 3
3、a
6.
5 n 1 m
(a )
2m
2 n 1
4、 ( x) ( x) ( x)
n 2m-3n
5、 5 125 25
若3
m
=8 , 3 =2 , 求 3
的值.
3 0 7、若 ( x ) 1, 求x的取值范围 . 2
P107、1、
加油!
• 探究:
(1)3 3
2 2
加油!
(2)10 10
3 3
10 10
(3)a a (a 0)
问题再探索
在 中,
当m n时你能得到什么?
规定:任何不等于0的数的0次幂
都等于1。
0 a
1(a 0)
思考???
(1)
(3.14π)
计算:
(1) (3)
x x
8
2
(2)
(a) (a )
5 2 (ab) (ab)
2 9 2 4 (a b) (a b)
(4) y n2 y3 (6)
(5)
同底数幂除法(解析版)

同底数幂除法【知识梳理】一、同底数幂的除法法则同底数幂相除,底数不变,指数相减,即m n m na a a −÷=(a ≠0,m n 、都是正整数,并且m n >)要点诠释:(1)同底数幂乘法与同底数幂的除法是互逆运算.(2)被除式、除式的底数相同,被除式的指数大于除式指数,0不能作除式. (3)当三个或三个以上同底数幂相除时,也具有这一性质. (4)底数可以是一个数,也可以是单项式或多项式. 二、零指数幂任何不等于0的数的0次幂都等于1.即01a =(a ≠0)要点诠释:底数a 不能为0,00无意义.任何一个常数都可以看作与字母0次方的积.因此常数项也叫0次单项式.【考点剖析】 题型一、同底数幂的除法例1、计算:(1)83x x ÷;(2)3()a a −÷;(3)52(2)(2)xy xy ÷;(4)531133⎛⎫⎛⎫−÷− ⎪ ⎪⎝⎭⎝⎭.【思路点拨】利用同底数幂相除的法则计算.(2)、(4)两小题要注意符号. 【答案与解析】解:(1)83835x x x x −÷==.(2)3312()a a a a −−÷=−=−.(3)5252333(2)(2)(2)(2)8xy xy xy xy x y −÷===. (4)535321111133339−⎛⎫⎛⎫⎛⎫⎛⎫−÷−=−=−=⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.【总结升华】(1)运用法则进行计算的关键是看底数是否相同.(2)运算中单项式的系数包括它前面的符号. 【变式1】(2021•上海)计算:x 7÷x 2= .【分析】根据同底数幂的除法法则进行解答即可. 【解答】解:x7÷x2=x7﹣2=x5, 故答案为:x5.【点评】此题考查了同底数幂的除法,熟练掌握同底数幂相除,底数不变指数相减是解题的关键. 【变式2】(2022•浦东新区二模)计算:(﹣a 6)÷(﹣a )2= . 【分析】根据同底数幂相除的法则:底数不变,指数相减即可得出答案. 【解答】解:(﹣a6)÷(﹣a )2=﹣(a6÷a2)=﹣a4. 故答案为:﹣a4.【点评】本题考查了同底数幂的除法,同底数幂相除的法则:底数不变,指数相减. 【变式3】计算:(1)()()151233−÷−;(2)853377⎛⎫⎛⎫÷− ⎪ ⎪⎝⎭⎝⎭;(3)10010099÷.【答案】(1)27−;(2)27343−;(3)1.【解析】(1)()()()()151215123333327−−÷−=−=−=−;(2)858533333277777343−⎛⎫⎛⎫⎛⎫⎛⎫÷−===⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭; (3)100100100100099991−÷===.【总结】本题考查了同底数幂的除法,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠.【变式4】计算: (1)107a a ÷;(2)102102x x −÷;(3)()()75a a −÷−.【答案】(1)3a ;(2)1−;(3)2a .【解析】(1)1071073a a aa −÷==; (2)10210210210201x x x x −−÷=−=−=−;(3)()()()()757522a a a a a −−÷−=−=−=.【总结】本题考查了同底数幂的除法,同底数幂相除,底数不变,指数相减. 【变式5】计算:(1)()()105x y x y +÷+;(2)()()97a b b a −÷−.【答案】(1)()5x y +;(2)222a ab b −+−.【解析】(1)()()()()1051055x y x y x y x y −+÷+=+=+;(2)()()()()()()9797972222a b b a b a b a b a b a a ab b −−÷−=−−÷−=−−=−−−+−.【总结】本题主要考查了同底数幂的除法. 题型二、科学记数法有关的同底数幂的除法例2.下雨时,常常是“先见闪电、后闻雷鸣”,这是因为光速比声速快的缘故.已知光在空气中的传播速度为8310⨯米每秒,而声音在空气中的传播速度约为300米每秒,你知道光速是声速的多少倍吗? 【答案】610.【解析】8631030010⨯÷=.【总结】本题考查了整式的除法,解题的关键是根据题意列出代数式,再根据除法运算法则求出答案. 【变式】月球距离地球大约53.8410⨯千米,一架飞机的速度约为2810⨯千米/时.如果乘坐此飞机飞行这么远的距离,大约需要多少时间? 【答案】480小时.【解析】()()()()52523.8410810 3.8481010480⨯÷⨯=÷⨯÷=(小时)【总结】本题考查了单项式除以单项式,用整式乘除法解决实际问题时要注意分清量与量之间存在的数量关系.题型三、同底数幂的除法的逆用例3、已知32m =,34n=,求129m n +−的值.【答案与解析】解:121222222221222244449(3)33333(3)399(3)33(3)(3)m m m m m m m nn n n n n n ++++−======.当32m =,34n=时,原式224239464⨯==. 【总结升华】逆用同底数除法公式,设法把所求式转化成只含3m ,3n的式子,再代入求值.本题是把除式写成了分数的形式,为了便于观察和计算,我们可以把它再写成除式的形式. 【变式1】(2020秋•宝山区期末)如果2021a =7,2021b =2.那么20212a﹣3b= .【分析】根据幂的乘方以及同底数幂的除法法则计算即可,幂的乘方法则:底数不变,指数相乘;同底数幂的除法法则:底数不变,指数相减. 【解答】解:∵2021a =7,2021b =2.∴20212a ﹣3b =20212a ÷20213b =(2021a )2÷(2021b )3=72÷23=.故答案为:.【点评】本题主要考查了同底数幂的除法以及幂的乘方,熟记相关运算法则是解答本题的关键.【变式2】已知2552m m⨯=⨯,求m 的值.【答案】解:由2552m m ⨯=⨯得1152m m −−=,即11521m m −−÷=,1512m −⎛⎫= ⎪⎝⎭,∵ 底数52不等于0和1,∴ 15522m −⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,即10m −=,1m =.题型四、同底数幂的除法有关的混合运算例4.(2020秋•浦东新区期末)计算:a •a 7﹣(﹣3a 4)2+a 10÷a 2.【分析】分别根据同底数幂的乘除法法则以及积的乘方运算法则化简后,再合并同类项即可. 【解答】解:a •a7﹣(﹣3a4)2+a10÷a2=a8﹣9a8+a8=﹣7a8.【点评】本题主要考查了同底数幂的乘除法以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.【变式1】(2022y 3•y 5÷(﹣y )4= . 【分析】利用同底数幂的乘除法运算法则进行计算. 【解答】解:原式=﹣y3•y5÷y4=﹣y3+5﹣4=﹣y4, 故答案为:﹣y4.【点评】本题考查同底数幂的乘除法,掌握同底数幂的乘法(底数不变,指数相加),同底数幂的除法(底数不变,指数相减)的运算法则是解题关键. 【变式2】计算: (1)()623x x x ÷⋅;(2)()1243x x x ⋅÷.【答案】(1)x ;(2)13x . 【解析】(1)()6236236565x x x x x x x x x+−÷⋅=÷=÷==;(2)()124312*********x x x x x x x x x −+⋅÷=⋅=⋅==.【总结】本题考查了同底数幂的乘法与除法,m n m n a a a +⋅=,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠.【变式3】.计算: (1)()()4334a a −÷−;(2)()()22237a a a a ⋅÷⨯−.【答案】(1)1−;(2)5a .【解析】(1)()()()433412121a a a a −÷−=÷−=−;(2)()()()22223757210725a a a a a a a a a −+⋅÷⨯−=÷⋅==.【总结】本题考查了同底数幂的乘法与除法,m nm na a a +⋅=,()nm mna a =,m n m na a a −÷=(0a ≠,m ,n 都是正整数),规定()010a a =≠,注意负数的奇次幂还是负数.【变式4】计算:(1)()3232942x x x x x ⋅−+÷;(2)54189t t t t ⋅−÷.【答案】(1)5628x x −;(2)0.【解析】(1)()3232942323945655628828x x x x x x x x x x x x x +⨯−⋅−+÷=−+=−+=−;(2)5418954189990t t t t t tt t +−⋅−÷=−=−=. 【总结】本题考查了同底数幂的乘法与除法以及幂的乘方,注意法则的准确运用.【过关检测】一、单选题1.(2022秋·上海·七年级专题练习)下列计算正确的是( )A .235a a ()=B .3232a b a b −−()= C .448a a a += D .532a a a ÷=【答案】D【分析】利用合并同类项的法则,同底数幂的除法的法则,幂的乘方的法则,单项式乘多项式的法则对各项进行运算即可.【详解】解:A 、623a a ()=,故A 不符合题意;B 、3(a ﹣2b )=3a ﹣6b ,故B 不符合题意;C 、4442a a a +=,故C 不符合题意;D 、532a a a ÷=,故D 符合题意;故选:D .【点睛】本题主要考查幂的乘方,同底数幂的除法,单项式乘多项式,合并同类项,解答的关键是对相应的运算法则的掌握.2.(2023·上海·七年级假期作业)在下列运算中,计算正确的是( ) A .3262()x y x y −= B .339x x x ⋅= C .224x x x += D .62322x x x ÷=【答案】A【分析】按照幂的乘方、积的乘方、合并同类项、同底数幂相乘、同底数幂相除的运算法则.【详解】解:3262x y x y =(-),故A 正确,符合题意; 336x x x ⋅=,故B 错误,不符合题意; 2222x x x +=,故C 错误,不符合题意; 62422x x x ÷=,故D 错误,不符合题意;故选:A .【点睛】本题考查了幂的乘方、积的乘方、合并同类项、同底数幂相乘、同底数幂相除等运算,熟练掌握相关运算法则是解题关键.【答案】B【分析】根据幂的公式逆运算即可求解.【详解】∵3,2m nx x ==,∴23m nx−=(mx )2÷(nx )3=32÷23=98故选B【点睛】此题主要考查幂的运算,解题的关键是熟知幂的运算公式.4.(2021秋·上海浦东新·七年级期末)下列运算中,正确的是( ) A .(﹣m )6÷(﹣m )3=﹣m 3 B .(﹣a 3)2=﹣a 6 C .(xy 2)2=xy 4 D .a 2•a 3=a 6【答案】A【分析】根据同底数幂的除法,幂的乘方,积的乘方,同底数幂的乘法逐项分析判断即可. 【详解】解:A 、(﹣m )6÷(﹣m )3=﹣m3,故本选项符合题意; B 、(﹣a3)2=a6,故本选项不符合题意; C 、(xy2)2=x2y4,故本选项不符合题意; D 、a2•a3=a5,故本选项不符合题意; 故选:A .【点睛】本题考查了幂的运算,掌握幂的运算是解题的关键. 5.(2023·上海·七年级假期作业)下列计算结果中,正确的是( ) A .a 3+a 3=a 6 B .(2a )3=6a 3 C .(a ﹣7)2=a 2﹣49 D .a 7÷a 6=a .【答案】D【分析】根据合并同类项法则、积的乘方的运算法则、完全平方公式、同底数幂的除法的运算法则逐项计算得出结果即可得出答案.【详解】解:A 、3332a a a +=,原计算错误,故此选项不符合题意;B 、33(2)8a a =,原计算错误,故此选项不符合题意;C 、22(7)1449a a a =−−+,原计算错误,故此选项不符合题意;D 、76a a a ÷=,原计算正确,故此选项符合题意.故选:D .【点睛】本题考查合并同类项、积的乘方、完全平方公式和同底数幂的除法.掌握各运算法则是解题关键. 6.(2023·上海·七年级假期作业)下列运算正确的是( ) A .()323a a = B .623a a a ÷= C .235a a a += D .235a a a ⋅=【答案】D【分析】根据幂的乘方,同底数幂的乘法和除法,以及合并同类项法则,逐一进行计算即可.【详解】解:A 、()326a a =,选项错误,不符合题意;B 、624a a a ÷=,选项错误,不符合题意;C 、235a a a +≠,选项错误,不符合题意;D 、235a a a ⋅=,选项正确,符合题意;故选D .【点睛】本题考查幂的乘方,同底数幂的乘法和除法,以及合并同类项法.熟练掌握相关法则,是解题的关键.二、填空题7.(2023·上海·七年级假期作业)42()()n n y y −÷−=________;4232()()()a b a b a b ⎡⎤⎡⎤−⨯−÷−=⎣⎦⎣⎦___________.【答案】 2n y 9()a b −【分析】利用同底数幂的乘法、除法、幂的乘方化简,先算乘方,再算乘除.【详解】解:42()()n n y y −÷−=42()n n y −−=2()ny −=2n y ,4232()()()a b a b a b ⎡⎤⎡⎤−⨯−÷−⎣⎦⎣⎦=124()()()a a b a b −⨯−÷−=124()()()a b a b a b −⨯−÷−=1214()a b +−−=9()a b −.故答案为:2n y ,9()a b −.【点睛】此题考查了同底数幂的乘法、除法、幂的乘方运算,解题的关键是掌握同底数幂的乘法、除法、幂的乘方的运算法则.8.(2023·上海·七年级假期作业)计算:结果用幂的形式表示94()()a b b a −÷−=_____. 【答案】5()a b −【分析】利用同底数幂的除法的法则进行运算即可.【详解】解:94()()a b b a −÷−94()()a b a b =−÷−5()a b =−.故答案为:5()a b −.【点睛】本题主要考查同底数幂的除法,解答的关键是对同底数幂除法法则的掌握.9.(2023秋·上海青浦·七年级校考期末)计算:()()2333142a b a b b −−−⋅÷=____________.(结果只含有正整数指数幂) 【答案】934b a【分析】根据幂的运算法则和整式的混合运算法则计算可得.【详解】解:()()2333142a b a b b −−−⋅÷293464a b a b b −−=⋅÷()492634a b +−−−=934a b −=394b a =.【点睛】本题主要考查整式的混合运算,解题的关键是熟练掌握幂的运算法则和整式的混合运算法则.10.(2022秋·上海·七年级专题练习)计算:62a a ÷(-)(-)=______. 【答案】4a −【分析】先依据公式得出正确的符号,再利用幂的除法公式计算.【详解】62624a a a a a −÷−−÷−()()=()=.故答案为:4a −.【点睛】本题考查幂的运算,正确运用公式是解题的关键.11.(2019秋·上海·七年级上海市张江集团中学校考期中)已知3m a =,5n a =,则32m n a +=_______________ 【答案】675【分析】根据幂的乘方以及同底数幂的乘法法则解答即可. 【详解】∵am=3,an=5,∴a3m+2n=(am)3•(an)2=33×52=27×25=675. 故答案为:675.【点睛】本题考查了幂的乘方与积的乘方以及同底数幂的乘法,熟记幂的运算法则是解答本题的关键.【答案】9【分析】根据同底数幂除法的逆用、幂的乘方的逆用进行计算即可得.【详解】解:因为102a =,109b=,所以112210100100b aa b −=÷1222(10)(10)b a=÷1222(10)10b a ⨯=÷2210b=÷49=÷49=,故答案为:49.【点睛】本题考查了同底数幂除法的逆用、幂的乘方的逆用,熟练掌握各运算法则是解题关键.13.(2023秋·上海静安·七年级新中初级中学校考期末)若15m x =,5n x =,则m n x −等于_____. 【答案】3【分析】逆向运算同底数幂的除法法则计算即可.同底数幂的除法法则:同底数幂相除,底数不变,指数相减.【详解】解:∵xm=15,xn=5, ∴xm-n=xm÷xn=15÷5=3. 故答案为:3.【点睛】本题考查了同底数幂的除法,掌握幂的运算法则是解答本题的关键.14.(2023·上海·七年级假期作业)已知5m a =,5n b =,则25m n +=______,235m n −=______.(请用含有a ,b 的代数式表示)【答案】 2a b /2ba 23a b【分析】逆用同底数幂的乘法,幂的乘方,同底数幂的除法运算法则,进行计算即可.【详解】解:∵5m a =,5nb =,∴()222255555m n m n m n a b+=⋅=⋅=;()()223232323355555m nmnm n a a b b −=÷=÷=÷=.故答案为:2a b ;23a b .【点睛】本题主要考查了同底数幂的乘法,同底数幂的除法,幂的乘方,解题的关键是熟练掌握同底数幂的乘法,幂的乘方,同底数幂的除法运算法则.15.(2023·上海·七年级假期作业)已知2m a =,3n a =,那么3m n a −=___________. 【答案】83【分析】根据同底数幂的除法底数不变指数相减,可得答案. 【详解】解:2m a =,3n a =,∴3m na−3mnaa =÷3()m na a =÷323=÷83=.故答案为:83.【点睛】本题考查了同底数幂的除法,逆用同底数幂除法的计算法则是解题关键.16.(2022秋·上海·七年级阶段练习)﹣y 3•y 5÷(﹣y )4=_____.【答案】﹣y4【分析】先计算幂的乘方,再计算同底数幂的乘、除法,注意负号的作用.【详解】解:﹣y3•y5÷(﹣y )4=﹣y8÷y4=﹣y4故答案为:﹣y4【点睛】本题考查幂的乘方、同底数幂的乘除法等知识,是基础考点,掌握相关知识是解题关键.17.(2022秋·七年级单元测试)已知5230x y −−=,则324x y ÷=________.【答案】8【分析】先求出523x y −=,然后逆用幂的乘方法则对所求式子变形,再根据同底数幂的除法法则计算.【详解】解:∵5230x y −−=,∴523x y −=,∴5253228324222x y x y x y −===÷=÷, 故答案为:8.【点睛】本题考查了代数式求值,涉及幂的乘方的逆用,同底数幂的除法,有理数的乘方运算,熟练掌握运算法则是解题的关键.18.(2023·上海·七年级假期作业)已知2320x y −−=,则927x y ÷的值为________.【答案】9【分析】先变形,再根据同底数幂的除法进行计算,最后整体代入求出即可.【详解】解:∵2320x y −−=,∴232x y −=,∴927x y ÷2333x y =÷233x y −=23=9= 故答案为9.【点睛】本题考查了同底数幂的除法、幂的乘方等知识点,能正确根据法则进行变形是解此题的关键.三、解答题19.(2023·上海·七年级假期作业)计算:(1)()()105x y x y +÷+;(2)()()97a b b a −÷−. 【答案】(1)()5x y +(2)222a ab b −+− 【分析】(1)利用同底数幂的除法进行运算;(2)先将底数均化为a b −,再利用同底数幂的除法运算.【详解】(1)解:1055()()()x y x y x y +÷+=+;(2)解:97()()a b b a −÷−97()()a b a b ⎡⎤=−÷−−⎣⎦2()a b =−−222a ab b =−+−. 【点睛】本题考查了同底数幂的除法,熟练掌握相关运算规则是解题的关键.20.(2022秋·上海·七年级校考期中)计算:()()222334222a a a a a a +−−÷ 【答案】6a【分析】根据同底数幂乘法的法则,积的乘方的运算法则,同底数幂除法的运算法则先化简计算,然后合并同类项即可.【详解】解:()()222334222a a a a a a +−−÷668244a a a a =+−÷66644a a a =+−6a = 【点睛】本题考查了整式的混合运算,解题的关键是掌握相关公式并灵活运用.幂的乘方法则:底数不变,指数相乘.积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘. 21.(2023·上海·七年级假期作业)计算:(1)()()4334a a −÷−; (2)()()22237a a a a ⋅÷⨯−. 【答案】(1)1−(2)5a【分析】(1)先计算幂的乘方,再计算同底数幂的除法;(2)先计算同底数幂的乘法、乘方,再计算同底数幂的乘法与除法.【详解】(1)解:()()()433412121a a a a −÷−=÷−=−;(2)解:()()()22223757210725a a a a a a a a a −+⋅÷⨯−=÷⋅==.【点睛】本题考查了同底数幂的乘法与除法,m n m n a a a +⋅=,()n m mn a a =,m n m n a a a −÷=(0a ≠,m ,n 都是正整数),注意负数的奇次幂还是负数.22.(2022秋·上海·七年级专题练习)已知3m =4,3n =5,分别求3m +n 与32m ﹣n 的值.【答案】20,165【分析】利用同底数幂的乘法的逆用法则,同底数幂的除法的逆用法则,幂的乘方的逆用法则对所求的式子进行整理,再代入运算即可.【详解】解:3334520m m n n +=⋅=⨯=;222233316(53)534m n m n m n −=÷=÷=÷=.【点睛】本题考查同底数幂的乘法的逆用,同底数幂的除法的逆用,幂的乘方的逆用.掌握各运算法则是解题关键.23.(2022秋·上海·七年级专题练习)已知34m =,35n =,分别求3m n +与23m n −的值.【答案】20,165【分析】同底数幂的除法的逆用法则,幂的乘方的逆用法则对所求的式子进行整理,再代入运算即可.【详解】解:3m n +33m n =⋅45=⨯20=;23m n −233m n =÷()233m n =÷245=÷165=.【点睛】本题考查同底数幂的乘法的逆用,同底数幂的除法的逆用,幂的乘方的逆用.掌握各运算法则是解题关键.24.(2022秋·上海·七年级校考期中)已知96,32b a ==,求323a b −的值. 【答案】43【分析】先根据幂的乘方求出3336,38b a ==,再逆用同底数幂的除法计算即可. 【详解】∵96,32b a ==, ∴233396,328b b a ====,∴3243863a b −=÷=.【点睛】本题考查了幂的乘方,同底数幂的除法,熟练掌握运算法则是解题的关键.25.(2021秋·上海浦东新·七年级期末)计算:a •a 7﹣(﹣3a 4)2+a 10÷a 2.【答案】﹣7a8【分析】根据同底数幂的乘除法,积的乘方运算法则,幂的乘方运算,最后合并同类项即可【详解】解:a•a7﹣(﹣3a4)2+a10÷a2=a8﹣9a8+a8=﹣7a8.【点睛】本题考查了同底数幂的乘除法,积的乘方运算法则,幂的乘方运算,掌握幂的运算是解题的关键.26.(2023·上海·七年级假期作业)若32x =,35y =,求23x y −的值. 【答案】45【分析】逆用幂的乘方,除法法则计算即可.【详解】()22233333x y x y x y −=÷=÷,把32x =,35y =代入得()224333455x y x y −=÷=÷=.【点睛】本题考查了同底数幂的乘方与除法,熟练掌握运算法则是解题的关键.。
15.4.1 同底数幂的除法(1)

20÷210) 所需时间为:(2
×12
温故而知新
m 1.a n=am+n (a≠0,m、n为正整数 a 、 为正整数 为正整数)
2. 若a b=q 则q÷a= ÷ =
b
被乘数×乘数= 被乘数×乘数=积 被除数÷除数= 被除数÷除数=商
3.计算 计算 102 × 103= 105 22 24= x5 · x7= x12
性质的应用
例1 计算:
(1) (2)
a9÷a3 =a9-3 = a6
212÷27 =212-7=25=32 (3) (- x)4÷(- x ) =(- x)4-1=(- x)3= - x3 11/(- 3)8 =(- 3)11-8=(- 3)3=- 27 (4) (- 3)
计算: 例2 计算
5-4+1=a3 (1) =a 7÷x2 = - x7÷x2= - x7-2= - x5 (2) (- x) (3) (ab)5÷(ab)2 =(ab)5-2=(ab)3 5÷a4.a2 a
同底数幂相除,底数不变,指数相减 同底数幂相除,底数不变,指数相减 相除
思考与讨论 为什么规定a≠0? m>n ?
归纳与梳理
已学过的幂运算性质
为正整数) (1)am·an=am+n (a≠0 m、n为正整数 ) 、 为正整数 (2)am÷an=am-n (a≠0 m、n为正整数 ) 、 为正整数 且m>n) 为正整数) (3)(am)n=amn (a≠0 m、n为正整数 ) 、 为正整数 为正整数) (4)(ab)n=anbn (a≠0 m、n为正整数 ) 、 为正整数
(4) (a+b)6÷(a+b)4 =(a+b)6-4=(a+b)2=a2+2ab+b2
第一章第03讲 同底数幂的除法(6类热点题型讲练)(原卷版)--初中数学北师大版7年级下册

第03讲同底数幂的除法(6类热点题型讲练)1.经历同底数幂的除法法则的探索过程,理解同底数幂的除法法则;2.理解零次幂和负整数指数幂的意义,并能进行负整数指数幂的运算;3.会用同底数幂的除法法则进行计算.知识点01同底数幂的除法m n m n a a a -÷=(其中,m n 都是正整数).即同底数幂相除,底数不变,指数相减.要点诠释:(1)同底数幂是指底数相同的幂,底数可以是任意的实数,也可以是单项式、多项式.(2)逆用公式:即=m nm n aa a -÷(,m n 都是正整数).知识点02零指数幂:01a =(a ≠0)知识点03负指数幂:1pp aa-=(a ≠0,p 是正整数)题型01同底数幂的除法【例题】(2023上·八年级课时练习)计算:(1)()()()722ab ab ab -÷-÷-;(2)()243m m ÷;(3)()()426x x x -⋅÷-.【变式训练】1.(2023上·全国·八年级课堂例题)计算:(1)93m m -÷;(2)63()()a a -÷-;(3)2366m m +÷.2.(2023上·全国·八年级课堂例题)计算:(1)1023a a a ÷÷;(2)255a a a ⋅÷;(3)()()5222x y x y ÷;(4)432()()()p q q p p q -÷-⋅-.题型02同底数幂除法的逆用【例题】(2023上·八年级课时练习)已知2a x =,6b x =.(1)求a b x -的值;(2)求2a b x -的值.【变式训练】1.(2023下·安徽安庆·七年级校考期中)已知3x a =,5y a =,求:(1)x y a -的值;(2)2x y a -的值.2.(2023上·河南南阳·八年级统考期中)根据条件求值:(1)已知3m a =,4n a =,求23m n a -的值;(2)已知129372n n +-=,求n 的值.题型03幂的混合运算【例题】(2023·上海·七年级假期作业)计算:(1)()()4334a a -÷-;(2)()()22237a a a a ⋅÷⨯-.【变式训练】题型04零指数幂题型05负整数指数幂【例题】计算:(1)2(5)--;(2)0(3)-;(3)510-;(4)3(0.25)--.【变式训练】题型06用科学计数法表示绝对值小于1的数一、单选题1.(2023上·河南濮阳·八年级校联考期中)下列各式运算结果为6x 的是()A .24x x ⋅B .()42x C .122x x ÷D .33x x +2.(2023上·四川宜宾·八年级统考期中)下列计算正确的是()A .426235a a a +=B .824a a a ÷=C .53822a a a ⋅=D .()236a ba b=3.(2023上·吉林松原·八年级校联考期末)经测算,一粒芝麻的质量约为0.00000201kg ,数据0.00000201用科学记数法表示为()A .320.110-⨯B .42.0110-⨯C .50.20110-⨯D .62.0110-⨯4.(2023上·河南濮阳·八年级校联考期中)若()021x +=,则x 的取值范围是()A .2x ≥-B .2x ≤-C .2x ≠-D .2x =-5.(2023上·河南新乡·八年级校考阶段练习)下列四个算式:①()()4322x x x -÷-=-;②()()2122242n n x x x +--÷-=-;③()2522a b a b a ÷=;④()2642221832a b a b a b ÷-=.其中计算不正确的是()A .①②B .①③C .②④D .②③(1)求m n a +的值;(2)求2m n a -的值.16.(2023上·陕西延安·八年级校联考阶段练习)按要求解答下面各题.(1)已知2430x y ++=,求981x y ⨯的值;(2)已知314748216a a a +++⨯÷=,求a 的值.17.(2023下·江苏泰州·七年级校联考期中)已知32a =,36b =,324c =.(1)求()23a 的值;(2)求3b c -的值;(3)直接写出a 、b 、c 之间的数量关系为______.18.(2023上·陕西延安·八年级陕西延安中学校考阶段练习)将幂的运算逆向思维可以得到m n m n a a a +=⋅,m nmnaa a -=÷,()=nmn m a a ,()=mm m a b ab ,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.(1)已知2m a =,3n a =,求3m n a -的值;(2)已知2328162x ⨯⨯=,求x 的值.。
同底数幂的除法1
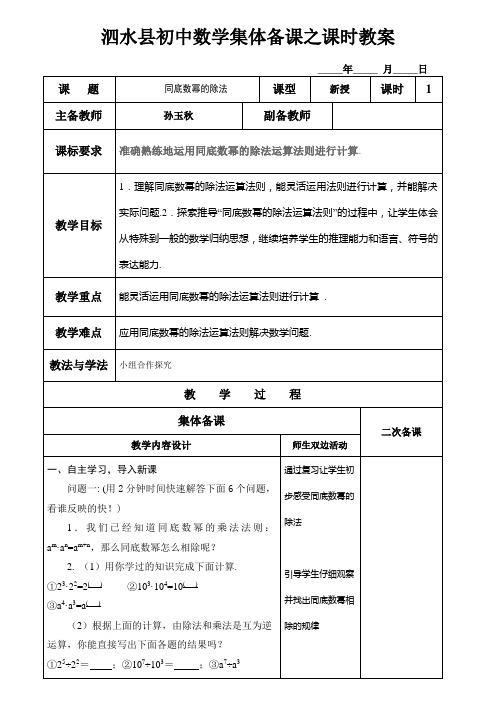
3
平方厘米,这个水池的深度是多少?
课堂总结 教后反思
3
÷ (a - 6)3 (3)y10n ÷ (y4n ÷ y2n) ; (4)x7 ÷ x2 + x· (–x)
4
; 4. (1)xm = 5,xn = 3,求 xm–n
⑵已知a m 8, a n 3, a k 2, 求a m3k 2n的算术平方根 5.有一容积为 16 10 立方厘米的长方体水池,测
)
步学习上,注意书 写格式
.
)-( )
(2)32÷ 32-( )
(3)a ÷ a =a 不为 0 的数的
=a
(
)
=1,也就是说,任何
教师可以让学生尝 做,然后说一下自 己的思路
次幂等于 1;
字母作底数,如果没有特别说明一般不为 0. 二、合作学习,获取新知
a8 a3 问题二: 1、 计算 (1)
642 x 82 x 4 16, 求x的值。
(2)
⑵已 知
⑶ 已 知 : 5m=3,25n=4 , 求 5m-2n+2 的 值 . ⑷若 3m-2n-2=0,求 106 m 1002 n 10 的立方根 四、理解运用,巩固提高 问题四:1.下列计算中正确的是( A. a5 a 3 a 2 C.
板书设计
(3)y10n ÷ (y4n ÷ y2n) ; (4)x7 ÷ x2 + x· (–x)4;
4. (1)xm = 5,xn = 3,求 xm–n ⑵已知a m 8, a n 3, a k 2, 求a m3k 2n的算术平方根
5. 有一容积为 16 10 立方厘米的长方体水池, 测得水面的面积为 16 10
同底数幂的除法(1)

课题:8.3同底数幂的除法(1)班级 姓名 学号【教学目标】1.掌握同底数幂的除法运算法则.2.会正确的运用同底数幂除法的运算性质进行运算,并能说出每一步运算的依据. 【重、难点】重点:熟练运用同底数幂除法的运算性质进行运算.难点:运用同底数幂除法的运算性质的逆用进行求幂的值. 【教学过程】 一、情境引入一颗人造地球卫星运行的速度是7.9×103 m/s ,一架喷气式飞机飞行的速度是1.0×103 km/h 。
人造卫星的速度是飞机速度的多少倍?问:怎样计算(7.9×103 ×3600)÷( 1.0×103×1000)?二、探索活动活动一 计算下列各式:(1)________;2______,22538==÷ (2)________;)3(______,)3()3(325=-=-÷- (3)________;)43(_______,)43()43(235==÷从上面的计算中,你发现了什么规律?活动二 同底数幂的除法法则的推导当a ≠0 , m 、n 是正整数 , 且m >n 时, a m ÷a n= (a ﹒a ﹒﹒a )÷(a ﹒a ﹒a)m 个 n( a ﹒a ﹒﹒﹒﹒a) (a ﹒a ﹒﹒a)(m-n) 个 n 个=a ﹒a ﹒﹒﹒﹒a n 个= a m-n所以a m ÷a n= (a ≠0 , m 、n 是正整数 , 且m >n)归纳同底数幂的除法法则:执笔:刘玲 审核:石云荣三、例题讲解例1.计算:(1)a 6÷a 2 (2) (-b)8÷(-b) (3)(ab)4÷(ab)2 (4)t 2m +3÷t 2(m 是正整数)例2.(1)若n 为正整数,,312a a a n =÷ 则求 n 的值; (2)若,2,4==n m a a 则求nm a -的值;(3)若,2,4==n m a a 则nm a 43-的值.四、反馈练习1. 计算:26÷22= ,(-3)6÷(-3)3= ,(21)7÷(21)4= , 2.已知 A ·x 2n+1= x 3nx ≠0那么A =3.若 x m = 2 , x n = 5 , 则x m+2n = , x m-2n= . 4.计算:(1)443÷(2)26)41()41(-÷- (3)37)()(ab ab -÷- (4)y yx x48÷(5)22333÷÷m(6)232432)()(z y x z y x -÷- (7)34)()(y x y x +÷--(8)(a 3 .a 2 ) 3÷(-a 2 ) 2 ÷a (9) (x 4 ) 2÷(x 4 ) 2 (x 2 ) 2 ·x 2(10)(ab ) 12÷[(ab ) 4÷(ab ) 3]25.4m .8m-1÷2m = 512 ,求m 的值.6.若4m .8m-1÷2m= 512 ,则求m 的值.七年级数学中午作业班级姓名学号1.下列各式计算正确的是( )A.(a+1)2=a2+1 B.a2+a3=a5C.a8÷a2=a6D.3a2-2a2=1 2.a m=3,a n=2,则a m-n的值是( )A.1.5 B.6 C.9 D.83.化简:6a6÷3a3=_______.4.(1)①195÷192=_______,②(-14)6÷(-14)2=_______,③(-m)8÷(-m)3=_______;(2)①x9a÷x4a=_______,②b2m÷b m-1=_______;(3)①(a-2)6÷(2-a)5=_______,②(-a-b)5÷(a+b)=_______;(4)①(-mn)9÷(mn)4=_______,②(a2)3÷(-a2)2=_______.5.(1)若a m+2÷a3=a5,则m=_______;(2)若a x=5,a y=3,则a y-x=_______.6.计算:(1)x10÷x5.x3;(2)-(-6)6.(-6)4÷(-6)8;(3)(a-b)10÷(b-a)7;(4)(x n+1)2÷(x2)n;(5)(-xy)7÷(-xy)4;(6)(-2a)6÷[-(2a)]3.7.已知3x=a,3y=b,则32x-y等于( )A.2abB.a2b C.2ab D.a2+1b8.计算(a2)3÷(a2)2的结果是( )A.a B.a2C.a3D.a4 9.若3x=4,9y=7,则3x-2y的值为( )A.47B.74C.-3 D.2710.(1)①(-a)3÷(-a2)=_______,②a10÷(a5÷a2)=_______;(2)①x n+1÷x2n-3=_______,②8m+1÷4m=_______ 11.(1)若32÷8n-1=2n,则n=_______;(2)若a m =3,a n =-2,则a m +n =_______,a m -n =_______. 12.计算:(1)(-x)3÷(-x 2); (2)(-x 2y 3)5÷(-x 2y 3)2; (3)(4×108)÷(8×105); (4)x 10÷(x 4÷x 2);(5)279÷97÷3; (6)(-a)7÷a 3.(-a)2;(7)(a 4)3÷(-a 3)2.(-a)3; (8)(x 3)2÷x 2.x 3-2x 3.(-x 5)2÷(x 2)3.13.已知3×9m ×27m =321,求(-m 2)3÷(m 3.m 2)的值.14.(1)若x m =10,x n =-1,x k =2,求x m -2k +3n 的值;(2)若3x =4,3y =6,求92x -y 的值.15.如图,65A ∠=︒,30ABD ∠=︒,72ACB ∠=︒,且CE 平分ACB ∠,求BEC ∠ 的度数。
《同底数幂的除法(1)》教学课件

(2) (-x)6÷(-x)3; (4) (xy)4÷(xy) ; (6) (m+n)8÷(m+n)3;
归纳总结
1、同底数幂的除法法则: am÷an=am-n, (a≠0,m,n是正整数,m>n). 底数可以是一个具体的数,也可以是单项
式或多项式.
2、计算时的几个注意点: (1)同底数幂的除法计算,直接应用法则,底数不 变,指数相减. (2)不是同底数幂时,应先化成同底数幂,再计算, 注意符号. (3)当底数是多项式时,应把这个多项式看成一个 整体. (4)混合运算时注意运算的顺序.
10×···×10 9个10
=10×10×10
=103
归纳法则
1.计算你列出的算式
2.计算下列各式,并说明理由(m>n)
(1)10m÷10n; (2)(-3)m÷(-3)n;
(3)( 1 )m ( 1 )n
2
2
3.你能用字母表示同底数幂的除法运算法则 并说明理由吗?
归纳法则
m个a
m-n个a
m
a
课后作业:
课本P55页,第1、2题
结束
÷ an
= —aa—··aa—······—····aa—
= a·a·····a
n个a
= a m-n
am ÷ an =am-n(a≠0,m,n都是正整数,且m>n)
同底数幂相除,底数 不变 ,指数 相减 .
巩固落实
例1 计算: (1)a6÷a2 (2)(-b)8÷(-b) (3)(ab)4÷(ab)2 (4)t2m+3÷t2(m是正整数)
解: (1)a6÷a2=a6-2=a4 (2)(-b)8÷(-b)= (-b)b)2= (ab)4-2 = (ab)2 = a2b2 (4)t2m+3÷t2=t2m+3-2=t2m+1
同底数幂的除法(1)

试一试 计算下列各式。
am an amn
1、 27 23;
2、 (-3)5 (-3)2;
3、 (- 3)6 33; 4、 ( x 2 y)7 ( x 2 y)3;
5、 (m - n)5 (n- m )2
例 2 . 计算:
(1) a5 a4 • a2;
am an amn
(2) (ab)5 (ab)2;
(3) b4 gb3 g( (b)14 ) b21; (4) c8 ( c3) c5.
(5) (a b)5 (b a)3 (a b)2
4、计算:
(1) a3n an ;
2 a8 a4 • a4 ;
3 y2 3 y3; 4 2 27 23 ;
5 (a b)5 a b2 ;
ቤተ መጻሕፍቲ ባይዱ
.
2. 若 812x 27x4 , 则 x
.
3. 已知 2x- 5y= 4,求4x 32y 的值.
温馨提示
1. 同底数幂相除,使用范围:底数相同,相除 方法: 底数不变,指数相减。
2. 应用时可以拓展: 底数和指数,它既可取具体数,也可取单项式或多项式。
3. 运用时注意不能与整式的加减和乘法混淆。 幂相乘→指数相加,幂相除→指数相减, 幂乘方→指数相乘。
例如: 46 42 462 44
例1. 计算:
am an amn
(1) a9 a3
(2) 212 27
(3) ( x)4 ( x)1
(3)11 (4) (3)8
5 a7 a7
(6) ( x)7 x3
注意: ➢注意法则使用的条件;
➢同底数幂相除时,指数是相减的; ➢不能疏忽指数为1的情况; ➢运算结果的底数一般应为正数. ➢若底数不同,先化为相同,后运用法则.
8.3 同底数幂的除法(1)

1.下列各式计算正确的是( )
A.(a+1)2=a2+1B.a2+a3=a5
C.a8÷a2=a6D.3a2-2a2=1
2.am=3,an=2,则am-n的值是( )
A.1.5B.6
C.9D.8
3.化简:6a6÷3a3=_______.
4.(1)①195÷192=_______,②(- )6÷(- )2=_______,③(-m)8÷(-m)3=_______;
重点
难点
重点:探索同底数幂的除法运算性质,会正确运用此性质进行计算.
难点:同底数幂的除法运算性质的探索.
作业
板书设计
教后反思
教学过程
教师活动
学生活动
个人复备
1、预习导学
如图,若已知这个长方形的面积为25cm2,长为23cm,则宽为多少cm?
二、探索活动
1.活动一.如何计算 ?
2.活动二.
计算下列各式:
学生独立思考,然后小组交流,再全班讨论,最后得出答案
学生抢答,说出结论,并说明理由.
先独立思考,再小组讨论.
学生独立思考,尝试完成.
自主小结,完善自身的知识体系
(3) ;
(4) (m是正整数)..
例2下面的计算是否正确?如有错误,请改正.
(1) ;(2) ;
(3) ;(4)
4、质疑拓展
1.已知3×9m×27m=321,求(-m2)3÷(m3.m2)的值.
2. (1)若xm=10,xn=-1,xk=2,求xm-2k+3n的值;
(2)若3x=4,3y=6,求92x-y的值.
积极思考,回答问题:
学生较容易度思考,积极发言.
学生可能回答 = = =4,也可能回答: = = =4,
14.1.4同底数幂的除法

(2)107 103 1_0__4___;aa221140024a102a10a10
a (3)a7 a3
4
______
a 0.
由上面的计算,我们发现
2 (1)25 23 _______2_;
(2)107
103
104
_______;
a x
2a
7106431
83
(2 a10 a3
(3 2a7 2a4
82aaa37ax537
5
(4 x6 x
练习:
(1)x8 x2 (2)m8 m7 (3)(a)10 (a)7 (4)(ab)5 (ab)2
(4) 6108 3105
解:原式= (63)1085
= 2103
多项式除以单项式的法则
知 识 点
∵(a+b)m=am+bm ∴(am+bm)÷m=_____a__+_b________ 又am÷m+bm÷m=___a__+__b_________
四 ∴(am+bm)÷m=am÷m+bm÷m
一般地,多项式除以单项式,先把这
个多项式的 每一项 除以这个单项式,
再 把所得的商 相加 .
温馨提示:把多项式除以单项式问题 转化为单项式除以单项式问题来解决.
例8 计算:
(3)12a3 6a 2 3a 3a
解:原式=12a3 ÷_3_a_- 6a 2÷_3_a_+3a÷3_a__ =___4_a_2__2_a___1____
5
练习:2.填空:
1) a3 a3 1
2) x4 x4 1
《同底数幂的除法》课件

规则概述
定义
同底数幂的除法规则是指当两个同底 数的幂相除时,其结果是该底数的幂 的差。
公式
适用范围
适用于任何实数底数 $a$,且 $m$ 和 $n$ 为整数。
$a^m div a^n = a^{m-n}$,其中 $a$ 是底数,$m$ 和 $n$ 是指数。
规则推导
推导过程
根据幂的性质,我们知道 $a^m times a^n = a^{m+n}$。由此,我们可以得 出 $a^m div a^n = a^m times frac{1}{a^n} = a^{m-n}$。
幂的运算法则
幂的乘法、除法、乘方等运算法则是幂运算的基本法则,是解决复 杂数学问题的关键。
幂的性质
幂的性质包括奇偶性、周期性、对称性等,这些性质在解决数学问 题时具有重要作用。
学生自我总结
学生应该回顾自己在本课中所学的知识点,包括同底数幂的除法法则、幂的运算法 则和幂的性质等,并思考这些知识点在实际问题中的应用。
运算技巧
通过对数性质,可以简化同底数幂的除法的计算过程。例如,利用对数的运算法 则,可以将复杂的幂次运算转化为简单的对数运算,从而简化计算过程。这种技 巧有助于提高学生的运算能力和数学思维能力。
与三角函数的关联
三角函数与指数形式
同底数幂的除法与三角函数之间存在一定的关联。例如,三角函数可以通过指数形式表示,而同底数幂的除法可 以与这种指数形式进行关联。这种关联有助于学生更好地理解三角函数和同底数幂的除法之间的关系。
进阶练习3
求值 (2^3)^2 ÷ (2^2)^3 = ?
进阶练习4
化简 (a^m × a^n) ÷ (a^m)^n = ?
综合练习
综合练习1
3.6同底数幂的除法(1) 浙教版 2014

火眼金睛辨真假 (1) a6÷ a3 = a2 (2) a5÷ a = a5
判断 (×) a6÷ a3 = a3
5÷ a = a4 a (×)
(3) -a6÷ a6 = -1 (
)
( ×)
(4)(-c)4 ÷(-c)2 =-c2 (-c)4 ÷ (-c)2 =c2
例2.计算:
m个a
(a 0,m,n都是正整数,且m>n)
=a a … a
(m-n)个a
=a
n个a m n
同底数幂的除法法则: 同底数幂相除,底数不变,指数相减.
即a
m
a =a
n
m n (a 0,m,n都是正整数,且m>n)
注意:
条件:①除法
②同底数幂
结果:①底数不变 ②指数相减
3.可以把整个代数式看作底.
4.运算结果能化简的要进行化简.
计算:
自 我 检 测
⑴ s9÷s3 ⑵ (-3)6 ÷(-3)2 ⑶ (ab)5÷(ab) ⑷ (x-y)8÷(x-y)3 11 2 ⑸ (-t) ÷t 5 4 ⑹ (a-b) ÷(b-a)
7 2 a a a ; (1) (2) ( x) x ; 5 4 2
6 4 ( a b ) ( a b ) ; (ab) (ab) ; (3) (4)
5
2
解题后的反思
1.乘除混合运算的顺序与有理数混合运算顺序
相同(即“从左到右”).
2.若底数不同,先化为同底数,后运用法则.
=a ( 1 )
= a(3 )-(2 )
m n (a 0,m,n都是正整数,且m>n) 猜想观察上面各题左右两边,底数、指数有什么关系? : 思考:
同底数幂的除法课件(共17张PPT)

0
2 1 .
解: 3 +
0
法
例3 计算:(a-b)3÷(b-a)2+(-a-b)5÷(a+b)4.
注意:符号的变化
解:原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4
=(a-b)-(a+b)
=a-b-a-b =-2b.
偶次幂下,减数和被减数可以任意交换位置, 其结果不变.
(3)(a)10 (a)3;
解:(a)10 (a)3 (a)103 (a)7 a7
(4)(2a)7 (2a)4 .
解:(2a)7 (2a)4 (2a)74 (2a)3 8a3
14.1.4.4 同底数幂的除法
思考 am÷am=? (a≠0)
am÷am=1,根据同底数幂的除法法则可得am÷am=am-m=a0.
am÷ an = am-n (a ≠ 0,m,n都是正整数,并 且m>n). 同底数幂相除,底数不变,指数相减.
零整数幂
a0 =1(a ≠0) 任何不等于0的数的0次幂都等于1.
14.1.4.4 同底数幂的除法
随堂练习
1.计算:16m÷4n÷2等于( D )
A.2m-n-1
B.22m-n-1
C.23m-2n-1
D.24m-2n-1
14.1.4.4 同底数幂的除法
2.下雨时,常常是“先见闪电,后听雷鸣”,这是由于光速比声速快.已 知光在空气中的传播速度约为3×108m/s,而声音在空气中的传播速度约 为3.4×102m/s,则光速是声速的多少倍?(结果保留1位小数)
14.1.4.4 同底数幂的除法
14.1.4.4 同底数幂的除法
学习目标
1.理解并掌握同底数幂的除法法则. 2.能够运用同底数幂的除法法则进行计算.
同底数幂的除法(1)

学生完成
教学难点
会正确的运用同底数幂除法的运算性质进行运算,并能说出每一步运算的依据
教学过程
教学内容
教师活动方式
学生活动方式
一预习展示
二合作探究
三问题置疑
分层训练
五当堂反馈
做一做:
计算下列各式:
(1) = =
(2) ==
(3) ==
(4) ==
你发现了什么?
同底数幂的除法法则的推导
当a≠0 , m、n是正整数,且m>n时
A、m=2n B、m=-2n C、m-2n=1 D、m-2n=1
2、计算:
(1)、 (2)、
(3)、 (4)、
(5)、 (6)、
(7)、 (8)、
(9)、
检查预习情况
教师引出概念。
教师指导强调分类的依据。。
。
教师指生回答。
学生尝试。
学生分类。
合作活动
学生动手操作后,总结三角形三边关系。
归纳法则:
同底数幂的除法:
★。
例题讲解
(1) (2)
(3) (4)
如果将上题中的第四小问中的 改为 又该怎么计算了?
(5)
(6)一颗人造地球卫星运行的速度是7.9×103 m/s,一架喷气式飞机的速度是1.0×103 km/h.人造卫星的速度是飞机速度的倍?
课堂练习:
1、如果 ,则m,n的关系是( )
年级:初一
学科:数学
课题:8.3同底数幂的除法(1)
课型:新授
执笔:颜彦
审核:初一年级组
讲学时间
教学目标
1.能说出同底数幂除法的运算性质,并会用符号表示.
2.会正确的运用同底数幂除法的运算性质进行运算,并能说出每一步运算的依据.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.3.1同底数幂的除法
备课人:余国霞 审核:八年级数学备课组 备课时间:11.18 上课时间:
学习目标:
1.理解和掌握同底数幂的除法和运算法则.
2.运用同底数幂的除法和运算法则,熟练、准确地进行计算.
学习重难点:准确、熟练地运用法则进行计算;根据乘、除互为逆运算关系得出法则. 学习过程
一、自学指导(课本102)
问题1: 叙述同底数幂乘法运算法则: 。
即n
m a a ⋅= (m 、n 是 )
问题2:一种数码照片的文件大小是8
2K ,一个存储量为6
2M (1M=10
2K )的移动存储器能存储多少张这样的数码照片?
问题3:16
2、8
2是同底数幂,同底数幂相除如何计算呢? 请先做如下运算: 填空:
(1)、()82⋅=16
2 (2)、()5355=⋅
(3)、()751010=⋅ (4)、()63a a =⋅
3、除法与乘法两种运算互逆,要求空内所填数,其实是一种除法运算,所以这四个小题等价于:
(1)、 816
22
÷=( ) (2)、3555÷=( ) (3)、571010÷=( ) (4)、3
6a a ÷=( )
问题4:从上述运算能否发现商与除数、被除数有什么关系?
问题5:对于除法运算,在同底数幂相除时,要求除数(或 )不为零,所以同底数幂相除时,底数不能为 。
由此可得到同底数幂的除法运算法则: 。
用符号语言叙述为:n
m
a a ÷= (a 0,m n)。
练习: 1、填空: ①(
)5
7a a ⋅= ②()38m m ⋅=
③()35
12x x x ⋅⋅= ④()()()35b b -⋅=-
2、下面的计算对不对?如果不对,应怎样改正? ①6x ÷3x =2x ②5z ÷5
z =z ③3
a ÷a =3
a ④()4
c -÷()2
c -=2
c -
问题6:先利用除法的意义填空,再利用同底数幂的除法运算法则计算,你能得出什么结论?
(1)、8
8
22÷= (2)、551010÷= (3)、()()7
733-÷-=
(4)、()()8
8
55-÷- = (5)m
m
a a ÷= (a ≠0)
由此得出结论:0
a = (a≠0)。
文字语言叙述为: 。
二、课堂展示
例1:计算⑴3
4
a a ÷ ⑵()4
a -÷()a - ⑶()5
ab ÷()2
ab ⑷2n y +÷2y
(5)、()34
a a ÷- (6)、()3
8a a -÷- (7)、()35
a a ÷- (8)、()0
368125⨯
展示一下自我:
计算①7
x ÷5
x ②()()38xy xy -÷- ③()()3
6xy xy ÷-
④()()3
5
xy xy ÷- ⑤ ()
221082+⨯- ⑥()()3
44
3x x ÷
⑦、()()2
5
y x y x -÷- ⑧、()()2
5
y x y x +-÷-
例2、若2,4==n m
x x
求n m x 23-的值。
分析:先把n
m x 23-化成同底数幂的除法,再运用幂的乘方来计算。
三、堂清检测
1、课本104练习题1
2、已知b a y x ==5,5,试用a ,b 表示y
x 325-。
2、已知3x-y-5=0,试求y
x
28÷的值。
