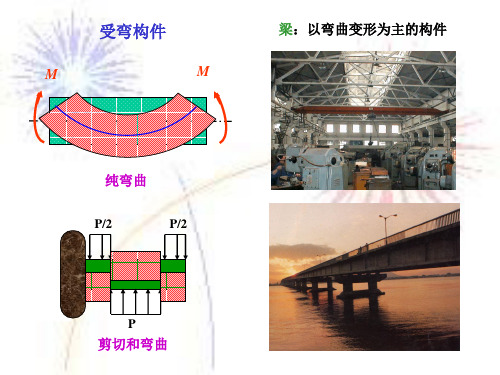
杆件内力计算
杆件与结构的内力计算

FS F Fl
| FS |max F | M |max Fl
M
例题 图示简支梁受均布荷载q的作用,作该梁的剪 力图和弯矩图。
q
A
解: 1、求支反力
B
x
FA
由对称性知: FA FB ql 2
l
FB
ql / 2
2、建立剪力方程和弯矩方程
ql FS ( x) FA qx 2 qx qx2 qLx qx2 M ( x) F x A 2 2 2
M /l
FS
Mb/ l
M
Ma / l
试确定截面C及截面D上的剪力和弯矩
FA
A
2Fl
C D
F
B
FCs F
FCs F
MC Fl
MC Fl
l
l
FCs
MA FA
A
MC 2Fl Fl 0
l
C
MC
MA
FCs
2Fl
MC
C D
FDs F
F
B
MD 0
l
FDs
MD
F
D
B
弯曲内力
FS ( x) FS ( x) dFS ( x) q( x) dx 0
dFS ( x ) q( x ) dx
d2 M ( x) dx
2
q( x )
目录
这些式子的几何意义是: 1、剪力图上某点处切线斜率等于该点处的横向荷载集度, 但符号相反; 2、弯矩图上某点处切线斜率等于该点处的剪力。
A
x
M
a
C
B b
FA
M M ; FB l l
工程力学第六章杆件与结构的内力计算

M
M
弯矩为正
M
M
弯矩为负
试确定截面C及截面D上的剪力和弯矩
FA
A
MA
FA
A
MA
2Fl
lC
l
FCs
l
C MC
2Fl
FCs
MC
C
l
F
B D
FCs F FCs F
M C Fl MC Fl
M C 2Fl Fl 0
F
B
D
FDs
MD
F
DB
FDs F MD 0
1.剪力、弯矩方程:
FS FS (x) M M (x)
F
拉杆
FF
F
压杆
§6–1轴向拉压杆的内力 轴力图
物体在受到外力作用而变形时,其内部各 质点间的相对位置将有变化。与此同时,各质 点间相互作用的力也发生了改变。相互作用力 由于物体受到外力作用而引起的改变量,就是 附加内力,简称内力。
内力分析是解决构件强度,刚度与稳定
性问题的基础。
§6–1轴向拉压杆的内力 轴力图
图和弯矩图。
q
解: 1、求支反力
A
x
B
l
FA
FB
由对称性知: ql
FA FB 2
ql / 2
2、建立剪力方程和弯矩方程
FS
FS (x)
FA
qx
ql 2
qx
ql / 2
M (x)
FA x
qx2 2
qLx 2
qx2 2
M
ql2 / 8
FS ,max
ql 2
M max
ql 2 8
例题 在图示简支梁AB的C点处作用一集中力F,作该
截面法求内力讲解
解: 1. 确定支座反力
B Fx 0 MA 0
FBy
Fy 0
FAx 0 2FPa FPa FBy 3a 0 FAy FBy 2FP 0
FBy
FP 3
FAy
5FP 3
2FP FQE
A 5FP
C E ME
3
Fy 0
2FP
FQE
5FP 3
0
C
a
FAy
b l
FPb l
+
FP a
-
l FQ图
FPab M图
l
B FBy
A FPb
l
FQ
M
MA 0
Fy 0
FBy
FP a l
FAy
FPb l
FQ
FQ
FPb l
(0 x a)
M
M FPb x (0 x a)
l
B
FQ
FP a l
(a x l)
FPa M FPa (l x)
平: 对留下部分写平衡方程求出内力的值
FQ(+)
FQ(+)
M(+)
M(+)
(1)平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 (2)取简单部分作为隔离体,列平衡方程时,尽量使一个方程含有一个未知量
例1 求E截面内力
A FAx
FAy
2FP FPa
C
D
1.5a E
a
a
a
2. 用截面法研究内力
M JK J
F QJK
M JK J
工程力学第4次作业解答杆件的内力计算与内力图

6 .剪力 F 、弯矩 M 与载荷集度 q 三者之间的微分关系是 dM ( x)= F ( x ) 、dx《工程力学》第 4 次作业解答(杆件的内力计算与内力图)2008-2009 学年第二学期一、填空题1.作用于直杆上的外力(合力)作用线与杆件的轴线重合时,杆只产生沿轴线方向的 伸长或缩短变形,这种变形形式称为轴向拉伸或压缩。
2.轴力的大小等于截面截面一侧所有轴向外力的代数和;轴力得正值时,轴力的方向 与截面外法线方向相同,杆件受拉伸。
3.杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时,杆件任意 两相邻横截面产生绕杆轴相对转动,这种变形称为扭转。
4.若传动轴所传递的功率为 P 千瓦,转速为 n 转/分,则外力偶矩的计算公式为M = 9549 ⨯ Pn。
5.截面上的扭矩等于该截面一侧(左或右)轴上所有外力偶矩的代数和;扭矩的正负, 按右手螺旋法则确定。
S S dF ( x )S dx= ±q ( x ) 。
7.梁上没有均布荷载作用的部分,剪力图为水平直线,弯矩图为斜直线。
8.梁上有均布荷载作用的部分,剪力图为斜直线,弯矩图为抛物线。
9.在集中力作用处,剪力图上有突变,弯矩图上在此处出现转折。
10.梁上集中力偶作用处,剪力图无变化,弯矩图上有突变。
二、问答题1.什么是弹性变形?什么是塑性变形?解答:在外力作用下,构件发生变形,当卸除外力后,构件能够恢复原来的大小和形状,则这种变形称为弹性变形。
如果外力卸除后不能恢复原来的形状和大小,则这种变形称为塑性变形。
2.如图所示,有一直杆,其两端在力 F 作用下处于平衡,如果对该杆应用静力学中“力的可传性原理”,可得另外两种受力情况,如图(b )、(c )所示。
试问:(1)对于图示的三种受力情况,直杆的变形是否相同? (2)力的可传性原理是否适用于变形体?问答题 2 图问答题 3 图。
解答:(1)图示的三种情况,杆件的变形不相同。
Mathcad - 杆件计算

+
1
Lpf = 15.537
cm
Lpl := 50
cm
(一)、面板采用花纹钢板:
δm := 4.5
mm
(二)、纵梁选用[10,布置见下图:
(三)、中间横梁选用I22a
1、荷载计算
a、自重: 钢材重度: γg := 7.85
t
γz := 1.2
m3
面板
qmb := δm⋅10− 3⋅Lj⋅γg
qmb = 0.106
δ := 12 mm
焊缝高度:
hf := 0.8 cm
焊缝的强度设计值:
1、上弦杆端节点: N1 := −58
ft := 16000
t
m2
N1 = −58
t
焊缝面积: 焊缝长度: 2、下弦杆端节点:
Af1 :=
N1 ⋅104 ft
Lf1 :=
Af1 2 ⋅ hf ⋅ 0.7
+1
N3 := 31.3
Af1 = 36.25
M :=
R 4
⋅⎛⎜ ⎝
aL
−
LB ⎞⎟ 2⎠
M = 3.02
t⋅m
Q := R 2
Q = 28.76
t
M
8
σlz :=
M
π 32
⋅dB3
t
σr := 1.45⋅104
m2
σlz = 9.114 × 103
t m2
3、轴承板 容许应力
采用 容许剪应力
σlz < σr 满足要求
τ := 4 ⋅ Q
3
Nmax1 := Pe1
Nmax1 = 6.53
t
σ51 :=
工程力学工程力学杆件内力

详细描述
在机械工程中,各种机械设备都需要进行杆 件内力分析。通过分析杆件的内力分布,可 以优化机械设备的结构设计,提高设备的稳 定性和使用寿命,确保机械设备在运行过程
中的安全可靠。
06 结论
总结
01
杆件内力是工程力学中的重要概念, 它描述了杆件在受力作用下的内部应 力分布情况。通过分析杆件的内力, 可以评估杆件的承载能力和安全性能 ,为工程设计和施工提供重要的依据 。
02
在本篇论文中,我们介绍了工程力学 中杆件内力的基本概念、计算方法和 应用实例。首先介绍了杆件内力的定 义和分类,然后详细阐述了如何通过 截面法和平衡法计算杆件的内力。此 外,还结合实际工程案例,介绍了如 何运用杆件内力分析解决实际问题。
03
通过对杆件内力的研究和分析,我们 可以更好地理解杆件在受力作用下的 行为和性能,为工程实践提供更加科 学和可靠的依据。同时,随着科学技 术的发展和工程实践的深入,我们需 要不断探索新的方法和手段,以更加 精确和高效地分析杆件内力,推动工 程力学的发展和应用。
弯曲力是杆件内力的一种,当杆件受到外力作用导致发生弯曲变形时,杆件内部会产生弯曲力。弯曲 力的方向与外力的方向相反,大小与外力和杆件截面积有关。弯曲力会导致杆件的弯曲变形,对结构 的承载能力和稳定性有一定影响。
04 内力分析的方法
解析法
总结词
通过数学解析公式计算杆件内力。
详细描述
解析法基于弹性力学理论,通过数学公式推导杆件的内力分布,适用于简单结构 和理想化的模型。
05 工程实例
桥梁工程中的杆件内力分析
总结词
桥梁工程中,杆件内力分析是确保结构安全和稳定的关键环节。
详细描述
在桥梁工程中,杆件内力分析是必不可少的环节。通过分析桥梁各部分杆件的内力分布, 可以确定杆件的承载能力和安全储备,从而优化结构设计,提高桥梁的稳定性和安全性。
第五章 杆件的内力与内力图

Mz (x) = m - FRAx = m (l -x ) / l (a < x≤ l ) 3°画 FQy (x)图和 Mz (x)图。
四、剪力、弯矩和荷载集度之间的关系
y FP
q(x) MZ(x) q(x) MZ(x)+d MZ(x) C FQY(x)+d FQY(x) dx
x
x dx
FQY(x)
FRA FQy
(KN)
FRB
60 20 x = 3.6m
Mz6 = 72 ×12 - 160 - 20×10 ×5 = 0
88
当FQY(x)=0时, Mz (x)有极值。
Mz x = 3.6m处, FQY(x)=0 。(KNm)
16 113.6 144
80
即
Mz7 = 72 ×5.6 - 160 - 20×3.6 ×3.6 / 2 = 113.6 KNm
MZ —— 弯矩
A FRA
x
m
C
MZ
m FQY
规 定:
∑FP
FQY 下剪力正, 反之为负
∑M
MZ
MZ
∑M
MZ:
上凹下凸弯矩正, 反之为负
a A
FP1
m m
FP2 B
由∑Fyi=0, FRA- FP1 - FQY =0
x
FRA y A
x
FRB FP1
m
C
得 FQY = FRA- FP1
x = 2m 时 , FN (x) = - 1KN。
3KN
A 2m 3
B 2KN/ m C 2m 2m
D 1KN
FN (KN) 1
规律:没有力作用的杆段,轴力为常数;
分布荷载为常数的杆段,轴力线性变化;
求杆件的内力方法

求杆件的内力方法
杆件的内力方法主要有以下几种:
1. 静力法:通过平衡条件,分析杆件的受力情况,求解各个连接点的内力。
2. 切割法:将杆件沿着一条或多条截面切割,分析切割面的内力平衡关系,求解切割面上的内力。
3. 弯矩法:将杆件看作是梁,根据梁的弯曲理论,通过计算弯矩来求解杆件内力。
4. 变形法:根据杆件的变形情况,利用杆件的本构关系和变形方程,求解杆件内力。
5. 外力法:根据外力作用在杆件上的情况,利用杆件的受力平衡条件,求解杆件内力。
根据具体的杆件结构和受力情况,可以选择合适的内力方法来求解杆件的内力。
不同的方法适用于不同的情况,有时也需要结合多种方法进行分析。
