t分布和标准正态分布
标准正态分布和t分布的关系和区别

标准正态分布和t分布的关系和区别
标准正态分布和 t 分布都是统计学中常用的概率分布,它们之间有一些关系和区别。
关系:
1、起源:
标准正态分布:是均值为0,标准差为1的正态分布,通常表示为 Z ~ N(0,1)。
t 分布:是由样本容量较小的情况下,对总体均值的抽样分布。
它在样本容量较大时趋向于标准正态分布。
2、形状:
标准正态分布:具有对称的钟形曲线。
t 分布:在样本容量较小的情况下,相比标准正态分布,其分布形状更加扁平,尖峭。
区别:
1、参数:
标准正态分布:完全由均值和标准差确定,无其他参数。
t 分布:需要指定自由度(degrees of freedom)作为参数。
自由度是样本容量与总体方差之比。
2、应用场景:
标准正态分布:通常用于处理已知总体方差的情况。
t 分布:用于处理总体方差未知,通过样本估计得到的情况。
3、形状稳定性:
标准正态分布:形状参数固定,与样本容量无关。
t 分布:随着自由度的增加,t 分布逐渐接近标准正态分布。
医学统计学__问答题

1、标准正态分布(u分布)与t分布有何异同?相同点:集中位置都为0,都是单峰分布,是对称分布,标准正态分布是t分布的特例(自由度是无限大时)不同点:t分布是一簇分布曲线,t 分布的曲线的形状是随自由度的变化而变化,标准正态分布的曲线的形状不变,是固定不变的,因为它的形状参数为1。
3、简述直线回归与直线相关的区别。
1资料要求上不同:直线回归分析适用于应变量是服从正态分布的随机变量,自变量是选定变量;直线相关分析适用于服从双变量正态分布的资料。
2 两种系数的意义不同:回归系数是表明两个变量之间数量上的依存关系,回归系数越大回归直线越陡峭,表示应变量随自变量变化越快;相关系数是表明两个变量之间相关的方向和紧密程度的,相关系数越大,两个变量的关联程度越大。
第一章医学统计中的基本概念2、抽样中要求每一个样本应该具有哪三性?从总体中抽取样本,其样本应具有“代表性”、“随机性”和“可靠性”。
(1)代表性: 就是要求样本中的每一个个体必须符合总体的规定。
(2)随机性: 就是要保证总体中的每个个体均有相同的几率被抽作样本。
(3)可靠性: 即实验的结果要具有可重复性,即由科研课题的样本得出的结果所推测总体的结论有较大的可信度。
由于个体之间存在差异, 只有观察一定数量的个体方能体现出其客观规律性。
每个样本的含量越多,可靠性会越大,但是例数增加,人力、物力都会发生困难,所以应以“足够”为准。
需要作“样本例数估计”。
3、什么是两个样本之间的可比性?可比性是指处理组(临床设计中称为治疗组)与对照组之间,除处理因素不同外,其他可能影响实验结果的因素要求基本齐同,也称为齐同对比原则。
实习一统计研究工作的基本步骤1、什么叫医学统计学?医学统计学与统计学、卫生统计学、生物统计学有何联系与区别?医学统计学:是运用统计学原理和方法研究生物医学资料的搜索、整理、分析和推断的一门学科统计学:是研究数据的收集、整理、分析与推断的科学。
卫生统计学:是把统计理论、方法应用于居民健康状况研究、医疗卫生实践、卫生事业管理和医学科研的一门应用学科。
t分布和f分布的表达式关系

t分布和f分布的表达式关系题目:t分布和f分布的表达式关系引言:概统课上,我们经常会接触到t分布和f分布,它们作为统计学中重要的概率分布函数,常常用于计算统计推断和假设检验。
本文将重点讨论t分布和f分布的定义、性质以及它们之间的关系。
通过一步一步的解析,我们将揭示t分布和f分布之间的密切联系。
第一部分:t分布的定义和性质(一)t分布的定义t分布是由英国统计学家William Gosset(更为众所周知的名字是“学生”)在1908年提出的。
它是通过正态分布的样本标准差来进行推断的。
具体而言,t分布是用来估计总体均值的分布,当总体标准差未知且样本容量较小时,t分布的应用更为广泛。
(二)t分布的概率密度函数t分布的概率密度函数表达式为:t分布的性质1. t分布的均值为0:t分布的平均值为0,即t分布的概率密度函数在t=0处达到最大值。
2. t分布的方差为n / (n-2):方差的计算公式为n / (n-2),其中n为自由度。
随着自由度的增加,t分布的方差越来越逼近于1。
第二部分:f分布的定义和性质(一)f分布的定义f分布是由英国统计学家Ronald Fisher在1920年提出的。
它是用来比较两个正态分布总体方差差异的分布。
一般而言,当我们希望比较两个总体方差时,就会使用f分布。
(二)f分布的概率密度函数f分布的概率密度函数表达式为:f分布的性质1. f分布的均值为(n / (n-2)) ×(n / (n-2)):均值的计算公式为(n / (n-2)) ×(n / (n-2)),其中n为第一个总体的自由度。
2. f分布的方差为[(2n^2(n+m-2))/(m(n-2)^2(n-4))] ×(m / (m-2)):方差的计算公式相对较复杂,涉及两个总体的自由度。
t分布公式了解t分布的关键公式

t分布公式了解t分布的关键公式t分布(t-distribution)是统计学中常用的概率分布之一,它在小样本情况下对总体均值的推断起到了重要作用。
学习和理解t分布的关键公式可以帮助我们更好地应用t分布进行统计推断和假设检验。
本文将介绍t分布的概念,并详细解释t分布的关键公式。
一、t分布的概念t分布是由英国统计学家威廉·塞特勒特(William Sealy Gosset)于1908年提出的。
在实际应用中,当总体标准差未知或样本容量较小时,使用t分布而不是正态分布来进行统计推断更为合适。
二、t分布的概率密度函数t分布的概率密度函数可以用以下公式表示:```latexf(t) = [Γ((v+1)/2) / √(πv)Γ(v/2)] * (1 + t²/v)^(-(v+1)/2),```其中,t为随机变量,v为自由度,Γ表示伽玛函数。
三、t分布的关键公式1. t值的计算当样本均值服从正态分布,而总体标准差未知时,我们可以通过将样本均值与总体均值进行比较,计算得到t值来进行统计推断。
计算t值的公式为:```latext = (x - μ) / (s/√n),```其中,x为样本均值,μ为总体均值,s为样本标准差,n为样本容量。
2. t分布的临界值在假设检验中,我们需要比较计算得到的t值与t分布的临界值来判断是否拒绝原假设。
t分布的临界值与显著性水平和自由度有关。
常见的t分布临界值有单侧临界值和双侧临界值。
以95%的显著性水平和自由度为例,双侧临界值分别为t0.025和-t0.025,单侧临界值为t0.05。
3. t分布与标准正态分布的关系当自由度足够大时(一般认为大于30),t分布近似于标准正态分布。
在实际应用中,当样本容量较大时,可以使用标准正态分布的临界值作为t分布的近似临界值,简化计算过程。
四、总结t分布是小样本条件下进行统计推断和假设检验的重要工具。
了解t分布的关键公式可以帮助我们理解和应用t分布,进行科学准确的统计分析。
t分布

第二节t分布一.t分布(t-distribution)(一)u分布在前一章中,我们已经讲述了正态分布(normal distribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
正态分布有两个参数,μ和σ,决定了正态分布的位置和形态。
为了应用方便,常将一般的正态变量X通过u变换[]转化成标准正态变量u,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standard normal distribution),亦称u分布。
根据中心极限定理,通过上述的抽样模拟试验表明,在正态分布总体中以固定n (本次试验n=10)抽取若干个样本时,样本均数的分布仍服从正态分布,即N (μ,σ)。
所以,对样本均数的分布进行u变换[],也可变换为标准正态分布N (0,1)(二)t分布由于在实际工作中,往往σ是未知的,常用s作为σ的估计值,为了与u变换区别,称为t变换t=,统计量t 值的分布称为t分布。
t分布有如下特征:1.以0为中心,左右对称的单峰分布;2.t分布是一簇曲线,其形态变化与n(确切地说与自由度ν)大小有关。
自由度ν越小,t分布曲线越低平;自由度ν越大,t分布曲线越接近标准正态分布(u分布)曲线,如图4.1。
t=图4.1自由度为1、5、∞的t分布对应于每一个自由度ν,就有一条t分布曲线,每条曲线都有其曲线下统计量t 的分布规律,计算较复杂。
因此,统计学家上根据自由度ν的大小与t分布曲线下面积的关系,编制了附表2,t界值表,以便于应用。
表中的横标目为自由度ν,纵标目为概率P,表中数字表示自由度ν为某值时,P为某值时,t的界值。
因t分布是以0为中心的对称分布,故附表中只列出正值,如果算出的t 值为负值,可以用绝对值查表。
t分布曲线下面积为95%或99%的界值不是一个常量,而是随着自由度大小而变化的,分别用和表示。
T分布(t-distribution)(一)u分布正态分布(normal distribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
t分布例题及答案

t分布例题及答案1、下列关于t分布的描述正确的是( )A.曲线在t= 1处最高B.t值只能是正数C.t分布的形态变化与自由度有关D.t分布就是标准正态分布E.t分布的概率密度曲线是一条曲线正确答案: C .2、下列关于分布与正态分布的关系,正确的是( )A.均以0为中心,左右对称B.随样本含量增大,t分布逼近标准正态分布C.样本含量无限增大,两者分布完全一致D.总体均数增大,曲线变得瘦长正确答案: B3、t分布与正态分布的区别是前者的分布形态是不对称的,后者是对称的。
A.正确B.错误正确答案: B4、t分布有( )个参数?A.3B.2C.1D.4正确答案: C5、当测量次数趋近于无穷时,u分布曲线就是分布曲线。
( )A.正确B.错误正确答案: B6、无限次的测量,随机误差服从t分布曲线。
( )A.正确B.错误.正确答案: B7、当正态总体的方差已知时,在小样本条件下,估计总体均值使用的分布是t 分布。
A.正确B.错误正确答案: B8.假设检验中的t检验统计量服从自由度为v的t分布。
A.正确B.错误.正确答案:错误9.样本量很大时,可用正态分布近似t分布来计算均数的可信区间。
A.正确B.错误.正确答案:正确10.若随机误差项服从t分布,则OLS估计量不再具有BLUE性质。
A.正确B.错误正确答案:错误11.下列关于以0为中心的t分布的叙述,错误的是( )A.t分布图是一簇曲线B.t分布图是单峰分布C.当v→∞时,t→uD.t分布图以0为中心,左右对称E.相同v时, |t |越大,P越大正确答案:相同v时,| t |越大,P越大12.当自由度趋向于无穷大时,t分布与( ) 分布重合。
正确答案:正态13.当随机变量t服从自由度为n- 1的t分布时,应记为( )A.t~t(n-1)B.t~t(n)C.t~t(n+1)D.t~t(1)正确答案: t~t(n-1)14.下列关于t分布与正态分布的描述正确的是( ) 。
t分布自由度大数定理

t分布自由度大数定理是指当自由度趋向于无穷大时,t分布逼近于标准正态分布的定理。
它是统计学中的一个重要定理,用于理解 t分布与正态分布之间的关系以及
t检验的有效性。
下面是关于 t分布自由度大数定理的详细解释:
1.t分布的定义:t分布是用于描述小样本情况下统计量(如样本均值)的分
布,它类似于标准正态分布,但具有更宽的尾部。
t分布取决于自由度参数,当自由度较小时,其形状更宽,随着自由度的增加,其形状逐渐趋于标准正
态分布。
2.大数定理:大数定理是数理统计学中的一个基本定理,它指出当样本容量
足够大时,样本均值会以很高的概率收敛于总体均值。
在 t分布自由度大数
定理中,它说明当 t分布的自由度足够大时,t分布会逐渐趋于标准正态分
布。
3.应用:t分布自由度大数定理对于统计推断是至关重要的,特别是在小样本
情况下。
它说明了当样本容量足够大时,t检验可以近似为标准正态分布的
检验,从而使得在实践中可以更准确地进行统计推断。
这对于理解和应用 t
检验、置信区间估计等具有重要意义。
总的来说,t分布自由度大数定理表明了 t分布和标准正态分布之间的关系,并指
出当自由度足够大时,t分布可以近似为标准正态分布。
这一定理在统计学中有着
重要的理论和应用意义。
t 分布

⑴ 自由度为(n-1),而不是n。
⑵ t分布表具有对称性,t值大于等 于某一特定值的概率与t值小于等于该
特定值相反数的概率相等。
9
数学期望与方差:
设T~t (n),则E(T)=0,D(T)= n/(n-2) (n≥2)
小组成员: 主讲: 叶娇旗14、 PPT制作: 侯晓爽04、刘雨49、李舒婷03、 收集资料:花蕾17、王茜13
t 分布
主讲人:叶娇旗 营销131班
1
定义:
设X~N(0, 1), Y~ 2(n),X与Y相互独立, 则称随机变量 X T Y n 所服从的分布为自由度为n的t分布。 记为T~t(n).又称为学生氏分布
2
图像:
3
特点:
1、t分布的概率密度函数是偶函数,所以图形关于y轴对称。 2、其形态变化与n(确切地说与自由度ν)大小有关 自由度n越小,t分布曲线越低平; 自由度n越大,t分布曲线越接近标准正态分布曲线
10
0.05
0.05
-1.812
0
1.812
6Leabharlann t分布表举例:例:变量 X表示面包房每日出售的面包量,在15天内,出 售面包的样本方差为16。假定真实的出售量为70条,求任 意15天内出售面包平均数量为74条的概率。 分析:本例中已知样本方差S² =16,则S=4,总体均值(真 实的出售量)=70,运用t变量公式得:
4
t分布的均值与标准正态分布均值相
同,为0,但方差为k/(k-2)。由此,在 求t分布的方差时定义自由度必须大于2。
标准正态分布的方差等于1,因此,t
分布方差总大于标准分布的方差,也就 是说,t分布比正态分布略“胖”些。
5
t分布表的使用:
卫生统计学名词解释

脉搏(次/分)、血压(KPa)等。
(2)计数资料:将观察单位按某种属性或类别分组,所得的观察单位数称为计数资料
(count data)。计数资料亦称定性资料或分类资料。其观察值是定性的,表现为互不相容的
值,记为P(A),P(A)越大,说明A事件发生的可能性越大。0﹤P(A)﹤1。
频率:在相同的条件下,独立重复做n次试验,事件A出现了m次,则比值m/n称为随
机事件A在n次试验中出现的频率(freqency)。当试验重复很多次时P(A)= m/n。
6.随机误差:随机误差(random error)又称偶然误差,是指排除了系统误差后尚存的
3、生存时间:是任何两个有联系事件之间的时间间隔。
4、截尾值:指在随访过程中,由于某种原因未能观察到病人的明确结局(即终止事件),所以不知道该病人的确切生存时间,它提供的生存时间的信息是不完全的。
5、生存函数:又称为累积生存率,简称生存率。表示具有协变量X的观察对象其生存时间T大于时间t的概率,常用S(t,X)=P(T>t,X)表示。
3均方:每种来源的离均差平方和用相应的自由度去除,可得到平均的离均差平方和,简称均方(mean square,MS)
4、LSD-t检验:即最小显著性差异t检验,适用于一对或几对在专业上有特殊意义的样本均数间的比较。
5、SNK(student-Newman-Keuls)法:又称q检验,是根据q值的抽样分布作出统计推论,适用于多个样本均数两两之间的全面比较。
3、Q型聚类:又称样品聚类,是指将n个样品归类的方法,其目的是找出样品间的共性。
1、潜在变量(latent variable):不能或不易直接观测得到的变量。这种变量往往是根据某种理论假设的。如:交感神经等。
5.3 t分布的概念与特征

第五章 参数估计基础三、t 分布的概念与特征正态分布2在统计应用中,可以把任何一个均数为µ,标准差为σ的正态分布N (µ , σ 2 )转变为 µ=0 σ=1的标准正态分布,即将正态变量值X 用 来代替。
由于 服从正态分布,故 服从标准正态分布N (0,1)。
X XX Z s m- = sm- = X Z 一、t 分布的概念3实际资料的分析中,由于σ 往往未知,故标准化转换演变为: 服从υ = n 1 的 t 分布,即:XS X t m- = nS X S X X / mm- = - 45υ=∞(标准正态分布)υ=5υ=1 0 1 2 3 4 51 2 3 4 5 f (t ) 0.10.20.361.t 分布曲线是单峰分布,它以0为中心,左右对称。
2.t 分布的形状与样本例数 n 有关。
自由度越小,则越大,t 值越分散,曲线的峰部越矮,尾部则偏高。
3.当 n →∞时,则 S 逼近 σ,t 分布逼近标准正态分布。
t 分布不是一条曲线,而是一簇曲线。
t 分布曲线特点:X S 8与单侧概率相对应的 t 值用 表示,与双侧概率相对应的t 值用 表示。
由于 t 分布是以0为中心的对称分布,表中只列出了正值,故查表时,不管 t 值正负只用绝对值表示。
正确使用 t 界值表( ) n a , t ( ) n a , 2 / t 9。
t分布 z分布 标准正态分布 泊松分布 二项分布

t分布 z分布标准正态分布泊松分布二项分布标题:深入理解统计学中的常见分布在统计学中,分布是一种描述数据分布情况的概率模型,常见的包括t 分布、z分布、标准正态分布、泊松分布和二项分布。
通过对这些分布的深入理解,我们可以更好地分析和解释数据,为决策提供支持。
本文将围绕这几种常见的分布展开探讨,并分享个人对这些分布的理解和观点。
1. t分布t分布是由威廉·塞韦里德(William Sealy Gosset)发现的,用于小样本量情况下总体标准差未知的抽样分布。
t分布的特点是钟形、对称,但比标准正态分布更加平缓。
在实际应用中,t分布常用于构建置信区间和进行假设检验,尤其适用于小样本量的情况。
与z分布相比,t分布更加灵活,因此在统计推断的过程中发挥着重要作用。
2. z分布z分布,又称标准正态分布,是一种特殊的正态分布,其均值为0,标准差为1。
在统计学中,z分布常用于大样本量情况下对总体均值的假设检验和置信区间估计。
通过z分布,我们可以进行标准化处理,将不同分布的数据转化为标准正态分布,从而进行比较和分析。
3. 标准正态分布标准正态分布是统计学中最为常见的分布之一,其概率密度函数呈现钟形曲线,均值为0,标准差为1。
在实际应用中,我们经常将不同数据转化为标准正态分布,以便进行统计分析和推断。
4. 泊松分布泊松分布描述了在特定时间或空间内随机事件发生的次数。
泊松分布的特点是取值范围为0至正无穷,且分布呈现右偏态。
在实际应用中,泊松分布常用于描述单位时间或单位空间内事件发生的概率,比如通信方式呼叫次数、交通事故发生次数等。
5. 二项分布二项分布描述了在n次独立重复实验中成功事件发生的次数。
二项分布的特点是取值范围为0至n,且分布呈现对称性。
在实际应用中,二项分布常用于描述二分类结果的概率,比如硬币抛掷结果、产品合格率等。
总结回顾:通过本文的探讨,我对t分布、z分布、标准正态分布、泊松分布和二项分布有了更加深入的理解。
浅谈正态分布与t分布
• t分布
少量数据的处理--t分布曲线
t分布
t分布的特点可归纳如下:
• • ①t分布的平均值为0。 ②是对于平均值0对称的分布,分布左侧t为负值,分布右侧 t为正 值。 ⑧t变量取值在-∞一+∞之间。
•
• ④当样本容量趋于∞时,t分布为正态分布,方差为1,而当n-1大于20 以上时,t分布接近正态分布,方差大于1,随n-1之增大而方差渐趋于 1,当n-1<20时,t分布与正态分布相差较大,随n-1减少,离散程度 (方差)越大,分布中间部分低面分布的尾部较高
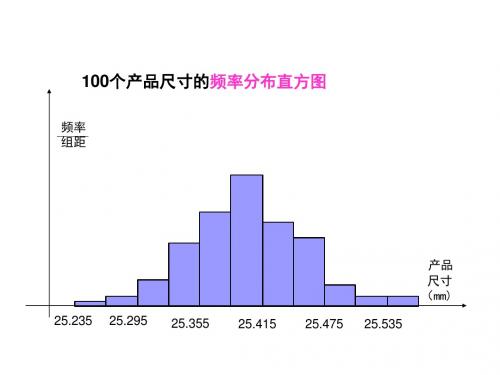
频率 组距
总体密度曲 线
产品 尺寸 (mm)
高尔顿板
11
Y
总体密度曲 线
0
X
定义
• 精确度不同对比
s的意义
总体平均数反映总体随机变量的 平均水平 总体标准差反映总体随机变量的 集中与分散的程度
s1 s2
平均数
产品 尺寸 (mm)
• 平均值和标准偏差
ቤተ መጻሕፍቲ ባይዱ
• 标准正态分布
正态总体的函数表示式 1 f ( x) e 2 s
• P和 α
• 例如:
• 置信区间
• 置信区间置信限
例1
• 续上
对比
例.
•延伸
对数正态分布
对数正态分布在分析上的应用
• 采集的土壤样品经风干后,用2mm的尼 龙筛筛除土壤中比较大的杂物和石砾,剩 余的土壤样品进一步用玛瑙研钵研磨,再 过100目的尼龙筛获得粒度比较均匀的样品。 样品采用HNO3-HCLO4-HF消解,元素(Pb、 Cu、Zn、Cd、V、Se、Ti)含量用电感耦合 等离子体原子发射光谱法测定。为了控制 测定的准确度,在进行上述元素分析时, 每10个测定样品用标准土壤样品校验。 10%-20%的平行样分析用于控制实验的精 密度。
T分布(近似标准正态分布)

T分布(近似标准正态分布)1.1 定义定义:假设X服从标准正态分布N(0,1),Y服从卡⽅分布,那么的分布称为⾃由度为n的t分布,记为。
T分布密度函数其中,Gam(x)为伽马函数。
可⽤于两组独⽴计量资料的假设检验。
由于在实际⼯作中,往往σ(总体⽅差)是未知的,常⽤s(样本⽅差)作为σ总体⽅差的估计值,为了与u变换(正态化变换)区别,称为t变换,统计量t 值的分布称为t分布。
【u分布也叫标准正态分布】u变换:[(X-µ)/σ]转化成标准正态变量u,以使原来各种形态的正态分布都转换为µ=0,σ=1的标准正态分布(standard normaldistribution),亦称u分布。
在和中,t-分布(t-distribution)⽤于根据⼩样本来估计呈且⽅差未知的总体的均值。
如果总体⽅差已知(例如在样本数量⾜够多时),则应该⽤正态分布来估计总体均值。
经常应⽤在对呈的总体的进⾏估计。
它是对两个差异进⾏测试的学⽣t测定的基础。
t检定改进了Z检定(en:Z-test),不论样本数量⼤或⼩皆可应⽤。
在样本数量⼤(超过120等)时,可以应⽤Z检定,但Z检定⽤在⼩的样本会产⽣很⼤的误差,因此样本很⼩的情况下得改⽤学⽣t检定。
t分布曲线形态与n(确切地说与⾃由度df)⼤⼩有关。
与标准正态分布曲线相⽐,⾃由度df越⼩,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈⾼;⾃由度df愈⼤,t分布曲线愈接近正态分布曲线,当⾃由度df=∞时,t分布曲线为标准正态分布曲线。
当总体的是未知的但却⼜需要估计时,我们可以运⽤t-分布。
【特征】:(1)以0为中⼼,左右对称的单峰分布;(2)其数学期望E(Z) = 0,n>1;⽅差D(Z)=n/n-2 , n>2 。
(3)t分布是⼀簇曲线,其形态变化与n(确切地说与df)⼤⼩有关。
⾃由度df越⼩,t分布曲线越低平;⾃由度df越⼤,t分布曲线越接近标准正态分布(u分布)曲线;(4)随着⾃由度逐渐增⼤,t分布逐渐接近标准正态分布。
卡方分布和正态分布的关系

卡方分布和正态分布的关系
联系:随看自由度增大t分布趋近于标准正态分布;当n\ue30时二者相差很小;当n∞时二者重合;区别:①正态分布是与自由度无关的一条曲线,t分布是依自由度而变的一组曲线。
t分布较正态分布顶部略低而尾部稍高,标准正态分布是正态分布的一种特殊形式,就像正方形与长方形的关系,前者包含于后者之中。
在概率论和统计学中,可简称为t分布,用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知,则应该用正态分布来估计总体均值。
t分布的概念及表和查表方法

t分布介绍在概率论和统计学中,学生t-分布(t-distribution),可简称为t分布,用于根据小样本来估计呈正态分布且方差未知的总体的均值。
如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
t分布曲线形态与n(确切地说与自由度df)大小有关。
与标准正态分布曲线相比,自由度df越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度df愈大,t分布曲线愈接近正态分布曲线,当自由度df=∞时,t分布曲线为标准正态分布曲线。
目录1历史2定义3扩展4特征5置信区间6计算历史在概率论和统计学中,学生t-分布(Student's t-distribution)经常应用在对呈正态分布的总体的均值进行估计。
它是对两个样本均值差异进行显著性测试的学生t测定的基础。
t检定改进了Z检定(en:Z-test),不论样本数量大或小皆可应用。
在样本数量大(超过120等)时,可以应用Z检定,但Z检定用在小的样本会产生很大的误差,因此样本很小的情况下得改用学生t检定。
在数据有三组以上时,因为误差无法压低,此时可以用变异数分析代替学生t检定。
当母群体的标准差是未知的但却又需要估计时,我们可以运用学生t-分布。
学生t-分布可简称为t分布。
其推导由威廉·戈塞于1908年首先发表,当时他还在都柏林的健力士酿酒厂工作。
因为不能以他本人的名义发表,所以论文使用了学生(Student)这一笔名。
之后t检验以及相关理论经由罗纳德·费雪的工作发扬光大,而正是他将此分布称为学生分布。
定义由于在实际工作中,往往σ是未知的,常用s作为σ的估计值,为了与u变换区别,称为t变换,统计量t 值的分布称为t分布。
假设X服从标准正态分布N(0,1),Y服从分布,那么的分布称为自由度为n 的t分布,记为。
分布密度函数,其中,Gam(x)为伽马函数。
扩展正态分布(normal distribution)是数理统计中的一种重要的理论分布,是许多统计方法的理论基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数理统计实验
t分布与标准正态分布
院(系):
班级:
成员:
成员:
成员:
指导老师:
日期:
目录
t分布与标准正态分布的关系 (1)
一、实验目的 (1)
二、实验原理 (1)
三、实验容及步骤 (1)
四、实验器材 (5)
五、实验结果分析 (5)
六、实验结论 (6)
t分布与标准正态分布的关系
一、实验目的
正态分布是统计中一种很重要的理论分布,是许多统计方法的理论基础。
正态分布有两个参数,μ和σ,决定了正态分布的本质。
为了应用和计算方便,常将一般的正态变量X通过μ变换[(X-μ)/σ]
转化成标准正态变量μ,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布,亦称μ分布。
对于标准正态分布来说,μ是
数据整体的平均值,σ是整体的标准差。
但实际操作过程中,人们往往难以获得μ和σ。
因此人们只能通过样本对这两个参数做出估计,用样本平均值和样本标准差代替整体的平均值和标准差,从而得出了
t分布。
另外从图像的层面说,正态分布的位置和形态只与μ和σ有关,而t分布不只与样本平均值和样本标准差有关,还与自由度相关。
通过实验了解t分布与标准正态分布之间的关系。
二、实验原理
运用EXCEL软件验证t分布与标准正态分布的关系,绘制相应的统计图表进行分析。
三、实验容及步骤
1.打开Excel文件,将“t分布与标准正态分布N(0,1)”合并并居中,黑体,20字号,红色;
2.选中文件,选项,自定义功能区,加载开发工具.在开发工具中插入滚动条,调节滚动条大小;
3.设置A2单元格格式,数字自定义区” !n=#,##0;[红
色]¥-#,##0”.然后左对齐,设置为红色;
4.设置滚动条格式,单元格连接为$A$2;
5.在A3中输入-4.0,单击开始,填充,序列,设置等差序列,步长0.1,当出现十字下拉即出现等差序列;
6.在B3中插入标准正态分布函数”=NORM.S.DIST(A3,0)”,十字出现向下拉;
7.在C3中插入t分布函数”=T.DIST(A3,$A$2,0)”,十字出现向下拉;
8.选中整体区域,作X,Y(散点图),设置标题,横纵截距,箭头方向。
四、实验器材
计算机办公软件
五、实验结果分析
t分布和标准正态分布的动态演示
0.45
0.40
0.35
0.30
0.25
0.20
0.15
0.10
0.05
0.00
-5.0-4.0-3.0-2.0-1.00.0 1.0 2.0 3.0 4.0 5.0
N(0,1)t(n)
六、实验结论
在讨论t分布与标准正态分布之间的关系时,运用电脑软件能较好的模拟出他们之间的关系,随看自由度增大t分布趋近于标准正态分布。
区别:
1.正态分布是与自由度无关的一条曲线;t分布是依自由度而变的一组曲线;
2.t分布较正态分布顶部略低而尾部稍高。
