七年级数学几何证明题(典型)

合集下载

(完整版)七年级几何证明题训练(含答案),推荐文档

1. 已知：如图11所示，∆ABC 中，∠=C 90于E ，且有AC AD CE ==。

求证：DE =122. 已知：如图求证：BC ＝3. 已知：如图13所示，过∆ABC 的顶点A ，在∠A 内任引一射线，过B 、C 作此射线的垂线BP 和CQ 。

设M 为BC 的中点。

求证：MP ＝MQ4. ∆ABC 中，∠=︒⊥BAC AD BC 90，于D ，求证：()AD AB AC BC <++14【试题答案】1. 证明：取ΘAC ADAF CDAFC =∴⊥∴∠= 又∠+∠=︒∠+∠=︒14901390，∴∠=∠=∴≅∴=∴=4312ΘAC CEACF CED ASA CF EDDE CD∆∆()2. 分析：本题从已知和图形上看好象比较简单，但一时又不知如何下手，那么在证明一条线段等于两条线段之和时，我们经常采用“截长补短”的手法。

“截长”即将长的线段截ΘΘCB CE BCD ECD CD CD CBD CEDB EBAC B BAC E=∠=∠=⎧⎨⎪⎩⎪∴≅∴∠=∠∠=∠∴∠=∠∆∆22又∠=∠+∠BAC ADE E∴∠=∠∴=∴==ADE E AD AEBC CE ，3. 证明：延长PM ΘCQ AP BP BP CQ PBM ⊥∴∴∠=∠，// 又BM CM =，∴≅∴=∆∆BPM CRMPM RM∴QM 是Rt QPR ∆斜边上的中线ΘAD BC AD AEBC AE AD⊥∴<∴=>，22()ΘAB AC BCBC AB AC BC AD AB AC BC AD AB AC BC +>∴<++∴<++∴<++2414。

七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角）∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB ≌△CEF ∴∠B ＝∠CFE∵∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° ∴∠D ＝∠CFA ∵AC 平分∠BAD ∴∠DAC ＝∠FAC ∵AC ＝AC∴△ADC ≌△AFC （SAS ）∴AD ＝AF∴AE ＝AF ＋FE ＝AD ＋BE6、如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

七年级下册数学期末考试几何大题证明必考题

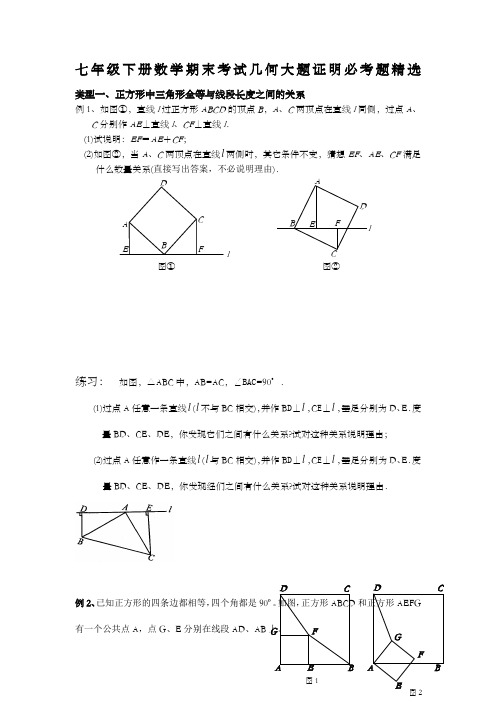
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习：如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

A E B 图1D CG FA BD CG FE图2（1）如图1，连结DF 、BF ，说明：DF ＝BF ；（2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线段DG 的长始终相等的线段？并以图2为例说明理由。

练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上画出示意图，并请求出这个大正方形的面积.附加：如图，△ABC 与△ADE 都是等边三角形，连结BD 、CE（1）BD 与CE 相等吗？请说明理由．A BCFDE GP32B（2）你能求出BD与CE的夹角∠BFC的度数吗？（3）若将已知条件改为：四边形ABCD与四边形AEFG都是正方形，连结BE、DG交点记为点M（如图）．请直接写出线段BE和DGF例3、正方形四边条边都相等，四个角都是90o．如图，已知正方形ABCD在直线MN 的上方，BC在直线MN上，点E是直线MN上一点，以AE为边在直线MN的上方作正方形AEFG．（1）如图1，当点E在线段BC上（不与点B、C重合）时：①判断△ADG与△ABE是否全等，并说明理由；②过点F作FH⊥MN，垂足为点H，观察并猜测线段BE与线段CH的数量关系，并说明理由；（2）如图2，当点E在射线CN上（不与点C重合）时：①判断△ADG与△ABE是否全等，不需说明理由；②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．图 2FG DA图 1FDA类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321．在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论；（3）证明图（4）所得结论．（4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ，R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为：；图（4）与图（6）中的等式有何关系？ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.CBAPDE2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中，点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的；（3）说明图（5）所得结论为什么是正确的．ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形，将一块含30o 角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立C图1吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是。

七年级数学几何证明题

七年级数学几何证明题1.如图，在ABC 中，D 在AB 上，且ΔCAD 和ΔCBE 都是等边三角形，求证：（1）DE=AB ，（2）∠EDB=60°2.如图，在ΔABC 中，AD 平分∠BAC ，DE||AC,EF ⊥AD 交BC 延长线于F 。

求证： ∠FAC=∠B3.已知，如图，在△ ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线，若∠B=30∠C=50°求：（1），求∠DAE 的度数。

（2）试写出 ∠DAE 与 ∠C - ∠B 有何关系?（不必证明）4、一个零件的形状如图，按规定∠A=90º ，∠ C=25º，∠B=25º，检验已量得∠BDC=150º，就判断这个零件不合格，运用三角形的有关知识说明零件不合格的理BACD由。

C5、如图,已知DF ∥AC,∠C=∠D,你能否判断CE ∥BD?试说明你的理由6、如图,△ABC 中,D 在BC 的延长线上,过D 作DE ⊥AB 于E,交AC 于F. 已知∠A=30°,∠FCD=80°,求∠D 。

7、如图，BE 平分∠ABD ，CF 平分∠ACD ，BE 、CF 交于G ，若∠BDC = 140°，∠BGC = 110°，则∠A ？G FEDCB A8、如图，AD ⊥BC 于D ，EG ⊥BC 于G ，∠E =∠1，求证AD 平分∠BAC 。

EDCBAE O DCBAEC BA 3219、如图，直线DE 交△ABC 的边AB 、AC 于D 、E ，交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°，∠AED ＝48°，求∠BDF 的度数.10、如图，将一副三角板叠放在一起，使直角的顶点重合于O ，则∠AOC+∠DOB11、如图，将两块直角三角尺的直角顶点C 叠放在一起. （1）若∠DCE=350，求∠ACB 的度数；（2）若∠ACB=1400，求∠DCE 的度数；（3）猜想：∠ACB 与∠DCE 有怎样的数量关系，并说明理由12、已知：直线AB 与直线CD 相交于点O ，∠BOC=45，（1）如图1，若EO ⊥AB ，求∠DOE 的度数；（2）如图2，若EO 平分∠AOC ，求∠DOE 的度数．13、已知AOB ∠，P 为OA 上一点．（1）过点P 画一条直线PQ ，使PQ ∥OB ；（2）过点P 画一条直线PM ，使PM ⊥OA 交OB 于点M ；（3）若︒=∠40AOB ，则=∠PMO ？14、如图。

初一几何证明题(精选多篇)

初一几何证明题(精选多篇)第一篇：初一几何证明题初一《几何》复习题201某--6—29姓名：一．填空题1．过一点2．过一点，有且只有直线与这条直线平行；3．两条直线相交的，它们的交点叫做；4．直线外一点与直线上各点连接的中，最短；a b 5．如果c[图1]6．如图1，ab、cd相交于o点，oe⊥cd，∠1和∠2叫做，∠1和∠3叫做，∠1和∠4叫做，∠2和∠3叫做；a7．如图2，ac⊥bc，cd⊥ab，b点到ac的距离是a点到bc的距离是，c点到ab的距离是d438．如图3，∠1=110°，∠2=75°，∠3=110°，∠4=；cb 二．判断题[图2][图3] 1．有一条公共边的两个角是邻补角；（）2．不相交的两条直线叫做平行线；（）3．垂直于同一直线的两条直线平行；（）4．命题都是正确的；（）5．命题都是由题设和结论两部分组成（）6．一个角的邻补角有两个；（）三．选择题1．下列命题中是真命题的是（）a、相等的角是对顶角b、如果a⊥b，a⊥c，那么b⊥cc、互为补角的两个角一定是邻补角d、如果a∥b，a⊥c，那么b⊥c 2.下列语句中不是命题的是（）a、过直线ab外一点c作ab的平行线cf b、任意两个奇数之和是偶数c、同旁内角互补，则两直线平行d、两个角互为补角，与这两个角所在位置无关a 3．如图4，已知∠1=∠2，若要∠3=∠4，则需（）da、∠1=∠3b、∠2=∠3c、∠1=∠4d、ab∥cdc [图4] 4．将命题“同角的补角相等”改写成“如果，那么”的形式，正确的是（）a．如果同角的补角，那么相等b．如果两个角是同一个角，那么它们的补角相等 c．如果有一个角，那么它们的补角相等d．如果两个角是同一个角的补角，那么它们相等四．解答下列各题：p 1. 如图5，能表示点到直线（或线段）的距离的线段qac 有、、；abf 2.如图6，直线ab、cd分别和ef相交，已知ab∥cd，orebba平分∠cbe，∠cbf=∠dfe，与∠d相等的角有∠[图5][图6]d∠、∠、∠、∠等五个。

初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇：初一下册几何证明题初一下册几何证明题1.已知在三角形ab中，be,f分别是角平分线，d是ef中点，若d到三角形三边b,ab,a的距离分别为x,,z，求证：x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me，me=2hd同理可证fp=2dj。

又因为fq=fp,em=en.fq=2dj，en=2hd。

又因为角fq，do，en都是90度，所以四边形fqne是直角梯形，而d是中点，所以2do=fq+en又因为fq=2dj，en=2hd。

所以do=hd+jd。

因为x=do,=h,z=dj.所以x=+z。

在正五边形abde中,m、n分别是de、ea上的点，bm与n相交于点o，若∠bon=108°，请问结论bm=n是否成立?若成立，请给予证明;若不成立，请说明理由。

当∠bon=108°时。

bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中，ab=a,角a=58°，ab的垂直平分线交a与n，则角nb=3°因为ab=a，∠a=58°，所以∠b=61°，∠=61°。

七年级数学几何证明题(典型)

EDC BAEODCBA七年级数学几何证明题1.如图，在ABC 中，D 在AB 上，且ΔCAD 和ΔCBE 都是等边三角形，求证：（1）DE=AB ，（2）∠EDB=60°2.如图，在ΔABC 中，AD 平分∠BAC ，DE||AC,EF ⊥AD 交BC 延长线于F 。

求证： ∠FAC=∠B3.已知，如图，在△ ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线，若∠B=30∠C=50°求：（1），求∠DAE 的度数。

（2）试写出 ∠DAE 与 ∠C - ∠B 有何关系?（不必证明） 4、一个零件的形状如图，按规定∠A=90o ，∠ C=25o，∠B=25o ，检验已量得∠BDC=150o ，就判断这个零件不合格，运用三角形的有关知识说明零件不合格的理由。

CDA B5、如图,已知DF ∥AC,∠C=∠D,你能否判断CE ∥BD?试说明你的理由6、如图,△ABC 中,D 在BC 的延长线上,过D 作DE ⊥AB 于E,交AC 于F. 已知∠A=30°,∠FCD=80°,求∠D 。

7、如图，BE 平分∠ABD ，CF 平分∠ACD ，BE 、CF 若∠BDC = 140°，∠BGC = 110°，则∠A ？8、如图，AD ⊥BC 于D ，EG ⊥BC 于G ，∠E =∠1，求证BAC 。

EB A 3219、如图，直线DE 交△ABC 的边AB 、AC 于D 、E ，交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°，∠AED ＝48°，求∠BDF 的度数. 10、如图，将一副三角板叠放在一起，使直角的顶点重合于O ，则∠AOC+∠DOB11、如图，将两块直角三角尺的直角顶点C 叠放在一起. （1）若∠DCE=350，求∠ACB 的度数；（2）若∠ACB=1400，求∠DCE 的度数；（3）猜想：∠ACB 与∠DCE 有怎样的数量关系，并说明理由 12、已知：直线AB 与直线CD 相交于点O ，∠BOC=45，（1）如图1，若EO ⊥AB ，求∠DOE 的度数；（2）如图2，若EO 平分∠AOC ，求∠DOE 的度数． 13、已知AOB ，P 为OA 上一点．（1）过点P 画一条直线PQ ，使PQ ∥OB ；（2）过点P 画一条直线PM ，使PM ⊥OA 交OB 于点M ；BA CD213FDCBH EG A（3）若︒=∠40AOB ，则=∠PMO ？14、如图。

初一数学几何证明题答案

初一典型几何证明题1、已知： AB=4，AC=2，D是BC中点， AD是整数，求AD解：延长A D到 E,使AD=DE∵D是 BC中点A ∴BD=DC在△ ACD和△ BDE中AD=DE∠BDE=∠ADC B CDBD=DC∴△ACD≌△ BDE∴AC=BE=2∵在△ ABE中AB-BE＜AE＜AB+BE∵AB=4即 4-2＜2AD＜4+21＜AD＜3∴AD=22、已知： BC=DE，∠B=∠E，∠ C=∠D，F 是 CD中点，求证：∠1=∠2A21B EC F D证明：连接BF和 EF∵BC=ED,CF=DF∠, BCF=∠EDF∴△BCF≌△ EDF 第1页共22 页∴BF=EF,∠CBF=∠DEFB E连接在△ BEF中,BF=EF∴∠EBF=∠BEF。

∵∠ABC=∠AED。

∴∠ABE=∠AEB。

∴AB=AE。

在△ ABF和△ AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△ AEF。

∴∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=D，E EF证明：连接EF ∵AB∥CD共22 页第9页∴∠B=∠C∴△BEM≌△CFM（ SAS）∵M是 BC中点∴CF=BE∴BM=CM在△BEM和△CFM中BE=CF∠B=∠CBM=CM7. 已知：如图所示，AB＝AD，BC＝DC，E、F 分别是DC、BC的中点，求证：AE＝AF。

证：连接AC DE=BF∵在△ ADC和△ABC中∴△ADE≌△ ABF（SAS）AD=AB ∴AE=AFDC=BCAC=AC∴△ADC≌△ ABC（SSS）D∴∠B=∠ DE∵E、F 分别是DC、BC的中点AC又∵ BC＝DCF∴DE=BFB∵在△ ADE和△ABF中AD=AB∠D=∠B8. 如图，在四边形ABCD中， E是AC上的一点，∠1=∠2，∠3=∠4，求证 : ∠5=∠6．证明：∵在△ADC和△ ABC中∴△DEC≌△ BEC（SAS）∠BAC=∠DAC ∴∠DEC=∠BEC∠BCA=∠DCAAC=AC∴△ADC≌△ ABC（AAS）D∵AB=AD，BC=CD在△ DEC与△ BEC中A12E5634CCE=CEB∠BCA=∠DCABC=CD9. 如图，在△ABC中， AD为∠ BAC的平分线，DE⊥AB于 E，DF⊥AC于 F。

初一数学几何图形的性质与证明练习题及答案

初一数学几何图形的性质与证明练习题及答案几何图形是数学中的一个重要概念，它们具有独特的性质和特征。

在初一的数学学习中，学生需要了解不同几何图形的性质，并且能够通过证明来验证这些性质。

本文将提供一些初一数学几何图形的性质与证明练习题及答案，帮助学生深入理解几何图形。

一、直线和线段的性质及证明性质1：两点确定一条直线。

证明：设有两点A和B，我们可以通过连接这两个点的直线来得到一条直线。

性质2：直线上的任意一点都在直线的同一侧。

证明：设直线上有一点C，在直线上我们可以找到一点D，并通过连接点C和D得到一条直线。

点C和点D的连接线与原始直线重合，因此点C和原始直线上的点A、B都在直线的同一侧。

性质3：线段的中点即为线段上到两个端点距离相等的点。

证明：设线段AB上有一点E，若点E到点A和点B的距离相等，则点E为线段AB的中点。

二、三角形的性质及证明性质4：三角形的内角和等于180度。

证明：设三角形ABC，我们可以通过在点B处做一条平行于边AC的直线，连接点A和点C，构成直线ABCD。

由于直线ABCD是一条直线，所以角ABC + 角BCD = 180度。

因此，三角形ABC的内角和等于180度。

性质5：等腰三角形的底边上的高线也是中位线。

证明：设等腰三角形ABC中，AB = AC，点D为底边BC上的中点，我们需要证明AD是三角形ABC的高线。

通过连接点A和点D，我们可以得到线段AD。

由于AB=AC，所以角BAD =角CAD，即角B = 角C。

又因为线段AD是BC的中点，所以BD = CD。

根据三角形的SAS相等性质，我们可以得知三角形ABD与三角形ACD全等。

根据全等三角形的性质，我们可以得出AD是三角形ABC的高线。

性质6：直角三角形的斜边平方等于两直角边平方和。

证明：设直角三角形ABC ，其中∠C为直角。

我们需要证明AB² = AC² + BC²。

通过在边AC上做一条垂直于AC的高线AD，我们可以将直角三角形ABC分为两个矩形，分别为ABCD和ABDE。

初一上册几何证明题(精选多篇)

初一上册几何证明题(精选多篇)第一篇：初一上册几何证明题初一上册几何证明题1.在三角形abc中，∠acb=90°，ac=bc，e是bc边上的一点，连接ae，过c作cf ⊥ae于f，过b作bd⊥bc交cf的延长线于d，试说明：ae=cd。

满意回答因为ae⊥cf,bd⊥bc所以∠afc=90°,∠dbc=90°又∠acb=90°，所以∠ace=∠dbc因为∠cae+∠aec=90°∠ecf+∠aec=90°所以∠cae=∠ecf又ac=bc所以△ace全等于△cbd(asa)所以ae=cd像这类题目，一般用全等较好做些2.如图所示，已知ad、bc相交于o，∠a=∠d，试说明∠c=∠b.解：证1：∠a=∠d=====>ab∥cd=====>∠c=∠b(内错角相等)证2：△abo内角和180=△cdo内角和180∠a=∠d∠aob=∠d0c∴∠c=∠b证明：显然有:∠aob=∠cod(两直线相交,对顶角相等)又∠a=∠d,且三角形三个内角的和等于180º∴一定有∠c=∠b.3.(1)d是三角形abc的bc边上的点且cd=ab，角adb=角bad，ae是三角形abd的中线，求证ac=2ae。

(2)在直角三角形abc中，角c=90度，bd是角b的平分线，交ac于d，ce垂直ab于e，交bd于o，过o作fg平行ab，交bc于f，交ac于g。

求证cd=ga。

延长ae至f，使ae=ef。

be=ed，对顶角。

证明abe全等于def。

=》ab=df，角b=角edf角adb=角bad=》ab=bd，cd=ab=》cd=df。

角ade=bad+b=adb+edf。

ad=ad=》三角形adf全等于adc=》ac=af=2ae。

题干中可能有笔误地方：第一题右边的e点应为c点，第二题求证的cd不可能等于ga，是否是求证cd=fa或cd=co。

初一几何证明题

初一几何证明题1.已知AB∥CD，∠1=∠2，证明：∠XXX∠XXX。

根据平行线内角相等的性质，可得∠1=∠2=∠XXX。

同时，因为AB∥CD，所以∠BEF+∠EFC=180°，即∠BEF=180°-∠XXX。

代入前面的等式，可得∠XXX∠XXX。

2.如图2，AB∥CD，∠3∶∠2＝3∶1，求∠1的度数。

根据平行线内角相等的性质，可得∠1=180°-∠2.又因为∠3∶∠2＝3∶1，所以∠3=3x，∠2=x。

代入前面的等式，可得∠1=180°-x。

因此，∠1+∠2+∠3=180°，即4x=180°，x=45°。

代入前面的等式，可得∠1=135°。

3.如图3，C在AB的延长线上，CE⊥AF于E，交FB于D，若∠F=40°，∠C=20°，求∠XXX的度数。

根据直角三角形的性质，可得∠CEA=90°。

又因为CE⊥AF，所以∠EAF=90°-∠F=50°。

根据三角形内角和为180°的性质，可得∠EFA=180°-∠F-∠EAF=90°。

因为AB∥CD，所以∠XXX∠EFA=90°。

4.如图4，EF∥AD，∠1=∠2，∠BAC=80°。

求证：∠AGD=100°。

因为EF∥AD，所以∠AGD=∠AGE。

又因为∠BAC=80°，所以∠XXX°-∠BAC/2=50°。

因为∠1=∠2，所以∠DGE=∠AGE=180°-∠1-∠GAC=50°。

因此，∠AGD=∠AGE=50°+∠DGE=100°。

5.如图5，B处在A处的南偏西57°的方向，C处在A处的南偏东15°方向，C处在B处的XXX°方向。

求∠C的度数。

根据题意，可画出如图6所示的图形。

(完整word版)七年级数学几何证明题

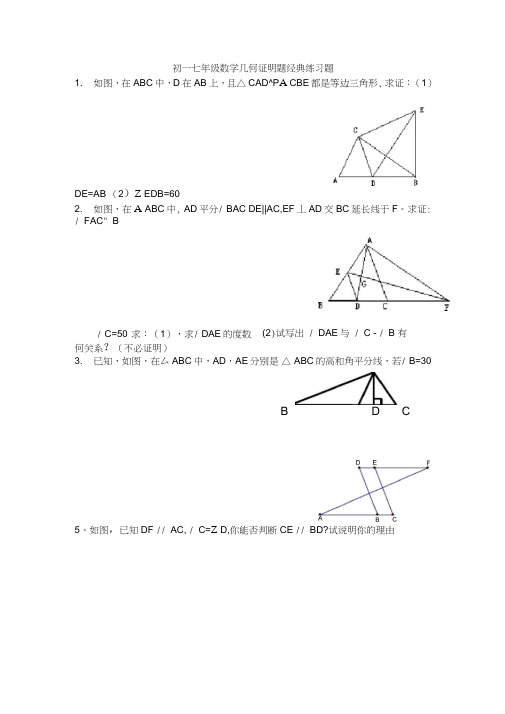
初一七年级数学几何证明题经典练习题1. 如图，在ABC 中，D 在AB 上，且△ CAD^P A CBE 都是等边三角形, 求证：（1）DE=AB （2）Z EDB=602. 如图，在A ABC 中, AD 平分/ BAC DE||AC,EF 丄AD 交BC 延长线于F 。

求证: / FAC " B3. 已知，如图，在厶ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线，若/ B=30 B D C5、如图，已知DF // AC, / C=Z D,你能否判断CE // BD?试说明你的理由/ C=50°求：（1），求/ DAE 的度数何关系？（不必证明）(2)试写出 / DAE 与 / C - / B 有6、如图,△ ABC中,D在BC的延长线上,过D作DE丄AB于E,交AC于F.已知/ A=30 ° ,Z FCD=80° ,求/D。

A87、如图，BE 平分/ ABD , CF 平分/ ACD , BE 、CF 交于 G , 若/ BDC = 140。

，/ BGC = 110。

，则 / A ?8、如图，AD 丄BC 于D , EG 丄BC 于G ,Z E =Z 1,求证 AD 平分/ BAC9、如图，直线。

丘交厶ABC 的边AB AC 于 D E,交BC 延长线于F ，若/ B = 67°,/ ACB= 74°,/ AED= 48°，求/ BDF 的度数•10、如图，将一副三角板叠放在一起，使直角的顶点重合于O,贝U/ AOC / DOB11、如图，将两块直角三角尺的直角顶点C 叠放在一起 (1) 若/ DCE=3&求/ ACB 的度数；(2) 若/ ACB=140,求/ DCE 的度数； (3) 猜想：/ ACB 与/ DCE 有怎样的数量关系，并说明理由 AE12、已知：直线AB 与直线CD 相交于点O ,/ B0C= 45° ,(1) 如图1，若E0丄AB ,求/ D0E 的度数；(2) 如图2，若E0平分/ AOC ，求/ DOE 的度数.13、已知 AOB , P 为0A 上一点. (1)过点P 画一条直线PQ ，使PQ // 0B ；(2)过点P 画一条直线PM ，使PM 丄0A 交0B 于点M ；14、如图。

(完整版)七年级下册数学全等三角形的经典证明

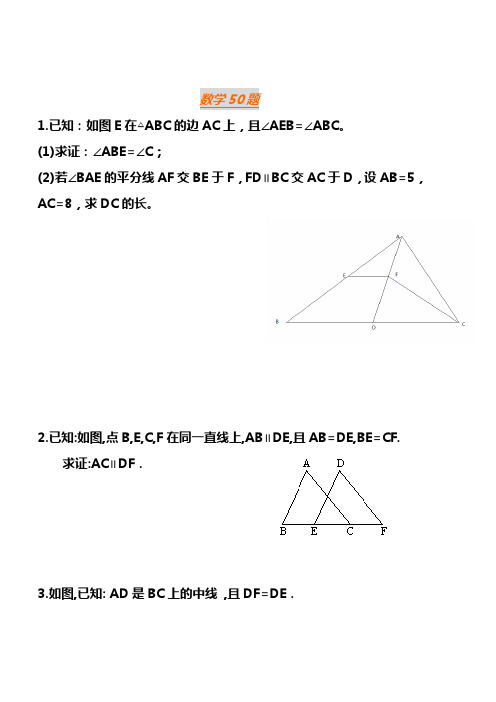
数学50题1.已知：如图E在△ABC的边AC上，且∠AEB=∠ABC。

(1)求证：∠ABE=∠C；(2)若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=5，AC=8，求DC的长。

2.已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF．3.如图,已知: AD是BC上的中线,且DF=DE．求证:BE∥CF．4.如图, 已知：AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF．求证：AC=EF．5.如图，在ΔABC中，AC=AB，AD是BC边上的中线。

求证：AD⊥BC，6.如图，已知AB=DE，BC=EF，AF=DC。

求证：∠EFD=∠BCAFGE DC BAAB C D EF AB CD7.如图，ΔABC 的两条高AD 、BE 相交于H ，且AD=BD ，试说明下列结论成立的理由。

（1）∠DBH=∠DAC ；（2）ΔBDH ≌ΔADC 。

8.已知等边三角形ＡＢＣ中，ＢＤ＝ＣＥ，ＡＤ与ＢＥ相交于点Ｐ，求∠ＡＰＥ的大小。

9.如图，在矩形ABCD 中，F 是BC 边上的一点，AF 的延长线交DC 的延长线于G ，DE ⊥AG 于E ，且DE ＝DC ，根据上述条件，请你在图中找出一对全等三角形，并证明你的结论。

ABCDEH10.已知：如图所示，BD 为∠ABC 的平分线，AB=BC ，点P 在BD 上，PM ⊥AD 于M ，•PN ⊥CD 于N ，判断PM 与PN 的关系．11.如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．12.在△ABC 中，,AB=AC ，在AB 边上取点D ，在AC 延长线上了取点E ，使CE=BD ，连接DE 交BC 于点F ，求证DF=EF .P D AC M NF E DCB AB13.如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF.求证：EG=EF;请你判断BE+CF与EF的大小关系，并说明理由。

初一几何证明题

初一几何证明题初一几何证明题1. 证明等腰三角形底角相等设等腰三角形ABC，其中AB=AC，要证明∠B=∠C。

证明：由已知可知∠A=180-∠B-∠C。

又因为∠B=∠C，代入可得∠A=180-2∠B。

由于三角形内角和定理，可得∠A+∠B+∠C=180。

代入上式可得180-2∠B+∠B+∠C=180。

化简得∠C-∠B=0。

即∠C=∠B。

所以等腰三角形底角相等得证。

2. 证明垂直的两条直线互相垂直设有两条直线AB和CD，其中AB⊥CD，要证明CD⊥AB。

证明：由于AB⊥CD，可以得到∠ABC=90度。

假设CD不⊥AB，即CD与AB不垂直，那么就存在另一条直线CE平行于AB，并且与CD相交于点E。

可以得到∠CED=90度。

那么∠CED+∠ABC=90+90=180度，这与角的和为180度的基本定理相矛盾。

所以假设不成立，CD⊥AB。

证毕。

3. 证明平行线的内错角相等设有两条平行线AB和CD，要证明∠1=∠2。

证明：由已知可以得到直线AB∥CD。

假设∠1≠∠2，即∠1>∠2。

通过点C引一条平行于AB的直线CE，并且与CD相交于点E。

根据平行线的性质，可以得到∠3=∠1>∠2。

由于∠2和∠3是同位角，所以∠2>∠3，这与刚才得到的结论相矛盾。

所以假设不成立，∠1=∠2。

证毕。

通过上述证明题，我们可以学习到几何证明的基本方法和常用推理。

几何证明是一种严谨的推理和论证，需要运用已知条件和几何性质来得出结论。

同时，几何证明也需要大量的绘图和图形分析。

进一步研究和掌握几何证明对于提高数学思维和解决实际问题有一定的帮助。