近五年全国2卷数学(理科)高考试题双向细目表
2016年-2018年高考数学(理)细目表(印刷版)
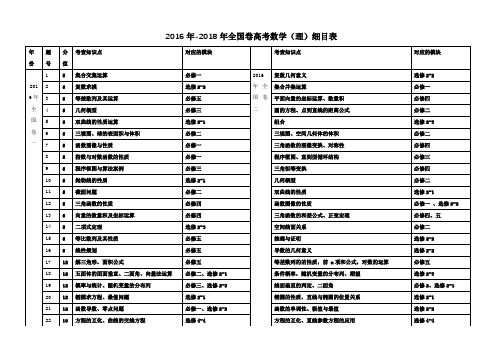
圆、折叠、三棱锥体积最值
必修2
抛物线焦点弦弦长
选修2-1
17
12
解三角形、面积公式、和角公式
必修五
解三角形、面积
必修五
18
12
面面垂直、二面角
必修二、选修2-1
直方图、独立性检验、中位数
必修三、选修2-319Leabharlann 12期望、正态分布
选修2-3
线面平行证明、线面角、二面角
必修二、选修2-1
20
12
椭圆方程、定点问题
选修2-2、选修2-3
三棱锥线面垂直、二面角
必修二、选修2-1
21
12
导数单调性、极值不等式
选修2-2
导数不等式、零点个数求参数
选修2-2
22
10
方程互化、曲线交点个数
选修4-4
椭圆参数方程、中点弦
选修4-4
2017年全国卷三
1
5
点集、交集运算
必修一
2018年全国卷三
集合交集
必修一
2
5
复数模
选修2-2
必修五
极值点、极小值
选修2-2
12
5
推理新概念
选修2-3
三角形、向量数量积(坐标法运算)
必修四
13
5
向量夹角、模
必修四
二项分布方差
选修2-3
14
5
线性规划
必修五
非齐次三角函数式最值(换元法、二次函数)
必修四
15
5
双曲线渐近线方程、离心率
选修2-1
等差数列基本计算(求首项、公差)裂项相消法求和
必修五
16
必修二
2016年-2018年高考数学(理)细目表(印刷版)
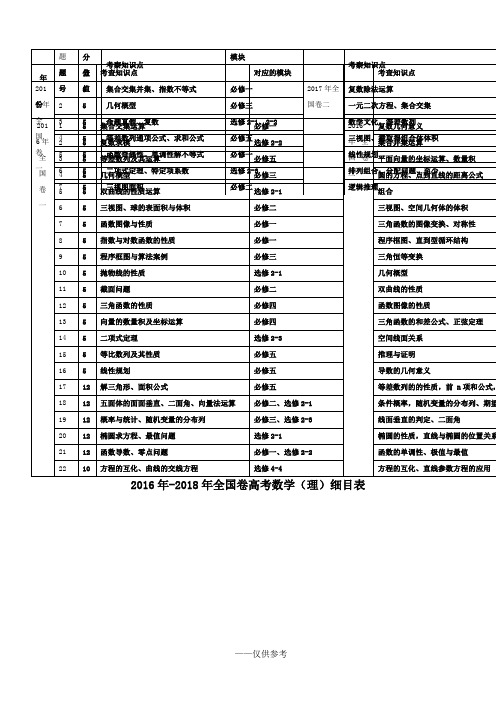
程序框图
必修三
8
5
直线与抛物线、韦达定理、数量积;抛物线性质。
选修2-2、必修四
数学文化古典概型
必修三
9
5
分段函数零点范围:化为图像交点
必修一
长方体异面直线所成角
必修二
10
5
数学文化、几何概型
必修三
三角函数单调性
必修四
11
5
双曲线渐近线、求弦长
选修2-1
函数性质:奇偶性、对称性
必修一
12
5
正方体线面角、截面面积最值
必修二
双曲线的性质
选修2-1
12
5
三角函数的性质
必修四
函数图像的性质
必修一、选修2-2
13
5
向量的数量积及坐标运算
必修四
三角函数的和差公式、正弦定理
必修四、五
14
5
二项式定理
选修2-3
空间线面关系
必修二
15
5
等比数列及其性质
必修五
推理与证明
选修2-2
16
5
线性规划
必修五
导数的几何意义
选修2-2
17
12
椭圆的性质,直线与椭圆的位置关系
选修2-1
21
12
函数导数、零点问题
必修一、选修2-2
函数的单调性、极值与最值
选修2-2
22
10
方程的互化、曲线的交线方程
选修4-4
方程的互化、直线参数方程的应用
选修4-4
2016年-2018年全国卷高考数学(理)细目表
题号
分值
考察知识点
模块
2023年数学新高考2卷细目表

2023年数学新高考2卷细目表一、代数部分1. 有理数及其运算1.1 有理数的概念1.2 有理数的加法、减法、乘法、除法1.3 有理数的比较大小1.4 有理数的应用题2. 整式及其加减法2.1 整式的概念2.2 整式的加法与减法2.3 整式的应用题3. 整式的乘法3.1 单项式乘法3.2 多项式乘法3.3 整式乘法的应用题4. 整式的除法4.1 单项式除法4.2 多项式除法4.3 整式除法的应用题5. 分式及其加减法5.1 分式的概念5.2 分式的加法与减法5.3 分式的应用题6. 分式的乘法和除法6.1 分式的乘法6.2 分式的除法6.3 分式的应用题7. 一次函数及其应用7.1 一次函数的概念7.2 一次函数的图像及性质7.3 一次函数的应用题8. 二次函数及其应用8.1 二次函数的概念8.2 二次函数的图像及性质8.3 二次函数的应用题9. 幂函数及其应用9.1 幂函数的概念9.2 幂函数的图像及性质9.3 幂函数的应用题二、几何部分1. 直线和角1.1 点、线、面1.2 直线及其性质1.3 角及其性质1.4 相交线及其应用题2. 多边形2.1 多边形的概念2.2 三角形及其性质2.3 四边形及其性质2.4 多边形的应用题3. 圆3.1 圆的概念3.2 圆的性质3.3 圆的应用题4. 相似4.1 相似的概念4.2 相似三角形4.3 相似的应用题5. 锐角三角函数5.1 正弦函数5.2 余弦函数5.3 正切函数5.4 锐角三角函数的应用题6. 三角恒等式6.1 三角函数的基本关系式6.2 三角函数的和差化积6.3 三角函数的应用题7. 数列和数学归纳法7.1 等差数列及其应用7.2 等比数列及其应用7.3 数学归纳法及其应用8. 平面向量8.1 向量的概念8.2 平面向量及其运算8.3 平面向量的应用题9. 解析几何9.1 坐标系9.2 点、直线、圆的方程9.3 解析几何的应用题三、概率与统计部分1. 随机事件与概率1.1 随机事件的概念1.2 随机事件的运算1.3 概率的性质1.4 概率的应用题2. 随机变量及其概率分布2.1 随机变量的概念2.2 随机变量的分布律2.3 随机变量的应用题3. 统计图及其应用3.1 统计图的类型3.2 统计图的绘制3.3 统计图的分析与应用4. 抽样与估计4.1 抽样的方法4.2 参数估计4.3 区间估计的应用以上便是2023年数学新高考2卷的细目表。
2015—2019高考数学双向细目表(理科)
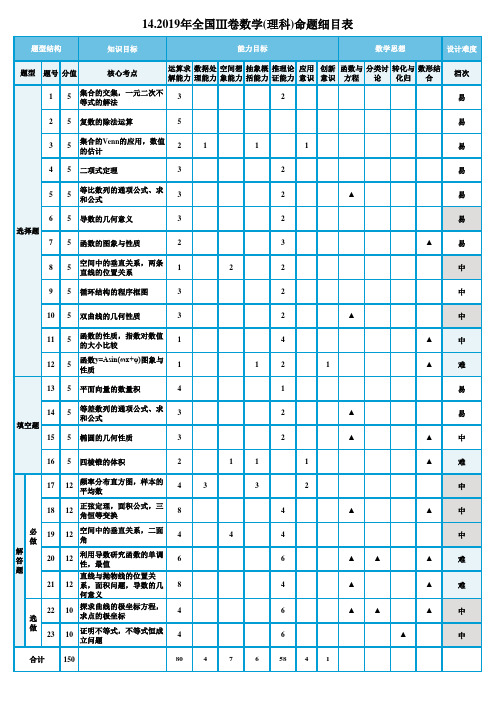
知识目标设计难度题号分值核心考点运算求解能力数据处理能力空间想象能力抽象概括能力推理论证能力应用意识创新意识函数与方程分类讨论转化与化归数形结合档次15集合的交集,一元二次不等式的解法32易25复数的除法运算5易35集合的Venn 的应用,数值的估计2111易45二项式定理32易55等比数列的通项公式、求和公式32▲易65导数的几何意义32易75函数的图象与性质23▲易85空间中的垂直关系,两条直线的位置关系122中95循环结构的程序框图32中105双曲线的几何性质32▲中115函数的性质,指数对数值的大小比较14▲中125函数y=Asin(ωx+φ)图象与性质1121▲难135平面向量的数量积41易145等差数列的通项公式、求和公式32▲易155椭圆的几何性质32▲▲中165四棱锥的体积2111▲难1712频率分布直方图,样本的平均数4332中1812正弦定理,面积公式,三角恒等变换84▲▲中1912空间中的垂直关系,二面角444中2012利用导数研究函数的单调性,最值66▲▲▲难2112直线与抛物线的位置关系,面积问题,导数的几何意义84▲▲难2210探求曲线的极坐标方程,求点的极坐标46▲▲▲中2310证明不等式,不等式恒成立问题46▲中150804765841合计解答题必做选做选择题填空题14.2019年全国Ⅲ卷数学(理科)命题细目表题型结构能力目标数学思想题型。
2010-2015山东卷高考命题双向细目表(理科数学)
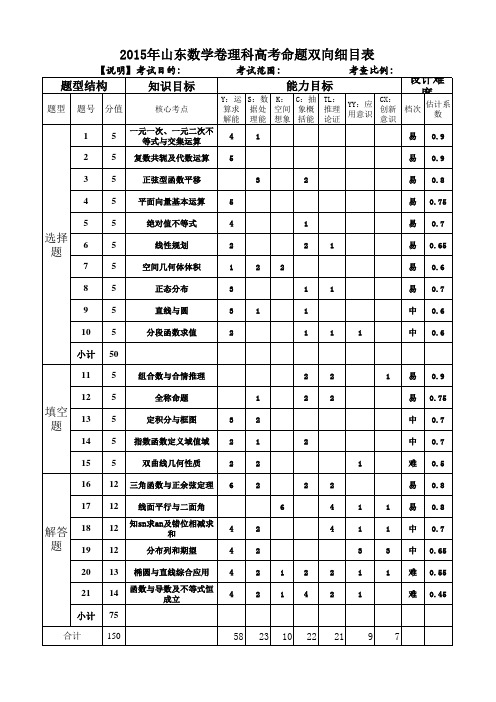
【说明】考试目的: 考试范围: 考查比例:
题型结构
题型 题号 1 2 3 4 5 分值 5 5 5 5 5 5 5 5 5 5 50 5 5 5 5 5 12 12 12 12 13 14 75 150
知识目标
核心考点 一元一次、一元二次不 等式与交集运算 复数共轭及代数运算 正弦型函数平移 平面向量基本运算 绝对值不等式 线性规划 空间几何体体积 正态分布 直线与圆 分段函数求值 5 4 2 1 3 3 2 1 2 2
能力目标
Y:运 S:数 K: C:抽 TL: CX: YY:应 算求 据处 空间 象概 推理 创新 档次 用意识 解能 理能 想象 括能 论证 意识 4 5 3 2 1 易 易 易 易 1 2 1 易 易 易 1 1 1 1 1 1 易 中 中
设计难 度 估计系
数 0.9 0.9 0.8 0.75 0.7 0.65 0.6 0.7 0.6 0.6
23
10
22
21
9
7
2 2
2 2
1
易 易 中
0.9 0.75 0.7 0.7 0.5 0.8 0.8 0.7 0.65 0.55 0.45
填空 题
13 14 15 16 17
2 1 2 2 4 4 1 1 3 2 4 2 2 1 1 1 1 3 1
中 难 易 易 中 中 难 难
解答 题
18 19 20 21 小计
合计
58
选择 题
6 7 8 9推理 全称命题 定积分与框图 指数函数定义域值域 双曲线几何性质 三角函数与正余弦定理 线面平行与二面角 知sn求an及错位相减求 和 分布列和期望 椭圆与直线综合应用 函数与导数及不等式恒 成立 4 4 4 4 2 2 2 2 1 1 3 2 2 6 1 2 1 2 2 6
2023新课标全国2卷数学双向细目表

2023新课标全国2卷数学双向细目表一、概述随着时代的发展和教育体制的不断改革,教育教学内容也在不断更新。
在教育领域,新课标的推出是一个重要的事件,它对学生的学习内容和学习方法,以及教师的教学内容和教学方法都有着重要的指导作用。
本文根据2023年新课标全国2卷数学的双向细目表,进行了详细解读和分析,旨在帮助教师和学生更好地了解新课标的要求,有效指导教学实践。
二、2023新课标全国2卷数学双向细目表解读1. 教材选择根据新课标的要求,教材的选择应当注重贴近学生的生活和实际应用,提倡多角度、立体化的教学。
2. 学习目标新课标强调培养学生的数学思维能力和解决问题的能力,要求学生在学习数学的过程中,不仅要掌握数学的基本知识,更要具备数学的思维方式和解决问题的能力。
3. 教学内容在教学内容方面,新课标重视数学知识的系统性和整合性,提倡数学知识的跨学科性和综合性。
教学内容涵盖了数学的基本概念、基本原理和基本方法,同时还包括了一些前沿的数学知识和数学应用。
4. 学习方法新课标要求教师在教学中注重培养学生的自主学习能力,引导学生学会提出问题、探究问题和解决问题的方法,注重培养学生的团队合作精神和交流能力。
5. 教学评价新课标提倡多样化的教学评价方式,不再仅仅依靠考试成绩来评价学生的学习水平,而是要注重以课堂表现、作业与项目、综合评价等多种方式来全面评价学生的学习情况。
三、教学实践与有效策略1. 加强课堂教学的互动性在教学实践中,教师应该注重通过提问、讨论、案例分析等方式,激发学生的学习兴趣,提高学生的学习积极性,培养学生的自主学习能力。
2. 组织丰富多样的教学活动除了传统的讲授和练习,教师还应该开展更多的实验、探究、研究性学习等活动,让学生在实践中掌握知识,提高解决问题的能力。
3. 引导学生进行综合性实践活动教师应该引导学生参与数学建模、数学应用等综合性实践活动,让学生将所学知识应用到实际中去,提高数学知识的实际运用能力。
2023年数学新高考2卷双细目表

2023年数学新高考2卷双细目表1. 代数与函数1.1. 一元二次方程及一元二次不等式1.1.1 解一元二次方程:通过因式分解、配方法、公式法等方法解一元二次方程,包括真分式方程的解法。
1.1.2 解一元二次不等式:通过因式分解、配方法、开平方法等方法解一元二次不等式,建立二次函数与一元二次不等式之间的通联。
1.2. 参数方程1.2.1 理解参数方程的概念与性质,掌握参数方程与直角坐标系之间的相互转换。
1.2.2 利用参数方程解曲线的方程,求参数方程的参数范围等。
2. 解析几何2.1. 直线与圆2.1.1 直线方程:掌握点斜式、斜截式、两点式等直线方程的表示与相互转换。
2.1.2 圆的方程:掌握标准方程、一般方程等圆的方程,并能够在坐标系中画出对应的图形。
2.2. 平面向量2.2.1 理解平面向量的概念与性质,掌握平面向量的加减、数量积、夹角等运算法则。
2.2.2 应用平面向量解决几何问题,包括线性运动、平面图形的性质等。
3. 概率论3.1. 随机事件与概率3.1.1 随机事件的定义与性质,包括基本事件、必然事件、互斥事件、对立事件等。
3.1.2 概率的定义与性质,包括样本空间、事件的概率等概念。
3.2. 条件概率与独立性3.2.1 条件概率的概念与性质,包括条件概率的计算、全概率公式、贝叶斯公式等。
3.2.2 独立事件与互不独立事件的概念与应用。
4. 数学模型4.1. 建立数学模型的基本方法4.1.1 复杂问题抽象为数学问题,建立数学模型的基本思想与方法。
4.1.2 通过实际问题建立具体的数学模型,求解数学模型的参数与条件。
4.2. 数学建模的实际应用4.2.1 运用数学模型解决实际问题,包括人口增长、经济发展、资源分配等领域。
4.2.2 分析数学模型的合理性与局限性,提出改进与优化方案。
5. 综合应用5.1. 数学知识的交叉应用5.1.1 将不同数学知识相互通联,解决具体问题。
5.1.2 利用数学模型、概率统计等方法分析解决现实问题。
-高考数学双向细目表(精)

2020届理科数学双向细目表模块知识点考查内容知识要求2015 分值2016 分值2017 分值备注了解理解掌握集合集合的含义与表示集合的含义、元素与集合的属于关系√列举法、描述法√集合间的基本关系包含与相等的含义√识别给定集合子集√全集与空集√集合的基本运算并集与交集含义与运算√补集含义与运算√韦恩图表达集合的关系与运算√函数概念与基本初等函数I 函数简单定义域值域,了解映射√图像法、列表法、解析法表示函数√分段函数√函数单调性、最值及几何意义√函数奇偶性√函数图像研究函数性质√指数函数指数函数模型背景√有理、实数指数幂、幂的运算√指数函数概念、单调性√指数函数图像过定点√对数函数对数的概念及其运算√换底公式、自然对数、常用对数√对数函数的概念、单调性√对数函数图像过定点√指数函数与对数函数互为反函数√幂函数幂函数概念√幂函数图像√函数与方程二次函数、零点与方程根√一元二次方程根的存在性及根的个数√结合图像,用二分法求近似解√函数模型及应用指、对、幂的增长特征√函数模型的应用√立体几何初步空间几何体柱锥台的结构特征√三视图√斜二测画出直观图√平行、中心投影√会画视图和直观图√球柱锥台的表面积和体积公式√点线面位置关系线面位置关系定义√线面平行判定√面面平行判定√线面垂直判定√面面垂直判定√线面平行性质√面面平行性质√线面垂直性质√面面垂直性质√用已获结论证明空间图形的位置关系√平面解析几何初步直线与方程结合图形,确定直线位置的几何要素√直线倾斜角和斜率√过两点的直线斜率计算公式√判定直线平行或垂直√点斜式、两点式、一般式√斜截式与一次函数的关系√两条相交直线的交点坐标√两点间距离公式√点到直线距离公式√两条平行直线间距离√圆与方程圆的几何要素,标准方程和一般方程√判断直线与圆的位置关系√判断两圆的位置关系√应用直线与圆的方程√代数方法处理几何问题的思想√空间直角坐标系空间直角坐标表示点的位置√空间两点间距离公式√算法初步算法的含义、程序框图算法的含义和思想√顺序、条件分支、循环逻辑结构√基本算法语句输入、输出、赋值、条件、循环语句√统计随机抽样会用简单随机抽样从总体中抽取样本√分层抽样和系统抽样√用样本估计总体频率分布表、频率分布直方图、折线图√茎叶图√数据标准差意义和作用√平均数和标准差√用样本估计总体思想√变量的相关性会画散点图,并认识变量间的相关关系√最小二乘法,线性回归方程√概率事件与概率频率与概率的意义√互斥事件的概率加法公式√古典概型古典概型计算公式√随机事件所含的基本事件数及发生概率√几何概型随机数的意义,运用模拟方法估计概率√几何概型的意义√基本初等函数II 任意角的概念、弧度制任意角的概念√弧度制的概念、弧度与角度的互化√三角函数理解正弦、余弦、正切的定义√单位圆的三角函数线√诱导公式√会画三角函数图像√三角函数周期性√正余弦单调性、最值与X轴交点等性质√正切函数性质√同角三角函数的基本关系式√正弦型函数参数对图像变化的影响√平面向量平面向量的实际背景及基本概念向量的实际背景√平面向量的概念√两个向量相等√向量的几何表示√向量的线性运算加法、减法、几何意义√数乘的运算、几何意义√两个向量共线的含义√线性运算的性质和几何意义√平面向量基本定理和坐标表示平面向量基本定理及意义√正交分解及坐标表示√加法、减法、数乘坐标运算√用坐标表示平面向量共线的条件√平面向量的数量积平面向量的数量积含义与物理意义√平面向量的数量积与向量投影关系√数量积坐标表达式与运算√用数量积表示夹角√用数量积判断两个向量的垂直关系√向量的应用解决平面几何问题√解决实际问题√三角恒等变换和与差的三角函数公式两角和与差的余弦、正弦、正切公式√二倍角公式√三角恒等变换积化和差、和差化积√半角公式√解三角形正弦定理余弦定理正弦定理√余弦定理√应用三角形度量问题√数列数列的概念与简单表示法数列的概念√列表、图像、通项公式表示方法√数列是自变量为正整数的函数√等差数列、等比数列等差数列概念√等差数列通项公式和求和公式√等比数列概念√等比数列通项公式和求和公式√等差数列与一次函数√等比数列与指数函数√不等式不等关系实际背景√一元二次不等式实际情景中抽象√与二次函数、一元二次方程联系√会解一元二次不等式,设计程序框图√二元一次不等式组与简单的线性规划问题实际情景抽象出二元一次不等式组√二元一次不等式组表示平面区域√二元线性规划问题√基本不等式了解证明过程√解决最值问题√常用基本逻辑用语命题及其关系命题的概念√四种命题及其关系√充分、必要、充要条件√简单的逻辑联结词或、且、非√全称量词与存在量词全称量词√存在量词√含有量词命题的否定√圆锥曲线与方程圆锥曲线实际背景√椭圆定义几何图形标准方程、简单性质√抛物线定义几何图形标准方程简单性质√双曲线定义几何图形标准方程简单性质√简单应用、数形结合思想√曲线与方程方程的曲线与曲线的方程√空间向量与立体几何空间向量及其运算空间向量概念、基本定理、坐标√空间向量线性运算√空间向量数量积√用空间向量数量积表示共线与垂直√空间向量的应用直线方向向量与平面的法向量√线线、线面、面面平行关系√线线、线面、面面垂直关系√三垂线定理√线线、线面、面面夹角计算√导数及其应用导数概念及几何意义导数概念实际背景√导数的几何意义√导数的运算求导运算法则√基本初等函数导数公式√在研究函数中应用单调性与导数关系√函数取极值的必要条件和充分条件√会求函数的极值√会求闭区间上的最值√生活中的优化问题实际问题√定积分与微积分定积分概念、实际背景、思想√微积分基本定理√推理与证明合情推理与演绎推理归纳和类比推理√演绎推理的基本模式√联系和差异√直接证明与间接证明分析法与综合法√反证法√数学归纳法数学归纳法√数系的扩充与复数的引入复数的概念复数的概念√复数相等的充要条件√复数代数表示法与几何意义√复数的四则运算四则运算√加减法运算的几何意义√计数原理分类加法、分步乘法分类加法√分步乘法√排列与组合排列概念与公式√组合概念与公式√二项式定理证明二项式定理√展开式有关问题√概率与统计概率离散型随机变量与分布列√超几何分布√条件概率√两个事件相互独立√N次独立重复试验与二项分布√均值、方差√正态分布曲线特点及意义√统计案例独立性检验√回归分析√坐标系与参数方程坐标系用极坐标表示点的位置√极坐标与直角坐标互化√简单图形的方程√柱坐标系、球坐标系表示空间中点位置√参数方程参数方程和参数的意义√直线、圆、圆锥曲线的参数方程√平摆线与渐开线√不等式选讲含绝对值不等式几何意义√绝对值三角不等式√柯西不等式不同形式√几何意义√柯西不等式一般情参数配方法√排序不等式向量递归法√伯努利不等式数学归纳法√均值不等式求极值√证明不等式方法比较、综合、分析、反证、放缩√。
全国新课标2卷近六年数学(理)科高考试题考点分布表

17
和与差的 三角函数 公式 正弦定理 、余弦定 理 数列的递 推公式、 等差数列 求和、等 比数列的 二元一次 不等式组 与简单线 性规划问 题
运算求 填空题 解能力 运算求 解答题 解能力
15
11
解三 (1)正弦定理和余弦 ①掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.①能够运用正弦定理、余弦定理等知识和方法 填空题 角形 定理 (2)应用 解决一些与测量和几何计算有关的实际问题. (1)数列的概念和简 单表示 数列 (2)等差数列、等比 数列 (1)不等关系 (2)一元二次不等式 不等 (3)二元一次不等式 式 组与简单线性规划问 题 (4)基本不等式 (1)命题及其关系 常用 (2)简单的逻辑联结 逻辑 词 (3)全称量词 用语 与存在量词 圆锥 曲线 与方 程 (1)圆锥曲线 (2)曲线与方程 ①了解数列的概念和几种简单的表示方法(列表、图像、通项公式).②了解数列是自变量为正整数的一类特殊函 数.①理解等差数列、等比数列的概念.②掌握等差数列、等比数列的通项公式与前n项和公式.③能在具体的问题 解答题 情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.④了解等差数列与一次函数、等比数列 与指数函数的关系. ①了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.①会从实际情境中抽象出一元二次不等 式模型.②通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.③会解一元二次不等式, 对给定的一元二次不等式,会设计求解的程序框图.①会从实际情境中抽象出二元一次不等式组.②了解二元一次 选择题 不等式的几何意义,能用平面区域表示二元一次不等式组.③会从实际情境中抽象出一些简单的二元线性规划问 题,并能加以解决.①了解基本不等式的证明过程.②会用基本不等式解决简单的最大(小)值问题. ①理解命题的概念.②了解"若p,则q"形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系. ③理解必要条件、充分条件与充要条件的意义.④了解逻辑联结词"或"、"且"、"非"的含义.⑤理解全称量词与存 在量词的意义.⑥能正确地对含有一个量词的命题进行否定. 选择题
2019年卷123高考理数细目表
9
5
等差数列的通项公 式,求和公式
3
10
5
椭圆的定义、方程、 几何性质
3
11
5
三角函数的图象与性 质
2
12
5
三棱锥的外接球,球 的体积
1
13 5 导数的几何意义
3
填空 14
5
等比数列的定义,求 和公式
3
题 15 5 二项分布
2
2
中
2
▲
中
2
▲
▲难
2
1
▲
▲难
2
2
▲
难
2
易
2
易
111
中
16 5 双曲线的几何性质
6
2
做 23
10
不等式的证明,均值 不等式
4
6
合计 150
难
▲
▲
中
中
▲
▲▲中
2
▲▲▲难
2▲
▲
难
2▲
▲▲中
▲
中
2019年全国课标数学卷(Ⅱ)理科高考命题双向细目表
设
题型结构 知识目标
能力目标
数学思想
计 难
题型
题 号
分 值
核心考点
度
Y: S: K: C: TL YY CX 函 分 转 数 档
运算 数 空 抽 : : : 数 类 化 形 次
档 次
1
5
集合的交集,一元二 次不等式的解法
3
2
易
2
5
复数的模,复数的几 何意义
3
3
5
指数、对数函数的性 质
1
4
5
近五年全国2卷数学(理科)高考试题双向细目表
⑷ 直线方程的三种形式
√
⑸ 斜截式与一次函数的关系
⑹ 两相交直线交点坐标
⑺ 两点,点到直线,平行线 距离
√
10
5
⑴ 圆的几何要素
√
⑵ 圆的标准与一般方程
√
⒉ 圆与方程
⑶ 直线和圆的方程简单应用
√
4
5
7
5
⑷ 代数方法处理几何问题 √
16
5
⑴ 空间直角坐标系
√
⒊ 空间直角坐标系
⑵ 空间点的坐标
√
⑶ 空间两点的距离公式 √
掌握
题号 14
分值 5
题号 5
分值 5
⒋ 基本不等式
⑴ 基本不等式的证明
√
⑵ 基本不等式解决简单最值 问题
√
⑴ 命题的概念
√
⑵ 四种命题的相互关系
√
常用逻辑用语
⑶充要条件 ⑷ 逻辑联结词
√ √
⑸ 全称与存在量词
√
⑹ 含一个量词的命题否定
√
⑴ 椭圆的定义,标准方程
√
20(1) 6
⑵ 椭圆的简单几何性质
√ √ √
⑷ 向量线性运算的性质及其 几何意义
√
⑴ 平面向量的基本定理及其 意义
√
⑵ 平面向量的正交分解及其
⒊ 平面向量的基本定理及坐标表
坐标表示
√
示
⑶ 坐标表示平面向量的加 法,减法与数乘运算
√
⑷ 坐标表示的平面向量共线 的条件
√
⑴ 数量积的含义及其物理意 义
√
⑵ 数量积与向量投影的关系 √
⒋ 平面向量的数量积
(一)坐标系与参数方程 (一)坐标系与参数方程
近五年全国Ⅱ卷数学(理科)高考试题双向细目表
命题双向细目表(参考模板)

命题双向细目表(参考模板) 学校考试试卷命题双向细目表学科年级题型答卷时间分钟满分命题人说明:1.题型包括:填空题、选择题、计算题、简答题、综合题等,根据学科有所区别。
2.试题来源包括:教材原题、学案原题、教材改编题、学案改编题、中考原题、原创题等。
3.目标层次:请根据学科标准要求填写,使用通用能力层级“识记、理解、应用、分析、综合”。
请用√符号表示。
4.题号指小题序号。
5.难度指标要点:容易题(0.90-0.75)、较易题(0.70左右)、较难题(0.55左右)、难题(0.45-0.20)。
6.注:合计分值为试题预计分值之和。
学科年级题型题号试题预计分值难度指标考查目标属性语文七年级填空题 1-10 10 0.75 理解√选择题 11-20 10 0.70 应用√计算题 21-25 15 0.55 分析√简答题 26-30 20 0.45-0.20 综合√数学八年级填空题 1-10 10 0.75 理解√选择题 11-20 10 0.70 应用√计算题 21-25 15 0.55 分析√简答题 26-30 20 0.45-0.20 综合√以下是学校考试试卷命题双向细目表:语文七年级的试卷包含填空题、选择题、计算题和简答题。
其中,填空题和选择题考查学生的理解和应用能力,计算题则考察学生的分析能力,而简答题则需要综合运用多种能力。
每一题都有预计分值和难度指标,难度指标分为容易、较易、较难和难四个级别。
数学八年级的试卷也包含了相同的题型,同样考查学生的不同能力。
学生需要根据题目要求,灵活运用所学知识,解决实际问题。
每一题都有预计分值和难度指标,难度指标分为容易、较易、较难和难四个级别。
这份双向细目表是由命题人根据学科标准要求、教材原题、学案原题、教材改编题、学案改编题、中考原题和原创题等来源制作而成。
通过这份表格,学生和教师都可以更好地了解试卷的命题情况,有利于提高学生的研究效果和教师的教学质量。
全国高考数学理科II双向细目表

11/5
抛物线
掌握
抛物线的标准方程及其几何性质
、
11/5
10/5
11/5
直线与圆锥曲线
掌握
综合
8/5
20
轨迹方程
掌握
综合
20
23
23
23
综合应用
熟练掌握
综合
20
空间直线
理解
平面的基本性质,斜二侧的画法;画出空间两条直线的各种位置关系的图形,根据图形想象它们的位置关系;直线与直线所成角、距离
10/5
9/5
14/5
13/5
图象与性质
掌握
会用三角函数线画正弦函数,正切函数的图象,由诱导公式画余弦函数的图象;理解它们的性质;会用"五点法"
12/5
的图象
理解
、 、 的物理意义
掌握
用"五点法"画函数 的简图;函数的平移问题
7/5
三角最值及综合应用
掌握
利用三角知识求最值
14/5
12/5
应用
掌握
运用所学二角知识解决实际问题
3/5
距离公式、定比分点
掌握
平面两点间的距离公式,线段的定比分点和中点坐标公式,
灵活运用
平移公式
正余弦定理
掌握
正弦定理、余弦定理,并能运用它们解斜三角形
13/5
17
4/5
17
不等式的概念性质
理解
不等式的性质
均值不等式
掌握
两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理.并会简单的应用;分析法、综合法、比较法证明简单的不等式
向量、向量的加法与减法、实数与向量的积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
要求 B C
2018
2017
2016
2015
2014
知道 理解 掌握 √ √
题号 分值 题号 分值 题号 分值 题号 分值 题号 分值
√ √ √ √
10
5 10 5
12
5
⒉ 三角函数
7
5
⒈ 平面向量的背景及 ⑵ 平面向量的概念和两个向 量相等的含义 基本概念 ⑶ 向量的几何表示 ⑴ 向量加法,减法运算其几 何意义 ⒉ 向量的线性运算 ⑵ 向量数乘的运算及其几何 意义 ⑶ 两个向量共线 ⑷ 向量线性运算的性质及其 几何意义 ⑴ 平面向量的基本定理及其 意义 ⒊ 平面向量的基本定 理及坐标表示 ⑶ 坐标表示平面向量的加 法,减法与数乘运算 ㈨ 平面向量 ⑵ 平面向量的正交分解及其 坐标表示 √
√
√ √ √ √ √ √ √
√
20(2) 6 19(2) 6 19(2) 6 19(2) 6
11
5
√ √ √ √
13
5
16
5
8
5
12
5
21(2) 6
20(1)
2
√ 21(1) 6
21(1) 6 21(1) 6
11
5
(十七) 导 数及其应用
知识点 A (十七) 导 数及其应用 必考 导数及其应用 ⑼ 导数求函数的极值 ⑽ 闭区间上函数的最值 ⑾ 导数解决实际问题 ⑿ 定积分与微积分 ⑴ 简单的归纳推理和类比推 理 (十八)推 理与证明 推理与证明 ⑵ 三段论 ⑶ 综合与分析法,反证法, ⑷ 数学归纳法 ⑴ 复数的概念,复数相等的 数系的扩充和复数的 重要条件 ⑵ 复数的几何意义 引入 ⑶ 复数代数形式的四则运算 ⑴ 分类加法,及其简单应用 ⑵分步乘法计数原理,及其简 单应用 ⑶ 排列概念及其公式,解决 简单问题 计算原理 ⑷ 组合的概念及公式,解决 简单问题 ⑸ 二项式定理解决与二项展 开式有关的简单问题 ⑴ 求有限个值的离散随机变 量及其分布列 ⑵ 超几何分布进行简单应用 ⑶条件概率的含义 √ ⑷ n次独立重复试验模型及二 项分布,解决简单问题 ⑸ 有限个值的离散型随机变 量的均值,方差,解决简单问 题 ⑹ 正态分布曲线特点及其意 义 ⑺ 回归分析的思想,方法及 其简单应用 ⑻ 独立性检验的思想,方法 及其初步应用 选考 (一)坐标 系与参数方 程 (1)坐标系的作用 (2)在平面直角坐标系伸缩 变换作用下平面图形的变化情 况 (3)极坐标的基本概念 (4)在极坐标系中用极坐标 刻画点的位置 (5)进行极坐标和直角坐标 的互化 (6)在极坐标系中给出简单 图形表示的极坐标方程 (7)参数方程 (8)参数的意义 √ √ √ √ √ √ √ √
√
15
5
14
5
√ √
6
5 17(2) 6 13 5 17 12
4
5
√
17(2) 6 √ √ 17 12 15 17(1) 6
√
⒊ 等比数列
⑸ 等比数列的概念 ⑹ 等比数列的通项公式与前n 项和公式 ⑺ 具体情境中识别等比数 列,利用等比数列的解决简单 应用 ⑻ 等比数列与指数函数关系 √ √ ⑴ 一元二次不等式模型 √
近五年全国Ⅱ卷数学(理科)高考试题双向细目表
知识点 A 必考 ⑴ 集合的含义 1.集合的含义与表示 ⑵ 元素与集合的关系 ⑶ 三种集合语言 ⑴ 包含与相等关系 ㈠ 集合 2.集合间的基本关系 ⑵ 子集 ⑶ 全集与空集 ⑴ 并集与交集 ⒊ 集合的基本运算 ⑵ 补集 ⑶ 韦恩图 ⑴ 函数的概念 ⑵ 函数的表示方法 ⑶ 分段函数 ⒈ 函数 ⑷ 单调性,最值 ⑸ 奇偶性 √ ⑹ 基本初等函数的图像分析 函数的性质 ⑴ 指数幂的含义 ⑵ 幂的运算 ⒉ 指数函数 ㈡ 函数概念 与基本初等 函数I ⒊ 对数函数 ⑶ 指数函数概念及单调性 ⑷ 指数函数的图像 ⑸ 指数函数模型 ⑴ 对数的概念及其运算性质 ⑵ 对数函数的概念及其单调 性 ⑶ 对数函数图像 ⑷ 对数函数模型 ⑸ 反函数 ⒋ 幂函数 ⑴ 幂函数的概念 ⑵ 五种常见幂函数图像 ⑴ 由二次函数图像零点与方 程根关系 ⑵ 方程的根的个数与存在性 √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ 14 14 5 5 18(1) 6 9 5 10 5 9 5 4 5 6 5 6 5 6 5 21(3) 5 √ √ √ √ √ 5 5 √ √ √ √ √ √ 11 √ √ √ 5 5 3 5 5 12 5 12 5 5 5 15 5 √ √ √ √ √ 2 5 2 5 1 5 1 5 √ √ √ √ 2 5 要求 B C 2018 2017 2016 2015 2014 题号 分值 题号 分值 题号 分值 题号 分值 题号 分值
√
7
5
8
5
8
5
8
5
7
5
√ √ √ √ √ √ √ 18(3) 6 3 5
⒈ 随机抽样
⒉ 用样本估计总体 ㈥ 统计
√
√ √ √ √ 8 5 18(1) 3 18 12
19
12
⑴ 随机数与模拟方法估计概 ⒊ 随机数与几何概型 率 ⑵ 几何概型的意义 ⑴ 任意角的概念和弧度制的 概念 ⑵ 弧度与角度的互化 ⑴ 正弦,余弦,正切的定义
√ √ √ 3 5 4 5 17 12
⒈ 不等关系
⒉ 一元二次不等式
⑵ 由图像了解一元二次不等 与相应二次函数,一元二次方 √ 程的联系 ⑶ 一元二次不等式解法以及 设计求解的程序框图 √
(十三)不 等式 ⒊ 简单线性规划问题
⑴ 实际情境中抽象二元一次 不等式组 ⑵ 平面区域表示二元一次不 等式组 ⑶ 简单的二元线性规划问题 ⑴ 基本不等式的证明 ⑵ 基本不等式解决简单最值 问题 ⑴ 命题的概念 ⑵ 四种命题的相互关系 ⑶充要条件 ⑷ 逻辑联结词
要求 B C √ √ √
Байду номын сангаас2018
2017
2016
2015
2014
知道 理解 掌握
题号 分值 题号 分值 题号 分值 题号 分值 题号 分值 21(1) 6 21(2) 6 21(2) 6 21(2) 12 21(2) 16 5 5
√ 7 √ √ √ √ √ √ √ √ 6 6 5 5 1 5 1 5 5
知道 理解 掌握
题号 分值 题号 分值 题号 分值 题号 分值 题号 分值
√
17(1) 6
9
5
运用两角和与差的正弦、余弦 ⒉ 简单的三角恒等变 、正切公式以及二倍角的正弦 换 、余弦、正切公式进行简单的 恒等变换 ⑴ 正弦定理,余弦定理 ⒈ 正弦定理和余弦定 ⑵ 正弦定理,余弦定理解决简 理 单的三角形度量问题 (十一) 解 三角形 ⑶正弦,余弦定理解决测量和 ⒉ 应用 几何计算有关的实际问题 ⒈ 数列的概念和简单 表示法 ⑴ 等差数列的概念 ⑵ 等差数列的通项公式与前n 项和公式 ⒉ 等差数列 (十二) 数列 ⑷ 等差数列与一次函数关系 √ ⑶ 具体情境中识别等差数 列,利用等差数列的解决简单 应用 √
√
√
√ √ √ √ √ √ √
14
5
5
5
14
5
9
5
⒋ 基本不等式
(十四) 常 用逻辑用语
常用逻辑用语
知识点 (十四) 常 用逻辑用语 常用逻辑用语 必考 ⑸ 全称与存在量词 ⑹ 含一个量词的命题否定 ⑴ 椭圆的定义,标准方程 ⑵ 椭圆的简单几何性质 ⑶ 直线与椭圆的位置关系 ⑷ 抛物线的定义,标准方程 (十五) 圆 锥曲线 圆锥曲线 ⑸ 抛物线的简单几何性质 ⑹ 直线与抛物线的位置关系 ⑺ 双曲线 ⑻ 曲线与方程的对应关系 ⑼ 数形结合思想 ⑽ 圆锥曲线的简单应用 ⑴ 空间向量概念,基本定理 及其意义 ⑵ 空间向量的正交分解及其 坐标表示 ⑶ 空间向量的线性运算及其 坐标表示 ⑷ 空间向量的数量积及其坐 标表示 (十六) 空 ⑸ 向量的数量积判断向量的 间向量与立 空间向量与立体几何 共线和垂直 体几何 ⑹ 直线的方向向量及平面的 法向量 ⑺ 向量语言表述线线,线 面,面面的平行和垂直关系 ⑻ 向量方法证明线面位置关 系 ⑼ 向量方法线线,线面,面 面的夹角 ⑴ 导数概念的实际背景 ⑵ 导数几何意义 ⑶导数的定义求导数 (十七) 导 数及其应用 导数及其应用 ⑷ 基本初等函数导数公式和 导数的四则运算 ⑸ 复合函数求导 ⑹ 函数的单调性与导数的关 系 ⑺ 导数研究函数的单调性, 会求函数的单调区间(不超过 三次) ⑻ 函数在某点取得极值的必 要与充分条件 导数及其应用 √ √ √ √ √ √ √ A
知道 理解 掌握
⒌ 函数与方程 6.函数图像 7. 函数模型及其应用
⑴ 柱锥台球及其简单组合体 的结构特征 ⑵ 简易组合体的三视图,及 其能够还原立体模型 ⒈ 空间几何体 ⑶ 斜二测画法 ⑷ 平行投影方法画图与直观 图 ㈢ 立体几何 ⑸ 球、棱柱、棱锥、台的表 初步 面积与体积 ⑴ 空间直线,平面位置关系 的定义 ⒉ 点直线平面之间的 ⑵ 四个公理+1个定理 ⑶ 线面平行性质与判定定理 位置关系 ⑷ 线面垂直性质与判定定理 ⑸ 证明空间位置的简单命题 ⑴ 直线位置的几何要素 ⑵ 倾斜角和斜率概念及其计 算 ⒈ 直线与方程
10
5
⒈ 任意角,弧度制
√
知识点 A 必考 ⑵ 利用单位圆推导的正弦, 余弦,正切的诱导公式 ⑶ 正弦,余弦,正切的图像 ㈧ 基本初等 函数II(三 角函数) ⑷ 三角函数的周期性 √ ⑸ 正弦,余弦在【0,2π 】上 的性质 ⑹ 正切函数在(-π /2,π /2 】的单调性 ⑺ 同角三角函数的基本关系 式 ⑻ y=Asin(wx+Φ )的图像与 性质 ⑼ 三角函数解决简单实际问 √ 题,三角函数模型 ⑴ 向量的实际背景 √
要求 B √ √ √ √ C
2018
2017
2016
2015
2014
知道 理解 掌握
题号 分值 题号 分值 题号 分值 题号 分值 题号 分值
