全等三角形证明题及答案(15道)
全等三角形经典题型50题(含答案)

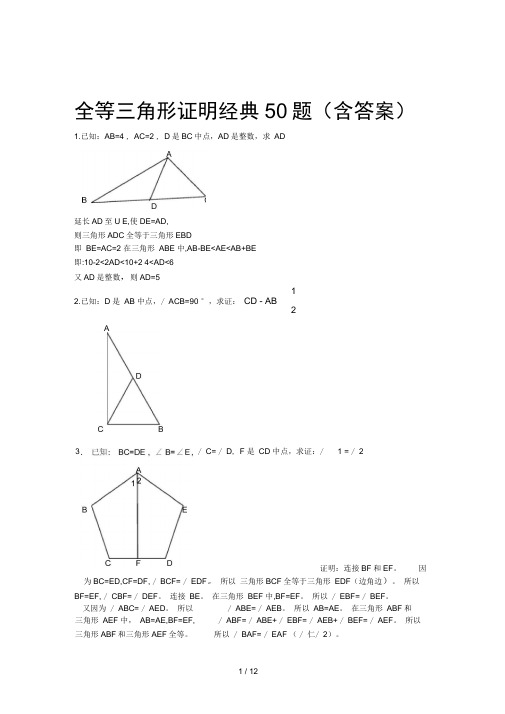
全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延伸 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连结 BF 和 EF。
由于 BC=ED,CF=DF,∠ BCF=∠ EDF。
因此三角形 BCF 全等于三角形 EDF(边角边 )。
因此 BF=EF,∠ CBF=∠ DEF。
连结 BE。
在三角形BEF 中 ,BF=EF。
因此∠ EBF=∠ BEF。
又由于∠ ABC=∠AED。
因此∠ABE=∠AEB。
因此 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
因此三角形 ABF 和三角形 AEF全等。
因此∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延伸线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD均分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连结(SASED∵ AD)均分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 均分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连结 CF 由于 CE⊥AB 因此∠CEB=∠ CEF= 90 °由于 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 由于∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°因此∠ D=∠ CFA 由于AC 均分∠ BAD 因此∠ DAC=∠ FAC 又由于AC= AC因此△ ADC≌ △ AFC( SAS)因此 AD= AF 因此 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别均分∠ ABC、∠ BCD,且点 E 在 AD 上。
全等三角形经典题型50题(含答案)
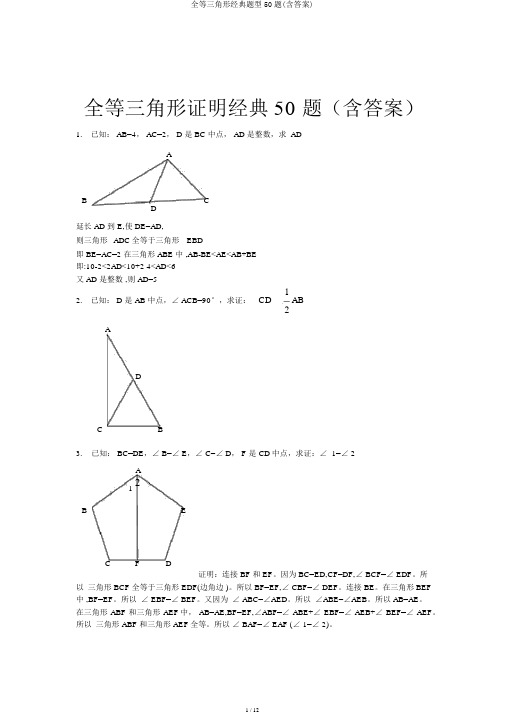
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
全等三角形经典题型50题(含答案)
全等三角形证明经典50 题(含答案)1. 已知: AB=4, AC=2, D 是 BC 中点, AD 是整数,求ADAB CD延长 AD 到 E,使 DE=AD,则三角形ADC全等于三角形EBD即 BE=AC=2 在三角形 ABE 中 ,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又 AD 是整数 ,则 AD=512. 已知: D 是 AB 中点,∠ ACB=90°,求证:CD AB2ADC B3.已知: BC=DE,∠ B=∠ E,∠ C=∠ D, F 是 CD中点,求证:∠ 1=∠ 2A21B EC F D证明:连接 BF 和 EF。
因为 BC=ED,CF=DF,∠ BCF=∠ EDF。
所以三角形 BCF 全等于三角形 EDF(边角边 )。
所以 BF=EF,∠ CBF=∠ DEF。
连接 BE。
在三角形BEF 中 ,BF=EF。
所以∠ EBF=∠ BEF。
又因为∠ ABC=∠AED。
所以∠ABE=∠AEB。
所以 AB=AE。
在三角形 ABF 和三角形 AEF中, AB=AE,BF=EF,∠ABF=∠ ABE+∠ EBF=∠ AEB+∠ BEF=∠ AEF。
所以三角形 ABF 和三角形 AEF全等。
所以∠ BAF=∠ EAF (∠ 1=∠ 2)。
A4. 已知:∠ 1=∠ 2, CD=DE, EF//AB,求证: EF=AC 1 2证明:过 E 点,作 EG//AC,交 AD 延长线于 G 则∠ DEG=∠ DCA,F ∠DGE=∠ 2又∵CD=DE∴ ⊿ADC≌ ⊿ GDE(AAS)∴EG=AC∵ EF//AB∴∠ DFE=∠ 1∵ ∠ 1=∠ 2∴ ∠ DFE=∠ DGE∴ EF=C EG∴ EF=AC DEB5.已知:AD平分∠ BAC,AC=AB+BD,求证:∠B=2∠C ACB D证明:在 AC上截取AD=AD∴ ⊿ AED≌ ⊿ ABD AE=AB,连接(SASED∵ AD)平分∠ BAC∴ ∠∴ ∠ AED=∠ BEAD=∠ BAD 又∵ AE=AB,,DE=DB∵ AC=AB+BDAC=AE+CE∴ CE=DE∴ ∠ C=∠ EDC∵∠ AED=∠ C+∠ EDC=2∠ C∴∠ B=2∠C6. 已知: AC 平分∠ BAD,CE⊥ AB,∠ B+∠ D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接 CF 因为 CE⊥AB 所以∠CEB=∠ CEF= 90 °因为 EB= EF, CE= CE,所以△CEB≌△CEF 所以∠B =∠ CFE 因为∠ B+∠ D= 180 ,°∠CFE+∠ CFA= 180°所以∠ D=∠ CFA 因为AC 平分∠ BAD 所以∠ DAC=∠ FAC 又因为AC= AC所以△ ADC≌ △ AFC( SAS)所以 AD= AF 所以 AE= AF+ FE= AD+ BE12.如图,四边形 ABCD 中, AB∥ DC, BE、 CE 分别平分∠ ABC、∠ BCD,且点 E 在 AD 上。
全等三角形证明经典50题(含答案)
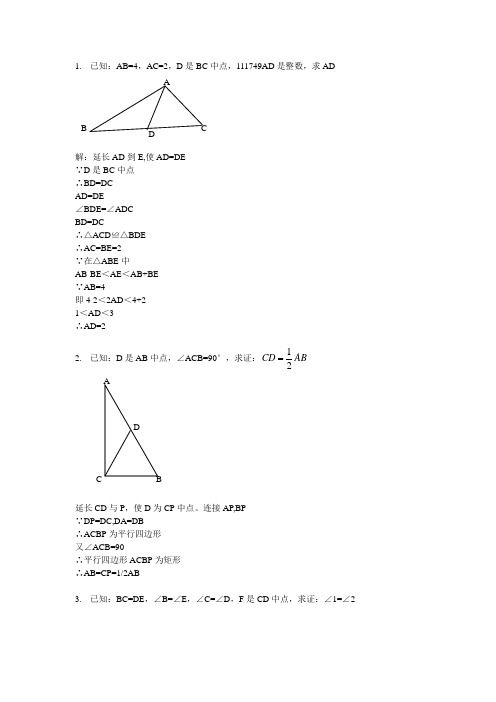
1. 已知:AB=4,AC=2,D 是BC 中点,111749AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DCAD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGBACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE (AAS )∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=E G ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明题及答案15道
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即:∠EAD=∠BAC,
在△EAD和△BAC中
∠B=∠E AB=AE
∠BAC=∠EAD ,
∴△ABC≌△AED(ASA),
∴BC=ED.
全等三角形的判定与性质.
如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF, AE=CF,BE=DF.求证:△ADE≌△CBF.
∴△BCF≌△CBD(ASA). 全等三角形的判定.
如图,在△ABC中,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F,BE=CF. 求证:AD是△ABC的角平分线.
证明:∵DE⊥AB,DF⊥AC, ∴Rt△BDE=Rt△DCF=90°. BD=DC BE=CF , ∴Rt△BDE≌Rt△DCF(HL), ∴DE=DF, 又∵DE⊥AB,DF⊥AC, ∴AD是角平分线.
直角三角形全等的判定
如图,△ABC中,∠ABC=∠BAC=45°,点 P在AB上,AD⊥CP,BE⊥CP,垂足分别为D, E,已知DC=2,求BE的长.
∵∠ABC=∠BAC=45° ∴∠ACB=90°,AC=BC ∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2.
:∵AC平分∠BAD, ∴∠BAC=∠DAC, 在△ABC和△ADC 中, AB=AD ∠BAC=∠DAC AC=AC , ∴Fra bibliotekABC≌△ADC.
全等三角形的判定.
9.如图,已知点E,C在线段BF上,BE=CF, AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
(完整版)全等三角形证明经典50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠24. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CDAB B A CDF2 1 EAC D E F 21 A D BC A6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
13.已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠C14. P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-AB15. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BED C B A FE PD A CB16. 已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC18.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .19.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA20.(5分)如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .21.如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.F AEDCB P E D CB A DC B A23.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点, (1)求证:△AED ≌△EBC . (2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):24.(7分)如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .证明:25、如图:DF=CE ,AD=BC ,∠D=∠C 。
三角形全等证明题目60题目(有详解)
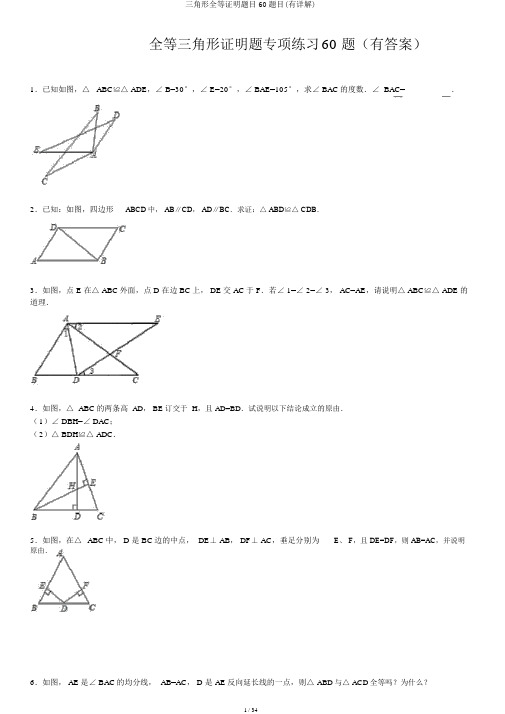
全等三角形证明题专项练习60 题(有答案)1.已知如图,△ABC≌△ ADE,∠ B=30°,∠ E=20°,∠ BAE=105°,求∠ BAC的度数.∠ BAC= _________.2.已知:如图,四边形ABCD中, AB∥CD, AD∥BC.求证:△ ABD≌△ CDB.3.如图,点 E 在△ ABC外面,点 D 在边 BC上, DE交 AC于 F.若∠ 1=∠ 2=∠ 3, AC=AE,请说明△ ABC≌△ ADE的道理.4.如图,△ ABC的两条高AD, BE订交于 H,且 AD=BD.试说明以下结论成立的原由.(1)∠ DBH=∠ DAC;(2)△ BDH≌△ ADC.5.如图,在△ABC中, D 是 BC边的中点, DE⊥ AB, DF⊥ AC,垂足分别为E、 F,且 DE=DF,则 AB=AC,并说明原由.6.如图, AE是∠ BAC的均分线, AB=AC, D 是 AE反向延长线的一点,则△ABD与△ ACD全等吗?为什么?第1页共28页7.以下列图,A、 D、 F、 B 在同素来线上,A F=BD, AE=BC,且 AE∥BC.求证:△ AEF≌△ BCD.8.如图,已知AB=AC, AD=AE, BE 与 CD订交于 O,△ ABE与△ ACD全等吗?说明你的原由.9.如图,在△ ABC中, AB=AC, D 是 BC的中点,点 E 在 AD上,找出图中全等的三角形,并说明它们为什么是全等的.10.以下列图, CD=CA,∠ 1=∠ 2, EC=BC,求证:△ ABC≌△ DEC.11.已知 AC=FE, BC=DE,点 A、 D、 B、F 在一条直线上,要使△ ABC≌△ FDE,应增加什么条件?并依照你所增加的条件证明:△ ABC≌△ FDE.12.如图,已知AB=AC, BD=CE,请说明△ ABE≌△ ACD.13.如图,△ ABC中,∠ ACB=90°, AC=BC,将△ ABC绕点 C 逆时针旋转角α( 0°<α< 90°)获取△ A1B1C,连接BB1.设 CB1交 AB于 D, A1B1分别交 AB, AC于 E, F,在图中不再增加其他任何线段的情况下,请你找出一对全等的三角形,并加以证明.(△ ABC与△ A1B1 C1全等除外)14.如图, AB∥ DE,AC∥ DF,BE=CF.求证:△ ABC≌△ DEF.15.如图, AB=AC, AD=AE, AB,DC订交于点M, AC, BE订交于点N,∠ DAB=∠EAC.求证:△ADM≌△ AEN.16.将两个大小不同样的含 45°角的直角三角板如图 1 所示放置在同一平面内.从图1中抽象出一个几何图形(如图2), B、 C、E 三点在同一条直线上,连接DC.求证:△ ABE≌△ ACD.优秀文档17.如图,已知△ ABC是等边三角形, D、E 分别在边 BC、AC上,且 CD=CE,连接 DE并延长至点 F,使 EF=AE,连接AF、 BE和 CF.请在图中找出所有全等的三角形,用符号“≌”表示,并选择一对加以证明.18.如图,已知∠1=∠ 2,∠ 3=∠ 4, EC=AD.(1)求证:△ ABD≌△ EBC.(2)你能够从中得出哪些结论?请写出两个.19.等边△ ABC边长为 8, D为 AB边上一动点,过点 D 作 DE⊥ BC于点 E,过点 E 作 EF⊥ AC于点 F.(1)若 AD=2,求 AF的长;(2)求当 AD取何值时, DE=EF.20.巳知:如图,AB=AC, D、E 分别是 AB、 AC上的点, AD=AE, BE与 CD订交于 G.(Ⅰ)问图中有多少对全等三角形?并将它们写出来.(Ⅱ)请你选出一对三角形,说明它们全等的原由(根椐所选三角形说理难易不同样给分,即难的说对给分高,易的说对给分低)21.已知:如图,AB=DC, AC=BD, AC、BD订交于点E,过 E 点作 EF∥ BC,交 CD于 F,(1)依照给出的条件,能够直接证明哪两个三角形全等?并加以证明.(2) EF 均分∠ DEC吗?为什么?22.如图,己知∠1=∠ 2,∠ ABC=∠ DCB,那么△ ABC与△ DCB全等吗?为什么?23.如图, B, F, E, D 在一条直线上,AB=CD,∠ B=∠ D,BF=DE.试证明:(1)△ DFC≌△ BEA;(2)△ AFE≌△ CEF.24.如图, AC=AE,∠ BAF=∠BGD=∠ EAC,图中可否存在与△ABE全等的三角形?并证明.25.如图, D 是△ ABC的边 BC的中点, CE∥ AB,E 在 AD的延长线上.试证明:△ ABD≌△ ECD.26.如图,已知AB=CD,∠ B=∠C, AC和 BD订交于点O,E 是 AD的中点,连接OE.(1)求证:△ AOB≌△ DOC;(2)求∠ AEO的度数.27.如图,已知AB∥ DE, AB=DE, AF=DC.(1)求证:△ ABF≌△ DEC;(2)请你找出图中还有的其他几对全等三角形.(只要直接写出结果,不要证明)28.如图:在△ ABC中, BE、CF分别是 AC、AB 两边上的高,在 BE 上截取 BD=AC,在 CF的延长线上截取CG=AB,连接 AD、 AG.(1)求证:△ ABD≌△ GCA;(2)请你确定△ ADG的形状,并证明你的结论.29.如图,点D、 F、 E 分别在△ ABC的三边上,∠ 1=∠ 2=∠ 3, DE=DF,请你说明△ ADE≌△ CFD的原由.30.如图,在△ ABC中,∠ ABC=90°, BE⊥ AC于点 E,点 F 在线段 BE 上,∠ 1=∠ 2,点 D在线段 EC上,给出两个条件:① DF∥BC;② BF=DF.请你从中选择一个作为条件,证明:△AFD≌△ AFB.31.如图,在△ ABC中,点 D在 AB 上,点 E 在 BC上, AB=BC, BD=BE,EA=DC,求证:△ BEA≌△ BDC.32.阅读并填空:如图,在△ ABC中,∠ ACB=90°, AC=BC, BE⊥ CE于点 E,AD⊥ CE于点 D.请说明△ ADC≌△ CEB的原由.解:∵ BE⊥CE于点 E(已知),∴∠ E=90°_________,同理∠ ADC=90°,∴∠ E=∠ ADC(等量代换).在△ ADC中,∵∠ 1+∠ 2+∠ ADC=180°_________,∴∠ 1+∠ 2=90°_________.∵∠ ACB=90°(已知),∴∠ 3+∠ 2=90°,∴_________ .在△ ADC和△ CEB中, .∴△ ADC≌△ CEB ( A. A. S)33.已知:以下列图,AB∥ DE,AB=DE, AF=DC.( 1)写出图中你认为全等的三角形(不再增加辅助线);( 2)选择你在(1)中写出的全等三角形中的任意一对进行证明.34.如图,点 E 在△ ABC外面,点 D在 BC边上, DE交 AC于点 F,若∠ 1=∠ 2=∠ 3, AC=AE.试说明以下结论正确的原由:(1)∠ C=∠ E;(2)△ ABC≌△ ADE.35.如图,在 Rt△ ABC中,∠ ACB=90°,AC=BC,D 是斜边 AB上的一点, AE⊥ CD于 E,BF⊥ CD交 CD的延长线于F.求证:△ ACE≌△ CBF.36.如图,在△ ABC中, D 是 BC的中点, DE∥ CA交 AB 于 E,点 P 是线段 AC上的一动点,连接PE.研究:当动点P 运动到 AC边上什么地址时,△APE≌△ EDB?请你画出图形并证明△APE≌△ EDB.37.已知:如图,AD∥ BC, AD=BC, E 为 BC上一点,且AE=AB.求证:( 1)∠ DAE=∠B;(2)△ ABC≌△ EAD.38.如图, D 为 AB边上一点,△ ABC和△ ECD都是等腰直角三角形,∠ ACB=∠ DCE=90°, CA=CB, CD=CE,图中有全等三角形吗?指出来并说明原由.39.如图, AB=AC, AD=AE,∠ BAC=∠ DAE.求证:△ ABD≌△ ACE.40.如图,已知D是△ ABC的边 BC的中点,过D 作两条互相垂直的射线,分别交AB于 E,交 AC于 F,求证: BE+CF >EF.41.以下列图,在△MNP中, H是高 MQ与 NE的交点,且QN=QM,猜想 PM与 HN有什么关系?试说明原由.42.如图,在△ ABC中, D 是 BC的中点,过 D 点的直线 GF交 AC于 F,交 AC的平行线 BG于 G点, DE⊥ GF,交 AB于点 E,连接 EG.(1)求证: BG=CF;(2)请你判断 BE+CF与 EF 的大小关系,并证明你的结论.43.如图,在△ ABC中,∠ ACB=90°, AC=BC, BE⊥ CE于 E, AD⊥ CE于 D,,,求 BE 的长.44.如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD, BC=AD,请说明:∠ A=∠ C 的道理,小明着手测量了一下,发现∠A确实与∠ C相等,但他不能够说明其中的道理,你能帮助他说明这个道理吗?试一试看.45.如图, AD是△ ABC的中线, CE⊥ AD于 E, BF⊥AD,交 AD的延长线于F.求证: CE=BF.46.如图,已知 AB∥ CD,AD∥ BC,F 在 DC的延长线上, AM=CF,FM交 DA的延长线上于E.交 BC于 N,试说明:AE=CN.47.已知:如图,△ABC中,∠ C=90°, CM⊥ AB于 M, AT均分∠ BAC交 CM于 D,交 BC于 T,过 D 作 DE∥ AB交 BC 于 E,求证: CT=BE.48.如图,已知AB=AD, AC=AE,∠ BAE=∠ DAC.∠ B 与∠ D 相等吗?请你说明原由.49. D 是 AB上一点, DF交 AC于点 E, DE=EF, AE=CE,求证: AB∥CF.50.如图, M是△ ABC的边 BC上一点, BE∥ CF,且 BE=CF,求证: AM是△ ABC的中线.优秀文档合用标准文案51.如图,在△ ABC中, AC⊥BC, AC=BC, D 为 AB上一点, AF⊥ CD交于 CD的延长线于点F, BE⊥ CD于点 E,求证:EF=CF﹣ AF.52.如图,在△ ABC中,∠ BAC=90°, AB=AC,若 MN是经过点 A 的直线, BD⊥ MN于 D,EC⊥ MN于 E.(1)求证: BD=AE;(2)若将 MN绕点 A 旋转,使 MN与 BC订交于点 O,其他条件都不变, BD与 AE边相等吗?为什么?(3) BD、 CE与 DE有何关系?53.已知:如图,△ABC中, AB=AC, BD和 CE为△ ABC的高, BD和 CE订交于点O.求证: OB=OC.54.在△ ABC中,∠ ACB=90°, D 是 AB边的中点,点 F 在 AC边上, DE与 CF平行且相等.试说明AE=DF的原由.55.如图,在△ ABC中, D 是边 BC上一点, AD均分∠ BAC,在 AB 上截取 AE=AC,连接 DE,已知 DE=2cm, BD=3cm,求线段 BC的长.优秀文档56.如图:已知∠B=∠ C, AD=AE,则 AB=AC,请说明原由.57.如图△ ABC中,点 D 在 AC上, E 在 AB上,且 AB=AC,BC=CD, AD=DE=BE.( 1)求证△ BCE≌△ DCE;( 2)求∠ EDC的度数.58.已知:∠ A=90°, AB=AC, BD均分∠ ABC, CE⊥ BD,垂足为E.求证: BD=2CE.59.如图,已知:AB=CD, AD=BC,过 BD上一点 O的直线分别交DA、 BC的延长线于E、 F.(1)求证:∠ E=∠ F;(2) OE与 OF相等吗?若相等请证明,若不相等,需增加什么条件就能证得它们相等?请写出并证明你的想法.60.以以下列图, AD是∠ BAC的均分线, DE垂直 AB于点 E, DF垂直 AC于点 F,且 BD=DC.求证: BE=CF.全等三角形证明题专项练习60 题参照答案:1.∵△ ABC≌△ ADE 且∠ B≠∠ E,∴∠ C=∠ E,∠ B=∠ D;∴∠ BAC=180°﹣∠ B﹣∠ C=180°﹣ 30°﹣ 20° =130°.2.∵ AB∥ CD, AD∥ BC,∴∠ ABD=∠ CDB、∠ ADB=∠CBD.又 BD=DB,∴△ ABD≌△ CDB(ASA).3.△ ADF与△ AEF中,∵∠ 2=∠ 3,∠ AFE=∠ CFD,∴∠ E=∠ C.∵∠ 1=∠ 2,∴∠ BAC=∠DAE.∵AC=AE,∴△ ABC≌△ ADE.4.( 1)∵∠ BHD=∠ AHE,∠ BDH=∠ AEH=90°∴∠ DBH+∠BHD=∠ HAE+∠ AHE=90°∴∠ DBH=∠HAE∵∠ HAE=∠DAC∴∠ DBH=∠DAC;(2)∵ AD⊥ BC∴∠ ADB=∠ADC在△ BDH与△ ADC中,∴△ BDH≌△ ADC.5.∵ DE⊥ AB, DF⊥ AC,∴△ DBE与△ DCF是直角三角形,∵BD=CD, DE=DF,∴Rt △ DBE≌ Rt △ DCF( HL),∴∠ B=∠ C,∴AB=AC.6.∵ AE 是∠ BAC的均分线,∴∠ BAE=∠CAE;∴180°﹣∠BAE=180°﹣∠CAE,即∠ DAB=∠DAC;又∵ AB=AC, AD=AD,∴在△ ABD和△ ACD中,∴△ ABD≌△ ACD( SAS)7.∵ AE∥ BC,∴∠ B=∠ C.∵AF=BD, AE=BC,∴△ AEF≌△ BCD( SAS).8.△ ABE与△ ACD全等.原由:∵ AB=AC,∠ A=∠ A(公共角), AE=AD,∴△ ABE≌△ ACD.9.图中的全等三角形有:△ABD≌△ ACD,△ABE≌△ ACE,△BDE≌△ CDE.原由:∵ D是 BC的中点,∴BD=DC, AB=AC, AD=AD∴△ ABD≌△ ACD( SSS);∵AE=AE,∠ BAE=∠ CAE, AB=AC,∴△ ABE≌△ ACE( SAS);∵BE=CE, BD=DC, DE=DE,∴△ BDE≌△ CDE( SSS).10.:∵∠ 1=∠ 2,∴∠ ACB=∠DCE,在△ ABC和△ DEC中,,∴△ ABC≌△ DEC( SAS)11.增加AB=DF.在△ ABC和△ FDE中,∴△ ABC≌△ FDE(SSS).12.∵ AB=AC, BD=CE,∴ AD=AE.又∵∠ A=∠ A,∴△ ABE≌△ ACD(SAS).13.△ CBD≌△ CA1F 证明以下:∵AC=BC,∴∠A=∠ ABC.∵△ ABC绕点 C 逆时针旋转角α( 0°<α< 90°)获取△ A1B1C1,∴∠ A1 =∠ A, A1C=AC,∠ ACA1=∠ BCB1=α.∴∠ A1 =∠ ABC(1 分), A1C=BC.∴△ CBD≌△ CAF( ASA)114.∵ AB∥DE, AC∥DF,∴∠ B=∠ DEF,∠ F=∠ ACB.∵BE=CF,∴BE+CE=CF+EC.∴BC=EF.∴△ ABC≌△ DEF ( ASA).15.∵ AB=AC, AD=AE,∠ DAB=∠ EAC,∴∠ DAC=∠AEB,∴△ ACD≌△ ABE,∴∠ D=∠ E,又 AD=AE,∠ DAB=∠EAC,∴△ ADM≌△ AEN16.∵△ ABC和△ ADE均为等腰直角三角形,∴AB=AC, AD=AE,∠ BAC=∠DAE=90,即∠ BAC+∠CAE=∠DAE+∠ CAE,∴∠ BAE=∠CAD,在△ ABE和△ ACD中,,∴△ ABE≌△ ACD17.答:△ BDE≌△ FEC,△ BCE≌△ FDC,△ ABE≌△ ACF;证明:(以△ BDE≌△ FEC为例)∵△ ABC是等边三角形,∴BC=AC,∠ ACB=60°,∵CD=CE,∴△ EDC是等边三角形,∴∠ EDC=∠DEC=60°,∴∠ BDE=∠FEC=120°,∵CD=CE,∴BC﹣ CD=AC﹣ CE,∴BD=AE,又∵ EF=AE,∴B D=FE,在△ BDE与△ FEC中,∵,∴△ BDE≌△ FEC( SAS).18.( 1)证明以下:∵∠ ABD=∠1+∠ EBC,∠ CBE=∠ 2+∠ EBC,∠ 1=∠2.∴∠ ABD=∠CBE.在△ ABD和△ EBC中∴△ ABD≌△ EBC( AAS);(2)从中还可获取 AB=BC,∠ BAD=∠ BEC19.( 1)∵ AB=8, AD=2∴BD=AB﹣ AD=6在 Rt △ BDE中∠BDE=90°﹣∠B=30°∴ BE= BD=3∴CE=BC﹣ BE=5在 Rt △ CFE中∠CEF=90°﹣∠C=30°∴ CF= CE=∴AF=AC﹣ FC= ;(2)在△ BDE和△ EFC中,∴△ BDE≌△ CFE( AAS)∴BE=CF∴BE=CF= EC∴BE= BC=∴BD=2BE=∴AD=AB﹣ BD=∴AD= 时, DE=EF20.( 1)图中全等的三角形有四对,分别为:①△ DBG≌△ EGC,②△ ADG≌△ AEG,③△ ABG≌△ ACG,④△ABE≌△ ACD;( 4 分)(Ⅱ)∵ AB=AC, AD=AE,∠ A 是公共角,∴△ ABE≌△ ACD( SAS)④;∵AB=AC, AD=AE,∴AB﹣ AD=AC﹣ AE,即 BD=CE;由④得∠ B=∠ C,又∵∠ DGB=∠ EGC(对顶角相等), BD=CE(已证),∴△ DBG≌△ EGC( AAS)①;由①得 BG=CG,由④得∠ B=∠C,又∵ AB=AC,∴△ ABG≌△ ACG( SAS)③;由①得 BG=CG,且 AD=AE, AG为公共边,∴△ ADG≌△ AEG( SSS)②;21.( 1)△ ABC≌△ DCB.证明:∵ AB=CD, AC=BD, BC=CB,∴△ ABC≌△ DCB.( SSS)(2) EF 均分∠ DEC.原由:∵ EF∥ BC,∴∠ DEF=∠EBC,∠ FEC=∠ ECB;由( 1)知:∠ EBC=∠ ECB;∴∠ DEF=∠FEC;∴ FE 均分∠ DEC22.△ ABC≌△ DCB.原由以下:∵∠ABC=∠ DCB,∠ 1=∠ 2,∴∠ DBC=∠ACB.∵BC=CB,∴△ ABC≌△ DCB23.( 1)∵ BF=DE,∴BF+EF=DE+EF.即 BE=DF.在△ DFC和△ BEA中,∵,∴△ DFC≌△ BEA( SAS).(2)∵△ DFC≌△ BEA,∴CF=AE,∠ CFD=∠ AEB.∵在△ AFE与△ CEF中,∵,∴△ AFE≌△ CEF( SAS)24.△ ABF与△ DFG中,∠ BAF=∠ BGD,∠ BFA=∠DFG,∴∠ B=∠ D,∵∠ BAF=∠EAC,∴∠ BAE=∠DAC,∵AC=AE,∠ BAE=∠ DAC,∠B=∠D,∴△ BAE≌△ DAC.答案:有.△ BAE≌△ DAC25.∵ CE∥AB,∴∠ ABD=∠ECD.在△ ABD和△ ECD中,,∴△ ABD≌△ ECD( ASA)26.( 1)证明:在△ AOB和△ COD中∵∴△ AOB≌△ COD( AAS)(2)解:∵△ AOB≌△ COD,∴ AO=DO∵ E 是 AD的中点∴OE⊥ AD∴∠ AEO=90°27. 1)证明:∵ AB∥ DE,∴∠ A=∠ D.∵AB=DE, AF=DC,∴△ ABF≌△ DEC.( 2)解:全等三角形有:△ ABC和△ DEF;△ CBF和△ FEC28.证明:( 1)∵ BE、 CF分别是 AC、 AB两边上的高,∴∠ AFC=∠AEB=90°(垂直定义),∴∠ ACG=∠DBA(同角的余角相等),又∵ BD=CA,AB=GC,∴△ ABD≌△ GCA;(2)连接 DG,则△ ADG是等腰三角形.证明以下:∵△ ABD≌△ GCA,∴AG=AD,∴△ ADG是等腰三角形.29.解:∵∠ 4+∠ 6=180°﹣∠ 3,∠ 5+∠ 6=180°﹣∠ 2,∠ 3=∠2,∴∠ 4+∠ 6=∠ 5+∠ 6,∴∠ 4=∠ 5,∵在△ ADE和△ CFD中,,∴△ ADE≌△ CFD( AAS).30.① DF∥BC.证明:∵ BE⊥ AC,∴∠ BEC=90°,∴∠ C+∠ CBE=90°,∵∠ ABC=90°,∴∠ ABF+∠CBE=90°,∴∠ C=∠ ABF,∵DF∥ BC,∴∠C=∠ ADF,∴∠ABF=∠ADF,在△ AFD和△ AFB中∴△ AFD≌△ AFB( AAS).31.在△ BEA和△ BDC中:,故△ BEA≌△ BDC(SSS).32.如图,在△ ABC中,∠ ACB=90°, AC=BC, BE⊥ CE于点 E, AD⊥CE于点 D.请说明△ ADC≌△ CEB的原由.解:∵ BE⊥CE于点 E(已知),∴∠ E=90°(垂直的意义),同理∠ ADC=90°,∴∠ E=∠ ADC(等量代换).在△ ADC中,∵∠ 1+∠ 2+∠ ADC=180°(三角形的内角和等于180°),∴∠ 1+∠ 2=90°(等式的性质).∵∠ ACB=90°(已知),∴∠ 3+∠ 2=90°,∴∠ 1=∠3(同角的余角相等).在△ ADC和△ CEB中, .∴△ ADC≌△ CEB ( A. A. S)33.( 1)△ ABF≌△ DEC,△ ABC≌△ DEF,△ BCF≌△ EFC;(2 分)(2)△ ABF≌△ DEC,证明:∵ AB∥ DE,∴∠ A=∠ D,( 3 分)在△ ABF和△ DEC中,(4 分)∴△ ABF≌△ DEC.(5 分)34.( 1)△ ADF与△ AEF中,∵∠ 2=∠ 3,∠ AFE=∠ CFD,∴∠ C=∠ E;(2)∵∠ 1=∠ 2,∴∠BAC=∠DAE.∵AC=AE,又∠ C=∠ E,∴△ ABC≌△ ADE.35.∵ AE⊥CD,∴∠ AEC=90°,∴∠ ACE+∠CAE=90°,(直角三角形两个锐角互余)∵∠ ACE+∠BCF=90°,∴∠ CAE=∠BCF,(等角的余角相等)∵AE⊥ CD,BF⊥ CD,∴∠ AEC=∠BFC=90°,在△ ACE与△ CBF中,∠ CAE=∠ BCF,∠ AEC=∠ BFC,AC=BC,∴△ ACE≌△ CBF( AAS).优秀文档36.当动点 P 运动到 AC边上中点地址时,△APE≌△ EDB,∵DE∥ CA,∴△ BED∽△ BAC,∴= ,∵D是BC的中点,∴ = ,∴= ,∴E 是 AB中点,∴DE= AC, BE=AE,∵DE∥ AC,∴∠ A=∠ BED,要使△ APE≌△ EDB,还缺少一个条件DE=AP,又有 DE= AC,∴ P 必定是 AC中点.37.( 1)∵ AE=AB,∴∠ B=∠ AEB,又∵ AD∥ BC,∴∠ AEB=∠DAE,∴∠ DAE=∠B;(2)∵∠ DAE=∠ B,AD=BC,AE=AB,∴△ ABC≌△ EAD.38.△ ACE≌△ BCD.∵△ ABC和△ ECD都是等腰直角三角形,∴∠ ECD=∠ACB=90°,∴∠ ACE=∠BCD(都是∠ ACD的余角),在△ ACE和△ BCD中,∵,∴△ ACE≌△ BCD.39.∵∠ BAC=∠ DAE,∴∠ BAC+∠CAD=∠ DAE+∠ CAD,即∠ BAD=∠EAC,在△ ABD和△ ACE中,∴△ ABD≌△ ACE.40.证明:延长FD到 M使 MD=DF,连接 BM,EM.∵D 为 BC中点,∴BD=DC.∵∠ FDC=∠BDM,∴△ BDM≌△ CDF.∴BM=FC.∵ED⊥ DF,∴EM=EF.∵BE+BM> EM,∴B E+FC> EF.41. PM=HN.原由:∵在△ MNP中, H是高 MQ与 NE的交点,∴∠ MEH=∠NQH=90°,∠ MQP=∠ NQH=90°∵∠ MHE=∠NHQ(对顶角相等),∴∠ EMH=∠QNH(等角的余角相等)在△ MPQ和△ NHQ中,,∴△ MPQ≌△ NHQ( ASA),∴MP=NH.42.( 1)∵ BG∥ AC,∴∠ DBG=∠DCF.∵D为BC的中点,∴ BD=CD又∵∠ BDG=∠ CDF,在△ BGD与△ CFD中,∵∴△ BGD≌△ CFD( ASA).∴BG=CF.(2)BE+CF>EF.∵△BGD≌△CFD,∴GD=FD, BG=CF.又∵ DE⊥ FG,∴EG=EF(垂直均分线到线段端点的距离相等).∴在△ EBG中, BE+BG> EG,即 BE+CF>EF.43.∵ BE⊥CE于 E,AD⊥ CE于 D∴∠ E=∠ ADC=90°∵∠ BCE+∠ACE=∠ DAC+∠ ACE=90°∴∠ BCE=∠DAC∵AC=BC∴△ ACD≌△ CBE∴CE=AD,﹣ 1.7=0.8 ( cm)44.∵ AB=CD, BC=AD,又∵ BD=DB,在△ ABD和△ CDB中,∴△ ABD≌△ CDB,∴∠ A=∠ C.45.∵ AD是△ ABC中 BC边上的中线,∴BD=CD.∵CE⊥ AD于 E, BF⊥AD,∴∠ BFD=∠CED.在△ BFD和△ CED中,∴△ BFD≌△ CED( AAS).∴CE=BF46.∵ AD∥BC,∴∠ E=∠ ENB,∵∠ ENB=∠CNF,∴∠ E=∠ CNF,∵AB∥ CD,∴∠A=∠B,∵∠ C=∠ B,∴∠ EAB=∠DCB,∵AM=CF,∴△ AME≌△ CFN,优秀文档47.证明:过T 作 TF⊥ AB于 F,∵A T 均分∠ BAC,∠ ACB=90°,∴CT=TF(角均分线上的点到角两边的距离相等),∵∠ ACB=90°, CM⊥AB,∴∠ ADM+∠DAM=90°,∠ ATC+∠ CAT=90°,∵AT 均分∠ BAC,∴∠DAM=∠CAT,∴∠ ADM=∠ATC,∴∠ CDT=∠CTD,∴CD=CT,又∵ CT=TF(已证),∴C D=TF,∵CM⊥ AB,DE∥ AB,∴∠ CDE=90°,∠ B=∠ DEC,在△ CDE和△ TFB 中,,∴△ CDE≌△ TFB( AAS),∴C E=TB,∴CE﹣ TE=TB﹣ TE,即 CT=BE.48.∵∠ BAE=∠ DAC∴∠ BAE+∠CAE=∠ DAC+∠ CAE即∠ BAC=∠DAE又∵ AB=AD, AC=AE,∴△ ABC≌△ ADE( SAS)∴∠ B=∠ D(全等三角形的对应角相等)49.∵ DE=EF, AE=CE,∠ AED=∠ FEC,∴△ AED≌△ FEC.∴∠ ADE=∠CFE.∴AD∥ FC.∵D是AB上一点,∴ AB∥ CF50.∵ BE∥CF,∴∠ CMF=∠BME,∠ FCM=∠ EBM.又∵ BE=CF,即 AM是△ ABC的中线51.∵ AC⊥BC, BE⊥CD,∴∠ ACF+∠FCB=∠ FCB+∠ CBE=90°.∴∠ FCA=∠EBC.∵∠ BEC=∠CFA=90°, AC=BC,∴△ BEC≌△ CFA.∴CE=AF.∴EF=CF﹣ CE=CF﹣ AF52.解:( 1)证明:由题意可知, BD⊥ MN与 D, EC⊥ MN与 E,∠BAC=90°,则△ ABD与△ CEA是直角三角形,∠ DAB=∠ ECA,在△ ABD与△ CEA中,∵,∴△ ABD≌△ CEA,∴B D=AE;(2)若将 MN绕点 A 旋转,与 BC订交于点 O,则 BD, CE与 MN垂直,∴△ABD与△CEA仍是直角三角形,两个三角形仍全等,∴BD与 AE边仍相等;(3)∵△ ABD≌△ CEA,∴B D=AE, AD=EC,∴DE=BD+EC或 DE=CE﹣ BD或 DE=BD﹣ CE.53.∵ AB=AC,∴∠ ABC=∠ACB,∵BD、CE分别为△ABC的高,∴∠ BEC=∠BDC=90°,∴在△ BEC和△ CDB中,∴△ BEC≌△ CDB,∴∠ 1=∠ 2,∴OB=OC∵∠ ACB=90°, D 是 AB 边的中点∴CD=AD,∠ DAC=∠ DCF∵DE与 CF平行且相等∴∠ EDA=∠DAC∴∠ EDA=∠DCF在△ AED和△ CFD中CD=AD,∠ EDA=∠ DCF, DE=CF∴△ AED≌△ CFD∴A E=DF.55.∵ AD均分∠ BAC∴∠ BAD=∠CAD在△ ADE和△ ADC中∵∴△ ADE≌△ ADC( SAS)∴DE=DC∴BC=BD+DC=BD+DE=2+3=5(cm)56.在△ AEB与△ ADC中,.∴△ AEB≌△ ADC( AAS).∴ AB=AC(全等三角形,对应边相等)57.( 1)证明:在△ BCE和△ DCE中∴△ BCE≌△ DCE( SSS).(2)解:∵ AD=DE,∴∠ A=∠ AED;∴∠ EDC=∠A+∠ AED=2∠ A,设∠ A=x,依照题意得,5x=180°,解得x=36°∴∠ EDC=2∠ A=72°证明:延长CE、 BA 交于点 F.∵CE⊥ BD于 E,∠ BAC=90°,∴∠ ABD=∠ACF.又 AB=AC,∠ BAD=∠ CAF=90°,∴△ ABD≌△ ACF,∴B D=CF.∵BD均分∠ ABC,∴∠ CBE=∠FBE.有 BE=BE,∴△ BCE≌△ BFE,∴C E=EF,∴C E= BD,∴B D=2CE.59.( 1)证明:在△ ABD和△ CDB中∵AB=CD,AD=BC,BD=DB,∴△ ABD≌△ CDB( SSS),∴∠ ADB=∠DBC,∴ DE∥ BF.∴∠ E=∠ F.(2)答:当 O是 BD中点时,OE=OF.证明以下:∵ O是 BD中点,∴OB=OD.又∵∠ ADB=∠ DBC,∠ E=∠ F,∴△ ODE≌△ OBF( AAS).∴OE=OF.(当 AE=CF时也可证得60.∵ DE⊥AB, DF⊥AC,∴∠ E=∠ DFC=90°.∵AD均分∠ EAC,∴ DE=DF.在 Rt △ DBE和 Rt △ DCF中,∴Rt △ DBE≌ Rt △ CDF( HL).∴BE=CF.。
(完整版)全等三角形证明经典50题(含答案)
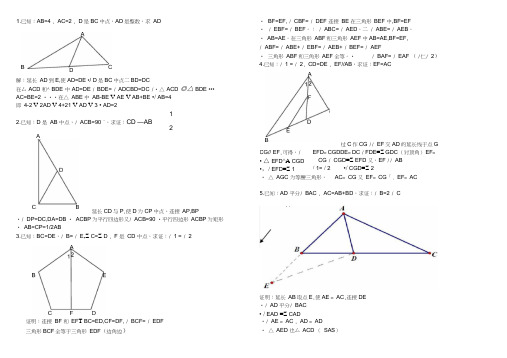
证明:连接 BF 和 EF T BC=ED,CF=DF, / BCF= / EDF 三角形BCF 全等于三角形 EDF (边角边)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 ADD • BF=EF, / CBF= / DEF 连接 BE 在三角形 BEF 中,BF=EF • / EBF= / BEF 。
: / ABC= / AED 。
二 / ABE= / AEB 。
• AB=AE 。
在三角形 ABF 和三角形 AEF 中AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF • 三角形 ABF 和三角形 AEF 全等。
•/ BAF= / EAF ( /仁/ 2)4.已知:/ 1 = / 2, CD=DE , EF//AB ,求证:EF=AC解:延长 AD 到E,使AD=DE •/ D 是BC 中点二BD=DC 在厶 ACD 和^ BDE 中 AD=DE / BDE= / ADCBD=DC /•△ ACD ◎△ BDE ••• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+21 V AD V 3 • AD=21 2.已知:D 是 AB 中点,/ ACB=90 °,求证:CD —AB 2A CG// EF ,可得,/• △ EFD ^A CGD•,/ EFD =Z 1过C 作CG // EF 交AD 的延长线于点GEFD = CGDDE = DC / FDE =Z GDC (对顶角) EF = CG / CGD =Z EFD 又,EF // AB / 1= / 2 •/ CGD =Z 2 • △ AGC 为等腰三角形, AC = CG 又 EF = CG 「. EF = AC 延长CD 与P ,使D 为CP 中点。
连接 AP,BP •/ DP=DC,DA=DB • ACBP 为平行四边形又/ ACB=90 •平行四边形 ACBP 为矩形 • AB=CP=1/2AB 3.已知:BC=DE ,/ B= / E ,Z C=Z D , F 是 CD 中点,求证:/ 1 = / 2 5.已知:AD 平分/ BAC , AC=AB+BD ,求证:/ B=2 / C证明:延长 AB 取点E ,使AE = AC ,连接DE •/ AD 平分/ BAC• / EAD =Z CAD•/ AE = AC , AD = AD • △ AED 也厶 ACD ( SAS )•••/ E = Z C•/ AC = AB+BD •AE = AB+BD•/ AE = AB+BE •BD = BE •••/ BDE =Z E •••/ ABC =Z E+ / BDE •••/ ABC = 2 / E •••/ ABC = 2 / C ••• AE = AF + FE = AD + BE12.如图,四边形ABCD中,AB 在AD上。
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
完整版)全等三角形经典例题(含答案)

完整版)全等三角形经典例题(含答案)全等三角形证明题精选1.在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F。
证明:△ADE≌△CBF;若AC与BD相交于点O,证明:AO=CO。
2.已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D。
证明:AC∥DE;若BF=13,EC=5,求BC的长。
3.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,AD=AE。
证明:BE=CD。
4.点O是线段AB和线段CD的中点。
证明:△AOD≌△BOC;AD∥BC。
5.点C是AE的中点,∠A=∠ECD,AB=CD。
证明:∠B=∠D。
6.已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC。
证明:AE=BC。
7.在△ABE和△DEF中,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF。
证明:AF=DF。
8.点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。
证明:AB∥DE。
9.在△ABC中,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB。
证明:AE=CE。
10.点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF。
证明:DE=CF。
11.点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD。
证明:AE=FB。
12.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.证明:BD=CE;∠M=∠N。
13.在△ABC中,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD。
证明:AB=AC。
14.在△ABC和△CED中,AB∥CD,AB=CE,AC=CD。
证明:∠B=∠E。
15.在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F。
证明:AB=AC;若AD=2,∠DAC=30°,求AC的长。
16.已知直角三角形ABC和直角三角形DBF,且它们相似,∠D=28°,求∠GBF的度数。
全等三角形证明50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC 在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=2ADBC2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP ∵DP=DC,DA=DB ∴ACBP 为平行四边形 又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边) ∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点G CG ∥EF ,可得,∠EFD =CGD DE =DC∠FDE =∠GDC (对顶角)BA CDF2 1 EEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF ∵CE ⊥AB∴∠CEB =∠CEF =90° ∵EB =EF ,CE =CE , ∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS ) ∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DEADB C∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC ∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=29.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF和EF。
全等三角形经典题型50题(含答案)
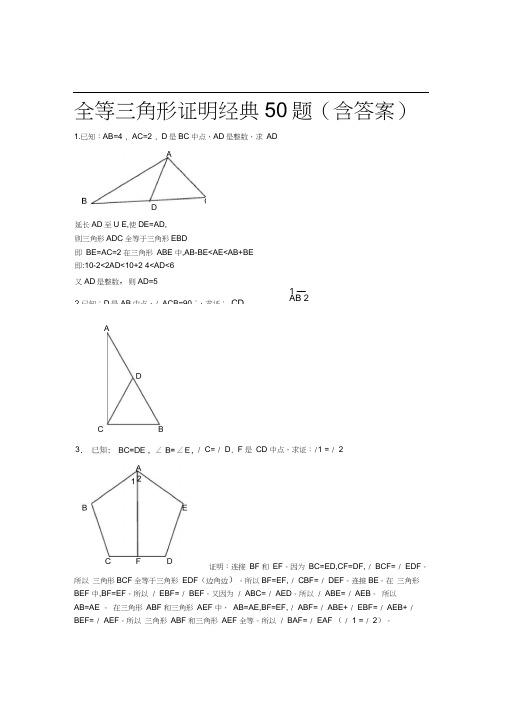
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D是BC中点,AD是整数,求AD/ C= / D, F 是CD 中点,求证:/ 1 = / 2证明:连接BF 和EF。
因为BC=ED,CF=DF, / BCF= / EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以BF=EF, / CBF= / DEF。
连接BE。
在三角形BEF 中,BF=EF。
所以 / EBF= / BEF。
又因为 / ABC= / AED。
所以 / ABE= / AEB。
所以AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF。
所以三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF (/ 1 = / 2)。
延长AD至U E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知:D是AB中点,/ ACB=90 °,求证:CD1 —AB 2A34. 已知:/ 仁/2, CD=DE , EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于 G 则/ DEG= / DCA , / DGE= / 2 又 •/ CD=DE U ADC 也"GDE ( AAS )••• EG=AC •/ EF//AB /-Z DFE= / 1 v/ 1 = / 2:丄 DFE= / DGE ••• EF=EG •: EF=AC5. 已知:AD 平分Z BAC , AC=AB+BD ,求证:Z B=2 / C证明:在 AC 上截取 AE=AB ,连接 ED •/ AD 平分Z BAC :•/ EAD= Z BAD 又 v AE=AB ,AD=AD :•" AED 6 ABD (SAS )•:Z AED= Z B ,DE=DB v AC=AB+BDAC=AE+CE •: CE=DE :-Z C=Z EDC vZ AED= Z C+ Z EDC=2 Z C -Z B=2 Z C 6. 已知:AC 平分Z BAD , CE 丄 AB , Z B+ Z D=180 °,求证: AE=AD+BE证明:在AE 上取F ,使EF = EB , 连接CF 因为CE 丄AB 所以Z CEB=Z CEF = 90° 因为 EB = EF , CE = CE , 所以△CEBCEF 所以Z B = Z CFE 因为Z B+ Z D = 180°, Z CFE +Z CFA = 180° 所以Z D = Z CFA 因为 AC 平分Z BAD 所以Z DAC=Z FAC 又因为 AC = AC 所以△ ADC AFC (SAS ) 所以 AD = AF 所以 AE = AF + FE=AD + BE12.如图,四边形 ABCD 中,AB // DC , BE 、CE 分别平分Z ABC 、Z BCD ,且点 E 在AD 上。
全等三角形经典题型50题(含答案)
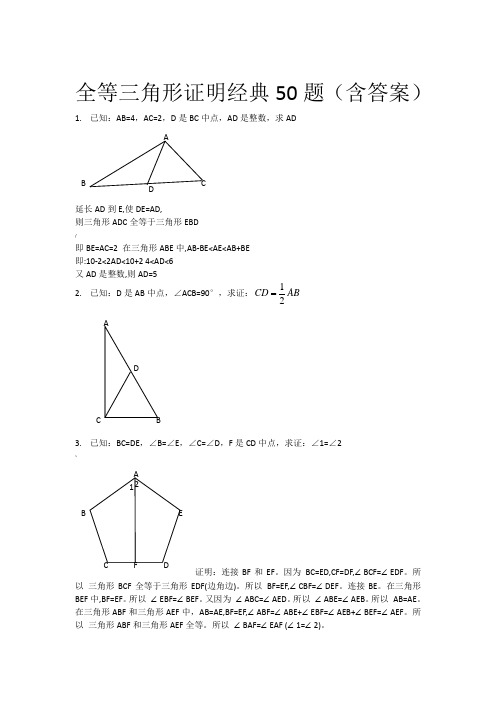
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD /即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2 ~证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC(4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB =∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典50题(含答案)
全等三角形证明经典50题1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CG∠CGD =∠EFD又,EF ∥AB∴,∠EFD =∠1∠1=∠2∴∠CGD =∠2∴△AGC 为等腰三角形,BA CD F2 1EAC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=28. 已知:D 是AB 中点,∠ACB=90°,求证:12CD ABAD BBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=29. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:∵AB∥CD,
∴∠BAC=∠ECD,
在△BAC和△ECD中
AB=EC ∠BAC=∠ECD
AC=CD ,
∴△BAC≌△ECD
(SAS),
∴CB=ED.
全等三角形的判定与性质.
7.如图,D、E分别是AB、AC上的点,且 AB=AC,AD=AE.求证:∠B=∠C.
在△ABE和△ACD中, ∵ AB=AC ∠A=∠A AE=AD , ∴△ABE≌△ACD(SAS), ∴∠B=∠C.
全等三角形的判定与性质.
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF. (1)求证:Rt△ABE≌Rt△CBF;
(1)证明:∵∠ABC=90°, ∴∠CBF=∠ABE=90°, 在Rt△ABE和Rt△CBF中, AE=CF AB=BC , ∴Rt△ABE≌Rt△CBF(HL);
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
全等三角形的判定与性质.
6.已知:如图,点E,A,C在同一直线上,AB∥CD, AB=CE,AC=CD.求证:BC=ED.
直角三角形全等的判定;全等三角形的性质.
如图,△ABC中,AB=AC, ∠1=∠2,求证:AD平分 ∠BAC.
解:∵AB=AC, ∴∠ABC=∠ACB. ∵∠1=∠2, ∴∠ABD=∠ACD,BD=CD. ∵AB=AC,BD=CD, ∴△ABD≌△ACD. ∴∠BAD=∠CAD. 即AD平分∠BAC.
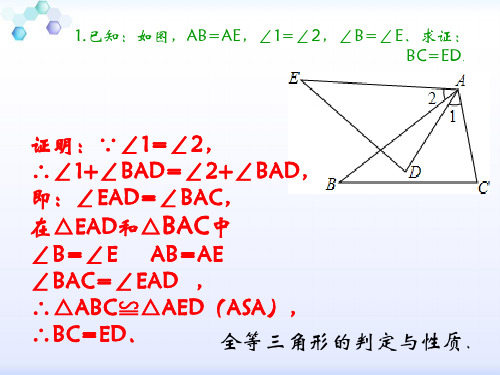
1.已知:如图,AB=AEቤተ መጻሕፍቲ ባይዱ∠1=∠2,∠B=∠E.求证: BC=ED.
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即:∠EAD=∠BAC,
在△EAD和△BAC中
∠B=∠E AB=AE
∠BAC=∠EAD ,
∴△ABC≌△AED(ASA),
∴BC=ED.
全等三角形的判定与性质.
2.如图,在△ABC中,∠C=90°,点D是AB边上的 一点,DM⊥AB,且DM=AC,过点M作ME∥BC交
直角三角形全等的判定
如图,△ABC中,∠ABC=∠BAC=45°,点 P在AB上,AD⊥CP,BE⊥CP,垂足分别为D, E,已知DC=2,求BE的长.
∵∠ABC=∠BAC=45° ∴∠ACB=90°,AC=BC ∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2.
系和位置关系?并加以证明.
证明:∵AB∥CD,
∴∠A=∠D,
∵在△ABF和 △DCE中
AB=CD ∠A=∠D AF=DE ,
∴△ABF≌△DCE,
∴CE=BF, ∠AFB=∠DEC,
∴CE∥全质BF等;,三平角 行形 线的 的判 判定 定与 与性 性质质.;平行线的性
5.如图,在△ABC中,AB=AC,AD平分∠BAC.求 证:∠DBC=∠DCB.
全等三角形的判定与性质.
8.已知AC平分∠BAD, AB=AD.求证:
:∵AC平分△∠ABBACD,≌△ADC.
∴∠BAC=∠DAC, 在△ABC和△ADC 中, AB=AD ∠BAC=∠DAC AC=AC , ∴△ABC≌△ADC .
全等三角形的判定.
9.如图,已知点E,C在线段BF上,BE=CF, AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
全等三角形的判定与性质.
如图,△ABC中,AB=AC,过点A作GE∥BC,角平 分线BD、CF相交于点H,它们的延长线分别交GE于 点E、G.试在图中找出3对全等三角形,并对其中
一对全等三角形给出证明.
:△BCF≌△CBD. △BHF≌△CHD. △BDA≌△CFA. 证明:在△BCF与△CBD中, ∵AB=AC. ∴∠ABC=∠ACB ∵BD、CF是角平分线. ∴∠BCF=1 2 ∠ACB,∠CBD=1 2 ∠ABC. ∴∠BCF=∠CBD, ∴ ∠BCF=∠CBD BC=BC ∠ABC=∠ACB
∴△BCF≌△CBD(ASA). 全等三角形的判定.
如图,在△ABC中,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F,BE=CF. 求证:AD是△ABC的角平分线.
证明:∵DE⊥AB,DF⊥AC, ∴Rt△BDE=Rt△DCF=90°. BD=DC BE=CF , ∴Rt△BDE≌Rt△DCF(HL), ∴DE=DF, 又∵DE⊥AB,DF⊥AC, ∴AD是角平分线.
证明:∵AB∥DE, ∴∠B=∠DEF. ∵BE=CF, ∴BC=EF. ∵∠ACB=∠F, ∴ ∠B=∠DEF BC=EF∠ACB=∠F , ∴△ABC≌△DEF.
全等三角形的判定;平行线的性质.
10.已知:如图,E、F在AC上,AD∥CB且AD=CB, ∠D=∠B. 求证:AE=CF.
证明:∵AD∥CB, ∴∠A=∠C, 在△ADF和△CBE中, ∠A=∠C AD=CB ∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即AE=CF.
证明:∵AE∥CF ∴∠AED=∠CFB, ∵DF=BE, ∴DF+EF=BE+EF, 即DE=BF, 在△ADE和△CBF中,
AE=CF ∠AED=∠CFB DE=BF , ∴△ADE≌△CBF (SAS).
全等三角形的判定.
4.如图,点E、F分别是AD上的两点,AB∥CD, AB=CD,AF=DE.问:线段CE、BF有什么数量关
角平分线的性质;全等三角形的判定与性质
AB于点E.求证:△ABC≌△MED。
证明:∵MD⊥AB, ∴∠MDE=∠C=90°, ∵ME∥BC, ∴∠B=∠MED, 在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC , ∴△ABC≌△MED(AAS).
全等三角形的判定.
如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF, AE=CF,BE=DF.求证:△ADE≌△CBF.
