工业机器人运动学-逆运动学
ppt机器人正逆运动学解析

将上面两个方程两边平方相加,并利用和差化积公式得到
S2 S23 C2C23 cos3
于是有:
C3
(
pxC1
py S1
C234a4 )2 ( pz 2a2a3
S234a4 )2
a22
a32
已知 S3 1 C32
于是可得到:
3
arctan
S3 C3
依次类推,分别在方程2.19两边左乘A1~A4的逆,可得到
O4
x2
z5
y5
x4
O5
y4
z2
y2
关节3
A1 连杆2
O2 坐标系2
x5
o3 , o4 , o5重合 d4 d5 0
关节2 O1
z1
坐标系1
y1 连杆1
x1
d2
关节1 坐标系0
ai—沿 xi 轴, zi-1 轴与 xi 轴交点到Oi 的距离 αi — 绕 xi 轴,由 zi-1 转向zi di — 沿 zi-1 轴,zi-1 轴和 xi 交点至Oi –1 坐标
系原点的距离 θi — 绕 zi-1 轴,由 xi-1转向 xi
连杆0
z0 y0
d1 x0
O0
解:
例2、PUMA560运动学方程(六个自由度,全部是旋转关节) 关节变量都是θ
θ2
θ1
θ3
θ5
θ4 θ6
PUMA560机器人的连杆及关节编号
A1
O1 O0
A2
为右手坐标系,Yi轴:按右手定则
C234a4 ) S234a4 )
进而可得:
4 234 2 3
机器人学导论第4章操作臂逆运动学

我们把操作臂的全部求解方法分成两大类:封闭解和数值解法。由于数值解 法的迭代性质,因此它一般要比相应的封闭解法的求解速度慢很多。实际上 在大多数情况下,我们并不喜欢用数值解法求解运动学问题。因为封闭解的 计算速度快,效率高,便于实时控制。而数值法不具有些特点为。
“封闭形式”意指基于解析形式的解法,或者意指对于不高于四次的多项式 不用迭代便可完全求解。可将封闭解的求解方法分为两类:代数法和几何法。 有时它们的区别又并不明显:任何几何方法中都引入了代数描述,因此这两 种方法是相似的。这两种方法的区别或许仅是求解过程的不同。
多重解问题
在求解运动学方程时可能遇到的另一个问题就是多重解问题。一个具有3个旋转关节的 平面操作臂,由于从任何方位均可到达工作空间内的任何位置,因此在平面中有较大的 灵巧工作空间(给定适当的连杆长度和大的关节运动范围)。图4-2所示为在某一位姿 下带有末端执行器的三连杆平面操作臂。虚线表示第二个可能的位形,在这个位形下, 末端执行器的可达位姿与第一个位形相同。
4.1 概述 • 在上一章中讨论了已知操作臂的关节角,计算工具 坐标系相对于用户工作台坐标系的位置和姿态的问 题。在本章中,将研究难度更大的运动学逆问题 :已 知工具坐标系相对于工作台坐标系的期望位置和姿 态,如何计算一系列满足期望要求的关节角? • 第3章重点讨论操作臂的运动学正问题,而本章重点 讨论操作臂的运动学逆问题。
4.4 代数解法与几何解法
代数解法:以第三章所介绍三连杆平面操作臂为例,其坐标和连杆参数如下
按第三章的方法,应用这些连杆参数可以求得这个机械臂的运动学方程:
c123 s 123 B 0 T T W 3 0 0
s123 c123 0 0
0 0 1 0
机械臂的运动学与逆运动学分析

机械臂的运动学与逆运动学分析机械臂是一种能够模拟人类手臂运动的自动化机器人。
它广泛应用于工业领域,用于完成各种复杂的操作任务。
机械臂的运动控制是实现其功能的关键,其中运动学和逆运动学分析是研究机械臂运动的基础。
一、机械臂的运动学分析运动学分析主要关注机械臂的位置、速度和加速度等运动参数的计算。
机械臂主要由关节连接的刚性杆件组成,每个关节可以沿特定方向进行旋转或平移运动。
在机械臂运动学中,我们关注的是机械臂末端执行器的位置和姿态。
1. 正运动学分析正运动学分析指的是根据机械臂各关节的运动参数,计算机械臂末端执行器的位置和姿态。
通常,我们采用坐标变换矩阵的方法来进行计算。
通过将各个关节的运动连续相乘,可以得到机械臂末端执行器相对于机械臂基座标系的位姿矩阵。
以一个3自由度的机械臂为例,设第一关节绕Z轴旋转角度为θ1,第二关节绕Y轴旋转角度为θ2,第三关节绕X轴旋转角度为θ3。
则机械臂末端执行器相对于基座标系的位姿矩阵可以表示为:[cos(θ2+θ3) -sin(θ2+θ3) 0 a1*cos(θ1)+a2*cos(θ1+θ2)+a3*cos(θ1+θ2+θ3)][sin(θ2+θ3) cos(θ2+θ3) 0 a1*sin(θ1)+a2*sin(θ1+θ2)+a3*sin(θ1+θ2+θ3)][0 0 1 d1+d2+d3][0 0 0 1]其中,a1、a2、a3和d1、d2、d3分别为机械臂的长度和位移参数。
通过这个矩阵,我们可以得到机械臂末端执行器的位置和姿态。
2. 速度和加速度分析除了机械臂末端执行器的位置和姿态,机械臂的速度和加速度也是非常重要的运动参数。
通过对机械臂运动学模型的导数运算,我们可以得到机械臂的速度和加速度表达式。
机械臂的速度可以表示为:v = J(q) * q_dot其中,v为机械臂末端执行器的速度向量,J(q)为机械臂的雅可比矩阵,q为机械臂各关节的角度向量,q_dot为各关节的角速度向量。
精品课件-机器人学简明教程(张奇志)-第4章

0
1
0
r32 0
r33 0
pz
1
1r31
0
1r32 0
1r33 0
1
pz
1
(4-6)
第4章 机器人逆运动学
式(3-22)的最后三个数如下:
1 1
px py
a2c2 d3
a3c23
d4s23
1 pz a3s23 a2s2 d4c23
令式(4-6)两边元素(2,4)相等,得到
-pxs1+pyc1=d3 为了求解式(4-8),做三角恒等变换
nx ox ax
Rzyz
ny
oy
a
y
nz oz ax
第4章 机器人逆运动学 根据欧拉变换方程式(2-40)可得如下9个方程:
nnxy
cc c sc c
s s c s
nz s c
ooxy
cc s sc s
sc cc
oazx
s s c s
ay ss
az c
(4-1)
第4章 机器人逆运动学
第4章 机器人逆运动学 第4章 机器人逆运动学
4.1 逆运动学问题的可解性 4.2 欧拉变换解 4.3 PUMA560逆运动学
第4章 机器人逆运动学 4.1 逆运动学问题的可解性
1.解的存在性 逆运动学问题解是否存在完全取决于机械臂的工作空间。 所谓工作空间是指机械臂末 端执行器所能达到的空间位姿的集合。一般来说,对于给 定的机械臂,其工作空间是固定的。而对于少于6个自由度的 机械臂,它在三维空间内不能达到全部位姿。所以通用工业机 器人一般都设计成6个自由度。当期望位姿位于机械臂的工作 空间之外时,逆运动学问题无解。如图4-1所示期望平面机械 臂末端达到B点,显然该逆运动学问题是无解的。
第4章机器人逆运动学(一)

第4章机器人逆运动学(一)引言概述:机器人逆运动学是研究机器人动作规划和控制的重要内容之一。
在工业领域和服务领域中,机器人逆运动学能够帮助机器人根据预设的目标位置和姿态,确定关节角度和长度,从而实现准确的动作控制。
本文将介绍机器人逆运动学的基本原理,以及逆运动学的求解方法和实际应用。
正文:1. 基本原理1.1 前向运动学和逆运动学的关系1.2 关节角度和长度的确定方法1.3 机器人姿态表示方法2. 逆运动学的求解方法2.1 解析法2.2 数值法2.3 迭代法2.4 优化算法2.5 约束条件的处理方法3. 逆运动学的实际应用3.1 机器人轨迹规划3.2 机器人运动控制3.3 机器人碰撞检测与避障3.4 机器人抓取和操作4. 逆运动学问题的局限性和挑战4.1 多解性问题4.2 存在性问题4.3 运动优化问题4.4 环境约束问题4.5 实时性和稳定性问题5. 逆运动学的发展趋势5.1 智能化和自适应控制5.2 机器学习与优化算法的结合5.3 非线性逆运动学求解方法的研究5.4 多机器人协同控制的逆运动学问题5.5 逆运动学在虚拟现实和增强现实中的应用总结:机器人逆运动学是机器人控制领域的重要研究方向之一。
本文介绍了机器人逆运动学的基本原理,包括前向运动学与逆运动学的关系、关节角度和长度的确定方法,以及机器人姿态表示方法。
同时,还介绍了逆运动学的求解方法和实际应用,包括机器人轨迹规划、运动控制、碰撞检测与避障,以及抓取和操作等。
此外,还探讨了逆运动学问题面临的局限性和挑战,并展望了逆运动学的发展趋势,包括智能化和自适应控制、机器学习与优化算法的结合等。
逆运动学的研究将有助于推动机器人应用在更广泛的领域中,提高机器人的灵活性和性能。
4.5.2工业机器人的逆运动学计算

例题解答
yA
3
oC l2
2
l3 oD
4
l1
oA
1 oB
xA
例题解答
图 机器人可能的姿态
该题也可采用机器人运动学 方程求得,此处不详写。
逆运动学求解的一般方法
nx ox ax px
n0T (q1, q2 ,
, qn )01T (q1)
n
3
oC
l2
2
l3 oD
4
l1
oA
1 oB
xA
例题
SCARA机器人俯视可以抽象为两关节
例题解答
yA
3
oC l2
2
l3 oD
4
oA l1 1 oB
xA
由题可知,第三关节的坐标可由末端执行 器的坐标求得:
9 xOC 2
3 4COS30 5 2
3
yOC
19 4 sin 30 15
z
oy oz
ay az
p
y
p
z
0 0 0 1
逆运动学求解的一般方法(两步): A、求出上述变换矩阵; B、由上式求出相应的关节变量。
实际应用逆运动学
• 要考虑关节活动范围,某些解无法实现 • “最短行程”原则 • “多移动小关节,少移动大关节”原则
总结
• 要理解和掌握工业机器人逆运动学计算的特点,包括多解、无解等 • 学习了机器人逆运动学计算方法 • 与实际机器人控制结合理解
例题
• 某个机器人有3个关节,分别位于
点,机械手中心为 OD
点,如图所示。 调整机器人各关节
使得末端操作器最终到达指定位置
(未沿Z轴发生平移),坐标系{A}
第三章工业机器人运动学3逆运动学

由于角φ已求出,比较式(3.48)等号两边矩阵第1行第3列和第3行第3 列元素相等有
sin f11(a) cos f13 (a)
或
(3.59) (3.60)
由此可得
sin cos ax sin ay cos az
tan 1 cos
ax sin az
ay
(3.61) (3.62)
(3.63)
同样比较式(3.48)等号两边矩阵的第2行第1列和第2行第2列元素可知
sin f12 (n)
(3.64)
cos f12 (o)
(3.65)
或
由此可得
sin sin nx cos ny cos sin ox cos oy
tan
1
sin sin
n o
x x
cos ny cos oy
1T6 =
C2( C4C5C6 - S4S6 ) - S2S5C6 S2( C4C5C6 - S4S6 ) + C2S5C6
S4C5C6 + C4C6
0
-C2( C4C5S6 + S4C6 )+ S2S5S6 -S2( C4C5 S6+ S4C6 )- C2S5S6
-S4C5S6 + C4C6
0
C2C4S5 + S2C5 S2C4S5 - C2C5
3.4 欧拉变换的逆运动学解 (Inverse solution of Euler Angles )
由前节知欧拉变换为
Euler (ø, θ,ψ) = Rot (z, ø) Rot (y, θ) Rot (z,ψ)
我们用T来表示欧拉变换的结果,即
T = Euler (ø, θ,ψ)
工业机器人运动学逆解的几何求解方法

工业机器人运动学逆解的几何求解方法黄晨华【摘要】工业机器人运动学逆解求解方法的不同,其计算量也有很大的差别。
常用的代数法求逆解存在计算繁琐,不易理解等缺点,几何法求逆解具有直观、计算量小的特点。
以5自由度工业机器人为算例,详细介绍了几何法求逆解的过程,总结出了几何法求逆解的一般步骤:首先对机器人的结构进行分析,确定影响机器人末端操作器位置的相关关节,按机器人的结构直接求出各相关关节的逆解,然后利用所求的位置关节的逆解,通过简单的矩阵运算,可求得剩余关节的逆解。
用仿真的方法验证了所求逆解的正确性:假设机器人各关节的转动不受限制,首先让各关节随机转过一定的角度,用机器人正运动学方程,获得机器人任意位姿,然后以此位姿为已知,用所求的逆解求相应的各关节所转过的角度,从而验证了方法的正确性。
【期刊名称】《制造业自动化》【年(卷),期】2014(000)015【总页数】4页(P109-112)【关键词】工业机器人;运动学方程;逆运动学;几何法【作者】黄晨华【作者单位】韶关学院物理与机电工程学院,韶关512005【正文语种】中文【中图分类】TP242.20 引言工业机器人的运动学是工业机器人控制与轨迹规划的基础,其内容包括正运动学和逆运动学。
当给定机器人所有关节转过的角度时,可以通过机器人的正动学方程来确定其末端操作器的位解;当已知机器人末端操作器的位置时,则可根据运行学逆解获得各关节需转过后角度。
机器人运动学建模的标准方法,即D-H建模,可以很方便地得到机器人的正运动学方程,而要获得机器人的逆运动学方程,则难度较大,求解的方法可以分成两大类:数值解和封闭解。
Tsai[2]等研究了通用的6自由度和5自由度的机械臂的数值解,Nakamura[3]等研究了适用了机器人控制的带有奇点鲁棒控制的数值逆解,Baker[4]等研究了冗余机械臂的数值逆解,数值解的最大不足就是计算时比较耗时,对系统造成较大的负担。
封闭解是基于解析形式的解法,其又可分为代数法和几何法,用代数法求逆解在很多机器人经典教材和文献中都有详细的论述[5~7],在此不作具体讨论,刘达[8]等为了使机器人获得更好的实时性,提出了一种解析和数值相结合的机器人逆解算法,陈庆诚[9]等提出基于旋量理论的逆运动学子问题求解算法。
机器人的逆运动学名词解释

机器人的逆运动学名词解释机器人的逆向运动学是,已知末端的位置和姿态,以及所有连杆的几何参数下,求解关节的位置。
二、两大类求解逆运动学的方法逆运动学求解通常有两大类方法:解析法、数值法。
1.解析法(Analytical Solution)特点:运算速度快(达到us级),通用性差,可以分为代数法与几何法进行求解。
串联机械臂有逆运动学解析解的充分条件是满足Pieper准则。
即如果机器人满足两个充分条件中的一个,就会得到封闭解,这两个条件是:•三个相邻关节轴相交于一点;•三个相邻关节轴相互平行。
现在的大多数商品化的工业机器人在设计构型时,都会尽可能满足满足Pieper准则,因为解析法求解能够很快的使用较少的算力,使用较低成本的控制器就能求解,之后随着芯片算力的提升,感觉在未来,机器人公司也会在是否采用满足解析解的构型和采用特定构型并开发对应的逆解算法之间找一个平衡。
以PUMA560机器人为例,它的最后3个关节轴相交于一点。
我们运用Pieper方法解出它的封闭解。
对于UR5机械臂,其第2、第3、第4关节轴平行,满足Pieper准则其中的一条,即三个相邻的关节轴两两平行。
2.数值法(Numerical Solution)特点:通用性高,但是求解速度较慢(ms级)。
除了一些特殊的机械臂构型外,机械臂逆运动学问题很难用解析解求解,因此在许多情况下会使用数值解求解。
通常设定一个优化目标函数,是把逆解求解问题转化为一个优化问题求数值解。
Newton-Raphson(NR)是数值解的一种方法。
它需要基本的雅可比矩阵。
然而,当且仅当原始方程的函数具有逆函数,且原始方程可解时,NR方法才会成功。
从运动学的角度来看,前一个条件意味着机器人需要非冗余,机器人在从初始配置到最终配置的运动过程中不通过奇异点。
后一个条件意味着机械臂的期望位置和方向需要在机器人的工作空间内,是可解的。
由于这些限制,NR方法不能保证全局收敛性,因此它在很大程度上取决于初始值。
机器人逆运动学求解方法

机器人逆运动学求解方法1. 嘿,你知道机器人逆运动学求解方法有多神奇吗?就像你要去一个陌生的地方,得先搞清楚怎么走!比如机器人要抓取一个杯子,它就得知道每个关节怎么动才能准确抓到。
2. 机器人逆运动学求解方法,哇哦,这可真是个厉害的玩意儿!好比解一道超级复杂的谜题,每一步都要精确无比。
想象一下机器人跳舞,那动作怎么来的,就是靠这个方法算出来的呀!3. 哎呀呀,机器人逆运动学求解方法可不简单呢!就如同在黑暗中摸索出一条正确的路。
像工业机器人精准焊接,没有这个方法可不行。
4. 机器人逆运动学求解方法真的是太重要啦!这简直就是机器人的“导航仪”啊!比如说机器人在仓库里搬运货物,靠的就是它来规划路线。
5. 哇塞,机器人逆运动学求解方法,这是让机器人变得聪明的关键呀!好比是给机器人装上了智慧的“大脑”。
你看那些能与人互动的机器人,就是因为有这个方法。
6. 嘿,想想机器人逆运动学求解方法,是不是很神奇?这就像是给机器人注入了灵魂!比如机器人医生做手术,每一个动作都依赖它。
7. 机器人逆运动学求解方法,那可是相当了不起啊!如同为机器人搭建了一座通往目标的桥。
像智能机器人给你送快递,怎么做到的?就是靠它呀!8. 哇,机器人逆运动学求解方法,这是开启机器人世界的钥匙啊!好比是一场刺激的冒险。
机器人踢足球,怎么精准射门,就靠这个方法啦。
9. 哎呀,机器人逆运动学求解方法真的超酷的!就像给机器人穿上了超级战甲。
比如机器人在危险环境中工作,全靠它保障安全和准确。
10. 机器人逆运动学求解方法,绝对是个厉害的存在!这就好像是机器人的魔法秘籍!像机器人在舞台上表演精彩节目,都是因为它呀!我的观点结论:机器人逆运动学求解方法是机器人领域中至关重要的一部分,它让机器人能够实现各种复杂而精确的动作,为我们的生活和工作带来了巨大的便利和可能性。
原创不易,请尊重原创,谢谢!。
第三章-工业机器人运动学-2运动学方程

(2.30)
cosθ -sinθ 0 0 1 0 0 a 1 0
00
sinθ cosθ 0 0 0 1 0 0 0 cosα -sinα 0
An = 0
0 1 0 0 0 1 d 0 sinα cosα 0
(2.31)
0
0 01 0001 0 0
01
cosθ -sinθcosα sinθsinα acosθ
对于棱形关节,an = 0,则式(2.32)A矩阵简化为
cosθ -sinθcosα sinθsinα 0
sinθ cosθcosα -cosθsinα 0
An = 0
sinα
cosα d
0
0
0
1
(2.33)
RPY(ø, θ, ψ) =
cosøcosθ cosøsinθsinψ – sinøcosψ cosøsinθcosψ + sinøsinψ 0
sinøcosθ sinøsinθsinψ + cosøcosψ sinøsinθcosψ–cosøsinψ 0
-sinθ
cosθsinψ
cosθcosψ
Sph(α,β,γ) = Rot(z,α)Rot(y,β)Trans(0,0,γ) Rot(y,-β) Rot(z,-α) (2.27)
Sph(α,β,γ) =
1 0 0 γcosαsinβ
0 1 0 γsinαsinβ
0 0 1 γcosβ
000
1
(2.28)
2.7 T6的确定 ( Specification of T6 )
Sph(α,β,γ) = Rot(z,α) Rot(y,β)
Trans(0,0,γ)
(2.23)
第二章 2.3工业机器人运动学(一)

第二章机器人基础知识2.3工业机器人运动学(一)【内容提要】本课主要学习工业机器人技术的运动学基础知识,涉及机器人正逆运动学的概念、平面二连杆机器人的运动学、以及机器人一般运动学的数学基础(位姿描述、齐次变换及运算)。
知识要点:✓机器人正逆运动学概念✓平面二连杆机器人的正逆运动学✓机器人的位姿描述✓齐次变换及运算重点:✓掌握机器人正逆运动学概念✓掌握平面二连杆机器人的正逆运动学✓理解机器人的位姿描述和齐次变换✓掌握齐次变换及运算难点:✓机器人的位姿描述、齐次变换及运算关键字:✓机器人正逆运动学、平面二连杆机器人、位姿描述、齐次变换及运算【本课内容相关资料】2.3机器人运动学从机构学的角度看,机器人可以看成开式运动链结构,由一系列连杆通转动或移动关节串联而成。
机器人运动学研究的是机器人各关节运动的几何关系,具体而言是各连杆之间的位移关系、速度关系和加速度关系。
本节仅研究位移关系,重点是研究手部相对于机座的位姿与各连杆之间的相互关系。
“位姿”是“位置和姿态”的简称。
工业机器人手部相对于机座的位姿与工业机器人各连杆之间的相互关系直接相关。
为了便于数学上的分析,一般将连杆和关节按空间顺序进行编号。
同时,选定一个与机座固联的坐标系,称为固定坐标系,并为每一个连杆(包括手部)选定一个与之固联的坐标系,称为连杆坐标系。
一般把机座也视为一个连杆,即零号连杆。
这样,连杆之间的相互关系可以用连杆坐标系之间的相互关系来描述。
工业机器人手部相对机座的位姿就是固联在手部的坐标系相对固定坐标系的位姿。
这样,就可以将“手部相对于机座的位姿”这样一个物理问题转化为一个数学问题,即,得到了工业机器人的运动学数学模型,便于用计算机进行分析计算。
工业机器人运动学主要包括正向运动学和反向运动学两类问题。
正向运动学是在已知各个关节变量的前提下,解决如何建立工业机器人运动学方程,以及如何求解手部相对固定坐标系位姿的问题。
反向运动学则是在已知手部要到达目标位姿的前提下,解决如何求出关节变量的问题。
六轴机器人逆运动学求解 8个解

六轴机器人逆运动学求解是机器人领域中的重要问题,六轴机器人具有复杂的结构与运动学特性,其逆运动学求解是指在给定末端执行器姿态时,求解机器人各关节的角度,以实现特定的末端执行器姿态。
在机器人的运动控制与路径规划中,逆运动学求解是一个至关重要的环节。
六轴机器人通常具有6个自由度,这意味着机器人的末端执行器可以沿着6个不同的轴线进行运动。
在实际应用中,需要对机器人的运动轨迹、姿态等进行精确控制,这就要求对六轴机器人的逆运动学问题进行求解,以实现机器人的精准操作。
逆运动学问题的求解涉及矩阵运算、三角函数关系等数学知识,需要对机器人各关节的几何结构和运动学参数有深入的了解。
在六轴机器人中,每个关节的位置、方向等特征都会对逆运动学求解造成影响,因此需要综合考虑机器人的整体结构和特性。
六轴机器人逆运动学求解可以衍生出多个解,这意味着在给定末端执行器姿态时,存在多组关节角度可以实现相同的末端姿态。
这些解称为「多解」,这种情况在实际应用中会给机器人的精确定位和操作带来挑战。
对于六轴机器人逆运动学求解的多解问题,可以通过以下方法进行处理:1. 增加约束条件:在逆运动学求解中,可以增加额外的约束条件,如关节运动范围、碰撞检测等,以限制多解的产生,使得机器人能够选择出最优的关节角度组合。
2. 引入优化算法:可以利用优化算法对多解进行评估与筛选,选取出最优的解,以满足运动控制和操作精度的要求。
3. 结合遗传算法等智能算法:利用智能算法对多解进行搜索与优化,找到最适合的关节角度组合,提高机器人的运动控制精度和操作效率。
在实际应用中,六轴机器人逆运动学求解的多解问题是一个具有挑战性的课题,需要综合应用数学、控制理论与算法等多个学科的知识,以满足对机器人运动控制精度和操作效率的要求。
六轴机器人逆运动学求解是一个复杂而重要的问题,对于解决这一问题有益于机器人的应用。
我们相信,通过不断的研究和探索,一定能够找到更加高效和精确的逆运动学求解方法,为机器人技术的发展做出更大的贡献。
工业机器人运动学

(2)圆柱坐标
由于这些变换都是相对于全局参考坐标系的坐标轴
的,因此由这三个变换所产生的总变换可以通过依
次左乘每一个矩阵而求得:
RTP Tcyl (r, ,l) Trans(0, 0,l)Rot(z, )Trans(r, 0, 0)
1 0 0 0 C S 0 0 1 0 0 r
动组成,运动顺序为:先沿z轴平移r ,再y轴旋转 β并 绕z轴旋转γ。这三个变换建立了手坐标系与参考坐标
系之间的联系。由于这些变换都是相对于全局参考坐
标系的坐标轴的,因此有这三个变换所产生的总变换
可以通过一次左乘每一个矩阵而求得:
RTP Tsph r, , Rotz, Roty, Trans0,0, r
解: 设定正运动学方程用式(3.31)中的RTP 矩阵表示,根据期望的位置可得知 如下结果:
1 0 0 Px 1 0 0 3
RTP
0 0
0
1 0 0
0 1 0
Py
0
Pz 1
0 0
1 0 0
0 1 0
4 7
或Px
3, Py
4, Pz
7
1
RTP
Tsph
C S S
C
0
S S
rS
S
C
rC
0
0
0
1
3.7 机器人的正逆运动学
例3-15假设要将球坐标机器人手坐标系原点放在3 4,7T 计算机器人的关节变量。
解: 设定正运动学方程用式(3.35)中的Txph 矩阵表示,根据期望的位置可得知 如下结果:
机械臂的运动学与逆运动学分析

机械臂的运动学与逆运动学分析引言:机械臂是一种工业机器人,能够模拟人的手臂运动,完成各种复杂的操作。
机械臂的运动学与逆运动学是研究机械臂动作学习和控制的基础知识。
通过研究机械臂的运动学与逆运动学分析,可以确定机械臂各个关节的运动规律,实现精确的位置控制。
本文将介绍机械臂的运动学和逆运动学,并探讨其在实际应用中的意义。
一、机械臂的运动学分析机械臂的运动学研究机械臂的姿态和位置随时间的变化规律。
运动学分析主要包括三个方面:位置、速度和加速度。
1. 位置机械臂的位置可以通过关节点的坐标来描述,常用的坐标系有笛卡尔坐标系和极坐标系。
笛卡尔坐标系通过XYZ三个坐标轴描述机械臂末端的位置,而极坐标系则通过距离和角度来描述。
根据不同的控制需求和操作环境,可以选择合适的坐标系来描述机械臂的位置。
2. 速度机械臂的速度是机械臂终端各关节点的速度值。
通过推导机械臂各关节点的速度,可以得出机械臂末端的速度。
机械臂的速度是根据位置变化率来计算的,可以通过微分方法求解。
在实际应用中,机械臂的速度需要根据具体任务进行调整,以实现精确控制。
3. 加速度机械臂的加速度是机械臂终端各关节点的加速度值。
通过推导机械臂各关节点的加速度,可以得出机械臂末端的加速度。
机械臂的加速度决定了机械臂能够完成的运动速度和周期。
加速度的分析可以帮助设计者了解机械臂的动态特性,并在控制系统中进行合理的参数调节。
二、机械臂的逆运动学分析机械臂的逆运动学是指已知机械臂末端位置,求解各关节的角度,从而实现确定的位置控制。
逆运动学分析是机械臂控制设计中的重要一环。
逆运动学的求解过程有多种方法,最常见的是几何法和代数法。
几何法是基于三角函数关系进行求解的,根据机械臂构型和关节参数,可以将位置坐标转化为关节角度。
代数法则是利用向量和矩阵的运算进行求解,将机械臂的位置坐标转化为向量形式,并通过矩阵运算求解逆运动学方程组。
逆运动学的求解是机械臂控制的关键步骤,可应用于自动化装配、物料搬运和危险环境作业等领域。
六自由度工业机器人正逆运动学

六自由度工业机器人正逆运动学
六自由度工业机器人具有6个关节,可以实现6个不同的运动自由度,分别是平移、转动、旋转、可在水平和垂直方向移动。
正运动学是指从机器人关节角度和长度参数计算出机器人末端执行器在空间中的位置和姿态的过程。
通过运动学方程,可以将关节角度和长度参数转换为空间中的位置和姿态。
逆运动学是指已知机器人末端执行器在空间中的位置和姿态,计算出机器人关节角度和长度参数的过程。
通过逆运动学方程,可以将空间中的位置和姿态转换为关节角度和长度参数。
正逆解的计算过程复杂且涉及到大量的三角函数和求解方程,需要使用数值计算方法进行求解。
此外,也需要考虑机器人的约束和限制条件,以确保计算得到的解是可行解。
机器人学基础第4章

4. 5 典型机器人的逆运动学举例
④求θ5。 由机械臂关节位姿矩阵推导可知:
由于前文已经求解出θ1 ~ θ3, 可以求解出 则根
据
可以求解出 的数值。令:
4. 5 典型机器人的逆运动学举例
得
解得
4. 5 典型机器人的逆运动学举例
下面分两种情况讨论θ4 和θ6 的解法。 当θ5≠0°时: ⑤求θ4 。 根据前文得:
4. 6 逆运动学对机器人的设计约束
根据4. 1 节的内容可以知道, 对于6 自由度机器人来 说, 当存在几个正交关节轴或者有多个αi 为0°或90°, 可能得到解析解。所以当设计6 自由度机械臂时, 通常 会有3 根相交轴, 并尽量使αi 为0°或90°。
此外, 为了使机械臂有更大的灵巧工作空间, 通常将机 械臂的末端连杆设计得短一些。
令式(4 -1) 和式(4 -2) 相等, 可以得到: 解得:
4.2 三个相邻关节轴线交于一点的 逆运动学求解
当θ2≠0 时, 可以解得:
当θ2 =0 时, 可以化作如下形式:
4.2 三个相邻关节轴线交于一点的 逆运动学求解
即:
可以解得: 同理当θ2 = π 时, 可以解得:
4. 3 逆运动学的几何解法
4.2 三个相邻关节轴线交于一点的 逆运动学求解
逆运动学没有通用的求解算法, 通常将机器人的逆运动学解法 分为数值解法和解析解法两类。数值解法是指通过迭代的方 法对运动学方程进行求解, 此种方法求解速度较慢, 且不能保 证求出全部的解。解析法是指通过代数或者几何的方法, 得到 关节角的数学表达式, 本课程主要讨论解析解法。解析法中几 何法与代数法并不完全区别, 几何法中可以引入代数描述, 代 数法可以通过几何性质来简化求解过程, 二者仅是求解过程不 同。
3)机器人逆运动学实验
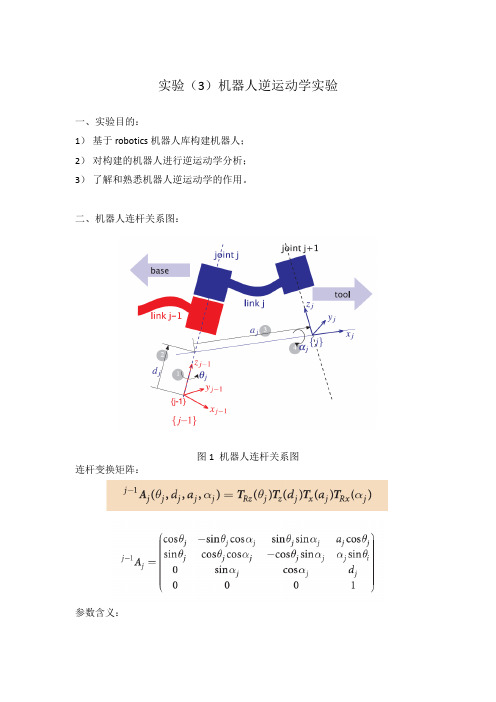
实验(3)机器人逆运动学实验一、实验目的:1)基于robotics机器人库构建机器人;2)对构建的机器人进行逆运动学分析;3)了解和熟悉机器人逆运动学的作用。
二、机器人连杆关系图:图1 机器人连杆关系图连杆变换矩阵:参数含义:三、基本函数介绍(1)2连杆机器人实例图2连杆机器人坐标系1)建立机器人DH参数表2)根据D-H参数创建机器人连杆对象3)根据连杆对象,建立机器人4)观测建立机器人的情况正运动学函数:1)正运动学函数的使用T=two_link.fkine([pi/4 pi/4])T = 0.0000 -1.0000 0 0.70711.0000 0.0000 0 1.70710 0 1.0000 00 0 0 1.00002)观测计算结果的情况,三维显示two_link.plot([pi/4 pi/4])3)逆运动学函数q=two_link.ikine(T,[0 0],[1 1 0 0 0 0])q =0.7854 0.7854 ikine 函数的参数说明:Q = R.ikine(T, Q0, M, OPTIONS)Q0为求解的初始值;M 为自由度数,也就是有运动关节,对应有关节的为1。
(2)对于六自由度机器人求解的逆解,以puma560为例。
1)函数ikine6s使用方法Q = R.ikine6s(T, CONFIG) 其中T 为机器人位姿矩阵。
CONFIG 为臂型'l' arm to the left (default) 'r' arm to the right 'u' elbow up (default) 'd' elbow down'n' wrist not flipped (default)'f' wrist flipped (rotated by 180 deg)XYZ2)puma560实例>> mdl_puma560 >>qn qn =0 0.7854 3.1416 0 0.7854 0 >> T = p560.fkine(qn) T =-0.0000 0.0000 1.0000 0.5963 -0.0000 1.0000 -0.0000 -0.1501 -1.0000 -0.0000 -0.0000 -0.0144 0 0 0 1.0000>>qi = p560.ikine6s(T) qi =2.6486 -3.9270 0.0940 2.5326 0.9743 0.3734>>qi = p560.ikine6s(T,’ru ’)qi = -0.0000 0.7854 3.1416 0.0000 0.7854 -0.0000 >>p560.plot(qi)XYZ六、实验内容(1)用机器人库建立下图的机器人,并且求解和显示下面几种情况讨论平面3自由度机器人的姿态逆运动学解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d3 S2 CLeabharlann px S1 py C2 pz(3.24) (3.25)
4
tan 1
C2
S1ax C1ay C1ax S1ay S2az
(3.26)
5
tan 1
C4
C2
C1ax
S1ay S2az S2 C1ax S1ay
S4 S1ax C2az
C1ay
1T6 =
C2( C4C5C6 - S4S6 ) - S2S5C6 S2( C4C5C6 - S4S6 ) + C2S5C6
S4C5C6 + C4C6
0
-C2( C4C5S6 + S4C6 )+ S2S5S6 -S2( C4C5 S6+ S4C6 )- C2S5S6
-S4C5S6 + C4C6
0
C2C4S5 + S2C5 S2C4S5 - C2C5
7
这里 其中
f11 = C1 x+S1 y
f12 = - z f13 = - S1 x+C1 y
(3.10) (3.11) (3.12)
x =[ nx ox ax px ]T, y =[ ny oy ay py ]T, z =[ nz oz az pz ]T 由前节得到的斯坦福机械手运动学方程式(2.48)为
3
3.1 引言 (Introduction)
所谓逆运动学方程的解,就是已知机械手直角坐标空间的位姿
(pose)T6,求出各节变量θn or dn 。
T6 = A1 A2 A3 A4 A5 A6
(3.1)
逆运动学方程解的步骤如下:
(1)根据机械手关节坐标设置确定An
An为关节坐标的齐次坐标变换,由关节变量和参数确定。关节变量 和参数有:
an-连杆长度;
αn-连杆扭转角;
dn-相邻两连杆的距离;
θn-相邻两连杆的夹角。
对于旋转关节θn为关节变量,而对于滑动关节dn为关节变量。其余为 连杆参数,由机械手的几何尺寸和组合形态决定。
4
(2) 根据任务确定机械手的位姿T6
T6为机械手末端在直角坐标系(参考坐标或基坐标)中的位姿,由 任务确定,即式( 2.37 )给出的表达式T6 = Z-1 X E-1确定。它是由三个 平移分量构成的平移矢量P(确定空间位置)和三个旋转矢量n,o,a (确定姿态)组成的齐次变换矩阵描述。
第三章 工业机器人的运动学-3
1
主要内容
数学基础——齐次坐标变换 机器人运动学方程的建立(正运动学) 机器人逆运动学分析(逆运动学)
2
三、逆运动学方程
( Inverse Kinematic Equations )
3.1 引言 3.2 逆运动学方程的解 3.3 斯坦福机械手的逆运动学解 3.4 欧拉变换的逆运动学解 3.5 RPY变换的逆运动学解 3.6 球坐标变换的逆运动学解 3.7 本章小结
S4S5
0
S2d3 -C2d3
d2
1
(3.13)
8
比较式(3.9)和式(3.13)矩阵中的第三行第四列元素相等得到
f13(p)= d2
或
- S1 px+C1 py = d2
令 其中
px = r cosΦ py = r sinΦ
r px2 py2
tan 1
py px
将式(3.16)和式(3.17)代入式(3.15)有
nx ox ax px
T6
ny
nz 0
oy oz 0
ay az 0
p
y
pz 1
(3)由T6和An(n=1,2,…,6)和式(4.1)求出相应的关节变量θn 或 dn。
5
3.2 逆运动学方程的解(Solving inverse kinematic equations)
根据式(3.1)
T6 = A1 A2 A3 A4 A5 A6
(3.20)
(3.21) (3.22)
9
由式(3.21)、(3.22)和(3.18)可得到第一个关节变量θ1的值
1
tan 1
py px
tan 1
d2 r2 d22
(3.23)
根据同样的方法,利用式(3.9)和式(3.13)矩阵元素相等建立的相关的方程
组,可得到其它各关节变量如下:
2
tan 1
C1 px S1 py pz
(3.27)
6
tan 1
C5
C4
C2
C1ox S1oy S4 C2
S2oz C1ox
S4 S1oy
S1ox C1oy S5 S2oz C4 S1ox
S2 C1ox C1oy
S1oy C2oz
(3.28)
10
注意:
在求解关节变量过程中如出现反正切函数的分子和分母太小, 则计算结果误差会很大,此时应重新选择矩阵元素建立新的方 程组再进行计算,直到获得满意的结果为止。同样,如果计算 结果超出了机械手关节的运动范围,也要重新计算,直到符合 机械手关节的运动范围。
sinΦconθ1-conΦsinθ1 = d2/r 由式(3.20)可得
( 0< d2/r ≤1 )
sin(Φ-θ1)= d2/r
(0< Φ-θ1 < )
con(Φ-θ1)=
1
d2
r
2
这里±号表示机械手是右肩结构(+)还是左肩结构(-)。
(3.14) (3.15) (3.16) (3.17) (3.18) (3.19)
(3.2) (3.3) (3.4) (3.5) (3.6)
根据上述五个矩阵方程对应元素相等,可得到若干个可解的代数方程,便可
求出关节变量θn或 dn。
6
3.3 斯坦福机械手的逆运动学解 ( Inverse solution of Stanford manipulator)
在第三章我们推导出 Stanford Manipulator 的运动方程和各关节齐次变换式。 下面应用式(3.2)~(3.6)进行求解:
分别用An(n=1,2,…,5)的逆左乘式(3.1)有
A1-1 T6 = 1T6 A2-1 A1-1 T6 = 2T6 A3-1A2-1 A1-1 T6 = 3T6 A4-1 A3-1A2-1 A1-1 T6 = 4T6 A5-1 A4-1 A3-1A2-1 A1-1 T6 = 5T6
( 1T6 = A2 A3 A4 A5 A6 ) ( 2T6 = A3 A4 A5 A6 ) ( 3T6 = A4 A5 A6 ) ( 4T6 = A5 A6 ) ( 5T6 = A6 )
