4.2 分枝定界法
智慧树答案管理运筹学(山东联盟)知到课后答案章节测试2022年

第一章1.运筹学的主要分支包括()答案:非线性规划;整数规划;图论;线性规划;目标规划2.运筹学是应用系统的、科学的、数学分析的方法,通过建模、检验和求解数学模型而获得最优决策的科学。
答案:对3.运筹学是用数学方法研究各种系统中最优化问题的科学,它主要用数学模型来求得合理运用现有条件的最优方案,为决策者提供科学决策的依据。
答案:对4.运筹学着重以管理、经济活动方面的问题及解决这些问题的原理和方法作为研究对象。
答案:对5.制定决策是运筹学应用的核心,而()则是运筹学方法的精髓。
答案:建立模型6.运筹学可用()来进行概括。
答案:寻优科学7.运筹学的简称是()。
答案:OR8.下列哪一项不是运筹学的特点()。
答案:主观的9.下列哪一项不是运筹学的研究步骤()。
答案:实施模型10.运筹学模型是以()模型为其主要形式。
答案:数学第二章1.线性规划问题的一般模型中不能出现等式约束。
答案:错2.用图解法求最优解时,只需求出可行域顶点对应的目标值,通过比较大小,就能找出最优解。
答案:对3.线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大。
答案:对4.单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负。
答案:对5.单纯形法的迭代运算过程是从一个可行解转换到目标函数值更大的另一个可行解。
答案:错6.检验数λj表示非基变量xj增加一个单位时目标函数值的改变量。
答案:对7.利用单纯形法求解线性规划问题的过程中,所有基变量的检验数必为零。
答案:对8.若某个bk≤0, 化为标准形式时原不等式( )。
答案:两边同乘负19.将线性规划问题转化为标准形式时,下列说法不正确的是:答案:若约束条件为=,则要增加一个人工变量10.标准形式的线性规划问题,其可行解()是基本可行解,最优解一定是可行解。
答案:不一定11.关于线性规划问题的图解法,下面()的叙述正确。
第15章分枝定界法

算法思想
从活结点表中选择下一个扩展结点通常有两种方式。 ①先进先出(FIFO)法。即从活结点表中取出结点的 顺序与加入结点的顺序相同,因此活结点表的性质与队 列的相同。
②最小耗费或最大收益法。由于解空间中每个结点都 有一个对应的耗费或收益,可将活结点表组织成一个优 先队列,并根据结点的耗费所确定的结点优先级别来选 取下一个结点。
最后G成为扩展结点,生成的结点为N和O,两者 所对应的解都不比当前的最优解更好,因此最优解保 持不变,两者都是叶结点而被删除,此时堆变为空, 搜索过程结束,到达结点L 的搜索为最优解。
已知n = 3, w = [20, 15, 15], p = [40, 25, 25], c = 30
算法思想
已知n = 3, w = [20, 15, 15], p = [40, 25, 25], c = 30
例15-1
A被删除,由于B的收益值比C的大,因此对B进行 扩展,得到结点D和E,D是不可行的而被删除,E加 入堆中。由于E具有收益值40,而C为0,因此E成为 下一个扩展结点,生成结点J和K,J不可行而被删除, K是一个可行的解,因此K作为目前能找到的最优解 而被记录下来,然后K被删除。
例15-1
接下来扩展结点F,它产生两个孩子L和M,L代表一 个可行的解且其收益值为50,M代表另一个收益值为 15的可行解。G是最后一个扩展结点,它的孩子N和O 都是可行的。由于活结点队列变为空,因此搜索过程 终止,最佳解的收益值为50。
从上述过程可看出,在解空间树上进行的FIFO分枝定界方法 类似于从根结点出发的广度优先搜索,它们的主要区别是在 FIFO分枝定界法中不可行的结点不会被搜索。
分枝定界法

4
x1
x2 x1
16.5 4
x1 0, x2 0
结论1 :(IP)的最优解一定在某个子问题中
2 :子问题的可行域 父问题的可行域 子问题的最优解 ≤ 父问题的最优值
3 :子问题中的整数解都是(IP)的可行解
二: 定界,以每个后继问题为一分枝标明求解结 果,在解的结果中,找出最优目标函数值最大者作 为新的上界.从已符合整数条件的各分支中,找出 目标函数值为最大者作为新的下界,若无,则下界 为0.
x1 x2 x3 x4 x5 解
检 0 0 -20/3 0 -50/3 Z-440/3
x2 0
x1 1 x4 0
1 1/3 0
00
0
0 -1/3 1
-2/3 17/6 13 -10/3 5/3
L1最优解:x1 3,x2 17 6 , x3 0
x4
5 3
,
x5
0,
最优值:z1
440 3
求解子问题L3 :
x1 x2 x3
检 0 0 -20/3
x2 0 1 1/3 x1 1 0 0 x4 0 0 -1/3
x6 0 1 0
x4 x5
x6
0 -50/3 0
00 1
解 Z-440/3 17/6 3 5/3
2
最优解:
xx14
35,/ 2x,2 x52, x03,
11 4,x2 0,x4
3, 52,
z3 130 得下界
x5 14 , x6 0
z4
285 2
z3
L5
:x1 x3
2,x2 0,x4
第五章整数规划

第五章 整数规划主要内容:1、分枝定界法; 2、割平面法; 3、0-1型整数规划; 4、指派问题。
重点与难点:分枝定界法和割平面法的原理、求解方法,0-1型规划模型的建立及求解步骤,用匈牙利法求解指派问题的方法和技巧。
要 求:理解本章内容,熟练掌握求解整数规划的方法和步骤,能够运用这些方法解决实际问题。
§1 问题的提出要求变量取为整数的线性规划问题,称为整数规则问题(简称IP )。
如果所有的变量都要求为(非负)整数,称之为纯整数规划或全整数规划;如果仅一部分变量要求为整数,称为混合整数规划。
例1 求解下列整数规划问题211020m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,13522445x x x x x x x x 如果不考虑整数约束,就是一个线性规划问题(称这样的问题为原问题相应的线性规划问题),很容易求得最优解为:96m ax ,0,8.421===z x x 。
用图解法将结果表示于图中画“+”号的点都是可行的整数解,为满足要求,将等值线向原点方向移动,当第一次遇到“+”号点(1,421==x x )时得最优解为1,421==x x ,最优值为z=90。
由上例可看出,用枚举法是容易想到的,但常常得到最优解比较困难,尤其是遇到变量的取值更多时,就更困难了。
下面介绍几种常用解法。
§2 分枝定界法分枝定界法可用于解纯整数或混合的整数规划问题。
基本思路:设有最大化的整数规划问题A ,与之相应的线性规划问题B ,从解B 开始,若其最优解不符合A 的整数条件,那么B 的最优值必是A 的最优值*z的上界,记为z ;而A 的任意可行解的目标函数值是*z的一个下界z ,采取将B 的可行域分枝的方法,逐步减少z 和增大z ,最终求得*z 。
现举例说明: 例2 求解A219040m ax x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,702075679x x x x x x x x 解:先不考虑条件⑤,即解相应的线性规划B (①--④),得最优解=1x 4.81, =2x 1.82,①② ③ ④ ⑤=0z 356(见下图)。
4.3.1 分枝定界法

四、分枝定界法求解实例
LP0 : 1 7 5 x1 3 , x 2 2 , Z 3 2 9 9 9
上界: 32 下界: 0 5 9
x1≤3
L P1 : 6 2 , Z 32 7 7
x1 ≥4
LP 2 : x 1 4 , x 2 1, Z 2 9
上界: 32 下界: 29 2 7
z 0, z 35 .5
x2≥7 无可行解
z 0, z 35 .3
x1≥5 LP5:X=(5,5) Z5=35 分枝过程图示
z 35, z 35
OR:SM
x* (5,5), z* 35
例2:
MaxZ 6 x1 5 x 2 2 x1 x 2 9 5 x 7 x 35 1 2 s .t . x1 , x 2 0 x1 , x 2 取整数
运筹学--管理科学方法
李军
桂林电子科技大学商学院
第三节 (I)分枝定界法
1.分枝定界法的创立者 2.分枝定界法求解依据 3. 分枝定界法求解步骤 4.分枝定界法求解实例 5.分枝定界法求解小结 6. 算法应用注意事项
2
OR:SM
一、分枝定界法的创立者
理查德·卡普(Richard Karp)教授1935年1月3日生 于波士顿,从小时起就兴趣广泛,聪明过人。在哈 佛大学时他文理兼修, 1955 年先获得文学学士学位 ,第二年又获得理科硕士学位。之后他进入哈佛大 学的计算实验室攻读博士,于 1959 年取得应用数学 博士学位。现任美国加州大学伯克利分校计算机科 学讲座教授,美国科学院、美国工程院、美国艺术 与科学院、欧洲科学院院士。因其在计算机科学领 域的杰出贡献曾获图灵奖、冯诺依曼奖、美国国家 科学勋章、哈佛大学百年奖章等奖项. 卡普和他的同事海尔特(M.Held)20世纪60年代,经过反复研究,提出 了一种称为“分枝限界法”(branch—and—bound method)的新方法。该方 法的要点是:对解集合反复进行分枝,每次分枝时,都对所得的子集计算最 优解的界。如果对某个子集求得的界不优于已知的允许解,则抛弃此子集不 再进行分枝;否则继续分枝以探索更好的解,直到所得的子集仅含有一个解 时为止。分枝限界法就其实质而言是一种求解策略而非算法,具体算法要根 据实际问题的特点去实现。但由于这种方法在求解许多问题中都非常实用, 因此常常被直呼为“分枝限界算法”。
运筹学_分支定界法

⑵
5 x1 6 x 2 3 0
x2
A 3 B
⑴x
1
x2 2
⑶
x1 4
1
1
3
x1 5 x 2 Z
x1
求(LP2) ,如图所示。
m a x Z x1 5 x 2 x1 x 2 2 5 x 6 x2 30 1 ( IP 2 ) x 1 4 x 2 1 x1 , x 2 0 且 为 整 数
x1 x 2 2 x1 x 2 2 5 x 6 x2 30 5 x 6 x2 30 1 1 x1 x1 4 4 ( IP 2 2 ) ( IP 2 1) 2 2 x1 x1 x x 4 3 2 2 x1 , x 2 0 且 为 整 数 x1 , x 2 0 且 为 整 数
第三节 分枝定界法
(一)、基本思路 考虑纯整数问题:
m ax Z
n
c
j 1
n
j
xj
a ij x j b i ( i 1 .2 m ) ( IP ) j 1 x 0 ,( j 1 .2 n ) 且 为 整 数 j
m ax Z
c
j 1
n
记为(IP)
解:首先去掉整数约束,变成一般线性规划问题
m a x Z x1 5 x 2 x1 x 2 2 5 x1 6 x 2 3 0 4 x1 x ,x 0 1 2
记为(LP)
用图解法求(LP)的最 优解,如图所示。
m a x Z x1 5 x 2 x1 x 2 2 5 x1 6 x 2 3 0 4 x1 x ,x 0 1 2
分枝定界法讲义_代码

第5 章分枝定界任何美好的事情都有结束的时候。
现在我们学习的是本书的最后一章。
幸运的是,本章用到的大部分概念在前面各章中已作了介绍。
类似于回溯法,分枝定界法在搜索解空间时,也经常使用树形结构来组织解空间(常用的树结构是第1 6章所介绍的子集树和排列树)。
然而与回溯法不同的是,回溯算法使用深度优先方法搜索树结构,而分枝定界一般用宽度优先或最小耗费方法来搜索这些树。
本章与第1 6章所考察的应用完全相同,因此,可以很容易比较回溯法与分枝定界法的异同。
相对而言,分枝定界算法的解空间比回溯法大得多,因此当内存容量有限时,回溯法成功的可能性更大。
算法思想分枝定界(branch and bound)是另一种系统地搜索解空间的方法,它与回溯法的主要区别在于对E-节点的扩充方式。
每个活节点有且仅有一次机会变成E-节点。
当一个节点变为E-节点时,则生成从该节点移动一步即可到达的所有新节点。
在生成的节点中,抛弃那些不可能导出(最优)可行解的节点,其余节点加入活节点表,然后从表中选择一个节点作为下一个E-节点。
从活节点表中取出所选择的节点并进行扩充,直到找到解或活动表为空,扩充过程才结束。
有两种常用的方法可用来选择下一个E-节点(虽然也可能存在其他的方法):1) 先进先出(F I F O)即从活节点表中取出节点的顺序与加入节点的顺序相同,因此活节点表的性质与队列相同。
2) 最小耗费或最大收益法在这种模式中,每个节点都有一个对应的耗费或收益。
如果查找一个具有最小耗费的解,则活节点表可用最小堆来建立,下一个E-节点就是具有最小耗费的活节点;如果希望搜索一个具有最大收益的解,则可用最大堆来构造活节点表,下一个E-节点是具有最大收益的活节点。
例5-1 [迷宫老鼠] 考察图16-3a 给出的迷宫老鼠例子和图1 6 - 1的解空间结构。
使用F I F O分枝定界,初始时取(1,1)作为E-节点且活动队列为空。
迷宫的位置( 1 , 1)被置为1,以免再次返回到这个位置。
分枝定界法的步骤

分枝定界法的步骤
分枝定界法是一种求解组合优化问题的方法,其步骤如下:
1. 确定问题的目标函数以及约束条件:首先需要明确问题的目标函数是什么,以及有哪些约束条件需要满足。
2. 构造初始问题:根据问题的要求,构造一个初始问题,并计算初始问题的目标函数值。
3. 分枝:在初始问题的基础上,对其中的某个变量(或几个变量)进行分枝操作。
将问题划分为多个子问题,每个子问题代表了某个变量取值的一个分支。
4. 计算下界:对于每个子问题,计算出一个下界值。
下界值是一个目标函数值的估计,它不会高于目标函数的最小值。
5. 判断分支:根据计算出的下界值,选择一个最有希望的子问题进行分支,即选择一个下界值最小的子问题。
6. 回溯:从步骤5选择的分支开始,回溯到父问题,跳过部分分支。
7. 重复:重复步骤3到步骤6,直到找到一个满足问题要求的解,或者找到一个可行解的上界值。
8. 定解:通过进一步确定上界值,并进行剪枝操作,选择最优解。
9. 输出:输出最优解及其对应的目标函数值。
需要注意的是,分枝定界法的关键在于如何计算下界值和进行剪枝操作,以减少问题的搜索空间。
常用的技巧有线性规划松弛、最小生成树、割集等。
分枝定界法

束——缩小可行域;将原整数规划问题分枝——分为两个子 规划,再解子规划的伴随规划……通过求解一系列子规划的 伴随规划及不断地定界 .最后得到原整数规划问题的整数最 优解 . 下面结合一个极大化例题来介绍分枝定界法的主要思路 .
例2 某公司计划建筑两种类型的宿舍.甲种每幢占地0.25 ×103m2, 乙种每幢地0.4×103m2.该公司拥有土地3×103m2. 计划甲种宿舍不超过 8 幢,乙种宿舍不超过4幢.甲种宿舍每 幢利润为10万元,乙种宿舍利润为每幢20万元.问该公司应
x2 3 x1, x2 0
问题 B4
max f 20 x1 10 x2
5x1 8x2 60
x1 8
s.t
x2 4 x1 6
x2 4 x1, x2 0
它们的可行域分别为 K3, K4 ( ). 见图3。
第21页/共34页
x2
因为 K4 ,问题 B4
4
无可行解,此问题已
3
作出问题 A1, 的A2伴随规划 B则1, 问B2题, 的可B1行, B2, 域为 K1, K见2图, 2(b). 以下我们将由同一问题分解出的两
个分枝问题称为"一对分枝".
第15页/共34页
x2
4
x2
3
2 1
O
246
8 x1
O
12 4
6
8
x1
(a)
(b)
图2 ( a )
4. 分别求解一对分枝
在一般情况下,对某个分枝问题(伴随规划)求解时,可能出现 以下几种可能:
x1, x2 0, 整数
(1)
第3页/共34页
若暂且不考虑 x1, x取2 整数这一条件.则(1)就变为下列 线性规划 :
分枝定界法的求解步骤

分枝定界法的求解步骤
分枝定界法是一种综合了暴力搜索与动态规划的算法,它能够处理复杂的最优化问题,比如带决策变量的规划问题、组合背包问题等。
在互联网应用中,这种算法常用于多次筛选的场景,例如实现分类系统中的排序任务或优化搜索时的推荐服务。
分枝定界法的求解步骤主要包括以下几步:
首先,建立一个由多个可变节点和边组成的多变量决策模型,这些可变节点即是这个最优化问题的变量,边则表示变量之间的关系;
其次,根据题意的约束条件,选取一条限制范围最宽的边作为参照标准,将决策模型中的叶子节点分成两个分支,尝试计算每个节点在不同尝试下的最佳解;
然后,依次向下求解每个叶子节点,根据其在不同尝试下的最优解,选取给定参数下最好的值,并将其保留下来;
最后,重复上述操作,不断地向下搜索,直至每个叶子节点都遍历完毕,即可获得最终的最优解。
总之,分枝定界法是一种能够在有多个可变节点的复杂问题中求解最优解的有效算法,在互联网领域中,它可用于实现精准推荐等功能,可谓运用广泛。
分支定界法

第三节 分枝定界法
• 分枝定界法基本思想 • 分枝定界法计算步骤
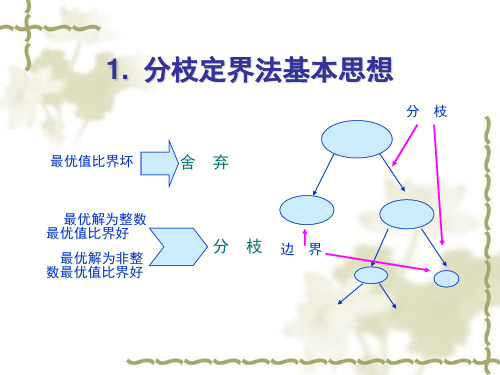
1. 分枝定界法基本思想
最优值比界坏
舍弃
最优解为整数 最优值比界好
最优解为非整 数最优值比界好
分 枝 边界
分枝
1. 分枝定界法基本思想续
0
N
I
B1N
cB B1b B 1b
xr br Z
br xr br 1
1. 分支定界法基本思想续
• 分枝的方法 min c x
Ax b s.t.x 0, x为整数
min c x
Ax b
s.t.xr
br
x 0, x为整数
1. 分枝定界法基本思想续
• 分枝方法示意图
1. 分枝定界法基本思想续
• 定界 1. 当前得到的最好整数解的目标函数值
2. 分枝后计算松弛的线性规划的最优解
整数解且目标值小于原有最好解的值则替代原有 最好解
整数解且目标值大于原有最好解的值则 删除该分 支其中无最优解
非整数解且目标值小于原有最好解的值则继续分 支
非整数解且目标值大于等于原有最好解的值则删 除该分支其中无最优解
2. 分枝定界法计算步骤
z z 3x52xz(2,1()1,332.2)5xx例((xPP2))(x231.25.,(1323) ,(52.Px))1z(P1解) (4xP答(x)P1)3 x 无解(2,x32) 2无z 解(P )72 5 1 5 13 T T 1 3 115 0 T 2T 0 3 12 1 6 2 2 T 2 4
2. 分枝定界法计算步骤-例题
• 例3.3.1
minZ (x1 x2 )
第4章 线性整数规划

线性整数规划的概念 例:用集装箱装运甲、乙两种货物,每种货物每包的体积、 重量和收益见下表。集装箱体积为 24m3 ,允许的最大 重量 14 吨,问每个集装箱应装两种货物各多少包才能
使收益最大?
货物 甲 乙 每包体积 (m3) 5 4 每包重量 (吨 ) 2 5 收益 (元/包) 1000 1500
线性整数规划的概念
二、线性整数规划的数学模型
在线性规划模型:
max S CX AX b s .t . X 0
中,若增加自变量取整数约束条件,则可得到线性整数 规划的数学模型:
max S CX AX b s.t . X 0且为整数
解:①解原问题的松弛问题P0: max S 40 x1 90 x2
9 x1 7 x2 56 s.t .7 x1 20 x2 70 x , x 0 1 2
分枝定界法 可用图解法求解。最优解为xl=4.809,x2=1.817,S=355.89 根据松弛问题的最优解可以确定原问题的目标函数值的 上界为S =355.89或 S =355,下界为 S =0(由于目标函数的 系数均为整数且大于0)。 ②将P0分解为两个子问题Pl和P2(分枝)
P3 的最优解为 x1=4 , x2=2 , S=340 ,因已得到一个整数 解,即原问题的一个可行解,故原问题目标函数下界 为:S=340。 P4的最优解为x1=1.428,x2=3,S=327.12,S4 327
分枝定界法
因S4 S,故没有必要继续对 P4分枝,应将 P4剪掉(称为剪枝 )。
线性整数规划的概念
三、整数规划的解法概述
由于对变量的整数约束限制了通常的连续型方法的应 用,因此,人们在刚接触整数规划问题时,往往会产 生两种原始的求解设想: ①因为纯整数规划的可行解是有限的,因此,可采用一 一比较的方法(穷举法)找出最优解; ②先不考虑整数约束,解相应的连续型问题 ( 松弛问题 ) , 然后用“四舍五入”的办法凑得一个较好的整数解作 为最优解。 这两种设想往往是行不通的。穷举法效率太低,只有 当可行解较少时才能行得通,当可行解很多时,需要 花很长的时间。凑整法不一定能得到问题的最优解。
3.2分枝定界法

L 3 : x = 3,x = 2, 1 2 L 4 x1 = 11 4,x2 = 3, : x3 = 5 / 2,x4 = 5 / 2, x3 = 0,x4 = 5 , x5 = 0, x6 = 0 2 z 3 = 130 得下界 x5 = 1 , x 6 = 0 4 z 4 = 285 ≥ z 3 2
x6
0 0 0 0
1
解 Z-440/3 17/6 3 5/3 -1/6
解 Z-440/3 17/6 3 5/3
x2 x1 x4
最优解: x1 = 11 ,x2 = 3, x3 = 0, 4 5 ,x = 1 , x = 0 x4 = 2 5 4 6 最优值:z 3 = 285 2
x3
-15 0 1/2 -2 -1/2
分枝定界法计算过程:
讨论松弛问题 L 0 : 1、 L0无最优解, 则(IP )无最优解 结束
上界
2、最优解 X *0 = ( x *01 , x *02 , , x * on ), 最优值 z 0 (1) X *0 为整数解 ,则X *0 为( IP)的最优解 结束 ( 2 ) X * 0 中至少有一个是分数,设x *01 是分数 :分枝
混合型
L 0 : x1 = 3.5,x 2 = 2.5, x3 = 0,x 4 = 0, z 0 = 155
松弛问题 L 0 ; max z = 30 x 1 + 20 x 2 2 x 1 + 3 x 2 + x 3 = 14 . 5 s .t 4 x 1 + x 2 + x 4 = 16 . 5 x1 , x 2 , x 3 , x 3 ≥ 0 L0的最优单纯型表:
剪枝
L6 :
求解子问题 L1 :
分枝定界法

§3 分枝定界法 (2)
x2 10 1)不受整数限制,作为 9 8 普通线性规划求解,可 得出最优解为:x1=10/3, 7 6 x2=4/3,z=26/3( 见 图 5 2-1)。 4 3 该解示如图2-4中的节 2 点①。 1
[解]
2x1+x2=8 最优解 x1+2x2=6 1 2 3 4 5 6 7 8 9 图2-1 x1
x1+2x2≥6
x1≤3 x2≥2 x1≥0,全取整。 其图解法见图2-5,最优解为x1=2,x2=2,z=10。
§3 分枝定界法 (9)
x1≤3 1 z =26/3 x1=10/3 x1≥4 x2=4/3 图2-4
2
z =9 x1=3 x2=3/2 3 不可行
x2
8 7 6 5 4 3 x2=2
目标函数 1 2 3 4 5 6 7 8 9 x1 图2-5
§3 分枝定界法 (10)
从对求解[例2-5]的过程,可归纳出求解整数规划的分枝 定界法有下述特点: (i) 既可求解全整数规划,亦可求解混合整数规划。 (ii)求解每个子集的最优整数解,都是首先放弃整数约束, 用线性规划解法求出无约束时的最优解,此时的目标函 数值即为该子集所有可行解的目标下界(对于求极小值 的规划而言)。
§3 分枝定界法 (3)
2)因为x1、x2当前均为非整数,故不满足整数要求,任 选1个进取分枝。设选x1进行分枝,把可行集分成2个子 集: x1≤[10/3]=3及x1≥[10/3]+1=4 3)x1≤3时 目标函数 min z=x1+4x2 约束条件 2x1+x2≤8
x1+2x2≥6
x1≤3 x1,x2≥0且为整数。
(iii)如果子集的非整数最优解的下界超过迄今已得到的最 好可行整数解目标值,或者子集无解,则这个子集将被 剪掉,又称剪枝。
《运筹学》试题及答案(二)

《运筹学》试题及答案19、简述线性规划模型主要参数(p11)(1)、价值系数:目标函数中决策变量前的系数为价值系数(2)、技术系数:约束条件中决策变量前的系数(3)、约束条件右边常数项15、简述线性规划解几种可能的结果(情形)(ppt第二章39或89页)(1).有唯一最优解 (单纯形法中在求最大目标函数的问题时,对于某个基本可行解,所有δj≤0)(2).无可行解,即可行域为空域,不存在满足约束条件的解,也就不存在最优解了。
(3).无界解,即可行域的范围延伸到无穷远,目标函数值可以无穷大或无穷小,一般来说,这说明模型有错,忽略了一些必要的约束条件(4).无穷多个最优解,则线段上的所有点都代表了最优解(5)退化问题,基变量有时存在两个以上相同的最小比值,这样在下一次迭代中就有一个或几个基变量等于零,用图解法无退化解1、简述单纯形法的基本思路(p70)从可行域中某一个顶点开始,判断此顶点是否是最优解,如不是,则再找另一个使得其目标函数值更优的顶点,称之为迭代,再判断此点是否是最优解。
直到找到一个顶点为其最优解,就是使得其目标函数值最优的解,或者能判断出线性规划问题无最优解为止。
17、简述线性规划中添加人工变量的前提(p85)在系数矩阵中直接找不到初始可行解,进而通过添加人工变量的方法来构造初始可行基,得出初始基本可行解10、简述线性规划对偶问题的基本性质(p122)(1)对称性(2)弱对偶性(3)强对偶性(4)最优性(5)互补松弛型原函数与对偶问题的关系1)求目标函数最大值的线性规划问题中有n 个变量 m个约束条件,它的约束条件都是小于等于不等式。
而其对偶则是求目标函数为最小值的线性规划问题,有m个变量n个约束条件,其约束条件都为大于等于不等式。
2)原问题的目标函数中的价值系数为对偶问题中的约束条件的右边常数项,并且原问题的目标函数中的第i个价值系数就等于对偶问题中的第i个约束条件的右边常数项。
3)原问题的约束条件的右边常数项为对偶问题的目标函数中价值系数。
分枝定界算法应用小结

分枝定界算法应用小结摘要本文首先总结了分枝定界算法的总体内容。
然后,我们列举了6个分枝定界算法应用的实例,它们分别:(1)基于分枝限界法的公交换乘算法设计;(2)分枝定界算法用于有机混合物的分析;(3)求解最大割问题的分枝定界算法;(4)弱有效集上凹函数极大问题的分枝定界算法;(5)分枝定界算法在食品分析中的应用—水果中有机酸的同时定性定量分析;(6)基于分枝定界法的环肋圆柱壳优化研究。
我们得知,分枝定界算法是一种常用算法,属于枚举算法,能够系统地搜索解空间,分枝定界算法的应用非常广泛。
一、分枝定界算法总述分枝定界算法也可以叫做分支限定法。
分枝定界法是一个用途十分广泛的算法,运用这种算法的技巧性很强,不同类型的问题解法也各不相同。
总的来说,“分支限定法求解问题的过程与图的广度优先方法类似。
它是把问题的各个结点的解看作是解空间树上的各个分支结点,求解过程是在解空间树中进行官广度优先搜索的过程。
”[1]分枝定界算法的具体内容如下:“步骤一:如果问题的目标为最小化,则设定目前最优解的值Z=∞。
步骤二:根据分枝法则(Branching rule),从尚未被洞悉(Fathomed)节点(局部解)中选择一个节点,并在此节点的下一阶层中分为几个新的节点。
步骤三:计算每一个新分枝出来的节点的下限值(Lower bound,LB)。
步骤四:对每一节点进行洞悉条件测试,若节点满足以下任意一个条件,则此节点可洞悉而不再被考虑:此节点的下限值大于等于Z值。
已找到在此节点中,具最小下限值的可行解;若此条件成立,则需比较此可行解与Z 值,若前者较小,则需更新Z值,以此为可行解的值。
此节点不可能包含可行解。
步骤五:判断是否仍有尚未被洞悉的节点,如果有,则进行步骤二,如果已无尚未被洞悉的节点,则演算停止,并得到最优解。
”[2]二、分枝定界算法的有关应用分枝定界算法是一种常用算法,属于枚举算法,能够系统地搜索解空间,分枝定界算法的应用非常广泛。
分支定界法
s.t.xr br
x 0, x为整数
1. 分枝定界法基本思想续
❖ 分枝方法示意图
1. 分枝定界法基本思想续
❖ 定界
1. 当前得到的最好整数解的目标函数值
2. 分枝后计算松弛的线性规划的最优解
➢ 整数解且目标值小于原有最好解的值则替代原有 最好解
➢ 整数解且目标值大于原有最好解的值则 删除该分 支其中无最优解
➢ 非整数解且目标值小于原有最好解的值则继续分 支
➢ 非整数解且目标值大于等于原有最好解的值则删 除该分支其中无最优解
2. 分枝定界法计算步骤
2. 分枝定界法计算步骤-例题
❖
例3.3.1
minZ
( x1
x2 )
s.t.44
x1 x1
2x2 2 x2
1 11
2x2 1
x1x2 整数
例x3.(33,5.) 1z 解 4答 0
T0
z z 3x52xz(2,1()1,332.2)5xx((xPP2))(21.25,12) (2Px) (P1 ) (xP(x)P1) 3 x 无解(2,x32) 2无z 解(P )72 5 1 5 13 T T 1 3 115 T 2 3 12 1 6 2 2 T 2 4
1. 分枝定界法基本思想ห้องสมุดไป่ตู้
分枝
最优值比界坏
舍弃
最优解为整数 最优值比界好
最优解为非整 数最优值比界好
分 枝 边界
1. 分枝定界法基本思想续
0
N
I
B1N
cB B1b B 1b
xr br Z
br xr br 1
1. 分支定界法基本思想续
❖ 分枝的方法 min c x
分枝定界法

§ 2 分枝定界法分枝定界法是求解整数规划的常用算法,既可用来解全部变量取值都要求为整数的纯整数规划,又可用以求解混合整数规划。
该算法的基本思路是:先不考虑整数限制,求出相应的线性规划的最优解,若此解不符合整数要求,则去掉不包含整数解的部分可行域,将可行域D分成、两部分(分枝),然后分别求解这两部分可行域对应的线性规划,如果它们的解仍不是整数解,则继续去掉不包含整数解的部分可行域,将可行域或分成与两部分,再求解与对应的线性规划,……,在计算中若已得到一个整数可行解,则以该解的目标函数值作为分枝的界限,如果某一线性规划的目标值Z≤,就没有必要继续分枝,因为分枝(增加约束)的结果所得的最优解只能比更差。
反之若Z>,则该线性规划分枝后,有可能产生比更好的整数解,一旦真的产生了一个更好的整数解,则以这个更好的整数解目标值作为新的界限,继续进行分枝,直至产生不出更好的整数解为止。
下面以实例来说明算法的步骤。
例2 求解下面整数规划解:先不考虑条件⑸,求解相应的线性规划问题L,得最优解=4.81,=1.82,=356(见图)该解不是整数解。
选择其中一个非整数变量,如=4.81,对问题L分别增加约束条件:≤4,≥5 将问题L分解为两个子问题,(分枝),也就是去掉问题L不含整数解的一部分可行域,将原可行域D变为、两部分(如图)因为没有得到整数解,所以继续对L1进行分解,增加约束:≤2,≥3 将分解成问题与,并求得最优解如下:问题的解已是整数解,它的目标值=340,大于问题L4的目标值,所以问题已无必要再分枝。
但由于问题的目标值大于,分解还有可能产生更好的整数解,因此继续对分枝。
增加约束≤1,≥2 将分解成问题与,并求解,结果如下:问题的,所以不必分解了;问题无可行解,于是可以断定问题的解:=4.00,=2.00即为最优整数解。
整个分枝定界过程如下图所示:用分枝定界法求解整数规划的步骤可总结如下:步骤1:求解与整数规划相对应的线性规划L,若L无可行解,则整数规划也没有可行解,计算停;若L的最优解是整数解,则该解即为整数规划的最优解,计算停;若L的最优解不是整数解,则转步骤2。
运筹学 选择题

运筹学选择题1. 线性规划问题的最优解一定在可行域的()上达到。
A. 内点B. 外点C. 顶点D. 边界答案:C解析:线性规划问题的最优解一定在可行域的顶点上达到。
2. 求解线性规划问题时,若最优解不唯一,则()。
A. 存在无穷多个最优解B. 目标函数值无界C. 没有可行解D. 以上都不对答案:A解析:若最优解不唯一,则存在无穷多个最优解。
3. 对于标准型的线性规划问题,其可行域()。
A. 有界B. 无界C. 可能有界也可能无界D. 是凸集答案:D解析:标准型线性规划问题的可行域是凸集。
4. 用单纯形法求解线性规划问题时,判断当前解是否为最优解的依据是()。
A. 检验数B. 基变量C. 非基变量D. 目标函数值答案:A解析:根据检验数来判断当前解是否为最优解。
5. 在对偶问题中,若原问题的约束条件为等式,则对偶变量()。
A. 无约束B. 大于零C. 小于零D. 等于零答案:A解析:若原问题的约束条件为等式,则对偶变量无约束。
6. 原问题与对偶问题都有可行解,则()。
A. 原问题与对偶问题都有最优解B. 原问题有最优解,对偶问题可能没有最优解C. 对偶问题有最优解,原问题可能没有最优解D. 原问题与对偶问题都可能没有最优解答案:A解析:原问题与对偶问题都有可行解时,原问题与对偶问题都有最优解。
7. 运输问题中,若某一非基变量的检验数为零,则该问题()。
A. 无最优解B. 有无穷多最优解C. 有唯一最优解D. 以上都不对答案:B解析:某一非基变量的检验数为零,有无穷多最优解。
8. 求解运输问题时,常用的方法是()。
A. 单纯形法B. 表上作业法C. 匈牙利法D. 以上都不对答案:B解析:求解运输问题常用表上作业法。
9. 动态规划的最优性原理是()。
A. 子问题的最优解可以组合成原问题的最优解B. 原问题的最优解包含子问题的最优解C. 无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略D. 以上都不对答案:C解析:动态规划的最优性原理是无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2分支定界算法
下面通过例子说明分支定界方法的算法思想和步骤。
例4.3 对如下整数规划
12
12121212max 4090975672070.,0,z x x x x x x s t x x x x =++≤⎧⎪⎪+≤⎪⎨≥⎪⎪⎪⎩整数
解:先不考虑整数条件,解相应的线性规划,得最优解:。
该解不符合整数条件。
对其中一个非整数变量解,如,显然,若要满足整数条件,必定有于是,对原问题增加两个新约束条件,将原问题分为两个子问题,即有
1 4.81x =1204.81=1.82356x x z ==,,1154x x ≥≤或
(B )121212112max 4090975672070.4,0z x x x x x x s t x x x =++≤⎧⎪⎪+≤⎪⎨≤⎪⎪≥⎪⎩12
1212112max 4090975672070.5,0
z x x x x x x s t x x x =++≤⎧⎪⎪+≤⎪⎨≥⎪⎪≥⎪⎩(A )问题(A )和(B )的可行域中包含了原整数规划问题的所有整数可行解,而在中不可能存在整数可行解。
145x <<
分别求解这两个线性规划问题,得到的解是:和变量仍不满足整数的条件,对问题(A ),必有,将(A )增加约束条件,得到124, 2.1,349x x z ===125, 1.57,341
x x z ===1212121212max 4090975672070.42,0z x x x x x x s t x x x x =++≤⎧⎪⎪+≤⎪⎪≤⎨⎪≤⎪⎪⎪≥⎩1212121212max 4090975672070.43,0
z x x x x x x s t x x x x =++≤⎧⎪⎪+≤⎪⎪≤⎨⎪≥⎪⎪⎪≥⎩2x 2232x x ≥≤或(A1)(A2)
求解(A1),得到;求解(A2),得到。
由于(A2)的最优值小于(A1)的最优值,原问题的最优值必大于等于340,尽管(A2)的解仍然不满足整数条件,(A2)已无必要继续分解。
124,2,340x x z ===121.42,3,327x x z ===2x 22x x ≥≤2或1125.44,1,308x x z ===对(B ),不满足整数条件,必有
,将这两个约束条件分别加到(B )中,得到(B1)和(B2),求解得到:(B1)的最优解为,(B2)无可行解。
至此,原问题的最优解为:上述求解过程称为分支定界算法.
124,2,340
x x z ===
分支过程。
在B 的最优解中任选一个不符合整数条件的变量
,若其值为,以表示小于的最大整数,构造两个约束条件:。
将这两个约束条件,分别加入问题B ,得到后续规划问题。
不考虑整数条件求解这两个后续问题。
定界过程。
以每个后续问题为一分支标明求解的结果,在其他问题解的结果中,找出最优目标函数值最大者作为新的上界。
从已符合整数条件的各分支中,找出目标函数值最大者作为新的下界,若无可行解,则。
j x j b []j b j b [][]1j j j j x b x b ≤≥+和12B B 和z z 0z =步骤1:分支定界过程
步骤2:
比较与剪支。
各分支的最优目标函数中若有小于者,则剪掉这支,以后不再考虑这个分支。
若大于,且不符合整数条
件,则重复步骤1,直到最后得到为止,得到最优整数解:z z *z z
=*,1,,j x j n =⋅⋅⋅。
