卓越联盟历年自主招生真题及模拟题
卓越联盟自主招生真题卷

卓越联盟—Part 1ClozeRoad politeness is not only good manners, but good sense too. It takes the most cool-headed and good-tempered drivers to ___1___ the temptation to take revenge when subjected to uncivilized behavior. ____2___ the other hand, a little politeness goes a long way towards relieving the ____3____ of motoring. A friendly nod or a wave of _____4____ in response to a ( an) ____5___ of politeness helps to create an atmosphere of goodwill and tolerance so necessary in modern traffic conditions. But such acknowledgements of politeness are all too ____6___ today. Many drivers nowadays don’t even seem able to ___7___ politeness when they see it.However, ____8___ politeness can be dangerous. Typical examples are the drivers who brakes ___9___ to allow a car to ___10____ from a side street to following traffic, when a few seconds later the road would be ____11___anyway; or the man who ___12___ a child across a zebra crossing into the path of oncoming vehicles that may be unable to stop in time. The same ___13___for encouraging old ladies to cross the road wherever and ____14___ they care to.A veteran driver told me it would help if motorists learn to filter correctly into traffic ___15___ one at a time without causing the total blockages that ___16___ rise to bad temper. Years ago the experts warned us that an ____19___ in car-ownership would demand a lot more give-and-take from all road users, It’s high time for all of us to take this message ___20___ heart.1. A. refuse B. resist C. avoid D. combat2. A. In B. At C. To D. On3. A. tension B. anxieties C. worries D. tightness4. A. appreciate B. gratitude C. tribute D. acknowledgement5. A. action B. move C. act D. step6. A. scare B. rare C. infrequent D. sparse7. A. recognize B. understand C. realize D. respect8. A. misgiving B. misleading C. misplaced D. mislaid9. A. violently B. cruelly C. forcefully D. severely10.A. arise B. rise C. submerge D. emerge11.A. obstructed B. clear C. open D. blocked12. A. waves B. sways C. signs D. shakes13. A. functions B. operates C. runs D. goes14. A. when B. while C. whenever D. however15. A. currents B. drifts C. rivers D. streams16. A. give B. take C. develop D. grow17. A. Though B. Unfortunately C. Although D. Spite18. A. delicate B. indirect C. profound D. subtle19. A. explosion B. outbreak C. outburst D. eruption20. A. on B. off C. to D. atReadingWhile awareness and mastery of skills are important steps in any learning process, it is only when conscious skills are put to work that you will experience the involvement and excitement that accompany personal growth. The infant mimicking sounds, the youngster practicing to ride hisbicycle, the teenager learning to drive, the adult preparing to buy a house---all experience a good deal of anticipation, but the anticipation pales next to the excitement of first communicating verbally or riding a bicycle solo or taking that first drive or moving into that first home. In other words, social interaction is the highest degree of personal involvement, the logical peak experience towards what awareness and mastery lead.More than any other experience it is social interaction by which a person defines, expands, and develops his own personality. Therefore, the more involved you are, the more experiences you have, the greater will be the actualization of your personality. If, for example, you are an active person in your community, your personality will express this activity by its positive and outgoing nature. If, on the other hand, you are passive, merely allowing yourself to be acted upon without any involvement in the day-to-day activities of your community, you risk boredom and dullness. Much has been written about the “ mass man” and about the inability of the average citizen to affect his own destiny. Involved persons are not mass men or passive citizens. Involvement in your community means developing your community and yourself by direct and relevant social interaction. Since this interaction could involve you in any and all of the functions of your community, we suggest here that you select for your involvement activities which are most meaningful to you. You might consider your future career plans, hobbies, or educational interests as guides for your decision. For once you begin to be involved in your community and once you experience your own growth in self-awareness through community awareness, you may very well find social interaction a life-time project, regardless of where your community may be or how it may change.1. Which of the following statements is not true according to the first paragraph?A. You can have your personal growth accompanied by involvement and excitement by employing conscious skills in any learning process.B. Involved persons do not anticipate anything.C. Social interaction is the logical peak experience.D. Involvement and excitement come from social interaction.2. Which of the following is characteristic of an active person?A. Being involved in social interaction.B. Risking boredom and dullness.C. Allowing oneself to be acted upon.D. All of the above.3. According to the author, involvement in a community should be____________.A. suggestiveB. decisiveC. comprehensiveD. selective4. Which of the following may be the best title for the passage?A. Self-awarenessB. Community AwarenessC. Social InteractionD. Mass Men5. After the passage, the author would most probably _________________________.A. tell us the difference between active citizens and passive ones.B. define the nature of social interactionC. explain why awareness helps actualize one’s personalityD. help us to be involved in social interactionSentence FillingA. The function of a microblog makes it easier for people to share and influence others’ opinions.B. Instant casualty updates, missing persons notices, charity announcements, microblogs are now the priority channel for sending and acquiring information. Of course, there are also rumors.C. Comparisons between China and Japan have been trending on microblogs of late.D. Still, rumors reached such a heightened point that they triggered a salt panic in China last week.E. When everybody has more freedom of speech, a principle is to tolerate different opinions.F. The disaster rose up to the focus of the whole world by microblogs, becoming the fastest information channel to make sure whether their relatives in Japan are safe or not.The power of microblogs has escalated to new heights in China after the devastating earthquake that has happened in Japan in March.In the days following the disaster, microblogs have transformed from a medium for gossiping and chatting to a swift information channel that outshone traditional media. Four hours after the quake, 4.5 million messages had already been sent in the Sina microblog.1._________________________________________Rumors tend to accompany catastrophes every time, and microblogs are rife for such spreading. From nuclear radiation fallout to malicious fake death news, the number of rumors rose to such level that Sina had to increase its manpower to screen them out.2._________________________________Behind the chaotic scene is the unprecedented freedom of speech the Chinese netizens enjoy on microblogs. Individuals have almost equal opportunity to have their voices heard as with the mainstream media.Sufficient information and thorough debate supposedly should result in more truth surfacing. But this is not always the case.3._____________________________________Disasters response in Japan and the Japanese’ way of surviving such a calamity have given Chinese netizens reasons to look at their domestic situation.4________________________.For the first few days, the opinion of Chinese microblogs was titled in favor of lauding the post-disaster order in Japan and the country’s flexibility in dealing with disasters.Those questioning voices were met with heavy verbal assault and quelled. Mere days later though, more objective facts about Japan’s disaster relief reality appeared on microblogs.The emergence of microblogs is changing how Chinese obtain information, and more importantly, shaping how they perceive the world.5.___________________________________________. Unfortunately this has not yet been widely adopted in China’s microblog community.Summary①In 1985 when a Japan Air Lines(JAL) jet crashed, its president, Yasumoto Takagi, called each victim’s family to apologize, and then promptly resigned. And in 1987, when a subsidiary of Toshiba sold sensitive military technology to the farmer Soviet Union, the chairman of Toshiba gave up his post.②These executive actions, which Toshiba calls “the highest form of apology,”may seem bizarre to US managers. No one at Boeing resigned after the JAL crash, which may have been caused by a faulty Boeing repair.③The difference between the two business cultures centers around different definitions of delegation. While US executives give both responsibility and authority to their employees,Japanese executives delegate only authority--- the responsibility is still theirs. Although the subsidiary that sold the sensitive technology to the Soviets had its own management, the Toshiba top executives said they “must take personal responsibility for not creating an atmosphere throughout the Toshiba group that would make such activity unthinkable, even in an independently run subsidiary.”④Such acceptance of community responsibility is not unique to business in Japan. School principles in Japan have resigned when their students committed major crimes after school hours. Even if they do not quit, Japanese executives will often accept primary responsibility in other ways, such as taking the first pay cut when a company gets into financial trouble. Such personal sacrifices, even if they are largely symbolic, help to create the sense of community and employee loyalty that is crucial to the Japanese way of doing business.⑤Harvard Business School professor George Lodge calls the ritual acceptance of blame “almost a feudal way of purging the community of dishonor,”and to some in the United States, such resignations look cowardly. However, in an era in which both business and governmental leaders seem particularly good at evading responsibility, many US managers would probably welcome an infusion of the Japanese sense of responsibility, if, for instance, US automobile company executives offered to reduce their own salaries before they asked their workers to take pay cuts, negotiations would probably take on a very different character.日本JAL航空公司在发生空难之后,总裁引咎辞职并向每一位受难家属致电道歉。
卓越联盟自主招生试题及答案 缺答案

卓越联盟自主招生试题及答案新一轮卓越联盟自主招生开始了,小编整理卓越联盟自主招生试题及答案供大家分享学习语文英语1.完型填空是乔布斯,这篇完型填空是作者以一名“果粉”的身份,表达了对乔布斯的怀恋,比较抒情。
2.阅读短文三篇第一篇阅读讲小镇居民对树的感情,思想性比较强。
第二篇阅读材料的内容是及“有机食品的研究”,主要讲的是有机食品问题,包括有机食品和常规食品的优缺点比较等第三篇阅读材料与“关于科学发展对教育的影响和作用”。
阅读内容偏向于社会时事。
3.完形填空的文章,谈到现代技术对教育的影响。
4..英语作文题的大意为“回顾过去与展望未来一样重要”。
英语写作内容与“回忆过去,展望未来”有关,并根据自己的理解进行写作,其字数要求120字左右。
数学1.数学6道填空题2.6道大题,涉及平面几何、立体几何、抛物线、等比数列、抛物线,导数等知识点。
化学则都是大题1.一道说明题要求考生比较碳元素和硅元素的差异2.大题为根据铁元素的性质,进行沉淀实验验证。
3.一道辩证推理题.4.最难的一道有机题.物理1.大题涉及到速度与电路问题。
2013年卓越联盟自主招生笔试试题16日上午9点,卓越联盟自主招生笔试结束,以下为考生对自主招生试题的回忆记录,供参考!语文作文题目:小作文,35分400到500字:是否认可煎饼人,煎饼人是指掌握多个领域的技能和知识的人,有人说煎饼人“面面会,面面松”,有人说煎饼人是复合型人才,谈谈对此的观点。
物理实验:力学方面数学题型有数列,平面几何2013年卓越联盟自主招生家长考生心态好上周末,“华约”、“北约”和“卓越”三大自主招生联盟同时进行了笔试,这引起了考生、家长和社会的广泛关注。
本报记者分赴三个联盟考点进行采访,通过与考生的直接交流获悉,今年三大联盟笔试试题争相“瘦身”,同时又各有特色。
“卓越”联盟家长考生心态好看重经历检验实力参加了北京理工大学等9所高校“卓越”联盟自主招生笔试后,考生表示,参考“瘦身”后的自主招生笔试没有太大压力。
“卓越联盟”自主招生模拟卷(7)

2014年自主招生考试数学模拟试卷(七)一、选择题:1.已知2014220140122014(1)x a a x a x a x +=++++,则48122012a a a a ++++= A.20112 B.20122 C.20132 D.201422.若a 为正数,[]a 表示a 的整数部分,{}[]a a a =-,如果,[],{}a a a 按照某种顺序组成等比数列,则a 的值是3.已知(0,2)x π∈且(1|cos |)sin (1|cos |)x x x -=+,则满足条件的所有x 的和是A.2π B.π C.32π D.2π 4.已知数列{}n a 满足1(a m m =为正整数),1231n n n n n a a a a a ++⎧⎪=⎨⎪⎩当为偶数时当为奇数时,若123 29a a a ++=,则m的值为A.3B.4 .C.5D.65.若自椭圆中心到焦点,长轴顶点,以及到准线的距离之长可以组成一个直角三角形,则该椭圆的离心率是6.正四棱锥P ABCD -中,5,6,PA AB M ==是PAD ∆的重心,则四面体MPBC 的体积是A.B.C.D.7.已知()f x 为R 上的单调递增函数,且对任意x R ∈,都有(()3)4x f f x -=,则(2)f 的值是A.8B.9C.10D.118.设函数()sin cos 1f x x x =+,若实数,,a b c 使得()()1af x bf x c +-=对任意x R ∈恒成立,则cos b c a的值是 A.1 B.1- C.0 D.1或1- 9.已知实数,,,a b c d 满足221ab c d =+=,则22()()a c b d -+-的最小值是A.3-B.3+C.3D.3+10.7个花色不同的小球放到编号分别为1,2,3的三个盒子内,要求各盒子内的小球数不小于其编号数,则不同的放法种数为A.105B.140C.210D.455二、解答题:11.锐角三角形ABC 的三条高分别为,,AD BE CF ,求证:DEF ∆的周长不超过ABC ∆的周长的一半.12.数列{}n a 满足22112211,2,1n n n n a a a a a a +++===+. (Ⅰ)求证:11(1,2,3,)n n na a n a +=+= (Ⅱ)求证n a ≤≤(Ⅲ)令1,2,3,)n b n ==判断n b 与1n b +的大小,并说明理由.13.已知(1,0)F 为一定点,(0,)P b 是y 轴上的一动点,点(,0)M a 满足0PM PF ⋅=,若点N 满足 20PN NM +=.(Ⅰ)求点N 的轨迹曲线C 的方程;(Ⅱ)求曲线C 的任何两条互相垂直的切线的交点轨迹.14.在长方体1111ABCD A BC D -中,已知11,2,AD AB AA t ===. (Ⅰ)若对角线1BD 上存在一点P ,使得11PB PC ⊥,求实数t 的取值范围;(Ⅱ)当对角线1BD 上存在唯一一点P ,使得11PB PC ⊥时,求平面11PB C 与平面PBC 所成锐二面角的余弦值.15.已知函数1()2ln(1)1(1)f x x x x =++-+ (Ⅰ)求()f x 在区间[1,)+∞上的最小值;(Ⅱ)求证:2*(1)ln1ln 2ln 3ln (,2)2n n n N n n-++++>∈≥ (Ⅲ)42222*3(1)ln 1ln 2ln 3ln (,2)4n n n N n n-++++>∈≥。
一道“卓越联盟”自主招生试题的赏析与探究

1 ( + 礼一1 一 (2 X  ̄ ) ) 2a l I.
 ̄2 - X2C1 L
— — .
B =
口 2 一 10 l Z l — X2
1一
X2
发展 2 设数列 { 满足0 n) 1= 0 0 , 2= b ,
2 n a +2 = 0 +1+ 0 n n,d = 0 ~ — + 2 n n a b
2 -2= nn+1+ 0n, 0nt - = 2n an +1 +1+ 2ha
n .
求
证: , } {n 为等 比数 列. 发展 4 设数列 _ 满足 n [ 0 1= 0 0 , 2= b ( 0< 6, a + ) 2 n 2= 0 + +a .求证: 2+ n1 札 n札 1<
0 n < n2 2 n一2 .
( 当 ≠ X 时, n: A 一 I 1 2 0 ) 一B 一 ; () l 2寸 0 Ⅱ 当X =X 日j :【+ n一1] _ . ( ) 。 例1 ( 卓越联盟 2 1 年 自主招生数学第 1 01 1 题) 设数列 _n. [ ] 0 满足0 1=0 0 , 2= b 2 2= ,a+
,
( )一 ) 一 ( 一
( 1. 扎≥ )
一
,
H
n
0
且 + 一 。 = n
、l ,
.
 ̄ a2 - al  ̄
。。 一 n =
an+ l - an
、
试题赏析
1 .试题 分 析
n + 一a = ( —a n1 l b )
此类 问题求 解的关键是 由二 阶线性递 推关
系 a+ = /a+ ,札求其通项. n2 ( la ) 本题中连续三
“卓越联盟”自主招生模拟卷(8)

2014年自主招生考试数学模拟试卷(八)一、选择题:1.444sin 10sin 50sin 70++的值是 A.32 B.54 C.76 D.982.在ABC ∆中,点O 为BC 的中点,过点O 的直线分别交直线,AB AC 于不同的两点,M N ,若 ,AB mAM AC nAN ==,则m n +的值是A.2B.3C.32 D.65 3.已知,,0a b c >且39a b c ++=,则23a b c ++的最小值是A.31B.2744.ABC ∆内接于单位圆,三个内角平分线延长后分别交圆于111,,A B C ,则 111cos cos cos 222sin sin sin A B C AA BB CC A B C++=++ A.1 B.2 C.3 D.45.一个球的内接圆锥的最大体积与这个球的体积之比为A.29 B.49 C.427 D.8276.设直线l 与曲线31y x x =++有三个不同的交点,,A B C且||||AB BC ==则直线l 的方程是A.1y x =+B.21y x =+C.1y x =-+D.21y x =-+ 7.从1,2,3,…,20中任取5个不同的数,其中至少有两个是相邻的数的概率为A.232323 B.155323 C.242323D.199323 8.实数,b c 满足221b c +=,且()sin cos f x ax b x c x =++的图象上存在两条互相垂直的切线,则实数a 的取值范围是A.(,0)-∞B.(0,)+∞C.{0}D.[1,1]-9.设M 是椭圆22143x y +=上的动点,点F 和P 的坐标分别是(1,0)和(3,1),则2||||MF MP -的最大值是A.1D.210.设()f x 是定义在(0,)+∞上的单调函数,且对于任意(0,)x ∈+∞都有2[()log ]6f f x x -=,若0x 是方程()'()4f x f x -=的一个根,且*0(1,)()x a a a N ∈-∈,则a 的值为A.1B.2C.3D.4二、解答题:11.在等腰ABC ∆中,,AB AC =设,M N 分别在边,BC AC 上且//MN AB ,记CMN ∆的外心为,D BN 的中点为E ,求证:90AED ∠=.12.已知函数3()(1)1x f x x x +=≠-+设数列{}n a 满足:111,()n n a a f a +==,数列{}n b 满足|n n b a =(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)求证:n b ≤13.已知曲线11:()()2x x C y f x e e -==+,曲线21:()()2x x C y g x e e -==-,直线x a =与曲线12,C C 分别交于,A B ,曲线1C 在点A 处的切线为1l ,曲线2C 在点B 处的切线为2l .(Ⅰ)证明:直线1l 与2l 必相交,且交点到直线AB 的距离为定值; (Ⅱ)设0a <,直线1l 与2l 的交点为P ,若PAB ∆为钝角三角形,求实数a 的取值范围.14.如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD ,边长为1,60BAD ∠=,再在α的上方,分别以ABD ∆与CBD ∆为底面安装上相同的正棱锥P ABD -与 Q CBD -,已知90APB ∠=.(Ⅰ)求二面角P BD Q --的余弦值;(Ⅱ)求点P 到平面QPB 的距离.15.已知椭圆2222:1(0)x y E a b a b+=>>的一个焦点为1(F ,且该椭圆经过点1)2H ,设椭圆的上,下顶点分别为12,A A ,点P 是椭圆上异于12,A A 的任一点,直线12,PA PA 分别交x 轴于点,M N ,若直线OT 与过点,M N 的圆G 相切,切点为T .(Ⅰ)求椭圆E 的方程;(Ⅱ)证明:线段OT 的长为定值,并求出这个定值.。
【2018-2019】卓越联盟自主招生报名系统word版本 (16页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==卓越联盟自主招生报名系统篇一:卓越联盟自主招生试题及答案卓越联盟自主招生试题及答案新一轮卓越联盟自主招生开始了,小编整理卓越联盟自主招生试题及答案供大家分享学习语文1.语文的古文阅读选取的是《左传》中的篇章。
一道现代文阅读,内容是关于“科学研究的范式”,即常规科学赖以运作的理论基础和规范。
文章偏于科学哲学范围,考察逻辑思维和理解能力。
2.小作文要求选取一个汉字来盘点201X年,并做阐述,篇幅不超过150字3.大作文:作题目大意为:在“见、贤、思、齐”这四个字中,任选一个字作为作文的主题,题目不限,文体不限,字数为800字左右。
英语1.完型填空是乔布斯,这篇完型填空是作者以一名“果粉”的身份,表达了对乔布斯的怀恋,比较抒情。
2.阅读短文三篇第一篇阅读讲小镇居民对树的感情,思想性比较强。
第二篇阅读材料的内容是及“有机食品的研究”,主要讲的是有机食品问题,包括有机食品和常规食品的优缺点比较等第三篇阅读材料与“关于科学发展对教育的影响和作用”。
阅读内容偏向于社会时事。
3.完形填空的文章,谈到现代技术对教育的影响。
4..英语作文题的大意为“回顾过去与展望未来一样重要”。
英语写作内容与“回忆过去,展望未来”有关,并根据自己的理解进行写作,其字数要求120字左右。
数学1.数学6道填空题2.6道大题,涉及平面几何、立体几何、抛物线、等比数列、抛物线,导数等知识点。
化学则都是大题1.一道说明题要求考生比较碳元素和硅元素的差异2.大题为根据铁元素的性质,进行沉淀实验验证。
3.一道辩证推理题.4.最难的一道有机题.物理1.大题涉及到速度与电路问题。
201X年卓越联盟自主招生笔试试题201X-03-16 14:07 来源:中国教育在线我要评论 16日上午9点,卓越联盟自主招生笔试结束,以下为考生对自主招生试题的回忆记录,供参考!语文作文题目:小作文,35分400到500字:是否认可煎饼人,煎饼人是指掌握多个领域的技能和知识的人,有人说煎饼人“面面会,面面松”,有人说煎饼人是复合型人才,谈谈对此的观点。
卓越联盟自招考题模拟试题(三)

C.S与 均为定值D.S与 均不为定值
6.记集合 将M中的元素按从大到小的顺序排列,则第2005个数是( )
A. B.
C. D.
7.设p是给定的奇质数,正整数k使得也是一个正整数,则k=;
8.已知数列a0,a1,a2,…,an,…满足关系式(3-an+1)(6+an)=18,且a0=3,则的值是;
A.B.C.D.
3.空间四点A、B、C、D满足 则 的取值()
A.只有一个B.有二个C.有四个D.有无穷多个
4. 内接于单位圆,三个内角A、B、C的平分线延长后分别交此圆于 、 、 。则 的值为()
A.2 B.4 C.6 D.8
5.如图, 为正方体。任作平面 与对角线 垂直,使得 与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为 .则()
自招模拟考题(三)
1.设三位数n=,若以a,b,c为三条边长可以构成一个等腰(含等边)三角形,则这样的三位数n有( )
A.45个B.81个C.165个D.216个
2.顶点为P的圆锥的轴截面是等腰直角三角形,A是底面圆周上的点,B是底面圆内的点,O为底面圆圆心,AB⊥OB,垂足为B,OH⊥PB,垂足为H,且PA=4,C为PA的中点,则当三棱锥O-HPC的体积最大时,OB的长为( )
9.在平面直角坐标系xOy中,给定两点M(-1,2)和N(1,4),点P在x轴上移动,当∠MPN取最大值时,点P的横坐标为;
10.如果自然数 的各位数字之和等于7,那么称 为“吉祥数”.将所有“吉祥数”从小到大排成一列 若 则 __________________.
11.已知,是方程4x2-4tx-1=0(t∈R)的两个不等实根,函数f(x)=的定义域为[,].
清北学长精心打造——卓越联盟自主招生物理模拟试题及参考答案(二)
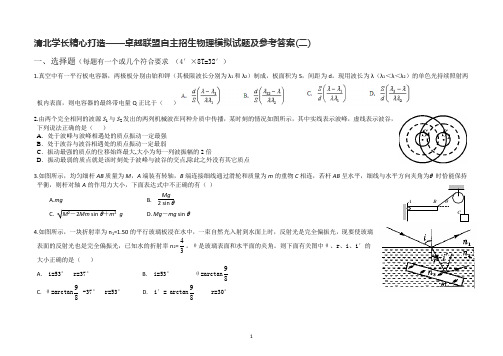
清北学长精心打造——卓越联盟自主招生物理模拟试题及参考答案(二)一、选择题(每题有一个或几个符合要求 (4′×8T=32′)1.真空中有一平行板电容器,两极板分别由铂和钾(其极限波长分别为λ1和λ2)制成,板面积为S ,间距为d 。
现用波长为λ(λ1<λ<λ2)的单色光持续照射两板内表面,则电容器的最终带电量Q 正比于( )2.由两个完全相同的波源S 1与S 2发出的两列机械波在同种介质中传播,某时刻的情况如图所示,其中实线表示波峰,虚线表示波谷,下列说法正确的是( )A .处于波峰与波峰相遇处的质点振动一定最强B .处于波谷与波谷相遇处的质点振动一定最弱C .振动最强的质点的位移始终最大,大小为每一列波振幅的2倍D .振动最弱的质点就是该时刻处于波峰与波谷的交点,除此之外没有其它质点3.如图所示,均匀细杆AB 质量为M ,A 端装有转轴,B 端连接细线通过滑轮和质量为m 的重物C 相连,若杆AB 呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则杆对轴A 的作用力大小,下面表达式中不正确的有( ) A.mgB.Mg2 sin θC.M 2-2Mm sin θ+m 2 gD. Mg -mg sin θ4.如图所示,一块折射率为n 1=1.50的平行玻璃板浸在水中,一束自然光入射到水面上时,反射光是完全偏振光,现要使玻璃表面的反射光也是完全偏振光,已知水的折射率n 2=34。
θ是玻璃表面和水平面的夹角。
则下面有关图中θ、r 、i 、i ′的大小正确的是( )A. i=53° r=37°B. i=53° θ=arctan 89 C. θ=arctan 89 -37° r=53° D. i ′= arctan 89r=30°5.如图所示的电路中,三个电容器完全相同,电源电动势ε1 = 3.0V ,ε2 = 4.5V ,开关K 1和K 2接通前电容器均未带电,则K 1和K 2接通后,有关三个电容器的电压U ao 、U bo 和U co 下列正确的是( )A .Uao=3.5V Ubo= —0.5VB .Uao=3.5V Uco=4.0VC .Ubo=0.5V Uco= —4.0VD .Uao=—3.5V Ubo=0.5V6.潮汐现象主要是由于月球对地球的不同部分施加不同的万有引力而产生的,可以近似认为地球表面均有水覆盖,如果地球与月球的相对位置如图所示,则在图中a 、b 、c 、d 四点中( ) A .a 点处于高潮,c 点处于低潮。
卓越联盟自主招生数学模拟试题及参考答案1

清北学长精心打造——卓越自主招生数学模拟试题及参考答案(一)一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中只有一项是符合题目要求的。
1.已知△ABC 的三边a ,b ,c 成等比数列,a ,b ,c 所对的角依次为A ,B ,C.则sinB+cosB 的取值范围是( ) A .(1,1+]23 B .[21,1+]23 C .(1,]2 D .[21,]2 2.一个口袋里有5个大小一样的小球,其中两个是红色的,两个是白色的,一个是黑色的,依次从中摸出5个小球,相邻两个小球的颜色均不相同的概率是( ) A 1/2 B 2/5 C 3/5 D 4/73.正四棱锥ABCD S -中,侧棱与底面所成的角为α,侧面与底面所成的角为β,侧面等腰三角形的底角为γ,相邻两侧面所成的二面角为θ,则α、β、γ、θ的大小关系( ) (A )θγβα<<<(B )γθβα<<<(C )βγαθ<<<(D )θβγα<<< 4. 已知f (x )=|x +1|+|x +2|+…+|x +2007|+|x -1|+|x -2|+…+|x -2007|(x ∈R ),且f (a 2-3a +2)=f (a -1).则a 的值有( ).(A )2个 (B )3个 (C )4个 (D )无数个5.平面上满足约束条件⎪⎩⎪⎨⎧≤--≤+≥01002y x y x x 的点(x ,y )形成的区域为D ,区域D 关于直线y=2x对称的区域为E ,则区域D 和区域E 中距离最近的两面三刀点的距离为( )A .556 B .5512 C .538 D .53166. 若m 、n ∈{x |x =a 2×102+a 1×10+a 0},其中a i ∈{1,2,3,4,5,6,7},i =0,1,2,并且m +n =636,则实数对(m ,n )表示平面上不同点的个数为( ).(A )60个 (B )70个 (C )90个 (D )120个 7.数列{}n a 定义如下:()1221211,2,2+++===-++n n n na a a a n n 201122012>+m a ,则正整数m 的最小值为( ). A 4025 B 4250 C 3650 D 4425 8. 用红、黄、蓝三种颜色之一去涂途中标号为9,,2,1的9个小正方形(如图),使得任意相邻(有公共边的)小正方形所涂颜色都不相同,且“3、5、7”号数字涂相同的颜色,则符合条件的所有涂法共有( )A 96B 108C 112 D120 9.设a n =2n ,b n =n ,(n=1,2,3,。
清北学长精心打造——卓越联盟自主招生数学模拟试题及参考答案(四)

用3种颜色:C=20种方法.
∴共有230种方法.
6.解:把圆心平移至原点,不影响问题的结果.故问题即求x2+y2=1992的整数解数.
(1)若函数 总存在有两个极值点 ,求 所满足的关系;
(2)若函数 有两个极值点 ,且存在 ,求 在不等式 表示的区域内时实数 的范围.
(3)若函数 恰有一个极值点 ,且存在 ,使 在不等式 表示的区域内,证明: .
3、对每一对实数(x,y),函数f(t)满足f(x+y)=f(x)+f(y)+xy+1。若f(-2)=-2,试求满足f(a)=a的所有整数a.
AG=EG=,BF=DF=,AE=2=2.
由cos∠AGE=cos∠BFD,得=.
∴=9b2=16a2,b=a,从而b=2,2a=3.
AE=2.即最远的两个顶点距离为3.
5.解:至少3种颜色:
6种颜色全用:上面固定用某色,下面可有5种选择,其余4面有(4-1)!=6种方法,共计30种方法;
用5种颜色:上下用同色:6种方法,选4色:C(4-1)!=30;6×30÷2=90种方法;.
2.解:z1满足|z-i|=1;argz1=,得z1=+i,=cos(-)+isin(-).
设z2的辐角为θ(0<θ<π),则z2=2sinθ(cosθ+isinθ).·z2=2sinθ[cos(θ-)+isin(θ-)],若其实部为0,则θ-=,于是θ=.z2=-+i.过的面积即可.
(A)π9(B)π11(C)π12(D)π13
3.存在整数n,使+是整数的质数p( )
(A)不存在(B)只有一个
(C)多于一个,但为有限个(D)有无穷多个
“卓越联盟”自主招生模拟卷

2014年自主招生考试数学模拟试卷(一)一、选择题:1.在ABC ∆中,,,A B C ∠的对边分别是,,a b c ,若22bc b a =-且80B A -=,则内角C 为 A.30B.40C.50D.602.设*111,(1),(1)n n n N x y nn+∈=+=+,则A.y x x y =B.y x x y >C.y x x y <D.yx 与x y 无法比较大小3.在ABC ∆中,,A B 是锐角,且22sin sin sin A B C +=,则 ABC ∆是A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形4.设椭圆与x 轴交于,A B 两点,已知对椭圆上不同于,A B 的任意一点P ,直线AP 与直线BP 的斜率之积为12-,则该椭圆的离心率为C.125.在半径为1的球面上有不共面的四个点,,,A B C D 且,,AB CD x BC DA y CA BD z ======,则222x y z ++等于A.2B.4C.8D.166.如果曲线2sin2xy =的两条互相垂直的切线交于P 点,则P 点坐标不可能是 A.(,)ππ B.(3,)ππ- C.(5,)ππ- D.(7,)ππ-7.如果不等式2|1|x x a <-+的解集是区间(3,3)-的子集,则实数a 的取值范围是 A.(,7)-∞ B.(,7]-∞ C.(,5)-∞ D.(,5]-∞ 8.复数z x yi =+满足||1z ≤,则x y xy +-的最大值是A.1B.2C.3D.49.设20141!(cos)2013nn k k x π==∑,则lim n n x →∞等于A.1952B.1953C.1954D.1955 10.已知定义在(0,)+∞上的函数()f x 为单调函数,且1()(())1f x f f x x⋅+=,则(1)f = A.1三、解答题11.已知在ABC ∆中,AB AC >,A ∠的一个外角平分线交ABC ∆的外接圆于点E ,过E 作EF AB ⊥,垂足为F ,求证:2AF AB AC =-.12.已知数列{}n a ,{}n b 满足:2*111111,1,,[1(2)],1n n n n n n a nb a b b b na n N a n +++==-==-∈+. (Ⅰ)求数列{}n a 和{}n b 的通项公式;(Ⅱ)若不等式12(1)(12)(1)n a a na +++≥*n N ∈恒成立,求实数m 的取值范围.13.在平面直角坐标系中,设,,A B C 是曲线1xy =上三个不同的点,,,D E F 分别是,,BC CA AB 的中点,求证:DEF ∆的外接圆经过原点O .14.设,αβ为实数,n 为正整数,且0,14n πβα≤≤≤>.(Ⅰ)求证:2tan tan 1tan αβαβα-≤-+,并给出等号成立的条件; (Ⅱ)求证:22114nk n kn π=<+∑.15.电脑每秒钟以相同的概率输出一个数字1或2,将输出的前n 个数字之和被3整除的概率记为n P . (Ⅰ)求证:11(1)2n n P P +=-; (Ⅱ)求证:201413P >.2014年自主招生考试数学模拟试卷(二)一、选择题:1.已知复数z 满足||2z z i +=+,则z =A.43i + B.34i + C.43i -+ D.34i -+ 2.如果{1,2,,9} 的某个非空子集中所有元素之和是3的倍数,则称该子集为 “忐忑”子集,那么“忐忑”子集的个数是A.133B.134C.173D.175 3.设,B C 是定点,且都不在平面α上,动点A 在平面α上且1sin 2ABC ∠=,那么A 点的轨迹是 A.椭圆 B.双曲线 C.抛物线 D.椭圆,双曲线,抛物线皆有可能4.sin12sin 48sin54=A.14C.185.设复数(,,z x yi x y R i =+∈是虚数单位)满足12z z ++则yx的最大值是A.5B.5C.5D.5-6.已知O 为ABC ∆的外心,1,2,120AC AB BAC ==∠=,若AO AB AC λμ=+ ,则λμ+=A.136B.138C.56D.437.设数列{}n a满足12121,(3)n n n a a a a n --===-≥,则2014a =A.12C.218.已知ABC ∆是边长为2013的正三角形,点,D E 分别在边,BC CA 上,且3,3BC BD CA CE ==,若AD 与BE 交于,P M 是线段DC 的中点,则PM 长是A.670B.671C.672D.6739.抛物线22(0)y px p =>的焦点为F ,已知点,A B 为抛物线上的两个动点,且满足120AFB ∠= ,过弦AB 的中点M 作抛物线准线的垂线,垂足为N ,则||||MN AB 的最大值是B.210.设[]x 表示不超过x 的最大整数,则2014120142[]2kk k +=+=∑ A.2012 B.2013 C.2014 D.2015二、解答题:11.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若角,,A B C 的大小成等比数列,且22b a ac -=,求B ∠的弧度数.12.定义函数()(1)1,2,(),n n f x x x n N *=+->-∈其导函数记为'()n f x . (Ⅰ)求证:();n f x nx ≥(Ⅱ)数列{}n a 满足'*'11()(1),()(1)n n n n n n f a f n N f a f ++=∈,求证111n n a n -<<+; (Ⅲ)求证:对*242,(1)(1)(1)n n N a a a ∈+++>13.如图,在直三棱柱111ABC A B C -中,190,,2,1BAC AB a AC AA ∠==== ,点D 在棱11B C 上,且113DC B D =. (Ⅰ)求证:1BD AC ⊥;(Ⅱ)当a 为何值时,二面角11B A D B --的大小为60?14.已知函数21()()()2xf x a ex a R =-+∈. (Ⅰ)若函数()f x 在区间(,0)-∞上单调递增,求实数a 的取值范围;(Ⅱ)若在区间(0,)+∞上,函数()f x 的图形恒在曲线2xy ae =的下方,求实数a 的取值范围.15.在椭圆中定义:过焦点且垂直于长轴的直线被椭圆截得的弦叫做椭圆的通径,如图,已知椭圆22221(0)x y a b a b +=>>的左,右焦点分别为12,,F F 其离心率为12,通径长为3,过1F 的直线交椭圆于,A B 两点,12,I I 分别为1212,F BF F AF ∆∆的内心,延长2BF 交椭圆于点M .(Ⅰ)求该椭圆的方程; (Ⅱ)求四边形1221F I F I 与2AF B ∆的面积的比值p ; (Ⅲ)在x 轴上是否存在点C ,使CM CB ⋅为常数,若存在,求出点C的坐标和这个常数,若不存在,请说明理由.2014年自主招生考试数学模拟试卷(三)一、选择题:1.设421111{||78||21|;,,||1}S z z i z z z z C z =--=-+∈=,则S 在复平面内所对应的区域的面积是A.4πB.8πC.16πD.32π2.设双曲线22221(0,0)x y a b a b -=>>的右焦点为F ,过点F 作与x 轴垂直的直线l 交两条渐近线于,A B 两点,P 是l 与双曲线的一个交点,设O 为坐标原点,若有实数,m n 使得OP mOA nOB =+且29mn =,则该双曲线的离心率是A.4B.98 D.23.在ABC ∆中,D 为AC 的中点,3,,AB BD BC ABC ==∆的面积是3,则A ∠的大小是A.6πB.4πC.3πD.2π4.函数y =B. D.35.正三棱锥D ABC -的底面ABC ∆的边长均为6,各侧棱长均为5,点I 是侧面DAB ∆的内心,则四面体I ABC -的体积是6.[]x 表示不超过x 的最大整数,则222[log 1][log 2][log 2014]+++ 的值是A.18084B.18094C.18104D.18114 7.各项均为正数的等比数列{}n a 中,4321228a a a a +--=,则872a a +的最小值为 A.18 B.36 C.54 D.728.设函数:,f R R →满足:(0)1,f =且对任意,x y R ∈都有(1)()()()2f xy f x f y f y x +=--+,则(2014)f 的值是A.2013B.2014C.2015D.2016 9.在ABC ∆中,10,AB AB =边上的高为3,当AC BC ⋅最小时,AC BC +的值是A. B. C. D.10.设两点,C D 在以线段AB 为直径的半圆弧上,线段AC 和线段BD 相交于点,10,8,E AB AC ==BD =则ABE ∆的面积为 A.1507 B.1307 C.1107 D.907二、解答题:11.已知焦点在x 轴上的椭圆222:18x y C b+=内含圆2218:3C x y +=,圆1C 的切线l 与椭圆C 交于,A B 两点,且满足0(OA OB O ⋅=为坐标原点.(Ⅰ)求2b 的值;(Ⅱ)求||AB 的取值范围.12.设递增数列{}n a 满足:*111,451,)n n a a a n n N +==+≥∈. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求证:121112na a a +++< .13. ABC ∆的内切圆I 分别切,BC CA 于点,D E 直线BI 交DE 于点G ,求证:AG BG ⊥.14.如图所示,在矩形ABCD 中,6,AB AD BD ==是对角线,过点A 作AE BD ⊥,垂足为O ,交CD 于点E ,以AE 为折痕将ADE ∆向上折起,使点D 到点P 的位置.(Ⅰ)若平面PAE 与平面ABCE 所形成的二面角P AE B --的大小为120,求四棱锥P ABCE -的体积; (Ⅱ)若PB =求二面角P AB E --的余弦值.15.已知函数2()ln(1)2(1f x x ax x =+++-+其中0)a > (Ⅰ)当1a =时,求()f x 的最小值;(Ⅱ)若[0,2]x ∈时,()0f x ≥恒成立,求实数a 的取值范围;2014年自主招生考试数学模拟试卷(四)一、选择题:1.设12,z z 为一对不相等的共轭复数,且2112||z z z =为实数,则12||z z -的值为C.3D.2.设,x y 满足约束条件122323x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,若224x y a +≥恒成立,则实数a 的最大值是A.1B.4C.52D.453.函数()|1||1|f x x x =++-A.[2B.[2C.[2D.[24.已知O 点在ABC ∆的内部,且324AB BC CA AO ++= ,记ABC ∆的面积为1,S OBC ∆的面积为2S ,则12:S S 的值为A.2B.3C.4D.55.在ABC ∆中,D 是BC 的中点,若0AD AC ⋅=,则tan 2tan A C +的值为A. B.0D.16.若锐角α=,则角α的度数为A.30B.40C.50D.607.将11个完全相同的小球放入6个各不相同的盒子中,使得至多有三个空盒子的放法种数是 A.3112 B.3912 C.4212D.45128.已知12,F F 分别为双曲线22:1927x y C -=的左,右焦点,点A 的坐标为9(2,则12F AF ∠的平分线与x 轴交点M 的坐标为A.(2,0)B.(2,0)-C.(4,0)D.(4,0)-9.在长方体1111ABCDA BC D -中,已知111,AC BC AB p ==,则长方体的体积最大时,p 等于10.方程1sin [[]]222x x x π=-+在区间[0,2]π内的所有实数解的和为A.8B.10C.12D.14 二、解答题:11.如图,四边形ABCD 是圆内接四边形,且,AB CD AD BC E ⋅=⋅是对角线AC 上的一点. (Ⅰ)若E 是AC 的中点,求证:ABE DBC ∠=∠;(Ⅱ)若ABE DBC ∠=∠,试问E 是否为AC 的中点?说明理由.12.已知函数ln(1)()x f x x+=. (Ⅰ)当0x >时,求证:2()2f x x >+;(Ⅱ)当1x >-且0x ≠时,不等式1()1kxf x x+<+恒成立,求实数k 的取值集合.13.如图,已知四棱锥E ABCD -的底面是菱形,且60,2,ABC AB EC AE BE ∠===== (Ⅰ)求证:平面EAB ⊥平面ABCD ; (Ⅱ)求二面角A EC D --的余弦值.14.数列{}n x 中,11x =且121n n n x x x ++=+. (Ⅰ)设n a =,求数列{}n a 的通项公式;(Ⅱ)设|n n b x =,数列{}n b 的前n 项和为n S ,求证:2n S <.15.已知椭圆221,4x y P +=是圆2216x y +=上任意一点,过P 作椭圆的切线,PA PB ,切点分别为,A B ,求PA PB ⋅的最大值和最小值.2014年自主招生考试数学模拟试卷(五)一、选择题:1.设实数1r >,如果复平面上的动点z 满足||z r =,则动点1w z z=+的轨迹是 A.焦距为4的椭圆 B.焦距为2的椭圆 C.焦距为2r 的椭圆 D.焦距为2r的椭圆 2.设P 是函数2(0)y x x x=+>的图象上任意一点,过点P 分别向直线y x =和y 轴作垂线,垂足分别是,A B ,则PA PB ⋅的值是A.2-B.C.D.1-3.设ABC ∆的内角,,A B C 所对的边分别是,,a b c 且满足5cos 5cos 3a B b C c -=,则tan :tan A B 的值是A.2 D.54.设,,[0,1]x y z ∈,则M =1 B.1 C.2 D.25.某情报站有,,,A B C D 四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周末使用的三种密码中等可能地随机选用一种,设第一周使用A 密码,那么第七周也使用A 密码的概率是A.59243 B.61243 C.65243 D.67243 6.半径为R 的球内部装有4个相同半径为r 的小球,则小球半径r 的可能的最大值是R R 7.[表示不超过实数x 的最大整数,则在平面直角坐标系xOy 中,满足2014的所有点(,)x y 组成的图形的面积是A.8B.16C.1007D.20148.若实数,x y 满足1x y xy +=-的值是9.设1616(1)i i i x a x =+=∑,则16ii ia==∑A.142 B.162 C.182 D.20210.已知平面,,αβγ两两垂直,点A α∈,点A 到平面,βγ的距离都是3,P 是平面α上的动点,点P 到平面β的距离是到A 点距离的2倍,则点P 到平面γ的距离的最小值是A.2B.3C.4D.5-二、解答题:11.在锐角ABC ∆中,,BD CE 分别是,AC AB 上的高,以AB 为直径作圆交CE 于点M ,在BD 上取点N ,使AN AM =,求证:AN CN ⊥.12.已知函数()x f x e x =-.(Ⅰ)若函数2()()1g x f x ax =--的导函数'()g x 在[0,)+∞上是增函数,试求实数a 的最大值; (Ⅱ)求证:111()()()234(2)nf f f n n n +++>++ .13.已知m 为非零实数,抛物线2:2(0)C y px p =>的焦点F 在直线2:02m l x my --=上.(Ⅰ)若2m =,求抛物线C 的方程;(Ⅱ)设直线l 与抛物线C 交于,A B 两点,过,A B 分别作抛物线C 的准线的垂线,垂足分别为11,A B ,11,AA F BB F ∆∆的重心分别为,,G H 求证:对任意非零实数m ,抛物线C 的准线与x 轴的交点在以线段GH 为直径的圆外.14.已知数列{}n a 满足;0n a ≥,22*1110,1()n n n a a a a n N ++=+-=∈,记12n n S a a a =+++112121111(1)(1)(1)(1)(1)n n T a a a a a a =+++++++++ 求证:当*n N ∈时, (Ⅰ)1n n a a +< (Ⅱ)2n S n >-(Ⅲ)3n T <15.设ABC ∆的三个角,,A B C 所对的边的长分别为,,a b c ,求证:2()()()3aA B C bB C A cC A B a b c π+++++<++2014年自主招生考试数学模拟试卷(六)一、选择题:1.函数(1y x =的最大值是A.3B.4C.D.22.设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并放入半径为r 的一个实心球,此时,球与容器壁及水面恰好都相切,则取出球后水面高为A.rB.2r3.任作椭圆221259x y +=的一条切线,与椭圆的两条对称轴分别交于,A B 两点,则线段AB 的长度的最小值是A.6B.8C.10D.124.已知数列{}n a 满足1(a m m =为正整数),1231n n n n n a a a a a ++⎧⎪=⎨⎪⎩当为偶数时当为奇数时,若4 7a =,则m 的所有可能的取值的和为A.9B.10 .C.56D.655.设,,a b c 均为非零复数,令12ω=-,若a b c b c a ==,则a b c a b c +--+的值为 A.1 B.ω± C.1或ω或2ω D.1或ω-或2ω-6.函数22|log |,04()2708,433x x f x x x x <≤⎧⎪=⎨-+>⎪⎩,若,,,a b c d 互不相等且()()()()f a f b f c f d ===,则 abcd 的取值范围是A.(32,35)B.(30,35)C.(31,36)D.(32,36)7.方程2(1)sin 10x x π-+=在区间[2,4]-内的所有解之和为 A.4 B.6 C.8 D.108.将各位数字之和为7的正整数按从小到大的顺序排成一个数列,则2014是该数列的第( )项A.64B.65C.66D.679.设[],0()(1),0x x x f x f x x -≤⎧=⎨->⎩,其中[]x 表示不超过x 的最大整数,若方程()0f x kx k --=有三个不同的实数解,则实数k 的取值范围是A.11(,)43B.11(,]43C.11[,)43D.11[,]43 10.设P 为ABC ∆内一点,角,,A B C 的对边分别是,,,a b c S 为ABC ∆的面积,则a PAb PBc PC S ⋅+⋅+⋅的最小值为 A.2 B.3 C.4 D.5二、解答题11.过直线07075:=--y x l 上的点P 作椭圆192522=+y x 的切线PM ,PN ,切点分别为M ,N ,连结.MN(Ⅰ)当点P 在直线l 上运动时,证明:直线MN 恒过定点Q ;(Ⅱ)当MN ∥l 时,定点Q 平分线段.MN12.ABC ∆的内切圆I 分别切,BC CA 于点,D E 直线BI 交DE 于点G ,求证:AG BG ⊥.13.在四面体ABCD 中,,,AB CD AC BD AD BC ===.(Ⅰ)求证:四面体的每个面的三角形都是锐角三角形;(Ⅱ)设三个面与底面BCD 所成的角分别为,,,αβγ求证:cos cos cos 1αβγ++=14.函数2()(1)ln ()f x x b x b R =-+∈.(Ⅰ)若函数在其定义域内是单调递增函数,求实数b 的取值范围;(Ⅱ)设3222,()3467a g x x a x a a >=-+-+,当12b =时,若存在12,[1,2]x x ∈,使得 121|()()|2f xg x -<,求实数a 的取值范围.15.已知函数2()1,,f x x x αβ=+-是方程()0f x =的两个根(),'()f x αβ>是()f x 的导数,设11()1,(1,2,)'()n n n n f a a a a n f a +==-= . (Ⅰ)求,αβ的值; (Ⅱ)证明:对任意的正整数n ,都有n a α>(Ⅲ)记ln(1,2,)n n n a b n a βα-==- ,求数列{}n b 的前n 项和n S .2014年自主招生考试数学模拟试卷(七)一、选择题:1.已知2014220140122014(1)x a a x a x a x +=++++ ,则48122012a a a a ++++=A.20112B.20122C.20132D.201422.若a 为正数,[]a 表示a 的整数部分,{}[]a a a =-,如果,[],{}a a a 按照某种顺序组成等比数列,则a 的值是3.已知(0,2)x π∈且(1|cos |)sin (1|cos |)x x x -=+,则满足条件的所有x 的和是A.2π B.π C.32π D.2π 4.已知数列{}n a 满足1(a m m =为正整数),1231n n n n n a a a a a ++⎧⎪=⎨⎪⎩当为偶数时当为奇数时,若123 29a a a ++=,则m的值为A.3B.4 .C.5D.65.若自椭圆中心到焦点,长轴顶点,以及到准线的距离之长可以组成一个直角三角形,则该椭圆的离心率是B.326.正四棱锥P ABCD -中,5,6,PA AB M ==是PAD ∆的重心,则四面体MPBC 的体积是A.B.C.D.7.已知()f x 为R 上的单调递增函数,且对任意x R ∈,都有(()3)4x f f x -=,则(2)f 的值是A.8B.9C.10D.118.设函数()sin cos 1f x x x =+,若实数,,a b c 使得()()1af x bf x c +-=对任意x R ∈恒成立,则cos b c a的值是 A.1 B.1- C.0 D.1或1- 9.已知实数,,,a b c d 满足221ab c d =+=,则22()()a c b d -+-的最小值是A.3-B.3+C.3D.3+10.7个花色不同的小球放到编号分别为1,2,3的三个盒子内,要求各盒子内的小球数不小于其编号数,则不同的放法种数为A.105B.140C.210D.455二、解答题:11.锐角三角形ABC 的三条高分别为,,AD BE CF ,求证:DEF ∆的周长不超过ABC ∆的周长的一半.12.数列{}n a 满足22112211,2,1n n n n a a a a a a +++===+. (Ⅰ)求证:11(1,2,3,)n n na a n a +=+= (Ⅱ)求证n a ≤≤(Ⅲ)令1,2,3,)n b n == 判断n b 与1n b +的大小,并说明理由.13.已知(1,0)F 为一定点,(0,)P b 是y 轴上的一动点,点(,0)M a 满足0PM PF ⋅= ,若点N 满足 20PN NM += .(Ⅰ)求点N 的轨迹曲线C 的方程;(Ⅱ)求曲线C 的任何两条互相垂直的切线的交点轨迹.14.在长方体1111ABCD A BC D -中,已知11,2,AD AB AA t ===. (Ⅰ)若对角线1BD 上存在一点P ,使得11PB PC ⊥,求实数t 的取值范围;(Ⅱ)当对角线1BD 上存在唯一一点P ,使得11PB PC ⊥时,求平面11PB C 与平面PBC 所成锐二面角的余弦值.15.已知函数1()2ln(1)1(1)f x x x x =++-+ (Ⅰ)求()f x 在区间[1,)+∞上的最小值;(Ⅱ)求证:2*(1)ln1ln 2ln 3ln (,2)2n n n N n n-++++>∈≥ (Ⅲ)42222*3(1)ln 1ln 2ln 3ln (,2)4n n n N n n-++++>∈≥2014年自主招生考试数学模拟试卷(八)一、选择题:1.444sin 10sin 50sin 70++的值是 A.32 B.54 C.76 D.982.在ABC ∆中,点O 为BC 的中点,过点O 的直线分别交直线,AB AC 于不同的两点,M N ,若 ,AB mAM AC nAN == ,则m n +的值是A.2B.3C.32D.653.已知,,0a b c >且39a b c ++=,则23a b c ++的最小值是 A.31 B.274C.24336-D.45- 4.ABC ∆内接于单位圆,三个内角平分线延长后分别交圆于111,,A B C ,则 111cos cos cos 222sin sin sin A B C AA BB CC A B C++=++ A.1 B.2 C.3 D.45.一个球的内接圆锥的最大体积与这个球的体积之比为A.29 B.49 C.427 D.8276.设直线l 与曲线31y x x =++有三个不同的交点,,A B C且||||AB BC ==则直线l 的方程是A.1y x =+B.21y x =+C.1y x =-+D.21y x =-+ 7.从1,2,3,…,20中任取5个不同的数,其中至少有两个是相邻的数的概率为A.232323 B.155323 C.242323D.199323 8.实数,b c 满足221b c +=,且()sin cos f x ax b x c x =++的图象上存在两条互相垂直的切线,则实数a 的取值范围是A.(,0)-∞B.(0,)+∞C.{0}D.[1,1]-9.设M 是椭圆22143x y +=上的动点,点F 和P 的坐标分别是(1,0)和(3,1),则2||||MF MP -的最大值是A.1D.210.设()f x 是定义在(0,)+∞上的单调函数,且对于任意(0,)x ∈+∞都有2[()log ]6f f x x -=,若0x 是方程()'()4f x f x -=的一个根,且*0(1,)()x a a a N ∈-∈,则a 的值为A.1B.2C.3D.4二、解答题:11.在等腰ABC ∆中,,AB AC =设,M N 分别在边,BC AC 上且//MN AB ,记CMN ∆的外心为,D BN 的中点为E ,求证:90AED ∠= .12.已知函数3()(1)1x f x x x +=≠-+设数列{}n a 满足:111,()n n a a f a +==,数列{}n b 满足|n n b a =(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)求证:n b ≤13.已知曲线11:()()2x x C y f x e e -==+,曲线21:()()2x x C y g x e e -==-,直线x a =与曲线12,C C 分别交于,A B ,曲线1C 在点A 处的切线为1l ,曲线2C 在点B 处的切线为2l .(Ⅰ)证明:直线1l 与2l 必相交,且交点到直线AB 的距离为定值; (Ⅱ)设0a <,直线1l 与2l 的交点为P ,若PAB ∆为钝角三角形,求实数a 的取值范围.14.如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD ,边长为1,60BAD ∠=,再在α的上方,分别以ABD ∆与CBD ∆为底面安装上相同的正棱锥P ABD -与 Q CBD -,已知90APB ∠= .(Ⅰ)求二面角P BD Q --的余弦值;(Ⅱ)求点P 到平面QPB 的距离.15.已知椭圆2222:1(0)x y E a b a b+=>>的一个焦点为1(F ,且该椭圆经过点1)2H ,设椭圆的上,下顶点分别为12,A A ,点P 是椭圆上异于12,A A 的任一点,直线12,PA PA 分别交x 轴于点,M N ,若直线OT 与过点,M N 的圆G 相切,切点为T .(Ⅰ)求椭圆E 的方程;(Ⅱ)证明:线段OT 的长为定值,并求出这个定值.。
卓越联盟自主招生数学模拟试题及参考答案(3)

绝密★启用前清北学长精心打造——卓越联盟自主招生数学模拟试题(三)考试范围:xxx ;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(5*6=30分)1.已知函数()()432,,,f x x a x b x c x d a b c d =++++为实常数的图象经过三点12,2A ⎛⎫ ⎪⎝⎭,13,3B ⎛⎫ ⎪⎝⎭,14,4C ⎛⎫ ⎪⎝⎭,则()()15f f +的值等于( ) A .0 B .1C .265D .252.函数f 定义在正整数有序对的集合上,并满足(,),(,)(,),f x x x f x y f y x ==()(,)(,)x y f x y yf x x y +=+,则(14,52)f 的值为( )A .364B .182C .91D .无法计算3.二次函数c bx ax y ++=2的图象的一部分如图,则a 的取 值范围是 ( )A .01<≤-aB .1->aC .01<<-aD .1-≤a4.关于x 、y 的方程20071111=++xy y x 的正整数解(x ,y )的个数为( )A .16B .24C .32D .48第II 卷(非选择题)二、填空题(6*6=36分)5.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x =的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.6. 平面上给定ΔA 1A 2A 3及点p 0,定义A s =A s-3,s ≥4,构造点列p 0,p 1,p 2,…,使得p k+1为绕中心A k+1顺时针旋转1200时p k 所到达的位置,k=0,1,2,…,若p 1986=p 0.则ΔA 1A 2A 3为 三角形。
清北学长精心打造——卓越联盟自主招生数学模拟试题及参考答案(六)

3.从正方体的棱和各个面上的对角线中选出k条,使得其中任意两条线段所在的直线都是异面直线,则k的最大值是_____.
4.设z1,z2都是复数,且|z1|=3,|z2|=5|z1+z2|=7,则arg()3的值是______.
4.解:cos∠OZ1Z3==-.即∠OZ1Z3==120°,
∴arg()=或.
∴arg()3=π.
5.解:anan+1an+2an+3=an+an+1+an+2+an+3,an+1an+2an+3an+4=an+1+an+2+an+3+an+4,
相减,得anan+1an+2(a4-an)=an+4-an,由anan+1an+21,得an+4=an.
6.解:f(20-x)=f[10+(10-x)]=f[10-(10-x)]=f(x)=-f(20+x).
∴f(40+x)=f[20+(20+x)]=-f(20+x)=f(x).∴是周期函数;
∴f(-x)=f(40-x)=f(20+(20-x)=-f(20-(20-x))=-f(x).∴是奇函数.选C.
PD=,QE=,RF=.
当D、E、F在K同侧时2QE=PD+RF,
=+.解之得d=
当D、E、F不全在K同侧时2QE=PD-RF,=-.无实解.
∴l与m距离为.
五
证明:⑴由yfn(x)fn-1(x)===fn+1(x).故证.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6. 高为 8 的圆台内有一个半径为 2 的球 O1,球心 O1 在圆台的轴上,球 O1 与圆台的上底面、侧面都相切,圆台内可再放入一个 半径为 3 的球 O2,使得球 O2 与球 O1、圆台的下底面及侧面都只有一个公共点,除球 O2,圆台内最多还能放入半径为 3 的球的个数 是( ) (A) 1 二.填空题 1 1. 集合{x|-1≤log110<- ,x∈N*}的真子集的个数是 2 x . (B) 2 (C) 3 (D) 4
(A)α3<α2<α1 (B)α1<α3<α2 (C)α3<α1<α2 (D)α2<α3<α1 )
1 5. 如果在区间[1,2]上函数 f(x)=x2+px+q 与 g(x)=x+ 2在同一点取相同的最小值,那么 f(x)在该区间上的最大值是( x 11 3 3 (A) 4+ 2+ 4 2 (C) 13 3 1- 2+ 4 2 53 3 (B) 4- 2+ 4 2 (D)以上答案都不对
(C)
2 等于
(D)
(A)
n 1 n 1
(B)
n n 1
n n 1
n 1 n 1
(3)在正方体 ABCD—A1B1C1D1 中,E 为棱 AA1 的中点,F 是棱 A1B1 上的点,且 A1F:FB1=1:3,则异面直线 EF 与 BC1 所成角的正弦值为
(A)
15 3
(B)
15 5
(C)
2 2 2 2
(C)(x+ 1-y )(y 1-x )=0 (D)(x 1-y )(y+ 1-x )=0 4 3.设四面体四个面的面积分别为 S1,S2,S3,S4,它们的最大值为 S,记λ=( (A)2<λ≤4 (B)3<λ<4 (C)2.5<λ≤4.5
y
1
Si)/S,则λ一定满足( Σ i=1
,Z2
1995
,…,Z20 所对应的不
1995
3. 如果甲的身高数或体重数至少有一项比乙大,则称甲不亚于乙,在 100 个小伙子中,如果某人不亚于其他 99 人,就称他为棒
相约学思,共创美好明天
小伙子,那么,100 个小伙子中的棒小伙子最多可能有( (A)1 个 (B)2 个 (C)50 个 1 2n+1 ) )
相约学思,共创美好明天
2011 卓越联盟自主招生数学
(1)向量 a,b 均为非零向量,(a-2b)⊥a,(b-2a)⊥b,则 a,b 的夹角为 (A)
6
(B)
3
(C)
2 3
2
(D)
5 6
(2)已知 sin2(+)=nsin2,则
tan( ) tan( )
相约学思,共创美好明天
(Ⅰ)设 bn=an+1-an,证明:若 a≠b,则{bn}是等比数列; (Ⅱ)若 lim (a1+a2+…+an)=4,求 a,b 的值.
n
(12)在△ABC 中,AB=2AC,AD 是 A 的角平分线,且 AD=kAC. (Ⅰ)求 k 的取值范围; (Ⅱ)若 S△ABC=1,问 k 为何值时,BC 最短? (13)已知椭圆的两个焦点为 F1(-1,0),F2(1,0),且椭圆与直线 y=x(Ⅰ)求椭圆的方程; (Ⅱ)过 F1 作两条互相垂直的直线 l1,l2,与椭圆分别交于 P,Q 及 M,N,求四边形 PMQN 面积的最大值与最小值. (14)一袋中有 a 个白球和 b 个黑球.从中任取一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一 个白球放到袋中.在重复 n 次这样的操作后,记袋中白球的个数为 Xn. (Ⅰ)求 EX1; (Ⅱ)设 P(Xn=a+k)=pk,求 P(Xn+1=a+k),k=0,1,…,b; (Ⅲ)证明:EXn+1=(1-
3. 存在整数 n,使 p+n+ n是整数的质数 p( (A)不存在 (C)多于一个,但为有限个
(B)只有一个 (D)有无穷多个 )
1 4. 设 x∈(- ,0),以下三个数 α1=cos(sinxπ),α2=sin(cosxπ),α3=cos(x+1)π 的大小关系是( 2
相约学思,共创美好明天
_ π 2. 复平面上,非零复数 z1,z2 在以 i 为圆心,1 为半径的圆上,z1· z2 的实部为零,z1 的辐角主值为 ,则 z2=_______. 6 3. 曲线 C 的极坐标方程是 ρ=1+cosθ,点 A 的极坐标是(2,0),曲线 C 在它所在的平面内绕 A 旋转一周,则它扫过的图形的面积是 _______. 4. 已知将给定的两个全等的正三棱锥的底面粘在一起,恰得到一个所有二面角都相等的六面体,并且该六面体的最短棱的长为 2, 则最远的两顶点间的距离是________. 5. 从给定的六种不同颜色中选用若干种颜色,将一个正方体的六个面染色,每 面恰染一种颜色,每两个具有公共棱的面染成不 同的颜色。则不同的染色方法共有_______种.(注:如果我们对两个相同的正方体染色后,可以通过适当的翻转,使得两个正方体 的上、下、左、右、前、后六个对应面的染色都相同,那么,我们就说这两个正方体的染色方案相同.) 6. 在直角坐标平面,以(199,0)为圆心,199 为半径的圆周上整点(即横、纵坐标皆为整数的点)的个数为________.
A M B N F C G P E H Q D
2013 大学自主招生模拟试题三
一.选择题 1 . 对 于 每 个 自 然 数 n , 抛 物 线 y=(n +n)x (2n+1)x+1 与 x 轴 交 于 An , Bn 两 点 , 以 |AnBn| 表 示 该 两 点 的 距 离 , 则
2 2
|A1B1|+|A2B2|++|A1992B1992|的值是(
6. 设 O 是正三棱锥 P—ABC 底面三角形 ABC 的中心,过 O 的动平面与 PC 交于 S,与 PA,PB 的延长线分别交于 Q,R,则 1 1 1 和式 + + PQ PR PS (A)有最大值而无最小值 (C)既有最大值又有最小值,两者不等 二.填空题 α 1. 设 α,β 为一对共轭复数,若|α-β|=2 3,且 2为实数,则|α|= β 2. 一个球的内接圆锥的最大体积与这个球的体积之比为
2
(B 有最小值而无最大值 (D)是一个与面 QPS 无关的常数
.
. .
3. 用[x]表示不大于实数 x 的最大整数, 方程 lg x-[lgx]-2=0 的实根个数是 y≤3x, x 4. 直角坐标平面上,满足不等式组 y≥3, 的整点个数是 x+y≤100 总数是 三.解答题 . .
3
相约学思,共创美好明天
4
2013 大学自主招生模拟试题一
一.选择题 1. 把圆 x2+(y-1)2=1 与椭圆 9x2+(y+1)2=9 的公共点,用线段连接起来所得到的图形为( (A)线段 (B)不等边三角形 (C)等边三角形 (D)四边形 ) )
1 2. 等比数列{an}的首项 a1=1536,公比 q=- ,用 πn 表示它的前 n 项之积。则 πn(n∈N*)最大的是( 2 (A)π9 (B)π11 (C)π12 (D)π13 )
(D)100 个
4. 已知方程|x-2n|=k x (n∈N*)在区间(2n-1,2n+1]上有两个不相等的实根,则 k 的取值范围是( (A)k>0 1 1 (C ) <k≤ 2n+1 2n+1 (B)0<k≤
(D)以上都不是
5. logsin1cos1,logsin1tan1,logcos1sin1,logcos1tan1 的大小关系是 (A ) (B ) (C) (D) logsin1cos1< logcos1sin1< logsin1tan1< logcos1tan1 logcos1sin1< logcos1tan1< logsin1cos1< logsin1tan1 logsin1tan1< logcos1tan1< logcos1sin1< logsin1cos1 logcos1tan1< logsin1tan1< logsin1cos1< logcos1sin1
5 3
(D)
5 5
(4)i 为虚数单位,设复数 z 满足|z|=1,则
z 2 2z 2 z 1 i
(C)
的最大值为
(A)
2 -1
(B)2-
2
2 +1
(D)2+
2
(5)已知抛物线的顶点在原点,焦点在 x 轴上,△ABC 三个顶点都在抛物线上,且△ABC 的重心为抛物线的焦点,若 BC 边所在直线 的方程为 4x+y-20=0,则抛物线方程为 (A)y =16x
2 (10)设是坐标平面按顺时针方向绕原点做角度为 7
再做,用 表示连续 k 次的变换,则 是(
k
2 3 4
的旋转,表示坐标平面关于 y 轴的镜面反射.用表示变换的复合,先做, ) (D)
2
(A)
4
(B)
5
(C)
2
(11)设数列{an}满足 a1=a,a2=b,2an+2=an+1+an.
3 相切.
1 )EXn+1. ab
(15)(Ⅰ)设 f(x)=xlnx,求 f′(x); (Ⅱ)设 0<a<b,求常数 C,使得
1 b | ln x C | dx 取得最小值; b a a
(Ⅲ)记(Ⅱ)中的最小值为 ma,b,证明:ma,b<ln2.
