变位直齿圆柱齿轮几何尺寸计算
齿轮几 何尺寸计算

பைடு நூலகம்a=m(z1+z2)/2
5 齿数比: u=z2/z1
举例分析:
已知标准直齿圆柱齿轮的齿数为z=40,测得其齿根圆 直径df=75mm。试求: (1)齿距p; (2)全齿高h; (3)分度圆直径d,齿顶圆直径da。 解:df=m(z-2.5) m=df/(z-2.5)=75/(40-2.5)=2mm (1)p=πm=3.14X2=6.28mm (2)h=2.25m=2.25X2=4.5mm (3)d=mz=2X40=80mm da=m(z+2)=2X(40+2)=84mm
新授知识:
三、外啮合标准直齿圆柱齿轮的几何尺寸计算
1、四圆的直径: d =mz da=m(z+2)
df=m(z-2.5) db=dcos20º
2、三高的计算:
ha=m
hf=1.25m h=ha+hf=2.25m
3、三弧的长度:
p=πm
e=s=p/2
4、一对标准直齿圆柱齿轮的中心距: a=d1/2+d2/2
学生练习:
有一对正常齿制的标准直齿圆柱齿轮,测得大 齿轮的齿根圆直径df2=123.75mm,大齿轮的 齿数z2=52,两轮孔中心距a=112.5mm,试 求新配的小齿轮齿数z1。 解:由df=m(z2-2.5)=123.75 → m=2.5mm a=m(z1+z2)/2=112.5 → z1=38
《机
械
胡 尧
基
础》
复习提问:
1、直齿圆柱齿轮:四圆。 2、直齿圆柱齿轮:三高。 3、直齿圆柱齿轮分度圆上的三个弧长。 4、直齿圆柱齿轮的基本参数。
教学内容:
外啮合标准直齿圆柱齿轮的几何尺寸计算
变位齿轮公法线长度公式

齿轮公法线的计算:
公法线长度计算(直齿圆柱齿轮)
1、外啮合齿轮
方法一:利用齿轮制作软件Geartrax2007做出圆柱齿轮图,再作出经过齿数k的两平行公法线,两公法线之间的距离即为公法线长度。
(其中跨测齿数k可从图中直接找出)
方法二:利用公法线长度计算公式:
Wk=mcosα[ (k-0.5) zinvα 2xtanα];其中: α为压力角;X为齿轮变位系数;
K为公法线跨齿数,由下面公式计算:
K= 0.5 ;当压力角α=20
Wk=m[2.9521(k-0.5) 0.014z 0.684x]=m( *)
其中:2.9521(k-0.5) 0.014z;*=0.684x;
方法三:利用公式Wk= m( *)查表;*都可查相关表格。
2、内啮合齿轮
方法同上,特别指出的是:内啮合齿轮的公法线跨测齿数指的是槽齿数,公法线长度的测量亦应相应改变。
注:公法线跨测齿数K对同一变位齿轮可取不同数值,但有一较佳值,可利用齿轮制作软件Geartrax2007做出圆柱齿轮图,从中得出较佳值。
尤其指出的是《机械设计手册》表格中的跨测齿数的选取有些不尽合理,有时在实际中根本无法测出。
8-齿轮传动-2

• 一对渐开线直齿圆柱齿轮啮合时,齿廓曲面的接触线是与
轴平行的直线。
• 啮合情况是沿着整个齿宽突然同时进入啮合和退出啮合,
• 传动平稳性差,冲击和噪声大。
2020/5/3
第八章 齿轮传动
24
① 渐开线直齿圆柱齿轮齿面的形成
k
渐开线形成2
k0
N' k'
k'0
当发生面沿基圆柱作纯滚动时, 若平行于齿轮的轴线的直线kk’在空间 的轨迹为直齿圆柱齿轮的齿面。
2020/5/3
第八章 齿轮传动
28
二、斜齿圆柱齿轮的基本参数和几何尺寸的计算
(一) 基本参数
1. 螺旋角:
• 斜齿圆柱齿轮的各圆柱面上的螺旋角 不同
• 通常指分度圆上的螺旋角,用β表示
2. 齿距和模数
① 斜齿圆柱齿轮有法面和端面之分
• 法面:与分度圆柱螺旋线垂直的平面, 参数mn、n、han*、cn* ,法面参数 为标准值。
▪ 第八节 斜齿圆柱齿轮传动 ▪ 第九节 齿轮传动的失效形式和材料 ▪ 第十节 圆柱齿轮传动的强度计算 ▪ 第十一节 圆锥齿轮传动 ▪ 第十二节 蜗杆传动 ▪ 第十三节 轮系 ▪ 第十四章 齿轮传动精度 ▪ 第十五章 齿轮传动的空间 ▪ 第十六章 齿轮传动链的设计
2020/5/3
第八章 齿轮传动
3
第七节 变位齿轮
2020/5/3
第八章 齿轮传动
5
二、变位齿轮及其特点
2. 与标准齿轮相比,变位齿轮的特点
① 两者截取的渐开线区段不同。各区段渐开线的曲率半径 不同,可利用变位的方法改善齿轮传动质量。
② 标准齿轮分度圆齿厚s=齿槽宽e;正变位齿轮s>e,负变 位齿轮s<e。
圆柱齿轮传动几何尺寸计算公式1

mz cos f
d f 1 153 .75 d f 2 256 .25
De1 163 .75 De2 266 .25 Di1 141 .25 Di2 243 .75
De
Di
De d f 2m fn
Di d f 2m( f n Cn )
ro
t
jn
ro
பைடு நூலகம்
一、直齿圆柱齿轮传动几何尺寸计数公式
名称 代号 公式 例 模数
m Z
m
tf
df z
m5
z1 30 z 2 50
齿数
z
cos
df
m
r0 rf
分度圆 压力角
f
df
De
f
f 20
d f 150
分度圆 直径 齿顶圆 直径 齿根圆 直径 基圆半 径 基节 周节
d f mz
fs
分 度 圆 螺旋角 分 度 圆 直径 齿 顶 圆 直径 齿 根 圆 直径 基 圆 半 径 法 向 基 节 端 面 基 节 法 向 周 节 端 面 周 节 齿顶高
f
df
cos f
zmn df
f 1 f 2 12 4049
d
f
d
f
mz cos
f1 f 2
153 .75 256 .25
d
De
De d f 2m(f n n )
Di d f 2m( f n n Cn )
De1 166 .75 De2 263 .25
Di
Di1 144 .25 Di2 240 .75
ro
(完整版)变位齿轮的计算方法

Wk=Wk*m+0.684xm
式中:Wk*——某齿数齿轮跨测k齿时,模数m=1的公法线长度。
表 2 变位齿轮的yz、xz、Δyz和啮合角α′(α=2ห้องสมุดไป่ตู้°)
α′
(分)
19°
20°
21°
yz
xz
Δyz
yz
xz
Δyz
yz
xz
Δyz
0
1
2
3
4
5
6
7
8
9
-0.00616
606
596
0.00107
118
129
139
150
161
172
183
194
205
0.00001
001
001
001
001
001
001
001
002
002
0.00768
779
790
802
813
825
836
847
859
870
0.00789
801
814
825
837
850
862
874
886
898
0.00022
023
023
024
236
246
257
268
279
290
301
312
0.00216
227
238
249
260
271
282
293
304
315
0.00002
002
002
003
003
直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算

外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1,直齿圆柱齿轮变位系数计算:Case1:a,此处例子仅计算用齿条型刀具加工时的情况(插齿刀加工见相关手册公式):小结:由此可知本例选取的齿数在不变位的情况也不会产生根切现象。
b,根据下图选择大小齿轮的变位系数和x∑。
本例在P6-P7区间取值。
即齿根及齿面承载能力较高区,进行选择。
因大小齿轮的齿数和为18+19=37。
所以本例选择的变位系数和x∑=0.8。
本例我们的两个齿轮在工作时属于减速运动,所以按减速运动的变位系数分配线图,进行2个齿轮的变位系数的选择。
先按(z1+z1)/2=18.5,作为横坐标,做一条垂线(图中蓝色的线),再按x∑/2=0.4,作为纵坐标,做一条水平线(图中橙色的线),接着沿着L线的趋势,穿过上面2条线的交点做一条射线(图中红色的线)最后按大小齿轮的齿数做相应的垂线(图中紫色的线),即得到需要的各自变位系数。
最后我们选择的变位系数即为:小齿轮x1=0.42,大齿轮x2=0.38。
【基本保障其和与之前x ∑一致,即可】。
c,验算变位后的齿顶厚度:注:一般要求齿顶厚Sa≥0.25m;对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式(因为当齿轮变位后,齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。
)。
分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结:计算发现变位后的齿轮齿顶厚满足设计需求。
根据上面确定的变位系数,计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。
变位齿轮几何参数计算

(invα '−invα )
invα '及invα 可根据 a' 、 a 由
表查得
χ ∑ = x1 + x2
χn∑
=
z1 + z2 2 tanα n
(invα 't −invαt )
invα '及invα 可根据 α 't 、α t 查得
χ n ∑ = xn1 + xn2
Δy 或 Δyn
Δy = χ ∑ − y
Δyn = χ n ∑ − yn
按线 图计
算
齿高变动系数 中心距变动系数
Δy 或 Δyn y 或 yn
根据 z∑ 及 χ ∑ 查得 y = χ ∑ − Δy
中心距
α'
α ' = a + ym
注:1.表内公式中的x、xn(xt)本身应带正负号代入;Δy、Δyt永为正号。 2.计算高度变位圆柱齿轮几何尺寸时,公式中的y或yt,Δy或Δyt均为零。
y = z1 + z2 ( cosα −1) 2 cosα '
α ' = a + ym
invat
'=
2(xn1 + xn2 ) z1 + z2
tanα n
+
invα t
yn
=
z1 + z2 2 cos β
( cosαt cosα 't
− 1)
α ' = a + ynmn
Δy 或 Δyn
Δy = χ ∑ − y
名称
代号
已知条件及要求项目
直齿轮
斜齿(人字齿)轮
已 知 z1、z2、m、a' 求 χ ∑ 及 已知 z1、z2、mn (mt )、β、a` 求 χ n ∑
角度变位直齿圆锥齿轮的计算公式

角度变位直齿圆锥齿轮的计算公式袁义刚【摘要】In order to meet the actual production of straight bevel gears and design needs, according to the angular displacement spur gear calculation formula and the equivalent of straight bevel gear derive formulas of the angular displacement gear, and then use computer programming languages VB generated calculation program. Practice has proved that the use of this method to derive the formula is reliable, and the angular displacement design is conducive to improving the quality of gear transmission.%为了满足直齿圆锥齿轮实际生产和设计的需要,根据角度变位直齿圆柱齿轮的计算公式和直齿圆锥齿轮当量齿轮推导出角度变位的计算公式,再利用计算机编程语言VB生成计算程序。
实践证明:运用此方法推导出的计算公式是可靠的,且角度变位设计有利于提高齿轮传动质量。
【期刊名称】《机电工程技术》【年(卷),期】2014(000)001【总页数】4页(P80-83)【关键词】角度变位;直齿锥齿轮;计算公式;当量齿轮【作者】袁义刚【作者单位】广东柳菱宏通实业有限公司,广东梅州 514016【正文语种】中文【中图分类】TH123直齿圆锥齿轮副是用来传递两相交轴之间的运动和动力,其有三种基本变位类型:高度变位、切向变位和角度变位[1]。
渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算

渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算齿轮各部分名称及符号此主题相关图片如下:此主题相关图片如下:此主题相关图片如下:此主题相关图片如下:渐开线标准直齿圆柱齿轮的基本参数及几何尺寸计算1 模数齿轮圆周上轮齿的数目称为齿数,用z表示。
根据齿距的定义知此主题相关图片如下:2 压力角此主题相关图片如下:此主题相关图片如下:3 齿数4 齿顶高系数h a=h a*m (h a*=1)5 顶隙系数c=c*m (c*= h f=(h a*+c*)m全齿高h=h a+h f=(2h a*+c*)m此主题相关图片如下:标准齿轮是指模数、压力角、齿顶高系数和顶隙系数均为标准值,且分度圆上的齿厚等于齿槽宽的齿轮。
表12-2 标准直齿圆柱齿轮的几何尺寸计算公式此主题相关图片如下:4. 内齿轮与齿条图示为一内齿圆柱齿轮,内齿轮的轮齿是分布在空心圆柱体的内表面上。
与外齿轮相比有下列几个不同点:1)内齿轮的齿厚相当于外齿轮的齿槽宽,内齿轮的齿槽宽相当于外齿轮的齿厚。
2)内齿轮的齿顶圆在它的分度圆之内,齿根圆在它的分度圆以外。
图示为一齿条,它可以看作齿轮的一种特殊型式。
与齿轮相比有下列两个主要特点:1)由于齿条的齿廓是直线,所以齿廓上各点的法线是平行的;传动时齿条是直线移动的,故各点的速度大小和方向均相同;齿条齿廓上各点的压力角也都相同,等于齿廓的倾斜角。
2)与分度线相平行的各直线上的齿距都相等。
此主题相关图片如下:渐开线直齿圆柱齿轮的任意圆周上齿厚的计算此主题相关图片如下:5.公法线长度测量齿轮公法线长度是检验齿轮精度常用的方法之一。
它具有测量方便、准确和易于掌握的优点。
测量齿轮公法线长度的原理:公法线长度是指渐开线齿轮上两反向齿廓间的基圆切线长度。
此主题相关图片如下:此主题相关图片如下:此主题相关图片如下:K为跨齿数(证明略)。
变位齿轮的计算方法

变位齿轮的计算方法1 变位齿轮的功用及变位系数变位齿轮具有以下功用:(1)避免根切;(2)提高齿面的接触强度和弯曲强度;(3)提高齿面的抗胶合和耐磨损能力;(4)修复旧齿轮;(5)配凑中心距。
对于齿数z=8~20的直齿圆柱齿轮,当顶圆直径d a=mz+2m+2xm时,不产生根切的最小变位系数x min,以及齿顶厚S a=0。
4m和S a=0时的变位系数x sa=0.4m和x sa=0如表1所列。
2 变位齿轮的简易计算将变位齿轮无侧隙啮合方程式作如下变换:总变位系数中心距变动系数齿顶高变动系数表 1 齿数z=8~20圆柱齿轮的变位系数z x min x sa=0.4m x sa=08 910111213141516171819 200。
53 0.47 0。
42 0.36 0。
30 0.24 0.18 0。
12 0.06 0-0。
05 -0.11 -0。
170.180.220。
270.310.350。
390。
430.460.500。
530.560.590。
620.560.630。
700。
760.820。
880。
930.981。
031。
081.131。
181.23或Δy=xΣ-y式中:α-—压力角,α=20°;α′--啮合角;z2、z1——大、小齿轮的齿数。
将上述三式分别除以,则得:由上述公式可以看出,当齿形角α一定时,x z、y z和Δy z均只为啮合角α′的函数。
在设计计算时,只要已知x z、y z、Δy z和α′四个参数中的任一参数,即可由变位齿轮的x z、y z、Δy z和啮合角α′的数值表(表2)中,查出其他三个参数,再进行下列计算。
一般齿轮手册上均列有此数值表。
式中正号用于外啮合,负号用于内啮合。
3 计算实例例1:已知一对外啮合变位直齿轮,齿数z1=18,z2=32,压力角α=20°,啮合角α′=22°18′,试确定总变位系数xΣ、中心距变动系数y及齿顶高变动系数Δy。
机械设计基础第6章

6.4.2 渐开线齿廓的根切 现象及最小齿数
1. 根切现象 如图6.9所示,用展成法加工齿轮时,若刀具的齿顶 线超过理论啮合线的极限点N1(如图中双点画线 齿条所示),则由基圆以内无渐开线的性质可知, 超过N1的刀刃不仅不能切出渐开线齿廓,而且会 将根部已加工的渐开线切去一部分,如图6.10所 示,这种现象称为根切。根切大大削弱了轮齿的 弯曲强度,降低了齿轮传动的平稳性和重合度, 故应避免。
图6.3 渐开线齿廓的啮合特性
2) 中心距的可分性 由图6.3可知,∆O1N1C∽∆O2N2C,可推得两轮 的传动比为
齿轮加工完成后,基圆大小就确定了,因此渐 开线齿轮啮合,在安装时若中心距略有变化也不 会改变传动比的大小,此特性称为中心距可分性。 该特性使渐开线齿轮对加工、安装的误差及轴承 的磨损不敏感,这一点对齿轮传动十分重要,这 是渐开线齿轮传动的一大优点。
(6) 分度圆:设计齿轮的基准圆,在此圆上具有 标准模数和标准压力角,分度圆上的所有参数不 带下标,如分度圆半径r,齿厚s,齿槽宽e,模数 m等。 (7) 齿宽:沿齿轮轴线方向测得的齿轮宽度,用b 表示。 (8) 齿顶高:分度圆与齿顶圆之间的径向距离, 用ha表示。 (9) 齿根高:分度圆与齿根圆之间的径向距离, 用hf表示。 (10) 全齿高:齿顶圆与齿根圆之间的径向距离, 用h表示,明显地,h=ha+hf。
表6-1标准直齿圆柱齿轮几何尺寸的计算公式
6.3.4 渐开线直齿圆柱齿轮 正确啮合的条件
一对渐开线齿廓能保证传动比恒定,但这并不 表明任意两个渐开线齿轮都能相互配对并正确啮 合传动,如图6.5所示,设相邻两齿同侧齿廓与啮 合线N1N2(同时为啮合点的法线)的交点分别为 K和K′,线段KK′的长度为齿轮的法向齿距,由于 两轮轮齿是沿啮合线啮合的,所以只有当两齿轮 在啮合线上的齿距即它们的法向齿距相等时,才 能保证两齿轮的相邻齿廓正确啮合。 而法向齿距等于两轮基圆上的齿距,因此两轮 正确啮合的条件可表述为pb1=pb2,pb=πmcosα,故 可得 πm1cosα1=πm2cosα2
变位圆柱齿轮跨测齿数的简便计算

变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工 周万峰摘要:本文给出一个简便的跨齿数计算的经验公式,并验证了该公式确定的跨齿数是合理的。
关键词:变位齿轮,跨齿数,公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样,五花八门:有教科书上公式,有各种手册上公式,有参考书上的公式,还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式注:早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出,表1中的几个公式大都比较复杂:平方、开放、三角函数等等项目很多,计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此,笔者通过分析研究,并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角020=α时,经验公式为:z ——齿数,斜齿时z z '用代入(n tinvzz α=',nt inv αα可查手册)。
x ——变位系数,斜齿时代入用n x x 。
p ——与变位系数正负有关的系数。
当变位系数为正()0>x 时p=1.4,当变位系数为负()0<x 时p=1.9。
通过大量的算例验证后得知,当变位系数为负时,由经验公式确定的跨齿数与表1中的公式(4)确定的跨齿数是完全一样的(见表2)。
当变位系数为正时,经验公式与表1中的(2)、(3)、(4)确定的跨齿数绝大多数是相同的,只在极少数情况下两者的跨齿数不同。
但在不同的情况下,经验公式的情况比理论公式的情况还好些(见表3)。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表(020=α)注:表2中的“理论公式”为表1中的公式(4)。
表3 角度变位直齿轮跨齿数计算公式比较)20 5(0==α,m注:表3中的“理论公式”为表1中的公式(4)2、经验公式合理性的验证众所周知,凡计算公法线长度首先应计算跨齿数k ,根据跨齿数k 计算跨k 个齿的公法线长度。
齿轮传动

(3)焊接或加骑缝螺钉固定。在图8-3-20中: 图a为焊接固定。 图b为加骑缝螺钉固定。
4.更换轮缘修复(见图8-3-21): (1)将齿轮轮齿车掉。 (2)按原齿轮外圆和车后直径配制一个新轮缘。 (3)将新制轮缘压入轮坯,并用焊接或铆接方 法将新轮缘固定。在图8-3-21中:图a为焊接 固定。 图b为铆接固定。 (4)在齿轮加工机床上按有关技术要求切制新 齿。 5.对于齿轮机构其他各零件的损坏,可根据实际 情况,分别按零件常用修理方法进行修复即可。
(2)直齿圆柱齿轮各部分名称 1)齿顶圆 2)齿根圆 3)齿厚、 齿槽宽、齿距 4)齿顶高 5)齿根高 6)全齿高
(3)直齿圆柱齿 轮几何尺寸计算
3.渐开线齿轮的正确啮合条件 一对标准直齿圆柱齿轮, 只有当两齿轮的模数和 压力角分别相等时才能 正确啮合,也就是当 m1= m2=m, α1=α2=20°时方能正 确啮合。
(3)对于过盈量较大的齿轮与轴的装 配,应采用温差法装配,即通过加热齿 轮或冷却轴的方法迅速准确地将齿轮装 套在轴上。 4.对以螺栓法兰盘连接的齿轮与轴的 装配,还必须将螺栓拧紧;对固定铆接 连接的齿轮与轴的装配,还必须铆接铆 钉。
5.对于精度要求较高的齿轮与轴的装配,齿轮 装配完后还必须作如下检查: (1)直接观察检查,见图8-3-5: 图a为齿轮 装配后严重 偏心。 图b为齿轮 偏斜。 图c为齿轮 端与轴肩未 贴紧。
三、变位齿轮简介 1.标准齿轮的概念及其局限性 标准齿轮设计、制造都较 方便,因而得到广泛的应 用。但是,在很多机械中, 采用标准齿轮则不能满足 某些特殊要求。 a12=72mm, a13=67.5mm
2.变位齿轮的概念及其特点 (1)变位齿轮——由于改变了刀具与轮坯的相 对位置而切制出的齿轮便称为变位齿轮。 (2)变位齿轮的特点 1)变位齿轮的齿廓曲线和标准齿轮的齿廓曲线 是同一基圆上形成的渐开线,只是部位不同。 2)变位齿轮的一些几何尺寸发生了变化。 3)变位齿轮传动按其中心距变动与否,分为高 度变位齿轮传动和角度变位齿轮传动两种。 高度变位齿轮传动——两齿轮变位系数之和为零。 角度变位齿轮传动——两齿轮变位系数之和不等于 零。
变位内啮合直齿圆柱齿轮传动的计算公式

变位内啮合直齿圆柱齿轮传动的计算公式1. 引言1.1 概述变位内啮合直齿圆柱齿轮传动是一种常见的机械传动方式,广泛应用于各种机械装置中。
在设计和分析变位内啮合直齿圆柱齿轮传动时,需要准确计算相关参数和力学特性,以确保传动系统的可靠性和高效性。
本文旨在介绍变位内啮合直齿圆柱齿轮传动的计算公式,帮助读者理解和应用这些公式。
1.2 文章结构本文主要分为四个部分:引言、变位内啮合直齿圆柱齿轮传动的计算公式、计算公式应用实例以及结论与展望。
下面将对每个部分进行详细说明。
1.3 目的本文的目的是介绍变位内啮合直齿圆柱齿轮传动的计算公式,并通过实际应用案例来说明其具体使用方法。
通过阅读本文,读者可以了解到如何根据给定的齿轮参数来计算接触比力和压力角,并学会分析结果和验证计算公式的准确性。
此外,本文还将展望后续研究方向和拓展,包括其他齿轮传动类型的计算公式研究。
通过本文的阅读,读者可以深入了解变位内啮合直齿圆柱齿轮传动,并在实际应用中灵活运用相关的计算公式。
2. 变位内啮合直齿圆柱齿轮传动的计算公式2.1 齿轮参数定义在变位内啮合直齿圆柱齿轮传动中,我们首先需要定义一些关键的齿轮参数。
这些参数包括:- 齿数:分别表示驱动轮和从动轮上的齿数,分别记为Z1和Z2。
- 模数:表示齿轮的常规参数,记为m。
- 压力角:表示啮合点处切线与轴线间的夹角,记为α。
- 分度圆直径:分别表示驱动轴和从动轴上的分度圆直径,分别记为D1和D2。
2.2 接触比力分析接触比力是变位内啮合直齿圆柱齿轮传动中一个重要的参数。
它可以用来评估传动过程中发生的载荷情况。
接触比力的计算公式如下所示:Ft = (P*D1*cosα)/Z1其中,Ft表示接触比力,P表示传递功率。
2.3 压力角计算方法压力角是变位内啮合直齿圆柱齿轮传动中另一个重要参数。
它影响着齿轮传动的性能和效率。
压力角的计算方法如下所示:cosα= cos(atan(tanα) - (1/m)*((Z2*sin(atan(tan α)))/sqrt(Z1^2-(Z2*cos(atan(tanα)))^2)))其中,cosα表示压力角,tanα表示压力角切线,Z1表示驱动轮的齿数,Z2表示从动轮的齿数。
4种齿轮计算公式

外啮合直齿圆柱齿轮传动几何尺寸计算外啮合斜齿圆柱齿轮传动几何尺寸计算压力角α20.0020.00齿顶高ha 2.00 2.00齿根高hf 2.50 2.50全齿高h 4.50 4.50分度圆直径d320.00160.00齿顶圆直径da324.00164.00齿根圆直径df315.00155.00分度圆齿厚s 6.28 6.28中心距a240.00齿宽计算m n=(da-df)/4.5计算螺旋角cosβ =m n z/(da-2mn)注注:☆蜗杆齿宽:当注:☆最大外圆直注:☆蜗轮齿宽:当注:模数为12,10注注:☆蜗杆螺纹长注:蜗杆在分度圆外啮合直齿锥齿轮传动几何尺齿顶高h a 齿根高hf 分度圆直径d1节圆直径dje1齿顶圆直径da1齿根圆直径df1分度圆螺旋导程角(弧度)γ法向模数m f 轴向齿距Px 分度圆柱螺旋导程P Z螺牙沿分度圆柱上的轴向齿厚S z1螺牙沿分度圆柱上的法向齿厚S f1齿厚测量高度h~齿数Z 2分度圆直径d2齿根圆直径df2齿顶圆直径da2最大外圆直径D2蜗轮宽度b2齿顶圆弧半径R a 齿根圆弧半径Rf注:☆磨削蜗杆需加长:m≤10时,加长25mm;10≤m≤16时,加长35mm;m>16时,加长40-50mm 注:☆蜗杆齿宽:当Z=1~2时取(13~16)m, 当Z=3~4时取(15~21)m注:☆最大外圆直径:当Z=1取≤da2+2m,当Z=2~3取≤da2+1.5m,当Z=4取≤da2+m注:☆蜗轮齿宽:当Z≤3时取≤0.75Ddi1, 当Z=4时取≤0.67Ddi1,包角2θ=45°~130°注:模数为12,10,8,6,5,4,3,2.5,2,1.5,1蜗 轮蜗 杆螺旋长度L☆注:蜗杆特性系数q为14,13,12,11,10,9,8注:☆蜗杆螺纹长度L:当Z=1~2时取大于(11+0.06Z2)m, 当Z=3~4时取大于(12.5+0.09Z2)m 注:蜗杆在分度圆上的轴向齿厚=1.498m,分度圆上的法向齿厚=1.498mcos γ齿齿齿轴向齿距轴向齿形齿齿分h高h 顶高h 根高 3:1a压力角齿根圆弧半d 顶圆直径L切制螺纹部分长度d 根圆直径d 度圆直径21f 1a 1P xa 1f 1(a )蜗杆(b几何尺寸计算mm;m>16时,加长40-50mm+1.5m,当Z=4取≤da2+m67Ddi1,包角2θ=45°~130°时取大于(12.5+0.09Z2)m 向齿厚=1.498mcosγ齿顶圆弧半径R齿根圆弧半径R a 2(b)蜗轮。
齿轮变位系数计算公式
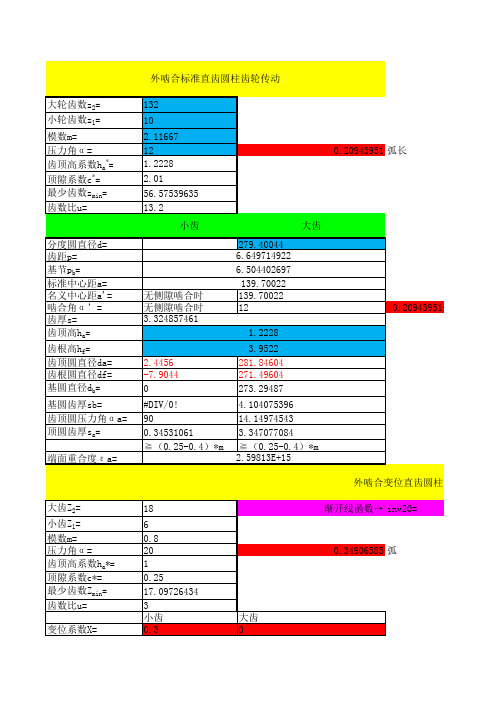
1.743355127
1.622393438
27.87834641
0.295868875
直齿外齿轮
公法线长度
公法线长度的计算 Wk=
标准齿轮 9.70116265
直齿外齿轮 斜齿外齿轮
跨测齿数 公法线长度 跨测齿厚
k= Wkn= k=
5.055555556
直齿外齿轮
公法线长度 跨测齿数
齿顶高hae1= 齿根高hfe1= 全齿高he1= 齿顶圆直径dae1= 分度圆直径de1= 齿根角Øf1= 齿顶角Øa1= 顶锥角δa1= 根锥角δf1= Ak1=
14.212488
齿根圆直径df=
11.14560191
基圆直径db=
12.5630209
法向齿距pn=
端面齿距pt=
5.199545947
法向基圆齿距pbn=
端面基圆齿距pbt=
基圆螺旋角βb=
21.46902352
法向齿厚sn=
2.35619449
端面齿厚st=
2.599772973
端面基圆齿厚sbt= 2.474242055
0.003117051
0.019 要查出,我没查,用时一定要
0.01
查
弧长
αa1
αa2
1.570796327 0.246959646
位直齿圆柱齿轮传动 0.014904
给定x∑求a' 0.320442451
αa1 0.743891086
αa2 0.479274389
inv20= invαa1= invαa2=
变位系数X=
18
6 0.8 20 1 0.25 17.09726434 3 小齿 0.3
变位齿轮齿顶圆齿根圆直径计算公式

变位齿轮齿顶圆齿根圆直径计算公式变位齿轮是一种常见的传动装置,用于传递动力和扭矩。
在设计和制造变位齿轮时,计算齿顶圆直径和齿根圆直径是非常重要的。
本文将介绍如何计算变位齿轮的齿顶圆直径和齿根圆直径的公式和方法。
变位齿轮的齿顶圆直径和齿根圆直径是通过模数来计算的。
模数是变位齿轮齿数与齿轮直径的比值。
齿顶圆直径和齿根圆直径的计算公式如下:齿顶圆直径 = (齿数+ 2) × 模数齿根圆直径 = (齿数+ 2) × 模数 - 2 × 齿高其中,齿数是指变位齿轮的齿数,齿高是变位齿轮齿槽的深度。
通过这两个公式,可以准确地计算出变位齿轮的齿顶圆直径和齿根圆直径。
在实际应用中,计算齿顶圆直径和齿根圆直径前,需要先确定变位齿轮的模数、齿数和齿高。
模数的选择需要考虑到变位齿轮的传动功率、转速和齿轮材料等因素。
齿数的确定通常根据设计要求和装配空间来确定。
齿高的选择需要满足变位齿轮的强度和传动效率要求。
在计算齿顶圆直径和齿根圆直径时,需要注意以下几点。
首先,齿数和齿高的单位必须一致,通常为毫米。
其次,计算结果应保留足够的有效数字,以确保计算的准确性。
最后,齿高的计算需要根据变位齿轮的齿型来确定,常见的齿型有直齿、渐开线齿和圆弧齿等。
通过计算齿顶圆直径和齿根圆直径,可以确定变位齿轮的几何尺寸。
这些尺寸对于变位齿轮的制造、装配和使用非常重要。
在制造过程中,需要根据计算结果来确定齿轮的加工工艺和机床设备。
在装配和使用过程中,需要根据齿顶圆直径和齿根圆直径来确定齿轮的配合间隙和传动效率。
计算变位齿轮的齿顶圆直径和齿根圆直径是非常重要的工作。
通过正确使用相应的公式和方法,可以准确地计算出变位齿轮的几何尺寸。
这对于变位齿轮的设计、制造和使用都具有重要意义。
希望本文能对读者理解和应用变位齿轮的计算公式有所帮助。
变位齿轮

标准齿轮的局限性: a)标准齿轮齿数 Z≥Zmin,否则根切 用范成法切制标准齿轮时,齿轮的齿数必须大于Z(17), 否则会产生根切(采用变位,则能制出小于Z(17)而无根切的 齿轮) b) 实际中心距 a′=标准中心距a 若a′>a,虽能保证定i=常数,但会出现过大C(齿侧间隙), 重合度下降 ,传动不连续。 若a′<a,因较大齿厚不能嵌入较小的齿槽宽中去,标准齿 轮无法安装,会卡死。 c)一对材质相同的标准齿轮啮合,小轮齿根厚度小于大轮齿根 厚度,抗弯能力有差别(Sb1<Sb2),小轮先坏(断) 为了弥补上述不足,出现了变位齿轮。它可以制造Z<17 而无根切的齿轮,可以实现非标准中心距无侧隙传动,可以使 大小齿轮的抗弯能力比较接近
外啮合变位直齿轮基本 尺寸的计算公式见表11.6
m
2
ห้องสมุดไป่ตู้ xmtg
2、变位齿轮传动的类型 根据变位系数之和的不同值,可分为两种类型,见表 11.7,标准齿轮传动可看作是零传动的特例
x1 x 2 0( x1 0, x 2 0)是标准齿轮传动 小齿轮取正 零传动 x1 x 2 0( x1 x 2 )等移距(等变位齿轮传动,且 大齿轮取负 正传动:x1 x 2 0,a ' , ' 负传动:x1 x 2 0,a ' a, '
(2)正传动 这样传动的一对齿轮的变位系数之和大于零,即x1+x2>0 正传动的啮合角大于分度圆压力角、节圆大于分度圆、实 际中心距大于标准中心距
正传动的特点: 可以提高齿轮传动的承载能力; 适当选择x1和x2,可以凑中心距; 必须成对设计、制造和使用 (3)负传动 这样传动的一对齿轮的变位系数之和小于零,即x1+x2<0 负传动的啮合角小于分度圆压力角、节圆小于分度圆、实 际中心距小于标准中心距。 负传动很少采用,仅用于凑中心距 3、变位齿轮传动的设计步骤 根据不同的已知条件,可采用不同的设计步骤,见书上
