定积分的近似计算.ppt

合集下载

高等数学定积分

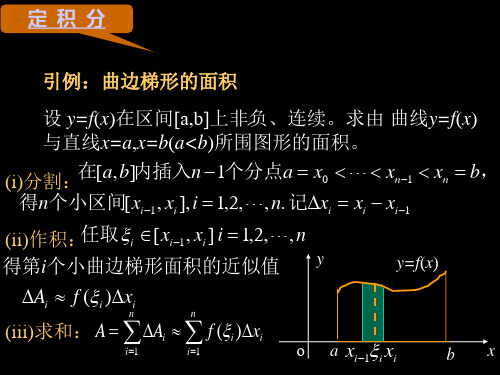
第五章定积分第一节定积分的概念第二节定积分的性质和中值定理第三节微积分基本公式第四节定积分的换元法第五节定积分的分部积分法第六节定积分的近似计算第七节广义积分问题的提出定积分的定义几何意义定积分存在定理第一节定积分的概念abxyo?=A 曲边梯形由连续曲线实例1 （求曲边梯形的面积）)(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围成.一、问题的提出)(x f y =ab xyoab x yo用矩形面积近似取代曲边梯形面积显然，小矩形越多，矩形总面积越接近曲边梯形面积．（四个小矩形）（九个小矩形）观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．观察下列演示过程，注意当分割加细时，矩形面积和与曲边梯形面积的关系．曲边梯形如图所示，,],[1210b x x x x x a b a n n =<<<<<=- 个分点，内插入若干在区间a bxyoi ξi x 1x 1-i x 1-n x ;],[],[11---=∆i i i i i x x x x x n b a 长度为，个小区间分成把区间形面积，曲边梯形面积用小矩上任取一点在每个小区间i i i x x ξ-],[1ii i x f A ∆ξ≈)(:))(],[(1近似为高为底，以i i i f x x ξ-（1）分割（2）近似ini i x f A ∆≈∑=)(1ξ曲边梯形面积的近似值为ini i x f A ∆=∑=→)(lim 10ξλ时，趋近于零即小区间的最大长度当分割无限加细)0(},,max{,21→∆∆∆=λλn x x x 曲边梯形面积为（3）求和（4）取极限实例2 （求变速直线运动的路程）设某物体作直线运动，已知速度)(t v v =是时间间隔],[21T T 上t 的一个连续函数，且0)(≥t v ，求物体在这段时间内所经过的路程.思路：把整段时间分割成若干小段，每小段上速度看作不变，求出各小段的路程再相加，便得到路程的近似值，最后通过对时间的无限细分过程求得路程的精确值．（1）分割212101T t t t t t T n n =<<<<<=- 1--=∆i i i t t t ii i t v s ∆≈∆)(τ部分路程值某时刻的速度（3）求和ii ni t v s ∆≈∑=)(1τ（4）取极限},,,max{21n t t t ∆∆∆= λini i t v s ∆=∑=→)(lim 10τλ路程的精确值（2）近似设函数)(x f 在],[b a 上有界，记},,,max{21n x x x ∆∆∆= λ，如果不论对],[b a 在],[b a 中任意插入若干个分点bx xx x x a nn =<<<<<=-121把区间],[b a 分成n 个小区间，各小区间的长度依次为1--=∆i i i x x x ，),2,1( =i ，在各小区间上任取一点i ξ（i i x ∆∈ξ），作乘积i i x f ∆)(ξ ),2,1( =i 并作和i i ni x f S∆=∑=)(1ξ，二、定积分的定义定义怎样的分法，⎰==ba I dx x f )(ii ni x f ∆∑=→)(lim 10ξλ被积函数被积表达式积分变量积分区间],[b a 也不论在小区间],[1i i x x -上点i ξ怎样的取法，只要当0→λ时，和S 总趋于确定的极限I ，我们称这个极限I 为函数)(x f 在区间],[b a 上的定积分，记为积分上限积分下限积分和几点说明：（1）定积分是一个数值，它仅与被积函数及积分区间有关，⎰b a dx x f )(⎰=b a dt t f )(⎰=ba duu f )(而与积分变量的字母无关.)( ,)()( 2⎰⎰⎰=-=aaabbadx x f dx x f dx x f 规定：）（.],[)(],[)( 3的取法无关的分法及的和式的极限与所表示上可积，则在区间若）（i bab a dx x f b a x f ξ⎰,0)(≥x f ⎰=ba Adx x f )(曲边梯形的面积,0)(≤x f ⎰-=ba Adx x f )(曲边梯形的面积的负值a b xyo)(x f y =AxyoabA -)(x f y =三、定积分的几何意义1A 2A 3A 4A 4321)(A A A A dx x f ba ⎰=-+-,],[)(变号时在区间b a x f 三、定积分的几何意义.)(是面积的代数和⎰badx x f几何意义：积取负号．轴下方的面在轴上方的面积取正号；在数和．之间的各部分面积的代直线的图形及两条轴、函数它是介于x x b x a x x f x ==,)(++--当函数)(x f 在区间],[b a 上连续时，定理1定理2 设函数)(x f 在区间],[b a 上有界，且只有有限个间断点，则)(x f 在四、定积分的存在定理区间],[b a 上可积.例1 利用定义计算定积分.12dx x ⎰解将]1,0[n 等分，分点为nix i =，(n i ,,2,1 =)小区间],[1i i x x -的长度nx i 1=∆，(n i ,,2,1 =)取i i x =ξ，(n i ,,2,1 =)i i n i x f ∆∑=)(1ξi i ni x ∆=∑=21ξ,12i ni ix x ∆=∑=.,102的选取无关及法故和式极限与区间的分可积因为i dx x ξ⎰n n i ni 121⋅⎪⎭⎫ ⎝⎛=∑=∑==n i i n 12316)12)(1(13++⋅=n n n n ,121161⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=n n ∞→⇒→n 0λdx x ⎰102i i ni x ∆=∑=→210lim ξλ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∞→n n n 121161lim .31= 几何上是曲线y=x 2,直线x=1及x 轴围成的曲边三角形面积.例2 利用定义计算定积分.121dx x⎰解在]2,1[中插入分点 12,,,-n q q q ,典型小区间为],[1ii q q -，（n i ,,2,1 =）小区间的长度)1(11-=-=∆--q qq q x i i i i ,取1-=i i qξ，（n i ,,2,1 =）i i ni x f ∆∑=)(1ξi ni ix ∆=∑=11ξ)1(1111-=-=-∑q q q i ni i ∑=-=ni q 1)1()1(-=q n 取2=nq即nq 12=),12(1-=n n )12(lim 1-+∞→xx x x xx 112lim1-=+∞→,2ln =)12(lim 1-∴∞→nn n ,2ln =dx x ⎰211i ni ix ∆=∑=→101lim ξλ)12(lim 1-=∞→n n n .2ln =i i ni x f ∆∑=)(1ξ原式⎥⎦⎤⎢⎣⎡π+π-++π+π=∞→n n n n n n n nsin )1(sin 2sin sin 1lim π=∑=∞→n i n n i n 1sin 1lim n n i ni n π⋅⎪⎭⎫ ⎝⎛ππ=∑=∞→1sin lim 1.sin 10⎰ππ=xdx ix ∆i ξ例3：将下列和式极限表示成定积分.⎥⎦⎤⎢⎣⎡-+++∞→n n n n n n πππ)(sin sin sin lim121 ：五、小结１．定积分的实质：特殊和式的极限．２．定积分的思想和方法：分割化整为零求和积零为整取极限精确值——定积分求近似以直（不变）代曲（变）取极限Z .思考n n n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dxx f e 2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n 证明n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫⎝⎛∞→ 21lim ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21lim ln n n n n f n f n f ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim 试证.1)(ln ⎰=dx x f e 利用对数的性质得⎪⎭⎫⎝⎛∑==∞→n i f n ni n e1ln 1lim n n i f ni n e1ln lim 1⋅⎪⎭⎫ ⎝⎛∑==∞→ 指数上可理解为：)(ln x f 在]1,0[区间上的一个积分和．分割是将]1,0[n 等分分点为nix i =，（n i ,,2,1 =）⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→=n n n n f n f n f e21ln lim 极限运算与对数运算换序得nn i f n i n 1ln lim 1⋅⎪⎭⎫ ⎝⎛∑=∞→⎰=10)(ln dx x f 故nn n n f n f n f ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∞→ 21lim.10)(ln ⎰=dxx f e 因为)(x f 在区间]1,0[上连续，且0)(>x f 所以)(ln x f 在]1,0[上有意义且可积 ,2：将和式极限，表示成定积分.⎥⎦⎤⎢⎣⎡-++-+-∞→2222241241141lim n n n n n ⎰∑-=-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++-+-=⎥⎦⎤⎢⎣⎡-++-+-=∞→∞→∞→1021222222222411)(41lim )(41)2(41)1(411lim 41241141lim dxx n ni n n n n n n n n n n i n n n 解第二节定积分的性质、中值定理1.定积分性质2.中值定理对定积分的补充规定:（1）当b a =时，0)(=⎰ba dx x f ；（2）当b a >时，⎰⎰-=abb adx x f dx x f )()(.说明在下面的性质中，假定定积分都存在，且不考虑积分上下限的大小．一、定积分性质和中值定理证⎰±ba dxx g x f )]()([i i i ni x g f ∆±=∑=→)]()([lim 10ξξλi i ni x f ∆=∑=→)(lim 10ξλii ni x g ∆±∑=→)(lim 10ξλ⎰=ba dx x f )(.)(⎰±ba dx x g ⎰±b a dx x g x f )]()([⎰=b a dx x f )(⎰±ba dx x g )(.（此性质可以推广到有限多个函数作和的情况）性质1⎰⎰=ba b a dx x f k dx x kf )()( (k 为常数).证⎰ba dx x kf )(ii ni x kf ∆=∑=→)(lim 10ξλi i n i x f k ∆=∑=→)(lim 1ξλii ni x f k ∆=∑=→)(lim 10ξλ.)(⎰=ba dx x f k 性质2⎰ba dx x f )(⎰⎰+=bcca dx x f dx x f )()(.补充：不论的相对位置如何, 上式总成立.c b a ,,例若,c b a <<⎰c a dx x f )(⎰⎰+=cb b a dx x f dx x f )()(⎰b a dx x f )(⎰⎰-=cb c a dxx f dx x f )()(.)()(⎰⎰+=bc ca dx x f dx x f （定积分对于积分区间具有可加性）假设bc a <<性质3dx b a ⋅⎰1dx ba⎰=a b -=.则0)(≥⎰dx x f ba. )(b a <证,0)(≥x f ,0)(≥ξ∴i f ),,2,1(n i =,0≥∆i x ,0)(1≥∆ξ∴∑=i i ni x f },,,max{21n x x x ∆∆∆= λi i ni x f ∆∴∑=→)(lim 1ξλ.0)(⎰≥=ba dx x f 性质4性质5如果在区间],[b a 上0)(≥x f ，例1 比较积分值dx e x⎰-20和dx x ⎰-20的大小.解令,)(x e x f x -=]0,2[-∈x ,0)(>x f ,0)(02>-∴⎰-dx x exdx ex⎰-∴2,02dx x ⎰->于是dx e x ⎰-2.20dx x ⎰-<性质5的推论：证),()(x g x f ≤ ,0)()(≥-∴x f x g ,0)]()([≥-∴⎰dx x f x g ba ,0)()(≥-⎰⎰ba ba dx x f dx x g 于是 dx x f ba ⎰)( dx x g ba ⎰≤)(.则dx x f ba ⎰)( dx x g ba ⎰≤)(. )(b a <如果在区间],[b a 上)()(x g x f ≤，（1）dx x f b a ⎰)(dx x f ba⎰≤)(.)(b a <证,)()()(x f x f x f ≤≤- ,)()()(dx x f dx x f dx x f ba ba ba ⎰⎰⎰≤≤-∴即dx x f ba ⎰)(dx x f ba⎰≤)(.说明：可积性是显然的.|)(x f |在区间],[b a 上的性质5的推论：（2）设M 及m 分别是函数证,)(M x f m ≤≤ ,)(⎰⎰⎰≤≤∴ba ba b a Mdx dx x f dx m ).()()(a b M dx x f a b m ba -≤≤-⎰（此性质可用于估计积分值的大致范围）则 )()()(a b M dx x f a b m ba -≤≤-⎰.)(x f 在区间],[b a 上的最大值及最小值，性质6例2 估计积分dx x⎰π+03sin 31值的范围.解,sin 31)(3xx f +=],,0[π∈∀x ,1sin 03≤≤x ,31sin 31413≤+≤x ,31sin 31410030dx dx x dx ⎰⎰⎰πππ≤+≤.3sin 31403π≤+≤π∴⎰πdx x例3 估计积分dx xx⎰ππ24sin 值的范围.解,sin )(xx x f =2sin cos )(x x x x x f -='2)tan (cos x x x x -=⎥⎦⎤⎢⎣⎡∈2,4ππx ,0<)(x f 在]2,4[ππ上单调下降,,22)4(π=π=f M ,2)2(π=π=f m ,442π=π-π=-a b ,422sin 4224π⋅π≤≤π⋅π∴⎰ππdx x x .22sin 2124≤≤∴⎰ππdx x x 如果函数)(x f 在闭区间],[b a 上连续，上的平均值在],[)()(1b a x f dxx f a b ba⎰-则在积分区间],[b a 上至少存在一个点 ξ，使dx x f b a ⎰)())((a b f -=ξ. )(b a ≤≤ξ性质7（定积分中值定理）积分中值公式证Mdx x f a b m ba≤-≤∴⎰)(1)()()(a b M dx x f a b m ba -≤≤-⎰ 由闭区间上连续函数的介值定理知在区间],[b a 上至少存在一个点 ξ,)(1)(⎰-=ξbadx x f a b f dx x f ba ⎰)())((ab f -=ξ.)(b a ≤≤ξ即在区间],[b a 上至少存在一个点ξ，1. 积分中值公式的几何解释：xyoa b ξ)(ξf 使得以区间],[b a 为以曲线)(x f y =底边，为曲边的曲边梯形的面积等于同一底边而高为)(ξf 的一个矩形的面积。

定积分的概念PPT课件

解
将[0,1]n 等分，分点为xi
i ，(i n
1,2,
,n)
小区间[ xi1 , xi ]的长度xi
1 ，(i n
1,2,
,n)
取i xi ，(i 1,2, , n)
n
n
n
f (i )xi i2xi xi2xi ,
i 1
i 1
i 1
n
i 1
i n
பைடு நூலகம்
2
1 n
1 n3
n
i 1
i2
1 n3
xi xi xi1，(i 1,2, )，在各小区间上任取
一点i （i xi ），作乘积 f (i )xi (i 1,2, )
n
并作和S f (i )xi ，
i 1
记 max{ x1 , x2 , , xn }，如果不论对[a, b]
怎样的分法，也不论在小区间[ xi1 , xi ]上
A
lim
0
i 1
f
(i )xi
n
s
lim
0
i 1
v(
i
)ti
(1)分割 (2)近似 (3)求和 (4)取极限
一、定积分的定义
定义设函数 f ( x)在[a, b]上有界，在[a, b]中任意插入
若干个分点 a x x x x x b
0
1
2
n1
n
把区间[a, b]分成n 个小区间，各小区间的长度依次为
Ai f (i )xi
近似
曲边梯形面积的近似值为
n
A f (i )xi
i 1
求和
当分割无限加细,即小区间的最大长度
max{x1, x2 , xn }

高二数学定积分概念.pptx

lim 0
n
ei
i 1
1 n
lim
iY
n n1
1
e lim
ni
en
n i1
n n n i1
1
1
lim
n
1 n
1
(e
n)
1
n
1
en
(1 e) lim n
n
1
1 en
1 en
e 1
第7页/共91页
第二节定积分的性质
定积分的性质
第8页/共91页
规定：(1)当a b时，b f (x)dx 0; a
1
xdx
1ln(1 x)dx.又在[0，1]上，x ln(1 x) 0，
0
0
故
1
xdx
1
ln(1 x)dx.
0
0
例2：估计下列积分值
（1）4 (x2 1)dx；（2）0 ex2xdx.
1
2
第12页/共91页
解： (1)2 x2 1 17，
2 (4 1) 4 (x2 1)dx 17 (4 1) 1
b
n
a
f (x)dx I
lim 0
i 1
f (i )xi
这里f(x)叫做被积函数，f(x)dx叫做被积表达式，x叫做积
分变量，a,b叫做积分下限和上限，[a,b]叫做积分区间。
n
Y
注意:(i) 当和 f (i )xi的极限存在时，其极限I仅与被积函数
i 1
f (x)及积分区间[a,b]有关，而与积分变量的记法无关，即
x f (t)dt也是f (x)的a一个原函数，从而
a
F(x) (x) C.令x a有F(a) C.即F(x) (x) F(a)

定积分的概念ppt课件

2
2
b a
(b
x)( x
a)dx
1
2
(b a )2 2
(b a)2
8
.
17
例1 利用定义计算定积分 1 x2dx. 0
解因为y x2在[0,1]上连续，积分存在.
将[0,1]n 等分，分点为 xi
i ，( i n
0,1,2,
,n
)
小区间[ xi1 ,
xi ]的长度xi
1 ，(i n
b
a
f
(u)du
（2）定义中区间的分法和介点i 的取法是任意的.
（3）当函数 f ( x)在区间[a,b]上的定积分存在时，
称 f ( x)在区间[a, b]上可积. 也称定积分为
Riemann 积分.
11
对定积分的补充规定:
（1）当a
b时， b a
f
(
x)dx
0；
（2）当a
b时， b a
f
( x)dx
1
一、问题的提出
实例1 （求曲边梯形的面积）
y
曲边梯形由连续曲线
y f (x)
y f ( x)( f ( x) 0)、
x轴与两条直线x a 、
x b所围成.
A?
oa
bx
2
用矩形面积近似取代曲边梯形面积
y
y
oa
b xo a
bx
（四个小矩形）
（九个小矩形）
显然，小矩形越多，矩形总面积越接近曲边梯形面积．
0
证明利用对数的性质得
lim n f 1 f 2 f n n n n n
eln lim n n
f
1 n

1-5-3 定积分的概念课件 (人教A版选修2-2)

i －1 ∴f(ξi)＝f(xi－1)＝1＋1＋ n i －1 ＝2＋ n . ∴ f(ξi)Δx＝
i＝1 n n n
i＝1
i－1 1 (2＋ )· n n
＝
i＝1
2 i－1 (n＋ n2 )
2 1 ＝ · n＋ 2[0＋1＋2＋…＋(n－1)] n n 1 nn－1 ＝2＋ 2· n 2 n－1 1 1 ＝2＋＝2＋－ 2n 2 2n 5 1 ＝2－2n. 5 1 5 ∴ (1＋x)dx＝lim (2－2n)＝2. n→∞
解 (1)由y＝图．
4－x2 知，x2＋y2＝4(y≥0)，其图像如下
被积函数的曲线是圆心在原点，半径为2的半圆周，由定积分的几何意义知，此定积分为半圆的面积，所以
2
-2
2 π·2 4－x2dx＝ 2 ＝2π.
π π (2)∵函数y＝sinx在x∈[－， ]是奇函数，由定积分的 2 2
1
0
1 1 2 1－x dx＝ ·π·1 ＝ π. 4 4
2
(2)∵函数y＝sinx＋x3在[－1,1]上为奇函数，
1 3 ∴ (sinx＋x )dx＝0.
-1
技能演练
nLeabharlann 积分下限积分下限积分区间
答案
积分变量
被积式曲边梯形的面积
2.连续恒有f(x)≥0
b 3.(1)k f(x)dx
a
b b (2) f1(x)dx± f2(x)dx
a c a
b (3) f(x)dx
名师讲解
正确理解定积分的概念及其几何意义 (1)定积分是一个数值(极限值)，它的值仅仅取决于被积函数与积分的上、下限，而与积分变量用什么字母表示无

定积分的近似计算之矩形法

知识文库第14期189定积分的近似计算之矩形法李喆一、新课导入上节课我们学习了定积分的定义，由定积分的定义可知，通过求特定和式的极限，可以计算定积分，然而在许多实际应用中，被积函数没有解析表达式，仅仅是一组离散采样值，这时只能利用近似方法计算定积分的近似值，计算定积分的近似值方法非常多，本节课学习其中最基础的一种方法，矩形法。

二、引例首先看一个具体的例子，汽车做直线运动，用84s 的时间从起点到终点，每隔6s 用雷达测速仪测速度(见下表)，求起点到终点的距离。

it iv分析：汽车从起点到终点的运动过程分为14个小时间段，每个时间段都是6s, 总距离为这14个小时间段所走过的距离之和。

在每个小时间段，汽车做变速直线运动，仅知道左端点和右端点的瞬时速度，方案一：用每个时间段左端点的速度近似这个小时间段的平均速度，左端点速度乘以小时间段的长度近似代替该小时间段汽车所走过的距离，求和累加，从而得到总距离的近似值。

方案二：用每个小时间段右端点的速度近似这个小时间段的平均速度，右端点速度*小时间段的长度，近似代替该小时间段汽车所走过的距离，求和累加，得到总距离的近似值。

借助于这种方法，来解决连续量的定积分的近似计算问题。

三、知识点回顾回顾定积分的定义，由定积分的定义给出定积分的近似计算公式，1()()nbi i ai f x dx f x ξ=≈∆∑⎰问题[a, b]如何划分，i ξ如何选取？四、讲授新课1、左矩形法和右矩形法通常将区间[a, b]n 等分， h 为每个小区间的长度，取1i i x ξ-= ，得出定积分近似计算的左矩形法11()()nbi ai f x dx h f x -=≈∑⎰。

取i i x ξ= ，得出定积分近似计算的左矩形法1()()nbi ai f x dx h f x =≈∑⎰。

几何上，左矩形法和右矩形法是分别用这样的红色小矩形的面积近似代替第i 个小曲边梯形的面积，整体上用台阶形的面积作为曲边梯形面积的近似值。

第32讲定积分的分部积分法与近似计算

2 所以： x f " x dx x f ' x f ' x 2 xdx 0 0
1 2
1
又 f x dx e C ，所以 f x e
x2
' 2 xe
x2
x2
，
再令 u1 x, v1 ' f ' x
2 0

2
I 1 2 sin xdx 1
0

续当 n 2k 1 时，
n 1 n 3 4 2 In I1 n n2 5 3 n 1 n 3 4 2 n n2 5 3
当n 2k 时， n 1 n 3 3 1 In I0 n n2 4 2
n 1 n 3 3 1 n n2 4 2 2
令x

2
t 可得第二式显然也成立。
e 例4 设 f x 的一个原函数是
2
x2
，求 x 2 f " x dx
0
1
解令 u x , v' f " x ，则 u ' 2 x, v f ' x
其误差分别为：
b a 2
2n
y ' ,
b a 3
12n 2
y" ,
b a 5
180n 4
y 4
a b
小结：

全面理解分部积分公式
熟练使用分部积分公式求积分
了解定积分的近似计算方法
作业：第P306Fra bibliotek习题5-5
4e 2e 2e

定积分的近似计算方法

定积分的近似计算方法定积分是微积分中的重要概念，它代表了曲线与坐标轴之间的有限面积。

在实际问题中，有时候我们需要计算一些函数在一定范围内的定积分，以获得其中一种物理量或求解其中一种问题的解析解。

然而，有些函数的原函数较复杂甚至难以找到，这时候我们就需要使用定积分的近似计算方法。

下面将介绍几种常用的定积分近似计算方法：1.矩形法：矩形法是最简单的一种近似计算方法。

它的思想是将积分区间等分成若干个小区间，然后在每个小区间上选择一个代表点，通过函数在这些代表点处的函数值与小区间长度的乘积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₁) + f(x₂) + ... + f(xₙ))其中，Δx=(b-a)/n，n为小区间个数，x₁、x₂等为代表点。

当n越大时，近似结果越接近真实结果。

2.梯形法：梯形法是将积分区间分成若干个小区间，然后在每个小区间上构造一个梯形，通过计算梯形的面积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₁) + f(x₂))/2 + Δx * (f(x₂) +f(x₃))/2 + ... + Δx * (f(xₙ-1) + f(xₙ))/2其中，Δx=(b-a)/n，n为小区间个数，x₁、x₂等为小区间的端点。

3.辛普森法：辛普森法是一种比矩形法和梯形法更精确的近似计算方法。

它的思想是将积分区间分成若干个小区间，然后在每个小区间上构造一个二次多项式，通过计算这些二次多项式的面积来近似计算定积分。

具体计算公式为：∫[a,b]f(x)dx ≈ Δx * (f(x₀)+4f(x₁)+f(x₂))/3 + Δx *(f(x₂)+4f(x₃)+f(x₄))/3 + ... + Δx * (f(xₙ-2)+4f(xₙ-1)+f(xₙ))/3其中，Δx=(b-a)/n，n为小区间个数，x₀、x₁、x₂等为小区间的端点。

4.蒙特卡洛法：蒙特卡洛法是通过随机抽取点的方法来近似计算定积分。

定积分近似计算方法

定积分的近似计算方法摘要本文主要讨论了一元函数常见的数值积分方法,例如插值型求积公式、龙贝格求积公式、高斯求积公式等近似计算方法,在用这些方法计算定积分时,会产生一些误差,为了减少误差, 可以利用复化求积公式、复化高斯公式等.本文围绕这些方法,系统介绍它们的计算公式以及截断误差,并用例题分析它们产生误差的大小、计算量等.关键词插值型积分龙贝格积分高斯积分误差分析近似计算1引言在计算定积分的值()b aI f x dx =⎰时,常常根据微积分学基本定理求出)(x f 的一个原函数)(x F ,再用牛顿-莱布尼茨公式求的积分,()()()baI f x dx F b F a ==-⎰.但在实际应用中,这种方法只限于解决一小部分定积分的求值问题.当函数没有具体表达式,只是一些实验测得数据形成的表格或图形或者是()F x 无法用初等函数表示,例如,2bx ae dx ⎰,2sin ba x dx ⎰等等,这就需要我们用一些近似方法求的积分值.与数值积分一样,把积分区间细分,在每个小区间上,找到简单函数)(x ϕ来近似代替()f x ,且()bax dx ϕ⎰的值容易求的.这样就把计算复杂的()baf x dx ⎰转化为求简单的积分值()bax dx ϕ⎰.因此,定积分的近似计算实质上是就是被积函数的近似计算问题.2常见数值方法 2.1牛顿-科茨数值方法牛顿-科茨求积公式是求积节点等距离分布的插值型求积公式.利用插值多项式来构造数值积分公式是最常用、最基本的方法,具体做法是：给定区间[,]a b 上一组节点01...n a x x x b =<<<=,以及节点处函数()(0,1,2,i f x i n =,作()f x 的n 次拉格朗日多项式()()()nn i i i x f x l x ϕ==∑,其中 011011()()()()()()()()()i i n i i i i i i i n x x L x x x x L x x l x x x L x x x x L x x -+-+----=----,将插值公式(1)1()()()()(1)!n n n f f x x x n ξϕω++=++. 其中 1012()()()()()n n x xx x xx x L x x ω+=----,[,]a b ξ∈,依赖于变量x , 上式积分得(1)1()()()()(1)!n bb bn n aa af f x dx x dx x dx n ξϕω++=++⎰⎰⎰(1)(1)0()()()()(1)!n nb biiin aai f f x l x dx x dx n ξω++==++∑⎰⎰(1)(1)0()()()()(1)!n nb bi i n aai f f x b l x dx x dxn ξω++==++∑⎰⎰若记 (),(0,1,2,bi ia A l x dx i ==⎰….. )n (1)(1)1()[]()(1)!n bn af R f x dxn ξω++=+⎰, (2)则有()()[]nbi i ai f x dx A f x R f ==+∑⎰(3)称式(3)为插值求型公式,其中(0,1,2,i A i =…. )n 与()f x 无关,叫求积系数, i x 为求积节点,[]R f 为求积公式余项,其中求积系数由(1)决定.2.1.1梯形求积公式1梯形公式当插值节点01,x x 分别选取区间端点,a b 时,由式(3)分别求出求积系数10012bb aa x x xb b aA dx dx x x a b ---===--⎰⎰,01102bb aa x x x ab a A dx dx x x b a ---===--⎰⎰.从而的求积公式()[()()]2bab af x dx f a f b -≈+⎰. (4) 称求积公式(4)为梯形求积公式,简称梯形公式.2梯形公式截断误差: 3*()[](),12b a R f f ξ-''=- *[,]a b ξ∈. (5) 3梯形求积公式的代数精度:1 当()1f x =时,式(5)中 1(1)2bab adx b a x b a -=-=+=-⎰. 精确成立.2.1.2 辛普森求积公式1辛普森求积公式当选取节点为012,,2a bx a x x b +===时,由式(1)求下列求积系数 1200102()()()()2()()6()()2b b a a a b x x b x x x x b a A dx dx a b x x x x a a b +-----===+----⎰⎰,0211002()()()()2()()()3()()22bb aa x x x x x a xb b a A dx dx a b a b x x x x a b -----===++----⎰⎰.0122021()()()()2()()6()()22b b a a a bx a x x x x x b a A dx dx a b a b x x x x a b +-----===++----⎰⎰ .从而求积公式()[()4()()]62bab a a bf x dx f a f f b -+≈++⎰. （6）称式(6)为抛物线积分公式或辛普森积分公式.2抛物线求积公式误差估计定理1.若()f x 在[,]a b 上有四阶连续导数,则抛物线公式(6)的余项为:5(4)**()[](),[,]2880b a R f f a b ξξ--=∈. (7) 3抛物线公式的代数精度为3.易验证,当23()1,,,f x x x x =时,式(6)精确成立,而当4()f x x =时,式(6)不能精确成立.2.1.3 牛顿-科茨公式1牛顿-科茨公式在等距离节点i x a ih =+下,其中(0,1,2b ah i n-==…. )n .作为变量替换x a th =+,那么由求积公式(1),得系数:10(1)(1)(1)()!(1)(1)!ni n t t t i t i t n A h dt i n ---+---==--⎰10(1)(1)...(1)(1)...()(0,1,2,...)!(1)!n nb a t t t i t i t n dt i n n i n -----+---=-⎰ (8)则 ()()n i iA b a C =- (9)于是差值求积公式为:()0()()()[]nbn i i ai f x dx b a C f x R f ==-+∑⎰(10)称公式(10)为牛顿-科茨求积公式,其中()n iC 称为科茨系数.显然,科茨系数与被积函数()f x 及积分区间[,]a b 无关,它指依赖于n ,且为多项式积分.因此,只要给出n ,就能看出i A ,并写出相应地牛顿-科茨公式.2牛顿-科茨公式的截断误差与代数精度.当1n =与2n =情况分析牛顿-科茨公式的截断误差为(1)()[]()()()(1)!n b b bn aaaf R f f x dx x dx x dxn ξϕω+=-=+⎰⎰⎰牛顿-科茨公式的截断误差还可以写成(2)*1()[]()((2)!n bn a f R f x dx n n ξω++=+⎰为偶数）(1)*1()[]()(1)!n bn af R f x dx n ξω++=+⎰ (n 为奇数） (11) 其中*[,]a b ξ∈,且不依赖于x ,101()()()...()n n x x x x x x x ω+=---,对()f x 为任何并不超过n 次多项式,均有(1)()0n fx +≡,因而[]0R f ≡,即0()()nbi i ai f x dx A f x ==∑⎰精确成立,也就是说,牛顿-科茨公式的代数精度至少为n ,牛顿-科茨公式在n 为偶数时,至少具有1n +次代数精度,在n 为奇数情况时,至少具有n 次代数精度.2.1.4复化梯形求积公式将区间[,]a b 等分,节点为i x a ih =+ (步长b ah n-=),0,1,2...,i n =)在每个小区间1[,]i i x x -上采用梯形公式(4)得11111()()[(()()]2ii nnbx i i i i ax i i x x f x dx f x dx f x f x ---==-=≈+=∑∑⎰⎰11[()()]2ni i i hf x f x +=+=∑11[()2()()]2n i n i hf a f x f b T -=++=∑ (12)称式(12)为复化梯形公式. 复化梯形公式余项为()2()()()12i n b a R f h f η-''=-(13) 2.1.5复化辛普森求积公式在每个小区间],[1+i i x x 上,辛普森公式(6)得11102()[()4()()]6n bi i ai i hf x dx f x f x f x -++==++∑⎰（14）111012[()4()2((6)]6n n i i i i hf a f x f x f --+===+++∑∑记 )]()(2)(4)([6111021b f x f x f a f hS n i i n i i n +++=∑∑-=-=+ (15)式中,21+i x为],[1+i i x x 的中点,即h x x i i 2121+=+.式(15)称为复化辛普森公式,其余项为∑-=-=-=10)4(4)()2(180)()(n i i n n f h h S f I f R η, 1(,).i i i x x η+∈ 故 ),(),()2(180)(R )4(4b a f h a b f n ∈--=ηη (16) 为复化辛普森的截断误差. 2.1.6复化科茨求积公式将区间[,]a b n 等分, 4n m =,m 为正整数,在每个子区间444[,]k k x x -上用科茨求积公式得到复化求积公式:412()[7()7()32()45mbk ak hf x dx f a f b f x -≈++∑⎰14241411112()32()14()mmm k k k N k k k f xf x f x C ---===+++=∑∑∑ (17)其中 4b a b ah n m--==, k x a kh =+ 其截断误差为6(6)2()[,](),()945n b a R f C h f a b ηη-=-<. 2.1.7 变步长复化求积方法复化求积公式虽然计算简单,也达到了提高精度的目的,但为了满足精度要求必须顾及误差,利用误差公式往往很困难,因为误差表达式中含有未知函数的导数,而估计各阶导数的最大值不太容易.我们可以采取把积分的区间[,]a b 细分的办法,在计算积分时将步长逐步折半,利用前后两次结果进行误差估计,如此继续,直到相邻两次结果相差不大,取最小的步长算出的结果为积分值,这种方法称为变步长积分法.以复化梯形公式为例,把区间[,]a b 分成n 等分,设复化梯形公式的近似值为n T ,原积分值为I ,由复化梯形公式误差公式(14)知:2"11()()()n b a b a I T f a b N N ηη--=-<<再把区间[,]a b 分成2n 等分,得近似值2n T ,则2222()()()122k b a b a I T f a b nηη--''=-<< 假定()f x ''在[,]a b 上变化不大,既有12()()f f ηη''''≈. 由上式得 .24kkI T I T -≈-于是 222211()()341n n n n n n I T T T T T T ≈+-=+-- (18) 式(18)表明若用2n T 作为I 的近似值,其截断误差约为2()3n n T T - (19)2.2 龙贝格求积公式龙贝格积分法的基本思想是采用复化梯形求积方法不断折半步长过程中,在积分结果中加入时候误差估计值进行补偿,使积分计算的收敛性加速,就可以加工出,,,...n n n S C R 精度较高的积分结果.由式(19), 2n T 的误差大致为23n nT T -,因此,可用这个误差值作为2n T 的一种补偿,加到2n T 上,则可得到积分准确值I ,比2n T 的更好近似值~T .222141()333n n n n nT T T T T T =+-=-2221(2)21n n T T =-- (20)式(20)左端1n =时记122121141()333S T T T T T =+-=- 112()()332a b T b a f +=+- [()4()()]62b a a b f a f f b -+=++恰好为[,]a b 上应用辛普生公式(16)的结果.在每个小区间应用辛普生公式:11[()2()()]2n n k k hT f a f x f b -==++∑121()112[()2()()2()]4n n n k k k k hT f a f x f b f x --===+++∑∑代入式(20)的左端得11111[()2()()2()32n nk k k k h f a f x f b f x -==+++--∑∑ 11[()2()()]2n k k h f a f x f b -++∑11111[()4()2()()]62n n k k k k f a f x f x f b -===+-++∑∑nS =从而复化辛普森公式与复化梯形公式公式有以下关系式2441n nn T T S -=- (21)类似也可以推证,在辛普森序列基础上,利用以下关系式22242161151541n n n n n S S C S S -=-=- (22)可以造出收敛速度更快的科茨序列12,...,...n C C C 将此推行下去,在科茨序列基础上,通过243431n nn C C R -=- (23)构造出收敛速度比科茨序列更快的龙贝格序列12,,......n R R R .以上这种通过逐步构造龙贝格序列的积分近似值法就称为龙贝格积分法.2.3高斯求积公式由定理()()()baf x F b F a =-⎰知,插值型求积公式的代数精度与求积节点的个数有关,具有1n +个节点的插值型求积公式至少具有n 次代数精度.不仅如此,代数精度与节点的选取有关,在构造牛顿-科茨求积公式时,为了简化处理过程,限定用等分节点作为求积节点,这样做,虽然公式确实得到简化,但同时也限制了公式的代数精度. 设积分,1,1=-=b a 本段讨论如下求积公式11()()ni i i f x A f x -==∑⎰(24)对任意积分区间[,]a b ,通过变 22ba t ab x ++-= 可以转换到区间]1,1[-上,这时11()()222bab a b a a bf x dx f t dt ---+=+⎰⎰ 此时,求积公式写为0()()222n bii ai b a a b b af x dx A f t =-+-=+∑⎰若一组节点]1,1[.....,10-∈n x x x 使插值型求积公式(24)具有21n +次代数精度,则称此组节点为高斯点,并称相应求积公式(24)为高斯求积公式.2.3.1 高斯求积公式的余项(2)2()[]()()()(22)!n nbb k k aa k f R f f x dx A f x x dx n ηω+==-=+∑⎰⎰ 其中 01()()()...(),[,]n x x x x x x x ab ωη=---∈,且不依赖于x .2.3.2 复化高斯求积公式复化高斯求积公式的基本思想是:将积分区间[,]a b 分成n个等长小区间1[,](1,...)i i t t i m -=,然后在低阶(2n =)高斯求积公式算出近似值,最后将他们相加的积分()baf t dt ⎰的近似值m G ,即11111111()()[]222ii mmbt i i i i i i at i i t t t t t t f t dt f t dt dt -----==-+-==+∑∑⎰⎰⎰1111[()]222m i h ha i h x dx-==+-+∑⎰101[()]222m n j j mi j h hA f a i h x G ==≈+-+≈∑∑ (25)其中mab h -=,j A 与(0,1,2,...,)j t j n =可由书中表中查出. 3 应用3.1插值型积分的应用例1 用牛顿-科茨公式(1,2,4n =)计算积分12211I x =+⎰. 解 1n =时2210112[]0.4512101()2I -≈+=++2n =时22211112[4]0.463725116101()1()42I -≈++=+++4n =时2222111112[7321232]0.46363311390101()1()1()848I =++++≈++++例2 利用复化梯形求积公式计算积分 12211I dx x =+⎰解设211)(xx f +=,分点个数为n =1,2,4,5时,求出相应积分n T , 111[(()())],21,2(),.n n i i i i i T f a f b f h b a h n n f x f x a ih ih -=⎧=++⎪⎪-⎪==⎨⎪=⎪⎪=+=⎩∑列表如下:n =1的计算结果见表1-1所列 n h0x 1x 0f1f1T10.50.00.51.0 0.8 0.45n =2的表格如下 n hx1x2xf1f2f2T20.250.00 0.25 0.50 1.00 0.941765 0.80 0.460294n =4时计算结果如下表 n h 0x1x2x3x4x40.1250.00 0.125 0.25 0.375 0.50f1f2f3f4f4T1.00 0.9846154 0.9411765 0.876712 0.80 0.462813n = 5时计算结果如下 n hx1x2x3x4x5x50.10.0 0.1 0.2 0.3 0.40.5f1f2f3f4f5f5T1.0 0.990099 0.9615385 0.91743 0.862069 0.80.463114例3 利用复化求积公式120x e dx ⎰,问积分区间为多少等分才能得证有5位有效数字？解由式（14）知322()[],()()1212n b a b a R f h f n f n n--''''=-=- 有1(),(),2x x f x e f x e b a ''==-=,当]21,0[∈x 时,在12|()|f x e ''≤,所以122|[]|96n eR f n≤ 由于120x e dx ⎰的准确值具有一位整数,所以要使近似值具有5位有效数字,n 必须满足4242211048,102196⨯≥⨯≤-e n n e 或取对数有 19=n .即将区间]21,0[19等分可满足给定的精度要求.例4 利用复化抛物线求积公式计算 120211I dx x =+⎰. 解设11)(2+=x x f ,取m =1,2, 3时,公式()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=+=====-=+++=+---=-=+∑∑.)12(,2),(),(),(,,242[31221212221111,1222h i a x ih a x x f f x f f b f f a f f m a b n f f f f h S i i i i i i b a m i m i i b a m当m =1,2,3时结果如下表所示当m =1时m h(0.0)f )25.0(f )5.0(f2S1 0.25 1.0 0.9411765 0.80 0.463725当m =2时mh(0.0)f(0.125)f (0.025)f (0.35)f )5.0(f4S20.125 1.0 0.9846154 0.9411765 0.8767123 0.80 0.463653当m =3时mh(0.0)f(0.08333)f (0.16667)f (0.35)f(0.33333)f (0.14166667)f )5.0(f4S30.83331.00.99310340.9729730.9411760.90.852070.80.4636例5 用复化梯形公式,辛普森公式和科茨公式计算积分10sin xdx x ⎰的近似值.解按精度要求确定]1,0[分多少等分,即确定步长,要使6441021)1(28801|],[|-⨯≤≤M m S f R n ,只需.4642880102M m ⨯≥令10sin ()cos xf x txdt x==⎰,则1()0sin ()()(cos )k kk k k d xd fx tx dt dx x dx==⎰ 1cos().2k t tx kdt π=+⎰dt ktx t x f k k |)2cos(|max )(|max 10)(π+≤⎰11.1k t d t t≤=+⎰)10(≤≤x (4)1max |()| 5.f x ≤所以只要,9.13831288010264=⨯⨯≥-m 取m =4即可, 当4n =时,在每个子区间上用式(25）,或(14),或(17),结果.9460829.0,9460833.0,9456911.0888===C S T3.2 龙贝格积分公式应用例6 用龙贝格算法计算积分1241I dx x=+⎰的近似值,要求误差小于510-. 解 .3,0,14)(2==+=b a x x f 步骤如下:2)1(,4)0()1(==f f 得.3)]1()0([211=+=f f T )2(计算,1.3)]21([21,516)21(12=+==f T T f 由此得301333334121=-=T T S . (3)算出），（43),41(f f 从而,3013118)]43()41([412124=++=f f T T,14157.334242=-=T T S .30142121516121=-=S S C(4)计算),87(),85(),83(),81(f f f f 从而得到:13899.3)]87()85()83()81([812148=++++=f f f f T T ,,14159.334482=-=T T S ,14059.31516242=-=S S C.1458.36364121=-=C C R (5)再计算),1615(),1613(),1611(),169(),167(),165(),163(),161(f f f f f f f f 从而得到: 14094.316=T30141598=S ,,14159.3,14159.324==R C 51210||-≤-R R , 所以12043.14159.1dx x ≈+⎰3.3高斯求积公式的应用例7 用两点复化高斯求积公式计算10,x I e dx =⎰要求允许误差.106-=ε解在本算法中取21=+n 时,,110==A A 其中;,)(mab h e x f x-== =++--=∑=)22(2201j jj b a x a b f A a b G.87189637800.1][21)32121()32121(=++-eem =2时, h =21, ]4121)21([4120202j i j j x i f A G +⨯-=∑∑==.57182571650.1)(41341333413341333413=+++=++--eeee m =3时, h =31. .37182769352.1]631)21([6130203=+⨯-=∑∑==j i j j x i f A G.101027.71||||56323--<⨯≈+-G G G3.4 几种方法的比较分析例8 计算积分211ln 2dx x =⎰，精确到0.001.(1)利用矩形公式计算, 因为对于x x f 1)(=,有320()2f x x''<=<(如果1<x <2),所以按照公式0)2(S =+-dx ba xb a . 0<n R <2112n . 如果取n =10,则我们公式的余项的余数得31010.84101200R -<<⨯,我们还必须加进由于在计算函数值实行四舍五入所产生的误差的界限相差于0.16⨯310-,为了这个目的只要计算1x的值到四位小数精确到0.00005就够了.我们有1232527292132152172192 1.051.151.251.351.551.651.751.851.95x x x x x x x x x =========5128.05405.05714.06061.06897.07407.08.08696.09524.02192172152132927252321=========y y y y y y y y y和6.928469284.0109284.6= (2) 按照梯形公式作同样的计算,在这种情况下,作公式 210,||6n n R R n<<在这儿也试一试取n =10,虽然此时仅可以证3107.16001||-⨯<<n R ,纵坐标是9.18.17.16.15.14.13.12.11.1987654321=========x x x x x x x x x 5263.05556.05882.06250.06667.07143.07692.08333.09091.0987654321=========y y y y y y y y y和1877.669377.01877.621500101=+）（ (3) 用辛普森公式做同样的计算作公式 .0))(()2(180)()4(45<≤≤⨯--=n n R b a f n a b R ξξ 并且n =5时有55104.1||-⨯<R .实行计算到五位数字,精确到0.0000058.16.14.12.14321====x x x x 45636.555556.062500.071429.083333.04321和====y y y y 9.17.15.13.11.12927252321=====x x x x x83820.1352632.058824.066667.076923.090909.029********和=====y y y y y.20.150==x x 50000.150000.060000.150和==y y6931525.083820.345636.550000.1301=++）（. 由此可见，用辛普森公式计算得到的值误差最小，计算量相对一般；而用矩形公式计算得到的值误差较大，计算量也比较大；用梯形公式计算的值误差比用矩形公式得到的值要误差小，计算量也是如此.所以我们计算定积分时用辛普森公式往往得到的值误差小，而对没有要求误差大小的，则可以选择辛普森或者是梯形公式，因为这两种方法计算量相对较小.结束语本文只讨论了一些一维数值积分方法及其它们的应用,误差分析等有关内容.其中最常用的方法是插值型积分以及复化方法、龙贝格积分方法和高斯积分方法,并讨论了相关求积方法的代数精度和误差分析,并给出了一些例题,分析各种方法的近似值,得出误差分析最小的近似方法.由于篇幅有限,对于高维数值积分方法本文便不再讨论.参考文献[1] 华东师范大学数学系，数学分析（第一版）[M]，北京:高等教育出版社,2001. [2] 李庆阳,关治,白峰杉，数值计算原理（第二版）[M]，北京: 清华大学出版社, 2008. [3] 肖筱南，现代数值计算方法（第一版）[M]，北京: 北京大学出版社, 1999.[4] 菲赫金格尔茨，微积分学教程（第三版）[M]，北京: 高等教育出版社, 2005. [5] 裴礼文，数学分析中的典型问题与方法（第一版）[M] ，北京: 北京大学出版社,2004. [6] 李桂成，计算方法（第三版）[M]，北京: 高等教育出版社,2010.[7] Yin Y uezhu ,Yang Zhonglian.Calculating Skillfully the Curve Integral and Surface Integral Type 2 bySymmetry, SCIENCE & TECHNOLOGY INFORMATION ,2008(30)The Approximate Numerical Method of the Definite IntegralAbstract This paper mainly discusses common numerical methods of unary function, such as approximate calculation method of interpolation integral, Lebesgue integral and Gauss integration. With these methods in calculating the integral, it will produce some error. In order to reduce the error, we can use after the formula for product and after the Gauss formula. This paper focus on these methods introducing formula of introduction and truncation errors .In addition they can provide examples to analysis size of the error and computation.Keywords interpolation integral Lebesgue integral Gauss integral error analysis approximate computation。

第七讲-定积分的近似计算

将自变量看成是向量
quad 举例
例：用 quad 计算定积分：
dx 0 1 x 2
1
解：
>> quad('1./(1+x.^2)',0,1)
>> quad('1./(1+x.^2)',0,1,10e-10) 函数表达式一定要用单引号括起来！涉及的运算一定要用数组运算！
dblquad
i 1
n
通常我们取
x1 x2 xn
h ba n
点 i [ xi 1, xi ] 可以任意选取，常见的取法有：左端点 xi 1 ，右端点
xi 和中点 ( xi 1 xi ) / 2 。
中点法
左点法
右点法
左点法、右点法和中点法
步长
xi h (b a) / n xi a ih, i 1,2, n
抛物线法
设过以上三点的抛物线方程为： y = x2 + x + = p1(x)
则在区间 [x0, x2] 上，有

x2
x0
f ( x)dx p1 ( x)dx x ( x2 x )dx
x2
0
x2
x0
x x x
3 2
x2
x2 x0 (y0 4y1 y2 ) 6 ba (y0 4 y1 y2 ) 6n
i 1 n
x2 i 2
f ( x )dx
ba ( y2i 2 4 y2i 1 y2i ) i 1 6n
抛物线法
整理后可得：

baຫໍສະໝຸດ b a f ( x)dx [ y0 y2n 4( y1 y3 y2n1 ) 6n 2( y2 y4 y2n2 )]

定积分的性质课件

定积分的概念之
定积分的性质
一、定积分问题举例
1.曲边梯形的面积
•曲边梯形设函数yf(x)在区间[a, b]上非负、连续. 由直线xa、xb、
y0及曲线yf (x)所围成的图形称为曲边梯形, 其中曲线弧称为曲边.
•观察与思考在曲边梯形内摆满小的矩形, 当小矩形的宽度减少时,
小矩形面积之和与曲边梯形面积之间的误差将如何变化?
e 1
n n
1
1e n
n
1
n(1e n )
利用几何意义求定积分
例例22 用定积分的几何意义求01(1 x)dx .
解函数 y1x在区间[0, 1]上的定积分是以y1x为曲边, 以区间[0, 1]为底的曲边梯形的面积.
因为以y1x为曲边, 以区间[0, 1]为底的曲边梯形是一个直角三角形, 其底边长及高均为1, 所以
b
a
f
(x)dx
abg(x)dx
(a<b).
•推论2
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
(a<b).
这是因为|f(x)|f(x)|f(x)|, 所以
ab|
f
(x)|dx
b
a
f
(x)dx
ab|
f
(x) | dx
,
即
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
.
•性质5 如果在区间[a, b]上 f (x)0, 则
f(x) ———被积函数, i1
f(x)dx ——被积表达式,
x ————积分变量,
a ————积分下限,

高等数学-第五章-定积分

则有
ab
c
c
b
c
a f (x)dx a f (x)dx b f (x)dx
b
c
c
a f (x)dx a f (x)dx b f (x)dx
c
b
a f (x)dx c f (x)dx
6. 若在 [a , b] 上
则
a<b
n
证: f (i ) xi 0
i1
b
n
a
f
( x) d
x
lim
d (x)
dx a
f (t) d t
f
[ ( x)] ( x)
d
dx
( x) (x)
f
(t) d t
d dx
a
f (t) d t
(x)
( x)
a
f
(t) d t
f [(x)](x) f [ (x)] (x)
例1. 求
0
0
解: 原式洛 lim ecos2 x ( sin x) 1
x
ba n
,
xi a i x (i 0,1, ,n)
记 f (xi ) yi (i 0,1, ,n)
1. 左矩形公式
O a xi1xi
bx
ab f (x)dx y0x y1x yn1x
2. 右矩形公式
ba n
(
y0
y1
yn1)
ab f (x)dx y1x y2x ynx
)
故
π 2 0
2
dx
π
2 f (x) dx
0
π
2 1dx
0
即
1
π
2 0

高等数学课件 PPT 第五章定积分

［a,b］上有界并不是可积的充分条件.例如，
在［0,1］上是有界函数，但不可积．因为不论对［0,1］怎样分割，在任意被分割的小区间［xi－1,xi］上，总能取到ξi为有理数，这时f(ξi)=1，也总能取到ξi为无理数，这时f(ξi)=0．所以对［0,1］的任何一种分法，我们总可以得到
一、定积分的概念
思考
一个函数在什么条件下可积？什么条件下不可积？
一、定积分的概念
3. 定积分存在的充分条件
若f(x)在［a,b］上无界，则f(x)在［a,b］上一定是不可积的．这是因为，若f(x)在［a,b］上无界，那么无论对［a,b］怎样分割，都至少有一个区间［xi－1,xi］，函数f(x)在其上无界．因此，在［xi－1,xi］上一定可以取一点ξi，使得f(ξi)大于任意一个正数M，因而也就使得和式 ∑ =1f(ξi)Δxi可以任意的大．当λ→0时，这个和就不可能趋向于任何极限．由此可知， f(x)在［a,b］上可积的必要条件是f(x)在［a,b］上有界．
一、变速直线运动中位置函数与速度函数之间的联系
为了讨论质点在变速直线运动中位置函数与速度函数间的联系，有必要沿质点的运动方向建立坐标轴.设时刻t时质点所在位置st，速度vtvt≥0. 已知质点在时间间隔T1,T2内经过的路程可以用速度函数vt在 T1,T2上的定积分
一、定积分的概念
在区间［a,b］上，f(x)既有正值又有负值时，函数y=f(x) 的图形某些部分在x轴的上方，而其他部分在x轴的下方．如果规定在x轴的上方的图形的面积为正，在x下方的图形面积为负，那么∫baf(x) 的几何意义就是介于曲线y=f(x)、x轴及两条直线 x=a,x=b之间的各部分面积的代数和，如图5-2所示．
把区间［a,b］分成个n小区间［x0,x1］,［x1,x2］,…,［xn－1,xn］，

定积分的近似计算方法

定积分的近似计算方法
定积分的近似计算方法有多种，其中常见的包括矩形法、梯形法和辛普森法。

矩形法是将积分区间分成若干小区间，然后在每个小区间中选取一个代表点，将代表点处的函数值作为该小区间的近似值，最后将所有小区间的近似值相加，得到定积分的近似结果。

梯形法是将积分区间分成若干小区间，然后在每个小区间中将函数图像近似为一个梯形，通过计算每个梯形的面积并相加，得到定积分的近似结果。

辛普森法利用抛物线与曲线之间的关系进行近似计算。

首先将积分区间分成若干小区间，然后在每个小区间中利用三个点的函数值构建抛物线，通过计算每个抛物线下的面积并相加，得到定积分的近似结果。

这些方法都是通过将积分区间离散化，并在离散化的点上计算函数值来进行近似计算的。

(整理)定积分的近似计算.

实验二定积分的近似计算一、问题背景与实验目的利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值，但它仅适用于被积函数的原函数能用初等函数表达出来的情形．如果这点办不到或者不容易办到，这就有必要考虑近似计算的方法．在定积分的很多应用问题中，被积函数甚至没有解析表达式，可能只是一条实验记录曲线，或者是一组离散的采样值，这时只能应用近似方法去计算相应的定积分．本实验将主要研究定积分的三种近似计算算法：矩形法、梯形法、抛物线法．对于定积分的近似数值计算，Matlab有专门函数可用．二、相关函数（命令）及简介1．sum(a)：求数组a的和．2．format long：长格式，即屏幕显示15位有效数字．（注：由于本实验要比较近似解法和精确求解间的误差，需要更高的精度）．3．double()：若输入的是字符则转化为相应的ASCII码；若输入的是整型数值则转化为相应的实型数值．4．quad()：抛物线法求数值积分．格式： quad(fun,a,b) ，注意此处的fun是函数，并且为数值形式的，所以使用*、/、^等运算时要在其前加上小数点，即 .*、./、.^等．例：Q = quad('1./(x.^3-2*x-5)',0,2);5．trapz()：梯形法求数值积分．格式：trapz(x,y)其中x为带有步长的积分区间；y为数值形式的运算（相当于上面介绍的函数fun）例：计算x=0:pi/100:pi;y=sin(x);trapz(x,y)6．dblquad()：抛物线法求二重数值积分．格式：dblquad(fun,xmin,xmax,ymin,ymax)，fun可以用inline定义，也可以通过某个函数文件的句柄传递．例1：Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)顺便计算下面的Q2，通过计算，比较Q1 与Q2结果（或加上手工验算），找出积分变量x、y的上下限的函数代入方法．Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi) 例2：Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi)这时必须存在一个函数文件integrnd.m：function z = integrnd(x, y)z = y*sin(x);7．fprintf（文件地址，格式，写入的变量）：把数据写入指定文件．例：x = 0:.1:1;y = [x; exp(x)];fid = fopen('exp.txt','w'); %打开文件fprintf(fid,'%6.2f %12.8f\n',y); %写入fclose(fid) %关闭文件8．syms 变量1 变量2 …：定义变量为符号．9．sym('表达式')：将表达式定义为符号．解释：Matlab中的符号运算事实上是借用了Maple的软件包，所以当在Matlab中要对符号进行运算时，必须先把要用到的变量定义为符号．10．int(f,v,a,b)：求f关于v积分，积分区间由a到b．11．subs(f，'x'，a)：将 a 的值赋给符号表达式 f 中的 x，并计算出值．若简单地使用subs(f)，则将f的所有符号变量用可能的数值代入，并计算出值。

定积分定义ppt课件

说明：定积分的值只与被积函数及积分区间有关, 而与积分变
量的记法无关, 即
a b f ( x ) d a b f ( t ) d x a b f ( u ) d t . u
上页下页返回退出
x 二、定积分定义
❖定积分的定义 ❖函数的可积性
a b f ( x ) d l 0 i n 1 f ( i ) D i x i . x m
已知物体直线运动的速度vv(t)是时间 t 的连续函数, 且 v(t)0, 计算物体在时间段[T1, T2]内所经过的路程S. (1)分割: T1t0<t1<t2< <tn1<tnT2, Dtititi1; (2)近似代替: 物体在时间段[ti1, ti]内所经过的路程近似为
DSiv(i)Dti ( ti1< i<ti );
于是
1exd x lim nen i 1li1 m (e1 n en 2 en n)
0
n i 1 nn n
1
1
1
lim 1en[1(en)n]lim en[1e]e1
n n
1
1en
n
1
n(1en)
上页下页返回退出
•利用几何意义求定积分
例例2 2 用定积分的几何意义求 0 1 ( 1 x ) d . x
•观察与思考在曲边梯形内摆满小的矩形, 当小矩形的宽度减少时,
小矩形面积之和与曲边梯形面积之间的误差将如何变化? 怎样求曲边梯形的面积？
上页下页返回退出
•求曲边梯形的面积 (1)分割: ax0< x1< x2< < xn1< xn b, Dxixixi1;
(2)近似代替: 小曲边梯形的面积近似为f(xi)Dxi (xi1<xi<xi);

定积分的近似计算

定积分的近似计算定积分的近似计算是数学中一种常用的方法，它可以帮助我们计算具体函数在一定区间上的面积或曲线长度。

在实际应用中，定积分的近似计算有多种方法，包括矩形法、梯形法、辛普森法等。

本文将侧重介绍这些方法的原理和应用。

1. 矩形法（Reimann和法）：矩形法是定积分近似计算的最简单方法之一、其基本思想是将给定区间等分为若干个小区间，然后在每个小区间内选择一个代表点，以该点处函数值与小区间长度的乘积作为该小区间的面积近似值，然后对所有小区间的面积近似值求和得到最终的近似计算结果。

具体而言，设函数f(x)在区间[a,b]上连续，将该区间分为n个小区间：x0=a, x1=a+h, x2=a+2h, ..., xn=a+nh=b其中h=(b-a)/n，xi为每个小区间的代表点。

此时，对于每个小区间，我们可以将其面积近似为S_i=h*f(xi)，然后对所有小区间的面积进行求和，即：S=a*h*f(x0)+a*h*f(x1)+...+a*h*f(xn-1)对于当n趋向于无穷大时，通过这一方法可以得到函数f(x)在区间[a,b]上的定积分值。

2.梯形法：梯形法是定积分近似计算的另一种常用方法。

与矩形法类似，梯形法也是将给定区间等分为若干个小区间，然后在每个小区间内用该区间两个端点处的函数值构造出一个梯形，以该梯形的面积作为小区间面积的近似值，最终对所有小区间的面积进行求和得到近似计算结果。

设函数f(x)在区间[a,b]上连续，将该区间分为n个小区间，并选取区间端点[a,b]分别作为梯形的上底和下底，连线得到梯形。

此时，对于每个小区间，梯形的面积可以近似表示为：S_i=(h/2)*(f(xi)+f(xi+1))其中h=(b-a)/n，xi为每个小区间的起点。

最后，对于所有小区间的面积近似值进行求和，即：S=(h/2)*[f(a)+2f(a+h)+2f(a+2h)+...+2f(b-h)+f(b)]对于当n趋向于无穷大时，通过这一方法也可以得到函数f(x)在区间[a,b]上的定积分值。

定积分的近似计算矩形法教学PPT课件

1 4 0 1 x2
dx
1 10
(
y0
y1
y9 )
3.2400，
1 4 d x 1 ( y y y ) 3.0400．
0 1 x2
10 1 2
10
梯形法
b a
f
(x)d
x
b
a n
(y0
y 1
y) n1
b
n
a( y1
y2
y) n
．
y
y f (x)
Oa
bx
b a
f
(x) d
x
b
a n
利用矩形法( n 10 )计算
14 0 1 x2
d
x．
解记 x i ， y 4 (i 0,1, 2,,10) ，
i 10
i 1 xi2
xi
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
yi 4.0000 3.9604 3.8462 3.6697 3.4483 3.2 2.9412 2.6846 2.4390 2.2099 2.0000
2
n
i xi
定积分 b f (x) d x ( f (x) 0) 的几何意义 a b f (x)d x A． a
y
y f (x)
Oa
A
bx
b a
f
(x)d
x
b
a n
( y0
y1
yn1 )
b a(y y y ) ．
n
1
2
n
y
y f (x)
左矩形法右矩形法
矩形法
Oa
bx
例
y0

定积分的近似计算.ppt

高等数学 定积分

定积分的概念PPT课件

高二数学定积分概念.pptx

定积分的概念ppt课件

1-5-3 定积分的概念 课件 (人教A版选修2-2)

定积分的近似计算之矩形法

第32讲 定积分的分部积分法与近似计算

定积分的近似计算方法

定积分近似计算方法

第七讲-定积分的近似计算

定积分的性质 课件

高等数学-第五章-定积分

高等数学 课件 PPT 第五章 定积分

定积分的近似计算方法

(整理)定积分的近似计算.

定积分定义ppt课件

定积分的近似计算

定积分的近似计算 矩形法 教学PPT课件

高等数学定积分

1-5-3 定积分的概念课件 (人教A版选修2-2)

第32讲定积分的分部积分法与近似计算

定积分的性质课件

高等数学课件 PPT 第五章定积分

定积分的近似计算矩形法教学PPT课件