最小二乘法求二次方程系数
多元二次回归方程

多元二次回归方程一、概述多元二次回归方程是一种用于分析多个自变量与因变量之间关系的统计方法。
与一元二次回归方程相比,多元二次回归方程能够更准确地描述复杂的非线性关系。
本文将详细介绍多元二次回归方程的定义、求解方法以及应用场景。
二、定义多元二次回归方程可以表示为:Y=β0+β1X1+β2X2+β3X12+β4X22+β5X1X2+ϵ其中,Y表示因变量,X1和X2表示自变量,β0、β1、β2、β3、β4和β5是回归系数,ϵ是误差项。
三、求解方法求解多元二次回归方程的回归系数可以采用最小二乘法,即通过最小化残差平方和(RSS)来估计回归系数。
最小二乘法的目标是找到使得RSS最小的回归系数组合。
具体的求解步骤如下: 1. 收集样本数据,包括因变量Y和自变量X1、X2的取值。
2. 对自变量进行预处理,包括去除缺失值、处理异常值等。
3. 构建多元二次回归模型,即将样本数据代入多元二次回归方程。
4. 计算残差平方和RSS,即将观测值与回归模型的预测值之差的平方求和。
5. 使用最小二乘法求解回归系数,即通过对RSS对回归系数求偏导数,将偏导数为零的方程组求解得到回归系数的估计值。
6. 检验回归模型的拟合优度,包括计算决定系数R2和残差的正态性等。
四、应用场景多元二次回归方程在实际应用中具有广泛的应用场景。
以下列举了几个常见的应用场景:1. 金融领域在金融领域,多元二次回归方程可以用于分析多个因素对某项金融指标的影响。
例如,可以使用多元二次回归方程来研究收入、利率和通胀率对股票价格的影响。
2. 经济学研究在经济学研究中,多元二次回归方程可以用于解释宏观经济变量之间的关系。
例如,可以使用多元二次回归方程来分析GDP、劳动力参与率和投资对就业率的影响。
3. 市场营销在市场营销中,多元二次回归方程可以用于分析多个市场因素对产品销量的影响。
例如,可以使用多元二次回归方程来研究广告投入、产品定价和竞争对销售额的影响。
最小二乘法转为二次方程

最小二乘法转为二次方程最小二乘法是一种用于求解最小化误差平方和的方法,具体应用在回归分析中。
可以将最小二乘法转化为二次方程的形式来求解。
假设有一组数据 (x1, y1), (x2, y2), ..., (xn, yn),其中 x 和 y 分别代表自变量和因变量。
我们假设二次方程 y = ax^2 + bx + c 可以拟合这组数据,其中 a、b、c 是待求的系数。
首先,我们需要构造误差函数 E,它是实际值 y 与预测值ax^2 + bx + c 的差的平方和:E = Σ(yi - axi^2 - bxi - c)^2接下来,我们需要将误差函数 E 对系数 a、b、c 分别求偏导数:∂E/∂a = -2Σxi^2(yi - axi^2 - bxi - c)∂E/∂b = -2Σxi(yi - axi^2 - bxi - c)∂E/∂c = -2Σ(yi - axi^2 - bxi - c)令三个偏导数等于0,我们得到一个包含三个未知数 a、b、c的线性方程组。
解出 a、b、c 的值,即可求出二次方程 y =ax^2 + bx + c。
但是,由于这个线性方程组比较复杂,通常需要使用矩阵运算来求解。
具体来说,我们可以将误差函数 E 写成以下形式:E = (Y - Xb)^T (Y - Xb)其中,Y 是一个 n×1 的向量,包含实际值 y1, y2, ..., yn;X 是一个 n×3 的矩阵,包含自变量的平方项 xi^2,一阶项 xi,和一个全为1的常数项 1;b 是一个 3×1 的向量,包含待求系数a、b、c。
通过对E 求偏导数,我们可以得到一个关于b 的线性方程组:X^T Xb = X^T Y解这个线性方程组,即可得到 b 向量的值,从而求出二次方程y = ax^2 + bx + c。
二次函数回归方程公式

二次函数回归方程公式y = ax^2 + bx + c其中,a、b和c是常数,x是自变量,y是对应的因变量。
Step 1: 收集和整理数据首先,需要收集一组自变量和因变量之间的实际观测数据。
这些数据可以来自于实验或现实世界的观测。
Step 2: 构建二次函数回归模型根据收集到的数据,我们可以假设二次函数回归模型为:y = ax^2 + bx + c其中,a、b和c是待定系数。
Step 3: 确定残差残差是实际观测值与回归模型预测值之间的差异。
我们定义残差e为:e = y - ax^2 - bx - cStep 4: 最小化残差的平方和最小二乘法的核心思想是使得残差的平方和最小化。
也就是要最小化以下目标函数:∑(e^2)其中,∑表示求和运算。
Step 5: 求解参数为了最小化目标函数,需要对参数a、b和c求导,并令导数等于零。
通过求解导数方程组,可以得到参数的解析解。
具体求解过程比较繁琐,可以使用数学软件或计算机程序来进行求解。
在实际应用中,一般使用现有的统计软件或编程语言来拟合二次函数回归方程。
例如,在Python编程语言中,可以使用NumPy、Scipy等库来进行二次函数回归的求解。
以下是Python代码的一个示例:```pythonimport numpy as npfrom scipy.optimize import curve_fit#自变量数据x = np.array([1, 2, 3, 4, 5])#因变量数据y = np.array([3, 7, 12, 18, 25])#定义二次函数模型def quadratic_func(x, a, b, c):return a * x**2 + b * x + c#使用最小二乘法拟合数据params, params_covariance = curve_fit(quadratic_func, x, y)a, b, c = params#打印拟合结果print("a =", a)print("b =", b)print("c =", c)```这段代码使用了Scipy库中的curve_fit函数来拟合二次函数回归方程。
二次多项式回归方程

二次多项式回归方程二次多项式回归方程是一种常用的数学模型,用于拟合二次曲线形状的数据。
它是基于多项式回归的扩展,通过引入平方项的系数来更好地适应具有非线性关系的数据。
二次多项式回归方程的一般形式如下:y = ax^2 + bx + c其中,y表示因变量(依赖变量),x表示自变量(独立变量),a、b、c表示二次多项式回归方程的系数。
在二次多项式回归中,我们通常使用最小二乘法来估计系数的值。
该方法旨在使模型的预测值与实际观测值之间的平方差尽量小。
通过求解最小二乘问题,可以得到最佳拟合的二次多项式回归方程。
为了求解系数a、b、c,可以利用已知的数据点进行拟合。
首先,我们需要收集足够数量的自变量x和对应的因变量y的数据对。
然后,我们可以使用数值计算方法或者统计软件来估计系数的值。
一种常见的方法是使用最小二乘法拟合二次多项式回归方程。
这种方法的基本思想是,通过选择合适的系数值,使得二次多项式回归方程的预测值与已知数据点的观测值之间的残差平方和最小化。
残差表示了预测值与观测值之间的差异。
求解最小二乘问题可以使用线性代数的方法,例如矩阵运算或者求解线性方程组。
具体步骤如下:1. 将数据点表示为矩阵形式:X = [x^2, x, 1]Y = [y]2. 使用最小二乘法的公式计算系数向量:θ = (X^T X)^-1 X^T Y其中,X^T表示X的转置,(X^T X)^-1表示X^T X的逆矩阵。
3. 得到系数向量后,可以得到二次多项式回归方程:y = θ[0]x^2 + θ[1]x + θ[2]这样,我们就得到了二次多项式回归方程,并可以使用该方程进行预测或拟合。
需要注意的是,二次多项式回归方程在某些情况下可能会产生过拟合的问题。
过拟合指的是模型过度拟合训练数据,导致在新数据上的表现不如预期。
为了解决过拟合问题,可以考虑使用正则化技术,如岭回归或Lasso回归,来减小高次项的系数。
另外,二次多项式回归方程也可以进一步扩展为更高阶的多项式回归方程,以适应更复杂的数据模式。
最小二乘法 范德蒙德行列式

最小二乘法范德蒙德行列式
摘要:
1.最小二乘法简介
2.范德蒙德行列式的概念
3.最小二乘法与范德蒙德行列式的关系
4.应用实例
正文:
【1.最小二乘法简介】
最小二乘法是一种数学优化技术,用于通过最小化误差的平方和来寻找最佳拟合函数。
在各种科学和工程领域中,例如经济学、物理学、统计学等,最小二乘法都有着广泛的应用。
【2.范德蒙德行列式的概念】
范德蒙德行列式,又称范德蒙德矩阵,是由一组数构成的矩阵,其元素是这些数的乘积。
范德蒙德行列式在数学中有着广泛的应用,包括线性代数、微积分、概率论等领域。
【3.最小二乘法与范德蒙德行列式的关系】
最小二乘法与范德蒙德行列式之间的关系主要体现在最小二乘法的解的求解过程中。
在最小二乘法中,我们需要求解一个线性方程组,而这个方程组的解可以直接由范德蒙德行列式来表示。
具体来说,如果一个线性方程组的系数矩阵的范德蒙德行列式不等于0,那么这个方程组就有唯一解,这个解可以直接由范德蒙德行列式求出。
【4.应用实例】
我们可以通过一个简单的实例来说明最小二乘法和范德蒙德行列式的应用。
假设我们有一组数据,描述的是一个二次函数y=ax^2+bx+c 的输出,而我们知道这个二次函数的某些点(x1, y1),(x2, y2),(x3, y3)。
我们的目标是找到这个二次函数的系数a、b、c。
这个问题就可以通过最小二乘法和范德蒙德行列式来解决。
我们首先通过最小二乘法构造一个线性方程组,然后通过范德蒙德行列式求解这个方程组,就可以得到系数a、b、c 的值。
最小二乘法公式

最小二乘法公式-CAL-FENGHAI.-(YICAI)-Company One1最小二乘法公式∑(X--X平)(Y--Y平)=∑(XY--X平Y--XY平+X平Y平)=∑XY--X平∑Y--Y平∑X+nX平Y平=∑XY--nX平Y平--nX平Y平+nX平Y平=∑XY--nX平Y平∑(X --X平)^2=∑(X^2--2XX平+X平^2)=∑X^2--2nX平^2+nX平^2=∑X^2--nX平^2最小二乘公式(针对y=ax+b形式)a=(NΣxy-ΣxΣy)/(NΣx^2-(Σx)^2)b=y(平均)-ax(平均)最小二乘法在我们研究两个变量(x, y)之间的相互关系时,通常可以得到一系列成对的数据(x1, y1),(x2, y2).. (xm , ym);将这些数据描绘在x -y直角坐标系中(如图1), 若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
Y计= a0 + a1 X (式1-1)其中:a0、a1 是任意实数为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用(式1-1)计算值(Y计=a0+a1X)的离差(Yi-Y计)的平方和〔∑(Yi - Y 计)²〕最小为“优化判据”。
令: φ = ∑(Yi - Y计)² (式1-2)把(式1-1)代入(式1-2)中得:φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)当∑(Yi-Y计)²最小时,可用函数φ 对a0、a1求偏导数,令这两个偏导数等于零。
(式1-4)(式1-5)m a0 + (∑Xi ) a1 = ∑Yi (式1-6)(∑Xi ) a0 + (∑Xi2 ) a1 = ∑(Xi, Yi) (式1-7)得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:a0 = (∑Yi) / m - a1(∑Xi) / m (式1-8)a1 = [∑Xi Yi - (∑Xi ∑Yi)/ m] / [∑Xi2 - (∑Xi)2 / m)] (式1-9)这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的元线性方程即:数学模型。
二次函数回归方程公式

二次函数回归方程公式f(x) = ax^2 + bx + c其中,a、b、c分别为二次项系数、一次项系数和常数项。
为了确定这三个系数的值,我们需要至少三个数据点,即(x1,y1)、(x2,y2)和(x3,y3)。
代入这三个数据点到方程中,得到以下三个方程:y1 = ax1^2 + bx1 + cy2 = ax2^2 + bx2 + cy3 = ax3^2 + bx3 + c将这三个方程整理成矩阵的形式,可以得到:⎡x1^2x11⎡⎡a⎡⎡y1⎡⎡x2^2x21⎡⎡b⎡=⎡y2⎡⎡x3^2x31⎡⎡c⎡⎡y3⎡这是一个形如AX=B的线性方程组,其中A是一个3x3的矩阵,X是矩阵⎡a⎡的解向量,B是由(y1,y2,y3)组成的列向量。
解这个线性方程组,可以使用线性代数中的方法,如求逆矩阵、高斯消元法或矩阵分解等。
解得向量X的分量即为二次项系数a、一次项系数b和常数项c的值。
在实际应用中,可以使用计算软件或编程语言来求解这个方程组,例如使用Python的NumPy库可以很方便地进行矩阵运算和求解线性方程组。
以下是一个简单的Python代码示例,使用最小二乘法拟合数据点,并得到二次函数的回归方程:```import numpy as npdef quadratic_regression(x, y):n = len(x)A = np.column_stack((x**2, x, np.ones(n)))B = np.array(y).reshape(n, 1)X = np.linalg.lstsq(A, B, rcond=None)[0]a, b, c = X.flattenreturn a, b, c#示例数据点x=[1,2,3,4,5]y=[3,6,11,18,27]#拟合数据点a, b, c = quadratic_regression(x, y)#打印回归方程print(f"f(x) = {a}x^2 + {b}x + {c}")```上述代码首先定义了一个quadratic_regression函数,该函数接受一组x和y的数值数据点作为输入,并返回二次函数的回归方程的系数a、b和c的值。
最小二乘法

第七章 最小二乘法最小二乘法是实验数据处理的一种基本方法。
它给出了数据处理的一条准则,即在最小二乘以一下获得的最佳结果(或最可信赖值)应使残差平方和最小。
基于这一准则所建立的一整套的理论和方法,为随机数据的处理提供了行之有效的手段,成为实验数据处理中应用十分广泛的基础内容之一。
自1805年勒让得(Legendre )提出最小二乘法以来,这一方法得到了迅速发展,并不断完善,成为回归分析、数理统计等方面的理论基础之一,广泛地应用于天文测量,大地测量及其他科学实验的数据处理中。
现代,矩阵理论的发展及电子计算机的广泛应用,为这一方法提供了新的理论工具和得力的数据处理手段。
随着计量技术及其他现代科学技术的迅速发展,最小二乘法在各学科领域将获得更为广泛的应用。
本章仅涉及独立的测量数据的最小二乘法处理。
以等精度线性参数的最小二乘法为中心,叙述最小二乘法原理,正规方程和正规方程的解,以及最小二乘估计的精度估计。
最后给出测量数据最小二乘法处理的几个例子。
7 .1 最小二乘法原理县考察下面的例子。
设有一金属尺,在温度()C t ︒条件下的长度可表示)1(0t y y t α+=式中 y 0——温度为0°C 时的金属尺的长度;α——金属材料的线膨胀系数; t ——测量尺长时的温度。
现要求给出y 0与α的数值。
为此,可在t 1与t 2两个温度条件下分别测得尺的长度l 1与l 2,得方程组()()⎭⎬⎫+=+=20210111t y l t y l αα由此可解得y 0与α。
事实上,由于测量结果l 1与l 2含有测量误差,所得到的y 0与α的值也含有误差。
显而易见,为减小所得y 0与α值的误差,应增加y t 的测量次数,以便利用抵偿性减小测量误差的影响。
设在n t t t ,,,21 温度条件下分别测得金属尺的长度n l l l ,,,21 共n 个结果,可列出方程组⎪⎪⎭⎪⎪⎬⎫+=+=+=)1()1()1(0202101n n t y l t y l t y l ααα)1(0t y y t α+=但由于方程式的数目n 多于待求量的数目,所以无法直接利用代数法求解上述方程组。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
曲线拟合的最小二乘法
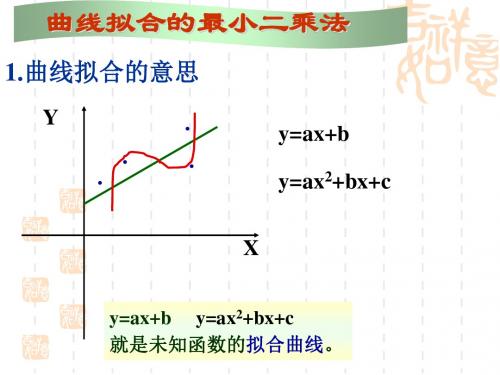
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
第四章参数的最小二乘法估计讲解

第四章 最小二乘法与组合测量§1 概述最小二乘法是用于数据处理和误差估计中的一个很得力的数学工具。
对于从 事精密科学实验的人们来说, 应用最小乘法来解决一些实际问题, 仍是目前必不 可少的手段。
例如,取重复测量数据的算术平均值作为测量的结果, 就是依据了 使残差的平方和为最小的原则, 又如,在本章将要用最小二乘法来解决一类组合 测量的问题。
另外,常遇到用实验方法来拟合经验公式, 这是后面一章回归分析 方法的内容,它也是以最小二乘法原理为基础。
最小二乘法的发展已经经历了 200 多年的历史,它最先起源于天文和大地测 量的需要, 其后在许多科学领域里获得了广泛应用, 特别是近代矩阵理论与电子 计算机相结合,使最小二乘法不断地发展而久盛不衰。
本章只介绍经典的最小二乘法及其在组合测量中的一些简单的应用, 一些深 入的内容可参阅专门的书籍和文献。
§2 最小二乘法原理最小二乘法的产生是为了解决从一组测量值中寻求最可信赖值的问题。
对某 量 x 测量一组数据 x 1,x 2, ,x n ,假设数据中不存在系统误差和粗大误差,相互独 立,服从正态分布,它们的标准偏差依次为: 1, 2, n 记最可信赖值为 x ,相 应的残差 v i x i x 。
测值落入 (x i ,x i dx)的概率。
根据概率乘法定理,测量 x 1,x 2, ,x n 同时出现的概率为P i2i 2 exp( 2v ii 2)dx1 1 v PP i1n exp[ 1( i )2 ](dx)n ii ( 2 )n 2 i i显然,最可信赖值应使出现的概率 P 为最大,即使上式中页指数中的因子达 最小,即2 v ii2 Min i i 22[ wvv]w i v i Min再用微分法,得最可信赖值 xnw i x ii1 x nw ii1这里为了与概率符号区别,以 i 表示权因子。
特别是等权测量条件下,有:[vv] v i 2 Min以上最可信赖值是在残差平方和或加权残差平方和为最小的意义下求得的, 称之为最小二乘法原理。
最小二乘法

数值分析作业最小二乘法最小二乘法是提供“观测组合”的主要工具之一,它依据对某事件的大量观测而获得最佳”结果或最可能”表现形式。
如已知两变量为线性关系y= a+ bx,对其进行n(n> 2)次观测而获得n对数据。
若将这n对数据代入方程求解a,b之值则无确定解。
最小二乘法提供了一个求解方法,其基本思想就是寻找最接近”这n 个观测点的直线。
最小二乘法不仅是19世纪最重要的统计方法,而且还可以称为数理统计学之灵魂。
相关回归分析、方差分析和线性模型理论等数理统计学的几大分支都以最小二乘法为理论基础。
作为其进一步发展或纠正其不足而采取的对策,不少近现代的数理统计学分支也是在最小二乘法基础上衍生出来的。
正如美国统计学家斯蒂格勒(S.M. Stigler)所说,最小二乘法之于数理统计学犹如微积分之于数学”最小二乘法创立的历史过程充满着丰富的科学思想,这些对今日的数学创造仍有着重要的启示意义。
本文旨在全面认识最小二乘法的历史系统发育过程以及创立者的思路。
一先驱者的相关研究天文学和测地学的发展促进了数理统计学及其他相关科学的发展。
丹麦统计史家哈尔德曾指出天文学在数理统计学发展中所起的作用。
“天文学自古代至18 世纪是应用数学中最发达的领域。
观测和数学天文学给出了建立数学模型及数据拟合的最初例子,在此种意义下,天文学家就是最初的数理统计学家。
天文学的问题逐渐引导到算术平均,以及参数模型中的种种估计方法,以最小二乘法为顶峰。
” 这也说明了最小二乘法的显著地位。
有关统计计算思想记载的著作要首推天文学家罗杰柯茨的遗作,即1715年其所发论文中所蕴含的统计方法,亦即对各种观测值赋予加权后求其加权平均。
尽管当时得到认可,然而事实证明如此计算的结果不太精确。
1749年,欧拉(L. Euler,1707—1783)在研究木星和土星之间相互吸引力作用对各自轨道影响时,最后得到一个含8个未知量75个方程的线性方程组。
欧拉的求解方法繁杂而奇特,只能看作是一次尝试。
第四讲线性方程组与最小二乘法

xn
a(1) 2,n1
a(2) 3n
xn
a(2) 3,n1
a x a (n1) nn n
( n 1) n,n1
其中,
a(k) ij
a(k 1) ij
mik
a(k kj
1),
i k 1, k 2, , n;j k 1, k 2, , n, n 1.
mik
a(k 1) ik
/
a(k kk
1),i
确定满足k≤μ≤n和k≤λ≤n,使得 |A(μ,λ)|=max{A(i,j)|i=k:n, j=k:n} A(k,1:n) ↔ A(μ,1:n) ; A(1:n,k) ↔ A(1:n,λ) ; T(k) ↔ T(λ);
if A(k,k)≠0 begin for i=k+1:n begin m=A(i,k)/A(k,k); for j=k+1:n A(i,j)=A(i,j)-m*A(k,j); end
3
➢
高斯消元法始终假设主元
a(k 1) kk
0,若
a(k 1) kk
0,则消元
过程无法进行;实际上,即使
a(k kk
1)
0,但
a(k 1) kk
很小
时,用它作除数对计算结果也是很不利的。
4.2 一般线性方程组求解
(2)全选主元高斯消元法
对于如下所示的方程组,有性质:
a11 a12 a21 a22 an1 an2
对于线性方程组 Ax b,写成分量形式为
n
aij x j bj,i 1, 2, , n.
j 1
若记 ai,n1 bi , i 1, 2, , n,则有
a11x1 a12 x2 a13x3
matlab 多点利用最小二乘法拟合二次函数方程

Matlab是一种用于数学计算和工程䇹算的高级语言和交互式环境。
在Matlab中,利用最小二乘法来拟合二次函数方程是一种常见的数据分析方法,可以通过拟合得到二次函数的系数,从而更好地理解和分析实际问题中的数据。
1. 理论基础最小二乘法是一种数学优化方法,用于寻找真实数据与拟合函数之间的最小误差。
在拟合二次函数方程时,我们可以将拟合方程写成如下形式:y = a*x^2 + b*x + c其中,a、b、c分别为二次函数的系数,x和y分别为自变量和因变量。
2. Matlab中的多点利用最小二乘法在Matlab中,可以使用polyfit函数来实现对多点数据进行二次函数拟合。
其基本语法为:p = polyfit(x, y, n)其中,x和y分别为输入的数据点,n为二次函数的次数。
3. 示例代码下面给出一个简单的示例代码来演示如何在Matlab中进行多点利用最小二乘法拟合二次函数方程:```Matlabx = [1, 2, 3, 4, 5];y = [3.1, 4.9, 7.2, 9.8, 12.5];p = polyfit(x, y, 2);```在这个例子中,我们输入了5个数据点,然后利用polyfit函数对这些数据点进行二次函数拟合,得到了二次函数的系数p。
4. 结果分析经过拟合得到的二次函数系数p为:p = [0.1, 0.2, 3]这意味着拟合得到的二次函数方程为:y = 0.1*x^2 + 0.2*x + 3通过这个拟合方程,我们可以更好地理解和分析实际数据的趋势和规律。
5. 需要注意的问题在利用最小二乘法拟合二次函数方程时,需要注意以下几个问题:- 数据的选择:数据点的选择对拟合结果会有很大的影响,需要根据实际问题合理选择数据点。
- 拟合精度:拟合得到的二次函数方程的精度取决于数据的质量和数量,需要谨慎选择拟合的次数。
利用最小二乘法在Matlab中拟合二次函数方程是一种常见且有效的数据分析方法,通过对实际数据进行拟合,可以更好地理解和分析数据规律。
一元二次方程 最小二乘法 克莱姆法则

一元二次方程最小二乘法克莱姆法则最小二乘法是一种常用的数学方法,用于求解一元二次方程的最优解。
而克莱姆法则是一种用于求解线性方程组的方法。
本文将介绍最小二乘法和克莱姆法则的原理及应用。
最小二乘法是一种通过最小化误差平方和来求解一元二次方程的方法。
它的基本思想是,通过找到一个最优解,使得方程的计算结果与观测值的差别最小化。
最小二乘法可用于拟合一条曲线到一组离散的数据点,以求得最优的拟合曲线。
最小二乘法的具体步骤如下:1. 假设一元二次方程的形式为 y = ax^2 + bx + c,其中a、b、c 为待求解的系数。
2. 假设有n个观测点,记为(x1, y1),(x2, y2),...,(xn, yn)。
3. 将观测点带入方程,得到n个方程:a(x1^2) + b(x1) + c = y1a(x2^2) + b(x2) + c = y2...a(xn^2) + b(xn) + c = yn4. 将这n个方程合并为一个矩阵形式:AX = Y,其中A为一个n×3的矩阵,X为一个3×1的矩阵,Y为一个n×1的矩阵。
5. 使用最小二乘法的原理,可以得到一个最优解X*,使得误差平方和最小。
最小二乘法的解析解为X* = (A^T A)^(-1) A^T Y。
6. 求得系数a、b、c后,即可得到拟合的一元二次方程。
克莱姆法则是一种用于求解线性方程组的方法。
它的基本思想是,通过求解方程组的行列式来得到未知数的值。
克莱姆法则适用于线性方程组的系数矩阵的行列式不为零的情况。
克莱姆法则的具体步骤如下:1. 假设有n个线性方程,形如:a11x1 + a12x2 + ... + a1nxn = b1a21x1 + a22x2 + ... + a2nxn = b2...an1x1 + an2x2 + ... + annxn = bn2. 将这n个方程的系数矩阵记为A,常数矩阵记为B,未知数矩阵记为X,即AX = B。
最小二乘法拟合二次方程

最小二乘法拟合二次方程一、概念与定义最小二乘法(Least Squares Method)是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配。
当处理的数据呈现某种趋势或模式时,如线性、二次或更高次的曲线,最小二乘法可以帮助我们找到最能代表这些数据的函数。
对于二次方程拟合,最小二乘法旨在找到一个形如(y = ax^2 + bx + c) 的二次函数,使得该函数与给定的数据点集之间的误差平方和最小。
这里的误差指的是每个数据点((x_i, y_i)) 到函数曲线上对应点((x_i, ax_i^2 + bx_i + c)) 的垂直距离。
二、性质最优性:最小二乘法得到的拟合曲线在误差平方和的意义下是最优的,即没有其他曲线能够使得误差平方和更小。
线性性:对于线性模型(包括二次模型),最小二乘法得到的解是线性的,即解可以通过数据的线性组合得到。
无偏性:在某些假设下(如误差项独立同分布,且期望为0),最小二乘法得到的估计量是无偏的,即估计量的期望等于真实参数值。
三、特点直观性:最小二乘法通过最小化误差平方和来寻找最佳拟合曲线,这一过程直观且易于理解。
计算简便:对于二次方程拟合,最小二乘法可以通过求解线性方程组来得到参数(a), (b), 和(c),计算过程相对简便。
适用性广:最小二乘法不仅适用于二次方程拟合,还可以扩展到更高次的多项式拟合以及其他类型的函数拟合。
四、规律在使用最小二乘法拟合二次方程时,我们通常会遵循以下步骤:收集数据:首先收集一组包含(x) 和(y) 值的数据点。
构建模型:根据数据点的分布趋势,构建一个形如(y = ax^2 + bx + c) 的二次模型。
计算误差平方和:对于给定的参数(a), (b), 和(c),计算每个数据点到模型曲线的垂直距离的平方和。
最小化误差平方和:通过调整参数(a), (b), 和(c) 的值,使得误差平方和达到最小。
这通常可以通过求解一个线性方程组来实现。
二元二次方程 最小二乘法

二元二次方程最小二乘法最小二乘法是一种常用的数据拟合方法,用来确定能够最小化观测数据和预测值之间的平方差的参数。
在统计学和数学建模领域中,最小二乘法被广泛应用于回归分析、数据拟合、误差分析等等。
在本文中,我们将重点讨论二元二次方程的最小二乘法拟合。
一元二次方程的标准形式为y = ax² + bx + c,其中a、b、c是待定参数。
同样地,二元二次方程的标准形式为z = ax² + by²+ cx + dy + e,其中a、b、c、d、e是待定参数。
现在的问题是,在给定一组观测数值(x, y, z)的情况下,我们如何通过最小二乘法估计这些参数的值。
首先,我们需要构建一个多元二次方程的矩阵方程。
令X = [x², y², x, y, 1]为待定参数的向量,令Z = [z]为观测值的向量。
那么,我们可以将二元二次方程表示为Z = AX,其中A是一个包含观测值的矩阵。
具体地,令X = [a, b, c, d, e],A = [[[x₁², y₁², x₁, y₁, 1] [x₂², y₂², x₂, y₂, 1] ... [xₙ², yₙ², xₙ, yₙ, 1]]]为一个n行5列的矩阵,Z = [z₁, z₂, ... , zₙ]为一个n行1列的向量。
那么,我们可以将AX表示为一个n行1列的向量。
接下来,我们需要最小化残差的平方和。
残差是观测值和预测值之间的差异,即r = Z - AX。
通过最小二乘法,我们可以最小化r的平方和来确定参数的值。
为了最小化残差平方和,我们需要求解方程A^TAX =A^TA^Z,其中^T表示矩阵的转置运算。
解得X = (A^TA)^(-1)A^TZ。
最后,我们可以使用计算机软件(如MATLAB、Python等)来实现最小二乘法的计算。
通过输入观测值的坐标和对应的数值,我们可以得到二元二次方程的最小二乘法拟合结果,包括参数的估计值以及拟合的曲面。
最小二乘法求二次方程系数

最小二乘法求二次方程系数例1:二次方程式计算Y=a0+a1x+a2 x2y=-6.3+2.4x+1.3x2下表为自动计算系数,给出9组x和y的数值,自动计算出系数。
x y x^2x^3x^4xy x^2y 11-2.6111-2.6-2.612 3.748167.414.81312.69278137.8113.41424.1166425696.4385.61538.2251256251919551654.93621612963291976.41774.24934324015193635.81896.16451240967696150.419120.681729656110859768.6求和945421.8285202515333303322997.4945285421.8452852025303328520251533322997.4系数系数值a0-6.30x ya1 2.40896.10a2 1.30原理与多项式拟合说明附后。
第一节 最小二乘法的基本原理和多项式拟合 一最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m)i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ,即误差 向量T m r r r r ),,(10 =的∞—范数;二是误差绝对值的和∑=mi ir 0,即误差向量r 的1—范数;三是误差平方和∑=mi ir02的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ),(i i y x (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即∑=mi ir 02=[]∑==-mi ii y x p 02min)(从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线)(x p y =(图6-1)。
f(x,y)的二次多项式拟合方程

f(x,y)的二次多项式拟合方程是指利用二元变量x和y的数值数据,通过二次多项式函数拟合出一个与实际数据最接近的方程。
这种拟合方程可以用于分析x和y之间的关系,并预测未知数据点的数值。
1. 二次多项式拟合方程的一般形式二次多项式拟合方程的一般形式如下:f(x,y) = ax^2 + by^2 + cxy + dx + ey + f其中,a、b、c、d、e、f为拟合方程的系数,x和y为自变量,f(x,y)为因变量。
2. 拟合方程的求解方法为了求解二次多项式拟合方程的系数,可以利用最小二乘法进行拟合。
最小二乘法是一种优化方法,旨在使拟合方程的预测值与实际观测值的误差平方和最小化。
具体求解过程可以通过数值计算软件进行,例如Matlab、Python等。
通过给定的x和y的数值数据,利用最小二乘法,可以得到拟合方程的系数,从而得到最终的拟合方程。
3. 拟合方程的应用二次多项式拟合方程在实际应用中具有广泛的用途。
在工程领域中,可以利用二次多项式拟合方程来分析材料的性能,预测材料的强度和耐久性等。
在经济学和金融学领域中,可以利用二次多项式拟合方程来分析市场变化趋势,预测股票价格等。
在科学研究中,二次多项式拟合方程也可以用于分析实验数据,寻找变量之间的关系等。
4. 拟合方程的评估在利用二次多项式拟合方程进行数据拟合时,需要对拟合结果进行评估,以确保拟合方程的准确性和可靠性。
常用的评估方法包括拟合曲线的拟合优度R²值、残差分析等。
拟合优度R²值是衡量拟合方程对原始数据拟合程度的指标,取值范围为0至1,值越接近1表示拟合效果越好。
残差分析是评估拟合方程预测值与实际观测值之间误差的方法,通过残差分析可以发现拟合方程的预测误差是否均匀分布、是否存在系统性偏差等。
5. 拟合方程的局限性尽管二次多项式拟合方程在许多领域有着广泛的应用,但也存在一定的局限性。
在一些非线性关系较强的数据拟合中,二次多项式拟合方程可能无法很好地反映实际关系;拟合方程的高阶项系数可能受噪声干扰较大,导致拟合效果不佳。
一元二次方程 最小二乘法 克莱姆法则

一元二次方程最小二乘法克莱姆法则一、一元二次方程一元二次方程是指形如ax²+bx+c=0的方程,其中a、b、c为已知实数,且a≠0。
这个方程的解可以通过求根公式或配方法来求得。
二、最小二乘法最小二乘法是一种数学优化方法,用于拟合数据,找到最佳的函数曲线与数据点的拟合程度。
它的基本思想是通过最小化数据点到拟合曲线的垂直距离的平方和,来确定拟合曲线的参数。
三、克莱姆法则克莱姆法则是一种求解线性方程组的方法,它通过计算方程组的系数行列式和各个未知数对应行列式的比值,来求得方程组的解。
克莱姆法则适用于未知数个数与方程个数相同的线性方程组。
下面我们将分别对一元二次方程最小二乘法和克莱姆法则进行详细解释。
一、一元二次方程最小二乘法在实际问题中,我们常常需要拟合一些数据,以便得到一个函数曲线来描述这些数据的分布规律。
而一元二次方程最小二乘法可以帮助我们找到最佳的二次函数曲线与数据点的拟合程度。
具体来说,我们可以通过最小化数据点到拟合曲线的垂直距离的平方和来确定二次函数曲线的参数。
这里的垂直距离就是数据点到拟合曲线的纵坐标的差值,平方和则是将所有数据点的垂直距离的平方相加。
通过求解这个平方和的最小值,我们可以得到最佳的二次函数曲线。
二、克莱姆法则克莱姆法则是一种求解线性方程组的方法,它通过计算方程组的系数行列式和各个未知数对应行列式的比值,来求得方程组的解。
对于一个线性方程组,如果未知数个数与方程个数相同,且系数行列式不为零,那么可以使用克莱姆法则来求解。
具体步骤如下:1. 计算方程组的系数矩阵的行列式,记为D。
2. 将方程组的右侧常数项依次替换系数矩阵的每一列,并计算其行列式,分别记为D1、D2、D3...。
3. 未知数的解依次为D1/D、D2/D、D3/D...。
需要注意的是,克莱姆法则虽然简单易懂,但在实际应用中往往不是最优解法。
当方程组的规模较大时,求解过程中需要计算大量的行列式,计算量非常大,效率较低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:二次方程式计算Y=a0+a1x+a2 x2y=-6.3+2.4x+1.3x2下表为自动计算系数,给出9组x和y的数值,自动计算出系数。
x y x^2x^3x^4xy x^2y 11-2.6111-2.6-2.612 3.748167.414.81312.69278137.8113.41424.1166425696.4385.61538.2251256251919551654.93621612963291976.41774.24934324015193635.81896.16451240967696150.419120.681729656110859768.6求和945421.8285202515333303322997.4945285421.8452852025303328520251533322997.4系数系数值a0-6.30x ya1 2.40896.10a2 1.30原理与多项式拟合说明附后。
第一节 最小二乘法的基本原理和多项式拟合 一 最小二乘法的基本原理从整体上考虑近似函数)(x p 同所给数据点),(i i y x (i=0,1,…,m)误差i i i y x p r -=)((i=0,1,…,m) 的大小,常用的方法有以下三种:一是误差i i i y x p r -=)((i=0,1,…,m)绝对值的最大值im i r ≤≤0max ,即误差 向量T m r r r r ),,(10 =的∞—范数;二是误差绝对值的和∑=mi ir 0,即误差向量r 的1—范数;三是误差平方和∑=mi ir02的算术平方根,即误差向量r 的2—范数;前两种方法简单、自然,但不便于微分运算 ,后一种方法相当于考虑 2—范数的平方,因此在曲线拟合中常采用误差平方和∑=mi ir02来 度量误差i r (i=0,1,…,m)的整体大小。
数据拟合的具体作法是:对给定数据 ),(i i y x (i=0,1,…,m),在取定的函数类Φ中,求Φ∈)(x p ,使误差i i i y x p r -=)((i=0,1,…,m)的平方和最小,即∑=mi ir 02=[]∑==-mi i i y x p 02min)(从几何意义上讲,就是寻求与给定点),(i i y x (i=0,1,…,m)的距离平方和为最小的曲线 )(x p y =(图6-1)。
函数)(x p 称为拟合 函数或最小二乘解,求拟合函数)(x p 的方法称为曲线拟合的最小二乘法。
在曲线拟合中,函数类Φ可有不同的选取方法.6—1二 多项式拟合假设给定数据点),(i i y x (i=0,1,…,m),Φ为所有次数不超过)(m n n ≤的多项式构成的函数类,现求一Φ∈=∑=nk k k n x a x p 0)(,使得[]min)(00202=⎪⎭⎫ ⎝⎛-=-=∑∑∑===mi mi n k i k i k i i n y x a y x p I (1)当拟合函数为多项式时,称为多项式拟合,满足式(1)的)(x p n 称为最小二乘拟合多项式。
特别地,当n=1时,称为线性拟合或直线拟合。
显然∑∑==-=m i nk i k i k y x a I 02)(为n a a a ,,10的多元函数,因此上述问题即为求),,(10n a a a I I =的极值 问题。
由多元函数求极值的必要条件,得n j x y x a a Im i j i nk i k i k j ,,1,0,0)(200==-=∂∂∑∑== (2)即nj y x a xn k mi i j i k mi k j i,,1,0,)(000==∑∑∑===+ (3)(3)是关于n a a a ,,10的线性方程组,用矩阵表示为⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+∑∑∑∑∑∑∑∑∑∑∑=====+==+====m i i n i m i i i m i i n mi n imi n imi n i mi n i mi im i imi nimi iy x y x y a a a x xx x xxx x m 00010020101020001(4) 式(3)或式(4)称为正规方程组或法方程组。
可以证明,方程组(4)的系数矩阵是一个对称正定矩阵,故存在唯一解。
从式(4)中解出k a (k=0,1,…,n),从而可得多项式∑==nk kk n x a x p 0)( (5)可以证明,式(5)中的)(x p n 满足式(1),即)(x p n 为所求的拟合多项式。
我们把[]∑=-mi i i ny x p2)(称为最小二乘拟合多项式)(x p n 的平方误差,记作[]∑=-=mi i i n y x p r0222)(由式(2)可得∑∑∑===-=mi nk mi i k i k i y x a y r222)( (6)多项式拟合的一般方法可归纳为以下几步:(1) 由已知数据画出函数粗略的图形——散点图,确定拟合多项式的次数n ;(2) 列表计算∑==mi j in j x)2,,1,0( 和∑==mi ij in j y x)2,,1,0( ;(3) 写出正规方程组,求出n a a a ,,10; (4) 写出拟合多项式∑==nk kk n x a x p 0)(。
在实际应用中,m n <或m n ≤;当m n =时所得的拟合多项式就是拉格朗日或牛顿插值多项式。
例1 测得铜导线在温度i T (℃)时的电阻)(Ωi R 如表6-1,求电阻R 与温度 T数为T a a R 10+=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡445.200295.56583.93253.2453.245710a a解方程组得921.0,572.7010==a a故得R 与T 的拟合直线为T R 921.0572.70+=利用上述关系式,可以预测不同温度时铜导线的电阻值。
例如,由R=0得T=-242.5,即预测温度 T=-242.5℃时,铜导线无电阻。
6-2例2 例2 已知实验数据如下表解 设拟合曲线方程为2210x a x a a y ++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡102514732253173017381301738152381529210a a a解得2676.06053.3,4597.13210=-==a a a故拟合多项式为22676.06053.34597.13x y +-=*三 最小二乘拟合多项式的存在唯一性定理1 设节点n x x x ,,,10 互异,则法方程组(4)的解存在唯一。
证 由克莱姆法则,只需证明方程组(4)的系数矩阵非奇异即可。
用反证法,设方程组(4)的系数矩阵奇异,则其所对应的齐次方程组⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+∑∑∑∑∑∑∑∑∑∑∑=====+==+====m i i n i m i i i m i i n mi n i mi n i m i n i mi n i mi im i imi nimi i y x y x y a a a x x x x x x x x m 00010020101020001(7) 有非零解。
式(7)可写为nj a xn k k mi k j i,,1,0,0)(0==∑∑==+ (8)将式(8)中第j 个方程乘以j a (j=0,1,…,n),然后将新得到的n+1个方程左右两端分别 相加,得∑∑∑===+=⎥⎦⎤⎢⎣⎡nj n k k m i k j i j a x a 00000)( 因为[]∑∑∑∑∑∑∑∑∑∑=======+===+===⎥⎦⎤⎢⎣⎡m i m i mi in n k ki k n j j i j n j n k k j i j k n j n k k m i k j i j x p x a x a x a a a x a 00020000000)())(()( 其中∑==nk kk n x a x p 0)(所以0)(=i n x p (i=0,1,…,m))(x p n 是次数不超过n 的多项式,它有m+1>n 个相异零点,由代数基本定理,必须有010===n a a a ,与齐次方程组有非零解的假设矛盾。
因此正规方程组(4)必有唯一解 。
定理2 设n a a a ,,1,0 是正规方程组(4)的解,则∑==nk kk n x a x p 0)(是满足式(1)的最小二乘拟合多项式。
证 只需证明,对任意一组数nb b b ,,1,0 组成的多项式∑==nk kk n x b x Q 0)(,恒有[][]∑∑==-≥-mi i i n m i i i n y x p y x Q 022)()(即可。
[][][][][][]()∑∑∑∑∑∑∑∑∑∑==========⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎥⎦⎤⎢⎣⎡-⋅-+≥-⋅-+-=---n j mi j i n k i ki k j j m i nj n k i k i k ji j j i i n mi i n i n m i i n i n mi i i n mi i i nx y x a a b y x a x a b y x p x p x Q x p x Q y x p y x Q00000002222)(20)()()(2)()()()(因为k a (k=0,1,…,n)是正规方程组(4)的解,所以满足式(2),因此有[][]0)()(022≥---∑∑==mi i i n mi i i n y x p y x Q故)(x p n 为最小二乘拟合多项式。
*四 多项式拟合中克服正规方程组的病态在多项式拟合中,当拟合多项式的次数较高时,其正规方程组往往是病态的。
而且①正规方程组系数矩阵的阶数越高,病态越严重;②拟合节点分布的区间[]m x x ,0偏离原点越远,病态越严重; ③i x (i=0,1,…,m)的数量级相差越大,病态越严重。
为了克服以上缺点,一般采用以下措施:①尽量少作高次拟合多项式,而作不同的分段低次拟合;②不使用原始节点作拟合,将节点分布区间作平移,使新的节点i x 关于原 点对称,可大大降低正规方程组的条件数,从而减低病态程度。
平移公式为:mi x x x x mi i ,,1,0,20 =+-= (9) ③对平移后的节点i x (i=0,1,…,m),再作压缩或扩张处理:m i x p x i i ,,1,0,==* (10) 其中r mi rix m p 202)()1(∑=+=,(r 是拟合次数) (11)经过这样调整可以使*i x 的数量级不太大也不太小,特别对于等距节点),,1,0(0m i ih x x i =+=,作式(10)和式(11)两项变换后,其正规方程组的系数矩阵设 为A ,则对1~4次多项式拟合,条件数都不太大,都可以得到满意的结果。
