运筹学第1章
《运筹学》课件 第一章 线性规划

10
解:令
xi=
1, Si被选中
min z= ci xi i 1 10
0, Si没被选中
xi 5
i 1
x1 x8 1 x7 x8 1
称为技术系数
b= (b1,b2, …, bm) 称为资源系数
2、非标准型
标准型
(1)Min Z = CX
Max Z' = -CX
(2)约束条件
• “≤”型约束,加松弛变量;
松弛变量
例如: 9 x1 +4x2≤360
9 x1 +4x2+ x3=360
• “≥”型约束,减松弛变量;
例、将如下问题化为标准型
数据模型与决策 (运筹学)
课程教材:
吴育华,杜纲. 《管理科学基础》,天津大学出版社。
绪论
一、运筹学的产生与发展
运筹学(Operational Research) 直译为“运作研究”。
• 产生于二战时期 • 60年代,在工业、农业、社会等各领域得到广泛应用 • 在我国,50年代中期由钱学森等引入
Min z x1 2x2 3x3
x1 x2 x3 7
s.t
.
x1 x2 x3 3x1 x2 2
x3
2
5
x1, x2 , x3 0
解:令 Min z Max z' (z' z) ,第一个约束加松弛变量x5,
第二个约束减松弛变量x6,得标准型:
Max z' x1 2x2 +3x3
x1 x2 x3 x4 7
s.t .
x1 x2 3x1
x3 x2
x5 2 2x3 5
x1 , , x5 0
运筹学-第一章-单纯形法基本原理
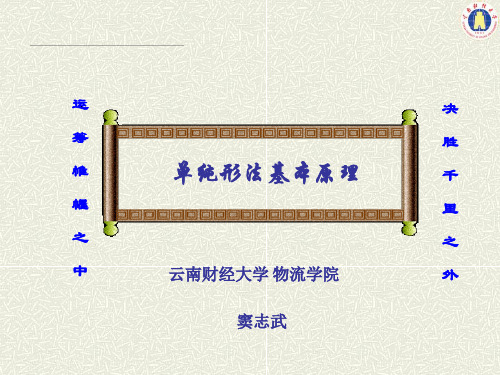
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义:两个基可行解称为相邻的,如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量,
X
凸集
顶点
凸集
不是凸集
顶点:如果凸集C中不存在任何两个不同的点X1,X2,使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1:若线性规划问题存在可行解,则该问题的可行域是 凸集。 定理2:线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3:若问题存在最优解,一定存在一个基可行解是最优 解。(或在某个顶点取得)
的左边变成一个单位矩阵,
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中: i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限,
运筹学第1章-线性规划

下一页 返回
图解法步骤:
(1)建立坐标系; (2)将约束条件在图上表示; (3)确立满足约束条件的解的范围; (4)绘制出目标函数的图形 (5)确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题,对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制,即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器,应如何裁剪,使做成的窗口的容积为最 大?
解:设 x1, x2分别表示从A,B两处采购的原油量(单
位:吨),则所有的采购方案的最优方案为:
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式,其中模型(1-7)较为常用。
运筹学基础及应用课后习题答案(第一二章习题解答)

运筹学基础及应用课后习题答案(第一二章习题解答)第一章:线性规划一、选择题1. 线性规划问题中,目标函数可以是()A. 最大化B. 最小化C. A和B都对D. A和B都不对答案:C解析:线性规划问题中,目标函数可以是最大化也可以是最小化,关键在于问题的实际背景。
2. 在线性规划问题中,约束条件通常表示为()A. 等式B. 不等式C. A和B都对D. A和B都不对答案:C解析:线性规划问题中的约束条件通常包括等式和不等式两种形式。
二、填空题1. 线性规划问题的基本假设是______。
答案:线性性2. 线性规划问题中,若决策变量个数和约束条件个数相等,则该问题称为______。
答案:标准型线性规划问题三、计算题1. 求解以下线性规划问题:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 83x + 4y ≤ 12x, y ≥ 0答案:最优解为 x = 4, y = 2,最大值为 Z = 14。
解析:画出约束条件的图形,找到可行域,再求目标函数的最大值。
具体步骤如下:1) 将约束条件化为等式,画出直线;2) 找到可行域的顶点;3) 将顶点代入目标函数,求解最大值。
第二章:非线性规划一、选择题1. 以下哪个方法适用于求解非线性规划问题()A. 单纯形法B. 拉格朗日乘数法C. 柯西-拉格朗日乘数法D. A和B都对答案:B解析:非线性规划问题通常采用拉格朗日乘数法求解,单纯形法适用于线性规划问题。
2. 非线性规划问题中,以下哪个条件不是K-T条件的必要条件()A. 梯度条件B. 正则性条件C. 互补松弛条件D. 目标函数为凸函数答案:D解析:K-T条件包括梯度条件、正则性条件和互补松弛条件,与目标函数是否为凸函数无关。
二、填空题1. 非线性规划问题中,若目标函数和约束条件都是凸函数,则该问题称为______。
答案:凸非线性规划问题2. 非线性规划问题中,K-T条件是求解______的必要条件。
运筹学课程章节

对照教学大纲
第1章 线性规划 章
• 线性规划基本理论:模型形式,解的概念, 线性规划基本理论:模型形式,解的概念, 解的性质等 • 线性规划应用:6类问题建模 线性规划应用: 类问题建模 类问题建模* • 图解法 图解法* • 单纯形法:基本单纯形法 ,大M法,两阶 单纯形法:基本单纯形法*, 法 段法, 段法,前者重要
第2章 线性规划的对偶理论
• • • • • 对偶问题的构建:对偶规划 对偶问题的构建:对偶规划* 对偶问题的性质 运用对偶性质进行线性规划求解* 运用对偶性质进行线性规划求解* 影子价格理解* 影子价格理解 灵敏度分析*和参数分析 灵敏度分析 和参数分析
第4章 目标规划
• 目标规划建模* 目标规划建模 • 图解法
第5章 运输问题和指派问题
• 运输问题表示:语言描述,表格表示,数 运输问题表示:语言描述,表格表示, 学模型表示, 学模型表示,几何图形表示 • 标准运输问题的表上作业法 标准运输问题的表上作业法* • 表格建模 :应用,建立运输问题的供需平 表格建模*:应用, 衡与单位运价表, 衡与单位各位同学的选择 • 祝各位同学 考试顺利通过并取得好成绩
• 指派问题表示:语言描述,表格表示,数 指派问题表示:语言描述,表格表示, 学模型表示, 学模型表示,几何图形表示 • 表格建模:应用,指派问题的指派平衡与 表格建模:应用, 单位效率表 • 指派问题的匈牙利算法
第6章 网络模型
• 最优生成树问题 :最小树,最大树 最优生成树问题*:最小树, • 最短路问题*:三种算法,有向图法,无向 最短路问题*:三种算法,有向图法, 图法, 图法,表格法 • 最大流问题 :可行流法,增广链法 最大流问题*:可行流法,
运筹学课程讲义

运筹学课程讲义第一部分线性规划第一章线性规划的基本性质1.1 线性规划的数学模型一、线性规划问题的特点胜利家具厂生产桌子和椅子两种家具。
桌子售价50 元/个,椅子售价30 元/个。
生产桌子和椅子需木工和油漆工两种工种。
生产一个桌子需要木工4 小时,油漆工2小时。
生产一个椅子需要木工3 小时,油漆工1 小时。
该厂每月可用木工工时为120 小时,油漆工工时为50 小时。
问该厂如何组织生产才能使每月的销售收入最大?max z 50x1 30x24x1 3x2 1202x1 x2 50x1,x2 0 例:某工厂生产某一种型号的机床。
每台机床上需要 2.9m、2.1m、1.5m的轴,分别为1根、2根和1根。
这些轴需用同一种圆钢制作,圆钢的长度为74m。
如果要生产100台机床,问应如何安排下料,才能用料最省?二、数学模型的标准型1. 繁写形式2. 缩写形式3. 向量形式4. 矩阵形式若原模型中变量 x j 有上下界,如何化为非负变量?三、 任一模型如何化为标准型?1. 若原模型要求目标函数实现最大化,如何将其化为最小化问题?2. 若原模型中约束条件为不等式,如何化为等式?3. 若原模型中变量 x k 是自由变量,如何化为非负变量?1. 2 图解法该法简单直观,平面作图适于求解二维问题。
使用该法求解线性规划问题时,不必把原模型化为标准型。
一、 图解法步骤1. 由全部约束条件作图求出可行域2. 作出一条目标函数的等值线3. 平移目标函数等值线,作图求解最优点,再算出最优值 max z 5x 1 6x 2 7x 3x 1 5x 23x 3 15 5x 1 6x 210x 3 20 x 1 x 2 x 3 5x 1 0,x 2 0,x 3无约束令 x 1' x 1,x 3 x 3' x 3'',x 3' ,x 3'' 0, Z 1Z ' 1 1 min z ' 5x 1' 6x 2 7x 3' 7x 3'' 0x 5 Mx 6 1 x 1' 5x 2 1 11 3x 3' 3x 3'' x 4 x 6 15 1 5x 1' 6x 2 10x 3' 10x 3'' x 5 20 1 x ' x 1 ' II '' 54.Mx 7 x 1, x 2 , x 3, x 3, x 4 , x 5 ,x 6, x 7 0从图解法看线性规划问题解的几种情况1. 有唯一最优解2. 有无穷多组最优解3. 无可行解4. 无有限最优解(无界解)min z 6x1 4x?2x〔X2 13 最优解(1,0),最优值33x14x2 22x1, x20直观结论:1)线性规划问题的可行域为凸集,特殊情况下为无界域(但有有限个顶点)或空集;2)线性规划问题若有最优解,一定可以在其可行域的顶点上得到。
运筹学

11
目录
(三)LP问题的标准型
1.为了讨论LP问题解的概念和解的性质以及对LP问题求 解方便,必须把LP问题的一般形式化为统一的标准型:
minz=c1x1+c2x2+…+cnxn
j =1 a11 x2 + a12 x2 + + a1n xn = b1 a x + a x + + a x = b n 2n n 2 21 2 22 2 简 aij x j = bi (i = 1,2, L , m) s.t 化 j =1 x j ≥ 0( j = 1,2,L , n) am1 x2 + am 2 x2 + + amn xn = bm x1 , x2 , , xn ≥ 0
A ( 0 ,3 ) 10 15 , ) B( 7 7 5 C ( ,0 ) 2
max
Z = 5 x1 + 4 x 2
3 x 1 + 5 x 2 ≤ 15 2 x1 + x 2 ≤ 5 2 x 1 + 2 x 2 ≤ 11 x1 , x 2 ≥ 0
Z=
110 7
2x1+2x2=11
C 2.5
5x1+4x2=0 红线为目标函数的等值线 等值线. 红线为目标函数的等值线
j i= 1
j
(1.4) (1.5) (1.6)
ì n a ij x j = s .t . j = 1 í 1.从代数的角度看: x j 0 1.
b
i
可行解(Feasible Solution): 满足约束条件(1.5)和(1.6)的 解X=(x1,x2,…,xn)T称为可行解。所有可行解构成可行解集, 即可行域。 最优解(Optimal Solution): 而使目标函数达到最大值的可 行解称为最优解,对应的目标函数值称为最优值。 求解LP问题就是求其最优解和最优值,但从代数的角 17 度去求是困难的。 目录
运筹学第1章:线性规划问题及单纯型解法

原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8
运筹学第一章 1.4 大M法和两阶段法

(2)写出初始基本可行解 )写出初始基本可行解——
根据“ 用非基变量表示基变量的表达式” 根据 “ 用非基变量表示基变量的表达式 ” , 非基变量取0 算出基变量, 非基变量取0,算出基变量,搭配在一起构成 初始基本可行解。 初始基本可行解。 2、建立判别准则: 建立判别准则: (1)两个基本表达式的一般形式 LP限制条件中全部是 LP限制条件中全部是“≤”类型约束,新 限制条件中全部是“ 类型约束, 增的松弛变量作为初始基变量的情况来描述: 增的松弛变量作为初始基变量的情况来描述 :
2、处理人工变量的方法: 处理人工变量的方法:
(1)大M法——在约束条件中人为地加入非负 在约束条件中人为地加入非负 的人工变量, 的人工变量,以便使它们对应的系数列向量构 成单位阵。 成单位阵。 问题:加入的人工变量是否合理?如何处理? 问题:加入的人工变量是否合理?如何处理? 目标函数中, 在目标函数中,给人工变量前面添上一个绝对 值很大的负系数M>>0 迭代过程中, 值很大的负系数 -M ( M>>0 ) , 迭代过程中 , 只要基变量中还存在人工变量, 只要基变量中还存在人工变量,目标函数就不 可能实现极大化——惩罚! 惩罚! 可能实现极大化 惩罚
σj =cj −zj =cj −∑ a c
i= 1
m
' n+i ij
(2)最优性判别定理
若 X = (0,0,L0,b ,b ,Lb ) 是对应于基B的基本 是对应于基B , , 可行解, 的检验数, 可行解,σ j 是非基变量 x (j0) 的检验数,若对 于一切非基变量的角指标j 于一切非基变量的角指标j,均有 σ j ≤0,则 X(0)为最优解。 为最优解。
最优性判别定理; 最优性判别定理;无“有限最优解”判断定理 有限最优解”
运筹学(重点)

两个约束条件
(1/3)x1+(1/3)x2=1
及非负条件x1,x2 0所代表的公共部分
--图中阴影区, 就是满足所有约束条件和非负
条件的点的集合, 即可行域。在这个区域中的每
一个点都对应着一个可行的生产方案。
22
5–
最优点
4–
l1 3B E
2D
(1/3)x1+(4/3)x2=3
l2 1–
0 1〡 2〡 3A 4〡 5〡 6〡 7〡 8〡 9〡C
运筹学 Operational Research
运筹帷幄,决胜千里
史记《张良传》
1
目录
绪论 第一章 线性规划 第二章 运输问题 第三章 整数规划 第四章 动态规划 第五章 目标规划 第六章 图与网络分析
2
运筹学的分支 数学规划: 线性规划、非线性规划、整数规划、 动态规划、目标规划、多目标规划 图论与网络理论 随机服务理论: 排队论 存储理论 决策理论 对策论 系统仿真: 随机模拟技术、系统动力学 可靠性理论
32
西北角
(一)西北角法
销地
产地
B1
0.3
A1
300
0.1 A2
0.7 A3
销量 300
B2
1.1
400
0.9
200
0.4
600
B3
0.3
0.2
200
1.0
300 500
B4
产量
1.0
700 ②
0.8
400 ④
0.5
600
900 ⑥
600
2000
①
③
⑤
⑥
34
Z
cij xij 0.3 300 1.1 400 0.9 200
运筹学第一章

30
1.1.3解的概念
概念: 1、可行解:满足所有约束条件的解。 2、可行域:即可行解的集合。所有约束条件的交 集,也就是各半平面的公共部分。满足所有约 束条件的解的集合,称为可行域。 3、凸集:集合内任意两点的连线上的点均属于这 个集合。如:实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
(无界解)
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
(无解)
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士?
5
例题2建模
目标函数:min Z=x1+x2+x3+x4+x5+x6 约束条件: x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束:xj ≥0,j=1,2,…6
OR1
6
例题3:运输问题
三个加工棉花的加工厂,并且有三个仓库供应棉花,各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示:问如何运输才能使总的运费最小?
OR1
14
总
结
从以上 5 个例子可以看出,它们都属于优化问题,它们 的共同特征: 1 、每个问题都用一组决策变量表示某一方案;这组决 策变量的值就代表一个具体方案,一般这些变量取值是 非负的。 2 、存在一定的约束条件,这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标,它可用决策变量的线性 函数(称为目标函数)来表示。按问题的不同,要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。
运筹学讲义第1章

(2) 和式: max z= cjxj
j=1
n
s.t.
aijxj≤bi (i=1,2,……,m)
j=1
n
xj≥ 0
(j=1,2,……,n)
其中:cj---------表示目标函数系数 aij---------表示约束条件系数 bi ---------表示约束右端项
2007/08
-7-
---第 1 章 线性规划---
起迄时间 2----6 时 6---10 时 10--14 时 14--18 时 18--22 时 22---2 时
2007/08
服务员人数 4 8 10 7 12 4
-18-
---第 1 章 线性规划---
建立线性规划模型要求:
(1)要求决策的量是连续的、可控的量,或 者是可以简化为连续取值的变量;
1
n
xj≥0
(j=1,2,……,n)
(1)可行解:满足所有约束方程和变量符号限制条件的一组变量的 取值。 (2)可行域:全部可行解的集合称为可行域。 (3)最优解:使目标函数达到最优值的可行解。
2007/08 -20-
---第 1 章 线性规划---
(4)基:设A为线性规划模型约束条件系数矩阵(m n,m<n), 而B为其mm子矩阵,若|B|≠0,则称B为该线性规划模型的一个基。
可行解:X=(0,0)T,X=(0,1)T,X=(1/2,1/3)T 等。 x3 x4 ——基变量 x x x x
1 2 3 4
设
A=
1 1
1 2
1
0
0
1
,令 B=
1
0
0
1
,则 | B |=1≠0,
运筹学

12X1 + 6X2 ≤ 600 X1≥0,X2 ≥0 使 max f(x)=7X1 + 5X2
3.合理配料模型
例1-5 用三种原料A1、A2、A3配制一种食品,要求该食品中 蛋白质、脂肪、碳水化合物和维生素的含量分别不低于150、 200、250、300个单位,这三种原料的单价及每单位原料所含各 种成份的数量如表1-6所示。问如何配制这种食品,使成本最低?
X2 = 18 maxf(x) = 2600
第三节
解的结构
线性规划的解有三种情况:有最优解、有解但无 最优解和无可行解。有最优解又有两种情况:有惟一 的最优解和有无穷多个最优解。 当线性规划的约束条件中出现矛盾约束时,即二 元一次不等式组无解时,线性规划问题无可行解。
在例2-1中,加一个约束条件: 求x1,x2
令f(x)=-f(x) ′ 则maxf(x)=-min[-f(x)] =-minf(x) ′
例1-14 将下列线性规划数学模型化为标准形式: 求 x1,x2,x3
2x1 +
x2 + x3
≤ 8
满足
x1
-
x2
x2
+
x3
≥ 3
3x1 -
– 2x3 ≤ -5
≥0,X3是自由变量
X1≥0,x2
使 maxf(x) = x1 – 2x2 + 3x3
解:令X3=X4-X5,其中X4≥0,X5≥0, 在第一个约束条件的左边加入一个松驰变量X6,化为等式; 在第二个约束条件的左边减去一个松驰变量X7,化为等式; 在第三个约束条件的左边加入一个松驰变量X8,化为等式; 并且等式两边同乘以-1; 将求 maxf(x) = X1 - 2X2 + 3X3 化为求
运筹学 第01章 线性规划问题

线性规划建模步骤
设定决策变量 明确约束条件并用决策变量的线性等式或 不等式表示 用变量的线性函数表示要达到的目标,并 确定是求极小还是求极大 根据变量的物理性质确定变量是否具有非 负性 注:其中最关键是设定决策变量这一步
生产计划问题(1)
某工厂用三种原料生产三种产品,已知的 条件如下表所示,试制订总利润最大的日 生产计划
线性规划问题解的有关概念(2)
基本解:令模型中所有非基变量的值等于零后,由 模型的约束方程组得到的一组解。 基本可行解:满足非负条件的基本解称为基本可行 解。 可行基:对应于基本可行解的基称为可行基。 退化解:基本可行解的非零分量个数小于m时,称 为退化解。 最优基:若对应于基B的基本可行解X是线性规划的 最优解,则称B为线性规划的最优基
人员安排问题(1)
医院护士24小时值班,不同时段需要的护 士人数不等(见下表)。每个护士每天连 续值班8小时,在各时段开始时上班。问最 少需要多少护士?
序号 1 2 3 4 时段 06—10 10—14 14—18 18—22 最少人数 60 70 60 50
5 6
22—02 02—06
20 30
人员安排问题(2)
设xj为第j时段开始值班的护士人数
目标函数为:使人数最少,则有
min f ( X ) x1 x2 x3 x4 x5 x6 x6 x1 60 x x 70 1 2 x2 x3 60 s.t. x3 x4 50 x x 20 5 4 x5 x6 30 x1 , x2 , x3 , x4 , x5 , x6 0且为整数
运筹学
第一章 线性规划问题
本章重点
线性规划建模 线性规划的图解法 线性规划的标准形式 单纯形法 两阶段法 大M法
运筹学1至6章习题参考答案
0
2
11/8
0
-3/4
0
9
X4
0
0
0
9/8
1
7/16
-1/4
27/4
6
X1
3
1
0
-1/2
0
1/4
0
3
M
X2
2
0
1
[11/16]
0
-3/32
1/8
1/8
0.181818
C(j)-Z(j)
0
0
0
0
-9/16
-1/4
37/4
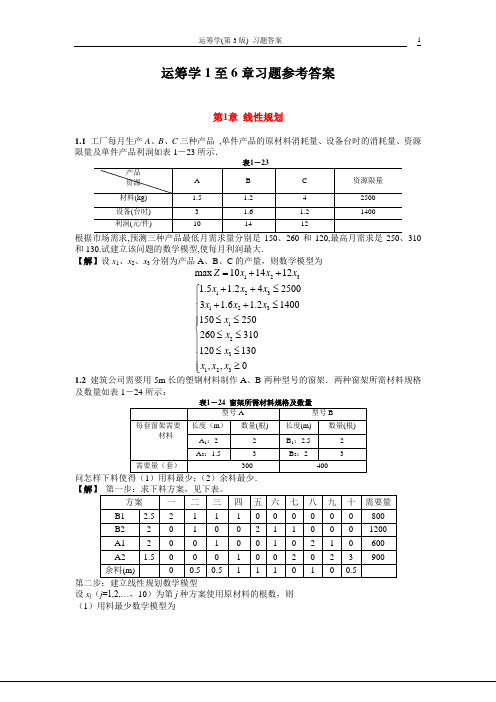
X3进基、X2出基,得到另一个基本最优解。
C(j)
3
2
-0.125
6重油
7残油
辛烷值
80
115
105
蒸汽压:公斤/平方厘米
1.0
1.5
0.6
0.05
每天供应数量(桶)
2000
1000
1500
1200
1000
1000
800
问炼油厂每天生产多少桶成品油利润最大,建立数学模型。
解设xij为第i(i=1,2,3,4)种成品油配第j(j=1,2,…,7)种半成品油的数量(桶)。
10
-5
1
0
0
0
* Big M
5
3
1
0
0
0
X1
10
1
3/5
1/5
0
1/5
2
X4
0
0
4
-9
1
1
25
C(j)-Z(j)
0
-11
-1
运筹学第1章线性规划及单纯形法复习题

max (min)
Z = CX
AX ≤ ( = , ≥ ) b X ≥ 0
3、线性规划的标准形式 、
ma0
4、线性规划问题的解 、 (一)求解方法
一 般 有 两种方法 图 解 法 单纯形法 两个变量、 两个变量、直角坐标 三个变量、 三个变量、立体坐标
适用于任意多个变量、 适用于任意多个变量、但需将 一般形式变成标准形式
(二)线性规划问题的解
1、解的概念 可行解:满足约束条件② 的解为可行解。 ⑴ 可行解:满足约束条件②、③的解为可行解。 所有解的集合为可行解的集或可行域。 所有解的集合为可行解的集或可行域。 最优解: 达到最大值的可行解。 ⑵ 最优解:使目标函数①达到最大值的可行解。 ⑶ 基:B是矩阵A中m×m阶非奇异子矩阵 是矩阵A ≠0), ),则 是一个基。 (∣B∣≠0),则B是一个基。
§2 图 解 法
例一、 例一、 max
Z = 2 x 2 x 2 x 4 x
2 2 1
+ 3 x
2
2 x1 + x + 1 4 x1 x1 ≥
≤ 12 ≤ 8 ≤ 16 ≤ 12
2
⑴ ⑵ ⑶ ⑷
2
0, x
≥ 0
max
Z = 2 x1 + 3 x 2 x 2 x
2 2
当xj=0时, 必有 j=zj=0, 因此 时 必有y
∑P x = ∑P y = ∑P z
j =1
r
r
r
r
j
j
j =1
j
j
j =1
j
j
=b
∑(y
j =1
j
− z j ) Pj = 0
运筹学第一章

第一章、 线性规划和单纯形法1.1 线性规划的概念一、线性规划问题的导出1.(引例) 配比问题——用浓度为45%和92%的硫酸配置100t 浓度为80%的硫酸。
取45%和92%的硫酸分别为x1和x2t,则有: 求解二元一次方程组得解。
目的相同,但有5种不同浓度的硫酸可选(30%,45%,73%,85%,92%)会出现什么情况?设取这5种硫酸分别为 x1、x2、x3、x4、x5 t, 则有: ⎩⎨⎧⨯=++++=++++1008.092.085.073.045.03.01005432154321x x x x x x x x x x 请问有多少种配比方案?为什么?哪一种方案最好?假设5种硫酸价格分别为:400,700,1400,1900,2500元/t ,则有:2.生产计划问题如何制定生产计划,使三种产品总利润最大?考虑问题:⎩⎨⎧⨯=+=+1008.092.045.01002121x x x x ⎪⎩⎪⎨⎧=≥⨯=++++=++++++++=5,,2,1,01008.092.085.073.045.03.0100..250019001400700400543215432154321 j x x x x x x x x x x x t s x x x x x MinZ j(1)何为生产计划?(2)总利润如何描述?(3)还要考虑什么因素?(4)有什么需要注意的地方(技巧)?(5)最终得到的数学模型是什么?二、线性规划的定义和数学描述(模型)1.定义:对于求取一组变量xj (j =1,2,......,n),使之既满足线性约束条件,又使具有线性表达式的目标函数取得极大值或极小值的一类最优化问题称为线性规划问题,简称线性规划。
2.配比问题和生产计划问题的线性规划模型的特点:用一组未知变量表示要求的方案,这组未知变量称为决策变量;存在一定的限制条件,且为线性表达式;有一个目标要求(最大化,当然也可以是最小化),目标表示为未知变量的线性表达式,称之为目标函数; 对决策变量有非负要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第三版)《运筹学》教材编写组编清华大学出版社运筹学第1章线性规划与单纯形法第1节线性规划问题及其数学模型二.线性规划与目标规划第1章线性规划与单纯形法第2章对偶理论与灵敏度分析第3章运输问题第4章目标规划第1章线性规划与单纯形法第1节线性规划问题及其数学模型第2节线性规划问题的几何意义第3节单纯形法第4节单纯形法的计算步骤第5节单纯形法的进一步讨论第6节应用举例第1节线性规划问题及其数学模型•1.1 问题的提出•1.2 图解法•1.3 线性规划问题的标准形式•1.4 线性规划问题的解的概念第1节线性规划问题及其数学模型线性规划是运筹学的一个重要分支。
线性规划在理论上比较成熟,在实用中的应用日益广泛与深入。
特别是在电子计算机能处理成千上万个约束条件和决策变量的线性规划问题之后,线性规划的适用领域更为广泛了。
从解决技术问题的最优化设计到工业、农业、商业、交通运输业、军事、经济计划和管理决策等领域都可以发挥作用。
它已是现代科学管理的重要手段之一。
解线性规划问题的方法有多种,以下仅介绍单纯形法。
1.1 问题的提出从一个简化的生产计划安排问题开始例1某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表1-1所示。
资源产品ⅠⅡ拥有量设备 1 2 8台时原材料A40 16kg原材料B0 4 12kg续例1该工厂•每生产一件产品Ⅰ可获利2元,•每生产一件产品Ⅱ可获利3元,•问应如何安排计划使该工厂获利最多?如何用数学关系式描述这问题,必须考虑称它们为决策变量。
产品的数量,分别表示计划生产设II I,,21x x ∙12416482212121≤≤≤+∙x ;x ;x x ,x ,x 这是约束条件。
即有量的限制的数量多少,受资源拥生产021≥∙x ,x ,即生产的产品不能是负值这是目标。
最大如何安排生产,使利润,∙数学模型⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0124164823221212121x ,x x x x x :x x z max 约束条件目标函数例2. 简化的环境保护问题靠近某河流有两个化工厂(见图1-1),流经第一化工厂的河流流量为每天500万立方米,在两个工厂之间有一条流量为每天200万立方米的支流。
图1-1续例2•第一化工厂每天排放含有某种有害物质的工业污水2万立方米,第二化工厂每天排放这种工业污水1.4万立方米。
从第一化工厂排出的工业污水流到第二化工厂以前,有20%可自然净化。
根据环保要求,河流中工业污水的含量应不大于0.2%。
这两个工厂都需各自处理一部分工业污水。
第一化工厂处理工业污水的成本是1000元/万立方米。
•第二化工厂处理工业污水的成本是800元/万立方米。
现在要问在满足环保要求的条件下,每厂各应处理多少工业污水,使这两个工厂总的处理工业污水费用最小。
建模型之前的分析和计算设:第一化工厂每天处理工业污水量为x 1万立方米,第二化工厂每天处理工业污水量为x 2万立方米100027004128021000250022211≤-+-≤-)]x .()x (.[)x (工厂后的水质要求:经第工厂前的水质要求:经第数学模型,4.126.18.018001000min 212121121≥≤≤≥+≥+=x x x x x x x x x z 约束条件目标函数共同的特征(1)每一个线性规划问题都用一组决策变量表示某一方案,这组决策变量的值就代表一个具体方案。
一般这些变量取值是非负且连续的;(2)要有各种资源和使用有关资源的技术数据,创造新价值的数据;()n x ,x ,x 21)n ,j ;m ,i (c ;a j ij 11==共同的特征(继续)(3)存在可以量化的约束条件,这些约束条件可以用一组线性等式或线性不等式来表示;(4)要有一个达到目标的要求,它可用决策变量的线性函数(称为目标函数)来表示。
按问题的不同,要求目标函数实现最大化或最小化。
它们的对应关系可用表格表示:n m mn m m n n n c c b b b a a a a a a a a a m x x x212121222211121121c 21价值系数动活资源决策变量线性规划的一般模型形式).(x ,,x ,x b ),(x a x a x a ).(b ),(x a x a x a b ),(x a x a x a ).(x c x c x c z max(min)n mn m m m n n n n nn 310211121221122222121112121112211≥≥=≤+++≥=≤+++≥=≤++++++=约束条件目标函数1.2 图解法例1是二维空间(平面)线性规划问题,可用作图法直观地来表述它的求解。
因存在必须在直角坐标的第1象限内作图,求解。
21 x ,x图1-2⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0124164223221212121x ,x x x x x x x z max图1-3 目标值在(4,2)点,达到最大值14目标函数2132x x z max +=表示一簇平行线33212z x x +-=可能出现的几种情况(1)无穷多最优解(多重最优解),见图1-4(2)无界解,见图1-5-1(3)无可行解,见图1-5-2图1-4 无穷多最优解(多重最优解)+4x2目标函数max z=2x1图1-5-1 无界解⎪⎩⎪⎨⎧≥≤-≤+-+=o x ,x x xx x x x z max 2121121242无可行解当存在矛盾的约束条件时,为无可行域。
85.121≥+x x 如果在例1的数学模型中增加一个约束条件:该问题的可行域为空集,即无可行解,图1-5-2 不存在可行域85121≥+x .x1.3线性规划问题的标准型式⎪⎪⎪⎩⎪⎪⎪⎨⎧≥=+++=+++=++++++=0a c z max 212211222221211121211122111n n n mn m m n n n n nn x ,,x ,x b x a x a x a b x a x a x a b x a x a x x c x c x :M 约束条件:目标函数:线性规划问题的几种表示形式⎪⎩⎪⎨⎧=≥===∑∑==n ,,,j ,x m ,,,i ,b x a x c z max :M j nj i j ij n j jj ' 21021111约束条件:目标函数:用向量表示为:()n ,,j ;b b b b ;a a a P ;x x x X ;c ,,c ,c C n ,,,j ,x b x P CXz max :M m mj j j j n n j nj j j '' 212102121212111=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==⎪⎩⎪⎨⎧=≥==∑=约束条件:目标函数:用矩阵表示为:()()Tn n mn m n ''x ,,x ,x X ;P ,P ,P a a a a A X bAX CXz max :M 21m 12111111b b b 0000=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛==⎪⎪⎪⎭⎫ ⎝⎛=⎩⎨⎧≥==决策变量向量:;资源向量:零向量:系数矩阵:约束条件:目标函数:如何变换为标准型:(1)若要求目标函数实现最小化,即min z=CX。
这时只需将目标函数最小化变换求目标函数最大化,即令z′=-z,于是得到max z′=-CX。
这就同标准型的目标函数的形式一致了。
(2)约束方程为不等式。
这里有两种情况:一种是约束方程为“≤”不等式,则可在“≤”不等式的左端加入非负松弛变量,把原“≤”不等式变为等式;另一种是约束方程为“≥”不等式,则可在“≥”不等式的左端减去一个非负剩余变量(也可称松弛变量),把不等式约束条件变为等式约束条件。
下面举例说明。
例3 将例1的数学模型化为标准型。
例1的数学模型,加松驰变量后⎪⎪⎩⎪⎪⎨⎧≥=+=+=++⇒⎪⎪⎩⎪⎪⎨⎧≥≤≤≤+++++=⇒+=0124164820124164823232432152413212121215432121x ,x ,x ,x ,x x x x x x x x x ,x x x x x x x x x x z max x x z max(3) 若存在取值无约束的变量x k ,可令,其中。
"'k k k x x x-=0,"'≥k k x x 例4将下述线性规划问题化为标准型⎪⎪⎩⎪⎪⎨⎧≥=++-≥+-≤++-+-=为无约束3213213213213210533732x ;x ,x x x x x x x x x x x x x z min处理的步骤:(1)用x4-x5替换x3,其中x4,x5≥0;(2)在第一个约束不等式≤号的左端加入松弛变量x6;(3)在第二个约束不等式≥号的左端减去剩余变量x7;(4)令z′=-z,把求min z改为求max z′,即可得到该问题的标准型例4的标准型⎪⎪⎩⎪⎪⎨⎧≥=-++-=+-+-=+-++++-+-=05232700327654214217542165421765421x ,x ,x ,x ,x ,x )x x (x x x )x x (x x x )x x (x x x x )x x (x x z max '1.4 线性规划问题的解的概念•1.可行解•2.基•3.基可行解•4.可行基1. 可行解满足约束条件(1-5),(1-6)式的解X=(x 1,x 2,…,x n )T ,称为线性规划问题的可行解,其中使目标函数达到最大值的可行解称为最优解。
⎪⎩⎪⎨⎧-=≥-==-=∑∑==)(n ,,,j ,x )(m ,,i ,b x a )(x c z max j nj i j ij n j jj 61210512141112. 基,基向量,基变量()()为基变量。
为基向量,为线性规划问题的基。
称阶非奇异子矩阵中的是系数矩阵)m ,,j ()m ,,j (P ,P ,P a a a a a a a a a B m m B m mm m m m m 21x 21P B 0B A j j 21212222111211===⎪⎪⎪⎪⎪⎭⎫⎝⎛=≠⨯3.基可行解满足非负条件(1-6)的基解,称为基可行解. 基可行解的非零分量的数目也不大于m ,并且都是非负的。
•是基可行解43210Q ,Q ,Q ,Q ,4. 可行基对应于基可行解的基,称为可行基。
•约束方程组(1-5)具有基解的数目最多是个。
一般基可行解的数目要小于基解的数目。
•以上提到的几种解的概念,它们之间的关系可用图1-6表明。
•另外还要说明一点,基解中的非零分量的个数小于m 个时,该基解是退化解。
