运筹学第一章:计算公式
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
《运筹学》第一章 线性规划

③
约束方程②的系数矩阵
2 2 1 0 0 0
A 1 4
2 0
0 0
1 0
0 1
0 0
p1
p2
p3
p4
p5
p6
0 4 0 0 0 1
确定初始基B
1 0 0 0
产量分别为 x1、x2
项目
Ⅰ
设备 A(h) 0
设备 B(h) 6 调试工序(h) 1 利润(元) 2
Ⅱ 每天可用能力
5
15
2
24
1
5
1
问:应如何安排生产计划,才 能使总利润最大?
2.目标函数:设总利润为z,则
max z = 2 x1 + x2 3.约束条件:
5x2 ≤ 15
s.t.
6x1+ 2x2 ≤ 24 x1+ x2 ≤ 5
凸集
顶点
凸集
不是凸集
顶点:如果凸集C中不存在任何两个不同的点X1, X2,使X成为这两个点连线上的一个点。
(三)基本定理
定理1 若线性规划问题存在可行解,则问题的 可行域是一个凸集。
定理2 线性规划的基可行解对应线性规划问题 可行域(凸集)的顶点。
定理3 若线性规划问题有最优解,一定存在一个 基可行解是最优解。
(2)常数项bi<0的转换:约束方程两边乘以(-1)。 (3) 约束方程的转换:由不等式转换为等式 。
aij xj bi aij xj bi
aij x j xni bi
xni 0 称为松弛变量
aij x j xni bi
xni 0 称为剩余变量
(4) 变量的变换
若存在取值无约束的变量 x,j可令
2x1
运筹学第一章 1.4 大M法和两阶段法(章节优讲)

优质教学
10
要求:
xx15
3 6
x2 x3 x4 3x2 6x3
0 x4
0
于是:
xx22
3/1
6/3
x2
min3/1,6 / 3
如果x2的系数列变成P2’=(-1,0)T,则用非 基变量表示基变量的表达式就变成;
x1 3 x2 x3 x4 0
x5
6 0x2
6x3
②W最优值=0——但人工变量中有等于0的基 变量,构成退化的基本可行解,可以转化为情 况①;如何转化?
选一个不是人工变量的非基变量进基, 把在基中的人工变量替换出来
优质教学
27
③W最优值>0——至少有一个人工变量取值 >0,说明基变量中至少有1个人工变量,表明原 问题没有可行解,讨论结束。
试比较
MinZ xn1 xn2 … xnm
优质教学
7
一般(经过若干次迭代),对于基B,
用非基变量表出基变量的表达式 为:
n
xni bi' ai'j x j , j 1
i 1,2, m
用非基变量表示目标函数的表达式:
n
Z Z0 jxj j1
m
j cj z j cj cniai'j i1
优质教学
8
(2)最优性判别定理
优质教学
25
(2) 两阶段法
第一阶段:建立辅助线性规划并求解, 以判断原线性规划是否存在基本可行解。
辅助线性规划的结构:目标函数W为所有 人工变量之和,目标要求是使目标函数极 小化,约束条件与原线性规划相同。
优质教学
26
求解结果
①W最优值=0——即所有人工变量取值全为0 (为什麽?),均为非基变量,最优解是原线 性规划的一个基本可行解,转入第二阶段;
运筹学-第一章-单纯形法基本原理
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义:两个基可行解称为相邻的,如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量,
X
凸集
顶点
凸集
不是凸集
顶点:如果凸集C中不存在任何两个不同的点X1,X2,使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1:若线性规划问题存在可行解,则该问题的可行域是 凸集。 定理2:线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3:若问题存在最优解,一定存在一个基可行解是最优 解。(或在某个顶点取得)
的左边变成一个单位矩阵,
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中: i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限,
运筹学第1章-线性规划

下一页 返回
图解法步骤:
(1)建立坐标系; (2)将约束条件在图上表示; (3)确立满足约束条件的解的范围; (4)绘制出目标函数的图形 (5)确定最优解
用图解法求解下列线性规划问题
max z 2x1 3x2
4x1 0x2 16
s.t
10xx11
4x2 2x2
12 8
x1, x2 0
1. 1.1问题举例
(1)生产计划问题。 生产计划问题是典型的已知资源求利润最大化的问题,对于此类
问题通常有三个假设:①在某一计划期内对生产做出的安排;②生产 过程的损失忽略不计;③市场需求无限制,即假设生产的产品全部 卖出。
下一页 返回
1.一般线性规划问题的数学模型
例1 用一块连长为a的正方形铁皮做一个容 器,应如何裁剪,使做成的窗口的容积为最 大?
解:设 x1, x2分别表示从A,B两处采购的原油量(单
位:吨),则所有的采购方案的最优方案为:
min z 200x1 290x2
0.15x1 0.50x2 150000
s.t
0.20x1 0.50x1
0.30x2 0.15x2
120000 120000
x1 0, x2 0
1. 1线性规划问题与模型
也可以写成模型(1-6)和模型(1-7)的形式,其中模型(1-7)较为常用。
运筹学-1、线性规划

则:
x1 x2 100
x1 ( x3 ) x4 x2 2
设x3为第二年新的投资; x4为第二年的保留资金;
则:
18
•设x5为第三年新的投资;x6为第三年的保留资金;
则:
x3 ( x5 ) x6 x4 2 x1 2
•设x7为第四年新的投资;第四年的保留资金为x8;
max Z 2 x7 x9 x1 x2 100 x 2x 2x 2x 0 2 3 4 1 4 x1 x3 2 x4 2 x5 2 x6 0 s.t 4 x3 x5 2 x6 2 x7 2 x8 0 4 x5 x7 2 x 8 2 x9 0 x 0, j 1, 2, , 9 j
13
例3:(运输问题)设有两个砖厂A1 、A2 ,产 量分别为23万块、27万块,现将其产品联合供应三 个施工现场B1 、 B2 、 B3 ,其需要量分别为17万 块、18万块、15万块。各产地到各施工现场的单位 运价如下表: 现场 砖厂 B1 B2 B3
A1 A2
5 6
14 18
7 9
问如何调运才能使总运费最省?
20
例5:(下料问题) 某一机床需要用甲、乙、 丙三种规格的钢轴各一根,这些轴的规格分别是 2.9,2.1, 1.5(m),这些钢轴需要用同一种圆钢来做,圆 钢长度为7.4m。现在要制造100台机床,最少要用多 少根圆钢来生产这些钢轴?
解:第一步:设一根圆钢切割成甲、乙、丙三 种钢轴的根数分别为y1,y2,y3,则切割方式可用不等 式2.9y1+2.1y2+1.5y3≤7.4 表示,求这个不等式的有实 际意义的非负整数解共有8组,也就是有8种不同的 下料方式,如下表所示:
运筹学第1章:线性规划问题及单纯型解法

原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8
1-《运筹学》-第一章-2010-至第3节

第一章 线性规划与单纯形法§1 线性规划问题及其数学模型[例] 利用现有机器台时及原料A 、B 生产两种产品,已知如下:求达最大利润的生产方案。
解:设生产产品一、二的数量分别为x 1, x 2 相应线性规划问题为:⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,1241648232max 21212121x x x x x x x x z线性规划问题的特点:1) 一组控制变量表示某一方案2) 关于控制变量线性的约束条件(等式或不等式) 3) 关于控制变量线性的目标函数线性规划问题的一般形式:⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≥=≤+++≥=≤++++++=++free x x x x x x x b x a x a xa b x a x a x a x c x c x c z n t t s s m n mn m m n n n n ,0,0,,),(),(max(min)11212211112121112211两个变量的线性规划问题的图解法 [例1]⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,1241648232max 21212121x x x x x x x x z唯一最优解(4,2),最优值=14 [例2]⎪⎪⎩⎪⎪⎨⎧≥≤≤≤++=0,1241648242max 21212121x x x x x x x x z无穷多最优解(4,2),(2,3)及其中间点,最优值=16 [例3]⎪⎩⎪⎨⎧≥≤-≤+-+=0,242max 21212121x x x x x x x x z无界解,+∞=z m ax [例4]⎪⎩⎪⎨⎧≥≥-≥+-+=0,242max 21212121x x x x x x x x z 无可行解,约束矛盾,可行域φ=D由两个变量的线性规划问题的图解法得出的直观结论: 1. 可行域D 及相应最优解与最优值的可能情况:φ=D :无可行解φ≠D 且D 有界:有有限的最优值(有唯一最优解或无穷多最优解) φ≠D 且D 无界:1) 有有限的最优值(有唯一最优解或无穷多最优解) 2) 无界解(+∞=z m ax 或-∞=z m in )2. 若φ≠D ,则可行域D 为有界凸多边形或无界凸区域3. 若有最优解,必可以在可行域D 的某个顶点达到4. 若在两个顶点同时达到最优值,则其连线之间任一点都是最优解,即为无穷多最优解情形。
运筹学讲义第一章
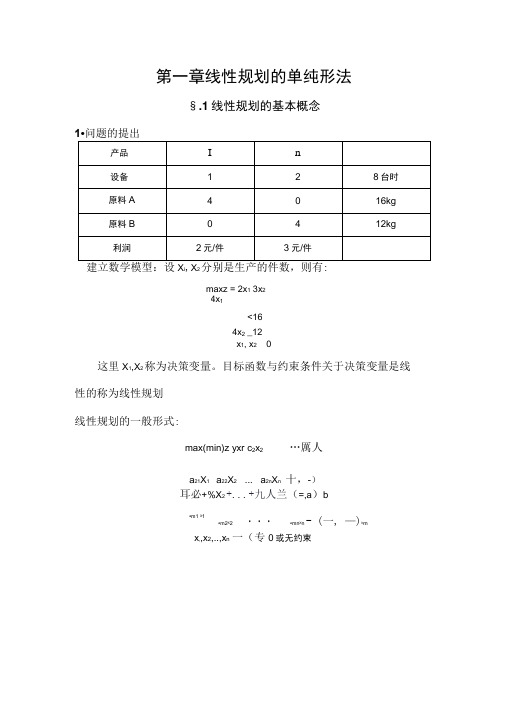
4x 1<164x 2 _12a 21X 1 a 22X 2 ... a 2n X n 十,-)b a m1 X 1第一章线性规划的单纯形法§.1线性规划的基本概念建立数学模型:设X i ,X 2分别是生产的件数,则有:maxz = 2x 1 3x 2x 1, x 2 0这里X 1,X 2称为决策变量。
目标函数与约束条件关于决策变量是线 性的称为线性规划线性规划的一般形式:max(min)z yxr c 2x 2 …厲人耳必+%X 2 +...+九人兰(=,a )ba m2X 2 ・・・ a mn X n - (一, —)bm x ,,x 2,..,x n 一(专0或无约束2. 线性规划的标准形maxz 二C1X1 …Cn X n"a^x, +ai2x2+••• + 印*人=Ra21^ +a22x2+... + a2n x n= b2a m1 为* a m2 X2 * …+ a mn 人=b m捲_ 0,X2_0,...,X n_0特点:目标函数求极大;等式约束;变量非负。
^令c =(G,c2,…,q), X = (X1,X2,…,x n) , A = (a ij )m n,b=(九^,…,b m ) 则线性规划标准形的矩阵表达式为:max z = exAx = bx _0约定:b — 0,m ^ n,秩A=m.如何化标准形:(I)目标函数实现极大化,即min z=cx,令w--z,则m w丸;(II )约束条件为不等式约束条件为“「不等式,则在约束条件的左端加上一个非负的松弛变量;约束条件为“ 一”不等式,则在约束条件的左端减去一个非负的松弛变量。
(III )若存在无约束的变量X k,可令X k = Xk - x k,其中x k 一0,x'k- 0.故有 x^ -B 4b 。
由此,得到Ax -b 的一个解例1.将线性规划min z = -捲 2x 2x-i x 2 x 3 _ 2* X i — X ? + X 3 乏 1论Z0,x 2兰0,x 3无约束化为标准形。
运筹学(简化)

第一部分 运筹学一、什么是运筹学?实例:一公司有:三个工厂:A 、B 、C 。
各工厂分别有140吨、120吨、50吨产品待运;三个仓库:甲、乙、丙。
甲库可存货60吨,乙库可存货100吨,丙库可存货150吨;直观思路:1、距离最短A -丙。
(140吨); 2、B -丙。
(10吨);依此类推。
可得调运方案:总吨公里数=140*1.5+60*12+50*13.5+10*3+50*4.5=1860。
最佳方案:对该问题如果利用数学符号(即建立数学模型)来表示,可如下讨论:设工厂A 向仓库甲、乙、丙的调运吨数分别为11x 、12x 、13x ,工厂B 向仓库甲、乙、丙的调运吨数分别为21x 、22x 、23x ,工厂C 向仓库甲、乙、丙的调运吨数分别为31x 、32x 、33x ,则调运货物的总吨公里数(相当于运输费用)为33323133222113121195.4635.13125.169x x x x x x x x x z ++++++++=现在需要求该函数的最小值,而限制条件为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=++=++=++=++=++=++0,,,,,,,,1501006050120140333231232221131211332313322212312111333231232221131211x x x x x x x x x x x x x x x x x x x x x x x x x x x运筹学:以系统为研究对象,把系统的功能和特点用模型表示,通过对模型的定量分析,从总体上寻求最优策略,为决策和揭露新问题提供数量根据,并以研究结果的应用为目的,保证系统高效运行。
运筹学建立模型的最终目的是实现系统的最优化,帮助管理者作出正确的决策,使系统正常有效地运行。
这里的最优化是指在一定条件下求最优解(可以是求最大值,也可以是求最小值)。
运筹学研究系统的基本方法由以下5个阶段构成:第一阶段:观察所要研究的系统,确定存在的问题、影响问题的因素、约束、假设以及准备优化的目标。
运筹学第一章

30
1.1.3解的概念
概念: 1、可行解:满足所有约束条件的解。 2、可行域:即可行解的集合。所有约束条件的交 集,也就是各半平面的公共部分。满足所有约 束条件的解的集合,称为可行域。 3、凸集:集合内任意两点的连线上的点均属于这 个集合。如:实心球、三角形。线性规划的可 行域是凸集。
OR1
OR1
27
线性规划图解法例题
(无界解)
max z x 2 y x y 1 2 x 4 y 3 x 0, y 0
OR1
28
线性规划图解法例题
(无解)
min z x 2 y x y 2 2 x 4 y 3 x 0, y 0
请问该 医院至 少需要 多少名 护士?
5
例题2建模
目标函数:min Z=x1+x2+x3+x4+x5+x6 约束条件: x1+x2 ≥70
x2+x3 ≥60 x3+x4 ≥ 50 x4+x5 ≥20 x5+x6 ≥30 非负性约束:xj ≥0,j=1,2,…6
OR1
6
例题3:运输问题
三个加工棉花的加工厂,并且有三个仓库供应棉花,各 供应点到各工厂的单位运费以及各点的供应量与需求量 分别如下表所示:问如何运输才能使总的运费最小?
OR1
14
总
结
从以上 5 个例子可以看出,它们都属于优化问题,它们 的共同特征: 1 、每个问题都用一组决策变量表示某一方案;这组决 策变量的值就代表一个具体方案,一般这些变量取值是 非负的。 2 、存在一定的约束条件,这些约束条件可以用一组线 性等式或线性不等式来表示。 3 、都有一个要求达到的目标,它可用决策变量的线性 函数(称为目标函数)来表示。按问题的不同,要求目 标函数实现最大化或最小化。 满足以上三个条件的数学模型称为线性规划的数学模型。
运筹学第一章 1.3.1 单纯形法的基本思路

L L
L L cn + m
0 0 M 1
b1 b2 M bm 0
-Z,Xn+1,…,Xn+m所对应的系数 列向量构成一个基
用矩阵的初等行变换将该基变成单位阵, 用矩阵的初等行变换将该基变成单位阵 , 变成0 这时 c n +1 , c n + 2 , L , c n + m 变成0,相应的增广 矩阵变成如下形式: 矩阵变成如下形式:
第二步:寻求初始可行基, 第二步:寻求初始可行基,确定基变量
1 2 1 0 0 A = ( P1,P2,P3,P4,P5 ) = 4 0 0 1 0 0 4 0 0 1
对应的基变量是
x3 x4 x5
第三步: 第三步:写出初始基本可行解和相应的 目标函数值
两个关键的基本表达式: 两个关键的基本表达式: ①用非基变量表示基变量的表达式
max Z = 2 x1 + 3 x2 x1 + 2 x2 ≤ 8 4 x ≤ 16 1 4 x2 ≤ 12 x1 , x2 ≥ 0
第一步:引入非负的松弛变量和剩余变量 第一步: x3,x4,x5, 将该LP化为标准型 将该LP化为标准型
max Z = 2 x1 + 3x2 + 0 x3 + 0 x4 + 0 x5 x1 + 2 x2 + x3 = 8 4 x1 + x4 = 16 4 x2 + x5 = 12 x j ≥ 0, j = 1, 2,L ,5
(2)表格设计依据: 表格设计依据: 将 -Z 看作不参与基变换的基变量 , 把目 看作不参与基变换的基变量, 标函数表达式改写成方程的形式, 标函数表达式改写成方程的形式 , 和原有的 m 个约束方程组成一个具有 n+m+1 个变量 、 个约束方程组成一个具有n+m+1 个变量、 m+1个方程的方程组: m+1个方程的方程组: a11x1 + a12 x2 + L+ a1n xn + xn+1 = b1 a x + a x + L+ a x + x = b 2n n n+2 2 21 1 22 2 L L L a x + a x + L+ a x + x = b mn n n+m m m1 1 m2 2 − Z + c1 x1 + c2 x2 + Lcn xn + cn+1 xn+1 + Lcn+m xn+m = 0
运筹学 第01章 线性规划问题

线性规划建模步骤
设定决策变量 明确约束条件并用决策变量的线性等式或 不等式表示 用变量的线性函数表示要达到的目标,并 确定是求极小还是求极大 根据变量的物理性质确定变量是否具有非 负性 注:其中最关键是设定决策变量这一步
生产计划问题(1)
某工厂用三种原料生产三种产品,已知的 条件如下表所示,试制订总利润最大的日 生产计划
线性规划问题解的有关概念(2)
基本解:令模型中所有非基变量的值等于零后,由 模型的约束方程组得到的一组解。 基本可行解:满足非负条件的基本解称为基本可行 解。 可行基:对应于基本可行解的基称为可行基。 退化解:基本可行解的非零分量个数小于m时,称 为退化解。 最优基:若对应于基B的基本可行解X是线性规划的 最优解,则称B为线性规划的最优基
人员安排问题(1)
医院护士24小时值班,不同时段需要的护 士人数不等(见下表)。每个护士每天连 续值班8小时,在各时段开始时上班。问最 少需要多少护士?
序号 1 2 3 4 时段 06—10 10—14 14—18 18—22 最少人数 60 70 60 50
5 6
22—02 02—06
20 30
人员安排问题(2)
设xj为第j时段开始值班的护士人数
目标函数为:使人数最少,则有
min f ( X ) x1 x2 x3 x4 x5 x6 x6 x1 60 x x 70 1 2 x2 x3 60 s.t. x3 x4 50 x x 20 5 4 x5 x6 30 x1 , x2 , x3 , x4 , x5 , x6 0且为整数
运筹学
第一章 线性规划问题
本章重点
线性规划建模 线性规划的图解法 线性规划的标准形式 单纯形法 两阶段法 大M法
运筹学第一章
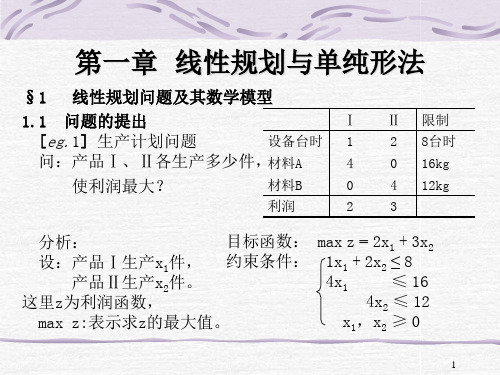
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
x1,x2 ≥ 0
1
[eg.2]污水处理问题
环保要求河水含污低于2‰,河水可自身净化20%。 问:化工厂1、2每天各处理多少污水,使总费用最少?
分析:
500万m3
化工厂1
2万m3 1000元/万m3 化工厂2
(2)不等式(≤,≥) 对于“≤”情况:在“≤”左边加上一个松弛变量(非
负),变为等式; 对于“≥”情况:在“≥”左边减去一个剩余变量(非
负),变为等式。 注意:松弛变量、剩余变量在目标函数中的价值系数为0。
(3)无约束变量 令xk = xk’ - xk”,xk’,xk” ≥ 0,代入即可。
13
[eg.7]将下述问题化为标准型
22
3、人工基
[eg.10]max z = x1 + 2x2 + 3x3
x1 + 3x2 + 2x3 = 3 2x1 + x2 + x3 = 4 x1,x2,x3 ≥ 0 分析: A= 1 3 2 211 ∵ 找不到单位矩阵基 ∴ 引入人工变量为初始基变量(2个)
23
3.2 最优性的检验与解的判别
min z = -x1+2x2-3x3 x1+ x2+ x3 ≤ 7 ① x1- x2+ x3 ≥ 2 ②
-3x1+ x2+2x3 = 5 ③ x1,x2 ≥ 0,x3无约束
解:令x3 = x3’-x3”,x3’,x3” ≥ 0;
①式加上一个松弛变量x4;②式减去一个剩余变量x5; 令z’ = -z
运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习
![运筹学[第一章线性规划与单纯形法]山东大学期末考试知识点复习](https://img.taocdn.com/s3/m/83512a81ba0d4a7303763a31.png)
第一章线性规划与单纯形法1.线性规划问题的数学模型(1)一般形式(2)标准型式]2.数学模型化为标准型(1)若目标函数实现最小化,则min z=-max z'(令z'=-z)(2)若约束方程为不等式,则若约束方程为“≤”不等式左端+松驰变量(≥0)=右端若约束方程为“≥”不等式左端-剩余变量(≥0)=右端(3)若存在取值无约束的变量x k(1≤k≤咒),则在标准型中x k=x'k-x"k(其中x k=x',x"k≥0)3.线性规划的解线性规划问题:(1)可行解:满足约束条件②和③的解X=(x1,x2,…,x n)T。
(2)最优解:使目标函数①达到最大值的可行解。
(3)基:设A为约束方程组②的m×n阶系数矩阵,设n>m,其秩为m,B 为矩阵A中的一个m×m阶的满秩子矩阵,则称B为线性规划问题的一个基。
不失一般性,设B中每一个列向量P j(j=1,2,…,m)称为基向量,与基向量PJ对应的变量x j称为基变量。
除基变量以外的变量为非基变量。
(4)基本解:在约束方程组②中,令所有非基变量x m+1=x m+2=…=x n=0,此时方程组②有唯一解X B=(x1,x2,…,x m)T,将此解加上非基变量取0的值有X=(x1,x2,…,x m,0,0…,0)T,称X为线性规划问题的基本解。
(5)基本可行解:满足非负条件③的基本解。
(6)可行基:对应于基本可行解的基。
4.初始基可行解的确定(1)直接从A中观察到存在一个初始可行基。
(2)对所有约束条件是“≤”形式的不等式,可利用化为标准型的方法,在每个约束条件左端加上一个松弛变量,这m个松弛变量就构成一个基变量,则对应的m个向量组成的单位矩阵B就是线性规划问题的一个可行基。
(3)对所有约束条件是“≥”形式的不等式以及等式约束情况,采用人造基的方法。
即对不等式约束的左端减去一个非负的剩余变量后,再加上一个非负的人工变量;对于等式约束的左端再加上一个非负的人工变量。
运筹学第一章

第一章、 线性规划和单纯形法1.1 线性规划的概念一、线性规划问题的导出1.(引例) 配比问题——用浓度为45%和92%的硫酸配置100t 浓度为80%的硫酸。
取45%和92%的硫酸分别为x1和x2t,则有: 求解二元一次方程组得解。
目的相同,但有5种不同浓度的硫酸可选(30%,45%,73%,85%,92%)会出现什么情况?设取这5种硫酸分别为 x1、x2、x3、x4、x5 t, 则有: ⎩⎨⎧⨯=++++=++++1008.092.085.073.045.03.01005432154321x x x x x x x x x x 请问有多少种配比方案?为什么?哪一种方案最好?假设5种硫酸价格分别为:400,700,1400,1900,2500元/t ,则有:2.生产计划问题如何制定生产计划,使三种产品总利润最大?考虑问题:⎩⎨⎧⨯=+=+1008.092.045.01002121x x x x ⎪⎩⎪⎨⎧=≥⨯=++++=++++++++=5,,2,1,01008.092.085.073.045.03.0100..250019001400700400543215432154321 j x x x x x x x x x x x t s x x x x x MinZ j(1)何为生产计划?(2)总利润如何描述?(3)还要考虑什么因素?(4)有什么需要注意的地方(技巧)?(5)最终得到的数学模型是什么?二、线性规划的定义和数学描述(模型)1.定义:对于求取一组变量xj (j =1,2,......,n),使之既满足线性约束条件,又使具有线性表达式的目标函数取得极大值或极小值的一类最优化问题称为线性规划问题,简称线性规划。
2.配比问题和生产计划问题的线性规划模型的特点:用一组未知变量表示要求的方案,这组未知变量称为决策变量;存在一定的限制条件,且为线性表达式;有一个目标要求(最大化,当然也可以是最小化),目标表示为未知变量的线性表达式,称之为目标函数; 对决策变量有非负要求。
运筹学第一章线性规划

线性规划解的概念 ——[3]基可行解
[3.1.2]基变量XB和非基变量XN
线性代数: 被表示变量 表示变量
2 x2 x4 x1 2 x2 x3 2 x4 1 x1 2 基变量: 2 x x x1 x 2 x1 4 x2 x3 x4 5 2 x3 41 待解的 4 2 1 x4 变量 x3
X=αx1+βx2 或C=αA +βB y=αy1+βy2
类似的我们有凸组合的概念
线规几何意义: 凸组合
设X1,X2,…XK为n维空间中的k个
点。若下式成立, 显然, X X 1 X例:阴影中任 原点,Q1,Q4的凸 2 ... K X K 类似的,上面X1,X2,…XK的 1 2 C=αA 组合则表示三角 +βB 一点,可表示 0 i 1, i 1 ( 0≤α,β≤1,α+β=1) 凸组合X,则表示由它们圈定 为:原点、 形(O,Q1,Q4)内 则称X为X1,X2,…XK的凸组合。 的封闭空间中任意一点。 是凸组合的一个特例,同时AB的凸 Q1、Q2、Q3、 的任一点 组合C表示AB连线上任一点。 Q4的凸组合
线性规划解的概念
——[3]基可行解 根据基解的定义,我们有:
在基解中
基变量 非零分量(待求变量) 非基变量 零分量(自由变量)
线性规划解的概念
——[3]基可行解
基可行解的定义:
定义1:可行的基解。 定义2:各分量均大于零的基解。
基可行解(m个方程,n个变量) 基可行解 基变量 正分量(待求变量) 正分量个数=m=方程个数=R(A) 非基变量 =n-m 零分量个数 零分量(自由变量)
运筹学第一章线性规划及

x2 x1+2x2=8
3 2 1
4x1=16 4x2=12
D
A(4,2)
0
1
2
3
4
x1
二、解的情况
*唯一解 *无穷多解例 *无界解例 *无可行解(课本)
可行基: 对应于基可行解的基称为可行基。
一、解的概念
以上提到的几种解的概念,可用下图来表示:
可 行 解
基 可 行 解
基 解
二、基本定理
定理 1 若线性规划问题存在可行解,则该问题的可 行域是凸集。
引理 线性规划问题的可行解为基可行解的充要条 件是X的正分量所对应的系数列向量是线性独立的。 定理2 线性规划问题的基可行解X对应线性规划问 题可行域(凸集)的顶点。
a12 a22 am 2
a1n a2 n amn
三、标准形式
标准型的主要特征:
① 目标最大;
② 约束等式; ③右端非负;
max z c1 x1 c 2 x 2 c n x n a11 x1 a12 x 2 a1n x n b1 a 21 x1 a 22 x 2 a 2 n x n b 2 st . a m 2 x 2 a mn x n b m a m1 x1 x1 , x 2 , , x n 0
第一节 线性规划问题及其数学模型
问题的提出 数学模型 模型的标准形式
一、问题的提出
例1:某工厂在计划期内安排生产Ⅰ、Ⅱ两种产品, 已知生产单位产品所需的设备台时、A、B两种原 材料的消耗及两种产品每件可获利润见如下表所 示: 设 备 原材料A 原材料B 利 润 I 1台时 4公斤 0公斤 2元/件 II 2台时 0公斤 4公斤 3元/件 资源总量 8 台时 16公斤 12公斤
运筹学第一章:计算公式

Z CB B b (C N CB B N )) X N
1
1
得到下列五个计算公式:
1. 2. Z 0 CB B b
1
(令XN=0)
1
N C N CB B N
C CB B 1 A
j c j ci aij
其中
3. 4. 5.
XB B b N B N
BX B b NX N X B B (b NX n ) B b B NX N
1 1 1
令非基变量XN=0,XB=B—1b,由 B是 可行基的假设, 则得到基本可行解 X=(B-1b,0)T 将目标函数写成
X B Z (C B , C N ) CB X B X N
再将第二行左乘-CB后加到第三行,得到
XB XN b
XB
λ N
I
0 λΝ
B-1N
CN-CBB-1N XB
B-1b
-CBB-1b
-Z0
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 7 of 13
五个公式的应用 【例1.17】线性规划
故基本可行解为
X (25,
0,0,0, ) ,
T
目标函数值为
25 145 Z 0 C B B b C B X B (1,) 35 2 3 3
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 10 of 13
1
B1
故单纯形乘子
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
再将第二行左乘-CB后加到第三行,得到
XB XN b
XB
λ N
I
0 λΝ
B-1N
CN-CBB-1N XB
B-1b
-CBB-1b
-Z0
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 7 of 13
五个公式的应用 【例1.17】线性规划
故基本可行解为
X (25,
0,0,0, ) ,
T
目标函数值为
25 145 Z 0 C B B b C B X B (1,) 35 2 3 3
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 10 of 13
(3) 求λ3
2 1 7 2 107 1 P3 , CB B P3 P3 ( , ) 9 3 5 9 5
3 c3 C B B 1 P 3
=- 1 =- 107 9 98 9
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 9 of 13
(2)基变量的解为
XB x1 1 B b x2
25 1 15 2 20 35 3 3
35 3,
1
1 3 1 9
max Z x1 2 x 2 x3
2 x1 3 x 2 2 x3 x 4 15 1 x1 x 2 5 x3 x5 20 3 x j 0, j 1, ,5
已知可行基
2 3 B1 1 1 3
求(1)单纯形乘子π; (2)基可行解及目标值; (3)求λ3; (4)B1是否是最优基,为什么; (5)当可行基为 B =1 3 时求λ1及λ3. 2 0 1
因λj≤0,j=1,…,5,故B1是最优基.
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 12 of 13
(5) 因B2是A中第四列与第二列组成的,x4、x2是基变 量x1、x3、x5是非基变量,这时有
C B (c 4 , c 2 ) (0,2) 1 3 1 1 B , C B B (0,2) 0 1 1 (1 , 3 ) (c1 , c3 ) C B B ( P P3 ) 1 .2 2 (1,1) (0,2) 1 5 3 ( ,9) 3 1
1
B1
故单纯形乘子
C B B 1
1 3 1 9
1 2 3
1 3 (1,2) 1 9
1 1 7 ( ,) 2 9 3 3
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
b (b1 , b2 , , bm )
T
T
X≥0应理解为X大于等于零向量,即xj≥0,j=1,2…,n。
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 2 of 13
不妨假设A=(P1,P2,…,Pn)中前m个列向量构成 一个可行基,记为B=(P1 ,P2 ,…,Pm)。矩阵A中后n -m列构成的矩阵记为N=(Pm+1,…Pn),则A可以写成 分 块 矩 阵 A= ( B , N ) 。 对 于 基 B , 基 变 量 为 xB= (x1,x2,…,xm )T, 非基变量为xN=(xm+1,xm+2,…xn)T. 则X可表示成 同理将C写成分块矩阵C=(CB, CN),CB=(c1,c2,…,cn), CN=(Cm+1Cm+2,…,cn) 则AX=b可写成
CN X N
CB ( B b B
1
1
1 N
X N ) CN X NFra bibliotek1 CB B b (C N CB B N )) X N
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 4 of 13
2012年11月1日星期四 Page 11 of 13
(4) 要判断B1是不是最优基,亦是要求出所有检验数 则否满足λj≤0,j=1…,5.x1,x2是基变量,
故λ1=0,λ2=0,而 得
3
98 9
剩下来求λ4,λ5,由λN计算公式 0,
1
(4 , 5 ) (c4 , c5 ) C B B ( P4 P5 ) 1 7 1 0 (0,0) ( , ) 9 3 0 1 1 7 ( , ) 9 3
即
1
1 3
, 3 9
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 13 of 13
本节不作重点要求!
The End of Chapter 1
第二章 对偶线性规划
Exit
1
1
i
aij ( B N ) j
1
CB B 1
称为单纯形算子
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 5 of 13
上述公式可用下面较简单的矩阵表格运算得到,
设初始矩阵单纯形表为
XB XB B CB XN N CN b b 0
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 8 of 13
【解】(1)因为B1 由A中第一列、第二列组成,故x1 、x2 为基变量,x3、x4、x5为非基变量,有关矩阵为
CB=(c1,c2)=(1,2) CN=(c3,c4,c5)=(1,0,0)
X B ( B,N ) BX B NX N b X N
X B X XN
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 3 of 13
因为r(B)=m(或|B|≠0)所以B —1存在,因此可有
BX B b NX N X B B (b NX n ) B b B NX N
1 1 1
令非基变量XN=0,XB=B—1b,由 B是 可行基的假设, 则得到基本可行解 X=(B-1b,0)T 将目标函数写成
X B Z (C B , C N ) CB X B X N
将B化为I(I为m阶单位矩阵),CB化为零,即求基本可 行解和检验数.用B-1左乘表中第二行,得到下表
XB XB I CB XN B-1N CN b B-1b 0
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 6 of 13
Z CB B b (C N CB B N )) X N
1
1
得到下列五个计算公式:
1. 2. Z 0 CB B b
1
(令XN=0)
1
N C N CB B N
C CB B 1 A
j c j ci aij
其中
3. 4. 5.
XB B b N B N
§1.7 计算公式 Calculate Formula
Ch1 Linear Programming
2012年11月1日星期四 Page 1 of 13
设有线性规划
max Z CX AX b X 0 其中Am×n且r(A)=m,
C=(c1 , c2 ,cn )
X ( x1 , x 2 , , x n )
