宁波大学考博历年初试真题之数字信号处理2009--2015年考博真题
宁波大学高级数字系统设计2015--2016,2018,2020年考博初试真题
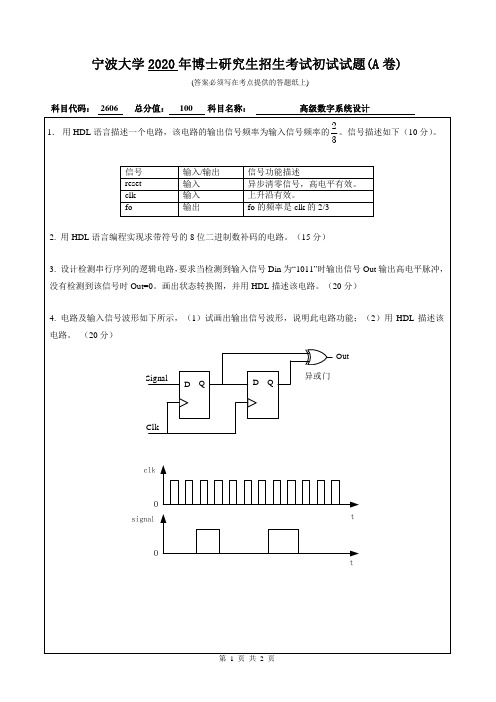
科目代码 : 2606 科目名称:
高级数字系统设计
四、(20 分)利用 ROM 和累加器设计一个频率分辨率小于 0.5Hz 的 DDS 正弦信号发生器,ROM 采用 256×8bit,频率控制字 M 为 8 位。
试给出:1. 相位累加器的最少位数,时钟频率,最高输出频率。(12 分) 2. 画出电路结构框图。(8 分)
③ 完成上述操作后,返回初始状态。
画出该数字系统的算法状态机图。(15 分)
6.简述数字电路设计中流水线技术提升电路运行速度的原理。(20 分)
第2页共2页
宁波大学 2018 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码 : 2606 科目名称:
高级数字系统设计
4. 电路及输入信号波形如下所示,(1)试画出输出信号波形,说明此电路功能;(2)用 HDL 描述该 电路。 (20 分)
Signal DQ
DQ
Out 异或 门
Clk
第1页共2页
宁波大学 2020 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 2606 总分值: 100 科目名称:
五、(20 分)设计 4 位乘 3 位二进制数乘法器的算法流程图,电路结构如图 1 所示。
Start
A4 B3
乘法电路
7P
图1
第3页共3页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
考试科目: 适用专业:
高级数字系统设计 微纳信息系统
科目代码: 2606
表1
第1页共3页
2015年宁波大学考博初试真题之3807数字通信B_2015年考博真题

考试科目: 适用专业: 数字通信 科目代码: 3807
通信与信息系统/信号与信息处理/移动计算与人机交互/微纳信息系统
一、填空(16 分)
1、QAM 信号的解调通常采用( )相干解调。 )。
2、设在 125s 内传输 256 个二进制码元,则码元传输速率是(
Orthogonal frequency division multiplexing (OFDM) has become a popular technique for transmission of signals over wireless channels. OFDM has been adopted in several wireless standards such as digital audio broadcasting (DAB), digital video broadcasting (DVB-T), the IEEE 802.11a local area network (LAN) standard and the IEEE 802.16a metropolitan area network (MAN) standard. OFDM is also being pursued for dedicated short-range communications (DSRC) for road side to vehicle communications and as a potential candidate for fourth-generation (4G) mobile wireless systems. OFDM converts a frequency-selective channel into a parallel collection of frequency flat subchannels. The subcarriers have the minimum frequency separation required to maintain orthogonality of their corresponding time domain waveforms, yet the signal spectra corresponding to the different subcarriers overlap in frequency. Hence, the available bandwidth is used very efficiently. If knowledge of the channel is available at the transmitter, then the OFDM transmitter can adapt its signaling strategy to match the channel. Due to the fact that OFDM uses a large collection of narrowly spaced subchannels, these adaptive strategies can approach the ideal water pouring capacity of a frequency selective channel. OFDM is a block modulation scheme where a block of information symbols is transmitted in parallel on subcarriers. The time duration of an OFDM symbol is times larger than that of a single carrier system. An OFDM modulator can be implemented as an inverse discrete Fourier transform (IDFT) on a block of information symbols followed by an analog-to-digital converter (ADC). To mitigate the effects of inter-symbol interference (ISI) caused by channel time spread, each block of IDFT coefficients is typically preceded by a cyclic prefix (CP) or a guard interval consisting of samples, such that the length of the CP is at least equal to the channel length. Under this condition, a linear convolution of the transmitted sequence and the channel is converted to a circular convolution. As a result, the effects of the ISI are easily and completely eliminated. Moreover, the approach enables the receiver to use fast signal processing transforms such as a fast Fourier transform (FFT) for OFDM implementation. Similar techniques can be employed in single-carrier systems as well, by preceding each transmitted data block of length by a CP of length , while using frequency domain equalization at the receiver. While the first mobile communications standards focused primarily on voice communication, the 第 2 页 共 4 页
宁波大学信息科学与工程学院《912信号与系统》历年考研真题专业课考试试题

2013年宁波大学912信号处理基础 (信号与系统+数字信号处理)
考研真题
2014年宁波大学912信号处理基础 (信号与系统+数字信号处理)
考研真题
2015年宁波大学912信号处理基础 (信号与系统+数字信号处理)
考研真题
2016年宁波大学912信号处理基础 (信号与系统+数字信号处理)
目 录
2013年宁波大学912信号处理基础(信号与系统+数字信号处理)考研 真题 2014年宁波大学912信号处理基础(信号与系统+数字信号处理)考研 真题 2015年宁波大学912信号处理基础(信号与系统+数字信号处理)考研 真题 2016年宁波大学912信号处理基础(信号与系统+数字信号处理)考研 真题 2017年宁波大学912信号与系统考研真题 2018年宁波大学912信号与系统考研真题 2019年宁波大学912信号与系统考研真题
考研真题
2017年宁波大学912信号与系统考 研真题
2018年宁波大学912信号与系统考 研真题
2019年宁波大学9
宁波大学随机过程2009--2020年考博初试真题

之间的关系是______________________,高斯随机过程通过线性系统后是否还是高斯随机过 程?
4. 若平稳随机过程 X(t) 的自相关函数为 Rx ( ) _________________。
a2 cos 3
,则其平均功率 1 2
Sx ( )d =
第1页共3页
宁波大学 2020 年博士研究生招生考试初试试题(B 卷)
3. 假 设 两 个 相 互 独 立 的 随 机 变 量 X 、Y 服 从 正 态 分 布 N (m1, s12) 和 N (m2, s22) , 则 随 机 变 量 Z = X + 2Y 服从_________分布。若令W [X,Y ]T ,则W 的协方差矩阵为_________。
j
=
2
sin
q
+ 2
j·cos
q
2
j
cos
q
+
cos
j
=
2
cos
+ 2
j·cos
q
2
j
一、概念题(每题 4 分,共 40 分)
sin a sin b
=
-
1 2
cos (a
+
b)-
cos (a
- b)
cos a cos b
=
1 2
cos (a
+
b) +
cos (a
- b)
sin
q
-
sin
j
=
2
cos
宁波大学 2020 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 2603 总分值: 100 科目名称:
宁波大学信号与系统考研真题试题2009年—2019年(缺13、14、15)

R
t=0
V
i(t)
C vC(t)
题图 4
5. (16 分) 某一离散时间因果 LTI 系统的差分方程为
y(n) 3 y(n 1) 1 y(n 2) x(n) ax(n 1) 。
4
8
(1) 若输入 x(n) (1)n 时,输出 y(n) 16 (1)n ,求系统函数 H(z),画出零极点图,标明 ROC 15
② 求该系统的频率响应,并判断该系统的稳定性;
③
当输入
x(n)
1 2
n
u(n)
,
y(1)
0,
y(2) 8 时,求该系统的零输入和零状态响应;
④
当输入
x(n)
3
1 2
n
u(n)
,
y(1)
0,
y(2) 4 时,求该系统的完全响应。
第3页共3页
宁波大学 2018 年硕士研究生招生考试初试试题(A 卷)
信号与系统
电路与系统 通信与信息系统 信号与信息处理 电子与通信工程 集成电路工程
1.(12 分)一系统由如下方程描述: y(t) x(t)sin(t) ,试论证如下问题:
① 该系统是不是线性系统?为什么? ② 该系统是不是时不变系统?为什么? ③ 该系统是不是因果系统?为什么?
2. ( 14 分 ) 一 线 性 时 不 变 系 统 , 在 相 同 起 始 状 态 下 , 当 激 励 为 f (t) 时 , 其 全 响 应 为 y1(t) 2et cos(2t), t 0 ;当激励为 2 f (t) 时,其全响应为 y2 (t) et 2 cos(2t), t 0 。 试求在同样起始状态下,当激励为 4 f (t) 时系统的全响应 y(t) 。
数字信号处理2009期末考试样卷

2008—2009 学年第3, 4 学期数字信号处理课程期末考试样卷注意:装订线左侧请不要答题,请不要在试卷上书写与考试无关的内容,否则将按相应管理规定处理。
院系:专业:班级:姓名:学号:题号一二三四五六七八九十总分得分考试时间:90分钟;试题数目:共五大题;试卷:共5页。
一、填空题(本大题20分,每空2分)1、/4()jnx n jeπ=的共轭对称部是0 。
2、假设)(nx的DTFT存在,当ωj eZ=时,)(nx的Z变换就是DTFT。
3、一个矩形窗长度为N,其频谱宽度(主瓣宽度)为2/N Hz。
4、ωω2cos)(=jeX的IDTFT为)2(41)2(41)(21)(-+++=nnnnxδδδ。
5、按频率抽取FFT的运算复杂度等于按时间抽取FFT 。
6、一个稳定系统的收敛域必包括为单位圆。
7、以20kHz的采样率对最高频率为10kHz的带限信号)(txa采样,N=500个采样点,频谱采样点之间的间隔是40 Hz。
8、以10kHz采样率对语音信号进行采样,并对其实时处理,所需的部分运算包括采集1024点语音值块、计算一个1024点DFT和一个1024点IDFT。
若每一次实乘所需时间为1sμ,那么计算DFT和IDFT后还剩40.96 ms来处理数据9、最小相位系统具有最小群延迟性质。
10、两序列的长度非别为1N和2N,当圆周卷积的点数L满足121-+≥NNL时,两序列的圆周卷积等于线性卷积。
二、判断题(本大题20分,每小题2分。
正确打√,错误打×)1. ()ax t为一连续信号,∑∞-∞=-=nsanTtts)()(δ,用)(txa调制)(tsa得)(txs,)(txs是离散信号。
(×)2.如果某个序列不能保证绝对可和,则这个序列不能进行DTFT。
(×)得分:得分:3.以采样频率s f 对频率为0f 的正弦信号采样时,得到的)(n x 所对应的模拟信离散信号号并不唯一。
宁波大学2602概率论与数理统计2015--2020年考博真题

第1页共1页
宁波大学 2016 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
考试科目: 适用专业:
概率论与数理统计 工程力学
科目代码: 2602
1. 某一地区患有癌症的人占 0.005,患者对一种试验反应是阳性的概率为 0.95,正常人对这种试 验反应是阳性的概率为 0.04,现抽查了一个人,试验反应是阳性,问此人是癌症患者的概率有多 大?(10 分)
第1页共1页
宁波大学 2019 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 2602 总分值: 100 科目名称:
概率论与数理统计
计算题(共 7 题,共 100 分)
1. (15 分) 有两种花籽,发芽率分别是 0.5,0.8,从中各取一颗,设各花籽是否发芽相互独立,求
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
考试科目: 适用专业:
概率论与数理统计 工程力学
科目代码: 2602
1. 市场上有甲、乙、丙三家工厂生产的同一品牌产品,已知三家工厂的市场占有率 分别为 1/4、1/4、1/2,且三家工厂的次品率分别为 2%、1%、3%,试求市场上 该品牌产品的次品率。(10 分)
X
7 2
。(20
分)
4. 公共汽车车门的高度是按男子与车门碰头的机会在 0.01 以下来设计的,设男子的身高
X ~ N(170,62) ,问车门的高度应如何确定? 已知: (2.33) 0.99 (10 分)
5. 设(X,Y)的概率密度是
f
x,
y
2e(2 x y) ,
宁波大学智能数据处理2019--2020年考博初试真题

满足 F (ti ) di , for i 1,..., N ,显然是不切实际的,在这种情况下,请给
出一个合理的解决方案,并设计具体的学习算法。
(13 分)
3. Boltzmann 机是一个全相联的随机型神经网络,如果将其简化处理,限定为只
含一个可见层和一个隐单元层,取消层内连接,仅保留层间的加权连接,这种
(1)试画出 ER 图,并在图上注明属性、联系的类型。 (2)将 ER 图转换成关系模型,并注明主键和外键。
9.( 8%) 数 据 库 的 并 发 操 作 会 带 来 哪 些 问 题 ? 如 何 解 决 ?
10.(6%,每个小题 2 分)设有关系模式 R(职工编号,日期,日营业额,部门 名,部门经理),该模式统计商店里每个职工的日营业额,以及职工所在的部 门和经理信息。如果规定:每个职工每天只有一个营业额;每个职工只在一个 部门工作;每个部门只有一个经理。试回答下列问题: (1)根据上述规定,写出模式 R 的基本 FD 和关键码; (2)说明 R 不是 2NF 的理由; (3)分解 R 成 3NF 模式集。
层后,要求输出尽量与输入接近,其处理数据的效果非常类似于 PCA 分析, 请为 AutoEncoder 设计一个合理的学习算法(建议采用梯度下降法)。(12 分)
2. 假设一个含 M 单元的 RBF 网络的输出为
M
F (x) wj (|| x xj ||) , j0
对于 N 个不同的学习样本 ti , i 1,..., N ,如果 N M ,要实现精确的插值,即
第2页共2页
宁波大学 2019 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 3809 总分值: 100 科目名称:
2014-2015年宁波大学考博真题2608资源与环境经济学 B

入学考试试题(B卷)(答案必须写在答题纸上)考试科目:资源与环境经济学科目代码:2608适用专业:渔业经济管理
1.自然资源核算的方法有哪些?谈谈你对绿色GDP的看法。
(25分)
2.低碳经济的内涵和特征,谈谈我国实行碳市场的意义。
(25分)
3.资源与环境管理的手段有哪些?试结合我国当前资源与环境问题论述之。
(25分)
4.环境变化是否有规律可循?谈谈生物多样性保护的经济价值。
(25分)
入学考试试题(B卷)(答案必须写在答题纸上)
考试科目: 资源与环境经济学科目代码:2608 适用专业: 渔业经济管理。
宁波大学2604半导体器件2015--2016,2018--2020年考博真题

(答案必须写在考点提供的答题纸上) A. 3 B. 2(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)考试科目:半导体器件科目代码:2604适用专业:微纳信息系统一、单项选择题:本大题共5小题,每小题5分,共25分。
在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题前的括号内。
错选、多选或未选均不得分。
()1.在半导体太阳能电池中,关于暗电流说法正确的是A.没有光照时电流B.由外加偏压产生C.其方向与光电流方向相同D.由光生电压降落在势垒区而产生()D正常工作时,其MOS单元半导体表面所处状态是A.强反型B.多子积累C.深耗尽D.多子耗尽()3.在以下复合跃迁中,非辐射复合跃迁是A.带间复合B.激子复合C.俄歇复合D.不存在()4.与LED量子效率有关的因素有A.结两侧参杂浓度B.结深C.表面反射D.以上都有关()5.太阳能电池工作时,对应P-N结内部处于:A.正偏电压B.反偏电压C.没有电压D.耗尽第1页共2页考试科目:半导体器件科目代码:2604适用专业:微纳信息系统二问答题(共35分)1.采用载流子扩散与漂移的观点分析PN结的单向导电性。
(10分)2.试述NPN双极型晶体管的四种工作模式。
(15分)3.试述金属-半导体接触:肖特基接触与欧姆接触的各自特点。
(10分)三.计算与推导(共40分)1.计算一硅p-n结在300K时的内建电势,其N A=1018cm-3和N D=1015cm-3.(10分)2.一理想晶体管其发射效率为0.999,集基极漏电流为10μA,假设I B=0,请算出由空穴所形成的放大模式发射极电流。
(15分)3.简述评估太阳能电池器件性能的四个基本参数,那些因素会影响太阳能电池器件性能(15分)第2页共2页考试科目:半导体器件科目代码:2604适用专业:微纳信息系统第1页共2页一、判断题(共20分,每题1分)1.()半导体材料的导电性能介于导体和绝缘体之间。
2019年宁波大学考博试题3807数字通信(B卷)

(答案必须写在考点提供的答题纸上)科目代码:3807总分值:100科目名称:数字通信一、填空(16分,每空格2分)1、假设信号的符号间隔为50ms ,为了保证信号的正交性,FSK 相干检测时要求的最小频率间隔为(),非相干检测时要求的最小频率间隔为()。
2、数字通信系统的有效性指标有()和(),线性编码是()。
3、某二维信号用向量表示为Si=[3,4],该信号的能量为()。
4、一个数字传输系统以1000符号/秒的码元速率传送16进制码元,该系统的信息速率是()bps 。
5、2PAM,2FSK,2PSK 和2DPSK 四种调制信号通过AWGN 信道传输。
假设发送信号的幅度相同,信息速率相同,噪声的功率谱密度N0相同,接收端都采用理想的相干最佳解调,那么,在大信噪比条件下,将这4种调制方式按误比特率从小到大排出的次序是()。
二、选择题(14分,每空格2分)从下面所列答案中选择出最合理的答案,填入后面的答题中。
每个空格只能选一个答案,不排除某一个答案被多次选择的可能性。
示例题:3+2=(p ),2×0=(n )(a)2w(b)sinc(t/T)(c)量化噪声(d)2FSK(e)慢(f)快(g)(h)相位错移(i)kb/slog 2M (j)kb/s log 102M (k)(l)循环稳定(m)时域均衡(n)0(o)高(p)5(r)12(s)4(t)倒 现象(u)21、周期为T 的信号通过带宽为wHz 的信道,要实现无ISI 传输,最大符号速率为()符号/s ,相应的脉冲x(t )为()。
(答案必须写在考点提供的答题纸上)科目代码:3807总分值:100科目名称:数字通信2、如果信道传输带宽为10kHz,信噪比为30dB,则该信道的最高信息传输速率理论值为()。
3、如果升余弦滚降系统的滚降系数 越大,则相应的系统总的冲激响应x(t)的拖尾衰减越()。
4、BPSK信号在接收端因为载波同步系统中的分频,可能产生载波相位状态转移,发生对信号的错误解调,这种现象称为()。
2015年宁波大学考博初试真题之2606高级数字系统设计B_2015年考博真题
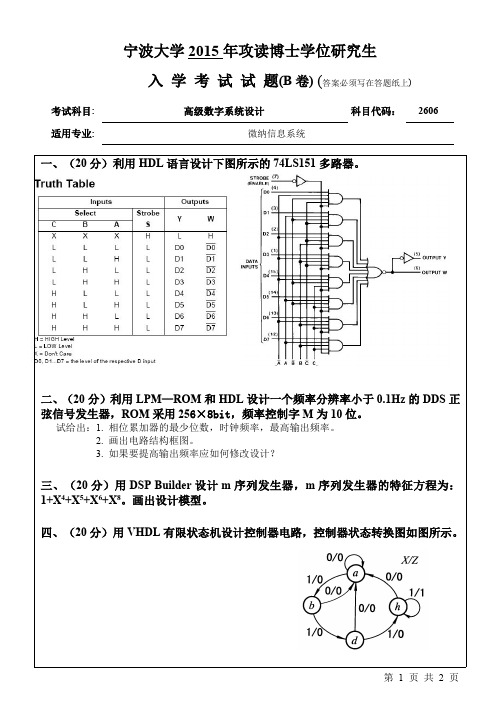
宁波大学2015
年攻读博士学位研究生
入学考试试题(B卷)(答案必须写在答题纸上)考试科目:高级数字系统设计科目代码:2606适用专业:微纳信息系统
第1页共2页
一、(20分)利用HDL语言设计下图所示的74LS151多路器。
二、(20分)利用LPM—ROM和HDL设计一个频率分辨率小于0.1Hz的DDS正弦信号发生器,ROM采用256×8bit,频率控制字M为10位。
试给出:1.相位累加器的最少位数,时钟频率,最高输出频率。
2.画出电路结构框图。
3.如果要提高输出频率应如何修改设计?
三、(20分)用DSP Builder设计m序列发生器,m序列发生器的特征方程为:1+X4+X5+X6+X8。
画出设计模型。
四、(20分)用VHDL有限状态机设计控制器电路,控制器状态转换图如图所示。
宁波大学2015年考研真题【010信息学院】912信号处理基础(信号与系统+数字信号处理)B

考试科目: 信号处理基础(信号与系统+数字信号处理) 科目代码:912
适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、
集成电路工程
考试科目: 信号处理基础(信号与系统+数字信号处理) 科目代码:912
适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、
集成电路工程
考试科目: 信号处理基础(信号与系统+数字信号处理) 科目代码:912
适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、
集成电路工程
考试科目: 信号处理基础(信号与系统+数字信号处理) 科目代码:912
适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、
集成电路工程
考试科目: 信号处理基础(信号与系统+数字信号处理) 科目代码:912
适用专业: 电路与系统、通信与信息系统、信号与信息处理、电子与通信工程、
集成电路工程。
2015年宁波大学考博初试真题之3808数字信号处理A_2015年考博真题

第 1 页 共 2 页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
考试科目: 适用专业: 数字信号处理 通信与信息系统/信号与信息处理 科目代码: 3808
Hale Waihona Puke 6.(12 分)设某一混合相位系统的系统函数为:
0π . 3 1 H ( z ) z (1 0e . j8 z ) ( j 0π e0 . .83 1 )z (1
0.9
)
试确定具有相同幅度响应特性的因果最小相位延时系统 H min ( z ) 和最大相位延时 系统 H max ( z ) 的系统函数表达式。 7.(12 分)用双线性变换法设计一个低通的巴特沃兹数字滤波器,确定满足下列指 标要求的低通滤波器阶次 N。已知,在 0 0.25 的通带范围内振幅衰减不超 过 0.75dB,在 0.4 的阻带范围内振幅衰减不小于 20dB。已知 T=10-4 秒。 8.(11 分)简述用窗函数法设计线性相位 FIR 数字滤波器的设计步骤。
第 2 页 共 2 页
1 2.(9 分)已知离散时间系统差分方程表示式为 y(n) y(n 1) x(n) 3
1 n 1 n ① 若系统的零状态响应为 y (n) 3 u (n) ,求激励信号 x(n) ; 2 3
② 粗略画出幅频响应特性曲线。 3.(12 分)已知有限长序列 x(n) (n 2) 4 (n 4) 。 ① 求其 8 点 DFT,即 X (k ) DFT x(n) , 0 k 7 ; ② 若 h(n)(0 n 7) 的 8 点 DFT 为 H (k ) W83k X (k ), 0 k 7 ,求 h(n) ; ③ 若 y(n)(0 n 7) 的 8 点 DFT 为 Y (k ) X (k ) H (k ), 0 k 7 ,求 y (n) 。 4.(12 分)对于 8 点序列 x(n) ,试画出基-2 按频率抽取法的 FFT 流图(采用输入 自然顺序,输出倒位序方式)。
2013-2015年宁波大学考博真题3816细胞生物学

入学考试试题(B卷)(答案必须写在答题纸上)考试科目:细胞生物学科目代码:3816适用专业:水产养殖、渔业资源一、名词解释(每个3分,共30分)1.亲核蛋白(karyophilic protein)2.管家基因(house-keeping genes)3.端粒(telomere)4.接触抑制(contact inhibition)5.分子伴侣(molecular chaperon)6.脂质体(liposome)7.内膜系统(endomembrane system)8.流动镶嵌模型(fluid mosail model)9.原代细胞(primary culture cell)10.细胞连接(cell junction)二、简答题(每个10分,共70分)1.请举出5种用于细胞形态结构观察的研究工具,并指明它们的主要用途。
2.简述物质的跨膜运输类型。
3.cAMP信号通路和磷脂酰肌醇信号通路有哪些联系和区别?4.微丝的结构与功能。
5.结合核仁的功能,谈谈为什么凡是蛋白质合成旺盛的细胞中核仁都明显偏大。
6.谈谈你对细胞核全能性和细胞全能性的认识。
7.细胞增殖的意义。
入学考试试题(B卷)(答案必须写在答题纸上)考试科目:细胞生物学科目代码:3816适用专业:水产养殖/渔业资源一、单项选择题:本大题共20小题,每小题1分,共20分。
在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题前的括号内。
错选、多选或未选均不得分。
()1.有关原核细胞与真核细胞的比较,下列说法错误的是:(A)现有资料证明真核细胞由原核细胞进化而来,自然界真核细胞的个体数量比原核细胞多。
(B)真核细胞内有一个较复杂的骨架体系,原核细胞内并没有明显的骨架系统。
(C)真核细胞基因表达具有严格的时空关系,并具有多层次的调控。
(D)真核细胞内膜系统分化,内部结构和功能的区域化和专一化,是进化过程的一次飞跃。
()2.下列结构中,原核细胞具备而真核细胞缺少的是:(A)内含子(B)操纵子(C)重复序列(D)线状DNA分子()3.建立分泌单克隆抗体的杂交瘤细胞是通过下列哪项技术构建的:(A)细胞融合(B)核移植(C)病毒转化(D)基因转移()4.细胞外基质中含量最高,刚性及抗张力强度最大的成分是:(A)胶原(B)氨基聚糖和蛋白聚糖(C)弹性蛋白(D)层粘连蛋白和纤连蛋白()5.下列对协助扩散的描述,不正确的是:(A)转运速率高,存在最大转运速率。
2013-2015年宁波大学考博真题3809智能系统 A

5. 对 5 个不同省份的发展情况进行调查统计后,得到 以下每个省份 两两间 的距离矩阵: 4 6 1 6 0 0 9 7 3 4 D 6 9 0 10 5 10 0 8 1 7 6 3 5 8 0 试用类平均法 ( 均值 ) 对其进行聚类, 分别给出聚成 2 类和 3 类的结果。 (12%) 6. 对于下图所示的Boltzmann机,假设每个结点的阈值都为0,连接权值如图所示, 如何采用模拟退火(Simulated Annealing)技术,使网络尽快达到系统平衡态? 如 果达到了平衡态,请计算系统处在状态{S1=1,S2=1,S3=1,S4=1}的概率是多少? 要求给出具体的计算过程。 (13%)
宁波大学 2014 年攻读博士学位研究生 入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
考试科目: 适用专业: 智能系统 移动计算与人机交互 科目代码: 3809
1. 试设计一个感知器, 将下图中带黑点标志的输入 (001, 101, 110, 111) 与其它输入(000, 010, 011, 100) 区分开来,要求给出详细的感知器结构和具体权值,单元个数尽可能的少。 (10%)
k k
请详细解释这二个计算公式的含义。
第 1 页, 共 3
(12%)
页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题 (A 卷)
考试科目: 适用专业: 智能系统 (A)
(答案必须写在答题纸上)
科目代码:
3809
移动计算与人机交互
4. 如图所示的特征脸(Eigenfaces)是机器视觉领域中用于人脸图像分析的一组特征 向量,通过主元分析(PCA)得到。请问: (a)进行 PCA 的主要步骤有哪些? (b)试给出运用 PCA 进行特征脸分析的详细过程,并指出如何进行高维人脸数 据降维。 (14%)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试科目: 适用专业: 数字信号处理 通信与信息系统、信号与信息处理 科目代码: 3808
1.(8 分)采用数字系统处理模拟信号,在 A/D 变换之前和 D/A 变换之后,都要让信号通过一 个低通滤波器,请说明这两个低通滤波器分别起到什么作用? 2.(12 分)采用 DFT 的 FFT 算法,可用圆周卷积快速完成线性卷积的计算。现欲计算 N1 点序 列 x( n) 与 N2 点序列 h( n) 的线性卷积 x( n) h( n) , 请写出采用圆周卷积完成线性卷积的具体 计算步骤。 3.(12 分)对于一离散时间系统 y ( n) n x( n n0 ) ,其中 x( n) 、 y ( n) 分别为其输入和输
1.(15 分)设某线性移不变离散时间系统的差分方程为 10 y(n 1) y(n) y(n 1) x(n) ,试求它的单位样值响应。它是不是因果的?是 3 不是稳定的?
1 2.(9 分)已知离散时间系统差分方程表示式为 y(n) y(n 1) x(n) 3
1 n 1 n ① 若系统的零状态响应为 y (n) 3 u (n) ,求激励信号 x(n) ; 2 3
n 5.(17 分)已知一个因果 LTI 离散时间系统,对于输入序列 x(n)=(0.4) u(n) ,有输
n n 1 出 y(n)=(0.5) u(n) 0.2(0.5) u(n 1)
① 确定该系统的传递函数 H ( z ) ; ② 写出该系统的差分方程; ③ 试用直接 II 型结构实现该系统; ④ 试用并联型结构实现该系统。
0.9
)
试确定具有相同幅度响应特性的因果最小相位延时系统 H min ( z ) 和最大相位延时 系统 H max ( z ) 的系统函数表达式。 7.(12 分)用双线性变换法设计一个低通的巴特沃兹数字滤波器,确定满足下列指 标要求的低通滤波器阶次 N。已知,在 0 0.25 的通带范围内振幅衰减不超 过 0.75dB,在 0.4 的阻带范围内振幅衰减不小于 20dB。已知 T=10-4 秒。 8.(11 分)简述用窗函数法设计线性相位 FIR 数字滤波器的设计步骤。
5.(17 分)一个 LTI 因果系统由下列差分方程描述: y ( n) x( n) x( n 1) 0.5 y ( n 1) ① 求系统函数 H ( z ) ; ② 画出系统幅频响应示意图,说明系统的滤波特性; ③ 若输入 x( n) 2 cos(0.5 ) ,求系统稳态输出的最大幅度。 6.(12 分)一个线性相位 FIR 滤波器的差分方程为:
2
6000Hz),要预畸。试确定数字低通滤波器的系统函数并画出直接 II 型(典范型)结构图。 第 1 页 共 1 页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
考试科目: 适用专业: 数字信号处理 通信与信息系统/信号与信息处理 科目代码: 3808
第 1 页 共 2 页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
考试科目: 适用专业: 数字信号处理 通信与信息系统/信号与信息处理 科目代码: 3808
6.(12 分)设某一混合相位系统的系统函数为:
0π . 3 1 H ( z ) z (1 0e . j8 z ) ( j 0π e0 . .83 1 )z (1
y ( n ) x ( n ) 4x ( n 1) 3x ( n 2) ax ( n 3) bx ( n 4) x ( n 5)
① 试确定系数 a 和 b 值; ② 试确定系统的群延时; ③ 画出 FIR 滤波器的线性相位型结构。 7.(12 分)两个 8 点实序列 x( n) 和 y ( n) 构成一个 8 点复序列 v ( n) x ( n) jy ( n) , 0 n 7 , 复序列 v( n) 的 DFT 为: V ( k ) 2 j 3,1 j 5, 4 j 7, 2 j 6, 1 j 3, 4 j ,3和 n0 为非零值,试推断该系统是不是 ①线性,②移不变,③因果,④稳定的? 4.(12 分)已知 x( n) 为一实因果序列,其离散时间傅里叶变换(DTFT)的实部为
X re (e j ) 1 cos ,试确定序列 x(n) 及其 DTFT 即 X (e j ) 。
0 k 7 ,试确定 8 点实序列 x(n) 和 y (n) 的 DFT: X (k ) 和 Y (k ) 。
8.(15 分)某二阶模拟低通滤波器(原型)的传递函数为 H a ( s )
1 , ( s / c ) 3( s / c ) 3 现采用双线性变换法设计一个数字低通滤波器,其 3dB 截止频率 f c =1000Hz(抽样频率 f s =
② 粗略画出幅频响应特性曲线。 3.(12 分)已知有限长序列 x(n) (n 2) 4 (n 4) 。 ① 求其 8 点 DFT,即 X (k ) DFT x(n) , 0 k 7 ; ② 若 h(n)(0 n 7) 的 8 点 DFT 为 H (k ) W83k X (k ), 0 k 7 ,求 h(n) ; ③ 若 y(n)(0 n 7) 的 8 点 DFT 为 Y (k ) X (k ) H (k ), 0 k 7 ,求 y (n) 。 4.(12 分)对于 8 点序列 x(n) ,试画出基-2 按频率抽取法的 FFT 流图(采用输入 自然顺序,输出倒位序方式)。
