余弦定理测试题(小题详解)
高一数学余弦定理试题答案及解析

高一数学余弦定理试题答案及解析1.在△ABC中,设AD为BC边上的高,且AD = BC,b,c分别表示角B,C所对的边长,则的取值范围是____________.【答案】.【解析】因为BC边上的高AD=BC=a,所以,则,又,所以,其中有tanA=2,又由基本不等式有所以的取值范围.【考点】三角形的面积公式,辅助角公式,余弦定理,基本不等式,正弦函数的定义域与值域.2.已知ABC的重心为G,内角A,B,C的对边分别为a,b,c,若,则角A为()A.B.C.D.【答案】A【解析】由于是的重心,,.代入得由于不共线,【考点】平面向量共线定理和余弦定理的应用.3.△中,若,则△的形状为()A.直角三角形B.等腰三角形C.等边三角形D.锐角三角形【答案】B【解析】由,结合余弦定理得,即有,此题也可运用正弦定理化边为角,从角来判定三角形的形状,可能不及运用余弦定理简便【考点】余弦定理和三角形形状的判定.4.在中,已知,则 .【答案】【解析】由得,由余弦定理,所以,即,在中,,那么.【考点】1.余弦定理;2.特殊角的三角函数值.5.在△ABC中,角A、B、C的对边分别为a、b、c,已知向量,,.(1)求角C的大小; (2)若,求角A的值.【答案】(1);(2)【解析】解题思路:(1)利用平面向量的垂直的判定得出三角形的三边的关系式,在利用余弦定理求角;(2)利用三角形的三角关系进行消元,使其变为关于角A的式子,再恒等变形求角的正弦值,结合角的范围求角.规律总结:对于以平面向量为载体考查三角函数问题,要正确利用平面向量知识化为三角函数关系式,再利用三角函数的有关公式进行变形.注意点:利用三角函数值求角时,一定要结合角所在的范围求角.试题解析:(1) 由整理得即又又因为,所以(2) 因为,所以故由即,所以.即.因为故所以【考点】1.平面向量垂直的判定;2余弦定理;3.三角恒等变换.6.某货轮在航行中不幸遇险,发出呼救信号,我海军护卫舰在A处获悉后,测得该货轮在北偏东45º方向距离为10海里的C处,并测得货轮正沿北偏东105º的方向、以每小时9海里的速度向附近的小岛靠拢.我海军护卫舰立即以每小时21海里的速度前去营救;则护卫舰靠近货轮所需的时间是小时.【答案】.【解析】由题意可画出如下示意图,假设经过小时处护卫舰靠近了货轮,则可得,,,∴在,由余弦定理可得:.【考点】余弦定理的运用.7.在△ABC中,,则A等于().A.60°B.120°C.30°D.150°【答案】B【解析】根据余弦定理:,根据,可得,所以在三角形中.【考点】余弦定理.8.已知的三条边的边长分别为4米、5米、6米,将三边都截掉米后,剩余的部分组成一个钝角三角形,则的取值范围是()A.05B.15C.13D.14【答案】C【解析】新三角形的三边分别为,其中边长为的边对的角最大记为角,所以角为钝角。
(完整版)余弦定理练习题及答案

积累巩固1.已知a ,b ,c 是∆ABC 中角A ,B ,C 的对边,若a =21,b =5,c =4,则A =.3,b =3,c =30︒,则A =.2.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知a =3.在△ABC 中,三个角A ,B ,C 的对边边长分别为a =3,b =4,c =6,则bc cos A +ca cos B +ab cos C 的值为.4.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为.5.在△ABC 中,已知a =1,b =7,B =60°,求边C .延伸拓展6.在△ABC 中,已知a =2,b =2,A =45°,解此三角形.7.已知a 、b 、c 分别是∆ABC 的三个内角A 、B 、C 所对的边,若∆ABC 面积S∆ABC=3,c =2,A =60︒,求a 、b 的值.28.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若a ⋅cos 2.C A 3+c ⋅cos 2=b ,求证:2229.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b +c =a +3bc ,求:(1)A 的大小;(2)2sin B cos C -sin(B -C )的值.10.设∆ABC 的内角A,B,C 的对边分别为a,b,c,且A=60o ,c=3b.求:(1)222cos B cos C a的值;(2)的值.+c sin B sin C 创新应用11.在△ABC 中,a 、b 是方程x -23x +2=0的两根,且2cos(A +B )=1.求:(1)角C 的度数;(2)c ;(3)△ABC 的面积.12.已知A 、B 、C 为∆ABC 的三内角,且其对边分别为a 、b 、c ,若2cos B cos C -sin B sin C =1.2(1)求A ;(2)若a =23,b +c =4,求∆ABC 的面积.13.当甲船位于A 处时获悉,在其正东方方向相距20海里的B 处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30°、相距10海里C 处的乙船,试问乙船直接赶往B 处救援最少要走多少海里?参考答案b 2+c 2-a 21=,∠A =60o .1.60解析:cos A =2bc 2o 2.解:由余弦定理可得c 2=3+9-2⨯3⨯3cos30o =3,解得c =a =3⇒A =C =30o (或).616+36-99+36-1616+9-36613.解:由余弦定理,所求式=++=.22224.解:设顶角为C ,因为l =5c ,∴a =b =2c ,由余弦定理得πa 2+b 2-c 24c 2+4c 2-c 27cos C ===.2ab 2⨯2c ⨯2c 85.解:由余弦定理得(7)2=1+c 2-2c cos60°,∴c 2-c -6=0,解得c 1=3,c 2=-2(舍去);∴c =3.6.解:由a 2=b 2+c 2-2bc cos A 得22=(2)2+c 2-22c cos45°,∴c 2-2c -2=0,解得c =1+3或c =1-3(舍去);∴c =1+3.c 2+a 2-b 222+(1+3)2-(2)23又cos B ===,且B 为三角形内角;2ca 22×2×(1+3)∴B =30°;∴C =180°-(A +B )=180°-(45°+30°)=105°.7.解:ΘS∆ABC=1bc sin A =3,∴1b ⋅2sin 60︒=3,得b =12222由余弦定理得a =b +c -2bc cos A =1+2-2⨯1⨯2⋅cos60︒=3,∴a =2222223.8.证明:由已知得:,∴,∴,∴,即222.9.解:(1)由余弦定理得a b c2bccosA,b2c2a23bc3故cosA,所以A.2bc2bc26(2)2sinB cosC sin(B C)2sin B cos C(sinB cos C cos B sinC)sinB cos C cos B sinC1sin(B C)sin(A)sin A.210.解:(1)由余弦定理得1117a7 a2b2c22b cosA(c)2c22g cg cg c2.3329c3(2)由余弦定理及(1)的结论有72212c c(c)a c b539. cosB2ac7272g cg c3222故sin B1cos2B1253. 282772122c c ca2b2c2919,同理可得cosC2ab71272g cg c33sin C1cos2C1133. 2827从而cosB cosC5114333. sinB sin C39911.解:(1)∵2cos(A +B )=1,∴cos C =-21,∴角C 的度数为120°.2(2)∵a 、b 是方程x -23x +2=0的两根,∴由求根公式计算得a +b =23,ab =2,222由余弦定理得c =a +b -2ab cos C =(a +b )-2ab (cos C +1)=12-2=10.2∴c =10.(3)S =13ab sin C =.2212.解:(1)Θcos B cos C -sin B sin C =又Θ0<B +C <π,∴B +C =22211,∴cos(B +C )=;223;ΘA +B +C =π,∴A =π2π.3(2)由余弦定理得a =b +c -2bc ⋅cos A ,∴(23)=(b +c )-2bc -2bc ⋅cos 222π,3即12=16-2bc -2bc ⋅(-),∴bc =4;12∴S∆ABC=113bc ⋅sin A =⋅4⋅=3.222o o o 13.解:在△ABC 中,∠BAC =90+30=120,∴BC =AB 2+AC 2-2AB g AC cos A =202+102-2⨯20⨯10cos120o =107.答:乙船直接赶往B 处救援最少要走107海里.。
高考正弦定理和余弦定理练习题及答案

高考正弦定理和余弦定理练习题及答案一、选择题1. 已知△ABC中,a=c=2,A=30°,则b=A. 错误!B. 2错误!C. 3错误!D. 错误!+1答案:B解析:∵a=c=2,∴A=C=30°,∴B=120°.由余弦定理可得b=2错误!.2. △ABC中,a=错误!,b=错误!,sin B=错误!,则符合条件的三角形有A. 1个B. 2个C. 3个D. 0个答案:B解析:∵a sin B=错误!,∴a sin B<b=错误!<a=错误!,∴符合条件的三角形有2个.3.2010·天津卷在△ABC中,内角A,B,C的对边分别是a,b,c.若a2-b2=错误! bc,sin C=2错误!sin B,则A=A.30° B.60°C.120° D.150°答案:A解析:利用正弦定理,sin C=2错误!sin B可化为c=2错误!b.又∵a2-b2=错误!bc,∴a2-b2=错误!b×2错误!b=6b2,即a2=7b2,a=错误!b.在△ABC中,cos A=错误!=错误!=错误!,∴A=30°.4.2010·湖南卷在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=错误!a,则A.a>b B.a<bC.a=b D.a与b的大小关系不能确定答案:A解析:由正弦定理,得错误!=错误!,∴sin A=错误!=错误!>错误!.∴A>30°.∴B=180°-120°-A<30°.∴a>b.5. 如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为A. 错误!B. 错误!C. 错误!D. 错误!答案:D解析:方法一:设三角形的底边长为a,则周长为5a,∴腰长为2a,由余弦定理知cosα=错误!=错误!.方法二:如图,过点A作AD⊥BC于点D,则AC=2a,CD=错误!,∴sin错误!=错误!,∴cosα=1-2sin2错误!=1-2×错误!=错误!.6. 2010·泉州模拟△ABC中,AB=错误!,AC=1,∠B=30°,则△ABC的面积等于A. 错误!B. 错误!C. 错误!或错误!D. 错误!或错误!答案:D解析:∵错误!=错误!,∴sin C=错误!·sin30°=错误!.∴C=60°或C=120°.当C=60°时,A=90°,S△ABC=错误!×1×错误!=错误!,当C=120°时,A=30°,S△ABC=错误!×1×错误!sin30°=错误!.即△ABC的面积为错误!或错误!.二、填空题7.在△ABC中,若b=1,c=错误!,∠C=错误!,则a=________.答案:1解析:由正弦定理错误!=错误!,即错误!=错误!,sin B=错误!.又b<c,∴B=错误!,∴A=错误!.∴a=1.8.2010·山东卷在△ABC中,角A,B,C所对的边分别为a,b,c.若a=错误!,b =2,sin B+cos B=错误!,则角A的大小为________.答案:错误!解析:∵sin B+cos B=错误!,∴sin B+错误!=1.又0<B<π,∴B=错误!.由正弦定理,知错误!=错误!,∴sin A=错误!.又a<b,∴A<B,∴A=错误!.9. 2010·课标全国卷在△ABC中,D为边BC上一点,BD=错误!DC,∠ADB=120°,AD=2.若△ADC的面积为3-错误!,则∠BAC=________.答案:60°解析:S△ADC=错误!×2×DC×错误!=3-错误!,解得DC=2错误!-1,∴BD=错误!-1,BC=3错误!-1.在△ABD中,AB2=4+错误!-12-2×2×错误!-1×cos120°=6,∴AB=错误!.在△ACD中,AC2=4+2错误!-12-2×2×2错误!-1×cos60°=24-12错误!,∴AC=错误!错误!-1,则cos∠BAC=错误!=错误!=错误!,∴∠BAC=60°.三、解答题10. 如图,△OAB是等边三角形,∠AOC=45°,OC=错误!,A、B、C三点共线.1求sin∠BOC的值;2求线段BC的长.解:1∵△AOB是等边三角形,∠AOC=45°,∴∠BOC=45°+60°,∴sin∠BOC=sin45°+60°=sin45°cos60°+cos45°sin60°=错误!.2在△OBC中,错误!=错误!,∴BC=sin∠BOC×错误!=错误!×错误!=1+错误!.11. 2010·全国Ⅱ卷△ABC中,D为边BC上的一点,BD=33,sin B=错误!,cos ∠ADC=错误!,求AD.解:由cos∠ADC=错误!>0知B<错误!,由已知得cos B=错误!,sin∠ADC=错误!,从而sin∠BAD=sin∠ADC-B=sin∠ADC cos B-cos∠ADC sin B=错误!×错误!-错误!×错误!=错误!.由正弦定理得错误!=错误!,AD=错误!=错误!=25.12. 2010·安徽卷设△ABC是锐角三角形,a,b,c分别是内角A,B,C所对边长,并且sin2A=sin错误!sin错误!+sin2B.1求角A的值;2若错误!·错误!=12,a=2错误!,求b,c其中b<c.解:1因为sin2A=错误!错误!+sin2B=错误!cos2B-错误!sin2B+sin2B=错误!,所以sin A=±错误!.又A为锐角,所以A=错误!.2由错误!·错误!=12,可得cb cos A=12.①由1知A=错误!,所以cb=24.②由余弦定理知a2=c2+b2-2cb cos A,将a=2错误!及①代入,得c2+b2=52,③③+②×2,得c+b2=100,所以c+b=10.因此c,b是一元二次方程t2-10t+24=0的两个根.解此方程并由c>b知c=6,b=4.。
正余弦定理练习题(含答案)

A.6B.2 C.3 D .26 2.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( ) A .42 B .43 C .46 D.3233.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =60°,a =43,b =42,则角B 为( ) A .45°或135°B .135°C .45°D .以上答案都不对.以上答案都不对 4.在△ABC 中,a ∶b ∶c =1∶5∶6,则sin A ∶sin B ∶sin C 等于( ) A .1∶5∶6B .6∶5∶1 C .6∶1∶5 D .不确定.不确定 解析:选A.由正弦定理知sin A ∶sin B ∶sin C =a ∶b ∶c =1∶5∶6. 5.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,若A =105°,B =45°,b =2,则c =( ) A .1 B.12 C .2 D.146.在△ABC 中,若cos A cos B =b.已知△ABC 中,AB =3,AC =1,∠B =30°,则△ABC C.32或3 D.34或3、b 、c .若c =2,b =6,B =120°,则a 等于( ) A.6 B .2 C.3 D.2 9.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若a =1,c =3,C =π3,则A =________. 10.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________. 11.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________. 12.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.13.在△ABC 中,A =60°,a =63,b =12,S △ABC =183,则a +b +csin A +sin B +sin C =________,c =________. 14.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C=________. 15.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________. 16.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.组解. 的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少?的距离是多少?18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2、c ,且cos cos 22A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值.的值.20.△ABC 中,ab =603,sin B =sin C ,△ABC 的面积为153,求边b 的长.的长.1.在△ABC 中,∠A =45°,∠B =60°,a =2,则b 等于( ) a,则△ABC 是( ) A .等腰三角形 B .等边三角形 C .直角三角形 D .等腰三角形或直角三角形.等腰三角形或直角三角形 7的面积为( ) A.32B.3428.△ABC 的内角A 、B 、C 的对边分别为a 17.如图所示,货轮在海上以40 40 km/h km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°A2,求A 、B 及b 、c . 19.(2009年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C 所对应的边分别为a 、b,那么26 6 6 =3-A.3 B.2 5 c 2+3bc =3A.π B.π C.π或5π D.π或2π =3,c A.3 .23 C.323 3,则边32=13,则=a +b -c 1为3,则(3-(3∶1023x 为2=2sin 的面积为1sin =5,-π)A.6B.2 3 6 应用正弦定理得:=,求得== 6. 42 43 46 D.32= 6. 3,42,则角由正弦定理=得:==2,又∵=2,则B.1 D.1,由=得=2×2×sin 30°sin 30°=中,若cos A =,则△∵=sin B ,∴cos A =sin B ,π. 3A.3 B.3 C.3或3 D.3或3D.=,求出=3,∵1AB ,6A.6 C.3 D.2 由正弦定理得6=2,= 2. 3,π,则=2=1. A =csin C, 所以sin A =a ·sin C c =12. 又∵a <c ,∴A <C =π3,∴A =π6. 答案:π610.在△ABC 中,已知a =433,b =4,A =30°,则sin B =________. 解析:由正弦定理得a sin A =bsin B ⇒sin B =b sin A a =4×12433=32. 答案:3211.在△ABC 中,已知∠A =30°,∠B =120°,b =12,则a +c =________. 解析:C =180°-120°-30°=30°,∴a =c ,由a sin A =b sin B 得,a =12×12×sin30°sin30°sin120°=43, ∴.在△ABC 中,A =60°,a =63,b =12,S △ABC =183,则a +b +csin A +sin B +sin C=________,c =________. 解析:由正弦定理得a +b +c sin A +sin B +sin C =a sin A =63sin60°=12,又S △ABC =12bc sin A ,∴12×12×12×sin60°sin60°sin60°××c =183, ∴c =6. 答案:12 6 14.已知△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,a =1,则a -2b +csin A -2sin B +sin C =________. 解析:由∠A ∶∠B ∶∠C =1∶2∶3得,∠A =30°,∠B =60°,∠C =90°, ∴2R =a sin A =1sin30°=2,又∵a =2R sin A ,b =2R sin B ,c =2R sin C , ∴a -2b +c sin A -2sin B +sin C =2R s in A -2sinB +sin C sin A -2sin B +sin C =2R =2. 答案:2 15.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________. 解析:由解析:由正弦定理正弦定理得:a sin a +c =8 3. 答案:83 12.在△ABC 中,a =2b cos C ,则△ABC 的形状为________.解析:由正弦定理,得a =2R ·sin A ,b =2R ·sin B , 代入式子a =2b cos C ,得,得 2R sin A =2·2·22R ·sin B ·cos C , 所以sin A =2sin B ·cos C ,即sin B ·cos C +cos B ·sin C =2sin B ·cos C , 化简,整理,得sin(B -C )=0. ∵0°<B <180°,0°<C <180°, ∴-180°<B -C <180°, ∴B -C =0°,B =C . 答案:答案:等腰三角形等腰三角形13解析:依题意,sin C =223,S △ABC =12ab s in C =43,解得b =2 3. 答案:23 16.在△ABC 中,b =43,C =30°,c =2,则此三角形有________组解.组解.解析:∵b sin C ==BC ·sin ∠ABCsin A =20sin30°sin45°=102(km).即货轮到达C 点时,与灯塔A 的距离是102 2 km. km. 18.在△ABC 中,a 、b 、c 分别为角A 、B 、C 的对边,若a =23,sin C 2cos C 2=14,sin B sin C =cos 2A2,求A 、B 及b 、c . 解:由sin C 2cos C 2=14,得sin C =12,又C ∈(0,π),所以C =π6或C =5π6. 由sin B sin C =cos 2A2,得,得sin B sin C =12[1-cos(B +C )], 即2sin B sin C =1-cos(B +C ), 即2sin B sin C +cos(B +C )=1,变形得,变形得 cos B cos C +sin B sin C =1, 即cos(B -C )=1,所以B =C =π6,B =C =5π6(舍去),A =π-(B +C )=2π3. 由正弦定理a sin A =b sin B =csin C ,得,得b =c =a sin B sin A =23×1232=2. 故A =2π3,B =π6,b =c =2. 19.(2009所对应的边分别为a 、b 、c ,且cos cos 22A =35,sin B =1010.(1)求A +B 的值;(2)若a -b =2-1,求a ,b ,c 的值.的值. 43×12=23且c =2,∴c <b sin C ,∴此三角形无解.,∴此三角形无解. 答案:0 17.如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方向线的水平转角)为140°的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110°,航行半小时后船到达C 点,观测灯塔A 的方位角是65°,则货轮到达C 点时,与灯塔A 的距离是多少?的距离是多少?解:在△ABC 中,BC =40×12=20,∠ABC =140°-110°=30°,∠ACB =(180°-140°140°))+65°=105°, 所以∠A =180°-(30°+105°105°))=45°, 由正弦定理得AC 年高考四川卷)在△ABC 中,A 、B 为锐角,角A 、B 、C=10,=1-sin 2B =310. =3,∴=5,25,25×310-5×10=2. π. 3π2==得5a =10b =2c 2b =5-b =2-,∴2=2-=2,c = 5. 603×3×sin =1,∴∠3,sin A =sin B ,∴215. 21,那么6 6 46 AC =AB 2+BC 2-2AB ·BC cos B = 42+62-2×2×4×4×4×6×6×13=6. .在△ABC 中,a =2,b =3A.3 2 C.5 2(3-2×((32. +3bc ==-3bc 2bc =-32,:603153=1153115. 4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =3ac ,则∠B 的值为( ) A.π6B.π3C.π6或5π6D.π3或2π3解析:选D.由(a 2+c 2-b 2)tan B =3ac 2-b 22ac =32·1tan B =32·cos Bsin B . 显然∠B ≠π2,∴sin B =32.∴∠B =π3或2π3. 5.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( ) A .a B .b +2m 2>c 2+2cm +m 2=(c +m )2, ∴三角形各角均为锐角,即新三角形为锐角三角形.∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,|AB →|=4,|AC →|=1 ) A .2 B .-2 C .4 D .-4 解析:选A.S △ABC =3=12|AB →|·|·||AC →|·|·sin sin A=12×4×4×1×1×1×sin sin A , ∴sin A =32,又∵△ABC 为锐角三角形,为锐角三角形,∴cos A =12,∴AB →·AC →=4×4×1×1×12=2. 8.在△ABC 中,b =3,c =3,B =30°,则a 为( ) A.3 B .23 C.3或23 D .2 解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-33a , ∴a 2-33a +6=0,解得a =3或2 3. 9.已知△ABC π3. 在△ABD 中,中,AD =AB 2+BD 2-2AB ·BD cos B= 1+4-2×2×1×1×1×2×2×12= 3. 答案:3 10.△ABC 中,sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10,求最大角的度数.,求最大角的度数. 解:∵sin A ∶sin B ∶sin C =(3-1)∶(3+1)∶10, ∴a ∶b ∶c =(3-1)∶(3+1)∶10. 设a =(3-1)k ,b =(3+1)k ,c =10k (k >0),,联想到余弦定理,代入得到余弦定理,代入得cos B =a 2+c C .c D .以上均不对.以上均不对解析:选C.a ·a 2+c 2-b 22ac +b ·b 2+c 2-a 22bc =2c 22c=c . 6.如果把.如果把直角三角形直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) A .锐角三角形三角形 B .直角三角形.直角三角形 C .钝角三角形.钝角三角形 D .由增加的长度决定.由增加的长度决定 解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2. 设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m ,△ABC 的面积为3,则AB →·AC →的值为( 的三个的三个内角内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的上的中线中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B ==-1,3,=1ab =3,∴===11,7,=-132,43=1,∴=22. 1ab 431·32·22=432 3. 答案:23 = =49+25-36 19,-19) ±12,又∵=21或61. 答案:21或61 ,则角1ab ==·1ab4=78. 答案:723x +2=0的两根,且2cos(A +B )=1,求AB 的长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=12,即cos C =-12. 又∵a ,b 是方程x 2-23x +2=0的两根,的两根,∴a +b =23,ab =2. ∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-12) =a 2+b 2+ab =(a +b )2-ab =(23)2-2=10, ∴AB =10. 18.已知△ABC AC =2+1,BC +AC =2AB , 两式相减,得AB =1. (2)由△ABC 的面积12BC ·AC ·sin C =AC 2+BC 2-AB 22AC ·BC=A C +BC 2-2AC ·BC -AB 22AC ·BC =12,所以C =60°60°. . 19.在△ABC 中,BC =5,AC =3,sin C =2sin A . (1)求AB 的值;的值;(2)求sin(2A -π4)的值.的值.解:(1)在△ABC 中,由正弦定理AB sin C =BCsin A ,得AB =sin Csin A BC =2BC =2 5. (2)在△ABC 中,根据余弦定理,得中,根据余弦定理,得cos A =AB 2+AC 2-BC 22AB ·AC =255, 于是sin A =1-cos 2A =55. 从而sin 2A =2sin A cos A =45, cos 2A =cos 2 A -sin 2 A =35. 所以sin(2A -π4)=sin 2A cos π4-cos 2A sin π4=210. 则îïíïìk 2+k -12-k +12<0k +k -1>k +1⇒2<k <4, ∴k =3,故三边长分别为2,3,4,∴最小角的∴最小角的余弦余弦值为32+42-222×2×3×3×817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-的周长为2+1,且sin A +sin B =2sin C . (1)求边AB 的长;的长; (2)若△ABC 的面积为16sin C ,求角C 的度数.的度数. 解:(1)由题意及由题意及正弦定理正弦定理得AB +BC +=16sin C ,得BC ·AC =13, 由余弦定理得cos C=. sin C ,所以=,得sin C =,。
专题4-3 正余弦定理与解三角形小题归类-(解析版)

专题4-3 正余弦定理与解三角形小题归类目录一、热点题型归纳【题型一】正余弦定理 .............................................................................................................................. 2 【题型二】求角 .......................................................................................................................................... 3 【题型三】判断三角形形状 ...................................................................................................................... 4 【题型四】面积与最值 .............................................................................................................................. 6 【题型五】周长与最值 .............................................................................................................................. 8 【题型六】角的最值 .................................................................................................................................. 9 【题型七】最值 ........................................................................................................................................ 11 【题型八】切弦互化求最值 .................................................................................................................... 13 【题型九】解三角形应用题 .................................................................................................................... 14 二、真题再现 ............................................................................................................................................ 17 三、模拟检测 .. (22)正余弦定理(1)正弦定理:a sin A =b sin B =csin C =2R ,其中R 为 外接圆半径 ;注意:正弦定理变式与性质:①边化正弦:a =2R sin A ,b =2R sin B ,c =2R sin C ; ②正弦化边:sin A sin B sin C =c2R ; ③a ∶b ∶c =sin_A ∶sin_B ∶sin_C ;④a +b +csin A +sin B +sin C= 2R ;(2)余弦定理:①a 2=b 2+c 2-2bc cos_A ; ②b 2=c 2+a 2-2ca cos_B ; ③c 2=a 2+b 2-2ab cos_C 注意:变式:①cos A =b 2+c 2-a 22bc;②cos B =c 2+a 2-b 22ac;③cos C =a 2+b 2-c 22ab(3)三角形面积 :①S △ABC =12ab sin C =12bc sin A =12ac sin B =abc4R②S △ABC =12(a +b +c )·r (r 是切圆的半径) 三角形中:①sin(A +B )=sin C ,cos(A +B )=-cos C ;②sinA +B 2=cosC 2, cos A +B 2=sin C2;③三角形中,任何一个角的正弦值恒大于0;④a >b ⇔A >B ⇔sin A >sin B ⇔cos A <cos B .【题型一】正余弦定理【典例分析】(2022·上海市松江一中高三阶段练习)在ABC 中,a 、b 、c 分别是角A 、B 、C 所对的边,B 是A 、C 的等差中项,则a c +与2b 的大小关系是( )A .2a c b +>B .2a c b +<C .2a c b +≥D .2a c b +≤ 【答案】D【分析】根据等差中项的性质及内角和的性质求出B ,再由余弦定理及基本不等式计算可得. 【详解】解:依题意,在ABC 中B 是A 、C 的等差中项,所以2A+C =B ,又A C B π++=,所以3B π=,由余弦定理2222cos b a c ac B =+-()22222233a c ac a c ac ac a c ac =+-=++-=+-,又22a c ac +⎛⎫≤ ⎪⎝⎭,当且仅当a c =时取等号,所以2332a c ac +⎛⎫-≥- ⎪⎝⎭, 所以()()()222213324a c a c ac a c a c +⎛⎫+-≥+-=+ ⎪⎝⎭,即()2214b a c ≥+,即()224b a c ≥+,所以2a c b +≤; 故选:D1..(2022·江西·丰城九中高三开学考试(文))已知ABC 的三个内角A ,B ,C 的对边分别为a ,b ,c ,且656cos a c b C =+,则cos B =( )A .78B .56C .34D .23【答案】B【分析】根据题意,利用正弦定理边化角,由三角形内角和定理,展开化简得cos B . 【详解】由656cos a c b C =+,边化角得6sin 5sin 6sin cos A C B C =+, 又()sin sin A B C =+,所以()6sin 5sin 6sin cos B C C B C +=+, 展开得6sin cos 6cos sin 5sin 6sin cos B C B C C B C +=+,所以6cos sin 5sin B C C =, 因为sin 0C >,所以5cos 6B =.故选:B . 2.(2023·全国·高三专题练习)在ABC 中,60,3,90C AC B ==>,则ba 的可能取值为( ) A .23B .43 C .53D .73【答案】D【分析】通过正弦定理将所求表达式表示为关于A 的三角函数,求出范围即可得结果. 【详解】因为60,3,90C AC B ==>,所以030A <<,0tan A <<1tan A >()1sin sin sin 11222sin sin sin 2tan A AA C bB a A A A A +====>,则b a 的可能取值为73,故选:D. 3.面积(无最值型)【题型二】求角【典例分析】(2022·山西吕梁·三模(文))在ABC 中,内角,,A B C 的对边分别为,,a b c ,若()(),6b c b c ac C π+-==,则B =( ) A .6πB .3π C .2π D .23π 【答案】B【分析】由22b c ac =+结合余弦定理以及正弦定理的边化角公式得出sin 2sin cos sin A C B C -=,再由内角和定理以及三角恒等变换得出B .【详解】由()()b c b c ac +-=得22b c ac =+,结合余弦定理2222cos b a c ac B =+-,可得2cos a c B c -=,再由正弦定理得sin 2sin cos sin A C B C -=,因为()()sin 2sin cos sin 2sin cos sin A C B B C C B B C -=+-=-, 所以()sin sin B C C -=,所以B C C -=,得2B C =.因为6C π=,所以3B π=.【变式演练】1.(2022·全国·高三专题练习)已知在ABC中,30,1B a b ===,则A 等于( ) A .45 B .135C .45或135D .120 【答案】C【分析】根据正弦定理,结合三角形中的边角关系,即可求得答案.【详解】由正弦定理sin sina b A B=,得1sin 2sin 12a B Ab ===, 因为1,(0,π)a b A ==∈,故45A =或135, 故选:C2.(2022·全国·高三专题练习)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知()22a b c =+-,则sin 4C π⎛⎫+= ⎪⎝⎭( )A B C .2D .1【答案】A【分析】根据三角形面积公式及余弦定理化简条件求角C ,由此可求sin 4C π⎛⎫+ ⎪⎝⎭.【详解】因为()22a b c =+-,又in 12s S ab C =,所以222sin 2C ab a b c -=+-,22212a b c C ab +--=,又222cos 2a b c C ab+-=cos 1C C -=,所以1sin 62C π⎛⎫-= ⎪⎝⎭,又()0,C π∈,所以3C π=,所以sin =sin sin cos cos sin 4343434C πππππππ⎛⎫⎛⎫++=+= ⎪ ⎪⎭⎝⎭所以sin 44C π⎛⎫+= ⎪⎝⎭A.3.(2023·全国·高三专题练习)已知ABC 的内角,,A B C 的对边分别为,,a b c ,设22(sin sin )sin (2sin B C A B C +=+2sin 0A B -=,则sin C = ( )A .12B C D 【答案】C【分析】根据给定条件利用正弦定理角化边,求出角A ,再求出角B 即可计算作答.【详解】在ABC 中,由22(sin sin )sin (2sin B C A B C +=+及正弦定理得:22()(2b c a bc +=+,即222b c a +-=,由余弦定理得:222cos 2b c a A bc +-==0180A <<,解得135A =,2sin 0A B -=得1sin 2B A ==,显然090B <<,则30B =,15C =,所以6sin sin(6045)sin 60cos 45cos 60sin 454C -=-=-=. 故选:C【题型三】判断三角形形状【典例分析】(2023·全国·高三专题练习)在ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,若222a b c -=且cos sin =b C a B ,则ABC 是( ) A .等腰直角三角形 B .等边三角形 C .等腰三角形D .直角三角形【答案】A【分析】由222a b c -=结合余弦定理可求得π4A =,由cos sin =b C a B 结合正弦定理可求得π4C =,从而可判断出三角形的形状【详解】由222a b c -=,得222b c a +-,所以由余弦定理得222cos 2b c a A bc +-===, 因为(0,π)A ∈,所以π4A =,因为cos sin =b C a B ,所以由正弦定理得sin cos sin sin B C A B =,因为sin 0B ≠,所以πcos sin sin 4C A ===,因为(0,π)C ∈,所以π4C =,所以πππππ442B AC =--=--=,所以ABC 为等腰直角三角形, 故选:A【变式演练】1..(2021·广东·高三阶段练习)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且222b c a bc +=+,若2sin sin sin B C A =,则△ABC 的形状是( ) A .等腰三角形 B .直角三角形C .等边三角形D .等腰直角三角形【答案】C【分析】先依据条件222b c a bc +=+求得π3A =,再利用2sin sin sinBC A =可以求得b c =,从而判断△ABC 的形状是等边三角形【详解】△ABC 中,222b c a bc +=+,则2221cos 222b c a bc A bc bc +-=== 又0πA <<,则π3A =由2sin sin sin B C A =,可得2a bc =,代入222b c a bc +=+则有222b c bc bc bc +=+=,则()20b c -=,则b c = 又π3A =,则△ABC 的形状是等边三角形故选:C2.(2023·全国·高三专题练习)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,若cos cos a bA B=,222c a b ab =+-,则ABC ∆是( )A .钝角三角形B .等边三角形C .直角三角形D .等腰直角三角形 【答案】B【分析】利用正余弦定理可确定边角关系,进而可判定三角形形状.【详解】在ABC ∆中,由正弦定理得sin sin a bA B =,而cos cos a b A B =,△ sin sin cos cos A B A B=,即tan tan A B =,又△A 、B 为ABC ∆的内角,△A B =,又△222c a b ab =+-,△222ab a b c =+-,△由余弦定理得:2221cos 22a b c C ab +-==,△3C π=,△ABC ∆为等边三角形.故选:B.3.(2023·全国·高三专题练习)已知三角形ABC ,则“222cos cos cos 1A B C +->”是“三角形ABC 为钝角三角形”的( )条件.A .充分而不必要B .必要而不充分C .充要D .既不充分也不必要 【答案】A【分析】利用同角的三角函数的基本关系式、正余弦定理可判断两个条件之间的推出关系,从而可得正确的选项.【详解】因为222cos cos cos 1A B C +->,故2221sin 1sin 1sin 1A B C -+--+>, 故222sin sin sin C A B >+,故222c a b >+,故222cos 02a b c C ab+-=<,而C 为三角形内角,故C 为钝角,但若三角形ABC 为钝角三角形,比如取2,63C B A ππ===,此时2221cos cos cos 14A B C +-=<,故222cos cos cos 1A B C +->不成立,故选:A.【题型四】面积与最值【典例分析】(2021·江苏·高三课时练习)在锐角三角形ABC 中,cos 2B B +=,且满足关系式cos cos sin sin 3sin B C A Bb c C +=,则ABC ∆的面积的最大值为( )AB .C .D .【答案】Ccos 2B B +=结合同角三角函数基本关系,可求出B ,根据正余弦定理由cos cos sin sin 3sin B C A Bb c C +=可得b ,再利用余弦定理及均值不等式求ac 最大值,代入面积公式即可.cos 2B B +=得cos 2B B =,所以2221cos sin 44sin B B B B =+=+-,即2(2sin 0B =,解得sin B =由锐角三角形知3B π=,cos cos sin sin 3sin B C A Bb c C+=, 22222222a c b a b c abc abc +-+-∴+=,即222a abc =b =2222126cos 122a c b ac B ac ac ac+--∴=≥=-,当且仅当a c =时等号成立,解得12ac ≤,11sin 1222ABC S ac B ∆=≤⨯=当且仅当a c =时等号成立,故选:C【变式演练】1.(2020·全国·高三课时练习)在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c,b =且ABC ∆面积为222)S b a c --,则ABC ∆面积S 的最大值为( ) A.2 B.4-C.8-D.16-【答案】B【解析】由已知利用三角形的面积公式可求tan B ,可得cos B ,sin B 的值,由余弦定理,基本不等式可求8(23)ac -,根据三角形的面积公式即可求解其最大值. 【详解】解:222331()(2cos )sin12122S b a c ac B ac B =--=-=,tan B ∴=,56B π=,cos B=,1sin 2B =, 又22b =228(23)a c ac =++,88(223ac∴=+, 当且仅当a c =时取等号,111sin 8(24222ABC S ac B ∆∴=⨯⨯=- ∴面积S 的最大值为4-B .2.(2023·全国·高三专题练习)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若22a bkab +=,则△ABC的面积为22c 时,k 的最大值是( )A .2BC .4D .【答案】B【分析】由三角形的面积公式,可得2sin c ab C =, 根据余弦定理,可得22sin 2cos a b ab C ab C +=+,则整理出以k 为函数值的三角函数,根据三角函数的性质,可得k 的最值.【详解】由题意得21sin 22ABC c S ab C ==,所以2sin c ab C =,又因为2222cos c a b ab C =+-,所以2222cos sin 2cos a b c ab C ab C ab C +=+=+,所以()22sin 2cos a b k C CC abϕ+==++,其中tan 2ϕ=,且0k >, 所以k 的取值范围为(,故选:B. 3.(2023·全国·高三专题练习)在ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,若8,sin 2sin cos 0ac B C A =+=,则ABC 面积的最大值为( ) A .1 B .3 C .2 D .4 【答案】C【分析】根据sin 2sin cos 0B C A +=利用三角恒等变换和正余弦定理得到2222b a c =-,再根据余弦定理和基本不等式可得cos B 的范围,由此得B 的范围,从而得到sin B 的最大值,从而根据1sin 2ABC S ac B =可求△ABC 面积的最大值.【详解】sin 2sin cos 0B C A +=,()sin 2sin cos 0A C C A ∴++=,即sin cos cos sin 2sin cos 0A C A C C A ++=, 即sin cos 3cos sin 0A C A C +=,则2222223022b a c b c a a c ab bc+-+-⋅+⨯⨯=,理得2222b a c =-, △2222222223232cos 2244a ca c a cb ac ac B ac ac ac ac -+-+-+====当且仅当a 2=3c 2⇔c =√√3a =√8√3时取等号,π10sin 62B B ⎛⎤∴∈∴ ⎥⎝⎦,,, 则111sin 82222ABCS ac B =⨯⨯=.故选:C .【题型五】周长与最值【典例分析】(2022·全国·高三专题练习)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若sin cos 6A A π⎛⎫++ ⎪⎝⎭4b c +=,则ABC ∆周长的取值范围是( )A .[)6,8B .[]6,8C .[)4,6D .[]4,6【答案】A【分析】利用三角函数恒等变换的应用化简已知可得3sin A π+=(),结合A 的范围可求A ,再由余弦定理求得2163a bc =- ,再由基本不等式,求得bc 的范围,即可得到a 的范围,进而可求周长的范围.【详解】△ sin 6A cos A π⎛⎫++ ⎪⎝⎭12sinA sinA ∴-=可得:3sin A π+=()40333A A ππππ∈+∈(,),(,),2 33A ππ∴+=,解得3A π=,△4b c +=, △由余弦定理可得222222163a bccosA b c bc bc bc =-=+--=-(),△由4b c +=,b c +≥,得04bc ≤<,△2416a ≤<,即24a ≤<.△ABC 周长4[68L a b c a =++=+∈,) .故选:A .【变式演练】1.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若sinA +cos(A +π6)=√32,b +c =4,则ABC ∆周长的取值范围是 A .[6,8) B .[6,8] C .[4,6) D .(4,6]【答案】A 【分析】利用三角函数恒等变换的应用化简已知可得sin (A +π3)=√32,结合A 的范围可求A ,再由余弦定理求得a 2=16−3bc ,再由基本不等式,求得bc 的范围,即可得到a 的范围,进而可求周长的范围. 【详解】△sinA +cos(A +π6)=√32,∴sinA +√32cosA −12sinA =√32,可得:sin (A +π3)=√32,∵A ∈(0,π),A +π3∈(π3,4π3),∴A +π3=2π3,解得A =π3,△b +c =4,△由余弦定理可得a 2=b 2+c 2−2bccosA =(b +c )2−2bc −bc =16−3bc ,△由b +c =4,b +c ≥2√bc ,得0<bc ≤4,△4≤a 2<16,即2≤a <4. △ABC 周长L =a +b +c =a +4∈[6,8) .故选A .2.(2022·贵州遵义·高三开学考试(文))在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sinsin 2B Cb a B +=,a =△ABC 周长的最大值为________.【答案】【分析】根据正弦定理,结合三角恒等变换可得3A π=,再根据余弦定理与基本不等式求解周长最大值即可.【详解】由正弦定理,sin sin 2B C b a B +=即sin sin sin sin 22A B A B π⎛⎫-= ⎪⎝⎭,又sin 0B ≠,故sin sin 22A A π⎛⎫-= ⎪⎝⎭,即cossin 2AA =. 由二倍角公式有cos2sin cos 222A A A =,因为0,22A π⎛⎫∈ ⎪⎝⎭,故cos 02A ≠,所以1sin 22A =,所以26A π=,即3A π=.222cos 3b c bc π=+-,结合基本不等式有()()2222332b c b c bc b c +⎛⎫=+-≥+-⨯ ⎪⎝⎭,即()2124b c +≤,()28b c +≤,故b c +≤b c ==.故△ABC 周长的最大值为a b c ++故答案为:3.(2022·全国·高三专题练习)在三角形ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin Aa ==,则该三角形周长的最大值为___________.【分析】利用正弦定理化简式子,求出tan B 的值,进而求出B 的大小,由余弦定理结合基本不等式即可求出a c +≤.【详解】由正弦定理变形有:sin sin A B a b =,又因为sin A a ==sin B B =,则tan 3B B π=2=1b ===又因为()()()()222222212cos 3344a cb ac ac B a c ac a c a c +=+-=+-≥+-⋅=+,所以()2264464a cb ac +≤=⨯=⇒+≤ “a c =”时取等.则该三角形周长的最大值为a b c ++==.【题型六】角的最值【典例分析】(2022·全国·高三专题练习(理)(文))已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2c sin C =(a +b )(sin B -sin A ),则当角C 取得最大值时,B =( ) A .3π B .6πC .2π D .23π【答案】D 【分析】利用正弦定理化简已知条件,结合余弦定理与基本不等式求得C 的最大值,再通过三角形的形状,即可求得此时对应的B .【详解】由正弦定理得2c 2=(a +b )(b -a ),即b 2-a 2=2c 2.又cos C =2222a b c ab +-=2234a b ab +当且仅当3a 2=b 2,即b 时,cos C C 取到最大值6π.当b 时,3a 2-a 2=2c 2,则a =c .所以A =C =6π,从而B =π-A -C =23π.故选:D .【变式演练】1.(2022·安徽淮南·一模(文))在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若函数()()322213f x x bx a c x =+++无极值点,则角B 的最大值是( )A .34πB .2πC .4π D .6π【答案】A【分析】由题知()()22220f x x bx a c '=+++=无解或有两个相等的解,即()()222240b a c ∆=-+≤,再由余弦定理得角B 的范围.【详解】解:因为()()322213f x x bx a c x =+++无极值点,所以()()22220f x x bx a c '=+++=无解或有两个相等的解,所以()()222240b a c ∆=-+≤,所以222cos 2a c b B ac +-=≥,因为()0,B π∈,所以304B π<≤.故选:A2. 2.(2022·全国·江西师大附中模拟预测(文))在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若2sin sin sin a A c C b B +=,则角A 的最大值为( )A .π6B .π4C .π3D .2π3【答案】A【分析】根据正弦定理先将角化边,再运用余弦定理和基本不等式得到cos A 的范围进而得到最后的结果 【详解】因为2sin sin sin a A c C b B += 所以2222a c b +=,进而可得2222a b c =-2222222221()32cos 224b c b c b c a b c A bc bc bc+--+-+===因为223b c +≥=,当且仅当b =时等号成立所以cos A ≥=又因为(0,)A π∈所以角A 的最大值为6π故选:A3.已知锐角△ABC 中,角、、A B C 对应的边分别为a b c 、、,△ABC的面积)222S a b c =+-,若24)tan bc a b B -=(, 则c 的最小值是ABCD【答案】C 【详解】分析:利用余弦定理列出关系式,代入已知等式中,并利用三角形面积公式化简求出C 的度数,再对24)tan bc a b B -=(进行化简整理,最后利用基本不等式求得.详解:)2221cos sin 2S a b c C ab C =+-==,即tan C =,6C π∴=.又A B C π++=,56A B π∴+=,又△ABC 为锐角三角形,∴025062B B πππ<<<-<,解得32B ππ<<, ∴)tan B ∈+∞,又24)tan bc a b B -=(,5sin 24246tan 242424242424sin sin B bc a a sinA B c c c b b B Bπ⎛⎫- ⎪-⎝⎭∴==-=-=-, 即1tan 24242tan B c B ⎛=- ⎝⎭1224tan tan c B B ∴-+≥=,当且仅当12tan tan B B =,即tan B =.24c ∴-≥c ≥故选C.【题型七】最值【典例分析】在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知6B π=且1ABC S =△,则22a cca c ac a +++的最小值为( )A .12B .2C .14D .4 四川省成都市成都市石室中学2020-2021学年高三下学期期中数学试题 【答案】A【分析】由1sin 2ABC S ac B =△可解得4ac =,结合基本不等式,知24a c ac +=;经过变形化简可将原式整理为222()2()a c a c ac ca c ac a ac a c +-+=+++,令t a c =+,则[4t ∈,)+∞,2818()()44t f t t t t-==-,结合函数的单调性即可得解.【详解】由1sin 2ABC S ac B =△可知,11122ac =⨯,解得4ac =,由基本不等式得,24a c ac +=.22222()2()()()()a c a c a c a c acca c ac a c a c a c a ac a c ac a c ++-+=+==++++++, 令t a c =+,则[4t ∈,)+∞,∴222818()()44a c t f t t ca c ac a t t-+===-++,在[4,)+∞上单调递增, ()min f t f ∴=(4)12=,即22a c ca c ac a +++的最小值为12. 故选:A .【变式演练】1..锐角△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若2sinA(acosC +ccosA)=√3a ,则cb 的取值范围是( ) A .(12,2)B .(√33,2√33)C .(1,2)D .(√32,1)【答案】B【分析】根据正弦定理,结合2sinA(acosC +ccosA)=√3a 可求得角B .又由三角形为锐角三角形,求得角C 的取值范围,即可求解.【详解】由正弦定理得,2sinA(sinAcosC +sinCcosA)=√3sinA ⇒sin(A +C)=√32⇒B =π3又∵A,C ∈(0,π2)∴π6<C <π2⇒12<sinC <1⇒c b=sinC sinB=2√33sinC ∈(√33,2√33) 故选B.2.在锐角ABC ∆中,A =2B ,则ABAC 的取值范围是A .(−1,3)B .(1,3)C .(√2,√3)D .(1,2)【答案】D【分析】根据在锐角ABC ∆中,每个角都是锐角确定B 的范围,利用正弦定理以及三倍角的正弦公式,化简表达式,求出范围即可.【详解】在锐角ABC ∆中,{0<2∠B <π20<∠B <π20<π−3∠B <π2可得π6<∠B <π4,cosB ∈(√22,√32),cos 2B ∈(12,34),所以由正弦定理可知AB AC=cb =sinC sinB=sin3B sinB=3sinB−4sin 3BsinB=3−4sin 2B =4cos 2B −1∈(1,2),故选D.3.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,设△ABC 的面积为S,若222c a b S --b a 的取值范围为A .(0,+∞)B .(1,+∞) C .(0D.)+∞【答案】A 【分析】根据222c a b S --=2222a b c C ab +-=,可得cos C C =,可得tan C =可得23C π=,再利用正弦定理可得sin sin b B a A =,12,根据A 的范围可得答案.【详解】由222c a b S --=得2221sin2a b c ab C +-= ,所以2222a b c C ab +-=,所以cos C C =,所以tan C =又0C π<<,所以23C π=, 所以sin()sin cos cos sin )sin 333sin sin sin A A A b B a A A A πππ--===1sin 122sin 2A AA -=,因为03A π<<,所以0tan A <<所以1tan A >所以102b a >=, 所以ba 的取值范围为(0,)+∞.故选:A【题型八】切弦互化求最值【典例分析】ABC 中,角,,A B C 的对边长分别为a,b,c ,若acosB −bcosA=35c ,则tan (A −B )的 最大值为 ( )A .43B .1C .34D 【全国百强校】黑龙江省鹤岗市第一中学2019届高三上学期第二次月考数学(理)试题 【答案】C 【分析】利用正弦定理,将已知等式化简整理得sinAcosB =4sinBcosA ,两边同除以cosAcosB ,得到tanA =4tanB ,利用两角差的正切公式,得tan (A −B )=31tanB+4tanB,最后利用基本不等式求最值 . 【详解】∵acosB −bcosA =35c ,∴结合正弦定理与sinC =sin (A +B ),可得sinAcosB −sinBcosA =35(sinAcosB +cosAsinB ),整理得sinAcosB =4sinBcosA , 同除以cosAcosB ,得tanA =4tanB ,由此可得tan (A −B )=tanA−tanB 1+tanAtanB =3tanB 1+4tan 2B =31tanB+4tanB ,∵A,B 是三角形内角,且tan A 与tan B 同号,∴A,B 都是锐角,即tanA >0,tanB >0,∴tan (A −B )=31tanB+4tanB ≤34,当且仅当1tanB=4tanB ,即tanB =12时,tan (A −B )的最大值为34,故选C.【变式演练】1.在ABC ∆中,若111tan tan tan B C A+=,则cos A 的取值范围为 A .20,3⎛⎤ ⎥⎝⎦B .2,13⎡⎫⎪⎢⎣⎭C .10,3⎛⎤ ⎥⎝⎦D .1,13⎡⎫⎪⎢⎣⎭【答案】B 【详解】分析:由已知等式正切化为弦,可得2sin cos sin sin AA B C=,结合正弦定理、余弦定理以及基本不等式求得cos A的最小值,从而可得结果.详解:111tan tan tan B C A +=,cos cos cos sin sin sin B C A B C A ∴+=,可得sin cos cos sin sin cos sin sin sin sin sin C B C B A A B C B C A +==, 2sin cos sin sin A A B C ∴=,又22,cos sin sin sin a b c a R A A B C bc ====,22222b c a a bc bc+-∴=,可得2223a b c =+,222222222223cos 22333b c b c b c a b c bc A bc bc bc bc ++-+-+∴===≥=,cos A ∴的取值范围是2,13⎡⎫⎪⎢⎣⎭,故选B. 2.在ABC 中,,,a b c 分别是角,,A B C 的对边,若a 2+b 2=2014c 2,则2tanA⋅tanBtanC(tanA+tanB)的值为A .2013B .1C .0D .2014【答案】A 【分析】由a 2+b 2=2014c 2,利用余弦定理可得a 2+b 2﹣c 2=2013c 2=2abcosC .利用三角函数基本关系式和两角和的正弦公式、正弦定理可得2tanA⋅tanBtanC(tanA+tanB)=2sinA cosA ⋅sinBcosB sinC cosC (sinA cosA +sinBcosB)=2sinAsinBcosC sinCsin(A+B)=2abcosCc 2即可得出.【详解】△a 2+b 2=2014c 2,△a 2+b 2﹣c 2=2013c 2=2abcosC . △2tanA⋅tanBtanC(tanA+tanB)=2sinA cosA ⋅sinBcosB sinC cosC (sinA cosA +sinBcosB)=2sinAsinBcosC sinCsin(A+B)=2abcosCc 2=2013.故答案为:A3.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,若ABC ∆为锐角三角形,且满足22b a ac -=,则1tanA−1的取值范围是A .⎛ ⎝⎭B .(1,√2)C .(2√33,√2) D .(1,+∞)【答案】A根据余弦定理以及正弦定理化简条件得A 、B 关系,再根据二倍角正切公式以及函数单调性求范围. 【详解】因为b 2−a 2=ac ,所以c 2−2accosB =ac ∴c −2acosB =a ∴sinC −2sinAcosB =sinA,sin(A +B)−2sinAcosB =sinA,∴sin(B −A)=sinA ∴B −A =A,B =2A因此1tanA−1tanB=1tanA−1tan2A=1tanA−1−tan 2A 2tanA=1+tan 2A 2tanA=12(tanA +1tanA), 因为ΔABC 为锐角三角形,所以0<A <π2,0<B =2A <π2,0<C =π−B −A =π−3A <π2∴π6<A <π4,√33<tanA <1因为y =12(x +1x )在(√33,1)上单调递减,所以1tanA−1tanB∈(1,2√33),选A.【题型九】解三角形应用题【典例分析】(2022·江苏·高三课时练习)如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小,若15,25,30AB cm AC cm BCM ==∠=︒,则tan θ的最大值是( ).(仰角θ为直线AP 与平面ABC 所成的角)A B C D 【答案】D【分析】由题可得,20BC =,过P 作PP BC '⊥,交BC 于P ',连接'AP ,则tan PP AP θ'=',设(0)BP x x '=>,分类讨论,若P '在线段BC 上,则20CP x '=-,可求出PP '和'AP ,从而可得出2320tan 225xx θ-=+,利用函数的单调性,可得出0x =时,取得最大值;若P '在CB 的延长线上,同理求出PP '和'AP ,可得出220tan 225x x θ+=+454x =时,函数取得最大值;结合两种情况的结果,即可得出结论.【详解】解:15,25AB cm AC cm ==,AB BC ⊥,由勾股定理知,20BC =,过点P 作PP BC '⊥交BC 于P ',连结'AP ,则tan PP AP θ'=',设(0)BP x x '=>,若P '在线段BC 上,则20CP x '=-,由30BCM ∠=︒,得tan30)PP CP x ''=︒-,在直角ABP '△中,AP '220tan 225x x θ-∴+令y =,则函数在[0x ∈,20]单调递减,0x ∴=时,;若P '在CB 的延长线上,tan30)PP CP x ''=︒+,在直角ABP '△中,AP '220tan 225xx θ+∴+22(20)225x y x +=+,则0y '=可得454x =. 故答案为:539.【变式演练】1.(2022·全国·高三课时练习)如图,某城市有一条公路从正西方MO 通过市中心O 后转向东北方ON ,为了缓解城市交通压力,现准备修建一条绕城高速公路L ,并在,MO ON 上分别设置两个出口,A B ,若AB 部分为直线段,且要求市中心O 与AB 的距离为20千米,则AB 的最短距离为( )A .)201千米B .)401千米C .)201D .)401【答案】D【分析】使用余弦定理及基本不等式,得到(22AB ab ≥,使用正弦定理及三角恒等变换得到ab ≥AB 的最短距离. 【详解】在ABC 中,135AOB ∠=︒,设,AO a BO b ==,则(222222cos1352AB a b ab a b ab =+-︒=+≥,当且仅当a b =时取等号,设BAO α∠=,则45ABO α∠=︒-,又O 到AB 的距离为20千米,所以20sin a α=,()20sin 45b α=︒-,故()400sin sin 45ab αα=︒-(22.5α=︒时取等号),所以)221600216001AB ≥=,得)401AB ≥,故选:D2.在一座尖塔的正南方地面某点A ,测得塔顶的仰角为2230'︒,又在此尖塔正东方地面某点B ,测得塔顶的仰角为6730︒',且A ,B 两点距离为540m ,在线段AB 上的点C 处测得塔顶的仰角为最大,则C 点到塔底O 的距离为( ) A .90m B .100m C .110m D .270m 【答案】A 【分析】作出图示,根据正切的二倍角公式和解直角三角形求得塔的高度,再运用等面积法可求得选项. 【详解】如下图所示,设,,OC z OA x OB y ===,则222540x y +=,22.5,67.5OAP OBP ∠=∠=,则22tan 22.5tan 4511tan 22.5==-,解得tan 22.521=,22tan 67.5tan13511tan 67.5==--,解得tan 67.52+1=,所以222540+=,解得z =所以1x ==)y ==要使点C 处测得塔顶的仰角为最大,则需tan PCO ∠最大,也即需OC 最小,所以OC AB ⊥,又1122ABOSOA OB AB OC =⨯⨯=⨯⨯,即(90540OA OB OC AB ⨯===, 所以C 点到塔底O 的距离为90m ,故选:A.3..某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD 的周长为4米,沿AC 折叠使B 到B′位置,AB′交DC 于P ,研究发现,当ΔADP 的面积最大时最节能,则最节能时ABCD 的面积为A .3−2√2B .C .2(√2−1)D .2【答案】C 【分析】本题可以先通过设AB 、DP 分别为x 、y ,再通过题目所给信息以及AD 2+DP 2=PA 2得出x 、y 之间的关系,然后通过ΔADP 的面积列出算式,当其最大时求出AB 的值,最后得出结果. 【详解】设AB 为x ,DP 为y ,因为四边形ABCD 是周长为4的长方形,AB 为x 所以AD 为2−x ,DC 为x , 因为DP 为y ,所以PC 为x −y , 由题意可知,PC =PA ,所以有AD 2+DP 2=PA 2,即(2−x )2+y 2=(x −y )2,化简得y =2−2x , 所以S ΔADP =12(2−x )(2−2x ),化简得S ΔADP =3−(2x +2),所以当x =√2时ΔADP 面积最大,此时S ABCD =√2(2−√2)=2(√2−1),故选C .1.(2020·山东·高考真题)在ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若222sin a b c ab C +=+,且sin cos +a B C sin cos c B A =,则tan A 等于( )A .3B .13-C .3或13- D .-3或13【答案】A【分析】利用余弦定理求出tan 2C =,并进一步判断4C π>,由正弦定理可得sin()sin A C B +=⇒=,最后利用两角和的正切公式,即可得到答案;【详解】222sin cos tan 222a b c CC C ab +-==⇒=,4C π∴>,2sin sin sin a b cR A B C===,sin sin cos sin sin cos A B C C B A B ∴⋅⋅+⋅⋅,sin()sin A C B ∴+=⇒=4B π∴=, tan 1B ∴=,∴tan tan tan tan()31tan tan B CA B C B C+=-+=-=-⋅,故选:A. 2.(2021·全国·高考真题(文))在ABC 中,已知120B =︒,AC 2AB =,则BC =( )A.1 B C D .3 【答案】D【分析】利用余弦定理得到关于BC 长度的方程,解方程即可求得边长. 【详解】设,,AB c AC b BC a ===,结合余弦定理:2222cos b a c ac B =+-可得:21942cos120a a c =+-⨯⨯⨯, 即:22150a a +-=,解得:3a =(5a =-舍去), 故3BC =. 故选:D.3.(2020·全国·高考真题(文))在△ABC 中,cos C =2,AC =4,BC =3,则tan B =( )A B .C .D .【答案】C【分析】先根据余弦定理求c ,再根据余弦定理求cos B ,最后根据同角三角函数关系求tan .B 【详解】设,,AB c BC a CA b ===22222cos 916234933c a b ab C c =+-=+-⨯⨯⨯=∴=2221cos sin tan 29a c b B B B ac +-==∴===故选:C4.(2014·江西·高考真题(文))在ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若32a b =,则2222sin sin sin B AA-的值为( )A .19B .13 C .1 D .72【答案】D【分析】根据正弦定理边化角求解即可.【详解】由正弦定理有22222222sin sin 221sin B A b a b A a a --⎛⎫==- ⎪⎝⎭.又3322b a b a =⇒=, 故297212142b a ⎛⎫-=⨯-= ⎪⎝⎭.故选:D5.(2020·全国·高考真题(理))在△ABC 中,cos C =23,AC =4,BC =3,则cos B =( )A .19B .13C .12D .23【答案】A【分析】根据已知条件结合余弦定理求得AB ,再根据222cos 2AB BC AC B AB BC+-=⋅,即可求得答案.【详解】在ABC 中,2cos 3C =,4AC =,3BC =根据余弦定理:2222cos AB AC BC AC BC C =+-⋅⋅2224322433AB =+-⨯⨯⨯可得29AB = ,即3AB =由22299161cos22339AB BC AC B AB BC +-+-===⋅⨯⨯故1cos 9B =.故选:A.6.(2019·全国·高考真题(文))△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A -b sin B =4c sin C ,cos A =-14,则bc =A .6B .5C .4D .3 【答案】A【分析】利用余弦定理推论得出a ,b ,c 关系,在结合正弦定理边角互换列出方程,解出结果. 【详解】详解:由已知及正弦定理可得2224a b c -=,由余弦定理推论可得 22222141313cos ,,,46422422b c a c c c b A bc bc c +---==∴=-∴=∴=⨯=,故选A .7.·湖南·高考真题(文))在△ABC 中,,BC=2,B =60°,则BC 边上的高等于A B C D 【答案】B2sin 60sin A A A =⇒==所以sin sin()sin cos cos sin C A B A B A B =+=+=则BC 边上的高h C ===,应选答案B .点睛:解答本题的思路是先运用正弦定理求出cos A ,再运用两角和的正弦公式求得sin C =,再解直角三角形可求得三角形的高h C =,从而使得问题获解.8.(2018·全国·高考真题(理))ABC 的内角A B C ,,的对边分别为a ,b ,c ,若ABC 的面积为2224a b c +-,则C =A .π2B .π3C .π4D .π6【答案】C【详解】分析:利用面积公式12ABC S absinC =和余弦定理2222a b c abcosC +-=进行计算可得.详解:由题可知222124ABC a b c S absinC +-==所以2222absinC a b c +-=由余弦定理2222a b c abcosC +-=所以sinC cosC =()C 0,π∈C 4π∴=故选C.9.(2022·浙江·高考真题)我国南宋著名数学家秦九韶,发现了从三角形三边求面积的公式,他把这种方法称为“三斜求积”,它填补了我国传统数学的一个空白.如果把这个方法写成公式,就是S =a ,b ,c 是三角形的三边,S是三角形的面积.设某三角形的三边2a b c ===,则该三角形的面积S =___________.【分析】根据题中所给的公式代值解出.【详解】因为S =S10.(2022·全国·高考真题(理))已知ABC 中,点D 在边BC 上,120,2,2ADB AD CD BD ∠=︒==.当AC AB取得最小值时,BD =________.1##-【分析】设220CD BD m ==>,利用余弦定理表示出22AC AB 后,结合基本不等式即可得解.【详解】设220CD BD m ==>,则在ABD △中,22222cos 42AB BD AD BD AD ADB m m =+-⋅∠=++, 在ACD △中,22222cos 444AC CD AD CD AD ADC m m =+-⋅∠=+-,所以()()()2222224421214441243424211m m m AC m m AB m m m m m m ++-++-===-+++++++44≥=- 当且仅当311m m+=+即1m =时,等号成立,所以当ACAB取最小值时,31m =-.故答案为:31-.11.(2022·上海·高考真题)在△ABC 中,3A π∠=,2AB =,3AC =,则△ABC 的外接圆半径为________【分析】运用正弦定理及余弦定理可得解.【详解】根据余弦定理:22212cos 4922372BC AB AC AB AC BAC =+-⋅∠=+-⨯⨯⨯=,得BC =△ABC 3sin 3=.故答案为 12.(2021·全国·高考真题(理))记ABC 的内角A ,B ,C 的对边分别为a ,b ,c 60B =︒,223a c +=,则b =________. 【答案】【分析】由三角形面积公式可得4ac =,再结合余弦定理即可得解.【详解】由题意,1sin 2ABC S ac B ==,所以224,12ac a c =+=,所以22212cos 122482b ac ac B =+-=-⨯⨯=,解得b =.故答案为:13.(2020·江苏·高考真题)在△ABC 中,43=90AB AC BAC ==︒,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-(m 为常数),则CD 的长度是________.【答案】185或0 【分析】根据题设条件可设()0PA PD λλ=>,结合32PA mPB m PC ⎛⎫=+- ⎪⎝⎭与,,B D C 三点共线,可求得λ,再根据勾股定理求出BC ,然后根据余弦定理即可求解.【详解】△,,A D P 三点共线,△可设()0PA PD λλ=>,△32PA mPB m PC ⎛⎫=+- ⎪⎝⎭,△32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭,即32m m PD PB PC λλ⎛⎫-⎪⎝⎭=+,若0m ≠且32m ≠,则,,B D C 三点共线,△321m m λλ⎛⎫-⎪⎝⎭+=,即32λ=,△9AP =,△3AD =,△4AB =,3AC =,90BAC ∠=︒,△5BC =,设CD x =,CDA θ∠=,则5BD x =-,BDA πθ∠=-.△根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅,()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-,△()cos cos 0θπθ+-=,△()()2570665x x x --+=-,解得185x =,△CD 的长度为185.当0m =时, 32PA PC =,,C D 重合,此时CD 的长度为0, 当32m =时,32PA PB =,,B D 重合,此时12PA =,不合题意,舍去.故答案为:0或185. 14.(2020·全国·高考真题(理))如图,在三棱锥P –ABC 的平面展开图中,AC =1,AB AD ==AB △AC ,AB △AD ,△CAE =30°,则cos△FCB =______________.【答案】14-【分析】在ACE 中,利用余弦定理可求得CE ,可得出CF ,利用勾股定理计算出BC 、BD ,可得出BF ,然后在BCF △中利用余弦定理可求得cos FCB ∠的值.【详解】AB AC ⊥,AB =1AC =,由勾股定理得2BC ,同理得BD BF BD ∴==ACE 中,1AC =,AE AD ==30CAE ∠=,由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=,1CF CE ∴==,在BCF △中,2BC =,BF =1CF =,由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯.故答案为:14-.15.(2019·全国·高考真题(文))ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b sin A +a cos B =0,则B =___________.【答案】34π.【分析】先根据正弦定理把边化为角,结合角的范围可得.【详解】由正弦定理,得sin sin sin cos 0B A A B +=.(0,),(0,)A B ∈π∈π,sin 0,A ∴≠得sin cos 0B B +=,即tan 1B =-,3.4B π∴=故选D .【点睛】本题考查利用正弦定理转化三角恒等式,渗透了逻辑推理和数学运算素养.采取定理法,利用转化与化归思想解题.忽视三角形内角的范围致误,三角形内角均在(0,)π范围内,化边为角,结合三角函数的恒等变化求角.16.(2019·全国·高考真题(理))ABC 的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===,则ABC的面积为__________.【答案】【分析】本题首先应用余弦定理,建立关于c 的方程,应用,a c 的关系、三角形面积公式计算求解,本题属于常见题目,难度不大,注重了基础知识、基本方法、数学式子的变形及运算求解能力的考查.【详解】由余弦定理得2222cos b a c ac B =+-,所以2221(2)2262c c c c +-⨯⨯⨯=,即212c =解得c c ==-2a c ==11sin 22ABC S ac B ∆==⨯=1.(2022·江西·模拟预测(文))在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足1cos A A +=,sin 6cos sin A B C =,则bc的值为( )A .1B .1+C .1+D .1+【答案】A【分析】由题设化简1cos A A +=可得120A =︒,余弦定理结合sin 6cos sin A B C =可得(1b c =,即可得出答案.【详解】由题设可得22sin cos 222A A A =,即tan 2A ,则120A =︒,故由余弦定理可得222a b c bc =++;。
余弦定理40道基础题必练题含详解

利用余弦定理可求 ab 的值,从而可求三角形的面积.
【详解】
因为 C 120 ,故 c2 a2 b2 2ab cos120 a2 b2 ab ,
而 a b2 c2 4 ,故 c2 a2 b2 2ab 4 a2 b2 ab ,
故 ab 4 ,故三角形的面积为 1 ab sin120 3 4 3 ,
由余弦定理可得: cos A b2 c2 a2 16 36 28 1
2bc
246 2
又 A 0, 所以 A
3
故选:C
4.C
【分析】
答案第 1页,总 21页
利用余弦定理即可求解. 【详解】
在 ABC 中,若 b2 c2 a2 2bc ,
所以 cos A b2 c2 a2 2bc 2 ,
【详解】
依题意,由正弦定理得 c2 2a bb a b a ,
c2 2ab b2 a2 ab , a2 b2 c2 ab , a2 b2 c2 1 ,
2ab
2
即 cos C 1 .由于 0 C ,
2 所以 C 2 .
3
故选:C
3.C
【分析】
由余弦定理求解可得结果. 【详解】
则C ( )
A. 6
B.
或
2
33
C. 2 3
D.
6
或
5 6
3.在 ABC 中,若 AC 4 , AB 6 , BC 2 7 ,则 A ( )
A. 6
B.
4
C.
3
4.在 ABC 中,若 b2 c2 a2 2bc ,则 A ( )
D.
2
A. 90
B.150
C.135
余弦定理练习题及答案

1.在△ABC 中,已知a =4,b =6,C =120°,则边c 的值是( )A .8B .217C .6 2D .219解析:选D.根据余弦定理,c 2=a 2+b 2-2ab cos C =16+36-2×4×6cos 120°=76,c =219.2.在△ABC 中,已知a =2,b =3,C =120°A.5719 C.338 解析:选A.c 2=a 2+b 2-2ab cos C=22+32-2×2×3×cos 120°=19.__________. 2a ,故顶角的余弦值为ABC 的形状.2b =a +c 可转化为2sin B =sin A +sin C .又∵B =60°,∴A +C =120°,∴C =120°-A ,∴2sin 60°=sin A +sin(120°-A ),整理得sin(A +30°)=1,∴A =60°,C =60°.∴△ABC 是正三角形.一、选择题1.在△ABC 中,符合余弦定理的是( )A .c 2=a 2+b 2-2ab cos CB .c 2=a 2-b 2-2bc cos AC .b 2=a 2-c 2-2bc cos AD .cos C =a 2+b 2+c 22ab 解析:选A.注意余弦定理形式,特别是正负号问题.2.(2011年合肥检测)在△ABC 中,若a =10,b =24,c =26,则最大角的余弦值是( ) A.1213 B.513C .0 D.23解析:选C.∵c >b >a ,∴c 所对的角C 0. 3.已知△ABC 的三边分别为2,3,4,则此三角形是( A .锐角三角形 B C .直角三角形 D 解析:选B.∵42=16>22+32=13,∴边长为4( )或2π3个 4个sin A =sin B cos C +sin C cos B =sin(B +C ),显然成立.对于④由正弦定理sin B =sin C sin A +sin A sin C =2sin A sin C ,则不一定成立.6.在△ABC 中,已知b 2=ac 且c =2a ,则cos B 等于( )A.14B.34C.24D.23解析:选B.∵b 2=ac ,c =2a ,∴b 2=2a 2,X k b 1 . c o m∴cos B =a 2+c 2-b 22ac =a 2+4a 2-2a 22a ·2a=34. 二、填空题7.在△ABC 中,若A =120°,AB =5,BC =7,则AC =________.解析:由余弦定理,得BC 2=AB 2+AC 2-2AB ·AC ·cos A ,即49=25+AC 2-2×5×AC ×(-12), AC 2+5AC -24=0.∴AC =3或AC =-8(舍去).答案:38.已知三角形的两边分别为4和5,它们的夹角的余弦值是方程2x 2+3x -2=0的根,则第三边长是________.解析:解方程可得该夹角的余弦值为12,由余弦定理得:42+52-2×4×5×12=21,∴第三边长是21.8,则B 的大小是________. C .解得c =5或c =-75(舍). 由余弦定理得cos C =a 2+b 2-c 22ab =16+9-252×4×3=0, ∵0°<C <180°,∴C =90°.11.在△ABC 中,a 、b 、c 分别是角A 、B 、C 所对的边长,若(a +b +c )(sin A +sin B -sin C )=3a sin B ,求C 的大小.解:由题意可知,(a +b +c )(a +b -c )=3ab ,于是有a 2+2ab +b 2-c 2=3ab ,即a 2+b 2-c 22ab =12, 所以cos C =12,所以C =60°. 12.在△ABC 中,b =a sin C ,c =a cos B ,试判断△ABC 的形状.解:由余弦定理知cos B =a 2+c 2-b 22ac,代入c =a cos B , 得c =a ·a 2+c 2-b 22ac,∴c 2+b 2=a 2, ∴△ABC 是以A 为直角的直角三角形.又∵b =a sin C ,∴b =a ·c a,∴b =c , ∴△ABC 也是等腰三角形.综上所述,△ABC 是等腰直角三角形.。
2021年高中数学《余弦定理》精选练习(含答案)

2021年高中数学《余弦定理》精选练习一、选择题1.在△ABC 中,已知a=9,b=23,C=150°,则c 等于( )A.39B.8 3C.10 2D.7 32.在△ABC 中,已知A=30°,且3a=3b=12,则c 的值为( )A.4B.8C.4或8D.无解3.在△ABC 中,已知(a +b +c)(b +c -a)=3bc ,则角A 等于( )A.30°B.60°C.120°D.150°4.在△ABC 中,若a=8,b=7,cos C=1314,则最大角的余弦值是( )A.-15B.-16C.-17D.-185.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若c 2-a 2-b22ab>0,则△ABC( )A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.是锐角或直角三角形6.若△ABC 的内角A ,B ,C 所对的边a ,b ,c 满足(a +b)2-c 2=4,且C=60°,则ab 的值为( )A.43B.8-4 3C.1D.237.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若C=120°,c=2a ,则a ,b 大小关系为( )A.a>bB.a<bC.a=bD.不能确定 8.在△ABC 中,有下列关系式:一定成立的有( )①asin B=bsin A;②a=bcos C+ccos B ;③a 2+b 2-c 2=2abcos C ;④b=csin A+asin C. A.1个 B.2个 C.3个 D.4个 9.锐角△ABC 中,b=1,c=2,则a 的取值范围是( )A.1<a<3B.1<a<5C.3<a< 5D.不确定10.在△ABC 中,cos 2B 2=a +c 2c,则△ABC 是( )A.正三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形二、填空题11.在△ABC 中,已知b=60 cm ,c=60 3 cm ,A=π6,则a=________cm ;12.在△ABC 中,a=1,b=2,cos C=14,则c= ;sin A= .13.在△ABC 中,若b=1,c=3,C=2π3,则a=________.14.在△ABC 中,A=120°,AB=5,BC=7,则sin Bsin C 的值为________.三、解答题15.在△ABC 中,a,b,c 分别是角A,B,C 的对边,,且满足错误!未找到引用源。
余弦定理练习题及答案

余弦定理练习题及答案1.已知三角形ABC的边长a=21,b=5,c=4,求角A的大小。
解析:根据余弦定理,cosA=(b^2+c^2-a^2)/(2bc),代入数值计算可得cosA=-61/40,因为-1≤cosA≤1,所以三角形ABC不存在角A,即无解。
2.已知三角形ABC的边长a=3,b=4,c=6,求XXX的值。
解析:根据余弦定理,cosA=(b^2+c^2-a^2)/(2bc),cosB=(a^2+c^2-b^2)/(2ac),cosC=(a^2+b^2-c^2)/(2ab),代入所求式计算可得答案为-11/2.3.已知三角形ABC的边长a=3,b=4,c=6,求边C的长度。
解析:根据余弦定理,cosC=(a^2+b^2-c^2)/(2ab),代入数值计算可得cosC=-1/2,因为0°≤C≤180°,所以C的大小为120°。
再根据正弦定理,c/sinC=a/sinA,代入已知数据可得c=2√3.4.如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为多少?解析:设等腰三角形的底边长为x,则周长为5x,由等腰三角形的性质可知,其两个等角为(180°-顶角)/2,所以顶角的大小为2(180°-顶角)/2=180°-顶角。
根据余弦定理,cos顶角=[(5x/2)^2+x^2-(5x/2)^2]/(2x^2)=3/4.5.已知三角形ABC的边长a=1,b=7,角B=60°,求边C 的长度。
解析:根据正弦定理,c/sinC=a/sinA,又因为A+B+C=180°,所以角A=180°-60°-arcs in(1/7)≈86.6°。
代入已知数据计算可得c≈7.5.6.已知三角形ABC的边长a=2,b=2,角A=45°,解此三角形。
解析:根据余弦定理,cosB=(a^2+c^2-b^2)/(2ac)=0,即角B为直角。
正余弦定理习题加答案详解超级详细

∴由余弦定理可得:cosC= = = .
故答案为: .
14.(2016•抚顺一模)已知△ABC的周长为 +1,且sinA+sinB= sinC,则边AB的长为1.
【解答】解:由题意及正弦定理,得:AB+BC+AC= +1.
BC+AC= AB,
两式相减,可得AB=1.
故答案为:1.
15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于1.
(1)求角A的值;
(2)若a= ,则求b+c的取值范围.
【解答】解:(1)在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2 =a﹣2a• ,
利用正弦定理可得(sinB﹣2sinC)cosA=sinA(﹣cosB),
即sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,
【解答】解:(1)∵ .
∴由正弦定理,得 ,化简得cosA= ,
∴A= ;
(2)∵∠B= ,∴C=π﹣A﹣B= ,
可知△ABC为等腰三角形,
在△AMC中,由余弦定理,得AM2=AC2+MC2﹣2AC•MCcos120°,即7= ,
解得b=2,
∴△ABC的面积S= b2sinC= = .
19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b﹣2c)cosA=a﹣2aco模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是( )
余弦定理练习题(含答案)

余弦定理练习题(含答案)本页仅作为文档封面,使月変T以删除This document is for reference onlyjar21year余弦定理练习题11. ABC中,如果BC=6, AB=4, cosB=§,那么AC 等于()A. 6B. 2、/i C・ 3、/i D・ 4、/i2. 在△ABC 中,a=29 b=\[l-l9 C=30\ 则 c 等于()D・23. 在A ABC中,,=匕2+以+羽be,则z &等于()A. 60°B. 45°C. 120°D. 150°4. ABC中,Z/k Z B. ZC的对边分别为a、H c,若0+呂_夕曲曲=羽却则Z B的值为()5TX2n或T 或亍5. 在△ ABC中,a、b、c分别是4、C的对边,则acosS+bcos4等于()A. aB. bC. cD.以上均不对6. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.由增加的长度决定8. 在AABC 中,b=g C=39 S=30°,贝!| a 为()B・ 2、/i 或2、/i D・ 29. 已知bABC的三个内角满足2B=A + C9且48=1, SC=4,则边BC上的中线AD的长为 __________________ ・10. A ABC中,sin4: sinB : sinC=({i —:L):(yfl+l):倔,求最大角的度数.已知a. b、c是bABC的三边,S是'ABC的面积,若a=4, b=5, S=5©则边c的值为______________________ ・12. 在AABC 中,sin A : sin S : sin C=2 : 3 : 4,贝Ij cos A : cos B : cos C= _______ ・13. ABC中,0=3^2, cos C=|, S^ABC=4y[39则b= __________________ ・/+,一c215・已知4 ABC的三边长分别是a、b. c,且面积S= ---------------- -------- ,则角C= __________ ・16.三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为_____________ •17・在AABC中,BC=a9 AC=b f a, b是方程只_2压+2 = 0的两根,且2cos(4 + B) = l,求48的长.18.已知"BC的周长为y/1+l,且sin A + sin B=y/lsin C.⑴求边AB的长;⑵若4 ABC的面积为^sin C,求角C的度数.19.在△ABC 中,BC=G AC=39 sin C=2sinA.(l)求AB 的值;(2)求sin(24的值.20.在4 ABC中,已知(a+b+c)(a+b-c)=3ab・且2cos Asin B=sinC,确定A ABC的形状.余弦定理答案在bABC 中,a=2, b=y[3-l 9 C=30°,则 c 等于(B ) D. 2 在4 ABC 中.a2=b2+w+羽矗,则ZA 等于(D )A ・ 60°B. 45°C. 120°D. 在b ABC 中,Z Z By ZC 的对边分别为 a. c 9 若(a 2+c 2—b 2)tanB=y/3ac 9亠5兀亠2TX 或T 或亍 解析:选D.由(a 24-c 2-b 2)tanS=V3ac,联想到余弦定理,代入得 c^+c 2—b2 y[3 1 羽 cosB n . 羽 n 2ncosB== 2ai = 2 t^B = 2 sin8•显然fi#2r •: S ,n8= 2 ••: Z 或亍.5. ABC 中.a 、b 、c 分别是久8、C 的对边,则acosS+bcosA 等于(C )A ・a B. S C. c D ・以上均不对6. 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.宜角三角形C ・钝角三角形 D.由增加的长度决定解析:选A.设三边长分别为a, b 9 c 且a 2+b 2=c 2.设增加的长度为m,则c+m>a+m 9 c+m>b+m, 又(a+m )2+(b+m )2=a 2+b 2+2 佃+b )E+2m2>c2+2cm+E2=(c+E )r•:三角形各角均为锐角,即新三角形为锐角三角形.8・在4ABC 中.b=g C =39 S=30°,贝!)a 为( )B ・ 2、/i 或 2、/iD ・ 2 解析:选 C ・在AABC 中,由余弦定理得 62=02+^—2accosS,即 3=a 2^9—3y[3a 9 :. a 2 —3^3a+6=0,解得 a=\[3或 2羽・9. 已知bABC 的三个内角满足2B=A+C 9且AB=l f BC=4,则边BC 上的中线AD 的长为 ___________________ ・ 解析:T 2B=A + C, 4 + B+C=n,・•・ 3=扌・在AABD 中,AD=\)AB 2-}-BD 2—2AB BDcosB= yj 1+4—2xlx2x^=^3.答案:羽10. A ABC 中,smA : sinB : sinC=^-l ):(羽+ 1): 嗣,求最大角的度数・解:・・ sin4 : sinB : sinC=(V3~l ) : (W+1):屈,・.a : b : c =(\(3-l ):(羽+1):伍・ 设 a=(羽一b=(y[3 + l )k 9 c=yjldk (k>O}fa 24~b 2—c 2 1 ・・・c 边最长,即角C 最大.由余弦定理,得cosC=―面一=一刁 又ce (o°, 180°), /. C=120°.11. 已知a 、b 、c 是6ABC 的三边,S 是b ABC 的面积,若a=4, b=5, S=5品 则边c 的值为 ___________________ ・ 解析:S=#absinC, sinC=^, /. C=60°或 120°./. cosC=#,又T c 2=a 2+b 2—2abcosC tA ^=21或61,・・,=回或佰•答案: 回或屈12. 在 AABC 中.sinA : sinB : sin C=2 : 3: 4,贝l| cos A : cos 8 : cos C= ________ ・解析:由正弦定理 a : b : c=sin A : sin B : sin C=2 : 3 : 4,2k 2+ 4k 2- 3/c 2 11IS 9 13.在△ ABC 中,a=3\(29 cos C=-: 解析:cos c=扌,sin2. 3. 4. 150° 则ZB 的值为(D )cP+c 2—b 2 设 a=2k (k>0),贝0 b=3k 9 c=4k, cos B=同理可得:cos 4=^, cos C=—右・・ cos A : cos B : cos C=14 : 11 : (—4).答案:14 : 11 : (—4)S AABC =4~\》,则 b= __________ ..又S AAB c=^absinC=4yj3t 即知3迄普=裁,二b=2品答案;2伍a 2-f-b 2—c 215.已知AABC 的三边长分别是a 、b. c,且面积S=——,则角C= ________________________ ・2x2kx4k1 a'+b2—c2,+堺一c2 ab 1解析:尹bsinC=S= ---------- - ------= --- 書^—=2obcosC, sinC=cosC, tanC=l, /. C=45°.答案:45°2ab16.三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为.疋+ k—1 2—k+1 2<0解析:设三边长为k-l9 k f k+l(k>29 kWN),则‘ 一亠-々=2VkV4,A+k—l>k+l32+4'—2? 7 7• • k=3,故三边长分别为2,3,4, 最小角的余弦值为2x3x4 =:答案:百17.在bABC中,BC=a, AC = b9 a, b是方程x z-2y(3x^2 = 0的两根,且2cos(A + S) = 1,求AB的长.1 1解:・.• A+B+C=TI且2cosS+B)=l, cos(n—C)=-t即cosC=—-又T 6 b是方程x2—2^/3x+2=0的两根,・・・a+b=2晶ab=2.・・.AB2=AC2+BC2-2AC BCcosC=a2+b2-2ab(-^=a2+b2+ab=(a+b)2—ab=(2yj3)2-2 = lQ9 /. AB=y[ld.18.已知AABC的周长为迄+1,且sinA+sinS=V2sinC・⑴求边AB的长;⑵若bABC的面积为fsinC,求角C的度数.解:⑴由题意及正弦定理得AB+BC+AC=7i+l, BC+AC=y/2AB,两式相减,得48=1.(2)由厶ABC的面积扌BC AC sin C=|sin C,得BC AC=^,在△ ABC 中,BC=G AC=3f sin C=2sinA・⑴求AB的值;(2)求sin(2A-为的值.解:⑴在BABC中,由正弦定理黒=鳥,得AB=^BC=2BC=2y/5. ▲毋+&7—BC2 2\[s(2)在△ ABC中,根据余弦定理,得cos A= 2AB AC = 5,于是si" … 4 3从而sin 24=2sin AcosA=^9 cos 24=cos2 4 —sin2 ^ = g-所以sin(2A—R = sin 2Acos^—cos 2Asin^=-J^・20.在b ABC中,已知(a+b+c)佃+b—c)=3cr® 且2cos4sin S=sinC,确定b ABC的形状. 」十7亠e ^sin C c .亠sinC c解:由正弦定理,得sin 8=匸由2cos Asin B=sin C,有cos4 = 2s j n g = 2b・b'+c2—ct2 c b'+c2—a'又根据余弦定理,得COS 4= 2bc ,所以沪2bc /即云=屏+以一a"所以a=b又因为(a+b+c)(a+b—c) = 3ab,所以(a+b)2—c2=3ab f所以4S2—c2=3S2, 所以b=6所以a=b=c f因此4 ABC为等边三角形.。
(完整版)余弦定理练习含答案

课时作业2余弦定理时间:45分钟 满分:100分课堂训练1.在△ABC 中,已知 a = 5, b =4,Z C = 120°.则 c 为()A. 41B. , 61C. 41 或 61D. , 21【答案】 B【解析】 c = ” a 2 + b 2 — 2abcosC=52 + 42 — 2X 5X 4X — 2 = 61.2.^ ABC 的内角A 、B 、C 的对边分别为a , b , c ,若a , b , c 满足 b 2 = ac ,且 c = 2a ,则 cosB =( )3B. 3C.【答案】 B【解析】 由b 2 = ac ,又c = 2a ,由余弦定理3. 在厶ABC 中,三个角A 、B 、C 的对边边长分别为a = 3、b = 4、c = 6,贝卩 bccosA + cacosB + abcosC =A*_ a 2 + c 2 — b 2 cosB = 2ac a 2+ 4a 2 — a x 2a 3 2a 2a — 4.b 2 +c 2— a 2bccosA + cacosB + abcosC = bc •c 2 + a 2 — b 2 a 2 + b 2 — c 2 1 1 1 ca -20c + ab • 2ab = 2(b 2 + c 2— a 2) + 2(c 2 + a 2 — b 2) + ^(a 2 + 1 61b 2—c 2) = 2(a 2 + b 2+ c 2)=亍4. 在△ ABC 中:(1) a = 1, b = 1,Z C = 120° 求 c ; (2) a = 3, b = 4, c = 37,求最大角; (3) a:b:c = 1: 3 :2,求/ A 、/ B 、/ C. 【分析】(1)直接利用余弦定理即可; (2) 在三角形中,大边对大角; (3) 可设三边为x , 3x,2x.【解析】(1)由余弦定理,得c 2 = a 2 + b 2— 2abcosC 1=12+ 12 — 2X 1 x 1 x (—刁=3,「・c = 3. (2) 显然/C 最大,a 2+b 2 —c 2 32+ 42— 37 1/cosC = —2ab — = 2x 3x 4 = — 2.AzC = 120°(3) 由于 a:b:c = 1: 3 :2, 可设 a = x , b = V3x , c = 2x(x>0).b 2+c 2 — a 2 3x 2 + 4/ — x 2 百由余弦定理,得 cosA = —2bc — = 2 • 3X 2X = ~2,/./\= 30 °【答案】 612 【解析】1同理cosB=2 cosC= O.「./3= 60 ,ZC= 90 .12,【规律方法】1. 本题为余弦定理的最基本应用,应在此基础上熟练地掌握余弦 定理的结构特征.2. 对于第(3)小题,根据已知条件,设出三边长,由余弦定理求 出/A ,进而求出其余两角,另外也可考虑用正弦定理求/ B ,但要注意讨论解的情况.课后作业一、选择题(每小题5分,共40分)ABC 中,下列结论:① a 2>b 2 + &,则厶ABC 为钝角三角形; ② a 2= b 2 + c 2 + be,则/ A 为 60° ③ a 2+ b 2>e 2,则△ ABC 为锐角三角形;④ 若/ A:Z B: / C = 1:2:3,贝卩 a:b:e = 1:2:3, 其中正确的个数为()A . 1B . 2 C. 3 D . 4【答案】 A•••么为钝角,正确;b 2 + e 2— a 2【解析】 ① eosA = b 2+ c 2—a 2 —2bc —<°,②eosA=—2be—12,a 2+b 2—c 2③ cosC = 2ab >0,•••©为锐角,但/ A 或/B 不一定为锐角,错误;④ Z A = 30 ° ZB = 60 ° ZC= 90 °a:b:c = 1: 3 :2,错误.故选 A.2.A ABC 的三内角A 、B 、C 所对边长分别为a 、b 、c ,设向量p =(a + c , b), q = (b — a , c — a).若 p// q ,则/ C 的大小为( )人nA~6nB.3nc.2【答案】 B【解析】 Tp = (a + c , b), q = (b — a , c — a)且 p 〃q , • .(a + c)(c — a) — b(b — a) = 0n zC= 3.冗 ,△ ABC 中,角A , B , C 的对边分别为a , b , c ,/ A =3 a=7, b = 1,则 c 等于()A . 2 2B . 3 C/ 3 + 1 D . 2 3【答案】 B【解析】 由余弦定理得,a 2= b 2 + c 2— 2bccosA ,即 a 2+ b 2— c 2= ab , 「•cosC = a 2+ b 2—c 2=_ab =1 2ab = 2ab =2.所以(7)= 1 + c2—2x 1 x e x cog.即c2—c—6= 0,解得c= 3 或c= —2(舍).故选 B.4.在不等边三角形ABC中,a为最大边,且a2vb2+ c2,则/ A 的取值范围是()A.(扌,n )B. (n, nC.(n,f)D. (0, n【答案】C【解析】因为a为最大边,所以/ A为最大角,即/A> ZB,/A>ZC,故2ZA>/B+/C.又因为Z B+ Z C= n-Z A,所以2ZA> n—Z A, 即Z Ag因为a2<b2+ c2,所以cosA=葺b—2>0,所以0<从W综上,n /A n3<zA<25. 在△ ABC 中,已知 a = 4,b= 6,Z C= 120° 则si nA 的值为() A语D「I?【答案】【解析】由余弦定理得c = a2+ b2—2ab cosC = 42+ 62—2X4X 6( —2)= 76,••c= 76.由正弦定理得轟=sinC,即蠢=sinLZQ ,4sin120。
(完整版)正余弦定理习题加答案详解超级详细

正余弦定理高中数学组卷一.选择题(共9小题)1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若,a=2,,则b的值为()A.B. C. D.2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.(2016•岳阳校级模拟)在△ABC中,A:B:C=1:2:3,则a:b:c等于()A.1:2:3 B.3:2:1 C.1::2 D.2::14.(2016•大连一模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形 D.等腰直角三角形5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且,则∠B=()A.B.C.D.6.(2016•宝鸡一模)在△ABC,a=,b=,B=,则A等于()A.B.C.D.或7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2 B.2C.D.8.(2016•新余二模)在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.角B的值为()A.B.C.D.9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则等于()A.B.C.D.二.填空题(共7小题)10.(2016•上海二模)△ABC中,,BC=3,,则∠C=.11.(2016•丰台区一模)在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,若b=2asinB,则角A等于.12.(2016•焦作一模)在△ABC中,已知a=8,∠B=60°,∠C=75°,则b等于.13.(2016•潍坊一模)已知△ABC中,a,b,c分别为内角A,B,C的对边,且a•cosB+b•cosA=3c•cosC,则cosC=.14.(2016•抚顺一模)已知△ABC的周长为+1,且sinA+sinB=sinC,则边AB的长为.15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于.16.(2016•湖南校级模拟)设△ABC的内角A,B,C的对边分别为a,b,c.若,,则b=.三.解答题(共4小题)17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知=(1)求角C的大小,(2)若c=2,求使△ABC面积最大时a,b的值.18.(2016•安徽校级一模)在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)求角A的值;(2)若∠B=,BC边上中线AM=,求△ABC的面积.19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b ﹣2c)cosA=a﹣2acos2.(1)求角A的值;(2)若a=,则求b+c的取值范围.20.(2016•鹰潭一模)已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosc=2a ﹣c(Ⅰ)求B;(Ⅱ)若△ABC的面积为,求b的取值范围.正余弦定理高中数学组卷参考答案与试题解析一.选择题(共9小题)1.(2016•太原校级二模)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若,a=2,,则b的值为()A.B. C. D.【解答】解:∵在锐角△ABC中,sinA=,S△ABC=,∴bcsinA=bc=,∴bc=3,①又a=2,A是锐角,∴cosA==,∴由余弦定理得:a2=b2+c2﹣2bccosA,即(b+c)2=a2+2bc(1+cosA)=4+6(1+)=12,∴b+c=2②由①②得:,解得b=c=.故选A.2.(2016•潍坊模拟)在△ABC中,sinA=sinB是△ABC为等腰三角形的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【解答】解:当sinA=sinB时,则有A=B,则△ABC为等腰三角形,故sinA=sinB是△ABC 为等腰三角形的充分条件,反之,当△ABC为等腰三角形时,不一定是A=B,若是A=C≠60时,则sinA≠sinB,故sinA=sinB是△ABC为等腰三角形的不必要条件.故选A.3.(2016•岳阳校级模拟)在△ABC中,A:B:C=1:2:3,则a:b:c等于()A.1:2:3 B.3:2:1 C.1::2 D.2::1【解答】解:在△ABC中,若∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=π所以∠A=,∠B=,∠C=.由正弦定理可知:a:b:c=sin∠A:sin∠B:sin∠C=sin:sin:sin=1::2.故选:C.4.(2016•大连一模)在△ABC中,a,b,c分别是角A,B,C的对边,且满足acosA=bcosB,那么△ABC的形状一定是()A.等腰三角形B.直角三角形C.等腰或直角三角形 D.等腰直角三角形【解答】解:根据正弦定理可知∵bcosB=acosA,∴sinBcosB=sinAcosA∴sin2A=sin2B∴A=B,或2A+2B=180°即A+B=90°,即有△ABC为等腰或直角三角形.故选C.5.(2016•河西区一模)已知△ABC的内角A,B,C的对边分别为a,b,c,且,则∠B=()A.B.C.D.【解答】解:已知等式利用正弦定理化简得:=,即c2﹣b2=ac﹣a2,∴a2+c2﹣b2=ac,∴cosB==,∵B为三角形的内角,∴B=.故选:C.6.(2016•宝鸡一模)在△ABC,a=,b=,B=,则A等于()A.B.C.D.或【解答】解:由正弦定理可得:sinA===∵a=<b=∴∴∠A=,故选:B.7.(2016•岳阳二模)△ABC的三个内角A、B、C所对的边分别为a,b,c,asinAsinB+bcos2A=a,则=()A.2 B.2C.D.【解答】解:∵△ABC中,asinAsinB+bcos2A=a,∴根据正弦定理,得sin2AsinB+sinBcos2A=sinA,可得sinB(sin2A+cos2A)=sinA,∵sin2A+cos2A=1,∴sinB=sinA,得b=,可得=.故选:C.8.(2016•新余二模)在△ABC中,a、b、c分别是角A、B、C的对边,且(2a+c)cosB+bcosC=0.角B的值为()A.B.C.D.【解答】解:由条件及正弦定理得sinBcosC+sinCcosB=﹣2sinAcosB.即sin(B+C)=﹣2sinAcosB.∵A+B+C=π,A>0∴sin(B+C)=sinA,又sinA≠0,∴cosB=﹣,而B∈(0,π),∴B=.故选:C.9.(2016•江西模拟)在△ABC中,角A,B,C的对边分别是a,b,c,且A=2B,则等于()A.B.C.D.【解答】解:∵A+B+C=π,A=2B,∴===.再结合正弦定理得:.故选:D.二.填空题(共7小题)10.(2016•上海二模)△ABC中,,BC=3,,则∠C=.【解答】解:由,a=BC=3,c=,根据正弦定理=得:sinC==,又C为三角形的内角,且c<a,∴0<∠C<,则∠C=.故答案为:11.(2016•丰台区一模)在锐角△ABC中,角A,B,C所对应的边分别为a,b,c,若b=2asinB,则角A等于30°.【解答】解:利用正弦定理化简b=2asinB得:sinB=2sinAsinB,∵sinB≠0,∴sinA=,∵A为锐角,∴A=30°.故答案为:30°12.(2016•焦作一模)在△ABC中,已知a=8,∠B=60°,∠C=75°,则b等于4.【解答】解:∵a=8,B=60°,C=75°,即A=45°,∴由正弦定理,得:b===4.故答案为:413.(2016•潍坊一模)已知△ABC中,a,b,c分别为内角A,B,C的对边,且a•cosB+b•cosA=3c•cosC,则cosC=.【解答】解:∵a•cosB+b•cosA=3c•cosC,∴利用余弦定理可得:a×+b×=3c×,整理可得:a2+b2﹣c2=,∴由余弦定理可得:cosC===.故答案为:.14.(2016•抚顺一模)已知△ABC的周长为+1,且sinA+sinB=sinC,则边AB的长为1.【解答】解:由题意及正弦定理,得:AB+BC+AC=+1.BC+AC=AB,两式相减,可得AB=1.故答案为:1.15.(2016•长沙一模)△ABC的周长等于2(sinA+sinB+sinC),则其外接圆半径等于1.【解答】解:设△ABC的三边分别为a,b,c,外接圆半径为R,由正弦定理得,∴a=2RsinA,b=2RsinB,c=2RsinC,∵a+b+c=2(sinA+sinB+sinC),∴2RsinA+2RsinB+2RsinC=2(sinA+sinB+sinnC),∴R=1.故答案为:1.16.(2016•湖南校级模拟)设△ABC的内角A,B,C的对边分别为a,b,c.若,,则b=2.【解答】解:B=π﹣A﹣C=,△ABC中,由正弦定理可得,∴b=2,故答案为:2.三.解答题(共4小题)17.(2016•白山一模)在△ABC中,角A,B,C所对的边分别为a,b,c,已知=(1)求角C的大小,(2)若c=2,求使△ABC面积最大时a,b的值.【解答】解:(1)∵A+C=π﹣B,即cos(A+C)=﹣cosB,∴由正弦定理化简已知等式得:=,整理得:2sinAcosC+sinBcosC=﹣sinCcosB,即﹣2sinAcosC=sinBcosC+cosBsinC=sin(B+C)=sinA,∵sinA≠0,∴cosC=﹣,∵C为三角形内角,∴C=;(Ⅱ)∵c=2,cosC=﹣,∴由余弦定理得:c2=a2+b2﹣2abcosC,即4=a2+b2+ab≥2ab+ab=3ab,∴ab≤,(当且仅当a=b时成立),∵S=absinC=ab≤,∴当a=b时,△ABC面积最大为,此时a=b=,则当a=b=时,△ABC的面积最大为.18.(2016•安徽校级一模)在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)求角A的值;(2)若∠B=,BC边上中线AM=,求△ABC的面积.【解答】解:(1)∵.∴由正弦定理,得,化简得cosA=,∴A=;(2)∵∠B=,∴C=π﹣A﹣B=,可知△ABC为等腰三角形,在△AMC中,由余弦定理,得AM2=AC2+MC2﹣2AC•MCcos120°,即7=,解得b=2,∴△ABC的面积S=b2sinC==.19.(2016•平果县模拟)已知在锐角△ABC中,a,b,c为角A,B,C所对的边,且(b ﹣2c)cosA=a﹣2acos2.(1)求角A的值;(2)若a=,则求b+c的取值范围.【解答】解:(1)在锐角△ABC中,根据(b﹣2c)cosA=a﹣2acos2=a﹣2a•,利用正弦定理可得(sinB﹣2sinC)cosA=sinA(﹣cosB),即sinBcosA+cosBsinA=2sinCcosA,即sin(B+A)=2sinCcosA,即sinC=2sinCcosA,∴cosA=,∴A=.(2)若a=,则由正弦定理可得==2,∴b+c=2(sinB+sinC)=2[sinB+sin(﹣B)]=3sinB+cosB=2sin(B+).由于,求得<B<,∴<B+<.∴sin(B+)∈(,1],∴b+c∈(3,2].20.(2016•鹰潭一模)已知a,b,c分别为△ABC三个内角A,B,C的对边,2bcosc=2a ﹣c(Ⅰ)求B;(Ⅱ)若△ABC的面积为,求b的取值范围.【解答】解:(1)由正弦定理,得2sinBcosC=2sinA﹣sinC,﹣﹣﹣﹣(2分)在△ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC,∴2cosBsinC=sinC,又∵C是三角形的内角,可得sinC>0,∴2cosB=1,可得cosB=,∵B是三角形的内角,B∈(0,π),∴B=.﹣﹣﹣﹣﹣(6分)(2)∵S△ABC==,B=∴,解之得ac=4,﹣﹣﹣﹣(8分)由余弦定理,得b2=a2+c2﹣2accosB=a2+c2﹣ac≥2ac﹣ac=ac=4,(当且仅当a=c=2时,“=”成立)∴当且仅当a=c=2时,b的最小值为2.﹣﹣﹣﹣(12分)综上所述,边b的取值范围为[2,+∞)﹣﹣﹣﹣(13分)。
高三数学余弦定理试题答案及解析

高三数学余弦定理试题答案及解析1.在△ABC中,角A,B,C所对边的长分别为a,b,c.已知a+c=2b,sinB=sinC,则cosA=.【答案】【解析】因为sinB=sinC,由正弦定理得:,由余弦定理得:【考点】正余弦定理2.已知的三个内角所对的边分别为.若△的面积,则的值是。
【答案】4【解析】得得。
【考点】三角形面积公式、余弦定理、商数关系.3.某人先向正东方向走了x km,然后他向右转150°,向新的方向走了3 km,结果他离出发点恰好为km,那么x的值为()A.B.2C.2或D.3【答案】C【解析】根据余弦定理可得:()2=x2+32-2×3x×cos(180°-150°),即x2-3x+6=0.∴x=2或.4.如图,某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是()A.5(+) km B.5(-) kmC.10(-) km D.10(+) km【答案】C【解析】由题意,知∠BAC=60°-30°=30°,∠ABC=30°+45°=75°,∠ACB=180°-75°-30°=75°,∴AC=AB=40×=20(km).由余弦定理,得BC2=AC2+AB2-2AC·AB·cos∠BAC =202+202-2×20×20×cos30°=800-400=400(2-),∴BC===10 (-1)=10(-)(km).5.在中,三个内角A,B,C所对的边分别是a,b,c,且.(1)求角的大小;(2)求的取值范围.【答案】(1);(2).【解析】(1)根据余弦定理的推论,代入到条件中可得,所以有,进一步根据角B的范围求出B 的大小;(2)由(1)知:所以把化成只含角一个变量的三角函数,利用三角函数的最值求解.解:(1)由余弦定理可得:,即由得 5分(2)由得, 6分. 9分∵,∴, 10分∴, 11分∴的取值范围为. 12分【考点】1、余弦绽理及其推论;2、两角各与差的三角函数公式;3、三角函数的最值问题.6.(13分)(2011•天津)在△ABC中,内角A,B,C的对边分别为a,b,c,已知.(Ⅰ)求cosA的值;(Ⅱ)的值.【答案】(Ⅰ)(Ⅱ)【解析】(I)利用三角形中的等边对等角得到三角形三边的关系;利用三角形的余弦定理求出角A的余弦.(II)利用三角函数的平方关系求出角A的正弦,利用二倍角公式求出角2A的正弦,余弦;利用两个角的和的余弦公式求出的值.解:(I)由B=C,可得所以cosA==(II)因为所以=点评:本题考查三角形的余弦定理、考查三角函数的平方关系、考查两角和的余弦公式.7.在中,角A,B,C的对边分别为若,则角B的值为()A.B.C.D.【答案】D【解析】由得.故选.【考点】余弦定理的应用.8.(2013•浙江)在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB=b.(Ⅰ)求角A的大小;(Ⅱ)若a=6,b+c=8,求△ABC的面积.【答案】(1)(2)【解析】(Ⅰ)由2asinB=b,利用正弦定理得:2sinAsinB=sinB,∵sinB≠0,∴sinA=,又A为锐角,则A=;(Ⅱ)由余弦定理得:a2=b2+c2﹣2bc•cosA,即36=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,∴bc=,又sinA=,则S=bcsinA=.△ABC9.在△ABC中,BC=,AC=1,以AB为边作等腰直角三角形ABD(B为直角顶点,C、D两点在直线AB的两侧).当变化时,线段CD长的最大值为.【答案】3【解析】设,,则在三角形BCD中,由余弦定理可知,在三角形ABC中,由余弦定理可知,可得,所以,令,则,当时等号成立.【考点】解三角形10.在△中,角、、所对的边长分别为、、,且.(1)若,,求的值;(2)若,求的取值范围.【答案】(1)或;(2).【解析】(1)已知两边,要求第三边,最好能求出已知两边的夹角,然后用余弦定理可求得,而由已知条件可得,从而可知,即,问题得解;(2)这是三角函数的一般性问题,解决它的一般方法是把函数化为的形式,然后利用正弦函数的知识解决问题,,首先用二倍角公式,降幂公式把二次式化为一次式,再利用两角和的正弦公式把两个三角函数化为一个三角函数,,接下来我们只要把作为一个整体,求出它的范围,就可借助于正弦函数求出的取值范围了.试题解析:(1)在△中,.所以.,所以. 3分由余弦定理,得.解得或. 6分(2). 9分由(1)得,所以,,则. ∴.∴.∴的取值范围是. 12分【考点】(1)余弦定理;(2)二倍角公式与降幂公式,三角函数的取值范围11.在△ABC中,角A,B,C的对边分别为a,b,c,C=,a=5,△ABC的面积为10.(1)求b,c的值;(2)求cos的值.【答案】(1)c=7(2)=absinC,即10=b·5sin,解得b=8. 【解析】(1)由已知,C=,a=5,因为S△ABC由余弦定理可得:c2=25+64-80cos=49,所以c=7.(2)由(1)有cosB=,由于B是三角形的内角,易知sinB=,所以cos=cosBcos+sinBsin=.12.在锐角△ABC中,角A、B、C所对的边长分别为a、b、c.向量m=(1,cosB),n=(sinB,-),且m⊥n.(1)求角B的大小;(2)若△ABC面积为10,b=7,求此三角形周长.【答案】(1)(2)20【解析】(1)m·n=sinB-cosB,∵m⊥n,∴m·n=0,∴sinB-cosB=0.∵△ABC为锐角三角形,∴cosB≠0,∴tanB=.∵0<B<,∴B=.=acsinB=ac,由题设ac=10,得ac=40.由72=a2+c2-2accosB,得(2)∵S△ABC49=a2+c2-ac,∴(a+c)2=(a2+c2-ac)+3ac=49+120=169.∴a+c=13,∴三角形周长是20.13.在△ABC中,a=,b=1,c=2,则A=________.【答案】60°【解析】由余弦定理,得cosA=,∵0<A<π,∴A=60°14.在△ABC中,a、b、c分别为角A、B、C所对的边,若a=2bcosC,则此三角形一定是________三角形.【答案】等腰【解析】因为a=2bcosC,所以由余弦定理得a=2b·,整理得b2=c2,故此三角形一定是等腰三角形.15.设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为()A.4∶3∶2B.5∶6∶7C.5∶4∶3D.6∶5∶4【答案】D【解析】因为a,b,c为连续的三个正整数,且A>B>C,可得a=c+2,b=c+1;①又因为3b=20acosA,由余弦定理可知cosA=,则3b=20a·,②联立①②,化简可得7c2-13c-60=0,解得c=4或c=-(舍去),则a=6,b=5.又由正弦定理可得,sinA∶sinB∶sinC=a∶b∶c=6∶5∶4.故应选D.16.在△ABC中,a、b、c分别是角A、B、C的对边,B=,且sinA∶sinC=3∶1,则b∶c的值为.【答案】【解析】sinA∶sinC=a∶c=3∶1,∴a=3c.由余弦定理cos==,∴=,7c2=b2,∴=7,∴=.17.在△ABC中,AC=,BC=2,∠B=60°,则△ABC的面积等于.【答案】【解析】设角A、B、C的对边分别为a、b、c,由余弦定理,cosB==,即=,∴c2-2c-3=0,∴c=3或c=-1(舍).∴S=acsinB=.△ABC18.在△ABC中,a、b、c分别为角A、B、C的对边,若m=(sin2,1),n="(-2,cos" 2A+1),且m⊥n.(1)求角A的度数;(2)当a=2,且△ABC的面积S=时,求边c的值和△ABC的面积.【答案】(1) π (2)C=B【解析】解:(1)由于m⊥n,所以m·n=-2sin2+cos 2A+1=1-2cos2+2cos2A-1=2cos2A-cosA-1=(2cosA+1)(cosA-1)=0.所以cosA=-或1(舍去),即角A的度数为π.(2)由S=及余弦定理得tanC=,∴C==B.又由正弦定理=得c=2,所以△ABC的面积S=acsinB=.19.在中,、、分别是角A、B、C所对的边,,则的面积S=______.【答案】【解析】由角A的余弦定理得,因为,所以三角形ABC为直角三角形,则,故填.【考点】余弦定理勾股定理面积=2,则b等20.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=1,B=45°,S△ABC于()A.5B.25C.D.5【答案】A【解析】∵S=ac sin B=2,∴×1×c×sin 45°=2.∴c=4.∴b2=a2+c2-2ac cos B=1+32-2×1×4×cos 45°.∴b2=25,b=5.21.△ABC中内角A,B,C的对边分别为a,b,c,已知a=b cos C+c sin B.(1)求B;(2)若b=2,求△ABC面积的最大值.【答案】(1)B=(2)+1【解析】(1)由已知及正弦定理,得sin A=sin B cos C+sin C sin B,①又A=π-(B+C),故sin A=sin(B+C)=sin B cos C+cos B sin C.②由①,②和C∈(0,π)得sin B=cos B.又B∈(0,π),所以B=.(2)△ABC的面积S=ac sin B=ac.由已知及余弦定理,得4=a2+c2-2ac cos.又a2+c2≥2ac,故ac≤,当且仅当a=c时,等号成立.因此△ABC面积的最大值为+1.22.在△ABC中,a、b、c分别为角A、B、C的对边,4sin2-cos 2A=.(1)求角A的度数;(2)若a=,b+c=3,求△ABC的面积.【答案】(1)A=60°.(2)【解析】(1)∵B+C=π-A,即=,由4sin2-cos 2A=,得4cos2-cos 2A=,即2(1+cos A)-(2cos2A-1)=,整理得4cos2A-4cos A+1=0,即(2cos A-1)2=0.∴cos A=,又0°<A<180°,∴A=60°.(2)由A=60°,根据余弦定理cos A=,得=.∴b2+c2-bc=3,①又b+c=3,②∴b2+c2+2bc=9. ③①-③得bc=2. ④解②④得或∴S=×1×2×sin 60°=.△ABC23.如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A.+1B.2+2C.-1D.2-2【答案】D【解析】分别过点作的垂线,垂足分别为,连结,设,则=,等腰梯形的周长,令则,所以,,所以,当即, ,此时, ,因为为双曲线的焦点,点在双曲线上,所以实轴长.故选D.【考点】1、双曲线的定义;2、余弦定理;3、二次函数的最值问题.24.在△ABC中,角A,B,C所对的边分别为a,b,c.若,,,则()A.B.C.D.【答案】D【解析】∴,由余弦定理得,,所以.【考点】1、诱导公式;2、余弦定理.25.已知三角形的一边长为4,所对角为60°,则另两边长之积的最大值等于 .【答案】16【解析】设三角形的边长为其中,则,即,所以,即,当且仅当时取等号,所以两边长之积的最大值等于16.【考点】余弦定理的应用,基本不等式.26.在⊿ABC中,三边所对的角分别为A,B,C,若,则角C为()A.30°B.45°C.150°D.135°【答案】B【解析】由余弦定理得,,又,∴.【考点】余弦定理.27.在△的内角、、的对边分别为、、,若,,,则 .【答案】【解析】由余弦定理可知.【考点】余弦定理.28.在中,设内角的对边分别为,向量,向量,若(1)求角的大小;(2)若,且,求的面积.【答案】(1);(2)16【解析】(1)先计算的坐标,由得关于的方程,再利用辅助角公式化为,则,然后根据,得范围,从而求值,进而确定;(2)在中,,确定,另外两边的关系确定,所以利用余弦定理列方程求,再利用求面积.试题解析:(1)又因为,故,∴;(2)由余弦定理得,即,解得,∴,∴.【考点】1、向量的模;2、向量运算的坐标表示;3、余弦定理.29.在中,,,,则的面积为().A.B.C.D.【答案】D.【解析】因为为三角形的内角,所以,所以三角形的面积,选D.【考点】三角形面积公式.30.在中,角所对的边分别为满足,,,则的取值范围是 .【答案】【解析】由得,得为钝角,故,由正弦定理可知:,,所以.【考点】正余弦定理,辅助角公式.31.已知△ABC的内角A、B、C所对应边分别为a、b、c,若,则角C的大小是_______________(结果用反三角函数值表示)【答案】【解析】,故.【考点】考查余弦定理及运算,属容易题。
【新人教版】初中数学余弦定理专项练习题含答案

人教版初中数学余弦定理专项练习题双基达标限时20分钟1.在△ABC中,已知a=9,b=23,C=150°,则c等于( ).A.39 B.8 3 C.10 2 D.7 3解析c2=a2+b2-2ab cos C=92+(23)2-2×9×23cos 150°=147=(73)2,∴c=7 3.答案 D2.在△ABC中,若a=7,b=43,c=13,则△ABC的最小角为( ).A.π3B.π6C.π4D.π12解析∵c<b<a,∴最小角为角C.∴cos C=a2+b2-c22ab=49+48-132×7×43=32.∴C=π6,故选B.答案 B3.在△ABC中,角A,B,C的对边分别为a,b,c,若c2-a2-b22ab>0,则△ABC( ).A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.是锐角或直角三角形解析∵c2-a2-b22ab>0,∴c2-a2-b2>0.∴a2+b2<c2.∴△ABC为钝角三角形.故选C.答案 C4.已知a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2=________.解析∵b2=a2+c2-2ac cos B=a2+c2-2ac cos 120°=a2+c2+ac.∴原式为0.答案 05.在△ABC 中,若(a -c )(a +c )=b (b +c ),则A =________.解析 ∵(a -c )(a +c )=b (b +c ),∴a 2-c 2=b 2+bc ,即b 2+c 2-a 2=-bc .∴cos A =b 2+c 2-a 22bc =-12. ∵0°<A <180°,∴A =120°.答案 120°6.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos A =14,a =4,b +c =6,且b <c ,求b ,c 的值.解 由余弦定理a 2=b 2+c 2-2bc cos A ,∴16=(b +c )2-2bc -12bc ∴bc =8,又∵b +c =6,b <c ,解方程组⎩⎨⎧ b +c =6,bc =8,得b =2,c =4或b =4,c =2(舍).∴b =2,c =4.综合提高 限时25分钟7.在△ABC 中,B =60°,b 2=ac ,则三角形一定是( ).A .直角三角形B .等边三角形C .等腰直角三角形D .钝角三角形解析 由余弦定理b 2=a 2+c 2-ac ,∴a 2+c 2-2ac =0,∴(a -c )2=0,∴a =c .∵B =60°,∴A =C =60°.故△ABC 为等边三角形.答案 B8.在△ABC 中,AB =5,AC =3,BC =7,则AB →·A C →等于( ).A.152 B .-152 C.1532 D .15 解析 ∵cos A =AB 2+AC 2-BC 22AB ·AC =52+32-722×5×3=-12, ∴AB →·AC →=|AB →|·|AC →|·cos ∠BAC=5×3×⎝ ⎛⎭⎪⎫-12=-152,故选B. 答案 B9.在锐角△ABC 中,边长a =1,b =2,则边长c 的取值范围是________. 解析 ∵c 2=a 2+b 2-2ab ·cos C =1+4-4cos C =5-4cos C . 又∵0<C <π2,∴cos C ∈(0,1). ∴c 2∈(1,5).∴c ∈(1,5).答案 (1,5)10.已知等腰△ABC 的底边BC =2,腰AB =4,则腰上的中线长为________.解析 ∵cos A =b 2+c 2-a 22bc =42+42-222×4×4=78. 设其中一腰中线长为x ,则x 满足:x 2=42+22-2×4×2cos A =20-16×78=6.∴x = 6. 答案 611.已知a ,b ,c 分别是△ABC 中角A ,B ,C 的对边,且a 2+c 2-b 2=ac .(1)求角B 的大小;(2)若c =3a ,求tan A 的值.解 (1)由余弦定理,得cos B =a 2+c 2-b 22ac =12. ∵0<B <π,∴B =π3. (2)法一 将c =3a 代入a 2+c 2-b 2=ac ,得b =7a .由余弦定理,得cos A =b 2+c 2-a 22bc =5714. ∵0<A <π,∴sin A =1-cos 2A =2114. ∴tan A =sin A cos A =35. 法二 将c =3a 代入a 2+c 2-b 2=ac ,得b =7a .由正弦定理,得sin B =7sin A .∵B =π3,∴sin A =2114. 又∵b =7a >a ,则B >A ,∴cos A =1-sin 2A =5714. ∴tan A =sin A cos A =35. 12.(创新拓展)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.解 (1)由已知,根据正弦定理得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc .由余弦定理a 2=b 2+c 2-2bc cos A , 故cos A =-12. 又A ∈(0,π),∴A =2π3. (2)由(1)中a 2=b 2+c 2+bc 及正弦定理,可得sin 2A =sin 2B +sin 2C +sin B sin C ,即⎝ ⎛⎭⎪⎫322=sin 2B +sin 2C +sin B sin C ,又sin B+sin C=1,得sin B=sin C=1 2,又0<B,C<π3,∴B=C,∴△ABC为等腰的钝角三角形.。
正余弦定理专题练习(含答案)

正余弦定理专题2020.3一、选择题1、在△ABC中,a=1,B=45°,S△ABC=2,则△ABC外接圆的直径为( )A.4B.60C.5D.6【解析】选C.因为由三角形的面积公式得:S=acsin B=×1×c×=2,所以c=4,又因为a=1,cos B=,根据余弦定理得:b2=1+32-8=25,解得b=5.所以△ABC的外接圆的直径为==5.2、在△ABC中,角A,B,C所对的边分别为a,b,c,如果c=a,B=30°,那么角C等于 ( )A.120°B.105°C.90°D.75°【解析】选A.因为c=a,所以sin C=sin A=sin(180°-30°-C)=sin(30°+C)=,即sin C=-cos C.所以tan C=-.又0°<C<180°,所以C=120°.3、在△ABC中,已知sin2A+sin2B-sin Asin B=sin2C,且满足ab=4,则该三角形的面积为( )A.1B.2C.D.【解析】选D.因为sin2A+sin2B-sin Asin B=sin2C,根据正弦定理得a2+b2-ab=c2,由余弦定理得2abcos C=ab,所以cos C=,所以sin C==,4、若△ABC为钝角三角形,三边长分别为2,3,x,则x的取值范围是( )A.(1,)B.(,5)C.(,)D.(1,)∪(,5)【解析】选D.(1)若x>3,则x对角的余弦值<0且2+3>x,解得<x<5.(2)若x<3,则3对角的余弦值<0且x+2>3,解得1<x<.故x的取值范围是(1,)∪(,5).所以S=absin C=×4×=.二、填空题5、在△ABC中,已知A=60°,tan B=,a=2,则c=________. 【解析】因为tan B=,所以sin B=,cos B=.又因为A=60°,所以sin C=sin[180°-(A+B)]=sin(120°-B)=sin 120°cos B-cos 120°sin B=+.由正弦定理,得=,即c===.答案:6、在△ABC中,角A,B,C的对边分别为a,b,c.若(a2+c2-b2)tan B=ac,则角B的度数为________.【解析】由余弦定理,得2accos B·tan B=ac,整理,得sin B=,所以B=60°或120°.答案:60°或120°7、△ABC的内角A,B,C的对边分别是a,b,c且满足acos B-bcos A=c,则△ABC的形状为________.【解析】根据正弦定理,得a=2Rsin A,b=2Rsin B,C=2Rsin C(其中R是△ABC外接圆的半径),代入acos B-bcos A=c得2Rsin Acos B-2Rsin Bcos A=2Rsin C,所以sin Acos B-sin Bcos A=sin (A+B),所以sin Acos B-sin Bcos A=sin Acos B+sin Bcos A,所以2sin Bcos A=0,又因为sin B≠0,所以cos A=0,又A∈(0,π),所以A=,所以该三角形为直角三角形.答案:直角三角形8、在△ABC中,若3b=2asin B,cos A=cos C,则△ABC的形状为________.【解析】由正弦定理知b=2R·sin B,a=2R·sin A,则3b=2a·sin B可化为:3sin B=2sin A·sin B.因为0°<B<180°,所以sin B≠0,所以sin A=,所以A=60°或120°,又cos A=cos C,所以A=C,所以A=60°,所以△ABC为等边三角形.答案:等边三角形9、在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=,b=,1+2cos(B+C)=0,则边BC上的高为________.【解析】由1+2cos(B+C)=0和B+C=π-A,得1-2cos A=0,所以cos A=,sin A=.再由正弦定理,得sin B==.由b<a知B<A,所以B不是最大角,B<,从而cos B==.由上述结果知sin C=sin(A+B)=×=.设边BC上的高为h,则有h=bsin C=.答案:10、在锐角三角形ABC中,a,b,c所对的角分别为A,B,C,A=2B,则的取值范围是________.【解析】在锐角三角形ABC中,A,B,C<90°,即所以30°<B<45°.由正弦定理知:===2cos B∈(,),故的取值范围是(,).答案:(,)三、解答题11、在△ABC中,a,b,c分别是角A,B, C所对的边且b=6,a=2,A=30°,求ac的值.【解析】由正弦定理=得sin B===.由条件b=6,a=2,b>a知B>A.所以B=60°或120°.(1)当B=60°时,C=180°-A-B=180°-30°-60°=90°.在Rt△ABC中,C=90°,a=2,b=6,c=4,所以ac=2×4=24.(2)当B=120°时,C=180°-A-B=180°-30°-120°=30°,所以A=C,则有a=c=2.所以ac=2×2=12.12、△ABC的内角A,B,C所对的边分别为a,b,c.向量m=(a,b)与n=(cos A,sin B)平行.(1)求A.(2)若a=,b=2,求sin C.【解析】(1)因为m∥n,所以asin B-bcos A=0.由正弦定理,得sin Asin B-sin Bcos A=0,又因为sin B≠0,从而tan A=.由于0<A<π,所以A=.(2)由正弦定理,得=,从而sin B=,又由a>b,知A>B,所以cos B=.故sin C=sin(A+B)=sin(B+)=sin Bcos +cos Bsin=.13、在△ABC中,求证:(1)=.(2)=.【证明】(1)由余弦定理,a2=b2+c2-2bccos A,于是==1-·2cos A=1-·2cos A===.(2)方法一:==·==.方法二:====.14、在△ABC中,已知(a+b+c)(a+b-c)=3ab,且2cos Asin B=sin C,确定△ABC的形状.【解析】由正弦定理得=,由2cos Asin B=sin C,有cos A==.又由余弦定理得cos A=,所以=,即c2=b2+c2-a2,所以a2=b2,所以a=b.又因为(a+b+c)(a+b-c)=3ab,所以(a+b)2-c2=3ab,所以4b2-c2=3b2,即b2=c2.所以b=c,所以a=b=c.15、所以△ABC为等边三角形.已知a,b,c分别为△ABC三个内角A,B,C的对边,+=.(1)求角A的大小.(2)若a=2,△ABC的面积为,求边b,c.【解析】(1)由+=及正弦定理得+=,得,sin Acos B+cos Asin B=2sin Ccos A,即 sin(A+B)=2sin CcosA. 因为sin(A+B)=sin(π-C)=sin C,且sin C≠0,所以,cos A=.又0<A<π,所以,A=.(2)因为△ABC的面积S=bcsin A=bcsin=,所以,bc=4.①由余弦定理得,a2=b2+c2-2bccos A,22=b2+c2-2bccos所以,b2+c2=8,②联立①②解得,b=c=2.16、在△ABC中,角A,B,C的对边分别为a,b,c,且a2-(b-c)2=(2-)bc,sin Asin B=cos2,BC边上的中线AM的长为.(1)求角A和角B的大小.(2)求△ABC的周长.【解析】(1)由a2-(b-c)2=(2-)bc,得a2-b2-c2=-bc所以cos A==.又0<A<π,所以A=.由sin Asin B=cos2,得sin B=,即sin B=1+cos C,则cos C<0,即C为钝角.所以B为锐角,且B+C=,则sin=1+cos C,化简得cos=-1,解得C=,所以B=.(2)由(1)知,a=b,在△ACM中,由余弦定理得AM2=b2+-2b··cos C=b2++=()2,解得b=2,所以a=2.在△ABC中c2=a2+b2-2abcos C=22+22-2×2×2×cos =12,所以c=2.所以△ABC的周长为4+2.。
余弦定理练习题(含答案)
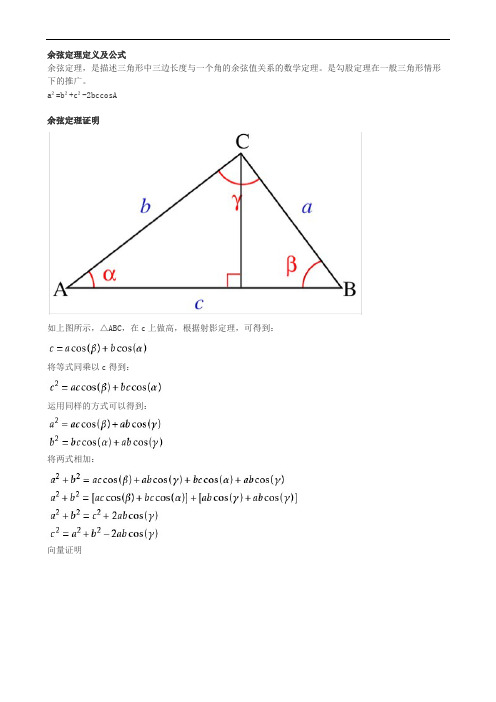
余弦定理定义及公式余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广。
a²=b²+c²-2bccosA余弦定理证明如上图所示,△ABC,在c上做高,根据射影定理,可得到:将等式同乘以c得到:运用同样的方式可以得到:将两式相加:向量证明正弦定理和余弦定理正弦定理 a/sinA=b/sinB=c/sinC=2R(1)已知三角形的两角与一边,解三角形(2)已知三角形的两边和其中一边所对的角,解三角形(3)运用a :b :c=sinA :sinB :sinC 解决角之间的转换关系直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值余弦定理练习题1.在△ABC 中,如果BC =6,AB =4,cos B =,那么AC 等于( )13A .6 B .2 C .3 D .46662.在△ABC 中,a =2,b =-1,C =30°,则c 等于( )3A. B. C. D .23253.在△ABC 中,a 2=b 2+c 2+bc ,则∠A 等于( )3A .60° B .45° C .120° D .150°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =ac ,则∠B 的值为( )3A. B. C.或 D.或π6π3π65π6π32π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定7.已知锐角三角形ABC 中,||=4,||=1,△ABC 的面积为,则·的值为( )AB → AC → 3AB → AC → A .2 B .-2 C .4 D .-48.在△ABC 中,b =,c =3,B =30°,则a 为( )3A. B .2 C.或2 D .233339.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.10.△ABC 中,sin A ∶sin B ∶sin C =(-1)∶(+1)∶,求最大角的度数.331011.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =5,则边c 的值为3________.12.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.13.在△ABC 中,a =3,cos C =,S △ABC =4,则b =________.213314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则·的值为________.AB → BC → 15.已知△ABC 的三边长分别是a 、b 、c ,且面积S =,则角C =________.a 2+b 2-c 2416.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________.17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-2x +2=0的两根,且2cos(A +B )=1,求AB 的3长.18.已知△ABC 的周长为+1,且sin A +sin B =sin C .(1)求边AB 的长;(2)若△ABC 的面积为sin 2216C ,求角C 的度数.19.在△ABC 中,BC =,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -)的值.5π420.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.余弦定理答案1.在△ABC 中,如果BC =6,AB =4,cos B =,那么AC 等于( )13A .6 B .26C .3D .466解析:选A.由余弦定理,得AC =AB 2+BC 2-2AB ·BC cos B ==6.42+62-2×4×6×132.在△ABC 中,a =2,b =-1,C =30°,则c 等于( )3A. B.32C. D .25解析:选B.由余弦定理,得c 2=a 2+b 2-2ab cos C=22+(-1)2-2×2×(-1)cos30°33=2,∴c =.23.在△ABC 中,a 2=b 2+c 2+bc ,则∠A 等于( )3A .60° B .45°C .120°D .150°解析:选D.cos ∠A ===-,b 2+c 2-a 22bc -3bc2bc 32∵0°<∠A <180°,∴∠A =150°.4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =ac ,则∠B 的值为( )3A. B.π6π3C.或D.或π65π6π32π3解析:选D.由(a 2+c 2-b 2)tan B =ac ,联想到余弦定理,代入得3cos B ==·=·.a 2+c 2-b 22ac 321tan B 32cos Bsin B 显然∠B ≠,∴sin B =.∴∠B =或.π232π32π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对解析:选C.a ·+b ·==c .a 2+c 2-b 22ac b 2+c 2-a 22bc 2c 22c 6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2.设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m +2m 2>c 2+2cm +m 2=(c +m )2,∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,||=4,||=1,△ABC 的面积为,则·的值为()AB → AC → 3AB →AC → A .2 B .-2C .4D .-4解析:选A.S △ABC ==||·||·sin A312AB →AC →=×4×1×sin A ,12∴sin A =,又∵△ABC 为锐角三角形,32∴cos A =,12∴·=4×1×=2.AB →AC → 128.在△ABC 中,b =,c =3,B =30°,则a 为( )3A. B .233C.或2 D .233解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-3a ,3∴a 2-3a +6=0,解得a =或2.3339.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B =.π3在△ABD 中,AD =AB 2+BD 2-2AB ·BD cos B==.1+4-2×1×2×123答案:310.△ABC 中,sin A ∶sin B ∶sin C =(-1)∶(+1)∶,求最大角的度数.3310解:∵sin A ∶sin B ∶sin C =(-1)∶(+1)∶,3310∴a ∶b ∶c =(-1)∶(+1)∶.3310设a =(-1)k ,b =(+1)k ,c =k (k >0),3310∴c 边最长,即角C 最大.由余弦定理,得cos C ==-,a 2+b 2-c 22ab 12又C ∈(0°,180°),∴C =120°.11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =5,则边c 的值为3________.解析:S =ab sin C ,sin C =,∴C =60°或120°.1232∴cos C =±,又∵c 2=a 2+b 2-2ab cos C ,12∴c 2=21或61,∴c =或.2161答案:或216112.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.解析:由正弦定理a ∶b ∶c =sin A ∶sin B ∶sin C =2∶3∶4,设a =2k (k >0),则b =3k ,c =4k ,cos B ===,a 2+c 2-b 22ac 2k 2+ 4k 2- 3k 22×2k ×4k 1116同理可得:cos A =,cos C =-,7814∴cos A ∶cos B ∶cos C =14∶11∶(-4).答案:14∶11∶(-4)13.在△ABC 中,a =3,cos C =,S △ABC =4,则b =________.2133解析:∵cos C =,∴sin C =.13223又S △ABC =ab sin C =4,123即·b ·3·=4,1222233∴b =2.3答案:2314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则·的值为________.AB → BC → 解析:在△ABC 中,cos B =AB 2+BC 2-AC 22AB ·BC=49+25-362×7×5=,1935∴·=||·||·cos(π-B )AB → BC → AB → BC → =7×5×(-)1935=-19.答案:-1915.已知△ABC 的三边长分别是a 、b 、c ,且面积S =,则角C =________.a 2+b 2-c 24解析:ab sin C =S ==·12a 2+b 2-c 24a 2+b 2-c 22ab ab 2=ab cos C ,∴sin C =cos C ,∴tan C =1,∴C =45°.12答案:45°16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________.解析:设三边长为k -1,k ,k +1(k ≥2,k ∈N ),则Error!⇒2<k <4,∴k =3,故三边长分别为2,3,4,∴最小角的余弦值为=.32+42-222×3×478答案:7817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-2x +2=0的两根,且2cos(A +B )=1,求AB 的3长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=,即cos C =-.1212又∵a ,b 是方程x 2-2x +2=0的两根,3∴a +b =2,ab =2.3∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-)12=a 2+b 2+ab =(a +b )2-ab=(2)2-2=10,3∴AB =.1018.已知△ABC 的周长为+1,且sin A +sin B =sin C .22(1)求边AB 的长;(2)若△ABC 的面积为sin C ,求角C 的度数.16解:(1)由题意及正弦定理得AB +BC +AC =+1,BC +AC =AB ,22两式相减,得AB =1.(2)由△ABC 的面积BC ·AC ·sin C =sin C ,得BC ·AC =,121613由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC ==,AC +BC 2-2AC ·BC -AB 22AC ·BC 12所以C =60°.19.在△ABC 中,BC =,AC =3,sin C =2sin A .5(1)求AB 的值;(2)求sin(2A -)的值.π4解:(1)在△ABC 中,由正弦定理=,AB sin C BCsin A 得AB =BC =2BC =2.sin Csin A 5(2)在△ABC 中,根据余弦定理,得cos A ==,AB 2+AC 2-BC 22AB ·AC 255于是sin A ==.1-cos2A 55从而sin 2A =2sin A cos A =,45cos 2A =cos 2 A -sin 2 A =.35所以sin(2A -)=sin 2A cos -cos 2A sin =.π4π4π421020.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.解:由正弦定理,得=.sin C sin B cb 由2cos A sin B =sin C ,有cos A ==.sin C 2sin B c2b 又根据余弦定理,得cos A =,所以=,b 2+c 2-a 22bc c 2b b 2+c 2-a 22bc 即c 2=b 2+c 2-a 2,所以a =b .又因为(a +b +c )(a +b -c )=3ab ,所以(a +b )2-c 2=3ab ,所以4b 2-c 2=3b 2,所以b =c ,所以a =b =c ,因此△ABC 为等边三角形.。
正弦定理、余弦定理练习题及答案

正弦定理、余弦定理练习题及答案正弦定理、余弦定理练习题年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共20题,题分合计100分)1.已知在△ABC中,sin A:sin B:sin C=3:2:4,那么cos C的值为A.-B.C.-D.2.在△ABC中,a=λ,b=λ,A=45°,则满足此条件的三角形的个数是A.0B.1C.2D.无数个3.在△ABC中,b cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形4.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为A.150°B.120°C.60°D.75°5.在△ABC中,=1,=2,(+)·(+)=5+2则边||等于A.B.5-2 C. D.6.在△ABC中,已知B=30°,b=50,c=150,那么这个三角形是A.等边三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形7.在△ABC中,若b2sin2C+c2sin2B=2bc cos B cos C,则此三角形为A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形8.正弦定理适应的范围是A.Rt△B.锐角△C.钝角△D.任意△9.已知△ABC中,a=10,B=60°,C=45°,则c=A.10+B.10(-1)C.(+1)D.1010.在△ABC中,b sin A<a<b,则此三角形有A.一解B.两解C.无解D.不确定11.三角形的两边分别为5和3,它们夹角的余弦是方程5x2-7x-6=0的根,则三角形的另一边长为A.52B.2C.16D.412.在△ABC中,a2=b2+c2+bc,则A等于A.60°B.45°C.120D.30°13.在△ABC中,,则△ABC是A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形14.在△ABC中,a=2,A=30°,C=45°,则△ABC的面积S△ABC等于A. B.2 C.+1 D.(+1)15.已知三角形ABC的三边a、b、c成等比数列,它们的对角分别是A、B、C,则sin A sin C 等于A.cos2BB.1-cos2BC.1+cos2BD.1+sin2B16.在△ABC中,sin A>sin B是A>B的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件17.在△ABC中,b Cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形18.△ABC中,sin2A=sin2B+sin2C,则△ABC为A.直角三角形B.等腰直角三角形C.等边三角形D.等腰三角形19.△ABC中,A=60°,b=1,这个三角形的面积为,则△ABC外接圆的直径为A. B. C. D.20.在△ABC中,,则k为A.2RB.RC.4RD.(R为△ABC外接圆半径)二、填空题(共18题,题分合计75分)1.在△ABC中,A=60°,C=45°,b=2,则此三角形的最小边长为.2.在△ABC中,= .3.在△ABC中,a∶b∶c=(+1)∶∶2,则△ABC的最小角的度数为.4.在△ABC中,已知sin A∶sin B∶sin C=6∶5∶4,则sec A= .5.△ABC中,,则三角形为_________.6.在△ABC中,角A、B均为锐角且cos A>sin B,则△ABC是___________.7.在△ABC中,若此三角形有一解,则a、b、A满足的条件为____________________.8.已知在△ABC中,a=10,b=5,A=45°,则B= .9.已知△ABC中,a=181,b=209,A=121°14′,此三角形解.10.在△ABC中,a=1,b=1,C=120°则c= .11.在△ABC中,若a2>b2+c2,则△ABC为;若a2=b2+c2,则△ABC为;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为.12.在△ABC中,sin A=2cos B sin C,则三角形为_____________.13.在△ABC中,BC=3,AB=2,且,A= .14.在△ABC中,B=,C=3,B=30°,则A= .15.在△ABC中,a+b=12,A=60°,B=45°,则a= ,b= .16.若2,3,x为三边组成一个锐角三角形,则x的范围为.17.在△ABC中,化简b cos C+c cos B= .18.钝角三角形的边长是三个连续自然数,则三边长为.三、解答题(共24题,题分合计244分)1.已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.2.已知△ABC的三边长a=3,b=4,c=,求三角形的最大内角.3.已知在△ABC中,∠A=45°,a=2,c=,解此三角形.4.在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求AB的长.5.在△ABC中,A最大,C最小,且A=2C,A+C=2B,求此三角形三边之比.6.证明:在△ABC中,.(其中R为△ABC的外接圆的半径)7.在△ABC中,最大角A为最小角C的2倍,且三边a、b、c为三个连续整数,求a、b、c的值.8.如下图所示,半圆O的直径MN=2,OA=2,B为半圆上任意一点,以AB为一边作正三角形ABC,问B在什么位置时,四边形OACB面积最大?最大面积是多少?9.在△ABC中,若sin A∶sin B∶sin C=m∶n∶l,且a+b+c=S,求a.10.根据所给条件,判断△ABC的形状(1)a cos A=b cos B(2)11.△ABC中,a+b=10,而cos C是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.12.在△ABC中,a、b、c分别是角A、B、C的对边,设a+c=2b,A-C=,求sin B的值.13.已知△ABC中,a=1,b=,A=30°,求B、C和c.14.在△ABC中,c=2,tan A=3,tan B=2,试求a、b及此三角形的面积.15.已知S△ABC=10,一个角为60°,这个角的两边之比为5∶2,求三角形内切圆的半径.16.已知△ABC中,,试判断△ABC的形状.17.已知△ABC的面积为1,tan B=,求△ABC的各边长.18.求值:19.已知△ABC的面积,解此三角形.20.在△ABC中,a=,b=2,c=+1,求A、B、C及S△.21.已知(a2+bc)x2+2=0是关于x的二次方程,其中a、b、c 是△ABC的三边,(1)若∠A为钝角,试判断方程根的情况.(2)若方程有两相等实根,求∠A的度数.22.在△ABC中,(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断△ABC的形状.23.在△ABC中,a>b,C=,且有tan A·tan B=6,试求a、b以及此三角形的面积.24.已知:k是整数,钝角△ABC的三内角A、B、C所对的边分别为a、b、c(1)若方程组有实数解,求k的值.(2)对于(1)中的k值,若且有关系式,试求A、B、C的度数.正弦定理、余弦定理答案一、选择题(共20题,合计100分)1 A 2A3C 4 B 5 C 6D 7A 8 D 9B 10 B 11 B 12C 13C 14C 15.B16. C 17:C 18A 19C 20. A二、填空题(共18题,合计75分)1. 2(-1)2 3. 45° 4. 8 5.等腰三角形 6.:钝角三角形7. a=b sin A或b<a8. 60°或120°9无10.11.钝角三角形直角三角形锐角三角形12.等腰三角形13. 120°14.或215. 36-1216.<x<17.a18. 2、3、4三、解答题(共24题,合计244分)1.a=B=105°b=2.∠C=120°3.∠B=75°或∠B=15°b=+1,∠C=60°,∠B=75°或b=-1,∠C=120°,∠B=15°4. AB的长为5.:此三角形三边之比为6∶5∶47.a=6,b=5,c=48.当θ=时,S四边形OACB最大,最大值为+29.10(1)△ABC是等腰三角形或直角三角形(2)△ABC为等边三角形11△ABC周长的最小值为12.13.B1=60°,B2=120°;C1=90°,C2=30°;c1=2, c2=114..15.16.等边三角形17.18.20. A=60°,B=45°,C=75°,S△=21. (1)没有实数根(2)60°22.等腰三角形或直角三角形23.24.(1)k=1,2,3 (2)C=45°,B=15°。
正弦定理余弦定理练习题及答案(供参考)

正弦定理、余弦定理练习题年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共20题,题分合计100分)1.已知在△ABC中,sin A:sin B:sin C=3:2:4,那么cos C的值为B.D.2.在△ABC中,a=λ,b=λ,A=45°,则满足此条件的三角形的个数是D.无数个3.在△ABC中,b cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形4.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为°°°°5.在△ABC中,=1,=2,(+)·(+)=5+2则边||等于A.C.D.6.在△ABC中,已知B=30°,b=50,c=150,那么这个三角形是A.等边三角形B.直角三角形C.等腰三角形D.等腰三角形或直角三角形7.在△ABC中,若b2sin2C+c2sin2B=2bc cos B cos C,则此三角形为A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形8.正弦定理适应的范围是△B.锐角△ C.钝角△ D.任意△9.已知△ABC中,a=10,B=60°,C=45°,则c=+(-1) C.(+1)10.在△ABC中,b sin A<a<b,则此三角形有A.一解B.两解C.无解D.不确定11.三角形的两边分别为5和3,它们夹角的余弦是方程5x2-7x-6=0的根,则三角形的另一边长为12.在△ABC中,a2=b2+c2+bc,则A等于°°°13.在△ABC中,,则△ABC是A.锐角三角形B.直角三角形C.钝角三角形D.任意三角形14.在△ABC中,a=2,A=30°,C=45°,则△ABC的面积S△ABC等于A.C.+1D.(+1)15.已知三角形ABC的三边a、b、c成等比数列,它们的对角分别是A、B、C,则sin A sin C 等于+cos2B+sin2B16.在△ABC中,sin A>sin B是A>B的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件17.在△ABC中,b Cos A=a cos B,则三角形为A.直角三角形B.锐角三角形C.等腰三角形D.等边三角形18.△ABC中,sin2A=sin2B+sin2C,则△ABC为A.直角三角形B.等腰直角三角形C.等边三角形D.等腰三角形19.△ABC中,A=60°,b=1,这个三角形的面积为,则△ABC外接圆的直径为A.B.C.D.20.在△ABC中,,则k为D.(R为△ABC外接圆半径)二、填空题(共18题,题分合计75分)1.在△ABC中,A=60°,C=45°,b=2,则此三角形的最小边长为.2.在△ABC中,= .3.在△ABC中,a∶b∶c=(+1)∶∶2,则△ABC的最小角的度数为.4.在△ABC中,已知sin A∶sin B∶sin C=6∶5∶4,则sec A= .5.△ABC中,,则三角形为_________.6.在△ABC中,角A、B均为锐角且cos A>sin B,则△ABC是___________.7.在△ABC中,若此三角形有一解,则a、b、A满足的条件为____________________.8.已知在△ABC中,a=10,b=5,A=45°,则B= .9.已知△ABC中,a=181,b=209,A=121°14′,此三角形解.10.在△ABC中,a=1,b=1,C=120°则c= .11.在△ABC中,若a2>b2+c2,则△ABC为;若a2=b2+c2,则△ABC为;若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为.12.在△ABC中,sin A=2cos B sin C,则三角形为_____________.13.在△ABC中,BC=3,AB=2,且,A= .14.在△ABC中,B=,C=3,B=30°,则A= .15.在△ABC中,a+b=12,A=60°,B=45°,则a= ,b= .16.若2,3,x为三边组成一个锐角三角形,则x的范围为.17.在△ABC中,化简b cos C+c cos B= .18.钝角三角形的边长是三个连续自然数,则三边长为.三、解答题(共24题,题分合计244分)1.已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.2.已知△ABC的三边长a=3,b=4,c=,求三角形的最大内角.3.已知在△ABC中,∠A=45°,a=2,c=,解此三角形.4.在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求AB的长.5.在△ABC中,A最大,C最小,且A=2C,A+C=2B,求此三角形三边之比.6.证明:在△ABC中,.(其中R为△ABC的外接圆的半径)7.在△ABC中,最大角A为最小角C的2倍,且三边a、b、c为三个连续整数,求a、b、c的值.8.如下图所示,半圆O的直径MN=2,OA=2,B为半圆上任意一点,以AB为一边作正三角形ABC,问B在什么位置时,四边形OACB面积最大?最大面积是多少?9.在△ABC中,若sin A∶sin B∶sin C=m∶n∶l,且a+b+c=S,求a.10.根据所给条件,判断△ABC的形状(1)a cos A=b cos B(2)11.△ABC中,a+b=10,而cos C是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.12.在△ABC中,a、b、c分别是角A、B、C的对边,设a+c=2b,A-C=,求sin B的值.13.已知△ABC中,a=1,b=,A=30°,求B、C 和c.14.在△ABC中,c=2,tan A=3,tan B=2,试求a、b及此三角形的面积.15.已知S△ABC=10,一个角为60°,这个角的两边之比为5∶2,求三角形内切圆的半径.16.已知△ABC中,,试判断△ABC的形状.17.已知△ABC的面积为1,tan B=,求△ABC 的各边长.18.求值:19.已知△ABC的面积,解此三角形.20.在△ABC中,a=,b=2,c=+1,求A、B、C及S△.21.已知(a2+bc)x2+2=0是关于x的二次方程,其中a、b、c是△ABC的三边,(1)若∠A为钝角,试判断方程根的情况.(2)若方程有两相等实根,求∠A的度数.22.在△ABC中,(a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断△ABC的形状.23.在△ABC中,a>b,C=,且有tan A·tan B=6,试求a、b以及此三角形的面积.24.已知:k是整数,钝角△ABC的三内角A、B、C所对的边分别为a、b、c(1)若方程组有实数解,求k的值.(2)对于(1)中的k值,若且有关系式,试求A、B、C的度数.正弦定理、余弦定理答案一、选择题(共20题,合计100分)1 A 2A3C 4 B 5 C 6D 7A 8 D 9B 10 B 11 B 12C 13C 14C 16. C 17:C 18A 19C 20. A二、填空题(共18题,合计75分)1.2(-1) 23. 45°4. 85.等腰三角形6.:钝角三角形7.a=b sin A或b<a8.60°或120°9无10.11.钝角三角形直角三角形锐角三角形12.等腰三角形13.120°14.或215. 36-1216.<x<17.a18. 2、3、4三、解答题(共24题,合计244分)=B=105°b=2.∠C=120°3.∠B=75°或∠B=15°b=+1,∠C=60°,∠B=75°或b=-1,∠C=120°,∠B=15°4. AB的长为5.:此三角形三边之比为6∶5∶4=6,b=5,c=48.当θ=时,S四边形OACB最大, 最大值为+29.10(1)△ABC是等腰三角形或直角三角形(2)△ABC为等边三角形11△ABC周长的最小值为12.=60°,B2=120°;C1=90°,C2=30°;c1=2,c2=114..15.16.等边三角形17.18.20. A=60°,B=45°,C=75°,S△=21. (1)没有实数根(2)60°22.等腰三角形或直角三角形23.24.(1)k=1,2,3 (2)C=45°,B=15°。
余弦定理

余弦定理一、选择题(每小题6分,共30分)1.(2013·泰安高二检测)在△ABC中,若c=,则角C的度数是()A.60°B.120°C.60°或120°D.45°2.在△ABC中,角A,B,C所对的边分别为a,b,c.若a=1,c=4,B=45°,则sinC等于()A. B. C. D.3.在△ABC中,若a=5,b=3,C=120°,则sinB= .4.(2013·潍坊高二检测)在△ABC中,B=60°,b2=ac,则三角形一定是()A.直角三角形B.等边三角形C.等腰直角三角形D.钝角三角形5.边长为5,7,8的三角形的最大角与最小角的和是()A.90°B.120°C.135°D.150°二、填空题(每小题8分,共24分)6.(2013·安徽高考)设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,则3sinA=5sinB,则角C= .7.已知a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2= .8.(2013·泉州高二检测)在△ABC中,角A,B,C所对的边分别是a,b,c,若sin2B+sin2C=sin2A+sinBsinC,且·=4,则bc= .三、解答题(9~10题各14分,11题18分)9.(2013·北京高考)在△ABC中,a=3,b=2,B=2A.(1)求cosA的值.(2)求c的值.10.(2013·吉林高二检测)在△ABC中,A,B,C是三角形的三内角,a,b,c是三内角对应的三边,已知b2+c2-a2=bc.(1)求角A的大小.(2)若sin2A+sin2B=sin2C,求角B的大小.答案解析1.【解析】选 B.因为c=,所以c2=a2+b2+ab,所以cosC==-,又因为0°<C<180°,故C=120°.2.【解析】选B.由余弦定理得b2=a2+c2-2accosB=1+32-8×=25,所以b=5.所以cosC==-,sinC==.【变式备选】【解析】c2=52+32-2×5×3×cos120°=49,所以c=7,由正弦定理得,sinB===.答案:3.【解析】选 B.由余弦定理得b2=a2+c2-2accosB=a2+c2-ac,所以a2+c2-2ac=0,即(a-c)2=0,a=c,又B=60°,故△ABC为等边三角形.5.【解析】选B.设中间角为θ,则cosθ==,所以θ=60°,最大角与最小角的和为120°.6.【解析】由题设条件可得⇒由余弦定理得cosC===-,所以C=.答案:7.【解析】因为b2=a2+c2-2accosB,所以a2+c2+ac-b2=ac+2accosB,又B=120°,所以ac+2accosB=ac-ac=0,即a2+c2+ac-b2=0.答案:08.【解题指南】由已知条件利用正弦定理可得b2+c2=a2+bc,再利用余弦定理可求出cosA,由·=4可以求出bc的值.【解析】由已知条件利用正弦定理可得b2+c2=a2+bc,所以bc=b2+c2-a2=2bc·cosA,所以cosA=,由·=4得bc·cosA=4,bc=8.答案:89.【解析】(1)由正弦定理得=,所以=,=,即cosA=.(2)由余弦定理得a2=b2+c2-2bccosA,所以32=(2)2+c2-2×2c×,即c2-8c+15=0,解得c=5或c=3(舍).10.【解析】(1)因为b2+c2-a2=bc,所以cosA==,又A∈(0,π),所以A=.(2)由正弦定理及sin2A+sin2B=sin2C得:+=.即:a2+b2=c2,故△ABC是以C为直角的直角三角形. 又因为A=,所以B=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同步分层能力测试题(一)A 组一.填空题(本大题共8小题,每小题5分,共40分)1.在△ABC 中, 若0,则边c= 。
1.a 2=c 2+b 2-2cb ·cosA,代入整理得c 2∴2. 在△ABC 中,已知A=450,B=600,c =1,则a= . 2. 213-。
提示:由A+B+C=180,得 C=1800-450-600=750。
由正弦定理,得 045sin a =075sin 1, ∴a=213-。
3. 在△ABC 中, 已知a=5,b=12,c=13.最大内角为 度。
3.90.提示:cosC=bca cb 2222-+= 222512132512+-⨯⨯=0,C=900. 4. 在△ABC 中,已知b=4,c=8,B=300.则a= 。
4. 23。
提示:(1)由正弦定理,得sin C=bB c sin =430sin 80=1。
所以 C=900, A=1800-900-300=600。
又由正弦定理,得 a=B A b sin sin =0030sin 60sin 4=23。
5. a,b,c 是△ABC 的三边,且B=1200,则a 2+ac+c 2-b 2的值为 .5.0.提示:由余弦定理,得b 2=a 2+c 2-2ac ·cosB= a 2+ac+c 2.6.在△ABC 中,若a=50,b=25 6 , A=45°则B= .6. 60°或120°。
提示:由正弦定理得050sin 45=,,故B=60°或120°。
7.在△ABC 中,有等式:①asinA=bsinB ;②asinB=bsinA ;③acosB=bcosA ;④sin sin sin a b c A B C+=+. 其中恒成立的等式序号为_______________. 7.②④。
提示:①不符合正弦定理;②两边同除以sinAsinB 即为正弦定理;③取A=900,便知等式不成立;④正弦定理结合等比定理可得。
8.在A B C ∆中,c b a ,,分别为三个内角A 、B 、C 所对的边,设向量(),,p a c b =+(),q b a c a =--,若向量//p q ,则角C 的大小为 。
8.3π.【解析】本题是向量与解三角形的综合问题,解决的关键是联想余弦定理求解。
由//p q 得(a+c)(c-a)=b(b-a),即a 2+b 2-c 2=ab.由余弦定理得2221cos ,223a b c C C ab π+-===. 二.解答题(本大题共4小题,共54分)9.在△ABC 中,a=3,,A=300,则角C 及b.9.解:由正弦定理得03sin 30=sinC=.∴C=120 或C=60 。
当C=120 时,B=1800-1200-300=300,b 2=32+()2-2×3× =9,b=3.同理当C=60 ,b=6. 故C=120 b=3。
或C=60 b=6。
10.在ABC ∆中, ⑴ 已知: acosB=bcosA ,试判断ABC ∆形状; ⑵求证:2222cos 2cos 211A B a b a b-=-。
10.解:(1)由正弦定理,得 a=2RsinA,b=2RsinB ,即 acosB =bcosA 。
∴sinA cosB=sinB cosA ,即 sinA cosB- cosA sinB=0, sin(A-B)=0。
∴ A-B=0 ,A=B ,∴ABC ∆为等腰三角形.(2) 证明:左边=222212sin 12sin A B a b ---=2211a b--2(2222sin sin A B a b -)。
由正弦定理,得2222sin sin A B a b =,故2222c o s 2c o s 211A B a b a b -=-成立。
已知: A a sin =B b cos =Cc cos ,试判断ABC ∆形状。
11.在锐角三角形中,边a 、b 是方程x 2-2 3 x+2=0的两根,角A 、B 满足2sin(A+B)- 3 =0,求角C 的度数,边c 的长度.11.解:由2sin(A+B)- 3 =0,得sin(A+B)=32, ∵△ABC 为锐角三角形, ∴A+B=120°, C=60°, 又∵a 、b 是方程x 2-2 3 x+2=0的两根, ∴a+b=2 3 , a ·b=2, ∴c 2=a 2+b 2-2a ·bcosC=(a+b)2-3ab=12-6=6, ∴c= 6 。
12. 在△ABC 中,已知角A 、B 、C 对应的边分别为a 、b 、c ,.且 C=2A .cos A=43 (1)求cosC 和cosB 的值;(2)当227=∙→→BC BA 时,求a 、b 、c 的值. 12.解:(1)cosC=cos2A=2cos 2A-1=81; sinA=47, cosC=873。
∴cosB=-cos(A+C)=sinAsinC-cosAcosC=169。
(2)227=∙→→BC BA 27cos 24.2ac B ac ⇒=⇒= 由正弦定理得32cos sin 2sin 2c a c A A A a =⇒==. 解得a=4,c=6.再由余弦定理知b 2=a 2+c 2-2ac ·cosB= 42+62-48×169=25,b=5.B 组一.填空题(本大题共6小题,每小题5分,共30分)1.在△ABC 中,若BC=5,CA=7,AB=8,则△ABC 的最大角与最小角之和是 。
1.1200.提示:由余弦定理知cosB=22258712582+-=⨯⨯,∴B=600,A+C=1200. 2.在△ABC 中,已知AB=2,∠C=50°,当∠B= 时,BC 的长取得最大值.2.400.提示:由正弦定理知02sin 50sin BC A =,∴BC=02sin sin 50A 。
故当A=900时,BC 最大。
此时B=400.3.在△ABC 中,AB =5,BC =7,AC =8,则AB BC = .. 3. -5.提示:∵ AB BC =-BA BC , BA BC =||||cos BA BC B =2221(||||||)2BA BC AC +-=5, ∴AB BC =-54.不等边三角形ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且最大边a 满足222c b a +<,则角A 的取值范围是 。
4.(3π,2π)。
提示:由余弦定理cosA=bc a c b 2222-+>0,可知A 是锐角。
又a 是最大边,则A 是最大角,故A ∈(3π,2π)。
5.在△ABC 中,已知2sinAcosB=sinC,那么△ABC 一定是 三角形。
5.等腰三角形。
提示:由2sinAcosB=sinC,知2sinAcosB=sin(A+B),∴2sinAcosB=sinAcosB+cosAsinB. ∴cosAsinB-sinAcosB=0.∴sin(B-A)=0. ∴B=A.另解:本题也可以借助正余弦定理来处理,但是稍微繁一点。
6.锐角三角形ABC 中,若2C B ∠=∠,则AB AC的范围是 .6..提示:本题是解三角形问题,解决的关键是利用正弦定理来解决。
sin sin 22cos .sin sin AB C B B AC B B===由锐角三角形ABC 、2C B ∠=∠两个条件可得,cos 2cos 6422B B B ππ<∠<<<< 二.解答题(本大题共2小题,共36分)7.在△ABC 中,已知边c=10, 又知cosA cosB =b a =43,求a 、b 及△ABC 的内切圆的半径。
7.解:由cosA cosB =b a ,sinB sinA =b a ,可得 cosA cosB =sinB sinA,变形为sinAcosA=sinBcosB ∴sin2A=sin2B, 又∵a ≠b, ∴2A=π-2B, ∴A+B=2π. ∴△ABC 为直角三角形. 由a 2+b 2=102和b a =43 ,解得a=6, b=8, ∴内切圆的半径为r=a+b-c 2 =6+8-102=2 8.锐角三角形ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,=(a-b,c), n =(a-c,a+b),且与n 共线。
(I )求角B 的大小;(II )设23cos sin 22C A C y -+=,求y 的最大值及此时∠C 的大小。
8.解(I )∵与共线,∴(a-b)(a+b)-c(a-c)=0, ∴212cos ,222222=-+==-+ac b c a B ac b c a . ∵.3,20ππ=∴<<B B (II )∵.323ππ=+∴=C A ,B )23cos(2cos 123cos sin 22C C C A C y -+-=-+=π ),62sin(12sin 232cos 2112sin 232cos 212cos 1π-+=+-=++-=C C C C C C ∴当262ππ=-C ,即3π=C 时,y 取最大值2。
