成都石室联合中学数学全等三角形易错题(Word版含答案)

合集下载

成都石室中学初中学校八年级数学上册第二单元《全等三角形》测试卷(有答案解析)

一、选择题1．如图，已知16AB AC +=，点O 为ABC ∠与ACB ∠的平分线的交点，且OD BC 于D ．若4OD =，则四边形ABOC 的面积是（）A ．36B ．32C ．30D ．642．如图，OP 平分AOB ∠，PC OA ⊥于点C ，PD OB ⊥于点D ，延长CP ，DP 交OB ， OA 于点E ，F ，下列结论错误的是（）A ．PC PD =B ．OC OD = C ．CPO DPO ∠=∠ D ．PC PE =3．如图，在ABC 中，B C ∠=∠，BD CE =，BF CD =，则EDF ∠等于（）A ．90A ︒-∠B ．1802A ︒-∠C ．1902A ︒-∠D ．11802A ︒-∠ 4．在平面直角坐标系xOy 中，以原点O 为圆心，任意长为半径作弧，分别交x 轴的负半轴和y 轴的正半轴于A 点，B 点，分别以点A ，点B 为圆心，AB 的长为半径作弧，两弧交于P 点，若点P 的坐标为(m ，n)，则下列结论正确的是（）A ．m ＝2nB ．2m ＝nC ．m ＝nD ．m ＝－n 5．下列四个命题中，真命题是（）A ．如果 ab ＝0，那么a ＝0B ．面积相等的三角形是全等三角形C ．直角三角形的两个锐角互余D ．不是对顶角的两个角不相等6．如图，ABC 的面积为26cm ，AP 垂直B 的平分线BP 于P ，则PBC 的面积为（）A ．21cmB ．22cmC ．23cmD ．24cm7．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙 8．如图，AB AC =，AD AE =，55A ︒∠=，35C ︒∠=，则DOE ∠的度数是（）A ．105︒B ．115︒C ．125︒D ．130︒9．如图，AB 与CD 相交于点E ，AD=CB ，要使△ADE ≌△CBE ，需添加一个条件，则添加的条件以及相应的判定定理正确的是（）A ．AE=CE ；SASB ．DE=BE ；SASC ．∠D=∠B ；AASD ．∠A=∠C ；ASA 10．到ABC 的三条边距离相等的点是ABC 的( )A ．三条中线的交点B ．三条边的垂直平分线的交点C ．三条高的交点D ．三条角平分线的交点 11．如图，在ABC 和△FED 中，AD FC =，AB FE =，下列条件中不能证明F ABC ED ≌△△的是（）A ．BC ED =B ．A F ∠=∠C ．B E ∠=∠D ．//AB EF 12．已知，如图，OC 是∠AOB 内部的一条射线，P 是射线OC 上任意点，PD ⊥OA ，PE ⊥OB ，下列条件中：①∠AOC ＝∠BOC ，②PD ＝PE ，③OD ＝OE ，④∠DPO ＝∠EPO ，能判定OC 是∠AOB 的角平分线的有（）A ．1个B ．2个C ．3个D ．4个二、填空题13．如图，△ABC ≌△DEF ，由图中提供的信息，可得∠D ＝__________°．14．如图，在Rt ABC △中，90C ∠=︒，以顶点A 为圆心，任意长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP 交BC 于点D ．若3CD =，10AB =，则ABD △的面积是______．15．如图，AB 与CD 相交于点O ，OC ＝OD ．若要得到△AOC ≌△BOD ，则应添加的条件是__________．（写出一种情况即可）16．如图，ABC 的面积为215cm ，以顶点A 为圆心，适当长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线AP ，过点C 作CD AP ⊥于点D ，连接DB ，则DAB 的面积是______2cm ．17．如图，AD 为∠CAF 的角平分线，BD=CD ，∠DBC=∠DCB ，∠DCA=∠ABD ，过D 作DE ⊥AC 于E ，DF ⊥AB 交BA 的延长线于F ，则下列结论：①△CDE ≌△BDF ；②CE=AB+AE ；③∠DAF=∠CBD ．其中正确的结论有_____．（填序号）18．如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，BD 平分ABC ∠．若P 是BC 边上一动点，则DP 长的最小值为______．19．ABC 中，4AB =，6AC =，则第三边BC 边上的中线m 的取值范围是______． 20．如图，在ABC 中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①120EDF ∠=︒；②DM 平分EDF ∠；③DE DF AD +=；④2AB AC AE +>；其中正确的有________(请将正确结论的序号填写在横线上)．三、解答题21．如图，点A ，D ，B ，E 依次在同一条直线上，BC DF =，AD BE =，ABC EDF ∠=∠，求证：A E ∠=∠．22．如图，Rt ABC 与Rt DEF △的顶点A ，F ，C ，D 共线，AB 与EF 交于点G ，BC 与DE 相交于点H ，90B E ∠=∠=︒，AF CD =，AB DE =．（1）求证：Rt ABC Rt DEF≌；（2）若1GF ，求线段HC的长．23．如图，在△ABD中，∠ABC=45°，AC，BF为△ABD的两条高，CM//AB，交AD于点M；求证：BE=AM+EM．24．我们知道，“对称补缺”的思想是解决与轴对称图形有关的问题时的一种重要的添加辅助线的策略．请参考这种思想，解决本题：如图，在△ABC中，AC＝BC，∠ACB＝90°，D 是AC上一点，AE⊥BD交BD的延长线于E，且BD是∠ABC的角平分线．求证：AE＝12 BD．25．如图，点B，F，C，E在一条直线上，FB=CE，AB∥ED，AC∥FD．求证：AB=DE．26．如图，一条河流MN旁边有两个村庄A，B，AD⊥MN于D．由于有山峰阻挡，村庄B 到河边MN的距离不能直接测量，河边恰好有一个地点C能到达A，B两个村庄，与A，B 的连接夹角为90°，且与A，B的距离也相等，测量C，D的距离为150m，请求出村庄B到河边的距离．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】过O 作OE ⊥AB 于E ，OF ⊥AC 于F ，连接OA ，根据角平分线的性质求出OE ＝OD ＝OF ＝4，根据三角形的面积公式求出即可．【详解】解：过O 作OE ⊥AB 于E ，OF ⊥AC 于F ，连接OA ，∵点O 为∠ABC 与∠ACB 的平分线的交点，OD ⊥BC 于D ，OD ＝4，∴OE ＝OD ＝4，OF ＝OD ＝4，∵AB +AC ＝16，∴四边形ABOC 的面积S ＝S △ABO +S △ACO ＝1122AB OE AC OF ⨯+⨯ ＝114422AB AC ⨯+⨯ ＝42×（AB +AC ）＝42×16 ＝32，故选：B ．【点睛】本题考查了角平分线的性质和三角形的面积，能根据角平分线的性质得出OD ＝OE ＝OF ＝3是解此题的关键．2．D解析：D【分析】根据角平分线的性质定理判断A 选项；证明△OPC ≌△OPD 判断B 选项；根据△OPC ≌△OPD 即可判断C 选项；证明△DPE ≌△CPF 判断D 选项．【详解】∵OP 平分AOB ∠，PC OA ⊥于点C ，PD OB ⊥于点D ，∴PC=PD ，故A 选项正确；∵∠ODP=∠OCP=90︒，又∵OP=OP ，PC=PD ，∴Rt △OPC ≌Rt △OPD ，∴OC=OD ，故B 选项正确；∵△OPC ≌△OPD ，∴CPO DPO ∠=∠，故C 选项正确；∵∠PDE=∠PCF=90︒，PD=PC ，∠DPE=∠CPF ，∴△DPE ≌△CPF ，∴PE=PF ，∵PF>PC ，∴PE>PC ，故D 选项错误；故选：D ．【点睛】此题考查三角形角平分线的性质定理，全等三角形的判定及性质，熟记角平分线的性质定理是解题的关键．3．C解析：C【分析】根据∠B=∠C ，BD=CE ，BF=CD ，可证出△BFD ≌△CDE ，继而得出∠BFD=∠EDC ，再根据三角形内角和定理及平角等于180︒，即可得出∠B=∠EDF ，进而得到答案．【详解】解：∵∠B=∠C ，BD=CE ，BF=CD ，∴△BFD ≌△CDE ，∴∠BFD=∠EDC ，∴∠B+∠BFD+∠BDF=∠BDF+∠EDF+∠EDC ，∴∠B=∠EDF ，又∵∠B=∠C=18019022A A ︒-∠=︒-∠， ∴∠EDF=1902A ︒-∠，故选：C ．【点睛】本题考查全等三角形的判定与性质、等腰三角形的性质以及三角形内角和定理，根据全等三角形的性质找出∠BFD=∠EDC是解题的关键．4．D解析：D【分析】根据角平分线的性质及第二象限内点的坐标特点即可得出结论．【详解】解：∵由题意可知，点C在∠AOB的平分线上，∴m=-n．故选：D．【点睛】本题考查的是作图−基本作图，熟知角平分线的作法及其性质是解答此题的关键．5．C解析：C【分析】根据有理数的乘法、全等三角形的概念、直角三角形的性质、对顶角的概念判断即可．【详解】解：A、如果ab＝0，那么a＝0或b＝0或a、b同时为0，本选项说法是假命题，不符合题意；B、面积相等的三角形不一定全等，本选项说法是假命题，不符合题意；C、直角三角形的两个锐角互余，本选项说法是真命题，符合题意；D、不是对顶角的两个角可能相等，本选项说法是假命题，不符合题意；故选：C．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题，判断命题的真假关键是要熟悉课本中的性质定理．6．C解析：C【分析】延长AP交BC于E，根据AP垂直∠B的平分线BP于P，即可求出△ABP≌△BEP，又知△APC和△CPE等底同高，可以证明两三角形面积相等，即可证明三角形PBC的面积．【详解】解：延长AP交BC于E，∵AP垂直∠B的平分线BP于P，∴∠ABP=∠EBP，∠APB=∠BPE=90∘，在△APB和△EPB中∠=∠⎧⎪=⎨⎪∠=∠⎩APB EPB BP BPABP EBP ∴△APB ≌△EPB (ASA )，∴APB EPB S S =△△，AP =PE ，∴△APC 和△CPE 等底同高，∴APC PCE S S =,∴PBC PCE PCE S S S =+△△△=12ABC S=1632⨯= 故选C ．【点睛】本题考查了三角形的面积和全等三角形的性质和判定的应用，关键是求出PBC PCE PCE S S S =+△△△=12ABC S ．7．B解析：B【分析】甲只有2个已知条件，缺少判定依据；乙可根据SAS 判定与△ABC 全等；丙可根据AAS 判定与△ABC 全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC 全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC 全等；丙三角形72°内角及所对边与△ABC 对应相等且均有50°内角，可根据AAS 判定乙与△ABC 全等；则与△ABC 全等的有乙和丙，故选：B ．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．8．C解析：C【分析】先判定△ABE ≌△ACD ，再根据全等三角形的性质，得出∠B=∠C=35︒，由三角形外角的性质即可得到答案．在△ABE 和△ACD 中，AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACD （SAS ），∴∠B=∠C ，∵∠C=35︒，∴∠B=35︒，∴∠OEC=∠B+∠A=355590︒+︒=︒，∴∠DOE=∠C+∠OEC=3590125︒+︒=︒，故选：C ．【点睛】本题考察全等三角形的判定与性质、三角形外角的性质，熟练掌握全等三角形的判定与性质是解题关键．9．C解析：C【分析】根据三角形全等的判定方法结合全等的判定方法逐一进行来判断．【详解】解：A.添加AE=CE 后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；B.添加DE=BE 后，根据已知两边和其中一边的对角对应相等，两个三角形不一定全等；故不符合题意；C.添加∠D=∠B ，根据AAS 可证明△ADE ≌△CBE ，故此选项符合题意；D.添加∠A=∠C ，根据AAS 可证明△ADE ≌△CBE ，故此选项不符合题意；故选：C【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、AAS 、ASA ．关键在于应根据所给的条件判断应证明哪两个三角形全等．10．D解析：D【分析】由于角平分线上的点到角的两边的距离相等，而已知一点到ABC 的三条边距离相等，那么这样的点在这个三角形的三条角平分线上，由此即可作出选择.【详解】解:∵到ABC 的三条边距离相等，角平分线上的点到角的两边的距离相等，∴这点在这个三角形三条角平分线上，即这点是三条角平分线的交点，【点睛】此题主要考查了三角形的角平分线的性质：三条角平分线交于一点，并且这一点到三边的距离相等.11．C解析：C【分析】由AD FC =推出AC=FD ，根据已知AB FE =添加夹角相等或第三边相等即可判定．【详解】∵AD FC =，∴AC=FD ，∵AB FE =，∴当A F ∠=∠（//AB EF 也可得到）或BC ED =时，即可判定F ABC ED ≌△△，故B E ∠=∠不能判定F ABC ED ≌△△，故选：C ．【点睛】此题考查添加一个条件证明两个三角形全等，熟记全等三角形的判定定理并熟练应用是解题的关键．12．D解析：D【分析】根据角平分线的性质、全等三角形的判定定理和性质定理判断即可．【详解】解：∵∠AOC ＝∠BOC ，∴OC 是∠AOB 的角平分线，① 符合题意；∵PD ⊥OA ，PE ⊥OB ，PD ＝PE ，∴OC 是∠AOB 的角平分线，② 符合题意；在Rt △POD 和Rt △POE 中，OD DE OP OP =⎧⎨=⎩， ∴Rt △POD ≌Rt △POE ，∴∠AOC ＝∠BOC ，∴OC 是∠AOB 的角平分线，③ 符合题意；∵∠DPO=∠EPO ，PD ⊥OA ，PE ⊥OB∴在△POD 和△POE 中，DPO EPO PDO PEO OP OP =⎧⎪=⎨⎪=⎩∠∠∠∠∴△POD≌△POE（AAS），∴∠AOC＝∠BOC，∴OC是∠AOB的角平分线，④ 符合题意，故选：D．【点睛】本题考查的是角平分线的性质、全等三角形的判定与性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键；二、填空题13．【分析】先根据三角形的内角和定理求出∠A的度数再利用全等三角形的性质求出答案即可【详解】∵∠A+∠B+∠C=∴∠A=-∠B-∠C=∵△ABC≌△DEF∴∠D=∠A=故答案为：【点睛】此题考查全等三角解析：70︒【分析】先根据三角形的内角和定理求出∠A的度数，再利用全等三角形的性质求出答案即可【详解】∵∠A+∠B+∠C=180︒，︒-︒-︒=︒，∴∠A=180︒-∠B-∠C=180506070∵△ABC≌△DEF，∴∠D=∠A=70︒，故答案为：70︒【点睛】此题考查全等三角形的性质：全等三角形的对应角相等，对应边相等，以及三角形的内角和定理．14．15【分析】如图过点D作DE⊥AB于E首先证明DE=CD=3再利用三角形的面积公式计算即可【详解】解：如图过点D作DE⊥AB于E由作图可知AD平分∠CAB∵CD⊥ACDE⊥AB∴DE=CD=3∴S△解析：15【分析】如图，过点D作DE⊥AB于E．首先证明DE=CD=3，再利用三角形的面积公式计算即可．【详解】解：如图，过点D作DE⊥AB于E．由作图可知，AD平分∠CAB，∵CD ⊥AC ，DE ⊥AB ，∴DE=CD=3，∴S △ABD =12•AB•DE=12×10×3=15，故答案为15．【点睛】本题考查了作图-基本作图，角平分线的性质定理等知识，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题．15．OA=OB （答案不唯一）【分析】全等三角形的判定方法有SASASAAASSSS 只要添加一个符合的条件即可【详解】解：OA=OB 理由是：在△AOC 和△BOD 中∴△AOC ≌△BOD （SAS ）故答案为：O解析：OA=OB ．（答案不唯一）【分析】全等三角形的判定方法有SAS ，ASA ，AAS ，SSS ，只要添加一个符合的条件即可．【详解】解：OA=OB ，理由是：在△AOC 和△BOD 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴△AOC ≌△BOD （SAS ）．故答案为：OA=OB ．（答案不唯一）【点睛】本题考查了全等三角形的判定的应用，通过做此题培养了学生的发散思维能力和对全等三角形的判定方法的灵活运用能力，题目答案不唯一，是一道比较好的题目．16．【分析】如图延长CD 交AB 于E 由题意得AP 平分∠CAB 证明△ADC ≌△ADE 得到CD=DE 由此得到推出即可得到答案【详解】如图延长CD 交AB 于E 由题意得AP 平分∠CAB ∴∠CAD=∠EAD ∵CD ⊥A 解析：152【分析】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，证明△ADC ≌△ADE ，得到CD=DE ，由此得到,ACD ADE BCD BED SS S S ==，推出ACD BCD ADE BED S S S S +=+，即可得到答案．【详解】如图，延长CD 交AB 于E ，由题意得AP 平分∠CAB ，∴∠CAD=∠EAD,∵CD ⊥AD ，∴∠ADC=∠ADE ，∵AD=AD ，∴△ADC ≌△ADE ，∴CD=DE ，∴,ACD ADE BCD BED SS S S ==， ∴ACD BCD ADE BED SS S S +=+， ∴12ABD ADE BED ABC S S S S =+==152，故答案为：152．．【点睛】此题考查三角形角平分线的作图方法，全等三角形的判定及性质，证出CD=DE 得到,ACD ADE BCD BED S S S S ==是解此题的关键．17．①②③【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF 再利用HL 证明Rt △CDE 和Rt △BDF 全等根据全等三角形对应边相等可得CE ＝AF 利用HL 证明Rt △ADE 和Rt △ADF 全等根据全等三解析：①②③．【分析】根据角平分线上的点到角的两边距离相等可得DE ＝DF ，再利用“HL”证明Rt △CDE 和Rt △BDF 全等，根据全等三角形对应边相等可得CE ＝AF ，利用“HL”证明Rt △ADE 和Rt △ADF 全等，根据全等三角形对应边相等可得AE ＝AF ，然后求出CE ＝AB ＋AE ；根据全等三角形对应角相等可得∠DBF ＝∠DCE ，利用“8字型”证明∠BDC ＝∠BAC ；根据三角形内角和定理及平角的性质，可得∠DAF ＝∠CBD ．【详解】解：如图∵AD 平分∠CAF ，DE ⊥AC ，DF ⊥AB ，∴DE ＝DF ，在Rt △CDE 和Rt △BDF 中，BD CD DE DF ⎧⎨⎩＝＝ ∴Rt △CDE ≌Rt △BDF （HL ），故①正确；∴CE ＝BF ，在Rt △ADE 和Rt △ADF 中，AD AD DE DF ＝＝⎧⎨⎩， ∴Rt △ADE ≌Rt △ADF （HL ），∴AE ＝AF ，∴CE ＝AB ＋AF ＝AB ＋AE ，故②正确；∵Rt △CDE ≌Rt △BDF ，∴∠DBF ＝∠DCE ，∵∠AOB ＝∠COD ，（设AC 交BD 于O ），∴∠BDC ＝∠BAC ，∵AD 平分∠FAE ，∴∠DAF ＝∠DAE∵BD ＝CD∴∠DBC ＝∠DCB∵∠BAC ＋∠DAF ＋∠DAE ＝180°，∠BDC ＋∠DBC ＋∠DCB ＝180°，∠BDC ＝∠BAC∴∠DAF ＋∠DAE ＝∠DBC ＋∠DCB∴∠DAF ＝∠CBD ，故③正确综上所述，正确的结论有①②③．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并准确识图判断出全等的三角形是解题的关键，难点在于需要二次证明三角形全等．18．3【分析】过D 作DE ⊥BC 于EDE 即为DP 长的最小值由题意可以得到△BAD ≌△BED 从而得到DE 的长度【详解】解：如图过D 作DE ⊥BC 于EDE 即为DP 长的最小值由题意知在△BAD 和△BED 中∴△BA解析：3【分析】过D 作DE ⊥BC 于E ，DE 即为DP 长的最小值，由题意可以得到△BAD ≌△BED ，从而得到DE 的长度．【详解】解：如图，过D 作DE ⊥BC 于E ，DE 即为DP 长的最小值，由题意知在△BAD 和△BED 中，A DEB ABD EBD BD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BAD ≌△BED ，∴ED=AD=3，故答案为3．【点睛】本题考查三角形全等的应用，熟练掌握三角形全等的判定和性质是解题关键． 19．【分析】如图延长AD 至点E 使得DE=AD 可证△ABD ≌△CDE 可得AB=CEAD=DE 在△ACE 中根据三角形三边关系即可求得AE 的取值范围即可解题【详解】解：延长AD 至点E 使得DE=AD ∵点D 是BC解析：15a <<【分析】如图延长AD 至点E ，使得DE=AD ，可证△ABD ≌△CDE ，可得AB=CE ，AD=DE ，在△ACE 中，根据三角形三边关系即可求得AE 的取值范围，即可解题．【详解】解：延长AD 至点E ，使得DE=AD ，∵点D 是BC 的中点，∴BD=CD在△ABD 和△CDE 中，AD DE ADB CDE BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△CDE （SAS ），∴AB=CE ，∵△ACE 中，AC-CE ＜AE ＜AC+CE ，即：AC-AB ＜AE ＜AC+AB ，∴2＜AE ＜10，∴1＜AD ＜5．故答案为：1＜AD ＜5．【点睛】本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ABD ≌△CDE 是解题的关键．20．①③【分析】由四边形内角和定理可求出；若DM 平分∠EDF 则∠EDM=60°从而得到∠ABC 为等边三角形条件不足不能确定故②错误；由题意可知∠EAD=∠FAD=30°故此可知ED=ADDF=AD 从而可解析：①③【分析】由四边形内角和定理可求出120EDF ∠=︒；若DM 平分∠EDF ，则∠EDM=60°，从而得到∠ABC 为等边三角形，条件不足，不能确定，故②错误；由题意可知∠EAD=∠FAD=30°，故此可知ED=12AD ，DF=12AD ，从而可证明③正确；连接BD 、DC ，然后证明△EBD ≌△CFD ，从而得到BE=FC ，从而可得AB+AC=2AE ，故可判断④．【详解】解：如图所示：连接BD 、DC ．（1）∵DE AB ⊥，DF AC ⊥，∴∠AED=∠AFD=90°，∵∠EAF=60°，∠EAF+∠AED+∠AFD+∠EDF=360°∴∠EDF=360°-∠EAF-∠AED-∠AFD=360°-60°-90°-90°=120°，故①正确；②由题意可知：∠EDA=∠ADF=60°．假设MD 平分∠EDF ，则∠ADM=30°．则∠EDM=60°，又∵∠E=∠BMD=90°，∴∠EBM=120°．∴∠ABC=60°．∵∠ABC 是否等于60°不知道，∴不能判定MD 平分∠EDF ，故②错误；③∵∠EAC=60°，AD 平分∠BAC ，∴∠EAD=∠FAD=30°．∵DE ⊥AB ，∴∠AED=90°．∵∠AED=90°，∠EAD=30°，∴ED=12AD ．同理：DF=12AD ． ∴DE+DF=AD ．故③正确．④∵DM 是BC 的垂直平分线，∴DB=DC ．在Rt △BED 和Rt △CFD 中DE DF BD DC ⎧⎨⎩＝＝， ∴Rt △BED ≌Rt △CFD ．∴BE=FC ．∴AB+AC=AE-BE+AF+FC又∵AE=AF ，BE=FC ，∴AB+AC=2AE ．故④错误．因此正确的结论是：①③，故答案为：①③．【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质以及四边形的内角和等知识，掌握本题的辅助线的作法是解题的关键．三、解答题21．证明见解析．【分析】先根据已知条件得出AB ED =，再利用SAS 证明ABC EDF △≌△，最后根据全等三角形的性质即可得出答案．【详解】证明：∵AD BE =，∴AD DB BE DB +=+，∴AB ED =．在ABC 和EDF 中，AB ED ABC EDF BC DF =⎧⎪∠=∠⎨⎪=⎩，∴()ABC EDF SAS △≌△，∴A E ∠=∠．【点睛】本题考查了全等三角形的判定及性质，熟练掌握全等三角形的判定方法是解题的关键． 22．（1）见详解；（2）1【分析】（1）先证明AC=DF ，再根据HL 证明Rt ABC Rt DEF ≌；（2）先证明∠AFG=∠DCH ，从而证明∆AFG ≅∆DCH ，进而即可求解．【详解】（1）∵AF CD =，∴AF+CF=CD+CF ，即AC=DF ，在Rt ABC 与Rt DEF △中，∵AC DF AB DE =⎧⎨=⎩， ∴Rt ABC ≅Rt DEF △（HL ）；（2）∵Rt ABC ≅Rt DEF △，∴∠A=∠D ，∠EFD=∠BCA ，∵∠AFG=180°-∠EFD ，∠DCH=180°-∠BCA ，∴∠AFG=∠DCH ，又∵AF CD =，∴∆AFG ≅∆DCH ，∴HC=GF =1．【点睛】本题主要考查全等三角形的判定和性质，熟练掌握HL 和ASA 证明三角形全等，是解题的关键．23．见解析【分析】求出∠CAD ＝∠EBC ，∠ACD ＝∠BCE ，AC ＝BC ，证出△BCE ≌△ACD ，求出CE ＝CD ，∠ECM ＝∠DCM ，证△ECM ≌△DCM ，推出DM ＝ME ，即可得出答案．【详解】∵AC 、BF 是高，∴∠BCE ＝∠ACD ＝∠AFE ＝90°，∵∠AEF ＝∠BEC ，∠CAD ＋∠AFE ＋∠AEF ＝180°，∠EBC ＋∠BCE ＋∠BEC ＝180°， ∴∠DAC ＝∠EBC ，∵∠ACB ＝90°，∠ABC ＝45°，∴∠BAC ＝45°＝∠ABC ，∴BC ＝AC ，在△BCE 和△ACD 中BCE ACD BC ACEBC DAC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BCE ≌△ACD （ASA ），∴BE ＝AD ．∵CM ∥AB ，∴∠MCE ＝∠BAC ＝45°，∵∠ACD ＝90°，∴∠MCD ＝45°＝∠MCE ，∵△BCE ≌△ACD ，∴CE ＝CD ，在△CEM 和△CDM 中CE CD ECM DCM CM CM =⎧⎪∠=∠⎨⎪=⎩∴△CEM ≌△CDM （SAS ），∴ME ＝MD ，∴BE ＝AD ＝AM ＋DM ＝AM ＋ME ，即BE ＝AM ＋EM ．【点睛】本题考查了全等三角形的性质和判定，平行线性质，三角形的内角和定理，垂直定义，等腰三角形的性质和判定的应用，主要考查学生综合运用定理进行推理的能力． 24．见解析【分析】如图，延长AE 、BC 交于点F ，构建三角形，证明△ACF ≌△BCD ，即可得出：AF=BD ，求证出AE=AF 即求证△ABE ≌△FBE ，即可求解．【详解】证明：如图，延长AE 、BC 交于点F∵AE ⊥BE ，∠ACB =90°∴∠BEF =∠BEA =90°,∠ACF =∠ACB =90°∴∠DBC +∠AFC =∠FAC +∠AFC =90°∴∠DBC =∠FAC在△ACF 和△BC D 中ACF BCD 90AC BCFAC DBC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△ACF ≌△BCD (ASA)∴AF =BD ．∵BD 是∠ABC 的角平分线∴∠ABE =∠FBE -在△ABE 和△FBE 中，BEA BEF BE BEABE FBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE ≌△FBE (ASA) ∴12AE EF AF ==∴12AE BD = 【点睛】本题主要考查的是三角形全等的性质及判定，熟练掌握三角形全等的判定定理，构建三角形是解答本题的关键．25．见详解【分析】先根据条件求出BC=EF ，根据平行线性质求出∠B=∠E ，∠ACB=∠DFE ，根据ASA 推出△ABC ≌△DEF 即可．【详解】∵FB ＝CE ，∴FB+FC=FC+CE ，即BC=FE ，又∵AB ∥ED ，AC ∥FD ，∴∠B=∠E ，∠ACB=∠DFE ，在△ABC 和△DEF 中，B E BC FEACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△DEF （ASA ）∴AB=DE ．【点睛】本题考查了平行线的性质和全等三角形的性质和判定的应用，主要考查学生的推理论证能力．26．150米【分析】根据题意，判断出△ADC ≌△CEB 即可求解．【详解】解：如图，过点B 作BE ⊥MN 于点E ，∵∠ADC ＝∠ACB ＝90°，∴∠A ＝∠BCE （同角的余角相等）．在△ADC 与△CEB 中，90ADC CEB A BCEAC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△CEB （AAS ）．∴BE ＝CD ＝150m ．即村庄B 到河边的距离是150米．【点睛】本题主要考查的是全等三角形的实际应用，熟练掌握全等三角形的判定及性质是解答本题的关键．。

四川省成都市石室中学数学三角形解答题(提升篇)(Word版含解析)

四川省成都市石室中学数学三角形解答题（提升篇）（Word版含解析）一、八年级数学三角形解答题压轴题（难）1．如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．(1)求证：∠A+∠C＝∠B+D；(2)如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD、AB分别相交于点M、N．①以线段AC为边的“8字型”有个，以点O为交点的“8字型”有个；②若∠B＝100°，∠C＝120°，求∠P的度数；③若角平分线中角的关系改为“∠CAP＝13∠CAB，∠CDP＝13∠CDB”，试探究∠P与∠B、∠C之间存在的数量关系，并证明理由．【答案】(1)证明见解析；(2)①3， 4；②∠P＝110°；③3∠P＝∠B+2∠C，理由见解析.【解析】【分析】(1)由三角形内角和得到∠A+∠C=180°﹣∠AOC，∠B+∠D=180°﹣∠BOD，由对顶角相等，得到∠AOC=∠BOD，因而∠A+∠C=∠B+∠D；(2)①以线段AC为边的“8字形”有3个，以O为交点的“8字形”有4个；②根据(1)的结论，以M为交点“8字型”中，∠P+∠CDP＝∠C+∠CAP，以N为交点“8字型”中，∠P+∠BAP＝∠B+∠BDP，两等式相加得到2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP，由AP和DP是角平分线，得到∠BAP＝∠CAP，∠CDP＝∠BDP，从而∠P=12(∠B+∠C)，然后将∠B=100º，∠C=120º代入计算即可；③与②的证明方法一样得到3∠P=∠B+2∠C.【详解】解：(1)在图1中，有∠A+∠C＝180°﹣∠AOC，∠B+∠D＝180°﹣∠BOD，∵∠AOC＝∠BOD，∴∠A+∠C＝∠B+∠D；(2)解：①以线段AC为边的“8字型”有3个：以点O为交点的“8字型”有4个：②以M为交点“8字型”中，有∠P+∠CDP＝∠C+∠CAP，以N为交点“8字型”中，有∠P+∠BAP＝∠B+∠BDP∴2∠P+∠BAP+∠CDP＝∠B+∠C+∠CAP+∠BDP，∵AP、DP分别平分∠CAB和∠BDC，∴∠BAP＝∠CAP，∠CDP＝∠BDP，∴2∠P＝∠B+∠C，∵∠B＝100°，∠C＝120°，∴∠P＝12（∠B+∠C）=12（100°+120°）＝110°；③3∠P＝∠B+2∠C，其理由是：∵∠CAP＝13∠CAB，∠CDP＝13∠CDB，∴∠BAP＝23∠CAB，∠BDP＝23∠CDB，以M为交点“8字型”中，有∠P+∠CDP＝∠C+∠CAP，以N为交点“8字型”中，有∠P+∠BAP＝∠B+∠BDP∴∠C﹣∠P＝∠CDP﹣∠CAP＝13（∠CDB﹣∠CAB），∠P﹣∠B＝∠BDP﹣∠BAP＝23（∠CDB﹣∠CAB）．∴2（∠C﹣∠P）＝∠P﹣∠B，∴3∠P＝∠B+2∠C．故答案为：(1)证明见解析；(2)①3， 4；②∠P＝110°；③3∠P＝∠B+2∠C，理由见解析.【点睛】本题考查了三角形内角和定理：三角形内角和是180°．也考查了角平分线的定义．2．在一个三角形中，如果一个角是另一个角的3倍，这样的三角形我们称之为“灵动三角形”．如，三个内角分别为120°，40°，20°的三角形是“灵动三角形”．如图，∠MON＝60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（规定0°< ∠OAC < 90°）．（1）∠ABO的度数为°，△AOB（填“是”或“不是”灵动三角形）；（2）若∠BAC＝60°，求证：△AOC为“灵动三角形”；（3）当△ABC为“灵动三角形”时，求∠OAC的度数．【答案】（1）30°；（2）详见解析；（3）∠OAC=80°或52.5°或30°.【解析】【分析】（1）根据垂直的定义、三角形内角和定理求出∠ABO的度数，根据“智慧三角形”的概念判断；（2）根据“智慧三角形”的概念证明即可；（3）分点C在线段OB和线段OB的延长线上两种情况，根据“智慧三角形”的定义计算．【详解】（1）答案为：30°；是；（2）∵AB⊥OM∴∠B AO＝90°∵∠BAC＝60°∴∠OAC＝∠B AO-∠BAC=30°∵∠MON＝60°∴∠ACO＝180°-∠OAC-∠MON＝90°∴∠ACO＝3∠OAC，∴△AOC为“灵动三角形”；（3）设∠OAC= x°则∠BAC=90-x, ∠ACB=60+x ,∠ABC＝30°∵△ABC为“智慧三角形”，Ⅰ、当∠ABC＝3∠BAC时，°，∴30＝3（90-x），∴x=80Ⅱ、当∠ABC＝3∠ACB时，∴30=3（60+x）∴x= -50 （舍去）∴此种情况不存在，Ⅲ、当∠BCA＝3∠BAC时，∴60+x＝3（90-x），∴x＝52.5°，Ⅳ、当∠BCA＝3∠ABC时，∴60+x＝90°，∴x＝30°，Ⅴ、当∠BAC＝3∠ABC时，∴90-x＝90°，∴x＝0°（舍去）Ⅵ、当∠BAC ＝3∠ACB 时，∴90-x ＝3（60+x ），∴x= -22.5（舍去），∴此种情况不存在，∴综上所述：∠OAC=80°或52.5°或30°。

成都石室联合中学数学全等三角形易错题(Word版含答案)

成都石室联合中学数学全等三角形易错题（Word版含答案）一、八年级数学轴对称三角形填空题（难）1．在等腰△ABC中，AD⊥BC交直线BC于点D，若AD=12BC，则△ABC的顶角的度数为_____．【答案】30°或150°或90°【解析】试题分析：分两种情况；①BC为腰，②BC为底，根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°，然后分AD在△ABC内部和外部两种情况求解即可．解：①BC为腰，∵AD⊥BC于点D，AD=12 BC，∴∠ACD=30°，如图1，AD在△ABC内部时，顶角∠C=30°，如图2，AD在△ABC外部时，顶角∠ACB=180°﹣30°=150°，②BC为底，如图3，∵AD⊥BC于点D，AD=12 BC，∴AD =BD =CD ， ∴∠B =∠BAD ，∠C =∠CAD ，∴∠BAD +∠CAD =12×180°=90°， ∴顶角∠BAC =90°，综上所述，等腰三角形ABC 的顶角度数为30°或150°或90°．故答案为30°或150°或90°．点睛：本题考查了含30°交点直角三角形的性质，等腰三角形的性质，分类讨论是解题的关键．2．如图，在等边ABC ∆中取点P 使得PA ，PB ，PC 的长分别为3， 4， 5，则APC APB S S ∆∆+=_________．【答案】9364+【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ，连接PD ，根据旋转的性质知△APD 是等边三角形，利用勾股定理的逆定理可得△PBD 为直角三角形，∠BPD ＝90︒，由△ADB ≌△APC 得S △ADB ＝S △APC ，则有S △APC ＋S △APB ＝S △ADB ＋S △APB ＝S △ADP ＋S △BPD ，根据等边3S △ADP ＋S △BPD ＝34×32＋12×3×4＝364+．【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ，连接PD∴AD ＝AP ，∠DAP ＝60︒，又∵△ABC 为等边三角形，∴∠BAC ＝60︒，AB ＝AC ，∴∠DAB ＋∠BAP ＝∠PAC ＋∠BAP ，∴∠DAB ＝∠PAC ，又AB=AC,AD=AP∴△ADB≌△APC∵DA＝PA，∠DAP＝60︒，∴△ADP为等边三角形，在△PBD中，PB＝4，PD＝3，BD＝PC＝5，∵32＋42＝52，即PD2＋PB2＝BD2，∴△PBD为直角三角形，∠BPD＝90︒，∵△ADB≌△APC，∴S△ADB＝S△APC，∴S△APC＋S△APB＝S△ADB＋S△APB＝S△ADP＋S△BPD＝34×32＋12×3×4＝9364+．故答案为：9364 +．【点睛】本题考查了等边三角形的性质与判定，解题的关键是熟知旋转的性质作出辅助线进行求解．3．如图，△ABC是等边三角形，高AD、BE相交于点H，BC=43，在BE上截取BG=2，以GE为边作等边三角形GEF，则△ABH与△GEF重叠（阴影）部分的面积为_____．53【解析】试题分析：如图所示，由△ABC是等边三角形，BC=43AD=BE=32BC=6，∠ABG=∠HBD=30°，由直角三角的性质，得∠BHD=90°﹣∠HBD=60°，由对顶角相等，得∠MHE=∠BHD=60°，由BG=2，得EG=BE﹣BG=6﹣2=4．由GE为边作等边三角形GEF，得FG=EG=4，∠EGF=∠GEF=60°，△MHE 是等边三角形；S △ABC =12AC•BE=12AC×EH×3EH=13BE=13×6=2．由三角形外角的性质，得∠BIF=∠FGE ﹣∠IBG=60°﹣30°=30°，由∠IBG=∠BIG=30°，得IG=BG=2，由线段的和差，得IF=FG ﹣IG=4﹣2=2，由对顶角相等，得∠FIN=∠BIG=30°，由∠FIN+∠F=90°，得∠FNI=90°，由锐角三角函数，得FN=1，IN=3．S 五边形NIGHM =S △EFG ﹣S △EMH ﹣S △FIN =223314231442⨯-⨯-⨯⨯=53，故答案为53．考点：1．等边三角形的判定与性质；2．三角形的重心；3．三角形中位线定理；4．综合题；5．压轴题．4．如图，将ABC ∆沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的1A 处，称为第1次操作，折痕DE 到BC 的距离记为1h ，还原纸片后，再将ADE ∆沿着过AD 中点1D 的直线折叠，使点A 落在DE 边上的2A 处，称为第2次操作，折痕11D E 到BC 的距离记为2h ，按上述方法不断操作下去…经过第2020次操作后得到的折痕20192019D E 到BC 的距离记为2020h ，若11h =，则2020h 的值为______．【答案】2019122-【解析】【分析】根据中点的性质及折叠的性质可得DA=DA ₁=DB,从而可得∠ADA ₁=2∠B,结合折叠的性质可得.，∠ADA ₁=2∠ADE,可得∠ADE=∠B,继而判断DE// BC,得出DE 是△ABC 的中位线，证得AA ₁⊥BC,AA ₁=2，由此发现规律：012122h =-=-₁同理21122h =-3211122222h =-⨯=-…于是经过第n 次操作后得到的折痕Dn-1 En-1到BC 的距离1122n n h -=-，据此求得2020h 的值．【详解】解：如图连接AA ₁,由折叠的性质可得：AA ₁⊥DE, DA= DA ₁ ,A ₂、A ₃…均在AA ₁上又∵ D 是AB 中点，∴DA= DB ,∵DB= DA ₁ ,∴∠BA ₁D=∠B ,∴∠ADA ₁=∠B +∠BA ₁D=2∠B,又∵∠ADA ₁ =2∠ADE ,∴∠ADE=∠B∵DE//BC,∴AA ₁⊥BC ,∵h ₁=1∴AA ₁ =2,∴012122h =-=-₁ 同理：21122h =-； 3211122222h =-⨯=-； …∴经过n 次操作后得到的折痕D n-1E n-1到BC 的距离1122n n h -=-∴20202019122h =-【点睛】本题考查了中点性质和折叠的性质，本题难度较大，要从每次折叠发现规律，求得规律的过程是难点．5．如图，在Rt△ABC中，∠ACB＝90°，AB的垂直平分线DE交BC的延长线于F，若∠F ＝30°，DE＝1，则EF的长是_____．【答案】2【解析】【分析】连接BE，根据垂直平分线的性质、直角三角形的性质，说明∠CBE＝∠F，进一步说明BE ＝EF，，然后再根据直角三角形中，30°所对的直角边等于斜边的一半即可.【详解】解：如图：连接BE∵AB的垂直平分线DE交BC的延长线于F，∴AE＝BE，∠A+∠AED＝90°，∵在Rt△ABC中，∠ACB＝90°，∴∠F+∠CEF＝90°，∵∠AED＝∠FEC，∴∠A＝∠F＝30°，∴∠ABE＝∠A＝30°，∠ABC＝90°﹣∠A＝60°，∴∠CBE＝∠ABC﹣∠ABE＝30°，∴∠CBE＝∠F，∴BE＝EF，在Rt△BED中，BE＝2DE＝2×1＝2，∴EF＝2．故答案为：2．【点睛】本题考查了垂直平分线的性质、直角三角形的性质，其中灵活利用垂直平分线的性质和直角三角形30°角所对的边等于斜边的一半是解答本题的关键.6．△ABC中，最小内角∠B＝24°，若△ABC被一直线分割成两个等腰三角形，如图为其中一种分割法，此时△ABC中的最大内角为90°，那么其它分割法中，△ABC中的最大内角度数为_____．【答案】117°或108°或84°．【解析】【分析】根据等腰三角形的性质进行分割，写出△ABC中的最大内角的所有可能值.【详解】①∠BAD＝∠BDA＝12（180°﹣24°）＝78°，∠DAC＝∠DCA＝12∠BDA＝39°，如图1所示：∴∠BAC＝78°+39°＝117°；②∠DBA＝∠DAB＝24°，∠ADC＝∠ACD＝2∠DBA＝48°，如图2所示：∴∠DAC＝180°﹣2×48°＝84°，∴∠BAC＝24°+84°＝108°；③∠DBA＝∠DAB＝24°，∠ADC＝∠DAC＝2∠DBA＝48°，如图3所示：∴∠BAC＝24°+48°＝72°，∠C＝180°﹣2×48°＝84°；∴其它分割法中，△ABC中的最大内角度数为117°或108°或84°，故答案为：117°或108°或84°．【点睛】本题考查了等腰三角形的性质，解题的关键是根据等腰三角形的性质进行分割找出所有情况.7．如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA2＝4，则△A n B n A n+1的边长为_____．【答案】2n．【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及A2B2＝2B1A2，得出A3B3＝4B1A2＝8，A4B4＝8B1A2＝16，A5B5＝16B1A2…进而得出答案．【详解】解：∵△A1B1A2是等边三角形，∴A1B1＝A2B1，∵∠MON＝30°，∵OA2＝4，∴OA1＝A1B1＝2，∴A2B1＝2，∵△A2B2A3、△A3B3A4是等边三角形，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴A2B2＝2B1A2，B3A3＝2B2A3，∴A3B3＝4B1A2＝8，A4B4＝8B1A2＝16，A5B5＝16B1A2＝32，以此类推△A n B n A n+1的边长为 2n．故答案为：2n．【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质，由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键．8．如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC=_____cm．【答案】8cm.【解析】【详解】解：如图，延长ED交BC于M，延长AD交BC于N，作DF∥BC，∵AB=AC，AD平分∠BAC，∴AN⊥BC，BN=CN，∵∠EBC=∠E=60°，∴△BEM为等边三角形，∴△EFD为等边三角形，∵BE=6cm，DE=2cm，∴DM=4，∵△BEM为等边三角形，∴∠EMB=60°，∵AN⊥BC，∴∠DNM=90°，∴∠NDM=36°，∴NM=2，∴BN=4，∴BC=8．9．如图，D 为ABC ∆内一点，CD 平分ACB ∠，BD CD ⊥，A ABD ∠=∠，若8AC =，5BC =，则BD 的长为_______.【答案】1.5【解析】【分析】延长BD 交AC 边于点E ，根据BD⊥CD,CD 平分∠ACB ，得到三角形全等，由此求出AE 的长，再根据A ABD ∠=∠，求出BE 的长即可求得BD.【详解】延长BD 交AC 于点E ，∵BD⊥CD，∴∠BDC=∠EDC=900，∵CD 平分∠ACB，∴∠BCD=∠ECD又∵CD=CD∴△BCD≌△ECD∴BD=ED,CE=BC=5，∴AE=AC -CE=8-5=3，∵A ABD ∠=∠,∴BE=AE=3，∴BD=1.5【点睛】此题考察等腰三角形的性质，延长BD 构建全等三角形是证明此题的关键.10．在下列结论中：①有三个角是60︒的三角形是等边三角形；②有一个外角是120︒的等腰三角形是等边三角形；③有一个角是60︒，且是轴对称的三角形是等边三角形；④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形．其中正确的是__________.【答案】①②③④【解析】【分析】依据等边三角形的定义，含有一个600角的等腰三角形是等边三角形判断即可.【详解】有三个角是600的三角形是等边三角形，故①正确；外角是1200时，邻补角为600，即有一个内角是600的等腰三角形是等边三角形，故②正确；轴对称的三角形是等腰三角形，且含有一个600角，因此是等边三角形，故③正确；一腰上的高也是中线，故底边等于腰长，所以此三角形是等边三角形，故④正确.故此题正确的是①②③④.【点睛】此题考查等边三角形的判定方法，熟记方法才能熟练运用.二、八年级数学轴对称三角形选择题（难）11．在平面直角坐标系中，等腰△ABC的顶点A、B的坐标分别为（0，0）、（2，2），若顶点C落在坐标轴上，则符合条件的点C有（）个．A．5 B．6 C．7 D．8【答案】D【解析】【分析】要使△ABC是等腰三角形，可分三种情况（①若AC=AB，②若BC=BA，③若CA=CB）讨论，通过画图就可解决问题．【详解】①若AC=AB，则以点A为圆心，AB为半径画圆，与坐标轴有4个交点；②若BC=BA，则以点B为圆心，BA为半径画圆，与坐标轴有2个交点（A点除外）；③若CA=CB，则点C在AB的垂直平分线上．∵A （0，0），B （2，2），∴AB 的垂直平分线与坐标轴有2个交点．综上所述：符合条件的点C 的个数有8个．故选D ．【点睛】本题考查了等腰三角形的判定、垂直平分线的性质的逆定理等知识，还考查了动手操作的能力，运用分类讨论的思想是解决本题的关键．12．如图，在ABC ∆中，120BAC ︒∠=，点,E F 分别是ABC ∆的边AB 、AC 的中点，边BC 分别与DE 、DF 相交于点,H G ，且,DE AB DF AC ⊥⊥，连接AD 、AG 、AH ，现在下列四个结论：①60EDF ︒∠=，②AD 平分GAH ∠，③B ADF ∠=∠，④GD GH =.则其中正确的结论有（）.A ．1个B ．2个C ．3个D ．4个【答案】A【解析】【分析】利用,DE AB DF AC ⊥⊥及四边形的内角和即可得到①正确；；根据三角形内角和与线段的垂直平分线性质得到∠BAH+∠GAC=60︒，无条件证明∠GAD=∠HAD,故②错误；由等量代换得B ADF ∠≠∠，故③错误；利用三角形的内角和与对顶角相等得到GD GH ≠，故④错误.【详解】∵,DE AB DF AC ⊥⊥，∴∠DEA=∠DFA=90︒，∵120BAC ︒∠=,∴∠EDF=360︒-∠DEA-∠DFA-∠BAC=60︒，故①正确；∵120BAC ︒∠=，∴∠B+∠C=60︒，∵点,E F 分别是ABC ∆的边AB 、AC 的中点，,DE AB DF AC ⊥⊥，∴BH=AH ，AG=CG ，∴∠BAH=∠B ，∠GAC=∠C ，∴∠BAH+∠GAC=60︒，∵无条件证明∠GAD=∠HAD,∴AD 不一定平分GAH ∠，故②错误；∵∠ADF+∠DAF=90︒，∠B=∠BAH,90BAH DAF ∠+∠≠,∴B ADF ∠≠∠，故③错误；∵90B BHE ∠+∠=，30B ∠≠ ，∴ 60BHE ∠≠，∴60DHG ∠≠，∴DHG HDG ∠≠∠,∴GD GH ≠，故④错误，故选：A.【点睛】此题考查线段的垂直平分线的性质，利用三角形的内角和，四边形的内角和求角度，利用对顶角相等，等角对等边推导边的关系.13．如图所示，在等边△ABC 中，E 是AC 边的中点，AD 是BC 边上的中线，P 是AD 上的动点，若AD =3，则EP ＋CP 的最小值为（）A ．2B ．3C ．4D ．5【答案】B【解析】由等边三角形的性质得，点B ，C 关于AD 对称，连接BE 交AD 于点P ，则EP+CP=BE 最小，又BE=AD ，所以EP+CP 的最小值是3.故选B.点睛：本题主要考查了等边三角形的性质和轴对称的性质，求一条定直线上的一个动点到定直线的同旁的两个定点的距离的最小值，常用的方法是，①确定两个定点中的一个关于定直线的对称点；②连接另一个定点与对称点，与定直线的交点就是两线段和的值最小时，动点的位置.14．如图，在等腰△ABC 中，AB=AC=6,∠BAC=120°，点P 、Q 分别是线段BC 、射线BA 上一点，则CQ+PQ 的最小值为（）A ．6B ．7.5C ．9D ．12【答案】C【解析】【分析】通过作点C 关于直线AB 的对称点，利用点到直线的距离垂线段最短，即可求解.【详解】解：如图，作点C 关于直线AB 的对称点1C ，1CC 交射线BA 于H ，过点1C 作BC 的垂线，垂足为P ，与AB 交于点Q ，CQ+PQ 的长即为1PC 的长.∵AB=AC=6,∠BAC=120°，∴∠ABC=30°，易得BC=3在Rt △BHC 中，∠ABC=30°，∴HC=33BCH=60°，∴163CC =在1Rt △PCC 中，1PCC ∠=60°，∴19PC =∴CQ+PQ 的最小值为9，故选：C.【点睛】本题考查了等腰三角形的性质以及利用对称点求最小值的问题，认真审题作出辅助线是解题的关键.15．如图，点P 、Q 分别是边长为4cm 的等边△ABC 边AB 、BC 上的动点，点P 从顶点A ，点Q 从顶点B 同时出发，且速度都为1cm/s ，连接AQ 、CP 交于点M ，下面四个结论:①BP ＝CM ；②△ABQ ≌△CAP ；③∠CMQ 的度数不变，始终等于60°；④当第43秒或第83秒时，△PBQ 为直角三角形，正确的有几个 ( )A．1 B．2 C．3 D．4【答案】C【解析】【分析】①等边三角形ABC中，AB=BC，而AP=BQ，所以BP=CQ．②根据等边三角形的性质，利用SAS证明△ABQ≌△CAP；③由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP，从而得到∠CMQ=60°；④设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，当∠PQB=90°时，因为∠B=60°，所以PB=2BQ，即4-t=2t故可得出t的值，当∠BPQ=90°时，同理可得BQ=2BP，即t=2（4-t），由此两种情况即可得出结论．【详解】①在等边△ABC中，AB=BC．∵点P、Q的速度都为1cm/s，∴AP=BQ，∴BP=CQ．只有当CM=CQ时，BP=CM．故①错误；②∵△ABC是等边三角形∴∠ABQ=∠CAP，AB=CA，又∵点P、Q运动速度相同，∴AP=BQ，在△ABQ与△CAP中，∵AB CAABQ CAP AP BQ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABQ≌△CAP（SAS）．故②正确；③点P、Q在运动的过程中，∠QMC不变．理由：∵△ABQ≌△CAP，∴∠BAQ=∠ACP，∵∠QMC=∠ACP+∠MAC，∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°．故③正确；④设时间为t秒，则AP=BQ=tcm，PB=（4-t）cm，当∠PQB=90°时，∵∠B=60°，∴PB=2BQ，即4-t=2t，t=43，当∠BPQ=90°时，∵∠B=60°，∴BQ=2BP，得t=2（4-t），t=83，∴当第43秒或第83秒时，△PBQ为直角三角形．故④正确．正确的是②③④，故选C．【点睛】此题是一个综合性题目，主要考查等边三角形的性质、全等三角形的判定与性质等知识．熟知等边三角形的三个内角都是60°是解答此题的关键．16．如果三角形有一个内角为120°，且过某一顶点的直线能将该三角形分成两个等腰三角形，那么这个三角形最小的内角度数是( )A．15°B．40 C．15°或20°D．15°或40°【答案】C【解析】【分析】依据三角形的一个内角的度数为120°，且过某一顶点能将该三角形分成两个等腰三角形，运用分类思想和三角形内角和定理，即可得到该三角形其余两个内角的度数．【详解】如图1，当∠A=120°，AD=AC，DB=DC时，∠ADC=∠ACD=30°，∠DBC=∠DCB=15°，所以，∠DBC=15°，∠ACB=30°+15°=45°；故∠ABC=60°，∠C=80°；如图2，当∠BAC=120°，可以以A为顶点作∠BAD=20°，则∠DAC=100°，∵△APB，△APC都是等腰三角形；∴∠ABD=20°，∠ADC=∠ACD=40°，如图3，当∠BAC=120°，以A为顶点作∠BAD=80°，则∠DAC=40°，∵△APB，△APC都是等腰三角形，∴∠ABD=20°，∠ADC=100°，∠ACD=40°．故选C．【点睛】本题主要考查了三角形内角和定理以及等腰三角形的性质的运用，解决问题的关键是掌握等腰三角形的性质以及三角形内角和定理．17．如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）．则∠OCD 等于（）A．108°B．114°C．126°D．129°【答案】C【解析】【分析】按照如图所示的方法折叠,剪开,把相关字母标上,易得∠ODC和∠DOC的度数,利用三角形的内角和定理可得∠OCD的度数．【详解】解:展开如图,五角星的每个角的度数是,180=36°.5∵∠COD =360°÷10=36°,∠ODC=36°÷2=18°,∴∠OCD =180°-36°-18°=126°,故选C ．【点睛】本题主要考查轴对称性质,解决本题的关键是能够理解所求的角是五角星的哪个角,解题时可以结合正五边形的性质解决．18．如图，ABC △，AB AC =，56BAC ︒∠=，BAC ∠的平分线与AB 的垂直平分线交于O ，将∠C 沿EF （E 在BC 上，F 在AC 上）折叠，点C 与O 点恰好重合，则∠OEC 的度数为（）A ．132︒B ．130︒C ．112︒D ．110︒【答案】C【解析】【分析】连接OB 、OC ，根据角平分线的定义求出∠BAO ，根据等腰三角形两底角相等求出∠ABC ，再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB ，根据等边对等角可得∠ABO=∠BAO ，再求出∠OBC ，然后判断出点O 是△ABC 的外心，根据三角形外心的性质可得OB=OC ，再根据等边对等角求出∠OCB=∠OBC ，根据翻折的性质可得OE=CE ，然后根据等边对等角求出∠COE ，再利用三角形内角和定理列式计算即可得出答案.【详解】如图，连接OB 、OC ，∵56BAC ︒∠=，AO 为BAC ∠的平分线∴11562822BAO BAC ︒︒∠=∠=⨯= 又∵AB AC =， ∴()()11180180566222ABC BAC ︒︒︒︒∠=-∠=-= ∵DO 是AB 的垂直平分线，∴OA OB =．∴28ABO BAO ︒∠=∠=，∴622834OBC ABC ABO ︒︒︒∠=∠-∠=-=∵DO 是AB 的垂直平分线，AO 为BAC ∠的平分线∴点О是ABC △的外心，∴OB OC =，∴34OCB OBC ︒∠=∠=，∵将C ∠沿EF （E 在BC 上，F 在AC 上）折叠，点C 与点O 恰好重合∴OE CE =，∴34COE OCB ︒∠=∠=，在OCE △中，1801803434112OEC COE OCB ︒︒︒︒︒∠=-∠-∠=--=【点睛】本题主要考查了线段垂直平分线上的点到线段两端点距离相等的性质，等腰三角形三线合一的性质，等边对等角的性质，以及翻折变换的性质，综合性较强，难度较大，做辅助线构造出等腰三角形是解决本题的关键.19．如图，已知，点A （0，0）、B （43，0）、C （0，4），在△ABC 内依次作等边三角形，使一边在x 轴上，另一个顶点在BC 边上，作出的等边三角形分别是第1个△AA 1B 1，第2个△B 1A 2B 2，第3个△B 2A 3B 3，…则第2017个等边三角形的边长等于（）A 3B 3C 3D 3【答案】A【解析】【分析】【详解】根据锐角三函数的性质，由OB=3OC=1，可得∠OCB=90°，然后根据等边三角形的性质，可知∠A 1AB=60°，进而可得∠CAA 1=30°，∠CA 1O=90°，因此可推导出∠A 2A 1B=30°，同理得到∠CA 2B 1=∠CA 3B 2=∠CA 4B 3=90°，∠A 2A 1B=∠A 3A 2B 2=∠A 4A 3B 3=30°，故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半，即OA 1=OCcos ∠CAA 1=3B 1A 2=1232⨯2017个等边三角形的边长为：201713()432⨯=. 故选A.【点睛】此题主要考查了等边三角形的性质，属于规律型题目，解题关键是仔细审图，得出：后一个等边三角形的边长等于前一个等边三角形的边长的一半.20．如图，ABC △中，60BAC ∠=︒，ABC ∠、ACB ∠的平分线交于E ，D 是AE 延长线上一点，且120BDC ∠=︒．下列结论：①120BEC ∠=︒；②DB DE =；③2BDE BCE ∠=∠．其中所有正确结论的序号有（）．A ．①②B ．①③C ．②③D ．①②③【答案】D【解析】分析：根据三角形内角和等于180°求出∠ABC+∠ACB ，再根据角平分线的定义求出∠EBC+∠ECB ，然后求出∠BEC=120°，判断①正确；过点D 作DF ⊥AB 于F ，DG ⊥AC 的延长线于G ，根据角平分线上的点到角的两边的距离相等可得DF=DG ，再求出∠BDF=∠CDG ，然后利用“角边角”证明△BDF 和△CDG 全等，根据全等三角形对应边相等可得BD=CD ，再根据等边对等角求出∠DBC=30°，然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ，根据等角对等边可得BD=DE ，判断②正确，再求出B ，C ，E 三点在以D 为圆心，以BD 为半径的圆上，根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ，判断③正确．详解：∵60BAC ∠=︒，∴18060120ABC ACB ∠+∠=︒-︒=︒，∵BE 、CE 分别为ABC ∠、ACB ∠的平分线，∴12EBC ABC ∠=∠，12ECB ACB ∠=∠， ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒， ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒，故①正确．如图，过点D 作DF AB ⊥于F ，DG AC ⊥的延长线于G ，∵BE 、CE 分别为ABC ∠、ACB ∠的平分线，∴AD 为BAC ∠的平分线，∴DF DG =，∴36090260120FDG ∠=︒-︒⨯-︒=︒，又∵120BDC ∠=︒，∴120BDF CDF ∠+∠=︒，120CDG CDF ∠+∠=︒．∴BDF CDG ∠=∠， ∵在BDF 和CDG △中，90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩， ∴BDF ≌()CDG ASA ，∴DB CD =，∴1(180120)302DBC ∠=︒-︒=︒， ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠，∵BE 平分ABC ∠，AE 平分BAC ∠，∴ABE CBE ∠=∠，1302BAE BAC ∠=∠=︒，根据三角形的外角性质， 30DEB ABE BAE ABE ∠=∠+∠=∠+︒，∴DEB DBE ∠=∠，∴DB DE =，故②正确．∵DB DE DC ==，∴B 、C 、E 三点在以D 为圆心，以BD 为半径的圆上，∴2BDE BCE ∠=∠，故③正确，综上所述，正确结论有①②③，故选：D ．点睛：本题考查了角平分线的性质，全等三角形的判定与性质，等角对等边的性质，圆内接四边形的判定，同弧所对的圆周角等于圆心角的一半性质，综合性较强，难度较大，特别是③的证明．。

成都石室联合中学数学轴对称填空选择易错题(Word版含答案)

成都石室联合中学数学轴对称填空选择易错题（Word 版含答案）一、八年级数学全等三角形填空题（难）1．如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，过点O 作EF ∥BC 交AB 于E ，交AC 于F ，过点O 作OD ⊥AC 于D ，下列四个结论：①EF =BE +CF ；②∠BOC =90°+12∠A ； ③点O 到△ABC 各边的距离相等；④设OD =m ，AE +AF =n ，则AEF S mn ∆=．其中正确的结论是____．（填序号）【答案】①②③【解析】【分析】由在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，根据角平分线的定义与三角形的内角和定理，即可求出②∠BOC =90°+12∠A 正确；由平行线的性质和角平分线的定义可得△BEO 和△CFO 是等腰三角形可得①EF =BE +CF 正确；由角平分线的性质得出点O 到△ABC 各边的距离相等，故③正确；由角平分线定理与三角形的面积求法，设OD=m ，AE+AF=n,则△AEF 的面积=12mn ，④错误. 【详解】在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC=12∠ABC ，∠OCB=12∠ACB ，∠A+∠ABC+∠ACB=180°， ∴∠OBC+∠OCB=90°-12∠A ， ∴∠BOC=180°-（∠OBC+∠OCB ）=90°，故②∠BOC =90°+12∠A 正确；在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，∴∠OBC=∠EOB ，∠OCB=∠OCF ，∵EF ∥BC ，∴∠OBC=∠EOB ，∠OCB=∠FOC ，∠EOB=∠OBE,∠FOC=∠OCF ，∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF，即①EF=BE+CF正确；过点O作OM⊥AB于M，作ON⊥BC于点N，连接AO，∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，∴ON=OD=OM=m，即③点O到△ABC各边的距离相等正确；∴S△AEF=S△AOE+ S△AOF=12AE·OM+12AF·OD=12OD·（AE+AF）=12mn，故④错误；故选①②③【点睛】此题主要考查角平分线的性质，解题的关键是熟知等腰三角形的判定与性质.2．如图，P为等边△ABC内一点，∠APC=150°，且∠APD=30°，AP=6，CP=3，DP=7，则BD的长为______.【答案】34【解析】【分析】将△CPA绕点C逆时针旋转60°得到△CEB，连接EP，由全等三角形的性质可得CE=CP，∠ECB=∠PCA，∠CEB=∠CPA=150°，BE=AP=6，结合等边三角形的性质可得出∠ECP=60°，进而证明△ECP为等边三角形，由等边△ECP的性质进而证明D、P、E三点共线以及∠DEB=90°，最后利用勾股定理求出BD的长度即可.【详解】将△CPA绕点C逆时针旋转60°得到△CEB，连接EP，∴CE=CP，∠ECB=∠PCA，∠CEB=∠CPA=150°，BE=AP=6，∵等边△ABC，∴∠ACP+∠PCB=60°，∴∠ECB+∠PCB=60°,即∠ECP=60°，∴△ECP为等边三角形，∴∠CPE=∠CEP=60°，PE=6，∴∠DEB=90°，∵∠APC=150°，∠APD=30°，∴∠DPC=120°，∴∠DPE=180°，即D、P、E三点共线，∴ED=3+7=10，∴BD=22=234.DE BE故答案为234.【点睛】本题主要考查全等三角形的性质、勾股定理、等边三角形的判定与性质以及三点共线的判定，运用旋转构造全等三角形是解题的关键.3．如图，在△ABC中，AB=AC，点D是BC的中点，点E是△ABC内一点，若∠AEB=∠CED=90°，AE=BE，CE=DE=2，则图中阴影部分的面积等于__________．【答案】4【解析】【分析】作DG⊥BE于G，CF⊥AE于F，可证△DEG≌△CEF，可得DG=CF，则是S△BDE=S△AEC，由D 是BC中点可得S△BED=2，即可求得阴影部分面积.【详解】作DG⊥BE于G，CF⊥AE于F，∴∠DGE=∠CFE=90°，∵∠AEB=∠DEC=90°，∴∠GED+∠DEF=90°，∠DEF+∠CEF=90°，∴∠GED=∠CEF，又∵DE=EC，∴△GDE≌△FCE，∴DG=CF，∵S △BED =12BE•DG ，S △BED =12AE•CF ，AE=BE ， ∴S △BED =S △BED ，∵D 是BC 的中点， ∴S △BDE =S △EDC =1222⨯⨯=2， ∴S 阴影=2+2=4，故答案为4.【点睛】本题考查了全等三角形的判定与性质，正确添加辅助线构造全等三角形是解题的关键.4．在△ABC 和△DEF 中，AC=DF ，BC=EF ，∠B=∠E ，且∠B 、∠E 都是锐角，∠C ＜90°，若∠B 满足条件：______________，则△ABC ≌△DEF ．【答案】∠B≥∠A ．【解析】【分析】虽然题目中∠B 为锐角,但是需要对∠B 进行分类探究会理解更深入：可按“∠B 是直角、钝角、锐角”三种情况进行，最后得出∠B 、∠E 都是锐角时两三角形全等的条件．【详解】解：需分三种情况讨论：第一种情况：当∠B 是直角时：如图①，在△ABC 和△DEF ，AC=DF ，BC=EF ，∠B=∠E=90°，可知：△ABC 与△DEF 一定全等，依据的判定方法是HL ；第二种情况：当∠B 是钝角时：如图②，过点C 作CG ⊥AB 交AB 的延长线于G ，过点F 作DH ⊥DE 交DE 的延长线于H ．∵∠B=∠E ，且∠B 、∠E 都是钝角．∴180°-∠B=180°-∠E ，即∠CBG=∠FEH ．在△CBG 和△FEH 中，CBG FEH G HBC EF ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△CBG ≌△FEH （AAS ），∴CG=FH ，在Rt △ACG 和Rt △DFH 中，AC DF CG FH⎧⎨⎩＝，＝ ∴Rt △ACG ≌Rt △DFH （HL ），∴∠A=∠D ，在△ABC 和△DEF 中，A DB EAC DF ∠∠⎧⎪∠∠⎨⎪⎩＝＝，＝∴△ABC ≌△DEF （AAS ）；第三种情况：当∠B 是锐角时：在△ABC 和△DEF 中，AC=DF ，BC=EF ，∠B=∠E ，且∠B 、∠E 都是锐角，小明在△ABC 中（如图③）以点C 为圆心，以AC 长为半径画弧交AB 于点D ，假设E 与B 重合，F 与C 重合，得到△DEF 与△ABC 符号已知条件，但是△AEF 与△ABC 一定不全等，所以有两边和其中一边的对角对应相等的两个三角形不一定全等；由图③可知，∠A=∠CDA=∠B+∠BCD ，∴∠A ＞∠B ，∴当∠B≥∠A 时，△ABC 就唯一确定了，则△ABC ≌△DEF ．故答案为：∠B≥∠A ．【点睛】本题是三角形综合题，考查全等三角形的判定与性质，应用与设计作图，熟练掌握三角形全等的判定方法是解题的关键．5．如图，CA ⊥AB ，垂足为点A ，射线BM ⊥AB ，垂足为点B ，AB=12cm ，AC=6cm ．动点E 从A 点出发以3cm/s 沿射线AN 运动，动点D 在射线BM 上，随着E 点运动而运动，始终保持ED=CB ．当点E 经过______s 时，△DEB 与△BCA 全等．【答案】0、2、6、8【解析】∵CA⊥AB，垂足为点A，射线BM⊥AB，垂足为点B，∴∠CAB=∠DBE=90°，∴△CAB和△EBD都是Rt△，∵点E运动过程中两三角形始终保持斜边ED=CB，∴当BE=BA=12cm或BE=AC=6cm时，两三角形全等，如图共有四种情形，此时AE分别等于0cm、6cm、18cm、24cm，又∵点E每秒钟移动3cm，∴当点E移动的时间分别为0秒、2秒、6秒和8秒时，两三角形全等.6．如图，在四边形ABCD中，∠DAB=∠DCB=90°，CB=CD，AC=6，则四边形ABCD的面积是_________.【答案】18．【解析】【分析】根据已知线段关系，将△ACD绕点C逆时针旋转90°，CD与CB重合，得到△CBE，证明A、B、E三点共线，则△ACE是等腰直角三角形，四边形面积转化为△ACE面积．【详解】∵CD=CB，且∠DCB=90°，∴将△ACD绕点C逆时针旋转90°，CD与CB重合，得到△CBE，∴∠CBE=∠D，AC=EC，∠DCA=∠BCE．根据四边形内角和360°，可得∠D+∠ABC=180°，∴∠CBE+∠ABC=180°，∴A、B、E三点共线，∴△ACE是等腰直角三角形，∴四边形ABCD面积=△ACE面积= 12AC2=18．故答案为：18．【点睛】本题考查了旋转的性质以及转化思想，解决这类问题要结合已知线段间的数量关系和位置关系进行旋转，使不规则图形转化为规则图形．7．如图，在ABC中，ACB90,CA CB∠==.点D在AB上，点F在CA的延长线上，连接FD并延长交BC于点E，若∠BED=2∠ADC，AF=2，DF=7，则ABC的面积为______．【答案】25 2【解析】【分析】作CD的垂直平分线交AD于M，交CD与N，根据垂直平分线的性质可得MC=MD，进而可得∠MDC=∠MCD，根据已知及外角性质可得∠AMC=∠BED，由等腰直角三角形的性质可得∠B=∠CAB=45°，根据三角形内角和定理可得∠ACM=∠BDE，进而可证明∠ADF=∠ACM，进而即可证明∠FCD=∠FDC，根据等腰三角形的性质可得CF=DF，根据已知可求出AC的长，根据三角形面积公式即可得答案.【详解】作CD的垂直平分线交AD于M，交CD与N，∵MN是CD的垂直平分线，∴MC=MD，∴∠MDC=∠MCD，∵∠AMC=∠MDC=∠MCD，∴∠AMC=2∠ADC，∵∠BED=2∠ADC，∴∠AMC=∠BED，∵∠ACB=90°，AC=BC，∴∠B=∠CAB=45°，∵∠ACM=180°-∠CAM-∠AMC，∠BDE=180°-∠B-∠BED，∴∠ACM=∠BDE，∵∠BDE=∠ADF，∴∠ADF=∠ACM，∴∠ADF+∠ADC=∠ACM+∠MCD，即∠FCD=∠FDC，∴FC=FD，∵AF=2，FD=7，∴AC=FC-AF=7-2=5，∴S△ABC=12×5×5=252.故答案为：25 2【点睛】本题考查了等腰三角形的判定与性质及线段垂直平分线的性质，线段垂直平分线上的点，到线段两端的距离相等；等腰三角形的两个底角相等；熟练掌握相关的定理及性质是解题关键.8．已知△ABC中，AB=BC≠AC，作与△ABC只有一条公共边，且与△ABC全等的三角形，这样的三角形一共能作出_____个．【答案】7【解析】只要满足三边对应相等就能保证作出的三角形与原三角形全等，以腰为公共边时有6个，以底为公共边时有一个，答案可得．解：以AB为公共边有三个，以CB为公共边有三个，以AC为公共边有一个，所以一共能作出7个．故答案为79．如图，已知AC平分∠DAB，CE⊥AB于点E，AB=AD+2BE，则下列结论：①AB+AD= 2AE；②∠DAB+∠DCB=180°；③CD=CB；④S ACE﹣S BCE=S ACD．其中正确的是______．【答案】①②③④．【解析】【分析】【详解】①在AE取点F，使EF＝BE，连接CF．∵AB＝AD＋2BE＝AF＋EF＋BE，EF＝BE，∴AB＝AD＋2BE＝AF＋2BE，∴AD＝AF，∴AB＋AD＝AF＋EF＋BE＋AD＝2AF＋2EF＝2(AF＋EF)＝2AE，∴AB+AD= 2AE，故①正确；②在AB上取点F，使EF＝BE，连接CF．在△ACD与△ACF中，∵AD＝AF，∠DAC＝∠FAC，AC＝AC，∴△ACD≌△ACF，∴∠ADC＝∠AFC．∵CE垂直平分BF，∴CF＝CB，∴∠CFB＝∠B．又∵∠AFC＋∠CFB＝180°，∴∠ADC＋∠B＝180°，∴∠DAB+∠DCB=180°故②正确；③由②知，△ACD≌△ACF，∴CD＝CF，又∵CF＝CB，∴CD＝CB，故③正确；④易证△CEF≌△CEB，∴S△ACE﹣S△BCE＝S△ACE﹣S△FCE＝S△ACF，又∵△ACD≌△ACF，∴S△ACF＝S△ADC，∴S△ACE﹣2S△BCE＝S△ADC，故④正确．综上所述，正确的结论是①②③④，故答案为①②③④．10．如图，在△ABC中，AB=AC＝10，BC＝12，AD是角平分线，P、Q分别是AD、AB边上的动点，则BP＋PQ的最小值为_______．【答案】9.6【解析】∵AB=AC，AD是角平分线，∴AD⊥BC，BD=CD，∴B点，C点关于AD对称，如图，过C作CQ⊥AB于Q，交AD于P，则CQ=BP+PQ的最小值，根据勾股定理得，AD=8，利用等面积法得：AB⋅CQ=BC⋅AD，∴CQ=BC ADAB⋅=12810⨯=9.6故答案为：9.6.点睛：此题是轴对称-最短路径问题，主要考查了角平分线的性质，对称的性质，勾股定理，等面积法，用等面积法求出CQ是解本题的关键.二、八年级数学全等三角形选择题（难）11．如图，四边形ABCD中，∠A、∠B、∠C、∠D的角平分线恰相交于一点P，记△APD、△APB、△BPC、△DPC的面积分别为S1、S2、S3、S4，则有（）A ．1324S S S S +=+B ．1234S S S S +=+C ．1423S S S S +=+D ．13S S =【答案】A【解析】【分析】作辅助线,利用角平分线性质定理,明确8个三角形中面积两两相等即可解题.【详解】四边形ABCD,四个内角平分线交于一点P,即点p 到四边形各边距离相等,（角平分线性质定理）,如下图,可将四边形分成8个三角形,面积分别是a 、a 、b 、b 、c 、c 、d 、d,则S 1=a+d, S 2=a+b, S 3=b+c, S 4=c+d,∴S 1+S 3=a+b+c+d= S 2+S 4故选A【点睛】本题考查了角平分线性质定理,作高线和理解角平分线性质定理是解题关键.12．如图，在△ABC 中，P 、Q 分别是BC 、AC 上的点，作PR ⊥AB ，PS ⊥AC ，垂足分别为R 、S ，若AQ =PQ ，PR =PS ，则下列四个结论：①PA 平分∠BAC ；②AS =AR ；③QP ∥AR ；④△BRP ≌△CSP ，其中结论正确的的序号为（）A ．①②③B ．①②④C ．②③④D ．①②③④【答案】A【解析】【分析】根据角平分线性质即可推出②，根据勾股定理即可推出AR =AS ，根据等腰三角形性质推出∠QAP=∠QPA，推出∠QPA=∠BAP，根据平行线判定推出QP∥AB即可；没有条件证明△BRP≌△QSP．【详解】试题分析：解：∵PR⊥AB，PS⊥AC，PR=PS，∴点P在∠A的平分线上，∠ARP=∠ASP=90°，∴∠SAP=∠RAP，在Rt△ARP和Rt△ASP中，由勾股定理得：AR2=AP2﹣PR2，AS2=AP2﹣PS2，∵AP=AP，PR=PS，∴AR=AS，∴②正确；∵AQ=QP，∴∠QAP=∠QPA，∵∠QAP=∠BAP，∴∠QPA=∠BAP，∴QP∥AR，∴③正确；没有条件可证明△BRP≌△QSP，∴④错误；连接RS，∵PR=PS，∵PR⊥AB，PS⊥AC，∴点P在∠BAC的角平分线上，∴PA平分∠BAC，∴①正确．故答案为①②③．故选A.点睛：本题考查了等边三角形的性质和判定，全等三角形的性质和判定，平行线的性质和判定，角平分线性质的应用，熟练掌握全等三角形的判定和性质是解题的关键．13．如图, AB=AC，AD=AE， BE、CD交于点O，则图中全等三角形共有（）A．五对B．四对C．三对D．二对【答案】A【解析】如图，由已知条件可证：①△ABE≌△ACD；②△DBC≌△ECB；③△BDO≌△ECO；④△ABO≌△ACO；⑤△ADO≌△AEO；∴图中共有5对全等三角形.故选A.14．下列条件中，不能判定两个直角三角形全等的是( )A．两条直角边对应相等B．有两条边对应相等C．斜边和一锐角对应相等D．一条直角边和斜边对应相等【答案】B【解析】根据全等三角形的判定SAS，可知两条直角边对应相等的两个直角三角形全等，故A不正确；根据一条直角边和斜边对应相等的两个直角三角形，符合全等三角形的判定定理HL，能判定全等；若两条直角边对应相等的两个直角三角形，符合全等三角形的判定定理SAS，也能判全等，但是有两边对应相等，没说明是什么边对应，故不能判定，故B正确．根据全等三角形的判定AAS，可知斜边和一锐角对应相等的两直角三角形全等，故C不正确；根据直角三角形的判定HL，可知一条直角边和斜边对应相等两直角三角形全等，故D不正确.故选B.点睛：此题主要考查了直角三角形全等的判定，解题时利用三角形全等的判定SSS，SAS，ASA，AAS，HL，直接判断即可.15．在△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB于点E，AB=18cm，则△DBE的周长为（）A．16cm B．8cm C．18cm D．10cm【答案】C【解析】因为∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB，易证△ACD≌△AED，所以AE=AC=BC，ED=CD.△DBE的周长=BE+DE+DB=BE+CD+DB=BE+BC=BE+AE=AB.因为AB=12，所以△DBE的周长=12.故选C.点睛：本题主要考查了全等三角形的判定的性质及角平分线的性质定理，角的平分线上的点到角的两边的距离相等，运用这个性质，结合等腰三角形有性质，将△DBE的周长转化为AB的长.16．如图所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是（）A．1+2B．1+22C．2-2D．2-1【答案】B 【解析】第一次折叠后，等腰三角形的底边长为1，腰长为22；第一次折叠后，等腰三角形的底边长为22，腰长为12，所以周长为112212222++=+.故答案为B.17．如图，将一个等腰Rt△ABC对折，使∠A与∠B重合，展开后得折痕CD，再将∠A折叠，使C落在AB上的点F处，展开后，折痕AE交CD于点P，连接PF、EF，下列结论：①tan∠CAE=2﹣1；②图中共有4对全等三角形；③若将△PEF沿PF翻折，则点E一定落在AB上；④PC=EC；⑤S四边形DFEP=S△APF．正确的个数是（）A．1个B．2个C．3个D．4个【答案】D【解析】【详解】①正确．作EM∥AB交AC于M．∵CA=CB，∠ACB=90°，∴∠CAB=∠CBA=45°，∵∠CAE=∠BAE=12∠CAB=22.5°，∴∠MEA=∠EAB=22.5°，∴∠CME=45°=∠CEM，设CM=CE=a，则2，∴tan ∠CAE=212CE AC a a==-+，故①正确， ②正确．△CDA ≌△CDB ，△AEC ≌△AEF ，△APC ≌△APF ，△PEC ≌△PEF ，故②正确， ③正确．∵△PEC ≌△PEF ，∴∠PCE=∠PFE=45°，∵∠EFA=∠ACE=90°，∴∠PFA=∠PFE=45°，∴若将△PEF 沿PF 翻折，则点E 一定落在AB 上，故③正确．④正确．∵∠CPE=∠CAE+∠ACP=67.5°，∠CEP=90°﹣∠CAE=67.5°，∴∠CPE=∠CEP ，∴CP=CE ，故④正确，⑤错误．∵△APC ≌△APF ，∴S △APC =S △APF ，假设S △APF =S 四边形DFPE ，则S △APC =S 四边形DFPE ，∴S △ACD =S △AEF ，∵S △ACD =12S △ABC ，S △AEF =S △AEC ≠12S △ABC ， ∴矛盾，假设不成立．故⑤错误． .故选D.18．如图，在Rt △ABC 中，AB AC =，D 、E 是斜边BC 上两点，且∠DAE =45°，将△ADC 绕点A 顺时针旋转90︒后，得到△AFB ，连接EF .列结论：①△ADC ≌△AFB ；②△ABE ≌△ACD ；③△AED ≌△AEF ；④BE DC DE += 其中正确的是( )A ．②④B ．①④C ．②③D ．①③【答案】D【解析】解：∵将△ADC 绕点A 顺时针旋转90︒后，得到△AFB ，∴△ADC ≌△AFB ，故①正确；②无法证明，故②错误；③∵△ADC ≌△AFB ，∴AF =AD ，∠FAB =∠DAC ．∵∠DAE =45°，∴∠BAE +∠DAC =45°，∠FA E =∠DAE =45°．在△FAE 和△DAE 中，∵AF =AD ，∠FAE =∠DAE ，AE =AE ，∴△FAE ≌△DAE ，故③正确；④∵△ADC ≌△AFB ，∴DC =BF ，∵△FAE ≌△DAE ，∴EF =ED ，∵BF +BE ＞EF ，∴DC +BE ＞ED ．故④错误．故选D ．19．如图，Rt ACB 中，90ACB ︒∠=，ABC 的角平分线AD 、BE 相交于点P ，过P 作PF AD ⊥交BC 的延长线于点F ，交AC 于点H ，则下列结论：①135APB ︒∠=；②PF PA =；③AH BD AB +=；④S 四边形23ABDE S ABP =，其中正确的个数是（）A ．4B ．3C ．2D ．1【答案】B【解析】【分析】根据三角形全等的判定和性质以及三角形内角和定理逐一分析判断即可．【详解】解：∵在△ABC 中，∠ACB=90°，∴∠CAB+∠ABC=90°∵AD 、BE 分别平分∠BAC 、∠ABC ，∴∠BAD=12CAB ∠，∠ABE=12ABC ∠ ∴∠BAD+∠ABE=111+=()45222CAB ABC CAB ABC ∠∠∠+∠=︒ ∴∠APB=180°-（∠BAD+∠ABE ）=135°，故①正确；∴∠BPD=45°，又∵PF ⊥AD ，∴∠FPB=90°+45°=135°∴∠APB=∠FPB又∵∠ABP=∠FBPBP=BP∴△ABP ≌△FBP （ASA ）∴∠BAP=∠BFP ，AB=AB ，PA=PF ，故②正确；在△APH 与△FPD 中∵∠APH=∠FPD=90°∠PAH=∠BAP=∠BFPPA=PF∴△APH ≌△FPD （ASA ），∴AH=FD ，又∵AB=FB∴AB=FD+BD=AH+BD ，故③正确；连接HD ，ED ，∵△APH ≌△FPD ，△ABP ≌△FBP∴APH FPD S S =，ABP FBP S S =，PH=PD ，∵∠HPD=90°，∴∠HDP=∠DHP=45°=∠BPD∴HD ∥EP ，∴EPH EPD S S =∵ABP BDP AEP EPD ABDE S S SS S =+++四边形 ()ABP AEP EPHPBD S S S S =+++ ABP APH PBDS S S =++ ABP FPD PBD SS S =++ ABP FBP S S =+2ABP S =故④错误，∴正确的有①②③，故答案为：B ．【点睛】本题考查了三角形全等的判定方法，判定两个三角形全等的方法有：SSS 、SAS 、AAS 、ASA 、HL ，注意AAA 和SAS 不能判定两个三角形全等．20．已知等边△ABC中，在射线BA上有一点D，连接CD，并以CD为边向上作等边△CDE，连接BE和AE，试判断下列结论：①AE=BD；②AE与AB所夹锐夹角为60°；③当D在线段AB或BA延长线上时，总有∠BDE-∠AED=2∠BDC；④∠BCD=90°时，CE2+AD2=AC2+DE2，正确的序号有（）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°，∠ACE=∠ACD+60°可得∠BCD=∠ACE，利用SAS可证明△BCD≌△ACE，可得AE=BD，①正确；∠CBD=∠CAE=60°，进而可得∠EAD=60°，②正确，当∠BCD=90°时，可得∠ACD=∠ADC=30°，可得AD=AC，即可得CE2+AD2=AC2+DE2，④正确；当D点在BA延长线上时，∠BDE-∠BDC=60°，根据△BCD≌△ACE可得∠AEC=∠BDC，进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，即可证明∠BDE-∠BDC=∠BDC+∠AED，即∠BDE-∠AED=2∠BDC，当点D在AB上时可证明∠BDE-∠AED=120°，③错误，综上即可得答案.【详解】∵∠BCA=∠DCE=60°，∴∠BCA+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，又∵AC=BC，CE=CD，∴△BCD≌△ACE，∴AE=BD，∠CBA=∠CAE=60°，∠AEC=∠BDC，①正确，∴∠BAE=120°，∴∠EAD=60°，②正确，∵∠BCD=90°，∠BCA=60°，∴∠ACD=∠ADC=30°，∴AC=AD，∵CE=DE，∴CE2+AD2=AC2+DE2，④正确，当D点在BA延长线上时，∠BDE-∠BDC=60°，∵∠AEC=∠BDC ，∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC ，如图，当点D 在AB 上时，∵△BCD ≌△∠ACE ，∴∠CAE=∠CBD=60°，∴∠DAE=∠BAC+∠CAE=120°，∴∠BDE-∠AED=∠DAE=120°，③错误故正确的结论有①②④，故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握21．如图，已知在正方形ABCD 中，点E F 、分别在BC CD 、上，△AEF 是等边三角形，连接AC 交EF 于G ，给出下列结论：①BE DF =； ② 15DAF ∠=;③AC 垂直平分EF ; ④BE DF EF +=．其中结论正确的共有( )．A ．1个B ．2个C ．3个D ．4个【答案】C【解析】试题分析：四边形ABCD 是正方形，∴AB=BC=CD=AD ，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．∴Rt△ABE≌Rt△ADF（HL），∴BE=DF （故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x．（故④错误）．∴综上所述，正确的有3个．考点：正方形的性质；全等三角形的判定与性质；线段垂直平分线的性质；等边三角形的性质．22．如图，与都是等边三角形，，下列结论中，正确的个数是( )①；②；③；④若，且，则．A．1 B．2 C．3 D．4【答案】C【解析】【分析】利用全等三角形的判定和性质一一判断即可.【详解】解：∵与都是等边三角形∴AD=AB,AC=AE,∠DAB=∠EAC=60°∴∠DAB+∠BAC=∠EAC +∠BAC即∠DAC=∠EAB∴∴，①正确；∵∴∠ADO=∠ABO∴∠BOD=∠DAB=60°，②正确∵∠BDA=∠CEA=60°，∠ADC≠∠AEB∴∠BDA-∠ADC≠∠CEA-∠AEB∴,③错误∵∴∠DAC+∠BCA=180°∵∠DAB=60°，∴∠BCA=180°-∠DAB-∠BAC=30°∵∠ACE=60°∴∠BCE=∠ACE+∠BCA=60°+30°=90°∴④正确故由①②④三个正确，故选：C【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、角平分线的判定定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．23．如图，Rt△ACB中，∠ACB=90°，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB=135°；②BF=BA；③PH=PD；④连接CP，CP平分∠ACB，其中正确的是（）A．①②③B．①②④C．①③④D．①②③④【答案】D【解析】分析：根据三角形内角和定理以及角平分线定义判断①；根据全等三角形的判定和性质判断②③；根据角平分线的判定与性质判断④．详解：在△ABC中，∵∠ACB=90°，∴∠BAC+∠ABC=90°，又∵AD、BE分别平分∠BAC、∠ABC，∴∠BAD+∠ABE=（∠BAC+∠ABC）=45°，∴∠APB=135°，故①正确．∴∠BPD=45°，又∵PF⊥AD，∴∠FPB=90°+45°=135°，∴∠APB=∠FPB，又∵∠ABP=∠FBP，BP=BP，∴△ABP≌△FBP，∴∠BAP=∠BFP，AB=FB，PA=PF，故②正确．在△APH和△FPD中，∵∠APH=∠FPD=90°，∠PAH=∠BAP=∠BFP，PA=PF，∴△APH≌△FPD，∴PH=PD，故③正确．∵△ABC的角平分线AD、BE相交于点P，∴点P到AB、AC的距离相等，点P到AB、BC的距离相等，∴点P到BC、AC的距离相等，∴点P在∠ACB的平分线上，∴CP平分∠ACB，故④正确．故选D．点睛：本题考查了角平分线的判定与性质，三角形全等的判定方法，三角形内角和定理．掌握相关性质是解题的关键．24．如图，点B，F，C，E在同一条直线上，点A，D在直线BE的两侧，AB∥DE，BF＝CE，添加一个适当的条件后，仍不能使得△ABC≌△DEF（）A．AC＝DF B．AC∥DF C．∠A＝∠D D．AB＝DE【答案】A【解析】【分析】根据AB∥DE证得∠B＝∠E，又已知BF＝CE证得BC＝EF，即已具备两个条件：一边一角，再依次添加选项中的条件即可判断.【详解】∵AB∥DE，∴∠B＝∠E，∵BF＝CE，∴BF+FC＝CE+FC，∴BC＝EF，若添加AC＝DF，则不能判定△ABC≌△DEF，故选项A符合题意；若添加AC∥DF，则∠ACB＝∠DFE，可以判断△ABC≌△DEF（ASA），故选项B不符合题意；若添加∠A ＝∠D ，可以判断△ABC ≌△DEF （AAS ），故选项C 不符合题意；若添加AB ＝DE ，可以判断△ABC ≌△DEF （SAS ），故选项D 不符合题意；故选：A ．【点睛】此题考查三角形全等的判定定理，熟练掌握定理，并能通过定理去判断条件是否符合全等是解决此题的关键.25．如图，AD 是ABC 的角平分线，DE AC ⊥；垂足为,//E BF AC 交ED 的延长线于点F ，若BC 恰好平分ABF ∠．给出下列三个结论：①DE DF =；②DB DC =；③AD BC ⊥．其中正确的结论共有（）个A ．0B ．1C ．2D ．3【答案】D【解析】【分析】由BF ∥AC ，AD 是ABC 的角平分线，BC 平分ABF ∠得∠ADB=90︒；利用AD 平分∠CAB 证得△ADC ≌△ADB 即可证得DB=DC ；根据DE AC ⊥证明△CDE ≌△BDF 得到DE DF =.【详解】∵DE AC ⊥,BF ∥AC,∴EF ⊥BF ，∠CAB+∠ABF=180︒，∴∠CED=∠F=90︒，∵AD 是ABC 的角平分线，BC 平分ABF ∠，∴∠DAB+∠DBA=12(∠CAB+∠ABF)=90︒， ∴∠ADB=90︒，即AD BC ⊥，③正确； ∴∠ADC=∠ADB=90︒，∵AD 平分∠CAB,∴∠CAD=∠BAD,∵AD=AD,∴△ADC≌△ADB,∴DB=DC，②正确；又∵∠CDE=∠BDF，∠CED=∠F，∴△CDE≌△BDF,∴DE=DF，①正确；故选：D.【点睛】此题考查平行线的性质，三角形全等的判定及性质，角平分线的定义.26．已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动，设点P的运动时间为t秒，当t的值为_____秒时，△ABP和△DCE全等．A．1 B．1或3 C．1或7 D．3或7【答案】C【解析】【分析】分两种情况进行讨论，根据题意得出BP=2t=2和AP=16-2t=2即可求得．【详解】解：因为AB=CD，若∠ABP=∠DCE=90°，BP=CE=2，根据SAS证得△ABP≌△DCE，由题意得：BP=2t=2，所以t=1，因为AB=CD，若∠BAP=∠DCE=90°，AP=CE=2，根据SAS证得△BAP≌△DCE，由题意得：AP=16-2t=2，解得t=7．所以，当t的值为1或7秒时．△ABP和△DCE全等．故选C．【点睛】本题考查全等三角形的判定，判定方法有：ASA，SAS，AAS，SSS，HL．27．如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：①△PFA≌△PEB，②EF=AP，③△PEF是等腰直角三角形，④当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），S四边形AEPF=12S△ABC，上述结论中始终正确有（）A．1个B．2个C．3个D．4个【答案】C【解析】∵AB=AC，∠BAC=90°，P是BC中点，∴AP⊥BC，AP=PB，∠B=∠CAP=45°，∵∠APF+∠FPA=90°，∠ APF+∠BPE=90°，∴∠APF=∠BPE，在△BPE和△APF中，∠B=∠CAP， BP=AP，∠BPE =∠APF，∴△PFA≌△PEB；故①正确；∵△ABC是等腰直角三角形点P是BC的中点，∴AP=12 BC，又∵EF不一定是△ABC的中位线，∴EF≠AP，故结论②错误；∵△PFA≌△PEB，∴PE=PF，又∵∠EPF=90°，∴△PEF是等腰直角三角形，故③正确；∵△PFA≌△PEB，∴S△PFA =S△PEB，∴S四边形AEPF=S△APE+S△APF=S△APE+S△BPE=S△APB=12S△ABC，故结论④正确；综上，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），始终正确的有3个结论.故选：C.点睛：本题意旋转为背景考查了全等三角形的判定和性质，解题时需要运用等腰直角三角形的判定和性质，综合性较强，根据题意得出△PFA≌△PEB是解答此题的关键.28．如图，在△ABC中，AB=AC，高BD，CE交于点O，AO交BC于点F，则图中共有全等三角形（）A ．8对B ．7对C ．6对D ．5对【答案】B【解析】【分析】易证△ABC 是关于AF 对称的图形，其中的小三角形也关于AF 对称，共可找出7对三角形.【详解】全等的三角形有：①△AFB≌△AFC；②△CEB≌△BDC；③△AEO≌△ADO；④△EOB≌△DOC；⑤△OBF≌△OFC；⑥△AOB≌△AOC；⑦△AEC≌△ADB证明①△AFB≌△AFC∵AB=AC，CE⊥AB，BD⊥AC 又∵1122ABC S AB CE AC BD == ∴CE=BD∴在Rt△BCE 和Rt△CBD 中BC BC CE BD=⎧⎨=⎩ ∴△BCE≌△CBD∴BE=CD，∴AE=AD在Rt△AEO 和Rt△ADO 中AE AD AO AO =⎧⎨=⎩∴△AEO≌△ADO∴∠EOD=∠DOA在△BAF 和△CAF 中AB AC BAF CAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△BAF≌△CAF，得证其余全等证明过程类似故选：B【点睛】本题考查全等的证明，解题关键是利用等腰三角形的性质，推导出图形中边的关系，为证全等作准备29．如图所示，OP 平分AOB ∠，PA OA ⊥，PB OB ⊥，垂足分别为A 、B ．下列结论中不一定成立的是（）．A ．PA PB =B ．PO 平分APB ∠C ．OA OB =D ．AB 垂直平分OP【答案】D【解析】【分析】根据角平分线上的点到角的两边距离相等可得出PA=PB ，再利用“HL ”证明△AOP 和△BOP 全等，可得出APO BPO ∠=∠，OA=OB ，即可得出答案．【详解】解：∵OP 平分AOB ∠，PA OA ⊥，PB OB ⊥∴PA PB =，选项A 正确；在△AOP 和△BOP 中，PO PO PA PB =⎧⎨=⎩， ∴AOP BOP ≅∴APO BPO ∠=∠，OA=OB ，选项B ，C 正确；由等腰三角形三线合一的性质，OP 垂直平分AB ，AB 不一定垂直平分OP ，选项D 错误．故选：D ．【点睛】本题考查的知识点是角平分线的性质以及垂直平分线的性质，熟记性质定理是解此题的关键．30．如图，AB ＝AC ，BD ⊥AC 于D ，CE ⊥AB 于E ，BD 、CE 交于O ，连结AO ，则图中共有全等三角形的对数为（）A ．2对B ．3对C ．4对D ．5对【答案】C【解析】【分析】先根据条件，利用AAS可知△ADB≌△AEC，然后再利用HL、ASA即可判断△AOE≌△AOD，△BOE≌△COD，△AOC≌△AOB.【详解】∵AB=AC，BD⊥AC于D，CE⊥AB于E，∴∠ADB=∠AEC=90°，∵∠A为公共角，∴△ADB≌△AEC，（AAS）∴AE=AD，∠B=∠C∴BE=CD，∵AE=AD，OA=OA，∠ADB=∠AEC=90°，∴△AOE≌△AOD（HL），∴∠OAC=∠OAB，∵∠B=∠C，AB=AC，∠OAC=∠OAB，∴△AOC≌△AOB.（ASA）∵∠B=∠C，BE=CD，∠ODC=∠OEB=90°，∴△BOE≌△COD（ASA）．综上：共有4对全等三角形，故选C.【点睛】本题考查三角形全等的判定方法和全等三角形的性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．做题时要从已知条件开始结合全等的判定方法逐一验证，由易到难，不重不漏．。

成都石室联合中学金沙校区数学三角形填空选择单元测试与练习(word解析版)

成都石室联合中学金沙校区数学三角形填空选择单元测试与练习（word 解析版）一、八年级数学三角形填空题（难）1．如图，在△ABC 中，∠C =90°，BC =8cm ，AC =6cm ，点E 是BC 的中点，动点P 从A 点出发，先以每秒2cm 的速度沿A →C 运动，然后以1cm /s 的速度沿C →B 运动．若设点P 运动的时间是t 秒，那么当t =___________________，△APE 的面积等于6．【答案】1.5或5或9【解析】【分析】分为两种情况讨论：当点P 在AC 上时：当点P 在BC 上时，根据三角形的面积公式建立方程求出其解即可．【详解】如图1，当点P 在AC 上．∵△ABC 中，∠C =90°，BC =8cm ，AC =6cm ，点E 是BC 的中点，∴CE =4，AP =2t ．∵△APE 的面积等于6，∴S △APE =12AP •CE =12AP ×4=6．∵AP =3，∴t =1.5．如图2，当点P 在BC 上．则t ＞3∵E 是DC 的中点，∴BE =CE =4． ∵PE ()43=7-PE t t =-- ，∴S =12EP •AC =12•EP ×6=6，∴EP =2，∴t =5或t =9．总上所述，当t =1.5或5或9时，△APE 的面积会等于6．故答案为1.5或5或9．【点睛】本题考查了直角三角形的性质的运用，三角形的面积公式的运用，解答时灵活运用三角形的面积公式求解是关键．2．如图，ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D ，点,E F 分别在线段BD 、CD 上，点G 在EF 的延长线上，EFD ∆与EFH ∆关于直线EF 对称，若60,84,A BEH HFG n ︒︒︒∠=∠=∠=，则n =__________.【答案】78.【解析】【分析】利用ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D 得到∠DBC=12∠ABC ，∠ACD=12(∠A+∠ABC)，根据三角形的内角和得到∠D=12∠A=30︒，利用外角定理得到∠DEH=96︒，由EFD ∆与EFH ∆关于直线EF 对称得到∠DEG=∠HEG=48︒，根据外角定理即可得到∠DFG=∠D+∠DEG=78︒.【详解】∵ABC ∆的ABC ∠的平分线与ACB ∠的外角平分线相交于点D∴∠DBC=12∠ABC ，∠ACD=12(∠A+∠ABC)， ∵∠DBC+∠BCD+∠D=180︒，∠A+∠ABC+∠ACB=180︒， ∴∠D=12∠A=30︒， ∵84BEH ︒∠=,∴∠DEH=96︒,∵EFD ∆与EFH ∆关于直线EF 对称，∴∠DEG=∠HEG=48︒，∠DFG=∠HFG n ︒=,∵∠DFG=∠D+∠DEG=78︒，∴n=78.故答案为：78.【点睛】此题考查三角形的内角和定理、外角定理，角平分线性质，轴对称图形的性质，此题中求出∠D=12∠A=30︒是解题的关键.3．如图，AB ∥CD ，点P 为CD 上一点，∠EBA 、∠EPC 的角平分线于点F ，已知∠F ＝40°，则∠E ＝_____度．【答案】80【解析】【详解】如图，根据角平分线的性质和平行线的性质，可知∠FMA=12∠CPE=∠F+∠1，∠ANE=∠E+2∠1=∠CPE=2∠FMA，即∠E=2∠F=2×40°=80°.故答案为80.4．如图，将一副直角三角板，按如图所示叠放在一起，则图中∠COB=____．【答案】105°．【解析】【分析】先根据直角三角形的特殊角可知：∠ECD=45°，∠BDC=60°，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【详解】如图，∠ECD=45°，∠BDC=60°，∴∠COB=∠ECD+∠BDC=45°+60°=105°．故答案为：105°．【点睛】此题考查三角形外角的性质，掌握三角形的一个外角等于与它不相邻的两个内角的和的性质是解题的关键．5．已知ABC 中，90A ∠=，角平分线BE 、CF 交于点O ，则BOC ∠= ______ ．【答案】135【解析】解：∵∠A =90°，∴∠ABC +∠ACB =90°，∵角平分线BE 、CF 交于点O ，∴∠OBC +∠OCB =45°，∴∠BOC =180°﹣45°=135°．故答案为：135°．点睛：本题考查了角平分线的定义、三角形的内角和定理：三角形的内角和等于180°．6．已知一个多边形的内角和与外角和的差是1260°，则这个多边形边数是．【答案】12【解析】试题解析：根据题意，得（n-2）•180-360=1260，解得：n=11．那么这个多边形是十一边形．考点：多边形内角与外角．7．如图，李明从A 点出发沿直线前进5米到达B 点后向左旋转的角度为α，再沿直线前进5米，到达点C 后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了45米，则每次旋转的角度α为_____．【答案】40︒．【解析】【分析】根据共走了45米，每次前进5米且左转的角度相同，则可计算出该正多边形的边数，再根据外角和计算左转的角度．【详解】连续左转后形成的正多边形边数为：4559÷=，则左转的角度是360940︒÷=︒．故答案是：40︒．【点睛】本题考查了多边形的外角计算，正确理解多边形的外角和是360°是关键．8．三角形的三个内角度数比为1：2：3，则三个外角的度数比为_____．【答案】5:4:3【解析】试题解析：设此三角形三个内角的比为x ，2x ，3x ，则x+2x+3x=180，6x=180，x=30，∴三个内角分别为30°、60°、90°，相应的三个外角分别为150°、120°、90°，则三个外角的度数比为：150°：120°：90°=5：4：3，故答案为5：4：3．9．将直角三角形（ACB ∠为直角）沿线段CD 折叠使B 落在B '处，若50ACB '︒∠=，则ACD ∠度数为________.【答案】20°.【解析】【分析】根据翻折的性质可知：∠BCD=∠B′CD ，又∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°，继而即可求出∠BCD 的值，又∠ACD+∠BCD=∠ACB=90°，继而即可求出∠ACD 的度数．【详解】解：∵△B′CD 时由△BCD 翻折得到的，∴∠BCD=∠B′CD，又∵∠BCD+∠B′CD=∠B′CB=∠ACB+∠ACB′=90°+50°=140°，∴∠BCD=70°，又∵∠ACD+∠BCD=∠ACB=90°，∴∠ACD=20°．故答案为：20°．【点睛】本题考查翻折变换的知识，难度适中，解题关键是掌握折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．10．如图，已知长方形纸片的一条边经过直角三角形纸片的直角顶点，若长方形纸片的一组对边与直角三角形的两条直角边相交成∠1，∠2，则∠2-∠1=____.【答案】90°【解析】【分析】【详解】如图：∵∠2+∠3=180°，∴∠3=180°﹣∠2．∵直尺的两边互相平行，∴∠4=∠3，∴∠4=180°﹣∠2．∵∠4+∠1=90°，∴180°﹣∠2+∠1=90°，即∠2﹣∠1=90°．故答案为90°.二、八年级数学三角形选择题（难）11．如图，ABC ∆中，100ABC ∠=︒，且AEF AFE ∠=∠，CFD CDF ∠=∠，则EFD ∠ 的度数为( )A ．80°B ．60°C ．40°D ．20°【答案】C【解析】【分析】连接FB ，根据三角形内角和和外角知识，进行角度计算即可．【详解】解：如图连接FB ，∵AEF AFE ∠=∠，CFD CDF ∠=∠，∴AEF AFE EFB EBF ∠=∠=∠+∠，CFD CDF BFD FBD ∠=∠=∠+∠∴AFE CFD EFB EBF BFD FBD ∠+∠=∠+∠+∠+∠，即AFE CFD EFD EBD ∠+∠=∠+∠，又∵180AFE EFD DFC ∠+∠+∠=︒，∴2180EFD EBD ∠+∠=︒，∵100ABC ∠=︒，∴180100=402EFD ︒-︒∠=︒，故选：C ．【点睛】此题考查三角形内角和和外角定义，掌握三角形内角和为180°，三角形一个外角等于不相邻两内角之和是解题关键．12．如图，△ABC的面积为3，BD：DC＝2：1，E是AC的中点，AD与BE相交于点P，那么四边形PDCE的面积为（）A．13B．710C．35D．1320【答案】B【解析】【分析】连接CP．设△CPE的面积是x，△CDP的面积是y．根据BD：DC=2：1，E为AC的中点，得△BDP的面积是2y，△APE的面积是x，进而得到△ABP的面积是4x．再根据△ABE的面积是△BCE的面积相等，得4x+x=2y+x+y，解得y=43x，再根据△ABC的面积是3即可求得x、y的值，从而求解．【详解】连接CP，设△CPE的面积是x，△CDP的面积是y．∵BD：DC=2：1，E为AC的中点，∴△BDP的面积是2y，△APE的面积是x，∵BD：DC=2：1∴△ABD的面积是4x+2y∴△ABP的面积是4x．∴4x+x=2y+x+y，解得y=43x．又∵△ABC的面积为3∴4x+x=32，x=310．则四边形PDCE的面积为x+y=710．故选B．【点睛】此题能够根据三角形的面积公式求得三角形的面积之间的关系．等高的两个三角形的面积比等于它们的底的比；等底的两个三角形的面积比等于它们的高的比．13．马小虎在计算一个多边形的内角和时，由于粗心少算了2个内角，其和等于830，则该多边形的边数是( )A．7B．8C．7或8D．无法确定【答案】C【解析】【分析】n边形的内角和是（n-2）•180°，即为180°的（n-2）倍，多边形的内角一定大于0度，小于180度，因而多边形中，除去2个内角外，其余内角和与180度的商加上2，以后所得的数值，比这个数值大1或2的整数就是多边形的边数．【详解】设少加的2个内角和为x度，边数为n．则（n-2）×180=830+x，即（n-2）×180=4×180+110+x，因此x=70，n=7或x=250，n=8．故该多边形的边数是7或8．故选C．【点睛】本题考查了多边形的内角和定理，正确理解多边形内角的大小的特点，以及多边形的内角和定理是解决本题的关键．14．能够铺满地面的正多边形组合是（）A．正三角形和正五边形B．正方形和正六边形C．正方形和正五边形D．正五边形和正十边形【答案】D【解析】【分析】正多边形的组合能否铺满地面，关键是要看位于同一顶点处的几个角之和能否为360°．若能，则说明能铺满；反之，则说明不能铺满．【详解】解：A、正五边形和正三边形内角分别为108°、60°，由于60m+108n=360，得m=6-95 n，显然n取任何正整数时，m不能得正整数，故不能铺满，故此选项错误；B、正方形、正六边形内角分别为90°、120°，不能构成360°的周角，故不能铺满，故此选项错误；C、正方形、正五边形内角分别为90°、108°，当90n+108m=360，显然n取任何正整数时，m不能得正整数，故不能铺满，故此选项错误；D、正五边形和正十边形内角分别为108、144，两个正五边形与一个正十边形能铺满地面，故此选项正确．故选：D．【点睛】此题主要考查了平面镶嵌，两种或两种以上几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．需注意正多边形内角度数=180°-360°÷边数．15．如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（）A．∠1＝∠2＋∠A B．∠1＝2∠A＋∠2C．∠1＝2∠2＋2∠A D．2∠1＝∠2＋∠A【答案】B【解析】试题分析：如图在∆ABC中，∠A+∠B+∠C=180°，折叠之后在∆ADF中，∠A+∠2+∠3=180°，∴∠B+∠C=∠2+∠3，∠3=180°-∠A-∠2，又在四边形BCFE中∠B+∠C+∠1+∠3=360°，∴∠2+∠3+∠1+∠3=360°∴∠2+∠1+2∠3=∠2+∠1+2（180°-∠A-∠2）=360°，∴∠2+∠1-2∠A-2∠2=0，∴∠1＝2∠A＋∠2.故选B点睛：本题主要考查考生对三角形内角和，四边形内角和以及三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角和的理解及掌握。

成都石室联合中学数学三角形填空选择易错题(Word版含答案)

成都石室联合中学数学三角形填空选择易错题（Word 版含答案）一、八年级数学三角形填空题（难）1．如图，BE 平分∠ABC，CE 平分外角∠ACD，若∠A＝42°，则∠E＝_____°．【答案】21°【解析】根据三角形的外角性质以及角平分线的定义可得．解：由题意得：∠E =∠ECD −∠EBC =12∠ACD −12∠ABC =12∠A =21°. 故答案为21°.2．如图，ABC 中，点D 在AC 的延长线上，E 、F 分别在边AC 和AB 上，BFE ∠与BCD ∠的平分线相交于点P ，若ABC ∠=70°FEC ∠=80°，则P ∠=______．【答案】85°【解析】【分析】根据四边形内角和等于360°，在四边形FECB 中∠B +∠BFE +∠FEC +∠BCE =360°，结合角平分线的定义计算即可得∠1-∠2=15°；再在四边形EFPC 中求出∠1-∠2+∠P =110°即可解答．【详解】解：∵∠BFE =2∠1，∠BCD =2∠2，又∵∠BFE +∠ABC +∠FEC +∠BCE =360°，ABC ∠=70°，FEC ∠=80°，∴2∠1+（180°-2∠2）+70°+80°=360°，∴∠1-∠2=15°；∵在四边形EFPC中，∠PFE+∠FEC+∠P+∠PCE=360°，∴∠1+80°+（180°-∠2）+∠P=360°，∴∠1-∠2+∠P=100°，∴∠P=85°，故答案为：85°．【点睛】本题考查的是三角形内角和定理和四边形内角和定理的应用，掌握三角形内角和等于180°和四边形内角和等于360°是解题的关键．3．直角三角形中，两锐角的角平分线所夹的锐角是_____度．【答案】45【解析】【分析】根据题意画出符合条件的图形，然后根据直角三角形的两锐角互余和角平分线的性质，以及三角形的外角的性质求解即可.【详解】如图所示△ACB为Rt△，AD，BE，分别是∠CAB和∠ABC的角平分线，AD，BE相交于一点F．∵∠ACB=90°，∴∠CAB+∠ABC=90°∵AD，BE，分别是∠CAB和∠ABC的角平分线，∴∠FAB+∠FBA=12∠CAB+12∠ABC=45°．故答案为45.【点睛】此题主要考查了直角三角形的两锐角互余和三角形的外角的性质，关键是根据题意画出相应的图形，利用三角形的相关性质求解.4．已知三角形的两边的长分别为2cm和8cm，设第三边中线的长为x cm，则x的取值范围是_______【答案】3＜x＜5【解析】【分析】延长AD至M使DM=AD，连接CM，先说明△ABD≌△CDM，得到CM=AB=8，再求出2AD的范围，最后求出AD的范围.【详解】解：如图：AB=8，AC=2，延长AD至M使DM=AD，连接CM在△ABD和△CDM中，AD MDADB MDCBD CD=⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△MCD（SAS），∴CM=AB=8．在△ACM中：8-2＜2x＜8+2，解得：3＜x＜5．故答案为：3＜x＜5．【点睛】本题考查了三角形的三边关系，解答的关键在于画出图形，数形结合完成解答.5．如图，在△ABC中，∠B和∠C的平分线交于点O，若∠A＝50°，则∠BOC＝_____．【答案】115°．【解析】【分析】根据三角形的内角和定理得出∠ABC+∠ACB=130°，然后根据角平分线的概念得出∠OBC+∠OCB，再根据三角形的内角和定理即可得出∠BOC的度数．【详解】解；∵∠A＝50°，∴∠ABC+∠ACB＝180°﹣50°＝130°，∵∠B和∠C的平分线交于点O，∴∠OBC ＝12∠ABC ，∠OCB ＝12∠ACB ， ∴∠OBC +∠OCB ＝12×（∠ABC +∠ACB ）＝12×130°＝65°， ∴∠BOC ＝180°﹣（∠OBC +∠OCB ）＝115°，故答案为：115°．【点睛】本题考查了三角形的内角和定理和三角形的角平分线的概念，关键是求出∠OBC +∠OCB 的度数．6．如图，七边形ABCDEFG 中，AB ，ED 的延长线交于点O ，若l ∠，2∠，3∠，4∠的外角和等于210，则BOD ∠的度数为______．【答案】30【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE 的内角和，则可求得∠BOD ．【详解】1∠、2∠、3∠、4∠的外角的角度和为210，12342104180∠∠∠∠∴++++=⨯，1234510∠∠∠∠∴+++=，五边形OAGFE 内角和()52180540=-⨯=，1234BOD 540∠∠∠∠∠∴++++=，BOD 54051030∠∴=-=．故答案为：30【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．7．如图，已知△ABC 中，AD 是BC 边上的高，点E 在线段BD 上，且AE 平分∠BAC ，若∠B=40°，∠C=78°，则∠EAD=____°．【答案】19°．【解析】【分析】根据三角形内角和定理求得∠BAC，再由AE平分∠BAC，可求得∠EAC，最后由∠ADC=90°，∠C=78°，可求得∠DAC，即∠EAD可求．【详解】解：∵∠B=40°，∠C=78°∴∠BAC=180°-∠B-∠C=62°∵AE平分∠BAC，∴∠EAC=1312BAC∠=，∵AD是BC边上的高∴∠ADC=90°∴∠DAC=90°-78°=12°∴∠EAD=∠EAC-∠DAC=19°故答案为：19°．【点睛】本题考查三角形内角和定理；三角形角平分线性质．8．如图，△ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF =_________度.【答案】74°【解析】【分析】【详解】试题分析：首先根据三角形的内角和定理求得∠ACB的度数，以及∠BCD的度数，根据角平分线的定义求得∠BCE的度数，则∠ECD可以求解，然后在△CDF中，利用内角和定理即可求得∠CDF的度数．∵∠A=40°，∠B=70°，∴∠ACB=180°﹣∠A﹣∠B=70°．∵CE平分∠ACB，∴∠ACE=12∠ACB=35°．∵CD⊥AB于D，∴∠CDA=90°，∠ACD=180°﹣∠A﹣∠CDA=50°．∴∠ECD=∠ACD﹣∠ACE=15°．∵DF⊥CE，∴∠CFD=90°，∴∠CDF=180°﹣∠CFD﹣∠DCF=75°．考点：三角形内角和定理．9．如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF＝AC，则∠ABC＝_____度．【答案】45【解析】【分析】根据三角形全等的判定和性质，先证△ADC≌△BDF，可得BD=AD，可求∠ABC=∠BAD=45°．【详解】∵AD⊥BC于D，BE⊥AC于E∴∠EAF+∠AFE=90°，∠DBF+∠BFD=90°，又∵∠BFD=∠AFE（对顶角相等）∴∠EAF=∠DBF，在Rt△ADC和Rt△BDF中，CAD FBDBDF ADCBF AC∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC≌△BDF（AAS），∴BD=AD，即∠ABC=∠BAD=45°．故答案为45．【点睛】三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．10．如图，五边形ABCDE的每一个内角都相等，则外角CBF=∠__________．【答案】72︒【解析】【分析】多边形的外角和等于360度，依此列出算式计算即可求解．【详解】360°÷5=72°．故外角∠CBF等于72°．故答案为：72︒．【点睛】此题考查了多边形内角与外角，关键是熟悉多边形的外角和等于360度的知识点．二、八年级数学三角形选择题（难）11．若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A．n·180°B．（n+2）·180°C．（2n-1）·180°D．（2n+1）·180°【答案】D【解析】【分析】当△ABC内的点的个数是1时，三角形内互不重叠的小三角形的个数是3；当△ABC内的点的个数是2时，三角形内互不重叠的小三角形的个数是5；依此类推得到当△ABC内的点的个数是3时，三角形内互不重叠的小三角形的个数是7；当△ABC内的点的个数是n 时，三角形内互不重叠的小三角形的个数2n+1，所以这些小三角形的内角和为（2n+1）·180°【详解】】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；图2中，当△ABC 内只有2个点时，可分割成5个互不重叠的小三角形；图3中，当△ABC 内只有3个点时，可分割成7个互不重叠的小三角形；根据以上规律，当△ABC 内有n 个点（P 1，P 2，…，P n ）时，可以把△ABC 分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°. 【点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．12．如图,△ABC 中,E 是 AC 的中点,延长 BC 至 D ,使 BC ：CD =3:2,以 CE ,CD 为邻边做▱CDFE ，连接 AF,BE,BF ，若△ABC 的面积为 9，则阴影部分面积是（）A ．6B ．4C ．3D ．2【答案】A【解析】【分析】根据三角形中位线性质结合三角形面积去解答.【详解】解：在ABC 中，E 是 AC 的中点,S ABC 9=, BC ：CD =3:2▱CDFE 中，CD=EF1S BCE 4.52S ABC ∴== 设BCE 的高为1h , ABC 的高为2.h11S BCE 4.52BC h ∴=⨯⨯= 13h =12:1:2h h =26h ∴=S AEF S EFB s ∴=+阴()2111122EF h h EF h =⨯⨯-+⨯⨯ 212EF h =⨯⨯ 1262=⨯⨯ 6.=【点睛】此题重点考察学生对三角形中位线和面积的理解，熟练掌握三角形面积计算方法是解题的关键.13．如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形ABCD内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为7、9、10，则四边形DHOG的面积为（）A．7B．8C．9D．10【答案】B【解析】分析：连接OC，OB，OA，OD，易证S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，S△OAE=S△OBE，所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，所以可以求出S四边形DHOG．详解：连接OC，OB，OA，OD，∵E、F、G、H依次是各边中点，∴△AOE和△BOE等底等高，∴S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，∵S四边形AEOH=7，S四边形BFOE=9，S四边形CGOF=10，∴7+10=9+S四边形DHOG，解得，S四边形DHOG=8．故选B.点睛：本题考查了三角形的面积．解决本题的关键将各个四边形划分，充分利用给出的中点这个条件，证得三角形的面积相等，进而证得结论．14．如图，是由相同的花盆按一定的规律组成的形如正多边形的图案，其中第1个图形一共有6个花盆，第2个图形一共有12个花盆，第3个图形一共有20个花盆，…则第8个图形中花盆的个数为（）A．56 B．64 C．72 D．90【答案】D【解析】【分析】根据题意找出规律得到第n个图形中花盆的个数为：（n+1）（n+2），然后将n=7代入求解即可.【详解】第1个图形的花盆个数为：（1+1）（1+2）；第2个图形的花盆个数为：（2+1）（2+2）=12；第3个图形的花盆个数为：（3+1）（3+2）=20；，第n个图形的花盆个数为：（n+1）（n+2）；则第7个图形中花盆的个数为：（7+1）（7+2）=72.故选：C.【点睛】本题考查图形规律题，解此题的关键在于根据题中图形找到规律.15．如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（）A．∠A=∠1+∠2 B．2∠A=∠1+∠2C．3∠A=2∠1+∠2 D．3∠A=2（∠1+∠2）【答案】B【解析】【分析】根据四边形的内角和为360°、平角的定义及翻折的性质，就可求出2∠A=∠1+∠2这一始终保持不变的性质．【详解】∵在四边形ADA′E中，∠A+∠A′+∠ADA′+∠AEA′=360°，则2∠A+(180°-∠2)+(180°-∠1)=360°，∴可得2∠A=∠1+∠2．故选：B【点睛】本题主要考查四边形的内角和及翻折的性质特点，解决本题的关键是熟记翻折的性质．16．一个多边形的每个内角都相等，并且它的一个外角与一个内角的比为1:3，则这个多边形为（）A．三角形B．四边形C．六边形D．八边形【答案】D【解析】【分析】一个外角与一个内角的比为1 : 3，则内角和是外角和的3倍，根据多边形的外角和是360°，即可求得多边形的内角的度数，依据多边形的内角和公式即可求解．【详解】解：多边形的内角和是：360°×3=1080°．设多边形的边数是n，则（n-2）•180=1080，解得：n=8．即这个多边形是正八边形．故选D．【点睛】本题考查了多边形的内角和定理以及多边形的外角和定理，注意多边形的外角和不随边数的变化而变化．17．已知一个正多边形的内角是140°，则这个正多边形的边数是（）A．9 B．8 C．7 D．6【答案】A【解析】分析：根据多边形的内角和公式计算即可.详解：.答:这个正多边形的边数是9.故选A.点睛：本题考查了多边形，熟练掌握多边形的内角和公式是解答本题的关键.18．一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为（）A．7 B．8 C．9 D．10【答案】A【解析】设这个多边形的边数为x，根据题意可得：x-=⨯+，180(2)2360180解得：7x=.故选A.19．如图，在△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于D点，∠A=50°，则∠D=（）A．15°B．20°C．25°D．30°【答案】C【解析】根据角平分线的定义和三角形的外角的性质即可得到∠D=12∠A．解：∵∠ABC的平分线与∠ACB的外角平分线相交于D点，∴∠1=12∠ACE，∠2=12∠ABC，又∠D=∠1﹣∠2，∠A=∠ACE﹣∠ABC，∴∠D=12∠A=25°．故选C．20．如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（）A．110︒B．115︒C．120︒D．125︒【答案】A【解析】【分析】根据三角形外角的性质三角形的一个外角等于和它不相邻的两个内角的和可得∠AEB=∠A+∠C=65°，∠DFE=∠B+∠AEC，进而可得答案．【详解】解：∵∠A=27°，∠C=38°，∴∠AEB=∠A+∠C=65°，∵∠B=45°，∴∠DFE=65°+45°=110°，故选：A．【点睛】此题主要考查了三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．。

成都石室联合中学小升初数学期末试卷易错题（Word版含答案）

成都石室联合中学小升初数学期末试卷易错题（Word 版含答案）一、选择题1．（1分）（2014•江东区模拟）一个体积25厘米×30厘米×60厘米的箱子里最多能装进棱长为1分米的立方体（）A ．45个B ．30个C ．72个D ．36个2．六年级同学参加兴趣小组，其中绘画小组有a 人，比书法小组的人数的2倍少4人。

书法小组有多少人？正确的算式是（）。

A ．2=4a B ．2=4a ÷ C ．24a ÷+ D ．()42a +÷ 3．如果一个三角形的三个内角度数之比为5∶4∶9，那么这个三角形是（）。

A ．锐角三角形B ．直角三角形C ．钝角三角形D ．无法确定4．一堆煤，用去了20%后，还剩下60吨，这堆煤共有多少吨？解：设这堆煤有x 吨。

所列方程正确的是（）。

A ．20%60x =B ．20%60+=x xC ．20%60x x -=D ．20%60x -=5．一个立方体的六个面上分别标上了数1点、2点、3点、4点、5点、6点，下图是从三个不同角度观察到的情况．“3点”这一面相对的面是（）A ．2点B ．4点C ．6点或4点6．如图所示，线段EF 、FG 、GH 的长度相等，下面叙述错误的是（）。

A ．线段EG 的长度是线段EF 长度的2倍B ．线段EF 比线段EG 短50%C ．线段EG 是线段EH 长度的34D ．线段EH 比线段EG 长127．如图所示，以点A 为圆心的圆内，三角形ABC 为等腰三角形．三角形为等腰三角形的证据，是运用了圆的什么特征？A ．同一个圆的半径相等B ．圆的周长为直径的3.14倍C ．同一个圆的直径为半径的2倍D ．直径的长度是圆周上的任意两点连成的线段中最长的8．一件商品原价180元，先降价110，再提价110，现价比原价（） A ．没变B ．提高了C ．降低了D ．无法确定9．观察下面点阵图找规律，第8个点阵图中有（）个点。

成都石室联合中学七年级下册数学期末试卷易错题(Word版含答案)

成都石室联合中学七年级下册数学期末试卷易错题（Word 版含答案）一、解答题1．如图，直线HD //GE ，点A 在直线HD 上，点C 在直线GE 上，点B 在直线HD 、GE 之间，∠DAB ＝120°．（1）如图1，若∠BCG ＝40°，求∠ABC 的度数；（2）如图2，AF 平分∠HAB ，BC 平分∠FCG ，∠BCG ＝20°，比较∠B ，∠F 的大小；（3）如图3，点P 是线段AB 上一点，PN 平分∠APC ，CN 平分∠PCE ，探究∠HAP 和∠N 的数量关系，并说明理由．2．已知：AB //CD ．点E 在CD 上，点F ，H 在AB 上，点G 在AB ，CD 之间，连接FG ，EH ，GE ，∠GFB ＝∠CEH ．（1）如图1，求证：GF //EH ；（2）如图2，若∠GEH ＝α，FM 平分∠AFG ，EM 平分∠GEC ，试问∠M 与α之间有怎样的数量关系（用含α的式子表示∠M ）？请写出你的猜想，并加以证明． 3．如图，直线//PQ MN ，一副直角三角板,ABC DEF ∆∆中，90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=．（1）若DEF ∆如图1摆放，当ED 平分PEF ∠时，证明：FD 平分EFM ∠．（2）若,ABC DEF ∆∆如图2摆放时，则PDE ∠=（3）若图2中ABC ∆固定，将DEF ∆沿着AC 方向平移，边DF 与直线PQ 相交于点G ，作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H （如图3），求GHF ∠的度数．（4）若图2中DEF ∆的周长35,5cm AF cm =，现将ABC ∆固定，将DEF ∆沿着CA 方向平移至点F 与A 重合，平移后的得到''D E A ∆，点D E 、的对应点分别是''D E 、，请直接写出四边形'DEAD 的周长．（5）若图2中DEF ∆固定，（如图4）将ABC ∆绕点A 顺时针旋转，1分钟转半圈，旋转至AC 与直线AN 首次重合的过程中，当线段BC 与DEF ∆的一条边平行时，请直接写出旋转的时间．4．如图，∠EBF ＝50°，点C 是∠EBF 的边BF 上一点．动点A 从点B 出发在∠EBF 的边BE 上，沿BE 方向运动，在动点A 运动的过程中，始终有过点A 的射线AD ∥BC ．（1）在动点A 运动的过程中，（填“是”或“否”）存在某一时刻，使得AD 平分∠EAC ？（2）假设存在AD 平分∠EAC ，在此情形下，你能猜想∠B 和∠ACB 之间有何数量关系？并请说明理由；（3）当AC ⊥BC 时，直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系．5．问题情境：如图1，AB ∥CD ，∠PAB ＝130°，∠PCD ＝120°．求∠APC 的度数．小明的思路是：过P 作PE ∥AB ，通过平行线性质，可得∠APC ＝∠APE +∠CPE ＝50°+60°＝110°．问题解决：（1）如图2，AB ∥CD ，直线l 分别与AB 、CD 交于点M 、N ，点P 在直线I 上运动，当点P 在线段MN 上运动时（不与点M 、N 重合），∠PAB ＝α，∠PCD ＝β，判断∠APC 、α、β之间的数量关系并说明理由；（2）在（1）的条件下，如果点P 在线段MN 或NM 的延长线上运动时．请直接写出∠APC 、α、B 之间的数量关系；（3）如图3，AB ∥CD ，点P 是AB 、CD 之间的一点（点P 在点A 、C 右侧），连接PA 、PC ，∠BAP 和∠DCP 的平分线交于点Q ．若∠APC ＝116°，请结合（2）中的规律，求∠AQC 的度数．二、解答题6．为更好地理清平行线相关角的关系，小明爸爸为他准备了四根细直木条AB 、BC 、CD 、DE ，做成折线ABCDE ，如图1，且在折点B 、C 、D 处均可自由转出．（1）如图2，小明将折线调节成50B ∠=︒，85C ∠=︒，35D ∠=︒，判断AB 是否平行于ED ，并说明理由；（2）如图3，若35C D ∠=∠=︒，调整线段AB 、BC 使得//AB CD 求出此时B 的度数，要求画出图形，并写出计算过程．（3）若85C ∠=︒，35D ∠=︒，//AB DE ，请直接写出此时B 的度数． 7．问题情境：如图1，AB ∥CD ，∠PAB =130°，∠PCD =120°，求∠APC 的度数．小明的思路是：如图2，过P 作PE ∥AB ，通过平行线性质来求∠APC ．（1）按小明的思路，易求得∠APC 的度数为度；（2）如图3，AD ∥BC ，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，∠ADP =∠α，∠BCP =∠β．试判断∠CPD 、∠α、∠β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你直接写出∠CPD 、∠α、∠β间的数量关系．8．如图，AB ⊥AK ，点A 在直线MN 上，AB 、AK 分别与直线EF 交于点B 、C ，∠MAB+∠KCF =90°．（1）求证：EF ∥MN ；（2）如图2，∠NAB 与∠ECK 的角平分线交于点G ，求∠G 的度数；（3）如图3，在∠MAB 内作射线AQ ，使∠MAQ =2∠QAB ，以点C 为端点作射线CP ，交直．线．AQ 于点T ，当∠CTA =60°时，直接写出∠FCP 与∠ACP 的关系式．9．已知，如图①，∠BAD =50°，点C 为射线AD 上一点（不与A 重合），连接BC ．（1）[问题提出]如图②，AB ∥CE ，∠BCD =73 °，则：∠B = ．（2）[类比探究]在图①中，探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系？并用平行．．．．线的性质．．．．说明理由．（3）[拓展延伸]如图③，在射线BC 上取一点O ，过O 点作直线MN 使MN ∥AD ，BE 平分∠ABC 交AD 于E 点，OF 平分∠BON 交AD 于F 点，//OG BE 交AD 于G 点，当C 点沿着射线AD 方向运动时，∠FOG 的度数是否会变化？若变化，请说明理由；若不变，请求出这个不变的值．10．已知：ABC 和同一平面内的点D ．（1）如图1，点D 在BC 边上，过D 作//DE BA 交AC 于E ，//DF CA 交AB 于F ．根据题意，在图1中补全图形，请写出EDF ∠与BAC ∠的数量关系，并说明理由；（2）如图2，点D 在BC 的延长线上，//DF CA ，EDF BAC ∠=∠．请判断DE 与BA 的位置关系，并说明理由．（3）如图3，点D 是ABC 外部的一个动点．过D 作//DE BA 交直线AC 于E ，//DF CA 交直线AB 于F ，直接写出EDF ∠与BAC ∠的数量关系，并在图3中补全图形．三、解答题11．在△ABC 中，射线AG 平分∠BAC 交BC 于点G ，点D 在BC 边上运动（不与点G 重合），过点D 作DE ∥AC 交AB 于点E ．（1）如图1，点D 在线段CG 上运动时，DF 平分∠EDB①若∠BAC ＝100°，∠C ＝30°，则∠AFD ＝；若∠B ＝40°，则∠AFD ＝； ②试探究∠AFD 与∠B 之间的数量关系？请说明理由；（2）点D 在线段BG 上运动时，∠BDE 的角平分线所在直线与射线AG 交于点F 试探究∠AFD 与∠B 之间的数量关系，并说明理由 12．解读基础：（1）图1形似燕尾，我们称之为“燕尾形”，请写出A ∠、B 、C ∠、D ∠之间的关系，并说明理由；（2）图2形似8字，我们称之为“八字形”，请写出A ∠、B 、C ∠、D ∠之间的关系，并说明理由：应用乐园：直接运用上述两个结论解答下列各题（3）①如图3，在ABC ∆中，BD 、CD 分别平分ABC ∠和ACB ∠，请直接写出A ∠和D ∠的关系；②如图4，A B C D E F ∠+∠+∠+∠+∠+∠= ．（4）如图5，BAC ∠与BDC ∠的角平分线相交于点F ，GDC ∠与CAF ∠的角平分线相交于点E ，已知26B ∠=︒，54C ∠=︒，求F ∠和E ∠的度数．13．如图所示，已知射线//,//,100CB OA AB OC C OAB ︒∠=∠=.点E 、F 在射线CB 上，且满足FOB AOB ∠=∠，OE 平分COF ∠ （1）求EOB ∠的度数；（2）若平行移动AB ，那么:OBC OFC ∠∠的值是否随之发生变化？如果变化，找出变化规律.若不变，求出这个比值；（3）在平行移动AB 的过程中，是否存在某种情况，使OEC OBA ∠=∠？若存在，求出其度数．若不存在，请说明理由.14．Rt △ABC 中，∠C=90°，点D 、E 分别是△ABC 边AC 、BC 上的点，点P 是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.（1）若点P 在线段AB 上，如图（1）所示，且∠α=50°，则∠1+∠2= °；（2）若点P 在边AB 上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：；（3）若点P 运动到边AB 的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.（4）若点P 运动到△ABC 形外，如图（4）所示，则∠α、∠1、∠2之间的关系为： . 15．已知AB //CD ，点E 是平面内一点，∠CDE 的角平分线与∠ABE 的角平分线交于点F ．（1）若点E 的位置如图1所示．①若∠ABE =60°，∠CDE =80°，则∠F = °； ②探究∠F 与∠BED 的数量关系并证明你的结论；（2）若点E 的位置如图2所示，∠F 与∠BED 满足的数量关系式是．（3）若点E 的位置如图3所示，∠CDE 为锐角，且1452E F ∠≥∠+︒，设∠F =α，则α的取值范围为．【参考答案】一、解答题1．（1）∠ABC ＝100°；（2）∠ABC ＞∠AFC ；（3）∠N ＝90°﹣∠HAP ；理由见解析．【分析】（1）过点B 作BMHD ，则HDGEBM ，根据平行线的性质求得∠ABM 与∠CBM ，便可求得最后解析：（1）∠ABC ＝100°；（2）∠ABC ＞∠AFC ；（3）∠N ＝90°﹣12∠HAP ；理由见解析．【分析】（1）过点B 作BM //HD ，则HD //GE //BM ，根据平行线的性质求得∠ABM 与∠CBM ，便可求得最后结果；（2）过B 作BP //HD //GE ，过F 作FQ //HD //GE ，由平行线的性质得，∠ABC ＝∠HAB +∠BCG ，∠AFC ＝∠HAF +∠FCG ，由角平分线的性质和已知角的度数分别求得∠HAF ，∠FCG ，最后便可求得结果；（3）过P 作PK //HD //GE ，先由平行线的性质证明∠ABC ＝∠HAB +∠BCG ，∠AFC ＝∠HAF +∠FCG ，再根据角平分线求得∠NPC 与∠PCN ，由后由三角形内角和定理便可求得结果．【详解】解：（1）过点B 作BM //HD ，则HD //GE //BM ，如图1，∴∠ABM＝180°﹣∠DAB，∠CBM＝∠BCG，∵∠DAB＝120°，∠BCG＝40°，∴∠ABM＝60°，∠CBM＝40°，∴∠ABC＝∠ABM+∠CBM＝100°；（2）过B作BP//HD//GE，过F作FQ//HD//GE，如图2，∴∠ABP＝∠HAB，∠CBP＝∠BCG，∠AFQ＝∠HAF，∠CFQ＝∠FCG，∴∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，∵∠DAB＝120°，∴∠HAB＝180°﹣∠DAB＝60°，∵AF平分∠HAB，BC平分∠FCG，∠BCG＝20°，∴∠HAF＝30°，∠FCG＝40°，∴∠ABC＝60°+20°＝80°，∠AFC＝30°+40°＝70°，∴∠ABC＞∠AFC；（3）过P作PK//HD//GE，如图3，∴∠APK＝∠HAP，∠CPK＝∠PCG，∴∠APC＝∠HAP+∠PCG，∵PN平分∠APC，∴∠NPC＝12∠HAP+12∠PCG，∵∠PCE＝180°﹣∠PCG，CN平分∠PCE，∴∠PCN＝90°﹣12∠PCG，∵∠N+∠NPC+∠PCN＝180°，∴∠N＝180°﹣12∠HAP﹣12∠PCG﹣90°+12∠PCG＝90°﹣12∠HAP，即：∠N ＝90°﹣12∠HAP ．【点睛】本题考查了角平分线的定义，平行线性质和判定：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用，理清各角度之间的关系是解题的关键，也是本题的难点．2．（1）见解析；（2），证明见解析．【分析】（1）由平行线的性质得到，等量代换得出，即可根据“同位角相等，两直线平行”得解；（2）过点作，过点作，根据平行线的性质及角平分线的定义求解即可．【详解析：（1）见解析；（2）902FME α∠=︒-，证明见解析．【分析】（1）由平行线的性质得到CEH EHB ∠=∠，等量代换得出GFB EHB ∠=∠，即可根据“同位角相等，两直线平行”得解；（2）过点M 作//MQ AB ，过点G 作//GP AB ，根据平行线的性质及角平分线的定义求解即可．【详解】（1）证明：//AB CD ，CEH EHB ∴∠=∠， GFB CEH ∠=∠，GFB EHB ∴∠=∠，//GF EH ∴；（2）解：902FME α∠=︒-，理由如下：如图2，过点M 作//MQ AB ，过点G 作//GP AB ，//AB CD ，//MQ CD ∴，AFM FMQ ∴∠=∠，QME MEC ∠=∠， FME FMQ QME AFM MEC ∴∠=∠+∠=∠+∠，同理，FGE FGP PGE AFG GEC ∠=∠+∠=∠+∠，FM 平分AFG ∠，EM 平分GEC ∠，2AFG AFM ∴∠=∠，2GEC MEC ∠=∠，2FGE FME ∴∠=∠，由（1）知，//GF EH ，180FGE GEH ∴∠+∠=︒，GEH α∠=，180FGE α∴∠=︒-，2180FME α∴∠=︒-，902FME α∴∠=︒-．【点睛】此题考查了平行线的判定与性质，熟记平行线的判定与性质及作出合理的辅助线是解题的关键．3．（1）见详解；（2）15°；（3）67.5°；（4）45cm ；（5）10s 或30s 或40s 【分析】（1）运用角平分线定义及平行线性质即可证得结论；（2）如图2，过点E 作EK ∥MN ，利用平行线性解析：（1）见详解；（2）15°；（3）67.5°；（4）45cm ；（5）10s 或30s 或40s 【分析】（1）运用角平分线定义及平行线性质即可证得结论；（2）如图2，过点E 作EK ∥MN ，利用平行线性质即可求得答案；（3）如图3，分别过点F 、H 作FL ∥MN ，HR ∥PQ ，运用平行线性质和角平分线定义即可得出答案；（4）根据平移性质可得D′A ＝DF ，DD′＝EE′＝AF ＝5cm ，再结合DE ＋EF ＋DF ＝35cm ，可得出答案；（5）设旋转时间为t 秒，由题意旋转速度为1分钟转半圈，即每秒转3°，分三种情况：①当BC ∥DE 时，②当BC ∥EF 时，③当BC ∥DF 时，分别求出旋转角度后，列方程求解即可．【详解】（1）如图1，在△DEF 中，∠EDF ＝90°，∠DFE ＝30°，∠DEF ＝60°，∵ED 平分∠PEF ，∴∠PEF＝2∠PED＝2∠DEF＝2×60°＝120°，∵PQ∥MN，∴∠MFE＝180°−∠PEF＝180°−120°＝60°，∴∠MFD＝∠MFE−∠DFE＝60°−30°＝30°，∴∠MFD＝∠DFE，∴FD平分∠EFM；（2）如图2，过点E作EK∥MN，∵∠BAC＝45°，∴∠KEA＝∠BAC＝45°，∵PQ∥MN，EK∥MN，∴PQ∥EK，∴∠PDE＝∠DEK＝∠DEF−∠KEA，又∵∠DEF＝60°．∴∠PDE＝60°−45°＝15°，故答案为：15°；（3）如图3，分别过点F、H作FL∥MN，HR∥PQ，∴∠LFA＝∠BAC＝45°，∠RHG＝∠QGH，∵FL∥MN，HR∥PQ，PQ∥MN，∴FL∥PQ∥HR，∴∠QGF＋∠GFL＝180°，∠RHF＝∠HFL＝∠HFA−∠LFA，∵∠FGQ和∠GFA的角平分线GH、FH相交于点H，∴∠QGH＝12∠FGQ，∠HFA＝12∠GFA，∵∠DFE＝30°，∴∠GFA＝180°−∠DFE＝150°，∴∠HFA＝12∠GFA＝75°，∴∠RHF＝∠HFL＝∠HFA−∠LFA＝75°−45°＝30°，∴∠GFL＝∠GFA−∠LFA＝150°−45°＝105°，∴∠RHG＝∠QGH＝12∠FGQ＝12（180°−105°）＝37.5°，∴∠GHF＝∠RHG＋∠RHF＝37.5°＋30°＝67.5°；（4）如图4，∵将△DEF沿着CA方向平移至点F与A重合，平移后的得到△D′E′A，∴D′A＝DF，DD′＝EE′＝AF＝5cm，∵DE＋EF＋DF＝35cm，∴DE＋EF＋D′A＋AF＋DD′＝35＋10＝45（cm），即四边形DEAD′的周长为45cm；（5）设旋转时间为t秒，由题意旋转速度为1分钟转半圈，即每秒转3°，分三种情况：BC∥DE时，如图5，此时AC∥DF，∴∠CAE＝∠DFE＝30°，∴3t＝30，解得：t＝10；BC∥EF时，如图6，∵BC∥EF，∴∠BAE＝∠B＝45°，∴∠BAM＝∠BAE＋∠EAM＝45°＋45°＝90°，∴3t＝90，解得：t＝30；BC∥DF时，如图7，延长BC交MN于K，延长DF交MN于R，∵∠DRM＝∠EAM＋∠DFE＝45°＋30°＝75°，∴∠BKA＝∠DRM＝75°，∵∠ACK＝180°−∠ACB＝90°，∴∠CAK＝90°−∠BKA＝15°，∴∠CAE＝180°−∠EAM−∠CAK＝180°−45°−15°＝120°，∴3t＝120，解得：t＝40，综上所述，△ABC绕点A顺时针旋转的时间为10s或30s或40s时，线段BC与△DEF的一条边平行．【点睛】本题主要考查了平行线性质及判定，角平分线定义，平移的性质等，添加辅助线，利用平行线性质是解题关键．4．（1）是；（2）∠B＝∠ACB，证明见解析；（3）∠BAC＝40°，AC⊥AD．【分析】（1）要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD解析：（1）是；（2）∠B＝∠ACB，证明见解析；（3）∠BAC＝40°，AC⊥AD．（1）要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则当∠ACB＝∠B时，有AD平分∠EAC；（2）根据角平分线可得∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则有∠ACB＝∠B；（3）由AC⊥BC，有∠ACB＝90°，则可求∠BAC＝40°，由平行线的性质可得AC⊥AD．【详解】解：（1）是，理由如下：要使AD平分∠EAC，则要求∠EAD＝∠CAD，由平行线的性质可得∠B＝∠EAD，∠ACB＝∠CAD，则当∠ACB＝∠B时，有AD平分∠EAC；故答案为：是；（2）∠B＝∠ACB，理由如下：∵AD平分∠EAC，∴∠EAD＝∠CAD，∵AD∥BC，∴∠B＝∠EAD，∠ACB＝∠CAD，∴∠B＝∠ACB．（3）∵AC⊥BC，∴∠ACB＝90°，∵∠EBF＝50°，∴∠BAC＝40°，∵AD∥BC，∴AD⊥AC．【点睛】此题考查了角平分线和平行线的性质，熟练掌握角平分线和平行线的有关性质是解题的关键．5．（1）∠APC=α+β，理由见解析；（2）∠APC=α-β或∠APC=β-α；（3）58°【分析】（1）过点P作PE∥AB，根据平行线的判定与性质即可求解；（2）分点P在线段MN或NM的延长线解析：（1）∠APC=α+β，理由见解析；（2）∠APC=α-β或∠APC=β-α；（3）58°【分析】（1）过点P作PE∥AB，根据平行线的判定与性质即可求解；（2）分点P在线段MN或NM的延长线上运动两种情况，根据平行线的判定与性质及角的和差即可求解；（3）过点P，Q分别作PE∥AB，QF∥AB，根据平行线的判定与性质及角的和差即可求解．解：（1）如图2，过点P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE=α，∠CPE=β，∴∠APC=∠APE+∠CPE=α+β．（2）如图，在（1）的条件下，如果点P在线段MN的延长线上运动时，∵AB∥CD，∠PAB=α，∴∠1=∠PAB=α，∵∠1=∠APC+∠PCD，∠PCD=β，∴α=∠APC+β，∴∠APC=α-β；如图，在（1）的条件下，如果点P在线段NM的延长线上运动时，∵AB∥CD，∠PCD=β，∴∠2=∠PCD=β，∵∠2=∠PAB+∠APC，∠PAB=α，∴β=α+∠APC，∴∠APC=β-α；（3）如图3，过点P，Q分别作PE∥AB，QF∥AB，∵AB∥CD，∴AB∥QF∥PE∥CD，∴∠BAP=∠APE，∠PCD=∠EPC，∵∠APC=116°，∴∠BAP+∠PCD=116°，∵AQ平分∠BAP，CQ平分∠PCD，∴∠BAQ=12∠BAP，∠DCQ=12∠PCD，∴∠BAQ+∠DCQ=12（∠BAP+∠PCD）=58°，∵AB∥QF∥CD，∴∠BAQ=∠AQF，∠DCQ=∠CQF，∴∠AQF+∠CQF=∠BAQ+∠DCQ=58°，∴∠AQC=58°．【点睛】此题考查了平行线的判定与性质，添加辅助线将两条平行线相关的角联系到一起是解题的关键．二、解答题6．（1）平行，理由见解析；（2）35°或145°，画图、过程见解析；（3）50°或130°或60°或120°【分析】（1）过点C作CF∥AB，根据∠B=50°，∠C=85°，∠D=35°，即可得C解析：（1）平行，理由见解析；（2）35°或145°，画图、过程见解析；（3）50°或130°或60°或120°【分析】（1）过点C作CF∥AB，根据∠B=50°，∠C=85°，∠D=35°，即可得CF∥ED，进而可以判断AB平行于ED；（2）根据题意作AB∥CD，即可∠B=∠C=35°；（3）分别画图，根据平行线的性质计算出∠B的度数．【详解】解：（1）AB平行于ED，理由如下：如图2，过点C作CF∥AB，∴∠BCF=∠B=50°，∵∠BCD=85°，∴∠FCD=85°-50°=35°，∵∠D=35°，∴∠FCD=∠D，∴CF∥ED，∵CF∥AB，∴AB∥ED；（2）如图，即为所求作的图形．∵AB∥CD，∴∠ABC=∠C=35°，∴∠B的度数为：35°；∵A′B∥CD，∴∠ABC+∠C=180°，∴∠B的度数为：145°；∴∠B的度数为：35°或145°；（3）如图2，过点C作CF∥AB，∵AB∥DE，∴CF∥DE，∴∠FCD=∠D=35°，∵∠BCD=85°，∴∠BCF=85°-35°=50°，∴∠B=∠BCF=50°．答：∠B的度数为50°．如图5，过C作CF∥AB，则AB∥CF∥CD，∴∠FCD=∠D=35°，∵∠BCD=85°，∴∠BCF=85°-35°=50°，∵AB∥CF，∴∠B+∠BCF=180°，∴∠B=130°；如图6，∵∠C=85°，∠D=35°，∴∠CFD=180°-85°-35°=60°，∵AB∥DE，∴∠B=∠CFD=60°，如图7，同理得：∠B=35°+85°=120°，综上所述，∠B的度数为50°或130°或60°或120°．【点睛】本题考查了平行线的判定与性质，解决本题的关键是区分平行线的判定与性质，并熟练运用．7．（1）110°；（2）∠CPD=∠α+∠β，见解析；（3）当P在BA延长线时，∠CPD=∠β-∠α；当P在AB延长线上时，∠CPD=∠α-∠β【分析】（1）过P作PE∥AB，通过平行线性质求∠A解析：（1）110°；（2）∠CPD=∠α+∠β，见解析；（3）当P在BA延长线时，∠CPD=∠β-∠α；当P在AB延长线上时，∠CPD=∠α-∠β【分析】（1）过P作PE∥AB，通过平行线性质求∠APC即可；（2）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；（3）画出图形，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案．【详解】解：（1）过点P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠A+∠APE=180°，∠C+∠CPE=180°，∵∠PAB=130°，∠PCD=120°，∴∠APE=50°，∠CPE=60°，∴∠APC=∠APE+∠CPE=110°．故答案为110°；（2）∠CPD=∠α+∠β，理由是：如图3，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠α+∠β；（3）当P在BA延长线时，∠CPD=∠β-∠α，理由是：如图4，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠CPE-∠DPE =∠β-∠α；当P在AB延长线时，∠CPD=∠α-∠β，理由是：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE -∠CPE =∠α-∠β．【点睛】本题考查了平行线的性质和判定的应用，主要考查学生的推理能力，题目是一道比较典型的题目，分类讨论是解题的关键．8．（1）见解析；（2）∠CGA=45°；（3）∠FCP=2∠ACP或∠FCP+2∠ACP=180°．【分析】（1）有垂直定义可得∠MAB+∠KCN=90°，然后根据同角的余角相等可得∠KAN=∠K解析：（1）见解析；（2）∠CGA=45°；（3）∠FCP=2∠ACP或∠FCP+2∠ACP=180°．【分析】（1）有垂直定义可得∠MAB+∠KCN=90°，然后根据同角的余角相等可得∠KAN=∠KCF，从而判断两直线平行；（2）设∠KAN=∠KCF=α，过点G 作GH ∥EF ，结合角平分线的定义和平行线的判定及性质求解；（3）分CP 交射线AQ 及射线AQ 的反向延长线两种情况结合角的和差关系分类讨论求解．【详解】解：（1）∵AB ⊥AK ∴∠BAC=90° ∴∠MAB+∠KAN =90° ∵∠MAB+∠KCF =90° ∴∠KAN=∠KCF ∴EF ∥MN（2）设∠KAN=∠KCF=α 则∠BAN=∠BAC+∠KAN=90°＋α ∠KCB=180°－∠KCF=180°－α ∵AG 平分∠NAB ，CG 平分∠ECK∴∠GAN=12∠BAN=45°＋12α，∠KCG=12∠KCB=90°－12α ∴∠FCG=∠KCG+∠KCF=90°＋12α 过点G 作GH ∥EF ∴∠HGC=∠FCG=90°＋12α 又∵MN ∥EF ∴MN ∥GH∴∠HGA=∠GAN=45°＋12α∴∠CGA=∠HGC －∠HGA=（90°＋12α）－（45°＋12α）=45°（3）①当CP 交射线AQ 于点T∵180CTA TAC ACP ∠+∠+∠=︒ ∴180CTA QAB BAC ACP ∠+∠+∠+∠=︒ 又∵=60,90CTA BAC ∠︒∠=︒ ∴30QAB ACP ∠+∠=︒由（1）可得：EF ∥MN ∴FCA MAC ∠=∠ ∵FCP FCA ACP ∠=∠+∠ ∴FCP MAC ACP ∠=∠+∠∵MAC MAQ QAB BAC ∠=∠+∠+∠，2MAQ QAB ∠=∠ ∴()390=330901803MAC QAB ACP ACP ∠=∠+︒︒-∠+︒=︒-∠ ∴1803FCP ACP ACP ∠=︒-∠+∠ 即∠FCP +2∠ACP=180°②当CP 交射线AQ 的反向延长线于点T ，延长BA 交CP 于点GFCP FCA ACP ∠=∠-∠，由EF ∥MN 得MAC FCA ∠=∠∴FCP MAC ACP ∠=∠-∠又∵TAG QAB ∠=∠，180BAC CAG ∠+∠=︒，90BAC ∠=︒ ∴18090CAG BAC ∠=︒-∠=︒90CAT CAG TAG QAB ∠=∠-∠=︒-∠ ∵180CAT CTA ACP ∠+∠+∠=︒，60CTA ∠=︒ ∴120CAT ACP ∠+∠=︒ ∴90120QAB ACP ︒-∠+∠=︒ ∴30QAB ACP ∠=∠-︒ 由①可得390MAC QAB ∠=∠+︒ ∴()=330903MAC ACP ACP ∠∠-︒+︒=∠∴32FCP MAC ACP ACP ACP ACP ∠=∠-∠=∠-∠=∠ 综上，∠FCP =2∠ACP 或∠FCP +2∠ACP=180°．【点睛】本题考查平行线的判定和性质以及角的和差关系，准确理解题意，正确推理计算是解题关键．9．（1）；（2），见解析；（3）不变，【分析】（1）根据平行线的性质求出，再求出的度数，利用内错角相等可求出角的度数；（2）过点作∥，类似（1）利用平行线的性质，得出三个角的关系；（3）运用解析：（1）23︒；（2）BCD A B ∠=∠+∠，见解析；（3）不变， 25FOG ∠=︒ 【分析】（1）根据平行线的性质求出50A DCE ∠=∠=︒，再求出BCE ∠的度数，利用内错角相等可求出角的度数；（2）过点C 作CE ∥AB ，类似（1）利用平行线的性质，得出三个角的关系；（3）运用（2）的结论和平行线的性质、角平分线的性质，可求出FOG ∠的度数，可得结论．【详解】（1）因为CE ∥AB ，所以50A DCE ∠=∠=︒，B BCE ∠=∠ 因为∠BCD =73 °，所以23BCE BCD DCE ∠=∠-∠=︒，故答案为：23︒ （2）BCD A B ∠=∠+∠，如图②，过点C 作CE ∥AB ，则A DCE ∠=∠，B BCE ∠=∠．因为BCD DCE BCE ∠=∠+∠，所以BCD BAD B ∠=∠+∠，（3）不变，设ABE x ∠=，因为BE 平分ABC ∠，所以CBE ABE x ∠=∠=．由（2）的结论可知BCD BAD ABC ∠=∠+∠，且50BAD ︒∠=，则：502BCD x ∠=︒+．因为MN ∥AD ，所以502BON BCD x ∠=∠=︒+，因为OF 平分BON ∠，所以1252COF NOF BON x ∠=∠=∠=︒+．因为OG ∥BE ，所以COG CBE x ∠=∠=，所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒．【点睛】本题考查了平行线的性质和角平分线的定义，解题关键是熟练运用平行线的性质证明角相等，通过等量代换等方法得出角之间的关系．10．（1）图见解析，，理由见解析；（2），理由见解析；（3）图见解析，或．【分析】（1）根据平行线的画法补全图形即可得，根据平行线的性质可得，由此即可得；（2）如图（见解析），先根据平行线的性质可解析：（1）图见解析，EDF BAC ∠=∠，理由见解析；（2）//DE BA ，理由见解析；（3）图见解析，EDF BAC ∠=∠或180EDF BAC ∠+∠=︒．【分析】（1）根据平行线的画法补全图形即可得，根据平行线的性质可得,EDF BFD B B D AC F ∠=∠∠∠=，由此即可得；（2）如图（见解析），先根据平行线的性质可得BAC BOD ∠=∠，再根据等量代换可得EDF BOD ∠=∠，然后根据平行线的判定即可得；（3）先根据点D 的位置画出如图（见解析）的两种情况，再分别利用平行线的性质、对顶角相等即可得．【详解】（1）由题意，补全图形如下：EDF BAC ∠=∠，理由如下： //DE BA ， EDF BFD ∴∠=∠，//DF CA ，BA BFD C ∴∠=∠， EDF BAC ∴∠=∠；（2）//DE BA ，理由如下：如图，延长BA 交DF 于点O ，//DF CA ，BAC BOD ∴∠=∠，EDF BAC ∠=∠， EDF BOD ∴∠=∠， //DE BA ∴；（3）由题意，有以下两种情况： ①如图3-1，EDF BAC ∠=∠，理由如下：//DE BA ，180E EAF ∴∠+∠=︒， //DF CA ，180E EDF ∴∠+∠=︒， EAF EDF ∴∠=∠，由对顶角相等得：BAC EAF ∠=∠，EDF BAC ∴∠=∠；②如图3-2，180EDF BAC ∠+∠=︒，理由如下：//DE BA ，180EDF F ∴∠+∠=︒， //DF CA ，BAC F ∴∠=∠， 180EDF BAC ∴∠+∠=︒．【点睛】本题考查了平行线的判定与性质等知识点，较难的是题（3），正确分两种情况讨论是解题关键．三、解答题11．（1）①115°；110°；②；理由见解析；（2）；理由见解析【分析】（1）①若∠BAC=100°，∠C=30°，由三角形内角和定理求出∠B=50°，由平行线的性质得出∠EDB=∠C=30°，由解析：（1）①115°；110°；②1902AFD B ∠=︒+∠；理由见解析；（2）1902AFD B ∠=︒-∠；理由见解析【分析】（1）①若∠BAC=100°，∠C=30°，由三角形内角和定理求出∠B=50°，由平行线的性质得出∠EDB=∠C=30°，由角平分线定义得出1502BAG BAC ∠=∠=︒，1152FDG EDB ∠=∠=︒，由三角形的外角性质得出∠DGF=100°，再由三角形的外角性质即可得出结果；若∠B=40°，则∠BAC+∠C=180°-40°=140°，由角平分线定义得出12BAG BAC ∠=∠，12FDG EDB ∠=∠，由三角形的外角性质即可得出结果；②由①得：∠EDB=∠C ，1502BAG BAC ∠=∠=︒，1152FDG EDB ∠=∠=︒，由三角形的外角性质得出∠DGF=∠B+∠BAG ，再由三角形的外角性质即可得出结论；（2）由（1）得：∠EDB=∠C ，12BAG BAC ∠=∠，1122BDH EDB C ∠=∠=∠,由三角形的外角性质和三角形内角和定理即可得出结论．【详解】（1）①若∠BAC=100°，∠C=30°，则∠B=180°-100°-30°=50°， ∵DE ∥AC ， ∴∠EDB=∠C=30°，∵AG 平分∠BAC ，DF 平分∠EDB ，∴1502BAG BAC ∠=∠=︒，1152FDG EDB ∠=∠=︒， ∴∠DGF=∠B+∠BAG=50°+50°=100°， ∴∠AFD=∠DGF+∠FDG=100°+15°=115°；若∠B=40°，则∠BAC+∠C=180°-40°=140°， ∵AG 平分∠BAC ，DF 平分∠EDB ，∴12BAG BAC ∠=∠，12FDG EDB ∠=∠，∵∠DGF=∠B+∠BAG ，∴∠AFD=∠DGF+∠FDG=∠B+∠BAG+∠FDG =()12B BAC C ∠+∠+∠ 1401402=︒+⨯︒4070110=︒+︒=︒故答案为：115°；110°； ②1902AFD B ∠=︒+∠；理由如下：由①得：∠EDB=∠C ，12BAG BAC ∠=∠，12FDG EDB ∠=∠，∵∠DGF=∠B+∠BAG ， ∴∠AFD=∠DGF+∠FDG =∠B+∠BAG+∠FDG =()12B BAC C ∠+∠+∠ ()11802B B =∠+︒-∠ 1902B =︒+∠；（2）如图2所示：1902AFD B ∠=︒-∠；理由如下：由（1）得：∠EDB=∠C ，12BAG BAC ∠=∠，1122BDH EDB C ∠=∠=∠，∵∠AHF=∠B+∠BDH ， ∴∠AFD=180°-∠BAG-∠AHF11802BAC B BDH=︒-∠-∠-∠1118022BAC B C =︒-∠-∠-∠()11802B BAC C =︒-∠-∠+∠ ()11801802B B =︒-∠-︒-∠ 1180902B B =︒-∠-︒+∠1902B =︒-∠．【点睛】本题考查了三角形内角和定理、三角形的外角性质、平行线的性质等知识；熟练掌握三角形内角和定理和三角形的外角性质是解题的关键．12．（1），理由详见解析；（2），理由详见解析：（3）①；②360°；（4）； . 【分析】（1）根据三角形外角等于不相邻的两个内角之和即可得出结论；（2）根据三角形内角和定理及对顶角相等即可得出结解析：（1）D A B C ∠=∠+∠+∠，理由详见解析；（2）A D B C ∠+∠=∠+∠，理由详见解析：（3）①1902D A ∠=︒+∠；②360°；（4）124E ∠=︒； =14F ∠︒. 【分析】（1）根据三角形外角等于不相邻的两个内角之和即可得出结论；（2）根据三角形内角和定理及对顶角相等即可得出结论；（3）①根据角平分线的定义及三角形内角和定理即可得出结论； ②连结BE ，由（2）的结论及四边形内角和为360°即可得出结论；（4）根据（1）的结论、角平分线的性质以及三角形内角和定理即可得出结论．【详解】（1）D A B C ∠=∠+∠+∠．理由如下：如图1，BDE B BAD ∠=∠+∠，CDE C CAD ∠=∠+∠，BDC B BAD C CAD B BAC C ∴∠=∠+∠+∠+∠=∠+∠+∠，D A B C ∴∠=∠+∠+∠；（2）A D B C ∠+∠=∠+∠．理由如下：在ADE ∆中，180AED A D ∠=︒-∠-∠，在BCE ∆中，180BEC B C ∠=︒-∠-∠，AED BEC ∠=∠，A D B C ∴∠+∠=∠+∠；（3）①180A ABC ACB ∠=︒-∠-∠，180D DBC DCB ∠=︒-∠-∠，BD 、CD 分别平分ABC∠和ACB ∠，∴1122ABC ACB DBC DCB ∠+∠=∠+∠，1111180()180(180)902222D ABC ACB A A ∴∠=︒-∠+∠=︒-︒-∠=︒+∠．故答案为：1902D A ∠=︒+∠． ②连结BE ． ∵C D CBE DEB ∠+∠=∠+∠，360A B C D E F A ABE F BEF ∴∠+∠+∠+∠+∠+∠=∠+∠+∠+∠=︒．故答案为：360︒；（4）由（1）知，BDC B C BAC ∠=∠+∠+∠，26B ∠=︒，54C ∠=︒，80BDC BAC ∴∠=︒+∠，402CDF CAE ∴∠=︒+∠，4BAC CAE ∠=∠，2BDC CDF ∠=∠，1902GDE CDF ∴∠=︒-∠，26180AGD B GDB CDF ∠=∠+∠=︒+︒-∠，3GAE CAE ∠=∠，3336064(2)644012422E GAE AGD GDE CAE CDF ∴∠=︒-∠-∠-∠=︒-∠-∠=︒+⨯︒=︒；180180(206)2262264014F AGF GAF CDF CAE CDF CAE ∠=︒-∠-∠=︒-︒-∠-∠=-︒+∠-∠=-︒+︒=︒．【点睛】本题考查了角平分线的性质，三角形内角和；熟练掌握角平分线的性质，进行合理的等量代换是解题的关键．13．（1）40°；（2）的值不变，比值为;（3）∠OEC=∠OBA=60°. 【分析】（1）根据OB 平分∠AOF ，OE 平分∠COF ，即可得出∠EOB=∠EOF+∠FOB=∠COA ，从而得出答案；（2解析：（1）40°；（2）:OBC OFC ∠∠的值不变，比值为12;（3）∠OEC=∠OBA=60°. 【分析】（1）根据OB 平分∠AOF ，OE 平分∠COF ，即可得出∠EOB=∠EOF+∠FOB=12∠COA ，从而得出答案；（2）根据平行线的性质，即可得出∠OBC=∠BOA ，∠OFC=∠FOA ，再根据∠FOA=∠FOB+∠AOB=2∠AOB ，即可得出∠OBC ：∠OFC 的值为1：2．（3）设∠AOB=x ，根据两直线平行，内错角相等表示出∠CBO=∠AOB=x ，再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠OEC ，然后利用三角形的内角和等于180°列式表示出∠OBA ，然后列出方程求解即可．【详解】（1）∵CB ∥OA ∴∠C+∠COA=180° ∵∠C=100°∴∠COA=180°-∠C=80° ∵∠FOB=∠AOB ，OE 平分∠COF∴∠FOB+∠EOF=12（∠AOF+∠COF ）=12∠COA=40°; ∴∠EOB=40°;（2）∠OBC ：∠OFC 的值不发生变化 ∵CB ∥OA∴∠OBC=∠BOA ，∠OFC=∠FOA ∵∠FOB=∠AOB ∴∠FOA=2∠BOA ∴∠OFC=2∠OBC ∴∠OBC ：∠OFC=1：2（3）当平行移动AB 至∠OBA=60°时，∠OEC=∠OBA ．设∠AOB=x ， ∵CB ∥AO ， ∴∠CBO=∠AOB=x ， ∵CB ∥OA ，AB ∥OC ，∴∠OAB+∠ABC=180°，∠C+∠ABC=180° ∴∠OAB=∠C=100°．∵∠OEC=∠CBO+∠EOB=x+40°，∠OBA=180°-∠OAB-∠AOB=180°-100°-x=80°-x ， ∴x+40°=80°-x ， ∴x=20°，∴∠OEC=∠OBA=80°-20°=60°．【点睛】本题主要考查了平行线、角平分线的性质以及三角形内角和定理，熟记各性质并准确识图理清图中各角度之间的关系是解题的关键．14．（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2解析：（1）140°；（2）∠1+∠2=90°+α；（3）∠1=90°+∠2+α,理由见解析;(4)∠2=90°+∠1﹣α．【详解】试题分析：（1）根据四边形内角和定理以及邻补角的定义，得出∠1+∠2=∠C+∠α，进而得出即可；（2）利用（1）中所求的结论得出∠α、∠1、∠2之间的关系即可；（3）利用三角外角的性质，得出∠1=∠C+∠2+α=90°+∠2+α；（4）利用三角形内角和定理以及邻补角的性质可得出∠α、∠1、∠2之间的关系．试题分析：（1）∵∠1＋∠2＋∠CDP＋∠CEP＝360°，∠C＋∠α＋∠CDP＋∠CEP＝360°，∴∠1＋∠2＝∠C＋∠α，∵∠C＝90°，∠α＝50°，∴∠1＋∠2＝140°，故答案为140；（2）由(1)得∠α＋∠C＝∠1＋∠2，∴∠1＋∠2＝90°＋∠α.故答案为∠1＋∠2＝90°＋∠α.（3）∠1＝90°＋∠2＋∠α.理由如下：如图③，设DP与BE的交点为M，∵∠2＋∠α＝∠DME，∠DME＋∠C＝∠1，∴∠1＝∠C＋∠2＋∠α＝90°＋∠2＋∠α.（4）如图④，设PE 与AC 的交点为F ，∵∠PFD ＝∠EFC ，∴180°－∠PFD ＝180°－∠EFC ，∴∠α＋180°－∠1＝∠C ＋180°－∠2，∴∠2＝90°＋∠1－∠α.故答案为∠2＝90°＋∠1－∠α点睛：本题考查了三角形内角和定理和外角的性质、对顶角相等的性质，熟练掌握三角形外角的性质是解决问题的关键.15．（1）①70；②∠F=∠BED ，证明见解析；（2）2∠F+∠BED=360°；（3）【分析】（1）①过F 作FG//AB ，利用平行线的判定和性质定理得到∠DFB=∠DFG+∠BFG=∠CDF+∠A解析：（1）①70；②∠F =12∠BED ，证明见解析；（2）2∠F+∠BED =360°；（3）3045α︒≤<︒ 【分析】（1）①过F 作FG//AB ，利用平行线的判定和性质定理得到∠DFB=∠DFG+∠BFG=∠CDF+∠ABF ，利用角平分线的定义得到∠ABE+∠CDE=2∠ABF+2∠CDF=2（∠ABF+∠CDF ），求得∠ABF+∠CDF=70︒，即可求解； ②分别过E 、F 作EN//AB ，FM//AB ，利用平行线的判定和性质得到∠BED=∠ABE+∠CDE ，利用角平分线的定义得到∠BED=2（∠ABF+∠CDF ），同理得到∠F=∠ABF+∠CDF ，即可求解；（2）根据∠ABE 的平分线与∠CDE 的平分线相交于点F ，过点E 作EG ∥AB ，则∠BEG+∠ABE=180°，因为AB ∥CD ，EG ∥AB ，所以CD ∥EG ，所以∠DEG+∠CDE=180°，再结合①的结论即可说明∠BED 与∠BFD 之间的数量关系；（3）通过对1452E F ∠≥∠+︒的计算求得30α≥︒，利用角平分线的定义以及三角形外角的性质求得45α<︒，即可求得3045α︒≤<︒．【详解】（1）①过F 作FG//AB ，如图：∵AB ∥CD ，FG ∥AB ，∴CD ∥FG ，∴∠ABF=∠BFG ，∠CDF=∠DFG ，∴∠DFB=∠DFG+∠BFG=∠CDF+∠ABF ，∵BF平分∠ABE，∴∠ABE=2∠ABF，∵DF平分∠CDE，∴∠CDE=2∠CDF，∴∠ABE+∠CDE=2∠ABF+2∠CDF=2（∠ABF+∠CDF）=60︒+80︒=140︒，∴∠ABF+∠CDF=70︒，∴∠DFB=∠ABF+∠CDF=70︒，故答案为：70；∠BED，②∠F=12理由是：分别过E、F作EN//AB，FM//AB，∵EN//AB，∴∠BEN=∠ABE，∠DEN=∠CDE，∴∠BED=∠ABE+∠CDE，∵DF、BF分别是∠CDE的角平分线与∠ABE的角平分线，∴∠ABE=2∠ABF，∠CDE=2∠CDF，即∠BED=2（∠ABF+∠CDF）；同理，由FM//AB，可得∠F=∠ABF+∠CDF，∠BED；∴∠F=12（3）2∠F+∠BED=360°．如图，过点E作EG∥AB，则∠BEG+∠ABE=180°，∵AB∥CD，EG∥AB，∴CD∥EG，∴∠DEG+∠CDE=180°，∴∠BEG+∠DEG=360°-（∠ABE+∠CDE），即∠BED=360°-（∠ABE+∠CDE），∵BF平分∠ABE，∴∠ABE=2∠ABF，∵DF平分∠CDE，∴∠CDE=2∠CDF ，∠BED=360°-2（∠ABF+∠CDF ），由①得：∠BFD=∠ABF+∠CDF ，∴∠BED=360°-2∠BFD ，即2∠F+∠BED=360°；（3）∵1452E F ∠≥∠+︒，∠F =α，∴2452αα≥+︒，解得：30α≥︒，如图，∵∠CDE 为锐角，DF 是∠CDE 的角平分线，∴∠CDH=∠DHB 190452<⨯︒=︒， ∴∠F <∠DHB 45<︒，即45α<︒，∴3045α︒≤<︒，故答案为：3045α︒≤<︒．【点睛】本题考查了平行线的性质、角平分线的定义以及三角形外角性质的应用，在解答此题时要注意作出辅助线，构造出平行线求解．。

四川省成都市石室中学数学三角形填空选择(提升篇)(Word版含解析)

四川省成都市石室中学数学三角形填空选择（提升篇）（Word 版含解析）一、八年级数学三角形填空题（难）1．如图，ABC ∆的面积为1，第一次操作：分别延长AB ，BC ，CA 至点111,,A B C ，使111,,A B AB B C BC C A CA ===，顺次连接111,,A B C ，得到111A B C ∆；第二次操作：分别延长111111,,A B B C C A 至点222,,A B C ，使2111A B A B =，2111B C B C =，2111C A C A =，顺次连接222,,A B C ，得到222A B C ∆，…；按此规律，要使得到的三角形的面积超过2020，最少需经过__________次操作.【答案】4【解析】【分析】连接111,,AC B A C B ，根据两个三角形等底同高可得111111111,C A B C AB A B C A BC B C A B CA ABC S S S S S S S ======从而得出第一次操作：11177A B C ABC S S ∆∆==＜2020；同理可得第二次操作22211127749A B C A B C S S ∆∆===＜2020……直至第四次操作4443334772401A B C A B C S S ∆∆===＞2020，即可得出结论．【详解】解：连接111,,AC B A C B∵111,,A B AB B C BC C A CA ===根据等底同高可得：111111111,,C A B C AB ABC A B C A BC ABC B C A B CA ABC S S S S SS S S S ====== ∴111111111,C A B C AB A B C A BC B C A B CA ABC S S S S S S S ======∴第一次操作：11177A B C ABC S S ∆∆==＜2020同理可得第二次操作22211127749A B C A B C S S ∆∆===＜2020第三次操作333222377343A B C A B C S S ∆∆===＜2020第四次操作4443334772401A B C A B C S S ∆∆===＞2020故要使得到的三角形的面积超过2020，最少需经过4次操作，故答案为：4．【点睛】此题考查的是三角形的面积关系和探索规律，掌握两个三角形等底同高时，面积相等是解决此题的关键．2．如图，在△ABC 中，∠B=50°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC =_______°.【答案】65【解析】如图，∵AE 平分∠DAC ，CE 平分∠ACF ，∴∠1=12∠DAC ，∠2=12∠ACF ， ∴∠1+∠2=12（∠DAC+∠ACF ），又∵∠DAC+∠ACF=（180°-∠BAC ）+（180°-∠ACB ）=360°-（∠BAC+∠ACB ），且 ∠BAC+∠ACB=180°-∠ABC=180°-50°=130°，∴∠1+∠2=12（360°-130°）=115°， ∴在△ACE 中，∠E=180°-（∠1+∠2）=180°-115°=65°.3．有公共顶点A ，B 的正五边形和正六边形按如图所示位置摆放，连接AC 交正六边形于点D，则∠ADE的度数为（）A．144°B．84°C．74°D．54°【答案】B【解析】正五边形的内角是∠ABC=()521805-⨯=108°，∵AB=BC，∴∠CAB=36°，正六边形的内角是∠ABE=∠E=()621806-⨯=120°，∵∠ADE+∠E+∠ABE+∠CAB=360°，∴∠ADE=360°–120°–120°–36°=84°，故选B．4．已知一个多边形的内角和与外角和的差是1260°，则这个多边形边数是．【答案】12【解析】试题解析：根据题意，得（n-2）•180-360=1260，解得：n=11．那么这个多边形是十一边形．考点：多边形内角与外角．5．等腰三角形一边长是10cm，一边长是6cm，则它的周长是_____cm或_____cm．【答案】22cm,26cm【解析】【分析】题目给出等腰三角形有两条边长为10cm和6cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】（1）当腰是6cm时，周长＝6+6+10＝22cm；（2）当腰长为10cm时，周长＝10+10+6＝26cm，所以其周长是22cm或26cm．故答案为：22，26．【点睛】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．6．如图所示，小明从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，…，照这样下去，他第一次回到出发地A点时，（1）左转了____次；（2）一共走了_____米．【答案】11120【解析】∵360÷30=12，∴他需要走12−1=11次才会回到原来的起点，即一共走了12×10=120米.故答案为11，120.7．如图，已知△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B=40°，∠C=78°，则∠EAD=____°．【答案】19°．【解析】【分析】根据三角形内角和定理求得∠BAC，再由AE平分∠BAC，可求得∠EAC，最后由∠ADC=90°，∠C=78°，可求得∠DAC，即∠EAD可求．【详解】解：∵∠B=40°，∠C=78°∴∠BAC=180°-∠B-∠C=62°∵AE平分∠BAC，∴∠EAC=1312BAC∠=，∵AD是BC边上的高∴∠ADC=90°∴∠DAC=90°-78°=12°∴∠EAD=∠EAC-∠DAC=19°故答案为：19°．【点睛】本题考查三角形内角和定理；三角形角平分线性质．8．如图，△ABC中，∠B与∠C的平分线交于点O，过O作EF∥BC交AB、AC于E、F，若△ABC的周长比△AEF的周长大12cm，O到AB的距离为4cm，△OBC的面积_____cm2．cm．【答案】242【解析】【分析】由BE=EO可证得EF∥BC，从而可得∠FOC=∠OCF，即得OF=CF；可知△AEF等于AB+AC，所以根据题中的条件可得出BC及O到BC的距离，从而能求出△OBC的面积．【详解】∵BE=EO，∴∠EBO=∠EOB=∠OBC，∴EF∥BC，∴∠FOC=∠OCB=∠OCF，∴OF=CF；△AEF等于AB+AC，又∵△ABC的周长比△AEF的周长大12cm，∴可得BC=12cm，根据角平分线的性质可得O到BC的距离为4cm，∴S△OBC=1×12×4=24cm2．2考点：1．三角形的面积；2．三角形三边关系．9．如图，在△ABC中，∠A=70°，点O到AB,BC,AC的距离相等，连接BO，CO，则∠BOC=________．【答案】125°【解析】【分析】根据角平分线性质推出O为△ABC三角平分线的交点，根据三角形内角和定理求出∠ABC+∠ACB，根据角平分线定义求出∠OBC+∠OCB，即可求出答案．【详解】：∵点O到AB、BC、AC的距离相等，∴OB平分∠ABC，OC平分∠ACB，∴12OBC ABC∠=∠，12OCB ACB∠=∠，∵∠A=70°，∴∠ABC+∠ACB=180°-70°=110°，∴1110552OBC OCB∠+∠=⨯︒=︒，∴∠BOC=180°-（∠OBC+∠OCB）=125°；故答案为：125．【点睛】本题主要考查平分线的性质，三角形内角和定理的应用，能求出∠OBC+∠OCB的度数是解此题的关键．10．如图，已知长方形纸片的一条边经过直角三角形纸片的直角顶点，若长方形纸片的一组对边与直角三角形的两条直角边相交成∠1，∠2，则∠2-∠1=____.【答案】90°【解析】【分析】【详解】如图：∵∠2+∠3=180°，∴∠3=180°﹣∠2．∵直尺的两边互相平行，∴∠4=∠3，∴∠4=180°﹣∠2．∵∠4+∠1=90°，∴180°﹣∠2+∠1=90°，即∠2﹣∠1=90°．故答案为90°.二、八年级数学三角形选择题（难）11．若△ABC内有一个点P1，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A．n·180°B．（n+2）·180°C．（2n-1）·180°D．（2n+1）·180°【答案】D【解析】【分析】当△ABC内的点的个数是1时，三角形内互不重叠的小三角形的个数是3；当△ABC内的点的个数是2时，三角形内互不重叠的小三角形的个数是5；依此类推得到当△ABC内的点的个数是3时，三角形内互不重叠的小三角形的个数是7；当△ABC内的点的个数是n 时，三角形内互不重叠的小三角形的个数2n+1，所以这些小三角形的内角和为（2n+1）·180°【详解】】解：图1中，当△ABC内只有1个点时，可分割成3个互不重叠的小三角形；图2中，当△ABC内只有2个点时，可分割成5个互不重叠的小三角形；图3中，当△ABC内只有3个点时，可分割成7个互不重叠的小三角形；根据以上规律，当△ABC内有n个点（P1，P2，…，P n）时，可以把△ABC分割成S=2n+1个互不重叠的三角形，所以这些小三角形的内角和为（2n+1）·180°.【点睛】此题考查了平面图形的有规律变化，要求学生通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．12．图1是二环三角形，S＝∠A1+∠A2+…+∠A6=360，图2是二环四边形，S＝∠A1+∠A2+…+∠A8=720，图3是二环五边形，S＝∠A1+∠A2+…+∠A10=1080…聪明的同学，请你直接写出二环十边形，S＝_____________度（）A．1440 B．1800 C．2880 D．3600【答案】C【解析】【分析】本题只看图觉得很复杂，但从数据入手，就简单了，从图2开始，每个图都比前一个图多360度．抓住这点就很容易解决问题了．【详解】解：依题意可知，二环三角形，S＝360度；二环四边形，S＝720＝360×2＝360×（4﹣2）度；二环五边形，S＝1080＝360×3＝360×（5﹣2）度；…∴二环十边形，S＝360×（10﹣2）＝2880度．故选：C．【点睛】本题考查了多边形的内角和，本题可直接根据S的度数来找出规律，然后根据规律表示出二环十边形的度数．A B C．再分13．如图，ABC的面积为1．分别倍长（延长一倍）AB，BC，CA得到111A B C．…… 按此规律，倍长2018次后得到的别倍长A1B1，B1C1，C1A1得到222A B C的面积为（）201820182018A．201787D．2018 6B．20186C．2018【答案】C【解析】分析：根据等底等高的三角形的面积相等可得三角形的中线把三角形分成两个面积相等的三角形，然后求出第一次倍长后△A1B1C1的面积是△ABC的面积的7倍，依此类推写出即可．详解：连接AB1、BC1、CA1，根据等底等高的三角形面积相等，△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等，所以，S△A1B1C1=7S△ABC，同理S△A2B2C2=7S△A1B1C1=72S△ABC，依此类推，S△AnBnCn=7n S△ABC．∵△ABC 的面积为1，∴S△AnBnCn=7n，∴S△A2018B2018C2018=72018．故选C．点睛：本题考查了三角形的面积，根据等底等高的三角形的面积相等求出一次倍长后所得的三角形的面积等于原三角形的面积的7倍是解题的关键．14．如图，七边形ABCDEFG 中，AB ，ED 的延长线交于点O ，若∠1，∠2，∠3，∠4的外角和等于215°，则∠BOD 的度数为( )A ．20°B ．35°C ．40°D ．45°【答案】B【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE 的内角和，则可求得∠BOD ．【详解】解：∵∠1、∠2、∠3、∠4的外角的角度和为215°，∴∠1+∠2+∠3+∠4+215°=4×180°，∴∠1+∠2+∠3+∠4=505°，∵五边形OAGFE 内角和=（5-2）×180°=540°，∴∠1+∠2+∠3+∠4+∠BOD=540°，∴∠BOD=540°-505°=35°，故选：B ．【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．15．如图，将一张三角形纸片ABC 的一角折叠，使点A 落在ABC ∆处的'A 处，折痕为DE .如果A α∠=，'CEA β∠=，'BDA γ∠=，那么下列式子中正确的是（）A ．2γαβ=+B ．2γαβ=+C ．γαβ=+D ．180γαβ=--【答案】A【解析】【分析】【详解】分析:根据三角形的外角得：∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，代入已知可得结论.详解:由折叠得：∠A=∠A'，∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，∵∠A=α，∠CEA′=β，∠BDA'=γ，∴∠BDA'=γ=α+α+β=2α+β，故选A.点睛：本题考查了三角形外角的性质，熟练掌握三角形的外角等于与它不相邻的两个内角的和是关键.16．如图所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米，又向左转24°，……，照这样走下去，他第一次回到出发地A点时，一共走的路程是（）A．140米B．150米C．160米D．240米【答案】B【解析】【分析】由题意可知小华走出了一个正多边形，根据正多边形的外角和公式可求解.【详解】已知多边形的外角和为360°，而每一个外角为24°，可得多边形的边数为360°÷24°=15，所以小明一共走了：15×10=150米．故答案选B．【点睛】本题考查多边形内角与外角，熟记公式是关键.17．如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG=2∠DCB；②∠DFB=∠CGE；③∠ADC=∠GCD；④CA平分∠BCG;其中正确的个数是（）A．1B．2C．3D．4【答案】C【解析】【分析】根据平行线、角平分线、垂直的性质及三角形内角和定理依次判断即可得出答案．【详解】①∵EG∥BC，∴∠CEG=∠ACB．又∵CD是△ABC的角平分线，∴∠CEG=∠ACB=2∠DCB，故正确；④无法证明CA平分∠BCG，故错误；③∵∠A=90°，∴∠ADC+∠ACD=90°．∵CD平分∠ACB，∴∠ACD=∠BCD，∴∠ADC+∠BCD=90°．∵EG∥BC，且CG⊥EG，∴∠GCB=90°，即∠GCD+∠BCD=90°，∴∠ADC=∠GCD，故正确；②∵∠EBC+∠ACB=∠AEB，∠DCB+∠ABC=∠ADC，∴∠AEB+∠ADC=90°+（∠ABC+∠ACB）=135°，∴∠DFE=360°﹣135°﹣90°=135°，∴∠DFB=45°=∠CGE，∴∠CGE=2∠DFB，∴∠DFB=∠CGE，故正确．故选C．点睛：本题主要考查的是三角形内角和定理，熟知直角三角形的两锐角互余是解答此题的关键．18．若一个凸多边形的内角和为720°，则这个多边形的边数为()A．4 B．5 C．6 D．7【答案】C【解析】【分析】设这个多边形的边数为n，根据多边形的内角和定理得到(n﹣2)×180°=720°，然后解方程即可．【详解】设这个多边形的边数为n，由多边形的内角和是720°，根据多边形的内角和定理得（n－2）180°=720°．解得n=6.故选C.【点睛】本题主要考查多边形的内角和定理，熟练掌握多边形的内角和定理是解答本题的关键.19．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（）A．108°B．90°C．72°D．60°【答案】C【解析】【分析】首先设此多边形为n边形，根据题意得：180（n-2）=540，即可求得n=5，再由多边形的外角和等于360°，即可求得答案．【详解】解：设此多边形为n边形，根据题意得：180（n-2）=540，解得：n=5，∴这个正多边形的每一个外角等于：3605=72°．故选C．【点睛】此题考查了多边形的内角和与外角和的知识．注意掌握多边形内角和定理：（n-2）•180°，外角和等于360°．20．若（a﹣3）2+|b﹣6|＝0，则以a、b为边长的等腰三角形的周长为（）A．12 B．15 C．12或15 D．18【答案】B【解析】【分析】根据非负数的和为零，可得每个非负数同时为零，可得a、b的值，根据等腰三角形的判定，可得三角形的腰，根据三角形的周长公式，可得答案．【详解】由（a﹣3）2+|b﹣6|＝0，得a﹣3＝0，b﹣6＝0．则以a、b为边长的等腰三角形的腰长为6，底边长为3，周长为6+6+3＝15，故选B．【点睛】本题考查了非负数的性质，利用非负数的和为零得出每个非负数同时为零是解题关键．。

成都市石室外语学校八年级数学上册第十二章《全等三角形》(含答案解析)

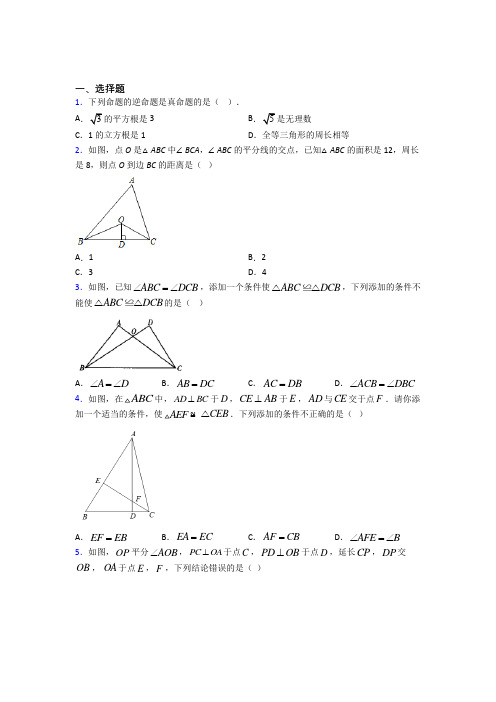
一、选择题1．下列命题的逆命题是真命题的是（）．A ．3的平方根是3B ．5是无理数C ．1的立方根是1D ．全等三角形的周长相等 2．如图，点O 是△ABC 中∠BCA ，∠ABC 的平分线的交点，已知△ABC 的面积是12，周长是8，则点O 到边BC 的距离是（）A ．1B ．2C ．3D ．4 3．如图，已知ABC DCB ∠=∠，添加一个条件使ABC DCB △△≌，下列添加的条件不能使ABC DCB △△≌的是（）A ．A D ∠=∠B ．AB DC = C ．AC DB =D ．ACB DBC ∠=∠ 4．如图，在ABC 中，AD BC ⊥于D ，CE AB ⊥于E ，AD 与CE 交于点F ．请你添加一个适当的条件，使AEF ≌CEB △．下列添加的条件不正确的是（）A ．EF EB = B ．EA EC = C ．AF CB =D ．AFE B ∠=∠ 5．如图，OP 平分AOB ∠，PC OA ⊥于点C ，PD OB ⊥于点D ，延长CP ，DP 交OB ， OA 于点E ，F ，下列结论错误的是（）A ．PC PD =B ．OC OD = C ．CPO DPO ∠=∠ D ．PC PE =6．如图，给出下列四组条件：①AB=DE ，BC=EF ，AC=DF ；②AB=DE ，∠B=∠E ，BC=EF ；③∠B=∠E ，BC=EF ，∠C=∠F ；④AB=DE ，AC=DF ，∠B=∠E ．其中，能使△ABC ≌△DEF 的条件共有（）A ．1组B ．2组C ．3组D ．4组 7．如图，∠ACB=90°，AC=BC ，AD ⊥CE ，BE ⊥CE ，垂足分别是点D 、E ，AD=3，BE=1，则DE 的长是（）A ．1.5B ．2C ．22D ．10 8．下列各命题中，假命题是（）A ．有两边及其中一边上的中线对应相等的两个三角形全等B ．有两边及第三边上高对应相等的两个三角形全等C ．有两角及其中一角的平分线对应相等的两三角形全等D ．有两边及第三边上的中线对应相等的两三角形全等9．如图，AB ＝4cm ，AC ＝BD ＝3cm ，∠CAB ＝∠DBA ，点P 在线段AB 上以1cm/s 的速度由点A 向点B 运动，同时，点Q 在线段BD 上由点B 向点D 运动．设运动时间为t （s ），当△ACP 与△BPQ 全等时，则点Q 的运动速度为（）cm/s ．A ．0.5B ．1C ．0.5或1.5D ．1或1.5 10．下列命题，真命题是（）A ．全等三角形的面积相等B ．面积相等的两个三角形全等C ．两个角对应相等的两个三角形全等D ．两边和其中一边的对角对应相等的两个三角形全等11．如图，已知AE 平分∠BAC ，BE ⊥AE 于E ，ED ∥AC ，∠BAE ＝34°，那么∠BED ＝（）A ．134°B ．124°C ．114°D ．104° 12．在尺规作图作一个角的平分线时的两个三角形全等的依据是（）A ．SASB ．AASC ．SSSD ．HL 13．根据下列条件，能画出唯一ABC 的是（）A ．3AB =，4BC =，7CA =B ．4AC =，6BC =，60A ∠=︒ C ．45A ∠=︒，60B ∠=︒，75C ∠=︒D ．5AB =，4BC =，90C ∠=︒ 14．如图，在Rt ABC 和Rt ADE △中，90,,ACB AED AB AD AC AE ∠=∠===，则下列说法不正确的是（）A ．BC DE =B ．BAE DAC ∠=∠ C ．OC OE =D ．EAC ABC ∠=∠ 15．如图，要判定△ABD ≌△ACD ，已知AB ＝AC ，若再增加下列条件中的一个，仍不能说明全等，则这个条件是（）A ．CD ⊥AD ，BD ⊥ADB ．CD ＝BDC ．∠1＝∠2D ．∠CAD ＝∠B AD二、填空题16．如图，已知在四边形ABCD 中，∠BCD ＝90°，BD 平分∠ABC ，AB ＝12，BC ＝18，CD ＝8，则四边形ABCD 的面积是____．17．如图，把等腰直角三角板放平面直角坐标系内，已知直角顶点C 的坐标为()0,3，另一个顶点B 的坐标为()8,8，则点A 的坐标为____________18．如图，△ABE ≌△ADC ≌△ABC ，若∠1＝130°，则∠α的度数为________．19．已知在△ABC 中，AB ＝9，中线AD ＝4，那么AC 的取值范围是____20．小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第____块去，这利用了三角形全等中的____原理．21．如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，交BC 边于点D ，若12AB =，4CD =，则ABD △ 的面积为__________．22．如图，△ABC ≌△A'B'C'，其中∠A ＝35°，∠C ＝25°，则∠B'＝_____．23．如图，在Rt △ABC 中，∠C ＝90°，D 、E 分别为边BC 、AB 上的点，且AE ＝AC ，DE ⊥AB ．若∠ADC ＝61°，则∠B 的度数为_____．24．已知△ABC ≌△DEF ，△ABC 的三边分别为3，m ，n ，△DEF 的三边分别为5，p ，q ．若△ABC 的三边均为整数，则m+n+p+q 的最大值为________．25．如图，在ABC 中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①120EDF ∠=︒；②DM 平分EDF ∠；③DE DF AD +=；④2AB AC AE +>；其中正确的有________(请将正确结论的序号填写在横线上)．26．如图，在△ABC 中，∠C =90°，∠A 的平分线交BC 于D ，若20ABD S ∆=cm 2，AB =10cm ，则CD 为__________cm ．三、解答题27．如图，点A ，E ，F ，B 在直线l 上，AE BF =，//AC BD ，且AC BD =，求证：ACF BDE ≅△△．28．（教材呈现）数学课上，赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法，方法如下：试一试如图，AOB ∠为已知角，试按下列步骤用直尺和圆规准确地作出AOB ∠的平分线.第一步：在射线OA 、OB 上，分别截取OD 、OE ，使0;OD E =第二步：分别以点D 和点E 为圆心，适当长(大于线段DE 长的一半)为半径作圆弧，在AOB ∠内，两弧交于点C ；第三步：作射线OC .射线OC 就是所要求作的AOB ∠的平分线（问题1）赵老师用尺规作角平分线时，用到的三角形全等的判定方法是__________________．（问题2）小明发现只利用直角三角板也可以作AOB ∠的角平分线，方法如下：步骤：①利用三角板上的刻度，在OA 、OB 上分别截取OM 、ON ，使OM ON =． ②分别过点M 、N 作OM 、ON 的垂线，交于点P ．③作射线OP ，则OP 为AOB ∠的平分线．请根据小明的作法，求证OP 为AOB ∠的平分线．29．如图，在△ABC 中，AD 是∠BAC 的角平分线，DE ⊥AB ，DF ⊥AC ，D 是BC 的中点，证明：∠B =∠C ．30．已知4,BC BA BC =⊥，射线CM BC ⊥，动点P 在BC 上，PD PA ⊥交CM 于D ．（1）如图1，当3,1BP AB ==时，求DC 的长；（2）如图2，连接AD ，当DP 平分ADC ∠时，求BP 的长．。

七年级上册成都石室联合中学数学期末试卷易错题(Word版含答案)

七年级上册成都石室联合中学数学期末试卷易错题（Word版含答案）一、初一数学上学期期末试卷解答题压轴题精选（难）1．如图 1，CE 平分∠ACD，AE 平分∠BAC，且∠EAC＋∠ACE=90°．（1）请判断 AB 与 CD 的位置关系，并说明理由；（2）如图2，若∠E=90°且AB 与CD 的位置关系保持不变，当直角顶点E 移动时，写出∠BAE 与∠ECD 的数量关系，并说明理由；（3）如图 3，P 为线段 AC 上一定点，点 Q 为直线 CD 上一动点，且 AB 与 CD 的位置关系保持不变，当点 Q 在射线 CD 上运动时(不与点 C 重合)，∠PQD，∠APQ 与∠ BAC 有何数量关系？写出结论，并说明理由．【答案】（1），理由如下：CE 平分，AE 平分，；（2），理由如下：如图，延长AE交CD于点F，则由三角形的外角性质得：；（3），理由如下：，即由三角形的外角性质得：又，即即．【解析】【分析】（1）根据角平分线的定义、平行线的判定即可得；（2）根据平行线的性质（两直线平行，内错角相等）、三角形的外角性质即可得；（3）根据平行线的性质（两直线平行，同旁内角互补）、三角形的外角性质、邻补角的定义即可得．2．点O为直线AB上一点，过点O作射线OC，使∠BOC＝65°，将一直角三角板的直角顶点放在点O处．（1）如图①，将三角板MON的一边ON与射线OB重合时，则∠MOC＝________；（2）如图②，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；（3）将三角板MON绕点O逆时针旋转至图③时，∠NOC＝∠AOM，求∠NOB的度数．【答案】（1）25°（2）解：∠BOC=65°，OC平分∠MOB∠MOB=2∠BOC=130°∠BON=∠MOB-∠MON=130°-90°=40°∠CON=∠COB-∠BON=65°-40°=25°（3）解：∠NOC= ∠AOM ∠AOM=4∠NOC ∠BOC=65°∠AOC=∠AOB-∠BOC=180°-65°=115°∠MON=90°∠AOM+∠NOC=∠AOC-∠MON=115°-90°=25°4∠NOC+∠NOC=25°∠NOC=5°∠NOB=∠NOC+∠BOC=70°【解析】【解答】解：（1）∠MON=90，∠BOC=65°∠MOC=∠MON-∠BOC=90°-65°=25°【分析】（1）根据∠MON和∠BOC的度数可以得到∠MON的度数；（2）根据角平分线的性质，由∠BOC=65°，可以求得∠BOM的度数，然后由∠NOM-90°，可得∠BON的度数，从而得解；（3）由∠BOC=65°，∠NOM=90°，∠NOC= ∠AOM，从而可求得∠NOC的度数，然后由∠BOC=65°，从而得解.3．如图，在平面直角坐标系中，已知点A（0，4），B（3，0），线段AB平移后对应的线段为CD，点C在x轴的负半轴上，B、C两点之间的距离为8．（1）求点D的坐标；（2）如图（1），求△ACD的面积；（3）如图（2），∠OAB与∠OCD的角平分线相交于点M，探求∠AMC的度数并证明你的结论．【答案】（1）解：∵B（3，0），∴OB＝3，∵BC＝8，∴OC＝5，∴C（﹣5，0），∵AB∥CD，AB＝CD，∴D（﹣2，﹣4）（2）解：如图（1），连接OD，∴S△ACD＝S△ACO+S△DCO﹣S△AOD＝﹣＝16（3）解：∠M＝45°，理由是：如图（2），连接AC，∵AB∥CD，∴∠DCB＝∠ABO，∵∠AOB＝90°，∴∠OAB+∠ABO＝90°，∴∠OAB+∠DCB＝90°，∵∠OAB与∠OCD的角平分线相交于点M，∴∠MCB＝，∠OAM＝，∴∠MCB+∠OAM＝＝45°，△ACO中，∠AOC＝∠ACO+∠OAC＝90°，△ACM中，∠M+∠ACM+∠CAM＝180°，∴∠M+∠MCB+∠ACO+∠OAC+∠OAM＝180°，∴∠M＝180°﹣90°﹣45°＝45°．【解析】【分析】（1）利用B的坐标，可得OB=3，从而求出OC=5，利用平移的性质了求出点D的坐标.（2）如图（1），连接OD，由S△ACD=S△ACO+S△DCO+S△AOD，利用三角形的面积公式计算即得.（3）连接AC，利用平行线的性质及直角三角形两锐角互余可得∠OAB+∠DCB＝90°，利用角平分线的定义可得∠MCB+∠OAM＝＝45°，根据三角形的内角和等于180°，即可求出∠M的度数.4．探究与发现：（1）探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系为：________（直接写出结果）．（2）探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图2，在△ADC中，DP，CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系为：________（直接写出结果）．（3）探究三：若将△ADC改为任意四边形ABCD呢？已知：如图3，在四边形ABCD中，DP，CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．【答案】（1）∠FDC+∠ECD=∠A+180°（2）∠P=90°+ ∠A（3）解：∵DP、CP分别平分∠ADC和∠BCD，【解析】【解答】（1）探究一：∵∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，故答案为：（ 2 ）探究二：∵DP、CP分别平分∠ADC和∠ACD，故答案为：【分析】（1）由三角形的一个外角等于和它不相邻的两个内角的和可得∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，再将两个等式两边分别相加并运用三角形的内角和定理即可求解；（2）由角平分线的定义可得∠PDC=∠ADC，∠PCD=∠ACD，再结合三角形的内角和定理即可求解；（3）由角平分线的定义可得∠PDC=∠ADC，∠PCD=∠BCD，再结合三角形的内角和定理和四边形的内角和定理即可求解。

成都石室中学初中学校数学全等三角形章末训练(Word版含解析)

成都石室中学初中学校数学全等三角形章末训练（Word版含解析）一、八年级数学轴对称三角形填空题（难）1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．【答案】4【解析】【分析】由A点坐标可得OA=22，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.【详解】（1）当点P在x轴正半轴上，①如图，以OA为腰时，∵A的坐标是（2，2），∴∠AOP＝45°，OA＝22，当∠AOP为顶角时，OA=OP=22，当∠OAP为顶角时，AO=AP，∴OPA=∠AOP=45°，∴∠OAP=90°，∴OP=2OA=4，∴P的坐标是（4，0）或（22，0）.②以OA为底边时，∵点A的坐标是（2，2），∴∠AOP=45°，∵AP=OP，∴∠OAP=∠AOP=45°，∴∠OPA=90°，∴OP=2，∴P 点坐标为（2，0）.（2）当点P 在x 轴负半轴上，③以OA 为腰时，∵A 的坐标是（2，2），∴OA ＝22，∴OA ＝OP ＝22，∴P 的坐标是（﹣22，0）．综上所述：P 的坐标是（2，0）或（4，0）或（2，0）或（﹣2，0）．故答案为：4．【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．2．在ABC ∆中，边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ，20DAE ∠=︒，则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意，点D 和点E 的位置不确定，需分析谁靠近B 点，则有如下图（图见解析）两种情况：（1）图1中，点E 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠，再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒，联立即可求得；（2）图2中，点D 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有3,4B C ∠=∠∠=∠，由三角形的内角和定理得180B C BAC ∠+∠+∠=︒，联立即可求得.【详解】由题意可分如下两种情况：（1）图1中，根据垂直平分线性质可知，,BD AD AE CE ==，1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠（等边对等角），两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠，又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒，由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠+︒+∠=︒，80BAC ∴∠=︒；（2）图2中，根据垂直平分线性质可知，,BD AD AE CE ==，3,4B C ∴∠=∠∠=∠（等边对等角），两式相加得34B C ∠+∠=∠+∠，又34DAE BAC ∠+∠+∠=∠，3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒，20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠-︒+∠=︒，100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质（垂直平分线上的点到线段两端点的距离相等）、等腰三角形的定义和性质（等边对等角）、以及三角形内角和定理，本题的难点在于容易漏掉第二种情况，出现漏解.3．如图，在01A BA △中，20B ∠=︒，01A B A B =，在1A B 上取点C ，延长01A A 到2A ，使得121A A AC =；在2A C 上取一点D ，延长12A A 到3A ，使得232A A A D =；…，按此做法进行下去，第n 个等腰三角形的底角n A ∠的度数为__________．【答案】11()802n -︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA 1 A 0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律即可得出第n 个等腰三角形的底角∠A n 的度数．【详解】解：∵在△A 0BA 1中，∠B=20°，A 0B=A 1B ， ∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°；同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n个等腰三角形的底角∠A n= 11()802n-︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA2A1，∠DA3A2及∠EA4A3的度数，找出规律是解答此题的关键．4．如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出下列四个结论：①AE=CF；②△EPF是等腰直角三角形；③EF=AB；④12ABCAEPFS S∆=四边形，当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合)，上述结论中始终正确的有________(把你认为正确的结论的序号都填上).【答案】①②④【解析】试题分析：∵∠APE、∠CPF都是∠APF的余角，∴∠APE=∠CPF，∵AB=AC，∠BAC=90°，P是BC中点，∴AP=CP，∴∠PAE=∠PCF，在△APE与△CPF中，{?PAE PCFAP CPEPA FPC∠=∠=∠=∠，∴△APE≌△CPF（ASA），同理可证△APF≌△BPE，∴AE=CF，△EPF是等腰直角三角形，S四边形AEPF=12S△ABC，①②④正确；而AP=12BC，当EF不是△ABC的中位线时，则EF不等于BC的一半，EF=AP，∴故③不成立．故始终正确的是①②④．故选D．考点：1．全等三角形的判定与性质；2．等腰直角三角形．5．如图，已知，点E是线段AB的中点，点C在线段BD上，8BD=，2DC=，线段AC交线段DE于点F，若AF BD=，则AC=__________.【答案】10.【解析】【分析】延长DE至G，使EG=DE，连接AG，证明BDE AGE∆≅∆，而后证明AFG∆、CDF∆是等腰三角形，即可求出CF的长，于是可求AC的长.【详解】解：如图，延长DE至G，使EG=DE，连接AG，∵点E是线段AB的中点，∴AE=BE,∴在BDE∆和AGE∆中，BE AEBED AEGDE EG=⎧⎪∠=∠⎨⎪=⎩,∴BDE AGE∆≅∆,∴AG=BD, BDE AGE∠=∠,∵AF=BD=8,∴AG=AF,∴AFG AGE∠=∠∵AFG DFC∠=∠,∴BDE DFC∠=∠,∴FC=DC,∴FC=2,∴AC=AF+FC=8+2=10.【点睛】本题考查了等腰三角形的性质与判定以及全等三角形的判定与性质，能利用中点条件作辅助线构造全等三角形是解题的关键.6．△ABC中，最小内角∠B＝24°，若△ABC被一直线分割成两个等腰三角形，如图为其中一种分割法，此时△ABC中的最大内角为90°，那么其它分割法中，△ABC中的最大内角度数为_____．【答案】117°或108°或84°．【解析】【分析】根据等腰三角形的性质进行分割，写出△ABC中的最大内角的所有可能值.【详解】①∠BAD＝∠BDA＝12（180°﹣24°）＝78°，∠DAC＝∠DCA＝12∠BDA＝39°，如图1所示：∴∠BAC＝78°+39°＝117°；②∠DBA＝∠DAB＝24°，∠ADC＝∠ACD＝2∠DBA＝48°，如图2所示：∴∠DAC＝180°﹣2×48°＝84°，∴∠BAC＝24°+84°＝108°；③∠DBA＝∠DAB＝24°，∠ADC＝∠DAC＝2∠DBA＝48°，如图3所示：∴∠BAC＝24°+48°＝72°，∠C＝180°﹣2×48°＝84°；∴其它分割法中，△ABC中的最大内角度数为117°或108°或84°，故答案为：117°或108°或84°．【点睛】本题考查了等腰三角形的性质，解题的关键是根据等腰三角形的性质进行分割找出所有情况.7．如图，∠AOB＝45°，点M、点C在射线OA上，点P、点D在射线OB上，且OD＝32，则CP+PM+DM的最小值是_____．34【解析】【分析】如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，根据轴对称的性质得到OC′＝OC＝2，OD′＝OD＝2，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，于是得到CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，于是得到结论．【详解】解：如图，作点C关于OB的对称点C′，作点D关于OA的对称点D′，连接OC′，PC′，D′M，OD′，C′D′，则OC′＝OC＝2，OD′＝OD＝2，CP＝C′P，DM＝D′M，∠C′OD＝′COD＝∠COD′＝45°，∴CP+PM+MD＝C′+PM+D′M≥C′D′，当仅当C′，P，M，D′三点共线时，CP+PM+MD最小为C′D′，作C′T⊥D′O于点T，则C′T＝OT＝2，∴D′T＝42，∴C′D′＝34，∴CP+PM+DM的最小值是34．故答案为：34．【点睛】本题考查了最短路径问题，掌握作轴对称点是解题的关键.8．如图，△ABC中，AC＝DC＝3，BD垂直∠BAC的角平分线于D，E为AC的中点，则图中两个阴影部分面积之差的最大值为________．【答案】9 2【解析】【分析】首先证明两个阴影部分面积之差＝S△ADC，当CD⊥AC时，△ACD的面积最大．【详解】延长BD交AC于点H．设AD交BE于点O．∵AD⊥BH，∴∠ADB＝∠ADH＝90°，∴∠ABD＋∠BAD＝90°，∠H＋∠HAD＝90°，∵∠BAD＝∠HAD，∴∠ABD＝∠H，∴AB＝AH，∵AD⊥BH，∴BD＝DH，∵DC＝CA，∴∠CDA＝∠CAD，∵∠CAD＋∠H＝90°，∠CDA＋∠CDH＝90°，∴∠CDH＝∠H，∴CD＝CH＝AC，∵AE＝EC，∴S△ABE＝14S△ABH，S△CDH＝14S△ABH，∵S△OBD−S△AOE＝S△ADB−S△ABE＝S△ADH−S△CDH＝S△ACD，∵AC＝CD＝3，∴当DC⊥AC时，△ACD的面积最大，最大面积为12×3×3＝92．故填：92．【点睛】本题考查等腰三角形的判定和性质，三角形中线的性质等知识，解题的关键是学会用转化的思想思考问题．9．如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB 以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P、Q同时出发，用t(s)表示移动的时间，当t=_____s时，△POQ是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，点P在BO上，分别计算，即可得解.【详解】当PO=QO时，△POQ是等腰三角形，如图1所示当点P在AO上时，∵PO=AO-AP=10-2t，OQ=t当PO=QO时，102t t-=解得103 t=当PO=QO时，△POQ是等腰三角形，如图2所示当点P在BO上时∵PO=AP-AO=2t-10，OQ=t当PO=QO时，210t t-=解得10t=故答案为：103或10【点睛】本题考查等腰三角形的性质及动点问题，熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.10．已知，∠MON=30°，点A1、A2、A3在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=a，则△A7B7A8的边长为______．【答案】64a【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，根据30°角所对直角边等于斜边的一半得到A2B2=2B1A2，进而得出A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2…从而得到答案．【详解】∵△A1B1A2是等边三角形，∴A1B1=A2B1，∠3=∠4=∠12=60°，∴∠2=120°．∵∠MON=30°，∴∠1=180°﹣120°﹣30°=30°．又∵∠3=60°，∴∠5=180°﹣60°﹣30°=90°．∵∠MON=∠1=30°，∴OA1=A1B1=a，∴A2B1=a．∵△A2B2A3、△A3B3A4是等边三角形，∴∠11=∠10=60°，∠13=60°．∵∠4=∠12=60°，∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，∴∠1=∠6=∠7=30°，∠5=∠8=90°，∴A2B2=2B1A2，B3A3=2B2A3，∴A3B3=4B1A2=4a，A4B4=8B1A2=8a，A5B5=16B1A2=16a，以此类推：A7B7=64B1A2=64a．故答案为：64a．【点睛】本题考查了等边三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质，根据已知得出A 3B 3=4B 1A 2，A 4B 4=8B 1A 2，A 5B 5=16B 1A 2进而发现规律是解题的关键．二、八年级数学轴对称三角形选择题（难）11．在Rt ABC ∆中，90ACB ∠=︒，以ABC ∆的一边为边画等腰三角形，使得它的第三个顶点在ABC ∆的其他边上，则可以画出的不同的等腰三角形的个数最多可画几个？（）A ．9个B ．7个C ．6个D ．5个【答案】B【解析】【分析】先以Rt ABC ∆三个顶点分别为圆心，再以每个顶点所在的较短边为半径画弧，即可确定等腰三角形的第三个顶点；也可以作三边的垂直平分线确定等腰三角形的第三个顶点即得．【详解】解：①如图1，以B 为圆心，BC 长为半径画弧，交AB 于点D ，则∆BCD 就是等腰三角形；②如图2，以A 为圆心，AC 长为半径画弧，交AB 于点E ，则∆ACE 就是等腰三角形； ③如图3，以C 为圆心，BC 长为半径画弧，交AB 于M ，交AC 于点F ，则∆BCM 、∆BCF 是等腰三角形；④如图4，作AC 的垂直平分线交AB 于点H ，则∆ACH 就是等腰三角形；⑤如图5，作AB 的垂直平分线交AC 于点G ，则∆AGB 就是等腰三角形；⑥如图6，作BC 的垂直平分线交AB 于I ，则∆BCI 就是等腰三角形．故选：B ．【点睛】本题考查等腰三角形的判定的应用，通过作垂直平分线或者画弧的方法确定相等的边是解题关键．12．如图所示，在ABC 中，AC BC =，90ACB ︒∠=，AD 平分BAC ∠，BE AD ⊥交AC 的延长线F ，E 为垂足．则有：①AD BF =；②CF CD =；③AC CD AB +=；④BE CF =；⑤2BF BE =，其中正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】D【解析】【分析】利用全等三角形的判定定理及其性质以及等腰三角形的三线合一的性质逐项分析即可得出答案．【详解】解：∵AC BC =，90ACB ︒∠=∴45CAB ABC ︒∠=∠=∵AD 平分BAC ∠∴22.5BAE EAF ︒∠=∠=∵90EAF F FBC F ︒∠+∠=∠+∠=∴EAF FBC ∠=∠∴ADC BFC ≅∴AD=BF ，CF=CD ，故①②正确；∵CD=CF，∴AC+CD=AC+CF=AF∵67.5F ︒∠=∵18018067.54567.5ABF F CAB ︒︒︒︒︒∠=-∠-∠=--=∴AF=AB ，即AC+CD=AB ，故③正确；由③可知，三角形ABF 是等腰三角形，∵BE AD ⊥∴12BE BF =若BE CF =，则30CBF ∠=︒与②中结论相矛盾，故④错误；∵三角形ABF 是等腰三角形，∵BE AD ⊥∴12BE BF = ∴BF=2BE ，故⑤正确；综上所述，正确的选项有4个．故选：D ．【点睛】本题考查的知识点是全等三角形的判定定理及其性质，等腰三角形的判定与性质，等腰直角三角形的性质，掌握以上知识点是解此题的关键．13．等边△ABC ，在平面内找一点P ，使△PBC 、△PAB 、△PAC 均为等腰三角形，具备这样条件的P 点有多少个？（）A ．1个B ．4个C ．7个D ．10个【答案】D【解析】试题分析：根据点P 在等边△ABC 内，而且△PBC 、△PAB 、△PAC 均为等腰三角形，可知P 点为等边△ABC 的垂心；由此可得分别以三角形各顶点为圆心，边长为半径，交垂直平分线的交点就是满足要求的．解：由点P 在等边△ABC 内，而且△PBC 、△PAB 、△PAC 均为等腰三角形，可知P 点为等边△ABC 的垂心；因为△ABC 是等边三角形，所以分别以三角形各顶点为圆心，边长为半径画弧，交垂直平分线的交点就是满足要求的，每条垂直平分线上得3个交点，再加三角形的垂心，一共10个．故选D ．点评：此题主要考查等腰三角形的性质和等边三角形的性质，有一定的拔高难度，属于中档题．14．如图，△ABC 的周长为32，点D 、E 都在边BC 上，∠ABC 的平分线垂直于AE ，垂足为Q ，∠ACB 的平分线垂直于AD ，垂足为P ，若BC ＝12，则PQ 的长为（）A ．3B ．4C ．5D ．6【答案】B【解析】【分析】首先判断△BAE 、△CAD 是等腰三角形，从而得出BA ＝BE ，CA ＝CD ，由△ABC 的周长为32以及BC ＝12，可得DE ＝8，利用中位线定理可求出PQ ．【详解】∵BQ 平分∠ABC ，BQ ⊥AE ，∴∠ABQ ＝∠EBQ ，∵∠ABQ+∠BAQ ＝90°，∠EBQ+∠BEQ ＝90°，∴∠BAQ ＝∠BEQ ，∴AB ＝BE ，同理：CA ＝CD ，∴点Q 是AE 中点，点P 是AD 中点（三线合一），∴PQ 是△ADE 的中位线，∵BE+CD ＝AB+AC ＝32﹣BC ＝32﹣12＝20，∴DE ＝BE+CD ﹣BC ＝8，∴PQ ＝12DE ＝4．故选：B ．【点睛】本题考查了三角形的中位线定理和等腰三角形的性质和判定，解答本题的关键是判断出△BAE 、△CAD 是等腰三角形，利用等腰三角形的性质确定PQ 是△ADE 的中位线．15．如图，在ABC ∆中，120BAC ︒∠=，点,E F 分别是ABC ∆的边AB 、AC 的中点，边BC 分别与DE 、DF 相交于点,H G ，且,DE AB DF AC ⊥⊥，连接AD 、AG 、AH ，现在下列四个结论：①60EDF ︒∠=，②AD 平分GAH ∠，③B ADF ∠=∠，④GD GH =.则其中正确的结论有（）.A ．1个B ．2个C ．3个D ．4个【答案】A【解析】【分析】利用,DE AB DF AC ⊥⊥及四边形的内角和即可得到①正确；；根据三角形内角和与线段的垂直平分线性质得到∠BAH+∠GAC=60︒，无条件证明∠GAD=∠HAD,故②错误；由等量代换得B ADF ∠≠∠，故③错误；利用三角形的内角和与对顶角相等得到GD GH ≠，故④错误.【详解】∵,DE AB DF AC ⊥⊥，∴∠DEA=∠DFA=90︒，∵120BAC ︒∠=,∴∠EDF=360︒-∠DEA-∠DFA-∠BAC=60︒，故①正确；∵120BAC ︒∠=，∴∠B+∠C=60︒，∵点,E F 分别是ABC ∆的边AB 、AC 的中点，,DE AB DF AC ⊥⊥，∴BH=AH ，AG=CG ，∴∠BAH=∠B ，∠GAC=∠C ，∴∠BAH+∠GAC=60︒，∵无条件证明∠GAD=∠HAD,∴AD 不一定平分GAH ∠，故②错误；∵∠ADF+∠DAF=90︒，∠B=∠BAH,90BAH DAF ∠+∠≠,∴B ADF ∠≠∠，故③错误；∵90B BHE ∠+∠=，30B ∠≠ ，∴ 60BHE ∠≠，∴60DHG ∠≠，∴DHG HDG ∠≠∠,∴GD GH ≠，故④错误，故选：A.【点睛】此题考查线段的垂直平分线的性质，利用三角形的内角和，四边形的内角和求角度，利用对顶角相等，等角对等边推导边的关系.16．如图，△ABC 中，AB ＝AC ，且∠ABC ＝60°，D 为△ABC 内一点，且DA ＝DB ，E 为△ABC 外一点，BE ＝AB ，且∠EBD ＝∠CBD ，连DE ，CE. 下列结论：①∠DAC ＝∠DBC ；②BE ⊥AC ；③∠DEB ＝30°. 其中正确的是（）A ．①...B ．①③...C ．② ...D ．①②③【答案】B【解析】【分析】连接DC,证ACD BCD DAC DBC ∠∠≅=得出①，再证BED BCD ≅，得出BED BCD 30∠∠==︒;其它两个条件运用假设成立推出答案即可.【详解】解：证明：连接DC，∵△ABC是等边三角形，∴AB=BC=AC，∠ACB=60°，∵DB=DA，DC=DC，在△ACD与△BCD中，AB BC DB DA DC DC=⎧⎪=⎨⎪=⎩,∴△ACD≌△BCD （SSS），由此得出结论①正确；∴∠BCD=∠ACD=130 2ACB∠=︒∵BE=AB，∴BE=BC，∵∠DBE=∠DBC，BD=BD，在△BED与△BCD中，BE BCDBE DBCBD BD=⎧⎪∠=∠⎨⎪=⎩,∴△BED≌△BCD （SAS），∴∠DEB=∠BCD=30°．由此得出结论③正确；∵EC∥AD，∴∠DAC=∠ECA，∵∠DBE=∠DBC，∠DAC=∠DBC，∴设∠ECA=∠DBC=∠DBE=∠1，∵BE=BA，∴BE=BC，∴∠BCE=∠BEC=60°+∠1，在△BCE中三角和为180°，∴2∠1+2（60°+∠1）=180°∴∠1=15°，∴∠CBE=30，这时BE是AC边上的中垂线，结论②才正确．因此若要结论②正确，需要添加条件EC∥AD.故答案为：B.【点睛】本题考查的知识点主要是全等三角形的判定与性质以及等边三角形的性质，通过已知条件作出恰当的辅助线是解题的关键点.17．如图，在△ABC 中，BC 的垂直平分线分别交AC ，BC 于点D ，E ,若△ABC 的周长为24，CE ＝4，则△ABD 的周长为（）A ．16B ．18C ．20D ．24【答案】A【解析】【分析】根据线段的垂直平分线的性质和三角形的周长公式进行解答即可.【详解】解：∵DE 是BC 的垂直平分线，∴DB=DC ，BC=2CE=8又∵AABC 的周长为24，∴AB+BC+AC=24∴AB+AC=24-BC=24-8=16∴△ABD 的周长=AD+BD+AB=AD+CD+AB=AB+AC=16，故答案为A【点睛】本题考查的是线段的垂直平分线的性质，理解并应用线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.18．如图，Rt ABC ∆中，90ACB ∠=，3AC =，4BC =，5AB =,将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，两条折痕与斜边AB 分别交于点E 、F ，则线段EF 的长为（）A ．52B ．125C ．4D ．53【答案】B【解析】【分析】先利用折叠的性质证明出△ECF 是一个等腰直角三角形，因此EF=CE ，然后再根据文中条件综合得出S △ABC =12AC∙BC=12AB∙CE ，求出CE 进而得出答案即可. 【详解】根据折叠性质可知：CD=AC=3，BC=B C '=4，∠ACE=∠DCE ，∠BCF=∠B 'CF ，CE ⊥AB ， ∴∠DCE+∠B 'CF=∠ACE+∠BCF ，∵∠ACB=90°，∴∠ECF=45°，又∵CE ⊥AB ，∴△ECF 是等腰直角三角形，∴EF=CE ，又∵S △ABC =12AC∙BC=12AB∙CE ， ∴AC∙BC=AB∙CE ， ∵3AC =，4BC =，5AB =,∴125CE =， ∴EF 125=. 所以答案为B 选项.【点睛】本题主要考查了直角三角形与等腰三角形性质的综合运用，熟练掌握相关概念是解题关键.19．如图，在△ABC 中，∠A =36°，AB =AC ，AB 的垂直平分线OD 交AB 于点O ，交AC 于点D ，连接BD ．有下列结论：①∠C =2∠A ；②BD 平分∠ABC ；③S △BCD =S △BOD ．其中正确的选项是（）A ．①③B ．②③C ．①②③D ．①②【答案】D【解析】 ①、∵∠A=36°，AB=AC ，∴∠C=∠ABC=72°，∴∠C=2∠A ，正确；②、∵DO 是AB 垂直平分线，∴AD=BD ．∴∠A=∠ABD=36°．∴∠DBC=72°﹣36°=36°=∠ABD ．∴BD 是∠ABC 的角平分线，正确；③，根据已知不能推出△BCD 的面积和△BOD 面积相等，错误；故选：D.20．如图，平面直角坐标系中，已知A(2，2)、B(4，0)，若在x轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是( )A．1 B．2 C．3 D．4【答案】D【解析】【分析】由点A、B的坐标可得到AB=22，然后分类讨论：若AC=AB；若BC=AB；若CA=CB，确定C点的个数．【详解】∵点A、B的坐标分别为(2，2)、B(4，0)．∴AB=22，如图，①若AC=AB，以A为圆心，AB为半径画弧与x轴有2个交点(含B点)，即(0，0)、(4，0)，∴满足△ABC是等腰三角形的C点有1个；②若BC=AB，以B为圆心，BA为半径画弧与x轴有2个交点，即满足△ABC是等腰三角形的C点有2个；③若CA=CB，作AB的垂直平分线与x轴有1个交点，即满足△ABC是等腰三角形的C点有1个；综上所述：点C在x轴上，△ABC是等腰三角形，符合条件的点C共有4个．故选D．【点睛】本题主考查了等腰三角形的判定以及分类讨论思想的运用，分三种情况分别讨论，注意等腰三角形顶角的顶点在底边的垂直平分线上．。

成都市青羊实验联合中学数学全等三角形易错题(Word版含答案)

成都市青羊实验联合中学数学全等三角形易错题（Word版含答案）一、八年级数学轴对称三角形填空题（难）1．如图，在菱形ABCD中，∠ABC=120°，AB=10cm，点P是这个菱形内部或边上的一点．若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为______cm．-【答案】10310【解析】解：连接BD，在菱形ABCD中，∵∠ABC=120°，AB=BC=AD=CD=10，∴∠A=∠C=60°，∴△ABD，△BCD都是等边三角形，分三种情况讨论：①若以边BC为底，则BC垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”，即当点P与点D重合时，PA最小，最小值PA=10；②若以边PB为底，∠PCB为顶角时，以点C为圆心，BC长为半径作圆，与AC相交于一点，则弧BD（除点B外）上的所有点都满足△PBC是等腰三角形，当点P在AC上时，AP-；最小，最小值为10310③若以边PC为底，∠PBC为顶角，以点B为圆心，BC为半径作圆，则弧AC上的点A与点D均满足△PBC为等腰三角形，当点P与点A重合时，PA最小，显然不满足题意，故此种情况不存在；-（cm）．综上所述，PA的最小值为10310-．故答案为：10310点睛：本题考查菱形的性质、等边三角形的性质，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．2．我们知道，经过三角形一顶点和此顶点所对边上的任意一点的直线，均能把三角形分割成两个三角形（1）如图，在ABC∆中，25,105A ABC∠=︒∠=︒，过B作一直线交AC于D，若BD 把ABC∆分割成两个等腰三角形，则BDA∠的度数是______．（2）已知在ABC∆中，AB AC=，过顶点和顶点对边上一点的直线，把ABC∆分割成两个等腰三角形，则A∠的最小度数为________．【答案】130︒1807︒⎛⎫⎪⎝⎭【解析】【分析】（1）由题意得：DA=DB，结合25A∠=︒，即可得到答案；（2）根据题意，分4种情况讨论，①当BD=AD，CD=AD，②当AD=BD，AC=CD，③AB=AC，当AD=BD=BC，④当AD=BD，CD=BC，分别求出A∠的度数，即可得到答案．【详解】（1）由题意得：当DA=BA，BD=BA时，不符合题意，当DA=DB时，则∠ABD=∠A=25°，∴∠BDA=180°-25°×2=130°．故答案为：130°；（2）①如图1，∵AB=AC，当BD=AD，CD=AD，∴∠B=∠C=∠BAD=∠CAD，∵∠BAC+∠B+∠C=180°，∴4∠B=180°，∴∠BAC=90°．②如图2，∵AB=AC，当AD=BD，AC=CD，∴∠B=∠C=∠BAD，∠CAD=∠CDA，∵∠CDA=∠B+∠BAD=2∠B，∴∠BAC=3∠B，∵∠BAC+∠B+∠C=180°，∴5∠B=180°，∴∠B=36°，∴∠BAC=108°．③如图3，∵AB=AC，当AD=BD=BC，∴∠ABC=∠C ，∠BAC=∠ABD ，∠BDC=∠C ，∵∠BDC=∠A+∠ABD=2∠BAC ，∴∠ABC=∠C=2∠BAC ，∵∠BAC+∠ABC+∠C=180°，∴5∠BAC=180°，∴∠BAC=36°．④如图4，∵AB=AC ，当AD=BD ，CD=BC ，∴∠ABC=∠C ，∠BAC=∠ABD ，∠CDB=∠CBD ，∵∠BDC=∠BAC+∠ABD=2∠BAC ，∴∠ABC=∠C=3∠BAC ，∵∠BAC+∠ABC+∠C=180°，∴7∠BAC=180°，∴∠BAC=180()7︒ ．综上所述，∠A 的最小度数为：180()7︒．故答案是：180()7︒．【点睛】本题主要考查等腰三角形的性质定理以及三角形内角和定理与外角的性质，根据等腰三角形的性质，分类讨论，是解题的关键．3．在ABC ∆中，边AB 、AC 的垂直平分线分别交边BC 于点D 、点E ，20DAE ∠=︒，则BAC ∠=______°.【答案】80或100【解析】【分析】根据题意，点D 和点E 的位置不确定，需分析谁靠近B 点，则有如下图（图见解析）两种情况：（1）图1中，点E 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有1,2B DAE C DAE ∠=∠+∠∠=∠+∠，再根据三角形的内角和定理可得180B C BAC ∠+∠+∠=︒，联立即可求得；（2）图2中，点D 距离点B 近，根据垂直平分线性质可知，,BD AD AE CE ==，从而有3,4B C ∠=∠∠=∠，由三角形的内角和定理得180B C BAC ∠+∠+∠=︒，联立即可求得.【详解】由题意可分如下两种情况：（1）图1中，根据垂直平分线性质可知，,BD AD AE CE ==，1,2B DAE C DAE ∴∠=∠+∠∠=∠+∠（等边对等角），两式相加得12B C DAE DAE ∠+∠=∠+∠+∠+∠，又12DAE BAC ∠+∠+∠=∠20B C BAC DAE BAC ∴∠+∠=∠+∠=∠+︒，由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠+︒+∠=︒，80BAC ∴∠=︒；（2）图2中，根据垂直平分线性质可知，,BD AD AE CE ==，3,4B C ∴∠=∠∠=∠（等边对等角），两式相加得34B C ∠+∠=∠+∠，又34DAE BAC ∠+∠+∠=∠，3420BAC DAE BAC ∴∠+∠=∠-∠=∠-︒，20B C BAC ∴∠+∠=∠-︒由三角形内角和定理得180B C BAC ∠+∠+∠=︒，20180BAC BAC ∴∠-︒+∠=︒，100BAC ∴∠=︒.故答案为80或100.【点睛】本题考查了垂直平分线的性质（垂直平分线上的点到线段两端点的距离相等）、等腰三角形的定义和性质（等边对等角）、以及三角形内角和定理，本题的难点在于容易漏掉第二种情况，出现漏解.4．如图，在ABC ∆中，点D 是BC 的中点，点E 是AD 上一点，BE AC =．若70C ∠=︒，50DAC ∠=︒ 则EBD ∠的度数为______．【答案】10︒【解析】【分析】延长AD 到F 使DF AD =，连接BF ，通过ACD FDB ≅，根据全等三角形的性质得到CAD BFD ∠=∠，AC BF =，等量代换得BF BE =，由等腰三角形的性质得到F BEF ∠=∠，即可得到BEF CAD ∠=∠，进而利用三角形的内角和解答即可得．【详解】如图，延长AD 到F ，使DF AD =，连接BF ：∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠，AD DF =∴ACD FDB ≅∴AC BF =， CAD F ∠=∠，C DBF ∠=∠∵AC BE =， 70C ︒∠=， 50CAD ︒∠=∴BE BF =， 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为：10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理，解题的关键在于通过倍长中线法构造全等三角形．5．如图，在△ABC 中，P ，Q 分别是BC ，AC 上的点，PR ⊥AB ，PS ⊥AC ，垂足分别是R ，S ，若AQ PQ =，PR PS =，那么下面四个结论：①AS AR =；②QP //AR ；③△BRP ≌△QSP ；④BRQS ，其中一定正确的是（填写编号）_____________.【答案】①，②【解析】【分析】连接AP，根据角平分线性质即可推出①，根据勾股定理即可推出AR=AS，根据等腰三角形性质推出∠QAP=∠QPA，推出∠QPA=∠BAP，根据平行线判定推出QP∥AB即可；在Rt△BRP和Rt△QSP中，只有PR=PS．无法判断△BRP≌△QSP也无法证明BR QS．【详解】解：连接AP①∵PR⊥AB，PS⊥AC，PR=PS，∴点P在∠BAC的平分线上，∠ARP=∠ASP=90°，∴∠SAP=∠RAP，在Rt△ARP和Rt△ASP中，由勾股定理得：AR2=AP2-PR2，AS2=AP2-PS2，∵AP=AP，PR=PS，∴AR=AS，∴①正确；②∵AQ=QP，∴∠QAP=∠QPA，∵∠QAP=∠BAP，∴∠QPA=∠BAP，∴QP∥AR，∴②正确；③在Rt△BRP和Rt△QSP中，只有PR=PS，不满足三角形全等的条件，故③④错误；故答案为：①②.【点睛】本题主要考查了角平分线的性质与勾股定理的应用，熟练掌握根据垂直与相等得出点在角平分线上是解题的关键.6．如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AE平分∠BAC，∠D=∠DBC=60°，若BD=5cm，DE=3cm，则BC的长是 ______cm．【答案】8．【解析】【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形，△EFD为等边三角形，从而得出BN的长，进而求出答案．【详解】解：延长DE交BC于M，延长AE交BC于N，作EF∥BC于F，∵AB=AC，AE平分∠BAC，∴AN⊥BC，BN=CN，∵∠DBC=∠D=60°，∴△BDM为等边三角形，∴△EFD为等边三角形，∵BD=5，DE=3，∴EM=2，∵△BDM为等边三角形，∴∠DMB=60°，∵AN⊥BC，∴∠ENM=90°，∴∠NEM=30°，∴NM=1，∴BN=4，∴BC=2BN=8（cm），故答案为8．【点睛】本题考查等边三角形的判定与性质；等腰三角形的性质．7．等腰三角形一边长等于4，一边长等于9，它的周长是__．【答案】22【解析】【分析】等腰三角形有两条边长为4和9，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形；【详解】解：因为4+4=8<9，0<4<9+9=18，∴腰的不应为4，而应为9，∴等腰三角形的周长=4+9+9=22.故答案为22.【点睛】本题主要考查了等腰三角形的性质和三角形的三边关系；求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去.8．如图，在△ABC中，AB＝AC，点D、E在BC的延长线上，G是AC上一点，且CG＝CD，F是GD上一点，且DF＝DE．若∠A＝100°，则∠E的大小为_____度．【答案】10【解析】【分析】由DF=DE，CG=CD可得∠E=∠DFE，∠CDG=∠CGD，再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E，∠ACB=∠CDG+∠CGD=2∠CD G，进而可得∠ACB=4∠E，最后代入数据即可解答.【详解】解：∵DF＝DE，CG＝CD，∴∠E＝∠DFE，∠CDG＝∠CGD，∵GDC＝∠E+∠DFE，∠ACB＝∠CDG+∠CGD，∴GDC＝2∠E，∠ACB＝2∠CDG，∴∠ACB＝4∠E，∵△ABC中，AB＝AC，∠A＝100°，∴∠ACB＝40°，∴∠E＝40°÷4＝10°．故答案为10．【点睛】本题考查等腰三角形的性质以及三角形外角的定义，解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.9．如图，△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点，如果点P在线段BC 上以v厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动。

全等三角形易错题(Word版含答案)

全等三角形易错题（Word版含答案）一、八年级数学轴对称三角形填空题（难）1．如图，点A的坐标是（2，2），若点P在x轴上，且△APO是等腰三角形，则点P有_____个．【答案】4【解析】【分析】由A点坐标可得OA=22，∠AOP＝45°，分别讨论OA为腰和底边，求出点P在x轴正半轴和负半轴时，△APO是等腰三角形的P点坐标即可.【详解】（1）当点P在x轴正半轴上，①如图，以OA为腰时，∵A的坐标是（2，2），∴∠AOP＝45°，OA＝22，当∠AOP为顶角时，OA=OP=22，当∠OAP为顶角时，AO=AP，∴OPA=∠AOP=45°，∴∠OAP=90°，∴OP=2OA=4，∴P的坐标是（4，0）或（22，0）.②以OA为底边时，∵点A的坐标是（2，2），∴∠AOP=45°，∵AP=OP，∴∠OAP=∠AOP=45°，∴∠OPA=90°，∴OP=2，∴P点坐标为（2，0）.（2）当点P在x轴负半轴上，③以OA为腰时，∵A的坐标是（2，2），∴OA＝22，∴OA＝OP＝22，∴P的坐标是（﹣22，0）．综上所述：P的坐标是（2，0）或（4，0）或（2，0）或（﹣2，0）．故答案为：4．【点睛】此题主要考查等腰三角形的判定及坐标与图形性质的综合运用，注意分类讨论思想的运用是解题关键．2．在直角坐标系中，O 为坐标原点，已知点 A（1，2），点 P 是 y 轴正半轴上的一点，且△AOP 为等腰三角形，则点P 的坐标为_____________．【答案】5 5),(0,4),0,4⎛⎫⎪⎝⎭【解析】【分析】有三种情况：①以O为圆心，以OA为半径画弧交y轴于D，求出OA即可；②以A为圆心，以OA为半径画弧交y轴于P，求出OP即可；③作OA的垂直平分线交y轴于C，则AC＝OC，根据勾股定理求出OC即可．【详解】有三种情况：①以O为圆心，以OA为半径画弧交y轴于D，则OA＝OD＝22125+=∴D（05）；②以A 为圆心，以OA 为半径画弧交y 轴于P ，OP ＝2×y A =4，∴P （0，4）；③作OA 的垂直平分线交y 轴于C ，则AC ＝OC ，由勾股定理得：OC ＝AC ＝()2212OC +-，∴OC ＝54， ∴C （0，54）；故答案为：5(0,5),(0,4),0,4⎛⎫ ⎪⎝⎭．【点睛】本题主要考查对线段的垂直平分线，等腰三角形的性质和判定，勾股定理，坐标与图形性质等知识点的理解和掌握，能求出符合条件的所有情况是解此题的关键．3．如图，线段AB ，DE 的垂直平分线交于点C ，且72ABC EDC ∠=∠=︒，92AEB ∠=︒，则EBD ∠的度数为 ________ ．【答案】128︒【解析】【分析】连接CE，由线段AB，DE的垂直平分线交于点C，得CA=CB，CE=CD，ACB=∠ECD=36°，进而得∠ACE=∠BCD，易证∆ACE≅∆BCD，设∠AEC=∠BDC=x，得则∠BDE=72°-x，∠CEB=92°-x，BDE中，∠EBD=128°，根据三角形内角和定理，即可得到答案．【详解】连接CE，∵线段AB，DE的垂直平分线交于点C，∴CA=CB，CE=CD，∵72ABC EDC∠=∠=︒=∠DEC，∴∠ACB=∠ECD=36°，∴∠ACE=∠BCD，在∆ACE与∆BCD中，∵CA CBACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩，∴∆ACE≅∆BCD（SAS），∴∠AEC=∠BDC，设∠AEC=∠BDC=x，则∠BDE=72°-x，∠CEB=92°-x，∴∠BED=∠DEC-∠CEB=72°-（92°-x）=x-20°，∴在∆BDE中，∠EBD=180°-（72°-x）-（x-20°）=128°．故答案是：128︒．【点睛】本题主要考查中垂线的性质，三角形全等的判定和性质定理以及三角形内角和定理，添加辅助线，构造全等三角形，是解题的关键．4．如图，点A,B,C在同一直线上,△ABD和△BCE都是等边三角形，AE,CD分别与BD,BE交于点F,G，连接FG，有如下结论：①AE=CD ②∠BFG= 60°；③EF=CG；④AD⊥CD⑤FG∥AC 其中，正确的结论有__________________. (填序号)【答案】①②③⑤【解析】【分析】易证△ABE ≌△DBC ，则有∠BAE ＝∠BDC ，AE ＝CD ，从而可证到△ABF ≌△DBG ，则有AF ＝DG ，BF ＝BG ，由∠FBG ＝60°可得△BFG 是等边三角形，证得∠BFG ＝∠DBA ＝60°，则有FG ∥AC ，由∠CDB ≠30°，可判断AD 与CD 的位置关系．【详解】∵△ABD 和△BCE 都是等边三角形，∴BD ＝BA ＝AD ，BE ＝BC ＝EC ，∠ABD ＝∠CBE ＝60°． ∵点A 、B 、C 在同一直线上，∴∠DBE ＝180°﹣60°﹣60°＝60°，∴∠ABE ＝∠DBC ＝120°．在△ABE 和△DBC 中，∵BD BA ABE DBC BE BC ∠∠=⎧⎪=⎨⎪=⎩，∴△ABE ≌△DBC ，∴∠BAE ＝∠BDC ，∴AE ＝CD ，∴①正确；在△ABF 和△DBG中，60BAF BDG AB DBABF DBG ∠∠∠∠=⎧⎪=⎨⎪==︒⎩，∴△ABF ≌△DBG ，∴AF ＝DG ，BF ＝BG ． ∵∠FBG ＝180°﹣60°﹣60°＝60°，∴△BFG 是等边三角形，∴∠BFG =60°，∴②正确； ∵AE ＝CD ，AF ＝DG ，∴EF =CG ；∴③正确；∵∠ADB ＝60°，而∠CDB =∠EAB ≠30°，∴AD 与CD 不一定垂直，∴④错误．∵△BFG 是等边三角形，∴∠BFG =60°，∴∠GFB ＝∠DBA ＝60°，∴FG ∥AB ，∴⑤正确．故答案为①②③⑤．【点睛】本题考查了等边三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质、平行线的判定和性质，证得△ABE ≌△DBC 是解题的关键．5．如图，已知AB AC =，AD 平分BAC ∠，60DEB EBC ∠=∠=︒，若3BE =，3DE =BC =____________．【答案】33+【解析】【分析】延长ED 交BC 于点M ，延长AD 交BC 于点N ，作DF ∥BC 于点F.由已知条件推出△BEM 是等边三角形，△FDE 是等边三角形，在△DNM 中求出NM 的长度，即可求出BC 的长度.【详解】如图，延长ED 交BC 于点M ，延长AD 交BC 于点N ，作DF ∥BC 于点F ，∵AB AC =，AD 平分BAC ∠，∴AN ⊥BC ，BN=CN ，∵60DEB EBC ∠=∠=︒，∴△BEM 是等边三角形，∴△FDE 是等边三角形， ∵3BE =，3DE =33DM =-∵△BEM 是等边三角形，∴∠EMB=60°，∵AN ⊥BC ，∴∠DNM=90°，∴∠NDM=30°，∴13322NM DM ==， ∴33333BN BM NM -+=-=-= ∴233BC BN ==+【点睛】本题考查了等边三角形的性质，解题的关键是作出辅助线构造等边三角形.6．如图，在平面直角坐标系中，点 A,B 的坐标分别是（1,5）、（5,1），若点 C 在 x 轴上，且 A,B,C 三点构成的三角形是等腰三角形，则这样的 C 点共有_____________个【答案】5【解析】【分析】分别以A、B为圆心，AB为半径画圆，及作AB的垂直平分线，数出在x轴上的点C的数量即可【详解】解：由图可知：点 C 在 x 轴上，且 A,B,C 三点构成的三角形是等腰三角形，则这样的 C 点共有5个故答案为:5【点睛】本题考查了等腰三角形的存在性问题，掌握“两圆一线”找等腰三角形是解题的关键7．如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB 以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P、Q同时出发，用t(s)表示移动的时间，当t=_____s时，△POQ是等腰三角形.【答案】103或10【解析】【分析】根据△POQ是等腰三角形，分两种情况进行讨论：点P在AO上，点P在BO上，分别计算，即可得解.【详解】当PO=QO时，△POQ是等腰三角形，如图1所示当点P在AO上时，∵PO=AO-AP=10-2t，OQ=t当PO=QO时，102t t-=解得103 t=当PO=QO时，△POQ是等腰三角形，如图2所示当点P在BO上时∵PO=AP-AO=2t-10，OQ=t当PO=QO时，210t t-=解得10t=故答案为：103或10【点睛】本题考查等腰三角形的性质及动点问题，熟练掌握等腰三角形的性质以及分类讨论思想是解题关键.8．如图：在ABC ∆中，D ，E 为边AB 上的两个点，且BD BC =，AE AC =，若108ACB ∠=︒，则DCE ∠的大小为______.【答案】036【解析】【分析】根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ，用∠A 表示∠AEC,用∠B 表示∠BDC，然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080，∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC,∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800，∴0180DCE CDE CED ∠=-∠-∠= 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质，注意两条等边所在三角形，依此判断对应的两个底角相等.9．如图，在边长为6的菱形ABCD 中，∠DAB=60°，E 是AB 的中点，F 是AC 上一个动点，则EF+BF 的最小值是________ .【答案】33【解析】试题解析：∵在菱形ABCD中，AC与BD互相垂直平分，∴点B、D关于AC对称，连接ED，则ED就是所求的EF+BF的最小值的线段，∵E为AB的中点，∠DAB=60°，∴DE⊥AB，∴ED=22-=22AD AE-=33，63∴EF+BF的最小值为33．10．如图，在四边形ABCD中，∠A=60°，∠ADC=∠ABC=90°，在AB、AD上分别找一点F、E，连接CE、EF、CF，当△CEF的周长最小时，则∠ECF的度数为______．【答案】60°【解析】【分析】此题需分三步：第一步是作出△CEF的周长最小时E、F的位置（用对称即可）；第二步是证明此时的△CEF的周长最小（利用两点之间线段最短）；第三步是利用对称性求此时∠ECF的值.【详解】分别作出C关于AD、AB的对称点分别为C1、C2，连接C1C2，分别交AD，AB于点E、F再连接CE、CF此时△CEF的周长最小，理由如下：在AD、AB上任意取E1、F1两点根据对称性：∴CE=C1E，CE1=C1E1，CF=C2F，CF1=C2F1∴△CEF的周长= CE＋EF＋CF= C1E＋EF＋C2F= C1C2而△CE1F1的周长= CE1＋E1F1＋CF1= C1E1＋E1F1＋C2F1根据两点之间线段最短，故C1E1＋E1F1＋C2F1＞C1C2∴△CEF的周长的最小为：C1C2.∵∠A=60°，∠ADC=∠ABC=90°∴∠DCB=360°－∠A－∠ADC－∠ABC=120°∴∠C C1C2＋∠C C2C1=180°－∠DCB=60°根据对称性：∠C C1C2=∠E CD，∠C C2C1=∠F CB∴∠E CD＋∠F CB=∠C C1C2＋∠C C2C1=60°∴∠ECF=∠DCB－（∠E CD＋∠F CB）=60°故答案为：60°【点睛】此题考查的是周长最小值的作图方法（对称点），及周长最小值的证法：两点之间线段最短，掌握周长最小值的作图方法是解决此题的关键.二、八年级数学轴对称三角形选择题（难）11．如图，已知一条线段的长度为a，作边长为a的等边三角形的方法是：①画射线AM；②连结AC、BC；③分别以A、B为圆心，以a的长为半径作圆弧，两弧交于点C；④在射线AM上截取AB＝a；以上画法正确的顺序是（）A．①②③④B．①④③②C．①④②③D．②①④③【答案】B【解析】【分析】根据尺规作等边三角形的过程逐项判断即可解答.【详解】解：已知一条线段的长度为a ，作边长为a 的等边三角形的方法是：①画射线AM ；②在射线AM 上截取AB ＝a ；③分别以A 、B 为圆心，以a 的长为半径作圆弧，两弧交于点C ；④连结AC 、BC ．△ABC 即为所求作的三角形．故选答案为B ．【点睛】本题考查了尺规作图和等边三角形的性质，解决本题的关键是理解等边三角形的作图过程.12．如图所示，等边三角形的边长依次为2，4，6，8，……，其中1(0,1)A ，()21,13A --，()31,13A -，4(0,2)A ，()52,223A --，……，按此规律排下去，则2019A 的坐标为（）A ．(673,6736733-B ．(673,6736733--C ．(0,1009)D ．(674,6746743- 【答案】A【解析】【分析】根据等边三角形的边长依次为2，4，6，8，……，及点的坐标特征，每三个点一个循环，2019÷3=673，A 2019的坐标在第四象限即可得到结论．【详解】∵2019÷3=673，∴顶点A 2019是第673个等边三角形的第三个顶点，且在第四象限．第673个等边三角形边长为2×673=1346，∴点A 2019的横坐标为 12⨯1346=673．点A 2019的纵坐标为673-134632⨯=673﹣6733．故点A 2019的坐标为：()673,6736733-．故选：A ．【点睛】本题考查了点的坐标、等边三角形的性质，是点的变化规律，主要利用了等边三角形的性质，确定出点A 2019所在三角形是解答本题的关键．13．如图，△ABC 、△CDE 都是等腰三角形，且CA ＝CB , CD ＝CE ,∠ACB ＝∠DCE ＝α,AD ,BE 相交于点O ，点M ,N 分别是线段AD ,BE 的中点，以下4个结论:①AD ＝BE ;②∠DOB ＝180°－α;③△CMN 是等边三角形；④连OC ,则OC 平分∠AOE .正确的是（）A ．①②③B ．①②④C ．①③④D ．①②③④【答案】B【解析】【分析】 ①根据全等三角形的判定定理得到△ACD ≌△BCE （SAS ），由全等三角形的性质得到AD=BE ；故①正确；②设CD 与BE 交于F ，根据全等三角形的性质得到∠ADC=∠BEC ，得到∠DOE=∠DCE=α，根据平角的定义得到∠BOD=180°-∠DOE=180°-α，故②正确； ③根据全等三角形的性质得到∠CAD=∠CBE ，AD=BE ，AC=BC 根据线段的中点的定义得到AM=BN ，根据全等三角形的性质得到CM=CN ，∠ACM=∠BCN ，得到∠MCN=α，推出△MNC 不一定是等边三角形，故③不符合题意；④过C 作CG ⊥BE 于G ，CH ⊥AD 于H ，根据全等三角形的性质得到CH=CG ，根据角平分线的判定定理即可得到OC 平分∠AOE ，故④正确．【详解】解：①∵CA=CB ，CD=CE ，∠ACB=∠DCE=α，∴∠ACB+∠BCD=∠DCE+∠BCD ，∴∠ACD=∠BCE ，在△ACD 和△BCE 中AC BC ACD BCE CD CE ⎪∠⎪⎩∠⎧⎨＝＝＝∴△ACD ≌△BCE （SAS ），∴AD=BE ；故①正确；②设CD 与BE 交于F ，∵△ACD ≌△BCE ，∴∠ADC=∠BEC ，∵∠CFE=∠DFO ，∴∠DOE=∠DCE=α，∴∠BOD=180°-∠DOE=180°-α，故②正确；③∵△ACD ≌△BCE ，∴∠CAD=∠CBE ，AD=BE ，AC=BC又∵点M 、N 分别是线段AD 、BE 的中点，∴AM=12AD ，BN=12BE ， ∴AM=BN ，在△ACM 和△BCN 中 AC BC CAM CBN AM BN ⎪∠⎪⎩∠⎧⎨＝＝＝ ∴△ACM ≌△BCN （SAS ），∴CM=CN ，∠ACM=∠BCN ，又∠ACB=α，∴∠ACM+∠MCB=α，∴∠BCN+∠MCB=α，∴∠MCN=α，∴△MNC 不一定是等边三角形，故③不符合题意；④过C 作CG ⊥BE 于G ，CH ⊥AD 于H ，∴∠CHD=∠ECG=90°，∵∠CEG=∠CDH ，CE=CD ，∴△CGE ≌△CHD （AAS ），∴CH=CG ，∴OC 平分∠AOE ，故④正确，故选：B ．【点睛】本题综合考查了全等三角形的性质和判定，三角形的内角和定理，等边三角形的性质和判定等知识点的应用，解此题的关键是根据性质进行推理，此题综合性比较强，有一定的代表性．14．如图所示，在等边△ABC中，E是AC边的中点，AD是BC边上的中线，P是AD上的动点，若AD=3，则EP＋CP的最小值为（）A．2 B．3 C．4 D．5【答案】B【解析】由等边三角形的性质得，点B，C关于AD对称，连接BE交AD于点P，则EP+CP=BE最小，又BE=AD，所以EP+CP的最小值是3.故选B.点睛：本题主要考查了等边三角形的性质和轴对称的性质，求一条定直线上的一个动点到定直线的同旁的两个定点的距离的最小值，常用的方法是，①确定两个定点中的一个关于定直线的对称点；②连接另一个定点与对称点，与定直线的交点就是两线段和的值最小时，动点的位置.15．如图，已知等边△ABC的边长为4，面积为43，点D为AC的中点，点E为BC的中点，点P为BD上一动点，则PE+PC的最小值为（）A．3 B．2C．3D．3【答案】C【解析】【分析】由题意可知点A、点C关于BD对称，连接AE交BD于点P，由对称的性质可得，PA=PC，故PE+PC=AE，由两点之间线段最短可知，AE即为PE+PC的最小值．【详解】解：∵△ABC是等边三角形，点D为AC的中点，点E为BC的中点，∴BD⊥AC，EC＝2，连接AE ，线段AE 的长即为PE+PC 最小值，∵点E 是边BC 的中点，∴AE ⊥BC ，∴PE+PC 的最小值是22AC E C -＝224223-=．故选C ．【点睛】本题考查的是轴对称-最短路线问题，熟知等边三角形的性质是解答此题的关键．16．如图，ABC △是等边三角形，ABD △是等腰直角三角形，∠BAD =90°，AE ⊥BD 于点E ．连CD 分别交AE ，AB 于点F ，G ，过点A 做AH ⊥CD 交BD 于点H ，则下列结论：①∠ADC =15°；②AF =AG ；③AH =DF ；④△ADF ≌△BAH ；⑤DF =2EH .其中正确结论的个数为（）A ．5B ．4C ．3D ．2【答案】B【解析】【分析】 ①根据△ABC 为等边三角形，△ABD 为等腰直角三角形，可以得出各角的度数以及DA=AC ，即可作出判断；②分别求出∠AFG 和∠AGD 的度数，即可作出判断；④根据三角形内角和定理求出∠HAB 的度数，求证EHG DFA ∠=∠，利用AAS 即可证出两个三角形全等；③根据④证出的全等即可作出判断；⑤证明∠EAH=30°，即可得到AH=2EH ，又由③可知AH DF =，即可作出判断.【详解】①正确：∵ABC △是等边三角形，∴60BAC ︒∠=，∴CA AB =．∵ABD △是等腰直角三角形，∴DA AB =．又∵90BAD ︒∠=，∴150CAD BAD BAC ︒∠=∠+∠=，∴DA CA=，∴()1180150152ADC ACD︒︒︒∠=∠=-=；②错误：∵∠EDF=∠ADB-∠ADC=30°∴∠DFE=90°-∠EDF=90°-30°=60°=∠AFG∵∠AGD=90°-∠ADG=90°-15°=75°∠AFG≠∠AGD∴AF≠AG③，④正确，由题意可得45DAF ABH︒∠=∠=，DA AB=，∵AE BD⊥，AH CD⊥．∴180EHG EFG︒∠+∠=．又∵180?DFA EFG∠+∠=，∴EHG DFA∠=∠，在DAF△和ABH中()AFD BHADAF ABH AASDA AB∠=∠⎧⎪∠=∠⎨⎪=⎩∴DAF△≌ABH．∴DF AH=．⑤正确：∵150CAD︒∠=，AH CD⊥，∴75DAH︒∠=，又∵45DAF︒∠=，∴754530EAH︒︒︒∠=-=又∵AE DB⊥，∴2AH EH=，又∵=AH DF，∴2DF EH=【点睛】本题考查了等边三角形的性质，等腰三角形的性质，三角形的内角和定理，三角形外角的性质，全等三角形的判定与性质，综合性较强，属于较难题目.17．如图，等腰三角形ABC的底边BC长为4，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，若△CDM周长的最小值为8，则△ABC的面积为（）A．12 B．16 C．24 D．32【答案】A【解析】【分析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM+MD的最小值，再根据三角形的周长求出AD的长，由此即可得出结论．【详解】连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∵EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∵△CDM周长的最小值为8，∴AD=8-12BC=8-2=6∴S△ABC=12BC•AD=12×4×6=12，故选A．【点睛】本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．18．如图，在△ABC中，AB=AC=8，BC=5，AB的垂直平分线交AC于D，则△BCD的周长为（）A．13B．15C．18D．21【答案】A【解析】根据线段垂直平分线的性质，可由AB=AC=8，BC=5，AB的垂直平分线交AC于D，得到AD=BD，进而得出△BCD的周长为：CD+BD+BC=AC+BC=8+5=13．故选A．点睛：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．19．如图，O是正三角形ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO′3⑤S△AOC+S△AOB 934）A．①②③⑤B．①③④C．②③④⑤D．①②⑤【答案】A【解析】试题解析：由题意可知，∠1+∠2=∠3+∠2=60°，∴∠1=∠3，又∵OB=O′B，AB=BC，∴△BO′A≌△BOC，又∵∠OBO′=60°，∴△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；如图①，连接OO′，∵OB=O′B，且∠OBO′=60°，∴△OBO′是等边三角形，∴OO′=OB=4．故结论②正确；∵△BO′A≌△BOC，∴O′A=5．在△AOO′中，三边长为3，4，5，这是一组勾股数，∴△AOO′是直角三角形，∠AOO′=90°，∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°，故结论③正确；S四边形AOBO′=S△AOO′+S△OBO′=12323故结论④错误；如图②所示，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．易知△AOO″是边长为3的等边三角形，△COO″是边长为3、4、5的直角三角形，则S△AO C+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=12×3×4+34×32=6+934，故结论⑤正确．综上所述，正确的结论为：①②③⑤．故选A．20．如图，在平面直角坐标系中，A(1，2)，B(3，2)，连接AB，点P是x轴上的一个动点，连接AP、BP，当△ABP的周长最小时，对应的点P的坐标和△ABP的最小周长分别为( )A．(1，0)，224+ B．(3，0)，224+ C．(2,0), 25D．(2,0),252+【答案】D【解析】作A关于x轴的对称点N（1，-2），连接BN与x轴的交点即为点P的位置，此时△ABP的周长最小.设直线BN的解析式为y kx b=+，∵N(1，-2)，B(3，2)，∴232k b k b +=-⎧⎨+=⎩，解得24k b =⎧⎨=-⎩， ∴24y x =-，当0y =时，240x -=，解得，2x =，∴点P 的坐标为（2，0）；∵A (1，2)，B (3，2)，∴AB //x 轴，∵AN ⊥x 轴，∴AB ⊥x 轴，在Rt △ABC 中，AB ＝2，AN ＝4，由勾股定理得，BN ==∵AP =NP ,∴△ABP 的周长最小值为：AB +BP +AP =AB +BP +PN =AB +BN 故选D.点睛：本题考查最短路径问题.利用轴对称作出点P 的位置是解题的关键.。

成都市石室外语学校数学全等三角形单元测试卷(含答案解析)

成都市石室外语学校数学全等三角形单元测试卷（含答案解析）一、八年级数学轴对称三角形填空题（难）1．如图，在△ABC和△DBC中，∠A=40°，AB=AC=2，∠BDC=140°，BD=CD，以点D为顶点作∠MDN=70°，两边分别交AB，AC于点M，N，连接MN，则△AMN的周长为___________．【答案】4【解析】【分析】延长AC至E，使CE=BM，连接DE．证明△BDM≌△CDE（SAS），得出MD=ED，∠MDB=∠EDC，证明△MDN≌△EDN（SAS），得出MN=EN=CN+CE，进而得出答案．【详解】延长AC至E，使CE=BM，连接DE．∵BD=CD，且∠BDC=140°，∴∠DBC=∠DCB=20°，∵∠A=40°，AB=AC=2，∴∠ABC=∠ACB=70°，∴∠MBD=∠ABC+∠DBC=90°，同理可得∠NCD=90°，∴∠ECD=∠NCD=∠MBD=90°，在△BDM和△CDE中，BM CEMBD ECDBD CD⎧⎪∠∠⎨⎪⎩＝＝，＝∴△BDM≌△CDE（SAS），∴MD=ED，∠MDB=∠EDC，∴∠MDE=∠BDC=140°，∵∠MDN=70°，∴∠EDN=70°=∠MDN，在△MDN和△EDN中，MD EDMDN EDNDN DN⎧⎪∠∠⎨⎪⎩＝＝，＝∴△MDN≌△EDN（SAS），∴MN=EN=CN+CE，∴△AMN的周长=AM+MN+AN=AM+CN+CE+AN=AM+AN+CN+BM=AB+AC=4；故答案为：4．【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识；证明三角形全等是解题的关键．2．如图，在01A BA△中，20B∠=︒，01A B A B=，在1A B上取点C，延长01A A到2A，使得121A A AC=；在2A C上取一点D，延长12A A到3A，使得232A A A D=；…，按此做法进行下去，第n个等腰三角形的底角n A∠的度数为__________．【答案】11()802n-︒⋅.【解析】【分析】先根据等腰三角形的性质求出∠BA1 A0的度数，再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1，∠DA3A2及∠EA4A3的度数，找出规律即可得出第n个等腰三角形的底角∠A n的度数．【详解】解：∵在△A0BA1中，∠B=20°，A0B=A1B，∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°， ∵A 1A 2=A 1C ，∠BA 1 A 0是△A 1A 2C 的外角，∴∠CA 2A 1= 108022BA A ︒∠= =40°；同理可得，∠DA 3A 2=20°，∠EA 4A 3=10°，∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，根据题意得出∠CA 2A 1，∠DA 3A 2及∠EA 4A 3的度数，找出规律是解答此题的关键．3．如图，在直角坐标系中，点()8,8B -，点()2,0C -，若动点P 从坐标原点出发，沿y 轴正方向匀速运动，运动速度为1/cm s ，设点P 运动时间为t 秒，当BCP ∆是以BC 为腰的等腰三角形时，直接写出t 的所有值__________________．【答案】2秒或6秒或14秒【解析】【分析】分两种情况：PC 为腰或BP 为腰.分别作出符合条件的图形，计算出OP 的长度，即可求出t 的值．【详解】解：如图所示，过点B 作BD ⊥x 轴于点D ，作BE ⊥y 轴于点E ，分别以点B 和点C 为圆心，以BC 长为半径画弧交y 轴正半轴于点F ，点H 和点G∵点B（-8，8），点C（-2，0），∴DC=6cm，BD=8cm，由勾股定理得：BC=10cm∴在直角三角形COG中，OC=2cm，CG=BC=10cm，∴OP=OG= 22-=，10246(cm)当点P运动到点F或点H时，BE=8cm，BH=BF=10cm，∴EF=EH=6cm∴OP=OF=8-6=2（cm）或OP=OH=8+6=14（cm），故答案为：2秒，46秒或14秒．【点睛】本题综合考查了勾股定理和等腰三角形在平面直角坐标系中的应用，通过作图找出要求的点的位置，利用勾股定理来求解是本题的关键．4．如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AE平分∠BAC，∠D=∠DBC=60°，若BD=5cm，DE=3cm，则BC的长是 ______cm．【答案】8．【解析】【分析】作出辅助线后根据等边三角形的判定得出△BDM为等边三角形，△EFD为等边三角形，从而得出BN的长，进而求出答案．【详解】解：延长DE交BC于M，延长AE交BC于N，作EF∥BC于F，∵AB=AC，AE平分∠BAC，∴AN⊥BC，BN=CN，∵∠DBC=∠D=60°，∴△BDM 为等边三角形，∴△EFD 为等边三角形，∵BD=5，DE=3，∴EM=2，∵△BDM 为等边三角形，∴∠DMB=60°，∵AN ⊥BC ，∴∠ENM=90°，∴∠NEM=30°，∴NM=1，∴BN=4，∴BC=2BN=8（cm ），故答案为8．【点睛】本题考查等边三角形的判定与性质；等腰三角形的性质．5．如图,在ABC 中, 90,ACB ABD ︒∠=是ABC 的轴对称图形,点E 在AD 上,点F 在AC 的延长线上.若点B 恰好在EF 的垂直平分线上,并且5AE =,13AF =,则DE =______．【答案】4．【解析】【分析】连接BE ，BF ，根据轴对称的性质可得△ABD ≌△ACB ，进而可得DB=CB ，AD=AC ，∠D=∠BCA=90°，再利用线段垂直平分线的性质可得BE=BF ，然后证明Rt △DBE ≌Rt △CBF 可得DE=CF ，然后可得ED 长．【详解】解：连接BE ，BF ，∵△ABD 是△ABC 的轴对称图形，∴△ABD ≌△ACB ，∴DB=CB ，AD=AC ，∠D=∠BCA=90°，∴∠BCF=90°，∵点B 恰好在EF 的垂直平分线上，∴BE=BF ，在Rt △DBE 和Rt △CBF 中BD BC EB FB =⎧⎨=⎩，∴Rt △DBE ≌Rt △CBF （HL ），∴DE=CF ，设DE=x ，则CF=x ，∵AE=5，AF=13，∴AC=AD=5+x ，∴AF=5+2x ，∴5+2x=13，∴x=4，∴DE=4，故答案为：4．【点睛】此题主要考查了轴对称和线段垂直平分线的性质，关键是掌握成轴对称的两个图形全等．6．如图，在△ABC 中，AB ＝AC ，点D 、E 在BC 的延长线上，G 是AC 上一点，且CG ＝CD ，F 是GD 上一点，且DF ＝DE ．若∠A ＝100°，则∠E 的大小为_____度．【答案】10【解析】【分析】由DF=DE ，CG=CD 可得∠E=∠DFE ，∠CDG=∠CGD ，再由三角形的外角的意义可得∠GDC=∠E+∠DFE=2∠E，∠ACB=∠CDG+∠CGD=2∠CD G，进而可得∠ACB=4∠E，最后代入数据即可解答.【详解】解：∵DF＝DE，CG＝CD，∴∠E＝∠DFE，∠CDG＝∠CGD，∵GDC＝∠E+∠DFE，∠ACB＝∠CDG+∠CGD，∴GDC＝2∠E，∠ACB＝2∠CDG，∴∠ACB＝4∠E，∵△ABC中，AB＝AC，∠A＝100°，∴∠ACB＝40°，∴∠E＝40°÷4＝10°．故答案为10．【点睛】本题考查等腰三角形的性质以及三角形外角的定义，解题的关键是灵活运用等腰三角形的性质和三角形的外角的定义确定各角之间的关系.7．在△ABC 中，∠ACB＝90º，D、E 分别在 AC、AB 边上，把△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，若△CFD 与△BFE 都是等腰三角形，则∠BAC 的度数为_________．【答案】45°或60°【解析】【分析】根据题意画出图形，设∠BAC的度数为x，则∠B=90°-x，∠EFB =135°-x，∠BEF=2x-45°，当△BFE 都是等腰三角形，分三种情况讨论，即可求解.【详解】∵∠ACB＝90º，△CFD是等腰三角形，∴∠CDF=∠CFD=45°，设∠BAC的度数为x，∴∠B=90°-x，∵△ADE 沿 DE 翻折得到△FDE，点 F 恰好落在 BC 边上，∴∠DFE=∠BAC=x，∴∠EFB=180°-45°-x=135°-x，∵∠ADE=∠FDE，∴∠ADE=（180°-45°）÷2=67.5°，∴∠AED=180°-∠ADE-∠BAC=180°-67.5° -x=112.5°-x，∴∠DEF=∠AED=112.5°-x，∴∠BEF=180°-∠AED-∠DEF=180°-（112.5°-x）-（112.5°-x）=2x-45°，∵△BFE 都是等腰三角形，分三种情况讨论：①当FE=FB时，如图1，则∠BEF=∠B，∴90-x=2x-45，解得：x=45；②当BF=BE时，则∠EFB=∠BEF，∴135-x=2x-45，解得：x=60，③当EB=EF时，如图2，则∠B=∠EFB，∴135-x=90-x，无解，∴这种情况不存在.综上所述：∠BAC 的度数为：45°或60°.故答案是：45°或60°.图1 图2【点睛】本题主要考查等腰三角形的性质定理，用代数式表示角度，并进行分类讨论，是解题的关键.8．如图，在△ABC中，AB＝BC＝8，AO＝BO，点M是射线CO上的一个动点，∠AOC＝60°，则当△ABM为直角三角形时，AM的长为______．【答案】或4【解析】【分析】分三种情况讨论：①当M在AB下方且∠AMB=90°时，②当M在AB上方且∠AMB=90°时，③当∠ABM=90°时，分别根据含30°直角三角形的性质、直角三角形斜边的中线的性质或勾股定理，进行计算求解即可．【详解】如图1，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OB=4，又∵∠AOC=∠BOM=60°，∴△BOM是等边三角形，∴BM=BO=4，∴Rt△ABM中，AM如图2，当∠AMB=90°时，∵O是AB的中点，AB=8，∴OM=OA=4，又∵∠AOC=60°，∴△AOM是等边三角形，∴AM=AO=4；如图3，当∠ABM=90°时，∵∠BOM=∠AOC=60°，∴∠BMO=30°，∴MO=2BO=2×4=8，∴Rt△BOM中，BM=∴Rt△ABM中，AM综上所述，当△ABM为直角三角形时，AM的长为4．故答案为或4．9．如图，在四边形ABCD中，∠A+∠C＝180°，E、F分别在BC、CD上，且AB＝BE，AD ＝DF，M为EF的中点，DM＝3，BM＝4，则五边形ABEFD的面积是_____．【答案】12【解析】【分析】延长BM至G，使MG＝BM，连接FG、DG，证明△BME≌△GMF（SAS），得出FG＝BE，∠MBE＝∠MGF，证出AB＝FG，证明△DAB≌△DFG（SAS），得出DB＝DG，由等腰三角形的性质即可得DM⊥BM，由五边形ABEFD的面积＝△DBG的面积，可求解．【详解】延长BM至G，使MG＝BM＝4，连接FG、DG，如图所示：∵M 为EF 中点，∴ME ＝MF ，在△BME 和△GMF 中，BM MG BME GMFME MF =⎧⎪∠=∠⎨⎪=⎩， ∴△BME ≌△GMF （SAS ），∴FG ＝BE ，∠MBE ＝∠MGF ，S △BEM ＝S △GFM ，∴FG ∥BE ，∴∠C ＝∠GFC ，∵∠A +∠C ＝180°，∠DFG +∠GFC ＝180°，∴∠A ＝∠DFG ，∵AB ＝BE ，∴AB ＝FG ，在△DAB 和△DFG 中，AB FG A DFGAD DF =⎧⎪∠=∠⎨⎪=⎩， ∴△DAB ≌△DFG （SAS ），∴DB ＝DG ，S △DAB ＝S △DFG ，∵MG ＝BM ，∴DM ⊥BM ，∴五边形ABEFD 的面积＝△DBG 的面积＝12×BG ×DM ＝12×8×3＝12，故答案为：12．【点睛】本题考查了全等三角形的判定与性质、平行线的性质、等腰三角形的判定与性质等知识；熟练掌握等腰三角形的判定由性质，证明三角形全等是解题的关键．10．如图，已知30AOB ∠=︒，点P 在边OA 上，14OD DP ==，点E ，F 在边OB 上，PE PF =.若6EF =，则OF 的长为____.【答案】18【解析】【分析】由30°角我们经常想到作垂线，那么我们可以作DM垂直于OA于M，作PN垂直于OB 于点N，证明△PMD≌△PND，进而求出DF长度，从而求出OF的长度.【详解】如图所示，作DM垂直于OA于M，作PN垂直于OB于点N.∵∠AOB=30°，∠DMO=90°，PD=DO=14，∴DM=7，∠NPO=60°，∠DPO=30°，∴∠NPD=∠DPO=30°，∵DP=DP，∠PND=∠PMD=90°，∴△PND≌△PMD，∴ND=7，∵EF=6，∴DF=ND-NF=7-3=4，∴OF=DF+OD=14+4=18.【点睛】本题考查了全等三角形的判定及性质定理，作辅助线构造全等三角形是解题的关键.二、八年级数学轴对称三角形选择题（难）11．边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）A ．511a 32⨯（） B ．511a 23⨯（） C ．611a 32⨯（） D ．611a 23⨯（）【答案】A【解析】连接AD 、DB 、DF ，求出∠AFD=∠ABD=90°，根据HL 证两三角形全等得出∠FAD=60°，求出AD ∥EF ∥GI ，过F 作FZ ⊥GI ，过E 作EN ⊥GI 于N ，得出平行四边形FZNE 得出EF=ZN=13a ，求出GI 的长，求出第一个正六边形的边长是13a ，是等边三角形QKM 的边长的13；同理第二个正六边形的边长是等边三角形GHI 的边长的13；求出第五个等边三角形的边长，乘以13即可得出第六个正六边形的边长．连接AD 、DF 、DB ．∵六边形ABCDEF 是正六边形， ∴∠ABC=∠BAF=∠AFE ，AB=AF ，∠E=∠C=120°，EF=DE=BC=CD ，∴∠EFD=∠EDF=∠CBD=∠BDC=30°，∵∠AFE=∠ABC=120°，∴∠AFD=∠ABD=90°，在Rt △ABD 和RtAFD 中AF=AB {AD=AD∴Rt △ABD ≌Rt △AFD （HL ），∴∠BAD=∠FAD=12×120°=60°， ∴∠FAD+∠AFE=60°+120°=180°，∴AD ∥EF ，∵G 、I 分别为AF 、DE 中点，∴GI ∥EF ∥AD ，∴∠FGI=∠FAD=60°，∵六边形ABCDEF是正六边形，△QKM是等边三角形，∴∠EDM=60°=∠M，∴ED=EM，同理AF=QF，即AF=QF=EF=EM，∵等边三角形QKM的边长是a，∴第一个正六边形ABCDEF的边长是13a，即等边三角形QKM的边长的13，过F作FZ⊥GI于Z，过E作EN⊥GI于N，则FZ∥EN，∵EF∥GI，∴四边形FZNE是平行四边形，∴EF=ZN=13a，∵GF=12AF=12×13a=16a，∠FGI=60°（已证），∴∠GFZ=30°，∴GZ=12GF=112a，同理IN=112a，∴GI=112a+13a+112a=12a，即第二个等边三角形的边长是12a，与上面求出的第一个正六边形的边长的方法类似，可求出第二个正六边形的边长是13×12a；同理第第三个等边三角形的边长是12×12a，与上面求出的第一个正六边形的边长的方法类似，可求出第三个正六边形的边长是13×12×12a；同理第四个等边三角形的边长是12×12×12a，第四个正六边形的边长是13×12×12×12a；第五个等边三角形的边长是12×12×12×12a，第五个正六边形的边长是13×12×12×12×12a ；第六个等边三角形的边长是12×12×12×12×12a ，第六个正六边形的边长是13×12×12×12×12×12a ，即第六个正六边形的边长是13×512（）a ，故选A ．12．如图所示，△ABP 与△CDP 是两个全等的等边三角形，且PA ⊥PD ，有下列四个结论：①∠PBC ＝15°，②AD ∥BC ，③PC ⊥AB ，④四边形ABCD 是轴对称图形，其中正确的个数为（）A ．1个B ．2个C ．3个D ．4个【答案】D【解析】【分析】根据周角的定义先求出∠BPC 的度数，再根据对称性得到△BPC 为等腰三角形，∠PBC 即可求出；根据题意：有△APD 是等腰直角三角形；△PBC 是等腰三角形；结合轴对称图形的定义与判定，可得四边形ABCD 是轴对称图形，进而可得②③④正确．【详解】根据题意，BPC 36060290150∠=-⨯-= ， BP PC =，()PBC 180150215∠∴=-÷=，①正确；根据题意可得四边形ABCD 是轴对称图形，④正确；∵∠DAB+∠ABC=45°+60°+60°+15°=180°，∴AD//BC ，②正确；∵∠ABC+∠BCP=60°+15°+15°=90°，∴PC ⊥AB ，③正确，所以四个命题都正确，故选D．【点睛】本题考查了等边三角形的性质、等腰直角三角形的性质、等腰三角形的判定与性质、轴对称图形的定义与判定等，熟练掌握各相关性质与定理是解题的关键.13．某平原有一条很直的小河和两个村庄，要在此小河边的某处修建一个水泵站向这两个村庄供水. 某同学用直线（虛线）l表示小河，,P Q两点表示村庄，线段（实线）表示铺设的管道，画出了如下四个示意图，则所需管道最短的是（）.A．B．C．D．【答案】C【解析】【分析】根据轴对称分析即可得到答案.【详解】根据题意，所需管道最短，应过点P或点Q作对称点，再连接另一点，与直线l的交点即为水泵站M，故选项A、B、D均错误，选项C正确，故选：C.【点睛】此题考查最短路径问题，应作对称点，使三点的连线在同一直线上，这是此类问题的解题目标，把握此目标即可正确解题.14．如图，在锐角△ABC中，AC＝10，S△ABC＝25，∠BAC的平分线交BC于点D，点M，N分别是AD和AB上的动点，则BM＋MN的最小值是（）A．4 B．245C．5 D．6【答案】C 【解析】试题解析：如图，∵AD 是∠BAC 的平分线，∴点B 关于AD 的对称点B′在AC 上，过点B′作B′N ⊥AB 于N 交AD 于M ，由轴对称确定最短路线问题，点M 即为使BM+MN 最小的点，B′N=BM+MN ，过点B 作BE ⊥AC 于E ，∵AC=10，S △ABC =25，∴12×10•BE=25，解得BE=5， ∵AD 是∠BAC 的平分线，B′与B 关于AD 对称，∴AB=AB′，∴△ABB′是等腰三角形，∴B′N=BE=5，即BM+MN 的最小值是5．故选C ．15．如图，Rt ACB ∆中，90ACB ∠=︒，ABC ∠的平分线BE 和BAC ∠的外角平分线AD 相交于点P ，分别交AC 和BC 的延长线于E ，D .过P 作PF AD ⊥交AC 的延长线于点H ，交BC 的延长线于点F ，连接AF 交DH 于点G .下列结论：①45APB ∠=︒；②PB 垂直平分AF ；③BD AH AB -=；④2DG PA GH =+；其中正确的结论有（）A ．4个B ．3个C ．2个D ．1个【答案】A【解析】【分析】①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP ，再根据角平分线的定义∠ABP ＝12∠ABC ，然后利用三角形的内角和定理整理即可得解；②先求出∠APB ＝∠FPB ，再利用“角边角”证明△ABP 和△FBP 全等，根据全等三角形对应边相等得到AB ＝BF ，AP ＝PF ；③根据直角的关系求出∠AHP ＝∠FDP ，然后利用“角角边”证明△AHP 与△FDP 全等，根据全等三角形对应边相等可得DF ＝AH ；④求出∠ADG ＝∠DAG ＝45°，再根据等角对等边可得DG ＝AG ，再根据等腰直角三角形两腰相等可得GH ＝GF ，然后根据即可得到DG GH =+. 【详解】解：①∵∠ABC 的角平分线BE 和∠BAC 的外角平分线，∴∠ABP ＝12∠ABC ， ∠CAP ＝12（90°＋∠ABC ）＝45°＋12∠ABC ，在△ABP 中，∠APB ＝180°−∠BAP−∠ABP ，＝180°−（45°＋12∠ABC ＋90°−∠ABC ）−12∠ABC ，＝180°−45°−12∠ABC−90°＋∠ABC−12∠ABC ，＝45°，故本小题正确；②∵PF ⊥AD ，∠APB ＝45°（已证），∴∠APB ＝∠FPB ＝45°，∵∵PB 为∠ABC 的角平分线，∴∠ABP ＝∠FBP ，在△ABP 和△FBP 中，APB FPB PB PBABP FBP ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△ABP ≌△FBP （ASA ），∴AB ＝BF ，AP ＝PF ；∴PB 垂直平分AF ，故②正确；③∵∠ACB ＝90°，PF ⊥AD ，∴∠FDP ＋∠HAP ＝90°，∠AHP ＋∠HAP ＝90°，∴∠AHP ＝∠FDP ，∵PF ⊥AD ，∴∠APH ＝∠FPD ＝90°，在△AHP 与△FDP 中，90AHP FDP APH FPD AP PF ∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△AHP ≌△FDP （AAS ），∴DF ＝AH ，∵BD ＝DF ＋BF ，∴BD ＝AH ＋AB ，∴BD−AH ＝AB ，故③小题正确；④∵AP ＝PF ，PF ⊥AD ，∴∠PAF ＝45°，∴∠ADG ＝∠DAG ＝45°，∴DG ＝AG ，∵∠PAF ＝45°，AG ⊥DH ，∴△ADG 与△FGH 都是等腰直角三角形，∴DG ＝AG ，GH ＝GF ，∴DG ＝GH ＋AF ，∴故DG GH =+.综上所述①②③④正确．故选：A ．【点睛】本题考查了直角三角形的性质，全等三角形的判定，以及等腰直角三角形的判定与性质，等角对等边，等边对等角的性质，综合性较强，难度较大，做题时要分清角的关系与边的关系．16．在平面直角坐标系中，等腰△ABC 的顶点A 、B 的坐标分别为(1，0)、(2，3)，若顶点C 落在坐标轴上，则符合条件的点C 有( )个.A ．9B ．7C ．8D ．6【答案】C【解析】【分析】要使△ABC 是等腰三角形，可分三种情况（①若CA =CB ，②若BC =BA ，③若AC =AB ）讨论，通过画图就可解决问题．【详解】①若CA =CB ，则点C 在AB 的垂直平分线上．∵A （1，0），B （2，3），∴AB 的垂直平分线与坐标轴有2个交点C 1，C 2．②若BC =BA ，则以点B 为圆心，BA 为半径画圆，与坐标轴有3个交点（A 点除外）C 3，C 4，C 5；③若AC =AB ，则以点A 为圆心，AB 为半径画圆，与坐标轴有4个交点C 6，C 7，C 8，C 9．而C 8（0，-3）与A 、B 在同一直线上，不能构成三角形，故此时满足条件的点有3个．综上所述：符合条件的点C 的个数有8个．故选C ．【点睛】本题考查了等腰三角形的判定、垂直平分线的性质的逆定理等知识，还考查了动手操作的能力，运用分类讨论的思想是解答本题的关键．17．如图，已知：∠MON =30°，点A 1、A 2、A 3 ···在射线ON 上，点1B 、2B 、3B ···在射线OM 上，△112A B A 、△223A B A 、△334A B A …均为等边三角形，若112OA =，则△667A B A 的边长为（）A ．6B ．12C ．16D ．32【答案】C【解析】【分析】根据等腰三角形与等边三角形性质以及直角三角形中30°角所对应的直角边等于斜边的一半111OA A B =，112122321122A B A B A B A B ===…以此类推得出答案即可【详解】∵△112A B A 是等边三角形，∴∠112A B A =∠112B A A =60°又∵∠MON =30°∴∠11OB A =30°∴∠12OB A =∠212A B B =90°，1112112A B OA A B ===又∵△223A B A 是等边三角形∴22A B ∥11A B∴∠22OB A =∠11OB A =30°∴在Rt△212A B B 中，22A B =212A B =1以此类推，得出△667A B A 的边长=1222222⋅⋅⋅⋅⋅=16 所以答案为C 选项【点睛】本题主要考查了等腰三角形与等边三角形性质以及30°角的直角三角形的性质，熟练掌握相关概念通过题目发现规律是解题关键18．如果一个三角形能被一条线段分割成两个等腰三角形，那么称这个三角形为特异三角形．若△ABC 是特异三角形，∠A=30°，∠B 为钝角，则符合条件的∠B 有（）个． A ．1B ．2C ．3D ．4【答案】B【解析】【分析】【详解】如下图，当30°角为等腰三角形的底角时有两种情况：∠B=135°或90°，当30°角为等腰三角形的顶角时有一种情况：∠B=112.5°，所以符合条件的∠B 有三个.又因为∠B为钝角，则符合答案的有两个，故本题应选B.点睛：因为不确定这个等腰三角形的底边，所以应当以点A为一个确定点进行分类讨论：①当以B为顶点时，即以B为圆心，AB长为半径画弧交AC于点D，构成等腰△BAD；②当以点A为顶点时，即以点A为圆心，AB长为半径画弧，交AC于点D，构成等腰△ABD；或作线段AB的垂直平分线交AC于点D构成等腰△DAB.19．已知等边△ABC中，在射线BA上有一点D，连接CD，并以CD为边向上作等边△CDE，连接BE和AE，试判断下列结论：①AE=BD；②AE与AB所夹锐夹角为60°；③当D在线段AB或BA延长线上时，总有∠BDE-∠AED=2∠BDC；④∠BCD=90°时，CE2+AD2=AC2+DE2，正确的序号有（）A．①②B．①②③C．①②④D．①②③④【答案】C【解析】【分析】由∠BCD=∠ACD+60°，∠ACE=∠ACD+60°可得∠BCD=∠ACE，利用SAS可证明△BCD≌△ACE，可得AE=BD，①正确；∠CBD=∠CAE=60°，进而可得∠EAD=60°，②正确，当∠BCD=90°时，可得∠ACD=∠ADC=30°，可得AD=AC，即可得CE2+AD2=AC2+DE2，④正确；当D点在BA延长线上时，∠BDE-∠BDC=60°，根据△BCD≌△ACE可得∠AEC=∠BDC，进而可得∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，即可证明∠BDE-∠BDC=∠BDC+∠AED，即∠BDE-∠AED=2∠BDC，当点D在AB上时可证明∠BDE-∠AED=120°，③错误，综上即可得答案.【详解】∵∠BCA=∠DCE=60°，∴∠BCA+∠ACD=∠DCE+∠ACD，∴∠BCD=∠ACE，又∵AC=BC，CE=CD，∴△BCD≌△ACE，∴AE=BD，∠CBA=∠CAE=60°，∠AEC=∠BDC，①正确，∴∠BAE=120°，∴∠EAD=60°，②正确，∵∠BCD=90°，∠BCA=60°，∴∠ACD=∠ADC=30°，∴AC=AD，∵CE=DE，∴CE2+AD2=AC2+DE2，④正确，当D点在BA延长线上时，∠BDE-∠BDC=60°，∵∠AEC=∠BDC，∴∠BDC+∠AED=∠AEC+∠AED=∠CED=60°，∴∠BDE-∠BDC=∠BDC+∠AED∴∠BDE-∠AED=2∠BDC，如图，当点D在AB上时，∵△BCD≌△∠ACE，∴∠CAE=∠CBD=60°，∴∠DAE=∠BAC+∠CAE=120°，∴∠BDE-∠AED=∠DAE=120°，③错误故正确的结论有①②④，故选C.【点睛】此题主要考查等边三角形的性质和全等三角形的判定与性质等知识点的理解和掌握20．如图，O是正三角形ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO′=6+33；⑤S△AOC+S△AOB=6+934．其中正确的结论是（）A．①②③⑤B．①③④C．②③④⑤D．①②⑤【答案】A【解析】试题解析：由题意可知，∠1+∠2=∠3+∠2=60°，∴∠1=∠3，又∵OB=O′B，AB=BC，∴△BO′A≌△BOC，又∵∠OBO′=60°，∴△BO′A可以由△BOC绕点B逆时针旋转60°得到，故结论①正确；如图①，连接OO′，∵OB=O′B，且∠OBO′=60°，∴△OBO′是等边三角形，∴OO′=OB=4．故结论②正确；∵△BO′A≌△BOC，∴O′A=5．在△AOO′中，三边长为3，4，5，这是一组勾股数，∴△AOO′是直角三角形，∠AOO′=90°，∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°，故结论③正确；S四边形AOBO′=S△AOO′+S△OBO′=12323故结论④错误；如图②所示，将△AOB绕点A逆时针旋转60°，使得AB与AC重合，点O旋转至O″点．易知△AOO″是边长为3的等边三角形，△COO″是边长为3、4、5的直角三角形，则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=12×3×4+34×32=6+34，故结论⑤正确．综上所述，正确的结论为：①②③⑤．故选A．。

成都石室中学(北湖校区)八年级数学上册第二单元《全等三角形》测试题(有答案解析)

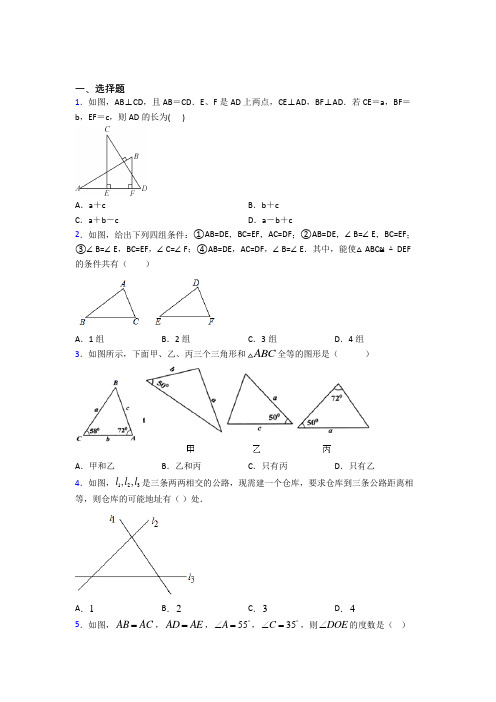
一、选择题1．如图，AB ⊥CD ，且AB ＝CD ．E 、F 是AD 上两点，CE ⊥AD ，BF ⊥AD ．若CE ＝a ，BF ＝b ，EF ＝c ，则AD 的长为( )A ．a ＋cB ．b ＋cC ．a ＋b －cD ．a －b ＋c2．如图，给出下列四组条件：①AB=DE ，BC=EF ，AC=DF ；②AB=DE ，∠B=∠E ，BC=EF ；③∠B=∠E ，BC=EF ，∠C=∠F ；④AB=DE ，AC=DF ，∠B=∠E ．其中，能使△ABC ≌△DEF 的条件共有（）A ．1组B ．2组C ．3组D ．4组3．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙 4．如图，123,,l l l 是三条两两相交的公路，现需建一个仓库，要求仓库到三条公路距离相等，则仓库的可能地址有（）处．A ．1B ．2C ．3D ．45．如图，AB AC =，AD AE =，55A ︒∠=，35C ︒∠=，则DOE ∠的度数是（）A ．105︒B ．115︒C ．125︒D ．130︒ 6．到ABC 的三条边距离相等的点是ABC 的( ) A ．三条中线的交点B ．三条边的垂直平分线的交点C ．三条高的交点D ．三条角平分线的交点7．对于ABC 与DEF ，已知∠A=∠D ，∠B=∠E ，则下列条件：①AB=DE ；②AC=DF ；③BC=DF ；④A B=EF 中，能判定它们全等的有（）A ．①②B ．①③C ．②③D ．③④ 8．如图，AB BC ⊥，CD BC ⊥，AC BD =，则能证明ABC DCB ≅的判定法是( )A ．SASB ．AASC ．SSSD ．HL9．如图，在OAB 和OCD 中，OA OB =，OC OD =，OA OC >，40AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ，下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠，其中正确的为（）A ．①②③B ．①②④C ．②③④D ．①②③④ 10．如图，点C ，D 在线段AB 上，AC DB =，AE //BF ，添加以下哪一个条件仍不能判定△AED ≌△BFC （）A ．ED CF =B ．AE BF =C ．E F ∠=∠D ．ED //CF11．如图，在下列条件中，不能判断△ABD ≌△BAC 的条件是（）A ．∠D=∠C ， ∠BAD=∠ABCB ．BD=AC ， ∠BAD=∠ABC C ．∠BAD=∠ABC ， ∠BAD=∠ABCD ．AD=BC ，BD=AC12．下列说法正确的是（） A ．一直角边对应相等的两个直角三角形全等 B ．斜边相等的两个直角三角形全等 C ．斜边相等的两个等腰直角三角形全等 D ．一边长相等的两个等腰直角三角形全等二、填空题13．如图，ABC 的三边AB 、BC 、CA 长分别是10、15、20，三条角平分线交于O 点，则::ABO BCO CAO S S S 等于__________．14．如图所示，在ABC 中，AB AC =，AD 是ABC 的角平分线，DE AB ⊥，DF AC ⊥，垂足分别是E ，F ．则下面结论中（1）DA 平分EDF ∠；（2）AE AF =，DE DF =；（3）AD 上的点到B ，C 两点的距离相等；（4）图中共有3对全等三角形．正确的有________ ．15．如图，线段AB ，CD 相交于点O ，AO=BO ，添加一个条件，能使AOC BOD ≅，所添加的条件的是___________________________．16．如图，四边形ABDC 中，对角线AD 平分BAC ∠，136ACD ∠=︒，44BCD ∠=︒，则ADB ∠的度数为_____17．如图，射线OC 是∠AOB 的角平分线，D 是射线OC 上一点，DP ⊥OA 于点P ，DP ＝5，若点Q 是射线OB 上一点，OQ ＝4，则△ODQ 的面积是__________．18．如图，AD 是ABC 中BAC ∠的平分线，DE AB ⊥交AB 于点E ，DF AC ⊥交AC 于点F ．若28ABC S =，4DE =，8AB =，则AC =_________．19．如图，在△ABC 和△DBC 中，∠ACB=∠DBC=90°，E 是BC 的中点，DE ⊥AB ，垂足为F ，AB=DE ．若BD=8cm ，则AC 的长为_________．20．如图，在△ABC 中，∠C =90°，∠A 的平分线交BC 于D ，若20ABD S ∆=cm 2，AB =10cm ，则CD 为__________cm ．三、解答题21．如图所示，△ABC 中，∠ACB=90°，AC=BC ，直线EF 经过点C ，BF ⊥EF 于点F ，AE ⊥EF 于点E ．（1）求证：△ACE ≌△CBF ；（2）如果AE 长12cm ，BF 长5cm ，求EF 的长．22．如图，已知A ABC ∠=∠，D CBD ∠=∠，ABD CBD ∠=∠，点E 在BC 的延长线上．求证：CD 平分ACE ∠．23．OAB 和ODE 均为等腰三角形，且AOB DOE β∠=∠=，OA OB =，OD OE =，连接AD 、BE ，它们所在的直线交于点F ．（1）观察发现：如图1，当60β︒=时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______；（2）探究证明：如图2，当90β︒=时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______，根据图2证明你的猜想；（3）拓展推广：当β为任意角时，线段AD 与BE 的数量关系是______，AFB ∠的度数是______．（用含β的式子表示）24．如图，在△ABD 中，∠ABD ＝90°，AB=BD ，点E 在线段BD 上，延长AB 使BC=BE ，连接AE 、CE 、CD ，点M 在线段AE 上，点N 在线段CD 上，BM ⊥BN ，易证△ABE ≌△DBC ；仔细观察，请逐一找出图中其他的全等三角形，并说明理由．25．如图①，∠BAD=90°，AB=AD ，过点B 作BC ⊥AC 于点C ，过点D 作DE ⊥CA 的延长线点E ，由∠1+∠2=∠D+∠2=90°，得∠1=∠D ，又∠ACB=∠AED=90°，AB=AD ，得△ABC ≌△DAE 进而得到AC=DE ，BC=AE ，我们把这个数学模型称为“K 字”模型或“一线三等角”模型．请应用上述“一线三等角”模型，解决下列问题：（1）如图②，∠BAD=∠CAE=90°，AB=AD ，AC=AE ，连接BC 、DE ，且BC ⊥AH 于点H ，DE 与直线AH 交于点G ，求证：点G 是DE 的中点．（2）如图③，在平面直角坐标系中，点A 为平面内任意一点，点B 的坐标为（4，1），若△AOB 是以OB 为斜边的等腰直角三角形，请直接写出点A 的坐标．26．如图，一条河流MN旁边有两个村庄A，B，AD⊥MN于D．由于有山峰阻挡，村庄B 到河边MN的距离不能直接测量，河边恰好有一个地点C能到达A，B两个村庄，与A，B 的连接夹角为90°，且与A，B的距离也相等，测量C，D的距离为150m，请求出村庄B到河边的距离．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】由“AAS”可证△ABF≌△CDE，根据全等三角形的性质可得AF＝CE＝a，BF＝DE＝b，则可推出AD＝AF＋DF＝a＋（b−c）＝a＋b−c．【详解】解：∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠AFB＝∠CED＝90°，∠A＋∠D＝90°，∠C＋∠D＝90°，∴∠A＝∠C，∵AB＝CD，∴△ABF≌△CDE（AAS），∴AF＝CE＝a，BF＝DE＝b，∵EF＝c，∴AD＝AF＋DF＝a＋（b−c）＝a＋b−c．故选：C．【点睛】本题考查了全等三角形的判定和性质，解题的关键是掌握全等三角形的判定方法并准确寻找全等三角形解决问题．2．C【分析】要使△ABC≌△DEF的条件必须满足SSS、SAS、ASA、AAS，可据此进行判断．【详解】解：第①组满足SSS，能证明△ABC≌△DEF．第②组满足SAS，能证明△ABC≌△DEF．第③组满足ASA，能证明△ABC≌△DEF．第④组只是SSA，不能证明△ABC≌△DEF．所以有3组能证明△ABC≌△DEF．故符合条件的有3组．故选：C．【点睛】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．3．B解析：B【分析】甲只有2个已知条件，缺少判定依据；乙可根据SAS判定与△ABC全等；丙可根据AAS判定与△ABC全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC全等；丙三角形72°内角及所对边与△ABC对应相等且均有50°内角，可根据AAS判定乙与△ABC 全等；则与△ABC全等的有乙和丙，故选：B．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．4．D解析：D【分析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点，把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．【详解】（1）三角形两个内角平分线的交点，共一处（2）三个外角两两平分线的交点，共三处，故选：D ．．【点睛】此题考查角平分线的性质：角平分线上的点到角两边的距离相等，熟记性质是正确解题的关键．5．C解析：C【分析】先判定△ABE ≌△ACD ，再根据全等三角形的性质，得出∠B=∠C=35︒，由三角形外角的性质即可得到答案．【详解】在△ABE 和△ACD 中，AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACD （SAS ），∴∠B=∠C ，∵∠C=35︒，∴∠B=35︒，∴∠OEC=∠B+∠A=355590︒+︒=︒，∴∠DOE=∠C+∠OEC=3590125︒+︒=︒，故选：C ．【点睛】本题考察全等三角形的判定与性质、三角形外角的性质，熟练掌握全等三角形的判定与性质是解题关键．6．D解析：D【分析】由于角平分线上的点到角的两边的距离相等，而已知一点到ABC 的三条边距离相等，那么这样的点在这个三角形的三条角平分线上，由此即可作出选择.【详解】解:∵到ABC 的三条边距离相等，角平分线上的点到角的两边的距离相等，∴这点在这个三角形三条角平分线上，即这点是三条角平分线的交点，故选：D.【点睛】此题主要考查了三角形的角平分线的性质：三条角平分线交于一点，并且这一点到三边的距离相等.7．A解析：A【分析】根据已知条件，已知两角对应相等，所以要证两三角形全等，可以根据角边角、角角边、边角边判定定理添加条件，再根据选项选取答案即可；【详解】题意已知：∠A=∠D ，∠B=∠E ，∴①根据“ASA”可添加AB=DE ，故①正确；②根据“AAS” 可添加AC=DF ，故②正确；③根据“AAS” 可添加BC=EF ，故③错误；④根据“ASA”可添加AB=DE ，故④错误；所以补充①②可判定两三角形全等；故选：A ．【点睛】本题主要考查了三角形全等的判定，根据不同的判定方法可选择不同的条件，所以对三角形全等的判定定理要熟练掌握并归纳总结；8．D解析：D【分析】直接证明全等三角形，即可确定判断方法.【详解】解：∵AB BC ⊥，CD BC ⊥，∴ABC 与△DCB 均为直角三角形，又AC DB =，BC CB =， ∴()ABC DCB HL ≅,故选：D.【点睛】本题考查全等三角形的判定定理，属于基础题.9．B解析：B【分析】由SAS 证明AOC BOD ≅得出OCA ODB ∠=∠，=AC BD ，①正确；由全等三角形的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，得出40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，由AAS 证明OCG ODH ≅（AAS ），得出OG=OH ，由角平分线的判定方法得出MO 平分BOC ∠，④正确；由AOB COD ∠=∠，得出当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM ，由AOC BOD ≅得出COM BOM ，由MO 平分BMC ∠得出∠=∠CMO BMO ，推出COM BOM ≅，得出OB=OC ，OA=OB ，所以OA=OC ，而OA OC >，故③错误；即可得出结论．【详解】∵40AOB COD ∠=∠=︒，∴AOB AOD COD AOD ∠+∠=∠+∠即AOC BOD ∠=∠在AOC △和BOD 中OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴AOC BOD ≅（SAS ）∴OCA ODB ∠=∠，=AC BD ，①正确；∴OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠，∴40AOB COD ∠=∠=︒，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=，在OCG 和ODH 中OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OCG ODH ≅（AAS ），∴OG=OH∴MO 平分BOC ∠，④正确；∴AOB COD ∠=∠∴当∠=∠DOM AOM 时，OM 平分BOC ∠，假设∠=∠DOM AOM∵AOC BOD ≅ ∴COM BOM ，∵MO 平分BMC ∠∴∠=∠CMO BMO ，在COM 和BOM 中OCM BOM OM OMCMO BMO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴COM BOM ≅（ASA ）∴OB=OC ，∵OA=OB ，∴OA=OC ，与OA OC >矛盾，∴③错误；正确的有①②④；故选：B【点睛】本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．10．A解析：A【分析】欲使△AED ≌△BFC ，已知AC=DB ，AE ∥BF ，可证明全等三角形判定定理AAS 、SAS 、ASA 添加条件，逐一证明即可；【详解】∵ AC=BD ，∴ AD=CE ，∵ AE ∥BF ，∴ ∠A=∠E ，A 、如添加ED=CF ，不能证明△AED ≌△BFC ，故该选项符合题意；B 、如添加AE=BF ，根据SAS ，能证明△AED ≌△BFC ，故该选项不符合题意；C 、如添加∠E=∠F ，利用AAS 即可证明△AED ≌△BFC ，故该选项不符合题意； D 、如添加ED ∥CF ，得出∠EDC=∠FCE ，利用ASA 即可证明△AED ≌△BFC ，故该选项不符合题意；故选：A．【点睛】本题考查了全等三角形的判定定理的理解和掌握，此类添加条件题，要求学生应熟练掌握全等三角形的判定定理；11．B解析：B【分析】本题已知条件是两个三角形有一公共边，只要再加另外两边对应相等或有两角对应相等即可，如果所加条件是一边和一角对应相等，则所加角必须是所加边和公共边的夹角对应相等才能判定两个三角形全等；【详解】A、符合AAS，能判断两个三角形全等，故该选项不符合题意；B、符合SSA，∠BAD和∠ABC不是两条边的夹角，不能判断两个三角形全等，故该选项符合题意；C、符合AAS，能判断两个三角形全等，故该选项不符合题意；D、符合SSS，能判断两个三角形全等，故该选项不符合题意；故选：B．【点睛】本题考查了全等三角形的判定方法，三角形判定定理中，最容易出错的是“边角边”定理，这里强调的是夹角，不是任意角；12．C解析：C【分析】根据全等三角形的判定定理：SSS、SAS、ASA、AAS、HL定理针对四个选项分别进行判断即可．【详解】A. 一直角边对应相等的两个直角三角形不一定全等，还要知道它的边或角才能证明，故此选项错误；B. 斜边相等的两个直角三角形不一定全等，还要知道它的边或角才能证明，故此选项错误；C. 斜边相等的两个等腰直角三角形全等，对应角相等，根据AAS即可证明全等，故此选项正确；D. 一边长相等的两个等腰直角三角形不一定全等，必须说明是对应边相等，故此选项错误．故选：C．【点睛】本题考查了全等三角形的判定，掌握证明三角形全等的条件尤其是必须含有边这个条件是解题的关键．二、填空题13．【分析】由角平分线的性质可得点O 到三角形三边的距离相等即三个三角形的ABBCCA 上的高相等利用面积公式即可求解【详解】解：过点O 作OD ⊥AC 于DOE ⊥AB 于EOF ⊥BC 于F ∵O 是三角形三条角平分线的解析：2:3:4【分析】由角平分线的性质可得，点O 到三角形三边的距离相等，即三个三角形的AB 、BC 、CA 上的高相等，利用面积公式即可求解．【详解】解：过点O 作OD ⊥AC 于D ，OE ⊥AB 于E ，OF ⊥BC 于F ，∵O 是三角形三条角平分线的交点，∴OD ＝OE ＝OF ．∵AB ＝10，BC ＝15，CA ＝20，∴::ABO BCO CAO S S S ＝(12•AB•OE )：(12•BC•OF )：(12•CA•OD )＝::AB BC CA ＝2:3:4．故答案为：2:3:4．【点睛】本题主要考查了角平分线的性质，掌握角平分线的性质定理和三角形面积的计算方法是解题的关键．14．（1）（2）（3）（4）【分析】在△ABC 中AB=ACAD 是△ABC 的平分线可知直线AD 为△ABC 的对称轴再根据图形的对称性逐一判断【详解】解：（1）∵在中是的角平分线∴∵∴∴∴平分故（1）正确；（解析：（1）（2）（3）（4）【分析】在△ABC 中，AB=AC ，AD 是△ABC 的平分线，可知直线AD 为△ABC 的对称轴，再根据图形的对称性，逐一判断．【详解】解：（1）∵在ABC 中，AB AC =，AD 是ABC 的角平分线，∴BAD CAD ∠=∠．∵DE AB ⊥，DF AC ⊥，∴ADE 90BAD ∠∠=︒-，ADF 90CAD ∠∠=︒-，∴ADE ADF ∠∠=， ∴DA 平分EDF ∠，故（1）正确；（2）由（1）可知，ADE ADF ∠∠=，在AED 和AFD 中，EAD FAD,AD AD,ADE ADF,∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AED AFD ASA ≅，∴AE AF =，DE DF =，故（2）正确；（3）在AD 上取一点M ，连结BM ，CM ．在ABM 和ACM 中，AB AC BAD CAD AM AM =⎧⎪∠=∠⎨⎪=⎩∴()ABM ACM SAS ≅，∴BM CM =，故（3）正确；（4）在ABD 和ACD 中，AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴()ABD ACD SAS ≅．∵DE AB ⊥，DF AC ⊥，∴∠AED=∠AFD=90°在ADE 和ADF 中，AED=AFD BAD CAD AD AD ∠∠⎧⎪∠=∠⎨⎪=⎩∴()ADE ADF AAS ≅． ∵ABD ACD ≅∴∠ABC=∠ACB ，BD=CD ，∵DE AB ⊥，DF AC ⊥，∴∠BED=∠CFD在BED 和CFD △中，EBD FCD BED CFD BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()BED CFD AAS ≅，∴图中共有3对全等三角形，故（4）正确．故答案为：（1）（2）（3）（4）．【点睛】本题考查了等腰三角形的性质，利用三角形全等是正确解答本题的关键．15．或或或【分析】先根据对顶角相等可得再根据三角形全等的判定定理即可得【详解】由对顶角相等得：当时由定理可证当时由定理可证当时由定理可证当时则由定理可证故答案为：或或或【点睛】本题考查了对顶角相等三角形解析：CO DO =或A B ∠=∠或C D ∠=∠或//AC BD【分析】先根据对顶角相等可得AOC BOD ∠=∠，再根据三角形全等的判定定理即可得．【详解】由对顶角相等得：AOC BOD ∠=∠，AO BO =，∴当CO DO =时，由SAS 定理可证AOC BOD ≅，当A B ∠=∠时，由ASA 定理可证AOC BOD ≅，当C D ∠=∠时，由AAS 定理可证AOC BOD ≅，当//AC BD 时，则A B ∠=∠，由ASA 定理可证AOC BOD ≅，故答案为：CO DO =或A B ∠=∠或C D ∠=∠或//AC BD ．【点睛】本题考查了对顶角相等、三角形全等的判定定理等知识点，熟练掌握三角形全等的判定定理是解题关键．16．【分析】先添加辅助线过点作交的延长线于点过点作交的延长线于点过点作于点根据角平分线的判定性质定义以及三角形外角的性质邻补角的定义角的和差等可求得【详解】解：过点作交的延长线于点过点作交的延长线于点过解析：46︒【分析】先添加辅助线“过点D 作DE AB ⊥交AB 的延长线于点E ，过点D 作DF AC ⊥交AC 的延长线于点F ，过点D 作DG BC ⊥于点G ”，根据角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等可求得()1462ADB CBE BAC ∠=∠-∠=︒．【详解】解：过点D 作DE AB ⊥交AB 的延长线于点E ，过点D 作DF AC ⊥交AC 的延长线于点F ，过点D 作DG BC ⊥于点G ，如图：∵AD 平分BAC ∠，DE AB ⊥，DF AC ⊥∴12BAD BAC ∠=∠，DE DF = ∵136ACD ∠=︒ ∴18044DCF ACD ∠=︒-∠=︒∵44BCD ∠=︒，92ACB ACD BCD ∠=∠-∠=︒∴CD 平分BCF ∠∵DF AC ⊥，DG BC ⊥∴DF DG =∴DE DG =∵DE AB ⊥，DG BC ⊥∴BD 平分CBE ∠∴12DBE CBE ∠=∠ ∴ADB DBE BAD ∠=∠-∠1122CBE BAC =∠-∠()12CBE BAC =∠-∠ 12BCA =∠ 46=︒．故答案是：46︒【点睛】本题考查了角平分线的判定、性质、定义以及三角形外角的性质、邻补角的定义、角的和差等，熟练掌握相关知识点是解题的关键． 17．10【分析】作DH ⊥OB 于点H 根据角平分线的性质得到DH=DP=5根据三角形的面积公式计算得到答案【详解】解：作DH ⊥OB 于点H ∵OC 是∠AOB 的角平分线DP ⊥OADH ⊥OB ∴DH=DP=5∴△OD解析：10【分析】作DH ⊥OB 于点H ，根据角平分线的性质得到DH=DP=5，根据三角形的面积公式计算，得到答案．【详解】解：作DH ⊥OB 于点H ，∵OC 是∠AOB 的角平分线，DP ⊥OA ，DH ⊥OB ，∴DH=DP=5，∴△ODQ 的面积=12×OQ×DH=12×4×5=10；故答案为：10．【点睛】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键． 18．【分析】首先由角平分线的性质可知DF=DE=4然后由S △ABC=S △ABD+S △ACD 及三角形的面积公式得出结果【详解】解：∵AD 是∠BAC 的平分线DE ⊥ABDF ⊥AC ∴DF=DE=4又∵S △ABC解析：【分析】首先由角平分线的性质可知DF=DE=4，然后由S △ABC =S △ABD +S △ACD 及三角形的面积公式得出结果．【详解】解：∵AD 是∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DF=DE=4．又∵S △ABC =S △ABD +S △ACD ，AB=8， ∴12×8×4+ 12×AC×4=28， ∴AC=6．故答案是：6．【点睛】本题主要考查了角平分线的性质；利用三角形的面积求线段的长是一种很好的方法，要注意掌握应用．19．4cm 【分析】由DE ⊥AB 可得∠BFE=90°由直角三角形两锐角互余可得∠ABC+∠DEB=90°由∠ACB=90°由直角三角形两锐角互余可得∠ABC+∠A=90°根据同角的余角相等可得∠A=∠DE解析：4cm ．【分析】由DE ⊥AB ，可得∠BFE=90°，由直角三角形两锐角互余，可得∠ABC+∠DEB=90°，由∠ACB=90°，由直角三角形两锐角互余，可得∠ABC+∠A=90°，根据同角的余角相等，可得∠A=∠DEB ，然后根据AAS 判断△ABC ≌△EDB ，根据全等三角形的对应边相等即可得到BD=BC ，AC=BE ，由E 是BC 的中点，得到BE=12BC=12BD=4．【详解】解：∵DE ⊥AB ，可得∠BFE=90°，∴∠ABC+∠DEB=90°，∵∠ACB=90°，∴∠ABC+∠A=90°，∴∠A=∠DEB ，在△ABC 和△EDB 中， ACB DBC A DEBAB DE ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ABC ≌△EDB （AAS ），∴BD=BC ，AC=BE ，∵E 是BC 的中点，BD=8cm ，∴BE=12BC=12BD=4cm ， ∴AC=4cm ．故答案为：4cm ．【点睛】此题考查了全等三角形的判定与性质，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等，本题是一道较为简单的题目，找准全等的三角形是解决本题的关键．20．4【分析】由角平分线的性质可知D到AB的距离等于DC可得出答案【详解】解：作DE⊥AB于E∵AD平分∠CAB且DC⊥ACDE⊥AB∴DE=DC∵S△ABD=20cm2AB=10cm∴•AB•DE=2解析：4【分析】由角平分线的性质可知D到AB的距离等于DC，可得出答案．【详解】解：作DE⊥AB于E．∵AD平分∠CAB，且DC⊥AC，DE⊥AB，∴DE=DC，∵S△ABD=20cm2，AB=10cm，∴1•AB•DE=20，2∴DE=4cm，∴DC=DE=4cm故答案为：4．【点睛】本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．三、解答题21．（1）证明见解析；（2）EF=17cm．【分析】（1）根据垂直的定义可得∠AEC=∠CFB=90°，然后求出∠EAC=∠FCB，再利用“角角边”证明即可；（2）由全等三角形的性质可得：AE=CF，CE=BF，再根据线段的和差求解即可．【详解】（1）证明：在Rt△ACB中，∵∠ACB=90°，∴∠ACE+∠BCF=90°∵AE⊥EF，BF⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE ≌△CBF(ASA)(2)由△ACE ≌△CBF 可得:AE=CF=12cm ， EC=BF=5cm ，∴EF=EC+CF=12+5=17cm ．【点睛】本题考查了全等三角形的判定与性质，同角的余角相等的性质，熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键．22．见解析【分析】根据题意，先证明//AB CD ，然后由平行线的性质以及等量代换，得到ACD DCE ∠=∠，即可得到结论成立．【详解】证明：D CBD ∠=∠，ABD CBD ∠=∠，D ABD ∴∠=∠，//AB CD ∴ABC DCE ∴∠=∠，A ACD ∠=∠又A ABC ∠=∠，ACD DCE ∴∠=∠，CD ∴平分ACE ∠．【点睛】本题考查了平行线的判定和性质，角平分线的判定，解题的关键是掌握所学的知识，正确得到//AB CD ．23．（1）AD BE =，60°；（2）AD BE =，90°，理由见解析；（3）AD BE =，β【分析】（1）设AF 交BD 于G ，证明AOD BOE ≌△△，推出AD BE =，OAD OBE ∠=∠，得到60AFB AOB ∠=∠=︒；（2）证明AOD BOE ≌△△，推出AD BE =，OAD OBE ∠=∠，根据OFA DFB ∠=∠及三角形内角和定理即可证得90AFB AOB ∠=∠=︒；（3）根据（1）与（2）直接得到结论．【详解】（1）证明：设AF 交BO 于G ，∵60AOB DOE ∠=∠=︒，∴AOB BOD DOE BOD ∠-∠=∠-∠，即AOD BOE ∠=∠，∵OA OB =，OD OE =，∴AOD BOE ≌△△，∴AD BE =，OAD OBE ∠=∠，∵OGA FGB ∠=∠，∴180180OGA OAD FGB OBE ∠-∠=∠--∠︒-︒，∴60AFB AOB ∠=∠=︒，故答案为：AD BE =，60°；（2）AD BE =，90°证明：设AF 交BO 于G ，∵90AOB DOE ︒∠=∠=，∴AOB BOD DOE BOD ∠+∠=∠+∠，即AOD BOE ∠=∠，∵OA OB =，OD OE =，∴AOD BOE ≌△△，∴AD BE =，OAD OBE ∠=∠，∵OGA DGB ∠=∠，∴90AFB AOB ∠=∠=︒；故答案为：AD BE =，90°；（3）证明：由（1）与（2）可得AD BE =，AFB AOB β∠=∠=故答案为：AD BE =，β．【点睛】此题考查全等三角形的判定及性质，等腰三角形的性质，熟练掌握全等三角形的判定及性质是解题的关键．24．△ABM ≌△DBN ，△BME ≌△BNC ，理由见解析．【分析】观察图形，可找出△ABM ≌△DBN ，△BME ≌△BNC ．①由△ABE ≌△DBC 可得到∠BAE=∠BDC ，根据BM ⊥BN 可得到∠AMB+∠MBE =∠DBN+∠MBE ，继而得到∠AMB=∠DBN ，AB=BD ，可得△ABM ≌△DBN ；②由△ABM ≌△DBN 可得BM=BN ，根据∠NBE+∠MBE =∠NBE+∠NBC ，可得∠MBE =∠NBC ，继而可证得△BME ≌△BNC ．【详解】解：全等三角形：△ABM ≌△DBN ，△BME ≌△BNC ，理由如下：由题意知△ABE ≌△DBC ，∴∠BAE=∠BDC ，∵BM ⊥BN ，∴∠MNB=90︒，∴∠ABM+∠MBE =∠DBN+∠MBE ，∴∠ABM=∠DBN ，AB=BD ，∴△ABM ≌△DBN ，∴BM=BN,∵∠NBE+∠MBE =∠NBE+∠NBC ，∴∠MBE =∠NBC ，∵BE=BC ，∴△BME ≌△BNC ．【点睛】本题考察全等三角形的判定与性质，熟知全等三角形的判定与性质是解题关键． 25．（1）见解析；（2）A(32，52)或(52，-32)．【分析】（1）过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ．根据“K 字模型”即可证明AH=DM 和AH=EN ，即EN=DM ，再根据全等三角形的判定和性质即可证明DG=EG ，即点G 是DE 的中点．（2）分情况讨论①当A 点在OB 的上方时，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．根据“K 字模型”即可证明AC BD OC AD DE ===，，再利用B 点坐标即可求出A 点坐标．②当A 点在OB 的下方时，作AP 垂直于y 轴，BM 垂直于x 轴，PA 和BM 的延长线交于点Q ．同理即能求出A 点坐标．【详解】（1）如图，过点D 作DM ⊥AM 交AG 于点M ，过点E 作EN ⊥AG 于点N ，则∠DMA=90°，∠ENG=90°．∵∠BHA=90 ，∴∠2+∠B=90°．∵∠BAD=90°，∴∠1+∠2=90°．∴∠B=∠1 ．在△ABH 和△DAM 中1BHA AMD B AB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABH ≅△DAM （AAS ），∴AH=DM ．同理 △ACH ≅△EAN （AAS ），∴ AH=EN ．∴EN=DM ．在△DMG 和△ENG 中MGD NGE DMG ENG DM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△DMG ≅△ENG （AAS ）．∴DG=EG ．∴点G 是DE 的中点．（2）根据题意可知有两种情况，A 点分别在OB 的上方和下方．①当A 点在OB 的上方时，如图，作AC 垂直于y 轴，BE 垂直于x 轴，CA 和EB 的延长线交于点D ．利用“K 字模型”可知ACO BDA ≅，∴AC BD OC AD DE ===，，设AC x =，则BD x =，∵1DE BD BE x =+=+，∴1OC AD DE x ===+，又∵4CD AD AC =+=，即14x x ++=，解得32x =， ∴32AC =，35122DE =+=．即点A 坐标为(32，52)．②当A点在OB的下方时，如图，作AP垂直于y轴，BM垂直于x轴，PA和BM的延长线交于点Q．根据①同理可得：52 AP=，32MQ=．即点A坐标为(52，32-)．【点睛】本题考查了三角形全等的判定和性质．熟练利用三角形的判定方法是解答本题的关键．26．150米【分析】根据题意，判断出△ADC≌△CEB即可求解．【详解】解：如图，过点B作BE⊥MN于点E，∵∠ADC＝∠ACB＝90°，∴∠A＝∠BCE（同角的余角相等）．在△ADC与△CEB中，90ADC CEBA BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△ADC≌△CEB（AAS）．∴BE＝CD＝150m．即村庄B到河边的距离是150米．【点睛】本题主要考查的是全等三角形的实际应用，熟练掌握全等三角形的判定及性质是解答本题的关键．。

成都石室联合中学小升初数学期末试卷易错题(Word版含答案)

成都石室联合中学小升初数学期末试卷易错题（Word 版含答案）一、选择题1．从12时到13时，钟的时针与分针可成直角的机会有（）。

A ．1次B ．2次C ．3次D ．4次2．将83除以32与41的差是多少？正确的算式是 ( ) A ．213-348÷ B ．213-348÷（） C ．312-843÷（） D ．321-834÷（） 3．一个三角形三个角度数的比是2:2:5，这个三角形是（）。

A ．等腰三角形 B ．等边三角形 C ．直角三角形 D ．等腰直角三角形 4．用5千克棉花的0.25和5千克铁的相比较，结果是（）．A ．5千克棉花的0.25重B ．5千克铁的重C ．一样重D ．无法比较5．用五个同样大小的正方体搭成下面的立体图形，从（）看到的形状是．A ．正面B ．右面C ．上面D ．左面6．下面语句中错误的是（）。

A ．要找到一张圆形纸片的圆心至少要对折2次B ．1吨煤，用去37吨后，还剩全部的47C ．产品增长率可能大于100%D ．圆形、三角形、正方形、长方形都是轴对称图形7．一个圆柱与圆锥，体积和底面积都相等。

圆柱与圆锥高的比是（）。

A ．1∶1B ．1∶3C ．3∶1D ．不能确定 8．春节期间，一家三口旅游，甲旅行社优惠条件是：父母全票，孩子半票，乙旅行社优惠条件是：三人都按80%收费。

两旅行社原来标价都相同，花钱少的是（）。

A ．甲社B ．乙社C ．不好确定 9．将一张正方形纸连续对折4次后展开，其中一份占这张正方形纸的( ) ． A ．12 B ．14 C ．18D ．116二、填空题10．325小时＝（________）分 40.8立方米＝（________）升 11．58的分数单位是（________），再增加（________）个这样的分数单位就成了最小的质数。

12．学校合唱队男生和女生人数的比是3∶5。

成都市青羊实验联合中学数学轴对称填空选择易错题(Word版含答案)

成都市青羊实验联合中学数学轴对称填空选择易错题（Word 版含答案）一、八年级数学全等三角形填空题（难）1．如图，MN ∥PQ ，AB ⊥PQ ，点A ，D ，B ，C 分别在直线MN 和PQ 上，点E 在AB 上，AD ＋BC ＝7，AD ＝EB ，DE ＝EC ，则AB ＝_____．【答案】7【解析】由MN ∥PQ ，AB ⊥PQ ，可知∠DAE=∠EBC=90°，可判定△ADE ≌△BCE ，从而得出AE=BC ，则AB=AE+BE=AD+BC=7．故答案为：7.点睛：本题考查了直角三角形全等的判定和性质以及平行线的性质，是基础知识，比较简单．2．如图，△ABC 的三边AB 、BC 、CA 的长分别为30、40、15，点P 是三条角平分线的交点，将△ABC 分成三个三角形，则APB S ∆︰BPC S ∆︰CPA S ∆等于____．【答案】6：8：3【解析】【分析】由角平分线性质可知，点P 到三角形三边的距离相等，即三个三角形的AB 、BC 、CA 边上的高相等，利用面积公式即可求解.【详解】解：过点P 作PD ⊥BC 于D ，PE ⊥CA 于E ，PF ⊥AB 于F∵P 是三条角平分线的交点∴PD=PE=PF∵AB=30，BC=40，CA=15∴APB S ∆︰BPC S ∆︰CPA S ∆=30∶40∶15=6∶8∶3故答案为6∶8∶3.【点睛】本题主要考查了角平分线的性质和三角形面积的求法. 角平分线上的点到两边的距离相等. 难度不大，作辅助线是关键.3．如图,CA ⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM ⊥BQ,垂足为B,动点P 从C 点出发以1cm/s 的速度沿射线CQ 运动,点N 为射线BM 上一动点,满足PN=AB,随着P 点运动而运动,当点P 运动_______秒时，△BCA 与点P 、N 、B 为顶点的三角形全等.(2个全等三角形不重合)【答案】0；4；8；12【解析】【分析】此题要分两种情况：①当P 在线段BC 上时，②当P 在BQ 上，再分别分两种情况AC ＝BP 或AC ＝BN 进行计算即可．【详解】解：①当P 在线段BC 上，AC ＝BP 时，△ACB ≌△PBN ，∵AC ＝2，∴BP ＝2，∴CP ＝6−2＝4，∴点P 的运动时间为4÷1＝4（秒）；②当P 在线段BC 上，AC ＝BN 时，△ACB ≌△NBP ，这时BC＝PN＝6，CP＝0，因此时间为0秒；③当P在BQ上，AC＝BP时，△ACB≌△PBN，∵AC＝2，∴BP＝2，∴CP＝2＋6＝8，∴点P的运动时间为8÷1＝8（秒）；④当P在BQ上，AC＝NB时，△ACB≌△NBP，∵BC＝6，∴BP＝6，∴CP＝6＋6＝12，点P的运动时间为12÷1＝12（秒），故答案为：0或4或8或12．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等时必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．4．如图，Rt△ABC中，AB＝AC，点D为BC中点．∠MDN＝90°，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论：①△DEF是等腰直角三角形；②AE＝CF；③△BDE≌△ADF；④BE+CF＝EF；⑤S四边形AEDF＝14AD2，其中正确结论是_____（填序号）【答案】①②③【解析】【分析】先由ASA证明△AED≌△CFD，得出AE＝CF，DE＝FD；再由全等三角形的性质得到BE+CF＝AB，由勾股定理求得EF与AB的值，通过比较它们的大小来判定④的正误；先得出S四边形AEDF＝S△ADC＝12AD2，从而判定⑤的正误．【详解】解：∵Rt△ABC中，AB＝AC，点D为BC中点，∴∠C＝∠BAD ＝45°，AD ＝BD ＝CD ，∵∠MDN ＝90°，∴∠ADE +∠ADF ＝∠ADF +∠CDF ＝90°，∴∠ADE ＝∠CDF ．在△AED 与△CFD 中，EAD C AD CDADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AED ≌△CFD （ASA ），∴AE ＝CF ，ED ＝FD ．故①②正确；又∵△ABD ≌△ACD ，∴△BDE ≌△ADF ．故③正确；∵△AED ≌△CFD ，∴AE ＝CF ，ED ＝FD ，∴BE +CF ＝BE +AE ＝AB ＝2BD ，∵EF ＝2ED ，BD ＞ED ，∴BE +CF ＞EF ．故④错误；∵△AED ≌△CFD ，△BDE ≌△ADF ，∴S 四边形AEDF ＝S △ADC ＝12AD 2．故⑤错误．综上所述，正确结论是①②③．故答案是：①②③．【点睛】考查了全等三角形的判定与性质，等腰直角三角形的性质，勾股定理，图形的面积等知识，综合性较强，有一定难度．5．如图，要在河流的南边，公路的左侧M 区处建一个工厂，位置选在到河流和公路的距离相等，并且到河流与公路交叉A 处的距离为1cm(指图上距离)，则图中工厂的位置应在_____.【答案】∠BAC 的平分线上，与A 相距1cm 的地方.【解析】【分析】由已知条件及要求满足的条件，根据角平分线的性质作答，注意距A1cm 处．【详解】工厂的位置应在∠BAC的平分线上，与A相距1cm的地方；理由：角平分线上的点到角两边的距离相等．【点睛】此题考查角平分线的性质：角平分线上的任意一点到角的两边距离相等．作图题一定要找到相关的知识为依托，同时满足多个要求时，要逐个满足．6．如图，OP平分∠AOB，∠AOP＝15°，PC∥OA，PC＝4，点D是射线OA上的一个动点，则PD的最小值为_____．【答案】2【解析】【分析】作PE⊥OA于E，根据角平分线的性质可得PE＝PD，根据平行线的性质可得∠ACP＝∠AOB＝30°，由直角三角形中30°的角所对的直角边等于斜边的一半，可求得PE，即可求得PD．【详解】当PD⊥OA时，PD有最小值，作PE⊥OA于E，∵∠AOP＝∠BOP，PD⊥OB，PE⊥OA，∴PE＝PD（角平分线上的点到角两边的距离相等），∵∠BOP＝∠AOP＝15°，∴∠AOB＝30°，∵PC∥OB，∴∠ACP＝∠AOB＝30°，∴在Rt△PCE中，PE＝12PC＝12×4＝2（在直角三角形中，30°角所对的直角边等于斜边的一半），∴PD＝PE＝2，故答案是：2．【点睛】此题主要考查角平分线的性质和平行线的性质，难度一般，作辅助线是关键．7．如图,在平面直角坐标系xOy中,点A、B分别在x轴的正半轴、y轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、八年级数学全等三角形解答题压轴题（难）1．如图1，等腰△ABC中，AC=BC＝42, ∠ACB=45˚，AO是BC边上的高，D为线段AO上一动点，以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45˚，连结BE.(1) 求证：△ACD≌△BCE；(2) 如图2，在图1的基础上，延长BE至Q, P为BQ上一点，连结CP、CQ,若CP＝CQ＝5,求PQ的长.(3) 连接OE，直接写出线段OE的最小值．【答案】（1）证明见解析；（2）PQ=6；（3）OE=422-【解析】试题分析：()1根据SAS即可证得ACD BCE≌；()2首先过点C作CH BQ⊥于H，由等腰三角形的性质，即可求得45DAC∠=︒，则根据等腰三角形与直角三角形中的勾股定理即可求得PQ 的长．()3OE BQ⊥时，OE取得最小值.试题解析：()1证明：∵△ABC与△DCE是等腰三角形，∴AC=BC,DC=EC,45ACB DCE∠=∠=，45ACD DCB ECB DCB∴∠+∠=∠+∠=，∴∠ACD=∠BCE；在△ACD和△BCE中，,AC BCACD BCEDC EC=⎧⎪∠=∠⎨⎪=⎩(SAS)ACD BCE∴≌；()2首先过点C作CH BQ⊥于H，(2)过点C作CH⊥BQ于H，∵△ABC是等腰三角形，∠ACB=45˚，AO是BC边上的高，45DAC∴∠=，ACD BCE≌，45PBC DAC∴∠=∠=，∴在Rt BHC中,2242422CH BC=⨯=⨯=，54PC CQ CH===，，3PH QH∴==，6.PQ∴=()3OE BQ⊥时，OE取得最小值.最小值为：42 2.OE=-2．（1）已知△ABC是等腰三角形，其底边是BC,点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE,若∠A等于60°（如图①）.求证：EB=AD；（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变（如图②），（1）的结论是否成立，并说明理由．【答案】（1）证明见解析（2）证明见解析【解析】试题分析：（1）作DF∥BC交AC于F，由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF是等边三角形，∠DFC=120°，得出AD=DF，由已知条件得出∠FDC=∠DEC，ED=CD，由AAS证明△DBE≌△CFD，得出EB=DF，即可得出结论；（2）作DF∥BC 交AC 的延长线于F ，同（1）证出△DBE≌△CFD，得出EB=DF ，即可得出结论.试题解析：（1）证明：如图，作DF ∥BC 交AC 于F ，则△ADF 为等边三角形∴AD=DF ，又∵ ∠DEC=∠DCB ，∠DEC+∠EDB=60°，∠DCB+∠DCF=60° ，∴ ∠EDB=∠DCA ，DE=CD ，在△DEB 和△CDF 中，120EBD DFC EDB DCF DE CD ，，∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△DEB≌△CDF ，∴BD=DF ，∴BE=AD .(2). EB=AD 成立；理由如下：作DF ∥BC 交AC 的延长线于F ，如图所示：同（1）得：AD=DF ，∠FDC=∠ECD ，∠FDC=∠DEC ，ED=CD ，又∵∠DBE=∠DFC=60°，∴△DBE ≌△CFD（AAS ），∴EB=DF ，∴EB=AD.点睛：此题主要考查了三角形的综合，考查等边三角形的判定与性质，全等三角形的判定与性质，等腰三角形的判定与性质，等腰直角三角形的判定与性质，平行线的性质等知识，综合性强，有一定的难度，证明三角形全等是解决问题的关键.3．如图，AB=12cm，AC⊥AB，BD⊥AB ，AC=BD=9cm，点P在线段AB上以3 cm/s的速度，由A向B运动，同时点Q在线段BD上由B向D运动．（1）若点Q的运动速度与点P的运动速度相等，当运动时间t=1（s），△ACP与△BPQ 是否全等？说明理由，并直接判断此时线段PC和线段PQ的位置关系；（2）将“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA”，其他条件不变．若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使△ACP与△BPQ全等.（3）在图2的基础上延长AC，BD交于点E，使C，D分别是AE，BE中点，若点Q以（2）中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿△ABE三边运动，求出经过多长时间点P与点Q第一次相遇．【答案】（1）△ACP≌△BPQ，理由见解析；线段PC与线段PQ垂直（2）1或32（3）9s 【解析】【分析】（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．（3）因为V Q＜V P，只能是点P追上点Q，即点P比点Q多走PB+BQ的路程，据此列出方程，解这个方程即可求得．【详解】（1）当t=1时，AP=BQ=3，BP=AC=9，又∵∠A=∠B=90°，在△ACP与△BPQ中，AP BQA BAC BP=⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△BPQ（SAS），∴∠ACP=∠BPQ，∴∠APC+∠BPQ=∠APC+∠ACP=90°，∠CPQ=90°，则线段PC与线段PQ垂直.（2）设点Q的运动速度x,①若△ACP≌△BPQ，则AC=BP，AP=BQ，912t t xt =-⎧⎨=⎩，解得31t x =⎧⎨=⎩， ②若△ACP ≌△BPQ ，则AC=BQ ，AP=BP ，912xt t t=⎧⎨=-⎩ 解得632t x =⎧⎪⎨=⎪⎩，综上所述，存在31t x =⎧⎨=⎩或632t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. （3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，设经过x 秒后P 与Q 第一次相遇，∵AC=BD=9cm ，C ，D 分别是AE ，BD 的中点；∴EB=EA=18cm.当V Q =1时，依题意得3x=x+2×9，解得x=9；当V Q =32时，依题意得3x=32x+2×9，解得x=12.故经过9秒或12秒时P 与Q 第一次相遇.【点睛】本题考查了一元一次方程的应用，解题的关键是熟练的掌握一元一次方程的性质与运算.4．如图，在ABC ∆中，90C ∠=︒，4cm AC BC ==，点D 是斜边AB 的中点．点E 从点B 出发以1cm/s 的速度向点C 运动，点F 同时从点C 出发以一定的速度沿射线CA 方向运动，规定当点E 到终点C 时停止运动．设运动的时间为x 秒，连接DE 、DF ．（1）填空：ABC S ∆=______2cm ；（2）当1x =且点F 运动的速度也是1cm/s 时，求证：DE DF =；（3）若动点F 以3cm /s 的速度沿射线CA 方向运动，在点E 、点F 运动过程中，如果存在某个时间x ，使得ADF ∆的面积是BDE ∆面积的两倍，请你求出时间x 的值．【答案】（1）8;(2)见解析；（3）45或4. 【解析】【分析】（1）直接可求△ABC 的面积；（2）连接CD ，根据等腰直角三角形的性质可求：∠A=∠B=∠ACD=∠DCB=45°，即BD=CD ，且BE=CF ，即可证△CDF ≌△BDE ，可得DE=DF ；（3）分△ADF 的面积是△BDE 的面积的两倍和△BDE 与△ADF 的面积的2倍两种情况讨论，根据题意列出方程可求x 的值．【详解】解：（1）∵S △ABC =12⨯AC×BC ∴S △ABC =12×4×4=8（cm 2）故答案为：8（2）如图：连接CD∵AC=BC ，D 是AB 中点∴CD 平分∠ACB又∵∠ACB=90°∴∠A=∠B=∠ACD=∠DCB=45°∴CD=BD依题意得：BE=CF∴在△CDF与△BDE中BE CFB DCABD CD=⎧⎪∠=∠⎨⎪=⎩∴△CDF≌△BDE（SAS）∴DE=DF（3）如图：过点D作DM⊥BC于点M，DN⊥AC于点N，∵AD=BD，∠A=∠B=45°，∠AND=∠DMB=90°∴△ADN≌△BDM（AAS）∴DN=DM当S△ADF=2S△BDE．∴12×AF×DN=2×12×BE×DM∴|4-3x|=2x∴x1=4，x2=45综上所述：x=45或4【点睛】本题考查了动点问题的函数图象，全等三角形的性质和判定，利用分类思想解决问题是本题的关键．5．如图，在ABC∆中，ACB∠为锐角，点D为射线BC上一动点，连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.（1）若AB AC =，90BAC ∠=︒①当点D 在线段BC 上时（与点B 不重合），试探讨CF 与BD 的数量关系和位置关系； ②当点D 在线段C 的延长线上时，①中的结论是否仍然成立，请在图2中面出相应的图形并说明理由；（2）如图3，若AB AC ≠，90BAC ∠≠︒，45BCA ∠=︒，点D 在线段BC 上运动，试探究CF 与BD 的位置关系.【答案】（1）①CF ⊥BD ，证明见解析；②成立，理由见解析；（2）CF ⊥BD ，证明见解析.【解析】【分析】（1）①根据同角的余角相等求出∠CAF=∠BAD ，然后利用“边角边”证明△ACF 和△ABD 全等，②先求出∠CAF=∠BAD ，然后与①的思路相同求解即可；（2）过点A 作AE ⊥AC 交BC 于E ，可得△ACE 是等腰直角三角形，根据等腰直角三角形的性质可得AC=AE ，∠AED=45°，再根据同角的余角相等求出∠CAF=∠EAD ，然后利用“边角边”证明△ACF 和△AED 全等，根据全等三角形对应角相等可得∠ACF=∠AED ，然后求出∠BCF=90°，从而得到CF ⊥BD ．【详解】解：（1）①∵∠BAC=90°，△ADF 是等腰直角三角形，∴∠CAF+∠CAD=90°，∠BAD+∠ACD=90°，∴∠CAF=∠BAD ，在△ACF 和△ABD 中，∵AB=AC ，∠CAF=∠BAD ，AD=AF ，∴△ACF ≌△ABD(SAS)，∴CF=BD ，∠ACF=∠ABD=45°，∵∠ACB=45°，∴∠FCB=90°，∴CF ⊥BD ；②成立，理由如下：如图2：∵∠CAB=∠DAF=90°，∴∠CAB+∠CAD=∠DAF+∠CAD，即∠CAF=∠BAD，在△ACF和△ABD中，∵AB=AC，∠CAF=∠BAD，AD=AF，∴△ACF≌△ABD(SAS)，∴CF=BD，∠ACF=∠B，∵AB=AC，∠BAC=90°，∴∠B=∠ACB=45°，∴∠BCF=∠ACF+∠ACB=45°+45°=90°，∴CF⊥BD；（2）如图3，过点A作AE⊥AC交BC于E，∵∠BCA=45°，∴△ACE是等腰直角三角形，∴AC=AE，∠AED=45°，∵∠CAF+∠CAD=90°，∠EAD+∠CAD=90°，∴∠CAF=∠EAD，在△ACF和△AED中，∵AC=AE，∠CAF=∠EAD，AD=AF，∴△ACF≌△AED(SAS)，∴∠ACF=∠AED=45°，∴∠BCF=∠ACF+∠BCA=45°+45°=90°，∴CF⊥BD．【点睛】本题考查全等三角形的动点问题，综合性较强，有一定难度，需要熟练掌握全等三角形的判定和性质进行综合运用.6．已知4AB cm=，3AC BD cm==.点P在AB上以1/cm s的速度由点A向点B运动，同时点Q在BD上由点B向点D运动，它们运动的时间为()t s．（1）如图①，AC AB⊥，BD AB⊥，若点Q的运动速度与点P的运动速度相等，当1t=时，ACP△与BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；（2）如图②，将图①中的“AC AB⊥，BD AB⊥”为改“60CAB DBA∠=∠=︒”，其他条件不变．设点Q的运动速度为/xcm s，是否存在实数x，使得ACP△与BPQ 全等？若存在，求出相应的x、t的值；若不存在，请说明理由．【答案】（1）全等，PC与PQ垂直；（2）存在，11tx=⎧⎨=⎩或232tx=⎧⎪⎨=⎪⎩【解析】【分析】（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．【详解】解：（1）当t=1时，AP=BQ=1，BP=AC=3，又∠A=∠B=90°，在△ACP和△BPQ中，AP BQA BAC BP=⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△BPQ（SAS）．∴∠ACP=∠BPQ，∴∠APC+∠BPQ=∠APC+∠ACP=90°．∴∠CPQ=90°，即线段PC与线段PQ垂直．（2）①若△ACP ≌△BPQ ，则AC=BP ，AP=BQ ，34t t xt =-⎧⎨=⎩，解得11t x =⎧⎨=⎩， ②若△ACP ≌△BQP ，则AC=BQ ，AP=BP ，34xt t t=⎧⎨=-⎩，解得232t x =⎧⎪⎨=⎪⎩，综上所述，存在11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等．【点睛】本题考查全等三角形的判定与性质，在解题时注意分类讨论思想的运用．7．（1）如图（a ）所示点D 是等边ABC 边BA 上一动点（点D 与点B 不重合），连接DC ，以DC 为边在BC 上方作等边DCF ，连接AF ．你能发现线段AF 与BD 之间的数量关系吗？并证明．（2）如图（b ）所示当动点D 运动至等边ABC 边BA 的延长线上时，其他作法与（1）相同，猜想AF 与BD 在（1）中的结论是否仍然成立？（直接写出结论）（3）①如图（c ）所示，当动点D 在等边ABC 边BA 上运动时（点D 与点B 不重合），连接DC ，以DC 为边在BC 上方、下方分别作等边DCF 和等边DCF '，连接AF 、BF '，探究AF 、BF '与AB 有何数量关系？并证明．②如图（d ）所示，当动点D 在等边ABC 边BA 的延长线上运动时，其他作法与（3）①相同，①中的结论是否成立？若不成立，是否有新的结论？并证明．【答案】（1）AF=BD ，理由见解析；（2）AF=BD ，成立；（3）①AF BF AB '+=，证明见解析；②①中的结论不成立新的结论是AF AB BF '=+，理由见解析【解析】【分析】（1）根据等边三角形的三条边、三个内角都相等的性质，利用全等三角形的判定定理SAS 可证得BCD ACF △≌△，然后由全等三角形的对应边相等知AF BD = ．（2）通过证明BCD ACF △≌△，即可证明AF BD =．（3）①'AF BF AB += ，利用全等三角形BCD ACF △≌△的对应边BD AF = ，同理'BCF ACD △≌△ ，则'BF AD = ，所以'AF BF AB +=；②①中的结论不成立，新的结论是'AF AB BF =+ ，通过证明BCF ACD △≌△，则'BF AD =（全等三角形的对应边相等），再结合（2）中的结论即可证得'AF AB BF =+ ．【详解】（1）AF BD =证明如下：ABC 是等边三角形，BC AC ∴=，60BCA ︒∠=．同理可得：DC CF =，60DCF ︒∠=．BCA DCA DCF DCA ∴∠-∠=∠-∠．即BCD ACF ∠=∠．BCD ACF ∴△≌△．AF BD ∴=．（2）证明过程同（1），证得BCD ACF △≌△，则AF BD =（全等三角形的对应边相等），所以当动点D 运动至等边△ABC 边BA 的延长线上时，其他作法与（1）相同，AF BD =依然成立．（3）①AF BF AB '+=证明：由（1）知，BCD ACF △≌△．BD AF ∴=．同理BCF ACD '△≌△．BF AD '∴=．AF BF BD AD AB '∴+=+=．②①中的结论不成立新的结论是AF AB BF '=+；BC AC =，BCF ACD '∠=∠，F C DC '=，BCF ACD '∴△≌△．BF AD '∴=．又由（2）知，AF BD =．AF BD AB AD AB BF '∴==+=+．即AF AB BF '=+．【点睛】本题考查了三角形的综合问题，掌握等边三角形的三条边、三个内角都相等的性质、全等三角形的判定定理、全等三角形的对应边相等是解题的关键．8．探究与发现：如图（1）所示的图形，像我们常见的学习用品一圆规，我们，不妨把这样图形叫做“规形图（1）观察“规形图（1）”，试探究∠BDC与∠A、∠B、∠C之间的数量关系，并说明理由；（2）请你直接利用以上结论，解决以下问题：①如图（2），把一块三角尺XYZ放置在△ABC上使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝40°，则∠ABX+∠ACX＝°．②如图（3），DC平分∠ADB，EC平分∠AEB，若∠DAE＝40°，∠DBE＝130°，求∠DCE 的度数．【答案】（1）∠BDC＝∠BAC+∠B+∠C，理由见解析；（2）①50；②∠DCE＝85°．【解析】【分析】（1）首先连接AD并延长至点F，然后根据外角的性质，即可判断出∠BDC＝∠BAC+∠B+∠C；（2）①由（1）可得∠A+∠ABX+∠ACX＝∠X，然后根据∠A＝40°，∠X＝90°，即可求解；（3）②由∠A＝40°，∠DBE＝130°，求出∠ADE+∠AEB的值，然后根据∠DCE＝∠A+∠ADC+∠AEC，求出∠DCE的度数即可.【详解】（1）如图，∠BDC＝∠BAC+∠B+∠C，理由是：过点A、D作射线AF，∵∠FDC ＝∠DAC+∠C ，∠BDF ＝∠B+∠BAD ，∴∠FDC+∠BDF ＝∠DAC+∠BAD+∠C+∠B ，即∠BDC ＝∠BAC+∠B+∠C ；（2）①如图（2），∵∠X ＝90°，由（1）知：∠A+∠ABX+∠ACX ＝∠X ＝90°，∵∠A ＝40°，∴∠ABX+∠ACX ＝50°，故答案为：50；②如图（3），∵∠A ＝40°，∠DBE ＝130°，∴∠ADE+∠AEB ＝130°﹣40°＝90°，∵DC 平分∠ADB ，EC 平分∠AEB ，∴∠ADC ＝12∠ADB ，∠AEC ＝12∠AEB ， ∴∠ADC+∠AEC ＝1(ADB AEB)2∠+∠＝45°， ∴∠DCE ＝∠A+∠ADC+∠AEC ＝40°+45°＝85°．【点睛】本题主要考查了三角形外角性质以及角平分线的定义的运用，熟知三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.9．如图，ABC ∆是等腰直角三角形，090BAC ∠=，点D 是直线BC 上的一个动点（点D 与点B C 、不重合），以AD 为腰作等腰直角ADE ∆，连接CE .（1）如图①，当点D 在线段BC 上时，直接写出,BC CE 的位置关系，线段,BC CD ，CE 之间的数量关系；（2）如图②，当点D 在线段BC 的延长线上时，试判断线段BC ，CE 的位置关系，线段,,BC CD CE 之间的数量关系，并说明理由；（3）如图③，当点D 在线段CB 的延长线上时，试判断线段,BC CE 的位置关系，线段,,BC CD CE 之间的数量关系，并说明理由.【答案】（1）见解析；（2）BC CE ⊥，CE BC CD =+，理由见解析；（3）,BC CE CD BC CE ⊥=+，理由见解析【解析】【分析】（1）根据条件AB=AC ，∠BAC=90°，AD=AE ，∠DAE=90°，判定△ABD ≌△ACE （SAS ），利用两角的和即可得出BC CE ⊥；利用线段的和差即可得出BC CE CD =+；（2）同（1）的方法根据SAS 证明△ABD ≌△ACE ，得出BD=CE ，∠ACE=∠ABD ，从而得出结论；（3）先根据SAS 证明△ABD ≌△ACE ，得出ADB AEC ∠=∠，BD CE =，从而得出结论．【详解】（1）∵△ABC 、△ADE 是等腰直角三角形，∴AB＝AC ，AE ＝AD ，在△△ABD 和△ACE 中90AB AC BAC DAE AD AE ⎧⎪∠∠=︒⎨⎪⎩＝＝＝， ∴△ABD ≌△ACE （SAS ），∴∠B ＝∠ACE ，BD=CE,又∵△ABC 是等腰直角三角形，∴∠B+∠ACB=90︒,∴∠ACE +∠ACB=90︒,即BC CE ⊥，∵BC=BD+CD, BD=CE ，∴BC CE CD =+；（2）BC CE ⊥，CE BC CD =+，理由如下：∵ABC ∆、ADE ∆是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC DAC DAE DAC ∠+∠=∠+∠即BAD CAE ∠=∠,在ABD ∆和ACE ∆中 AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩＝＝ ∴()ABD ACE SAS ∆≅∆∴BD CE =∵BD BC CD =+∴CE BC CD =+，∴ABD ACE ∠=∠，∵090ABD ACE ∠+∠=∴090ACE ACB ∠+∠=∴BC CE ⊥.（3）,BC CE CD BC CE ⊥=+，理由如下：∵ABC ADE ∆∆、是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC BAE DAE BAE ∠-∠=∠-∠，即BAD CAE ∠=∠，在ABD ∆和ACE ∆中 AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩＝＝ ∴()ABD ACE SAS ∆≅∆，∴ADB AEC ∠=∠，BD CE =，∵CD BD BC =+，∴CD CE BC =+，∵090ADE AED ∠+∠=，即090ADB CDE AED ∠+∠+∠=∴090AEC CDE AED ∠+∠+∠=，∴090DCE ∠=，即BC CE ⊥.【点睛】考查了全等三角形的判定与性质以及等腰直角三角形的性质的运用，解题关键是根据利用两边及其夹角分别对应相等的两个三角形全等判定三角形全等．10．（1）如图（1），已知：在△ABC 中，∠BAC=90°，AB=AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．求证：DE=BD+CE ．（2）如图（2），将（1）中的条件改为：在△ABC 中，AB=AC ，D 、A 、E 三点都在直线m 上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）如图（3），D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为∠BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD 、CE ，若∠BDA=∠AEC=∠BAC ，求证:△DEF 是等边三角形．【答案】(1)见解析；（2）成立，理由见解析；(3)见解析【解析】【分析】（1）因为DE=DA+AE ，故通过证BDA AEC ≅△△，得出DA=EC ，AE=BD ，从而证得DE=BD+CE.（2）成立，仍然通过证明BDA AEC ≅△△，得出BD=AE ，AD=CE ，所以DE=DA+AE=EC+BD.（3）由BDA AEC ≅△△得BD=AE ，=BDA AEC ∠∠，ABF 与ACF 均等边三角形，得==60BA AC ︒∠F ∠F ，FB=FA ，所以=BA BA AC AC ∠F ＋∠D ∠F ＋∠E ，即FBD FAB ≅∠∠，所以BDF AEF ≅△△，所以FD=FE ，BFD AFE ≅∠∠，再根据=60BFD FA BFA =︒∠＋∠D ∠，得=60AF FA =︒∠E ＋∠D ，即=60FE =︒∠D ，故DFE △是等边三角形.【详解】证明：(1)∵BD ⊥直线m ，CE ⊥直线m∴∠BDA＝∠CEA=90°，∵∠BAC＝90°∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°∴∠CAE=∠ABD，又AB=AC ，∴△ADB≌△CEA∴AE=BD，AD=CE，∴DE=AE+AD= BD+CE(2)∵∠BDA =∠BAC=α，∴∠DBA+∠BAD=∠BAD +∠CAE=180°—α∴∠DBA=∠CAE ，∵∠BDA=∠AEC=α，AB=AC∴△ADB≌△CEA，∴AE=BD，AD=CE∴DE=AE+AD=BD+CE（3）由（2）知，△ADB≌△CEA， BD=AE，∠DBA =∠CAE∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE∵BF=AF，∴△DBF≌△EAF∴DF=EF，∠BFD=∠AFE∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°∴△DEF为等边三角形.【点睛】利用全等三角形的性质证线段相等是证两条线段相等的重要方法.。

成都石室联合中学数学全等三角形易错题(Word版 含答案)

成都石室中学初中学校八年级数学上册第二单元《全等三角形》测试卷(有答案解析)

四川省成都市石室中学数学三角形解答题(提升篇)(Word版 含解析)

成都石室联合中学数学全等三角形易错题(Word版 含答案)

成都石室联合中学数学轴对称填空选择易错题(Word版 含答案)

成都石室联合中学金沙校区数学三角形填空选择单元测试与练习(word解析版)

成都石室联合中学数学三角形填空选择易错题(Word版 含答案)

成都石室联合中学小升初数学期末试卷易错题（Word版 含答案）

成都石室联合中学七年级下册数学期末试卷易错题(Word版 含答案)

四川省成都市石室中学数学三角形填空选择(提升篇)(Word版 含解析)

成都市石室外语学校八年级数学上册第十二章《全等三角形》(含答案解析)

七年级上册成都石室联合中学数学期末试卷易错题(Word版 含答案)

成都石室中学初中学校数学全等三角形章末训练(Word版 含解析)

成都市青羊实验联合中学数学全等三角形易错题(Word版 含答案)

全等三角形易错题(Word版 含答案)

成都市石室外语学校数学全等三角形单元测试卷(含答案解析)

成都石室中学(北湖校区)八年级数学上册第二单元《全等三角形》测试题(有答案解析)

成都石室联合中学小升初数学期末试卷易错题(Word版 含答案)

成都市青羊实验联合中学数学轴对称填空选择易错题(Word版 含答案)

成都石室联合中学数学全等三角形易错题(Word版含答案)

四川省成都市石室中学数学三角形解答题(提升篇)(Word版含解析)

成都石室联合中学数学全等三角形易错题(Word版含答案)

成都石室联合中学数学轴对称填空选择易错题(Word版含答案)

成都石室联合中学数学三角形填空选择易错题(Word版含答案)

成都石室联合中学小升初数学期末试卷易错题（Word版含答案）

成都石室联合中学七年级下册数学期末试卷易错题(Word版含答案)

四川省成都市石室中学数学三角形填空选择(提升篇)(Word版含解析)

七年级上册成都石室联合中学数学期末试卷易错题(Word版含答案)

成都石室中学初中学校数学全等三角形章末训练(Word版含解析)

成都市青羊实验联合中学数学全等三角形易错题(Word版含答案)

全等三角形易错题(Word版含答案)

成都石室联合中学小升初数学期末试卷易错题(Word版含答案)

成都市青羊实验联合中学数学轴对称填空选择易错题(Word版含答案)