第一章 质点运动学作业答案
质点运动学一章习题解答

2υ cos θ g
代入(3)式得
sin θ =
a 2υ cos θ a cos θ ⋅ = 2υ g g
由此式可得
tgθ = a g
a θ = arctg( ) g
习题 1—9 一无风的下雨天,一列火车以 v1=20.0m/s 的速度匀速前
进,在车内的旅客看见玻璃窗外的雨滴和垂线成 75°角下降,求雨 滴下落的速度 v2。(设下降的雨滴作匀速运动) 解:根据相对运动,雨滴下落的速度满足伽利略速度变换式
v=
dx = 9t − 6t 2 dt
令 t=2s,则可得质点在第二秒末的瞬时速度为
v(2) = 9 × 2 − 6 × 2 2 = −6 m/s
(3) 因为质点的速度方向在第二秒内有所改变,所以求路程 时需分两段进行考虑。由
v = 9t − 6t 2 = 0
可解得 t = 1.5s 即 在 t=1.5s 时 ,质点运动开始转向。此时质点坐标达到极大,
x = (-10m/s)t + (30m/s–2)t2 和 y = (15m/s)t-(20m/s–2)t2。
试求:(1) 初速度的大小和方向;(2) 加速度的大小和方向。 解:(1) 由运动方程可得
dx = −10 + 60t dt dy vy = = 15 − 40t dt vx =
当 t = 0s 时
vM
hv dx = = 1 dt h1 − h2
x
X
习题 1—4 一物体作如图所示的斜抛运动, 测得在轨道 A 点处速度 v 的大小为 v, 其方向与水平方向夹角为 30°, 则物体在 A 点的切向加 速度 at= ,轨道的曲率半径 ρ = 。
�
分析:斜抛运动是加速度恒定的平面曲线运动,在轨道的任一位
01第一章质点运动学作业答案.doc

[C ] 1、[基础训练1]如图所示,湖中有一小船, 轮拉湖中的船向岸边运动.设该人以匀速率%收绳, 是(A)匀加速运动.(C)变加速运动.有人用绳绕过岸上一定高度处的定滑 绳不伸长、湖水静止,则小船的运动(B)匀减速运动.(D)变减速运动.(E) 匀速直线运动.设船离岸边x 米,dx I dl dt x dtVx 2 + /i 2dldlx dt dt第二色质点运动学一 .选择题:[B ] 2、[基础训练2〕一质点沿x 轴作直线运动,其*1曲线如图所示,如仁0时,质 点位于坐标原点,则/=4.5 s 时,质点在x 轴上的位置为(A) 5m. (B) 2m. (C)0. (D) -2 m. (E) -5 m. 4.5s【提示】x= J vdt,质点在工轴上的位置即为这段时间 0 内V-t 曲线下的面积的代数和:x = (1 + 2.5)x24-2-(24-1)x14-2 = 2(772)[B ] 3、(自测提高3)质点沿半径为R 的圆周作匀速率运动,每7秒转一圈.在27 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2nR/T, I TI R/T.(C) 0,0. (B) 0,2nR/T (D) 2nRIT , 0. 【提示】平均速度大小:i7 |Ar| 八 —_ A S 2丸 R ,=——=0 平均速率:v ==(注意定义式及符号的规范)[C ]4、[自测提高6]某物体的运动规律为du/dl = -ku 气,式中的人为大于零的常量.当 f = 0时,初速为功),则速度P 与时间,的函数关系是 1 , 2 (A) V — —kt + V (}, 21 7 2(B) v = ---- kt + V (},2【提示】如图建坐标系,可见,加速度与速度同向,且加速度随时间变化。
【提示】dv/dt = -kv2t,分离变量并积分,J47小1 kt2 1 =一ktdt,得一= ----- 1 --- 0 v 2 %1 kt2 1(C)丁项+私[B ]5、[自测提高7]在相对地面静止的坐标系内,A、B二船都以2 m/s速率匀速行驶, A船沿尤轴正向,8船沿y轴正向.今在A船上设置与静止坐标系方向相同的坐标系(X、方向单位矢用亍、/表示),那么在A船上的坐标系中,8船的速度(以m/s为单位)为(A)2f +2 J . (B)-2f +2 J . (C) ~2i ~2j .(D)2z*-2j •【提示】礼对A =%对地“地私=京对地一总对地=2J-2F=-2F+2;(m/s).(速度变换式是矢量式,应加上矢量符号)二.填空题1、[基础训练8]质点沿半径为R的圆周运动,运动学方程为。
大学物理 质点运动学 习题及答案

第1章 质点运动学 习题及答案1.|r ∆|与r ∆ 有无不同?t d d r 和dr dt 有无不同? t d d v 和dv dt有无不同?其不同在哪里?试举例说明. 解: |r ∆|与r ∆ 不同. |r ∆|表示质点运动位移的大小,而r ∆则表示质点运动时其径向长度的增量;t d d r 和dr dt 不同. t d d r 表示质点运动速度的大小,而dr dt则表示质点运动速度的径向分量;t d d v 和dv dt 不同. t d d v 表示质点运动加速度的大小, 而dv dt则表示质点运动加速度的切向分量. 2.质点沿直线运动,其位置矢量是否一定方向不变?质点位置矢量方向不变,质点是否一定做直线运动?解: 质点沿直线运动,其位置矢量方向可以改变;质点位置矢量方向不变,质点一定做直线运动.3.匀速圆周运动的速度和加速度是否都恒定不变?圆周运动的加速度是否总是指向圆心,为什么? 解: 由于匀速圆周运动的速度和加速度的方向总是随时间发生变化的,因此,其速度和加速度不是恒定不变的;只有匀速圆周运动的加速度总是指向圆心,故一般来讲,圆周运动的加速度不一定指向圆心.4.一物体做直线运动,运动方程为2362x t t =-,式中各量均采用国际单位制,求:(1)第二秒内的平均速度(2)第三秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
解: 由于: 232621261212x(t )t t dx v(t )t t dtdv a(t )t dt=-==-==- 所以:(1)第二秒内的平均速度: 1(2)(1)4()21x x v ms --==- (2)第三秒末的速度: 21(3)1236318()v ms -=⨯-⨯=-(3)第一秒末的加速度:2(1)121210()a ms -=-⨯=(4)物体运动的类型为变速直线运动。
5.一质点运动方程的表达式为2105(t t t =+r i j ),式中的,t r 分别以m,s 为单位,试求;(1)质点的速度和加速度;(2)质点的轨迹方程。
(完整版)大学物理01质点运动学习题解答

第一章质点运动学一选择题1.以下说法中,正确的选项是:()A.一物体若拥有恒定的速率,则没有变化的速度;B.一物体拥有恒定的速度,但仍有变化的速率;C.一物体拥有恒定的加快度,则其速度不行能为零;D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解:答案是 D。
2.长度不变的杆 AB,其端点 A 以 v0匀速沿 y 轴向下滑动, B 点沿 x 轴挪动,则 B 点的速率为:()A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解:答案是 C。
简要提示:设 B 点的坐标为 x, A 点的坐标为 y,杆的长度为l,则x2y2l 2对上式两边关于时间求导:dx dy0,因dxv,dyv0,所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示,路灯距地面高为 H,行人身高为 h,若人以匀速 v 背向路灯行走,灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为()H h Hv h HA.vB.H H h H h 解:答案是 B 。
简要提示:设人头影子到灯杆的距离为 x ,则x s h , x Hs , x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x = 3t-5t 3 + 6 (SI),则该质点作A. 匀加快直线运动,加快度沿 x 轴正方向.B. 匀加快直线运动,加快度沿 x 轴负方向.C. 变加快直线运动,加快度沿 x 轴正方向.D. 变加快直线运动,加快度沿x 轴负方向.()解: 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是: ()v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解:答案是 C 。
大学物理上册第一章 质点运动学 习题及答案

第一章 质点运动学一、简答题1、运动质点的路程和位移有何区别?答:路程是标量,位移是矢量;路程表示质点实际运动轨迹的长度,而位移表示始点指向终点的有向线段。
2、质点运动方程为()()()()k t z j t y i t x t r ++=,其位置矢量的大小、速度及加速度如何表示? 答:()()()t z t y t x r 222r ++==()()()k t z j t y i t xv ++= ()()()k t z j t y i t x a ++=3、质点做曲线运动在t t t ∆+→时间内速度从1v 变为到2v ,则平均加速度和t时刻的瞬时加速度各为多少? 答:平均加速度 t v v a ∆-=12 ,瞬时加速度()()dt v d t v v a t t lim t 120 =∆-=→∆4、画出示意图说明什么是伽利略速度变换公式? 其适用条件是什么?答:牵连相对绝对U V +=V ,适用条件宏观低速5、什么质点? 一个物体具备哪些条件时才可以被看作质点?答:质点是一个理想化的模型,它是实际物体在一定条件下的科学抽象。
条件:只要物体的形状和大小在所研究的问题中属于无关因素或次要因素,物体就能被看作质点。
二、选择题1、关于运动和静止的说法中正确的是 ( C )A 、我们看到的物体的位置没有变化,物体一定处于静止状态B 、两物体间的距离没有变化,两物体就一定都静止C 、自然界中找不到不运动的物体,运动是绝对的,静止是相对的D 、为了研究物体的运动,必须先选参考系,平时说的运动和静止是相对地球而言的2、下列说法中正确的是 ( D )A 、物体运动的速度越大,加速度也一定越大B 、物体的加速度越大,它的速度一定越大C 、加速度就是“加出来的速度”D 、加速度反映速度变化的快慢,与速度大小无关3、质点沿x 轴作直线运动,其t v-曲线如图所示,如s t 0=时,质点位于坐标原点,则s .t 54=时,质点在x 轴的位置为 ( B )A 、5 mB 、2 mC 、0 mD 、-2 m4、质点作匀速率圆周运动,则 ( B )A 、线速度不变B 、角速度不变C 、法向加速度不变D 、加速度不变5、质点作直线运动,某时刻的瞬时速度为s /m v 2=,瞬时加速度为22s /m a -=,则一秒钟后质点的速度 ( D )A 、等于0B 、等于s /m 2-C 、等于s /m 2D 、不能确定6、质点作曲线运动,r 表示位置矢量的大小,s 表示路程,z a 表示切向加速度的大小,v 表示速度的大小。
大学物理第一章 质点运动学-习题及答案

第一章 质点运动学1-1 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at += (其中b a ,为常量) 则该质点作(A )匀速直线运动 (B )变速直线运动(C )抛物线运动 (D )一般曲线运动 [B]解:由j i rv bt at t 22d d +==知 v 随t 变化,质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动,r 表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v (A )只有(1)、(4)是对的。
(B )只有(2)、(4)是对的。
(C )只有(2)是对的。
(D )只有(3)是对的。
[D]解:由定义:t vt a d d d d ≠=v ; t r t s t v d d d d d d ≠==r ; t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内,A 、B 二船都以21s m -⋅的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x ,y 方向单位矢用j i ,表示),那么在A 船上的坐标系中,B 船的速度(以1s m -⋅为单位)为(A )j i 22+ (B )j i 22+-(C )j i 22-- (D )j i 22- [B]解:由i v 2=对地A ,j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= (1s m -⋅)1-4 一质点沿x 方向运动,其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅,则当t 为3s 时,质点的速度1s m 23-⋅=v解:⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=,则在t 由0至4s 的时间间隔内,质点的位移大小为 8m ,在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
第一章质点运动学习题答案

第一章质点运动学习题答案1-1 质点做直线运动,运动方程为其中以s为单位,以m为单位,求:(1)=4s时,质点的位置、速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4) 做出-t图、-t图、-t图.解:(1) 根据直线运动情况下的定义,可得质点的位置、速度和加速度分别为(1)(2)(3)当=4s时,代入数字得:mm/sm/s(2)当质点通过原点时,=0,代入运动方程得:=0解得:,代入(2)式得:m/s=-12m/s(3) 将代入(2)式,得解得:s代入(1)式得:12m-6m=6m1.2一质点在平面上运动,运动方程为=3+5,=2+3-4.式中以 s计,,以m计.(1)以时间为变量,写出质点位置矢量的表示式;(2)求出=1 s 时刻和=2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算=0s时刻到=4s时刻内的平均速度;(4)求出质点速度矢量表示式,计算=4s 时质点的速度;(5)计算=0s 到=4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算=4s 时质点的加速度.解:(1)(2)将,代入上式即有(3)∵∴(4)则(5)∵(6)这说明该点只有方向的加速度,且为恒量.1-4 一质点沿一直线运动,其加速度为,式中的单位为m,的单位为m/s,试求该质点的速度与位置坐标之间的关系.设时,=4m/s解:依题意积分得1-5质点沿直线运动,加速度,如果当=3时,,,求质点的运动方程. (其中以m/s为单位,以s为单位,以m为单位,以m/s为单位)解:加速度表示式对积分,得将=3s,=9m,m/s代入以上二式,得积分常数m/s,=0.75m,则1-6 当物体以非常高的速度穿过空气时,由空气阻力产生的反向加速度大小与物体速度的平方成反比,即,其中为常量. 若物体不受其他力作用沿方向运动,通过原点时的速度为,试证明在此后的任意位置处其速度为.解:根据加速度定义得:,因,代入上式,分离变量,整理后得:,应用初始条件,两边积分得得即有:1-7试写出以矢量形式表示的质点做匀速圆周运动的运动学方程,并证明做匀速圆周运动质点的速度矢量和加速度矢量的标积等于零,即解:以直角坐标表示的质点运动学方程为以矢量形式表示的指点运动学方程为速度和加速度分别为所以1-8一质点在平面内运动,其运动方程为,其中均为大于零的常量.(1)试求质点在任意时刻的速度;(2)证明质点运动的轨道为椭圆;(3)证明质点的加速度恒指向椭圆的中心.解:(1)质点在任意时刻的速度(2)由消去,可得轨道方程可见是椭圆方程,表明质点作椭圆运动(3)加速度因为>0,所以的方向恒与反向,即恒指向椭圆中心.1-9路灯离地面高度为,一个身高为的人,在灯下水平路面上以匀速度步行. 如图所示,求当人与灯的水平距离为时,他的头顶在地面上的影子移动的速度的大小.解:建立如图所示的坐标,时刻头顶影子的坐标为,设头顶影子的移动速度为,则由图中可看出有,则有所以有1-10 1.10质点沿半径为的圆周按=的规律运动,式中为质点离圆周上某点的弧长,,都是常量,求:(1)时刻质点的加速度;(2)为何值时,加速度在数值上等于.解:(1)则加速度与半径的夹角为(2)由题意应有即∴当时,1-11质点做半径为20cm的圆周运动,其切向加速度恒为5cm/s,若该质点由静止开始运动,需要多少时间:(1)它的法向加速度等于切向加速度;(2)法向加速度等于切向加速度的二倍.解:质点圆周运动半径=20cm,切向加速度=5cm/s,时刻速度为,法向加速度为,因此有(1)当时,s(2)当时,s1-12 (1)地球的半径为6.37m,求地球赤道表面上一点相对于地球中心的向心加速度. (2)地球绕太阳运行的轨道半径为1.5m,求地球相对于太阳的向心加速度. (3)天文测量表明,太阳系以近似圆形的轨道绕银河系中心运动,半径为2.8m,速率为2.5m/s,求太阳系相对于银河系的向心加速度.解:(1)地球赤道表面一点相对于地球中心的向心角速度为m/s(2)地球相对太阳的向心加速度为m/s(3)太阳系相对银河系的向心加速度m/s1-13 以初速度=20抛出一小球,抛出方向与水平面成60°的夹角,求:(1)球轨道最高点的曲率半径;(2)落地处的曲率半径.解:设小球所作抛物线轨道如题1-13图所示.题1-13图(1)在最高点,又∵∴(2)在落地点,,而∴1-14一架飞机在水平地面的上方,以174m/s的速率垂直俯冲,假定飞机以圆形路径脱离俯冲,而飞机可以承受的最大加速度为78.4m/s,为了避免飞机撞到地面,求飞机开始脱离俯冲的最低高度. 假定整个运动中速率恒定.解:设飞机以半径为圆形路径俯冲,其加速度为当为飞机所能承受的最大加速度时,即为最小,所以m1-15一飞轮以速度rev/min转动,受制动而均匀减速,经s 静止,求(1) 角加速度和从制动开始到静止飞轮转过的转数;(2) 求制动开始后,s时飞轮的角速度;(3) 设飞轮半径=1m,求s时,飞轮边缘上一点的速度和加速度.解:(1)飞轮的初角速度,当s时,;代入得从开始到静止,飞轮转过的角度及其转数为:radrev(2)s 时,飞轮的角速度为rad/s(3)s 时,飞轮边缘上一点的速度为m/s相应的切线和法线加速度为m/sm/s1-16一质点沿半径为1m的圆周运动,运动方程为,式中以弧度计,以秒计,求:(1)=2s时,质点的切向和法向加速度;(2)当加速度的方向和半径成角时,其角位移是多少?解:(1)时,(2)当加速度方向与半径成角时,有即亦即则解得于是角位移为1-17一圆盘半径为3m,它的角速度在=0时为3.33rad/s,以后均匀地减小,到=4s时角速度变为零. 试计算圆盘边缘上一点在=2s时的切向加速度和法向加速度的大小.解:角速度均匀减小,因此,角加速度为rad/s圆盘做匀角加速度,故有当s时,rad/s法向和切向加速度分别为m/s=-7.8 m/s1-18某雷达站对一个飞行中的炮弹进行观测,发现炮弹达最高点时,正好位于雷达站的上方,且速率为,高度为,求在炮弹此后的飞行过程中,在(以s为单位)时刻雷达的观测方向与铅垂直方向之间的夹角及其变化率(雷达的转动角速度)解:以雷达位置为坐标原点,取坐标系如图所示,根据题意,炮弹的运动方程为可解得:(1)则将(1)式两边对求导数,得则有1-19 汽车在大雨中行驶,车速为80km/h,车中乘客看见侧面的玻璃上雨滴和铅垂线成角,当车停下来时,他发现雨滴是垂直下落的,求雨滴下落的速度.解:取车为运动参考系,雨滴相对于车的速度为,雨滴对地速度为,车对地的速度为,相对运动速度合成定理为见如图所示的速度合成图,则有m/s1-20一升降机以加速度1.22m/s上升,当上升速度为2.44 m/s时,有一螺帽自升降机的天花板松落,天花板与升降机底面相距 2.74m,计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.解:以升降机外固定柱子为参考系,竖直向上为坐标轴正向,螺帽松落时升降机底面位置为原点. 螺帽从=2.74m处松落,以初速度=2.44m/s做竖直上抛运动,升降机底面则从原点以同样的初速度做向上的加速运动,加速度=1.22m/s,它们的运动方程分别为螺帽:底面:螺帽落到底面上时,,由以上两式得=0.705s(2)螺帽相对于升降机外固定柱子的下降距离为m1-21某人骑自行车以速率向西行使,北风以速率吹来(对地面),问骑车者遇到风速及风向如何?解:地为静系E,人为动系M。
(完整版)大学物理01质点运动学习题解答

第一章 质点运动学一 选择题1. 下列说法中,正确的是:( )A. 一物体若具有恒定的速率,则没有变化的速度;B. 一物体具有恒定的速度,但仍有变化的速率;C. 一物体具有恒定的加速度,则其速度不可能为零;D. 一物体具有沿x 轴正方向的加速度而有沿x 轴负方向的速度。
解:答案是D 。
2. 长度不变的杆AB ,其端点A 以v 0匀速沿y 轴向下滑动,B 点沿x 轴移动,则B 点的速率为:( )A . v 0 sin θB . v 0 cos θC . v 0 tan θD . v 0 / cos θ 解:答案是C 。
简要提示:设B 点的坐标为x ,A 点的坐标为y ,杆的长度为l ,则222l y x =+ 对上式两边关于时间求导:0d d 2d d 2=+t y y t x x ,因v =tx d d ,0d d v -=t y ,所以 2x v -2y v 0 = 0 即 v =v 0 y /x =v 0tan θ所以答案是C 。
3. 如图示,路灯距地面高为H ,行人身高为h ,若人以匀速v 背向路灯行走,则人头影子移动的速度u 为( ) A.v H h H - B. v h H H - C. v H h D. v hH 解:答案是B 。
v x选择题2图灯s选择题3图简要提示:设人头影子到灯杆的距离为x ,则H h x s x =-,s hH H x -=, v hH H t s h H H t x u -=-==d d d d 所以答案是B 。
4. 某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作A. 匀加速直线运动,加速度沿x 轴正方向.B. 匀加速直线运动,加速度沿x 轴负方向.C. 变加速直线运动,加速度沿x 轴正方向.D. 变加速直线运动,加速度沿x 轴负方向. ( )解:答案是D5. 一物体从某一确定高度以v 0的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是:( ) A. g 0v v -t B. g 20v v -t C. g 202v v -t D. g2202v v -t 解:答案是C 。
(完整版)01质点运动学习题解答汇总,推荐文档

第一章 质点运动学一 选择题1. 下列说法中,正确的是 ()A. 一物体若具有恒定的速率,则没有变化的速度B. 一物体具有恒定的速度,但仍有变化的速率C. 一物体具有恒定的加速度,则其速度不可能为零D. 一物体具有沿x 轴正方向的加速度,其速度有可能沿x 轴的负方向解:答案是D 。
2. 某质点作直线运动的运动方程为x =3t -5t 3 + 6 (SI),则该质点作 ( )A. 匀加速直线运动,加速度沿x 轴正方向B. 匀加速直线运动,加速度沿x 轴负方向C. 变加速直线运动,加速度沿x 轴正方向D. 变加速直线运动,加速度沿x 轴负方向解:答案是D3. 如图示,路灯距地面高为H ,行人身高为h ,若人以匀速v 背向路灯行走,则人头影子移动的速度u 为( )A.B.C.D. v HhH -v hH H-v Hhv hH 解:答案是B 。
设人头影子到灯杆的距离为x ,则,,H h x s x =-s h H Hx -=v hH Ht s h H H t x u -=-==d d d d 所以答案是B 。
4. 一质点的运动方程为,其中t 1时刻的位矢为。
j i r )()(t y t x +=j i r )()(111t y t x +=问质点在t 1时刻的速率是()A.B.C.D. d d 1t r d d 1tr 1d dt t t=r 122)d d ()d d (t t ty t x =+解 根据速率的概念,它等于速度矢量的模。
本题答案为D 。
5. 一物体从某一确定高度以v 0的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是 ( )s选择题3图A.B.C.D.g 0v v -t g20v v -t g202v v -t g2202v v -t 解:答案是C 。
,,所以答案是C 。
gt t ty =-=202v v v g t t /202v v -=6. 质点作圆周运动时,下列说表述中正确的是 ()A. 速度方向一定指向切向,加速度方向一定指向圆心B. 速度方向一定指向切向,加速度方向也一般指向切向C. 由于法向分速度为零,所以法向加速度也一定为零D. 切向加速度仅由速率的变化引起解 答案是D 。
第1章 质点运动学——习题解答

第1章 质点运动学1-1 一运动质点某一瞬时位于径矢()r x y ,的端点处,关于其速度的大小有4种不同的看法,即 (1)d d tr; (2)d d t r; (3)d d sr;(4下列判断正确的是( ). (A) 只有(1)和(2)正确 (B) 只有(2)正确 (C) 只有(3)和(4)正确 (D) (1)(2)(3)(4)都正确 答案:(C )解析:瞬时速度的大小等于瞬时速率,故(3)正确;速度可由各分量合成,故(4)正确。
1-2 一质点的运动方程为22cos cos sin sin x At Bt y At Bt θθθθ⎧⎪⎨⎪⎩=+,=+,式中A ,B ,θ均为常量,且A >0,B >0,则该质点的运动为( ). (A) 一般曲线运动(B) 匀速直线运动 (C) 匀减速直线运动(D) 匀加速直线运动答案:(D )解析:由tan yxθ=可知,质点做直线运动.a x =2B cos θa y =2B sin θa =2B加速度a 为定值,故质点做匀加速直线运动.1-3 一质点沿半径为R 的圆周运动,其角速度随时间的变化规律为ω=2bt ,式中b 为正常量.如果t =0时,θ0=0,那么当质点的加速度与半径成45°角时,θ角的大小为( ) rad.(A) 12(B) 1 (C) b (D) 2b答案:(A )解析: a t =R β=2bRa n =R 2ω=4Rb 2t 2a t =a n t 2=b21θ=20tω⎰d t =bt 2=211-4 一人沿停靠的台阶式电梯走上楼需时90 s ,当他站在开动的电梯上上楼,需时60 s .如果此人沿开动的电梯走上楼,所需时间为( ).(A) 24 s (B) 30 s (C) 36 s (D) 40 s答案:(C )解析:设电梯长度为s ,则=+9060s s st , 解得t =36 s.1-5 已知质点的加速度与位移的关系式为32a x =+,当t =0时,v 0=0,x 0=0,则速度v 与位移x 的关系式为________. 答案:v 2=3x 2+4x 解析: d d d d d d d d v v x v a v t x t x ===, d d v v a x =,d =(3+2)d vxv v x x ⎰⎰,v 2=3x 2+4x .1-6 在地面上以相同的初速v 0,不同的抛射角θ斜向上抛出一物体,不计空气阻力.当θ=________时,水平射程最远,最远水平射程为________. 答案:45°20v g解析:对于斜抛运动:0cos x v t θ⋅=201sin 2y v t gt θ⋅=-当y =0时,解得02sin v t gθ=物体的水平射程20sin 2v x gθ=当θ=45°时有最远水平射程,其大小为20max v x g=1-7 某人骑摩托车以115m s -⋅的速度向东行驶,感觉到风以115m s -⋅的速度从正南吹来,则风速的大小为________ m·s -1,方向沿________.答案:m/s 东偏北45° 解析:如答案1-7图所示,由图可知=+v v v 风地风人人地故风速大小m/s v 风地=方向为东偏北45°.v 地风v 人地15v 人风15答案1-7图1-8 一质点作直线运动,加速度2sin a A t ωω=,已知t =0时,x 0=0,v 0=-ωA ,则该质点的运动方程为_______________. 答案:sin x A t ω=-,解析: d d v a t =20d sin d vtAv A t t ωωω-=⎰⎰解得,该质点的速度为cos v A t ωω=-d d x v t =d cos d xtx A t t ωω=-⎰⎰解得,该质点的运动方程为sin x A t ω=-1-9 一质点在xOy 平面上运动,运动方程为x =3t +5,y =12t 2+3t -4式中,t 以s 计,x ,y 以m 计.(1) 以时间t 为变量,写出质点位置矢量的表示式; (2) 计算第1 s 内质点的位移;(3) 计算t =0 s 时刻到t =4 s 时刻内的平均速度;(4) 求出质点速度矢量表示式,计算t =4 s 时质点的速度; (5) 计算t =0 s 到t =4 s 内质点的平均加速度;(6) 求出质点加速度矢量的表示式,计算t =4 s 时质点的加速度. (位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式) 解:(1) 质点t 时刻位矢为21(35)342r t i t t j ⎛⎫=+++- ⎪⎝⎭(m)(2) 第1 s 内位移为11010()()r x x i y y j ∆=-+-2213(10)(10)3(10)23 3.5()i ji j m ⎡⎤=-+-+-⎢⎥⎣⎦=+(3) 前4 s 内平均速度为11(1220)35(m s )4r v i j i j t -∆==⨯+=+⋅∆ (4) 质点速度矢量表示式为1d 3(3)(m s )d rv i t j t-==++⋅ t =4 s 时质点的速度为143(43)37(m s )v i j i j -=++=+⋅(5) 前4 s 内平均加速度为240731(m s )4s 4v v v a j j t -∆--====⋅∆(6) 质点加速度矢量的表示式为2d 1(m s )d va j t-==⋅t =4 s 时质点的加速度为241(m s )a j -=⋅1-10 质点沿直线运动,速度v =(t 3+3t 2+2) m·s -1,如果当t = 2 s 时,x =4 m ,求:t =3 s 时,质点的位置、速度和加速度. 解: 32d 32d x v t t t==++ 431d d 24x x v t t t t c ===+++⎰⎰当t =2时,x =4,代入可得c =-12.则质点的位置、速度和加速度的表达式分别为4312124x t t t =++-32232d 36d v t t v a t tt=++==+ 将t =3 s 分别代入得上述各式,解得1233341.25m 56m s 45m s x v a --==⋅=⋅,,1-11 质点的运动方程为2[4(32)] m r t i t j =++,t 以s 计.求: (1) 质点的轨迹方程;(2) t =1 s 时质点的坐标和位矢方向; (3) 第1 s 内质点的位移和平均速度; (4) t =1 s 时质点的速度和加速度.解:(1) 由运动方程2432x t y t⎧=⎨=+⎩消去t 得轨迹方程2(3)0x y --=(2) t =1 s 时,114m 5m x y ==,,故质点的坐标为(4,5). 由11tan 1.25y x α==得51.3α=︒,即位矢与x 轴夹角为53.0°. (3) 第1 s 内质点的位移和平均速度分别为1(40)(53)42(m)r i j i j ∆=-+-=+1142(m s )r v i j t-∆==+⋅∆ (4) 质点的速度与加速度分别为d 82d r v ti j t ==+d 8d va i t==故t =1 s 时的速度和加速度分别为1182m s v i j -=+⋅() 218m s a i -=⋅()1-12 以速度v 0平抛一球,不计空气阻力,求:t 时刻小球的切向加速度a t 和法向加速度a n 的量值. 解:小球下落过程中速度为v故切向加速度为2t d d v a t =由222n t a g a =-得,法向加速度为n a =1-13 一种喷气推进的实验车,从静止开始可在1.80 s 内加速到1 600 km·h -1的速率.按匀加速运动计算,它的加速度是否超过了人可以忍受的加速度25g ?这1.80 s 内该车跑了多少距离?解:实验车的加速度为3222160010m /s 2.4710m/s 3600 1.80v a t ⨯===⨯⨯故它的加速度略超过25g . 1.80 s 内实验车跑的距离为3160010 1.80m 400m 223600v s t ⨯==⨯=⨯ 1-14 在以初速率-1015.0 m s v ⋅=竖直向上扔一块石头后,(1) 在1.0 s 末又竖直向上扔出第二块石头,后者在h =11.0 m 高度处击中前者,求第二块石头扔出时的速率;(2) 若在1.3 s 末竖直向上扔出第二块石头,它仍在h =11.0 m 高度处击中前者,求这一次第二块石头扔出时的速率.解:(1) 设第一块石头扔出后经过时间t 被第二块击中,则2012h v t gt =-代入已知数据得2111159.82t t =-⨯解此方程,可得二解为111.84s 1.22s t t ==,′第一块石头上升到顶点所用的时间为10m 15.0s 1.53s 9.8v t g ===1m t t >,这对应于第一块石头回落时与第二块相碰;1m t t <′,这对应于第一块石头上升时被第二块赶上击中.设20v 和20v ′分别为在t 1和1t ′时刻两石块相碰时第二石块的初速度,则由于22011111()()2h v t t g t t =--- 所以2211201111()119.8(1.841)22m/s 17.2m/s 1.841h g t t v t t +-∆+⨯⨯-===-∆- 同理,2211201111()119.8(1.221)22m/s 51.1m/s 1.221h g t t v t t +-∆+⨯⨯-===-∆-′′′ (2) 由于211.3s t t ∆=>′,所以第二块石头不可能在第一块上升时与第一块相碰。
大学物理第一章质点运动学习题解详细完整

第一章 质点运动学1–1 描写质点运动状态的物理量是 ;解:加速度是描写质点状态变化的物理量,速度是描写质点运动状态的物理量,故填“速度”;1–2 任意时刻a t =0的运动是 运动;任意时刻a n =0的运动是 运动;任意时刻a =0的运动是 运动;任意时刻a t =0,a n =常量的运动是 运动;解:匀速率;直线;匀速直线;匀速圆周;1–3 一人骑摩托车跳越一条大沟,他能以与水平成30°角,其值为30m/s 的初速从一边起跳,刚好到达另一边,则可知此沟的宽度为 )m/s 102=g ;解:此沟的宽度为m 345m 1060sin 302sin 220=︒⨯==g R θv1–4 一质点在xoy 平面内运动,运动方程为t x 2=,229t y -=,位移的单位为m,试写出s t 1=时质点的位置矢量__________;s t 2=时该质点的瞬时速度为__________,此时的瞬时加速度为__________;解:将s t 1=代入t x 2=,229t y -=得2=x m,7=y ms t 1=故时质点的位置矢量为j i r 72+=m由质点的运动方程为t x 2=,229t y -=得质点在任意时刻的速度为m/s 2d d ==t x x v ,m/s 4d d t tx y -==v s t 2=时该质点的瞬时速度为j i 82-=v m/s质点在任意时刻的加速度为0d d ==ta x x v ,2m/s 4d d -==t a y y v s t 2=时该质点的瞬时加速度为j 4-m/s 2;1–5 一质点沿x 轴正向运动,其加速度与位置的关系为x a 23+=,若在x =0处,其速度m/s 50=v ,则质点运动到x =3m 处时所具有的速度为__________;解:由x a 23+=得x xt x x t 23d d d d d d d d +===v v v v 故x x d )23(d +=v v积分得⎰⎰+=305d )23(d x x v v v则质点运动到x =3m 处时所具有的速度大小为 61=v m/s=s ;1–6 一质点作半径R =的圆周运动,其运动方程为t t 323+=θ,θ以rad 计,t 以s 计;则当t =2s 时,质点的角位置为________;角速度为_________;角加速度为_________;切向加速度为__________;法向加速度为__________;解: t =2s 时,质点的角位置为=⨯+⨯=23223θ22rad由t t 323+=θ得任意时刻的角速度大小为36d d 2+==t tθω t =2s 时角速度为 =+⨯=3262ω27rad/s任意时刻的角速度大小为t t12d d ==ωα t =2s 时角加速度为 212⨯=α=24rad/s 2t =2s 时切向加速度为=⨯⨯==2120.1t αR a 24m/s 2t =2s 时法向加速度为=⨯==22n 270.1ωR a 729m/s 2;1–7 下列各种情况中,说法错误的是 ;A .一物体具有恒定的速率,但仍有变化的速度B .一物体具有恒定的速度,但仍有变化的速率C .一物体具有加速度,而其速度可以为零D .一物体速率减小,但其加速度可以增大解:一质点有恒定的速率,但速度的方向可以发生变化,故速度可以变化;一质点具有加速度,说明其速度的变化不为零,但此时的速度可以为零;当加速度的值为负时,质点的速率减小,加速度的值可以增大,所以A 、C 和D 都是正确的,只有B 是错误的,故选B;1–8 一个质点作圆周运动时,下列说法中正确的是 ;A .切向加速度一定改变,法向加速度也改变B .切向加速度可能不变,法向加速度一定改变C .切向加速度可能不变,法向加速度不变D .切向加速度一定改变,法向加速度不变解:无论质点是作匀速圆周运动或是作变速圆周运动,法向加速度a n 都是变化的,因此至少其方向在不断变化;而切向加速度a t 是否变化,要视具体情况而定;质点作匀速圆周运动时,其切向加速度为零,保持不变;当质点作匀变速圆周运动时,a t 值为不为零的恒量,但方向变化;当质点作一般的变速圆周运动时,a t 值为不为零变量,方向同样发生变化;由此可见,应选B;1–9 一运动质点某瞬时位于位置矢量),(y x r 的端点处,对其速度大小有四种意见: 1t r d d 2t d d r 3t s d d 422d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 下述判断正确的是 ;A .只有1,2正确B .只有2,3正确C .只有3,4正确D .只有1,3正确 解:tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中为质点的径向速度,是速度矢量沿径向的分量;t d d r 表示速度矢量;t s d d 是在自然坐标系中计算速度大小的公式;22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 是在真角坐标系中计算速度大小的公式;故应选C;1–10 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at +=其中a 、b 为常量,则该质点作 ;A .匀速直线运动B .变速直线运动C .抛物线运动D .一般曲线运动解:由j i r 22bt at +=可计算出质点的速度为j i bt at 22+=v ,加速度为j i b a 22+=a ;因质点的速度变化,加速度的大小和方向都不变,故质点应作变速直线运动;故选B;1–11 一小球沿斜面向上运动,其运动方程为S =5+4t –t 2SI,则小球运动到最高点的时刻是 ;A .t =4sB .t =2sC .t =8sD .t =5s解:小球到最高点时,速度应为零;由其运动方程为S =5+4t –t 2,利用ts d d =v 得任意时刻的速度为 t 24-=v令024=-=t v ,得s 2=t故选B;1–12 如图1-1所示,小球位于距墙MO 和地面NO 等远的一点A ,在球的右边,紧靠小球有一点光源S 当小球以速度V 0水平抛出,恰好落在墙角O 处;当小球在空中运动时,在墙上就有球的影子由上向下运动,其影子中心的运动是 ;A .匀速直线运动B .匀加速直线运动,加速度小于gC .自由落体运动D .变加速运动解:设A 到墙之间距离为d ;小球经t 时间自A 运动至B;此时影子在竖直方向的位移为S ;t V x 0=, 221gt y = 根据三角形相似得d S x y //=,所以得影子位移为2/V gt x yd S == 由此可见影子在竖直方向作速度为02V g 的匀速直线运动;故选A;1–13 在相对地面静止的坐标系内,A 、B 二船都以2m/s 的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向;今在A 船上设置与静止坐标系方向相同的坐标系x 、y 方向单位矢量用i 、j 表示,那么在A 船上的坐标系中,B 船的速度以m/s 为单位为 ;A .j i 22+B .j i 22+-C .j i 22--D .j i 22+解:选B 船为运动物体,则B 船相对于地的速度为绝对速度j 2=v ,A 船相对于地的速度为牵连速度i 2=0v ,则在A 船的坐标系中,B 船相对于A 船的速度为相对速度v ';因v v v 0'+=,故j i 22+-='v ,因此应选B1–14 2004年1月25日,继“勇气”号之后,“机遇”号火星探测器再次成功登陆火星;在人类成功登陆火星之前,人类为了探测距离地球大约5103⨯km 的月球,也发射了一种类似四轮小车的月球探测器;它能够在自动导航系统的控制下行走,且每隔10s 向地球发射一次信号;探测器上还装着两个相同的减速器其中一个是备用的,这种减速器可提供的最大加速度为5m/s 2;某次探测器的自动导航系统出现故障,从而使探测器只能匀速前进而不再能自动避开障碍物;此时地球上的科学家必须对探测器进行人工遥控操作;下表为控制中心的显示屏的数据:图1-1y BM9:10:40 12 已知控制中心的信号发射与接收设备工作速度极快;科学家每次分析数据并输入命令最少需要3s;问: 1经过数据分析,你认为减速器是否执行了减速命令2假如你是控制中心的工作人员,应采取怎样的措施加速度需满足什么条件,才可使探测器不与障碍物相撞请计算说明;解:1设在地球和月球之间传播电磁波需时为0t ,则有s 10==c s t 月地从前两次收到的信号可知:探测器的速度为m/s 21032521=-=v 由题意可知,从发射信号到探测器收到信号并执行命令的时刻为9:10:34;控制中心第3次收到的信号是探测器在9:10:39发出的;从后两次收到的信号可知探测器的速度为m/s 2101232=-=v 可见,探测器速度未变,并未执行命令而减速;减速器出现故障;(2)应启用另一个备用减速器;再经过3s 分析数据和1s 接收时间,探测器在9:10:44执行命令,此时距前方障碍物距离s =2m;设定减速器加速度为a ,则有222≤=as v m,可得1≥a m/s 2,即只要设定加速度1≥a m/s 2,便可使探测器不与障碍物相撞;1–15 阿波罗16号是阿波罗计划中的第十次载人航天任务1972年4月16日,也是人类历史上第五次成功登月的任务;1972年4月27日成功返回;照片图1-2显示阿波罗宇航员在月球上跳跃并向人们致意;视频显示表明,宇航员在月球上空停留的时间是;已知月球的重力加速度是地球重力加速度的1/6;试计算宇航员在月球上跳起的高度;解:宇航员在月球上跳起可看成竖直上抛运动,由已知宇航员在空中停留的时间为,故宇航员从跳起最高处下落到月球表面的时间为t =,由于月球的重力加速度是地球的重力加速度的1/6,即g g 61M =,所以 m 43.0725.08.961212122M =⨯⨯⨯==t g h1–16 气球上吊一重物,以速度0v 从地面匀速竖直上升,经过时间t 重物落回地面;不计空气对物体的阻力,重物离开气球时离地面的高度为多少;解:方法一:设重物离开气球时的高度为x h ,当重物离开气球后作初速度为0v 的竖直上抛运动,选重物离开气球时的位置为坐标原点,则重物落到地面时满足图1-220021)(x x x gt h t h --=-v v 其中x h -表示向下的位移,0v x h 为匀速运动的时间,x t 为竖直上抛过程的时间,解方程得 gt t x 02v = 于是,离开气球时的离地高度可由匀速上升过程中求得,其值为)2()(000gt t t t h x x v v v -=-= 方法二:将重物的运动看成全程做匀速直线运动与离开气球后做自由落体运动的合运动;显然总位移等于零,所以0)(21200=--v v x h t g t 解得 )2(00g t t h x v v -=1–17 在篮球运动员作立定投篮时,如以出手时球的中心为坐标原点,作坐标系Oxy 如图1–3所示;设篮圈中心坐标为x ,y ,出手高度为H ,于的出手速度为0v ,试证明球的出手角度θ应满足⎥⎥⎦⎤⎢⎢⎣⎡+-±=)2(211tan 2022020v v v gx y g gx θ才能投入;证明:设出手后需用时t 入蓝,则有 θt t x x cos 0v v ==20221sin 21gt t gt t y y -=-=θv v 消去时间t ,得 θgx gx αx θgx θx y 22022022202tan 22tan cos 21tan v v v --=-= 图1-3整理得02tan tan 22022202=++-v v gx y θx θgx解之得⎥⎥⎦⎤⎢⎢⎣⎡+-±=)2(211tan 2022020v v v gx y g gx θ1–18 有一质点沿x 轴作直线运动,t 时刻的坐标为32254t t .x -=SI;试求:1第2s 内的平均速度;2第2s 末的瞬时速度;3第2s 内的路程;解:1将t =1s 代入32254t t .x -=得第1s 末的位置为m 5.225.41=-=x将t =2s 代入32254t t .x -=得第2s 末的位置为m 0.22225.4322=⨯-⨯=x则第2s 内质点的位移为0.5m 2.5m -m 0.212-==-=∆x x x第2s 内的平均速度-0.5m/s 10.5=-=∆∆=t x v 式中负号表示平均速的方向沿x 轴负方向;2质点在任意时刻的速度为269d d t t tx -==v 将s 2=t 代入上式得第2s 末的瞬时速度为 m/s 626292-=⨯-⨯=v式中负号表示瞬时速度的方向沿x 轴负方向;3由069d d 2=-==t t tx v 得质点停止运动的时刻为s 5.1=t ;由此计算得第1s 末到末的时间内质点走过的路程为m 875.05.25.125.15.4321=-⨯-⨯=s 第末到第2s 末的时间内质点走过的路程为m 375.10.25.125.15.4322=-⨯-⨯=s则第2s 内的质点走过的路程为m 25.2375.1875.021=+=+=s s s1–19 由于空气的阻力,一个跳伞员在空中运动不是匀加速运动;一跳伞员在离开飞机到打开降落伞的这段时间内,其运动方程为)e (/k t k t c b y -+-=SI,式中b 、c 和k 是常量,y 是他离地面的高度;问:1要使运动方程有意义,b 、c 和k 的单位是什么2计算跳伞员在任意时刻的速度和加速度;解:1由量纲分析,b 的单位为m,c 的单位为m/s,k 的单位为s;2任意时刻的速度为)e 1(d d /k t c ty -+-==v 当时间足够长时其速度趋于c -;任意时刻的加速度为k t kc t a /ed d -==v 当时间足够长时其加速度趋于零;1–20 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2d d v v K t-=,式中K 为常量;试证明电艇在关闭发动机后又行驶x 距离时的速度为Kx -=e 0v v 其中0v 是发动机关闭时的速度; 证明:由2d d v v K t-=得 2d d d d d d v v v v K xt x x -== 即x K d d -=vv 上式积分为⎰⎰-=x x K 0d d 0v v v v 得 Kx -=e 0v v1–21 一质点沿圆周运动,其切向加速度与法向加速度的大小恒保持相等;设θ为质点在圆周上任意两点速度1v 与2v 之间的夹角;试证:θe 12v v =;证明:因R a 2n v =,ta d d t v =,所以 t R d d 2v v =dsv v d d = 即vv d d =R s 对上式积分⎰⎰=2d d 0v v v v s R s得 12ln v v =R s 12ln v v ==R s θ 所以 θe 12v v =1–22 长为l 的细棒,在竖直平面内沿墙角下滑,上端A 下滑速度为匀速v ,如图1-4所示;当下端B 离墙角距离为xx<l 时,B 端水平速度和加速度多大解:建立如图所示的坐标系;设A 端离地高度为y ;∆AOB 为直角三角形,有222l y x =+ 方程两边对t 求导得 0d d 2d d 2=+t y y t x x所以B 端水平速度为 t y x y t x d d d d -=v xy =v x x l 22-= B 端水平方向加速度为v 222d /d d /d d d x tx y t y x t x-=232v x l -=1–23 质点作半径为m 3=R 的圆周运动,切向加速度为2t ms 3-=a ,在0=t 时质点的速度为零;试求:1s 1=t 时的速度与加速度;2第2s 内质点所通过的路程;图1-4解:1按定义ta d d t v =,得 t a d d t =v ,两端积分,并利用初始条件,可得 ⎰⎰⎰==t t t a t a 0t 0t 0d d d v v t t a 3t ==v当s 1=t 时,质点的速度为 m/s 3=v方向沿圆周的切线方向;任意时刻质点的法线加速度的大小为2222n m/s 39t Rt R a ===v 任意时刻质点加速度的大小为242n 2t m/s 99t a a a +=+=任意时刻加速度的方向,可由其与速度方向的夹角θ给出;且有22t n 33tan t t a a ===θ 当s 1=t 时有24m/s 23199=⨯+=a ,1tan =θ注意到0t >a ;所以得︒=45θ2按定义ts d d =v ,得t s d d v =,两端积分可得 ⎰⎰⎰==t t t s d 3d d v故得经t 时间后质点沿圆周走过的路程为C t s +=223 其中C 为积分常数;则第2s 内质点走过的路程为:m 5.4)123()223()1()2(22=+⨯-+⨯=-=∆C C s s s1–24 一飞机相对于空气以恒定速率v 沿正方形轨道飞行,在无风天气其运动周期为T ;若有恒定小风沿平行于正方形的一对边吹来,风速为)1(<<=k k V v ;求飞机仍沿原正方形对地轨道飞行时周期要增加多少解:依题意,设飞机沿如图1-5所示的ABCD 矩形路径运动,设矩形每边长为l ,如无风时,依题意有 vl T 4= 1 图1-5当有风时,设风的速度如图1-5所示,则飞机沿AB 运动时的速度为v v v k V +=+,飞机从A 飞到B 所花时间为vv k l t +=1 2 飞机沿CD 运动时的速度为v v v k V -=-,飞机从C 飞到D 所花时间为vv k l t -=2 3 飞机沿BC 运动和沿DA 运动所花的时间是相同的,为了使飞机沿矩形线运动,飞机相对于地的飞行速度方向应与运动路径成一夹角,使得飞机速度时的速度v 在水平方向的分量等于v k -,故飞机沿BC 运动和沿DA 运动的速度大小为222v v k -,飞机在BC 和DA 上所花的总时间为22232v v k lt -= 4综上,飞机在有风沿此矩形路径运动所花的总时间,即周期为2223212vv v v v v k l k l k l t t t T -+-++=++=' 5 利用1式,5式变为)1(4)4()1(4)11(22222k k T k k T T --≈--+='飞机在有风时的周期与无风时的周期相比,周期增加值为43)1(4)4(222T k T k k T T T T =---≈'-=∆。
质点运动学习题答案

第一章 质点运动学P23.1.1 一质点沿直线运动,运动方程为x (t ) = 6t 2 - 2t 3.试求: (1)第2s 内的位移和平均速度;(2)1s 末及2s 末的瞬时速度,第2s 内的路程; (3)1s 末的瞬时加速度和第2s 内的平均加速度. [解答](1)质点在第1s 末的位移大小为x (1) = 6×12 - 2×13 = 4(m).在第2s 末的位移大小为x (2) = 6×22 - 2×23 = 8(m).在第2s 内的位移大小为Δx = x (2) – x (1) = 4(m),经过的时间为Δt = 1s ,所以平均速度大小为v =Δx /Δt = 4(m·s -1). (2)质点的瞬时速度大小为v (t ) = d x /d t = 12t - 6t 2,因此v (1) = 12×1 - 6×12 = 6(m·s -1),v (2) = 12×2 - 6×22 = 0,质点在第2s 内的路程等于其位移的大小,即Δs = Δx = 4m .(3)质点的瞬时加速度大小为a (t ) = d v /d t = 12 - 12t ,因此1s 末的瞬时加速度为a (1) = 12 - 12×1 = 0, 第2s 内的平均加速度为a = [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2).[注意]第几秒内的平均速度和平均加速度的时间间隔都是1秒.1.2 一质点作匀加速直线运动,在t = 10s 内走过路程s = 30m ,而其速度增为n = 5倍.试证加速度为22(1)(1)n sa n t -=+.由上述数据求出量值.[证明]依题意得v t = nv o , 根据速度公式v t = v o + at ,得a = (n – 1)v o /t , (1)根据速度与位移的关系式v t 2 = v o 2 + 2as ,得a = (n 2 – 1)v o 2/2s ,(2)(1)平方之后除以(2)式证得22(1)(1)n sa n t-=+. 计算得加速度为22(51)30(51)10a -=+= 0.4(m·s -2).1.3 一人乘摩托车跳越一个大矿坑,他以与水平成22.5°的夹角的初速度65m·s -1从西边起跳,准确地落在坑的东边.已知东边比西边低70m ,忽略空气阻力,且取g = 10m·s -2.问:(1)矿坑有多宽?他飞越的时间多长?(2)他在东边落地时的速度?速度与水平面的夹角?[解答]方法一:分步法.(1)夹角用θ表示,人和车(他)在竖直方向首先做竖直上抛运动,初速度的大小为v y 0 = v 0sin θ = 24.87(m·s -1).取向上的方向为正,根据匀变速直线运动的速度公式v t - v 0 = at ,这里的v 0就是v y 0,a = -g ;当他达到最高点时,v t = 0,所以上升到最高点的时间为t 1 = v y 0/g = 2.49(s).再根据匀变速直线运动的速度和位移的关系式v t 2 - v 02 = 2a s ,可得上升的最大高度为h 1 = v y 02/2g = 30.94(m).他从最高点开始再做自由落体运动,下落的高度为h 2 = h 1 + h = 100.94(m).根据自由落体运动公式s = gt 2/2,得下落的时间为2t =. 因此他飞越的时间为t = t 1 + t 2 = 6.98(s). 他飞越的水平速度为v x 0 = v 0cos θ = 60.05(m·s -1),所以矿坑的宽度为x = v x 0t = 419.19(m).(2)根据自由落体速度公式可得他落地的竖直速度大小为v y = gt = 69.8(m·s -1),落地速度为v = (v x 2 + v y 2)1/2 = 92.08(m·s -1),与水平方向的夹角为φ = arctan(v y /v x ) = 49.30º, 方向斜向下.方法二:一步法.取向上的方向为正,他在竖直方向的位移为y = v y 0t - gt 2/2,移项得时间的一元二次方程图1.3201sin 02gt v t y θ-+=, 解得0(sin t v g θ=.这里y = -70m ,根号项就是他落地时在竖直方向的速度大小,由于时间应该取正值,所以公式取正根,计算时间为t = 6.98(s).由此可以求解其他问题.1.4 一个正在沿直线行驶的汽船,关闭发动机后,由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度,即d v /d t = -kv 2,k 为常数.(1)试证在关闭发动机后,船在t 时刻的速度大小为11kt v v =+; (2)试证在时间t 内,船行驶的距离为01ln(1)x v kt k=+. [证明](1)分离变量得2d d vk t v=-, 积分 020d d vtv vk t v =-⎰⎰,可得11kt v v =+. (2)公式可化为001v v v kt=+,由于v = d x/d t ,所以00001d d d(1)1(1)v x t v kt v kt k v kt ==+++积分0001d d(1)(1)xtx v kt k v kt =++⎰⎰.因此 01ln(1)x v kt k=+. 证毕. [讨论]当力是速度的函数时,即f = f (v ),根据牛顿第二定律得f = ma . 由于a = d 2x /d t 2, 而 d x /d t = v , 所以 a = d v /d t , 分离变量得方程d d ()m vt f v =,解方程即可求解.在本题中,k 已经包括了质点的质量.如果阻力与速度反向、大小与船速的n 次方成正比,则d v /d t = -kv n .(1)如果n = 1,则得d d vk t v=-, 积分得ln v = -kt + C .当t = 0时,v = v 0,所以C = ln v 0,因此ln v/v 0 = -kt ,得速度为v = v 0e -kt .而d v = v 0e -kt d t ,积分得0e `ktv x C k-=+-. 当t = 0时,x = 0,所以C` = v 0/k ,因此(1-e )kt v x k-=. (2)如果n ≠1,则得d d nvk t v =-,积分得 11nv kt C n-=-+-. 当t = 0时,v = v 0,所以101n v C n-=-,因此 11011(1)n n n kt v v --=+-.如果n = 2,就是本题的结果. 如果n ≠2,可得1(2)/(1)020{[1(1)]1}(2)n n n n n v kt x n v k----+--=-, 读者不妨自证.1.5 一质点沿半径为0.10m 的圆周运动,其角位置(以弧度表示)可用公式表示:θ = 2 + 4t 3.求:(1)t = 2s 时,它的法向加速度和切向加速度;(2)当切向加速度恰为总加速度大小的一半时,θ为何值? (3)在哪一时刻,切向加速度和法向加速度恰有相等的值? [解答](1)角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1),法向加速度为a n = rω2 = 230.4(m·s -2);角加速度为β = d ω/d t = 24t = 48(rad·s -2), 切向加速度为a t = rβ = 4.8(m·s -2).(2)总加速度为a = (a t 2 + a n 2)1/2, 当a t = a /2时,有4a t 2 = a t 2 + a n 2,即n a a =由此得2r r ω= 即22(12)24t = 解得36t =. 所以3242(1t θ=+==3.154(rad).(3)当a t = a n 时,可得rβ = rω2, 即 24t = (12t 2)2,解得 t = (1/6)1/3 = 0.55(s).1.6 一飞机在铅直面内飞行,某时刻飞机的速度为v = 300m·s -1,方向与水平线夹角为30°而斜向下,此后飞机的加速度为as -2,方向与水平前进方向夹角为30°而斜向上,问多长时间后,飞机又回到原来的高度?在此期间飞机在水平方向飞行的距离为多少? [解答]建立水平和垂直坐标系,飞机的初速度的大小为v 0x = v 0cos θ,v 0y = v 0sin θ.加速度的大小为a x = a cos α,a y = a sin α. 运动方程为 2012x x x v t a t =+,2012y y y v t a t =-+.即 201c o s c o s 2x v t a t θα=⋅+⋅, 201sin sin 2y v t a t θα=-⋅+⋅.令y = 0,解得飞机回到原来高度时的时间为t = 0(舍去);02sin sin v t a θα==.将t 代入x 的方程求得x = 9000m .[注意]选择不同的坐标系,例如x 方向沿着a 的方向或者沿着v 0的方向,也能求出相同的结果.1.7 一个半径为R = 1.0m 的轻圆盘,可以绕一水平轴自由转动.一根轻绳绕在盘子的边缘,其自由端拴一物体A .在重力作用下,物体A 从静止开始匀加速地下降,在Δt = 2.0s 内下降的距离h = 0.4m .求物体开始下降后3s 末,圆盘边缘上任一点的切向加速度与法向加速度.[解答]圆盘边缘的切向加速度大小等于物体A 下落加速度.由于212t h a t =∆,所以0.2(m·s -2). a t = 2h /Δt 2 = 物体下降3s 末的速度为 0.6(m·s -1),v = a t t =这也是边缘的线速度,因此法向加速度为2n v a R== 0.36(m·s -2).1.8 一升降机以加速度1.22m·s -2上升,当上升速度为2.44m·s -1时,有一螺帽自升降机的天花板上松落,天花板与升降机的底面相距2.74m .计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.[解答]在螺帽从天花板落到底面时,升降机上升的高度为21012h v t at =+;螺帽做竖直上抛运动,位移为22012h v t gt =-.由题意得h = h 1 - h 2,所以21()2h a g t =+, 解得时间为t .算得h 2 = -0.716m ,即螺帽相对于升降机外固定柱子的下降距离为0.716m .[注意]以升降机为参考系,钉子下落时相对加速度为a + g ,而初速度为零,可列方程h = (a + g )t 2/2,由此可计算钉子落下的时间,进而计算下降距离.1.9 有一架飞机从A 处向东飞到B 处,然后又向西飞回到A 处.已知气流相对于地面的速度为u ,AB 之间的距离为l ,飞机相对于空气的速率v 保持不变.图1.7(1)如果u = 0(空气静止),试证来回飞行的时间为02l t v =; (2)如果气流的速度向东,证明来回飞行的总时间为01221/t t u v=-; (3)如果气流的速度向北,证明来回飞行的总时间为2t =[证明](1)飞机飞行来回的速率为v ,路程为2l ,所以飞行时间为t 0 = 2l /v .(2)飞机向东飞行顺风的速率为v + u ,向西飞行逆风的速率为v - u ,所以飞行时间为1222l l vl t v u v u v u =+=+-- 022222/1/1/t l v u v u v==--. (3)飞机相对地的速度等于相对风的速度加风相对地的速度.为了使飞机沿着AB 之间的直线飞行,就要使其相对地的速度偏向北方,可作矢量三角形,其中沿AB 方向的速度大小为V =,所以飞行时间为22l t V ===证毕.1.10 如图所示,一汽车在雨中沿直线行驶,其速度为v 1,下落雨的速度方向与铅直方向的夹角为θ,偏向于汽车前进方向,速度为v 2.今在车后放一长方形物体,问车速v 1为多大时此物体刚好不会被雨水淋湿?[解答]雨对地的速度2v 等于雨对车的速度3v 加车对地的速度1v ,由此可作矢量三角形.根据题意得tan α = l/h .方法一:利用直角三角形.根据直角三角形得v 1 = v 2sin θ + v 3sin α,其中v 3 = v ⊥/cos α,而v ⊥ = v 2cos θ, 因此v 1 = v 2sin θ + v 2cos θsin α/cos α, 即 12(sin cos )lv v hθθ=+. 证毕.方法二:利用正弦定理.根据正弦定理可得12sin()sin(90)v v θαα=+︒-,所以12sin()cos v v θαα+=AB AB vv + u v - uABvu uvv图1.101h l α2sin cos cos sin cos v θαθαα+=2(sin cos tan )v θθα=+,即 12(sin cos )lv v hθθ=+. 方法三:利用位移关系.将雨滴的速度分解为竖直和水平两个分量,在t 时间内,雨滴的位移为l = (v 1 – v 2sin θ)t , h = v 2cos θ∙t .两式消去时间t 即得所求. 证毕.。
大学物理上学习指导作业参考答案(1)

大学物理上学习指导作业参考答案(1)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 质点运动学课 后 作 业1、一质点沿x 轴运动,其加速度a 与位置坐标x 的关系为 a =2+6 x 2 (SI)如果质点在原点处的速度为零,试求其在任意位置处的速度.解:设质点在x 处的速度为v ,62d d d d d d 2x txx t a +=⋅==v v 2分 ()x x xd 62d 020⎰⎰+=v v v2分()2 213x x +=v 1分2、一质点沿x 轴运动,其加速度为a 4t (SI),已知t 0时,质点位于x10 m 处,初速度v 0.试求其位置和时间的关系式.解: =a d v /d t 4=t , d v 4=t d t ⎰⎰=vv 0d 4d tt tv 2=t 2 3分v d =x /d t 2=t 2 t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI) 2分3、一质点沿半径为R 的圆周运动.质点所经过的弧长与时间的关系为221ct bt S += 其中b 、c 是大于零的常量,求从0=t 开始到切向加速度与法向加速度大小相等时所经历的时间.解: ct b t S +==d /d v 1分c t a t ==d /d v 1分 ()R ct b a n /2+= 1分根据题意: a t = a n 1分即 ()R ct b c /2+=解得 cbc R t -=1分4、如图所示,质点P 在水平面内沿一半径为R =2 m 的圆轨道转动.转动的角速度与时间t 的函数关系为2kt =ω (k 为常量).已知s t 2=时,质点P 的速度值为32 m/s .试求1=t s 时,质点P 的速度与加速度的大小.O RP解:根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω 1分24t =ω, 24Rt R ==ωvs t 1=时, v = 4Rt 2 = 8 m/s 1分 2s /168/m Rt dt d a t ===v 1分22s /32/m R a n ==v 1分()8.352/122=+=nt a a a m/s 2 1分5、一敞顶电梯以恒定速率v =10 m/s 上升.当电梯离地面h =10 m 时,一小孩竖直向上抛出一球.球相对于电梯初速率200=v m/s .试问: (1) 从地面算起,球能达到的最大高度为多大? (2) 抛出后经过多长时间再回到电梯上?解:(1) 球相对地面的初速度=+='v v v 030 m/s 1分抛出后上升高度 9.4522='=gh v m/s 1分 离地面高度 H = (45.9+10) m =55.9 m 1分(2) 球回到电梯上时电梯上升高度=球上升高度2021)(gt t t -+=v v v 1分08.420==gt vs 1分6、在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如图所示.当人以0υ(m ·1-s )的速率收绳时,试求船运动的速度和加速度的大小.解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知222s h l +=将上式对时间t 求导,得tss t l l d d 2d d 2=题1-4图根据速度的定义,并注意到l ,s 是随t 减少的,∴ tsv v t l v d d ,d d 0-==-=船绳即 θcos d d d d 00v v s l t l s l t s v ==-=-=船 或 sv s h s lv v 02/1220)(+==船 将船v 再对t 求导,即得船的加速度3202220202002)(d d d d d d sv h s v s l s v slv s v v s t sl t l st v a =+-=+-=-==船船第二章 运动与力课 后 作 业1、 一人在平地上拉一个质量为M 的木箱匀速前进,如图. 木箱与地面间的摩擦系数μ=0.6.设此人前进时,肩上绳的支撑点距地面高度为h =1.5 m ,不计箱高,问绳长l 为多长时最省力解:设绳子与水平方向的夹角为θ,则l h /sin =θ. 木箱受力如图所示,匀速前进时, 拉力为F , 有F cos θ-f =0 2分F sin θ+N -Mg =0 f =μN得 θμθμsin cos +=MgF 2分令 0)sin (cos )cos sin (d d 2=++--=θμθθμθμθMg F ∴ 6.0tg ==μθ,637530'''︒=θ 2分且 0d d 22>θF∴ l =h / sin θ=2.92 m 时,最省力.N2、一质量为60 kg 的人,站在质量为30 kg 的底板上,用绳和滑轮连接如图.设滑轮、绳的质量及轴处的摩擦可以忽略不计,绳子不可伸长.欲使人和底板能以1 m/s 2的加速度上升,人对绳子的拉力T 2多大?人对底板的压力多大 (取g =10 m/s 2)解:人受力如图(1) 图2分a m g m N T 112=-+ 1分 底板受力如图(2) 图2分 a m g m N T T 2221=-'-+ 2分212T T = 1分 N N ='由以上四式可解得 a m m g m g m T )(421212+=--∴ 5.2474/))((212=++=a g m m T N 1分5.412)(21=-+=='T a g m N N N 1分3、一条轻绳跨过一轻滑轮(滑轮与轴间摩擦可忽略),在绳的一端挂一质量为m 1的物体,在另一侧有一质量为m 2的环,求当环相对于绳以恒定的加速度a 2沿绳向下滑动时,物体和环相对地面的加速度各是多少环与绳间的摩擦力多大m 1m 22a解:因绳子质量不计,所以环受到的摩擦力在数值上等于绳子张力T .设m 2相对地面的加速度为2a ',取向上为正;m 1相对地面的加速度为a 1(即绳子的加速度),取向下为正. 1分111a m T g m =- 2分 222a m g m T '=- 2分 212a a a -=' 2分 解得 2122211)(m m a m g m m a ++-= 1分21212)2(m m m m a g T +-= 1分2121212)(m m a m g m m a +--=' 1分4、一条质量分布均匀的绳子,质量为M 、长度为L ,一端拴在竖直转轴OO ′上,并以恒定角速度ω在水平面上旋转.设转动过程中绳子始终伸直不打弯,且忽略重力,求距转轴为r 处绳中的张力T ( r ).解:取距转轴为r 处,长为d r 的小段绳子,其质量为 ( M /L ) d r . (取元,画元的受力图) 2分由于绳子作圆周运动,所以小段绳子有径向加速度,由牛顿定律得: T ( r )-T ( r + d r ) = ( M / L ) d r r ω2令 T ( r )-T (r + d r ) = - d T ( r )得 d T =-( M ω2/ L ) r d r 4分 由于绳子的末端是自由端 T (L ) = 01分有r r L M T Lrr T d )/(d 2)(⎰⎰-=ω ∴ )2/()()(222L r L M r T -=ω 3分LOO ′rO O ′ d r T (r ) T (r +d )第三章 动量与角动量课 后 作 业hAv1、如图,用传送带A 输送煤粉,料斗口在A 上方高h =0.5 m 处,煤粉自料斗口自由落在A 上.设料斗口连续卸煤的流量为q m =40 kg/s ,A 以v =2.0 m/s 的水平速度匀速向右移动.求装煤的过程中,煤粉对A 的作用力的大小和方向.(不计相对传送带静止的煤粉质重)解:煤粉自料斗口下落,接触传送带前具有竖直向下的速度gh 20=v 1分设煤粉与A 相互作用的∆t 时间内,落于传送带上的煤粉质量为t q m m ∆=∆ 1分设A 对煤粉的平均作用力为f,由动量定理写分量式:0-∆=∆v m t f x 1分)(00v m t f y ∆--=∆ 1分 将 t q m m ∆=∆代入得 v m x q f =, 0v m y q f =∴ 14922=+=y x f f f N 2分f与x 轴正向夹角为α = arctg (f x / f y ) = 57.4° 1分由牛顿第三定律煤粉对A 的作用力f ′= f = 149 N ,方向与图中f相反.2分30°F2、质量为1 kg 的物体,它与水平桌面间的摩擦系数μ = 0.2 .现对物体施以F = 10t (SI)的力,(t 表示时刻),力的方向保持一定,如图所示.如t = 0时物体静止,则t = 3 s 时它的速度大小v 为多少?解:由题给条件可知物体与桌面间的正压力mg F N +︒=30sin 1分物体要有加速度必须 N F μ≥︒30cos 2分即 mg t μμ≥-)3(5, 0s 256.0t t =≥ 1分物体开始运动后,所受冲量为 ⎰-︒=tt t N F I 0d )30cos (μ)(96.1)(83.3022t t t t ---= t = 3 s, I = 28.8 N s 2分则此时物体的动量的大小为 I m =v速度的大小为 8.28==mIv m/s 2分3、一炮弹发射后在其运行轨道上的最高点h =19.6 m 处炸裂成质量相等的两块.其中一块在爆炸后1秒钟落到爆炸点正下方的地面上.设此处与发射点的距离S 1=1000 m ,问另一块落地点与发射地点间的距离是多少( 空气阻力不计,g =9.8 m/s 2)解:因第一块爆炸后落在其正下方的地面上,说明它的速度方向是沿竖直方向的.利用 2t g t h '+'=211v , 式中t '为第一块在爆炸后落到地面的时间. 可解得v 1=14.7 m/s ,竖直向下.取y 轴正向向上, 有v 1y =-14.7 m/s 2分设炮弹到最高点时(v y =0),经历的时间为t ,则有 S 1 = v x t ①h=221gt ②由①、②得 t =2 s , v x =500 m/s 2分 以2v表示爆炸后第二块的速度,则爆炸时的动量守恒关系如图所示.x v v m m x =221③0==+y y m m m v v v 1y 22121 ④解出 v 2x =2v x =1000 m/s , v 2y =-v 1y =14.7 m/s 3分 再由斜抛公式 x 2= S 1 +v 2x t 2 ⑤y 2=h +v 2y t 2-22gt 21 ⑥落地时 y 2 =0,可得 t 2 =4 s , t 2=-1 s (舍去) 故 x 2=5000 m 3分Mmv4、质量为M =1.5 kg 的物体,用一根长为l =1.25 m 的细绳悬挂在天花板上.今有一质量为m =10 g 的子弹以v 0=500 m/s 的水平速度射穿物体,刚穿出物体时子弹的速度大小v =30 m/s ,设穿透时间极短.求: (1) 子弹刚穿出时绳中张力的大小; (2) 子弹在穿透过程中所受的冲量.解:(1) 因穿透时间极短,故可认为物体未离开平衡位置.因此,作用于子弹、物体系统上的外力均在竖直方向,故系统在水平方向动量守恒.令子弹穿出时物体的水平速度为v '有 m v 0 = m v +M v 'v ' = m (v 0 - v )/M =3.13 m/s 2分 T =Mg+M v 2/l =26.5 N 2分(2) s N 7.40⋅-=-=∆v v m m t f (设0v方向为正方向) 2分负号表示冲量方向与0v方向相反. 2分第四章 功和能课 后 作 业1、一质量为m 的质点在Oxy 平面上运动,其位置矢量为j t b i t a rωωsin cos +=(SI)式中a 、b 、ω是正值常量,且a >b . (1)求质点在A 点(a ,0)时和B 点(0,b )时的动能;(2)求质点所受的合外力F 以及当质点从A 点运动到B 点的过程中F的分力x F和y F 分别作的功.解:(1)位矢 j t b i t a rωωsin cos += (SI) 可写为 t a x ωcos = , t b y ωsin =t a t x x ωωsin d d -==v , t b ty ωωcos d dy-==v在A 点(a ,0) ,1cos =t ω,0sin =t ωE KA =2222212121ωmb m m y x =+v v 2分在B 点(0,b ) ,0cos =t ω,1sin =t ωE KB =2222212121ωma m m y x =+v v 2分(2) j ma i ma F y x +==j t mb i t ma ωωωωsin cos 22-- 2分由A →B ⎰⎰-==020d cos d a a x x x t a m x F W ωω=⎰=-022221d a ma x x m ωω 2分⎰⎰-==b b y y t b m y F W 020dy sin d ωω=⎰-=-b mb y y m 022221d ωω 2分2、劲度系数为k 的轻弹簧,一端固定,另一端与桌面上的质量为m 的小球B 相连接.用外力推动小球,将弹簧压缩一段距离L 后放开.假定小球所受的滑动摩擦力大小为F 且恒定不变,滑动摩擦系数与静摩擦系数可视为相等.试求L 必须满足什么条件时,才能使小球在放开后就开始运动,而且一旦停止下来就一直保持静止状态.解:取弹簧的自然长度处为坐标原点O ,建立如图所示的坐标系.在t =0时,静止于x =-L 的小球开始运动的条件是kL >F ① 2分小球运动到x 处静止的条件,由功能原理得222121)(kL kx x L F -=+- ② 2分由② 解出 kFL x 2-=使小球继续保持静止的条件为 F k FL k x k ≤-=2 ③ 2分 所求L 应同时满足①、③式,故其范围为 k F <L kF3≤ 2分3、一链条总长为l ,质量为m ,放在桌面上,并使其部分下垂,下垂一段的长度为a .设链条与桌面之间的滑动摩擦系数为μ.令链条由静止开始运动,则 (1)到链条刚离开桌面的过程中,摩擦力对链条作了多少功?al -a(2)链条刚离开桌面时的速率是多少?解:(1)建立如图坐标.某一时刻桌面上全链条长为y ,则摩擦力大小为g lymf μ= 1分 摩擦力的功 ⎰⎰--==00d d a l a l f y gy l my f W μ 2分=022a l y l mg -μ =2)(2a l lmg--μ 2分(2)以链条为对象,应用质点的动能定理 ∑W =2022121v v m m -其中 ∑W = W P +W f ,v 0 = 0 1分W P =⎰la x P d =l a l mg x x l mg la 2)(d 22-=⎰ 2分由上问知 la l mg W f 2)(2--=μ所以222221)(22)(v m a l l mg l a l mg =---μ 得 []21222)()(a l a l lg ---=μv 2分αh0v4、一物体与斜面间的摩擦系数μ = 0.20,斜面固定,倾角α = 45°.现给予物体以初速率v 0 = 10 m/s ,使它沿斜面向上滑,如图所示.求: 物体能够上升的最大高度h ;该物体达到最高点后,沿斜面返回到原出发点时的速率v .解:(1)根据功能原理,有 mgh m fs -=2021v 2分 ααμαμsin cos sin mgh Nh fs ==mgh m mgh -==2021ctg v αμ 2分 )ctg 1(220αμ+=g h v =4.5 m 2分(2)根据功能原理有 fs m mgh =-221v 1分αμctg 212mgh mgh m -=v 1分[]21)ctg 1(2αμ-=gh v =8.16 m/s 2分第五章 刚体的转动课 后 作 业1、一轻绳跨过两个质量均为m 、半径均为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 和2m 的重物,如图所示.绳与滑轮间无相对滑动,滑轮轴光滑.两个定滑轮的转动惯量均为221mr .将由两个定滑轮以及质量为m 和2m的重物组成的系统从静止释放,求两滑轮之间绳内的张力.解:受力分析如图所示. 2分 2mg -T 1=2ma 1分T 2-mg =ma 1分T 1 r -T r =β221mr 1分 T r -T 2 r =β221mr 1分a =r β 2分解上述5个联立方程得: T =11mg / 8 2分2、一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的半径为R ,质量为M / 4,均匀分布在其边缘上.绳子的A 端有一质量为M 的人抓住了绳端,而在绳的另一端B 系了一质量为21M 的重物,如图.设人从静止开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B 端重物上升的加速度?(已知滑轮对通过滑轮中心且垂直于轮面的轴的转动惯量J =MR 2 / 4 )解:受力分析如图所示.设重物的对地加速度为a ,向上.则绳的A 端对地有加速度a 向下,人相对于绳虽为匀速向上,但相对于地其加速度仍为a 向下. 2分 根据牛顿第二定律可得:对人: Mg -T 2=Ma ① 2分对重物: T 1-21Mg =21Ma ② 2分根据转动定律,对滑轮有(T 2-T 1)R =J β=MR 2β / 4 ③ 2分因绳与滑轮无相对滑动, a =βR ④ 1分 ①、②、③、④四式联立解得 a =2g / 7 1分3、一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示).解:设绳子对物体(或绳子对轮轴)的拉力为T ,则根据牛顿运动定律和转动定律得:mg T =ma ① 2分 T r =J β ② 2分由运动学关系有: a = r β ③ 2分由①、②、③式解得: J =m ( g -a ) r 2 / a ④ 又根据已知条件 v 0=0∴ S =221at , a =2S / t 2 ⑤ 2分将⑤式代入④式得:J =mr 2(Sgt 22-1) 2分Am 1 ,l1v2俯视图4、有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动.另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相碰撞,设碰撞时间极短.已知小滑块在碰撞前后的速度分别为1v 和2v,如图所示.求碰撞后从细棒开始转动到停止转动的过程所需的时间.(已知棒绕O 点的转动惯量2131l m J =)解:对棒和滑块系统,在碰撞过程中,由于碰撞时间极短,所以棒所受的摩擦力 矩<<滑块的冲力矩.故可认为合外力矩为零,因而系统的角动量守恒,即1分m 2v 1l =-m 2v 2l +ω2131l m ① 3分碰后棒在转动过程中所受的摩擦力矩为gl m x x l m g M l f 10121d μμ-=⋅-=⎰ ② 2分由角动量定理 ω210310l m dt M tf -=⎰ ③ 2分由①、②和③解得 g m m t 12122μv v += 2分第六章 狭义相对论基础课 后 作 业1、一体积为V 0,质量为m 0的立方体沿其一棱的方向相对于观察者A 以速度v 运动.求:观察者A 测得其密度是多少?解:设立方体的长、宽、高分别以x 0,y 0,z 0表示,观察者A 测得立方体的长、宽、高分别为 221cx x v -=,0y y =,0z z =. 相应体积为 2201cV xyz V v -== 3分观察者A测得立方体的质量 2201cm m v -=故相应密度为 V m /=ρ22022011/c V c m v v --=)1(2200cV m v -=2分2、在O 参考系中,有一个静止的正方形,其面积为 100 cm 2.观测者O '以 0.8c 的匀速度沿正方形的对角线运动.求O '所测得的该图形的面积.解:令O 系中测得正方形边长为a ,沿对角线取x 轴正方向(如图),则边长在坐标轴上投影的大小为a a x 221=,a a y 221= 面积可表示为: x y a a S ⋅=2 2分在以速度v 相对于O 系沿x 正方向运动的O '系中2)/(1c a a x x v -=' =0.6×a 221 a a a yy 221==' 在O '系中测得的图形为菱形,其面积亦可表示为606.022=='⋅'='a a a S x y cm 23分aaO y x3、一艘宇宙飞船的船身固有长度为L 0 =90 m ,相对于地面以=v 0.8 c (c 为真空中光速)的匀速度在地面观测站的上空飞过.(1) 观测站测得飞船的船身通过观测站的时间间隔是多少? (2) 宇航员测得船身通过观测站的时间间隔是多少?解:(1) 观测站测得飞船船身的长度为 =-=20)/(1c L L v 54 m则 ∆t 1 = L /v =2.25×10-7 s 3分(2) 宇航员测得飞船船身的长度为L 0,则∆t 2 = L 0/v =3.75×10-7 s 2分4、半人马星座α星是距离太阳系最近的恒星,它距离地球S = 4.3×1016 m .设有一宇宙飞船自地球飞到半人马星座α星,若宇宙飞船相对于地球的速度为v = 0.999 c ,按地球上的时钟计算要用多少年时间如以飞船上的时钟计算,所需时间又为多少年解:以地球上的时钟计算: 5.4≈=∆vSt 年 2分 以飞船上的时钟计算: ≈-='∆∆221ct t v 0.20 年 3分5、在惯性系S 中,有两事件发生于同一地点,且第二事件比第一事件晚发生∆t =2s ;而在另一惯性系S '中,观测第二事件比第一事件晚发生∆t '=3s .那么在S '系中发生两事件的地点之间的距离是多少?解:令S '系与S 系的相对速度为v ,有2)/(1c tt v -='∆∆, 22)/(1)/(c t t v -='∆∆则 2/12))/(1(t t c '-⋅=∆∆v ( = 2.24×108 m ·s -1 ) 4分那么,在S '系中测得两事件之间距离为:2/122)(t t c t x ∆∆∆∆-'='⋅='v = 6.72×108 m 4分6、要使电子的速度从v 1 =1.2×108 m/s 增加到v 2 =2.4×108 m/s 必须对它作多少功? (电子静止质量m e =9.11×10-31 kg)解:根据功能原理,要作的功 W = ∆E根据相对论能量公式 ∆E = m 2c 2- m 1c 2 2分根据相对论质量公式 2/12202])/(1/[c m m v -=2/12101])/(1/[c m m v -= 1分 ∴ )1111(22122220c c c m W v v ---==4.72×10-14 J =2.95×105 eV 2分第七章 振动课 后 作 业1、一个轻弹簧在60 N 的拉力作用下可伸长30 cm .现将一物体悬挂在弹簧的下端并在它上面放一小物体,它们的总质量为4 kg .待其静止后再把物体向下拉10 cm ,然后释放.问:(1) 此小物体是停在振动物体上面还是离开它?(2) 如果使放在振动物体上的小物体与振动物体分离,则振幅A 需满足何条件二者在何位置开始分离解:(1) 小物体受力如图.设小物体随振动物体的加速度为a ,按牛顿第二定律有(取向下为正) ma N mg =- 1分)(a g m N -=当N = 0,即a = g 时,小物体开始脱离振动物体,已知 1分A = 10 cm ,N/m 3.060=k 有 50/==m k ω rad ·s -1 2分 系统最大加速度为 52max ==A a ω m ·s -2 1分 此值小于g ,故小物体不会离开. 1分(2) 如使a > g ,小物体能脱离振动物体,开始分离的位置由N = 0求得x a g 2ω-== 2分 6.19/2-=-=ωg x cm 1分即在平衡位置上方19.6 cm 处开始分离,由g A a >=2max ω,可得2/ωg A >=19.6 cm . 1分2、一质点在x 轴上作简谐振动,选取该质点向右运动通过A 点时作为计时起点( t = 0 ),经过2秒后质点第一次经过B 点,再经过2秒后质点第二次经过B 点,若已知该质点在A 、B 两点具有相同的速率,且AB = 10 cm 求: (1) 质点的振动方程; (2) 质点在A 点处的速率.解: T = 8 s , ν = (1/8) s -1, ω = 2πν = (π /4) s -1 3分(1) 以AB 的中点为坐标原点,x 轴指向右方. t = 0时, 5-=x cm φcos A =t = 2 s 时, 5=x cm φφωsin )2cos(A A -=+= 由上二式解得 tg φ = 1因为在A 点质点的速度大于零,所以φ = -3π/4或5π/4(如图) 2分25cos /==φx A cm 1分∴ 振动方程 )434cos(10252π-π⨯=-t x (SI) 1分(2) 速率 )434sin(41025d d 2π-π⨯π-==-t t x v (SI) 2分 当t = 0 时,质点在A 点221093.3)43sin(10425d d --⨯=π-⨯π-==t x v m/s 1分3、一质量为m 的质点在力F = -π2x 的作用下沿x 轴运动.求其运动的周期.解:将F = -π2x 与F = -kx 比较,知质点作简谐振动, k = π2. 3分 又 mm k π==ω 4分m T 22=π=ω3分4、一物体同时参与两个同方向的简谐振动: )212cos(04.01π+π=t x (SI), )2cos(03.02π+π=t x (SI)求此物体的振动方程.解:设合成运动(简谐振动)的振动方程为 )cos(φω+=t A x则 )cos(2122122212φφ-++=A A A A A ① 2分 以 A 1 = 4 cm ,A 2 = 3 cm ,π=π-π=-212112φφ代入①式,得5cm 3422=+=A cm 3分又 22112211cos cos sin sin arctg φφφφφA A A A ++= ②≈127°≈2.22 rad 3分 ∴ )22.22cos(05.0+π=t x (SI) 2分5、在竖直悬挂的轻弹簧下端系一质量为 100 g 的物体,当物体处于平衡状态时,再对物体加一拉力使弹簧伸长,然后从静止状态将物体释放.已知物体在32 s 内完成48次振动,振幅为5 cm . (1) 上述的外加拉力是多大?(2) 当物体在平衡位置以下1 cm 处时,此振动系统的动能和势能各是多少?解一:(1) 取平衡位置为原点,向下为x 正方向.设物体在平衡位置时弹簧的伸长量为∆l ,则有l k mg ∆=, 加拉力F 后弹簧又伸长x 0,则0)(0=+-+∆x l k mg F解得 F = kx 0 2分由题意,t = 0时v 0 = 0;x = x 0则02020)/(x x A =+=ωv 2分又由题给物体振动周期4832=T s, 可得角频率 Tπ=2ω, 2ωm k = ∴ 444.0)/4(22=π==A T m kA F N 1分(2) 平衡位置以下1 cm 处: )()/2(2222x A T -π=v 2分221007.121-⨯==v m E K J 2分2222)/4(2121x T m kx E p π== = 4.44×10-4 J 1分解二:(1) 从静止释放,显然拉长量等于振幅A (5 cm ),kA F = 2分2224νωπ==m m k ,ν = 1.5 Hz 2分∴ F = 0.444 N 1分(2) 总能量 221011.12121-⨯===FA kA E J 2分当x = 1 cm 时,x = A /5,E p 占总能量的1/25,E K 占24/25. 2分∴ 21007.1)25/24(-⨯==E E K J , 41044.425/-⨯==E E p J 1分6、如图,有一水平弹簧振子,弹簧的劲度系数k = 24 N/m ,重物的质量m = 6 kg ,重物静止在平衡位置上.设以一水平恒力F = 10 N 向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05 m 时撤去力F .当重物运动到左方最远位置时开始计时,求物体的运动方程.解:设物体的运动方程为 )cos(φω+=t A x .恒外力所做的功即为弹簧振子的能量: F ×0.05 = 0.5 J . 2分当物体运动到左方最远位置时,弹簧的最大弹性势能为0.5 J ,即:5.0212=kA J , ∴ A = 0.204 m . 2分A 即振幅. 4/2==m k ω (rad/s)2ω = 2 rad/s . 2分按题目所述时刻计时,初相为φ = π.∴ 物体运动方程为 2分)2cos(204.0π+=t x (SI). 2分第八章 波动课 后 作 业1、一平面简谐波沿x 轴正向传播,波的振幅A = 10 cm ,波的角频率ω = 7π rad/s.当t = 1.0 s 时,x = 10 cm 处的a 质点正通过其平衡位置向y 轴负方向运动,而x = 20 cm 处的b 质点正通过y = 5.0 cm 点向y 轴正方向运动.设该波波长λ >10 cm ,求该平面波的表达式.解:设平面简谐波的波长为λ,坐标原点处质点振动初相为φ,则该列平面简谐波的表达式可写成 )/27cos(1.0φλ+π-π=x t y (SI) 2分 t = 1 s 时 0])/1.0(27cos[1.0=+π-π=φλy 因此时a 质点向y 轴负方向运动,故π=+π-π21)/1.0(27φλ ① 2分 而此时,b 质点正通过y = 0.05 m 处向y 轴正方向运动,应有 05.0])/2.0(27cos[1.0=+π-π=φλy且 π-=+π-π31)/2.0(27φλ ② 2分由①、②两式联立得 λ = 0.24 m 1分3/17π-=φ 1分∴ 该平面简谐波的表达式为]31712.07cos[1.0π-π-π=x t y (SI) 2分或 ]3112.07cos[1.0π+π-π=x t y (SI)(m) -2、图示一平面简谐波在t = 0 时刻的波形图,求(1) 该波的波动表达式; (2) P 处质点的振动方程.解:(1) O 处质点,t = 0 时 0cos 0==φA y , 0sin 0>-=φωA v所以 π-=21φ 2分又 ==u T /λ (0.40/ 0.08) s= 5 s 2分故波动表达式为 ]2)4.05(2cos[04.0π--π=x t y (SI) 4分(2) P 处质点的振动方程为]2)4.02.05(2cos[04.0π--π=t y P )234.0cos(04.0π-π=t (SI) 2分3、沿x 轴负方向传播的平面简谐波在t = 2 s 时刻的波形曲线如图所示,设波速u = 0.5 m/s . 求:原点O 的振动方程.解:由图,λ = 2 m , 又 ∵u = 0.5 m/s ,∴ ν = 1 /4 Hz , 3分T = 4 s .题图中t = 2 s =T 21.t = 0时,波形比题图中的波形倒退λ21,见图. 2分此时O 点位移y 0 = 0(过平衡位置)且朝y 轴负方向运动,∴ π=21φ 2分∴ )2121cos(5.0π+π=t y (SI) 3分4、一平面简谐波沿Ox 轴正方向传播,波的表达式为 )/(2cos λνx t A y -π=, 而另一平面简谐波沿Ox 轴负方向传播,波的表达式为 )/(2cos 2λνx t A y +π= 求:(1) x = λ /4 处介质质点的合振动方程; (2) x = λ /4 处介质质点的速度表达式.解:(1) x = λ /4处)212cos(1π-π=t A y ν , )212cos(22π+π=t A y ν 2分∵ y 1,y 2反相 ∴ 合振动振幅 A A A A s =-=2 , 且合振动的初相φ 和y 2的初相一样为π21. 4分合振动方程 )212cos(π+π=t A y ν 1分(2) x = λ /4处质点的速度 )212sin(2/d d π+ππ-== v t A t y νν)2cos(2π+ππ=t A νν 3分5、设入射波的表达式为 )(2cos 1Ttx A y +π=λ,在x = 0处发生反射,反射点为一固定端.设反射时无能量损失,求(1) 反射波的表达式; (2) 合成的驻波的表达式; (3) 波腹和波节的位置.解:(1) 反射点是固定端,所以反射有相位突变π,且反射波振幅为A ,因此反 射波的表达式为 ])//(2cos[2π+-π=T t x A y λ 3分(2) 驻波的表达式是 21y y y +=)21/2cos()21/2cos(2π-ππ+π=T t x A λ 3分(3) 波腹位置: π=π+πn x 21/2λ, 2分λ)21(21-=n x , n = 1, 2, 3, 4,… 波节位置: π+π=π+π2121/2n x λ 2分λn x 21= , n = 1, 2, 3, 4,…6、如图所示,一平面简谐波沿x 轴正方向传播,BC 为波密媒质的反射面.波由P 点反射,OP = 3λ /4,DP = λ /6.在t = 0时,O 处质点的合振动是经过平衡位置向负方向运动.求D 点处入射波与反射波的合振动方程.(设入射波和反射波的振幅皆为A ,频率为ν.)解:选O 点为坐标原点,设入射波表达式为])/(2cos[1φλν+-π=x t A y 2分则反射波的表达式是 ])(2cos[2ππ++-+-=φλνxOP OP t A y 2分合成波表达式(驻波)为 )2cos()/2cos(2φνλ+ππ=t x A y 2分在t = 0时,x = 0处的质点y 0 = 0, 0)/(0<∂∂t y ,故得 π=21φ 2分因此,D 点处的合成振动方程是)22cos()6/4/32cos(2π+π-π=t A y νλλλt A νπ=2sin 3 2分第九章 温度和气体动理论课 后 作 业1、黄绿光的波长是5000A (1A =10 -10 m).理想气体在标准状态下,以黄绿光的波长为边长的立方体内有多少个分子?(玻尔兹曼常量k =1.38×10- 23J ·K -1)解:理想气体在标准状态下,分子数密度为n = p / (kT )=2.69×1025 个/ m 3 3分 以5000A 为边长的立方体内应有分子数为N = nV =3.36×106个. 2分2、已知某理想气体分子的方均根速率为 400 m ·s -1.当其压强为1 atm 时,求气体的密度.解: 223131v v ρ==nm p∴ 90.1/32==v p ρ kg/m 3 5分3、一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为 w = 6.21×10-21 J .试求:(1) 氧气分子的平均平动动能和方均根速率. (2) 氧气的温度.(阿伏伽德罗常量N A =6.022×1023 mol -1,玻尔兹曼常量k =1.38×10-23 J ·K -1)解:(1) ∵ T 相等, ∴氧气分子平均平动动能=氢气分子平均平动动能w=6.21×10-21 J .且 ()()483/22/12/12==m w vm/s 3分(2) ()k w T 3/2==300 K . 2分4、某理想气体的定压摩尔热容为29.1 J ·mol -1·K -1.求它在温度为273 K 时分子平均转动动能. (玻尔兹曼常量k =1.38×10-23 J ·K -1 )解: R R iR i C P +=+=222, ∴ ()5122=⎪⎭⎫⎝⎛-=-=R C R R C i P P ,2分 可见是双原子分子,只有两个转动自由度.211077.32/2-⨯===kT kT r ε J 3分5、一超声波源发射超声波的功率为10 W .假设它工作10 s ,并且全部波动能量都被1 mol 氧气吸收而用于增加其内能,则氧气的温度升高了多少?(氧气分子视为刚性分子,普适气体常量R =8.31 J ·mol -1·K -1 )解: A = Pt = T iR v ∆21, 2分∴ ∆T = 2Pt /(v iR )=4.81 K .3分6、1 kg 某种理想气体,分子平动动能总和是1.86×106 J ,已知每个分子的质量是3.34×10-27 kg ,试求气体的温度. (玻尔兹曼常量 k =1.38×10-23 J ·K -1)解: N = M / m =0.30×1027 个 1分==N E w K / 6.2×10-21 J 1分kwT 32== 300 K 3分第十章 热力学第一定律课 后 作 业1、一定量的单原子分子理想气体,从初态A 出发,沿图示直线过程变到另一状态B ,又经过等容、等压两过程回到状态A .(1) 求A →B ,B →C ,C →A 各过程中系统对外所作的功W ,内能的增量∆E 以及所吸收的热量Q .(2) 整个循环过程中系统对外所作的总功以及从外界吸收的总热量(过程吸热的代数和).1 2 3 12 OV (10-3 m 3) 5 A BC解:(1) A →B : ))((211A B A B V V p p W -+==200 J . ΔE 1=ν C V (T B -T A )=3(p B V B -p A V A ) /2=750 JQ =W 1+ΔE 1=950 J . 3分B →C : W 2 =0ΔE 2 =ν C V (T C -T B )=3( p C V C -p B V B ) /2 =-600 J .Q 2 =W 2+ΔE 2=-600 J . 2分C →A : W 3 = p A (V A -V C )=-100 J .150)(23)(3-=-=-=∆C C A A C A V V p V p T T C E ν J .Q 3 =W 3+ΔE 3=-250 J 3分(2) W = W 1 +W 2 +W 3=100 J .Q = Q 1 +Q 2 +Q 3 =100 J 2分2、1 mol 双原子分子理想气体从状态A (p 1,V 1)沿p -V 图所示直线变化到状态B (p 2,V 2),试求: 气体的内能增量. 气体对外界所作的功. 气体吸收的热量. 此过程的摩尔热容.解:(1) )(25)(112212V p V p T T C E V -=-=∆ 2分 (2) ))((211221V V p p W -+=, W 为梯形面积,根据相似三角形有p 1V 2= p 2V 1,则)(211122V p V p W -=. 3分(3) Q =ΔE +W =3( p 2V 2-p 1V 1 ). 2分(4) 以上计算对于A →B 过程中任一微小状态变化均成立,故过程中 ΔQ =3Δ(pV ). 由状态方程得 Δ(pV ) =R ΔT , 故 ΔQ =3R ΔT ,摩尔热容 C =ΔQ /ΔT =3R . 3分BAOVp p 2V 1V 2(摩尔热容C =T Q ∆∆/,其中Q ∆表示1 mol 物质在过程中升高温度T ∆时所吸收的热量.)3、一定量的理想气体,由状态a 经b 到达c .(如图, abc 为一直线)求此过程中1 2 3 1 2 3 a bcV (L)p (atm)气体对外作的功; 气体内能的增量;气体吸收的热量.(1 atm =1.013×105 Pa)解:(1) 气体对外作的功等于线段c a 下所围的面积W =(1/2)×(1+3)×1.013×105×2×10-3 J =405.2 J 3分 (2) 由图看出 P a V a =P c V c ∴T a =T c 2分内能增量 0=∆E . 2分(3) 由热力学第一定律得Q =E ∆ +W =405.2 J . 3分4、如图所示,abcda 为1 mol 单原子分子理想气体的循环过程,求:Oadcbp (×105 Pa)V (×10-3 m 3)2312(1) 气体循环一次,在吸热过程中从外界共吸收的热量; (2) 气体循环一次对外做的净功;(3) 证明 在abcd 四态, 气体的温度有T a T c =T b T d .解:(1) 过程ab 与bc 为吸热过程, 吸热总和为 Q 1=C V (T b -T a )+C p (T c -T b ))(25)(23b b c c a a b b V p V p V p V p -+-==800 J 4分(2) 循环过程对外所作总功为图中矩形面积W = p b (V c -V b )-p d (V d -V a ) =100 J 2分(3) T a =p a V a /R ,T c = p c V c /R , T b = p b V b /R ,T d = p d V d /R ,T a T c = (p a V a p c V c )/R 2=(12×104)/R 2T b T d = (p b V b p d V d )/R 2=(12×104)/R 2∴ T a T c =T b T d 4分5、一定量的理想气体经历如图所示的循环过程,A →B 和C →D 是等压过程,B →C 和D →A 是绝热过程.已知:T C = 300 K ,T B = 400 K . 试求:此循环的效率.(提示:循环效率的定义式η =1-Q 2 /Q 1,Q 1为循环中气体吸收的热量,Q 2为循环中气体放出的热量) A BC DO Vp解: 121Q Q -=η Q 1 = ν C p (T B -T A ) , Q 2 = ν C p (T C -T D ) )/1()/1(12B A B C D C A B D C T T T T T T T T T T Q Q --=--= 4分 根据绝热过程方程得到:γγγγ----=D D AA T p T p 11, γγγγ----=C CB B T p T p 11 ∵ p A = p B , pC = pD ,∴ T A / T B = T D / T C 4分故 %251112=-=-=BC T T Q Q η 2分6、一卡诺热机(可逆的),当高温热源的温度为 127℃、低温热源温度为27℃时,其每次循环对外作净功8000 J .今维持低温热源的温度不变,提高高温热源温度,使其每次循环对外作净功 10000 J .若两个卡诺循环都工作在相同的两条绝热线之间,试求:(1) 第二个循环的热机效率;(2) 第二个循环的高温热源的温度.解:(1) 1211211T T T Q Q Q Q W -=-==η 2111T T T W Q -= 且 1212T T Q Q = ∴ Q 2 = T 2 Q 1 /T 1即 212122112T T T W T T T T T Q -=⋅-==24000 J 4分 由于第二循环吸热 221Q W Q W Q +'='+'=' ( ∵ 22Q Q =') 3分 =''='1/Q W η29.4% 1分 (2) ='-='η121T T 425 K 2分。
第1章质点运动学(部分答案)

一、选择题:1. 某质点沿半径为R 的圆周运动一周,它的位移和路程分别为(B) A. πR ,0; B. 0,2πR ;C. 0,0;D. 2πR ,2πR 。
2. 质点作直线运动,运动方程为242x t t =--(SI 制),则质点在最初2秒内的位移为(C)A. -6 m ;B. 4 m ;C. -4 m ;D. 6 m 。
3.一质点在平面上作一般曲线运动,其瞬时速度为v ,瞬时速率为v ,某一时间内的平均速度为v ,平均速率为v ,它们之间的关系必定有( D ) A. v v =,v v =;B. v v ≠,v v =;C. v v ≠,v v ≠;D. v v =,v v ≠。
4.质点作曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,S 表示路程,a t 表示切向加速度,下列表达式中( D ) (1) a t = d /d v , (2) v =t r d /d ,(3) v =t S d /d , (4) t a t =d /d v。
A. 只有(1)、(4)是对的; B. 只有(2)、(4)是对的; C. 只有(2)是对的;D.只有(3)是对的。
5. 一运动质点在某瞬时位于矢径()y x r ,的端点处,其速度大小为( D )A.d d rt ; B.d d r t ;C.d d r t;6. 一质点作直线运动,某时刻的瞬时速度v =2m/s ,瞬时加速度a =-2m/s 2,则一秒钟后质点的速度(D)A.等于零;B.等于-2 m/s ;C.等于2 m/s ;D.不能确定。
7. 沿直线运动的物体,其速度大小与时间成反比,则其加速度的大小与速度大小有如下关系( B )A.与速度大小成正比;B.与速度大小的平方成正比;C.与速度大小成反比;D.与速度大小的平方成反比。
8. 下列说法中,正确的是( D )A. 物体走过的路程越长,它的位移也越大;B. 质点在时刻t 和t +Δt 的速度分别为1v 和2v ,则在时间Δt 内的平均速度为()122v v +;C. 如物体的加速度为常量,则它一定做匀变速直线运动;D. 在质点的曲线运动中,加速度的方向与速度的方向总是不一致的。
(完整版)大学物理课后习题答案详解

r r r r r r rr、⎰ dt⎰0 dx = ⎰ v e⎰v v1122v v d tv v d tvg 2 g h d tdt [v 2 + ( g t ) 2 ] 12 (v 2 + 2 g h ) 12第一章质点运动学1、(习题 1.1):一质点在 xOy 平面内运动,运动函数为 x = 2 t, y = 4 t 2 - 8 。
(1)求质点 的轨道方程;(2)求 t = 1 s 和 t = 2 s 时质点的位置、速度和加速度。
解:(1)由 x=2t 得,y=4t 2-8可得: r y=x 2-8r 即轨道曲线(2)质点的位置 : r = 2ti + (4t 2 - 8) jr r rr r 由 v = d r / d t 则速度: v = 2i + 8tjr r rr 由 a = d v / d t 则加速度: a = 8 jrr r r r r r r 则当 t=1s 时,有 r = 2i - 4 j , v = 2i + 8 j , a = 8 j r当 t=2s 时,有r = 4i + 8 j , v = 2i +16 j , a = 8 j 2 (习题 1.2): 质点沿 x 在轴正向运动,加速度 a = -kv , k 为常数.设从原点出发时速度为 v ,求运动方程 x = x(t ) .解:dv = -kvdt v1 v 0 vd v = ⎰ t - k dt 0v = v e - k tdx x= v e -k t0 t0 -k t d t x = v0 (1 - e -k t )k3、一质点沿 x 轴运动,其加速度为 a = 4 t (SI),已知 t = 0 时,质点位于 x 0=10 m 处,初速 度 v 0 = 0.试求其位置和时间的关系式.解:a = d v /d t = 4 td v = 4 t d tv 0d v = ⎰t 4t d t v = 2 t 2v = d x /d t = 2 t 2⎰x d x = ⎰t 2t 2 d t x = 2 t 3 /3+10 (SI)x4、一质量为 m 的小球在高度 h 处以初速度 v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; d r d v d v (3)落地前瞬时小球的 ,,.d td td t解:(1)x = v t式(1)v v v y = h - gt 2 式(2)r (t ) = v t i + (h - gt 2 ) j0 (2)联立式(1)、式(2)得y = h -vd r(3) = v i - gt j而落地所用时间t =0 gx 22v 22hgvd r所以 = v i - 2gh jvd vdv g 2t= - g j v = v 2 + v 2 = v 2 + (-gt) 2= =x y 0 0vv v d rv d v 2) v = [(2t )2+ 4] 2 = 2(t 2+ 1)2t t 2 + 1, V a = a - a = m + M m + Mvg gvv v 5、 已知质点位矢随时间变化的函数形式为 r = t 2i + 2tj ,式中 r 的单位为 m , 的单位为 s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。
第一章质点运动学习题及答案

(A)加速度恒定不变时,物体的运动速度也不变,
(B)平均速率等于平均速度的大小,
(C)质点作曲线运动时,质点速度大小的变化产生切向加速度,
(D)当物体的速度为零时,加速度必定为零.Fra bibliotek二、填空题
1 、 一 质 点 在 Oxy 平 面 内 运 动 , 运 动 学 方 程 为 ������ = 2������ + (19 − 2������2)������
位置矢量: r0 2i 19 j; r1 2i 11j
位移矢量: r r1 r0 8 j
2、36������ ������2, 1296������ ������2
解:角速度:
d dt
9t2 ;
(t
2s)
36(rad
/ s)
角加速度:
d dt
(SI).则在第 2 秒末的瞬时速度为������2=
������ ������,第 2 秒末的加速度为
������2 =
������ ������2,从 t=0s 到 t=2s 该质点的位移Δ ������=
m.
2、一质点沿半径为 1 m 的圆周运动,运动方程为 =2+3 t 3 ,式中 以
第一章 质点运动学 习题
一、选择题
1、
一运动质点在某瞬时位
于
矢
径
r(
x,
y)
的
端点处,其速度大小
为
()
(A) dr
dt
(C) d | r |
dt
(B) dr
dt
(D) ( dx )2 ( dy )2
dt dt
2、质点作曲线运动,
第一章质点运动学 作业答案
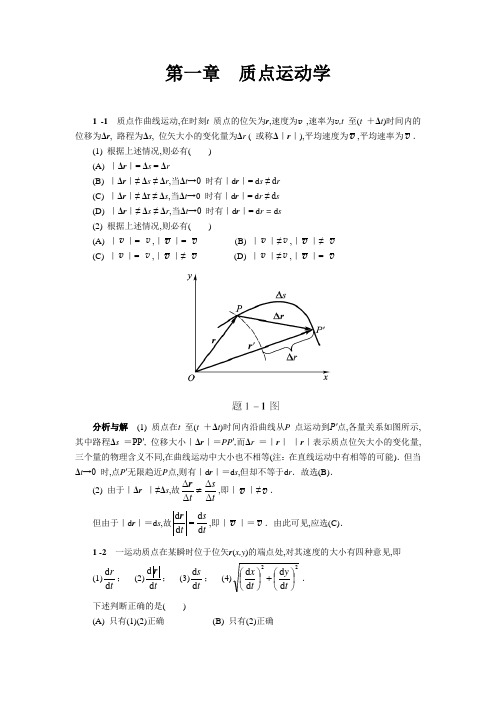
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts tΔΔΔΔ≠r ,即|v |≠v .但由于|d r |=d s ,故ts td d d d =r ,即|v |=v .由此可见,应选(C).1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t rd d ; (2)t d d r; (3)t sd d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确 分析与解tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式ts d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的 分析与解td d v 表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;tr d d 在极坐标系中表示径向速率v r (如题1 -2 所述);ts d d 在自然坐标系中表示质点的速率v ;而td d v 表示加速度的大小而不是切向加速度at.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -5 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx 来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d tx 两式计算.题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x (2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4sm 48d d -=⋅-==t tx v2s0.422m.s36d d -=-==t tx a1 -6 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -=这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图1 -16 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b ts a t -==22d d , Rbt Ra n 202)(-==v v故加速度的大小为R)(402222bt b a aa a t tn-+=+=v其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n20)(arctan arctan v(2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v =(3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为bs s s t 220v =-=因此质点运行的圈数为bRRs n π4π22v ==1 -19 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1o12sm 36.575tan -⋅==v v。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一. 选择题:
[
C ]1、[基础训练
1]
如图所示,湖中有一小船,有人用绳绕过岸上一定高度处得定滑轮
拉湖中得船向岸边运动.设该人以匀速率收绳,绳不伸长、湖水静止,则小船得运动就是
(A) 匀加速运动. (B) 匀减速运动.
(C) 变加速运动. (D) 变减速运动. (E) 匀速直线运动.
【答】如图建坐标系,设船离岸边x 米,
,,
,,
,可见,加速度与速度同向,且加速度随时间变化。
[ D ]2、[基础训练3] 一运动质点在某瞬时位
于矢径得端点处, 其速度大小为
(A) (B)
(C) (D)
【答】
[ C ]3、[基础训练6] 一飞机相对空气得
速度大小为 200 km/h, 风速为56 km/h,方向从
西向东.地面雷达站测得飞机速度大小为 192
km/h,则飞机飞行方向就是
(A) 南偏西16、3°;(B) 北偏东16、3°;
(C) 向正南或向正北; (D) 西偏北16、3°;
(E) 东偏南16、3°.
【答】根据三个速率得数值关系,以及伽利略速
度变换式,可以画出三个速度之间得矢量关系,
如图所示。
=200km/h, 56/, =192km/h km h v v v →→→=机空气空气地机地,根据余弦定理,,解得:,所
以、
[ B ]4、(自测提高3)质点沿半径为R 得圆周作匀速率运动,每T 秒转一圈.在2T 时间间
隔中,其平均速度大小与平均速率大小分别为
(A) 2πR /T , 2πR/T . (B) 0 , 2πR /T
(C) 0 , 0. (D) 2πR /T , 0、
【答】平均速度大小: 平均速率:
[ C ] 5、[自测提高6]某物体得运动规律为,式中得k 为大于零得常量.当时,初速为v 0,
则速度与时间t 得函数关系就是
(A) , (B) ,
(C) , (D)
【答】,分离变量并积分,,得、
[ B ]6、[自测提高7]在相对地面静止得坐标系内,A 、B 二船都以2 m/s 速率匀速行驶,A
船沿x 轴正向,B 船沿y 轴正向.今在A 船上设置与静止坐标系方向相同得坐标系(x 、y 方向单
位矢用、表示),那么在A 船上得坐标系中,B 船得速度(以m/s 为单位)为
(A) 2+2. (B) -2+2. (C) -2-2. (D) 2-2.
【答】=+ =- =、
二、填空题
1、[基础训练7] 已知质点得运动学方程为(SI),当t = 2 s时,加速度得大小为a = ;加速度与x轴正方向间夹角
α= .
【答】,,
,
大小;
与x轴正方向间夹角
2、[基础训练10] 一物体作如图所示得斜抛运动,测得在
轨道A点处速度得大小为v,其方向与水平方向夹角成30°,则物体在A点得切向加速度a t = -0、5g ,轨道得曲率半径、(重力加速度为g)
【答】如图,
22
00
sin300.5,cos30
cos30
t n
v v
a g g a g
g
ρ
ρ
=-=-==∴=
3、[基础训练12] 一质点沿直线运动,其运动学方程为x = 6 t-t2(SI),则在t由0至4s 得时间间隔内,质点得位移大小为,在t由0到4s得时间间隔内质点走过得路程为.
【答】(1)x = 6 t-t2(SI),位移大小;
(2),可见,t<3s时,>0;t=3s时,=0;而t>3s时,<0;所以,路程=
4、[自测提高9] 一质点从静止出发沿半径R=1m得圆周运动,其角加速度随时间t得变化规律为,则质点得角速度ω=;加速度切向分量a t =。
【答】(1),,;
(2);
5、[自测提高11]一质点从O点出发以匀速率1 cm/s作顺时针转向得圆周运动,圆得半径为1 m,如图所示.当它走过2/3圆周时,走过得路程就是__4、19(m),这段时间内得平均速度大小为,方向就是__与x轴正方向逆时针成600.
【答】
3
r2cos30
v 4.1310(/)
S
t400
v
m s
π
-
∆⨯
====⨯
∆
v
v
平均速度大小;方向如图。
三.计算题
1、[基础训练16 ]有一质点沿x轴作直线运动,t时刻得坐标为x = 4、5 t2– 2 t3(SI) .试求:
(1)第2秒内得平均速度;
(2)第2秒末得瞬时速度;
(3)第2秒内得路程.
解:(1)t1=1s时,x1=2、5m ; t2=2s时,x2=2m ;
,
(2)
(3)令, 得:、此时
第二秒内得路程()()m ....x'x x x's 2522375352375321=-+-=-+-=
2、[基础训练17 ] 倾斜上抛一小球,抛出时初速度与水平面成600角,1、00秒钟后小球仍然斜向上升,但飞行方向与水平面成450角。
试求:
(1)小球到达最高点得时间;
(2)小球在最高点得速度。
解 :以抛出点为原点、水平向右为x 轴、竖直向上为y 轴,建立坐标系。
(1)设初速度为v 0,则有 ,
任意时刻t:,
依题意,时,速度v 与水平方向成450,则有, ∴
解得 :
小球到达最高点时,,即,解得:
(2)小球在最高点时得速度沿水平方向,其大小为
3、[基础训练19 ]质点沿半径为R 得圆周运动,加速度与速度得夹角保持不变,求该质点得速度随时间而变化得规律,已知初速为。
解: 将,代入,得,
分离变量并积分:
002000tan 11, tan tan tan v
t v v R dv dt t v v R v v R R v t ϕϕϕϕ=-+=∴=-⎰⎰ 4、[自测提高15 ]质点按照得规律沿半径为R 得圆周运动,其中s 就是质点运动得路
程,b 、c 就是常量,并且b 2 >cR 。
问当切向加速度与法向加速度大小相等时,质点运动了多少
时间?
解:,,
切向加速度大小,法向加速度大小;
当切向加速度与法向加速度大小相等时:, (负号表示反向运动),
即 , 得
5、[自测提高17 ] 一敞顶电梯以恒定速率v =10 m/s 上升.当电梯离地面h =10 m 时,一小孩竖直向上抛出一球.球相对于电梯初速率 m/s.试问:
(1) 从地面算起,球能达到得最大高度为多大?
(2) 抛出后经过多长时间再回到电梯上?
解:(1) 根据伽利略速度变换式,可得球相对地面得初速度:方向向上,大小为 30 m/s 球到达最高点时,对地得速度为零。
可得最大高度为 m/s
离地面高度为 H = (45、9+10) m =55、9 m
(2) 以地面作为参考系:球回到电梯上时,电梯上升得高度=球上升得高度,即
解得: s
【若以电梯作为参考系:则再回到电梯上时,满足,得:t = 4、08s 】
附加题:[ 自测提高16 ] 一飞机相对于空气以恒定速率v 沿正方形轨道飞行,在无风天气其运动周期为T .若有恒定小风沿平行于正方形得一对边吹来,风速为.求飞机仍沿原正方形(对地)轨道飞行时周期要增加多少.
解:如图,设,正方形边长为L,根据求解。
(1)A →B,
;
(2)B→C,,
;
(3)C→D得飞行时间与A→B得飞行时间相等,;
(4)D→A,
所以,有恒定小风时飞行周期为,
与无风时相比,周期增加了。
根据上述计算结果,可得
因为,所以将与展开,并保留到项,
得。
