第二章matlab数据描述
使用MATLAB进行数据分析和建模

使用MATLAB进行数据分析和建模第一章:引言数据分析和建模是现代信息时代中至关重要的技术之一。
在涉及大量数据的情况下,使用MATLAB进行数据分析和建模能够帮助我们从数据中提取有用的信息,并使用这些信息来做出预测和决策。
本章将介绍使用MATLAB进行数据分析和建模的基本概念和方法。
第二章:MATLAB基础在开始进行数据分析和建模之前,我们首先需要了解MATLAB的基础知识。
这包括MATLAB的安装和配置,MATLAB的基本语法和数据类型,以及MATLAB中常用的数据分析和建模工具。
本章将对这些内容进行详细介绍。
第三章:数据导入和预处理在进行数据分析和建模之前,我们通常需要将原始数据导入到MATLAB中,并对数据进行一些预处理操作,例如数据清洗、数据归一化等。
本章将介绍如何使用MATLAB进行数据导入和预处理,以便为后续的数据分析和建模做准备。
第四章:数据可视化数据可视化是数据分析和建模中非常重要的环节,能够帮助我们更好地理解和解释数据。
MATLAB提供了多种数据可视化工具和函数,例如绘制散点图、折线图、直方图等。
本章将介绍如何使用MATLAB进行数据可视化,并通过实例演示如何将数据可视化应用于数据分析和建模中。
第五章:数据分析方法数据分析是从数据中寻找有意义的模式、关系和规律的过程。
MATLAB提供了多种数据分析方法和函数,例如回归分析、聚类分析、主成分分析等。
本章将介绍这些常用的数据分析方法,并通过实例演示如何使用MATLAB进行数据分析和解释。
第六章:数据建模方法数据建模是根据已有数据构建数学模型,并利用该模型进行预测和决策的过程。
MATLAB提供了丰富的数据建模工具和函数,例如线性回归模型、支持向量机模型、神经网络模型等。
本章将介绍这些常用的数据建模方法,并通过实例演示如何使用MATLAB进行数据建模和预测。
第七章:模型评估和优化在进行数据建模之后,我们需要评估所建立的模型的准确性和可靠性,并对模型进行优化。
MATLAB数据分析方法第2章数据描述性分析

MATLAB数据分析⽅法第2章数据描述性分析2.1 基本统计量与数据可视化1.均值、中位数、分位数、三均值均值、中位数:mean(A)、media(A)分位数:prctile(A,P),P∈[0,100]prctile(A,[25,50,75]) %求A的下、中、上分位数三均值:w=[0.25,0.5,0.75];SM=w*prctile(A,[25,50,75])%例:计算安徽16省市森林资源统计量A=xlsread('senlin.xls','sheet1')M=mean(A); %均值,MD=median(A); %中位数SM=[0.25,0.5,0.25]*prctile(A,[25,50,75]); %三均值[M;MD;SM]2.⽅差、标准误、变异系数⽅差:var(A,flag),flag默认0表⽰修正的⽅差,取1为未修正标准差:std(A,flag),同上变异系数:v=std(A)./abs(mean(A))k阶原点矩、中⼼距:ak=mean(A.^k)bk=mean((A-mean(A)).^k)%中⼼距系统命令bk=moment(A,k)3.极差、四分位极差(上、下分位数之差)R=rangr(A)R1=iqr(A)4.异常点判别(截断点)XJ=parctile(A,[25])-1.5*R1SJ=parctile(A,[75])+1.5*R15.偏度、峰度偏度:sk=skewness(A,flag),默认1,取0为样本数据修正的偏度峰度:ku=kurtosis(A,flg)-3,同上2.1.2 多维样本数据协⽅差:cov(A)相关系数:corr(A)标准化:zscore(A)2.1.3 样本数据可视化1.条形图bar(x)%样本数据x的条形图,横坐标为1:length(x)bar(x,y)%先把x和y⼀⼀对应,然后将x从⼩到⼤排序画图2.直⽅图hist(x,n)%数据x的直⽅图,n为组数,确省时n=10[h,stats]=cdfplot(x)%x的经验分布函数图,stats给出数据最⼤最⼩值、中位数、均值、标准差直⽅图基础上附加正态密度曲线histfit(x)histfit(x,nbins)%nbins指定bar个数,缺省时为x中数据个数的平⽅根3.盒图,五个数值点组成:最⼩值、下四分位数、中位数、上四分位数、最⼤值。
第二章MATLAB数据及其运算

显然,linspace(a,b,n) =a:(b-a)/(n-1):b
17
矩阵元素的引用
方法一:通过下标(subscript)引用矩阵的元素
– 例如 A(3,2)=200
方法二:采用矩阵元素的序号(index)来引用矩阵元素。
例:利用M文件建立MYMAT矩阵
– (1) 启动有关编辑程序或MATLAB文本编辑器,并输入待建矩阵: MYMAT=[101,102,103,104,105,106,107,108,109; 201,202,203,204,205,206,207,208,209; 301,302,303,304,305,306,307,308,309];
主要内容 MATLAB 数据的特点 变量及其操作 MATLAB矩阵的表示 MATLAB数据的运算 字符串 结构数据和单元数据
1
MATLAB数据的特点
矩阵是MATLAB最基本、最重要的数据对象 – MATLAB的大部分运算或命令都是在矩阵运算的意义 下执行的
问题: – 单个数据如何用矩阵表示?x=5 – 1*1矩阵 – 向量如何用矩阵表示?a=[1,2,3] – 行向量:1*n矩阵;列向量:n * 1矩阵
A(1,2) = [ ] 出错!
A(1,2) = 0
可以
21
主要内容 MATLAB 数据的特点 变量及其操作 MATLAB矩阵的表示 MATLAB数据的运算 字符串 结构数据和单元数据
22
MATLAB数据的运算
算术运算
– 基本算术运算 » +(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方)
第2章--MATLAB数据及其运算-习题答案教学内容

第2章--M A T L A B数据及其运算-习题答案第2章 MATLAB数据及其运算习题2一、选择题1.下列可作为MATLAB合法变量名的是()。
D A.合计 B.123 C.@h D.xyz_2a 2.下列数值数据表示中错误的是()。
CA.+10 B.1.2e-5 C.2e D.2i3.使用语句t=0:7生成的是()个元素的向量。
A A.8 B.7 C.6 D.54.执行语句A=[1,2,3;4,5,6]后,A(3)的值是()。
B A.1 B.2 C.3 D.45.已知a为3×3矩阵,则a(:,end)是指()。
D A.所有元素 B.第一行元素C.第三行元素 D.第三列元素6.已知a为3×3矩阵,则运行a (1)=[]后()。
A A.a变成行向量 B.a变为2行2列C.a变为3行2列 D.a变为2行3列7.在命令行窗口输入下列命令后,x的值是()。
B >> clear>> x=i*jA.不确定 B.-1 C.1 D.i*j 8.fix(354/100)+mod(354,10)*10的值是()。
D A.34 B.354 C.453 D.439.下列语句中错误的是()。
BA.x==y==3 B.x=y=3C.x=y==3 D.y=3,x=y10.find(1:2:20>15)的结果是()。
CA.19 20 B.17 19C.9 10 D.8 911.输入字符串时,要用()将字符括起来。
C A.[ ] B.{ } C.' ' D." " 12.已知s='显示"hello"',则s的元素个数是()。
A A.9 B.11 C.7 D.1813.eval('sqrt(4)+2')的值是()。
BA.sqrt(4)+2 B.4 C.2 D.2, 214.有3×4的结构矩阵student,每个结构有name(姓名)、scores(分数)两个成员,其中scores是以1×5矩阵表示的5门课的成绩,那么要删除第4个学生的第2门课成绩,应采用的正确命令是()。
第2章 MATLAB数据及其运算.

8 1 d 3 5
(2)利用空矩阵删除矩阵的元素 a=[ ] a的维数为0。 例:a( 2 , : )= [ ]; 8 1 6 得: 3 5 7 a a= 4 9 2 8 1 6 4 9 2
2.3.5
复数(Com part)和虚部(imaginary part)组 成。 虚数单位用i或j来表示。 6+5i = 6+5j
format bank format rat
2.3 MATLAB矩阵的表示
2.3.1 矩阵 MATLAB中最基本的数据结构是矩阵(matrix)。 1*1的矩阵----标量(scalar): [5] 只有一行或一列的矩阵-----向量(vector): [1 3 5 7]
2 4 6 8
2.4 Matlab数据的运算(Operators ) 运算符(Operators )
+ Addition
*
Subtraction
Multiplication
/
\
Division
Left division
^
Power
2.4.1 算术运算 (1)矩阵加减运算: 两个同维矩阵,才能进行加减运算,对应无素相加减。 一个标量与矩阵相加减时,结果为这个标量与矩阵的 每一个元素相加减。 x=[2,-1,0;3 2 -4]; y=ones(2,3); x-y=? [1,-2,-1;2,1,-5] x+1=? [3,0,1;4,3,-3]
在线性代数中,本没有矩阵除法,它是由逆 矩阵引申来的。 MATLAB中,矩阵求逆(Matrix inverse)的函 数为: Y = inv(X) 方程A*X=B的解为:X=inv(A)*B=A\B, A\B称为A左除B,左除时要求两矩阵行数相等。 方程X*A=B的解为:X=B*inv(A)=B/A, A/B称为A右除B,右除时要求两矩阵列数相等。
MATLAB课件 第2章 MATLAB数据

ans =
27 79 45 8 10
2748795 10
>> reshape(A,8,1)
ans =
4. 建立大矩阵 大矩阵可由方括号中的小矩阵建立起来。例如
>> A=[1 2 3;4 5 6;7 8 9]; C=[A,eye(size(A)); ones(size(A)),A]
C= 123100 456010 789001 111123 111456 111789
eps:在决定诸如奇异性和秩时,可作为一个容许 误差,eps=2.22*10-16,用户也可将此变量置 为其它任何值。
pi:即л Inf:表示正无穷大,当输入1/0时会产生Inf NaN:表示不定值,它由Inf/Inf或0/0运算产生。
2.2.2 赋值语句 MATLAB赋值语句有两种格式: (1) 变量=赋值表达式 如:S=1+2*pi (2) 表达式 如:1+2*pi
几个产生特殊矩阵的函数:zeros、ones、 eye、 rand(均匀分布的随机矩阵,随机数均匀分布在 (0,1]内)、randn(正态分布的随机矩阵)。
这几个函数的调用格式相似,下面以产生零矩阵 的zeros函数为例进行说明。其调用格式是:
zeros(m)
产生m×m零矩阵
zeros(m,n) 产生m×n零矩阵。
如
>> format short %设置定点格式,显 示5位 >> pi
ans =
3.1416 >> format long %设置定点格式,显示 15位 >> pi
ans =
3.14159265358979
2.2.4 内存变量的管理 1. 内存变量的显示与删除 who和whos这两个命令用于显示在MATLAB工作空 间中已经驻留的变量名清单。 例:若要检视现存於工作空间(Workspace)的变数, 可键入who: <<who Your variables are: testfile x clear命令用于删除MATLAB工作空间中的变量。 注意,预定义变量不能被删除。
第2章 MATLAB数值计算

第2章 MATLAB数值计算MATLAB的数学计算=数值计算+符号计算其中符号计算是指使用未定义的符号变量进行运算,而数值计算不允许使用未定义的变量。
2.1 变量和数据2.1.1数据类型数据类型包括:数值型、字符串型、元胞型、结构型等数值型=双精度型、单精度型和整数类整数类=无符号类(uint8、uint16、uint32、uint64)和符号类整数(int8、int16、int32、int64)。
2.1.2数据1. 数据的表达方式▪可以用带小数点的形式直接表示▪用科学计数法▪数值的表示范围是10-309~10309。
以下都是合法的数据表示:-2、5.67、2.56e-56(表示2.56×10-56)、4.68e204(表示4.68×10204)2. 矩阵和数组的概念在MATLAB的运算中,经常要使用标量、向量、矩阵和数组,这几个名称的定义如下:▪标量:是指1×1的矩阵,即为只含一个数的矩阵。
▪向量:是指1×n或n×1的矩阵,即只有一行或者一列的矩阵。
▪矩阵:是一个矩形的数组,即二维数组,其中向量和标量都是矩阵的特例,0×0矩阵为空矩阵([])。
▪数组:是指n维的数组,为矩阵的延伸,其中矩阵和向量都是数组的特例。
3. 复数复数由实部和虚部组成,MATLAB用特殊变量“i”和“j”表示虚数的单位。
复数运算不需要特殊处理,可以直接进行。
复数可以有几种表示:z=a+b*i或z=a+b*jz=a+bi 或z=a+bj(当b 为标量时) z=r*exp(i*theta)● 得出一个复数的实部、虚部、幅值和相角。
a=real(z) %计算实部 b=imag(z) %计算虚部 r=abs(z) %计算幅值 theta=angle(z) %计算相角 说明:复数z 的实部a=r*cos(θ); 复数z 的虚部b=r*sin(θ); 复数z 的幅值22b a r +=;复数z 的相角theta=arctg(b/a),以弧度为单位。
MATLAB实验报告第二章
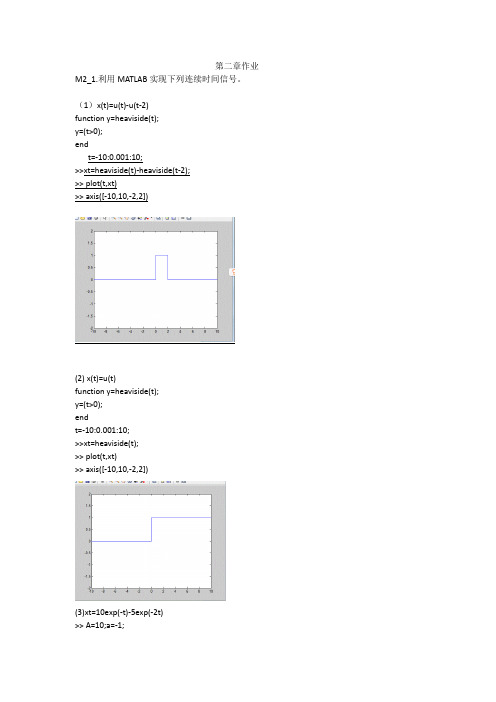
第二章作业M2_1.利用MATLAB实现下列连续时间信号。
(1)x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)(5)xt=2|sin(10pit+pi/3)| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3,写出书中图示波形函数,并画出xt,x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。
数据分析方法MATLAB实现ppt课件

MATLAB数据分析方法(机械工业出版社)
第2章 数据描述性分析
5/24
虽然均值与中位数都是描述数据集中位置的
数字特征,但是均值用了数据的全部信息,中位数
只用了部分信息(位置信息),因此通常情况下均
值比中位数有效.当数据有异常值时,中位数比较
稳健。为了兼顾两者的优势,因此人们提出三均值
17/24
例2.1.3 根据2007年华东地区各高校教职工数据, 计算专任教师、 行政人员、教辅人员以及工勤人
员占在职教工的百分比,以及百分比的极差、四分 位极差以及上、下截断点.
表2.4 2007年华东地区各高校教职工数据
地 区 在职教工 专任教师 行政人员 教辅人员
上海 江苏 浙江 安徽 福建
61385 134215 67763 59149 47864
第2章 数据描述性分析
1/24
第2章 数据描述性分析
数据描述性分析是从样本数据出发,概括分析数
据的集中位置、分散程度、相互关联关系等,分析数 据分布的正态或偏态特征.描述性分析是进行数据进一 步分析的基础.对不同类型量纲的数据有时还要进行变 换,然后再作出合理分析.本章主要介绍样本数据的基 本统计量、数据的可视化、数据分布检验及数据变换 等内容.
v s / x,或 s / | x | (2.1.9) 变异系数是一个无量纲的量,一般用百分数表示. 在MATLAB中,计算方差命令var,调用格式
S=var(x); 计算标准差命令std,调用格式
d=std(x) 其中输入x是样本数据,输出S为方差,d为标准差.当 输入x是矩阵时,输出x每列数据的方差与标准差. 由均值与方差命令,可设计变异系数的计算程序为 v=std(x)./mean(x),或者v=std(x)./abs(mean(x)) 当输入x是矩阵时,输出x每列数据的变异系数.
第2章 MATLAB数据

例2.4 产生5阶随机方阵 A,其元素为[10,90]区间 的随机整数,然后判断A 的元素是否能被3整除。
(1) 生成5阶随机方阵A。
A=fix((90-10+1)*rand(5)+10)
(2) 判断A的元素是否可 以被3整除。 P=rem(A,3)==0
2.4.3 逻辑运算 MATLAB 提 供 了 3 种 逻 辑运算符:&(与)、|(或) 和~(非)。
与字符串有关的另一个重要函 数是eval,其调用格式为: eval(t) 其中t为字符串。 它的作用是把字符串的内容作 为对应的MATLAB语句来执行。
例如: t=pi; m='[t,sin(t),cos(t)]'; y=eval(m)
2.6 结构和单元
2.6.1 结构数据
MATLAB通过使用结构 (Structure)数据类型把一组不 同类型的数据同时又是在逻辑上 相关的数据组成一个有机的整体, 以便于管理和引用。
2.MATLAB数据类型
MATLAB的数据类型
Array
char
numeric double
cell
struct user object
2.2 变量和赋值
2.2.1 变量的命名
作为一种编程语言,MATLAB也具 有与其它计算机语言类似的变量命名 规则: » 变量名大小写区别对待; » 变量名以字母开头,由字母、数 字、下划线组成; » 变量名长度不超过19个字符,第 19个字符之后的字符被忽略。
2.3.2 冒号表达式 冒号表达式的一般格式: e1:e2:e3 还可以用linspace函数产生 行向量:linspace(a,b,n) linspace(a,b,n)与a:(b-a)/(n1):b等价。
matlab-第二章

1,在一个MA TLAB命令中,6+7i和6+7*i有何区别?i和I有何区别?第一个i代表一个变量,6+7i是一个函数,第二个代表虚数,6是实部,7代表虚步.I只代表变量.2,.设A和B是两个同大小的矩阵,试分析A*B和A.*B、A./B和B.\A、A/B和B/A的区别?如果A和B是两个标量数据,结论又如何?A *B是矩阵相乘,A.*B表示A和B单个元素之间对应相乘。
A./B和B.\A值相等,是一样的。
A/B等效于B的逆右乘A的矩阵,B\A等效于B矩阵逆左乘A矩阵。
如果A和B是两个标量数据,结论是都没有区别。
3,写出完成下列操作的命令。
(1)删除矩阵A的第7号元素A(7)=[](2)将向量t的0元素用机器零来代替t(find(t==0))=eps(3)将含有12个元素的向量x转换成3*4矩阵newA=reshape(A,3,4)(4) 求一个字符串的ASCIIch=['a b c';'1 2 3'];abs ch(5) 产生和A同样大小的幺矩阵ones(size(A))(6) 从矩阵A提取主对角线元素,并以这些元素构成对角阵B。
A=[1 2 3;4 5 6;7 8 9];D=diag(A)B=diag([1,5,9])4, .要生产均值为3,方差为1的500个正态分布的随机序列,写出相应的表达式y=3+sqrt(1)*randn(500)5,(1)主对角元素1 1 5 9上三角矩阵1 -1 2 30 1 -4 20 0 5 20 0 0 9下三角矩阵1 0 0 05 1 0 03 0 5 011 15 0 9逆矩阵-0.1758 0.1641 0.2016 -0.0227-0.1055 -0.1016 -0.0391 0.0664-0.0508 -0.0859 0.1516 0.00230.3906 -0.0313 -0.1813 0.0281行列式的值1280秩4范数A1=norm(A,1)=20 A2=norm(A)= 21.3005 A3=norm(A,inf)=35条件数A1=cond(A,1)= 14.4531 A2=cond(A,2)= 11.1739 A3=cond(A,inf)= 22.0938迹16(2)主对角元素0.43 4上三角矩阵0.4300 43.0000 2.00000 4.0000 21.0000下三角矩阵0.4300 0 0-8.9000 4.0000 0逆矩阵0.0022 -0.01750.0234 -0.0017-0.0035 0.0405行列式的值秩2范数B1=norm(B,1)= 47 B2=norm(B)= 43.4271 B3=norm(B,inf)= 45.4300 条件数B2=cond(B,2)= 1.9354迹4.43006,all(A)=0any(A)=1isnan(A)= 0 1 0 0 0 0 0isinf(A)= 0 0 1 1 0 0 0isfinite(A)= 1 0 0 0 1 1 1。
MATLAB第二章实验报告

MATLAB数据及基本操作班级:11电信一班姓名:何得中学号:20111060108实验目的:1.熟悉MATLAB的组体成体系及工作环境;2.了解MATLAB的帮助系统;3.掌握MATLAB的数据类型及变量的基本操作;4.掌握矩阵建立的基本方法及其运算;5.掌握矩阵索引与分析方法;6.熟悉字符串单元及结构数据的建立及基本操作。
实验仪器:MA TLAB软件,电脑实验数据:>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> A=[1 2 34 5 67 8 9]A = 1 2 34 5 67 8 9>> x=0:pi/8:2*pi;>> y=cos(x)y = Columns 1 through 101.0000 0.9239 0.7071 0.3827 0.0000 -0.3827 -0.7071 -0.9239 -1.0000 -0.9239Columns 11 through 17-0.7071 -0.3827 -0.0000 0.3827 0.7071 0.9239 1.0000>> B=ones(3,5)B = 1 1 1 1 11 1 1 1 11 1 1 1 1>> zeros(3)ans = 0 0 00 0 00 0 0>> C=rand(3,4)C = 0.9501 0.4860 0.4565 0.44470.2311 0.8913 0.0185 0.61540.6068 0.7621 0.8214 0.7919>> D=randn(2,3)D = -0.4326 0.1253 -1.1465-1.6656 0.2877 1.1909>> eye(3)ans = 1 0 00 1 00 0 1>> M=magic(4)M = 16 2 3 135 11 10 89 7 6 124 14 15 1>> T=toeplitz(1:5,1:6)T = 1 2 3 4 5 62 1 234 53 2 1 2 3 44 3 2 1 2 35 4 3 2 1 2>> H=hilb(5)H = 1.0000 0.5000 0.33330.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111>> a=3:18a =3 4 5 6 7 8 9 10 1112 13 14 15 16 17 18>> b=1:0.2:6b =Columns 1 through 91.0000 1.2000 1.4000 1.600 1.80002.0000 2.2000 2.4000 2.6000 Columns 10 through 182.80003.0000 3.2000 3.40003.6000 3.80004.0000 4.2000 4.4000 Columns 19 through 264.6000 4.80005.0000 5.20005.4000 5.6000 5.80006.0000>> linspace(1,15,10)ans =Columns 1 through 91.00002.5556 4.1111 5.6667 7.2222 8.7778 10.3333 11.8889 13.4444Column 1015.0000>> y=[0.9 0.3 0.4 0.1 0.5 0.6 0.2 ]; >> [sorted,index]=sort(y)sorted =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.9000 index =4 7 2 3 5 6 1>> A=rand(4,5)A = 0.9218 0.9355 0.0579 0.13890.27220.7382 0.9169 0.3529 0.2028 0.19880.1763 0.4103 0.8132 0.1987 0.01530.4057 0.8936 0.0099 0.6038 0.7468>> [a,b]=min(A)a =0.1763 0.4103 0.0099 0.13890.0153b = 3 3 4 1 3>> min(A(:))ans = 0.0099>> V=[1 2 3 4]V = 1 2 3 4>> norm(V,2)ans =5.4772>> norm(V,1)ans = 10>> norm(V,inf)ans = 4>> V=[2 5 6 8 4 9]V = 2 5 6 8 4 9>> min(V)ans = 2>> V=[4 9 6;7 8 9;4 5 6]V = 4 9 67 8 94 5 6>> min(V)ans = 4 5 6>> max(V)ans = 7 9 9>> mean(V)ans = 5.0000 7.3333 7.0000>> median(V)ans = 4 8 6>> std(V)ans = 1.7321 2.0817 1.7321>> diff(V)ans =3 -1 3-3 -3 -3>> sort(V)ans =4 5 64 8 67 9 9>> length(V)ans = 3>> norm(V)ans =19.9125>> sum(V)ans = 15 22 21>> prod(V)ans =112 360 324>> cumsum(V)ans = 4 9 611 17 1515 22 21 >> cumprod(V)ans = 4 9 628 72 54112 360 324>> V=[1 2 8]V = 1 2 8>> U=[3; 4;7]U = 347>> dot(V,U)ans =67>> cross(V,U)ans =-18 17 -2>> A=[5 6 4;7 8 9;4 5 6]A = 5 6 47 8 94 5 6>> B=[6 2 7 ;7 5 8;4 6 8]B = 6 2 77 5 84 6 8>> C=A-BC = -1 4 -30 3 10 -1 -2>> C=A*BC = 88 64 115134 108 18583 69 116>> C1=A\BC1 =0.6667 -6.4444 -7.66670.6667 4.8889 7.3333-0.3333 1.2222 0.3333>> C2=B/AC2 = -3.0000 8.3333 -9.3333-1.6667 5.5556 -5.88890.0000 -1.3333 3.3333>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> D=A^2D = 30 36 4266 81 96102 126 150>> E=A^0.1E = 0.8466 + 0.2270i 0.3599 + 0.0579i -0.0967 - 0.1015i0.4015 + 0.0216i 0.4525 + 0.0133i 0.4432 - 0.0146i-0.0134 - 0.1740i 0.4848 - 0.0509i 1.0132 + 0.0820i>> A=[1+2*i 3;4 2+i]A =1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A'ans = 1.0000 - 2.0000i 4.00003.0000 2.0000 - 1.0000i>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> B=[3 4 6;7 9 8;5 2 01]B = 3 4 67 9 85 2 1>> C=A.*BC = 3 8 1828 45 4835 16 9>> D=A./BD = 0.3333 0.5000 0.50000.5714 0.5556 0.75001.4000 4.0000 9.0000>> E=A.\BE = 3.0000 2.0000 2.00001.7500 1.8000 1.33330.7143 0.2500 0.1111>> A=[1+2*i 3;4 2+i]A = 1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A.^2ans = -3.0000 + 4.0000i 9.000016.0000 3.0000 + 4.0000i>> A.'ans = 1.0000 + 2.0000i 4.00003.0000 2.0000 + 1.0000i>> x=0.1:0.1:0.8x =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> y=sin(2*x).*cos(2*x)y =0.1947 0.3587 0.4660 0.4998 0.4546 0.3377 0.1675 -0.0292>> y=sin(x)y =0.0998 0.1987 0.2955 0.3894 0.4794 0.5646 0.6442 0.7174>> y=cos(x)y =0.9950 0.9801 0.9553 0.9211 0.8776 0.8253 0.7648 0.6967>> y=tan(x)y =0.1003 0.2027 0.3093 0.4228 0.5463 0.6841 0.8423 1.0296>> y=cot(x)y =9.9666 4.9332 3.2327 2.3652 1.8305 1.4617 1.1872 0.9712>> y=sec(x)y = 1.0050 1.0203 1.0468 1.0857 1.1395 1.2116 1.3075 1.4353>> y=csc(x)y = 10.0167 5.0335 3.3839 2.5679 2.0858 1.7710 1.5523 1.3940>> y=asin(x)y = 0.1002 0.2014 0.3047 0.4115 0.5236 0.6435 0.7754 0.9273>> y=acos(x)y = 1.4706 1.3694 1.2661 1.1593 1.0472 0.9273 0.7954 0.6435>> y=atan(x)y =0.0997 0.1974 0.2915 0.3805 0.4636 0.5404 0.6107 0.6747>> y=acot(x)y = 1.4711 1.3734 1.2793 1.1903 1.1071 1.0304 0.9601 0.8961>> y=asec(x)y =Columns 1 through 60 + 2.9932i 0 + 2.2924i0 + 1.8738i 0 + 1.5668i 0 +1.3170i 0 + 1.0986iColumns 7 through 80 + 0.8956i 0 + 0.6931i>> y=sinh(x)y =0.1002 0.2013 0.3045 0.4108 0.5211 0.6367 0.7586 0.8881>> y=cosh(x)y =1.0050 1.0201 1.0453 1.0811 1.1276 1.1855 1.2552 1.3374>> y=tanh(x)y = 0.0997 0.1974 0.2913 0.3799 0.4621 0.5370 0.6044 0.6640>> y=coth(x)y = 10.0333 5.0665 3.4327 2.6319 2.1640 1.8620 1.6546 1.5059>> y=sech(x)y = 0.9950 0.9803 0.9566 0.9250 0.8868 0.8436 0.7967 0.7477>> y=csch(x)y = 9.9834 4.9668 3.2839 2.4346 1.9190 1.5707 1.3182 1.1260>> y=asinh(x)y = 0.0998 0.1987 0.2957 0.3900 0.4812 0.5688 0.6527 0.7327>> y=acosh(x)y =Columns 1 through 60 + 1.4706i 0 + 1.3694i0 + 1.2661i 0 + 1.1593i 0 +1.0472i 0 + 0.9273iColumns 7 through 80 + 0.7954i 0 + 0.6435i>> y=atanh(x)y = 0.1003 0.2027 0.3095 0.4236 0.5493 0.6931 0.8673 1.0986>> y=acoth(x)y = Columns 1 through 60.1003 + 1.5708i 0.2027 + 1.5708i 0.3095 + 1.5708i 0.4236 + 1.5708i 0.5493 + 1.5708i 0.6931 + 1.5708i Columns 7 through 80.8673 + 1.5708i 1.0986 + 1.5708i >> y=asech(x)y = 2.9932 2.2924 1.8738 1.5668 1.3170 1.0986 0.8956 0.6931>> y=acsch(x)y = 2.9982 2.3124 1.9189 1.6472 1.4436 1.2838 1.1545 1.0476>> y=log(x)y =-2.3026 -1.6094 -1.2040 -0.9163 -0.6931 -0.5108 -0.3567 -0.2231>> y=log10(x)y = -1.0000 -0.6990 -0.5229 -0.3979 -0.3010 -0.2218 -0.1549 -0.0969>> y=log2(x)y =-3.3219 -2.3219 -1.7370 -1.3219 -1.0000 -0.7370 -0.5146 -0.3219>> c=complex(a,b)c = 0.1763 + 3.0000i 0.4103 + 3.0000i0.0099 + 4.0000i 0.1389 + 1.0000i 0.0153 + 3.0000i>> zc=conj(x)zc =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> b=imag(x)b = 0 0 0 0 0 00 0>> a=real(x)a = 0.1000 0.2000 0.3000 0.40000.5000 0.6000 0.7000 0.8000>> y=fix(x)y = 0 0 0 0 0 0 0 0>> y=floor(x)y =0 0 0 0 0 0 0 0 >> y=ceil(x)y = 1 1 1 1 1 1 1 1>> y=round(x)y = 0 0 0 0 1 1 1 1>> y=sign(x)y = 1 1 1 1 1 1 1 1>> S=rats(x)S =1/10 1/5 3/10 2/5 1/2 3/5 7/10 4/5>> [N,D]=rat(x)N = 1 1 3 2 1 37 4D = 10 5 10 5 2 510 5>> A=[2 4 6;3 5 7;8 10 9]A = 2 4 63 5 78 10 9>> B=[4 1 5;7 5 0;9 3 6]B = 4 1 57 5 09 3 6>> A>Bans = 0 1 10 0 10 1 1>> A<Bans = 1 0 01 0 01 0 0>> A>=Bans = 0 1 10 1 10 1 1>> A<=Bans = 1 0 01 1 01 0 0>> A==Bans = 0 0 00 1 00 0 0>> A~=Bans =1 1 11 0 11 1 1>> A&Bans = 1 1 11 1 01 1 1>> A|Bans = 1 1 11 1 11 1 1>> ~Aans = 0 0 00 0 00 0 0>> ~Bans = 0 0 00 0 10 0 0>> x=0:pi/100:3*pi;>> y=sin(x);>> plot(x,y);>> y1=(x<pi|x>2*pi).*y;>> figure,plot(x,y1);>> r=(x>pi/3&x<2*pi/3)|(x>7*pi/3&8*pi/3);>> rn=~r;>> y2=r*sin(pi/3)+rn.*y1;>> figure,plot(x,y2)>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x =0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> all(x)ans =0>> any(x)ans = 1>> find(x)ans =2 3 4 5 6 7 8 9 10 11 12 13 14 15>> isempty(x)ans =>> isglobal(x)Warning: isglobal is obsolete and will be discontinued. Type "help isglobal" for more details.ans =0>> isinf(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isnan(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isfinite(x)ans =1 1 1 1 1 1 1 1 1 1 1 1 1 1 1>> issparse(x)ans = 0>> isstr(x)ans =0>> not(x)ans =1 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y =59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y = 59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x = 0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> A=[4 -40 2; 23 50 17;18 29 14]A = 4 -40 223 50 1718 29 14>> [r,c]=find(A>=20&A<=30)r = 23c = 12>> bitand(12,6)ans = 4>> bitshift(12,1)ans = 24>> bitxor(12,1)ans =13>> bitset(12,1)ans = 13 >> bitget(12,1)ans =0>> A =[ 87 59 56 85 66 21 12 35 62 64 69 88 99 81]A =87 59 56 85 66 21 1235 62 64 69 88 99 81>> A(2)ans =59>> A([1,2,8])ans =87 59 35>> A([9,6,2])ans =62 21 59>> A([end-4:end])ans =64 69 88 99 81>> A([1:5,5:-1:1])ans = 87 59 56 85 66 66 85 56 59 87>> A(3)=-1A = 87 59 -1 85 66 2112 35 62 64 69 88 99 81>> A(15)=-8A =87 59 -1 85 66 2112 35 62 64 69 88 99 81 -8>> A(20)=-1A = Columns 1 through 1687 59 -1 85 66 21 12 35 62 64 69 88 99 81 -8 0Columns 17 through 200 0 0 -1>> A=rand(8)A = 0.9501 0.8214 0.9355 0.13890.4451 0.8381 0.3046 0.37840.2311 0.4447 0.9169 0.2028 0.9318 0.0196 0.1897 0.86000.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.85370.4860 0.7919 0.8936 0.6038 0.4186 0.3795 0.6822 0.59360.8913 0.9218 0.0579 0.2722 0.8462 0.8318 0.3028 0.49660.7621 0.7382 0.3529 0.1988 0.5252 0.5028 0.5417 0.89980.4565 0.1763 0.8132 0.0153 0.2026 0.7095 0.1509 0.82160.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3,3)ans =0.4103>> A(8)ans =0.0185>> sub2ind(size(A),3,3)ans =19>> [i,j]=ind2sub(size(A),19)i =3j =3>> A(:,4)ans =0.13890.20280.19870.60380.27220.19880.01530.7468>> A(3,:)ans =0.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.8537>> A(end,:)ans =0.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3:4,5:6)ans =0.4660 0.68130.4186 0.3795>> A(2:2:4,1:2:5)ans =0.2311 0.9169 0.93180.4860 0.8936 0.4186>> A=reshape(A,5,5)A = 1 6 11 16 212 7 12 17 223 8 13 18 234 9 14 19 245 10 15 20 25>> A(:)'ans =Columns 1 through 161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 17 through 2517 18 19 20 21 22 23 24 25>> A(:,1:2:5)=[]A = 6 167 178 189 1910 20>> A=[9 8 7;6 5 4;3 2 1];>> D=diag(A)D =951>> D1=diag(A,1)D1 =84>> D2=diag(A,-1)D2 =62>> V=[1 2 3 4];>> diag(V)ans = 1 0 0 00 2 0 00 0 3 00 0 0 4>> diag(1:3,-1)ans = 0 0 0 01 0 0 00 2 0 00 0 3 0>>A=[17,1,0,15;5,7,14,16;4,0,13,0;10,12,19,21]; >> D=diag(4:-1:1);>> D*Aans = 68 4 0 6015 21 42 488 0 26 010 12 19 21>> triu(A)ans =17 1 0 150 7 14 160 0 13 00 0 0 21>> triu(A,1)ans = 0 1 0 150 0 14 160 0 0 00 0 0 0>> B=A'B =17 5 4 101 7 0 120 14 13 1915 16 0 21>> rot90(A)ans =15 16 0 210 14 13 191 7 0 1217 5 4 10>> rot90(A,3)ans =10 4 5 1712 0 7 119 13 14 021 0 16 15>> B=fliplr(A)B = 15 0 1 1716 14 7 50 13 0 421 19 12 10>> B=flipud(A)B = 10 12 19 214 0 13 05 7 14 1617 1 0 15>> A=[4 5 6 9;7 8 9 5;4 5 6 9;7 8 9 5]; >> det(A)ans =0>> rank(A)ans =2>> cond(A)ans =1.0968e+017>> inv(A)Warning: Matrix is singular to working precision.ans = Inf Inf Inf InfInf Inf Inf InfInf Inf Inf InfInf Inf Inf Inf>> A=[4 8 9;8 2 7;6 3 8];>> inv(A)ans = 0.0568 0.4205 -0.43180.2500 0.2500 -0.5000-0.1364 -0.4091 0.6364>> [V,D]=eig(A)V = -0.6438 -0.7444 -0.5061-0.5467 0.6392 -0.5515-0.5354 0.1931 0.6631D = 18.2776 0 00 -5.2030 00 0 0.9254>> [U,S,D]=svd(A)U = -0.6378 0.7375 -0.2220-0.5426 -0.6348 -0.5500-0.5465 -0.2304 0.8051S = 18.9278 0 00 5.2884 00 0 0.8791D = -0.5374 -0.6639 -0.5200-0.4135 0.7449 -0.5236-0.7350 0.0663 0.6749>> [L,U]=lu(A)L = 0.5000 1.0000 01.0000 0 00.7500 0.2143 1.0000U = 8.0000 2.0000 7.00000 7.0000 5.50000 0 1.5714>> [Q,R]=qr(A)Q = -0.3714 0.9114 -0.1774-0.7428 -0.4063 -0.5322-0.5571 -0.0659 0.8278 R =-10.7703 -6.1279 -12.99870 6.2808 4.83140 0 1.3009>> a=1234a = 1234>> class(a)ans =double>> size(a)ans = 1 1>> b='1234'b =1234>> class(b)ans =char>> size(b)ans = 1 4>> 'I am astudent'ans =I am astudent>> a='This is No.2.23 Example!'a =This is No.2.23 Example!>> b=a(1:7)b =This is>> c=a(12:end)c =2.23 Example!>> a='Good';>> b='Noon';>> length(a)==length(b)ans = 1>> c=[a,'',b]c =GoodNoon>> d=[a;b]d =GoodNoon>> size(c)ans = 1 8>> size(d)ans = 2 4>> a='Good Noon';>> b=double(a)b = 71 111 111 100 32 78 111 111 110>> c='再见!'c =再见!>> c='再见!'>> d=double(c)d = 20877 35265 65281>> char(d)ans =再见!>> a='The first string';>> b='The second string';>> c=strcmp(a,b)c =0>> d=strncmp(a,b,4)d =1>> X='A friend in need is a friend indeed'; >> Y='friend';>> a=findstr(Y,X)a = 3 23>> b=strfind(Y,X)b = []>> S=['1 2 3';'2 3 4'];>> A=str2num(S)A = 1 2 32 3 4>> B=str2num('6-8i')B = 6.0000 - 8.0000i>> D=num2str(rand(2,3),6)D =0.950129 0.606843 0.8912990.231139 0.485982 0.762097>> d=189;>> h=dec2hex(d)h =BD>> c=dec2base(d,7)c =360>> b=dec2bin(d)b =10111101>> bin2dec(b)ans = 189>> A={ones(3,3,3),'Welcome';30.34,1:200} A = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>>B=[{ones(3,3,3)},{'Welcome'};{30.34},{1:20 0}]B = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>> C={5}C = [5]>> C(2,3)={7}C = [5] [] [][] [] [7]>> isequal(A,B)ans =1>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> b=A(1,2)b = 'Welcome'>> class(B)ans =cell>> C=A{1,2}C =Welcome>> class Cans =char>> D=A{1,2}(6)D =m>> E=A{2,2}([end:-1:190])E =200 199 198 197 196 195 194 193 192 191 190>> class(E)ans =double>> N=A{3}([1 3 5 7])N =Wloe>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> B=cell(2);>> B(:,1)={char('Good','Morning');1:10}B = [2x7 char ] [][1x10 double] []>> C=[A,B]C = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D=[A,B;C]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D(4,:)=[]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] []>> E=reshape(D,2,3,2)E(:,:,1) = [3x3x3 double] [3x3x3 double] [1x200 double][ 30.3400] 'Welcome' 'Welcome'E(:,:,2) = [2x7 char ] [2x7 char] [][1x10 double] [] []>>A={randn(3,3,2),'Good',pi;29,4+7*i,zeros(4)} A = [3x3x2 double] 'Good' [ 3.1416][ 29] [4.0000+ 7.0000i] [4x4 double]>> B=cellfun('isreal',A)B = 1 1 11 0 1>> C=cellfun('length',A)C = 3 4 11 1 4>> Member.code='09021';>> ='Liu';>> Member.age=22;>> Member.grade=uint16(3);>> MemberMember =code: '09021'name: 'Liu'age: 22grade: 3>> Member(4).name='Wang';>> Member(4).grade=2;>> Member(2)ans = code: []name: []age: []grade: []>>Memebr=struct('code','09021','name','Liu','a ge',22,'grade',uint16(3))Memebr = code: '09021'name: 'Liu'age: 22grade: 3>>Member=struct('code',{'09021','09034'},'name' ,{'Liu','Wamg'},'age',{22,24},'grade',{2,3}) Member = 1x2 struct array with fields:codenameagegrade>>Member=struct('code',{},'name',{},'age',{},'gr ade',{})Member = 0x0 struct array with fields:codenameagegrade>>Member=struct('code',{'09021','09034'},'na me',{'Liu','Wang'},'age',{22,24},'grade',{2,3},' score',{[78 89;90 68],[91 76;89 97]}) Member = 1x2 struct array with fields:codenameagegradescore>> Member(1).scoreans =78 8990 68>> Member(2).score(2,:)ans =89 97>> Member.codeans =09021ans =09034>> Member.('name')ans =Liuans =Wang>> ='Liu';M.ID=1;>> M(2,2).name='Wang';M(2,2).ID=2; >> M2=setfield(M,{2,1},'name','Zhang'); >> ans =Liuans =[]ans = []ans =Wang>> ans =Liuans =Zhangans = []ans =Wang>> fieldnames(M)ans = 'name''ID'>> M3=orderfields(M)M3 = 2x2 struct array with fields:IDname。
第2章MATLAB的基本语法课件

handmard
Handmard矩 rosser 阵
hankel hilb invhilb
Hankel矩阵 toeplize Hilbert矩阵 vander
Hilbert逆矩 wilkinson 阵
魔方矩阵
Pascal矩阵
经典的对称 特征值测试 矩阵 Toeplize矩阵
Vanderm阵
此外,常用的函数还有reshape(A,m,n),它在 矩阵总元素保持不变的前提下,将矩阵A重新 排成m×n的二维矩阵。
4. 建立大矩阵 大矩阵可由方括号中的小矩阵建立起来。 例如
A=[1 2 3;4 5 6;7 8 9]; C=[A,eye(size(A)); ones(size(A)),A]
C=
3. 内存变量文件 ❖利用MAT文件(.mat)可以把当前MATLAB
工作空间中的一些有用变量长久地保留下 来。
❖MAT文件的生成和装入由save和load命令 来完成。常用格式为:
save 文件名 [变量名表] [-append][-ascii]
load 文件名 [变量名表] [-ascii]
2.3 MATLAB矩阵
• 数据输出时用户可以用format命令设置或改 变 数 据 输 出 格 式 。 format 命 令 的 格 式 为 : format 格式符
• 注意,format命令只影响数据输出格式,而 不影响数据的计算和存储。
2.2.4 预定义变量
在MATLAB工作空间中,还驻留几个由 系统本身定义的变量。它们有特定的含 义,在使用时,应尽量避免对这些变量 重新赋值。
❖ 变量的元素用圆括号“( )”中的数字 (下标)表示。一维矩阵(数组)中的
元素用一个下标表示;二维矩阵用两个 下标表示,以逗号分开
Matlab基础及其应用 第2章 MATLAB数据对象

y=
0.5690 + 1.3980i
2.2 变量及其操作
2.2.1 变量与赋值
3.预定义变量
MATLAB基础与应用教程
2.2 变量及其操作
MATLAB基础与应用教程
2.2.2 变量的管理
1.内存变量的显示与修改
who函数按字母顺序列出当前工作区中的所有变量,whos函 数工作区中按字母顺序列出当前工作区中的所有变量及大小、 类型。
2.2 变量及其操作
MATLAB基础与应用教程
2.2.1 变量与赋值
1.变量命名 在MATLAB中,变量名是以字母开头,后跟字母、数字或下划 线的字符序列,最多63个字符。 变量名区分字母的大小写。 不能使用MATLAB的关键字作为变量名。
2.2 变量及其操作
MATLAB基础与应用教程
2.2.1 变量与赋值
构建二维字符数组可以使用创建数值数组相同的方法matlab基础与应用教程25字符数据及操作251字符向量与字符数组matlab还有许多与字符处理有关的函数matlab基础与应用教程25字符数据及操作例22建立一个字符串向量然后对该向量做如下处理
MATLAB基础与应用教程
第2章 MATLAB数据对象
【本章学习目标】 掌握MATLAB数据对象的特点。 掌握变量的创建与管理。 掌握矩阵的生成、转换与运算。 掌握MATLAB基本的运算规则。
0 -2 -4 -6 -8
2.3 MATLAB数组
MATLAB基础与应用教程
2.3.1 构造数组
2.构造行向量 用linspace函数构建线性等间距的行向量,logspace函数构 建对数等间距的行向量: linspace(a, b, n) logspace(a, b, n) 其中,参数a和b是生成向量的第1个和最后1个元素,选项n 指定向量元素个数。当n省略时,默认生成100个元素。
MATLAB第二章

function [egg1,egg2,chicken1]=myegg(n)
% egg1 隔1天的蛋个数 % egg2 隔2天的蛋个数 % chicken1 过n天后母鸡个数 if n==1
egg1=1; egg2=0; chicken1=1; elseif n==2 egg1=1; egg2=1; chicken1=1;
27
>> x=0:0.1:2*pi; >> y=sin(x); >> plot(x,y) >> plot(x,y,‘ro’) %默认是蓝色曲线 >> x=[0 1 2 5];y=[4 -2 1 2]; >> plot(x,y) >> fplot(‘x^2+4*x+1’,[-15 15]) %函数用字符串表示
1 -8 4 9 -4 5 7 -9 >> fun=@myfun5 %例28中的函数 fun =
@myfun5 >> y=fun(A) %直接调用 y=
1 -13 16 81 -5 25 49 -15 >> y=feval(fun,A) %利用feval y=
1 -13 16 81 -5 25 49 -15
1 4 9 16 5 10 15 20
2024/7/5
第二章 MATLAB编程与作图
24
>> k=5;
>> ff=@(x)x^2+2*x+k %可以使用空间中的变量k
ff =
@(x)x^2+2*x+k
>> ff(5)
ans =
40
>> A=[1 2 ;3 4]
MATLAB实用教程第二章

1.矩阵的合并
矩阵的合并就是把两个或者两个以上的矩阵 连接成一个新矩阵矩阵构造符 可用于构造矩阵并 可以作为一个矩阵合并操作符 ➢ 表达式C=A B在水平方向合并矩阵A和B; ➢ 表达式C=A;B在竖直方向合并矩阵A和B
具有相同行数的两个矩阵合并为一个新矩阵
12 34 56 3×2
1.访问单个元素
2.线性引用元素
➢ 对于矩阵A线性引用元素的格式为 Ak通常这样的引用用于行向量或列 向量但也可用于二维矩阵
➢ MATLAB按列优先排列的一个长列向量格 式线性引用元素来存储矩阵元素
3.访问多个元素
操作符:可以用来表示矩阵的多个元 素若A是二维矩阵其主要用法如下: ➢ A:: 返回矩阵A的所有元素 ➢ Ai: 返回矩阵A第i行的所有元素
3.用满矩阵和稀疏矩阵存储方式分别构造下述矩 阵:
4.采用向量构造符得到向量159…41 5.按水平和竖直方向分别合并下述两个矩阵:
6. 分别删除第5题两个结果的第2行 7. 分别将第5题两个结果的第2行最后3列的数值
改为11 12 13 8. 分别查看第5题两个结果的各方向长度 9. 分别判断pi是否为字符串和浮点数 10.分别将第5题两个结果均转换为29的矩阵 11.计算第5题矩阵A的转秩 12.分别计算第5题矩阵A和B的A+B、A.* B和
行运算; ➢ 不同优先级的运算符采用先进行优先高的
运算
运算符的优先等级表
由表中可以看到括号的优先级别最高因此可 以用括号来改变默认的优先等级
2.4 字符串处理函数
2.4.1 字符串的构造 2.4.2 字符串的比较 2.4.3 字符串的查找和替换 2.4.4 字符串与数值间的转换
第2章 MATLAB应用基础-1

14
• 相反,char函数可以把ASCII码矩阵转换为字符 重新调整矩阵的行数、 串矩阵。 列数、维数
• 例如 显示一个3行32列的ASCII 字符变量串: ascii = char(reshape(32:127,32,3)') 输出结果为 表示转置 ascii = !"#$%&'()*+,-./0123456789:;<=> ? @ABCDEFGHIJKLMNOPQRSTUV WXYZ[\]^_ 'abcdefghijklmnopqrstuvwxyz{|}~
矩阵是MATLAB最基本、最重要的数据对 象,MATLAB的大部分运算或命令都是在矩 阵运算的意义下执行的,而且这种运算定义 在复数域上。向量和单个数据都可以作为矩 阵的特例来处理。 数值数据:双精度型、单精度数、带符号整 数和无符号整数、复数 字符数据。 结构体(Structure)和单元(Cell)数据类型。 稀疏矩阵(Sparse)。 逻辑型数据。在MATLAB中,以数值1(非零 )表示‚真‛,以数值0表示‚假‛。用 logical()函数将任何非零的数值转换为true, 将数值0转换为false
含义 字符串变小写 将字符串转换成数值 字符串连接,同[] 字符串比较 字符串变大写
19
讲在结构和单元矩阵之前:矩阵的建立
1.直接输入法 最简单的建立矩阵的方法是采用矩阵构造符‚[]”从 键盘直接输入矩阵的元素。 • 构造1×n矩阵(行向量)时,可以将各元素依次 放入矩阵构造符[]内,并且以空格或者逗号分隔; • 构造m×n矩阵时,每行如上处理,并且行与行之 间用分号分隔。 例:a=1;b=2;c=3; x=[5 b c;a*b,a+c,c/b] 2.利用M文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立 一个M文件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 Matlab 数据描述
1 在命令窗口中输入 原则: 1. 矩阵的元素排列在方括号内 2. 按行输入,每行内的元素使用空格或逗号(,)隔开 3. 行与行之间用分号(;)或回车键隔开 4. 矩阵生成不但可以使用纯数字(含复数),也可以使用变 量和表达式
第二章 Matlab 数据描述
2 语句生成 (1)等差数列向量矩阵 A=a:h:b 或 A=[a:h:b]
第二章 Matlab 数据描述
符号变量和符号表达式的创建 MATLAB提供了两个建立符号变量的命令:syms 和 sym 1 用syms创建符号量 格式:syms a1 a2 a3…
说明: 1. a1 a2 a3...为需要定义为符号变量的标识符,不能是数字、函 数表达式或方程式。 2. a1 a2 a3...均不用引号界定,而用空格分开。
第二章 Matlab 数据描述
第二章 Matlab 数据描述
第二章 Matlab 数据描述
第二章 Matlab 数据描述
第二章 Matlab 数据描述
例 2.2.8
save 文件名 变量名 将变量列中所列出的变量保存到磁盘文件中,变量列表中, 各个不同的变量之间不能用逗号,只能用空格来分隔。
load 文件名 变量名 作空间。
将以前用save命令保存的变量从磁盘文件中调入MATLAB工
第二章 Matlab 数据描述 2.3 Matlab矩阵创建与引用
MATLAB中不用描述矩阵的类型和维数, 它们由输入的格式和内容决定。 常用的创建矩阵变量的方法: 1.在命令窗口中输入。 2.语句生成。 3.函数生成 4.小矩阵生成大矩阵
求: a ^ 2
a.^ 2 2.^ a a.^ b
第二章 Matlab 数据描述
关系运算符
操作符 说 等于 不等于 大于 小于 大于等于 小于等于 明
== ~= > <
>=
<=
逻辑运算符
操作符 说 明
&
| ~
逻辑与
逻辑或 逻辑非
参与逻辑运算的是两个同 维数矩阵;或者一个是矩 阵,另一个是标量; 若 参与运算的是两个矩阵, 逻辑运算是将两个矩阵对 应元素逐一进行逻辑运算, 逻辑运算的结果是一个同 维数矩阵,其元素值为 “0”或“1” 。 若参与运 算的一个是矩阵,另一个 是标量,则是矩阵中每个 元素与该标量进行逻辑运 算,最终产生一个同维数 矩阵,其元素值为“0”或 “1” 。 逻辑操作符认定任何非零 元素都为真,给出“1”, 任何零元 素都为假,给出“0”.
第二章 Matlab 数据描述
2.4 Matlab的运算
Matlab对数值矩阵提供了两种不同的运算方法:
矩阵算法 把矩阵看作一个整体,各种运算完全按照线性代数代表的矩 阵运算法则进行,运算的书写形式和运算符号都与矩阵理论 完全相同。
数组算法 把矩阵看作由其元素构成的一组数据(数组),各种运算是 在参与运算矩阵的对应元素之间进行的数与数的运算,这种 运算方便对大批数据的处理和一次求出多个函数值。 数组算法的运算符主要有 .* ./ .\ .^
第二章 Matlab 数据描述
2 用sym创建符号量、符号表达式 格式:标识符=sym(A) 说明: 1. 输入参量A可以是数字、字符串也可以是字符串变量名、字符表达 式或字符方程。 2. 回车后将A定义成符号量并赋值给标识符。
第二章 Matlab 数据描述
第二章 Matlab 数据描述
m
例2.2.1 求
2.2 Matlab的变量
MATLAB 不需要在输入变量的时候进行声明,也不需要指定 其阶数,若输入的变量已经存在,则新变量替换原有变量。
变量的命名规则(标识符): 1. 2. 3. 4. 变量名应以字母开头。 变量名可以由字母、数字、和下划线组成。 字符长度不大于63个。 区分大小写。
如 Record_1 record_1
求:
ab a2
第二章 Matlab 数据描述
1 2 3 例2.2.4 已知 a 4 5 6 7 8 9 1 0 0 b 0 1 0 求: a * b a. * b a * 2 a. * 2 0 0 1
第二章 Matlab 数据描述
第二章 Matlab 数据描述
2.矩阵的拆分 1. A(:,j)表示取A矩阵的第j列全部元素; 2. A(i,:)表示A矩阵第i行的全部元素; 3. A(i:i+m,:)表示取A矩阵第i~i+m行的全部元素; 4. A(:,k:k+m)表示取A矩阵第k~k+m列的全部元素; 5. A(i:i+m,k:k+m)表示取A矩阵第i~i+m行内,并在第k~k+m列 中的所有元素。
1
realmax
最大正实数1.797693134862316×10+308
第二章 Matlab 数据描述
对变量操作的命令
变 量 who whos clear 说 明
显示当前工作空间中所有变量的一个简单列表 列出变量的大小、数据格式等详细信息 清除工作空间中所有的变量
clear 变量名
清除指定的变量
第二章 Matlab 数据描述
1 2 3 例 2.2.7已知 a 4 5 6 7 8 9 1 0 0 b 0 1 0 0 0 1
求:
a 2 a b a &2 a &b
第二章 Matlab 数据描述
第二章 Matlab 数据描述
第二章 Matlab 数据描述
第二章 Matlab 数据描述
/串接成高维数组
第二章 Matlab 数据描述
4 小矩阵生成大矩阵 Matlab中,可以将小矩阵连接起来生成较大的矩阵。
第二章 Matlab 数据描述
矩阵的引用
1.引用矩阵元素 ① 通过下标引用矩阵的元素 ② 矩阵元素的序号来引用矩阵元素。按列排序, m×n矩 阵A,矩阵元素A(i,j)的序号为(j-1)*m+i。
第二章 Matlab 数据描述
MATLAB 语句 一般形式为: 变量 = 表达式
说明: 1. 输入一个语句并以回车结束,则在工作区中显示计算的结果; 2. 若变量和“=”省略,则名为ans的变量自动建立; 3. 如果语句以分号“;”结束,MATLAB只进行计算,不显示计算的结果; 4. 如果一个表达式太长,可以用续行号 … 将其延续到下一行。 5. 一行中可以写几个语句,它们之间要用逗号或分号分开。 6. 表达式中的变量必须是已经定义的。
矩阵右除 A/B =A*B-1 数组右除 A./B 矩阵乘方 A^p
./
^ .^
数组乘方 A.^p A中每个元素的p次方
第二章 Matlab 数据描述
1 2 3 例 2.2.3已知 a 4 5 6 7 8 9 1 0 0 b 0 1 0 0 0 1
例2.2.5 已知
1 2 c 3 4
5 6 d 7 8
c-1*d
求: c
1
c \ d c / d c. \ d c. / d
c*d-1
第二章 Matlab 数据描述
1 2 3 例2.2.6 已知 a 4 5 6 7 8 9 1 0 0 b 0 1 0 0 0 1
lim
xa
x a xa
m
limit(F,x,a) takes the limit of the symbolic expression F as x -> a.
第二章 Matlab 数据描述
MATLAB固定变量
变 量 ans i j pi Inf NaN realmin 虚数单位,定义 圆周率 无穷大 如1/0 不确定量 如0/0 最小正实数2.225073858507201×10-308 说 明 用于结果的缺省变量名
其中a为起始值,h为步长,b为终止值。当步长为1时可省略h参 数;另外h也可以取负数。
第二章 Matlab 数据描述
2 语句生成 (2)A=linspace(a,b,n) 在线性空间上,行矢量的值从a到b,数据个数为n,缺省 n为100。与 A=a:(b-a)/(n-1):b相同
第二章 Matlab 数据描述
第二章 Matlab 数据描述
例2.2.2
第二章 Matlab 数据描述
Matlab运算符
操作符 说 加 减 明
+ * .* \ .\ /
A+B A B必须大小相同,或一个是标量 A-B A B必须大小相同,或的行数,一个可以是标量 数组乘 A.*B A B必须大小相同,一个可以是标量 矩阵左除 A\B =A-1* B 数组左除 A.\B Bij/Aij 等效于X*B=A求X Aij/Bij A自乘p次 等效于A*X=B求X A-1=inv(A)
MATLAB 的三种基本类型数据 1. 数值型数据:输入的数据为数值数据,包括实数和复数 2. 字符串型数据:用英文格式单引号加以界定的数字、字符、各种符号、表达 式、方程式和汉字等。 3. 符号型数据:用sym或syms把字符、表达式、方程、矩阵等定义成数学符号, 运算结果为数学表达式。
第二章 Matlab 数据描述
3 函数生成 常用创建矩阵函数 函 数 说 明 产生 mXn 全 1 矩阵 产生 mXn 随机矩阵 产生 mXn 对角线全1矩阵 返回矩阵最长的维的长度
ones(m,n) rand(m,n) eye(m,n) length(X)
zeros(m,n) 产生 mXn 全 0 矩阵
size(X)
返回矩阵每一维的长度
第二章 Matlab 数据描述
第二章 Matlab 数据描述
2.1 Matlab数据类型 2.2 Matlab的变量 2.3 Matlab矩阵创建与引用 2.4 Matlab的运算
