最新正态概率图(normal probability plot)
正态性检验的几种方法

正态性检验的几种方法一、引言正态分布是自然界中一种最常见的也是最重要的分布。
因此,人们在实际使用统计分析时,总是乐于正态假定,但该假定是否成立,牵涉到正态性检验。
目前,正态性检验主要有三类方法:一是计算综合统计量,如动差法、Shapiro-Wilk 法(W 检验)、D ’Agostino 法(D 检验)、Shapiro-Francia 法(W ’检验)。
二是正态分布的拟合优度检验,如2χ检验、对数似然比检验、Kolmogorov-Smirov 检验。
三是图示法(正态概率图Normal Probability plot),如分位数图(Quantile Quantile plot ,简称QQ 图)、百分位数(Percent Percent plot ,简称PP 图)和稳定化概率图(Stablized Probability plot ,简称SP 图)等。
而本文从不同角度出发介绍正态性检验的几种常见的方法,并且就各种方法作了优劣比较,还进行了应用。
二、正态分布2.1 正态分布的概念定义1若随机变量X 的密度函数为()()()+∞∞-∈=--,,21222x e x f x σμπσ其中μ和σ为参数,且()0,,>+∞∞-∈σμ则称X 服从参数为μ和σ的正态分布,记为()2,~σμN X 。
另我们称1,0==σμ的正态分布为标准正态分布,记为()1,0~N X ,标准正态分布随机变量的密度函数和分布函数分别用()x ϕ和()x Φ表示。
引理1 若()2,~σμN X ,()x F 为X 的分布函数,则()⎪⎭⎫⎝⎛-Φ=σμx x F由引理可知,任何正态分布都可以通过标准正态分布表示。
2.2 正态分布的数字特征引理2 若()2,~σμN X ,则()()2,σμ==x D x E 引理3 若()2,~σμN X ,则X 的n 阶中心距为()()N k kn k k n kn ∈⎩⎨⎧=-+==2,!!1212,02σμ定义2 若随机变量的分布函数()x F 可表示为:()()()()x F x F x F 211εε+-= ()10<≤ε其中()x F 1为正态分布()21,σμN 的分布函数,()x F 2为正态分布()22,σμN 的分布函数,则称X 的分布为混合正态分布。
SPSS-5-假设检验与推断统计

二、SPSS的实现
3、正态性检验
许多统计过程,如方差分析,要求各组样本数据来自是有相同方差 的正态总体。因此,在选定统计假设之前,我们需要检验假设:各组数 据有相同方差,或者,所有样本来自正态总体。 由于正态分布对于统计推断非常重要,因此,我们经常想考察“我 们的数据来自一个正态分布”这样一个假设。
原假设 H0:各分组数据的方差是相等的(或齐性的); 研究假设 H1:各分组数据的方差是不等的(或非齐性的) 。 SPSS实现:
Analyze → Descriptive Statistics → Explore →Plots… → Untransformed
4、方差齐性检验(Levene检验)
案例分析:检验2000级学生课堂调查数据.sav中男女生“身高”数据的离散程度
一、相关的概念
3、假设检验(Hypothesis Test)
(1)根据实际问题的需要提出假设,包括: 原假设: H0 研究假设:H1 原假设被否定时,即接受研究假设。
例:某高校的英语四级平均成绩是67.5分,改进教学 方法后,学生的英语四级成绩是否有显著变化?是 否有显著提高?是否有显著下降? 是否有显著变化? H : 1000
0
H1 :
1000
是否有显著提高? 是否有显著下降?
H0 : H1 : H0 : H1 :
1000 1000 1000 1000
一、相关的概念
3、假设检验(Hypothesis Test)
(2)选择适当统计量及其分布
假设检验,基本上是根据抽样分布的原理。根 据H0假设来确定一个抽样分布,由此抽样分布来计 算各种情况出现的概率,如果实际样本出现的事件 属于小概率事件,然而小概率事件在一次抽样中就 出现了,这时我们就要怀疑所作的H0假设了,即: 否定H0,接受H1。
normal prob plot p值0.05

正态概率图和p值0.05【概述】1. 正态概率图是一种常用的统计工具,用于检验数据是否符合正态分布。
2. p值是在假设检验中常用的统计学概念,用于判断样本数据对某个假设的支持程度。
3. 本文将介绍正态概率图和p值的相关概念,以及它们在统计学中的应用。
【正态概率图的概念及作用】4. 正态概率图是一种用于检验数据是否服从正态分布的方法。
5. 在正态概率图中,样本数据被转换成标准分位数,然后与正态分布的理论值进行比较。
6. 如果数据符合正态分布,则图上的点应该近似落在一条直线上。
7. 利用正态概率图可以直观地判断数据是否呈现出明显的偏离正态分布的特征。
【p值的概念及意义】8. p值是在假设检验中用于判断样本数据对某个假设的支持程度的统计量。
9. 在假设检验中,首先提出一个原假设和一个备择假设,然后利用样本数据计算出p值。
10. 当p值小于事先设定的显著水平(通常是0.05),就会拒绝原假设。
11. p值的大小代表了样本数据对原假设的支持程度,越小表示越不支持原假设。
【正态概率图与p值在统计学中的应用】12. 在统计学中,正态概率图和p值常常用于检验数据的正态性和假设检验。
13. 通过正态概率图可以直观地观察数据的分布特征,快速判断数据是否符合正态分布。
14. 利用p值可以对实验结果的可靠性进行判断,帮助做出合理的统计推断。
【结语】15. 正态概率图和p值是统计学中常用的两种工具,它们为我们提供了检验数据分布和假设检验的有效手段。
16. 合理地利用正态概率图和p值,可以帮助我们更加客观地分析实验数据,做出科学的统计决策。
扩写新内容:【正态概率图的绘制方法】17. 正态概率图的绘制方法包括以下几个步骤:1) 将所研究的数据按照从小到大的顺序排列。
2) 计算出每个数据点对应的累积概率值,即计算累积分布函数。
3) 根据所得的累积概率值,查找对应的标准正态分布的理论值,通常利用正态分布的标准分位数来进行匹配。
可以使用统计软件或统计图表来实现这一步骤。
正态概率图(normal probability plot)精编版
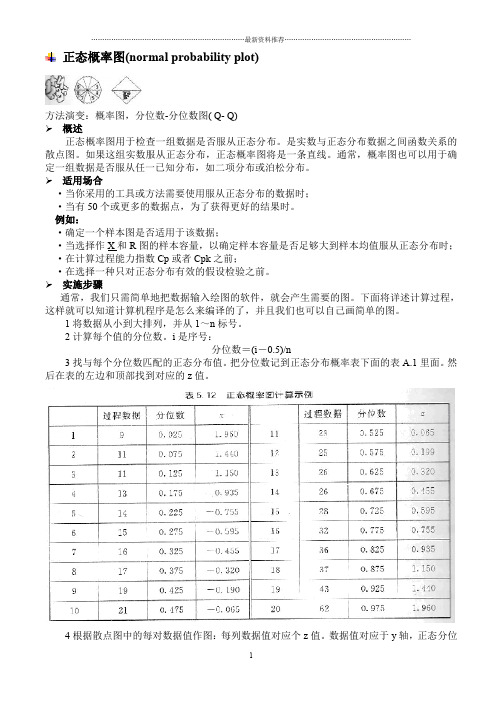
正态概率图(normal probability plot)方法演变:概率图,分位数-分位数图( Q- Q)概述正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
适用场合·当你采用的工具或方法需要使用服从正态分布的数据时;·当有50个或更多的数据点,为了获得更好的结果时。
例如:·确定一个样本图是否适用于该数据;·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;·在选择一种只对正态分布有效的假设检验之前。
实施步骤通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
示例为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20以此类推直到最后1个分位数=19. 5÷20。
数据的正态分布

数据的正态性检验汇总2012-11-21 00:01:04| 分类:统计学习|字号订阅如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的"偏度和峰度都接近0……可以认为……近似服从正态分布"并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。
由此可见,部分SPSS教材里面关于"Shapiro – Wilk 适用于样本量3-50之间的数据"的说法实在是理解片面,误人子弟。
正态概率图(normal probability plot)

正态概率图(normal probability plot)之阳早格格创做要领演变:概率图,分位数-分位数图( Q- Q)➢概括正态概率图用于查看一组数据是可遵循正态分集.是真数与正态分集数据之间函数闭系的集面图.如果那组真数遵循正态分集,正态概率图将是一条直线.常常,概率图也不妨用于决定一组数据是可遵循任一已知分集,如二项分集大概泊紧分集.➢适用场合·当您采与的工具大概要领需要使用遵循正态分集的数据时;·当有50个大概更多的数据面,为了赢得更佳的截止时.比圆:·决定一个样本图是可适用于该数据;·当采用做X战R图的样本容量,以决定样本容量是可脚够大到样本均值遵循正态分集时;·正在估计历程本领指数Cp大概者Cpk之前;·正在采用一种只对付正态分集灵验的假设考验之前.➢真施步调常常,咱们只需简朴天把数据输进画图的硬件,便会爆收需要的图.底下将详述估计历程,那样便不妨知讲估计机步调是怎么去编译的了,而且咱们也不妨自己画简朴的图.1将数据从小到大排列,并从1~n标号.2估计每个值的分位数.i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分集值.把分位数记到正态分集概率表底下的内里.而后正在表的左边战顶部找到对付应的z值.4根据集面图中的每对付数据值做图:每列数据值对付应个z值.数据值对付应于y轴,正态分位数z值对付应于x轴.将正在仄里图上得到n 个面.5画一条拟合大普遍面的直线.如果数据庄重意思上遵循正态分集,面将形大概一条直线.将面产死的图形与画的直线相比较,推断数据拟合正态分集的佳坏.请参阅注意事项中的典型图形.不妨估计相闭系数去推断那条直线战面拟合的佳坏.➢示例为了便于底下的估计,咱们仅采与20个数据.表5. 12中有逆序次排佳的20个值,列上标明“历程数据”.下一步将估计分位数.如第一个值9,估计如下:共理,第2个值,估计如下:÷20,第4个分位数=3 5÷20以此类推直到末尾1个分位数=19. 5÷20.当前不妨正在正态分集概率表中查找z值.z的前二个阿推伯数字正在表的最左边一列,末尾1个阿推伯数字正在表的最顶端一止.如第1个分位数=0.025,它位于止家与0.06天圆列的接叉处,故z=-1.96.用相共的办法找到每个分位数.如果分位数正在表的二个值之间,将需要用插值法举止供解.比圆:第4个分位数为0. 175,它位于0.1736与0.1762之间.0.1736对付应的z值为-0.94,0.1762对付应的z值为-0.93,故那二数的中间值为z=-0.935.当前,不妨用历程数据战相映的z值做图.图表5. 127隐现了截止战脱过那些面的直线.注意:正在图形的二端,面位于直线的上侧.那属于典型的左偏偏态数据.图表5.128隐现了数据的直圆图,可举止比较.➢概率图( probability plot)该要领不妨用于考验所有数据的已知分集.那时咱们没有是正在正态分集概率表中查找分位数,而是正在感兴趣的已知分集表中查找它们.➢分位数-分位数图(quantile-quantile plot)共理,任性二个数据集皆不妨通过比较去推断是可遵循共一分集.估计每个分集的分位数.一个数据集对付应于x轴,另一个对付应于y轴.做一条45°的参照线.如果那二个数据集去自共一分集,那么那些面便会靠拢那条参照线.➢注意事项·画造正态概率图有很多要领.除了那里给定的步调以中,正态分集还不妨用概率战百分数去表示.本质的数据不妨先举止尺度化大概者间接标正在x轴上.·如果此时那些数据产死一条直线,那么该正态分集的均值便是直线正在y轴截距,尺度好便是直线斜率.·对付于正态概率图,图表5.129隐现了一些罕睹的变形图形.短尾分集:如果尾部比仄常的短,则面所产死的图形左边往直线上圆蜿蜒,左边往直线下圆蜿蜒——如果倾斜背左瞅,图形呈S型.标明数据比尺度正态分集时间越收集结靠拢均值.少尾分集:如果尾部比仄常的少,则面所产死的图形左边往直线下圆蜿蜒,左边往直线上圆蜿蜒——如果倾斜背左瞅,图形呈倒S型.标明数据比尺度正态分集时间有更多偏偏离的数据.一个单峰分集也大概是那个形状.左偏偏态分集:左偏偏态分集左边尾部短,左边尾部少.果此,面所产死的图形与直线相比进与蜿蜒,大概者道呈U型.把正态分集左边截去,也会是那种形状.左偏偏态分集:左偏偏态分集左边尾部少,左边尾部短.果此,面所产死的图形与直线相比背下蜿蜒.把正态分集左边截去,也会是那种形状.·如果翻转正态概率图的数轴,那么蜿蜒的形状也跟着翻转.比圆,左偏偏态分集将是一个U型的直线.·记着历程该当正在受控状态下对付图形做出灵验推断.·纵然做直圆图能赶快知讲数据的分集,但是它却没有是推断那些数据是可去自共一特定分集的佳办法.人眼没有克没有及很佳天判别直线,其余的分集也大概产死相似的形状.而且,用遵循正态分集的少量数据集做成的直圆图大概瞅起去没有是正态的.果此,正态概率图是推断数据分集的较佳要领.·推断数据分集的另一种要领是使用拟合良佳性检定,比圆Shapiro-Wilk考验,Kolmogorov-Smirnov考验,大概者Lilliefors考验.闭于那些考验的简直形貌,没有正在本书籍的计划范畴,那些考验正在大普遍的统计硬件上皆能真止.背统计教家接洽怎么样采用精确的考验并阐明其截止.请参阅“假设考验”以明白那些考验战所得到的论断的普遍准则.·最佳的要领是使用统计硬件得到正态概率图并做拟合性考验.分离使用不妨对付数据战统计尺度有直瞅的明白,以此判决是可为正态.END。
《正态分布曲线》课件

使用Python绘制正态分布曲线
count, bins, ignored = plt.hist(data, 30, density=True)
plt.plot(bins, (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(- (bins - mu)2 / (2 * sigma2)), linewidth=2, color='r')
密度等。正态分布曲线可以用来描述这些物理量的分布情况。
03
社会调查
在社会调查中,许多调查数据呈现正态分布特征,例如民意调查、市场
调查等。正态分布曲线可以用来描述这些调查数据的分布情况。
CHAPTER 05
正态分布曲线的扩展知识
正态分布的假设检验
假设检验基本原理
假设检验是统计学中用于判断样本数据是否符合某种假设的一种方法。在正态分布的情境 下,通常假设数据符合正态分布,然后通过检验统计量进行判断。
THANKS
[ 感谢观看 ]
置信区间的应用
置信区间在统计学中有着广泛的应用,如回归分析、方差分析、实验设计等。在正态分布的情境下,我 们可以通过计算置信区间来评估样本数据的可靠性和稳定性。
正态分布与其他分布的比较
01 02 03
正态分布的优势
正态分布是一种非常重要的概率分布,其概率密度函数具 有许多优良的性质,如对称性、可加性等。此外,许多自 然现象和随机变量都呈现出近似正态分布的特性,因此正 态分布在统计学中具有广泛的应用。
《正态分布曲线》ppt 课件
CONTENTS 目录
• 正态分布曲线的定义 • 正态分布曲线的性质 • 正态分布曲线的绘制 • 正态分布曲线的应用 • 正态分布曲线的扩展知识
利用SPSS10进行多元线性回归分析

3 利用SPSS10.0进行多元线性回归分析【例】同上例。
第一步,录入或调入数据。
完全类同于一元线性回归分析,不赘述(图1)。
图1 录入或调入的数据第二步,回归操作。
多元线性分析的详细步骤的基本进程与一元线性回归分析相似,稍有不同。
⑴打开线性回归对话框。
即沿着主菜单的Analyse→Regression→Linear…路径打开Linear Regression选项框(图2)。
⑵将“运输业产值”置于因变量(Dependent)的空白栏,将“工业产值”、“农业产值”和“固定资产投资”置于自变量(Independent(s))的空白栏(图3)。
⑶在统计(Statistics)选项框中,除了选择“Durbin-Watson”外,还应该选择“Part and partial correlations”(部分与偏相关,给出零阶相关系数、偏相关系数和部分相关系数)以及“Collinearity diagnostics(共线性诊断)”。
然后继续。
⑷在Plot选项框中,除了可以选择“Histogram”(直方图)和“Normal probability plot”(正态概率图)外,还可选择“Produce all partial plot(s)”(给出所有自变量与因变量的残差散点图)。
然后继续。
⑸修改显著性水平或置信度,可以进入Save对话框,改变Prediction intervals的Confidence intervals(置信区间);修改逐步回归的F临界值,可以进入Option选项框,改变Stepping method criteria中的F值或者F概率。
如果对此缺乏足够的知识,可由系统默认。
然后继续。
⑹在线性回归对话框中,Method一栏由系统默认为enter(让所有的自变量都参入回归)。
完成上述设置以后,点击“OK”确定(图3),立即可以得到回归结果(Output)。
图2 线性回归对话框图3 设置变量图4 统计选项框的设置图5 图形对话框的设置在Variables Entered/Removed (变量取舍即变量的输入或剔除)表中,给出的采用的变量、剔除的变量和回归方法(enter ),此表中没有剔除变量。
正态性检验的一般方法汇总

正态性检验的一般方法汇总1. 引言正态性检验是统计学中一项重要的方法,用于确定数据是否服从正态分布。
正态分布在许多统计分析和假设检验中起着关键的作用,因此正态性检验对于数据分析的准确性和可靠性至关重要。
本文将综合介绍正态性检验的一般方法,包括直方图和正态概率图的可视化检验方法以及统计量检验方法。
2. 直方图检验直方图是一种用柱状图表示数据分布情况的可视化工具。
在正态性检验中,直方图可以帮助我们初步判断数据是否服从正态分布。
具体操作时,我们将数据划分为若干个区间,并统计每个区间内数据的频数。
如果直方图呈现钟形曲线,则表明数据具有较好的正态性。
反之,如果直方图呈现偏态分布,则可能说明数据不符合正态分布。
3. 正态概率图检验正态概率图是一种常用的正态性检验方法,其基本原理是将数据的分位数与标准正态分布的分位数进行比较。
通过在图上绘制数据的累积分布函数与标准正态分布的理论分布函数之间的关系,我们可以直观地判断数据是否服从正态分布。
在正态概率图中,数据点应当分布在一条直线上,如果数据点在直线上,则说明数据分布接近正态分布。
4. 统计量检验除了可视化方法,我们还可以使用统计量进行正态性检验。
常见的统计量检验方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验和D'Agostino-Pearson检验等。
这些检验方法都基于假设检验的原理,通过计算统计量并与理论分布进行比较,从而判断数据是否服从正态分布。
4.1 Kolmogorov-Smirnov检验Kolmogorov-Smirnov检验是一种常见的非参数检验方法,用于检验数据是否来自特定的分布。
在正态性检验中,Kolmogorov-Smirnov检验可以用来检验数据是否符合正态分布。
该检验基于经验分布函数和理论分布函数之间的最大差异,通过计算统计量并与临界值进行比较,可以判断数据的正态性。
4.2 Shapiro-Wilk检验Shapiro-Wilk检验是一种适用于小样本数据的正态性检验方法,其原理是通过计算统计量来衡量数据与正态分布之间的偏差程度。
Normal Probability Distributions7正态概率分布

Example: Male Height
64%
16%
16%
67.2 70 72.8
精选ppt
Reexpression of Non-Normal Variables
• Many biostatistical variables are not Normal • We can reexpress non-Normal variables
• Because the total AUC adds to 100%, 32% are in the tails below 67.2˝ and above 72.8˝
• Because of symmetry, half of this 32% (i.e., 16%) is below 67.2˝ and 16% is above 72.8˝
0.8
• 95% of ln(PSA) falls in
μ ± 2σ = −0.3 ±
(2)(0.8) = −1.9 to 1.3
• Thus, 2.5% are above
ln(PSA) 1.3; take anti-
log of 1.3: e1.3 = 3.67 精选ppt
§7.2: Determining Normal Probabilities
• Normal pdfs are recognized by their familiar bell-shape
This is the age distribution of a pediatric population. The overlying curve represents its Normal pdf model
精选ppt
Example: Normal Probability Step 1. Statement of Problem
PROBABILITYPLOT:概率图

PURPOSEGenerates a probability plot for one of 38 distributions.DESCRIPTIONA probability plot is a graphical data analysis technique for determining how well the specified distribution fits the data set. Linearity inthe probability plot is indicative of a good distributional fit. The probability plot consists of:Vertical axis=ordered observations;Horizontal axis=order statistic medians.DATAPLOT has extensive probability plot capabilities--38 distributions/distributional families are available. When distributionalfamilies are specified, then the LET command is used before the PROBABILITY PLOT command to specify fully which member of the distributional family is desired. For example,LET GAMMA = 5.3WEIBULL PROBABILITY PLOT YThe name of the distributional parameter for families is given in the list below.SYNTAX 1<dist> PROBABILITY PLOT <x><SUBSET/EXCEPT/FOR/qualification>where <x> is the variable of raw data values under analysis;<dist> is one of the following distributions:UNIFORMSEMI-CIRCULARTRIANGULAR(C, defaults to 0)NORMALLOGISTICDOUBLE EXPONENTIALCAUCHYTUKEY LAMBDA(LAMBDA)LOGNORMALHALFNORMALT(NU)CHI-SQUARED(NU)F(NU1, NU2)EXPONENTIALGAMMA(GAMMA)BETA(ALPHA, BETA)WEIBULL(GAMMA)EXTREME V ALUE TYPE 1EXTREME V ALUE TYPE 2(GAMMA)PARETO(GAMMA)BINOMIAL(N, P)GEOMETRIC(P)POISSON(LAMBDA)NEGATIVE BINOMIAL(N, K, P)WALD(GAMMA)INVERSE GAUSSIAN(GAMMA)RIG(GAMMA)FL(GAMMA)GENERALIZED PARETO(GAMMA)DISCRETE UNIFORM(N)NON-CENTRAL T(NU, LAMBDA)NON-CENTRAL F(NU1, NU2, LAMBDA)NON-CENTRAL CHI-SQUARE(NU, LAMBDA)NON-CENTRAL BETA(ALPHA, BETA, LAMBDA)DOUBLY NON-CENTRAL F(NU1, NU2, LAMBDA1, LAMBDA2)DOUBLY NON-CENTRAL T(NU, LAMBDA1, LAMBDA2)HYPERGEOMETRIC(K, N, M)VON MISES(B)and where the <SUBSET/EXCEPT/FOR qualification> is optional.This syntax is used for raw data.SYNTAX 2<dist> PROBABILITY PLOT <y> <x><SUBSET/EXCEPT/FOR/qualification>where <y> is the variable of pre-computed frequencies;<x> is the variable of distinct values for the variable under analysis;<dist> is as above;and where the <SUBSET/EXCEPT/FOR qualification> is optional.This syntax is used for pre-computed frequencies.EXAMPLESNORMAL PROBABILITY PLOT XCAUCHY PROBABILITY PLOT XTUKEY LAMBDA PROBABILITY PLOT XLOGNORMAL PROBABILITY PLOT XWEIBULL PROBABILITY PLOT XEXTREME V ALUE TYPE 1 PROBABILITY PLOT XPOISSON PROBABILITY PLOT XNORMAL PROBABILITY PLOT F XCAUCHY PROBABILITY PLOT F XTUKEY LAMBDA PROBABILITY PLOT F XLOGNORMAL PROBABILITY PLOT F XWEIBULL PROBABILITY PLOT F XEXTREME V ALUE TYPE 1 PROBABILITY PLOT F XPOISSON PROBABILITY PLOT F XNOTE 1For distributions that have a family of parameters, the PPCC PLOT can be used to find the optimal value of the parameter to use for generating the probability plot.NOTE 2The PROBABILITY PLOT command fits a least squares line to the resulting probability plot and automatically saves the following internal parameters:PPCC=the correlation coefficient between the vertical and horizontal axis variablesPPA0=the intercept of the fitted linePPA1=the slope of the fitted lineSDPPA0=standard deviation of PPA0SDPPA1=standard deviation of PPA1PPRESSD=residual standard deviation from fitted linePPRESDF=residual degrees of freedom from fitted lineThese parameters can be printed or used in subsequent computations if desired.NOTE 3The Weibull, extreme value type II, and generalized Pareto distributions can be based on either the minimum or maximum orderstatistic. The command SET MINMAX <1/2> is required before the PROBABILITY PLOT command for these distributions. A value of 1 specifies the minimum order statistic and a value of 2 specifies the maximum order statistic. Currently, the generalized Pareto distribution is only supported for the maximum order statistic (i.e., enter SET MINMAX 2).DEFAULTNoneSYNONYMSEV2 and FRECHET are synonyms for EXTREME V ALUE TYPE 2.EV1 and GUMBEL are synonyms for EXTREME V ALUE TYPE 1.FATIGUE LIFE is a synonym for FL.RECIPROCAL INVERSE GAUSSIAN is a synonym for RIG.IG is a synonym for INVERSE GAUSSIAN.LAPLACE is a synonym for DOUBLE EXPONENTIAL.RELA TED COMMANDSFREQUENCY PLOT=Generates a frequency plot.HISTOGRAM=Generates a histogram.PIE CHART=Generates a pie chart.PERCENT POINT PLOT=Generates a percent point plot.PPCC PLOT=Generates probability plot correlation coefficient plot.PLOT=Generates a data or function plot.APPLICA TIONSDistributional AnalysisIMPLEMENTA TION DATEPre-1987 (the saving of the various internal parameters was implemented 93/12, many distributions were added after 1987)PROGRAM 1MULTIPLOT 2 2; MULTIPLOT CORNER COORDINATES 0 0 100 100TITLE AUTOMATIC; X1LABEL THEORETICAL V ALUE; Y1LABEL DATA V ALUE .LET Y = NORMAL RANDOM NUMBERS FOR I = 1 1 100NORMAL PROBABILITY PLOT Y .LET NU = 5LET Y = CHI-SQUARE RANDOM NUMBERS FOR I = 1 1 100CHI-SQUARE PROBABILITY PLOT Y .LET Y = EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 100EXPONENTIAL PROBABILITY PLOT Y .LET Y = CAUCHY RANDOM NUMBERS FOR I = 1 1 1000LEGEND 1 CAUCHY RANDOM NUMBERS NORMAL PROBABILITY PLOT Y END OF MULTIPLOTNORMAL PROBABILITY PLOT YTHEORETICAL VALUE D A T A V A L U ECHI-SQUARE PROBABILITY PLOT YTHEORETICAL VALUED A T A V A L U E0EXPONENTIAL PROBABILITY PLOT YTHEORETICAL VALUE D A T A V A L U ENORMAL PROBABILITY PLOT YTHEORETICAL VALUED A T A V A L U EPROGRAM 2. ALASKA PIPELINE RADIOGRAPHIC DEFECT BIAS CURVE . PERFORM A LINEAR REGRESSION SKIP 25READ BERGER1.DAT TRUE MEAS CAPTURE FIT_1_OUT.DAT FIT MEAS TRUE END OF CAPTURE .MULTIPLOT 2 2 ; MULTIPLOT CORNER COORDINATES 0 0 100 100TITLE ORIGINAL DATAX1LABEL TRUE DEPTH (IN .001 INCH)Y1LABEL MEASURED DEPTH CHARACTERS X LINES BLANK PLOT MEAS TRUETITLE PREDICTED V ALUES PLOT MEAS PRED VS TRUE TITLE RESIDUALS Y1LABELPLOT RES VS TRUE X1LABELTITLE NORMAL PROBABILITY PLOT NORMAL PROBABILITY PLOT RES END OF MULTIPLOTORIGINAL DATATRUE DEPTH (IN .001 INCH)M E A S U R E D D E P T H00PREDICTED VALUESTRUE DEPTH (IN .001 INCH)M E A S U R E D D E P T HRESIDUALSTRUE DEPTH (IN .001 INCH)NORMAL PROBABILITY PLOT。
4.2.5 正态分布 课件(共44张PPT)- 高中数学人教B版(2019)选择性必修第二册.ppt

为正态分布的“3 原则”.
例 2 假设某个地区高二学生的身高服从正态分布,且均值为 170(单位: cm, 下同),标准差为 10. 在该地区任意抽取一名高二学生,求这名学生的身高:
(1)不高于 170 的概率; (2)在区间 [160,180] 内的概率; (3)不高于 180 的概率.
假设 ∼ (100,0.5),那么 ( ) = 50, ( ) = 25 ,用正态分布
近似二项分布的话有 ∼ (50,52),那么 P(X 50) P(49.5 X 50.5)
P
0.1
X
50 5
0.1
.
又因为
X
5
50
N
(0,1)
,所以
P
0.1
X
5
50
0.1
=
Φ(0.1)
−
Φ( − 0.1) = Φ(0.1) − [1 − Φ(0.1)] = 2 Φ(0.1) − 1 = 2 × 0.5398 − 1 = 0.0796.
(4)所有矩形的面积之和为 1.
事实上,很多服从二项分布的随机变量分布列的直观图都具有类似的特点. 例如,若
∼
50 ,1 2
,则其 分布列 可用图 (1)表示 ;若
∼
100
,1 2
,则其
分布列 可用图 (2)表示
.
由以上三图可以看出,当 充分大时, ∼ ( , ) 的直观表示总是具有中间 高、两边低的“钟形”. 而且,对不同的参数,只是钟形的宽度和高度不一样而已. 那 么,是否存在一个函数 ( ),它对应的图象能够近似这些钟形(如图(2)所示) 呢?如果这样的函数存在的话,要计算 落在某区间内的概率,只需计算对应曲 线与 轴在适当区间所围成的面积即可.
SPSS统计分析最全中英文对照表

SPSS 专业技术词汇、短语的中英文对照索引%of cases 各类别所占百分比1—tailed 单尾的2 Independent Samples 两个独立样本的检验2 Related Samples 两个相关样本检验2—tailed 双尾的3—D (=dimensional) 三维——〉三维散点图AAbove 高于Absolute 绝对的—->绝对值Add 加,添加Add Cases 合并个案Add cases from.。
. 从……加个案Add Variables 合并变量Add variables from。
从……加变量Adj。
(=adjusted)standardized 调整后的标准化残差Aggregate 汇总—->分类汇总Aggregate Data 对数据进行分类汇总Aggregate Function 汇总函数Aggregate Variable 需要分类汇总的变量Agreement 协议Align 对齐-—〉对齐方式Alignment 对齐——〉对齐方式All 全部,所有的All cases 所有个案All categories equal 所有类别相等All other values 所有其他值All requested variables entered 所要求变量全部引入Alphabetic 按字母顺序的—->按字母顺序列表Alternative 另外的,备选的Analysis by groups is off 分组分析未开启Analyze 分析——>统计分析Analyze all cases, do not create groups 分析全部个案,不建立分组Annotation 注释ANOV A Table ANOV A表ANOV A table and eta (对分组变量)进行单因素方差分析并计算其η值Apply 应用Apply Data Dictionary 应用数据字典Apply Dictionary 应用数据字典Approximately 大约Approximately X%of all cases 从所有个案中随机选择约X%的个案Approximation 近似估计Area 面积Ascend 上升Ascending counts 按频数的升序排列Ascending means 按均值升值排序Ascending values 按变量值的升序排列Assign 指定,分配Assign Rank 1 to 把秩值1 分配给Assume 假定Asymp。
Normal Probability Plot+QQ Plot

右偏态
左偏态
Confidential
Page
Normal Probability Plot
正态概率图(Normal Probability Plot) • 概述:正态概率图用于检查一组数据是否服从正态分布,是实数与正态分布数据之间 函数关系的散点图。如果这组数据服从正态分布,正态概率图会是一条直线。 • 适用条件:(1)当你采用的工具或者方法需要使用服从正态分布的数据 (2)当有50个或更多数据点,为了获得更好的结果 • 计算原理:(1)将数据从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 (3)从正态分布概率表中找到各分位数对应的Z值 (4)将数据点作散点图:实际数据值对应Y轴,正态分位数Z值对应X轴 (5)画一条拟合大多数点的直线与点形成的图形相比较,判断拟合正态 分布的好坏
Confidential
Page
QQ-Plot
分位数-分位数图(quantile-quantile plot) • 概述:QQ图的主要作用是判断样本是否近似于某种类型的分布,或者验证两组数据是 否来自同一分布。这里的“QQ”是两个Quantiles的大写字母,即两个分位数。 • 适用条件:检验一组数据是否来自某个分布或者两组数据是否来自同一分布 • 计算原理:(1)将数据按照从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 ( 3 )将数据点作散点图:第一组数据的分位数对应 X 轴,另一组数据的 分位数对应Y轴 ( 4 )作 y=x 的直线,如果两个分布相似,则该 Q-Q 图趋近于落在 y=x 线上。 如果两分布线性相关,则点在Q-Q图上趋近于落在一条直线上,但不一定在y=x线上。
中职—信息技术—回归方程—课件

对相同的两个变量进行重复测量时, 可以提供这两个变量之间因果关系的某 种信息(坎贝尔1963年)。
交叉滞后组相干分析研究CLPC
样本A 观测1 rA1B1=0.5
样本B 观测1 时间轴
rA1A2=0.8 rA1B2=0.6
rB1A2=0.45 rB1B2=0.8
样本A 观测2
rA2B2=0.5
样本B 观测2
实行统计分析进程中,“土壤成分”、“化肥”将成 为自变量无条件进入方程,而“种谷物的产量”将不显现 在方程中,其它自变量将根据其对方程的作用显著程度决 定是否进入方程。
“Selection Variable”为指定抽样变量以及抽样规则。 例如:以年份year为抽样变量,并指定抽样规则为1985年 以后的个案,则可以指定“Selection Variable” 为year。
在定义抽样规则项“Define Selection rule ”中定义: Greater than 1985。
⒊统计量的运算 单击运算统计按钮:“Statistics” 在运算统计对话窗 口中,可以见到以下几方面的内容:
⑴回来系数的运算Regression Coefficients: ①“Estimates”运算各个自变量的回来系数B、相干系 数R、标准误SEB、标准化回来系数Beta、t检验的双侧概 率以及容忍度Tolerance。 ②“Confidence interval”回来系数的95%的置信区间。 ③“Covariance matrix”生成协方差矩阵。
非线性回来分析 一、非线性回来分析原理 建立某种非线性的数学模型并做检验。 假定:二次方程、三次方程、n次方程、指数方程、对数方程等。 以二次方程为例,
Y=B2X2+B1X+B0 只要肯定了三个系数B2、B1、B0 (也就是Constant) 方程就肯定了。
MINITAB处理能力的分析和评估

0
Zshift 和 Zst
Report 8B: Product Benchmarks
Zone of Average Technology
Zone of Typical Control
World-Class Performance
1
2
3
4
5
6
Z.Bench (Short-Term)
Nominal:
40
Opportunity:
10,000 1000 100 10 1 0
10
20
30
40
50
Process Benchmarks
Actual (LT) Potential (ST)
Sigma
(Z.Bench)
1.38
1.55
PPM 83192.3 60454.5
Zlt
Zst
Report 2: Process Capability for C1
L1 任务单 (团圆值的 sigma 分值的计算) 目的: 计算在以后的 sigma 值中以后的 CTQ 特征值〔团圆值〕假设定位。 作用:
1) 了解以后的形状以便于可以决议能否做出改良或在目的值设定的状况下 在做出决议时作为数据运用。
8. 相关性剖析和回归剖析
相关性
1) 输入到数据窗口 获取 Minitab 规范数据。 阅读 Minitab 数据文件夹中的 〝 \MTBWIN\Data\Exh_regr.mtw〞。
North
-0.849 -0.634 -0.117 0.000 0.000 0.545
Time
-0.351 -0.584 -0.065 0.062 0.001 0.737
疲劳试验方法_标准_概述说明以及解释

疲劳试验方法标准概述说明以及解释1. 引言1.1 概述疲劳试验方法是一种重要的工程实验方法,用于评估材料或构件在循环加载条件下的耐久性和可靠性。
在现代工程设计和材料科学领域,疲劳试验方法被广泛应用于各种应用中,如航空航天、汽车制造、机械工程等。
通过模拟真实使用环境下的循环负载,疲劳试验可以揭示材料和构件在长时间使用过程中存在的弱点和故障机理。
1.2 文章结构本文将详细介绍疲劳试验方法及其标准,并对其进行解释和讨论。
文章由引言、疲劳试验方法、疲劳试验标准、疲劳试验概述说明、解释与讨论以及结论等部分组成。
引言部分将给出关于疲劳试验方法的整体概述,并简单介绍文章结构。
1.3 目的本文旨在提供对疲劳试验方法及其标准的全面理解。
通过对常见的疲劳试验方法和标准进行介绍和解析,读者将了解到选择适当的疲劳试验方法的考虑因素,以及疲劳试验标准的重要性和作用。
此外,本文还将详细说明疲劳试验的基本原理和过程概述,以及分析疲劳试验结果、对不同标准进行疲劳试验比较和解读疲劳断口特征及其含义的常用方法。
最后,通过总结疲劳试验方法和标准的重要性,并对未来发展进行展望,希望能够促进相关领域的研究与应用。
(文章正文内容根据实际需求填写即可)2. 疲劳试验方法2.1 定义和背景疲劳试验方法是用于评估材料、结构或设备在重复加载下的耐久性能的实验方法。
疲劳是指物体在反复循环载荷作用下逐渐损坏的现象,它可能导致结构失效或材料断裂。
疲劳试验方法旨在模拟实际使用条件下的循环荷载以确定材料或结构的疲劳极限、寿命和可靠性。
2.2 常见的疲劳试验方法常见的疲劳试验方法包括:- 轴向拉压疲劳试验:通过施加轴向拉力或压力来对材料进行循环加载,以评估其抗拉/压疲劳性能。
- 弯曲疲劳试验:施加弯曲力以模拟结构在实际使用中所受到的曲度变化,并评估材料或结构的抗弯曲疲劳性能。
- 扭转疲劳试验:通过扭转加载对材料进行循环应变,以评估其抗扭转疲劳性能。
- 振动疲劳试验:通过施加振动载荷模拟实际使用条件下的震动环境,评估材料或结构的抗振动疲劳性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态概率图(normal probability plot)
方法演变:概率图,分位数-分位数图( Q- Q)
➢概述
正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
➢适用场合
·当你采用的工具或方法需要使用服从正态分布的数据时;
·当有50个或更多的数据点,为了获得更好的结果时。
例如:
·确定一个样本图是否适用于该数据;
·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;
·在选择一种只对正态分布有效的假设检验之前。
➢实施步骤
通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:
分位数=(i-0.5)/n
3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位
数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
➢示例
为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个
值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:
分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025
同理,第2个值,计算如下:
分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075
可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20
以此类推直到最后1个分位数=19. 5÷20。
现在可以在正态分布概率表中查找z值。
z的前两
个阿拉伯数字在表的最左边一列,最后1个阿拉伯数
字在表的最顶端一行。
如第1个分位数=0. 025,它位
于-1.9在行与0.06所在列的交叉处,故z=-1.96。
用相同的方式找到每个分位数。
如果分位数在表的两个值之间,将需要用插值法
进行求解。
例如:第4个分位数为0. 175,它位于0.1736
与0.1762之间。
0.1736对应的z值为-0.94,0.1762
对应的z值为-0.93,故
这两数的中间值为z=-0.935。
现在,可以用过程数据和相应的z值作图。
图表5. 127显示了结果和穿过这些点的直线。
注意:在图形的两端,点位于直线的上侧。
这属于典型的右偏态数据。
图表5.128显示了数据的直方图,可进行比较。
➢概率图( probability plot)
该方法可以用于检验任何数据的已知分布。
这时我们不是在正态分布概率表中查找分位数,而是在感兴趣的已知分布表中查找它们。
➢分位数-分位数图(quantile-quantile plot)
同理,任意两个数据集都可以通过比较来判断是否服从同一分布。
计算每个分布的分位数。
一个数据集对应于x轴,另一个对应于y轴。
作一条45°的参照线。
如果这两个数据集来自同一分布,那么这些点就会靠近这条参照线。
➢注意事项
·绘制正态概率图有很多方法。
除了这里给定的程序以外,正态分布还可以用概率和百分数来表示。
实际的数据可以先进行标准化或者直接标在x轴上。
·如果此时这些数据形成一条直线,那么该正态分布的均值就是直线在y轴截距,标准差
就是直线斜率。
·对于正态概率图,图表5.129显示了一些常见的变形图形。
短尾分布:如果尾部比正常的短,则点所形成的图形左边朝直线上方弯曲,右边朝直线下方弯曲——如果倾斜向右看,图形呈S型。
表明数据比标准正态分布时候更加集中靠近均值。
长尾分布:如果尾部比正常的长,则点所形成的图形左边朝直线下方弯曲,右边朝直线上方弯曲——如果倾斜向右看,图形呈倒S型。
表明数据比标准正态分布时候有更多偏离的数据。
一个双峰分布也可能是这个形状。
右偏态分布:右偏态分布左边尾部短,右边尾部长。
因此,点所形成的图形与直线相比向上弯曲,或者说呈U型。
把正态分布左边截去,也会是这种形状。
左偏态分布:左偏态分布左边尾部长,右边尾部短。
因此,点所形成的图形与直线相比向下弯曲。
把正态分布右边截去,也会是这种形状。
·如果翻转正态概率图的数轴,那么弯曲的形状也跟着翻转。
比如,左偏态分布将是一个U型的曲线。
·记住过程应该在受控状态下对图形作出有效判断。
·尽管作直方图能马上知道数据的分布,但它却不是判断这些数据是否来自同一特定分布的好办法。
人眼不能很好地判别曲线,其他的分布也可能形成相似的形状。
并且,用服从正态分布的少量数据集作成的直方图可能看起来不是正态的。
因此,正态概率图是判断数据分布的较好方法。
·判断数据分布的另一种方法是使用拟合良好性检定,比如Shapiro-Wilk检验,Kolmogorov-Smirnov检验,或者Lilliefors检验。
关于这些检验的具体描述,不在本书的讨论范围,这些检验在大多数的统计软件上都能实现。
向统计学家咨询如何选择正确的检验并解释其结果。
请参阅“假设检验”以理解这些检验和所得到的结论的一般原则。
·最好的方法是使用统计软件得到正态概率图并作拟合性检验。
结合使用可以对数据和统计标准有直观的理解,以此判定是否为正态。
END佛经中的经典句子(350句)
1.凡所有相,皆是虚妄。
若见诸相非相,即见如来。
2.一切有为法,如梦幻泡影,如露亦如电,应作如是观。
3.知幻即离,不假方便;离幻即觉,亦无渐次。
4.世间无常,国土危脆,四大苦空,五阴无我生灭变异,虚伪无主,心是恶源,形为罪薮。
5.我观是南阎浮提众生,举心动念无不是罪。
6.复次地藏,未来世中,若有善男子、善女人,于佛法中所种善根,或布施供养,或修补塔寺,或装理经典,乃至一毛一尘、一沙一渧。
如是善事,但能回向法界,是人功德,百千生中,受上妙乐。
如但回向自家眷属,或自身利益,如是之果,即三生受乐,舍一得万报。
是故地藏,布施因缘,其事如是。
7.复次地藏,若未来世,有诸国王,至婆罗门等,遇先佛塔庙,或至经像,毁坏破落,乃能发心修补。
是国王等,或自营办,或劝他人,乃至百千人等布施结缘。
是国王等,百千生中,常为转轮王身。
如是他人同布施者,百千生中,常为小国王身。
更能于塔庙前,发回向心,如是国王,乃及诸人,尽成佛道。
以此果报,无量无边。
8.若人欲了知,三世一切佛。
应观法界性,一切唯心造。
9.人在爱欲之中独生独死,独去独来。
苦乐自当,无有代者。
10.觉了一切法,犹如梦幻响。
11.佛言:当念身中四大,各自有名,都无我者,我既都无。
其如幻耳。
12.阿字十方三世佛,弥字一切诸菩萨。
陀字八万诸圣教,三字之中是具足。
一句弥陀是佛王、法王、咒王、功德之王。
专念「南无阿弥陀佛」一佛,即是总持总念诸佛、诸菩萨、诸经咒、诸行门。
所谓「八万四千法门,六字全收。
」亦谓「赅罗八教,圆摄五宗。
」既得临终往生净土,亦获现世身心安乐。
13.念阿弥陀佛功德,多于念地藏菩萨百千万倍。
何以得知?准《观音经》,有一人供养六十二亿恒河沙菩萨,乃至一时,不如礼拜供养观世音菩萨。
《十轮经》云:“一百劫念观世音,不如一食顷念地藏菩萨。
”《群疑论》曰:“一大劫念地藏菩萨,不如一声念阿弥陀佛。
”何以故?佛是法王,菩萨为法臣,如王出时,臣必随从,大能摄小。
佛是觉满果圆,超诸地位,所以积念者功德最多,过于地藏百千万倍。
菩萨未属佛地,果未**,故功德最少。
"
14.心有所住,即为非住。
应无所住而生其心。
15.诸行无常,一切皆苦。
诸法无我,寂灭为乐。
