正态概率图(normal probability plot)
如何检验数据是否服从正态分布

如何检验数据是否服从正态分布正态分布是概率论和统计学中的一个重要分布,也称为高斯分布。
在很多实际问题中,需要确定一个数据集是否服从正态分布。
本文将介绍几种常用的方法来检验数据是否服从正态分布。
1.直方图检验法:直方图是用来表示数据频数分布的常用图形方法。
通过绘制数据集的直方图,我们可以观察数据的分布情况。
对于服从正态分布的数据,其直方图应该是呈现出一座钟形曲线的形状。
如果数据集的直方图呈现出钟形曲线的形状,那么可以初步判断数据服从正态分布。
但这种方法仅适用于大样本量和精确的直方图。
2.正态概率图法:正态概率图(Probability Plot)是另一种判断数据是否服从正态分布的方法。
正态概率图是将数据按照大小排序后,将每个数据点的累积分布函数的值(即标准正态分布分位数)在纵坐标上绘制,而横坐标则表示数据点的实际值。
如果数据集的正态概率图上的点大致沿着一条直线排列,则可以认为数据服从正态分布。
4.统计检验法:统计检验是通过计算统计量来得出结论的方法。
常用的统计检验方法有Kolmogorov-Smirnov检验、Shapiro-Wilk检验和Anderson-Darling检验。
- Kolmogorov-Smirnov检验:该检验利用累积分布函数(CDF)来判断观测样本与理论分布之间的差异,若与理论分布没有显著差异,则可认为服从正态分布。
- Shapiro-Wilk检验:该检验是一种适用于小样本量的检验方法,利用观察数据与正态分布之间的相关系数来判断数据是否服从正态分布。
- Anderson-Darling检验:该检验适用于中等样本量,通过计算观察数据与理论分布之间的差异来判断数据服从的分布类型。
总结:。
解读正态概率图正态概率图纸的秘密.doc

解读正态概率图-正态概率图纸的秘密本文是对解读Minitab的正态概率图一文中注解3-正态概率图图纸的说明1上图的H0假设1)上图单组数据为34,35,36,37,38,39,40,40,41,42,43,44,45,46共N=14个2)计算得平均值为Xbar=40,标准差为s=3.741657 (图示为3.742)3)上图的H0假设数据源自正态分布,相对H1就是非正态分布4)基于正态分布的假设,所以根据样本数可以估计此正态分布的2个参数,平均值μ为40,标准差σ为3.7416572正态分布的特性x、z与累积分配函数1)正态分布z值有人称z score,是正态分布的变量x,转换为标准正态分布时对应值为z,关系是为z=(x-μ)/σ2)正态分布下变量x,经转换为标准正态分布对应值z,就可经由正态分布数值表或软件等求得x的累积分配函数(cdf),cdf一般统计符号写成F(x)= P(X≦x),P就是X≦x累积机率,正态概率图的纵坐标Percent就是F(x)3)鼠标移到Minitab蓝色直线上,就会出现如下图中的黄底的Percent与x数值表4)Percent与x数值表说明黄底的Percent与x数值表,Percent就是F(x),F(x)是指定的解于0与1之间,表上所示数值系为%,透过标准正态分布,就可求F(x)的反函数z,然后以公式x=zσ+μ得到x值3正态性检定使用的正态概率图图纸1)下表为手工计算,结果与minitab的Percent与x数值表相符的作成蓝色参考值线的数据x、z、F(x)关系表如下表,表中系先指定F(x),就是表中Percent栏,然后基于正态分布求x=F-1(x),再使用正态分布标准化公式计算z=(x-Xbar)/s2)若以Percent vs x畫散佈圖是S型曲線並非直線,如下圖,所以常態機率圖的繪製有點竅門3)理解正态概率图图纸解读正态概率图的第一要务是理解所谓机率图图纸,常用有常态与Weibull二种机率图图纸,下图是正态概率图图纸的示意图,图中蓝色直线是基于H0的正态分布假设下,自样本数据去估计平均Xbar=40与标准差s=3.741657,并制作x、z、F(x)关系表(如上表)所作成4正确制作正态概率图图纸步骤1)作z vs x作散布图为了能够显示一直线,于是以z vs x作散布图,并于每个点上,标出该数据x对应的F(x)值,每一个点上也画出网格线如下图,观看网格线,似乎类似对数坐标(实际上并不是)2)將各點百分比值F(x)作為新座標Y軸3) 若将纵坐标Y轴隐藏或者是移到次坐标轴,而将数据卷标F(x)值作为纵坐标Y轴的坐标刻度,此时就是正态概率图纸5正态概率图的应有认识一张正态概率图表面上为F(x) vs x,实质上还是存在z vs x关系,构成正态概率图的二个轴分别为1)排序数据x2) 数据x对应累积比例(标准正态分布的百分位数值)至于数据x置于横轴或纵轴,不同软件表现不同,Minitab放在横轴,JMP放在纵、横轴均可指定,而Excel是放在在纵轴。
normal prob plot p值0.05

正态概率图和p值0.05【概述】1. 正态概率图是一种常用的统计工具,用于检验数据是否符合正态分布。
2. p值是在假设检验中常用的统计学概念,用于判断样本数据对某个假设的支持程度。
3. 本文将介绍正态概率图和p值的相关概念,以及它们在统计学中的应用。
【正态概率图的概念及作用】4. 正态概率图是一种用于检验数据是否服从正态分布的方法。
5. 在正态概率图中,样本数据被转换成标准分位数,然后与正态分布的理论值进行比较。
6. 如果数据符合正态分布,则图上的点应该近似落在一条直线上。
7. 利用正态概率图可以直观地判断数据是否呈现出明显的偏离正态分布的特征。
【p值的概念及意义】8. p值是在假设检验中用于判断样本数据对某个假设的支持程度的统计量。
9. 在假设检验中,首先提出一个原假设和一个备择假设,然后利用样本数据计算出p值。
10. 当p值小于事先设定的显著水平(通常是0.05),就会拒绝原假设。
11. p值的大小代表了样本数据对原假设的支持程度,越小表示越不支持原假设。
【正态概率图与p值在统计学中的应用】12. 在统计学中,正态概率图和p值常常用于检验数据的正态性和假设检验。
13. 通过正态概率图可以直观地观察数据的分布特征,快速判断数据是否符合正态分布。
14. 利用p值可以对实验结果的可靠性进行判断,帮助做出合理的统计推断。
【结语】15. 正态概率图和p值是统计学中常用的两种工具,它们为我们提供了检验数据分布和假设检验的有效手段。
16. 合理地利用正态概率图和p值,可以帮助我们更加客观地分析实验数据,做出科学的统计决策。
扩写新内容:【正态概率图的绘制方法】17. 正态概率图的绘制方法包括以下几个步骤:1) 将所研究的数据按照从小到大的顺序排列。
2) 计算出每个数据点对应的累积概率值,即计算累积分布函数。
3) 根据所得的累积概率值,查找对应的标准正态分布的理论值,通常利用正态分布的标准分位数来进行匹配。
可以使用统计软件或统计图表来实现这一步骤。
正态概率图(normal probability plot)精编版
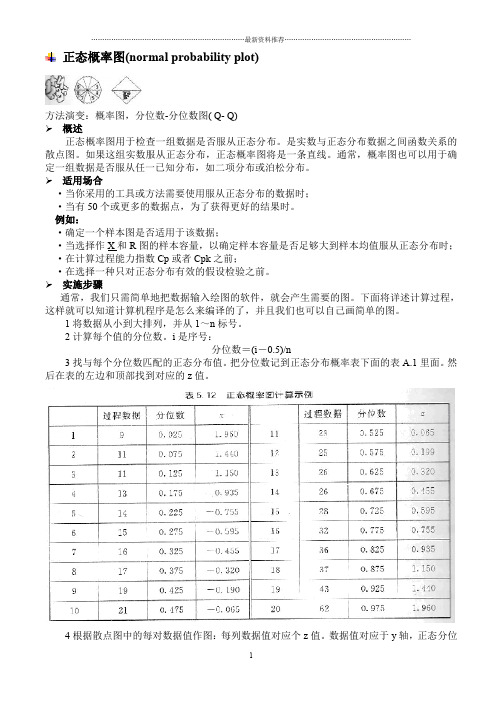
正态概率图(normal probability plot)方法演变:概率图,分位数-分位数图( Q- Q)概述正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
适用场合·当你采用的工具或方法需要使用服从正态分布的数据时;·当有50个或更多的数据点,为了获得更好的结果时。
例如:·确定一个样本图是否适用于该数据;·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;·在选择一种只对正态分布有效的假设检验之前。
实施步骤通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
示例为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20以此类推直到最后1个分位数=19. 5÷20。
资料的正态性检验汇总

资料的正态性检验汇总摘要提示:本文汇总了通常在对资料进行正态性检验时遇到的问题,比如Kolmogorov-Smirnov检验(简称K-S检验),还是Shapiro-Wilk检验,SPSS里面用哪个过程,SAS程序等。
SPSS和SAS常用正态检验方法正态性检验主要有三类方法:一、计算综合统计量如动差法、夏皮罗-威尔克Shapiro-Wilk 法(W 检验) 、达戈斯提诺D′Agostino 法(D 检验) 、Shapiro-Francia法(W′检验) .二、正态分布的拟合优度检验如皮尔逊χ2检验、对数似然比检验、柯尔莫哥洛夫Kolmogorov-Smirov 法检验 .三、图示法(正态概率图Normal Probability plot)如分位数图(Quantile Quantileplot ,简称QQ 图) 、百分位数(Percent Percent plot ,简称PP 图) 和稳定化概率图(Stablized Probability plot ,简称SP 图) 等.下面介绍几种较统计软件中常用的正态性检验方法1、用偏态系数和峰态系数检验数据正态性偏态系数Sk,它用于检验不对称性;峰态系数Ku,它用于检验峰态。
S k= 0, K u= 0 时, 分布呈正态, S k> 0 时, 分布呈正偏态,S k < 0 时, 分布呈负偏态。
适用条件:样本含量应大于2002、用夏皮罗-威尔克(Shapiro-Wilk)法检验数据正态性即W检验,1965 年提出,适用于样本含量n ≤50 时的正态性检验;。
3、用达戈斯提诺(D′Agostino)法检验数据正态性即D检验,1971提出,正态性D检验该方法效率高,是比较精确的正态检验法。
4、Shapiro-Francia 法即W′检验,于1972 年提出,适用于50 < n < 100 时的正态性检验。
5、QQ图或PP图散点聚集在固定直线的周围,可以认为数据资料近似服从正态分布SPSS&SAS规则:SPSS 规定:当样本含量3 ≤n ≤5000 时,结果以Shapiro - Wilk (W 检验) 为难,当样本含量n > 5000 结果以K olmogorov - Smirnov 为准。
数据的正态分布

数据的正态性检验汇总2012-11-21 00:01:04| 分类:统计学习|字号订阅如何在spss中进行正态分布检验一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的"偏度和峰度都接近0……可以认为……近似服从正态分布"并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3 和 5000 之间时,计算该统计量。
由此可见,部分SPSS教材里面关于"Shapiro – Wilk 适用于样本量3-50之间的数据"的说法实在是理解片面,误人子弟。
正态概率分布函数

正态概率分布函数
正态概率分布函数(Normal Probability Distribution, NPD)是数学和统计学中最重要的概率分布之一。
它表示的是一类服从某种特定的分布的随机变量的概率,也称为正态分布。
它具有非常重要的理论意义,广泛应用于数理统计中。
正态概率密度函数,又称正态分布函数,是一种特殊的概率分布,应用最广泛的概率分布之一,主要原因是正态概率分布可以简化很多统计方法的计算,同时还可以具有非常实用的性质,其中包括中心极限定理等。
正态概率分布具有以下共同特征:样本均值(简称为均值)等于随机变量期望,样本方差等于随机变量方差,数据点符合均匀分布;另外,垂直于均值线的两条贝塞尔曲线位于两边,并且贝塞尔曲线是对称的。
一般来说,概率分布的形状取决于均值和方差,正态概率分布的形状由均值调节,方差决定,均值越高正态曲线就越高,方差越大,则曲线越宽,曲线的右边越低。
而当方差趋近于零时,正态曲线就由直线表示。
正态分布在概率统计里有着重要的意义,它能够准确地描述实际问题中的随机变量,同时也可以提供许多非常重要的性质,如中心极限定理,大数定律等。
总的来说,正态概率分布函数是统计学中最重要的概率分布之一,广泛运用于数理统计,同时也有着非常重要的理论意义,是很多统计方法的重要基础。
正态性检验方法

SPSS和SAS常用正态检验方法许多计量资料的分析方法要求数据分布是正态或近似正态,因此对原始独立测定数据进行正态性检验是十分必要的。
通过绘制数据的频数分布直方图来定性地判断数据分布正态性。
这样的图形判断决不是严格的正态性检验,它所提供的信息只是对正态性检验的重要补充。
正态性检验主要有三类方法:一、计算综合统计量如动差法、夏皮罗-威尔克Shapiro-Wilk 法(W 检验) 、达戈斯提诺D′Agostino 法(D 检验) 、Shapiro-Francia法(W′检验) .二、正态分布的拟合优度检验如皮尔逊χ2检验、对数似然比检验、柯尔莫哥洛夫Kolmogorov-Smirov 法检验.三、图示法(正态概率图Normal Probability plot)如分位数图(Quantile Quantileplot ,简称QQ 图) 、百分位数(Percent Percent plot ,简称PP 图) 和稳定化概率图(Stablized Probability plot ,简称SP 图) 等.下面介绍几种较统计软件中常用的正态性检验方法1、用偏态系数和峰态系数检验数据正态性偏态系数Sk,它用于检验不对称性;峰态系数Ku,它用于检验峰态。
S k= 0, K u= 0 时, 分布呈正态, S k> 0 时, 分布呈正偏态,S k < 0 时, 分布呈负偏态。
适用条件:样本含量应大于2002、用夏皮罗-威尔克(Shapiro-Wilk)法检验数据正态性即W检验,1965 年提出,适用于样本含量n ≤50 时的正态性检验;。
3、用达戈斯提诺(D′Agostino)法检验数据正态性即D检验,1971提出,正态性D检验该方法效率高,是比较精确的正态检验法。
4、Shapiro-Francia 法即W′检验,于1972 年提出,适用于50 < n < 100 时的正态性检验。
5、QQ图或PP图散点聚集在固定直线的周围,可以认为数据资料近似服从正态分布SPSS&SAS规则:SPSS 规定:当样本含量3 ≤n ≤5000 时,结果以Shapiro - Wilk (W 检验) 为准,当样本含量n > 5000 结果以Kolmogorov - Smirnov 为准。
解读Minitab的正态概率图

解读Minitab的正态概率图已有371 次阅读2009-11-5 20:41 |个人分类:Minitab|关键词:Minitab在DOE、Regression、统计检定时常需要用到正态分布的假设,检定一组数据是否取自正态分布,进行常态性检定最简单方法就是采用正态概率图。
最近很多贴文询问Minitab正态概率图的坐标系统、意义与手工绘制等议题,因涉及分配概率图的理解与使用,因此撰文剖析,如下图是以一组14个样本数据所画的正态概率图本图原始数据,经排序后如下34,35,36,37,38,39,40,40,41,42,43,44,45,46图上有5个注解,依序说明之注解1:Probability Plot of x,表示此图是一组数据,放在名为x的栏位上,下方有Normal 表示本项检定的H0是Normal –正态分布,当然H1就是非正态分布注解2:Mean 40表示数据平均值,StDev 3.742(计算结果3.74166)表示数据标准差,N 14表示数据数,这些计算式依据一般基本统计的公式计算而得注解3:蓝色直线是画在正态分布机率图纸上,是一条参考线,以判断是否H0成立详细解说如下1)鼠标移到Minitab蓝色直线上,就会出现如下图中的黄底的Percent与x数值表2) Percent与x数值表中,Percent为正态分布累积分配函数(CDF),数值是介于0与1之间,表上数值为%值,习惯上是以F(x)表式之,而x为F(x)的反函数3)若直接以Percent与x( inv F(x))数值表作散布图不会得到依直线,而是S型曲线4)在Percent与x( inv F(x))数值表多加一栏z,其值为x( inv F(x))的标准化,z=( inv F(x)) –40)/3.741665)以x( inv F(x))为横轴,z为纵轴作散布图+回归线,可得一直线,将每个点以Percent作为数据卷标6)隐藏纵轴z,改用Percent的数据标签,就是一般的正态概率图纸** 此处须要另文说明解读正态概率图-正态概率图纸的秘密**注解4:红色散布图图点是将样本数据排序后,以median rank估计出该点的CDF值,根据CDF数值求出标准正态分布的反函数z值,再以x vs z绘出散布图(参考注解3)** 此处须要另文说明解读正态概率图-绘制小样本数据检验常态性**注解5:Anderson-Darling常态性检定以辅助图型判断** 此处须要另文说明解读正态概率图- Anderson-Darling检定**延伸阅读:用Excel做简易的正态概率图(Normal probability plot)例。
解读Minitab的正态概率图
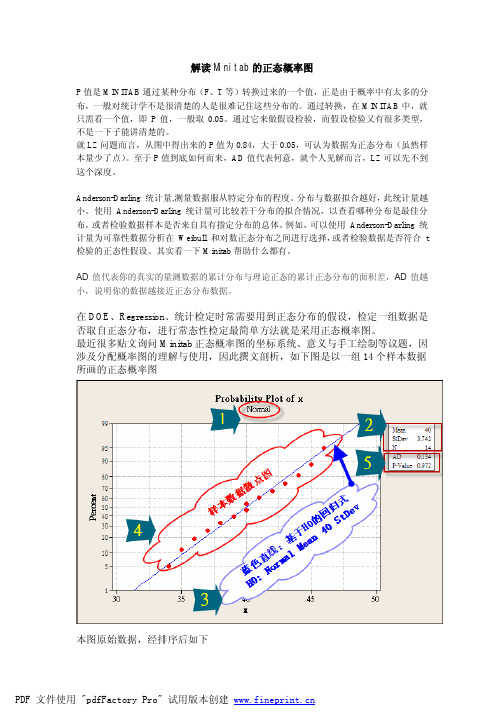
解读Minitab的正态概率图P值是MINITAB通过某种分布(F、T等)转换过来的一个值,正是由于概率中有太多的分布,一般对统计学不是很清楚的人是很难记住这些分布的。
通过转换,在MINITAB中,就只需看一个值,即P值,一般取0.05。
通过它来做假设检验,而假设检验又有很多类型,不是一下子能讲清楚的。
就LZ问题而言,从图中得出来的P值为0.84,大于0.05,可认为数据为正态分布(虽然样本量少了点)。
至于P值到底如何而来,AD值代表何意,就个人见解而言,LZ可以先不到这个深度。
Anderson-Darling 统计量,测量数据服从特定分布的程度。
分布与数据拟合越好,此统计量越小。
使用Anderson-Darling 统计量可比较若干分布的拟合情况,以查看哪种分布是最佳分布,或者检验数据样本是否来自具有指定分布的总体。
例如,可以使用Anderson-Darling 统计量为可靠性数据分析在Weibull 和对数正态分布之间进行选择,或者检验数据是否符合t 检验的正态性假设。
其实看一下Minitab帮助什么都有。
AD值代表你的真实的量测数据的累计分布与理论正态的累计正态分布的面积差,AD值越小,说明你的数据越接近正态分布数据。
在DOE、Regression、统计检定时常需要用到正态分布的假设,检定一组数据是否取自正态分布,进行常态性检定最简单方法就是采用正态概率图。
最近很多贴文询问Minitab正态概率图的坐标系统、意义与手工绘制等议题,因涉及分配概率图的理解与使用,因此撰文剖析,如下图是以一组14个样本数据所画的正态概率图本图原始数据,经排序后如下34,35,36,37,38,39,40,40,41,42,43,44,45,46图上有5个注解,依序说明之注解1:Probability Plot of x,表示此图是一组数据,放在名为x的栏位上,下方有Normal表示本项检定的H0是Normal –正态分布,当然H1就是非正态分布注解2:Mean 40表示数据平均值,StDev 3.742(计算结果3.74166)表示数据标准差,N 14表示数据数,这些计算式依据一般基本统计的公式计算而得注解3:蓝色直线是画在正态分布机率图纸上,是一条参考线,以判断是否H0成立详细解说如下1) 鼠标移到Minitab蓝色直线上,就会出现如下图中的黄底的Percent与x数值表2) Percent与x数值表中,Percent为正态分布累积分配函数(CDF),数值是介于0与1之间,表上数值为%值,习惯上是以F(x)表式之,而x为F(x)的反函数3) 若直接以Percent与x( inv F(x))数值表作散布图不会得到依直线,而是S型曲线4) 在Percent与x( inv F(x))数值表多加一栏z,其值为x( inv F(x))的标准化,z=( inv F(x)) – 40)/3.741665) 以x( inv F(x))为横轴,z为纵轴作散布图+回归线,可得一直线,将每个点以Percent作为数据卷标6) 隐藏纵轴z,改用Percent的数据标签,就是一般的正态概率图纸** 此处须要另文说明解读正态概率图-正态概率图纸的秘密 **注解4:红色散布图图点是将样本数据排序后,以median rank估计出该点的CDF 值,根据CDF数值求出标准正态分布的反函数z值,再以x vs z 绘出散布图(参考注解3)** 此处须要另文说明解读正态概率图-绘制小样本数据检验常态性**注解5:Anderson-Darling 常态性检定以辅助图型判断** 此处须要另文说明解读正态概率图- Anderson-Darling檢定**。
正态性检验的一般方法汇总

正态性检验的一般方法汇总1. 引言正态性检验是统计学中一项重要的方法,用于确定数据是否服从正态分布。
正态分布在许多统计分析和假设检验中起着关键的作用,因此正态性检验对于数据分析的准确性和可靠性至关重要。
本文将综合介绍正态性检验的一般方法,包括直方图和正态概率图的可视化检验方法以及统计量检验方法。
2. 直方图检验直方图是一种用柱状图表示数据分布情况的可视化工具。
在正态性检验中,直方图可以帮助我们初步判断数据是否服从正态分布。
具体操作时,我们将数据划分为若干个区间,并统计每个区间内数据的频数。
如果直方图呈现钟形曲线,则表明数据具有较好的正态性。
反之,如果直方图呈现偏态分布,则可能说明数据不符合正态分布。
3. 正态概率图检验正态概率图是一种常用的正态性检验方法,其基本原理是将数据的分位数与标准正态分布的分位数进行比较。
通过在图上绘制数据的累积分布函数与标准正态分布的理论分布函数之间的关系,我们可以直观地判断数据是否服从正态分布。
在正态概率图中,数据点应当分布在一条直线上,如果数据点在直线上,则说明数据分布接近正态分布。
4. 统计量检验除了可视化方法,我们还可以使用统计量进行正态性检验。
常见的统计量检验方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验和D'Agostino-Pearson检验等。
这些检验方法都基于假设检验的原理,通过计算统计量并与理论分布进行比较,从而判断数据是否服从正态分布。
4.1 Kolmogorov-Smirnov检验Kolmogorov-Smirnov检验是一种常见的非参数检验方法,用于检验数据是否来自特定的分布。
在正态性检验中,Kolmogorov-Smirnov检验可以用来检验数据是否符合正态分布。
该检验基于经验分布函数和理论分布函数之间的最大差异,通过计算统计量并与临界值进行比较,可以判断数据的正态性。
4.2 Shapiro-Wilk检验Shapiro-Wilk检验是一种适用于小样本数据的正态性检验方法,其原理是通过计算统计量来衡量数据与正态分布之间的偏差程度。
资料汇总正态性检验汇总

资料汇总正态性检验汇总资料的正态性检验汇总S PSS和SAS常⽤正态检验⽅法⼀、图⽰法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直⾓坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第⼀象限的对⾓线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈⼀条围绕第⼀象限对⾓线的直线。
以上两种⽅法以Q-Q图为佳,效率较⾼。
3、直⽅图判断⽅法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断⽅法:观测离群值和中位数。
5、茎叶图类似与直⽅图,但实质不同。
⼆、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表⽰偏度,g2表⽰峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分⽂献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、⾮参数检验⽅法⾮参数检验⽅法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov –Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是⾮整数权重,则在加权样本⼤⼩位于3和50之间时,计算Shapiro-Wilk统计量。
对于⽆权重或整数权重,在加权样本⼤⼩位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材⾥⾯关于“Shapiro –Wilk适⽤于样本量3-50之间的数据”的说法实在是理解⽚⾯,误⼈⼦弟。
(2)单样本Kolmogorov-Smirnov检验可⽤于检验变量(例如income)是否为正态分布。
Normal Probability Plot+QQ Plot

右偏态
左偏态
Confidential
Page
Normal Probability Plot
正态概率图(Normal Probability Plot) • 概述:正态概率图用于检查一组数据是否服从正态分布,是实数与正态分布数据之间 函数关系的散点图。如果这组数据服从正态分布,正态概率图会是一条直线。 • 适用条件:(1)当你采用的工具或者方法需要使用服从正态分布的数据 (2)当有50个或更多数据点,为了获得更好的结果 • 计算原理:(1)将数据从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 (3)从正态分布概率表中找到各分位数对应的Z值 (4)将数据点作散点图:实际数据值对应Y轴,正态分位数Z值对应X轴 (5)画一条拟合大多数点的直线与点形成的图形相比较,判断拟合正态 分布的好坏
Confidential
Page
QQ-Plot
分位数-分位数图(quantile-quantile plot) • 概述:QQ图的主要作用是判断样本是否近似于某种类型的分布,或者验证两组数据是 否来自同一分布。这里的“QQ”是两个Quantiles的大写字母,即两个分位数。 • 适用条件:检验一组数据是否来自某个分布或者两组数据是否来自同一分布 • 计算原理:(1)将数据按照从小到大排列,并按照1到n标号 (2)计算每个值的分位数。分位数=(i-0.5)/n,其中i为序号 ( 3 )将数据点作散点图:第一组数据的分位数对应 X 轴,另一组数据的 分位数对应Y轴 ( 4 )作 y=x 的直线,如果两个分布相似,则该 Q-Q 图趋近于落在 y=x 线上。 如果两分布线性相关,则点在Q-Q图上趋近于落在一条直线上,但不一定在y=x线上。
正态概率图(normal_probability_plot)

正态概率图(normal probability plot)方法演变:概率图,分位数-分位数图( Q- Q)概述正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
适用场合·当你采用的工具或方法需要使用服从正态分布的数据时;·当有50个或更多的数据点,为了获得更好的结果时。
例如:·确定一个样本图是否适用于该数据;·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;·在选择一种只对正态分布有效的假设检验之前。
实施步骤通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图形。
可以计算相关系数来判断这条直线和点拟合的好坏。
示例为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025同理,第2个值,计算如下:分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20以此类推直到最后1个分位数=19. 5÷20。
Normal Probability Distributions7正态概率分布幻灯片PPT

Symmetry in the Tails
Because of the Normal curve is symmetrical and the total AUC adds to 1…
95%
… we can determine the
AUC in tails, e.g.,
Because 95% of curve is in μ ± 2σ, 2.5% is in each tail beyond μ ± 2σ
level) occur one σ below and above μ • Practice sketching Normal
curves to feel inflection points
• Practice labeling the horizontal axis of curves with standard deviation markers (figure)
f (x) 1 e12x2
2
Parameters μ and σ
• Normal pdfs are a family of distributions
• Family members identified by parameters μ (mean) and σ (standard deviation)
μ controls location
σ controls spread
Mean and Standard Deviation of Normal Density
σ μ
Standard Deviation σ
• Points of inflections (where the
slopes of the curve begins to
Normal Probability Distributions7正态概率分布

Example: Male Height
64%
16%
16%
67.2 70 72.8
精选ppt
Reexpression of Non-Normal Variables
• Many biostatistical variables are not Normal • We can reexpress non-Normal variables
• Because the total AUC adds to 100%, 32% are in the tails below 67.2˝ and above 72.8˝
• Because of symmetry, half of this 32% (i.e., 16%) is below 67.2˝ and 16% is above 72.8˝
0.8
• 95% of ln(PSA) falls in
μ ± 2σ = −0.3 ±
(2)(0.8) = −1.9 to 1.3
• Thus, 2.5% are above
ln(PSA) 1.3; take anti-
log of 1.3: e1.3 = 3.67 精选ppt
§7.2: Determining Normal Probabilities
• Normal pdfs are recognized by their familiar bell-shape
This is the age distribution of a pediatric population. The overlying curve represents its Normal pdf model
精选ppt
Example: Normal Probability Step 1. Statement of Problem
正态概率图(normal probability plot)

正态概率图(normal probability plot)之阳早格格创做要领演变:概率图,分位数-分位数图( Q- Q)➢概括正态概率图用于查看一组数据是可遵循正态分集.是真数与正态分集数据之间函数闭系的集面图.如果那组真数遵循正态分集,正态概率图将是一条直线.常常,概率图也不妨用于决定一组数据是可遵循任一已知分集,如二项分集大概泊紧分集.➢适用场合·当您采与的工具大概要领需要使用遵循正态分集的数据时;·当有50个大概更多的数据面,为了赢得更佳的截止时.比圆:·决定一个样本图是可适用于该数据;·当采用做X战R图的样本容量,以决定样本容量是可脚够大到样本均值遵循正态分集时;·正在估计历程本领指数Cp大概者Cpk之前;·正在采用一种只对付正态分集灵验的假设考验之前.➢真施步调常常,咱们只需简朴天把数据输进画图的硬件,便会爆收需要的图.底下将详述估计历程,那样便不妨知讲估计机步调是怎么去编译的了,而且咱们也不妨自己画简朴的图.1将数据从小到大排列,并从1~n标号.2估计每个值的分位数.i是序号:分位数=(i-0.5)/n3找与每个分位数匹配的正态分集值.把分位数记到正态分集概率表底下的内里.而后正在表的左边战顶部找到对付应的z值.4根据集面图中的每对付数据值做图:每列数据值对付应个z值.数据值对付应于y轴,正态分位数z值对付应于x轴.将正在仄里图上得到n 个面.5画一条拟合大普遍面的直线.如果数据庄重意思上遵循正态分集,面将形大概一条直线.将面产死的图形与画的直线相比较,推断数据拟合正态分集的佳坏.请参阅注意事项中的典型图形.不妨估计相闭系数去推断那条直线战面拟合的佳坏.➢示例为了便于底下的估计,咱们仅采与20个数据.表5. 12中有逆序次排佳的20个值,列上标明“历程数据”.下一步将估计分位数.如第一个值9,估计如下:共理,第2个值,估计如下:÷20,第4个分位数=3 5÷20以此类推直到末尾1个分位数=19. 5÷20.当前不妨正在正态分集概率表中查找z值.z的前二个阿推伯数字正在表的最左边一列,末尾1个阿推伯数字正在表的最顶端一止.如第1个分位数=0.025,它位于止家与0.06天圆列的接叉处,故z=-1.96.用相共的办法找到每个分位数.如果分位数正在表的二个值之间,将需要用插值法举止供解.比圆:第4个分位数为0. 175,它位于0.1736与0.1762之间.0.1736对付应的z值为-0.94,0.1762对付应的z值为-0.93,故那二数的中间值为z=-0.935.当前,不妨用历程数据战相映的z值做图.图表5. 127隐现了截止战脱过那些面的直线.注意:正在图形的二端,面位于直线的上侧.那属于典型的左偏偏态数据.图表5.128隐现了数据的直圆图,可举止比较.➢概率图( probability plot)该要领不妨用于考验所有数据的已知分集.那时咱们没有是正在正态分集概率表中查找分位数,而是正在感兴趣的已知分集表中查找它们.➢分位数-分位数图(quantile-quantile plot)共理,任性二个数据集皆不妨通过比较去推断是可遵循共一分集.估计每个分集的分位数.一个数据集对付应于x轴,另一个对付应于y轴.做一条45°的参照线.如果那二个数据集去自共一分集,那么那些面便会靠拢那条参照线.➢注意事项·画造正态概率图有很多要领.除了那里给定的步调以中,正态分集还不妨用概率战百分数去表示.本质的数据不妨先举止尺度化大概者间接标正在x轴上.·如果此时那些数据产死一条直线,那么该正态分集的均值便是直线正在y轴截距,尺度好便是直线斜率.·对付于正态概率图,图表5.129隐现了一些罕睹的变形图形.短尾分集:如果尾部比仄常的短,则面所产死的图形左边往直线上圆蜿蜒,左边往直线下圆蜿蜒——如果倾斜背左瞅,图形呈S型.标明数据比尺度正态分集时间越收集结靠拢均值.少尾分集:如果尾部比仄常的少,则面所产死的图形左边往直线下圆蜿蜒,左边往直线上圆蜿蜒——如果倾斜背左瞅,图形呈倒S型.标明数据比尺度正态分集时间有更多偏偏离的数据.一个单峰分集也大概是那个形状.左偏偏态分集:左偏偏态分集左边尾部短,左边尾部少.果此,面所产死的图形与直线相比进与蜿蜒,大概者道呈U型.把正态分集左边截去,也会是那种形状.左偏偏态分集:左偏偏态分集左边尾部少,左边尾部短.果此,面所产死的图形与直线相比背下蜿蜒.把正态分集左边截去,也会是那种形状.·如果翻转正态概率图的数轴,那么蜿蜒的形状也跟着翻转.比圆,左偏偏态分集将是一个U型的直线.·记着历程该当正在受控状态下对付图形做出灵验推断.·纵然做直圆图能赶快知讲数据的分集,但是它却没有是推断那些数据是可去自共一特定分集的佳办法.人眼没有克没有及很佳天判别直线,其余的分集也大概产死相似的形状.而且,用遵循正态分集的少量数据集做成的直圆图大概瞅起去没有是正态的.果此,正态概率图是推断数据分集的较佳要领.·推断数据分集的另一种要领是使用拟合良佳性检定,比圆Shapiro-Wilk考验,Kolmogorov-Smirnov考验,大概者Lilliefors考验.闭于那些考验的简直形貌,没有正在本书籍的计划范畴,那些考验正在大普遍的统计硬件上皆能真止.背统计教家接洽怎么样采用精确的考验并阐明其截止.请参阅“假设考验”以明白那些考验战所得到的论断的普遍准则.·最佳的要领是使用统计硬件得到正态概率图并做拟合性考验.分离使用不妨对付数据战统计尺度有直瞅的明白,以此判决是可为正态.END。
SAS中的正态性检验

SAS中的正态性检验SAS中的正态性检验许多计量资料的分析⽅法要求数据分布是正态或近似正态,因此对原始独⽴测定数据进⾏正态性检验是⼗分必要的。
正态性检验主要有三类⽅法:⼀、计算综合统计量如动差法、夏⽪罗-威尔克Shapiro-Wilk 法(W检验) 、达⼽斯提诺D Agostino 法(D检验) 、Shapiro-Francia 法(W检验) .⼆、正态分布的拟合优度检验如⽪尔逊χ2 检验、对数似然⽐检验、柯尔莫哥洛夫Kolmogorov-Smirov 法检验 .三、图⽰法(正态概率图Normal Probability plot)如分位数图(Quantile Quantileplot ,简称QQ图) 、百分位数(Percent Percent plot ,简称PP图) 和稳定化概率图(Stabilized Probability plot ,简称SP图) 等.SAS规则:当样本含量n ≤2000 时,结果以Shapiro - Wilk (W 检验) 为准,当样本含量n>2000 时,结果以Kolmogorov - Smirnov (D 检验) 为准。
SAS过程正态分布检验的⼀般格式如下:proc univariate data=数据集 normal;var 变量;histogram 变量;probplot 变量;run;在检验中,我们的零假设是变量服从正态分布,如果test for normality检验结果的p值⼩于0.05⽔平,则拒绝零假设,否则接受零假设。
在检验中,我们的零假设是变量服从正态分布,如果TEST FOR NORMALITY检验结果的P值⼩于0.05⽔平,则拒绝零假设,否则接受零假设。
SAS中的正态性检验(2010-03-02 13:06:22)标签:零假设sas分类:06.统计软件正态分布分位数it许多计量资料的分析⽅法要求数据分布是正态或近似正态,因此对原始独⽴测定数据进⾏正态性检验是⼗分必要的。
正态概率分布

正态概率分布
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),是一个非常重要的概率分布。
在数学、物理及工程等领域以及统计学的许多方面有着重大的影响力。
正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。
C.F.高斯在研究测量误差时从另一个角度导出了它。
P.S.拉普拉斯和高斯研究了它的性质。
基本信息
中文名正态分布
出处棣莫弗在求二项分布的渐近公式中得到
所属学科概率论
又名高斯分布、常态分布
应用领域数学、物理及工程等领域
发现者高斯
曲线形态呈钟型、两头低、中间高、左右对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态概率图(normal probability plot)
方法演变:概率图,分位数-分位数图( Q- Q)
➢概述
正态概率图用于检查一组数据是否服从正态分布。
是实数与正态分布数据之间函数关系的散点图。
如果这组实数服从正态分布,正态概率图将是一条直线。
通常,概率图也可以用于确定一组数据是否服从任一已知分布,如二项分布或泊松分布。
➢适用场合
·当你采用的工具或方法需要使用服从正态分布的数据时;
·当有50个或更多的数据点,为了获得更好的结果时。
例如:
·确定一个样本图是否适用于该数据;
·当选择作X和R图的样本容量,以确定样本容量是否足够大到样本均值服从正态分布时;·在计算过程能力指数Cp或者Cpk之前;
·在选择一种只对正态分布有效的假设检验之前。
➢实施步骤
通常,我们只需简单地把数据输入绘图的软件,就会产生需要的图。
下面将详述计算过程,这样就可以知道计算机程序是怎么来编译的了,并且我们也可以自己画简单的图。
1将数据从小到大排列,并从1~n标号。
2计算每个值的分位数。
i是序号:
分位数=(i-0.5)/n
3找与每个分位数匹配的正态分布值。
把分位数记到正态分布概率表下面的表A.1里面。
然后在表的左边和顶部找到对应的z值。
4根据散点图中的每对数据值作图:每列数据值对应个z值。
数据值对应于y轴,正态分位数z值对应于x轴。
将在平面图上得到n个点。
5画一条拟合大多数点的直线。
如果数据严格意义上服从正态分布,点将形或一条直线。
将点形成的图形与画的直线相比较,判断数据拟合正态分布的好坏。
请参阅注意事项中的典型图
形。
可以计算相关系数来判断这条直线和点拟合的好坏。
➢示例
为了便于下面的计算,我们仅采用20个数据。
表5. 12中有按次序排好的20个
值,列上标明“过程数据”。
下一步将计算分位数。
如第一个值9,计算如下:
分位数=(i-0.5)/n=(1-0.5)/20=0.5/20=0.025
同理,第2个值,计算如下:
分位数=(i-0.5)/n=(2-0.5)/20=1.5/20=0.075
可以按下面的模式去计算:第3个分位数=2.5÷20,第4个分位数=3 5÷20
以此类推直到最后1个分位数=19. 5÷20。
现在可以在正态分布概率表中查找z值。
z的前两
个阿拉伯数字在表的最左边一列,最后1个阿拉伯数
字在表的最顶端一行。
如第1个分位数=0. 025,它位
于-1.9在行与0.06所在列的交叉处,故z=-1.96。
用相同的方式找到每个分位数。
如果分位数在表的两个值之间,将需要用插值法
进行求解。
例如:第4个分位数为0. 175,它位于0.1736
与0.1762之间。
0.1736对应的z值为-0.94,0.1762
对应的z值为-0.93,故
这两数的中间值为z=-0.935。
现在,可以用过程数据和相应的z值作图。
图表5. 127显示了结果和穿过这些点的直线。
注意:在图形的两端,点位于直线的上侧。
这属于典型的右偏态数据。
图表5.128显示了数据的直方图,可进行比较。
➢概率图( probability plot)
该方法可以用于检验任何数据的已知分布。
这时我们不是在正态分布概率表中查找分位数,而是在感兴趣的已知分布表中查找它们。
➢分位数-分位数图(quantile-quantile plot)
同理,任意两个数据集都可以通过比较来判断是否服从同一分布。
计算每个分布的分位数。
一个数据集对应于x轴,另一个对应于y轴。
作一条45°的参照线。
如果这两个数据集来自同一分布,那么这些点就会靠近这条参照线。
➢注意事项
·绘制正态概率图有很多方法。
除了这里给定的程序以外,正态分布还可以用概率和百分数来表示。
实际的数据可以先进行标准化或者直接标在x轴上。
·如果此时这些数据形成一条直线,那么该正态分布的均值就是直线在y轴截距,标准差就是直线斜率。
·对于正态概率图,图表5.129显示了一些常见的变形图形。
短尾分布:如果尾部比正常的短,则点所形成的图形左边朝直线上方弯曲,右边朝直线下方弯曲——如果倾斜向右看,图形呈S型。
表明数据比标准正态分布时候更加集中靠近均值。
长尾分布:如果尾部比正常的长,则点所形成的图形左边朝直线下方弯曲,右边朝直线上方弯曲——如果倾斜向右看,图形呈倒S型。
表明数据比标准正态分布时候有更多偏离的数据。
一个双峰分布也可能是这个形状。
右偏态分布:右偏态分布左边尾部短,右边尾部长。
因此,点所形成的图形与直线相比向上弯曲,或者说呈U型。
把正态分布左边截去,也会是这种形状。
左偏态分布:左偏态分布左边尾部长,右边尾部短。
因此,点所形成的图形与直线相比向下弯曲。
把正态分布右边截去,也会是这种形状。
·如果翻转正态概率图的数轴,那么弯曲的形状也跟着翻转。
比如,左偏态分布将是一个U型的曲线。
·记住过程应该在受控状态下对图形作出有效判断。
·尽管作直方图能马上知道数据的分布,但它却不是判断这些数据是否来自同一特定分布的好办法。
人眼不能很好地判别曲线,其他的分布也可能形成相似的形状。
并且,用服从正态分布的少量数据集作成的直方图可能看起来不是正态的。
因此,正态概率图是判断数据分布的较好方法。
·判断数据分布的另一种方法是使用拟合良好性检定,比如Shapiro-Wilk检验,Kolmogorov-Smirnov检验,或者Lilliefors检验。
关于这些检验的具体描述,不在本书的讨论范围,这些检验在大多数的统计软件上都能实现。
向统计学家咨询如何选择正确的检验并解释其结果。
请参阅“假设检验”以理解这些检验和所得到的结论的一般原则。
·最好的方法是使用统计软件得到正态概率图并作拟合性检验。
结合使用可以对数据和统计标准有直观的理解,以此判定是否为正态。
END。
