第三讲--托勒密定理及其应用
托勒密定理

感谢观看
托勒密定理
数学几何学术语ຫໍສະໝຸດ 01 定理提出03 验证推导 05 运用要点
目录
02 定理定义 04 定理推广
托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。原文:圆的内接四 边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。从这个定理 可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本 性质.
定理定义
指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
验证推导
一、(以下是推论的证明,托勒密定理可视作特殊情况。) 在任意凸四边形ABCD中(如图1),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE. 则△ABE∽△ACD 所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD, 所以△ABC∽△AED. BC/ED=AC/AD,即ED·AC=BC·AD (2) (1)+(2),得 A C ( B E + E D ) = A B ·C D + A D ·B C 又因为BE+ED≥BD (仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”) 复数证明
定理提出
图1一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
摘出并完善后的托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
定理表述:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩 形的面积之和。
托勒密定理及应用_沈文选

∠ ★数学竞赛初级讲座 ★托 勒 密 定 理 及 应 用湖南师大数学奥林匹克研究所 沈文选上依次排列的四点, 则1 基础知识托勒密定理 圆内接四边形的两组对边乘积之和等于两对角线的乘积.证明:如图 1, 四边形 ABCD 内接 ⊙O , 在 BD 上 取点 P , 使 ∠PAB = ∠CAD , 则 ■ ABP ∽ ■ ACD , 于是AB ·CD +BC · A D =AC ·BD . ④ 四边形中的托勒密定理 设四边形 ABCD 为任意凸四边形, 则 AB ·CD +BC · AD ≥AC ·BD . ⑤当且仅当 A 、B 、C 、D 四点共圆时取等号. 证 明:如 图 2, 取 点 E 使 ∠BAE = ∠CAD , ∠ABE = ∠ACD , 则■ABE ∽ ■ACD , 即有 AB = BP*AB · C D = AC · AD = AC , 且 AC = CD , 即AC CD AE AB AB BE BP .又■ABC ∽■ APD , 有 BC · AD = AC · P D .上述两乘积式相加, 得AB ·CD +BC · A D =AC (BP +PD )=AC ·BD .① 注:此定理有多种证法, 例如也可这样证:作 AE ∥BD 交⊙O 于 E , 连结 EB 、ED , 则知四边形 BDAE 为等腰梯形, 有 EB = AD , ED = AB , ∠ABD =∠BDE =θ, 且∠EBC +∠EDC =180°, 令 ∠BAC =φ, AC 与 BD 交于点 G , 则S 四边形ABCD = 1 AC ·BD ·sin ∠ AGD = 1AC ·BD ·AB ·CD =AC ·BE . (*)又 ∠DAE = ∠CAB , 有■ ADE ∽■ACB , 亦有 AD ·BC =AC ·ED . (**)由(*)式与(**)式, 注意到 BE +ED ≥BD , 有 AB ·CD +BC · A D =AC ·(BE +ED )≥ AC · B D . 其中等号当且仅当 E 在BD 上, 即∠ABD =∠ACD 时成立.此时 A 、B 、C 、D 四点共圆.由此, 即有托勒密定理的逆定理 在凸四边形 ABCD 中, 若 AB ·CD +BC · A D =AC ·BD , 则 A , B , C , D 四点 共圆.2 综合应用2 sin (θ+φ)= 1 AC · B D ·sin ∠EDC , 2 S 四边形EBCD = S ■EBC + S ■ECD = 21EB · BC 22 .1 恰当地选择或作出四边形, 是应用托勒密定理的关键例 1 在■ABC 中, 角 A 、B 、C 的对边分别为 a 、 ·sin ∠EBC + 1 ED · D C ·sin ∠EDC = 1 (EB · B C +b 、c .若角 A 、B 、C 的大小成等比数列, 且 b 2 -a 2 = 2 2ac , 则角 B 的弧度数等于多少? (1985 年全国高中联 ED · DC )· sin ∠EDC = 1(AD · BC + AB · DC )2·sin ∠EDC .易知 S 四边形AB CD =S E BC D , 从而有 AB · DC +BC · AD = AC · B D .推论 1 (三弦定理)如果 A 是圆上任意一点, AB , AC , AD 是该圆上顺次的三条弦, 则AC · sin ∠BAD = AB · sin ∠CAD + AD · sin ∠CAB . ② 事实上, 由①式, 应用正弦定理将 BD , DC , BC 换掉即得②式.推论 2 (四角定理)四边形 ABCD 内接于 ⊙O , 则 sin ∠ADC ·sin ∠BAD =sin ∠ABD · sin ∠BDC + sin ∠ADB ·sin ∠DBC . ③ 事实上, 由①式, 应用正弦定理将六条线段都换掉即得③式.直线上的托勒密定理 若 A 、B 、C 、D 为一直线赛题)解:如图 3 , 过点 C 作 CD ∥ AB 交■ ABC 的外接圆于D , 连结AD , 则 四边形 ABCD 为 等腰梯形.由托勒密定理, 有 b 2 =a 2 + c ·CD .由已知有 b 2 = a 2 + c · a , 则CD =a , 从而 AD =DC = CB , 即 ADC =2 BC , 亦即 ∠B =2 ∠BAC .又因为在■ ABC 中, ∠A 、∠B 、∠C 的大小成等比数列, 则公比 q = ∠B=2 .从而, ∠A +∠B + ∠CA=∠A +2 ∠A +4 ∠ A =7 ∠ A =π, 故∠ A = π, ∠B7=2π为所求. 7例 2 凸四边形 ABCD 中, ∠ABC =60°, ∠BAD3 331°= =∠BCD =90°, AB =2, CD =1, 对角线 AC 、BD 交于 点O , 如图 4, 求 sin ∠AOB .(1996 年北京中学生数学竞赛题)解:因∠BAD =∠BCD =90°, 则 A 、 B 、 C 、D 四 点共 圆, 延 长 BA , CD 交 于 P , 则 ∠ ADP = ∠ABC =60°.设 AD =x , 有 AP = 3 x , DP =2 x .由割线定理, 有(2 + x )· 3 x =2 x (1 +2 x ).求得 AD = x =AB · AF ·sin (α+β)+1AC · A F ·sin α 2= AF(AB · C D + AC · B D ), 4R其中 R 为外接圆半径 .又 S 四边形AMDN = 1 AM · AD ·sin α+ 1AD · AN ·2 2sin (α+β)= 2AD [ AF · c o s (α+ β)· s in α+ AF ·c o s α· sin (α+β)]= 1 AD · A F ·sin (2α+β)= AF AD ·BC . 2 -2, BC =BP=4 - 3 . 2 4R2对四边形 ABCD 应用托勒密定理, 有由托勒密定理, 有 AB ·CD +AC ·BD =AD ·BC . 故 S 四边形AMDN =S ■ABC . BD ·AC =(4- 3)(2 -2)+2·1 =10 3-12.例 5 如图 7 , 在■ABC 中, ∠A =60°, AB >AC , 又 S 四边形ABCD =S ■ABD +S ■BC D =(2 3 -2)+ 12·(4- 3)=3 3.2点 O 是外心, 两条高 BE , CF 交于 H 点, 点 M , N 分别在线段BH , HF 上, 且满足 BM =CN .求M H +NHOH的值.(2002 年全国高中联赛题)从而, 1 (10 2 sin ∠AOB =15+6 26-12)· sin ∠AOB = 3 3 .故 2.解法 1 :参见文[ 1] 中的解法 2 .解法 2:同解法 1 , 知 B , C , H , O 四点共 圆, 有 ∠OBH = 例 3 如图 5, 已知在 ■ABC 中, AB > AC , ∠A 的一个外角的角平分线交 ■ABC 的外接圆于点E , 过 E 作 EF ⊥AB , 垂足为 F .求证:2 AF = AB - AC .(1989 年全 国高中联赛题)证明:在 FB 上取点D , 使 FD =FA , 连结 ED 并延长交圆于 G ,连结 AG 、EC , 则 ∠ACE = ∠AGD , ∠ ADG =180°- ∠OCH , 而 BO = OC , BM = CN , 则■OB M ≌■OCN , 从而 OM = ON , ∠BMO = ∠CNO , 由此知 O , M , H , N 四点共圆,且等腰■OMN 的顶角∠MON =∠N HE =120°, 即知 MN =sin 120° 3 .OM sin 30 对四边形 OMHN , 应用托勒密定理, 有 MH · O N+NH · O M = OH · MN , 故 MH +N H = MN = 3 为∠ADE = 180°- ∠EAH = ∠EAC , 从 而 ■ADG ∽ ■ E A C , 且BC = A G .于是, 注意 BC = A G , 有 AD =所求. OH OMAE ·BC , 故 2 AF = A E · B C . 2 .2 注意托勒密定理逆定理的应用和拓广的托勒密定理或托勒密定理推论的应用 EC EC连结 EB , 对四边形 AEBC 应用托勒密定理, 有AB ·EC =AE ·BC +BE · A C ,即 AE ·BC =AB · E C -BE · A C .于是 2 AF = AB ·EC -BE · A C=AB -AC .EC其中 EC =BE 可由 ∠EAB =∠EAH =∠EBC 推得. 例4 如图 6, 在锐角 ■ABC 的 BC 边上有两点 E 、F , 满足∠BAE = ∠CAF , 作 FM ⊥AB , 重足为 M , FN ⊥AC , 垂足为 N , 延长 AE 交 ■ABC 的外接圆于点 D .证 明:四 边 形 AMDN 与 ■ ABC 的面积相等.(2000 年全国高中联赛题)证明:设 ∠BAE = ∠CAF =α, ∠E AF =β , 有 S ■AB C = 1·2例 6 若有四个圆都与第五个圆内切, 第一个与 第二个圆的外公切线的长用 l 12表示, 其他前四个圆中的两两的外公切线也用同样的方法来标记, 且前四个圆以顺时针的顺序排列, 试证明依次以 l 12 、l 23 、l 34 、l 41为边长, 以 l 13 , l 24 为对角线所构成的凸四边形的四个顶点共圆.(《中等数学》数学奥林区克问题高 79)证明:如图 8, 设前四个圆 分 别 为 ⊙O 1 、 ⊙O 2 、 ⊙O 3 、 ⊙O 4 , 第五个圆为⊙O .前四个圆与⊙O 分别内切于 A 、B 、C 、D , 则易知 A 、O 1 、O 三点共线.类似地, 有 B 、O 2 、O ;C 、O 3 、O ;D 、O 4 、O 三点共线.设五 个圆 的 半径 分 别 为 r 1 、r 2 、r 3 、r 4 、R ;∠AOB =α、∠BOC =β 、∠COD =γ、3 312 2 = = ∠DOA =δ;OO 1 =a 、OO 2 =b 、OO 3 =c 、OO 4 =d , 则 a =R -r 1 , b =R -r 2 , c =R -r 3 , d =R -r 4 . BC · C A .试确定 D 点的几何位置, 并证明你的结论. (1998 年 CM O 试题)从而 l 2=O 1 O 2-(r 1 -r 2)2=a 2+b 2-2 ab cos α此题我们改证比其更强的命题如下:-(a -b )2=4ab sin 2 α.2故 l 12 =2 ab sin α.2同理, 可求得 l 23 , l 34 , l 41 , l 13 , l 24 . 要证明以 l 12 、l 23 、l 34 、l 41 为边长, 以 l 13 , l 24 为对角线所构成的凸四边形的四个顶点共圆, 只要证明 l 12 · l 34 +l 23· l 41 =l 13· l 24 , 化简后只要证明 sin α sin r设 D 为锐角■ ABC 内部一点, 求证: DA · D B · AB +DB · DC · BC +DC · D A · C A ≥ AB ·BC ·CA ,等号当且仅当 D 为■ABC 的垂心时才成立.证明:如 图 10 , 作 ED ∥BC , FA ∥ED , 则四边形 BCDE 和四边形 ADEF 均是平行四边 +sin β ·sin δsinα+β sin β +γ2 · 2 形.连结 BF 和 AE .显然四边形BCAF 也 是平行四边 形.于 是 2 2 = 2 · 2, (*)即 sin ∠ADB · s in ∠DBC + sin ∠BDC · sin ∠ ABD = sin ∠ADC ·sin ∠BAD .这由托勒密定理的推论 2 即证.注:对于(*)式也可由正弦定理 AB =2 R sin α2式转换成 AB ·CD +BC ·DA = AC · BD 即证.此例是一个富有应用价值的问题.托勒密定理是这个问题中四个圆均变为点(过该点的线成了“ 点圆”的切线)的情形.例 7 经过 ∠X OY 的平分线上 的一点 A , 任 作一直 线与OX 及 OY 分别相交于P , Q .求AF = E D = B C , EF = AD , EB = CD , BF = AC .对 四 边 形ABEF 和四边形 AEBD , 应用四边形中的托勒密定理(或托勒密不等式)有 AB ·EF +AF · BE ≥ AE ·BF , BD · AE +AD ·BE ≥ AB ·ED , 即 AB · AD +BC · C D ≥AE · A C , BD ·AE + AD ·CD ≥AB ·BC . (*)对上述(*)式中前一式两边同乘 DB 后, 两边同加上 DC ·DA · AC , 然后注意到上述(*)式中的后一式, 有DB ·DA · AB +DB ·DC ·BC +DC ·DA · AC ≥DB · A E · A C +DC ·DA · AC , 证:1 OP + 1等于定值.OQ 即 DB (AB · A D +BC · C D )+DC ·DA ·C A≥ AC (DB · A E +DC · A D )≥AC · A B ·BC . 解:如图 9 , 过 O , P , Q 三点 作 圆, 交 射 线 OA 于 B .设 ∠POA = ∠QOA =α, 对四边形 OPBQ 中的三条弦 OP , OB , OQ应用托勒密定理的推论 1 , 有BO ·sin2 α=OP ·sin α+OQ ·sin α.即 OP + OQ = BO ·sin2α= 2BO ·sin α·c o s α =故 DA ·DB · A B +DB · DC ·BC +DC ·DA · CA ≥ AB ·BC ·CA .其中等号成立的充分必要条件是(*)式中两个不等式中的等号同时成立, 即等号当且仅当四边形 ABEF 及四边形 AEBD 都是圆内接四边形时成立 , 亦即五边形AFEBD 恰是圆内接五边形时等号成立.由于四边形 AFED 为平行四边形 , 所以条件等价于四边形 AFED sin α sin α为矩形(即 AD ⊥BC ), 且 ∠ABE =∠ ADE =90°, 亦等 2 BO ·c o s α. (*)连结 BQ , 由■OPA ∽■OBQ , 有OP ·OQ =OA ·OB . 由(*)式除以上式, 得 1 + 1 =2c o s α 定值).价于 AD ⊥BC 且CD ⊥AB , 所以所证不等式等号成立的充分必要条件是 D 为■ABC 的垂心 .3 强化训练OP OQ OA (注:类似于此例, 应用托勒密定理的推论 1 也可求解如下问题:过平行四边形 ABCD 的顶点 A 作一圆分别与AB , AC , AD 相交于E , F , G .则有 AE · A B + AG · A D =AF · AC .事实上, 若设∠BAC =α, ∠CAD =β , 则有 AE · sin β+ AG ·sin α= AF ·sin (α+ β).对此式两边同乘 AB · AC · AD , 利用三角形的面积公式有 AE · AB · S ■A DC +AG · AD ·S ■ABC =AF · AC ·S ■A B D .而在º ABCD 中, 有 S ■ADC = S ■ABC =S ■ABD , 由 (1)■ABC 为⊙O 内接三角形, AB > AC >BC .点 D 在BC 上, 从 O 点分别作 AB 、AC 的垂线交 AD 于E 、F , 射线 BE 、CF 交于P 点.则 PB =PC +PO 的充要条件是∠BAC =30°. (2) 证明:设 ■ABC 中, ∠ A 、∠B 与 ∠C 的三条 角平分线分别交 ■ABC 的外接圆于 A 1 , B 1 , C 1 , 则 A A 1 +BB 1 +CC 1 >AB +BC +CA .(1982 年澳大利亚 竞赛题)(3) 设六边形 ABCDEF 是凸六边形, 且 AB =BC , 此即证.例 8 设 D 为锐角 ■ABC 内部一点, 且满足条 CD =DE , EF =FA .证明:BC + DE +FA ≥ 3 , 并指BE DA FC 2件:DA ·DB · AB +DB ·DC · B C +DC ·DA ·CA = AB ·出等式在什么条件下成立.(I M O 38 预选题)等,= > (= ( > ( > ()= ( + + +z 3 a b c 3 BC ≥ b c a (4)在 ■ABC 中, ∠A =90°, ∠B < ∠C .过 A 点 = AM .令 ∠ABC =∠EBC =θ, 有BX = BX =c o s2θ, 作■ ABC 的外接圆⊙O 的切线, 交直线 BC 于点D , 设点 A 关于直线BC 的对称点为点E , 作 AX ⊥BE , 垂足为 X , Y 为AX 的中点, BY 与⊙O 交于Z .证明:BD ME 即 AM =c o s2θ. MEEB AB 为■ADZ 的外接圆的切线.(I M O 39 预选题)(5)⊙O 为正■ABC 的外接圆, AD 为 ⊙O 的直 径, 在BC 上任取一点 P (P ≠B , P ≠C ), 设 E 、F 分别为■PAB 、■PAC 的内心, 证明 PD =l PE -PF l.(6)设 G 为■ ABC 的重心, 在■ABC 所在平面上 确定点 P 的位置, 使得 AP · AG +BP · B G +CP · CG 对四边形 ABEZ 应用托勒密定理有 AZ ·BE + AB ·EZ =AE ·BZ .(*)注意 AE =2 AB sin θ=2BE sin θ及∠AZ M = ∠EZ M , 有 AZ = AM=c o s2θ, *式变为EZ MEAZ =2sin θ·c o s2θ BZ 1+c o s2θ由 ∠ABC =θ, 有 ∠CAD =θ, ∠ ADC =90°-2θ,有最 小 值, 并 用 ■ ABC 的 边 长 表 示 这 个最 小 值 (I M O 42 预选题)有 AC AD = cos2θ sin θ 注 意 AC = BC sin θ, 有 AC = BD 2sin θ·c o s2θ AC AZ AC BD训练题解答(1) 先证必要性.连结 OB , OC , 知■EAB , ■FAC 均为等 腰三角形, 且 ∠BPC = ∠AEP + ∠CFD = 2 (∠BAD +∠CAD )=2 ∠B AC = ∠BOC , 知 B , C , P ,O 共圆.由托勒密定理, 有 PB · OC =PC · OB+PO · BC .由 PB =PC +PO 得 OC =BC , 即■OBC为正三角形, 推得∠BAC 1 ∠BOC =30°.2 再证充分性.由∠B AC =30°, 知 ■OBC 为正三角形, 且由∠BPC =∠BOC 知 B , C , P , O 共圆.由托氏定理有 PB · OC =PC · OB +PO · BC , 及 OC =OB = BC , 即得 PB =PC +PO .(2) 对四边形 ACA 1 B 应用托勒密定理, 有 AA 1·BC =AB · A 1 C + AC · A 1 B .令 A 1 B = A 1 C = x , 注意ABx + A 1 C1+c o s2θ .即BD =BZ , 亦即 AZ =BZ , 再由 ∠ZBD=∠CAZ 知 ■ZBD ∽■ZAC , 有 ∠ZCA =∠ZDB .又 ∠ZCA = ∠ABZ = ∠ZAD , 所以 ∠ZAD = ∠ZDC .即 证.(5) 设 P 在BD 内部, 取 AB , AC 中点 M , N , 可证 P 、E 、 M ;P 、F 、N 分别共线.由 ME = AM = AN = NF . 可 证 ■DME ≌■DNF 及 ∠EPF =60°= ∠EDF , 知 P 、D 、F 、E 共圆, 在此圆中应用托勒密定理, 有 PD·EF +PE ·DF =PF · DE .再由■DEF 为正三角形即 证得PD +PE=PF , 若 P 在DC 上有PD +PF =PE .即 证. (6) 设 a , b , c 分别为 ■ ABC 顶点 A , B , C 所对边长.2 x = A 1 B + A 1 C > BC , 有 2 AA 1 =2 BC =下证所求最小值当 P 为重心 G 时取到, 且最小值(AB +AC )·2 x >AB +AC , 即 AA 1 1AB +AC ). 为 AG 2 +BG 2 +CG 2 1 a 2+b 2 +c 2).BC 2 3同理 BB 1 1 BA +BC ), CC 1 1CA +CB ).此三 2 2式相加即证.(3) 令 AC =a , CE =b , AE =c .对四边形 ACEF 应用托勒密不等式, 有 AC ·EF +CE · AF ≥ AE · C F ,设 Γ是过 B 、G 、C 的圆, 中线 AL 交 Γ于 G (在■ ABC 内)和 K , 令 ∠BGK =θ, ∠AGN =φ, ∠BGN=δ(N 为AB 中点).由 L 为BC 中点, 知 B 、C 到 GL的距离相等.即 BG ·sin θ=CG sin φ, 故 BG = C G.同注意 EF = AF , 有FA ≥ c .同理, DE ≥ b , BC≥理 AG = BG . sin φ sin θFC a +b DA c +a BEsin δ sin φ a . b +c1 x +z -y设 R 为圆 Γ的半径, 则 BK =2R ·sin θ, CK =2R·sin φ, BC =2R ·sin δ, 即AG =BG = CG.(*)又设 P令 x =a +b , y =c +a , z =b +c , 有 2 ( yBC CK BK+x +y -z +y +z -x 1 x y x + z y z x 2 y x z x z , 即知 + +≥ (*).故BE +DE +FA 3 .其中等号成立, 即要(*)式中等号 是■ ABC 所在平面上任意一点, 由托勒密不等式, 有 PK · BC ≤BP ·CK +CP ·BK , 等号当且仅当 P 在圆 Γ 上成立.由(*)式, 有 PK · AG ≤BP · BG +CP · C G , 两边同加 AP · AG 得(AP +PK )· AG ≤ AP · A G +BP ·BG DA FC 2成立, 亦即每次应用托氏不等式中等号也成立.从而四边形 ACEF 、四边形 ABCE 、四边形 ACDE 都是圆内接四边形.即六边形 ABCDEF 为圆内接六边形且 a =b =c 成立.即为正六边形时成立.(4) 连结 AE 交BZ 于 M , 连结 ZE 、ZC , 对 ■AXE及截线BY M 应用梅氏定理有EB · XY · AM =1, 即BXBX Y A ME EB.+GP·CG .而AK ≤AP +PK ,则AK ·A G ≤AP·AG +BP·BG +CP·CG.等号当且仅当P 在线段AK 上,且点P 在圆Γ上成立, 即等号当且仅当P 与G 重合时成立.参考文献1 广隶,陆珂.2002 年全国高中数学联赛加试几何题的几种解法.中学数学教学参考, 2002 , 12。
第三章托勒密定理及应用答

第三章 托勒密定理及应用习题A1.由CDE BAE △∽△和CBE DAE △∽△,有4BE AB CE =,4DEAD CE=,对四边形ABCD 应用托勒密定理,有()()416BE DEBD AE CE AB AD CE+⋅+=+=⋅.令CE x =,得方程26160x x +-=,求得2x =(舍去了负值).于是12BE DE CE AE ⋅=⋅=.又8BD BC DC <+=,求得3BE =,4DE =或4BE =,3DE =,总之7BD =为所求.2.连EF ,DF ,由FBC FBD FED FAC ∠=∠=∠=∠,ABF EBF EDF ACF ∠=∠=∠=∠,知EDF EDF △∽△,即EF DE DFAF AC CF==.设其比值为k (k 为参数),则EF kAF =,DE kAC DF kCF =⋅=,对四边形BEFD 应用托勒密定理.有()BE EF DF BF DE +=⋅,即()BE k AF k CF BF k AC ⋅+⋅=⋅⋅注意到BE AC =,消去k ,得BF AF CF =+.3.连AC ,在四边形APCD 中应用托勒密定理,有PA PC AC PB AB += 4.连11l l 11,,B D DC B C ,设CAD α∠=,BAD β∠=,O ⊙的半径为R .由AD 为BC 上中线,可令12ABC ACD ABC S S S k ===△△△.由正弦定理有112sin B D R β=⋅,112sin()C D R αβ=⋅+.对四边形111AB D C 应用托勒密定理,有1112sin 2sin 2sin()AB R αAC R βAD R αβ⋅⋅+⋅⋅=⋅⋅+,消去2R ,两边同乘以 12AB AC AD ⋅⋅得111122ACD ABD ABC AB AB S AC AC S AD AD S ⋅⋅+⋅⋅=⋅⋅△△△,亦即 1112AB AB AC AC AD AD ⋅+⋅=⋅,由此即证.5.连1535,A A A A ,则1514A A A A =,3513A A A A =.对四边形1345A A A A 应用托勒密定理,有 3413151435()A A A A A A A A A A ⋅+=⋅,即1213141413()A A A A A A A A A A +=⋅,由此整理即证.6.对四边形AB A B ''应用托勒密定理,有11a b cc AB A B '''=+⋅,即11111a b c cc c AB A B c '''=+⋅⋅,同理,对四边形B CA C ''',AB BC '',AA BC ''分别应用托勒密定理,有1AB A B c AB B C b AB A C a '''''''⋅⋅=⋅⋅+⋅⋅,1AB B C b abc bb b '''⋅⋅=+,1AB A C a a b c aa a '''''''⋅⋅=+.由此四式即证得结论.7.设圆心O 到AB ,BC ,CA 的距离分别为1x ,2x ,3x ,连接BO 并延长与O ⊙交于D ,连AD ,DC ,则12AD x =,22CD x =,对四边形ABCD 应用托勒密定理有12222x a x c Rb +=.同理,23222x b x a Rc +=,13222x b x c Ra +=.加之1232()2()2()2()x a b x b c x c a R a b c +=+++=++,但123()cx ax bx r a b c ++=++,以上两式相加得123x x x R r ++=+.但11x R h =-,22x R h =-,33x R h =-,由此即证.8.作一直径(11)AB x x =≥的圆,在B 的两侧分别取C ,D 二点,使2BC =,11BD =,于是AC =,AD =,对四边形ABCD 应用托勒密定理,有211CD x ⋅=,将此式与原方程比较得CD =BCD △中,由余弦定理,有1cos 2CBD ∠==-,知120CBD ∠=︒,故14sin120CDx AB ===︒为所求.9.作直径1AC =的圆,并作弦AB b =,AD a =的圆内接四边形ABCD,则DC =BC =.应用托勒密定理,有AD BC AB CD AC BD ⋅+⋅=⋅,即1a b BD =⋅,由此得1BD =,即BD 也是圆的直径,故221a b +=.10.当0x =时,1y =,当0x ≠时,作代换222x t x +=,1122x x t x x =+=+≥sin cos t θy t θ+=+,即1sin cos yt θy θ-=-⋅,以1AB =为直径作圆,作弦sin AC θ=,作弦AD =,则BD =cos BC θ=.由托勒密定理及1CD AB ≤=,有sin cos θy θ+,亦有sin cos sin cos yt t θy θθy θ-=-≤+11t y y ⋅-≤-≤,故22y ≤≤+11.连AC ,CE ,AE ,对四边形APCE 应用托勒密定理,有AC PE AE PC CE PA ⋅=⋅+⋅,而AC AE CE ==,有PE PA PC =+.同理,PD PB PF =+,由此即证. 12.不失一般性,令P 点位于OBF △内部(其中O 为C AB △中心),作1PP AD ⊥于1P ,2PP BE ⊥于2P ,3PP CF ⋅于3P .由P ,O ,1P ,2P 四点共圆,有23180PP O PPO ∠+=︒,知1P ,3P ,O ,2P 四点共圆,即P ,3P ,O ,l P ,2P 共圆,推知l 23PP P △是正三角形,在312PP PP 中,有123213312PP P P PP PP PP PP ⋅=⋅+⋅,即123PP PP PP =+,故PAD PCF S S +△△.13.作ABC △外接圆的直径CF ,并设AF x =,BF y =,则60BFC A ∠=∠=︒,直径2CF d y ==.对四边形BCAF 应用托勒密定理,有cd ax by =+.从而tan tan tan tan 2221tan tan tan tan 2a b A B BFC AFC ax by ax by by cd by by c by x a b A B BFC AFC ax by ax by cd c y cy x--∠-∠-+-=-======-=+∠+∠++⋅+.14.令AB AC a ==,对四边形ABPC 应用托勒密定理,有a PB a PC BC PA ⋅+⋅=⋅,即有PA aPB PC BC =+.对四边形BCAQ 应用托勒密定理,有QA BC a QB a QC ⋅+⋅=⋅,即QA aQC QB BC=-. 15.对四边形ABCD 应用托勒密定理,BC AD BD AC AB CD ⋅+⋅=⋅,即AD AC BC BD CD AB AB ⋅+⋅=.又ABD MCP △∽△及ABC MDQ △∽△,有AD MPAB MC =,AC MQ AB MD =,于是MP MQBC BD CD MC MD⋅+⋅=,注意到=22CD MC MD =即证.16.连EG ,FG 和EF ,对四边形BFGE 应用托勒密定理,有BE FG BF EG BG EF ⋅+⋅=⋅,又FEG FBG ADB ∠=∠=∠,EFG EBG ∠=∠,则EFG ABD △∽△,有FG EG EFAB AD BD==,令其比值为t ,则t BE AB t BF AD t BG BD ⋅⋅+⋅⋅=⋅⋅,消去t ,注意到AD BC =即证.17.作DG AF ∥交1O ⊙于G ,则AG FD =,GF AD =.对四边形AGDF 应用托勒密定理,AD FG AG FD AF GD ⋅=⋅+⋅.由AD 平分BAF ∠,知FD BD =,即AG BD =,由此知GB DA ∥,有GD AB =.故 222AD FD AF GD FD AF AB =+⋅=+⋅. 同理,有22AE FE AF AC =+⋅.此两式相减有2222DA EA DF EF -=-,故DE AF ⊥.18.在直径2AB x =>的圆中,在两个半圆上分别取点C 和,使2AC =,1AD =,则BC =,BD =CD x ⋅,与原方程比较得CD =.在ACD △中,由余弦定理,有1cos 2CAD ∠=-,则120CAD ∠=︒,故sin CD x CAD =∠.19.由222+=,在直径AB =的圆中,在一半圆上取点C ,使AC BC D ,则AD BD =.连CD ,知CD AB ≤2AB CD =⋅≤,即y =又在ABC △中,AC BC AB +≥(当C 与A 或B 重合时,取等号)y ≤≤ 20.设222x y a +=,则01a ≤≤.当0a =时,命题显然成立,当01a <≤时,在直径AB a =的一半圆上取点C ,使AC x =,BC y =,因2222x y a +=+=,则可在另一半圆上取点D ,使BD =,AD =,由托勒密定理,有2x y AB CD a +=⋅≤,即2()()x x y y x y ++-≤≤但222()()()()x xy y x x y y x y x x y y x y +-=++-≤++-21.设点T 在劣弧AB 上,连AT ,BT ,CT ,分别交小圆于点D ,E ,F .连DE ,EF ,FD ,过点T 作公切线RQ .由DFT RTD RTA ACT ∠=∠=∠=∠,有AC DF ∥,有AD ATCF CT=.又 2AM AD AT =⋅,2CP CF CT =⋅,有2222AM AD AT AT CP CF CT CT =⋅=,即AM AT CP CT=.同理,BN BTCP CT=.对圆内接四边形ATBC 应用托勒密定理,有AT BC BT AC TC AB ⋅+⋅=⋅,而AB BC CA ==,则AT BT CT +=,故AM BN CP ++.22.令BC a =,AC b =,AB c =.由BE 平分ABC ∠,有AE AB EC BC =,亦有AE ABAC BC AB=+,即bc AE a c =+.同理,bcAF a b=+.由AE PQ ∥,有AEF Q ∠=∠,从而AEF PCB ∠=∠,注意到FAE BPC ∠=∠,有AEF PCB △∽△,即PB AF a cPC AE a b+==+,即()PB b PC a c PB a ⋅=⋅+-⋅.在圆内接四边形PABC 中,应用托勒密定理,有PB b PC c PA a ⋅=⋅+⋅,故()PC a c PB a PC c PA a +-⋅=⋅+⋅,因此,PC PA PB ++. 23.由()BE AC AF FC AC ⋅=+⋅,AC ,()()AF BC AB FC AF BD CD FC BE AE AF ⋅+⋅=⋅++-=⋅()()AC AF CD FC AC FC AE AF FC AC AF CD FC AE +⋅+⋅-⋅=+⋅+⋅-⋅,又AF CD FC AE ⋅=⋅,则BF AC AF BC AB FC ⋅=⋅+⋅,由托勒密定理之逆,知ABCF 有外接圆.24.连EA ,ED ,由BAE ECD ∠=∠,且CDE EAD ABE ∠=∠=∠,有ABE CDE △∽△,亦有AE AB EC CD=, 即EC AB EA CD ⋅=⋅.在圆内接四边形AEBC 中,应用托勒密定理,有EA BC EB AC EC AB⋅+⋅=⋅,于是222111EB AC EA BC EA BC BC BD BD BD EC AB EC AB EA CD CD CD BD CD DA ⋅⋅⋅=-=-=-===⋅⋅⋅⋅.又ABD CAD ∠=∠,ADB ADC ∠=∠,有ABD CAD △∽△,有AB BDAC AD=.于是22EB AC AB EC AB AC ⋅=⋅,故33EB AB EC AC =. 习题B1.在弧ADC 上取点H ,使AH CD c ==,连HC ,HB ,令AC m =,BD n =,BH p =,易证AHC CDA △∽△,即HC AD d ==.对四边形ABCD ,ABCH 分别应用托勒密定理,有ac bd mn +=,ad bc pm +=.又在弧BCH 上取点K ,使BK CH d ==,由CHB KBH △∽△,有HK BC b ==对四边形ABKH 应用托勒密定理,有ab cd AK p +=⋅.又由KHA BCD =,有AK BD n ==.于是2()()ac bd ad bc m ab cd ++=+,2()()ac bd ab cd n ad bc++=+,由此即求得AC ,BD .2.作AGH △的外接圆1O ,分别截AC ,AD AB 于点H ,Q ,G .易证BCD APE △∽△,即DC BC PE AP =,BD BC AE AP =,即PE AK CD BC BC AP AP =⋅=⋅,AE BD BC AP =⋅.对四边形ABDC 应用托勒密定理,有AE AKAD BC BD AC DC AB BC BC AB AP AP⋅=⋅+⋅=⋅+⋅⋅,故AP AD AE AE AK AB ⋅=⋅+⋅.(*) 同理,由托勒密定理,有AP AQ AE AE AK AG ⋅=⋅+⋅.于是2()AP AQ AP AP PQ AP AP PQ AE AH AK AG ⋅=+=+⋅=⋅+⋅, 即22AP PG PH AP AP PQ AE AH AK AG +⋅++⋅=⋅+⋅从而2AP AE AH AK AG PG PH =⋅+⋅-⋅.由(*)式减去上式,有()()() AP AD AP AE AC AH AK AB AG PG PH -=-+-+⋅,即PA PD PK PI PE PF PG PH ⋅=⋅+⋅+⋅.又22221()24PK PI EF KI KI++≤≤,214PE PF EF ⋅≤,214PG PH GH ⋅≤,故224EF KI GH PA PD ++≥⋅,其中等号当且仅当P 为ABCV △的中心时取得.3.设四边形1234A A A A 内接于以O 为圆心,半径为R 的圆,设点O 在弦13A A ,12A A ,23A A ,34A A ,41A A ,上的射影分别为点0H ,1H ,2H ,3H ,4H .记(0,1,,4)i i h OH i ==…,1S ,2S 与1p ,2p 为123A A A △与34l A A A △的面积与半周长,1r ,2r 为它们的内切圆半径. 考虑含点O 的三角形,不妨设O 在123A A A △内,分别对四边形302A H OH ,110A H OH ,221A H OH ,应用托勒密定理,并注意02H H ,01H H ,12H H 是123A A A △的中位线,有1102()R r p R H H +=⋅.01121023203011102121()()(R H H R H H S h H A h H A h H A h H A h H A h +⋅+⋅+=⋅+⋅+⋅+⋅+⋅+⋅2211222003112011)()()2H A h A A h A A h A A h h h p +⋅+⋅+⋅=++⋅,故1120R r h h h +=++.考虑O 在三角形外部的情形,考虑341A A A △,对四边形140A H H O ,330A H H O ,413A H OH 应用托勒密定理,有220404033434010413()()(R r p R H H R H H R H H R H H S h H A h H A h +=⋅+⋅+⋅+⋅+=⋅-⋅+⋅0303343434433444101334021)()()()2H A h H A h H A h H A h A A h A A h A A h h h p -⋅+⋅-⋅+⋅+⋅-⋅=+-⋅,故2340R r h h h +=+-.在上述情形下,1212342r r h h h h R +=+++-.对一般情形,所求内切圆半径之和等于1h ,2h ,3h ,4h ,2R 并赋以一定的符号之和,这些符号只与点O 相对四边形1234A A A A 的位置有关.因此,这个和与对角线的选取无关. 4.设圆1C 的圆心为O ,半径为r ,连i OA ,(1,2,,)i OB i n =…,在四边形112OA B B 中应用托勒密不等式,有112211112OA B B CO A B OB A B ⋅+⋅≥⋅,即1211222()r B B λr A B λr A A A B →⋅+⋅≥+),故12111222()B B λA B λA A A B +≥+. 同理,迭用托勒密不等式,有23222333()B B λA B λA A A B '+≥+;34333444()B B λA B λA A A B +⋅≥+;…;1111()n n n n n n n B λA B λA A A B ----+⋅≥+,1111()n n n n B B λA B λA A A B +≥+. 将上述几个同向不等式相加,得1223111223-11()n n n n n B B B B B B B B λA A A A A An A A -+++≥+++……+,故21p λp ≥.由托勒密不等式中等号成立的条件是当且仅当四边形112OA B B ,223OA B B ,…,1n n OA B B ,都是圆内接四边形,由圆内接四边形性质,知2323OA A OB B ∠=∠,2132OA A OB B ∠=∠,但2332OB B OB O ∠=∠,则2123OA A OA A ∠=∠,从而1223OA A OA A △∽△,因此1223A A A A =.同理, 23341n A A A A A A ===…,即n 边形12n A A A …为正n 边形.反之,若12n A A A …为正n 边形,将其绕点O 逆时针方向旋转2πn,知12A A →,23A A →,…,1n A A →,从而12B B →,23B B →,…,1n B B →.于是知12n B B B …也是正n 边形,因此有122312n A A A A A A r ===⋅…πsin n,12231π2sin n B B B B B B λr n ====⋅….此时有21p λp =.5.作1O ⊙,O ⊙的公共直径GMK ,其中GM 是1O ⊙的直径,GK 是O ⊙的直径,连CG 交1O ⊙于点N .显然MN KC ∥,于是CN KM KG =,222CN KMf CN CG CG CG CG KG=⋅=⋅=⋅,即f CG =d AG =e BG =ABGC 中应用托勒密定理,有b BGc CG a AG ⋅+⋅=⋅bd ce af +=. 6.首先证EF GH =,MN PQ =.由切线长定理,有()()()()AC BC BD DA AF BF BE AE -+-=-+-=()()2AF AE BE BF EF-+-=,()()()()()AC DA BD BC CH DH DG CG CH CG -+-=-+-=-+()2DG DH GH -=,而()()()()AC B BD DA AC DA BD BC -+-=-+-,故EF GH =.同理MN PQ =.连1O A ,1O E ,3O C ,3O G ,由BAD ∠与BCD ∠互补,知1O AE ∠与3O CG ∠互余,有 13390O AE O CG CO G ∠=︒-∠=∠,即13AE CO G △∽△.于是1313AE CG O E O G R R ⋅=⋅=⋅.同理,24BM DP R R ⋅=⋅.令AE AQ a ==,BM BF b ==,CG CN c ==,DP DH d ==,EF GH m ==,MN PQ n ==.于是,AB a b m =++,CD c d m =++,BC b c n =++,DA d a n =++,()()AC AF CM a m c n =+=+++,()()BD BE DQ b m d n =+=+++.对ABCD 应用托勒密定理,有AC BD AB CD BC DA⋅=⋅+⋅,即()()()()()()a c m nb d m n a b mcd m b c n d a n +++⋅+++=+++++++++,亦即mn ac bd =+.即证.7.设BAN NAC a ∠=∠=,对AB ,AN ,AC 应用三弦定理,则有2cos AN αAB AC ⋅=+,因1sin ()2ABC ABL ACL S S S AL αAB AC ++=⋅⋅+△△△,则cos sin ABC AN AL αα=⋅⋅⋅△S .又在Rt ALK △中,cos AL αAK ⋅=,则sin 2ANK S ABC AN AK αS =⋅⋅=△△.又易知AK AM =,即知ANK ANM △∽△,于是12ANK ANM AKNM S S S ==△△四边形,即证.8.必要性:连OB ,OC ,知EAB △,FAC △均为等腰三角形,且2()2BPC AEP CFD BAD CAD BAC BOC ∠=∠+∠=∠+∠=∠=∠,知B ,C ,P ,O 共圆,由托勒密定理,有PB OC PC OB OP BC ⋅=⋅+⋅,由PB PC PO =+得OC BC =,即OBC △为正三角形,推得1302BAC BOC ∠=∠=︒.充分性:由30BAC ∠=︒,知OBC △为正三角形,且由BPC BOC ∠=∠知B ,C ,P ,O 共圆,由托勒密定理,有PB OC PC OB PO BC ⋅=⋅+⋅,及OC OB BC ==,即得PB PC PO =+. 9.对四边形1ACA B 应用托勒密定理,有111AA BC AB AC AC A B ⋅=⋅+⋅,令11A B AC x ==,注意112x A B ACK BC =+>,有11222()ABx AC x AA AB AC AB AC BC BC+==+⋅>+,即11()2AA AB AC >+.同理,11()2BB BA BC >+,11()2CC CA CB >+,此三式相加即证.10.令AC a =,CE b =,AE c =.对四边形ACEF 应用托勒密不等式,有AC EF CE AF AE CF ⋅+⋅≥⋅,注意EF AF =,有FA c FC a b ≥+.同理。
托勒密定理及圆的其它定理

托勒密定理及圆的其它定理托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理提出定理的内容。
摘出并完善后的托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
定理表述:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理内容指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.则△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,所以△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式: (a−b)(c−d) + (a−d)(b−c) = (a−c)(b −d) ,两边取模,运用三角不等式得。
第3章 托勒密定理及应用

第三章 托勒密定理及应用【基础知识】托勒密定理 圆内接四边形的两组对边乘积之和等于两对角线的乘积. 证明 如图3-1,四边形ABCD 内接于O e ,在BD 上取点P ,使PAB CAD =∠∠,则△ABP ∽△ACD ,于是A图3-1AB BPAB CD AC BP AC CD=⇒⋅=⋅. 又ABC △∽△APD ,有BC AD AC PD ⋅=⋅. 上述两乘积式相加,得 AB CD BC AD AC BP PD AC BD ⋅+⋅=+=⋅().①注 此定理有多种证法,例如也可这样证:作AE BD ∥交o e 于E ,连EB ,ED ,则知BDAE 为等腰梯形,有EB AD =,ED AB =,ABD BDE θ==∠∠,且180EBC EDC +=︒∠∠,令BAC ϕ=∠,AC 与BD 交于G ,则111sin sin()sin 222ABCD S AC BD AGD AC BD AC BD EDC θϕ=⋅⋅=⋅⋅+=⋅⋅∠∠,11sin sin 22EBCD EBC ECD S S S EB BC EBC ED DC EDC =+=⋅⋅+⋅⋅△△∠∠()()11sin sin 22EB BC ED DC EDC AD BC AB DC EDC =⋅+⋅⋅=⋅+⋅⋅∠∠. 易知 ABCD EBCD S S =,从而有AB DC BC AD AC BD ⋅+⋅=⋅.推论1(三弦定理) 如果A 是圆上任意一点,AB ,AC ,AD 是该圆上顺次的三条弦,则sin sin sin AC BAD AB CAD AD CAB ⋅=⋅+⋅∠∠∠.② 事实上,由①式,应用正弦定理将BD ,DC ,BC 换掉即得②式.推论2(四角定理) 四边形ABCD 内接于O e ,则sin sin sin sin ADC BAD ABD BDC ⋅=⋅∠∠∠∠sin sin ADB DBC +⋅∠∠.③ 事实上,由①式,应用正弦定理将六条线段都换掉即得③式.直线上的托勒密定理(或欧拉定理) 若A ,B ,C ,D 为一直线上依次排列的四点,则AB CD BC AD AC BD ⋅+⋅=⋅.注 由直线上的托勒密定理有如下推论:若A ,B ,C ,D 是一条直线上顺次四点,点P 是直线AD 外一点,则sin sin sin sin sin sin APB CPD APD BPC APC BPD ⋅+⋅=⋅∠∠∠∠∠∠.事实上,如图3-2,设点P 到直线AD 的距离为h ,DC BA P图3-2由AB CD AD BC AC BD ⋅+⋅=⋅,有 PAB PCD PAD PBC PAC PBD S S S S S S ⋅+⋅=⋅△△△△△△,用两边及夹角正弦形式的三角形面积表示上式后,两边同除以14PA PB PC PD ⋅⋅⋅即得推论.由上述推论也可证明圆内接四边形中的托勒密定理.证明 如图3-3,在图上取一点P ,连PA 、PB 、PC 、PD ,设PB 交AD 于B ',PC 交AD 于C '.由正弦定理 sin 2AB APB R =∠,sin 2CD CPD R =∠,sin 2AD APD R =∠,sin 2BC BPC R =∠,sin 2ACAPC R=∠,sin 2BDBPD R=∠,其中R 为圆的半径. B'C 'DCBAP图3-3对A 、B '、C '、D 应用直线上的托勒密定理的推论,有sin sin sin sin sin sin sin sin APB CPB APD BPC APB C PD APD B PC ''''⋅+⋅=⋅+⋅∠∠∠∠∠∠∠∠sin sin sin sin APC B PD APC BPD ''=⋅=⋅∠∠∠∠. 故AB CD AD BC AC BD ⋅+⋅=⋅.四边形中的托勒密定理(或托勒密不等式) 设ABCD 为任意凸四边形,则AB CD BC AD ⋅+⋅≥ AC BD ⋅,当且仅当A ,B ,C ,D 四点共圆时取等号.证明 如图3-4,取点E 使BAE CAD =∠∠,ABE ACD =∠∠,则△ABE ∽△ACD ,即有AD ACAE AB=,且AC CDAB BE=,即CB图3-4AB CD AC BE ⋅=⋅.①又DAE CAB =∠∠,有△ADE ∽△ACB ,亦有AD BC AC ED ⋅=⋅.② 由①式与②式,注意到BE ED BD +≥,有AB CD BC AD AC BE ED AC BD ⋅+⋅=⋅+⋅()≥.其中等号当且仅当E 在BD 上,即ABD ACD =∠∠时成立.此时A ,B ,C ,D 四点共圆.由此,即有托勒密定理的逆定理 在凸四边形ABCD 中,若AB CD BC AD AC BD ⋅+⋅=⋅,则A ,B ,C ,D 四点共圆.【典型例题与基本方法】1.恰当地作出或选择四边形,是应用托勒密定理的关键例 1 在ABC △中,角A ,B ,C 的对边分别为a ,b ,c .若角A ,B ,C 的大小成等比数列,且22b a ac =-,则角B 的弧度数等于多少?(1985年全国高中联赛题) 解 如图3-5,过点C 作CD AB ∥交ABC △的外接圆于D ,连AD ,则四边形ABCD 为等腰梯形.由托勒密定理,有22b a c CD =+⋅.cbaDCBA图3-5由已知有22b a c a =+⋅,则CD a =,从而AD DC CB ==,即¼»2ADC BC =,亦即2B BAC =∠∠. 又因为在ABC △中,角A ,B ,C 的大小成等比数列,则公比2Bq A==∠∠,从而A B C ++=∠∠∠ 247πA A A A ++==∠∠∠∠,故π7A =∠,2π7B =∠为所求. 例2 凸四边形ABCD 中,60ABC =︒∠,90BAD BCD ==︒∠∠,2AB =,1CD =,对角线AC ,BD交于点O .如图3-6,求sin AOB ∠. (1996年北京中学生竞赛题)DC BAPO图3-6解 因90BAD BCD ==︒∠∠,则A ,B ,C ,D 四点共圆.延长BA ,CD 交于P ,则ADP ABC =∠∠ 60=︒.设AD x =,有AP =,2DP x =,由割线定理,有(2)2(12)x x +⋅=+.求得2AD x ==,42BPBC == 对ABCD 应用托勒密定理,有(42)2112BD AC ⋅=+⋅=-.又ABCD ABD BCD S S S =+△△12)(42=-+=.从而,112)sin 2AOB ⋅=∠.故sin AOB =∠例3 如图3-7,已知在ABC △中,AB AC >,A ∠的一个外角的平分线交ABC △的外接圆于点E ,过E 作EF AB ⊥,垂足为F .求证:2AF AB AC =-. (1989年全国高中联赛题)H GF EDCBA图3-7证明 在FB 上取点D ,使FD FA =,连ED 并延长交圆于G ,连AG ,EC ,则ACE AGD =∠∠,180180ADG ADE EAH EAC =︒-=︒-=∠∠∠∠(H 在CA 的延长线上),从而△ADG ∽△EAC ,且»»BC AG =.于是,注意BC AG =,有C AE B AD EC ⋅=,故2AE BCAF EC⋅=. 连EB ,对四边形AEBC 应用托勒密定理,有AB EC AE BC BE AC ⋅=⋅+⋅,即AE BC AB EC BE AC ⋅=⋅-⋅.于是2AB EC BE ACAF AB AC EC⋅-⋅==-.其中EC BE =可由EAB EAH EBC ==∠∠∠推得. 注 (1)也可应用三弦定理证明.设DAE EAB α==∠∠,则180FAC α=︒-∠,1802BAC α=︒-∠.对AB ,AE ,AC 应用三弦定理,得sin 180sin 1802sin AB AE AC ααα⋅︒-=⋅︒-+⋅()(),即sin22cos sin AE AB AC AE ααα⋅-==⋅.又在Rt AEF △中,cos AE AF α⋅=,故2AF AB AC =-.(2)也可以应用阿基米德折弦定理证明.由BF FA AC ==,有AB AF FA AC -=+,即2AF AB AC =-. 例4 如图3-8,在锐角ABC △的BC 边上有两点E ,F ,满足BAE CAF =∠∠,作FM AB ⊥于M ,FN AC ⊥于N ,延长AE 交ABC △的外接圆于点D .证明:四边形AMDN 与ABC △的面积相等.(2000年全国高中联赛题)F E DCBAMN图3-8证明 设BAE CAF α==∠∠,EAF β=∠,有11sin()sin 22ABC S AB AF AC AF αβα=⋅⋅++⋅⋅=△ ()4AFAB CD AC BD R⋅+⋅,其中R 为外接圆半径. 又11sin sin()22AMDN S AM AD AD AN ααβ=⋅⋅+⋅⋅+四边形 1[cos()sin cos sin()]2AD AF AF αβαααβ=⋅+⋅+⋅⋅+ 1sin(2)24AF AD AF AD BC Rαβ=⋅⋅+=⋅. 由托勒密定理,有AB CD AC BD AD BC ⋅+⋅=⋅,例5 如图3-9,在ABC △中,60A =︒∠,AB AC >,点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM CN =.求MH NHOH+的值. (2002年全国高中联赛题)O HF EBAMN图3-9解法 1 连OB ,OC ,由三角形外心及垂心性质,知2120BOC A ==︒∠∠,180BHC =︒-∠ 180(90)(90)180120HBC HCB C B A -=︒-︒--︒-=︒-=︒∠∠∠∠∠,即B ,C ,H ,O 四点共圆.在此圆中对四边形BCHO 应用托勒密定理,有 BO CH OH BC BH OC ⋅+⋅=⋅.设ABC △的外接圆半径为R ,则BO OC R ==,且由60A =︒∠,知BC =,即有R CH ⋅+OH BH R =⋅,亦即BH CH H -.而()()MH NH BH BM CN CH BH CH +=-+-=-, 故MH NHOH+=解法2 同解法1,知B ,C ,H ,O 四点共圆,有OBH OCH =∠∠,而BO OC =,BM CN =,则△OBM OCN ≌△,从而OM ON =,BMO CNO =∠∠,由此知O ,M ,H ,N 四点共圆,且等腰△OMN 的顶角120MON NHE ==︒∠∠,即知sin120sin30MN OM ︒=︒对四边形OMHN ,应用托勒密定理,有MH ON NH OM OH MN ⋅+⋅=⋅,故MH NH MNOH OM+==为所求.注 此例的其他证法可参见第四章例2,第十五章例17.例6 已知ABC △内切圆I e 分别与边AB 、BC 切于点F 、D ,直线AD 、CF 分别与I e 交于另一点H 、K .求证:3FD HKFH DK⋅=⋅. (2010年东南奥林匹克题) 证明 设内切圆AC 于点Q ,联结FQ 、DQ 、KQ 、HQ (图略).由△CDK ∽△CFD 及△CQK ∽CFQ △,有DK DC FD FC=及QC QK FC FQ =. 注意到DC QC =,有DK FQ FD QK ⋅=⋅. 同理,有FH DQ FD HQ ⋅=⋅.分别对四边形FDKQ 及FDQH 应用托勒密定理,有 2KF DQ DK FQ ⋅=⋅,2HD FQ FH DQ ⋅=⋅.这两式相乘,有4KF HDFH DK⋅=⋅.又由托勒密定理,有KF HD DF HK FH DK ⋅=⋅+⋅.故43KF HD FD HKFH DK FH DK⋅⋅=⇔=⋅⋅.2.注意托勒密定理逆定理的应用和拓广的托勒密定理或托勒密定理推论的应用例7 若右四个圆都与第五个圆内切,第一个与第二个圆的外公切线的长用12l 表示,其他前四个圆中的两两的外公切线也用同样的方法来标记,且前四个圆以顺时针的顺序排列,试证明依次以12l ,23l ,34l ,41l 为边长,以13l ,24l 为对角线所构成的凸四边形的四个顶点共圆.(《中等数学》1999年第5期高中奥林匹克题)证明 如图3-10,设前四个圆分别为1O e ,2O e ,3O e ,4O e ,第五个圆为O e ,前四个圆与O e 分别内切于A ,B ,C ,D ,则易知A ,1O ,O 三点共线.类似地,有B ,2O ,O ;C ,3O ,O ;D ,4O ,O 三点共线.D图3-10设五个圆的半径分别为1r ,2r ,3r ,4r ,R ;AOB α=∠,BOC β=∠,COD γ=∠,DOA δ=∠;1OO a =,2OO b =,3OO c =,4OO d =,则1a R r =-,2b R r =-,3c R r =-,4d R r =-.从而,2222222121212()2cos ()4sin 2lO O r r a b ab a b ab αα=--=+---=⋅.故12sin2l α=.同理,可求得23l ,34l ,41l ,13l ,24l .要证明以12l ,23l ,34l ,41l 为边长,以13l ,24l 为对角线所构成的凸四边形的四个顶点共圆,只要证明123423411324l l l l l l ⋅+⋅=⋅,化简后只要证明sinsinsinsinsinsin222222αγβδαββγ++⋅+⋅=⋅,①即sin sin sin sin sin sin ADB DBC BDC ABD ADC BAD ⋅+⋅=⋅∠∠∠∠∠∠.这由托勒密定理的推论2即证.注 对于①也可由正弦定理2sin2AB R α=转换成AB CD BC DA AC BD ⋅+⋅=⋅即证.此例是一个富有应用价值的问题.托勒密定理是这个问题中四个圆均变为点(过该点线成了“点圆”的切线)的情形.例8 经过XOY ∠的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q .求证:11OP OQ +为定值.证明 如图3-11,过O ,P ,Q 三点作圆,交射线OA 于B .设POA QOA α==∠∠,对四边形OPBQ 中的三条弦OP ,OB ,OQ 应用托勒密定理的推论1,有BAPQO图3-11sin 2sin sin BO OP OQ ααα⋅=⋅+⋅.即sin 22sin cos 2cos sin sin BO BO OP OQ BO αααααα⋅⋅⋅+===⋅.①连BQ ,由△OPA ∽△OBQ ,有OP OQ OA OB ⋅=⋅.由①式除以上式,得112cos OP OQ OA α+=(定值). 注 类似于此例,应用托勒密定理的推论1,也可求解如下问题:过平行四边形ABCD 的顶点A 作一圆分别与AB ,AC ,AD 相交于E ,F ,G ,则有AE AB AG AD AF AC ⋅+⋅⋅=.事实上,若设BAC α=∠,CAD β=∠,则有sin sin sin()AE AG AF βααβ⋅+⋅=⋅+.对此式两边同乘AB AC AD ⋅⋅,利用三角形的面积公式有ADC ABC ABD AE AB S AG AD S AF AC S ⋅⋅+⋅⋅=⋅⋅△△△.而在ABCD Y 中,有ADCABC ABD SS S ==△△△,由此即证.例9 设D 为锐角ABC △内部一点,且满足条件:DA DB AB DB DC BC DC DA CA ⋅⋅+⋅⋅+⋅⋅ AB BC CA =⋅⋅.试确定D 点的几何位置,并证明你的结论.(1998年CMO 试题)此题我们改证比其更强的命题如下:设D 为锐角ABC △内部一点,求证:DA DB AB DB DC BC DC DA CA AB BC CA ⋅⋅+⋅⋅+⋅⋅⋅⋅≥,并且等号当且仅当D 为ABC △的垂心时才成立.证明 如图3-12,作ED BC ∥,FA ED ∥,则BCDE 和ADEF 均是平行四边形.连BF 和AE ,显然BCAF也是平行四边形,于是AF ED BC ==,EF AD =,EB CD =,BF AC =.对四边形ABEF 和四边形AEBD ,应用四边形中的托勒密定理(或托勒密不等式)有AB EF AF BE AE BF ⋅+⋅⋅≥,BD AE AD BE AB ED ⋅+⋅⋅≥,即AB AD BC CD AE AC ⋅+⋅⋅≥,BD AE AD CD AB BC ⋅+⋅⋅≥.① 对上述①式中前一式两边同乘DB 后,两边同加上DC DA AC ⋅⋅,然后注意到上述①式中的后一式,有 DB DA AB DB DC BC DC DA AC DB AE AC DC DA AC ⋅⋅+⋅⋅+⋅⋅⋅⋅+⋅⋅≥.FEDCBA图3-12即 ()()DB AB AD BC CD DC DA CA AC DB AE DC AD AC AB BC ⋅+⋅+⋅⋅⋅+⋅⋅⋅≥≥. 故 DA DB AB DB DC BC DC DA CA AB BC CA ⋅⋅+⋅⋅+⋅⋅⋅⋅≥.其中等号成立的充分必要条件是①式中两个不等式中的等号同时成立,即等号当且仅当ABEF 及AEBD 都是圆内接四边形时成立,亦即AFEBD 恰是圆内接五边形时等号成立.由于AFED 为平行四边形,所以条件等价于AFED 为矩形(即AD BC ⊥)且90ABE ADE ==︒∠∠,亦等价于AD BC ⊥且CD AB ⊥,所以所证不等式等号成立的充分必要条件是D 为ABC △的垂心. 【解题思维策略分析】1.推导某些重要结论的工具例10 圆内接六边形ABCDEF 的对角线共点的充要条件是1AB CD EFBC DE FA ⋅⋅=.(见第一角元形式的塞瓦定理的推论) 证明 必要性:如图3-13,设AD ,BE ,CF 交于一点P ,则易知△APB ∽△EPD ,△CPD ∽△APF ,△EPF ∽△CPB ,从而,,AB BP CD DP EF FPDE DP FA FP BC BP===.此三式相乘即证. P(C ')FEDC BA图3-13充分性:设1AB CD EFBC DE FA⋅⋅=,AD BE ⋅交于P ,连FP 并延长交圆于C ',连BC ',C D ',则由必要性知1AB C D EF BC DE FA '⋅⋅=',和已知式比较得CD C D BC BC '=',即CD BC BC C D ''⋅=⋅.连BD ,CC ',对四边形BCC D '应用托勒密定理,得BC C D BD CC CD BC '''⋅+⋅=⋅,由此得0BD CC '⋅=.因0BD >,所以0CC '=,即C '与C 重合,于是AD ,BE ,CF 三线共点.例11 O e 是ABC △的外接圆,I 是ABC △的内心,射线AI 交O e 于D .求证:AB ,BC ,CA 成等差数列的充要条件是IBC DBC S S =△△.证明 如图3-14,由5123242BID DBI ==+=+=+=∠∠∠∠∠∠∠∠∠,知DI BD DC ==.D图3-14必要性:若AB ,BC ,CA 成等差数列,即2AB AC BC +=,而△IBA ,△ICA ,IBC △有相等的高,则2IAB IAC IBC S S S +=△△△.又由托勒密定理,有AB DC AC BD AD BC ⋅+⋅=⋅,即()AB AC DI +⋅AD BC =⋅,2AD AB ACDI BC +==,即I 是AD 的中点,于是AIB IBD S S =△△,IAC ICD S S =△△,2IBC IAB S S =+△△ IAC IBD ICD BDC IBC BDC S S S S S S =+==+△△△△△△,故IBC DBC S S +△△.充分性:若IBC DBC S S =△△,即1111sin sin 2222IB BC B DB BC A ⋅⋅=⋅⋅∠∠,有11sin sin 22IB DB A B =∶∠∶∠.比较上述两式,得IA BD =,但DI DB =,即知2AD DI =,仿前由托勒定理知2AB AC ADBC DI+==,即2AB AC BC +=,故AB ,BC ,CA 成等差数列.例12 如图3-15,设I 为ABC △的内心,角A ,B ,C 所对的边长分别为a ,b ,c .求证:22IA IB bc ac++21IC ab=. FEDCBAI图3-15证明 设I 在三边上的射影分别为D ,E ,F .设ABC △的外接圆半径及内切圆半径分别为R ,,则ID IE IF r ===.由B ,D ,I ,F 四点共圆,且IB 为其圆的直径,应用托勒密定理,有DF IB ID BF IF BD ⋅=⋅+⋅ ()r BD BF =+.由正弦定理,有sin 2bDF IB B IB R=⋅=⋅∠,即有()22b IB Rr BD BF ⋅=+.同理,有22()a IB Rr AF AE ⋅=+,22()c IC Rr CD CE ⋅=+,从而2222()a IA b IB c IC Rr a b c ⋅+⋅+⋅=++.又由1()24ABC abc S r a b c R =++=△,有2()Rr a b c abc ++=,故222a IA b IB c IC abc ⋅+⋅+⋅=,即2221IA IB IC bc ac ab++=. 例13 如图3-16,若ABC △与△A B C '''的边长分别为a ,b ,c 与a ',b ',c ',且B B '=∠∠,180A A '+=︒∠∠,则aa bb cc '''=+.A′B'C 'c'b'a'bcbaDCBA图3-16证明 作ABC △的外接圆,过C 作CD AB ∥交圆于D ,连AD ,BD .因180A A A D '+=︒=+∠∠∠∠,BCD B B '==∠∠∠,则A D '=∠∠,B BCD '=∠∠,从而△A B C DCB '''∽△,有A B B C A C DC CB DB ''''''==,即 c a b DC a DB '''==,故ab DC a '='. 又AB CD ∥,知BD AC b ==,AD BC a ==.由托勒密定理,得AD BC AB DC AC BD ⋅=⋅+⋅,即2ac ab a c b a a ''=⋅+⋅''. 故 aa bb cc '''=+.例14 已知O e 的内接锐角ABC △,点O 到ABC △的三边a ,b ,c 的距离分别为a H ,b H ,c H .试证:O e 的半径R 为方程3222()20ab c a b c x H H H x H H H -++-=的根. (《数学通报》1991年第11期问题征解题)证明 如图3-17,设AO ,BO ,CO 的延长线分别交O e 于M ,N ,P .连AP ,BP ,BM ,MC ,NC ,NA .因O 在ABC △内部,则2c BM H =,2b MC H =,2a NC H =,2c NA H =,2b PA H =,2a PB H =.H aH b cb a CBMNOP图3-17在O e 的内接四边形ABMC ,ABCN ,APBC 中分别应用托勒密定理,得 222b c R a c MC b BM H c H b ⋅=⋅+⋅=⋅+⋅, 222c a R b a NA c NC H a H c ⋅=⋅+⋅=⋅+⋅, 222b a R c a PA b PB H a H b ⋅=⋅+⋅=⋅+⋅.即有 000c b c a ba b R a H b H c H a R b H c H a H R c ⋅⎧⋅-⋅-⋅=⎪⋅-⋅+⋅=⎨⎪⋅+-⋅=⎩,,.显然,该方程组关于a ,b ,c 有非零解,于是有 0c bc a baRH H H R H H H R---=-.展开整理,得关于R 的方程为 322220a b c a b c R H H H R H H H ++-=-(),命题获证.例15 如图3-18,在ABC △中,1B ,1C 分别是AB ,AC 延长线上的点,1D 为11B C 的中点,连1AD 交ABC △外接圆于D .求证:1112AB AB AC AC AD AD ⋅+⋅=⋅.(《中等数学》2001年第4期高中训练题)αβD 1B 11DCB图3-18证明 连BD ,CD .设BAD α=∠,CAD β=∠,ABC △外接圆的半径为R .因1D 为11B C 的中点,知11111112AB D AC D AB C S S S ==△△△.在△BCD 中,由正弦定理,有2sin BD R α=⋅,2sin CD R β=⋅,2sin()BC R αβ=⋅+.在圆内接四边形ABCD 中,由托勒密定理得AB CD AC BD AD BC ⋅+⋅=⋅,即2sin 2AB R AB R β⋅⋅+⋅ sin 2sin()AD R ααβ⋅=⋅⋅+, 两边同乘以11114AB AC AD R⋅⋅⋅,得 111111111AC D AB D AB C AB AB S AC AC S AD AD S ⋅⋅+⋅⋅=⋅⋅△△△,即 1112AB AB AC AC AD AD ⋅+⋅=⋅.例16 如图3-19,设1C ,2C 是同心圆,2C 的半径是1C 半径的2倍.四边形1234A A A A 内接于1C ,将41A A 延长交圆2C 于1B ,12A A 延长交圆2C 于2B ,23A A 延长交圆2C 于3B ,34A A 延长交圆2C 于4B .试证四边形1234B B B B 的周长2⨯≥四边形1234A A A A 的周长,并请确定等号成立的条件.(1988年第三届冬令营试题)C 图3-19证明 设同心圆圆心为O ,连1OA ,1OB ,2OB .在四边形112OA B B 中应用推广的托勒密定理,有112112211OB A B OA B B OB A B ⋅⋅+⋅≤.因1212OB OB OA ==,则12121122A B B B A B +≤, 从而 12122211222B B A A A B A B +-≥.①同理,23233322222B B A A A B A B +-≥,34344433222B B A A A B A B +-≥,41411144222B B A A A B A B +-≥. 以上四式相加,得12233441122334412()B B B B B B B B A A A A A A A A ++++++≥.②为使②式中等号成立,当且仅当所加的四式均为等式.而①式等号成立,当且仅当四边形112OA B B 内接于圆.这时,12122141O OA A OB B OB B A A ===∠∠∠∠,即1OA 为412A A A ∠的平分线.同理,2OA ,3OA ,4OA 分别为123A A A ∠,234A A A ∠,341A A A ∠的平分线.这意味着O 为四边形1234A A A A 的内切圆的圆心,故知四边形1234A A A A 为正方形,即当且仅当四边形1234A A A A 为正方形时②式等号成立.例17 如图3-20,设ABCDEF 是凸六边形,满足AB BC CD ==,DE EF FA ==,BCD EFA =∠∠ 60=︒.设G 和H 是这六边形内部的两点,使得120AGB DHE ==︒∠∠.试证:AG GB GH DH +++ HE CF +≥.(第36届IMO 试题)F'C 'E DC BAGH图3-20证明 以直线BE 为对称轴,作C 和F 关于该直线的轴对称点C '和F ',于是C F CF ''=,且ABC '△和△DEF '都是正三角形,G 和H 分别在这两个三角形的外接圆上.由托勒密定理,有 C G AB AG C B GB C A '''⋅=⋅+⋅,即有C G AG GB '=+,同理,HF DH HE '=+.于是 AG GB GH DH HE C G GH HF C F CF ''''++++=++=≥.例18 如图3-21,设M ,N 是ABC △内部的两个点,且满足MAB NAC =∠∠,MBA NBC =∠∠.证明:1AM AN BM BN CM CN AB AC BA BC CA CB⋅⋅⋅++=⋅⋅⋅.(第39届IMO 预选题)KCBAMN图3-21证明 设K 是射线BN 上的点,且满足BCK BMA =∠∠.因BMA ACB >∠∠,则K 在ABC △的外部.又MBA CBK =∠∠,则△ABM ∽△KBC ,即有AB BM AMBK BC CK==. 由ABK MBC =∠∠,AB BM KB BC =,知ABK MBC △≌△,于是AB BK AKBM BC CM==. 由CKN MAB NAC ==∠∠∠,知A ,N ,C ,K 四点共圆.应用托勒密定理,有AC NK AN KC ⋅=⋅+ CN AK ⋅,或()AC BK BN AN KC CN AK ⋅-⋅+⋅∶,将AM BC KC BM ⋅=,BK CM AK BM ⋅=,AB BCBK BM⋅=代入,得AB BC AN AM BC CN BK CMAC BN BM BM BM ⋅⋅⋅⋅⋅⎛⎫-=+ ⎪⎝⎭,即 1AM AN BM BN CM CN AB AC BA BC CA CB ⋅⋅⋅++=⋅⋅⋅.例19 如图3-22,在ABC △中,AB AC =.线段AB 上有一点D ,线段AC 延长线上有一点E ,使得DE AC =.线段DE 与ABC △的外接圆交于T ,P 是线段AT 延长线上的一点.证明:点P 满足PD PE AT +=的充分必要条件是点P 在△ADE 的外接圆上.(2000年国家集训队选拔试题)T ED CBAP图3-22证明 充分性:连BT ,CT .由A ,B ,T ,C ;A ,D ,P ,E 分别四点共圆,知CBT CAT EDP ==∠∠∠,BCT BAT DEP ==∠∠∠,于是△BTC ∽△DPE ,可设DP PE DEk BT CT BC ===.对四边形ABTC 应用托勒密定理,有 AC BT AB CT BC AT ⋅+⋅=⋅.将上式两边同乘以k ,并用前一比例式代入,得 AC DP AB PE DE AT ⋅+⋅=⋅.注意到AB AC DE ==,即得PD PE AT +=.必要性:以D ,E 为两个焦点,长轴长等于AT 的椭圆与直线AT 至多有两个交点,而其中在DE 的一侧,即线段AT 延长线上的交点至多一个,由前面的充分性证明,知AT 的延长线与△ADE 的外接圆的交点Q 在这个椭圆上;而依题设点P 同时在AT 的延长线上和椭圆上,故点P 与点Q 重合,命题获证.2.求解代数问题的一条途径例20 若0a b c >≥≥,且a b c <+,解方程ax =.(1993年南昌市竞赛题)解 因0a b c >≥≥,且a b c <+,所以a ,b ,c 为边可以作一个三角形.作ABC △,使BC a =,AC b =,AB c =,分别作AC ,AB 的垂线,它们交于点D .则四边形ABDC 内接于圆,如图3-23.此时,AD为直径,sin BDBAD AD=∠,sin CDCAD AD==∠,sin aCAB AD=∠.DCA图3-23对AD ,AC ,AB 应用托勒密定理推论1或三弦定理,有sin sin AC BAD AB CAD AD ⋅+⋅=⋅∠∠sin CAB ∠,即ab c AD AD⋅+=⋅,即b c a AD ⋅. 由1sin 22ABC abcS bcCAB AD =⋅=△∠,而ABC S =△,其中1()2P a b c =++,从而AD =例21已知a ,b 是不相等的正数,求函数()f x =的值域.CA图3-24解 因222+=,则可以ACAB =,BC =.如图3-24,在另一半圆上取中点D ,则CD AD ==ABCD 应用托勒密定理,有())f x AB CD BC AD AC BD =⋅+⋅=⋅=.不妨取a b >,则,即AB .而当AB CD ==()max f x =.AB ()f x 是AB 的单调递增函数,()min f x ==AB 时,()f x 是AB 的单调递减函数,从而当AB ,BC ,()min f x=故()f x 在定义域上,()min f x =()f x 的值域为.注 对于一般的函数,()()()f x a A x b B x =⋅+⋅,只要()()22A x B x +=定值,就可以构造圆的内接四边形,灵活运用托勒密定理求其极值或值域. 3.注意广义托勒密定理的应用前面给出的例6是一个很有价值的问题,甚至,我们可以称之为广义托勒密定理.当一个圆的半径无限趋近于0时,圆就趋近于一点,过该点的直线就成了“点圆”的切线.托勒密定理就是例6中内切于O e 的四个圆均变为点的情形. 利用广义托勒密定理可以处理如下问题:例22 已知1O e 与2O e 分别与O e 内切,作1O e 和2O e 的两条内公切线交O e 于A ,B ,作1O e 和2O e 的外公切线,切点为E 和F .求证:EF AB ∥.证明 如图3-25,设G ,H 分别为1O e 与2O e 的内公切线的切点,EF 交O e 于C ,D 两点,记1O e 和2O e 的内公切线长为d .用[]****表示一组与O e 内切的“圆”,并应用广义托勒密定理,则C 'D 图3-25对于1[]A C O D ,,,e ,有 AG CD AC DE CE AD ⋅=⋅+⋅,①对于2[]B D C O ,,,e ,有 BH CD BD CF DF BC ⋅=⋅+⋅ ()BD CE EF DF BC =++⋅.②对于2[]A C D O ,,,e ,有()()AG d CD AC DF AD CE EF +⋅=⋅+⋅+. ③对于1[]B D C O ,,,e ,有()()BH d CD BD CE BC DF EF +⋅=⋅++.④ 由①,③得()()AC DF AD CE EF DC d AC EF FD CE AD ⋅+⋅+-⋅=⋅++⋅,即AD EF DC d AC EF ⋅-⋅=⋅.⑤ 由②,④得()()BD CE BC DF EF DC d BD CE EF DF BC ⋅+⋅+-⋅=⋅++⋅,即BC EF DC d BD EF ⋅-⋅=⋅.⑥ 由⑤与⑥得 ()EF AD AC DC d -=⋅,()EF BC BD DC d -=⋅.故 BC BD AD AC -=-.若四边形ABCD 中不含圆心O ,那ABC ∠,BAD ∠均为锐角.不妨设ABC BAD >∠∠,则AC BD >. 又BDC ACD >∠∠,则BC AD >.所以BC BD AD AC ->-,矛盾.故一定有ABC BAD =∠∠.此时AB DC ∥.若四边形中含圆心,则与之“对称”的四边形A B C D ''''(A ',B ',C ',D '的定义方式与A ,B ,C ,D 的定义方式相似)不含圆心.设CD 交AA '于Y ,C D ''交BB '于X .由已证结论A B C D ''''∥,因为A B B A AB '''=∠∠,C XB DYA ''=∠∠,A B B C XB '''=∠∠,所以DYA A AB ''=∠∠,故AB DC ∥. 例23 如图3-26,1G e 和2G e 内切于G e 的一段弧,并且两圆彼此外切于点W .设A 是1G 和2G 的内公切线与该段弧的交点,而B 和C 是G 中1G 与2G 的外公切线弦的端点,证明:W 是ABC △的内切圆圆心.(IMO -33预选题)图3-26证明 设AW 与BC 的交点为D ,1G e ,2G e 与BC 的切点分别为E ,F ,并设各线段之长为BE x =,CF y =,BD k =,CD h =,AD d =,于是,有DE k x =-,DF h y =-.又因DE DW DF ==,故k x h y -=-,AW d k x d h y =-+=-+.用(A ,1G e )表示点圆A 与1G e 的公切线的长,则()1,A d k x G =-+e .同理,(),A b c =,(),A c b =,()1,B x G =e ,()1,C a x G =-e ,(),B C a =.对1[,,,]A B C G e 应用广义托勒密定理,有()()d k x a b x c a x -+⋅+⋅=⋅-,令()12p a b c =++,则由上式,有()2a x k c d p =+-.同理,对[B ,C ,2G e ,A ],有()2ay h b d P=+-, 注意到k x h y -=-,则()()22a ak k c d h h b d p p -+-=-+-,即有()()b c k ac b c h ab +⋅-=+⋅-,亦即()()()b c k h a c b +-=⋅-.而BD DC BC +=,即k h a +=,于是,()()()()b c k h k h c b +-=+-,即c h b k ⋅=⋅,亦即k ch b=. 此表明BD AB CD AC =,即知AD 平分BAC ∠.所以ac k b c =+,abh b c=+. 得 22ac a ac adk x c d b c p b c p ⎛⎫-=-+-=⎪++⎝⎭. 因而22d d p a b cad k x a ap++===-,于是 111AW AD d a b c b c c BAac DW DW k x a a BD b c+++=-=-=-===-+.由此,即知BW 平分ABC ∠.故W 是ABC △的内心. 【模拟实战】习题A1.A ,B ,C ,D 四点在同一圆周上,且4BC CD ==,E 为AC 与BD 的交点,且6AE =,线段BE 和DE 的长都是整数,则BD 的长等于多少? (1988年全国初中联赛题) 2.在ABC △中,AB AC BC <<,D 在BC 上,E 在BA 的延长线上,且BD BE AC ==,△BDE 的外接圆与ABC △的外接圆交于F 点.求证:BF AF CF =+. (1991年全国初中联褰题)3.已知P 是正方形ABCD 的外接圆»AD 上任一点,求PA PCPB +的值. 4.O e 过ABC △的顶点A ,且分别与AB ,AC 和BC 上的中线AD 相交于1B ,1C ,1D ,则1AB AB ⋅,1AD AD ⋅,1AC AC ⋅成等差数列.5.已知正七边形12A A …7A ,求证:121314111A A A A A A =+. (第21届全俄奥林匹克题)6.在圆内接六边形AB CA BC '''中,令BC a '=,B C a ''=,CA b =,C A b ''=,AB c '=,A B c ''=,1AA a '=,1BB b '=,1CC c '=.求证:111111a b c abc a b c aa a bb b cc c ''''''=++++.7.R ,分别为ABC △的外接圆和内切圆的半径,m ,n ,p 分别在弧»AB ,»BC ,»CA 上,1h ,2h ,3h 分别为弓形AmB ,BnC 和CPA 的高.求证:1232h h h R r ++=-. 8.解方程=.9.已知1=,且01a ≤≤,01b ≤≤.求证:221a b +=. 10.求函数222sin 22cos 2x x y x x θθ+⋅+=+⋅+的值域(θ为参数).11.已知ABC △中,最大角B 与最小角C 的差为»AB 上任一点.求证:PD PE PA PB PC PF +=+++. 12.AD ,BE ,CF 是正ABC △的三条高,任取一点P .试证:在△PAD ,△PBE ,△PCF 中,最大一个的面积等于其余两个的面积之和.13.已知ABC △的60A =︒∠,令BC a =,CA b =,AB c =.求证:tan tan tan tan A B c bA B c --=+. 14.已知P 为等腰ABC △(AB AC =)外接圆»BC 上的一点,Q 为»AB 上一点.求证:PAPB PC=+QAQC QB-.15.已知AB 为O e 的直径,圆周上的点C ,D 分别在AB 的两侧,过CD 中点M 分别作AC ,AD 的垂线,垂足为P ,Q .求证:22BC MP BD MQ MC ⋅+⋅=.16.已知平行四边形ABCD 中,过B 的圆分别交AB ,BC ,BD 于E ,F ,G 求证:BE AB BF BC ⋅+⋅ BG BD =⋅.17.设AF 为1O e 与2O e 的公共弦,点B ,C 分别在1O e ,2O e 上,且AB AC =,BAF ∠,CAF ∠的平分线交1O e ,2O e 于点D ,E 求证:DE AF ⊥.18.19.求函数,)y a b +=∈R 的值域.20.已知221(,)x y x y ++∈R ≤.求证:222x xy y +-21.已知两圆内切于点T ,ABC △是大圆的内接正三角形,过A ,B ,C 作小圆的切线AM ,BN ,CP ,且M ,N ,P 为切点.求证:CP ,AM ,BN 三条线段中,一条线段等于另外两条线段之和.22.在ABC △中,BC AC AB >>,外接圆为Γ.三条内角平分线分别交BC ,CA 和AB 于点D ,E 和F ,通过点B 的直线平行于EF 交圆Γ于点Q ,点P 在圆Γ上,且QP AC ∥.求证:PC PA PB =+. 23.在四边形ABCF 中,BF AF FC +=.点D 在BC 上,点E 在BA 的延长线上,且BD BE AC ==,AF CD FC AE ⋅=⋅.求证:四边形ABCF 有外接圆.24.1O e 与2O e 相交于A ,E 两点,1O e 的一条弦BC 与2O e 相切于点D ,且AD 与1O e 相切于点A .求证:33EB AB EC AC=. 习题B1.设圆内接四边形ABCD 的四边AB a =,BC b =,CD c =,DA d =.求对角线AC 和BD 的长(用a ,b ,c ,d 表示).2.已知ABC △内接于O e ,P 为ABC △内任一点,过点P 引AB ,AC ,BC 的平行线,分别交BC ,AC 于F ,E ,交AB ,BC 于K ,I ,交AB ,AC 于G ,H ,AD 为O e 过点P 的弦.试证:2224EF KI GH PA PD ++⋅≥.(《数学通报》1991年第9期问题)3.圆内接四边形被它的一条对角线分成两个三角形,证明:这两个三角形的内切圆半径之和与对角线的选取无关. (IMO -23预选题) 4.设1C ,2C 是同心圆,2C 的半径是1C 的半径的λ(1λ>)倍.n 边形12A A …n A 内接于1C ,延长1n A A .12A A ,…,1n n A A -分别交圆2C 于1B ,2B ,…n B ,若n 边形12A A …n A ,12B B …n B 的周长分别为1p ,2p .试证:21p p λ≥,其中等号当且仅当n 边形12A A …n A 是正n 边形时成立.(IMO -21预选题) 5.已知边长分别为a ,b ,c 的ABC △内接于O e ,1O e 内切于O e ,切点G 在»BC上,由点A ,B ,C 分别引1O e 的切线长顺次为d ,e ,f .证明:ad be cf =+.6.在圆内接四边形ABCD 中,1O e ,2O e ,3O e ,4O e 分别是△ABD ,△BCA ,△CDB ,△DAC 的内切圆.设AB ,BC ,CD ,DA 上的切点依次是E ,F ,M ,N ,G ,H ,P ,Q ,设i O e 的半径为i R (i =1,2,3,4).求证:1324EF MN R R R R ⋅=+.7.设锐角ABC △的A ∠的平分线交BC 于L ,交外接圆于N ,自点L 分别向AB 和AC 作垂线LK 和LM ,垂足为K 和M .求证:ABC △的面积等于四边形AKNM 的面积.(IMO -28试题)8.ABC △为O e 内接三角形,AB AC BC >>.点D 在»BC上,从O 点分别作AB ,AC 的垂线交AD 于E 、F ,射线BE ,CF 交于P 点.则PB PC PO =+的充要条件是30BAC =︒∠.9.证明:设ABC △中,A ∠,B ∠与C ∠的三条角平分线分别交ABC △的外接圆于1A ,1B ,1C ,则111AA BB CC AB BC CA ++>++.(1982年澳大利亚竞赛题)10.设ABCDEF 是凸六边形,且AB BC =,CD DE =,EF FA =.证明:32BC DE FA BE DA FC ++≥,并指出等式在什么条件下成立. (IMO -38预选题) 11.在ABC △中,90A =︒∠,A C <∠∠,过A 点作ABC △的外接圆O e 的切线,交直线BC 于D ,设点A 关于BC 的对称点为E ,作AX BE ⊥于X ,Y 为AX 的中点,BY 与O e 交于Z .证明:BD 为△ADZ 的外接圆的切线. (IMO -39预选题)12.O e 为正ABC △的外接圆,AD 为O e 的直径,在»BC上任取一点P (P B ≠,P C ≠),设E ,F 分别为△PAB ,PAC △的内心.证明PD PE PF =-.13.设G 为ABC △的重心,在ABC △所在平面上确定点P 的位置,使得PA AG BP BG CP CG ⋅+⋅+⋅有最小值,并用ABC △的边长表示这个最小值.(IMO -42预选题)14.设12A A …n A (4n ≥)为凸n 边形.证明:12A A …n A 为圆内接多边形的充分必要条件是对每个顶点j A 对应一组实数()j j b c ,1,2,,j n =…,满足(1)i j j i i j A A b c b c i j n =-<≤≤.(IMO -41预选题)。
托勒密定理(学生版)

托勒密定理1.托勒密定理原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.翻译:在四边形ABCD中,若A、B、C、D四点共圆,则AC BD AB CD AD BC⋅=⋅+⋅.DCBA2.证明:在线段BD上取点E,使得∠BAE=∠CAD,易证△AEB∽△ADC,∴AB BEAC CD=,即AC BE AB CD⋅=⋅,当∠BAE=∠CAD时,可得:∠BAC=∠EAD,易证△ABC∽△AED,∴AD DEAC CB=,即AC DE AD BC⋅=⋅,∴AC BE AC DE AB CD AD BC⋅+⋅=⋅+⋅,∴AC BD AB CD AD BC⋅=⋅+⋅.3.推广(托勒密不等式):对于任意凸四边形ABCD,有AC BD AB CD AD BC⋅≤⋅+⋅AB CD证明:如图1,在平面中取点E使得∠BAE=∠CAD,∠ABE=∠ACD,易证△ABE∽△ACD,∴AB BEAC CD=,即AC BE AB CD⋅=⋅①,图1图2连接DE,如图2,∵AB AEAC AD=,∴AB ACAE AD=,又∠BAC=∠BAE+∠CAE=∠DAC+∠CAE=∠DAE,∴△ABC∽△AED,∴AD DEAC BC=,即AC DE AD BC⋅=⋅②,将①+②得:AC BE AC DE AB CD AD BC⋅+⋅=⋅+⋅,∴()AC BD AC BE DE AB CD AD BC⋅≤⋅+=⋅+⋅即AC BD AB CD AD BC⋅≤⋅+⋅,当且仅当A、B、C、D共圆时取到等号.4.托勒密定理在中考题中的应用(1)当△ABC是等边三角形时,如图1,当点D在弧AC上时,根据托勒密定理有:DB AC AD BC AB CD⋅=⋅+⋅,又等边△ABC有AB=AC=BC,故有结论:DB DA DC=+.图1证明:在BD 上取点E 使得DE =DA ,易证△AEB ∽△ADC ,△AED ∽△ABC ,利用对应边成比例,可得:DB DA DC =+.如图2,当点D 在弧BC 上时,结论:DA =DB +DC .图2【小结】虽然看似不同,但根据等边的旋转对称性,图1和图2并无区别. (2)当△ABC 是等腰直角三角形,如图3,当点D 在弧BC 上时,根据托勒密定理:AD BC AB CD AC BD ⋅=⋅+⋅, 又::AB ACBC =BD CD =+.图3如图4,当点 D 在弧AC 上时,根据托勒密定理:AD BC AB CD AC BD ⋅=⋅+⋅, 又::AB ACBC =BD CD =+.图4(3)当△ABC 是一般三角形时,若记BC :AC :AB =a :b :c , 根据托勒密定理可得:a AD b BD c CD ⋅=⋅+⋅1.(2019·仙桃)已知ABC ∆内接于O ,∠BAC 的平分线交O 于点D ,连接DB ,DC . (1)如图①,当120BAC ∠=︒时,请直接写出线段AB ,AC ,AD 之间满足的等量关系式: ;(2)如图②,当90BAC ∠=︒时,试探究线段AB ,AC ,AD 之间满足的等量关系,并证明你的结论;(3)如图③,若5BC =,4BD =,求ADAB AC+的值.图3图1图22.(2019·威海)(1)方法选择如图①,四边形ABCD 是O 的内接四边形,连接AC ,BD ,AB BC AC ==.求证:BD AD CD =+.小颖认为可用截长法证明:在DB 上截取DM AD =,连接AM ⋯ 小军认为可用补短法证明:延长CD 至点N ,使得DN AD =⋯ 请你选择一种方法证明. (2)类比探究 【探究1】如图②,四边形ABCD 是O 的内接四边形,连接AC ,BD ,BC 是O 的直径,AB AC =.试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论. 【探究2】如图③,四边形ABCD 是O 的内接四边形,连接AC ,BD .若BC 是O 的直径,30ABC ∠=︒,则线段AD ,BD ,CD 之间的等量关系式是 .(3)拓展猜想如图④,四边形ABCD 是O 的内接四边形,连接AC ,BD .若BC 是O 的直径,::::BC AC AB a b c =,则线段AD ,BD ,CD 之间的等量关系式是 .图4图3图2图13.(2017·临沂)数学课上,张老师出示了问题:如图1,AC ,BD 是四边形ABCD 的对角线,若60ACB ACD ABD ADB ∠=∠=∠=∠=︒,则线段BC ,CD ,AC 三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB 到E ,使BE CD =,连接AE ,证得△ABE ≌△ADC ,从而容易证明ACE ∆是等边三角形,故AC CE =,所以AC BC CD =+. 小亮展示了另一种正确的思路:如图3,将ABC ∆绕着点A 逆时针旋转60︒,使AB 与AD 重合,从而容易证明ACF ∆是等边三角形,故AC CF =,所以AC BC CD =+. 在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“60ACB ACD ABD ADB ∠=∠=∠=∠=︒”改为“45ACB ACD ABD ADB ∠=∠=∠=∠=︒”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明. (2)小华提出:如图5,如果把“60ACB ACD ABD ADB ∠=∠=∠=∠=︒”改为“ACB ACD ABD ADB α∠=∠=∠=∠=”,其它条件不变,那么线段BC ,CD ,AC 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.图5ABCD图4DBA 图3FDBAEDBA图1ABD图24.(2016·淮安中考)问题背景:如图①,在四边形ADBC 中,90ACB ADB ∠=∠=︒,AD BD =,探究线段AC ,BC ,CD 之间的数量关系.小吴同学探究此问题的思路是:将BCD ∆绕点D ,逆时针旋转90︒到AED ∆处,点B ,C 分别落在点A ,E 处(如图②),易证点C ,A ,E 在同一条直线上,并且CDE ∆是等腰直角三角形,所以CE,从而得出结论:AC BC +=. 简单应用:(1)在图①中,若ACBC =CD = . (2)如图③,AB 是O 的直径,点C 、D 在上,AD BD =,若13AB =,12BC =,求CD 的长.拓展规律:(3)如图④,90ACB ADB ∠=∠=︒,AD BD =,若AC m =,()BC n m n =<,求CD 的长(用含m ,n 的代数式表示)(4)如图⑤,90ACB ∠=︒,AC BC =,点P 为AB 的中点,若点E 满足13AE AC =,CE CA =,点Q 为AE 的中点,则线段PQ 与AC 的数量关系是 .图5图1图2图3图4ACDAB BED CB AA BCD。
托勒密定理及其推广和应用

托勒密定理及其推广和应用1什么是托勒密定理及其推广和应用托勒密定理(Pythagorean Theorem)或者又被称为“勾股定理”,是古希腊数学家托勒密(Pythagoras)提出的一个定理,可以用来求三角形的斜边长度。
定理的内容是,如果一个三角形中,两条直角边的长度分别是a和b,那么斜边的长度c就等于根号下(a²+b²)。
2历史沿革托勒密定理在西元前600年由古希腊数学家托勒密首先提出,是一项里程碑式的数学理论,它被看做是世界三大数学定理之一,也是最古老、最广为人知的数学定理。
3推广和应用定理的推广和应用非常广泛,在四边形和多边形的求周长中占有重要的地位,它与三角函数的涉及将二元一次方程的解法推广到三元一次方程。
此外,在几何概念上勾股定理也可以应用于球面和曲面上,已经广泛运用于航海、地质、地理等科学中。
在数学证明上,勾股定理只有一个精辟而有力的自然证明,这也是它被广泛认可的原因。
可以说它改变了人们的数学思维,它的提出让很多已有的数学概念有了研究深刻的定义,更多的数学猜想也借此得以验证。
4扩展应用勾股定理的扩展应用至今来,也可以用于三次方程求解,它的推广也涉及到全部的多项式方程求解(又称厄米-伯拉斯特),它也在微积分中有重要的作用,在体积也有着深远的意义;此外,勾股定理也是测地学(地形测量和测绘,即建筑师和土木工程师所必须熟悉的学科)的基础,在远程精确测量地形细节的时候,投影的误差也是在计算过程中要考虑的重要因素。
5结论托勒密定理(Pythagorean theorem)经过几千年的发展变化,仍然是数学界一项最为重要的理论和定义,不仅在几何和数学上有着广泛的应用,也被用在了科学和文化领域,它深深地影响着我们对数学理解的方式。
它也给人们提供了很多对数学发展的启示,使人们在理解数学和科学以及其他文化领域知识时有一个更开放的思维框架。
赣县中学北校区高二数学竞赛平几讲义(三) (学生)

赣县中学北校区高二数学竞赛平几讲义(三)整理人:彭福星 2015-11-15一、托勒密定理及其逆定理1.托勒密定理:圆内接四边形两组对边乘积之和,等于两条对角线的乘积。
已知:四边形ABCD 内接于圆,如图,求证:AB·CD+BC·AD=AC·BD2.托勒密定理的逆定理:如果凸四边形两组对边的积的和,等于两对角线的积,此四边形必内接于圆。
已知四边形ABCD 满足AB·CD+BC·AD=AC·BD ,求证:A 、B 、C 、D 四点共圆。
3.托勒密定理的推广:在四边形ABCD 中,恒有AB·CD+BC·AD≥AC·DB ,当且仅当四边形ABCD 内接于圆时等号成立。
二、应用托勒密定理以其简介而优美的形式著称,在有关圆内接四边形问题及证四点共圆时有其独特的功效。
(1)证线段的和、差关系。
例1.在△ABC 中,AB<AC<BC ,D 点在BC 上,E点在BA 的延长线上,且BD=BE=AC ,△BDE 的外接圆与△ABC 的外接圆交于F 点,求证:BF=AF+CF 。
(2)求最值例2.已知圆周被其上二定点A 、B (A ≠B )分成两端狐,试指出弧上的动点P 在其中指定一段弧的哪个位置时,P A+PB 取最大值?证明你的结论并求出这个最大值。
(3)证四点共圆例3.已知D 为正△ABC 。
的∠ABC 内一点,且DA=DB+DC ,求证:A ,B ,C ,D 四点共圆。
(4)解方程例4.若a ≥b ≥c >0,且a <b +c ,解方程ax b x c c x b =-+-2222。
(5)证定值问题例5.如图,圆O 外接于正方形ABCD ,P 为弧AD 上的任意一点,求证PB PC PA +为定值。
(6)证不等关系例6.设1C ,2C 是同心圆,2C 的半径是1C 半径的2倍,四边形4321A A A A 内接于1C ,将14A A 延长交圆2C 于1B ,21A A 延长交圆2C 于2B ,32A A 交圆2C 于3B ,43A A 延长交圆2C 于4B ,试证:四边形4321B B B B 的周长≥2×四边形4321A A A A 的周长,并请确定等号成立的条件。
托勒密定理及应用

托勒密定理及应用
托勒密定理及应用
一、托勒密定理
托勒密定理是由富兰克林在1732年提出的数学定理,它认为“如果一个正三角形的三边长各不相同,它的每个内角都等于180度,那么已知此三角形的两边和其夹角等于定值的话,就可求出此三角形的另外一条边的长度。
”这就是托勒密定理。
二、托勒密定理的应用
1. 计算夹角
托勒密定理可用于计算夹角。
例如,若已知三角形的两边长数值,那么可以使用托勒密定理计算出它们之间的夹角。
2. 计算边长
托勒密定理也可以用于计算三角形边长。
例如,假设一个正三角形的另外一条边和它们之间的夹角都已知,那么可以通过托勒密定理计算这两边的长度。
3. 绘图测量
此外,使用托勒密定理也可以很方便地进行曲率量测,椭圆重心量测
等等。
例如,由于一个圆的另一条边和它们之间的夹角总是相等的,
因此很容易通过托勒密定理计算出这两部分的数值。
4. 求解方程
此外,可以使用托勒密定理来求解复杂方程。
最常见的用法就是将正
三角形边长和它们之间的夹角式子带入方程,从而求解圆形及抛物线
方程。
5. 电子学
此外,托勒密定理也用于电子学中,用于计算一个电机的磁励磁和电
路的阻抗特性。
通过托勒密定理,可以精准求出直流电路中的无功功
率和有功功率,也可以求得交流电路中的量度电压和电流的关系。
三、总结
托勒密定理是一个非常简单又实用的数学定理,它可以用于计算夹角、求出三角形边长,也可以用于测量、求解方程,甚至在电子学中也有
应用。
第三讲--托勒密定理及其应用.docx
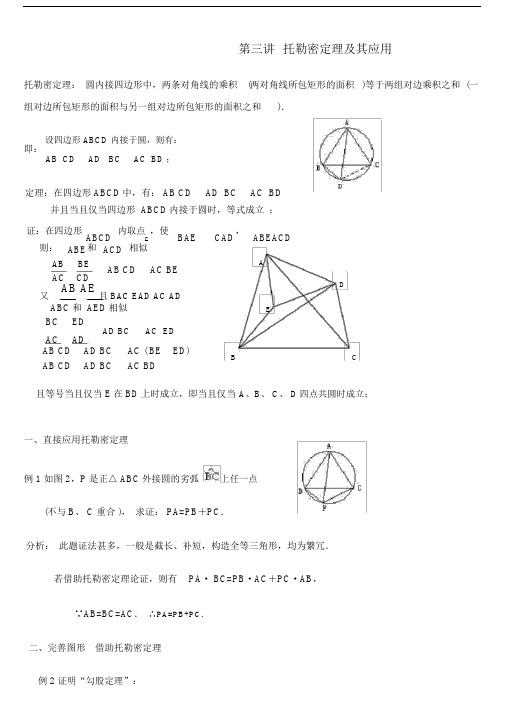
第三讲托勒密定理及其应用托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和 (一组对边所包矩形的面积与另一组对边所包矩形的面积之和).设四边形 ABCD 内接于圆,则有:即:AB CD AD BC AC BD ;定理:在四边形 ABCD中,有: AB CD AD BC AC BD并且当且仅当四边形 ABCD内接于圆时,等式成立;证:在四边形ABCD 内取点,使BAE CAD,ABEACD E则:ABE和ACD相似AB BE AC CD AB CD AC BEAD又AB AE且 BAC EAD AC AD ABC和 AED相似BC EDAD BC AC ED AC ADAB CD AD BC AC ( BE ED) AB CD AD BC AC BDEB C且等号当且仅当 E在 BD上时成立,即当且仅当A、B、 C、 D四点共圆时成立;一、直接应用托勒密定理例 1 如图 2,P 是正△ ABC外接圆的劣弧上任一点(不与 B、 C 重合 ),求证: PA=PB+PC.分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA· BC=PB·AC+PC·AB,∵AB=BC=AC.∴PA=PB+PC.二、完善图形借助托勒密定理例 2 证明“勾股定理”:在Rt△ABC中,∠ B=90°,求证: AC2 =AB2+ BC2证明:如图,作以 Rt△ABC的斜边 AC为一对角线的矩形ABCD,显然 ABCD是圆内接四边形.由托勒密定理,有AC·BD=AB·CD+AD·BC.①又∵ ABCD是矩形,∴AB=CD, AD=BC, AC=BD.②把②代人①,得AC2 =AB2+ BC2.例3 如图,在△ ABC中,∠ A 的平分线交外接∠圆于 D,连结 BD,求证: AD·BC=BD(AB+AC).证明:连结 CD,依托勒密定理,有AD·BC= AB· CD+AC·BD.∵∠ 1=∠ 2,∴ BD=CD.故 AD·BC=AB·BD+AC· BD=BD(AB+ AC).三、构造图形借助托勒密定理例4 若 a、b、x、y 是实数,且 a2+b2=1,x2+y2=1.求证: ax+by≤ 1.证明:如图作直径 AB=1的圆,在 AB 两边任作 Rt△ACB和 Rt△ADB,使AC=a,BC=b,BD= x, AD= y.由勾股定理知 a、 b、 x、y 是满足题设条件的.据托勒密定理,有 AC· BD+BC·AD=AB·CD.∵CD≤AB= 1,∴ ax+by≤1.四、巧变原式妙构图形,借助托勒密定理例 5 已知 a、 b、 c 是△ ABC的三边,且 a2 =b(b+c),求证:∠ A=2∠B.分析:将 a2 =b(b+c)变形为 a·a=b·b+ bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为 b,两对角线为 a,一底边为 c.证明:如图,作△ ABC的外接圆,以 A 为圆心, BC为半径作弧交圆于D,连结 BD、DC、 DA.∵AD=BC,∴∠ ABD=∠BAC.又∵∠ BDA=∠ ACB(对同弧 ),∴∠ 1=∠2.依托勒密定理,有BC·AD=AB·CD+BD· AC.①而已知 a2 =b(b+c),即 a·a=b· c+b2.②∴∠ BAC=2∠ABC.五、巧变形妙引线借肋托勒密定理例 6 在△ ABC中,已知∠ A∶∠ B∶∠ C=1∶2∶4,分析:将结论变形为 AC·BC+ AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图,作△ ABC的外接圆,作弦BD=BC,边结 AD、CD.在圆内接四边形ADBC中,由托勒密定理,有AC·BD+ BC·AD=AB·CD易证 AB=AD,CD=AC,∴ AC·BC+BC·AB=AB· AC,1.已知△ ABC中,∠ B=2∠ C。
平面几何3--托勒密定理及应用

平面几何(3)----托勒密定理及应用托勒密定理:圆内接四边形的两组对边乘积之和等于两对角线的乘积推论1(三弦定理) 如果A 是圆上任意一点,AB ,AC ,AD 是该圆上顺次的三条弦,则sin sin sin AC BAD AB CAD AD CAB ⋅∠=⋅∠+⋅∠推论2(四角定理) 四边形ABCD 内接于O ,则sin sin sin sin sin sin ADC BAD ABD BDC ADB DBC ∠⋅∠=∠⋅∠+∠⋅∠直线上的托勒密定理(或欧拉定理) 若A ,B ,C ,D 为一直线上依次排序的四点,则AB CD BC AD AC BD ⋅+⋅=⋅四边形中的托勒密定理:设ABCD 为任意凸四边形,则,AB CD BC AD AC BD ⋅+⋅≥⋅当且仅当A ,B ,C ,D 四点共圆时取等号托勒密定理的逆定理: 在凸四边形ABCD 中,若AB CD BC AD AC BD ⋅+⋅=⋅,则A ,B ,C ,D 四点共圆例1:在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若角A ,B ,C 的大小成等比数列,且22b a ac -=,则角B 的弧度数等于多少?例2:凸四边形ABCD 中,60,90o o ABC BAD BCD ∠=∠=∠=,AB=2,CD=1,对角线AC ,BD 交于点O ,如图,求sin AOB ∠例3:如图,在锐角ABC 的BC 边上有两点E ,F ,满足,BAE CAF ∠=∠作FM AB ⊥于M ,FN AC ⊥于N ,延长AE 交ABC 的外接圆于点D ,证明:四边形AMDN 与ABC 的面积相等.例4:如图,在ABC 中,60o A ∠=,,AB AC >点O 是外心,两条高BE ,CF 交于H 点,点M ,N 分别在线段BH ,HF 上,且满足BM=CN ,求MH NH OH+的值例5:若有四个圆都与第五个圆内切,第一个与第二个圆的外公切线长用12l 表示,其他前四个圆中的两两的外公切线也用同样的方法来标记,且前四个圆以顺时针的顺序排列,试证明依次以12233441,,,l l l l 为边长,以1324,l l 为对角线所构成的凸四边的四个顶点共圆.例6:经过XOY ∠的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P,Q ,求证:11OP OQ+为定值例7:圆内接六边形ABCDEF 的对角线共点的充要条件是1AB CD EF BC DE FA ⋅⋅=。
托勒密定理的证明及其应用

托勒密定理的证明及其应用
托勒密定理是数论中一个古老的定理,由古希腊数学家托勒密(Euclid)在他的著作《几何原本》中提出来的,它指出给定集合中
任意两个质数之间存在一个乘积为其积的合数。
托勒密定理的证明非
常简单而有效,它可以这样表述:
假设存在两个质数p和q,它们的乘积不能被表示为两个质数乘
积的积形式,也就是说,p × q ≠ m × n (其中m,n两个质数)。
使用反证法可以得出它们之间存在合数的结论:
反证:假设p和q之间没有合数,那么p × q只能由质数乘积
的形式来表示。
也就是说,p × q = m × n,m,n是任意的质数。
然而,根据前面的假设,我们知道p × q≠ m × n,于是得出矛盾,即
p和q之间存在合数。
托勒密定理的应用可以追溯到古罗马时代,当年人们经常会利用
它来求解各种猜想问题(比如判断数字是不是质数)。
直到19世纪,
它还可以用来测量太空物体距离地球的距离,还有工程精细化的计算。
近年来,随着计算机科技的发展,托勒密定理的应用也在不断的拓展,比如数论的信息安全方面,可以应用于数字签名算法,非常实用。
托勒密定理及其应用——初中生数学竞赛训练用

托勒密定理及其应用——初中生数学竞赛训练用提出“地心说”的托勒密,在几何上留有有著名的托勒密定理。
托勒密定理托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和。
如下图已知:四边形ABCD内接于⊙O中,求证AC.BD=AB.DC+BC.AD证明:以B点为顶点,AB为一边做∠BAE=∠DAC与BD相交于E ⊿ABE与⊿ACD中,∵∠BAE=∠CAD,∠ABE=∠ACD(同弧度所对圆周角)∴⊿ABE~⊿ACD(三角形两角相等三角形相似)AB:AC=BE:DC=>AB.DC=BE.AC (1)⊿BAD与⊿BEC中,∠BAC=∠EAD∠BCA=∠EDA∴⊿BCA~⊿EDA(三角形两角相等三角形相似)∴BC:ED=AC:AD=>BC.AD=ED.AC (2)(1)+(2)得到AB.DC+BC.AD=BE.AC+EF.AC=(BE+ED).AC=BD.AC托勒密定理证明几何题例题1.等边三角形ABC外一点D,∠BDC=1200,求证:AD=BD+BC 证明:A,B,C,D四点共圆,令正三角形边长为a由托勒密定理AB.DC+AC.BD=AD.BC即a.DC+a.BD=a.BC∴DC+BD=BC例题2.锐角三角形ABC中O是外心,A1,B1,C1是各边中点,求证OA1+OB1+OC1=R+r,其中R是ABC外接圆半径,r是内切圆半径。
证明:设AB=c,BC=a,CA=b。
如图C1,B1是AB,AC中点,所以C1B1=1/2BC=1/2a,AB1=1/2AC=1/2b,AC1=1/2AB=1/2cOC1⊥AB,OC2⊥AC,A,C1,O,B1四点共圆。
由托勒密定理:OA.C1B1=AC1.OB1+AB1.OC1R.1/2 a=1/2c.OB1+1/2b.OC1c.OB1+b.OC1=a.R (1)同理c.OA1+a.OC1=b.R (2)a.OB1+b.OA1=c.R (3)而a. OA1+b.OB1+c.OC1=2S⊿ABC=(a+b+c).r (4)由(1),(2),(3),(4)得(OA1+OB1+OC1).(a+b+c)=(a+b+c).(R+r)从而得到:OA1+OB1+OC1= R+r托勒密定理直观说明三角公式和角公式我们在直径为1的圆中,作下图:根据托勒密定理我们有:AB.DC+AD.BC=AC.BDAC=1,也就是说:sin(α+β)=sinα.cosβ+cosα.cosβ差角公式在上图中我们有:sin(α-β)= sinα.cosβ-cosα.cosβ接着我们代数推导cos(α+β)=?cos(α+β)=sin(900-α-β)=sin(900-α)cosβ-cos(900-α)sinβ=cosαcosβ-sinαsinβcos(α-β)的公式作为习题,请自己推导。
托勒密定理的证明及应用

托勒密定理的证明及应用
托勒密定理:圆的内接四边形中,两条对角线的积等于两组对边乘积之和!
证明过程如下,先作辅助线如下:
具体过程如下:
下面,我们看看使用托勒密定理证明两个重要其他定理:勾股定理和余弦定理
(1)利用托勒密定理证明勾股定理如下:
具体过程为:
(2)利用托勒密定理证明余弦定理
具体过程如下:
是不是感觉很强大呢?
下面我们再来看看使用托勒密定理的其他应用,用题目说话吧:题目一:
添加辅助线如下:
具体证明过程如下:
题目二:
本题直接使用托勒密定理,甚是简洁!
题目三:
附辅助线如下:。
第三讲--托勒密定理及其应用
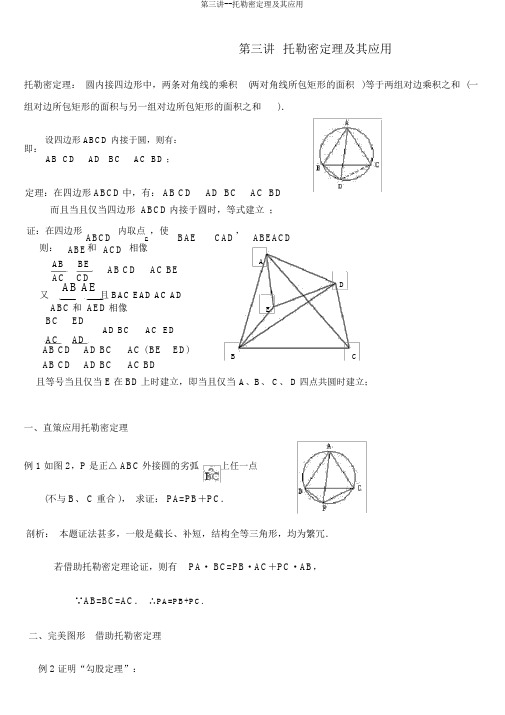
第三讲托勒密定理及其应用托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和 (一组对边所包矩形的面积与另一组对边所包矩形的面积之和).设四边形 ABCD 内接于圆,则有:即:AB CD AD BC AC BD ;定理:在四边形 ABCD中,有: AB CD AD BC AC BD而且当且仅当四边形 ABCD内接于圆时,等式建立;证:在四边形ABCD 内取点,使BAE CAD,ABEACD E则:ABE 和ACD 相像AB BE AC CD AB CD AC BEAD又AB AE且 BAC EAD AC AD ABC和 AED相像BC EDAD BC AC ED AC ADAB CD AD BC AC ( BE ED) AB CD AD BC AC BDEB C且等号当且仅当 E在 BD上时建立,即当且仅当A、B、 C、 D四点共圆时建立;一、直策应用托勒密定理例 1 如图 2,P 是正△ ABC外接圆的劣弧上任一点(不与 B、 C 重合 ),求证: PA=PB+PC.剖析:本题证法甚多,一般是截长、补短,结构全等三角形,均为繁冗.若借助托勒密定理论证,则有PA· BC=PB·AC+PC·AB,∵AB=BC=AC.∴PA=PB+PC.二、完美图形借助托勒密定理例 2 证明“勾股定理”:在Rt△ABC中,∠ B=90°,求证: AC2 =AB2+ BC2证明:如图,作以 Rt△ABC的斜边 AC为一对角线的矩形ABCD,明显 ABCD是圆内接四边形.由托勒密定理,有AC·BD=AB·CD+AD·BC.①又∵ ABCD是矩形,∴AB=CD, AD=BC, AC=BD.②把②代人①,得AC2 =AB2+ BC2.例3 如图,在△ ABC中,∠ A 的均分线交外接∠圆于 D,连结 BD,求证: AD·BC=BD(AB+AC).证明:连结 CD,依靠勒密定理,有AD·BC= AB· CD+AC·BD.∵∠ 1=∠ 2,∴ BD=CD.故 AD·BC=AB·BD+AC· BD=BD(AB+ AC).三、结构图形借助托勒密定理例4 若 a、b、x、y 是实数,且 a2+b2=1,x2+y2=1.求证: ax+by≤ 1.证明:如图作直径 AB=1的圆,在 AB 两边任作 Rt△ACB和 Rt△ADB,使AC=a,BC=b,BD= x, AD= y.由勾股定理知 a、 b、 x、y 是知足题设条件的.据托勒密定理,有 AC· BD+BC·AD=AB·CD.∵CD≤AB= 1,∴ ax+by≤1.四、巧变原式妙构图形,借助托勒密定理例 5 已知 a、 b、 c 是△ ABC的三边,且 a2 =b(b+c),求证:∠ A=2∠B.剖析:将 a2 =b(b+c)变形为 a·a=b·b+ bc,从而联想到托勒密定理,从而结构一个等腰梯形,使两腰为 b,两对角线为 a,一底边为 c.证明:如图,作△ ABC的外接圆,以 A 为圆心, BC为半径作弧交圆于D,连结 BD、DC、 DA.∵AD=BC,∴∠ ABD=∠BAC.又∵∠ BDA=∠ ACB(对同弧 ),∴∠ 1=∠2.依靠勒密定理,有BC·AD=AB·CD+BD· AC.①而已知 a2 =b(b+c),即 a·a=b· c+b2.②∴∠ BAC=2∠ABC.五、巧变形妙引线借肋托勒密定理例 6 在△ ABC中,已知∠ A∶∠ B∶∠ C=1∶2∶4,剖析:将结论变形为 AC·BC+ AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,从而结构圆内接四边形.如图,作△ ABC的外接圆,作弦BD=BC,边结 AD、CD.在圆内接四边形ADBC中,由托勒密定理,有AC·BD+ BC·AD=AB·CD易证 AB=AD,CD=AC,∴ AC·BC+BC·AB=AB· AC,1.已知△ ABC中,∠ B=2∠ C。
用托勒密定理

用托勒密定理托勒密定理是几何学中的一个重要定理,它被广泛应用于各种几何问题的解决中。
本文将从三个方面介绍托勒密定理的应用。
一、求正方形对角线长托勒密定理可以用来求正方形对角线长。
我们知道,正方形的对角线长等于边长的根号二倍,即d=a√2。
而托勒密定理告诉我们,对于任意四边形ABCD,有AB×CD+BC×AD=AC×BD。
因此,对于正方形ABCD,有AB×CD+BC×AD=2a×2a=4a^2,其中a为正方形的边长。
又因为正方形的对角线AC和BD相等,所以AC×BD=d^2。
将这两个式子联立,得到d=a√2。
二、求圆内接四边形对角线长托勒密定理还可以用来求圆内接四边形对角线长。
我们知道,圆内接四边形的对角线相互垂直且相等。
设四边形ABCD的对角线AC和BD 的长度分别为d,AB=a,BC=b,CD=c,DA=d,则托勒密定理告诉我们,有AB×CD+BC×AD=AC×BD。
又因为四边形ABCD内接于圆,所以AB+CD=BC+DA。
将这两个式子联立,得到d^2=a^2+c^2+2ac。
三、求三角形内切圆半径托勒密定理还可以用来求三角形内切圆半径。
我们知道,三角形内切圆的半径r等于三角形面积S除以半周长s的差值,即r=S/(s-a)。
而托勒密定理告诉我们,对于任意四边形ABCD,有AB×CD+BC×AD=AC×BD。
因此,对于三角形ABC,有AB×BC+AC×CB=2s×r,其中s=(a+b+c)/2为半周长。
将这个式子变形,得到r=S/(s-a)。
综上所述,托勒密定理是一个非常有用的几何定理,它可以用来解决各种几何问题,如求正方形对角线长、圆内接四边形对角线长和三角形内切圆半径等。
在学习几何学时,我们应该认真掌握托勒密定理的应用,以便更好地解决几何问题。
2021年中考二轮专题 构造旋转-托勒密定理的应用

2.证明:在线段BD 上取点E ,使得∠BAE =∠CAD ,易证△AEB ∽△ADC ,∴AB BEAC CD=,即AC BE AB CD ⋅=⋅,ααDCBAEEA B CD当∠BAE =∠CAD 时,可得:∠BAC =∠EAD ,易证△ABC ∽△AED ,∴AD DE AC CB=,即AC DE AD BC ⋅=⋅,∴AC BE AC DE AB CD AD BC ⋅+⋅=⋅+⋅,∴AC BD AB CD AD BC ⋅=⋅+⋅.构造旋转-托勒密定理的应用托勒密定理原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
翻译:在四边形ABCD 中,若A 、B 、C 、D 四点共圆,则AC ·BD=AB ·CD+AD ·BC.托勒密定理在中考题中的应用(1)当△ABC 是等边三角形时,如图1,当点D 在弧AC 上时,根据托勒密定理有:又等边△ABC 有AB =AC =BC ,故有结论:=+.图1托勒密定理在中考题中的应用(1)当△ABC 是等边三角形时,如图1,当点D 在弧AC 上时,根据托勒密定理有:DB ·AC=AD ·BC+AB ·CD, 又等边△ABC 有AB=AC=BC,故有结论:DB=DA+DC.2)当△ABC 是等腰直角三角形,如图3,当点D 在弧BC 上时,根据托勒密定理:⋅=⋅+⋅,又::AB AC BC =BD CD =+.图34,当点D 在弧AC 上时,根据托勒密定理:⋅=⋅+⋅,又::AB AC BC =,代入可得结论:BD CD =+.图4(2)当ΔABC 是等腰直角三角形,如图3,当点D 在弧BC 上时,根据托勒密定理:AD ·BC=AB ·CD+AC ·BD, 又AB:AC:BC=1:1:2,代入可得结论:2AD=BD+CD.如图4,当点D 在弧AC 上时,根据托勒密定理:AD ·CD+AC ·BD, 又AB:AC:BC=1:1:2,代入可得结论:BD=2AD+CD.证明:在BD 上取点E 使得DE =DA ,易证△AEB ∽△ADC ,△AED ∽△ABC ,利用对应边成比例,可得:DB DA DC =+.如图2,当点D 在弧BC 上时,结论:DA =DB +DC .图2【小结】虽然看似不同,但根据等边的旋转对称性,图1和图2并无区别.3)当△ABC 是一般三角形时,若记BC :AC :根据托勒密定理可得:a ⋅=⋅+⋅cbaABC D O(3)当ΔABC 是一般三角形时,若记BC:AC:AB=a :b :c , 据托勒密定理可得:a ·AD=b ·BD+c ·CD(2019•湖北)已知△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,连接DB ,DC . (1)如图①,当∠BAC=120°时,①AD 上是否存在点E ,使ΔABE 是等边三角形?证明你的结论. ②请直接写出线段AB ,AC ,AD 之间满足的等量关系式并加以证明;(2)如图②,当∠BAC=90°时,试探究线段AB ,AC ,AD 之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求 ACAB AD+的值.【分析】关于托勒密定理的简单探究.(1)由∠BAC =120°可得∠BDC =60°,又AD 平分∠BAC ,∴BD =CD ,即△BCD 是等边三角形.∴AD =AB +AC .(2)过点B 作BE ⊥AD 交AD 于点E ,易证△BED ∽△BAC ,∴DE BDAC BC =,即DE BC AC BD ⋅=⋅,易证△BEA ∽△BDC ,∴AE ABDC BC =,即AE BC AB CD ⋅=⋅,∴DE BC AE BC AC BD AB CD ⋅+⋅=⋅+⋅,∴AD BC AB CD AC BD ⋅=⋅+⋅.若∠BAC =90°,则∠BDC=90°,又BD =CD ,∴△BCD 是等腰直角三角形,∴::BD CD BC =AB AC =+.(3)CD =BD =4,根据托勒密定理,可得544AD AB AC =+,45AD AB AC =+.【说明】托勒密定理在解题不可直接使用,用前需证明.。
托勒密定理及其应用

托勒密定理及其应用
熊斌;郑仲义
【期刊名称】《数学学习与研究:中考考生适用》
【年(卷),期】2007(000)002
【摘要】托勒密定理在圆内接四边形中,两条对角线长度之积等于两对对边乘积之和.
【总页数】3页(P58-60)
【作者】熊斌;郑仲义
【作者单位】华东师范大学;复旦大学附属中学
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.掌握著名定理探寻实际应用--托勒密定理纵横谈 [J], 张东海
2.托勒密定理的复数证法及其应用 [J], 彭康青
3.托勒密定理的证明及应用 [J], 马福宝
4.托勒密定理的两个应用 [J], 徐道
5.掌握著名定理探寻实际应用——托勒密定理纵横谈 [J], 张东海
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).
即:
;内接于圆,则有:设四边形BD AC BC AD CD AB ABCD ⋅=⋅+⋅ ;内接于圆时,等式成立并且当且仅当四边形中,有:定理:在四边形ABCD BD
AC BC AD CD AB ABCD ⋅≥⋅+⋅
一、直接应用托勒密定理
例1 如图2,P 是正△ABC 外接圆的劣弧上任一点
(不与B 、C 重合), 求证:PA=PB +PC .
分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.
若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,
∵AB=BC=AC . ∴PA=PB+PC .
二、完善图形 借助托勒密定理
例2 证明“勾股定理”:
在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2
证明:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形. 由托勒密定理,有
AC ·BD=AB ·CD +AD ·BC . ①
四点共圆时成立;、、、上时成立,即当且仅当在且等号当且仅当相似
和且又相似和则:,,使内取点证:在四边形D C B A BD E BD AC BC AD CD AB ED BE AC BC AD CD AB ED AC BC AD AD ED AC BC AED ABC EAD BAC AD AE AC AB BE AC CD AB CD BE AC AB ACD ABE ACD ABE CAD BAE E ABCD ⋅≥⋅+⋅∴+⋅=⋅+⋅∴⋅=⋅⇒=∴∆∆∴∠=∠=⋅=⋅⇒=∴∆∆∠=∠∠=∠)
( E D C B A
又∵ABCD是矩形,
∴AB=CD,AD=BC,AC=BD.②
把②代人①,得AC2=AB2+BC2.
例3如图,在△ABC中,∠A的平分线交外接∠圆于D,连结BD,求证:AD·BC=BD(AB+AC).
证明:连结CD,依托勒密定理,
有AD·BC=AB·CD+AC·BD.
∵∠1=∠2,∴ BD=CD.
故 AD·BC=AB·BD+AC·BD=BD(AB+AC).
三、构造图形借助托勒密定理
例4若a、b、x、y是实数,且a2+b2=1,x2+y2=1.
求证:ax+by≤1.
证明:如图作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB,
使AC=a,BC=b,BD=x,AD=y.
由勾股定理知a、b、x、y是满足题设条件的.
据托勒密定理,有AC·BD+BC·AD=AB·CD.
∵CD≤AB=1,∴ax+by≤1.
四、巧变原式妙构图形,借助托勒密定理
例5已知a、b、c是△ABC的三边,且a2=b(b+c),求证:∠A=2∠B.
分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c.
证明:如图,作△ABC的外接圆,以 A为圆心,BC为半径作弧交圆于D,连结BD、DC、DA.
∵AD=BC,
∴∠ABD=∠BAC.
又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.
依托勒密定理,有BC·AD=AB·CD+BD·AC.①
而已知a2=b(b+c),即a·a=b·c+b2.②
∴∠BAC=2∠ABC.
五、巧变形妙引线借肋托勒密定理
例6在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4,
分析:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.
如图,作△ABC的外接圆,作弦BD=BC,边结AD、CD.
在圆内接四边形ADBC中,由托勒密定理,
有AC·BD+BC·AD=AB·CD
易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC,
1.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC ·BD=AD ·BC+CD ·AB 。
2. 已知正七边形A 1A 2A 3A 4A 5A 6A 7。
求证: 。
(第21届全苏数学竞赛)
PM AB PL AC PK BC PN PL PK AB AC BC P BC ABC +=∆求证:,
和、作垂线与、分别向边上一点外接圆的弧由.3
PM AB PL AC PK BC PM CP PM AB PL BP PL AC PK AP PK BC PM CP PL BP PL BP PK AP PA PB PL PK LAP Rt KBP Rt LAP KBP PM CP PM AB PL BP PL AC PK AP PK BC CP AB BP AC AP BC ABPC PC PB PA +=⋅⋅+⋅⋅=⋅⋅∴⋅=⋅⋅=⋅⇒=∴∆∆∠=∠⋅⋅+⋅⋅=⋅⋅⋅+⋅=⋅可得:由同理可得:相似和可知由即:利用托勒密定理有:,对于四边形、、证:连接。
