薄壁杆件力学
材料力学-第三章扭转
3、物理方程 mA a mA a AC 2GI p GI p
BC
2 mB a GI p
4 解得: m A 7 T 3 mB T 7
AB AC BC 0
例:由实心杆 1 和空心杆 2 组成的组合轴,受扭矩 T, 两者之间无相对滑动,求各点切应力。 T 解: 设实心杆和空心杆承担的扭矩分别为 G 2 Ip 2 M n 1 、 M n2 。 R2
二 刚度条件
M 180 刚度 n 0.50~1.0 / m 一般轴 l G Ip 条件
0.25~0.5 / m 精密轴
1.0 ~3.0 / m 粗糙轴
例 传动主轴设计,已知:n = 300r/m,P1 = 500kW,P2=200kW P3=300kW,G=80GPa [ ] 40MPa , [] 0.3 求:轴的直径d 解:1、外力分析
圆轴扭转的强度条件
max
Mn D Mn I p 2 Wp
Wp
2I p D
Mn
D 3 D 3 Wp 1 4 抗扭截面系数Wp : W p 16 16
强度条件:
Mn max Wp
例 已知汽车传动主轴D = 90 mm, d = 85 mm [ ] 60MPa, T = 1.5 kNm
Mn d
3
圆形优于矩形
Aa
= 0.208
3
a
3
4
3
d 0.886 d
2
Mn
a
2
Mn 0.208 0.886 d
b
6.913
力学英文词汇

索引(按照汉语拼音字母顺序)A安全系数 safety factorB半桥接法 half bridge闭口薄壁杆件 thin-walled tubes比例极限 proportional limit边界条件 boundary conditions变截面梁 beam of variable cross section变形 deformation变形协调方程 compatibility equation标距 gage length泊松比 Poisson’s ratio补偿片 compensating blockC材料力学 mechanics of materials冲击荷载 impact load初应力,预应力 initial stress纯剪切 pure shear纯弯曲 pure bending脆性材料 brittle materialsD大柔度杆 long columns单位荷载 unit load单位力偶 unit couple单位荷载法 unit-load method单向应力 uniaxial stress等强度梁 beam of constant strength低周疲劳 low-cycle fatigue电桥平衡 bridge balancing电阻应变片 resistance strain gage电阻应变仪 resistance strain indicator叠加法 superposition method叠加原理 superposition principle动荷载 dynamic load断面收缩率 percentage reduction in area多余约束 redundant restraintE二向应力状态 state of biaxial stressF分布力 distributed force复杂应力状态 state of triaxial stress复合材料 composite materialG杆,杆件 bar刚度 stiffness刚架 frame刚节点 rigid joint高周疲劳 high-cycle fatigue各向同性材料 isotropical material功的互等定理 reciprocal-work theorem工作应变计 active strain gage工作应力 working stress构件 structural member惯性半径 radius of gyration of an area惯性积 product of inertia惯性矩 moment of inertia广义胡克定律 generalized Hook’s lawH横向变形 lateral deformation胡克定律 Hook’s law滑移线 slip-linesIJ基本系统 primary system畸变能理论 distortion energy theory畸变能密度 distortional strain energy density 极惯性矩 polar moment of inertia极限应力 ultimate stress极限荷载 limit load挤压应力 bearing stress剪力 shear force剪力方程 equation of shear force剪力图 shear force diagram剪力流 shear flow剪切胡克定律 Hook’s law for shear剪切 shear交变应力,循环应力 cyclic stress截面法 method of sections截面几何性质 geometrical properties of an area 截面核心 core of section静不定次数,超静定次数 degree of a statically indeterminate problem静不定问题,超静定问题 statically indeterminate problem静定问题 statically determinate problem静荷载 static load静矩 static moment颈缩 neckingK开口薄壁杆件 bar of thin-walled open cross section抗拉强度 ultimate stress in tension抗扭截面系数 section modulus in torsion抗扭强度 ultimate stress in torsion抗弯截面系数 section modulus in bendingL拉压刚度 axial rigidity拉压杆 axially loaded bar理想弹塑性假设 elastic-perfectly plastic assumption力法 force method力学性能 mechanical properties连续梁 continuous beam连续条件 continuity condition梁 beams临界应力 critical stress临界荷载 critical loadM名义屈服强度 offset yielding stress莫尔强度理论 Mohr theory of failure敏感栅 sensitive gridN挠度 deflection挠曲线 deflection curve挠曲线方程 equation of deflection curve挠曲线近似微分方程 approximately differential equation of the deflection curve 内力 internal forces扭矩 torsional moment扭矩图 torque diagram扭转 torsion扭转极限应力 ultimate stress in torsion扭转角 angel of twist扭转屈服极限 yielding stress in torsion扭转刚度 torsional rigidityO欧拉公式 Euler’s formula疲劳极限 endurance limit疲劳破坏 fatigue rupture疲劳寿命 fatigue life偏心拉伸 eccentric tension偏心压缩 eccentric compression平均应力 average stress平面弯曲 plane bending平面应力状态 state of plane stress平行移轴定理 parallel axis theorem平面假设 plane cross-section assumptionQ强度 strength强度理论 theory of strength强度条件 strength condition切变模量 shear modulus切应变 shear strain切应力 shear stress切应力互等定理 theorem of conjugate shearing stress 屈服 yield屈服强度 yield strength全桥接线法 full bridgeR热应力 thermal stressS三向应力状态 state of triaxial stress三轴直角应变花 three-element rectangular rosette三轴等角应变花 three-element delta rosette失稳 buckling伸长率 elongation圣维南原理 Saint-Venant’s principle实验应力分析 experimental stress analysis塑性变形 plastic deformation塑性材料 ductile materials塑性铰 plastic hingeT弹性变形 elastic deformation弹性模量 modulus of elasticity体积力 body force体积改变比能 density of energy of volume change体积应变 volume strainUW弯矩 bending moment弯矩方程 equation of bending moment弯矩图 bending moment diagram弯曲 bending弯曲刚度 flexural rigidity弯曲正应力 normal stress in bending弯曲切应力 shear stress in bending弯曲中心 shear center位移法 displacement method位移互等定理 reciprocal-displacement theorem稳定条件 stability condition稳定性 stability稳定安全系数 safety factor for stabilityX细长比,柔度 slenderness ratio线性弹性体 linear elastic body相当长度 equivalent length相当应力 equivalent stress小柔度杆 short columns形心轴 centroidal axis形心主惯性矩 principal centroidal moments of inertia 形心主轴 principal centroidal axis许用应力 allowable stress许用应力法 allowable stress method许用荷载 allowable load许用荷载法 allowable load methodY应变花 strain rosette应变片 strain gage应变能 strain energy应变比能 strain energy density应力 stress应力速率 stress ratio应力比 stress ratio应力幅 stress amplitude应力状态 state of stress应力集中 stress concentration应力集中系数 stress concentration factor应力-寿命曲线,S-N曲线 stress-cycle curve应力-应变图 stress-strain diagram应力圆,莫尔圆 Mohr’s circle for stresses约束扭转 constraint torsionZ正应变 normal strain正应力 normal stress中面 middle plane中柔度杆 intermediate columns中性层 neutral surface中性轴 neutral axis轴 shaft轴力 axial force轴力图 axial force diagram轴向变形 axial deformation轴向拉伸 axial tension轴向压缩 axial compression主平面 principal planes主应力 principal stress主应力迹线 principal stress trajectory主轴 principal axis主惯性矩 principal moment of inertia转角 angel of rotation转轴公式 transformation equation自由扭转 free torsion组合变形 combined deformation组合截面 composite area最大拉应力理论 maximum tensile stress theory 最大拉应变理论 maximum tensile strain theory 最大切应力理论 maximum shear stress theory最大应力 maximum stress最小应力 minimum stress。
材料力学第3章扭转

试问:纵向截面里的切应力是由什么内力平衡的?
§3.8 薄壁杆件的自由扭转
薄壁杆件:杆件的壁厚远小于截面的其它尺寸。 开口薄壁杆件:杆件的截面中线是不封闭的折线或曲
线,例如:工字钢、槽钢等。 闭口薄壁杆件:杆件的截面中线是封闭的折线或曲线,
例如:封闭的异型钢管。
一、开口薄壁杆的自由扭转
= Tl
GI t
变形特点:截面发生绕杆轴线的相对转动 本章主要研究圆截面等直杆的扭转
§3.2 外力偶矩的计算 扭矩和扭矩图
功率: P(kW) 角速度:ω 外力偶矩:Me
P = Meω
转速:n(r/min)
2n/ 60
Me
1000 P=9549
P n
(N
m)
内力偶矩:扭矩 T 求法:截面法
符号规则: 右手螺旋法则 与外法线同向“ + ” 与外法线反向“-”
max
T max
It
It
1 3
hi
3 i
二、闭口薄壁杆的自由扭转
max
T
2 min
TlS
4G 2
其中:ω截面为中线所围的面积
S 截面为中线的长度
闭口薄壁杆的应力分布:
例: 截面为圆环形的开口和闭口薄壁杆件如图所 示,设两杆具有相同平均半径 r 和壁厚δ,试 比较两者的扭转强度和刚度。
开=3 r 闭 开=3( r )2 闭
8FD3n Gd 4
C
ห้องสมุดไป่ตู้
Gd 4 8D3n
F C
§3.7 矩形截面杆扭转的概念
1) 翘曲
变形后杆的横截面不再保持为平面的现象。
2) 自由扭转和约束扭转
自由扭转:翘曲不受限制的扭转。 各截面翘曲程度相同,纵向纤维无伸缩, 所以,无正应力,仅有切应力。
薄壁结构的热变形与材料力学性能分析

薄壁结构的热变形与材料力学性能分析薄壁结构是一种在工程设计中经常使用的结构形式。
这种结构主要由薄壁杆件组成,它们具有较大的长度和相对较小的截面尺寸。
由于材料特性和力学原理的影响,薄壁结构在受到温度变化时会发生热变形。
这种热变形会对结构的力学性能产生重要影响,因此对薄壁结构的热变形与材料力学性能进行分析是非常必要的。
首先,我们来探讨薄壁结构的热变形原因。
当薄壁结构受到温度变化时,其内部不同部分会因为温度差异而发生热膨胀或热收缩。
这样的热膨胀或热收缩会导致结构产生内部应力,从而引起结构的形变。
薄壁结构在受热时,表面层的温度升高速度较快,而内部温度变化较为缓慢,这会导致结构产生热弯曲变形。
而在整个结构内部,由于不同部分的温度差异,还可能发生由于热膨胀引起的轴向拉伸或压缩变形。
因此,热变形是薄壁结构在受到温度变化时不可忽视的影响因素。
接下来,我们来分析热变形对薄壁结构的力学性能的影响。
首先,由于热变形导致的内部应力,会使得薄壁结构的刚度发生变化。
当结构受到热弯曲变形时,会出现曲率变化,从而影响结构的刚度。
当结构受到轴向拉伸或压缩变形时,会出现长度的变化,也会影响结构的刚度。
这样的刚度变化会对结构的整体强度产生影响,因此在设计薄壁结构时需要考虑热变形对结构刚度的影响。
其次,热变形还会对薄壁结构的稳定性产生重要影响。
在薄壁结构受到热变形时,结构的截面形状会发生改变,可能导致结构的稳定性问题。
例如,在弯曲变形下,结构的截面变形可能会导致截面失稳,从而使得结构整体失稳。
因此,对薄壁结构的热变形进行分析,可以帮助工程师更好地把握结构的稳定性问题。
最后,薄壁结构的材料力学性能也会受到热变形的影响。
当结构受到热变形时,材料内部的应力状态也会发生变化。
由于材料的非线性特性,在温度变化下,材料的本构关系也会发生变化。
这会导致材料的强度、刚度等力学性能发生变化。
因此,在设计薄壁结构时,必须考虑材料在热变形下的力学性能,以确保结构的安全可靠性。
材料力学习题

材料⼒学习题材料⼒学习题训练22-1.求图⽰阶梯状直杆横截⾯1-1﹑2-2和3-3上的轴⼒,并作轴⼒图。
如横截⾯⾯积,,,求各横截⾯上的应⼒。
2-5.图⽰结构中,已知杆之横截⾯为的矩形,当杆横截⾯上的最⼤正应⼒为时,求此时的值。
2-6.直杆在两侧⾯受有沿轴线⽅向均匀分布的载荷(仅在段),其集度为;在端受集中⼒作⽤,。
已知杆横截⾯⾯积,,材料的弹性模量。
求:1、画出轴⼒图; 2、两截⾯的铅垂位3、过两点与轴线夹⾓斜截⾯上的螺杆所⽤材料的屈服点MPa,规定的安全系数n=1.5。
(1)试按强度要求选择⽴柱的直径D;(2)若螺杆的内径d=40mm试校核其强度。
3-1 夹剪如图所⽰。
销⼦C的直径d=5mm。
当加⼒P=0.2kN,剪直径与销⼦直径相同的铜丝时,求铜丝与销⼦横截⾯的平均剪应⼒。
已知a=30mm,b=150mm。
3-2 结构受⼒如图所⽰,若已知⽊材的许⽤切应⼒,试校核⽊接头剪切强度是否安全。
3-3 ⽊梁由柱⽀撑如图所⽰,今测得柱中的轴向压⼒为,若已知⽊梁所能承受的许⽤挤压应⼒。
确定柱与⽊梁之间垫板的尺⼨。
3-4 ⽊构件和由两⽚层合板⽤胶粘接在⼀起,承受轴向载荷作⽤,3-5 ⽔轮发电机组的卡环尺⼨如图所⽰。
已知轴向荷载P=1450kN,卡环材料的许⽤剪应⼒=80MPa,许⽤挤压应⼒=150MPa。
试对卡环进⾏强度校核。
3-6 拉⼒P=80kN的螺栓连接如图所⽰。
已知b=80mm,t=10mm,d=22mm,螺栓的许⽤剪应⼒=130MPa,钢板的许⽤挤压应⼒=300MPa,许⽤拉应⼒ =170MPa。
试校核该接头的强度。
3-7 ⼀托架如图所⽰。
已知外⼒P=35kN,铆钉的直径d=20mm,铆钉都受单剪。
求最危险的铆钉横截⾯上剪应⼒的数值及⽅向。
3-8 销钉式安全离合器如图所⽰,允许传递的外⼒偶矩m=30kN·cm,销钉材料的剪切强度极限=360MPa,轴的直径3-9 图⽰为测定剪切强度极限的试验装置。
薄壁杆件截面几何特性计算的比拟有限元法_周建春

工
程
力
学
Vol.19 No. 1 Feb. 2002
ENGINEERING
MECHANICS
文章编号: 1000-4750(2002)01-038-04
薄壁杆件截面几何特性计算的比拟有限元法
周建春 1,刘光栋 2,魏
(1. 华南理工大学, 广东
琴1
广州 510640; 2. 湖南大学, 湖南 长沙 410082)
4 任意形式截面几何特性的计算
取一任意形式的薄壁杆件截面如图 2 所示,其 中 XOY 为用户选定的初始坐标轴,xo’y 为截面形 心主坐标轴, α 为 X 轴和 x 轴之间的夹角。设 A 为 截面面积, C x 、 C y 为截面形心对 X 轴和 Y 轴的距 离,I x、I y 和 I xy 分别为截面对 X 轴和 Y 轴的惯性矩 和惯性积,由材料力学可得 N 1 N A = ∑ t k l k , C x = ∑ t k l k ( x i + x j ) A, 2 k =1 k =1 N 1 C y = ∑ tk lk ( y i + y j ) A 2 k =1 1 N I x = ∑ t k l k ( y i2 + y i y j + y 2j ) A, 3 k =1 1 N I y = ∑ t k l k ( x i2 + x i x j + x 2j ) A 3 k =1
由最小能量原理 ( 即整个截面中翘曲变形的分 布应使整个截面上的剪应变能 V 为最小),并考虑 单元 k 的起点、终点扇性坐标的关系,对每一个单 元的节点可得
∑±t
k =1
Ne
k
(h k −
ω j − ωi lk
) =0
薄壁杆件力学 主扇性坐标的求解

∙
2������ ∙ ������ ∙ 2 + ������
2 ∙ 2������
=
������ 3
并作出坐标 y 图如图 2 所示。以腹板中点 O 为参考极点,腹板与上翼缘板
交点 1 为积分起点,作出参考扇性坐标 ω1 图如图 3 所示。
图 2 坐标 y 图
图 3 参考扇性坐标 ω1 图
利用图 2 和图 3,由公式������������������ = ∫ ������1������������������ = ∫0������ ������1������������������������,可求出
作出坐标 x 图如图 5 所示。以腹板与上翼缘板交点 O 为参考极点,腹板与 下翼缘板交点 1 为积分起点,作出参考扇性坐标 ω1 图如图 6 所示。
图 5 坐标 x 图
图 6 参考扇性坐标 ω1 图
利用图 5 和图 6,由公式������������������ = ∫ ������1������������������ = ∫0������ ������1������������������������,可求出
1 6
������4������
5 6
������3������
=
1 5
������
因此剪心在
O
点下侧1
5
������处,由此作出主扇性坐标
ω0
图如图
7
所示。
图 7 主扇性坐标 ω0 图
问题:利用参考扇性坐标确定如图 1 所示各断面的扭心位置,并作出主扇性坐标 ω0 图。
(a)
(b)
图 1 断面尺寸图
解:(a) 槽型断面 此断面具有横向对称轴,故形心在该对称轴上,形心 C 到腹板中线的距离������������
薄壁杆件力学

薄壁杆件力学一、引言薄壁杆件力学是结构力学的一个重要分支,主要研究薄壁杆件的受力和变形规律。
薄壁杆件广泛应用于航空、航天、汽车、机械等领域,因此对其力学性能的研究具有重要意义。
二、薄壁杆件的基本概念1. 薄壁杆件的定义薄壁杆件是指截面尺寸相对较小,且轴向载荷较大的结构元件。
在实际工程中常见的薄壁杆件有圆管、方管、角钢等。
2. 薄壁杆件的特点(1)强度高:由于其截面尺寸相对较小,因此强度相对较高。
(2)重量轻:由于其截面尺寸相对较小,因此重量相对较轻。
(3)易于加工:由于其截面尺寸相对较小,因此易于加工成各种形状。
三、薄壁杆件受力分析1. 轴向载荷作用下的受力分析当薄壁杆件受到轴向载荷作用时,其受力分析可以采用杆件理论进行计算。
根据杆件理论,薄壁杆件的应力为:σ= F/A其中,σ为应力,F为轴向载荷,A为截面积。
2. 弯曲载荷作用下的受力分析当薄壁杆件受到弯曲载荷作用时,其受力分析可以采用梁理论进行计算。
根据梁理论,薄壁杆件的弯矩为:M= EI/ρ其中,M为弯矩,E为弹性模量,I为截面惯性矩,ρ为曲率半径。
3. 剪切载荷作用下的受力分析当薄壁杆件受到剪切载荷作用时,其受力分析可以采用剪切变形理论进行计算。
根据剪切变形理论,薄壁杆件的剪应力为:τ= F/As其中,τ为剪应力,F为剪切载荷,As为截面面积。
四、薄壁杆件的变形规律1. 轴向变形规律当薄壁杆件受到轴向载荷作用时,其轴向变形规律可以采用杆件理论进行计算。
根据杆件理论,薄壁杆件的轴向变形为:δ= FL/EA其中,δ为轴向变形,F为轴向载荷,L为杆件长度,E为弹性模量,A为截面积。
2. 弯曲变形规律当薄壁杆件受到弯曲载荷作用时,其弯曲变形规律可以采用梁理论进行计算。
根据梁理论,薄壁杆件的弯曲变形为:δ= M L/ EI其中,δ为弯曲变形,M为弯矩,L为跨度长度,E为弹性模量,I为截面惯性矩。
3. 剪切变形规律当薄壁杆件受到剪切载荷作用时,其剪切变形规律可以采用剪切变形理论进行计算。
结构力学

1、结构按其几何形状可分为杆件结构、薄壁板壳结构和实体结构。
2、结构力学的研究对象是杆件结构。
它是一门研究杆件结构强度、刚度、稳定性和合理组成的科学。
3、杆件结构按其受力特性可分为梁、拱、刚架、桁架、组合结构。
4、结点分为铰结点和刚结点。
铰结点之产生杆端轴力和剪力,不引起杆端弯矩;刚结点除产生杆端轴力和剪力,还引起杆端弯矩,当结构发生变形时,汇交于刚结点各杆端的切线之间的夹角将保持不变。
5、支座的类型:可动铰支座、固定铰支座、固定支座、定向滑动支座。
6、本来是几何可变,经微小位移后又成几何不变的体系称为几何瞬变体系。
7、顺便体系能否应用于工程结构?P8可见,即使荷载不大,也会使杆件产生非常大的内力和变形。
因此,瞬变体系在工程中不能采用,对于接近瞬变的体系也应避免。
8、凡减少一个自由度装置,称一个约束。
一根链杆相当于一个约束;一个单铰相当于两个约束;一个刚性联结相当于三个约束;联结n个刚片的复铰相当于(n-1)个单铰(n为刚片数)9、以刚片作为组成体系的基本部件进行计算的方法称为刚片法。
10、计算自由度W W=3m-2h-r (m刚片数 h 联结刚片的单铰数目r 支座链杆数目)11、平面体系几何不变的必要条件:W>0,表明体系缺少足够的约束,因此是几何可变的;W=0,表明体系具有成为几何不变所必须的最少约束数目;W<0,表明体系具有多余的约束。
12、体系本身为几何不变时必须满足W≤3的条件。
必须指出,W≤0只是几何不变的必要条件,不是充分条件。
13、静定结构与超静定结构的区别:静定结构的几何组成特征是几何不变且无多余约束;超静定结构的几何组成特征是几何不变且有多余约束;仅用静力平衡条件就可以求解的结构称为静定结构;综合运用平衡条件与位移协调条件求解的结构,称为超静定结构。
14、内力图绘制:梁上无荷载(q=0)的区段,Q图为一水平线,M图为一斜直线;梁上有均布荷载(q=常数)的区段,Q图为一斜直线,M图为二次抛物线;集中力作用点的两侧,剪力有突变,其差值等于该集中力,在集中力作用点处,M图是连续的,但因集中力偶两侧的剪力值相同,所以两侧M图的切线应相互平行;集中力偶作用处,剪力无变化,但在集中力偶两侧弯矩有突变,其差值等于该集中力偶,在M图中形成台阶,又因集中力偶两侧的剪力值相同,所以两侧M图的切线应相互平行。
船舶结构力学名词解释

弹性固定端:它受梁端力矩M作用后产生一个等于力矩M的转角Ɵ即存在如下关系Q0=A0M。
几何不变体系:是指如果不考虑材料应变所产生的变形,体系在受到任何载荷作用后能够保持其固有的几何形状和位置的体系。
不可动节点简单刚架:在实际结构中,大多数刚架受力变形后节点线位移可以不计,于是计算强度时在节点处可加上固定铰支座,故称为不可动节点刚架。
位移法:以杆系结构节点处的位移作为基本未知量的方法。
翘曲:非圆截面杆件扭转变形后,杆件的截面已不再保持为平面,而是变为曲面,这种现象称为翘曲。
用李兹法求结构问题是,要求所选挠度曲线必须满足位移边界线。
(错,还含有其他)薄壁杆件约束扭转时,杆件各横截面上没有正应力,只有扭转引起的剪应力。
(对,杆件上平行于杆轴的直线在变形后长度不变且仍为直线)简述复杂弯曲梁的叠加原理:当梁上同时受到几个不同的横向荷重及一定的轴向力作用时,分别求出在该轴向力作用下的各个横向荷重单独作用于梁时的弯曲要素,然后进行叠加,即得到在该轴向力作用下几个不同的横向荷重同时作用于梁时的弯曲要素。
矩阵位移法中,为什么要进行坐标转移?对哪些量要进行坐标转换?答:建立节点静力平衡方程是在总坐标系中进行的,因此,一般来说在矩阵位移法中有一个坐标转换问题。
要把各杆元在其局部坐标系中的节点位移向量,杆端力向量以及刚度矩阵,转换成坐标系中的节点位移向量,杆端力向量以及刚度矩阵。
杆元固端力向量也要换成坐标系中的杆元固端力向量。
简述薄板弯曲理论中的三条基本假定。
1板变形前垂直于中面的法线在板变形后仍为直线,且是变形后中面的法线,这一假定称为直法线假定。
2垂直于板面的应力分量与其他应力分量相比可以忽略不计,即假定其=0。
3薄板中面内的各点都没有平行于中面的位移,即假定不计因板发生弯曲而产生的中面的变形,从而不计板弯曲产生的中面力。
简述欧拉力计算公式的的适用范围,为什么要研究非弹性稳定性问题?只有当压杆的柔度大于极限值时才能使用欧拉公式若压杆的柔度X<Xp,则欧拉应力大于材料比例,这属于超比例极限的压杆稳定性问题,即非弹性稳定性问题,这时欧拉公式不能使用。
结构力学薄壁杆件扭转
§9-2 薄壁杆件的自由扭转
沿整个截面积分可得总扭矩为:
M s 2qA
式中A——闭口截面壁厚中心线所围的总面积。从
而沿截面的剪流为:
q
t
Ms
2A
(9-8)
再来推导扭率和扭矩常数计算公式。若从薄壁杆件
中取出长度为dx的微段,其受扭矩Ms作用产生的扭
角为dφ,则扭矩所做的功为:
dW
1 2
M s d
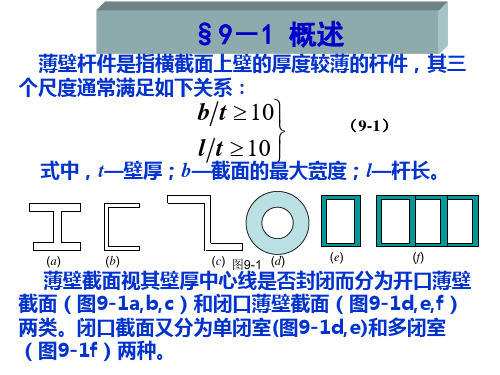
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
如果薄壁杆件受到扭矩作用,由于存在支座或其他 约束,扭转时不能自由变形,则这种扭转称为约束扭 转。薄壁杆件约束扭转时,各横截面的翘曲程度是不 相同的,这将引起相邻两截面间纵向纤维的长度改变, 于是横截面上除了有扭转而引起的剪应力之外,还有 因翘曲而产生的正应力。由于翘曲正应力在横截面上 分布不均匀,就会导致薄壁杆件发生弯曲,并伴随产 生弯曲剪应力。这样,薄壁杆件约束扭转时,截面上 就存在二次剪应力。二次剪应力又将在截面上形成一 个附加扭矩,称之为二次扭矩,于是杆件截面上的扭 矩就等于自由扭转扭矩与二次扭矩之和。由此可见, 薄壁杆件约束扭转是比较复杂的。
§9-2 薄壁杆件的自有扭转
开口薄壁杆件自由扭转时的扭率计算公式如下:
Ms
GI t
(9-2)
式中,—剪切模量;It—截面扭转惯性矩(扭转
常数)。
I t
1 3
i
hi
t
3 i
(9-3)
式中,hi、ti—截面上第i个狭长矩形的高度(长边)
和厚度(短边)。若截面的壁厚中心线是一根曲线,
§9-2 薄壁杆件的自由扭转
微段扭转变性能为:
结构力学第九章薄壁杆件扭转 28页

§9-2 薄壁杆件的自由扭转
作业2、3、5
考试
考试题型: (1)选择填空 (2)判断题(不要解释理由,只要判断对错)
以上两项共54分,可能会增加题量,减小每题的分值 (3)计算题(基本运算)46分 计算题比作业题目简单,运算量小 重点在后面章节,与材料力学重复率低的章节 试验报告+作业=平时分 考试时计算题先把关键公式写下
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
§9-1 概述
如果薄壁杆件受到扭矩作用,由于存在支座或其 他约束,扭转时不能自由变形,则这种扭转称为约束 扭转。薄壁杆件约束扭转时,各横截面的翘曲程度是 不相同的,这将引起相邻两截面间纵向纤维的长度改 变,于是横截面上除了有扭转而引起的剪应力之外, 还有因翘曲而产生的正应力。由于翘曲正应力在横截 面上分布不均匀,就会导致薄壁杆件发生弯曲,并伴 随产生弯曲剪应力。这样,薄壁杆件约束扭转时,截 面上就存在二次剪应力。二次剪应力又将在截面上形 成一个附加扭矩,称之为二次扭矩,于是杆件截面上 的扭矩就等于自由扭转扭矩与二次扭矩之和。由此可 见,薄壁杆件约束扭转是比较复杂的。
壁截面(图9-1a,b,c)和闭口薄壁截面(图9-1d,e,f)
两类。闭口截面又分为单闭室(图9-1d,e)和多闭室
(图9-1f)两种。
§9-1 概述
除薄壁圆管外,薄壁杆件通常是非圆截面杆件。 材料力学中已经指出,非圆截面杆件在扭转变形后, 杆件的截面已不再保持为平面,而是变为曲面,这种 现象称为翘曲。
qds dA o
x tb b
a ta
b ds
dx
§9-2 薄壁杆件的自由扭转
btb atad x 0
或
qbtbata (9-7)
材料力学——剪切中心与牵连位移
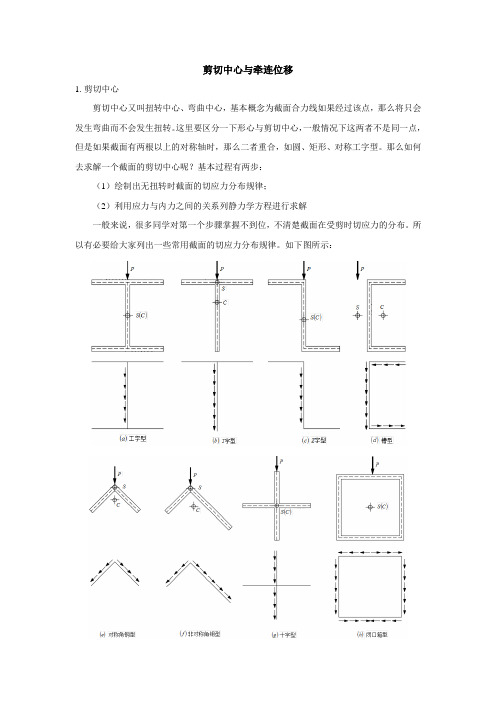
剪切中心与牵连位移1.剪切中心剪切中心又叫扭转中心、弯曲中心,基本概念为截面合力线如果经过该点,那么将只会发生弯曲而不会发生扭转。
这里要区分一下形心与剪切中心,一般情况下这两者不是同一点,但是如果截面有两根以上的对称轴时,那么二者重合,如圆、矩形、对称工字型。
那么如何去求解一个截面的剪切中心呢?基本过程有两步:(1)绘制出无扭转时截面的切应力分布规律;(2)利用应力与内力之间的关系列静力学方程进行求解一般来说,很多同学对第一个步骤掌握不到位,不清楚截面在受剪时切应力的分布。
所以有必要给大家列出一些常用截面的切应力分布规律。
如下图所示:图1:常见薄壁杆件的切应力分布规律和剪切中心位置注图1中S 表示剪切中心,C 表示形心知道了切应力的分布规律,那么就可以根据静力学关系进行求解了。
静力学关系公式如下:P dA F A s ==⎰τ0==⎰A dA d T τ截面扭转为0,截面合剪力为P 。
从图1中的截面切应力分布规律我们可以得出如下结论:(1)剪力中心是截面特性,与外荷载无关;(2)薄壁杆件开口杆件与闭口杆件的切应力分布有区别(有兴趣的同学可以查资料)(3)薄壁杆件的切应力分布与受力荷载有关。
下面我们来看一个算例:上图非对称工字型薄壁钢受水平力P ,求作用何处是无扭转产生。
很明显,需要求剪切中心,那么可以按照下图的计算模型进行计算:顶板承担剪力1s F ,底板承担剪力2s F 。
根据静力学关系有:P F F s s =+21()021=--e h F e F s s对上下顶板的最大切应力分别从整体和单独一块板应力切应力公式有: 顶板最大切应力I S P I S F s ⨯⨯=⨯⨯=δδτ11111max ;底板最大切应力IS P I S F s ⨯⨯=⨯⨯=δδτ22221max 其中21I I 、分别为上下顶板的惯性矩,且有21I I I +=。
故而: I I P F s 11⨯=,II P F s 22⨯= 所以:h I I h I e e h e I I 9821121=+=⇒-=(结论:剪切中心与上下板的刚度比有关) 2. 牵连位移这里主要讨论一下支座链杆的位移对杆件的影响。
薄壁杆件力学 主扇形静矩

薄壁杆件力学主扇形静矩
薄壁杆件力学是固体力学的一个分支,专门研究薄壁结构(如桥梁、建筑框架、航空航天器等)的力学行为。
在薄壁杆件的分析中,主扇形静矩是一个重要的概念,它对于理解杆件的受力特性和进行稳定性分析具有重要意义。
主扇形静矩,又称为扇形惯性矩或扇形面积矩,是描述截面形状对某一点转动惯性的量度。
在薄壁杆件中,由于截面形状通常较为复杂,不能简单地用常规的惯性矩来描述其受力特性。
因此,引入主扇形静矩来更准确地描述杆件截面在不同方向上的转动惯性。
主扇形静矩的计算通常涉及到复杂的积分运算,需要根据杆件截面的具体形状和尺寸来确定。
在计算过程中,需要选择合适的坐标系和积分路径,以确保计算结果的准确性。
在薄壁杆件的分析中,主扇形静矩的应用主要体现在以下几个方面:
稳定性分析:通过计算杆件截面的主扇形静矩,可以评估杆件在不同方向上的稳定性。
这对于预测杆件在受力过程中的变形和失稳行为具有重要意义。
应力分析:主扇形静矩还可以用于计算杆件截面上的应力分布。
通过对比不同方向上的主扇形静矩,可以了解杆件在不同受力状态下的应力特点,从而为杆件的设计和优化提供依据。
优化设计:在薄壁杆件的设计过程中,通过调整杆件截面的形状和尺寸,可以优化其主扇形静矩的分布。
这有助于提高杆件的承载能力和稳定性,同时降低材料消耗和制造成本。
总之,主扇形静矩是薄壁杆件力学中一个重要的概念,它对于理解杆件的受力特性和进行稳定性分析具有重要意义。
在未来的研究中,可以进一步探讨主扇形静矩在复杂薄壁结构分析中的应用,以及如何通过优化杆件截面形状来提高其力学性能。
工程力学 第9章 杆件横截面上的切应力分析

第 9 章 弹性杆件横截面上的切应力分析
对于实心截面杆件以及某些薄壁截面杆件,当其横截面上仅有 扭矩(Mx)或剪力(FQy 或 FQz)时,与这些内力分量相对应的分布 内力,其作用面与横截面重合。这时分布内力在一点处的集度,即为 切应力。 分析与扭矩和剪力对应的切应力方法不完全相同。对于扭矩存 在的情形,依然借助于平衡、变形协调与物性关系,其过程与正应力 分析相似。对于剪力存在的情形,在一定的前提下,则仅借助于平衡 方程。 本章重点介绍圆截面杆在扭矩作用下其横截面切应力以及薄壁 杆件的弯曲切应力分析。
§ 9-1 圆轴扭转时横截面上的切应力
9-1-1 圆轴扭转变形特征 -反对称性论证圆轴扭转时横截面保持平面 9-1-2 变形协调方程 9-1-3 物性关系-剪切胡克定律 9-1-4 静力学方程 9-1-5 圆轴扭转时横截面上的切应力表达式
§ 9-2 非圆截面杆扭转时的切应力
图 9-8 例 9-2 图
解: 1.各轴所承受的扭矩 各轴所传递的功率分别为 P1 =14 kw , P 2 = P3 =P 1 /2=7 kw 转速分别为 n1 = 120 r/min
n 3=n1 ×
据此,算得各轴承受的扭矩:
z1 36 =120 × r/min =360r/min z3 12
14 M x1 = M e1 = 9549 × N ⋅ m = 1114 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 557 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 185 .7 N ⋅ m 360
2.计算最大切应力 E 、H、C 轴横截面上的最大切应力分别为
材料力学课件-第四章 扭转-薄壁杆件的扭转

例2:某等壁厚d闭口薄壁杆受扭矩T,中心线周长S,轴的最大扭转切应力与扭转变形:(1)在 S/2中心线长度上壁厚增加一倍到2d;(2)在很小的局部受损伤壁厚减薄到d/2。
解:(2)第2种情形
局部减薄对积分值影响甚微,可以忽略不计。
最大应力增加一倍。
定性研究结论:强度是局部量,刚度是整体量。
例3:比较扭转切应力与扭转变形
解:
R0
R0
比较
(1)闭口薄壁圆管
(2)开口薄壁圆管
(狭长矩形)
作业 4-22 4-27 4-35 4-36
谢谢
薄壁圆管
思考:公式的精度?
在线弹性情况下,精确解为
思考:公式(1)和(2)的适用范围?
(1)
(2)
误差
T
dx
a
b
c
d
二、闭口薄壁杆的扭转变形
dx
ds
分析方法讨论:
由静力学、几何和物理三方面求解所遇到的困难:几何形状复杂。
新方法探索:
尝试能量法。
一未知量
无未知量
问题可解
二、闭口薄壁杆的扭转变形
假设:切应力沿壁厚均匀分布,其方向平行于中心线 假设依据:
T
dx
a
b
c
d
a
b
c
d
2
1
dx
1
1
2
2
薄,切应力互等定理
利用切应力互等定理,转化为研究纵向截面切应力,利用平衡方程求解.
截面中心线所围面积 的2倍
思考:O点位置可否任选,如截面外?
ds
o
ds
材料力学杆件常见支撑形式_概述说明以及解释__

材料力学杆件常见支撑形式概述说明以及解释1. 引言1.1 概述本文旨在介绍材料力学中的杆件常见支撑形式,并对其进行说明和解释。
杆件是工程中常用的结构元素,其功能主要是承受和传递外部载荷。
而不同的支撑形式会对杆件的受力分布和性能产生影响。
因此,了解各种支撑形式及其特点对于合理设计和安全运用杆件具有重要意义。
1.2 文章结构本文分为五个部分。
首先,在引言部分我们会简单概述文章内容和目的。
接下来,在第二部分中,我们将重点介绍常见的杆件支撑形式,包括支座支撑、固定支撑和弹性支撑,并详细解释每种形式的原理及适用条件。
第三部分将对材料力学中杆件的应力分析进行讨论,包括受力、应变和应力的分析方法与计算公式。
第四部分将探讨杆件常见的故障和破坏形式,具体包括弯曲破坏、屈服破坏以及断裂破坏等。
最后,在结论部分我们会总结全文,并展望未来研究的方向和可能的发展。
1.3 目的本文的目的是为读者提供关于材料力学中杆件常见支撑形式的全面了解。
通过对不同支撑形式原理及其在实际应用中的作用进行解释,有助于读者对结构物和工程设计中如何选择合适的支撑形式有更深入的认识。
同时,通过讨论杆件受力分析和常见故障破坏形式,读者可以更好地理解杆件结构性能和使用时需要注意的问题。
希望本文内容能够提供给读者在相关领域进行研究和实践时的参考依据,并促进该领域研究工作的进一步发展。
2. 常见支撑形式2.1 支座支撑在材料力学中,支座支撑是一种常见的杆件支撑形式。
它通常由固定在基础上的支座来提供支持。
这种支撑形式可以使杆件在运载荷作用下的位移受到限制,从而起到稳定结构的作用。
例如,在梁上施加一个负载时,通过使用两个直立的垂直墩柱作为支撑点,可以将梁固定在适当的位置上。
2.2 固定支撑固定支撑是另一种常见的材料力学杆件的支撑形式。
这种形式利用了端部约束条件来限制结构位移,并使其保持刚性。
通常情况下,在固定端具有零位移和零转角约束条件时,才能实现真正的固定。
