12简谐振动
(完整版)大学物理授课教案第十二章机械振动

第四篇 振动与颠簸第十二章机械振动§ 12-1 简谐振动1、弹簧振子运动如图所取坐标,原点 O 在 m 均衡地点。
现将 m 略向右移到 A ,而后松开,此时,由于弹簧伸长而出现指向均衡地点的弹性力。
在弹性 力作用下,物体向左运动,当经过地点O 时,作用在 m 上弹性力等于 0,可是因为惯性作用, m 将持续向 O 左侧运动,使弹簧压缩。
此时,因为弹簧被压缩, 而出现了指向均衡地点的弹性力并将阻挡物体向左 运动,使 m 速率减小,直至物体静止于B (刹时静止),以后物体在弹性力作用下改变方向,向右运动。
这样在弹性力作用下物体左右来去运动,即作机械振动。
图 12-12、简谐振动运动方程由上剖析知, m 位移为 x (相对均衡点 O )时,它遇到弹性力为(胡克定律) :Fkx(12-1)式中: 当x即位移沿 +x 时,F 沿 -x ,即F0 当 x即位移沿 -x 时,F 沿+x ,即F 0k为弹簧的倔强系数, “—”号表示力 F 与位移 x (相对 O 点)反向。
定义:物体受力与位移正比反向时的振动称为简谐振动。
由定义知,弹簧振子做谐振动。
由牛顿第二定律知,m加快度为aF kxmm( m为物体质量)ad 2 xd 2 x k x∵dt 2∴ dt2mk2∵ k、 m均大于 0,∴可令m可有:d 2 x2 x 0(12-2)dt 2式 (12-2) 是谐振动物体的微分方程。
它是一个常系数的齐次二阶的线性微分方程,它的解为x Asin t'(12-3)或x Acos t(12-4)'2式 (12-3)(12-4) 是简谐振动的运动方程。
所以,我们也能够说位移是时间t 的正弦或余弦函数的运动是简谐运动。
本书顶用余弦形式表示谐振动方程。
3、谐振动的速度和加快度物体位移:xAcos tdxAsin tV(12-5)速度:dtd 2 xa2 Acos t 2 x加快度:dt 2(12-6)可知:Vmax A amax 2 Ax t、V t 、 at 曲线以下图 12-2图 12-3第十二章机械振动沈阳工业大学郭连权(教授)说明:(1)Fkx 是谐振动的动力学特点;(2) a2 x是谐振动的运动学特点;(3)做谐振动的物体往常称为谐振子。
简谐振动的规律和特点

简谐振动的规律和特点
简谐振动是一种特殊的振动,其规律和特点可以总结如下:
恢复力与位移成正比: 简谐振动的主要特点之一是恢复力与振动物体的位移成正比。
即,物体偏离平衡位置越远,恢复力越大。
速度和加速度的正弦关系:在简谐振动中,物体的速度和加速度是正弦函数关系。
速度达到最大值时,加速度为零,反之亦然。
振动周期恒定: 简谐振动的周期是物体完成一次完整振动所需的时间。
在简谐振动中,周期是恒定的,与振幅无关。
频率和周期的关系:频率是振动的周期的倒数,即频率 = 1 / 周期。
频率和周期之间存在反比关系。
能量转换:在简谐振动中,势能和动能之间存在周期性的转换。
当物体经过平衡位置时,动能最大,而势能为零;反之,当物体达到最大位移时,势能最大,动能为零。
振动方向和恢复力方向相反: 当物体偏离平衡位置时,恢复力的方向总是指向平衡位置。
这导致振动物体沿着恢复力的方向振动。
频率不受振幅影响: 简谐振动的频率不受振幅的影响。
无论振幅的大小如何,频率始终保持不变。
这些规律和特点使得简谐振动成为一个数学上非常可控和可预测的振动模型。
简谐振动在物理学、工程学和其他科学领域中都有广泛的应用。
简谐振动

x x1 x 2
x1
v0
O x0
k • 频率 ω M m
2 v A x0 2 02 ω
x
v0 φ0 tg ωx0
1
( M m) g Mg mg x0 k k k
掌握初始条件 的确定方法
14
简谐振动总结
分析振动系统 求动力学方程 求运动学方程
• •
动力学特征
1. 动能
1 1 2 2 2 Ek mv kA sin ( t ) 2 2
1 t T 1 2 Ek Ek dt kA T t 4
2. 势能
1 2 Ek max kA 2 E k min 0
1 2 1 2 E p kx kA cos 2 ( t ) 2 2
3. 机械能
1 2 E Ek E p kA (简谐振动系统机械能守恒) 2
11
例 物理摆 如图所示, 设刚体对轴的转动惯量为J. 设 t = 0 时摆角向右最大为 0. 求 振动周期和振动方程.
解 M m g h sin J
mgh sin 0 J
5 时 , sin
mgh 0 J
振动方程
mgh J
单 摆
J T 2 mgh
h T 2 g
12
0 cosω t
例
竖直方向的弹簧振子,求振动方程。 解 分析系统受力
线性回复力
l0
k O
f
x
i
mg k (Δl x ) mg k Δ l kx kx
l
m
x
d x k x0 2 dt m
简谐振动的特性

简谐振动的特性简谐振动是物体在受到一个恢复力作用下,沿着某一直线定点运动的一种运动形式。
它具有周期性、振幅恒定以及频率稳定等特点。
本文将从频率、周期和振幅等几个方面介绍简谐振动的特性。
一、频率简谐振动的频率是指单位时间内振动的次数,通常用赫兹(Hz)来表示。
频率与振动周期之间有如下关系:频率 = 1 / 周期频率的倒数就等于振动周期。
例如,一个物体的振动周期为0.1秒,则它的频率为1 / 0.1秒 = 10Hz。
二、周期简谐振动的周期是指一个完整的振动所经过的时间。
周期与频率之间的关系已在上一部分中提到。
简谐振动的周期与其运动物体的质量以及弹性系数密切相关。
当质量和弹性系数不变时,周期始终保持不变。
三、振幅振幅是简谐振动中物体在振动过程中离开平衡位置的最大偏移距离。
振幅大小与振动物体的能量有关,而能量的大小与振幅平方成正比。
振幅越大,物体具有的机械能越大。
四、受力特性在简谐振动中,物体受到的恢复力与其偏离平衡位置的距离成正比,且方向相反。
根据胡克定律,恢复力的大小与物体偏离平衡位置的距离呈线性关系。
五、相位简谐振动的相位是指振动物体相对于某一特定时刻的位置关系。
相位用角度或弧度来表示。
相位角正负号表示了物体相对于平衡位置的偏移方向。
相位的变化规律可由三角函数来表示。
六、谐振现象谐振现象指的是当外力的频率与物体自身振动频率相同时,物体表现出的振幅增大的现象。
这是由于外力与物体振动频率的共振效应所引起的。
当共振发生时,外力与物体发生能量传递,使振幅增大。
七、应用范围简谐振动在日常生活和工程领域中得到了广泛的应用。
例如钟表的摆线引入了简谐振动的原理,以实现精准的时间测量。
在机械振动工程中,简谐振动的特性被广泛应用于减振器的设计和振动分析中。
结语简谐振动具有周期性、振幅恒定和频率稳定等特点,在自然界和工程中都有广泛的应用。
通过对简谐振动特性的研究和理解,可以更好地掌握和应用振动学的相关知识。
拓宽对简谐振动的认识,有助于我们更深入地探索振动现象的奥秘。
简谐振动的特点与描述

简谐振动的特点与描述简谐振动是指一个物体在固定位置附近做往复振动的运动,其特点是周期性、均衡运动和振幅恒定。
简谐振动广泛应用于物理、工程等领域,如弹簧振子、摆钟等,具有重要的理论和实际意义。
本文将从简谐振动的描述、特点和应用三个方面进行阐述。
一、简谐振动的描述简谐振动的描述通常使用正弦(sin)函数或余弦(cos)函数,根据时间t表示物体的位置x或速度v。
振动的位置可以表示为:x = A sin(ωt + φ)其中,x为位置,A为振幅,ω为角频率,t为时间,φ为初相位。
角频率ω与周期T的关系为:ω = 2π/T角频率反映了振动的频率,周期T表示振动从一个位置到达相同位置所需的时间。
初相位φ则是振动的起始点。
速度v可以表示为:v = Aωcos(ωt + φ)根据简谐振动的描述公式,我们可以确定物体的位置和速度随时间的变化规律。
二、简谐振动的特点1. 周期性:简谐振动具有明显的周期性,物体会在一个固定的时间间隔内完成一次完整的振动。
周期性的特征使得我们可以预测振动的未来状态,并对振动进行分析和研究。
2. 均衡运动:简谐振动的均衡位置是振动的中心位置,物体在均衡位置附近的振动是以均衡位置为基准的往复运动。
均衡位置是简谐振动的稳定状态,物体在外力作用下会向均衡位置回复。
3. 振幅恒定:简谐振动的振幅是指物体在振动过程中达到的最大位移,振幅决定了振动的幅度大小。
简谐振动的特点之一是振幅恒定,即振幅不受时间和频率的影响,保持不变。
4. 无摩擦和阻尼:简谐振动假设在振动过程中没有外界摩擦和阻尼的存在,即物体在振动中不受阻力影响。
这样的假设可以简化振动系统的分析,使得我们可以更好地研究其特性。
三、简谐振动的应用1. 物理实验:简谐振动广泛应用于物理实验中,可通过自由振动的系统来研究和验证振动的规律。
例如,利用弹簧振子实验可以研究简谐振动的周期和相位。
2. 工程应用:简谐振动的理论在工程中有重要的应用,例如建筑物的结构振动分析和振动控制。
简谐振动的特征与简谐振动的公式

简谐振动的特征与简谐振动的公式简谐振动是物理学中常见的一种振动方式,它具有许多特征和可以用公式进行描述。
本文将介绍简谐振动的特征以及常用的简谐振动公式。
1. 特征描述简谐振动是指物体在回复力的作用下,沿某一直线方向上做连续、周期性的往复运动。
简谐振动具有以下几个特征:(1) 幅度恒定:在简谐振动中,物体的振幅是恒定的,即振动的最大偏离位置。
(2) 频率恒定:简谐振动的频率是恒定的,即单位时间内的振动周期数。
(3) 相位差恒定:简谐振动中,不同物体的振动状态可以用相位角来描述,相位差的差别决定了振动状态的差异。
2. 简谐振动公式简谐振动的运动可以用以下公式进行描述:x = A*sin(ωt + φ)其中,x是物体的位移,A是振幅,ω是角频率,t是时间,φ是初始相位。
振幅A表示物体从平衡位置最大的位移距离,角频率ω表示单位时间内完成的往复运动的周期数,并且与振动的频率f有以下关系:ω = 2πf,其中π是圆周率。
初始相位φ表示物体在某一时刻位于位移最大的正方向上的位置。
3. 简谐振动的特殊情况除了上述一般情况的简谐振动公式,还存在几种特殊情况:(1) 无初相位差的简谐振动:当两个物体的简谐振动的振动频率相同且初相位差为0时,它们的振动状态完全一致。
(2) 反向偏移的简谐振动:若两个物体的简谐振动的振幅相等,振动频率相同,但初相位差为π或180°时,它们的位移与时间的关系将呈现反向的偏移。
(3) 超前偏移的简谐振动:若两个物体的简谐振动的振幅相等,振动频率相同,但初相位差为π/2或90°时,它们的位移与时间的关系将呈现超前的偏移。
4. 应用举例简谐振动广泛应用于许多物理学和工程学的领域,例如:(1) 机械振动:对于工程结构的振动现象,可以通过简谐振动公式进行分析和计算。
(2) 光学领域:光的波动也可以描述为简谐振动,例如光的干涉、衍射和偏振现象等。
(3) 电路中的交流电信号:电路中的交流电信号也可以用简谐振动的公式进行描述和分析。
简谐振动的规律和特点

简谐振动的规律和特点简谐振动是一种重要的物理现象,它在自然界和人类生活中都有广泛的应用。
本文将详细介绍简谐振动的规律和特点,并从多个角度进行描述。
一、简谐振动的规律和特点1. 定义:简谐振动是指物体在一个平衡位置附近做往复振动的运动。
它的运动方式具有周期性和对称性,是一种非常规律的振动。
2. 弹簧振子的例子:弹簧振子是最常见的简谐振动的例子之一。
当弹簧振子受到外力拉伸或压缩后,当外力移除时,它会以平衡位置为中心作往复振动。
3. 动力学规律:简谐振动的运动规律可以由胡克定律和牛顿第二定律得出。
根据胡克定律,当弹性体受力时,其恢复力与位移成正比。
牛顿第二定律则表明物体的加速度与作用力成正比,与质量成反比。
结合这两个定律,可以推导出简谐振动的运动方程。
4. 运动方程:简谐振动的运动方程可以表示为x = A * sin(ωt + φ),其中x是物体的位移,A是振幅,ω是角频率,t是时间,φ是相位差。
这个运动方程描述了物体在平衡位置两侧往复振动的过程。
5. 特点一:周期性。
简谐振动的最基本特点是其运动是周期性的,即物体在一个周期内重复完成相同的运动。
周期T是指物体完成一个完整振动所需的时间,与角频率ω的倒数成正比。
6. 特点二:振幅和频率。
简谐振动的振幅A表示物体在振动过程中最大的位移,频率f表示单位时间内完成的振动次数。
振幅和频率都是简谐振动的重要参数,它们与物体的质量、劲度系数、外力等因素有关。
7. 特点三:相位差和初相位。
相位差是指两个简谐振动之间的时间差,初相位是指物体在某一时刻的位移相对于平衡位置的位置。
相位差和初相位对于描述简谐振动的运动状态和相互作用非常重要。
8. 特点四:能量转化。
简谐振动是一种能量在不同形式之间转化的过程。
在振动过程中,物体的动能和势能会不断相互转化,当物体通过平衡位置时,动能最大,而位移最大时,势能最大。
9. 特点五:应用广泛。
简谐振动的规律和特点在物理学、工程学、生物学等领域都有广泛的应用。
简 谐 振 动

国际单位制中,周期的单位为秒(s);频率的单位为赫兹 (Hz);角频率的单位为弧度每秒(rad/s)。
对弹簧振子,由于
k
m
故有:
T 2π m k
1 k
2π m
由上式可以看出,弹簧振子的周期和频率都是由物体的质量 m和弹簧的劲度系数k所决定的,即只与振动系统本身的物理性 质有关。因此,我们将这种由振动系统本身的性质所决定的周期 和频率称为固有周期和固有频率。
v dx Asin(t )
dt
a
d2x dt 2
2 Acos(t
)
【例10-1】如下图所示,一质量为m、长度为l的均质细棒 悬挂在水平轴O点。开始时,棒在垂直位置OO′,处于平衡状态。 将棒拉开微小角度θ后放手,棒将在重力矩作用下,绕O点在竖 直平面内来回摆动。此装置是最简单的物理摆,又称为复摆。 若不计棒与轴的摩擦力和空气阻力,棒将摆动不止。试证明在 摆角很小的情况下,细棒的摆动为简谐振动。
由胡克定律可知,在弹性限度内,物体受到的弹力F的大小 与其相对平衡位置的位移x成正比,即F=-kx
上式中,负号表示弹力的方向与位移的方向相反,始终指向 平衡位置,因此,此力又称为回复力。
根据牛顿第二定律可知,物体的加速度为:
a F k x mm
因k和m都是正值,其比值可用一个常数ω的平方表示,即ω2 =k/m,故上式可写为:
物理学
简谐振动
物体运动时,如果离开平衡位置的位移(或角位移)按余 弦函数或正弦函数的规律随时间变化,则这种运动称为简谐振 动。在忽略阻力的情况下,弹簧振子的振动及单摆的小角度摆 动等都可视为简谐振动。
1.1 简谐振动的运动方程
如下图所示,一轻弹簧(质量可忽略不计)放置在光滑水平 面上,一端固定,另一端连一质量为m的物体。这样的系统称为 弹簧振子,它是物理学中的又一理想模型。
大学物理12机械振动2

A
x x−t 图
T
ω v = − A ω sin( ω t + ϕ )
π = Aω cos(ωt +ϕ + ) 2 2 a = − A ω cos( ω t + ϕ )
= Aω cos(ωt +ϕ + π)
2
T=
2π
取ϕ = 0
− Aω
v v −t图 Aω o T
l = l0 1− (v / c)2
在飞船B上测得飞船 相对于飞船 的速度: 在飞船 上测得飞船A相对于飞船 的速度: 上测得飞船 相对于飞船B的速度
v = l / ∆t = (l0 / ∆t) 1−(v / c)
解得:v = l0 / ∆t 1 + (l0 / c∆t )
2
2
= 2.68 ×10
8
∆φ > π 3π 称振动( )落后于振动( ) φ2 −φ1 > 0 例:φ2 −φ1= 2 称振动(2)落后于振动(1) 2π − ∆φ
分别作出四种情况的矢量图! 分别作出四种情况的矢量图!
2 4
∆ϕ21 = (ω t + ϕ2 ) - (ω t + ϕ1) = ϕ2 - ϕ1
φ2 −φ1 < 0 例:φ2 −φ1= − 3π称振动(2)超前振动(1) 2π + ∆φ 称振动( )超前振动( )
90
v am
ω
0
ω t+ϕ
·
x
1、用旋转矢量方法确定初相位ϕ: 、 要求条件: 的关系, 要求条件:已知 x0 与A的关系,初速度的方向。 的关系 初速度的方向。 例1: 已知一物体做简谐振动。1)x0=(1/2)A且向位移的 : 已知一物体做简谐振动。 ) 且向位移的 且向位移的正方向运动。 负方向运动; ) 且向位移的正方向运动 负方向运动; 2)x 0= 0且向位移的正方向运动。试求 两种情况下的初相。 两种情况下的初相。 ϕ = π/3
简谐振动特征方程

简谐振动特征方程简谐振动是物理学中一个重要的概念,它描述了许多自然界中的现象,例如弹簧振子、摆钟等等。
简谐振动的特征方程是用来描述振动系统的运动规律的,下面我们来详细介绍一下。
简谐振动是指一个物体在一个平衡位置附近做往复运动的现象。
这个物体可以是一个质点、一个弹簧振子、一个摆钟等等。
这些物体在平衡位置附近的运动可以用一个数学模型来描述,即简谐振动的特征方程。
简谐振动的特征方程可以写成如下的形式:m * a + k * x = 0其中,m是物体的质量,a是物体的加速度,k是振动系统的劲度系数,x是物体的位移。
这个方程描述了物体在振动过程中的运动规律。
我们可以从这个方程中得到一些重要的结论。
首先,当物体的位移为0时,即物体处于平衡位置时,方程变为0 = 0,这意味着物体处于静止状态。
其次,当物体受到外力作用时,例如一个弹簧的拉力或一个摆钟的重力,方程变为m * a + k * x = F,其中F是外力。
这意味着物体在外力作用下会发生加速度,从而产生振动。
根据简谐振动的特征方程,我们可以推导出振动系统的运动方程。
假设物体在t时刻的位移为x(t),速度为v(t),加速度为a(t),则有以下关系:x(t) = A * cos(ωt + φ)v(t) = -A * ω * sin(ωt + φ)a(t) = -A * ω^2 * cos(ωt + φ)其中,A是振幅,表示物体的最大位移;ω是角频率,表示物体在单位时间内完成的振动周期数;φ是初相位,表示物体在t=0时刻的相位。
从上面的方程可以看出,简谐振动的运动是周期性的,物体在单位时间内完成的振动周期数是固定的。
振幅决定了物体振动的幅度大小,角频率决定了物体振动的快慢,初相位决定了物体振动的起始位置。
简谐振动的特征方程不仅仅在物理学中有重要的应用,还在其他领域中有广泛的应用。
例如在工程学中,简谐振动的特征方程可以用来描述机械振动系统的运动规律,从而帮助工程师设计和优化振动系统。
大学物理习题答案12简谐振动

大学物理练习题十二一、选择题1. 一质点作简谐振动,振动方程为)cos(φω+=t A x ,当时间t=21T (T 为周期)时,质点的速度为 [ B ](A) φωsin A - (B) φωsin A(C) φωcos A - (D) φωcos A解: 当2/T t =,即π=π=ω=ω2/22/T t 时,()()=+-=+-==φπωφωωsin sin A t A dtdx v φωsin A2. 一物体作简谐振动,振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻,物体的加速度为 [ B ](A) 2212ωA - (B) 2212ωA(C) 2213ωA - (D) 2213ωA解: 当4/T t =,即2/4/24/T t π=π=ω=ω时, )4/cos(222πωω+-==t A dtxda=+-=)4/2/cos(2ππωA3. 劲度系数分别为k 1和k 2的两个轻弹簧串联在一起,下面挂着质量为m 的物体,构成一个竖挂的弹簧振子,则该系统的振动周期为 [ C ](A) 21212)(2k k k k m T +π= (B) )(221k k mT +π=(C) 2121)(2k k k k m T +π= (D) 2122k k mT +π=解: 由kx x k x k ==2211,21x x x +=可得21212111212111/1/1k k k k k k k x x k x x x k k +=+=+=+=,mk T /22ππ==ω4. 一质点沿x 轴作简谐振动,振动方程为()ππ3122cos 104+⨯=-t x (SI)。
从t=0时刻起,到质点位置在x= -2cm 处,且向X 轴正方向运动的最短时间间隔 (A) 1/8s (B) 1/4s (C) 1/2s (D) 1/3s (E) 1/6s [ C ]解: 由题意作知量图如右,πω=∆t,)(212s t ===∆ππωπ5.一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为 [ B ]二、填空题1. 如图所示,一质量为m 的滑块,两边分别与倔强系数为k 1和k 2的轻弹簧连接,两弹簧的另外两端分别固定在墙上。
简谐振动
G A
H
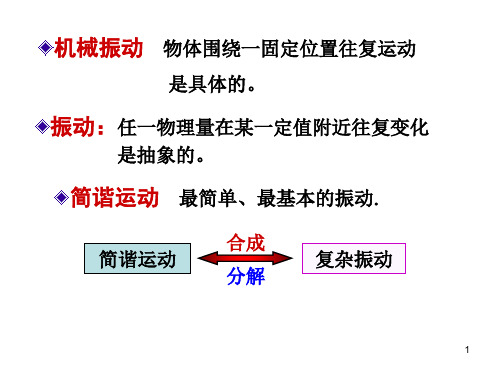
简谐振动曲线如图 以上描述简谐振动的方法称为简 谐振动的矢量图解法.
T
N
J
M
K T
L
t
12
旋转矢量
自Ox轴的原点 O作一矢量 A,使 它的模等于振动的 振幅A,并使矢量 A A 在 Oxy平面内绕点 t 0 O作逆时针方向的 o x0 x 匀角速转动,其角 x0 A cos 速度 与振动频率 相等,这个矢量就 叫做旋转矢量.
18
解:设物体沿x 轴作简谐振动
A = 10.0 cm = 0.100 m
m 0.500 当t = 0 时 ,x = A ,cos =1 ,
所以 x = 0.100 cos 8.00 t m
k
32.0
rad s
1
8.00 rad s
-1
即 =0
速度、加速度的最大值为 vm = A = 8.00×0.100 m s1 = 0.800 ms1 am= 2 A = (8.00)2 ×0.100 m s2 = 6.40 ms2 所以 v = 0.800 sin 8.00 t ms1
x0 A cos
2 A x0
2
2 v0
v0 Asin
v0 t an x0
10
对给定振动系统,周期由系统本身性质决定, 振幅和初相由初始条件决定.
讨论
已知 t
0, x 0, v 0 求
π A sin 0 取 2 o π x A cos( t ) A 2
π 2 v0 A sin 0
0 A cos
v
x
x
T 2
简谐振动的周期

简谐振动的周期简谐振动是指物体在受到一个恢复力作用下,沿着一个固定轴向来回运动的现象。
这种现象在自然界和科学实验中都有广泛的应用,包括钟摆的摆动、弹簧的振动等等。
在本文中,我将介绍简谐振动的周期及其相关内容。
首先,让我们来了解一下简谐振动的周期是什么。
周期是指一个振动完成一次往复运动所需要的时间。
对于简谐振动而言,其周期是恢复力的特性决定的。
具体来说,简谐振动的周期可以用以下公式表示:T = 2π√(m/k)在这个公式中,T代表振动的周期,m代表物体的质量,k代表恢复力的系数(也被称为弹性常数)。
根据这个公式,我们可以看到周期与质量和恢复力的关系。
质量越大,需要较长的时间来完成一次振动;恢复力越大,需要较短的时间来完成一次振动。
接下来,我将解释为什么简谐振动的周期与恢复力有关。
对于一个完全简谐振动的系统,如果物体偏离平衡位置,恢复力将被激活,试图将物体拉回平衡位置。
这种恢复力是根据钩定律来计算的,即F = -kx,其中F是恢复力,k是恢复力的系数,x是物体离平衡位置的位移。
根据牛顿第二定律,可以得到F = ma,其中m是物体的质量,a是物体的加速度。
结合这两个公式,可以得到恢复力与位移和质量的关系。
将恢复力代入振动的周期公式中,即可计算得到周期与质量、恢复力的关系。
当物体偏离平衡位置时,恢复力会导致物体沿着轴向来回振动。
振动的频率可以用频率f来表示,它等于周期的倒数。
即f = 1/T。
频率与周期是互相关联的,它们是描述简谐振动的重要参数。
简谐振动的周期和频率在许多领域都有应用。
在钟摆中,重物通过重力的作用产生简谐振动,其周期与钟摆的长度和重力加速度有关。
在弹簧系统中,弹簧的弹性系数和物体的质量决定了振动的周期。
这些应用都遵循简谐振动的基本原理。
简谐振动的周期是一个重要的物理概念。
它允许我们对物体的振动特性进行量化,并帮助我们理解振动现象的起源和影响因素。
通过研究简谐振动的周期,我们可以更深入地了解自然界中的各种振动现象,并应用这些原理来解决实际问题。
大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动(001)

解得 ω = ωr = ω02 − 2β 2
则
A=
2mβ
F0
ω02 − β 2
= Amax
A
β2 β3
β1
ω
β1 > βω2 0> β3
23
2.速度共振—使速度振幅达最大值的状态
v = dx = − Aω sin(ωt − δ )
dt
速度振幅 vm = Aω
而 Aω =
F0ω
m (ω02 − ω2 ) + 4β 2ω2
●合振幅A的大小由两个分振动的初相差决定。
当 Δϕ = ϕ2 − ϕ1 = ±2kπ
(k = 0,1,2") 同相
Y ωK
A2
ωK
A ωK
A = A1 + A2 = Amax
θ2
Δθ θ1
A1
合振动加强
x2 θ x1 x x
4
当 Δϕ = ϕ2 −ϕ1 = ±(2k +1)π 反相
(k = 0,1,2")
ϕ =0
t
19
2. β =ω0(临界阻尼) x = e −βt (C1 + C 2t)
●在临界阻尼时,质点到达平衡位置时速度即减为 零,振动不可能发生。
◆原理常用于阻尼天平等,以减少摆动时间.
3. β >ω0(过阻尼)
x = e − βt (C 1e ω1t + C 2 e −ω1t )
●过阻尼时,质点的速度 x
F强 = F0 cosωt
v = dx = Aω cos ωt v与强迫力同位相。
dt
●在整个周期内外力的方向和物体运动方向一致, 不断对物体作正功,使振动最强。 ◆外力的周期性变化与物体的固有振动“合拍”。
大学物理111简谐振动课件
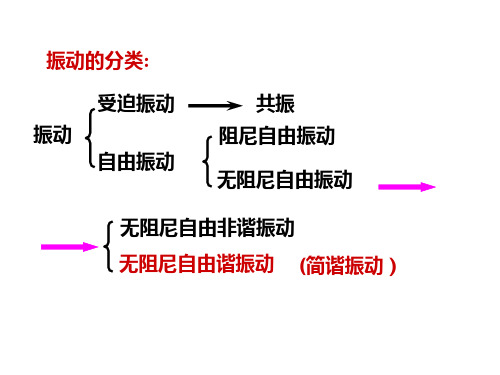
1. 平衡位置 2. 建立坐标 3.受力分析
弹性力 f kx
4.牛顿运动方程
kx
ma
m
d2 dt
x
2
令 k 2 整理得
m
d 2 x 2 x 0 简谐振动动力学方程
dt 2
解微分方程可得
x A cos(t 0 )
简谐振动运动学方程
二、简谐振动的三个特征量
1.振幅 物体离开平衡位置的最大位移的绝对值 A, 由初始条件决定,描述振动的空间范围。
2.周期 振动状态重复一次所需要的时间,描述振 动的快慢.
Acos[(t T ) 0] Acos(t 0)
T 2π T 2π
1
T
物体在单位时间内发生完全振动的次
数,称振动的频率.
2π 称圆频率(角频率).
k T 2 m 1 k
m
k
2 m
反映了系统的固有特性,分别称为谐振子系统 的固有圆频率、固有周期和固有频率.
圆频率 k 由系统决定,与初始条件无关
m
振幅 反映振动的强弱,由初始条件决定.
由
x Acos t 0 v A sin t 0
x0 Acos0
t=0时 v0 A sin0 可得
A
x02
v02
2
初相位 0 已知初始振动状态,用旋转矢量确定
x0<0 v0<0
x0=0 v0<0
x0>0 v0<0
例6 某简谐振动的振动曲线如图,写出振动方程。 x(cm)
O
t(s)
-1
1
-2
解: 设振动方程为 x A cos(t 0 )
则由振动曲线: A=2 cm
xA
简谐振动周期的计算

简谐振动周期的计算简谐振动是一种在没有外力干扰的情况下,运动物体按照正弦或余弦函数规律进行周期性振动的现象。
在物理学中,计算简谐振动的周期是一个重要的问题。
本文将介绍如何计算简谐振动的周期。
简谐振动的周期是指振动系统从一个极值到达下一个相同极值所需的时间。
设一个简谐振动的质点在任意时刻 t 时的位移为 x(t),振动的周期记为 T。
根据简谐振动的特性,振动系统在一个周期内的任意时刻的位移和时间之间存在着特定的关系。
根据物理学原理,可以得到简谐振动的周期公式:T = 2π√(m/k)其中,T 表示周期,m 表示质点的质量,k 表示振动系统的弹性系数(也称为劲度系数或者弹簧常数)。
这个公式表明,简谐振动的周期与质点的质量和振动系统的弹性系数有关。
不同类型的简谐振动有着不同的周期计算方法。
接下来,将分别介绍弹簧振子和单摆两种常见的简谐振动类型的周期计算方法。
1. 弹簧振子的周期计算弹簧振子是指通过一根弹簧与一个质点相连接的振动系统。
弹簧振子的周期计算需要知道质点的质量 m 和弹簧的劲度系数 k。
根据上述公式,弹簧振子的周期可以计算为:T = 2π√(m/k)2. 单摆的周期计算单摆是指通过一根质量可忽略不计的绳子或者杆与一个质点相连接的振动系统,常见于钟摆等物体。
单摆的周期计算需要知道质点的质量 m 和振动角度的大小θ。
根据上述公式,单摆的周期可以计算为:T = 2π√(L/g)其中,L 表示单摆的摆长,g 表示重力加速度。
除了弹簧振子和单摆,其他类型的简谐振动也可以利用上述公式进行周期的计算,只需根据具体情况确定质量、劲度系数或者振动角度的大小。
需要注意的是,在实际问题中,振动系统的其他因素也可能会对简谐振动的周期产生影响。
例如,阻尼力和驱动力等外力的作用可能导致振动周期发生变化。
如果考虑到这些因素,需要在计算中引入相应的修正项。
综上所述,计算简谐振动周期的关键是确定振动系统的质量和劲度系数,或者振动角度的大小。
大学物理-简谐振动讲义

t
A
a v
o·
t=0
x· x
v Asin(t )
Acos( t )
2
Av cos( t v )
a 2 Acos( t ) Aa cos( t a )
简谐振动旋转矢量表示法的应用
应用: 可以方便地确定初相位φ和相位
x0 0 x0 0 v0 0 v0 0
b a
a4 b3
F
(dF dr
) r r0
x
a4 b3
x
kx
其中
k
a4 b3
,为等效劲度系数.
➢ 结论: 原子在平衡位置附近的微振动是谐振动.
周期为:
T 2
m 2π k
b3 a4
m
角频率为:
a4 b3m
例题 质量为 m 的比重计,放在密度为 的液体中。
已知比重计圆管的直径为 d 。试证明在竖直方向的 振动为简谐振动,并计算周期。
x
A
= 2
O
t
-A
❖ 相位差
x1 A1 cos(1t 1) x2 A2 cos(2t 2 )
(2t 2 ) (1t 1) 2 1 (当2 1时)
k1
m1
k2 m2
x1
O
x2
若 2 1 2kπ
若 2 1 (2k 1)π
A1 x
x1
A2
o
x2
T
A1 x
A2
x1
x0 0 x0 0
x
v0 0 v0 0
M1 φ1
P φ2
M
2
[例1] 已知某质点作简谐运动, 振动曲线如图. 试根据图中数据
写出振动表达式.
简谐振动图文

二、简谐运动
物体在跟偏离平衡位置的位移大小成正比, 并且总是指向平衡位置的回复力作用下的振动, 叫做简谐运动
1、简谐运动是一种理想化的运动,振动过程中 无阻力,所以振动系统机械能守恒。
2、简谐运动是一种非匀变速运动。 3、最常见的两种简谐运动:弹簧振子、单摆
1、弹簧振子
思考:弹簧振子(理想模型)条件有:1、2、3、
(t1+t2)=0.24 s,
所以质点的振动周期的可能值为0.72 s和0.24 s.
9、 一个弹簧振子经a,b两Fra bibliotek时速度相同,从a到b经历的最短
时间为0.2 s,再从b到a的时间为0.3 s,则振子的周期为( ) C
A.1 s
B.0.8 s
C.0.6 s
D.1.2 s
解析:振子经过a,b两点时速度相同,从a到b经历的最短时间为 0.2 s,而由b到a的时间为0.3 s,由以上信息可知,a、b在平衡位置 两侧关于平衡位置对称,如图所示,O为平衡位置,tab=0.2. tba=0.3 s,则 tbb′=(0.3-0.2) s=0.1 s. 故周期T=(0.2+0.3+0.1)s=0.6 s. 答案:C
B.振子从最低点向平衡位置运动过程中,弹簧弹 力始终做负功
C.振子在振动过程中的回复力由弹簧的弹力和振 子的重力的合力提供
D.振子在振动过程中,系统的机械能一定守恒
4、有一个在光滑水平面内的弹簧振子,第一次用 力把弹簧压缩x后释放,第二次把弹簧压缩2x后释 放,则先后两次振动的周期和振幅之比分别为多 少?
T1:T2=1:1
A1:A2=1:2
5、弹簧振子以O点为平衡位置,在B、C两点之间做简 谐振动,B、C相距20cm,某时刻振子处于B点,经过 0.5s,振子首次到达C点,求:
《简谐振动》教学设计

<简谐振动>教学设计一、教学目标:1.认知目标:让学生知道机械振动是一种普遍的运动形式。
理解机械振动产生的条件和它的特性。
理解F=-kx的物理意义。
知道振动图象。
知道单摆在摆角很小的情况下(不大于5°)作的是简谐振动。
2.能力目标:培养学生观察能力、发现问题的能力和归纳能力。
二、教学重点:简谐振动的条件。
三、教学难点:1.简谐振动的条件。
2.简谐振动的图象。
四、教学器材:1.多媒体课件。
2.弹簧振子、气垫导轨、节拍器、单摆等。
五、教学设计说明:本节课着眼于简谐振动概念的形成过程和培养学生的观察、分析,归纳能力。
具体设计时,首先通过对演示实验的观察、分析,归纳出振动的概念及其特点,通过举例使学生知道机械振动是一种普遍的运动形式。
通过观察弹簧振子在全过程中各段的运动情况及对振子的受力分析,归纳出振动的条件和回复力概念。
进一步分析弹簧振子的回复力与位移的关系,归纳出简谐振动的条件,得到简谐振动的概念。
在研究单摆的振动时,同研究弹簧振子的振动一样,先观察单摆在全振动过程中各段的运动情况,然后分析单摆在振动过程中所受的力,使学生了解单摆振动的回复力。
同时让学生知道单摆在摆角很小的情况下(不大于5°时)作的是简谐振动。
利用多媒体课件描述振动中回复力和位移的变化,使回复力和位移的变化过程变得直观、形象。
通过电脑模拟振动图象,使学生对振动图象易于理解和接受。
小学常用歇后语1.八仙过海--------各显神通2.不入虎穴--------焉得虎子3.蚕豆开花--------黑心4.车到山前--------必有路5.打破砂锅--------问到底6.和尚打伞--------无法无天7.虎落平阳--------被犬欺8.画蛇添足--------多此一举9.箭在弦上--------不得不发10.井底青蛙--------目光短浅11.大海捞针--------没处寻12.竹篮打水--------一场空13.打开天窗--------说亮话14.船到桥头--------自会直15.飞蛾扑火-----自取灭亡16.百米赛跑--------分秒必争17.拔苗助长-----急于求成18.仇人相见--------分外眼红19.芝麻开花----节节高20.新官上任--------三把火21.瞎子点灯--------白费蜡22.兔子尾巴--------长不了23.偷鸡不成----蚀把米24.王婆卖瓜--------自卖自夸25.老虎屁股---- 摸不得26.老虎拉车--------谁敢27.老鼠过街-----人人喊打28.麻雀虽小--------五脏俱全29.墙上茅草----随风两边倒30.三十六计--------走为上计31.塞翁失马----焉知祸福32.壶中无酒--------难留客33.丈二和尚----摸不着头脑34.有借有还--------再借不难35.猫哭耗子---假慈悲36.铰子破皮--------露了馅37.扁担挑水---一心挂了两头38.对牛弹琴--------白费劲39.八仙聚会--------神聊40.霸王敬酒--------不干也得干41.板上订钉--------跑不了42.背鼓上门--------讨打43.草把做灯-----粗心(芯)44.竹笋出土--------节节高45.菜刀切豆腐----两面光46.钉头碰钉子--------硬碰硬47.高山上敲鼓--四面闻名(鸣)48.铁打的公鸡-----一毛不拔49.关公走麦城----骄必败50.狗咬吕洞宾--------不识好人心51.鸡蛋碰石头----不自量力52.姜太公钓鱼--------愿者上钩53.脚踏西瓜皮--滑到哪里是哪里54.孔夫子搬家--------净是书55.老鼠钻风箱-----两头受气56.留得青山在--------不怕没柴烧57.门缝里看人---把人看扁了58.泥菩萨过河--------自身难保59.泼出去的水----收不回60.骑驴看唱本--------走着瞧61.千里送鹅毛--礼轻情意重62.肉包子打狗--------有去无回63.山中无老虎---猴子称大王64.司马昭之心--------路人皆知65.外甥打灯笼---照旧(舅)66.王八吃年糕--------铁了心67.王小二过年---一年不如一年68.小葱拌豆腐-----一清二白69.小和尚念经----有口无心70.周瑜打黄盖--------两厢情愿71.赶鸭子上架----吃力不讨好72.擀面杖吹火----- -一窍不通73.瞎子戴眼镜----装饰74.猴子捞月亮--------空忙一场75.秀才遇到兵----有理讲不清76.三个臭皮匠--------顶个诸葛亮77.黄牛追兔子---有劲使不上78.和尚训道士--------管得宽79.过年娶媳妇----双喜临门80.聋子见哑巴--------不闻不问六字短语81.铜钣上钉铆钉---一是一,二是二82.里弄里扛竹竿---直来直去83.苦水里泡黄连----苦上加苦84.驴唇不对马嘴----答非所问85.猪鼻子里插葱-----装象86.只许州官放火---不许百姓点灯87.猪八戒照镜子--里外不是人88.放风筝断了线-----没指望了89.池塘里的风波-----大不了90.关门掩着耗子-----急(挤)死91.顶风顶水划船----硬撑92.东北的二人转--------一唱一和93.东洋人戴高帽----假充大个94.到火神庙求雨--------找错了门95.鲁班门前耍斧----有眼无珠96.老太太吃汤圆--------囫囵吞97.出太阳下暴雨---假情(晴)98.挂羊头卖狗肉--------虚情假意99.担着胡子过河----谦虚过度100.唱歌不看曲本--------离谱小学常用歇后语1.八仙过海--------各显神通2.不入虎穴--------焉得虎子3.蚕豆开花--------黑心4.车到山前--------必有路5.打破砂锅--------问到底6.和尚打伞--------无法无天7.虎落平阳--------被犬欺8.画蛇添足--------多此一举9.箭在弦上--------不得不发10.井底青蛙--------目光短浅11.大海捞针--------没处寻12.竹篮打水--------一场空13.打开天窗--------说亮话14.船到桥头--------自会直15.飞蛾扑火-----自取灭亡16.百米赛跑--------分秒必争17.拔苗助长-----急于求成18.仇人相见--------分外眼红19.芝麻开花----节节高20.新官上任--------三把火21.瞎子点灯--------白费蜡22.兔子尾巴--------长不了23.偷鸡不成----蚀把米24.王婆卖瓜--------自卖自夸25.老虎屁股---- 摸不得26.老虎拉车--------谁敢27.老鼠过街-----人人喊打28.麻雀虽小--------五脏俱全29.墙上茅草----随风两边倒30.三十六计--------走为上计31.塞翁失马----焉知祸福32.壶中无酒--------难留客33.丈二和尚----摸不着头脑34.有借有还--------再借不难35.猫哭耗子---假慈悲36.铰子破皮--------露了馅37.扁担挑水---一心挂了两头38.对牛弹琴--------白费劲39.八仙聚会--------神聊40.霸王敬酒--------不干也得干41.板上订钉--------跑不了42.背鼓上门--------讨打43.草把做灯-----粗心(芯)44.竹笋出土--------节节高45.菜刀切豆腐----两面光46.钉头碰钉子--------硬碰硬47.高山上敲鼓--四面闻名(鸣)48.铁打的公鸡-----一毛不拔49.关公走麦城----骄必败50.狗咬吕洞宾--------不识好人心51.鸡蛋碰石头----不自量力52.姜太公钓鱼--------愿者上钩53.脚踏西瓜皮--滑到哪里是哪里54.孔夫子搬家--------净是书55.老鼠钻风箱-----两头受气56.留得青山在--------不怕没柴烧57.门缝里看人---把人看扁了58.泥菩萨过河--------自身难保59.泼出去的水----收不回60.骑驴看唱本--------走着瞧61.千里送鹅毛--礼轻情意重62.肉包子打狗--------有去无回63.山中无老虎---猴子称大王64.司马昭之心--------路人皆知65.外甥打灯笼---照旧(舅)66.王八吃年糕--------铁了心67.王小二过年---一年不如一年68.小葱拌豆腐-----一清二白69.小和尚念经----有口无心70.周瑜打黄盖--------两厢情愿71.赶鸭子上架----吃力不讨好72.擀面杖吹火----- -一窍不通73.瞎子戴眼镜----装饰74.猴子捞月亮--------空忙一场75.秀才遇到兵----有理讲不清76.三个臭皮匠--------顶个诸葛亮77.黄牛追兔子---有劲使不上78.和尚训道士--------管得宽79.过年娶媳妇----双喜临门80.聋子见哑巴--------不闻不问六字短语81.铜钣上钉铆钉---一是一,二是二82.里弄里扛竹竿---直来直去83.苦水里泡黄连----苦上加苦84.驴唇不对马嘴----答非所问85.猪鼻子里插葱-----装象86.只许州官放火---不许百姓点灯87.猪八戒照镜子--里外不是人88.放风筝断了线-----没指望了89.池塘里的风波-----大不了90.关门掩着耗子-----急(挤)死91.顶风顶水划船----硬撑92.东北的二人转--------一唱一和93.东洋人戴高帽----假充大个94.到火神庙求雨--------找错了门95.鲁班门前耍斧----有眼无珠96.老太太吃汤圆--------囫囵吞97.出太阳下暴雨---假情(晴)98.挂羊头卖狗肉--------虚情假意99.担着胡子过河----谦虚过度100.唱歌不看曲本--------离谱。
高考一轮复习:12.1《简谐运动》ppt课件

7
关闭
解析 考点一 考点二
答案
第十二章
第一节
简谐运动 15 -15-
规律总结分析简谐运动的技巧 (1)分析简谐运动中各物理量的变化情况时,一定要以位移为桥梁,位移 增大时,振动质点的回复力、加速度、势能均增大,速度、动能均减小;反之, 则产生相反的变化。另外,各矢量均在其值为零时改变方向。 (2)分析过程中要特别注意简谐运动的周期性和对称性。
Ⅰ Ⅱ Ⅰ Ⅰ Ⅰ Ⅱ Ⅱ Ⅰ Ⅰ 实 验
权威解读 1.理解简谐运动的概念、表达式和图象; 熟记单摆的周期公式 ; 掌握产生共振的 条件。 2.理解机械波的特点和分类, 掌握波速、 波长和频率的关系 , 会分析波的图象 ; 理 解波的干涉、衍射现象和多普勒效应 , 掌握波的干涉和衍射的条件。 3.分析近几年高考可以看出, 单纯对简谐 运动的考查相对较少 , 主要考查振动和 波动相结合, 机械波的形成、波的图象以 及波长、波速、频率的关系, 题型以选择 题和填空题为主 , 也有小型计算题 , 难度 中等偏下, 有时会考查综合运用运动学、 动力学和能量等知识, 分析机械振动、机 械波的运动特点及规律。 重点考查用公式法和图象法计算重力加 速度
解析 答案
第十二章
第一节
简谐运动 11
基础自测
1
2
3
4
4. ( 多选)如图所示,两木块 A 和 B 叠放在光滑水平面上,质量分别为 m 和 M,A 与 B 之间的最大静摩擦力为 Ffm,B 与劲度系数为 k 的轻质弹簧连接构 成弹簧振子,为使 A 和 B 在振动过程中不发生相对滑动,则( )
M+m F kM fm M+m B.它们的振幅不能大于 F km fm F������������
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理练习题十二一、选择题1. 一质点作简谐振动,振动方程为)cos(φω+=t A x ,当时间t=21T (T 为周期)时,质点的速度为 [ B ] (A) φωsin A - (B) φωsin A (C) φωcos A - (D) φωcos A解: 当2/T t =,即π=π=ω=ω2/22/T t 时,()()=+-=+-==φπωφωωsin sin A t A dtdx v φωsin A2. 一物体作简谐振动,振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻,物体的加速度为 [ B ] (A) 2212ωA - (B) 2212ωA (C) 2213ωA -(D) 2213ωA解: 当4/T t =,即2/4/24/ππωω===T t 时, )4/cos(222πωω+-==t A dtx d a =+-=)4/2/cos(2ππωA 222ωA3. 劲度系数分别为k 1和k 2的两个轻弹簧串联在一起,下面挂着质量为m 的物体,构成一个竖挂的弹簧振子,则该系统的振动周期为 [ C ] (A) 21212)(2k k k k m T +π= (B) )(221k k m T +π=(C) 2121)(2k k k k m T +π= (D) 2122k k mT +π=解: 由kx x k x k ==2211,21x x x +=可得21212111212111/1/1k k k k k k k x x k x x x k k +=+=+=+=,mk T /22ππ==ω4. 一质点沿x 轴作简谐振动,振动方程为()ππ3122cos 104+⨯=-t x (SI)。
从t=0时刻起,到质点位置在x= -2cm 处,且向X 轴正方向运动的最短时间间隔 [ C ] (A) 1/8s (B) 1/4s (C) 1/2s (D) 1/3s (E) 1/6s解: 由题意作知量图如右,πω=∆t ,)(212st ===∆ππωπ 5.一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为A 21,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为 [ B ]1mk 2二、填空题1. 如图所示,一质量为m 的滑块,两边分别与倔强系数为k 1和k 2的轻弹簧连接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
将滑块m 向右移动到x 0,自静止释放,并从释放时开始计时。
取坐标如图所示,则其振动方程为 。
解: 由()kx x k k x k x k f f f =+=+=+=212121知,等效弹簧21k k k +=,mk k 21+=ω;由0=t 时,00=v 知0x A =,0=φ,振动方程为 ⎥⎦⎤⎢⎣⎡+=t mk k x x 210cos2.一质点作简谐振动.其振动曲线如图所示.根据此图,它的周期T =___________,用余弦函数描述时初相图表ϕ =___________。
解: 设)cos(φω+=t A x ,由t=0时0sin ,cos 2/00>-==-=φωφA v A A x ,得32πφ-=或34πφ=再由t=2时0)2cos()cos(2=+=+=φωφωA t A x ,0)2sin(2<+-=φωωA v 可得22πφω=+,127)]32(2[21)2(21πππφπω=--=-=, 7242==ωπT (s ) 3. 一质点作简谐振动,其运动速度与时间的曲线如图所示。
若质点的振动规律用余弦描述,则其初相位为___________。
解:A v t A v m ωφωω=+-=,)sin( 由图知,0=t 时0sin 21>-=φωA v m ,6πφ-=或67πφ=,根据不到四分之一周期的时间后,速度m v v =可知,取67πφ=。
4.图中所示为两个简谐振动的振动曲线.若以余弦函数表示这两个振动的合成结果,则合振动的方程为=+=21x x x (SI)解: 2=T (s ),ππω==T2t x πsin 08.01=, t x πsin 04.02-=)2/cos(04.0sin 04.021πππ-==+=t t x x x5.一弹簧振子,弹簧的劲度系数m N k /250=,当物体以J 2.0初动能振动时,振幅为0.04米;当动能和势能相等时,位移为 ±0.028 米。
解: 04.02502.02kE 2A 0=⨯==,由022121E kx E E pk ===知,028.05020±=±=±=kE x6. 一物体悬挂在弹簧下方作简谐振动,当这物块的位移等于振幅的一半时,其动能是总能量的 。
(设x (m )t (s)O x 1x 2120.08-0.04x(m ) t (s)O 4 -22v (m/s)t (s)Ov mm v 21平衡位置处势能为零)当这物块在平衡位置时,弹簧的长度比原长长l ∆,这一振动系统的周期为 。
解: 4/2212E A k E p =⎪⎭⎫⎝⎛=,=-=pk EE E E 43,=∆==lmg m km T /22ππgl 2∆π三、计算题1. 在一轻弹簧下端悬挂m 0=100g 砝码时,弹簧伸长8cm 。
现在这根弹簧下端悬挂m=250g 的物体,构成弹簧振子。
将物体从平衡位置向下拉动4cm ,并给以向上的21cm/s 的初速度(这时t=0)。
选X 轴向下,求振动方程的数值式。
解:(1) ∆=k g m 0,25.1244908.08.91.00==⨯=∆=g m k N/m ,)/(725.04/49s rad mk ===ω(2)设振动方程为)cos(φω+=t A x 由题意知,t=0时 ⎩⎨⎧-=-===scm A v cm A x /21sin 4cos 00φωφ)21()41(象限或在象限或在φφ联系解得 cm A 5=,54arccos=φ )1(象限在第φ, )54arccos7cos(05.0+=t x注:初相位也可以记作)(64.0rad 、53arcsin 、43arctan。
2. 如图,有一水平弹簧振子,弹簧的倔强系数k=24N/m ,重物的质量m=6kg ,重物静止在平衡位置上。
设以一水平恒力F=10N 向左作用于物体(不计摩檫),使之由平衡位置向左运动了0.05m ,此时撤去力F 。
当重物运动到左方最远位置时开始计时,求物体的运动方程。
解: )/(2624s rad m k ===ω振动系统的初始能量等于外力F 做的功J FS E 5.005.0100=⨯==,)(204.0245.0220m kE A =⨯==重物运动到左方最远位置时开始计时,即πϕ=,振动方程为 )2cos(204.0π+=t x3. 一轻弹簧在60N 的拉力下伸长30cm 。
现把质量为4kg 的物体悬挂在该弹簧的下端并使之静止,再把物体向下拉10cm ,然后由静止释放并开始计时。
选X 轴向下,求 (1) 物体的振动方程;(2) 物体在平衡位置上方5cm 时弹簧对物体的拉力。
(3) 物体从第一次越过平衡位置时刻起到它运动到上方5cm 处所需要的最短时间。
解: )/(2003.0/60/m N f k ==∆= )/(07.7504/200/s rad m k ≈===ω(1) 0,1.0==φm A ⎩⎨⎧<-====0sin 0cos 1.000φωφA v A x解得0,1.0==φm A ,所以t x 07.7cos 1.0=(2)力与位移的正方向均向下,在平衡位置上方5cm 处,x=-0.05(m ),kx mg F F -=+=拉合,=-⨯-⨯-=--=)05.0(2008.94kx mg F 拉2.29-(N ),方向向上。
(3)由题意作旋转矢量图,6πω=∆t ,===∆6026πωπt 074.0(S )注:(2-3)有多种解法!计算题1、3中的重力加速度不能取2/10s m 。
*4. 一质量为m 、长为L 的均匀细杆,上端挂在无摩檫的水平轴上,杆下端用一轻弹簧连在墙上,如图所示。
弹簧的劲度系数为k 。
当杆竖直静止时弹簧处于水平原长状态。
求杆作微小振动的周期。
(杆绕其一端轴的转动惯量为31mL 2) 解: 重力与弹簧力对杆的力矩分别为θsin 2L mgMG=,θθcos sin)(cos L L k L kx fd Mk⋅=⋅==考虑到微振动1cos ,sin ≈≈θθθ,并且两力矩的作用效果均与角位移的正向(逆时针)相反,应取负值。
合力矩θθcos sin)(sin 2L L k L mgMMMkG ⋅--=+=合θ)2(2kL L mg+-=由定轴转动定理22dtd JM θ=有0)2()31(2222=++θθkL L mgdt d mL ,0)2(322=++θθmk Lg dtd)2(32mk Lg +=ω,)2(3222kL mg mL T +==πωπ[补充题] 一长度为l 、倔强系数为k 的均匀轻弹簧分割成长度分别为l 1和l 2的两部分,且l 1=n l 2,n 为整数,则相应的倔强系数k 1和k 2为 [ B ] (A) ).1(,121+=+=n k k n kn k (B) .1,)1(21+=+=n k k n n k k(C) ).1(,)1(21+=+=n k k nn k k (D) .1,121+=+=n k k n kn k解: 由21nl l =知21x n x ∆=∆, 221)1(x n x x x ∆+=∆+∆= 由kx x k x k f =∆=∆=2211 有 22211)1(x n k x k x n k ∆+=∆=∆ 故nkn k k n k )1( , )1(12+=+=。
