(完整版)含参不等式(有解、无解问题)(人教版)含答案

(完整版)专题--含参一元一次不等式组(1)

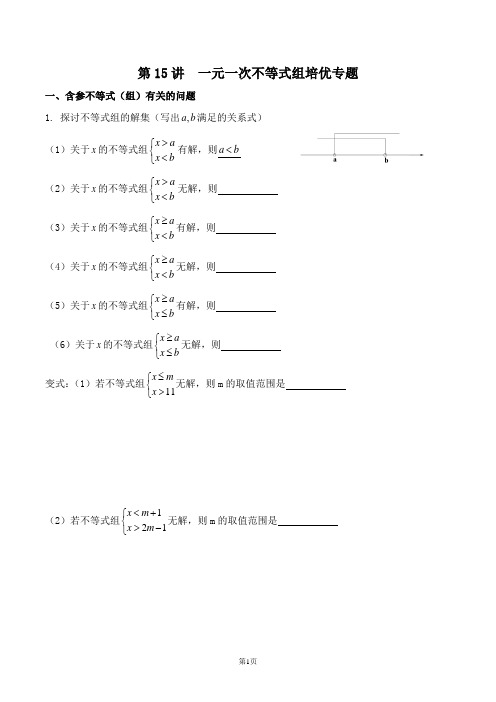
第15讲一元一次不等式组培优专题一、含参不等式（组）有关的问题1. 探讨不等式组的解集（写出,a b 满足的关系式）（1）关于x 的不等式组x a x b >⎧⎨<⎩有解，则a b < （2）关于x 的不等式组x a x b>⎧⎨<⎩无解，则（3）关于x 的不等式组x a x b ≥⎧⎨<⎩有解，则（4）关于x 的不等式组x a x b≥⎧⎨<⎩无解，则（5）关于x 的不等式组x a x b ≥⎧⎨≤⎩有解，则（6）关于x 的不等式组x a x b≥⎧⎨≤⎩无解，则变式：（1）若不等式组⎩⎨⎧>≤11x m x 无解，则m 的取值范围是（2）若不等式组121x m x m <+⎧⎨>-⎩无解，则m 的取值范围是(3)若不等式组⎩⎨⎧>≤<kx x ,21有解，则k 的取值范围是(4)如果关于x 的不等式组x a x b >⎧⎨<⎩无解，则关于y 的不等式组11y a y b +>⎧⎨+<⎩的解如何？2. (1)若不等式组的解集为，那么的值等于_______⎩⎨⎧>-<-3212b x a x 11<<-x )3)(3(+-b a(2)如果关于x 的不等式组7060x m x n -≥⎧⎨-<⎩的整数解仅为1，2，3，那么适合这个不等式组的整数对(),m n 共有对.（3）已知关于x 的不等式x －2a ＜3的最大整数解是-5，求a 的取值范围3.已知不等式13a x ->的每一个解都是21122x -<的解，求a 的取值范围变式：如果关于x的不等式组224x ax a>-⎧⎨<-⎩有解，并且所有解都是不等式组－6＜x≤5的解，求a的取值范围．4. 若关于x的不等式组2113xxx k-⎧>-⎪⎨⎪-<⎩的解集为2x<，求k的取值范围5.不等式组1235a x ax-<<+⎧⎨<<⎩的解集是3x<<2a+，求a的取值范围6.已知不等式组111x x x k >-⎧⎪<⎨⎪<-⎩（1）当2k =-时，不等式组的解集是__ ___，当3k =时，不等式组的解集是___ __；（2）由（1）可知，不等式组的解集是随数k 的值的变化而变化．当k 为任意有理数时，写出不等式组的解集．二、不等式（组）与方程（组）7.已知关于x 的方程23x k kx -=-无负数解，求k 的取值范围.变式：已知关于x 的方程20142014a x x -=只有负数解，求a 的取值范围8.已知非负实数x ,y ,z 满足123234x y z ---==，记345W x y z =++，求W 的最大值与最小值.三.绝对值不等式（1）若x a <(0)a >，则a x a -<< 不等式2x <的解集为（2）若x a >(0)a >，则x a >或x a <- 不等式>5x 的解集为。

含参不等式(有解、无解问题)(人教版)含答案

含参不等式（有解、无解问题）（人教版）含答案含参不等式（有解、无解问题）（人教版）一、单选题(共10道，每道10分)1.若不等式组的解集为，则m的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）2.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）3.若不等式组有解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）4.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）5.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）6.关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）7.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）8.已知关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）9.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）10.若关于x的不等式组无解，则m的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）第11页共11页。

含参不等式与分式方程(含答案)

一．不等式组无含参不等式组与分式方程解1．若数a使关于x的不等式组{x-3(x-a)≤8x-12＞2x-13+32无解，且使关于y的分式方程7y y-1+5=2a-11-y的解为正数，则符合条件的所有整数a的和为（）A．﹣7B．﹣4C．﹣3D．0 2．若数a既使关于x的不等式组{x-a2+1≤x+a3x-2a＞6无解，又使关于x的分式方程x+a x+2-a x-2=1的解小于4，则满足条件的所有整数a的个数为（）A．2B．3C．4D．53．从3，﹣1，12，1，﹣3这5个数中，随机抽取一个数记为a，若数a使关于x的不等式组{13(2x+7)≥3x-a＜0无解，且使关于x的分式方程xx-3-a-23-x=-1有整数解，那么这5个数中所有满足条件的a的值之积是（）A．12B．3C．﹣3D．-324．若关于x的分式方程1x-1=x-m(x-1)(x-3)-3x-3的解为正数，且关于y的不等式组{3y+24＞y+m2y≤3(y+4)-6无解，则符合条件的所有整数m的和为（）A．9B．11C．12D．145．如果关于x的分式方程ax-2+1=x+ax+2的解为负数，且关于x的不等式组{-12(x-a)≥0x-1≥2x+23无解，那么符合条件的所有整数a的和是（）A．7B．8C．9D．10二．不等式组有解6．若关于x的分式方程a x+22-x+4x-2=-3的解为正数，且关于y的一元一次不等式组{y≥-1a-y2≥y+1有解，则符合条件的所有整数a的和为（）A．1B．2C．3D．4 7．若关于x的不等式组{x-3(x-2)＞-2a+x2＜x有解，关于y的分式方程a y-14-y+3y-4=-2有整数解，则符合条件的所有整数a的和为（）A．0B．1C．2D．58．若整数a使关于x的分式方程2x-2+x+a2-x=1的解为正整数，且使关于y的不等式组{y+1≥2y-13-12(y-a)＞0有解，则满足条件的整数a的值之积是（）A．﹣4B．0C．16D．64 9．使得关于x的不等式组{-x2≤-m2+1-2x+1≥4m-1有解，且使得关于y的分式方程1y-2-m-y2-y=2有非负整数解的所有的m的和是（）A．﹣7B．﹣1C．0D．210．若关于x的不等式组{x+43-1≥x-22x+2≤2(x-a)有解，且关于y的分式方程1-2y y-1+a-y1-y=-3的解为非负数，则所有满足条件的整数a的值之积是（）A．﹣6B．0C．4D．12三．指定解集（同大取大，同小取小）11．若关于x 的一元一次不等式组{3x +1≤2(x -2)x -2a 3＜1的解集为x≤﹣5，且关于y 的分式方程2+a y 3-y +2=4y -3有非负整数解，则符合条件的所有整数a 的和为（）A ．﹣6B ．﹣4C ．﹣2D ．012．若整数a 使得关于x 的不等式组{x +1＞3x +42x -4≤2(a -x )的解集为x ＜﹣2，且关于y 的分式方程a y +1=2-yy +1+3的解为负数，则所有符合条件的整数a 的和为（）A ．0B ．﹣3C ．﹣5D ．﹣813．已知关于x 的一元一次不等式组{4(3-x )+2＜-2xx +a ≥2的解集为x ＞7，且关于y 的分式方程a y +5y -3-1=43-y的解为正整数，则满足条件的所有整数a 的和为（）A ．﹣3B ．﹣6C ．﹣8D ．﹣1114．若关于x 的一元一次不等式组{3x +14＞x -1x -a ≤0的解集为x ≤a ，且关于y 的分式方程y -a y -2+5-2y 2-y=1有正整数解，则所有满足条件的整数a 的和为（）A ．2B ．3C ．7D ．815．若关于x 的一元一次不等式组{3x -16-1≤13x 1314(a -x )≥0的解集为x ≤a ，且关于y 的分式方程y -a 2-y -3y -4y -2=-1有非负整数解，则所有满足条件的整数a的和为（）A．10B．8C．6D．1四．有且仅有几个整数解（共10小题）16．若数a 使关于x 的不等式组{3x -12＜7(x +47)5x -a ≤3有且仅有三个整数解，且使关于y 的分式方程3y y -2+a +122-y=1有整数解，则满足条件的所有a 的值之和是（）A ．﹣6B ．﹣10C ．﹣12D ．﹣1817．如果关于x 的分式方程2x -2+m +12-x=1有非负整数解，关于y 的不等式组{y 2≥y +23-1，5(y -1)＜y -(m +3)有且只有三个整数解，则所有符合条件的整数m 的个数为（）A ．0B ．1C ．2D ．318．如果关于x 的分式方程x x -2+m +12-x=2有非负整数解，关于y 的不等式组{y 2+1≥y +235(y -1)＜y -(m +3)有且只有3个整数解，则所有符合条件的m 的和是（）A ．﹣3B ．﹣2C ．0D ．219．若关于x 的分式方程x x -2+a +12-x=2有非负整数解，关于y 的不等式组{y 2+1≥y +235(y -2)＜y +a -3有且只有4个整数解，则所有符合条件的a 的和是（）A ．﹣3B ．﹣2C ．1D ．220．若数a 关于x 的不等式组{x 2-1≤13(x -2)3x -a ≥-2(1+x )恰有三个整数解，且使关于y 的分式方程1-3y y -1-2a 1-y=-2的解为正数，则所有满足条件的整数a的值之和是（）A．2B．3C．4D．521．已知关于x 的分式方程1-a x 2-x +3x -2-1=0有整数解，且关于x 的不等式组{4x ≥3(x -1)2x -x -12＜a 有且只有4个整数解，则符合条件的所有整数a 的个数为（）A ．1B ．2C ．3D ．422．若整数a 是使得关于x 的不等式组{x -16＞x 4-126x -a ≥5有且只有2个整数解，且使得且关于y 的分式方程2y +3y -1+a +11-y=a 有非负数解，则所有满足条件的整数a 的个数为（）A ．6B ．5C ．4D ．323．若整数a 使关于x 的不等式组{x 2-1≤13(x -2)3x -a ≥2(1-x )有且只有两个整数解，且关于y 的分式方程1-3y y -1-2a1-y=-2的解为正数，则满足上述条件的a 的和为（）A ．3B ．4C ．5D ．624．若关于x 的一元一次不等式组{3x -12＜x +25x -2≥x +a有且仅有3个整数解，且关于x 的分式方程a x -2x -1+31-x=1有正数解，则所有满足条件的整数a 的和为（）A ．12B ．13C ．14D ．1525．如果关于x的不等式组{m-5x≥2x-112＜3(x+12)有且仅有四个整数解，且关于y的分式方程2-m y2-y-8y-2=1有非负数解，则符合条件的所有整数m的和是（）A．13B．15C．20D．22五．至多几个整数解26．若实数a 使关于x 的不等式组{x 3+1≥x +32x -1≥a 2+x 2有解且最多有5个整数解，且使关于y 的方程3y y +3-a -2y +3=1的解为整数，则符合条件的所有整数a 的和为（）A ．﹣12B ．﹣14C ．﹣16D ．﹣2127．若实数a 使关于x 的不等式组{x 3+1≥x +32x -1≥a +x 2有解且最多有4个整数解，且使关于y 的方程3y y +3-a -2y +3=1的解是整数，则符合条件的所有整数a 的个数是（）A ．4B ．3C ．2D ．128．若数m 使关于y 的方程1y 2-y +m -5y 2+y =m -1y 2-1无解，且使关于x 的不等式组{5x +32＞x 3x -2m ≤-2有整数解且至多有4个整数解，则符合条件的m 之和为（）A ．18B ．15C ．12D ．929．若关于x 的分式方程x x -2-m -12-x=3的解为正整数，且关于y 的不等式组{2(y -m2)≤51+y 2＞y +26至多有六个整数解，则符合条件的所有整数m 的取值之和为（）A ．1B ．0C ．5D ．630．若整数a使得关于x的方程2-32-x=ax-2的解为整数，且关于y的不等式组{y+2≥y-123y+2-a≤0有偶数解且至多有3个偶数解，则所有符合条件的整数a的和为（）A．﹣12B．﹣9C．12D．15六．至少几个整数解31．若关于x 的方程x +3x -3+a x 3-x=1有正整数解，且关于y 的不等式组{2y -55＜2a -y -1≤0至少有四个整数解，则满足条件的整数a 有（）个．A ．0B ．1C ．2D ．332．若数a 使关于x 的不等式组{x -52+1≤x +135x -2a ＞2x +a至少有五个整数解，关于y 的分式方程a -3y -1-21-y=2有非负整数解，则满足条件的所有整数a 之和是（）A ．15B ．14C ．8D ．733．若数a 使关于x 的一元一次不等式组{x +15≥x2-1x +a ＜6x +3至少有4个整数解，且使关于y 的分式方程y +a y -3+2y3-y=1有非负整数解，则符合条件的所有整数a 的值之和为（）A ．9B ．12C ．15D ．1934．如果关于x 的方程x +3x -3+a x 3-x=1有正整数解，且关于y 的不等式组{2y -55＜1a -y -1≤0至少有两个偶数解，则满足条件的整数a 有（）个．A ．0B ．1C ．2D ．335．若关于x 的方程x +3x -3+a x 3-x=1有正整数解，且关于y 的不等式组{2y -55＜2a -y -1≤0至少有两个奇数解，则满足条件的整数a有（）个A．0B．1C．2D．3七．奇（偶）数解36．若数a使关于x的分式方程1-a x2-x=1-3x-2有整数解，且关于y的不等式组{y-12-2＜7-2y22y+1＞a-2y恰好有两个奇数解，则符合条件的所有整数a的和是（）A．7B．5C．2D．137．如果关于x的不等式组{m-x＞4x-5≤3(x-3)有且只有三个奇数解，且关于x的分式方程2-m x2-x-30x-2=13有整数解，则符合条件的整数m有（）个A．1B．2C．3D．4 38．如果关于x的不等式组{2x+33≥x-14x-6＞a-4有且只有两个奇数解，且关于y的分式方程3y y-2-a-102-y=1的解为非负整数，则符合条件的所有整数a的和为（）A．8B．16C．18D．2039．若数a使关于x的方程a x+12=-7x3-1有非负数解，且关于y的不等式组{y-12-2＜7-2y22y+1＞a-2y恰好有两个偶数解，则符合条件的所有整数a的和是（）A．﹣22B．﹣18C．11D．12含参不等式组与分式方程参考答案一．不等式组无解1．B；2．B；3．C；4．B；5．A；二．不等式组有解6．A；7．B；8．A；9．A；10．D；三．指定解集11．D；12．D；13．C；14．A；15．C；四．有且仅有几个整数解16．C；17．D；18．A；19．A；20．A；21．A；22．C；23．C；24．B；25．B；五．至多几个整数解26．B；27．D；28．D；29．A；30．A；六．至少几个整数解31．C；32．D；33．A；34．C；35．D；七．奇（偶）数解36．C；37．A；38．B；39．B；。

七年级数学下册《含参数的一元一次不等式与不等式组》练习题及答案(人教版)

七年级数学下册《含参数的一元一次不等式与不等式组》练习题及答案（人教版)一、选择题1. 已知点P(−1,a)在第二象限，则a的取值范围是( )A. a=0B. a>1C. a>0D. a<02. 若关于x的不等式(a−1)x<1的解集是x>1a−1，则a的取值范围是( )A. a>0B. a<0C. a>1D. a<13. 关于x的不等式2x−a≤−1的解集如图所示，则a的取值是( )A. −1B. −2C. −3D. 04. 关于x的方程a−1x+1=1的解是负数，则a的取值范围是( )A. a<2B. a>1C. a>1，且a≠2D. a<2，且a≠15. 若关于x，y的方程组{x+y=m2x−y=2的解满足x>y，则m的取值范围是( )A. m<1B. m<2C. m<3D. m<46. 关于x的不等式组{x−m<03x−1>2(x−1)有解，那么m的取值范围为( )A. m≤−1B. m<−1C. m≥−1D. m>−17. 若关于x的不等式(m+1)x>m+1的解集为x<1，则m的取值范围是( )A. m<−1B. m>−1C. m>0D. m<08. 关于x、y的二元一次方程组{x+3y=2+a3x+y=−4a的解满足x+y>2，则a的取值范围为( )A. a<−2B. a>−2C. a<2D. a>29. 不等式组{x+9<5x+1x>a+1的解集是x>2，则a的取值范围是( )A. a≤2B. a≥2C. a≤1D. a>110. 若不等式组{1<x≤2x>k有解，则k的取值范围是( )A. k<2B. k≥2C. k<1D. 1≤k<2二、填空题11. 若关于x的一元一次方程4x+m+1=x−1的解是负数，则m的取值范围是______．12. 若不等式(m−2)x>1的解集是x<1m−2，则m的取值范围是______．13. 若不等式组{x+2a≥51−2x>x−2有解，则a的取值范围是______．14. 关于x、y的二元一次方程组{2x+y=2m+1x+2y=3的解满足不等式x−y>4，则m的取值范围是______．15. 不等式组{2x−a<1x−2b>3的解集为−1<x<1，则(a+2)(b−2)的值等于______ ．三、解答题16.已知关于x、y的方程组{x+y=2a+7x−2y=4a−3．(1)若a=2，求方程组的解；(2)若方程组的解x、y满足x>y，求a的取值范围．17.已知关于x，y的二元一次方程组{x+y=1−ax−y=3a+7的解是一对正数．(1)求a的取值范围；(2)化简：|a+4|−|a|+|2a+3|．18.已知关于x，y的二元一次方程组{x+2y=12 x−y=3m(1)用含有m的代数式表示方程组的解；(2)如果方程组的解x，y满足x+y>0，求m的取值范围．19. 已知方程{x+y=−7−ax−y=1+3a的解x为非正数，y为负数，求a的取值范围．20.已知2x+3=2a，y−2a=4并且a−34<x+y≤2a+112．(1)求a的取值范围；(2)化简：|2a−6|+2|a+2|的结果是______；(3)比较a2+2a−5与a2+a−1的大小．参考答案1.C 2.D 3.A 4.D 5.D6.D7.A8.A9.C10.A11.m>−212.m<213.a>214.m>315.−1216.解：(1)当a=2时{x+y=11①x−2y=5②①−②得3y=6y=2将y=2代入①得x+2=11x=9则方程组的解为{x=9 y=2；(2)解方程组得{x=8a+113y=10−2a3∵x>y∴8a+113>10−2a3解得a>−110．17.解：(1){x+y=1−a①x−y=3a+7②①+②得2x=2a+8解得x=a+4代入①得y=−2a−3．故方程组的解为：{x=a+4y=−2a−3∵x>0，y>0∴{x=a+4>0y=−2a−3>0解得：−4<a<−1.5；(2)由(1)得a+4>0，a<0，2a+3<0∴原式=a+4−(−a)+(−2a−3) =a+4+a−2a−3=1．18.解：(1){x+2y=12 ①x−y=3m ②①−②，得3y=12−3m解得y=4−m．将y=4−m代入②，得x−(4−m)=3m解得x=2m+4．故方程组的解可表示为{x=2m+4 y=4−m；(2)∵x+y>0∴2m+4+4−m>0解得m>−8．故m的取值范围是m>−8．19.解：{x+y=−7−ax−y=1+3a得，{x=a−3y=−2a−4．∵{x≤0y<0∴{a−3≤0−2a−4<0．解得−2<a≤3．20.解：（1）由2x+3=2a，得到x=，由y-2a=4，得到y=2a+4代入得：可化为：由①去分母得：4a-3＜4a-6+8a+16，即8a＞-13，解得a＞-；由②去分母得：2a-3+4a+8＜4a+11，即2a＜6，解得a＜3∴不等式组的解集为：；（2）由（1）求出的a的范围得：2a-6≤0，a+2＞0则|2a-6|+2|a+2|=6-2a+2（a+2）=6-2a+2a+4=10；故答案为：10；（3）∵（a2+2a-5）-（a2+a-1）=a2+2a-5-a2-a+1=a-4＜0∴a2+2a-5＜a2+a-1．。

完整版含参不等式有解无解问题人教版含答案

含参不等式（有解、无解问题）（人教版）一、单选题洪10道，每道10分）1•若不等式组山弋麹的解集为玄门，贝U m的取值范围是（）粮± ?B.轉W ?A.C.疋- E D「；-答案：A解题思路：©解不等式组，得x<m②利用口快“小小取小”确定大致范围：心③验证端点値r当m=3^,不等式组可化为解集为"久符合题意<3综上.冊的取值范围是故选、试题难度：三颗星知识点：含参不等式（组）'兀 > ①+ 2q2•若关于x的不等式组有解，则a的取值范围是（）A—.Bf口>0答案：B解题思路：①■/不等式组有解二根据口诀污大小小大中间找阳可徐口的大致范围为土g-l■ ■ £?A】②脸证端点值：当吋，［"1不等式组无解，不符合题蕙xW 3综上』a的取值范围是Q>1故选B试题难度：三颗星知识点：含参不等式（组）蛊一兌②=03•若不等式组1 —> T—21 有解，则a的取值范围是（A.八B & E：-C.•「…D.「1 答案：D解题思路：©解不等式组，得严：X <1②利用口诀“大小小大中间找抿确定大致范围■ 0 <1③脸证端点值*r T> 1当农=1时，不等式组可化为q -,不等式组无解，不符合题意X £1h综上，口的取值范围是a <1故选D.试题难度：三颗星知识点：含参不等式（组）x>a-2<\_2x +■ 1 孑 4 盘—14.若关于x的不等式组L 有解，则a的取值范围是（）答案：B解题思路：①解不等式组：\ >a- 2x W一2应+1②丁不等式组有解二根据口快"大小小大中间找"可得，a的大致范囿対日-2盂-2「1二X]③验证端点值；当尸1时，P>_1,不等式坐无解"不符含题意综上，住的取值范围是口<1故选B.试题难度：三颗星知识点：含参不等式（组）[4（工-1）+2忌x-1 <—-—5•若关于x的不等式组L ' 有解，则a的取值范围是（）A 口>?B富兴2C—dH答案：C解题思路：①解不等式组，得F沁,X+ 7②T不等式组有解•:根据口快"知卜小大中间找"可角口的大致范围为a^~5③验证端点值，当日=巧时，f 不等式组无解，不符合题惫x < 2综上，a的取値范園是f故选C・试题难度：三颗星知识点：含参不等式（组）6•关于x的不等式组L^<3a~2无解，则a的取值范围是（）M 2 B Q > —2C ；£ 一ID L厂芯2答案：D解题思路：a-b2①解不等式组「得；：［万 < 3a②利用口诀确定Q的大致范凰丁原不等式组无解二根据口快"大大小小找不着■"可律口的大致范围为口十詰加-2'■ a <2③验证端点值’当片2时，｛：：；,不等式组无解，符合题意综上* /的取值范围为“W2 故选D.试题难度：三颗星知识点：含参不等式（组）x < 3a-27•若关于x的不等式组2 加7无解，贝U a的取值范围是（）答案：D解题思路:①解不等式组J得②确定大致范園：T不等式组无解二根据口诀"■大大小小找乔着”'可得；口的夭致范園为3—2 <2^-5二 a <-3③验证端点值，当^-3时.不等式蚩无解，符合题意—11综上，□的取值范围是凸芝-？故选D・试题难度：三颗星知识点：含参不等式（组）5-2Q-18•已知关于x的不等式组L “―“孑。

含参不等式习题及答案

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载含参不等式习题及答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容含参不等式习题及答案一．选择题（共20小题）1．关于x的不等式（m+1）x＞m+1的解集为x＜1，那么m的取值范围是（）A．m＜﹣1 B．m＞﹣1 C．m＞0 D．m＜02．已知关于x的不等式（a﹣2）x＞1的解集为x＜，则a的取值范围（）A．a＞2 B．a≥2C．a＜2 D．a≤23．如果不等式（2﹣a）x＜a﹣2的解集为x＞﹣1，则a必须满足的条件是（）A．a＞0 B．a＞2 C．a≠1D．a＜14．关于x的不等式（1﹣m）x＜m﹣1的解集为x＞﹣1，那么m的取值范围为（）A．m＞1 B．m＜1 C．m＜﹣1 D．m＞﹣15．如果关于x的不等式（1﹣a）x≥3解集为x≤，则a的取值范围是（）A．a≤1 B．a≥1C．a＞1 D．a＜16．如果关于x的不等式（1﹣k）x＞2可化为x＜﹣1，则k的值是（）A．1 B．﹣1 C．3 D．﹣37．关于x的不等式组有解，那么m的取值范围为（）A．m≤﹣1 B．m＜﹣1 C．m≥﹣1 D．m＞﹣18．已知关于x的不等式组有解，则a的取值不可能是（）A．0 B．1 C．2 D．﹣29．若关于x的一元一次不等式组有解，则a的取值范围是（）A．a＞1 B．a≥1C．a＜1 D．a≤110．已知关于x的不等式组有解，则m的取值范围为（）A．m＞6 B．m≥6C．m＜6 D．m≤611．如果关于x的不等式组有解，则a的取值范围是（）A．a≤3 B．a≥3C．a＞3 D．a＜312．若关于x的不等式组无解，则a的取值范围是（）A．a≤﹣3 B．a＜﹣3 C．a＞3 D．a≥313．已知关于x的不等式组无解，则实数a的取值范围是（）A．B．C．D．14．已知不等式组无解，则a的取值范围是（）A．a≥3 B．a≥﹣3 C．a≤3D．a≤﹣315．若不等式组无解，那么m的取值范围是（）A．m＞2 B．m＜2 C．m≥2D．m≤216．若不等式组有三个整数解，则a的取值范围是（）A．﹣3＜a≤﹣2 B．2＜a≤3C．2＜a＜3 D．a＜317．若关于x的不等式组的整数解只有3个，则a的取值范围是（）A．6≤a＜7 B．5≤a＜6 C．4＜a≤5D．5＜a≤618．关于x的不等式组的解中恰有4个整数解，则a的取值范围是（）A．18≤a≤19B．18≤a＜19 C．18＜a≤19D．18＜a＜19 19．关于x的不等式组恰好只有4个整数解，则a的取值范围为（）A．﹣2≤a＜﹣1 B．﹣2＜a≤﹣1 C．﹣3≤a＜﹣2 D．﹣3＜a≤﹣220．如果不等式组恰有3个整数解，则a的取值范围是（）A．a≤1 B．a＜﹣1 C．﹣2＜a≤﹣1 D．﹣2≤a＜﹣1二．填空题（共10小题）21．若不等式组有解，则a的取值范围是．22．若关于x的一元一次不等式组有解，则a的取值范围是．23．已知关于x的不等式组有解，则a的取值范围是．24．若不等式组无解，则a的取值范围是．25．若不等式组无解，则a的取值范围是．26．不等式组有3个整数解，则实数a的取值范围是．27．若关于x的不等式组有2个整数解，则a的取值范围是．28．关于x的不等式组无整数解，则a的取值范围为．29．已知关于x的不等式组恰有三个整数解，则t的取值范围为．30．已知关于x的不等式组恰好有2个整数解，则整数a的值是．含参不等式习题及答案参考答案与试题解析一．选择题（共20小题）1．关于x的不等式（m+1）x＞m+1的解集为x＜1，那么m的取值范围是（）A．m＜﹣1 B．m＞﹣1 C．m＞0 D．m＜0解：∵不等式（m+1）x＞m+1的解集为x＜1，∴m+1＜0，即m＜﹣1，故选：A．2．已知关于x的不等式（a﹣2）x＞1的解集为x＜，则a的取值范围（）A．a＞2 B．a≥2C．a＜2 D．a≤2解：∵不等式（a﹣2）x＞1的解集为x＜，∴a﹣2＜0，∴a的取值范围为：a＜2．故选：C．3．如果不等式（2﹣a）x＜a﹣2的解集为x＞﹣1，则a必须满足的条件是（）A．a＞0 B．a＞2 C．a≠1D．a＜1解：∵不等式（2﹣a）x＜a﹣2的解集是x＞﹣1，∴2﹣a＜0，解得 a＞2．故选：B．4．关于x的不等式（1﹣m）x＜m﹣1的解集为x＞﹣1，那么m的取值范围为（）A．m＞1 B．m＜1 C．m＜﹣1 D．m＞﹣1解：∵关于x的不等式（1﹣m）x＜m﹣1的解集为x＞﹣1，∴1﹣m＜0，﹣m＜﹣1，解得：m＞1，故选：A．5．如果关于x的不等式（1﹣a）x≥3解集为x≤，则a的取值范围是（）A．a≤1 B．a≥1C．a＞1 D．a＜1解：∵关于x的不等式（1﹣a）x≥3解集为x≤，∴1﹣a＜0，解得，a＞1，故选：C．6．如果关于x的不等式（1﹣k）x＞2可化为x＜﹣1，则k的值是（）A．1 B．﹣1 C．3 D．﹣3解：∵不等式（1﹣k）x＞2可化为x＜﹣1，∴1﹣k＝﹣2解得：k＝3．故选：C．7．关于x的不等式组有解，那么m的取值范围为（）A．m≤﹣1 B．m＜﹣1 C．m≥﹣1 D．m＞﹣1解：，解不等式x﹣m＜0，得：x＜m，解不等式3x﹣1＞2（x﹣1），得：x＞﹣1，∵不等式组有解，∴m＞﹣1．故选：D．8．已知关于x的不等式组有解，则a的取值不可能是（）A．0 B．1 C．2 D．﹣2解：∵关于x的不等式组有解，∴a＜2，∵0＜2，1＜2，﹣2＜2，∴a的取值可能是0、1或﹣2，不可能是2．故选：C．9．若关于x的一元一次不等式组有解，则a的取值范围是（）A．a＞1 B．a≥1C．a＜1 D．a≤1解：解不等式①得，x＞a，解不等式②得，x＜1，∵不等式组有解，∴a＜1，故选：C．10．已知关于x的不等式组有解，则m的取值范围为（）A．m＞6 B．m≥6C．m＜6 D．m≤6解：不等式组由①得x＞m﹣3，由②得x＜，∵原不等式组有解∴m﹣3＜解得：m＜6故选：C．11．如果关于x的不等式组有解，则a的取值范围是（）A．a≤3 B．a≥3C．a＞3 D．a＜3解：解不等式x+1＜4，得：x＜3，∵x＞a且不等式组有解，∴a＜3，故选：D．12．若关于x的不等式组无解，则a的取值范围是（）A．a≤﹣3 B．a＜﹣3 C．a＞3 D．a≥3解：∵关于x的不等式组无解，∴a﹣1≥2，∴a≥3，故选：D．13．已知关于x的不等式组无解，则实数a的取值范围是（）A．B．C．D．解：由不等式|x+1|＜4x﹣1得x＞，关于x的不等式组无解，所以a≤，故选：B．14．已知不等式组无解，则a的取值范围是（）A．a≥3 B．a≥﹣3 C．a≤3D．a≤﹣3解：∵不等式组无解，∴2a﹣5≥3a﹣2，解得：a≤﹣3，故选：D．15．若不等式组无解，那么m的取值范围是（）A．m＞2 B．m＜2 C．m≥2D．m≤2解：由①得，x＞2，由②得，x＜m，又因为不等式组无解，所以根据“大大小小解不了”原则，m≤2．故选：D．16．若不等式组有三个整数解，则a的取值范围是（）A．﹣3＜a≤﹣2 B．2＜a≤3C．2＜a＜3 D．a＜3 解：，解不等式x+a≥0得：x≥﹣a，解不等式1﹣2x＞x﹣2得：x＜1，∵此不等式组有3个整数解，∴这3个整数解为﹣2，﹣1，0，∴a的取值范围是﹣3＜a≤﹣2．故选：A．17．若关于x的不等式组的整数解只有3个，则a的取值范围是（）A．6≤a＜7 B．5≤a＜6 C．4＜a≤5D．5＜a≤6解：解不等式x﹣a≤0，得：x≤a，解不等式5﹣2x＜1，得：x＞2，则不等式组的解集为2＜x≤a，∵不等式组的整数解只有3个，∴5≤a＜6，故选：B．18．关于x的不等式组的解中恰有4个整数解，则a的取值范围是（）A．18≤a≤19B．18≤a＜19 C．18＜a≤19D．18＜a＜19 解：不等式组整理得：，解得：a﹣2＜x＜21，由不等式组恰有4个整数解，得到整数解为17，18，19，20，∴16≤a﹣2＜17，解得：18≤a＜19，故选：B．19．关于x的不等式组恰好只有4个整数解，则a的取值范围为（）A．﹣2≤a＜﹣1 B．﹣2＜a≤﹣1 C．﹣3≤a＜﹣2 D．﹣3＜a≤﹣2解：不等式组整理得：，解得：a+1＜x＜，由解集中恰好只有4个整数解，得到整数解为0，1，2，3，∴﹣1≤a+1＜0，解得：﹣2≤a＜﹣1，故选：A．20．如果不等式组恰有3个整数解，则a的取值范围是（）A．a≤1 B．a＜﹣1 C．﹣2＜a≤﹣1 D．﹣2≤a＜﹣1解：∵不等式组恰有3个整数解，∴﹣2≤a＜﹣1，故选：D．二．填空题（共10小题）21．若不等式组有解，则a的取值范围是a＞2 ．解：解不等式x+2a≥5得：x≥5﹣2a，解不等式1﹣2x＞x﹣2得：x＜1，∵该不等式组有解，∴5﹣2a＜1，解得：a＞2，故答案为：a＞2．22．若关于x的一元一次不等式组有解，则a的取值范围是a＜1 ．解：∵关于x的一元一次不等式组有解，∴a＜1，故答案为：a＜1．23．已知关于x的不等式组有解，则a的取值范围是a＜8 ．解：，由不等式①，得x＞﹣2，由不等式②，得x≤，∵关于x的不等式组有解，∴﹣2＜，解得，a＜8，故答案为：a＜8．24．若不等式组无解，则a的取值范围是a≥2．解：，由①得，x＜1+a，由②得，x＞2a﹣1，由于不等式组无解，则2a﹣1≥1+a解得：a≥2．故答案为：a≥2．25．若不等式组无解，则a的取值范围是a≥2．解：4﹣2x＞0，解得：x＜2，∵不等式组无解，∴无解，则a的取值范围是：a≥2．故答案为：a≥2．26．不等式组有3个整数解，则实数a的取值范围是13≤a＜18 ．解：解不等式3x﹣5＞1，得：x＞2，解不等式5x﹣a≤12，得：x≤，∵不等式组有3个整数解，∴其整数解为3，4，5，则5≤＜6，解得：13≤a＜18，故答案为：13≤a＜18．27．若关于x的不等式组有2个整数解，则a的取值范围是0≤a＜1 ．解：解不等式得：x≤2，解不等式得：x＞a，∵不等式组有2个整数解，∴不等式组的解集为：a＜x≤2，且两个整数解为：2，1，∴0≤a＜1，即a的取值范围为：0≤a＜1．故答案为：0≤a＜1．28．关于x的不等式组无整数解，则a的取值范围为a≥2．解：不等式组整理得：不等式组的解集是：a＜x＜，∵不等式组无整数解，∴a≥2．29．已知关于x的不等式组恰有三个整数解，则t的取值范围为．解：解不等式①得：x＞，解不等式②得：x＜3﹣2t，则不等式组的解集为：＜x＜3﹣2t，∵不等式组有3个整数解，∴一定存在一个整数k，满足满足下列关系：，解不等式组①得，，解不等式组②得，，（1）当，即时，则，于是，，解得，，∴＜k≤，∵k为整数，∴k＝3，此时，；（2）当时，即时，不存在整数k，∴此时无解；（3）当，此时无解；（4）当，即k时，则，于是，，解得，，∴，不存在整数k，∴此时无解．综上，＜t≤．故答案为：．30．已知关于x的不等式组恰好有2个整数解，则整数a的值是﹣4，﹣3 ．解：不等式组，由①得：ax＜﹣4，当a＜0时，x＞﹣，当a＞0时，x＜﹣，由②得：x＜4，又∵关于x的不等式组恰好有2个整数解，∴不等式组的解集是﹣＜x＜4，即整数解为2，3，∴1≤﹣＜2（a＜0），解得：﹣4≤a＜﹣2，则整数a的值为﹣4，﹣3，故答案为：﹣4，﹣3．。

高二数学专题一：含参不等式及参数问题知识精讲人教版

高二数学专题一：含参不等式及参数问题知识精讲人教版一. 本周教学内容：专题一：含参不等式及参数问题二. 重点、难点：含参数的不等式有着丰富的内容，解决含参数不等式的问题不仅需要很熟练的运算能力，而且还需要有明确的数学思想指导，灵活深刻的思维品质。

应注意以下几个问题： 1. 解含有参数的不等式。

2. 已知不等式成立的条件，求参数的X 围。

3. 不等式恒成立，能成立，恰成立的问题。

【典型例题】[例1] 解不等式012>+-x x ax 。

解：0)1(2>+-⇔x x ax（1）当0=a 时，0)1(>-x x 解为)1,0(∈x（2）当0>a 时，0)11(2>+-⋅ax a x xa a 412-=∆①),41(∞+∈a 时，解为),0(∞+∈x②41=a 时，解为),2()2,0(∞+⋃∈x③)41,0(∈a 时，解为),2411()2411,0(∞+-+⋃--∈a a a a x （3）0<a 时，0)11(2<+-x a x a x 0412>-=∆a a解为：)2411,0()2411,(aaa a --⋃-+-∞ [例2] 设na n n x f x x x x ⋅+-++++=)1(321lg )( ，其中R a ∈，2≥n ，*N n ∈，n为常数。

若)(x f 在（∞-，1）上成立，求a 的取值X 围。

解：依题意：0)1(21>+-+++nan n x x x 即0)1(21>+-++a n n x x x ])1()2()1[(x x x n n n n a -+++-> 令])1()1[()(xx nn n x g -++-=x n y )1(=↓……↓-=x nn y )1(∴)(x g y = R 上↑∴∈x （∞-，1） 21)1(max ng y -== ∴21n a ->∴∈a （21n-，∞+） [例3] }09log 5log 1|{<-+=x x x A ，}0)2(2|{2<+--=a a x x x B ，若B B A =⋃，求a 的取值X 围。

不等式含参问题

含参不等式专题一．利用基本性质对比求解.已知关于x 的不等式()132>--x a 的解集为24-<a x ，则a 的取值范围是；二．已知解集求参数的值1.关于x 的不等式22521-≥-x x 与不等式3x 的解集相同，则=a 2.若关于x 的不等式1232->-a a x 与5<a x的解相同，则=a3.若关于x 的不等式132≤--ax x 的解集在数轴上表示如图所示，则=a三．利用解的范围构造不等式求解1.关于x 的不等式32521+≥-x x 的解都是012≤+-a x 的解，则a 的取值范围是 2.关于x 的不等式1232+≤-a a x 的解都是1215312≥+--x x 的解，则a 的取值范围是4．借助数轴求解例4．不等式a x ≤3只有2个正整数解，则a 的最小值为变式：已知不等式02≥+a x 的负整数解恰好有1-、2-、3-，则a 的取值范围是三、方程（组）与不等式的联手解答 1．方程联手不等式例1．若关于x 的方程44232+-=-x m m x 的解不小于3187m--，求m 的最小值。

变式1：已知025253=+-++b a a ，求关于x 的不等式()()241213--<+-x b x ax 的最小非负整数解；变式2：若不等式()()716825+-<+-x x 的最小整数解是关于x 的方程32=-ax x 的解，求aa 144-的值。

2．方程组联手不等式例1．已知方程组⎩⎨⎧-=++=-8423332m y x m y x 的解满足15<+y x ，则m 的取值范围是变式：已知方程组⎩⎨⎧=+=-a y x y x 624的解满足3<-y x ，则a 的取值范围是四、含有两个参数不等式解集的解法例1．已知关于x 的不等式()n m x n m 52>--的解集为413<x ，求关于x 的不等式()n m x n m +>-的解集。

含参不等式(实数解问题)(人教版)

含参不等式(实数解问题)(人教版)一、简介本文档主要讨论含参不等式的实数解问题。

含参不等式是指在不等式中含有未知数的不等式，我们将通过实例详细介绍解决这类问题的方法和步骤。

二、解决方法解决含参不等式的实数解问题可以采取以下步骤：1. 确定不等式的范围：首先，要确定不等式的范围，即确定未知数的取值范围。

这可以通过对不等式进行变形和化简来实现。

2. 根据范围解不等式：根据确定的范围，将未知数代入不等式，并求解。

可以采用试探法、代入法或图像法等方法求解。

3. 验证解的有效性：求解出不等式的解之后，需要验证这些解是否满足原始的不等式。

通过将解代入不等式并判断不等式是否成立来验证解的有效性。

三、实例分析以下是一个实例分析，展示了如何解决含参不等式的实数解问题：例题：求解不等式 |x - a| < b，其中 a > 0，b > 0。

解：首先，根据不等式 |x - a| < b 的定义，可以得到两个不等式：1) x - a < b；2) -(x - a) < b。

将两个不等式进行化简：1) x < a + b；2) x > a - b。

因此，不等式的解是 a - b < x < a + b。

需要注意的是，这个解是根据 a > 0，b > 0 的条件得出的。

接下来，我们需要验证解的有效性。

将解代入原始不等式 |x - a| < b 可得：1) |(a - b) - a| = b，成立；2) |(a + b) - a| = b，成立。

因此，解 a - b < x < a + b 是原始不等式的实数解。

四、总结通过本文档的介绍，我们了解到解决含参不等式实数解问题的方法和步骤。

关键是确定范围、带入求解，并验证解的有效性。

通过实例的分析，我们可以更好地掌握和应用这些方法，解决含参不等式的实数解问题。

以上是对含参不等式(实数解问题)(人教版)的文档概述，希望对您有所帮助。

（完整版）一元一次不等式含参问题

一元一次不等式含参问题类型一根据不等式租的整数解情况确定字母的取值范围例1．不等式组有3个整数解，则m的取值范围是．变式练习1．不等式组有3个整数解，则m的取值范围是．变式练习2．已知关于x的不等式组只有3个整数解，则实数a的取值范围是．变式练习 3.已知关于x的不等式组{4??+2>3(??+??)2??>3(??-2)+5,仅有4个整数解，则实数a的取值范围是．变式练习 4.已知关于x的不等式组{5??+2>3(??-1)12≤8-32??+2??,仅有4个整数解，则实数a的取值范围是．类型二根据不等式组的解集确定字母的取值范围例2.已知关于x的不等式组无解，则a的取值范围是．变式练习1．若关于x的不等式组有解，则实数a的取值范围是．变式练习2．若不等式的解集为x＞3，则a的取值范围是．变式练习3．若关于x的不等式的解集为x＜2，则a的取值范围是．变式练习4．已知不等式组无解，则a的取值范围是．类型三根据未知数解集或者未知数间的关系确定字母的取值范围例3.已知方程组m y x my x 12312满足??+??<0,求m 的取值范围变式练习1.若关于x ，y 的二元一次方程组的解满足x+y ＜2，则a 的取值范围为．2.已知12242k y x k yx 且的取值范围为则k y x ,01-．例4. 已知关于x 的不等式（1﹣a ）x ＞2的解集为x ＜，则a 的取值范围是．变式练习1．不等式（x ﹣m ）＞3﹣m 的解集为x ＞1，则m 的值为．2．若关于x 的不等式3m ﹣2x ＜5的解集是x ＞3，则实数m 的值为．3．若不等式ax+b ＜0的解集是x ＞﹣1，则a ，b 应满足的条件有．综合练习1．关于x的一元一次不等式≤﹣2的解集为x≥4，则m的值为（）A．14B．7C．﹣2D．22．不等式组的解集是x＞﹣1，则a的取值范围是．3．若关于x的一元一次不等式组无解，则a的取值范围是．4．若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为．5．已知关于x的不等式组无解，则a的取值范围是．6.不等式组的解是0＜x＜2，那么a+b的值等于．7．已知关于x的不等式组只有3个整数解，则实数a的取值范围是．8．已知关于x的不等式组的整数解共有6个，则a的取值范围是．。

含参不等式(有解、无解问题)(人教版)

含参不等式（有解、无解问题）（人教版）一、单选题(共10道，每道10分)
1.若不等式组的解集为，则m的取值范围是( )
A. B.
C. D.
2.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
3.若不等式组有解，则a的取值范围是( )
A. B.
C. D.
4.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
5.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
6.关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
7.若关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
8.已知关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
9.若关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
10.若关于x的不等式组无解，则m的取值范围是( )
A. B.
C. D.。

(完整版)含参不等式(有解、无解问题)(人教版)含答案

含参不等式（有解、无解问题）（人教版）一、单选题(共10道，每道10分)1.若不等式组的解集为，则m的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）2.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）3.若不等式组有解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）4.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）5.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）6.关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）7.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）8.已知关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）9.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）10.若关于x的不等式组无解，则m的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）。

含参不等式(整数解问题)(人教版)含答案

含参不等式（整数解问题）（人教版）一、单选题(共10道，每道10分)1.若关于x的不等式只有4个正整数解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）2.若关于x的不等式只有3个正整数解，则m的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）3.若关于x的不等式组有且只有1个整数解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）4.若关于x的不等式组有且只有3个整数解，则a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）5.若关于x的不等式组有且只有4个整数解，则实数a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）6.若关于x的不等式组有且只有3个整数解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）7.若关于x的不等式组恰有5个整数解，则t的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）8.若不等式组恰有2个整数解，则实数a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）9.若不等式组的所有整数解的和为5，则实数a的取值范围是( )A. B.C. D.答案：A试题难度：三颗星知识点：含参不等式（组）10.若关于x的不等式组的所有整数解的和是-7，则m的取值范围是( )A. B.C. D.答案：C。

含参不等式(整数解问题)(人教版)含答案

含参不等式（整数解问题）（人教版）含答案含参不等式（整数解问题）（人教版）一、单选题(共10道，每道10分)1.若关于x的不等式只有4个正整数解，则a 的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）2.若关于x的不等式只有3个正整数解，则m的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）3.若关于x的不等式组有且只有1个整数解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）4.若关于x的不等式组有且只有3个整数解，则a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）5.若关于x的不等式组有且只有4个整数解，则实数a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）6.若关于x的不等式组有且只有3个整数解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）7.若关于x的不等式组恰有5个整数解，则t的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）8.若不等式组恰有2个整数解，则实数a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）9.若不等式组的所有整数解的和为5，则实数a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）10.若关于x的不等式组的所有整数解的和是-7，则m的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）。

含参不等式(整数解问题)(人教版)含答案-10页文档资料

含参不等式（整数解问题）（人教版）一、单选题（共10道，每道10分）1•若关于x 的不等式只有4个正整数解，则a 的取值范围是（）A .丄 m:B . ' 一 • _c.4答案：C解题思路：① 画数轴确定大致範围:-10 12 3 4 5丁不等式只有4个正整数解，/■ a 的大致范围是4<cj<5.② 验证端点值：当e4时，工V4,不等式有3个正整数解，不符合题意;当时,.r<5t 不等式有4个正整数解，符合题意. 综上，□的取值范围是4<^5, 故选C.试题难度：三颗星知识点：含参不等式（组）① 解不等式，得^<増② 画数轴确定大致范ffih A.— 1「冷.」■-.< -.'13 ~^m<2C .】D .-答案：D解题思路：2.若关于x -X-刑 <0的不等式1 只有3个正整数解, m 的取值范围是（_ ■ ___ I ___ I ___ 丄占—I --0 1 2 3 2ws 4T不等式只有3个正整数解，：.lm的大致范围为3<2w<4,/. m的大致范围为—VJW <2 ”2③验证端点值*当杭二彳时…X?,不等式有2个正螯数解，不符合题意,当叩W时，工7 不等式有3个正整数解，符合题意.综上，w的取值范围是£ <搐宅2 .故选D*试题难度：三颗星知识点：含参不等式（组）3•若关于x的不等式组卩一2兀>1有且只有1个整数解，则a的取值范围是（）A.O<X1B.O <©W1C OSI D.O唤1答案：C解题思路：①解不等式组，得“才；x < 2②画数轴确定大致范围；在数轴上表示固定的盘二0 a 1 2V不等式组只有1个整数解，「虫的大致范围为0<a<l.③验证端点值：T Q当eo时，r u,不竽式组有i个整数解，符合题意,z < 2当Q1时，（A>1S不等式组没有整数解，不符合题意. z < 2综上，a的取值范31是0Wo cl*故选u试题难度：三颗星知识点：含参不等式（组）2x-1^34•若关于x的不等式组有且只有3个整数解，则a的取值范围是（）A.4"%5B.4約<5c.5 <mW6D.5Wm <6答案：A 解题思路:①解不等式组，得x < a②画数轴确定大致范围：在数轴上表示固定的忑比2----- ------- ! ---- !■2 3 4 a 5T不等式组有且只有3个整数解，•"的大致范園为③验证端点值：当戸4时，’，不等式组有二个整数解，不符合题意；x<4匕「炷2当尸5时，「不等式组有§个整数解，符合题惹.z <5综上，山的取值范围是4<（sW故选A・试题难度：三颗星知识点：含参不等式（组）5•若关于x的不等式组I」宀I有且只有4个整数解，则实数a的取值范围是（）A.-3 <m <_2 B.-3 W-2c.-3 W 左< -2 D_3W 住W -2答案：B解题思路：①解不等式组，得不步:x < 2.②画数轴确定大致范围：在数轴上表示固定的;^2-3 a -2 -1 0 1V不等式组有且只有4个整数解，二口的大致SS围^-3<a <-2,③脸证端点值：当3时・不等式组可化为不等式组有5个整数解，z < 2-不符合题意；当戸P时，不等式组可化为不等式组有4个整数解, x < 2符合题意.综上"的取值范围为茲故选B.试题难度：三颗星知识点：含参不等式（组）4（x-l）+2 > 3xx-16•若关于x的不等式组〔丫有且只有3个整数解，则a的取值范围是（A.—U.a<： -1 B.~1W 住 <一1c.—2〔厂三 T D.—2 <^ < _1答案：C解题思路:① 解不等式组，得“； y < 7 + a■-② 画数轴确定犬致范Bh 在数轴上表示固定的XA 20 1 2 3 4 和+附T 不等式组有且只有3个整数解，二7“的大致范围为5<7+a <6,/. a 的取值范围为-2 << -1 *③ 验证端点值：当歼7时，不等式组可化为不等式组有2个整数解, x <5不符合题意；X > 2 当金=-1时，不等式组可化为,不等式组有3个整数解,x <6 * 符合题意.综上，a 的取值范围为-2. 故选C*试题难度：三颗星知识点：含参不等式（组） ① 解不等式组，得[x > 3- 2£② 画数轴确定大致范围：在数轴上表示固定的x<20M 3-2/15 16 17 18 19 20T 不等式组有5个整数解，3-2f 的大致范围为14 <3-2（ <15,7•若关于x 的不等式组恰有5个整数解，则 t 的取值范围是（A. -B. 2答案：B解题思路:二啲大致范围为③验证端点值；当尸—6时，不等式组可化为[“巴不等式组有4个整数解，|^x> 15不符合题意；当尸-口时，不等式组可化为不等式组有5个整数解，2[x >14符合题意.综上，『的取值范围为2故选B.试题难度：三颗星知识点：含参不等式（组）x x + 1 A一+--- > 02 3勿+4 4 ”、x + —-—> —（x+l）+ a8•若不等式组I $ 孑恰有2个整数解，则实数a的取值范围是（）31sW —斗/ mA. B.1 ■---Cd <1 l“wiC. D.]答案：D解题思路：_ 2①解不等式组，得?>_5< 2a②画数轴确定大致范围’2在数轴上表示固定的x>-|-1 2 0 1 2a3 35■/不等式组有［个整数解，二2”的大致范围为1<鮎<2・- a的大致范围为j C a C1・③验证端点值！当"舟时，不等式组可化为艮不等式组有1个整数解，2<1Z■-不符合题意，・_2当口“时，不等式组可化为J>_5 ,不等式组有2个整数解，j < 2£符合题意*综上，农的取值范围为!<亦01・故选D,试题难度：三颗星知识点：含参不等式（组）x-2 <2x {a + 2x------ <19•若不等式组I 4 的所有整数解的和为5,则实数a的取值范围是（）A.'-.一-：二B. ' Jc.-4 W M W -2 D._4<_2答案：A解题思路:>-2①解不等式组，得4-ax < ---I 2②画数轴确定大致范围：在数轴上表示固定的z>-22V不等式组的所有整数解的和为5,二辛的大致范围为3<^<<■ \ a的大致范围为-4 <a <-2 .③验证端点值：当4时，不等式组可化为卩>・2, 兀<4不等式组有亍个整数解，分别为：7, 0, b 2,灵所有整数解的和为5,符合题意；当^=^2时，不等式组可化为P>_\z <3■.不等式组有斗个整数解，分别为* -1, 0. L 2. 所有整数解的和为乙不符合题意.综上空的取值范围为-A^a <-2 .故选A,试题难度：三颗星知识点：含参不等式（组）盂+21 .------ >3- x210.若关于x的不等式组的所有整数解的和是-，则m的取值范围是（）A. 1 •.、；；一一JB. J ■- Jc.-3 5W -2或2 <用W 3D-3W怖・2或20 tn <3答案：c解题思路:2. 画数轴确定大致范围’ 在数轴上表示固定的x>-5,___ 打 ll II ■ ■ I ■Il-5 -4 -3 -2 -1 0 1 2 V 不等式组所有整数解的和是二原不等式组的整数解可能有两种情况*① T,② 7 T, -2, -l f O f 1, 2.m 的大致范围是T < m u-2或2 <m < 3.3. 验证端点值】① 当啣“3时，不等式组可化为$八1不等式组有1个整数解.[乂 <-3 为T,所有啓数解的和为T,不符合题意；当附=7时，不等式组可化为不等式组有2个整数解， x <-2为7和-灵所有整数解的和为符合题意. :、m 的取值范围为_3 —2 .（x>-5② 当豹W 时，不等式组可化为 \ ,\x <2不等式组的整数有6个整数解，为T, -3, -2, -1, 0, 1, 所有整数解的和为-9,不符合题意，当时，不等式组可化为$[x <3不等式组有了个整数解，为T, T, -2, -1, 0, 1, 2, 所有整数解的和为-入符合题意.二怕的取值范围为？ 5W3综上眄的取值范围为-3 <-2或2吒翊W 3.故选C,试题难度：三颗星知识点：含参不等式（组）1.解不等式组，得 x <m。

(完整版)含参数的一元二次不等式的分类讨论

复习引入：一元一次的分类讨论：2(2)(31)2(2)0k x k x x +--+->、含参数的一元二次不等式——分类讨论1. 优先考虑十字相乘，若两根大小不确定，即分121212,,x x x x x x >=<三种情况．2. 若不能十字相乘，则考虑按判别式∆的正负分类，即分0,0,0∆>∆=∆<三种情况，结合图像法求解。

3. 按二次项系数正负是否确定：当二次项系数含参数时，按2x 项的系数a 的符号分类，即分0,0,0a a a >=<三种情况．1.2(1)0x a x a -++< 2.22560x ax a -+> 3.223()0x a a x a -++> 4.2(1)0x a x a -++< 5.2(2)20x a x a +--< 6.21()10 x a x a -++< 7.22210 x x a -+-≥1.2210x mx m -++> 2.220x kx k +-≤ 3.240x ax ++> 4.2(2)0x a x a +-+>2560()x ax ax a a R -+>∈解关于的不等式1.2210ax x ++< 2.210.ax ax +-< 3.220ax x a -+<1.21)10ax a x -++<（ 2.21)10ax a x +-->（ 3.22(1)40 mx m x -++< 4.2(32)60 ax a x -++< 5.22(1)40 ax a x -++<综合提高题1. 集合{}{}2222(1)0,540A x x a x a a B x x x =-+++<=-+≥，且A B ⊆，求a 的范围2. 集合{}(){}22320,10A x x x B x x a x a =-+≤=-++≤，且A B ⊆，求a 的范围 3. 设全集U=R ，集合{}{}22(41)40,21A x x a a B x a x a =-++≤=≤≤+，且B A ⊆，求a 的范围4. 集合{}{}22540,220A x x x B x x ax a =-+≤=-++≤，且B A ⊆，求a 的范围含参数的一元二次不等式—恒成立和无解问题（数形结合） 1.220x x a ++>的解集为R ，求a 范围 2.220x x a ++≥的解集为R ，求a 范围 3.210x ax -+≥的解集为R ，求a 范围 4.()2140x k x +-+>的解集为R ，求a 范围5.2(1)10ax a x a +-+->恒成立，求a 范围 6.210ax ax -+>恒成立，求a 范围 7.23208kx kx ++<恒成立，求k 范围 8.22(2)0ax ax a +-+<恒成立，求k 范围 9. 2(3)10mx m x -+-<恒成立，求m 范围10. 2(2)(2)10a x a x -+-+≥恒成立，求a 范围11. 2(2)2(2)-40a x a x -+-<恒成立，求a 范围12. 22(1)(1)10a x a x ----<恒成立，求a 范围13. 22(1)(1)10t x t x -+-->恒成立，求t 范围14. 22(23)(3)10m m x m x -----<恒成立，求m 范围15. 2(1)1mx m x m x m --+-函数的图像在轴下方，求实数的取值范围。

含参不等式以及含参不等式组的解法

含参不等式以及含参不等式组的解法不等式在中考中的运用，往往掺杂参数来增加难度，我们只要读清楚题目找到解题思路便能迎刃而解了。

本节课我们就重点讲讲如何读题去寻找解题思路。

含参不等式：解不等式5（x-1）<3x+1通过去括号、移项、合并同类项等一系列运算可以求出解为：x<3 求不等式57x -<32-x 的最小整数解. 通过去括号、移项、合并同类项等一系列运算可以求出解为：x>831,故可以得出最小整数为4.那么含参不等式如下：解含参不等式ax<b若解ax ≤b 呢分类情况解集情况解集情况a>0时 X<a b X ≤a b a<0时 X>abX ≥aba=0时若b>0，则解集为任意数若b ≥0，则解集为任意数若b ≤0，则这个不等式无解若b<0，则这个不等式无解在这些需要讨论的情况下，等号最后讨论才方便，不会讨论重合。

例题：1、求不等式kx+2>2x-3的解集移项、合并同类项、讨论取值2、（1）求不等式解集mx+a>nx+b 移项、合并同类项、讨论取值（2）（m-1）x>a 2+1对于任意x 都成立，则参数m 的值为练习：1、求不等式kx+2>3的解集2、（1）求不等式mx-2<-7-nx 的解集（2）求不等式m 2x+1<-x+5的解集3、关于x 的方程5x-2m=-4-x 的解满足2<x<10，求m 的取值范围。

含参不等式组：观察下列不等式组的解集 ⎩⎨⎧>>31x x⎩⎨⎧<<31x x ⎩⎨⎧<>31x x ⎩⎨⎧><31x x 同大取大同小取小大小小大中间找大大小小无限了例题：1、（1）求不等式x-a ）（x-b ）>0的解集。

（2）求不等式320-x +518-x +716-x +914-x +1112-x >5的解集。

含参不等式(有解、无解问题)(人教版)含答案7页word

含参不等式（有解、无解问题）（人教版）一、单选题(共10道，每道10分)1.若不等式组的解集为，则m的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）2.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）3.若不等式组有解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）4.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）5.若关于x的不等式组有解，则a的取值范围是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：含参不等式（组）6.关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）7.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）8.已知关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：含参不等式（组）9.若关于x的不等式组无解，则a的取值范围是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：含参不等式（组）10.若关于x的不等式组无解，则m的取值范围是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：含参不等式（组）。

(整理)含参不等式(有解、无解问题)(人教版)

含参不等式（有解、无解问题）（人教版）一、单选题(共10道，每道10分)
1.若不等式组的解集为，则m的取值范围是( )
A. B.
C. D.
2.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
3.若不等式组有解，则a的取值范围是( )
A. B.
C. D.
4.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
5.若关于x的不等式组有解，则a的取值范围是( )
A. B.
C. D.
6.关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
7.若关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
8.已知关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
9.若关于x的不等式组无解，则a的取值范围是( )
A. B.
C. D.
10.若关于x的不等式组无解，则m的取值范围是( )
A. B.
C. D.。

(完整版)含参不等式(有解、无解问题)(人教版)含答案

(完整版)专题--含参一元一次不等式组(1)

含参不等式(有解、无解问题)(人教版)含答案

含参不等式与分式方程(含答案)

七年级数学下册《含参数的一元一次不等式与不等式组》练习题及答案(人教版)

完整版含参不等式有解无解问题人教版含答案

含参不等式习题及答案

高二数学专题一：含参不等式及参数问题 知识精讲 人教版

不等式含参问题

含参不等式(实数解问题)(人教版)

（完整版）一元一次不等式含参问题

含参不等式(有解、无解问题)(人教版)

(完整版)含参不等式(有解、无解问题)(人教版)含答案

含参不等式(整数解问题)(人教版)含答案

含参不等式(整数解问题)(人教版)含答案

含参不等式(整数解问题)(人教版)含答案-10页文档资料

(完整版)含参数的一元二次不等式的分类讨论

含参不等式以及含参不等式组的解法

含参不等式(有解、无解问题)(人教版)含答案7页word

(整理)含参不等式(有解、无解问题)(人教版)

高二数学专题一：含参不等式及参数问题知识精讲人教版