齿轮强度计算
齿轮疲劳强度计算公式

齿轮疲劳强度计算公式齿轮疲劳强度是评估齿轮在长期使用条件下承受载荷的能力。
齿轮在传递动力时经常会受到不断的变负载,存在疲劳断裂的风险。
为了确保齿轮的可靠性和安全性,需要进行疲劳强度的计算。
本文将介绍齿轮疲劳强度的计算公式以及相关参数和注意事项。
齿轮疲劳强度计算公式可以通过公式如下表示:\[S = Y \cdot Z \cdot F \cdot Y_N \cdot K_H \cdot K_X \cdot K_V \cdot K_A\]其中,S表示齿轮的疲劳强度,单位为MPa。
下面依次介绍每个参数的含义:Y:齿轮基本强度系数,是齿轮的材料和硬度的函数。
齿轮的基本强度系数可以通过查询相关的标准进行获取。
Z:齿数。
齿数是指齿轮上的齿的数量。
通常情况下,大齿数齿轮的疲劳强度较高。
F:载荷系数。
是描述齿轮所承受载荷大小的参数。
载荷系数可以根据载荷的类型和工况条件进行计算。
Y_N:安全系数。
是为了确保齿轮具有足够的安全边际而引入的。
通常情况下,安全系数会根据齿轮的质量等级和使用条件进行选择。
K_H:应力循环系数。
考虑齿轮在使用过程中遇到高低温、湿润和杂质等因素引起的不同的应力循环。
K_X:位错系数。
表示齿轮的制造精度和装配精度对疲劳强度的影响。
通常情况下,制造工艺的精度越高,位错系数越小。
K_V:动载系数。
描述齿轮承受动载的影响。
K_A:危险系数。
考虑齿轮在特定工况下的工作环境和振动等因素对疲劳强度的影响。
上述的公式中,各个参数的计算方法一般可以参考相关标准、手册和理论知识。
同时,在实际应用中,还需要根据具体情况进行修正和调整。
当计算得到齿轮的疲劳强度之后,通常需要将其与应力计算强度进行比较,以确定齿轮的可靠性。
如果疲劳强度大于应力计算强度,则齿轮在设计工作条件下是可靠的。
然而,如果疲劳强度小于应力计算强度,则需要重新考虑齿轮的材料、设计和制造等方面,以提高其可靠性。
总而言之,齿轮疲劳强度的计算公式是评估齿轮承受载荷能力的一个重要工具。
齿轮疲劳强度计算公式

齿轮疲劳强度计算公式齿轮是一种广泛运用于机械设备传动系统中的机械元件。
由于长时间使用和不可避免的载荷,在齿轮中会出现疲劳现象。
其严重程度甚至可能导致齿轮的失效,因此在齿轮的设计和选择时,需要对齿轮的疲劳强度进行评估和计算。
下面我们介绍一下齿轮疲劳强度的计算公式和相关参考内容。
一、齿轮疲劳强度的计算公式齿轮的疲劳强度指齿轮在循环载荷作用下能承受的极限应力,是齿轮设计时必须考虑的重要参数。
目前,齿轮疲劳强度的计算公式主要包括两种:1. 安全性系数法安全性系数法是齿轮疲劳强度计算中最基本的方法,其计算公式为:S_h = K_h \cdot S_N式中,S_h 为齿轮疲劳强度,K_h 为齿轮强度系数,S_N 为材料的疲劳极限强度。
2. AGMA方法AGMA方法是美国齿轮制造商协会制定的齿轮强度计算方法,其计算公式为:S_h = S_F \cdot S_G \cdot S_I \cdot (1 + S_K \cdot S_H)式中,S_F 为载荷系数,S_G 为几何系数,S_I 为材料系数,S_K 为动载系数,S_H 为表面硬化系数。
二、齿轮疲劳强度计算参考内容齿轮疲劳强度的计算涉及到多个参数和方法,具体参考内容如下:1. 齿轮疲劳强度计算手册近年来,国内外多个机械设计机构纷纷出版齿轮疲劳强度计算手册,内容包括安全性系数法和AGMA方法,详细介绍了齿轮强度计算的各个参数如何确定、如何计算等,是齿轮设计师必备的参考资料。
2. 齿轮强度计算软件为了方便齿轮设计师进行疲劳强度计算,多家厂商推出了齿轮强度计算软件,其中不乏国内外知名企业,如Gearotic、KISSsoft等,可实现齿轮的一些增效功能,如自动计算载荷系数、自动选型等,提高了工作效率。
3. 材料手册齿轮的疲劳强度受到材料性能的影响,因此需要用到材料手册,了解不同种类材料的优缺点、极限应力等数据,为正确选择材料提供参考。
总的来说,齿轮疲劳强度的计算是齿轮设计中不可或缺的环节。
标准直齿圆柱齿轮传动的强度计算

6.3 标准直齿圆柱齿轮传动的强度计算 (一)轮齿的受力分析 进行齿轮的强度计算时,首先要知道齿轮上所受的力,这就需要对齿轮传动作受力分析。
当然,对齿轮传动进行力分析也是计算安装齿轮的轴及轴承时所必需的。
齿轮传动一般均加以润滑,啮合轮齿间的摩擦力通常很小,计算轮齿受力时,可不予考虑。
垂直于齿面,为了计算方便,将法向 沿啮合线作用在齿面上的法向载荷Fn在节点P处分解为两个相互垂直的分力,即圆周力F t与径向力F r, 。
由此载荷Fn得F t=2T1/d1; F r=F t tanα ; FF t/cosα (a)n=—小齿轮传递的转矩,N·mm; 式中:T1—小齿轮的节圆直径,对标准齿轮即为分度圆直径,mm; d1 α—啮合角,对标准齿轮,α=20°。
(二)齿根弯曲疲劳强度计算 轮齿在受载时,齿根所受的弯矩最大 ,因此齿根处的弯曲疲劳强度最弱。
当轮齿在齿顶处啮合时,处于双对齿啮合区,此时弯矩的力臂虽然最大,但力并不是最大,因此弯矩并不是最大。
根据分析,齿根所受的最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。
因此,齿根弯曲强度也应按载荷作用于单对齿啮合区最高点来计算。
由于这种算法比较复杂,通常只用于高精度的齿轮传动(如6级精度以上的齿轮传动)。
对于制造精度较低的齿轮传动(如7,8,9级精度),由于制造误差大,实际上多由在齿顶处啮合的轮齿分担较多的载荷,为便于计算,通常按全部载荷作用于齿顶来计算齿根的弯曲强度。
当然,采用这样的算法,齿轮的弯曲强度比较富余。
右边动画所示为齿轮轮齿啮合时的受载情况。
动画演示为齿顶受载时,轮齿根部的应力图。
下一页 在齿根危险截面AB处的压应力σc仅为弯曲应力σF的百分之几,故可忽略,仅按水平分力p c a cosγ所产生的弯矩进行弯曲强度计算。
假设轮齿为一悬臂梁,则单位齿宽(b=1)时齿根危险截面的弯曲应力为 取,并将(a)式代入。
对直齿圆柱齿轮,齿面上的接触线长L即为齿宽b(mm),得 令 Y Fa是一个无量纲系数,只与齿轮的齿廓形状有关,而与齿的大小(模数m)无关。
齿轮传动强度设计计算

直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 1.齿轮箱外形尺寸不变,n2=3600r/min, m2=4mm,求P2? 弯曲 模数变化4/3,转速变化3600/3000, P2=120*4/3KW 接触 体积不变,转速变化3600/3000,P2=120KW;弯曲变化机理:齿形变大 接触变化机理:P=T*n/9550已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 2.齿轮箱齿数不变,n2=3600r/min, m2=4mm,求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW 接触 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW2 2 2 2弯曲变化机理:力臂和曲率半径增大 接触变化机理:单位齿宽负载和直径增大已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 3.齿轮箱尺寸放大4/3倍,n2=3600r/min, 求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW 接触 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW2 2 3 3弯曲变化机理:齿宽b,模数m增大 接触变化机理:齿宽b,模数m增大已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 4.齿轮材料选用1.2倍σ,n2=3600r/min, 求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*1.2KW 接触 模数变化4/3,转速变化3600/3000, P =120*(1.2) KW2 2 2弯曲变化机理:材料增强 接触变化机理:材料增强已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm。
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
2模数齿轮强度

2模数齿轮强度齿轮是机械传动中常见的元件,其作用是将电机或发动机的转速通过齿轮传递到其他装置上。
而齿轮的强度则是衡量齿轮是否能够承受传动力和传动扭矩的重要指标之一。
本文将以2模数齿轮强度为主题,探讨齿轮强度的相关内容。
一、齿轮强度的概念与意义齿轮强度是指齿轮材料在承受传动力和传动扭矩时的抗弯强度。
齿轮承受的载荷主要有两种:弯曲载荷和接触载荷。
弯曲载荷是由于齿轮的齿向力而引起的,而接触载荷则是由于齿轮齿面间的接触而产生的。
齿轮强度的计算与材料的强度、几何参数以及工作条件等因素密切相关。
齿轮强度的高低直接影响到齿轮的使用寿命和可靠性。
如果齿轮强度不足,容易导致齿轮齿面磨损、齿面断裂等故障,从而影响到机械设备的正常运行。
因此,对于齿轮的设计和选择来说,保证齿轮强度是至关重要的。
二、2模数齿轮强度的计算方法2模数齿轮是常用的一种齿轮规格,其齿距和齿轮齿数的关系可以通过特定的计算公式来确定。
在计算2模数齿轮的强度时,常用的方法有两种:弯曲强度计算和接触强度计算。
1. 弯曲强度计算弯曲强度是指齿轮在承受弯曲载荷时的抗弯能力。
常用的计算公式是根据齿轮的几何参数和材料的弯曲强度来确定的。
具体计算步骤如下:(1)根据齿轮模数、齿轮齿数和压力角等参数计算齿轮的几何参数,包括齿高、齿顶高、齿根高等;(2)根据齿轮的几何参数和材料的弯曲强度,计算齿轮的弯曲强度;(3)将齿轮的弯曲强度与工作条件下的弯曲载荷进行比较,判断齿轮是否强度足够。
2. 接触强度计算接触强度是指齿轮在承受接触载荷时的抗弯能力。
常用的计算公式是根据齿轮的几何参数和材料的接触强度来确定的。
具体计算步骤如下:(1)根据齿轮模数、齿轮齿数和压力角等参数计算齿轮的几何参数,包括齿距、齿顶圆直径等;(2)根据齿轮的几何参数和材料的接触强度,计算齿轮的接触强度;(3)将齿轮的接触强度与工作条件下的接触载荷进行比较,判断齿轮是否强度足够。
三、2模数齿轮强度的改善方法如果在计算中发现2模数齿轮的强度不足,可以通过以下几种方法来改善齿轮的强度:1. 选择更高强度的材料,如使用高强度钢材料制造齿轮;2. 优化齿轮的几何参数,如增加齿轮的齿数、增大齿宽等;3. 改变齿轮的传动方式,如使用多级齿轮传动来降低单级齿轮的载荷;4. 在齿轮表面进行热处理,如渗碳、淬火等,增加齿轮的表面硬度和强度。
齿轮强度计算公式.

二.
1.
2.
设计式:
3.
1)YFa、YSa---齿形系数和应力修正系数。Zv=Z/cos3YFa、YFa
2)Y---螺旋角系数。
3)初步设计计算
在设计式中,K等与齿轮尺寸参数有关,故需初步估算:
d)初取K=Kt
e) 计算mnt
f)修正mn
第8节
一.
二.
1. 锥齿轮设计计算简化
Fa1=Ft1tansin1(=Fr2)
方向:
四.
1.
1)计算公式:
按齿宽中点当量直齿圆柱齿轮计算,并取齿宽为0.85b,则:
以齿轮大端参数代替齿宽中点当量直齿圆柱齿轮参数,代入
整理得:
校核式:
对于a=200的标准齿轮ZH=2.5。
故:
设计式:
2)参数说明
a)K=KAKvKK
Kv---按平均分度圆速度查取。
锥弯曲
思考题
1.什么是开式、闭式齿轮传动?软齿面、硬齿面齿轮传动?
2.齿轮的失效形式有哪些?提高抗轮齿表面失效的措施有哪些?
3.开式齿轮传动的主要失效形式是什么?设计准则是什么?
4.闭式软齿面齿轮传动的主要失效形式是什么?设计准则是什么?
5.齿轮材料的选择及热处理的原则是什么?为什么?
6.已知直齿圆柱齿轮传动小齿轮分度圆直径、扭矩。Ft1=?、Fr1=?、
考虑轮齿啮合时的效率
考虑搅油时的效率
轴承的效率
小
第十二章齿轮传动小结
1.齿轮传动特点
2.分类:开式、闭式、半开式;软(硬)齿面齿轮传动
轮齿折断
疲劳点蚀
3. 失效形式及设计准则磨损
塑性变形
胶合
4.选材及热处理原则
齿轮的强度的计算

齿轮的强度的计算齿轮的设计者根据作用在齿轮上的负荷,旋转数,期待寿命等要素决定齿轮的式样。
在这里,简单的介绍齿轮强度中重要的弯曲强度和齿面强度。
直齿轮及斜齿齿轮的弯曲强度计算公式 JGMA401-01在轮齿上作用了超过极限值的力时,如图所示轮齿会从齿根部出现裂痕以致造成轮齿断裂。
弯曲强度计算公式如下所示。
图 7.1 弯曲应力不足符号名称影响因素/规格等σFlim 容许齿根弯曲应力材料/热处理mn 法向模数轮齿大小b 齿宽齿轮的大小提高弯曲强度需要将容许圆周力计算公式(7.1)中的分母减小,分子增大。
(a)使用高强度材料(容许齿根弯曲压力增加)(b)增大齿轮体积(大模数 / 宽齿面)(c)高强度齿形(减小齿形系数)- 大压力角 - 正变位(d)提高重合率(减小重合度系数)- 小压力角 - 增加齿高(e)提高齿轮精度直齿轮及斜齿齿轮的齿面强度计算公式 JGMA402-01齿面强度是基于齿面的接触应力计算轮齿抵抗点蚀(Pitting)发生的强度。
相对齿面强度的容许圆周力 Ftlim图 7.2 接触应力符号名称影响因素/规格等σHlim 容许接触应力材料/热处理d01 小齿轮的分度圆直径齿轮(小)的大小(直径)bH 有效齿宽齿轮的大小i 齿数比( z2 / z1 )轮齿数的比ZH 区域系数螺旋角/变位系数ZM 材料弹性系数齿轮材料的配合Zε重合度系数端面/纵向重合度Zβ螺旋角系数设为 1.00(未知)ZHL 寿命系数期待寿命ZL 润滑剂系数润滑油及动粘度ZR 粗糙度系数齿面的粗糙度ZV 润滑速度系数圆周速度/表面硬度提高齿面强度需要(a)使用经过淬火处理的硬质材料(增大容许接触应力)(b)增大齿轮体积(大节圆直径/增加有效齿宽)(c)提高重合率(减小重合度系数)(d)提高齿轮精度齿轮的强度计算方法很多, 也比较复杂。
齿轮的强度计算

直齿圆柱齿轮的强度计算受力分析:圆周力F t =112d T 径向力αtan ∙=t r F F 法向载荷αcos t n F F = 1T :小齿轮传递的转矩,mm N ∙ 1d :小齿轮的节圆直径,mm α:啮合角,对标准齿轮, 20=α齿根弯曲疲劳强度的计算: 校核公式:[]F d Sa Fa Sa Fa F z m Y Y KT bmd Y Y KT σφσ≤==21311122 计算公式:[]32112F d Sa Fa z Y Y KT m σφ≥d φ:齿宽系数,1d b d =φ Fa Y :齿形系数 Sa Y :应力校正系数齿面接触疲劳强度的计算: 校核公式:[]H E H uu bd KT Z σσ≤±∙=125.2211 设计公式:[]3211132.2⎪⎪⎭⎫ ⎝⎛∙±∙=H E d Z u u KT d σφ标准斜齿圆柱齿轮的强度计算 受力分析: 圆周力:112d T F T = 径向力:βαcos tan n t r F F ∙= 轴向力:βtan ∙=t a F F齿根弯曲疲劳强度计算: 校核公式:[]F n Sa Fa t F bm Y Y Y KF σεσαβ≤=设计计算:[]32121cos 2F Sa Fa d n Y Y z Y KT m σεφβαβ∙=齿面接触疲劳强度计算: 校核计算:H E H Z Z uu bd KT ∙±∙=111αεσ 设计计算:[]321112⎪⎪⎭⎫ ⎝⎛∙±∙≥H Sa Fa d Y Y u u KT d σεφαu :齿数比标准锥齿轮的强度计算 受力分析:11212m t t d T F F == 121cos tan δαt a r F F F == 121cos tan δαt r a F F F == αcos 1t n F F =齿根弯曲疲劳强度计算: 校核公式:()[]F R Sa Fa t F bm Y Y KF σφσ≤-=5.01 设计公式:()[]32212115.014F Sa Fa R R Y Y u z KT m σφφ∙+-≥齿面接触疲劳强度计算: 校核公式:()[]H R R E H u d KT Z σφφσ≤-=31215.015设计公式:[]()321215.0192.2u KT Z d R R H E φφσ-∙⎪⎪⎭⎫ ⎝⎛≥。
齿轮传动的强度设计计算
1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中,由于赫兹应力是齿面间应力的主要指标,故把赫兹应力作为齿面接触应力的计算基础,并用来评价接触强度。
齿面接触疲劳强度核算时,根据设计要求可以选择不同的计算公式。
用于总体设计和非重要齿轮计算时,可采用简化计算方法;重要齿轮校核时可采用精确计算方法。
分析计算表明,大、小齿轮的接触应力总是相等的。
齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。
实际使用和实验也证明了这一规律的正确。
因此,在齿面接触疲劳强度的计算中,常采用节点的接触应力分析齿轮的接触强度。
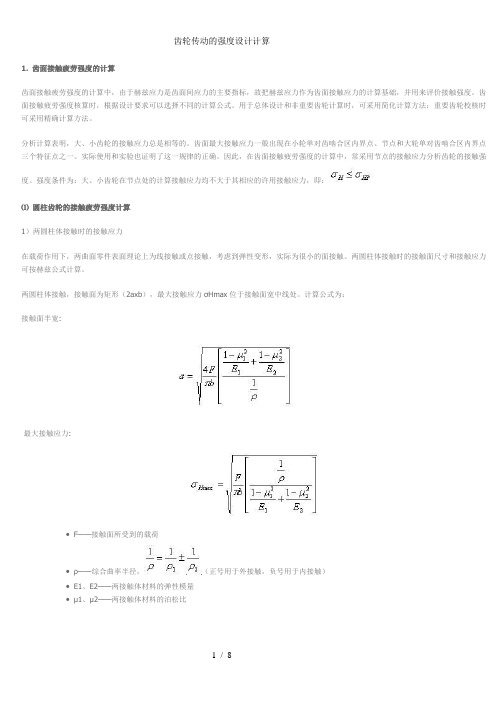
强度条件为:大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力,即:⑴圆柱齿轮的接触疲劳强度计算1)两圆柱体接触时的接触应力在载荷作用下,两曲面零件表面理论上为线接触或点接触,考虑到弹性变形,实际为很小的面接触。
两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。
两圆柱体接触,接触面为矩形(2axb),最大接触应力σHmax位于接触面宽中线处。
计算公式为:接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径,(正号用于外接触,负号用于内接触)•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2)齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况,都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。
在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。
节点附近处的ρ虽然不是最小值,但节点处一般只有一对轮齿啮合,点蚀也往往先在节点附近的齿根表面出现,因此,接触疲劳强度计算通常以节点为最大接触应力计算点。
参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为,3)圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式,并考虑各载荷系数的影响,得到:接触疲劳强度的校核公式为:接触疲劳强度的设计公式为:•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力,N;•T1——端面内分度圆上的名义转矩,N.mm;•d1——小齿轮分度圆直径,mm;•b ——工作齿宽,mm,指一对齿轮中的较小齿宽;•u ——齿数比;•ψd——齿宽系数,指齿宽b和小齿轮分度圆直径的比值(ψd=b/d1)。
齿轮强度的计算

一、轮齿的接触应力ζj 的计算:ζj=0.418√FE(1/ρz+1/ρb )/bF=F1/(cos αcos β)F1=2Tg/dd 为节圆的直径Tg 为计算载荷ρz 、ρb 分别为主从动齿轮节点处的曲率半径:直齿轮:ρz=r z sin α ρb= r b sin α斜齿轮:ρz=(r z sin α)/cos 2β ρb=( r b sin α)/cos 2βr z r b为主,从动齿轮节圆半径 二、轮齿弯曲应力ζw 的计算:直齿轮:ζw=F1K ζK f /bty=2TgK ζK f /πm 3ZK c y斜齿轮:ζw=2Tgcos βK ζ/∏m 3n ZK c yK εK ε为重合度系数,一般取K ε=2.0K ζ集中应力系数,一般直齿轮取K ζ=1.65,斜齿轮取K ζ=1.50y 为齿形系数,一般在0.16---0.18之间K c 为齿宽系数,一般在4.5---8.0之间K f 为摩擦力系数,主动轮取1.1,从动轮取0.9 A B δf Fa LbX一、初选轴的直径已知中心距A。
第二轴与中间轴中部直径:d≈0.45A,轴的最大直径d和支承间距离L的比值:d/L=0.16--0.18;对二轴:d/L=0.18--0.21;第一轴花键部分直径d可按下试初选:d=K 3√T emax式中,K为经验系数,K=4.0---4.6;T emax为发动机最大转矩(N.m)二、轴的强度计算1.轴的刚度计算:轴在垂直面内绕度:f c=F1a2b2/3EIL轴在水平面内绕度:f s=F2a2b2/3EIL轴在水平面内转角: δ=F1ab(b-a)/3EIL式中,F1为齿轮齿宽中间平面上的径向力(N),F2为齿轮齿宽中间平面上的圆周力(N),E为弹性模量,E=2.1×105MPa;I为惯性矩(mm4),对于实心轴,I=πd4/64;d为轴的直径(mm),花键外按平均直径计算;a,b为齿轮上的作用力矩A,B的距离(mm),L为支座间的距离(mm)。
齿面 硬度 强度计算公式

齿面硬度强度计算公式摘要,本文介绍了齿面硬度和强度的计算公式,通过分析齿轮的材料、几何形状和工作条件等因素,计算出齿轮的硬度和强度,为齿轮设计和选型提供了理论依据。
引言。
齿轮是一种常见的传动装置,广泛应用于机械设备中。
齿轮的硬度和强度是影响其使用性能和寿命的重要因素。
通过计算齿轮的硬度和强度,可以为齿轮的设计和选型提供理论依据,保证齿轮在工作条件下具有足够的耐用性和可靠性。
一、齿面硬度计算公式。
齿面硬度是指齿轮齿面的硬度,通常用洛氏硬度(HRC)来表示。
齿面硬度的计算公式如下:HRC = 185 / (T + 18)。
其中,T为齿轮的表面硬度(HB)。
在实际应用中,可以根据齿轮的材料和热处理工艺来确定齿轮的表面硬度,然后通过上述公式计算出齿面硬度,从而评估齿轮的耐磨性和耐用性。
二、齿面强度计算公式。
齿面强度是指齿轮齿面的承载能力,通常用齿面接触应力来表示。
齿面强度的计算公式如下:σH = (2KmF) / (bd)。
其中,σH为齿面接触应力(MPa),Km为齿轮载荷分布系数,F为齿轮传递的力(N),b为齿轮的面宽(mm),d为齿轮的分度圆直径(mm)。
在实际应用中,可以根据齿轮的工作条件和载荷来确定齿轮的载荷分布系数和传递的力,然后通过上述公式计算出齿面接触应力,从而评估齿轮的承载能力和工作可靠性。
三、影响齿面硬度和强度的因素。
1. 材料选择,齿轮的材料直接影响其硬度和强度,通常选择高强度和高硬度的合金钢或表面经过渗碳渗氮处理的材料。
2. 几何形状,齿轮的模数、齿数、齿宽等几何参数会影响其齿面硬度和强度,通常通过几何设计来优化齿轮的硬度和强度。
3. 热处理工艺,热处理工艺可以提高齿轮的硬度和强度,包括淬火、渗碳、渗氮等工艺。
4. 工作条件,齿轮在不同的工作条件下承受不同的载荷和速度,这会影响其齿面硬度和强度的要求。
四、应用实例。
以某型号齿轮为例,其材料为20CrMnTi合金钢,经过渗碳淬火处理,齿轮的模数为3,齿数为20,齿宽为30mm,分度圆直径为60mm,工作条件下承受的力为5000N。
齿轮强度计算载荷系数

齿轮强度计算载荷系数齿轮是机械传动中常用的零件,用于传递和改变力和运动的方向。
在齿轮设计中,强度是一个重要的考虑因素。
齿轮强度的计算涉及到载荷系数的应用。
本文将详细介绍齿轮强度计算中载荷系数的概念、计算方法以及其在齿轮设计中的应用。
一、载荷系数的概念载荷系数是用来衡量齿轮所承受载荷的大小和性质的参数。
它是根据齿轮工作条件和使用要求来确定的。
载荷系数包括动载荷系数、静载荷系数和冲击载荷系数等。
1. 动载荷系数:动载荷系数是用来计算齿轮传递动力时的载荷大小的参数。
它与齿轮传递的功率、转速、传动比等因素有关。
动载荷系数的计算方法一般根据齿轮的标准或经验公式来确定。
2. 静载荷系数:静载荷系数是用来计算齿轮在静止状态下所承受的载荷大小的参数。
它与齿轮的材料、齿轮的几何形状等因素有关。
静载荷系数的计算方法一般考虑齿轮的强度和刚度等因素。
3. 冲击载荷系数:冲击载荷系数是用来计算齿轮在冲击载荷下所承受的载荷大小的参数。
它与齿轮传递的冲击力、冲击时间等因素有关。
冲击载荷系数的计算方法一般根据齿轮的工作条件和使用要求来确定。
二、载荷系数的计算方法载荷系数的计算方法一般根据齿轮的工作条件和使用要求来确定。
具体的计算方法可以通过齿轮的标准或经验公式来确定。
以下是一些常用的计算方法:1. 动载荷系数的计算方法:动载荷系数可以通过齿轮的标准或经验公式来计算。
一般来说,动载荷系数与齿轮的传动功率、转速、传动比等因素有关。
在计算动载荷系数时,需要考虑齿轮的工作条件和使用要求,并根据相关标准或经验公式进行计算。
2. 静载荷系数的计算方法:静载荷系数可以通过齿轮的材料、齿轮的几何形状等因素来计算。
一般来说,静载荷系数与齿轮的材料强度、齿轮的几何形状等因素有关。
在计算静载荷系数时,需要考虑齿轮的强度和刚度等因素,并根据相关标准或经验公式进行计算。
3. 冲击载荷系数的计算方法:冲击载荷系数可以通过齿轮的工作条件和使用要求来计算。
一般来说,冲击载荷系数与齿轮的冲击力、冲击时间等因素有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 正火 正火能消除内应力、细化晶粒、改善力学性能和切
削性能。机械强度要求不高的齿轮可用中碳钢正火处 理。大直径的齿轮可用铸钢正火处理。
5. 渗氮 渗氮是一种化学处理。渗氮后齿面硬度可达
11章 齿轮的强度计算
齿轮强度计算
11-2 齿轮材料及热处理
1.对齿轮材料性能的要求
齿轮的齿体应有较高的抗折断能力,齿面应有较强
的抗点蚀、抗磨损和较高的抗胶合能力,即要求:齿
面硬、芯部韧。
2.常表用11齿-1轮材常料用齿轮材料及其机械性能
钢材的韧性好,耐冲击,通过热处理和化学处理可
改善材料的机械性能,最适于用来制造齿轮。
表面淬火、渗碳淬火、渗氮处理后齿面硬度高,属 硬齿面。其承载能力高,但一般需要磨齿。常用于结 构紧凑的场合。
齿轮强度计算
§11-3 齿轮传动的精度
制造和安装齿轮时,会产生误差,如齿形误差、齿距误 差、齿向误差、两轴线不平行等。
误差对传动带来以下三个方面的影响: 1. 影响传动准确性,啮合齿轮在一转范围内,实际转角与理论转 角不一致。
1.表面淬火 渗氮 一般用于中碳钢和中碳合金钢,如45、40Cr等。表
面淬火后轮齿变形小,可不磨齿,硬度可达52~56HRC, 面硬芯软,能承受一定冲击载荷。
2. 渗碳淬火 渗碳钢为含碳量0.15~0.25%的低碳钢和低碳合金钢,
如20、20Cr等。齿面硬度达56~62HRC,齿面接触强 度高,耐磨性好,齿芯韧性高。常用于受冲击载荷的 重要传动。通常渗碳淬齿火轮强后度计要算 磨齿。
锻钢
含碳量为(0.15~0.6)%的碳素钢或合金钢。 一般用齿轮用碳素钢,重要齿轮用合金钢。
常用齿 轮材料
铸钢 耐磨性及强度较好,常用于大尺寸齿轮。
铸铁
常作为低速、轻载、不太重要的场合的齿 轮材料;
非金属材料齿轮适噪强用声度计于的算 高场速合、。轻载、且要求降低
齿轮材料的热处理和化学处理
表面淬火 ----高频淬火、火焰淬火 渗碳淬火 热处理方法 调质 正火
O(1主动)
1 1 (21) 2(d2 d1) u1 2 1 1 2 12 d1d2 sin u d1si n
齿轮强度计算
钢制标准齿轮传动的齿面接触疲劳强度校核公式:
H335bKa21T(uu1)3 [H]
引入齿宽系数:ψa=b/a 得设计公式: a(u1)3 Ka.uT1 [33]H52 一对齿轮啮合,其接触应力σH反映了大小齿轮在 节点处相互啮合引起的表面应力, σH完全由两轮 的参数共同决定, σH1= σH2 注意:因两个齿轮的σH1= σH2 ,故按此强度准则设计齿 轮传动时,公式中应代入[σH] 1和[σH] 2中较小者。
580 320 650 350 580 290
齿轮强度计算
170~241 187~255 197~269 147~241 229~302
156~217 169~229 162~217
217~255 40~50HRC 241~286 48~55HRC
3.调质 调质一般用于中碳钢和中碳合金钢,如45、40Cr、
α----压力角
齿轮强度计算
二、计算载荷
法向力Fn 为名义载荷
由于制造、安装误差及受载时的变形等影响, 使载荷沿齿宽不是均匀分布,造成载荷局部集中。 轴和轴承的刚度越小、齿宽b越宽,载荷集中越严 重。此外,由于各种原动机和工作机的特性不同等 原因。
计算载荷=KFn K——载荷系数,其值由表11-3查取。
2. 影响传动的平稳性。瞬时传动比不能保持恒定,齿轮在一转 范围内会出现多次重复的转速波动。
3. 齿向误差影响载荷分布均匀性。当传递较大转矩时,易引 起早期损坏。
国标GB10095--88对圆柱齿轮及齿轮副规定了12个精度等级, 其中1级最高,12级最低,常用的是6—9级精度。
表11-2 列出了齿轮传动精度等级的选择及应用。
齿轮强度计算
§11-4 标准直齿圆柱齿轮传动的作用力及计算载荷10-5
为了计算轮齿强度,设计轴和轴承,有必要分析轮齿上的作用力。
一、轮齿受力分析
O2
O2
各作用力的方向如图
α ω2
圆周力: Ft
2T1 d1
径向力:Fr1Fr2Ftt g
法向力:Fn Ft /cos
小齿齿轮强度计算
11-5 直齿圆柱齿轮齿面接触疲劳强度计算 齿轮强度计算是根据齿轮可能出现的失效形式来进行的。在一般 闭式齿轮传动中,轮齿的失效主要是齿面接触疲劳点蚀和轮齿弯
曲疲劳折断。齿面疲劳点蚀与齿面接触应力的大小有关,而齿面
的最大接触应力可近似用赫兹公式进行计算。
1 1 O2
赫兹公式: H
Fn
60~62HRC。氮化处理温度低,轮齿变形小,适用于难 以磨齿的场合,如内齿轮齿轮。强度材计算料为:38CrMoAlA.
特点及应用: 调质、正火处理后的硬度低,HBS ≤ 350,属软齿
面,工艺简单、用于一般传动。当大小齿轮都是软齿 面时,因小轮齿根薄,弯曲强度低,故在选材和热处 理时,小轮比大轮硬度高: 20~50HBS
c
N2 αt t
N1
Fn
d1 T1 2
N1
α
Fr
Fn N2 α
t
c Ft
T1
d1 2
T 116 0 P 19.5 516 0n P 1
α ω1 NmmO(1主动)
α ω1 (主动)
O1
P为传递的功率(KW) ω1----小齿轮上的角速度,
n1----小齿轮上的转速 d1----小齿轮上的分度圆直径,
L
•
1 1 12
2 1 22
α ω2 (从动)
E1
E2
节“+圆”用处于齿外廓啮曲合率,半“径-:”用实生验点于表蚀明,内:故齿取根节啮部点分处合靠的近应节力点作处为最计容算易依发据t。 1N1Cd1s2in 2N2Cd2s2in N1
d2 2
Cc ρ1
α
ρ2 N2 αt
d1 T1 2
ω1
齿数比: u= z2 /z1 = d2 /d1 = ρ2 /ρ1 ≥ 1
表11-1 常用齿轮材料及其机械性能
材料牌号
热处理方法
强度极限
σB / MPa
屈服极限 硬度 (HBS) σS / Mpa 齿芯部 齿面
HT250 HT300 HT350 QT500-5 QT600-2 ZG310-570 ZG340-640
45 45 40Cr
常化
调质后表 面淬火
250 300 350 500 600
