遗传算法与优化问题重要 有代码
智能优化算法 python 解方程

智能优化算法 python 解方程智能优化算法在解方程方面的应用是一项非常有意义的研究领域。
通过利用智能算法,我们可以自动地找到方程的解,大大提高了解方程的效率和准确性。
本文将介绍一些常见的智能优化算法在解方程问题中的应用,并通过Python代码示例来说明其实现方法。
我们来介绍一种常用的智能优化算法——遗传算法。
遗传算法是模拟生物进化过程的一种优化算法。
其基本思想是通过模拟生物的遗传、变异和选择等过程,逐步演化出最优解。
在解方程问题中,遗传算法可以用来寻找方程的根。
下面我们以一个简单的一元二次方程为例,来说明遗传算法在解方程中的应用。
假设我们要解方程:x^2 - 3x + 2 = 0。
首先,我们需要定义一个适应度函数,用来评估每个个体的适应度。
在这个例子中,我们可以使用方程的根与0的距离作为适应度函数的值。
接下来,我们需要定义遗传算法的参数,如种群大小、交叉概率、变异概率等。
然后,我们随机生成初始种群,并通过遗传算法的操作(选择、交叉和变异)对种群进行迭代优化,直到找到满足适应度函数要求的最优解。
下面是使用Python实现遗传算法解方程的示例代码:```pythonimport random# 定义适应度函数def fitness_function(x):return abs(x**2 - 3*x + 2)# 定义遗传算法参数population_size = 100crossover_rate = 0.8mutation_rate = 0.01max_generations = 100# 随机生成初始种群population = [random.uniform(-10, 10) for _ in range(population_size)]# 迭代优化for generation in range(max_generations):# 计算适应度值fitness_values = [fitness_function(x) for x in population]# 选择操作selected_population = random.choices(population, weights=[1/fitness for fitness in fitness_values], k=population_size)# 交叉操作offspring_population = []for i in range(0, population_size, 2):parent1 = selected_population[i]parent2 = selected_population[i+1]if random.random() < crossover_rate:offspring1 = (parent1 + parent2) / 2offspring2 = (parent1 - parent2) / 2else:offspring1 = parent1offspring2 = parent2offspring_population.extend([offspring1,offspring2])# 变异操作for i in range(population_size):if random.random() < mutation_rate:offspring_population[i] += random.uniform(-0.1, 0.1)# 更新种群population = offspring_population# 输出最优解best_solution = min(population, key=fitness_function)print("最优解为:", best_solution)```上述代码通过遗传算法迭代优化的方法,最终得到了方程的最优解。
MATLAB课程遗传算法实验报告及源代码

硕士生考查课程考试试卷考试科目:考生姓名:考生学号:学院:专业:考生成绩:任课老师(签名)考试日期:年月日午时至时《MATLAB 教程》试题:A 、利用MATLAB 设计遗传算法程序,寻找下图11个端点最短路径,其中没有连接端点表示没有路径。
要求设计遗传算法对该问题求解。
ae h kB 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
C 、利用MATLAB 编程实现:三名商人各带一个随从乘船渡河,一只小船只能容纳二人,由他们自己划行,随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人越货,但是如何乘船渡河的大权掌握在商人手中,商人们怎样才能安全渡河?D 、结合自己的研究方向选择合适的问题,利用MATLAB 进行实验。
以上四题任选一题进行实验,并写出实验报告。
选择题目:B 、设计遗传算法求解f (x)极小值,具体表达式如下:321231(,,)5.12 5.12,1,2,3i i i f x x x x x i =⎧=⎪⎨⎪-≤≤=⎩∑ 要求必须使用m 函数方式设计程序。
一、问题分析(10分)这是一个简单的三元函数求最小值的函数优化问题,可以利用遗传算法来指导性搜索最小值。
实验要求必须以matlab 为工具,利用遗传算法对问题进行求解。
在本实验中,要求我们用M 函数自行设计遗传算法,通过遗传算法基本原理,选择、交叉、变异等操作进行指导性邻域搜索,得到最优解。
二、实验原理与数学模型(20分)(1)试验原理:用遗传算法求解函数优化问题,遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法。
其采纳了自然进化模型,从代表问题可能潜在解集的一个种群开始,种群由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体;初始种群产生后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的解:在每一代,概据问题域中个体的适应度大小挑选个体;并借助遗传算子进行组合交叉和主客观变异,产生出代表新的解集的种群。
遗传算法excel

遗传算法excel
遗传算法是一种模拟自然选择和遗传机制的优化算法,它可以
用于解决复杂的优化问题。
在Excel中,可以使用VBA(Visual Basic for Applications)编程语言来实现遗传算法。
下面我将从
几个方面来介绍在Excel中实现遗传算法的基本步骤和方法。
1. 设计遗传算法的基本流程:
遗传算法的基本流程包括初始化种群、选择、交叉、变异和
适应度评估等步骤。
在Excel中,可以使用VBA编写代码来实现这
些步骤。
首先,需要定义个体的编码方式,然后随机生成初始种群。
接着进行选择操作,选择适应度高的个体作为父代,然后进行交叉
和变异操作生成新的个体,最后进行适应度评估,更新种群。
2. 编写VBA代码实现遗传算法:
在Excel中,可以使用VBA编辑器编写代码来实现遗传算法。
首先需要打开Excel,按下Alt + F11组合键打开VBA编辑器,然
后在模块中编写遗传算法的相关代码,包括种群的初始化、选择、
交叉、变异等操作,以及适应度函数的编写。
通过VBA代码,可以
实现遗传算法的各个步骤,并在Excel中进行运行和调试。
3. 应用范围:
在Excel中实现遗传算法可以用于解决各种优化问题,比如旅行商问题、工程优化、资源分配等。
通过编写VBA代码,可以将遗传算法应用到实际的数据分析和决策问题中,帮助优化问题的求解。
总的来说,在Excel中实现遗传算法需要使用VBA编程语言,通过编写相应的代码来实现遗传算法的各个步骤,从而解决各种复杂的优化问题。
希望以上介绍能够对你有所帮助。
(完整版)遗传算法简介及代码详解

遗传算法简述及代码详解声明:本文内容整理自网络,认为原作者同意转载,如有冒犯请联系我。
遗传算法基本内容遗传算法为群体优化算法,也就是从多个初始解开始进行优化,每个解称为一个染色体,各染色体之间通过竞争、合作、单独变异,不断进化。
遗传学与遗传算法中的基础术语比较染色体:又可以叫做基因型个体(individuals)群体/种群(population):一定数量的个体组成,及一定数量的染色体组成,群体中个体的数量叫做群体大小。
初始群体:若干染色体的集合,即解的规模,如30,50等,认为是随机选取的数据集合。
适应度(fitness):各个个体对环境的适应程度优化时先要将实际问题转换到遗传空间,就是把实际问题的解用染色体表示,称为编码,反过程为解码/译码,因为优化后要进行评价(此时得到的解是否较之前解优越),所以要返回问题空间,故要进行解码。
SGA采用二进制编码,染色体就是二进制位串,每一位可称为一个基因;如果直接生成二进制初始种群,则不必有编码过程,但要求解码时将染色体解码到问题可行域内。
遗传算法的准备工作:1) 数据转换操作,包括表现型到基因型的转换和基因型到表现型的转换。
前者是把求解空间中的参数转化成遗传空间中的染色体或者个体(encoding),后者是它的逆操作(decoding)2) 确定适应度计算函数,可以将个体值经过该函数转换为该个体的适应度,该适应度的高低要能充分反映该个体对于解得优秀程度。
非常重要的过程。
遗传算法基本过程为:1) 编码,创建初始群体2) 群体中个体适应度计算3) 评估适应度4) 根据适应度选择个体5) 被选择个体进行交叉繁殖6) 在繁殖的过程中引入变异机制7) 繁殖出新的群体,回到第二步实例一:(建议先看实例二)求 []30,0∈x 范围内的()210-=x y 的最小值1) 编码算法选择为"将x 转化为2进制的串",串的长度为5位(串的长度根据解的精度设 定,串长度越长解得精度越高)。
遗传算法解释及代码(一看就懂)【精品毕业设计】(完整版)

遗传算法( GA , Genetic Algorithm ) ,也称进化算法。
遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。
因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ):包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。
适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。
那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。
这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取);首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。
这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。
遗传算法多目标优化matlab源代码

遗传算法多目标优化matlab源代码遗传算法(Genetic Algorithm,GA)是一种基于自然选择和遗传学原理的优化算法。
它通过模拟生物进化过程,利用交叉、变异等操作来搜索问题的最优解。
在多目标优化问题中,GA也可以被应用。
本文将介绍如何使用Matlab实现遗传算法多目标优化,并提供源代码。
一、多目标优化1.1 多目标优化概述在实际问题中,往往存在多个冲突的目标函数需要同时优化。
这就是多目标优化(Multi-Objective Optimization, MOO)问题。
MOO不同于单一目标优化(Single Objective Optimization, SOO),因为在MOO中不存在一个全局最优解,而是存在一系列的Pareto最优解。
Pareto最优解指的是,在不降低任何一个目标函数的情况下,无法找到更好的解决方案。
因此,在MOO中我们需要寻找Pareto前沿(Pareto Front),即所有Pareto最优解组成的集合。
1.2 MOO方法常见的MOO方法有以下几种:(1)加权和法:将每个目标函数乘以一个权重系数,并将其加和作为综合评价指标。
(2)约束法:通过添加约束条件来限制可行域,并在可行域内寻找最优解。
(3)多目标遗传算法:通过模拟生物进化过程,利用交叉、变异等操作来搜索问题的最优解。
1.3 MOO评价指标在MOO中,我们需要使用一些指标来评价算法的性能。
以下是常见的MOO评价指标:(1)Pareto前沿覆盖率:Pareto前沿中被算法找到的解占总解数的比例。
(2)Pareto前沿距离:所有被算法找到的解与真实Pareto前沿之间的平均距离。
(3)收敛性:算法是否能够快速收敛到Pareto前沿。
二、遗传算法2.1 遗传算法概述遗传算法(Genetic Algorithm, GA)是一种基于自然选择和遗传学原理的优化算法。
它通过模拟生物进化过程,利用交叉、变异等操作来搜索问题的最优解。
遗传算法matlab程序代码

遗传算法matlab程序代码遗传算法是一种优化算法,用于在给定的搜索空间中寻找最优解。
在Matlab中,可以通过以下代码编写一个基本的遗传算法:% 初始种群大小Npop = 100;% 搜索空间维度ndim = 2;% 最大迭代次数imax = 100;% 初始化种群pop = rand(Npop, ndim);% 最小化目标函数fun = @(x) sum(x.^2);for i = 1:imax% 计算适应度函数fit = 1./fun(pop);% 选择操作[fitSort, fitIndex] = sort(fit, 'descend');pop = pop(fitIndex(1:Npop), :);% 染色体交叉操作popNew = zeros(Npop, ndim);for j = 1:Npopparent1Index = randi([1, Npop]);parent2Index = randi([1, Npop]);parent1 = pop(parent1Index, :);parent2 = pop(parent2Index, :);crossIndex = randi([1, ndim-1]);popNew(j,:) = [parent1(1:crossIndex),parent2(crossIndex+1:end)];end% 染色体突变操作for j = 1:NpopmutIndex = randi([1, ndim]);mutScale = randn();popNew(j, mutIndex) = popNew(j, mutIndex) + mutScale;end% 更新种群pop = [pop; popNew];end% 返回最优解[resultFit, resultIndex] = max(fit);result = pop(resultIndex, :);以上代码实现了一个简单的遗传算法,用于最小化目标函数x1^2 + x2^2。
遗传算法及其MATLAB程序代码

遗传算法及其MATLAB程序代码遗传算法及其MATLAB实现主要参考书:MATLAB 6.5 辅助优化计算与设计飞思科技产品研发中⼼编著电⼦⼯业出版社2003.1遗传算法及其应⽤陈国良等编著⼈民邮电出版社1996.6主要内容:遗传算法简介遗传算法的MATLAB实现应⽤举例在⼯业⼯程中,许多最优化问题性质⼗分复杂,很难⽤传统的优化⽅法来求解.⾃1960年以来,⼈们对求解这类难解问题⽇益增加.⼀种模仿⽣物⾃然进化过程的、被称为“进化算法(evolutionary algorithm)”的随机优化技术在解这类优化难题中显⽰了优于传统优化算法的性能。
⽬前,进化算法主要包括三个研究领域:遗传算法、进化规划和进化策略。
其中遗传算法是迄今为⽌进化算法中应⽤最多、⽐较成熟、⼴为⼈知的算法。
⼀、遗传算法简介遗传算法(Genetic Algorithm, GA)最先是由美国Mic-hgan⼤学的John Holland于1975年提出的。
遗传算法是模拟达尔⽂的遗传选择和⾃然淘汰的⽣物进化过程的计算模型。
它的思想源于⽣物遗传学和适者⽣存的⾃然规律,是具有“⽣存+检测”的迭代过程的搜索算法。
遗传算法以⼀种群体中的所有个体为对象,并利⽤随机化技术指导对⼀个被编码的参数空间进⾏⾼效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定等5个要素组成了遗传算法的核⼼内容。
遗传算法的基本步骤:遗传算法是⼀种基于⽣物⾃然选择与遗传机理的随机搜索算法,与传统搜索算法不同,遗传算法从⼀组随机产⽣的称为“种群(Population)”的初始解开始搜索过程。
种群中的每个个体是问题的⼀个解,称为“染⾊体(chromos ome)”。
染⾊体是⼀串符号,⽐如⼀个⼆进制字符串。
这些染⾊体在后续迭代中不断进化,称为遗传。
在每⼀代中⽤“适值(fitness)”来测量染⾊体的好坏,⽣成的下⼀代染⾊体称为后代(offspring)。
遗传算法和粒子群算法结合代码python

遗传算法和粒子群算法结合代码python遗传算法和粒子群算法是两种非常实用的优化算法,在实际应用中具有广泛的适用性。
在本篇文章中,我们将介绍如何将遗传算法和粒子群算法结合起来,以实现更加高效和准确的优化过程。
具体来说,我们将以python语言为基础,编写代码来实现这种结合。
1. 遗传算法遗传算法是一种类似于进化过程的优化算法,它通过模拟生物进化过程来实现优化。
基本思路是将问题的可行解按照一定的方式编码成染色体序列,然后通过交叉、变异等操作产生新的染色体,按照适应度进行筛选,最终得出最优解。
在python中,我们可以使用遗传算法库DEAP(Distributed Evolutionary Algorithms in Python)快速地实现遗传算法。
以下是一段使用DEAP库实现遗传算法的代码:```import randomfrom deap import base, creator, tools# 定义一个求最小值的适应度函数def eval_func(individual):return sum(individual),# 创建遗传算法工具箱creator.create("FitnessMin", base.Fitness, weights=(-1.0,))creator.create("Individual", list, fitness=creator.FitnessMin)toolbox = base.Toolbox()# 注册染色体初始化函数(0或1)toolbox.register("attr_bool", random.randint, 0, 1)# 定义遗传算法实现函数def ga_algorithm():pop = toolbox.population(n=50)CXPB, MUTPB, NGEN = 0.5, 0.2, 50# 迭代遗传算法for gen in range(NGEN):# 交叉offspring = tools.cxBlend(pop, alpha=0.1)# 变异for mutant in offspring:if random.random() < MUTPB:toolbox.mutate(mutant)del mutant.fitness.values# 评估适应度fits = toolbox.map(toolbox.evaluate, offspring)for fit, ind in zip(fits, offspring):ind.fitness.values = fit# 选择pop = toolbox.select(offspring + pop, k=len(pop))gen_count += 1# 输出每代最小适应度和均值fits = [ind.fitness.values[0] for ind in pop]print("第 %d 代:最小适应度 %f, 平均适应度 %f" % (gen_count, min(fits), sum(fits) / len(pop)))# 返回最优解best_ind = tools.selBest(pop, 1)[0]print("最优解:", best_ind)```上述代码中,我们首先定义了一个求最小值的适应度函数,然后使用DEAP库创建了遗传算法工具箱。
遗传算法matlab代码

function youhuafunD=code;N=50; % Tunablemaxgen=50; % Tunablecrossrate=0.5; %Tunablemuterate=0.08; %Tunablegeneration=1;num = length(D);fatherrand=randint(num,N,3);score = zeros(maxgen,N);while generation<=maxgenind=randperm(N-2)+2; % 随机配对交叉A=fatherrand(:,ind(1:(N-2)/2));B=fatherrand(:,ind((N-2)/2+1:end));% 多点交叉rnd=rand(num,(N-2)/2);ind=rnd tmp=A(ind);A(ind)=B(ind);B(ind)=tmp;% % 两点交叉% for kk=1:(N-2)/2% rndtmp=randint(1,1,num)+1;% tmp=A(1:rndtmp,kk);% A(1:rndtmp,kk)=B(1:rndtmp,kk);% B(1:rndtmp,kk)=tmp;% endfatherrand=[fatherrand(:,1:2),A,B];% 变异rnd=rand(num,N);ind=rnd [m,n]=size(ind);tmp=randint(m,n,2)+1;tmp(:,1:2)=0;fatherrand=tmp+fatherrand;fatherrand=mod(fatherrand,3);% fatherrand(ind)=tmp;%评价、选择scoreN=scorefun(fatherrand,D);% 求得N个个体的评价函数score(generation,:)=scoreN;[scoreSort,scoreind]=sort(scoreN);sumscore=cumsum(scoreSort);sumscore=sumscore./sumscore(end);childind(1:2)=scoreind(end-1:end);for k=3:Ntmprnd=rand;tmpind=tmprnd difind=[0,diff(t mpind)];if ~any(difind)difind(1)=1;endchildind(k)=scoreind(logical(difind));endfatherrand=fatherrand(:,childind);generation=generation+1;end% scoremaxV=max(score,[],2);minV=11*300-maxV;plot(minV,'*');title('各代的目标函数值');F4=D(:,4);FF4=F4-fatherrand(:,1);FF4=max(FF4,1);D(:,5)=FF4;save DData Dfunction D=codeload youhua.mat% properties F2 and F3F1=A(:,1);F2=A(:,2);F3=A(:,3);if (max(F2)>1450)||(min(F2)<=900)error('DATA property F2 exceed it''s range(900,1450]')end% get group property F1 of data, according to F2 value F4=zeros(size(F1));for ite=11:-1:1index=find(F2<=900+ite*50);F4(index)=ite;endD=[F1,F2,F3,F4];function ScoreN=scorefun(fatherrand,D)F3=D(:,3);F4=D(:,4);N=size(fatherrand,2);FF4=F4*ones(1,N);FF4rnd=FF4-fatherrand;FF4rnd=max(FF4rnd,1);ScoreN=ones(1,N)*300*11;% 这里有待优化for k=1:NFF4k=FF4rnd(:,k);for ite=1:11F0index=find(FF4k==ite);if ~isempty(F0index)tmpMat=F3(F0index);tmpSco=sum(tmpMat);ScoreBin(ite)=mod(tmpSco,300);endendScorek(k)=sum(ScoreBin);endScoreN=ScoreN-Scorek;遗传算法实例:% 下面举例说明遗传算法 %% 求下列函数的最大值 %% f(x)=10*sin(5x)+7*cos(4x) x∈[0,10] %% 将 x 的值用一个10位的二值形式表示为二值问题,一个10位的二值数提供的分辨率是每为 (10-0)/(2^10-1)≈0.01 。
遗传算法介绍并附上Matlab代码
1、遗传算法介绍遗传算法,模拟达尔文进化论的自然选择和遗产学机理的生物进化构成的计算模型,一种不断选择优良个体的算法。
谈到遗传,想想自然界动物遗传是怎么来的,自然主要过程包括染色体的选择,交叉,变异(不明白这个的可以去看看生物学),这些操作后,保证了以后的个基本上是最优的,那么以后再继续这样下去,就可以一直最优了。
2、解决的问题先说说自己要解决的问题吧,遗传算法很有名,自然能解决的问题很多了,在原理上不变的情况下,只要改变模型的应用环境和形式,基本上都可以。
但是遗传算法主要还是解决优化类问题,尤其是那种不能直接解出来的很复杂的问题,而实际情况通常也是这样的。
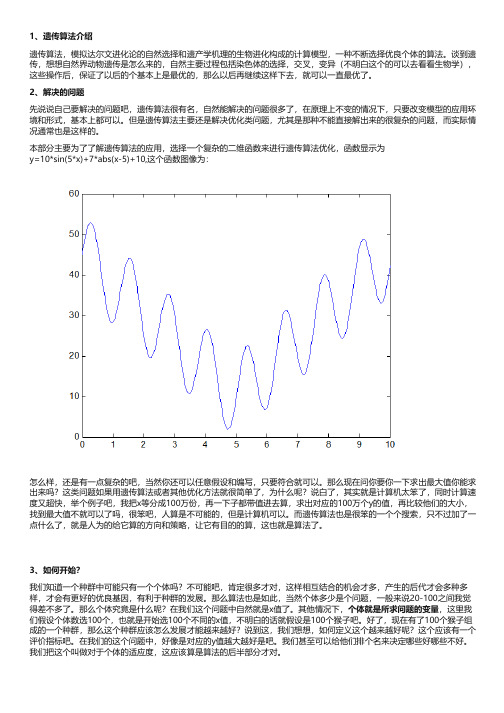
本部分主要为了了解遗传算法的应用,选择一个复杂的二维函数来进行遗传算法优化,函数显示为y=10*sin(5*x)+7*abs(x-5)+10,这个函数图像为:怎么样,还是有一点复杂的吧,当然你还可以任意假设和编写,只要符合就可以。
那么现在问你要你一下求出最大值你能求出来吗?这类问题如果用遗传算法或者其他优化方法就很简单了,为什么呢?说白了,其实就是计算机太笨了,同时计算速度又超快,举个例子吧,我把x等分成100万份,再一下子都带值进去算,求出对应的100万个y的值,再比较他们的大小,找到最大值不就可以了吗,很笨吧,人算是不可能的,但是计算机可以。
而遗传算法也是很笨的一个个搜索,只不过加了一点什么了,就是人为的给它算的方向和策略,让它有目的的算,这也就是算法了。
3、如何开始?我们知道一个种群中可能只有一个个体吗?不可能吧,肯定很多才对,这样相互结合的机会才多,产生的后代才会多种多样,才会有更好的优良基因,有利于种群的发展。
那么算法也是如此,当然个体多少是个问题,一般来说20-100之间我觉得差不多了。
那么个体究竟是什么呢?在我们这个问题中自然就是x值了。
其他情况下,个体就是所求问题的变量,这里我们假设个体数选100个,也就是开始选100个不同的x值,不明白的话就假设是100个猴子吧。
21装配生产线任务平衡问题的遗传算法MATLAB源代码

装配生产线任务平衡问题的遗传算法MATLAB源代码下面的源码实现了装配生产线任务平衡优化问题(ALB问题)的遗传算法,算法主要参考下面这篇文献,并对其进行了改进。
陈永卿,潘刚,李平.基于混合遗传算法的装配线平衡[J].机电工程,2008,25(4):60-62.。
function[BestX,BestY,BestZ,AllFarm,LC1,LC2,LC3,LC4,LC5]=GSAALB(M,N,Pm,Pd,K,t0,alpha,TaskP, TaskT,TaskV,RT,RV)% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%% 装配生产线任务平衡问题的遗传算法%% 输入参数列表% M------------遗传算法进化代数% N------------种群规模,取偶数% Pm-----------变异概率调节参数% Pd-----------变异程度调节参数,0<Pd<1,越大,变异的基因位越多% K------------同一温度下状态跳转次数% T0-----------初始温度% Alpha--------降温系数% Beta---------浓度均衡系数% TaskP--------任务优先矩阵,n×n矩阵,Pij=1表示任务i需在j之前完成,Pij=0时任务i 和j没有优先关系% TaskT--------任务时间属性,n×1向量% TaskV--------任务体积属性,n×1向量% RT-----------时间节拍约束% RV-----------工位体积约束%% 输出参数列表% BestX--------最好个体的编码% BestY--------最好个体对应的装配方案% BestZ--------最好个体的目标函数值% LC1----------最优个体适应值的收敛曲线,M×1% LC2----------种群平均适应值的收敛曲线,M×1% LC3----------工位个数收敛曲线,M×1% LC4----------时间利用率及平衡度综合度量参数收敛曲线,M×1% LC5----------空间利用率及平衡度综合度量参数收敛曲线,M×1% AllFarm------各代种群的集合,M×1的细胞结构%% -----------------------初始化----------------------------------n=size(TaskP,1);[AA,BB]=QJHJ(TaskP);%调用子函数,建立每一个任务的前任务集和后任务集farm=Initialization(N,TaskP,AA,BB);%调用子函数,种群初始化%输出参数初始化BestX=zeros(1,n);BestY=zeros(1,n);BestZ=0;LC1=zeros(M,1);LC2=zeros(M,1);LC3=zeros(M,1);LC4=zeros(M,1);LC5=zeros(M,1);AllFarm=cell(M,1);%控制参数初始化m=1;%迭代计数器t=t0;%温度指示器BestPos=1;%初始时任意指定被保护个体%% -----------------------迭代过程---------------------------------while m<=M%设置停止条件%% ----------------------变异退火算子------------------------------for i=1:Nif rand>Pm&&i~=BestPos%如果随机数大于变异概率门限值,并且不属于保护个体,就对其实施变异I=farm(i,:);%取出该个体k=1;while k<=K%每一个温度下的状态转移次数%调用变异子函数J=Mutation(I,Pd,AA,BB);%调用计算适应值子函数[YI,ZI,FI,TGWI,VGWI,f1I,f2I]=Fitness(I,TaskT,TaskV,RT,RV);[YJ,ZJ,FJ,TGWJ,VGWJ,f1J,f2J]=Fitness(J,TaskT,TaskV,RT,RV);if FJ>FIfarm(i,:)=J;elseif rand<exp((FJ-FI)/(FI*t))farm(i,:)=J;elsefarm(i,:)=I;endk=k+1;endendend%% -----------------------交叉算子---------------------------------newfarm=zeros(size(farm));Ser=randperm(N);%用这个函数保证随机配对for i=1:2:(N-1)FA=farm(Ser(i),:);FB=farm(Ser(i+1),:);[SA,SB]=CrossOver(FA,FB);newfarm(i,:)=SA;newfarm(i+1,:)=SB;end%新旧种群合并FARM=[farm;newfarm];%% -----------------------选择复制--------------------------------- FIT_Y=zeros(2*N,n);FIT_Z=zeros(2*N,1);FIT_F=zeros(2*N,1);FIT_f1=zeros(2*N,1);FIT_f2=zeros(2*N,1);fit_Y=zeros(N,n);fit_Z=zeros(N,1);fit_F=zeros(N,1);fit_f1=zeros(N,1);fit_f2=zeros(N,1);for i=1:(2*N)XX=FARM(i,:);[Y,Z,F,TGW,VGW,f1,f2]=Fitness(XX,TaskT,TaskV,RT,RV);FIT_Y(i,:)=Y;FIT_Z(i)=Z;FIT_F(i)=F;FIT_f1(i)=f1;FIT_f2(i)=f2;endSer=randperm(2*N);for i=1:Nff1=FIT_F(Ser(2*i-1));ff2=FIT_F(Ser(2*i));if ff1>=ff2farm(i,:)=FARM(Ser(2*i-1),:);fit_Y(i,:)=FIT_Y(Ser(2*i-1),:);fit_Z(i)=FIT_Z(Ser(2*i-1));fit_F(i)=FIT_F(Ser(2*i-1));fit_f1(i)=FIT_f1(Ser(2*i-1));fit_f2(i)=FIT_f2(Ser(2*i-1));elsefarm(i,:)=FARM(Ser(2*i),:);fit_Y(i,:)=FIT_Y(Ser(2*i),:);fit_Z(i)=FIT_Z(Ser(2*i));fit_F(i)=FIT_F(Ser(2*i));fit_f1(i)=FIT_f1(Ser(2*i));fit_f2(i)=FIT_f2(Ser(2*i));endend%% -----------------------记录与更新------------------------------- maxF=max(fit_F);meanF=mean(fit_F);LC1(m)=maxF;LC2(m)=meanF;pos=find(fit_F==maxF);BestPos=pos(1);BestX=farm(BestPos,:);BestY=fit_Y(BestPos,:);BestZ=fit_Z(BestPos);LC3(m)=fit_Z(BestPos);LC4(m)=fit_f1(BestPos);LC5(m)=fit_f2(BestPos);AllFarm{m}=farm;disp(m);m=m+1;t=t*alpha;end源代码运行结果展示。
人工智能遗传算法及python代码实现

人工智能遗传算法及python代码实现人工智能遗传算法是一种基于生物遗传进化理论的启发式算法,常用于求解复杂的优化问题。
它的基本思想是通过自然选择和基因交叉等机制,在种群中不断进化出适应性更强的个体,最终找到问题的最优解。
遗传算法通常由以下几个步骤组成:1. 初始化种群:从问题空间中随机生成一组解作为初始种群。
2. 评价适应度:利用一个适应度函数来评价每个解的适应性,通常是优化问题的目标函数,如最小化代价、最大化收益等。
3. 选择操作:从种群中选择一些具有较高适应度的个体用于产生新的种群。
选择操作通常采用轮盘赌选择方法或精英选择方法。
4. 交叉操作:将两个个体的染色体进行交叉、重组,生成新的子代个体。
5. 变异操作:对新产生的子代个体随机变异一些基因,以增加种群的多样性。
6. 生成新种群:用选择、交叉和变异操作产生新的种群,并进行适应度评价。
7. 终止条件:如果达到终止条件,算法停止,否则返回步骤3。
遗传算法的优点是可以适应各种优化问题,并且求解精度较高。
但由于其需要进行大量的随机操作,因此效率相对较低,也较容易陷入局部最优解。
在实际应用中,遗传算法常与其他算法结合使用,以求得更好的结果。
以下是使用Python实现基本遗传算法的示例代码:import randomimport math# 定义适应度函数,用于评价每个个体的适应程度def fitness_func(x):return math.cos(20 * x) + math.sin(3 * x)# 执行遗传算法def genetic_algorithm(pop_size, chrom_len, pcross, pmutate, generations):# 初始化种群population = [[random.randint(0, 1) for j in range(chrom_len)] for i in range(pop_size)]# 迭代指定代数for gen in range(generations):# 评价种群中每个个体的适应度fits = [fitness_func(sum(population[i]) / (chrom_len * 1.0)) for i in range(pop_size)]# 选择操作:轮盘赌选择roulette_wheel = []for i in range(pop_size):fitness = fits[i]roulette_wheel += [i] * int(fitness * 100)parents = []for i in range(pop_size):selected = random.choice(roulette_wheel)parents.append(population[selected])# 交叉操作:单点交叉for i in range(0, pop_size, 2):if random.uniform(0, 1) < pcross:pivot = random.randint(1, chrom_len - 1)parents[i][pivot:], parents[i+1][pivot:] = parents[i+1][pivot:], parents[i][pivot:]# 变异操作:随机翻转一个基因for i in range(pop_size):for j in range(chrom_len):if random.uniform(0, 1) < pmutate:parents[i][j] = 1 - parents[i][j]# 生成新种群population = parents# 返回种群中适应度最高的个体的解fits = [fitness_func(sum(population[i]) / (chrom_len * 1.0)) for i in range(pop_size)]best = fits.index(max(fits))return sum(population[best]) / (chrom_len * 1.0)# 测试遗传算法print("Result: ", genetic_algorithm(pop_size=100, chrom_len=10, pcross=0.9, pmutate=0.1, generations=100))上述代码实现了遗传算法,以优化余弦函数和正弦函数的和在某个区间内的最大值。
基于遗传算法PID控制寻优实现(有代码超详细)

基于遗传优化算法对离散PID控制器参数的优化设计摘要PID控制作为一种经典的控制方法,从诞生至今,历经数十年的发展和完善,因其优越的控制性能业已成为过程控制领域最为广泛的控制方法;PID控制器具有结构简单、适应性强、不依赖于被控对象的精确模型、鲁棒性较强等优点,其控制性能直接关系到生产过程的平稳高效运行,因此对PID控制器设计和参数整定问题的研究不但具有理论价值更具有很大的实践意义,遗传算法是一种借鉴生物界自然选择和自然遗传学机理上的迭代自适应概率性搜索算法。
本论文主要应用遗传算法对PID调节器参数进行优化。
关键词:遗传优化算法PID控制器参数优化1.前言PID调节器是最早发展起来的控制策略之一,因为它所涉及的设计算法和控制结构都是简单的,并且十分适用于工程应用背景,此外PID控制方案并不要求精确的受控对象的数学模型,且采用PID控制的控制效果一般是比较令人满意的,所以在工业实际应用中,PID调节器是应用最为广泛的一种控制策略,也是历史最久、生命力最强的基本控制方式。
调查结果表明: 在当今使用的控制方式中,PID型占84. 5% ,优化PID型占68%,现代控制型占有15%,手动控制型66%,人工智能(AI)型占0.6% 。
如果把PID型和优化PID型二者加起来,则占90% 以上,这说明PID控制方式占绝大多数,如果把手动控制型再与上述两种加在一起,则占97.5% ,这说明古典控制占绝大多数。
就连科学技术高度发达的日本,PID控制的使用率也高达84.5%。
这是由于理论分析及实际运行经验已经证明了PID调节器对于相当多的工业过程能够起到较为满足的控制效果。
它结构简单、适用面广、鲁棒性强、参数易于调整、在实际中容易被理解和实现、在长期应用中己积累了丰富的经验。
特别在工业过程中,由于控制对象的精确数学模型难以建立,系统的参数又经常发生变化,运用现代控制理论分析综合要耗费很大的代价进行模型辨识,但往往不能达到预期的效果,所以不论常规调节仪表还是数字智能仪表都广泛采用这种调节方式。
遗传算法挖掘因子 python代码

遗传算法是一种优化搜索技术,它是通过模拟自然选择和遗传过程来寻找最优解的。
以下是一个使用Python实现的简单遗传算法的例子,用于挖掘因子。
pythonimport numpy as np# 适应度函数def fitness_function(solution):# 此处是一个例子,具体的适应度函数应根据你的问题来定义return sum(solution)# 遗传算法def genetic_algorithm(population_size, gene_length, generations):# 初始化种群population = np.random.randint(2, size=(population_size, gene_length))for generation in range(generations):# 计算适应度值fitness = np.array([fitness_function(ind) for ind in population])# 选择操作parents = population[np.random.choice(population_size, population_size, replace=False)][:, np.random.choice(gene_length, gene_length, replace=False)] parents = parents[(fitness[np.arange(population_size)[:, None], parents] > fitness[parents, np.arange(gene_length)]).all()]# 交叉操作children = np.empty((0, gene_length), dtype=int)while len(children) < population_size:parent1 = parents[np.random.randint(0, len(parents))]parent2 = parents[np.random.randint(0, len(parents))]if parent1 != parent2:child = np.where(np.random.randint(2, size=(gene_length, 2)) > 0, parent1, parent2)children = np.append(children, child, axis=0)parents = np.delete(parents, np.where((parents == parent1).all() | (parents == parent2).all())[0])population = children# 变异操作for i in range(population_size):if np.random.rand() < 0.01: # 变异率可以根据实际情况调整for j in range(gene_length):if np.random.rand() < 0.5: # 变异点可以在这里调整population[i][j] = 1 if population[i][j] == 0 else 0 # 返回最优解return population[np.argmax(fitness)]# 运行遗传算法best_solution = genetic_algorithm(100, 10, 1000)print("Best solution:", best_solution)print("Best solution fitness:", fitness_function(best_solution))注意:这只是一个基础的遗传算法实现,实际应用中可能需要进行更复杂的操作,例如更复杂的编码方式、更复杂的交叉和变异操作、精英策略等。
matlab遗传算法函数

matlab遗传算法函数MATLAB遗传算法函数是一种高效的优化算法,它基于生物学的遗传进程和自然选择机制建立数学模型,并利用进化算法中的遗传操作和适应度评估方法,搜索最优的解。
该算法广泛应用于多个领域,如工程优化、控制系统、机器学习、生物信息学、图象处理等。
本文将对常用的MATLAB遗传算法函数进行描述和介绍。
1. ga(遗传算法)ga是MATLAB中常用的遗传算法函数,用于寻找多目标函数的最优解。
这个函数可以用来解决最优化问题,包括线性优化、非线性优化、混合整数线性优化等。
例如,如果需要在约束条件下最小化一个多项式函数,可以使用以下代码:x = ga(fun, nvars, A, b, Aeq, beq, lb, ub, nonlcon, options)其中,fun是目标函数,nvars是决策变量的数量,A和b是线性不等式限制条件,Aeq和beq是线性等式限制条件,lb和ub是变量的上下限非线性限制条件由nonlcon定义,options 是定义遗传算法的参数和配置的结构体数组。
3. gaoptimset(算法选项)gaoptimset函数是用于设置MATLAB遗传算法函数的选项和参数的函数。
通过修改选项,可以控制遗传算法的行为和表现。
常用的选项包括:PopulationSize:种群大小Generations:进化代数CrossoverFraction:交叉概率EliteCount:精英个数MutationFcn:变异函数SelectionFcn:选择函数例如,以下代码设置种群大小为50、进化代数为100、交叉概率为0.8、精英个数为2、变异函数为mutationuniform:options =gaoptimset('PopulationSize',50,'Generations',100,'CrossoverFraction',0.8,'Elit eCount',2,'MutationFcn',@mutationuniform);4. mutationgaussian(高斯变异)mutationgaussian是MATLAB中默认的变异函数之一,它可以引入随机扰动以增加解的多样性。
遗传算法求解选址问题的python代码

遗传算法求解选址问题的python代码选址问题是一种组合优化问题,其中目标是最小化总成本,总成本通常由多个因素决定,例如运输成本、设施成本等。
遗传算法是一种启发式搜索算法,可以用于求解这类问题。
以下是一个使用遗传算法求解选址问题的Python代码示例:```pythonimport numpy as npimport random定义适应度函数def fitness_func(individual):计算总成本total_cost = 0for i in range(len(individual) - 1):total_cost += abs(individual[i] - individual[i + 1])total_cost += abs(individual[-1] - individual[0])return total_cost定义遗传算法参数pop_size = 100 种群大小chrom_length = 10 染色体长度(即候选地址数量)num_generations = 100 迭代次数mutation_rate = 变异率初始化种群pop = (0, chrom_length, (pop_size, chrom_length))进行迭代进化for generation in range(num_generations):计算适应度值fitness = ([fitness_func(chrom) for chrom in pop]) 选择操作:轮盘赌选择法idx = (pop_size, size=pop_size, replace=True, p=fitness/()) pop = pop[idx]交叉操作:单点交叉for i in range(0, pop_size, 2):if () < :cross_point = (1, chrom_length-1)temp = pop[i][:cross_point] + pop[i+1][cross_point:]pop[i] = temppop[i+1] = temp[::-1]变异操作:位反转变异法for i in range(pop_size):if () < mutation_rate:flip_point = (0, chrom_length-1)pop[i][flip_point] = pop[i][flip_point] + (1 if pop[i][flip_point] % 2 == 0 else -1) % chrom_length```。
matlab智能算法代码

matlab智能算法代码MATLAB是一种功能强大的数值计算和科学编程软件,它提供了许多智能算法的实现。
下面是一些常见的智能算法及其在MATLAB中的代码示例:1. 遗传算法(Genetic Algorithm):MATLAB中有一个专门的工具箱,称为Global Optimization Toolbox,其中包含了遗传算法的实现。
以下是一个简单的遗传算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置遗传算法参数。
options = gaoptimset('Display', 'iter','PopulationSize', 50);% 运行遗传算法。
[x, fval] = ga(fitness, 1, options);2. 粒子群优化算法(Particle Swarm Optimization):MATLAB中也有一个工具箱,称为Global Optimization Toolbox,其中包含了粒子群优化算法的实现。
以下是一个简单的粒子群优化算法示例代码:matlab.% 定义目标函数。
fitness = @(x) x^2;% 设置粒子群优化算法参数。
options = optimoptions('particleswarm', 'Display','iter', 'SwarmSize', 50);% 运行粒子群优化算法。
[x, fval] = particleswarm(fitness, 1, [], [], options);3. 支持向量机(Support Vector Machine):MATLAB中有一个机器学习工具箱,称为Statistics and Machine Learning Toolbox,其中包含了支持向量机的实现。
遗传算法优化的matlab案例

遗传算法(Genetic Algorithm,GA)是一种模拟生物进化过程的搜索和优化算法,通过模拟生物的遗传、交叉和变异操作来寻找问题的最优解。
它以一种迭代的方式生成和改进解决方案,并通过评估每个解决方案的适应度来选择下一代解决方案。
在Matlab中,遗传算法优化工具箱提供了方便的函数和工具,可以帮助用户快速开发和实现遗传算法优化问题。
下面,我们以一个简单的最优化问题为例,演示在Matlab中如何使用遗传算法优化工具箱进行优化。
假设我们要优化一个简单的函数f(x),其中x是一个实数。
我们的目标是找到使得f(x)取得最小值的x值。
具体来说,我们将优化以下函数: f(x) = x² - 4x + 4首先,我们在Matlab中定义目标函数f(x)的句柄(用于计算函数值)和约束条件(如果有的话)。
代码如下:function y = testfunction(x)y = x^2 - 4*x + 4;end接下来,我们需要使用遗传算法优化工具箱的函数ga来进行优化。
我们需要指定目标函数的句柄、变量的取值范围和约束条件(如果有的话),以及其他一些可选参数。
以下是一个示例代码:options = gaoptimset('Display', 'iter'); % 设置显示迭代过程lb = -10; % 变量下界ub = 10; % 变量上界[x, fval] = ga(@testfunction, 1, [], [], [], [], lb, ub, [], options);在上面的代码中,gaoptimset函数用于设置遗传算法的参数。
在这里,我们使用了可选参数'Display',它的值设置为'iter',表示显示迭代过程。
变量lb和ub分别指定了变量的取值范围,我们在这里将其设置为-10到10之间的任意实数。
横线[]表示没有约束条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验十遗传算法与优化问题一、问题背景与实验目的遗传算法(Genetic Algorithm —GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是由美国Michigan大学的J.Holland教授于1975 年首先提出的•遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理及应用范围广等显著特点,奠定了它作为21世纪关键智能计算之一的地位.本实验将首先介绍一下遗传算法的基本理论,然后用其解决几个简单的函数最值问题,使读者能够学会利用遗传算法进行初步的优化计算.1. 遗传算法的基本原理遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程. 它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体.这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代. 后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程. 群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解.值得注意的一点是,现在的遗传算法是受生物进化论学说的启发提出的,这种学说对我们用计算机解决复杂问题很有用,而它本身是否完全正确并不重要(目前生物界对此学说尚有争议).(1)遗传算法中的生物遗传学概念由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法;故而在这个算法中要用到各种进化和遗传学的概念.首先给出遗传学概念、遗传算法概念和相应的数学概念三者之间的对应关系.这些概念如下:(2)遗传算法的步骤遗传算法计算优化的操作过程就如同生物学上生物遗传进化的过程,主要有三个基本操作(或称为算子):选择(Selection)、交叉(Crossove)、变异(Mutation).遗传算法基本步骤主要是:先把问题的解表示成“染色体”,在算法中也就是以二进制编码的串,在执行遗传算法之前,给出一群“染色体”,也就是假设的可行解.然后,把这些假设的可行解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉、变异过程产生更适应环境的新一代“染色体”群.经过这样的一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解.下面给出遗传算法的具体步骤,流程图参见图1:第一步:选择编码策略,把参数集合(可行解集合)转换染色体结构空间;第二步:定义适应函数,便于计算适应值;第三步:确定遗传策略,包括选择群体大小,选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数;第四步:随机产生初始化群体;第五步:计算群体中的个体或染色体解码后的适应值;第六步:按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体;第七步:判断群体性能是否满足某一指标、或者是否已完成预定的迭代次数,不满足则返回第五步、或者修改遗传策略再返回第六步.图1 一个遗传算法的具体步骤遗传算法有很多种具体的不同实现过程,以上介绍的是标准遗传算法的主要 步骤,此算法会一直运行直到找到满足条件的最优解为止.2. 遗传算法的实际应用例 1:设 f (x)二-X 2 2x 0.5,求 max f (x), x 二[-1,2].注:这是一个非常简单的二次函数求极值的问题,相信大家都会做•在此我 们要研究的不是问题本身,而是借此来说明如何通过遗传算法分析和解决问题.在此将细化地给出遗传算法的整个过程. (1)编码和产生初始群体首先第一步要确定编码的策略,也就是说如何把-1到2这个区间内的数用计 算机语言表示出来.编码就是表现型到基因型的映射,编码时要注意以下三个原则:完备性:问题空间中所有点(潜在解)都能成为 GA 编码空间中的点(染色 体位串)的表现型;健全性:GA 编码空间中的染色体位串必须对应问题空间中的某一潜在解; 非冗余性:染色体和潜在解必须一一对应.这里我们通过采用二进制的形式来解决编码问题, 将某个变量值代表的个体 表示为一个{0,1}二进制串.当然,串长取决于求解的精度.如果要设定求解精 度到六位小数,由于区间长度为2—(一1) = 3,则必须将闭区间[-1,2]分为3 106 等分.因为2097152 =221 ::: 3 106 ::: 222 =4194304所以编码的二进制串至少需要 22位.将一个二进制串(b 21b 20b 19, b 1b 0)转化为区间[-1,2]内对应的实数值很简单, 只需采取以下两步(Matlab 程序参见附录4):1) 将一个二进制串(b 21b 20b 19, b 1b 0)代表的二进制数化为10进制数:21(b 21b 20b1^b l b 0)^ = (' b i 2)10 二 x 'i =02) x'对应的区间[-1,2]内的实数:例如,一个二进制串 a=<1000101110110101000111 表示实数 0.637197. x' =(1000101110110101000111)=2288967 x - -12288967 撐 0.6371972 -1二进制串 <0000000000000000000000> <1111111111111111111111>则分别 表示区间的两个端点值-1和2.利用这种方法我们就完成了遗传算法的第一步 编码, 这种二进制编码的 方法完全符合上述的编码的三个原则.首先我们来随机的产生一个个体数为 4个的初始群体如下:'2-(-1) 222 -1pop(1)={<1101011101001100011110> <1000011001010001000010> <0001100111010110000000> <0110101001101110010101>}化成十进制的数分别为: %% a1 %% a2 %% a3%% a4 (Matlab 程序参见附录2)pop(1)={ 1.523032, 0.574022 , -0.697235 , 0.247238 }接下来我们就要解决每个染色体个体的适应值问题了. (2) 定义适应函数和适应值由于给定的目标函数f (x^^x 2 2x 0.5在[-1,2]内的值有正有负,所以必须通过建立适应函数与目标函数的映射关系, 标函数的优化方向应对应于适应值增大的方向, 打下基础.对于本题中的最大化问题,定义适应函数f(x) - F min ,若 f (X )- F min 0g(x"0, 其他式中F min 既可以是特定的输入值,也可以是当前所有代或最近K 代中f(x)的最小值,这里为了便于计算,将采用了一个特定的输入值.若取F min 二- •1,则当f(x)=1时适应函数g(x)=2 ;当f(x) = -1.1时适应函数g(x) =0 .由上述所随机产生的初始群体,我们可以先计算出目标函数值分别如下 (Matlab 程序参见附录3):f [pop(1)]={ 1.226437,1.318543 , -1.380607,0.933350 }然后通过适应函数计算出适应值分别如下 (Matlab 程序参见附录5、附录6):取 F min1,g[pop(1)]= { 2.226437,2.318543 ,0,1.933350 }(3) 确定选择标准这里我们用到了适应值的比例来作为选择的标准,得到的每个个体的适应值 比例叫作入选概率.其计算公式如下:对于给定的规模为n 的群体pop={ a 1,a 2,a 3/ ,a n },个体a i 的适应值为g(a i ), 则其入选概率为P s (a i)n,I _ 1,2,3, , n、g(a i )i 壬由上述给出的群体,我们可以计算出各个个体的入选概率. 首先可得4Z g(a )= 6. 478330i d4然后分别用四个个体的适应值去除以 、g(a i ),得:i =1P(a1)=2.226437 / 6.478330 = 0.343675 %% a1 P(a2)=2.318543 / 6.478330 = 0.357892 %% a2P(a3)= 0 / 6.478330 = 0 %% a3P(a4)=1.933350 / 6.478330 = 0.298433 %% a4 (Matlab 程序参见附录 7) (4)产生种群计算完了入选概率后,就将入选概率大的个体选入种群,淘汰概率小的个体, 并用入选概率最大的个体补入种群, 得到与原群体大小同样的种群(Matlab 程序 参见附录&附录11).保证映射后的适应值非负,而且目 也为以后计算各个体的入选概率 g(x),采用下述方法:要说明的是:附录11的算法与这里不完全相同•为保证收敛性,附录 11的算法作了修正,采用了最佳个体保存方法(elitist model ),具体内容将在后面给 出介绍.由初始群体的入选概率我们淘汰掉 a3,再加入a2补足成与群体同样大小的 种群得到newpop(1)如下:n ewpop(1)={<1101011101001100011110> %%a1 <1000011001010001000010〉, %%a2 <1000011001010001000010> %%a2 <0110101001101110010101〉}%%a4(5) 交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体, 然后得到新的染色体组,组成新的群体(Matlab 程序参见附录9).我们把之前得到的n ewpop(1)的四个个体两两组成一对,重复的不配对,进 行交叉.(可以在任一位进行交叉)<1101011叭 / 1001100011110> <1101011101010001000010>交叉得:<100001100 1010001000010〉 <1000011001001100011110> <1000011001010010010101>交叉得:通过交叉得到了四个新个体,得到新的群体jchpop (1)如下:jchpop(1)={<1101011101010001000010> <1000011001001100011110> <1000011001010010010101> <0110101001101101000010>}这里采用的是单点交叉的方法,当然还有多点交叉的方法,不过有些烦琐, 这里就不着重介绍了. (6) 变异变异也就是通过一个小概率改变染色体位串上的某个基因 (Matlab 程序参见附录10).现把刚得到的jchpop(1)中第3个个体中的第9位改变,就产生了变异,得到 了新的群体pop(2)如下:pop(2)= {<1101011101010001000010> <1000011001001100011110> <1000011011010010010101>, <0110101001101101000010> }然后重复上述的选择、交叉、变异直到满足终止条件为止. (7) 终止条件10010101>,<0110101001101101000010> <10000110010100 <0110101001101101000010>,遗传算法的终止条件有两类常见条件:(1采用设定最大(遗传)代数的方法,一般可设定为50代,此时就可能得出最优解•此种方法简单易行,但可能不是很精确(Matlab 程序参见附录1); (2)根据个体的差异来判断,通过计算种群中基因多样性测度,即所有基因位相似程度来进行控制.3. 遗传算法的收敛性前面我们已经就遗传算法中的编码、适应度函数、选择、交叉和变异等主要操作的基本内容及设计进行了详细的介绍•作为一种搜索算法,遗传算法通过对这些操作的适当设计和运行,可以实现兼顾全局搜索和局部搜索的所谓均衡搜索,具体实现见下图2所示.选择/变异图2均衡搜索的具体实现图示应该指出的是,遗传算法虽然可以实现均衡的搜索,并且在许多复杂问题的求解中往往能得到满意的结果,但是该算法的全局优化收敛性的理论分析尚待解决.目前普遍认为,标准遗传算法并不保证全局最优收敛•但是,在一定的约束条件下,遗传算法可以实现这一点.下面我们不加证明地罗列几个定理或定义,供读者参考(在这些定理的证明中,要用到许多概率论知识,特别是有关马尔可夫链的理论,读者可参阅有关文献).定理1如果变异概率为P m(0,1),交叉概率为巳• [0,1],同时采用比例选择法(按个体适应度占群体适应度的比例进行复制),则标准遗传算法的变换矩阵P是基本的.定理2标准遗传算法(参数如定理1)不能收敛至全局最优解.由定理2可以知道,具有变异概率P m ■ (0,1),交叉概率为P c • [0,1]以及按比例选择的标准遗传算法是不能收敛至全局最最优解.我们在前面求解例1时所用的方法就是满足定理1的条件的方法.这无疑是一个令人沮丧的结论.然而,庆幸的是,只要对标准遗传算法作一些改进,就能够保证其收敛性.具体如下:我们对标准遗传算法作一定改进,即不按比例进行选择,而是保留当前所得的最优解(称作超个体).该超个体不参与遗传.最佳个体保存方法(elitist model)的思想是把群体中适应度最高的个体不进行配对交叉而直接复制到下一代中.此种选择操作又称复制(copy). De Jong 对此方法作了如下定义:定义设到时刻t (第t代)时,群体中a* (t)为最佳个体•又设A (t + 1) 为新一代群体,若A (t + 1)中不存在a* (t),则把a*(t)作为A (t + 1)中的第n+1个个体(其中,n为群体大小)(Matlab程序参见附录11).采用此选择方法的优点是,进化过程中某一代的最优解可不被交叉和变异操作所破坏•但是,这也隐含了一种危机,即局部最优个体的遗传基因会急速增加而使进化有可能限于局部解•也就是说,该方法的全局搜索能力差,它更适合单峰性质的搜索空间搜索,而不是多峰性质的空间搜索•所以此方法一般都与其他选择方法结合使用.定理3具有定理1所示参数,且在选择后保留当前最优值的遗传算法最终能收敛到全局最优解.当然,在选择算子作用后保留当前最优解是一项比较复杂的工作,因为该解在选择算子作用后可能丢失.但是定理3至少表明了这种改进的遗传算法能够收敛至全局最优解.有意思的是,实际上只要在选择前保留当前最优解,就可以保证收敛,定理4描述了这种情况.定理4具有定理1参数的,且在选择前保留当前最优解的遗传算法可收敛于全局最优解.例2:设f(x)=3-x,x,求maxf(x), x [0,2],编码长度为5,采用上述定理4所述的“在选择前保留当前最优解的遗传算法”进行.此略,留作练习.二、相关函数(命令)及简介本实验的程序中用到如下一些基本的Matlab函数:ones, zeros, sum, size, length, subs, double等,以及for, while等基本程序结构语句,读者可参考前面专门关于Matlab的介绍,也可参考其他数学实验章节中的“相关函数(命令) 及简介”内容,此略.三、实验内容上述例1的求解过程为:群体中包含六个染色体,每个染色体用22位0—1码,变异概率为0.01,变量区间为[-1,2],取Fmin=-2,遗传代数为50代,则运用第一种终止条件(指定遗传代数)的Matlab程序为:[Cou nt,Result,BestMember]=Ge netic1(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,50)执行结果为:Count =50Result =1.0316 1.0316 1.0316 1.0316 1.0316 1.03161.4990 1.4990 1.4990 1.4990 1.4990 1.4990BestMember= 1.03161.4990图2例1的计算结果(注:上图为遗传进化过程中每一代的个体最大适应度; 而下图为目前为止的个体最大适应度单调递增)我们通过Matlab 软件实现了遗传算法,得到了这题在第一种终止条件下的最 优解:当 x 取 1.0316 时,Max f(x) =1.4990 .当然这个解和实际情况还有一点出入(应该是x 取1时,Max f(x) =1.5000 ), 但对于一个计算机算法来说已经很不错了.我们也可以编制Matlab 程序求在第二种终止条件下的最优解.此略,留作练 习.实践表明,此时的遗传算法只要经过10代左右就可完成收敛,得到另一个“最优解”,与前面的最优解相差无几.四、自己动手1 .用Matlab 编制另一个主程序 Genetic2.m ,求例1的在第二种终止条件下的最 优解.提示:一个可能的函数调用形式以及相应的结果为:[Cou nt,Result,BestMember]=Ge netic2(22,6,'-x*x+2*x+0.5',-1,2,-2,0.01,0.00001) Count =13 Result =1.03921.03921.0392 1.0392 1.0392 1.0392 1.4985 1.4985 1.4985 1.4985 1.4985 1.4985 BestMember =1.03921.49851.4985可以看到:两组解都已经很接近实际结果,对于两种方法所产生的最优解差异很小.可见这两种终止算法都是可行的,而且可以知道对于例1的问题,遗传算法只要经过10代左右就可以完成收敛,达到一个最优解.2•按照例2的具体要求,用遗传算法求上述例2的最优解.3•附录9子程序Crossing.m中的第3行到第7行为注解语句•若去掉前面的% 号,则程序的算法思想有什么变化?4. 附录9子程序Cross in g.m中的第8行至第13行的程序表明,当Dim(1)>=3 时,将交换数组Population的最后两行,即交换最后面的两个个体.其目的是什么?5. 仿照附录10子程序Mutatio n.m,修改附录9子程序Cross in g.m,使得交叉过程也有一个概率值(一般取0.65~0.90);同时适当修改主程序Genetic1.m或主程序Genetic2.m,以便代入交叉概率.6. 设f(x) - -x2-4x 1,求max f (x), [ -2,2],要设定求解精度到15位小数.五、附录附录1:主程序Genetid.mfun ctio n[Cou nt,Result,BestMember]=Ge netic1(MumberLe ngth,MemberNumber,Fu nctio nFitn ess,MinX,MaxX,Fmi n, Mutatio nProbability,Ge n)Populatio n=Populatio nln itialize(MumberLe ngth,MemberNumber);global Count;global Curren tBest;Cou nt=1;Populatio nCode=Populati on;Populatio nFit ness=Fit ness(Populatio nCode,F un ctio nFitness,MinX,MaxX,Mumbe rLen gth);Populatio nFit nessF=Fit nessF(Populatio nFit ness,Fmi n);Populatio nProbability=Probability(Populatio nFit nessF);[Populatio n,Curre ntBest,EachGe nMaxFit ness]=Elitist(PopulationCode,Populatio nF it ness,MumberLe ngth);EachMaxFit ness(Co un t)=EachGe nM axFit ness;MaxFit ness(Cou nt)=Curre ntBest(le ngth(Curre ntBest));while Cou nt<GenNewPopulatio n=Select(Populatio n,Populatio nProbability,MemberNumber);Populatio n=NewPopulatio n;NewPopulatio n=Crossi ng(Populatio n,Fun ctio nFit ness,MinX,MaxX,MumberLe ngth);Populatio n=NewPopulatio n;NewPopulatio n=Mutatio n(Populatio n,Mutatio nProbability);Populatio n=NewPopulatio n;Populatio nFit ness=Fit ness(Populatio n,Fun ctio nFit ness,MinX,MaxX,MumberLe ngth);Populatio nFit nessF=Fit nessF(Populatio nFit ness,Fmi n);Populatio nProbability=Probability(Populatio nFit nessF); Cou nt=Cou nt+1;[NewPopulatio n,Curre ntBest,EachGe nM axFit ness]=Elitist(Populatio n,Populatio nF it n ess,MumberLe ngth);EachMaxFit ness(Co un t)=EachGe nM axFit ness;;MaxFit ness(Cou nt)=Curre ntBest(le ngth(Curre ntBest));Populatio n=NewPopulatio n;endDim=size(Populatio n);Result=o nes(2,Dim(1));for i=1:Dim(1)Result(1,i)=Tra nslate(Populatio n(i,:),MinX,MaxX,MumberLe ngth);endResult(2,:)=Populati onF it ness;BestMember(1,1)=Tra nslate(Curre ntBest(1:MumberLe ngth),MinX,MaxX,Mumb erLe ngth);BestMember(2,1)=Curre ntBest(MumberLe ngth+1);close allsubplot(211)plot(EachMaxFit ness)subplot(212)plot(MaxFit ness)【程序说明】主程序Genetic1.m包含了8个输入参数:(1) MumberLength: 表示一个染色体位串的二进制长度. (例1中取22)(2) MemberNumber:表示群体中染色体的个数.(例1中取6个)(3) Fun ctio nFit ness:表示目标函数,是个字符串,因此用表达式时,用单引号括出.(例1中是f (x) = —x22x 0.5)⑷MinX : 变量区间的下限.(例1中是[-1,2]中的)(5) MaxX : 变量区间的上限.(例1中是[一1,2]中的2)⑹Fmin: 定义适应函数过程中给出的一个目标函数的可能的最小值,由操作者自己给出.(例1中取Fmin= —2)(7) MutationProbability : 表示变异的概率,一般都很小.(例1中取0.01)(8) Gen:表示遗传的代数,也就是终止程序时的代数. (例1中取50)另外,主程序Genetic1.m包含了3个输出值:Count表示遗传的代数;Result 表示计算的结果,也就是最优解;BestMember表示最优个体及其适应值.附录2:子程序Populationlnitialize.mfun ctio n Populatio n=Populatio nln itialize(MumberLe ngth,MemberNumber) Temporary=ra nd(MemberNumber,MumberLe ngth);Populatio n=(Temporary>=0.5* on es(size(Temporary)));【程序说明】子程序PopulationInitialize.m用于产生一个初始群体.这个初始群体含有MemberNumber个染色体,每个染色体有MumberLength个基因(二进制码).附录3:子程序Fitness.mfunction Populati onF it ness=Fit ness(Populatio nCode,Fu nctio nFit ness,MinX,MaxX,MumberLe ngth) Dim=size(Populati on Code);Populatio nFit ness=zeros(1,Dim(1));for i=1:Dim(1)Populatio nF it ness(i)=Tran sfer(Populatio nCode(i,:),Fu nctio nFit ness,MinX,MaxX,MumberLe ngth);end【程序说明】子程序Fitness.m用于计算群体中每一个染色体的目标函数值.子程序中含有5个输入参数:PopulationCode表示用0—1代码表示的群体,Fun ctio nFit ness表示目标函数,它是一个字符串,因此写入调用程序时,应该用单引号括出,MumberLength表示染色体位串的二进制长度. MinX和MaxX分别指变量区间的上下限.附录4:子程序Translate.mfun cti on Populatio nData=Tra nslate(Populatio nCode,MinX,MaxX,MumberLe ngth) Populati on Data=0;Dim=size(Populati on Code);for i=1:Dim(2)Populatio nData=Populatio nData+Populatio nCode(i)*(2A(MumberLe ngth-i));endPopulatio nData=MinX+Populatio nData*(MaxX-MinX)/(2Pim(2)-1);【程序说明】子程序Translate.m把编成码的群体翻译成变量的数值•含有4个输入参数,PopulationCode, MinX, MaxX, MumberLength .附录5:子程序Transfer.mfunction Populati onF it ness=Tran sfer(Populatio nCode,F un ctio nFit ness,MinX,MaxX,MumberLe ngth) Populati onF it ness=0;Populatio nData=Tra nslate(Populatio nCode,MinX,MaxX,MumberLe ngth);Populatio nF it ness=double(subs(F un cti onF it ness,'x',sym(Populatio nData)));【程序说明】子程序Transfer把群体中的染色体的目标函数值用数值表示出来,它是Fitness的重要子程序.其有5个输入参数分别为PopulationCode, FunctionFitness, MinX, MaxX , MumberLength.附录6:子程序FitnessF.mfunction Populati onF it nessF=Fit nessF(Populati onF it ness,F min)Dim=size(Populatio nFit ness);Populatio nFit nessF=zeros(1,Dim(2));for i=1:Dim(2)if Populati onF it ness(i)>F minPopulati onF it nessF(i)=Populatio nF it ness(i)-F min;endif Populati onF it ness(i)<=FminPopulati onF it nessF(i)=0;endend【程序说明】子程序FitnessF.m是用于计算每个染色体的适应函数值的.其输入参数如下:PopulationFitness为群体中染色体的目标函数值,Fmin为定义适应函数过程中给出的一个目标函数的可能的最小值.附录7:子程序Probability.mfun ctio n Populatio nProbability=Probability(Populatio nFit ness)SumPopulati onF it ness=sum(Populati onF it ness);Populatio nProbability=Populatio nFit ness/SumPopulatio nFit ness;【程序说明】子程序Probability.m用于计算群体中每个染色体的入选概率,输入参数为群体中染色体的适应函数值Populatio nFit ness附录8子程序Select.mfun ctio n NewPopulati on=Select(Populatio n,Populatio nProbability,MemberNumber)CProbability(1)=Populatio nProbability(l);for i=2:MemberNumberCProbability(i)=CProbability(i-1)+Populatio nProbability(i);endfor i=1:MemberNumberr=ra nd(1);In dex=1;while r>CProbability(I ndex)In dex=In dex+1;endNewPopulati on (i,:)=Populati on (I ndex,:);end【程序说明】子程序Select.m根据入选概率(计算累计概率)在群体中按比例选择部分染色体组成种群,该子程序的3个输入参数分别为:群体Population,入选概率PopulationProbability,群体中染色体的个数MemberNumber.附录9:子程序Crossing.mfun ctio n NewPopulati on=Cross in g(Populatio n,Fun cti onF it ness, MinX, MaxX,MumberLe ngth) %%Populati onF it ness=%% Fit ness(Populatio n,Fu nctio nFit ness,MinX,MaxX,MumberLe ngth);%%Populatio nProbability=Probability(Populatio nFitness); %%[SortResult,SortSite]=sort(Populatio nProbability);%%Populatio n=Populatio n(SortSite,:);Dim=size(Populatio n);if Dim⑴>=3Temp=Populatio n( Dim(1),:);Populatio n(Dim(1),:)=Populatio n(Dim(1)-1,:);Populatio n(Dim(1)-1,:)=Temp;endfor i=1:2:Dim(1)-1SiteArray=ran dperm(Dim(2));Site=SiteArray(1);Temp=Populati on (i,1:Site);Populatio n(i,1:Site)=Populatio n(i+1,1:Site);Populatio n(i+1,1:Site)=Temp;endNewPopulatio n=Populatio n;【程序说明】子程序Cross in g.m用于群体中的交叉并产生新群体.其输入参数为:Population, FunctionFitness MinX , MaxX , MumberLength.附录10:子程序Mutation.mfun ctio n NewPopulatio n=Mutatio n(Populatio n,Mutatio nProbability)Dim=size(Populatio n);for i=1:Dim(1)Probability=ra nd(1);Site=ra ndperm(Dim(2));if ProbabilityvMutatio nProbabilityif Populatio n(i,Site(1))==1Populatio n(i,Site(1))=0;endif Populatio n(i,Site(1))==0Populatio n(i,Site(1))=1;endendendNewPopulatio n=Populatio n;【程序说明】子程序Mutation.m用于群体中少量个体变量并产生新的群体.输入参数为:群体Population和变异概率MutationProbability .附录11:子程序Elitist.mfun ctio n [NewPopulatio nln cludeMax,Curre ntBest,EachGe nMaxFit ness]= Elitist(Populatio n,Populatio nFit ness,MumberLe ngth)global Count Curren tBest;[Mi nFit ness,Mi nSite]=mi n( Populatio nFit ness);[MaxFit ness,MaxSite]=max(Populati onF it ness);EachGe nMaxFit ness=MaxFit ness;if Cou nt==1Curre ntBest(1:MumberLe ngth)=Populatio n(MaxSite,:);Curre ntBest(MumberLe ngth+1)=Populatio nFit ness(MaxSite);elseif Curre ntBest(MumberLe ngth+1)<Populatio nFit ness(MaxSite);Curre ntBest(1:MumberLe ngth)=Populatio n(MaxSite,:);Curre ntBest(MumberLe ngth+1)=Populatio nFit ness(MaxSite);endPopulatio n(Mi nSite,:)=Curre ntBest(1:MumberLe ngth);endNewPopulatio nln cludeMax=Populatio n;【程序说明】子程序Elitist.m用到最佳个体保存方法(“优胜劣汰”思想).输入参数为:群体Population,目标函数值PopulationFitness和染色体个数MumberLe ngth.。
