浅谈因子分析方法在多指标综合评价中的运用(下)
因子分析在学生成绩综合评价中的应用

因子分析在学生成绩综合评价中的应用
综观当今的学校教育,学生的成绩对老师、家长和学生都有着非常重要的意义。
因此如何合理地综合评价学生的成绩,起着至关重要的作用。
本文的主要目的,就是利用因子分析等方法,来探索学生成绩综合评价的有效性和可靠性。
首先,我们来谈谈因子分析。
因子分析是一种数据分析技术,它可以把复杂的观察变量拆分成一组较少的根本因素,从而揭示数据中隐藏的潜在构成。
在调查学生成绩综合评价方面,可以采用多元因子分析,将学生成绩的各个维度,如学习表现、学习习惯、社会行为等,通过因子分析,分解并重新组合,形成新的综合评价体系。
此外,我们还可以从更宏观的角度,利用因子分析来探究学生成绩综合评价的有效性和可靠性。
因子分析可以通过不断地改进综合评价体系,把各项综合评价指标综合起来,并且不断校正和完善,使之成为最能反映学生实际情况的综合评价体系。
最后,在因子分析的基础上,我们还可以进一步对学生成绩综合评价进行深入的研究,比如探究一些特殊学生群体的成绩综合评价情况,这样可以更好的了解学生的学习表现,从而更好地跟踪其学习过程。
从以上分析可以发现,因子分析是一种可以帮助学校来综合评价学生成绩的有效方法。
它可以把观察变量拆分成一组较少的根本因素,通过对综合评价指标的不断校正和完善,最终构建最能反映学生实际情况的综合评价体系。
因此,学校和教育主管部门有必要在构建学生
成绩综合评价体系时,充分考虑因子分析的作用,以更好地为学生提供客观、全面、准确的成绩评价。
综上所述,因子分析在学生成绩综合评价中有着十分重要的作用,可以帮助教师、家长以及学校管理者更好地了解学生的表现,以便更加有效的帮助他们提高学习水平。
因子分析法在企业经济效益的综合分析与评价中的应用

王增民
(北京邮电大学经济管理学院 ,北京 100876)
摘 要 :企业经济效益评价往往涉及众多指标 ,利用多指标评价企业经济效益 ,使评价问题变得复
杂 。本文采用多元统计中的因子分析法来解决这一问题 ,介绍了分析 、评价过程 。
关键词 :因子分析 ;经济效益 ;综合评价
A synthetic evaluation on the economic benef it of enterprises ———The appl ication of main composition method
WAN G Zeng2min
( Institute of economics and management BU P T ,Beijing 100876) Abstract :The evaluating economic benefit of enterprises sometimes deal wit h many target , it is a complicated question as a result of many target . This paper settles t his matter by adopitng factor analysis met hod , introduces t he process of analysis and evaluation. Key words :factor analysis ; economic benefit ; synt hetic evaluation
得分 1. 223 . 950 2. 474 1. 117 2. 466 21. 258 1. 319 2. 681 21. 457 . 068 . 517 2. 856
因子分析在企业财务能力综合分析与评价中的应用

因子分析在企业财务能力综合分析与评价中的应用摘要:企业财务能力评价问题往往因涉及众多指标而变得复杂,文章采用多元统计中的因子分析法来解决这一问题。
以多元统计理论为手段运用SPSS统计软件,结合二十一家工业企业进行因子分析法的实例研究,旨在说明因子分析法在企业财务能力综合分析评价中的应用。
关键词:因子分析;财务能力;综合评价企业的财务能力是企业正常运转的根本前提,也是企业形成有效竞争力的必要条件。
运用会计信息对企业财务绩效进行评价,对促进企业加强监督管理,优化企业财务状况具有重要意义,使企业在激烈的市场竞争中立于不败之地。
企业财务能力的评价指标体系中涉及众多财务指标,不但在一定程度上增加了问题分析的复杂性,而且反映的信息在一定程度上也存在重复;同时,在多指标综合评价方法中传统方法对于权重的设置还往往带有一定的主观随机性。
为避免上诉问题,文章采用因子分析法对企业的财务能力进行综合分析与评价。
1 因子分析法的基本原理因子分析法是把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。
其具体思想是根据相关性大小把原始变量分组,每组变量代表一个基本结构,称之为公共因子。
评价总体有n个样本,每个样品观测量为p个指标,则其模型为:Xi=ai1F1+ ai2F2+…+aimFm+?着i (i=1,2,…,p)其中,X1,X2,…,Xp使均值为零、方差为1的标准化变量;F1,F2,…,Fm主因子(m<p);?着i为特殊因子;aij称为因子负荷,揭示了第i个变量在第j个主因子上的相对重要性。
在因子分析过程中,还可以用变量的观测值的线性表达式来计算各主因子的得分以及综合因子的得分值。
本文求解过程借助SPSS13.0统计分析软件来进行。
2 财务能力的综合分析与评价2.1 样本及变量指标的选取本文选取15个指标以构成一个比较完备的指标体系进行分析,X1~X15分别为:资产负债率、已获利息倍数、流动比率、速动比率、总资产周转率、应收账款周转率、固定资产周转率、存货周转率、销售收入增长率、销售利润增长率、总资产增长率、总资产报酬率、净资产收益率、销售利润率、成本费用利润率。
因子分析法在医院科室综合效益评价中的应用
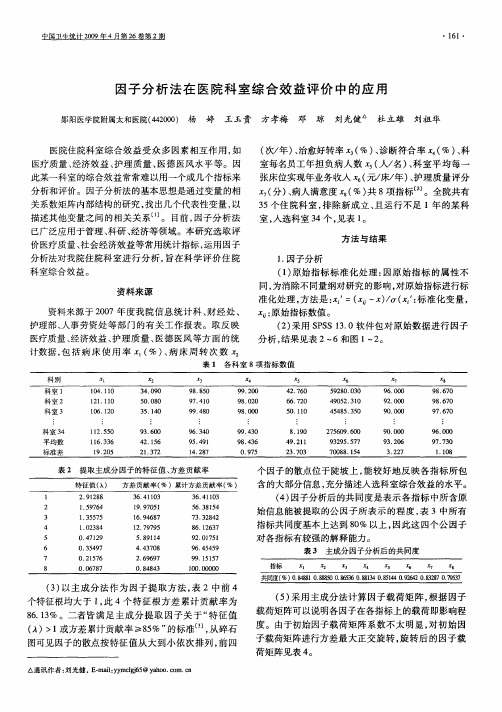
() 3 以主成分法作 为因子提 取方法 , 2中前 4 表 个特征根均大于 1 此 4个特征根方差累计贡献率为 , 8.3 6 1%。二者皆满足主成分提取 因子关于 “ 特征值 () 1 A > 或方差累计贡献率 I8 %” > 5 的标准 , 从碎石 图可见 因子 的散点 按 特征 值 从 大 到 小依 次 排 列 , 四 前
对 各指标 有较 强 的解释 能力 。
表 3 主 成 分 因 子 分 析 后 的 共 同 度
指标 3 4 向 8
共同度( 0881 . 800856081 . 14096208270757 %) . 8 8 5 .63 . 3 08 4 . 4 . 8 .93 4 08 84 5 2 3
关 系数矩 阵 内部结 构 的研 究 , 出几 个代 表性 变量 , 找 以
张床位实现年业务收人 (r f/ 、 Y/ . _ 年) 护理质量评分
X( ) 病人满 意度 X( ) 8项 指标 。全 院共 有 ,分 、 % 共 3 住 院科 室 , 除新 成 立 、 运 行 不 足 1年 的某 科 5个 排 且
荷 矩 阵见表 4 。
Chn s o m a fHe lhSait s, r2 0 Vo. 6。 . ieeJ u lo at tt i Ap 0 9, 12 No 2 sc
表 4 旋转后的因子载荷矩 阵
y 2= 0 8 3 0 l +0 2 9 2 2 +0 3 1 6 3 + .6 9 x . 12x .4 8 x
医疗质 量 、 经济效 益 、 护理 质 量 、 医德 医 风水 平 等 。 因
( 年) 治愈好转率 , %) 诊断符合率 ( 、 次/ 、 ( 、 %) 科
室 每名员 工年 担 负 病 人 数 ( / ) 科 室 平 均 每 一 人 名 、
因子分析在学生成绩综合评价中的应用

因子分析在学生成绩综合评价中的应用作者:张永福赵洪章穆扬来源:《现代电子技术》2008年第06期摘要:在教学管理中,需要科学合理地对学生成绩进行综合评价。
目前,应用较多的如简单相加法和标准分法都存在各种缺点。
运用主成分分析的方法对学生成绩进行因子分析,并通过分析的结果做出一个综合评价,这样可以比较有效地解决其他分析方法存在的问题。
通过对学生在校期间各科成绩进行因子分析的具体实例研究,找出影响学生知识和能力的主要方面因子,并据此对学生成绩做出一个客观、综合的评价。
关键词:因子分析;各科成绩;综合评价;实例分析中图分类号:TP391;O212 文献标识码:B 文章编号:1004-373X(2008)06-137-04Application of Factor Analysis to Comprehensive Evaluation on Students′ GradeZHANG Yongfu ZHAO Hongzhang MU Yang2(1.School of Astronautics,Northwestern Polytechnical University,Xi′an,710072,China;2.School of Educational Experimentation,Northwestern Polytechnical University,Xi′an,710072,China)Abstract:We need to have a comprehensive evaluation on the students′ grade scientifical ly and reasonably in the field of teaching management.At present,the methods which are mostly used in the aspect include simple addition and standard marks which both have their own limitations.Making use of the method of factor analysis in evaluating the students′ grade by using the principal component analysis can give us a more comprehensive evaluation from the analytical results than before-mentioned methods.In this paper,we find out the primary factors which can have an influence on the students′ knowl edge and ability by studying on an example and then make an objective and comprehensive assessment on the students′ grade.Keywords:factor analysis;grade of various subjects;comprehensive evaluation;example analysis1 引言在各大专院校中经常遇到评定各类奖学金,择优分配,推荐研究生等问题。
因子分析在企业绩效评价中的应用指南(四)

因子分析在企业绩效评价中的应用指南一、引言企业绩效评价是企业管理中一项至关重要的工作。
它不仅涉及到企业的发展方向和战略规划,还关系到员工的薪酬和晋升。
而因子分析作为一种多元统计分析方法,可以帮助企业更准确地评价绩效,提高管理效率。
本文将探讨因子分析在企业绩效评价中的应用指南。
二、因子分析的基本原理因子分析是一种多元统计分析方法,其基本原理是通过对多个变量的分析,找出它们之间的共性因素。
通过对这些共性因素的分析,可以将原始的多个变量简化为较少的若干个共性因子,从而揭示出变量之间的内在联系。
在企业绩效评价中,可以将多个绩效指标归因于几个共性因素,简化评价体系,更好地理解绩效的内在结构。
三、因子分析在企业绩效评价中的应用1. 确定绩效指标在进行因子分析之前,需要先确定要评价的绩效指标。
这些指标可以包括财务绩效、市场绩效、内部流程、学习与成长等多个方面。
确定好绩效指标后,将其转化为相应的变量,用于因子分析。
2. 数据收集与整理数据的收集是进行因子分析的基础。
在企业绩效评价中,可以通过问卷调查、财务报表等多种方式来收集数据。
在收集到数据后,需要对数据进行整理和清洗,剔除掉一些无效数据,确保数据的可靠性。
3. 因子提取在进行因子分析时,需要通过一定的数学方法来提取共性因子。
这其中包括主成分分析、最大方差法、最大似然法等多种方法。
通过这些方法,可以将原始的多个绩效指标简化为较少的若干个共性因子,更好地理解绩效的内在结构。
4. 因子旋转在进行因子分析后,可能会出现因子之间相关性较高的情况。
为了更好地理解共性因子的内在含义,需要对这些因子进行旋转。
常用的旋转方法包括正交旋转和斜交旋转,通过旋转可以使得因子更加清晰地呈现出来。
5. 因子解释因子分析的最终目的是为了更好地理解变量之间的内在联系。
因此,在得到共性因子后,需要对这些因子进行解释。
通过对因子的解释,可以帮助企业更好地理解绩效指标之间的内在联系,从而指导管理决策。
因子分析法在教师课堂教学质量综合评价中的应用

因子分析在学生成绩综合评价中的应用

因子分析在学生成绩综合评价中的应用杨宝军【摘要】采用因子分析法并利用SPSS软件对学生在校期间的各科成绩进行分析,得出累计贡献率达到69.753的9个主要因子.指出因子分析和平均成绩在学生评价中存在差异,并据此对学生成绩进行一个客观、综合的评价.【期刊名称】《宜宾学院学报》【年(卷),期】2010(010)006【总页数】3页(P37-39)【关键词】因子分析;学生成绩;综合评价【作者】杨宝军【作者单位】太原大学外语师范学院数学系,山西太原,030012【正文语种】中文【中图分类】O212.1%O424.7学生成绩能反映学生掌握知识和各种能力的程度,综合得分是评价一个学生学习好坏的重要指标,这涉及如何进行学生成绩分析以及评定.学生成绩分析是整个教学过程的一个重要环节,尤其在各大专院校中经常遇到评定各类奖学金等问题.学生成绩评定的含义通常是指学校根据一定的标准,对教学过程中学生所产生的思想、学业、行动和个性等方面的变化作出恰如其分的评断.解决这类问题的关键是如何对学生在校期间的表现给予综合的评价,而评价的基础是学生在校期间各门课程学习所获得的多方面的知识和能力.这些能力和知识具体表现在对课程的掌握上,即各科成绩.目前,对学生成绩综合评价的方法很多,大部分学校或系部采取原始分数求和法或平均学分成绩法,用这两种方法比较简单,但也有缺点:掩盖了学生的个性,不能反映学生的专业能力或其特长,这对学生的综合评价不是很理想.另外还有主成分分析法、专家调查法 -主成分分析法、因子分析法等,吴海英《大学数学》对这几种方法进行了比较,并指出因子分析法的优点[1].本文通过对学生在校期间的各科成绩进行因子分析,找出影响知识和能力的主要因素,并据此对学生成绩的综合评价提供较合理的方法.1.1 因子分析基本思想[2]因子分析是用少数几个因子去描述多个变量之间的关系,被描述的变量一般都是能实际观测的随机变量,而那些因子是不可观测的潜在变量.因子分析的基本思想是把联系比较紧密的变量归为一个类别,而不同类别的变量之间的相关性则较低.在同一个类别内的变量,可以想象是受到了某个共同因素的影响才彼此高度相关的,这个共同因素称为公共因子.1.2 因子分析的步骤[2](1)对原始数据进行标准化以消除量纲的影响,计算标准化指标的协方差即相关系数矩阵.(2)求相关系数矩阵的特征值和相应的特征向量、特征值的贡献率以及累计贡献率.(3)按照特征值大于 1.00的原则选取公共因子个数. (4)计算因子载荷矩阵并进行方差最大化旋转,得到旋转后的因子载荷矩阵,进而建立因子模型.(5)利用回归法得出因子得分系数,进而得出因子得分函数.(6)构建因子评价模型,实施综合评价分析.由于开始对数据进行了标准化处理,消除了量纲的影响,所以以各因子的方差贡献率占总方差贡献率的比重作为权重对各因子得分进行加权汇总,得出综合得分.以太原大学外语师范学院数学系 05级学生的 28门课程的成绩作为对象分析.用SPSS软件进行处理.由 SPSS的输出结果可得[3],这些变量之间的相关系数在 0.5左右的很多,而且其对应的相关性检验值大都小于 0.01(由于科目较多,输出的相关系数矩阵较大,具体输出略),这说明变量之间存在着较为显著的相关性,说明有进行因子分析的必要.同时,由结果可得 K MO检验值为0.757,说明了用因子分析的效果较好.利用 SPSS软件求其相关系数矩阵的特征值和特征向量,按照特征根大于 1的原则,选择 9个公共因子,其累计方差贡献率为 69.753%,也就是说总体近 70%的信息可用这 9个公共因子来解释,本文采取这前 9个公共因子进行分析.为了更好地解释原始变量在各个因子上的载荷值,我们对因子载荷矩阵进行方差最大正交旋转,得到旋转后的因子载荷矩阵,如表 2所示.由表 2可以看出,因子 1在三学期的英语、三学期的数分及高代、空解、小数竞和数论上的载荷比较大,可命名为专业知识水平,因子2、因子5、因子6和因子9在大学语文、计算机、毛概、邓论和马原上的载荷比较大,可命名为公共知识水平;因子 3在空解、小数理、小教法和两学期的普物上的载荷比较大,可命名为数学应用能力,因子 4在三学期的体育上的载荷较大,命名为身体素质因素,因子 7和因子 8在心理和班管上的载荷较大,命名为教师基本知识.从以上分析可以看出,在所有因子中,因子 1的贡献较大,因此求因子分析的总分时比重比较大,事实上因子 1的课程均为学生专升本或当小学教师的重要课程,学生都比较重视,说明了因子分析与实际相符.由回归法估计出因子得分,并对 9个因子的得分进行加权汇总,得出各个学生的综合得分(只显示排名前十位的同学),如表 3所示.从表 3可以看出,因子分析排名和按照均分排名还是有一定差距的.编号为 46的学生在大部分因子上的得分都不错,因子均分也较高,但从因子分析可以看出,该生在因子 4的得分较高,说明其具有体育特长;编号 24的学生均分排名第 3,但因子分析排在第 7位,通过表 3可以发现该生在因子 1上的得分较高,但是在因子 8和因子 9的得分较低,说明虽然专业成绩都较好,但基本教师素质和身体素质较差,通过调查也是与实际相符的.因子分析作为一种重要的多指标综合评价方法,在对学生的成绩做综合评价时有自己的优点,能反映出学生的特长和缺点,能对学生的培养提出较好的依据.但也有自己的缺点,这种方法完全依赖数据,可能把一些不重要的课程看为较重要的,可能产生偏差.为了避免这一缺点,可以采用学分和方差贡献率合成为权重来评价,可得到进一步的完善和改进.【相关文献】[1]吴海英,张杰.学生成绩排名的综合评价模型 [J].大学数学, 2006,8(4):142-145.[2]何晓群.现代统计分析方法与应用[M].北京:中国人民大学出版社,2003:316-319.[3]杜强,贾丽艳.SPSS统计分析从入门到精通[M].北京:人民邮电出版社,2009:543-554.。
因子分析与综合评价

因子分析在综合评价中的应用摘要:因子分析方法是一种降维、简化数据的技术。
将因子分析运用于统计指标体系的综合评价中,克服了传统评价方法在处理指标高度相关和权重设定上的缺陷,但所构造的因子得分模型仅适用于对评价对象的静态比较,并不适用于动态比较 。
文探将深入探讨因子分析法进在综合评价的作用以及应注意的一些问题。
关键词:因子分析法;综合评价在多指标综合评价方法中,传统方法对于权重的设置往往带有一定的主观随意性,将多元统计引入综合评价方法,如因子分析法,可以克服人为确定权数的缺陷,使得综合评价结果唯一,而且客观合理。
许多学者在因子分析方法的运用上存在着一些问题,削弱了实证分析研究的解释力和信服力。
本文试从如何正确运用因子分析法进行综合评价作一些探讨。
下面将从两个方面进行介绍:一、因子分析方法的基本思想和运用因子分析法是把一些具有错综复杂关系的变量归结为少数几个无关的新的综合因子的一种多变量统计分析方法。
其基本思想是根据相关性大小对变量进行分组,使得同组内的变量之间相关性较高,不同组的变量相关性较低。
每组变量代表一个基本结构,因子分析中将之称为公共因子。
假设观测系统 (即评价总体), 有k 个评价指标,n 个观测单位,因子分析的数学模型就是把 n 个观测单位分别表示为p<k 个公共因子和一个独特因子的线性加权和,即i p i i i F F F εααα++++=p 12211...x (n i ,...,2,1=) (1-1) 其中:P F F F ,...,,21为公共因子,它是各个指标中共同出现的因子,因子之间通常是彼此独立的;i ε是各对应变量i x 所特有的因子,称为特殊因子,通常假定()2i i 0~δε,N ;系数ij α是第i 个变量在第j 个公共因子上的系数,称为因子负荷量,它揭示了第i 个变量在第j 个公共因子上的相对重要性。
因此,通过因子模型建立综合评价函数的步骤如下:(1)根据原始变量矩阵估计因子载荷矩阵。
浅谈因子分析方法在多指标综合评价中的运用

浅谈因子分析方法在多指标综合评价中的运用因子分析方法是一种统计分析方法,主要用于研究多个变量之间的关系,其基本思想是将多个变量通过线性组合进行综合评价。
因子分析方法在多指标综合评价中的运用,可以帮助我们识别出具有代表性的综合指标,从而简化评价过程,提高评价准确性。
首先,因子分析方法在多指标综合评价中的应用可以帮助我们减少指标冗余。
在评价过程中,可能存在大量指标,但很多指标之间可能存在高度相关性。
通过因子分析,我们可以找到一些潜在因子来代表这些相关性,从而减少指标数量,简化评价模型。
这不仅可以节约评价成本,还可以提高评价效率。
另外,因子分析方法可以帮助我们确定主导因素和评价指标的权重。
在多指标综合评价中,不同指标对于评价结果的贡献是不同的。
通过因子分析,我们可以确定各个因子的权重,并进一步计算出各个指标的权重。
这有助于我们合理地设置各个指标的权重,避免主观随意性,提高评价结果的科学性和客观性。
此外,因子分析方法还可以帮助我们解决指标间的共线性问题。
在多指标综合评价中,指标之间可能存在高度相关性,导致评价结果不准确。
通过因子分析,我们可以将这些相关性较高的指标进行合并,生成新的综合指标,从而避免共线性问题对评价结果的影响。
最后,因子分析方法还可以帮助我们进行评价结果的解释和解读。
通过因子分析,我们可以得到各个因子的得分和权重,从而更好地解释评价结果的形成机制。
这有助于我们深入理解评价对象的特征和潜在问题,为进一步改进和优化提供依据。
总之,因子分析方法在多指标综合评价中的运用可以帮助我们简化评价过程,减少指标冗余,理清指标之间的内在关系,确定主导因素和指标的权重,解决指标共线性问题,以及解释评价结果的形成机制。
因此,合理运用因子分析方法可以提高多指标综合评价的科学性和客观性,为决策提供有效的支持。
因子分析在教育评估中的应用实例(六)

因子分析在教育评估中的应用实例教育评估是对教育质量和效果进行客观评价的过程,其结果对于学校改进和教学质量提升至关重要。
随着数据分析技术的不断发展,因子分析作为一种多变量统计方法,逐渐在教育评估中得到广泛应用。
本文将从实际案例出发,探讨因子分析在教育评估中的应用实例。
一、数据收集在某市一所高中,教育部门希望对学生的综合素质进行评估,以了解学生的学习状况、心理健康、社交能力等方面的情况。
为此,教育部门收集了一系列指标,包括学生成绩、学生评价问卷、心理测试结果等。
这些数据体现了学生在不同方面的表现,是进行因子分析的基础。
二、因子提取在收集到的数据中,有很多指标可能是相关的,但并不是所有的指标都是独立的。
因子分析可以帮助我们找到隐藏在数据背后的因子结构,从而减少数据的维度,提取出更有意义的变量。
通过因子提取,我们可以发现学生成绩、学生评价问卷和心理测试结果之间的潜在联系。
三、因子旋转在因子提取之后,往往会得到一些模糊的因子结构,这时需要进行因子旋转。
因子旋转可以让我们更好地理解因子之间的关系,从而找到更加可解释的因子结构。
在这个案例中,通过因子旋转,我们可能会发现学生成绩和学生评价问卷之间存在一定的相关性,而心理测试结果则与其他因子有较强的区分度。
四、结果解释通过因子分析,我们可以得到一些潜在的因子,比如“学习成绩”、“社交能力”、“心理健康”等。
这些因子能够更好地反映学生的综合素质,从而为教育部门提供更有针对性的评估结果。
例如,如果某个学校的学生在“学习成绩”方面表现较好,但在“社交能力”和“心理健康”方面存在较大的改进空间,教育部门可以有针对性地进行改进计划,提高学生的综合素质。
五、局限性与展望当然,因子分析也存在一定的局限性。
首先,因子分析依赖于数据的准确性和完整性,如果数据存在缺失或者错误,将会影响因子分析的结果。
其次,因子分析的结果需要结合实际情况进行解释,不能简单地依赖因子分析的结果。
未来,可以结合其他统计方法,比如回归分析、聚类分析等,进行更加全面的教育评估。
因子分析在学生成绩综合评价中的应用

第30卷第3期2010年6月惠州学院学报(自然科学版)JOURNAL OF HU I Z HOU UN I V ERSI TY Vol 1301No 13Jun 12010收稿日期:2010-04-21作者简介:张 琼(1971-),女,广东东莞人,助理研究员,研究方向为高等教育管理。
因子分析在学生成绩综合评价中的应用张 琼(惠州学院 美术系,广东 惠州 516000) 摘 要:本文简介了运用因子分析法对学生成绩进行综合评价的基本原理及步骤,提出了因子分析过程中的注意事项,通过实例分析,证实因子分析在学生成绩综合评价中的可行性和必要性。
关键词:因子分析;主成分分析;综合评价;学生成绩中图分类号:O213 文献标识码:A 文章编号:1671-5934(2010)03-0040-061 引言因子分析是“对现实生活中众多的相关、重叠信息进行合并和综合,它以最少的信息丢失,将原始的众多变量和指标变成较少的几个综合变量,以利于分析判定。
在研究中,因子分析得到的结果经常用于综合判定。
”[1]在高校的学生管理中,管理者经常会对学生成绩进行综合评价。
如奖学金的评定、先进的评选、各项推优工作等。
如何用科学、合理的方法对学生成绩进行综合评价?并依据评价的结果作出决定。
目前,对学生的成绩进行综合评价应用较多的方法是加权综合评分法或将各科成绩简单地相加。
由于加权评分法中的权重设置容易受人为的因素的影响,而各科成绩简单地相加又不能体现学生综合的学习能力等,这些方法都存在着各自的缺点。
而通对学生成绩进行因子分析并做综合评价,比较有效的解决了以上评价办法存在的问题,通过对学生各科成绩的因子分析,找出影响知识和能力的主要方面,对学生成绩进行综合评价。
2 因子分析的基本原理及步骤211 基本原理对学生成绩进行综合分析是对学生的各科成绩作因子分析,是把每个学生的各科成绩分解成两个部分:一部分是由所有成绩共同具有的少数几个因子构成的,即公共因子;另一部分是仅对某一个成绩产生影响,为某一个成绩所特有的,即所谓特殊因子[2]。
浅谈因子分析方法在多指标综合评价中的运用(下)

专题讲座??>>??正文专题讲座??>>??正文浅谈因子分析在多指标综合评价中的运用(上)* 2012-12一、相关概念简介1.综合评价简介所谓综合评价是指对以多属性体系结构描述的对象系统作出全局性、整体性的评价,即对评价对象的全体,根据所给的条件,采用一定的方法给每个评价对象赋予一个评价值(又称评价指数),再据此择优或排序的过程。
常见的综合评价方法有主成分法、基于主成分的因子分析法、熵权法,以及基于模糊数学的多层模糊综合评判法,等等。
2.因子分析简介:因子分析是利用降维的思想,在力保数据丢失最少的原则下,对高维变量空间进行降维处理,把多指标转化为少数几个综合指标的多元统计分析方法。
它的特点是在评价指标的相关性比较高时,能消除指标间信息的重叠,而且根据指标所提供的原始信息生成非人为的权重系数。
采用因子分析法进行多指标的综合评价具有以下优势:因子分析的降维处理技术能较好地解决多指标评价的要求。
1. 因子分析将原始变量变换为主因子的过程中, 同时形成了反映成分和指标包含信息量的权数, 以计算综合评价值, 这比人为地确定权数更为客观有效, 也有助于保证真实地反映样本间的现实关系。
2. 减少了指标选择的工作量。
在因子分析中由于可以消除评价指标间的相关影响, 因而在指标选择上相对容易些,另外因子分析可以保留原始评价指标的大部分信息。
3. 随着电子计算机技术的发展, SAS、SPSS等商品化统计分析软件的推广与应用, 使得因子分析在各类综合评价实践中的广泛应用成为现实。
基于上述几点,因子分析法在各类综合指标评估中得以广泛应用。
二、因子分析法在综合评估中的运用(实例讲解)下面,笔者将以某项目的多指标综合评估分析过程为例进行详细讲解。
需要说明的是,在进行综合评估之前,首要的工作是建立一套可靠完整的指标体系。
而确立评估指标的方法很多,包括主观、客观法,如常见的Delphi专家评估法、灰色关联度分析法、极小极大离差法和最小均方差法,等等。
浅论因子分析法在飞行能力的综合分析与评价中的应用

浅论因子分析法在飞行能力的综合分析与评价中的应用浅论因子分析法在飞行能力的综合分析与评价中的应用我国民航事业的开展,需要大量的飞行员.飞行员的培养质量是我国民航进一步持续、快速、安康开展的重要根底,是事关航空平安的大事.高素质的飞行员由诸多因素所决定,其中,很重要的一个决定性因素就是飞行员自身的飞行能力.由于飞行能力的差异,每一个飞行学员未必都能成为飞行员,即使有的成为飞行员,在飞行驾驶技术上也参差不齐.这种现状不仅在培训方面给国家带来了损失,而且还会给民航的飞行平安带来一定的影响.因此,提高飞行员的培养质量,尤为重要.笔者认为:做好以下两方面的工作是重要的:一是选择飞行能力强的学生;二是在学习训练阶段,不连续地加强学员飞行能力的培养,提高他们的飞行能力.这样,我们就能为中国民航事业培养出高素质的飞行员,满足持续、快速、安康开展的中国民航对飞行员的需求.我院教师曾在“预测飞行能力”方面作了首次尝试.他们利用逐步回归法选出6个评价飞行员飞行能力的指标,建立了评价飞行能力的回归方程,然后对飞行学员的飞行能力作评价,定等级,但是,效果不太理想.其原因在于:①选出的评价飞行能力的指标虽然都在不同程度上反映了一个学员的飞行能力的某些信息,但是各指标之间存在一定的相关关系,反映的信息在一定程度上有重叠;②评价飞行能力等级界限确实定,人的主观因素参与较多,影响了评价等级的客观性.因此,有必要寻找和设计较少的几个指标,来综合各指标携带的信息,这几个综合指标相互独立,所代表的信息既不重叠,又包含了原指标的大局部信息.因子分析正表达了这一思想,因此,因子分析法是解决该问题的一个好方法.本文利用因子分析法,对飞行能力进行综合分析与评价,取得较好评价结果,为民航飞行员的选拔提供科学的参考依据.因子分析通过研究可观测变量的相关矩阵或协方差矩阵的内部依赖关系,把多个变量综合为少数几个称为公因子或主因子的因子,并用这几个不可观测的公因子的线性函数与特定因子之和来描述原来观测的每一变量,既找到可观测变量受公因子支配的规律,从而尽可能合理地解释存在于可观测的原始变量之间的相关性,并起到简化变量维数与结构的作用。
基于因子分析的股票技术指标评价

基于因子分析的股票技术指标评价股票技术分析是指通过对股价走势、成交量等市场数据的分析和研究,以确定未来股价走势的方法。
在实践中,投资者往往会运用各种技术指标来辅助决策,以获取更好的投资收益。
市场上存在着大量的技术指标,投资者往往难以选择合适的指标进行分析和决策。
基于因子分析的方法为投资者提供了一种新的角度和思路,以评价和筛选技术指标的有效性。
本文将通过对基于因子分析的股票技术指标评价进行探讨,帮助投资者更好地理解和运用技术指标。
一、因子分析在股票技术指标评价中的应用因子分析是一种用于发现多个相互关联变量之间共同变异的统计方法。
在股票技术指标评价中,投资者通常将多个指标作为分析对象,以求得相互关联的指标的共同变异特征,从而可以简化冗余信息,提取主要信息特征。
因子分析的基本思想是将多个相关指标综合为少数几个综合指标,通过降维和提取主要信息特征,简化问题的复杂度,从而更好地进行分析和决策。
因子分析在股票技术指标评价中具有很高的应用价值。
在股票技术指标评价中,因子分析可以运用在以下几个方面:1. 提取主要技术指标特征。
通过对不同的技术指标进行因子分析,可以发现其共同的变异特征,从而提取主要的市场信息特征,简化技术指标的分析和应用。
2. 评价技术指标的有效性。
通过对技术指标进行因子分析,可以发现其共同变异的模式和特点,从而评价技术指标的有效性和适用性,帮助投资者筛选和确定合适的技术指标。
3. 构建综合指标体系。
通过对多个相关的技术指标进行因子分析,可以构建出综合的指标体系,更全面地反映市场的变化和趋势,提高投资决策的准确性和稳定性。
在进行基于因子分析的股票技术指标评价时,需要注意以下几点:1. 选择合适的技术指标。
需要选择一些具有代表性和关联性的技术指标进行分析评价,避免出现选取冗余和无关的指标,影响因子分析结果的准确性和稳定性。
2. 合理设置因子分析参数。
在进行因子分析时,需要合理设置因子数和旋转方法,以确保提取结果具有较好的解释性和可解释性。
因子分析在教育质量评估中的应用指南(六)

因子分析在教育质量评估中的应用指南教育质量评估是教育领域的一个重要议题,对于学校、教师以及学生的成长和发展至关重要。
因子分析作为一种统计学方法,在教育质量评估中发挥着重要的作用。
本文将从因子分析的基本理论、应用步骤以及在教育质量评估中的具体应用进行探讨,旨在为教育工作者提供一份实用的应用指南。
一、因子分析的基本理论因子分析是一种多元统计技术,旨在发现变量之间的内在结构和相关关系。
在教育领域,因子分析常常被用来分析学生的学习成绩、学习动机、学习兴趣等方面的数据,从而揭示出潜在的内在特征和结构。
通过因子分析,可以将多个变量归纳为较少的几个因子,从而简化数据分析和解释。
在进行因子分析时,需考虑以下几个基本概念:共性方差、特殊方差、因子载荷矩阵、旋转等。
共性方差是指多个变量共同所具有的方差,而特殊方差则是每个变量特有的方差。
因子载荷矩阵则反映了变量与因子之间的相关程度,通过旋转可以更好地理解因子之间的关系。
理解这些基本概念对于进行因子分析至关重要。
二、因子分析的应用步骤在进行因子分析时,需要经过一系列的步骤,包括数据收集、数据预处理、因子提取、因子旋转和结果解释等。
首先,需要收集与教育质量评估相关的数据,可以是学生的成绩、问卷调查结果等。
接着,对数据进行预处理,包括数据清洗、缺失值处理、标准化等,以保证因子分析结果的准确性。
在因子提取阶段,可以使用主成分分析或者最大方差法来提取公共因子。
通过提取出的公共因子,可以简化数据结构,帮助我们更好地理解数据的内在特征。
而在因子旋转阶段,可以通过正交旋转或者斜交旋转来得到更加清晰、可解释的因子结构。
最后,需要对因子分析的结果进行解释和应用,以指导教育质量评估的实际工作。
三、因子分析在教育质量评估中的具体应用因子分析在教育质量评估中有着广泛的应用。
例如,在学生综合素质评价方面,可以通过因子分析揭示出不同维度的素质特征,如学习成绩、学科能力、学习动机等,从而更全面地评估学生的素质。
因子分析法在中小板块上市公司综合业绩评价中的应用

因子分析法在中小板块上市公司综合业绩评价中的应用从理论层面来看,因子分析法是一种基于统计学原理的分析方法,可以将多个指标综合起来,评价企业的综合业绩。
通过因子分析,可以将大量指标降维至少数几个通用因子,通过这些通用因子来评价企业的业绩,从而更加简洁和全面地评估企业的表现。
在综合业绩评价中,我们通常需要考察企业的多个方面,包括财务状况、经营能力、管理水平、市场竞争力等等。
而这些方面通常涉及多个指标,例如资产负债表、利润表、现金流量表等财务指标,同时还包括企业的市场份额、市场增长率、市场开拓能力等非财务指标。
因此,使用因子分析可以将这些复杂的指标体系转化为更少的几个因子,简化评价的过程。
在应用层面,因子分析法可以通过以下步骤来评价中小板块上市公司的综合业绩:第一步,确定评价指标。
在综合评价中,我们需要选取适合的指标来评价企业的综合业绩。
这些指标可以包括财务指标、非财务指标以及自定义的指标。
选取指标时需要考虑指标的客观性、可量化性和代表性。
第二步,进行因子分析。
在因子分析中,需要对选定的指标进行数据处理和变换,例如标准化处理或对数化处理。
然后使用因子分析方法,通过计算主成分或因子得分,将多个指标降维至少数几个通用因子。
第三步,解释因子结果。
在因子分析中,我们可以通过因子载荷矩阵和因子解释度等方式来解释因子结果。
因子载荷矩阵可以帮助我们理解每个指标与因子之间的关系,根据各指标在不同因子上的载荷大小,可以进行因子命名和因子解释。
第四步,评价企业综合业绩。
通过计算企业在各个因子上的得分,可以得到企业在不同方面的综合表现。
根据因子得分的大小,可以对企业的综合业绩进行排名和评价。
首先,因子分析法能够对庞杂的指标体系进行降维处理,简化评价的过程。
这样既能减少冗余指标的影响,又能保留重要指标的信息。
其次,因子分析法能够更准确地反映企业的综合业绩。
通过综合考虑多个指标,可以更全面地评估企业的表现,避免单一指标的片面性。
因子分析法在我国区域综合经济实力评价中的应用

( 江西农业大学经贸学院,江西 南昌 304) 305
ቤተ መጻሕፍቲ ባይዱ
摘要 :文章依 据 区域 经济发展 理论和我 国的 实际情况 。选 为公共 因子 , f l , ) ( , … 为特殊因子。下面结合主成分 因子分 =2
取反映 经济发展规模与水平的七项指标 ,运 用因子分析法对我 析法 ,根据实际情况整理出来的分析步骤 :
一
、
引言
4 解特 . 征值l一 E= , R 2 I0 计算相关矩阵的 特征值 , 若
≥ … ≥ 0,则根据方差 累计贡献率 ( 一般 取值在8 %以 5
我 国自从改革开放 以来 ,经济建设取得了令 人瞩 目的成绩 。
区的经济实力。本文 在遵循科学性 、完整性 、可 比性 和可操作
具体的指标如下 :
行标准化 , 可建立变量的相关系数矩阵R 的特征值及贡献率 。R
表1R的特征值和贡献率
所 国内生产总值,反 映一省 的经济 总量 ;全 社会固定 资产投 如 表 1 示 :
资 ,反映一省的总体投 资水平 ;社会 消费品零售总额 ,反映一 省的总体消费水平 ;进出 口商品总值 ,反 映一省总体 外贸水平 ; 实际利用外商投资额 ,反映一省 的外资 利用水平 ;教育经费 , 反映一省的教育投 资水平 ;年底 就业人员 数 ,反映一省的总体
国各 地 区的 统 计 数 据 进行 综合 评 价 。依 此反 映 我 国各 地 区的 综
1 .建立指标体系和原始矩阵z 。
合经济实力,为各地 区的发展提供参考。
关键词 :综合经济实力;因子分析 ;实证分析
2 .原始数据标准化 ,得到标准化矩阵x ( 个指标存在 如各 数据单位不 同,或者数量级不同) 。 3 .计算z 或者x 得相关系数矩 阵R。
因子分析在教育质量评估中的应用指南(四)

因子分析在教育质量评估中的应用指南在当今社会,教育质量的评估越来越受到重视。
学校、教育机构和政府部门都希望能够通过科学的方法来评估教育质量,从而为教育改进和决策提供依据。
因子分析作为一种多元统计分析方法,被广泛应用于教育质量评估中。
本文将探讨因子分析在教育质量评估中的应用指南,希望能够为相关研究和实践提供一定的指导。
一、因子分析的基本原理首先,我们需要了解因子分析的基本原理。
因子分析是一种用于揭示变量之间关联结构的统计方法。
它可以帮助我们理解多个变量之间的内在联系,将多个相关变量归纳为较少的几个因子,从而简化数据分析和解释。
在教育质量评估中,我们可以使用因子分析来分析学生的学术成绩、学习动机、学习环境等多个指标,揭示它们之间的内在联系和结构。
二、因子分析在教育质量评估中的应用接下来,我们将探讨因子分析在教育质量评估中的具体应用。
首先,我们可以利用因子分析来构建教育质量评估的指标体系。
通过对学生的学术成绩、学习动机、学习环境等多个指标进行因子分析,我们可以得到几个关键因子,如学习成绩因子、学习动机因子、学习环境因子等,从而构建一个更加全面和准确的教育质量评估指标体系。
其次,因子分析还可以帮助我们识别影响教育质量的关键因素。
通过对学生的各项指标进行因子分析,我们可以找到影响学生成绩的关键因素,如学习动机、学习方法、家庭教育背景等。
这有助于学校和教育机构找出影响教育质量的关键因素,从而有针对性地进行改进和干预。
另外,因子分析还可以帮助我们进行不同学校、不同地区教育质量的比较。
通过对不同学校、不同地区学生的各项指标进行因子分析,我们可以揭示它们之间的异同,找出各自的优势和不足,为教育改进和政策决策提供依据。
三、因子分析在教育质量评估中的应用指南最后,我们将总结因子分析在教育质量评估中的应用指南。
首先,进行因子分析前,需要明确研究的目的和问题,明确分析的变量和数据类型。
其次,要选择合适的因子提取方法和旋转方法,确保得到可靠和有效的因子结构。
因子分析在学生成绩综合评价中的应用

因子分析在学生成绩综合评价中的应用
张永福;赵洪章;穆扬
【期刊名称】《现代电子技术》
【年(卷),期】2008(31)6
【摘要】在教学管理中,需要科学合理地对学生成绩进行综合评价.目前,应用较多的如简单相加法和标准分法都存在各种缺点.运用主成分分析的方法对学生成绩进行因子分析,并通过分析的结果做出一个综合评价,这样可以比较有效地解决其他分析方法存在的问题.通过对学生在校期间各科成绩进行因子分析的具体实例研究,找出影响学生知识和能力的主要方面因子,并据此对学生成绩做出一个客观、综合的评价.
【总页数】4页(P137-140)
【作者】张永福;赵洪章;穆扬
【作者单位】西北工业大学,航天学院,陕西,西安,710072;西北工业大学,航天学院,陕西,西安,710072;西北工业大学,教育实验学院,陕西,西安,710072
【正文语种】中文
【中图分类】TP391;O212
【相关文献】
1.因子分析在学生成绩综合评价中的应用 [J], 杨宝军
2.因子分析在学生成绩综合评价中的应用 [J], 张琼
3.因子分析法在学生Java成绩及学习行为中的应用 [J], 贺红敏;张艳
4.因子分析法在学生成绩综合评价中的应用 [J], 韩宇;包红
5.因子分析与聚类分析在学生成绩综合评价中的应用 [J], 田宏;于晓秋
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题讲座??>>??正文专题讲座??>>??正文浅谈因子分析在多指标综合评价中的运用(上)* 2012-12一、相关概念简介1.综合评价简介所谓综合评价是指对以多属性体系结构描述的对象系统作出全局性、整体性的评价,即对评价对象的全体,根据所给的条件,采用一定的方法给每个评价对象赋予一个评价值(又称评价指数),再据此择优或排序的过程。
常见的综合评价方法有主成分法、基于主成分的因子分析法、熵权法,以及基于模糊数学的多层模糊综合评判法,等等。
2.因子分析简介:因子分析是利用降维的思想,在力保数据丢失最少的原则下,对高维变量空间进行降维处理,把多指标转化为少数几个综合指标的多元统计分析方法。
它的特点是在评价指标的相关性比较高时,能消除指标间信息的重叠,而且根据指标所提供的原始信息生成非人为的权重系数。
采用因子分析法进行多指标的综合评价具有以下优势:因子分析的降维处理技术能较好地解决多指标评价的要求。
1. 因子分析将原始变量变换为主因子的过程中, 同时形成了反映成分和指标包含信息量的权数, 以计算综合评价值, 这比人为地确定权数更为客观有效, 也有助于保证真实地反映样本间的现实关系。
2. 减少了指标选择的工作量。
在因子分析中由于可以消除评价指标间的相关影响, 因而在指标选择上相对容易些,另外因子分析可以保留原始评价指标的大部分信息。
3. 随着电子计算机技术的发展, SAS、SPSS等商品化统计分析软件的推广与应用, 使得因子分析在各类综合评价实践中的广泛应用成为现实。
基于上述几点,因子分析法在各类综合指标评估中得以广泛应用。
二、因子分析法在综合评估中的运用(实例讲解)下面,笔者将以某项目的多指标综合评估分析过程为例进行详细讲解。
需要说明的是,在进行综合评估之前,首要的工作是建立一套可靠完整的指标体系。
而确立评估指标的方法很多,包括主观、客观法,如常见的Delphi专家评估法、灰色关联度分析法、极小极大离差法和最小均方差法,等等。
本例采取的是专家评估法,限于篇幅,在此不再赘述,本文是假定已完成指标体系的建立及数据无量纲处理的前提下,进行的分析过程。
1.步骤一:数据检验在进行因子分析前,应检验数据间的相关性程度,判断是否适合采用因子分析。
1)KMO检验:KMO检验:是用于比较变量间简单相关系数和偏相关系数的指标,KMO统计量是取值在0和1之间。
当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO值接越近1,意味着变量间的相关性越强,原有变量越适合作因子分析;当所有变量间的简单相关系数平方和接近0时,意味着变量间的相关性越弱,原有变量越不适合作因子分析。
KMO 值在0.9以上表示非常适合;0.8表示适合;0.7表示一般;0.5以下表示极不适合。
2)巴特利球型检验:用于检验相关矩阵是否是单位矩阵,即各变量是否独立。
它是以变量的相关系数矩阵为出发点,零假设:相关系数矩阵是一个单位矩阵。
如果统计值较大,且对应的相伴概率值小于用户给定的显著性水平,则应拒绝零假设,即各变量间存在公因子;反之,则不能拒绝零假设,认为相关系数矩阵可能是一个单位阵,这些变量间可能各自独立提供一些信息,缺少公因子,不适合做因子分析。
3)实例数据SPSS软件操作过程:Analyze——Data Reduction——Factor,在因子分析主对话框中,点击Descriptives,然后勾选KMO and Bartlett's Test of Sphericity。
下表1是本例的输出结果:KMO>0.5满足分析的要求;其次,巴特利球体检验统计值为P = 0. 000 <0. 05 ,可以拒绝零假设,证明各变量间存在公因子,通过了显著度检验。
小结:本文简单介绍了综合评价及因子分析的相关概念,了解了因子分析的数据检验要求及操作过程。
限于篇幅,我们将在下次继续讲解本例的实证分析结果。
浅谈因子分析方法在多指标综合评价中的运用(下)* 2013-06在上一篇专题文章之中,笔者简单介绍了多指标综合评价的相关概念及方法,了解了因子分析数据检验要求及操作过程,本次将为大家继续讲解相关的操作步骤及实证分析结果。
一、实证结果分析一:主因子的提取和确定???依据因子分析的原理,运用统计软件SPSS16.0进行分析,可得到10个指标相关矩阵R 的特征值、方差贡献率和累计方差贡献率,如表2所示。
按照特征值λ>1 的原则,选出5个主因子,其旋转前的累计方差贡献率为75.020%(即前5个主因子可以解释75%的方差),表明选取5个主要成分因子就能基本反映原指标的信息。
而旋转后5个主因子的累计方差贡献率仍为75.020%,表明因子旋转不改变模型对数据的拟合。
一、实证结果分析二:主因子的命名及解释?? 在因子分子中,计算指标的载荷矩阵时,一般需进行因子旋转,使得各个因子的典型代表指标意义更为明确,我们利用spss 软件将主因子经过正交旋转后,其载荷矩阵见表3。
由表3的因子载荷矩阵可以看出:第一个因子在X2、X3上有较大载荷,称之为投诉客户因子;第二个因子在X6、X7上有较大载荷,称之为投诉责任因子;第三个因子在X4、X5上有较大载荷,我们称之为投诉处理满意度因子;第四个因子在X1、X8、X9上有较大载荷,称为投诉焦点因子;第五个因子在X10上有较大载荷,称之为投诉频率因子。
一、实证结果分析三:因子表达式?? 根据spss统计软件我们得到旋转后各主因子的得分系数矩阵(见下表4),则旋转后的因子得分表达式为:?? 投诉客户因子得分F1=0.097*X1+0.492 *X2+0.492*X3+(-0.002)*X4+……+0.033*X10,同理可得:???投诉责任因子得分F2=(-0.028)*X1+0.000*X2……+0.007*X10?? 投诉满意度因子得分F3=(-0.005)*X1+(-0.008)*X2……+0.007*X10?? 投诉焦点因子得分F4=(-0.539)*X 1+0.013*X2……+(-0.144)*X10?? 投诉频率因子得分F5=0.127*X1+0.014*X 2+……+0.876*X10??(注意:Xi为每个投诉用户在该指标上的原始得分经过标准化处理后的值)且从下表5的因子得分协方差矩阵可以看出,旋转后因子间已无相关关系,说明因子提取是成功的。
二、投诉综合评估模型的构建?? 根据实证结果一,我们得到各因子的方差贡献率Wi (这里我们选取的是旋转后的方差贡献率,见附表A) ,可以据此确定各因子的权重系数,进而构建投诉综合评价模型: (注:Wi为权重系数,即各因子的方差贡献率;Fi 为第i 个主因子相应的因子得分) F = W1*F1 + W2*F2 + W3*F3 + W4*F4 + W5*F5??????=19.38%*F1+18.68%*F2+15.93%*F3+10.65%*F4+10.39%*F5????????????????? (式一)根据实证结果三,我们已经得到了5个主因子F1—F5的的表达式(见附表B)。
现将附表B的表达式代入式一,即可算出每一个投诉用户的F值,F值即称为投诉综合评估因子得分。
结论:因子得分越高,表示该投诉用户的综合评定系数级别越高,越需要进行关系修复。
专题讲座??>>??正文SMART原则* 2013-04目标管理是管理人员常用的一种工具,通过实施目标管理不但是有利于员工更加明确高效地工作,更是为未来的绩效考核制定了目标和考核标准,但如何确定目标呢?既要保证目标科学可行,又要能尽可能激发员工的潜能,灵活运用SMART原则可以帮助我们。
SMART原则首次出现在1981年12月发行的《管理评论》, SMART是五个英文字母的开头,分别是:S=Specific、M=Measurable、A=Attainable、R=Realistic、T=Time-based,目标确定的SMART原则具体内容如下:1. 目标必须是具体的(Specific)指要用具体的语言清楚地说明要达成的行为标准。
明确的目标几乎是所有成功团队的一致特点。
2. 目标必须是可以衡量的(Measurable)衡量性就是指目标应该是明确的,而不是模糊的。
应该有一组明确的数据,作为衡量是否达成目标的依据。
3. 目标必须是可以达到的(Attainable)目标是要可以让执行人实现、达到的,如果上司利用一些行政手段,利用权利性的影响力一厢情愿地把自己所制定的目标强压给下属,下属典型的反映是一种心理和行为上的抗拒:“我可以接受,但是否完成这个目标,有没有最终的把握,这个可不好说。
”一旦有一天这个目标真完成不了的时候,下属有一百个理由可以推卸责任:“你看我早就说了,这个目标肯定完成不了,但你坚持要压给我。
”4. 目标必须和其他目标具有相关性(Relevant)目标的相关性是指实现此目标与其他目标的关联情况。
如果实现了这个目标,但对其他的目标完全不相关,或者相关度很低,那这个目标即使被达到了,意义也不是很大。
5. 目标必须具有明确的截止期限(Time-based)目标特性的时限性就是指目标是有时间限制的。
无论是制定团队的工作目标还是员工的绩效目标都必须符合上述原则,五个原则缺一不可。
制定的过程也是自身能力不断增长的过程,管理人员必须和员工一起在不断制定高绩效目标的过程中共同提高绩效能力。
专题讲座??>>??正文浅谈用户细分* 2012-12用户细分是指根据用户属性划分的客户集合,它是分门别类研究用户、进行有效用户评估、合理分配服务资源、成功实施用户策略的基本原则之一,为企业充分获取用户价值提供理论和方法指导;用户细分理论原理是:每类产品的用户群不是一个群体,根据用户群的文化观念,消费收入、消费习俗、生活方式的不同细分新的类别,企业根据消费者的不同制定品牌推广战略和营销策略,将资源针对目标用户集中使用。
——————————以上摘自互联网————————说到用户细分,其实在一般消费者研究过程中或多或少的涉及到了,以通信领域的研究而言,我们常把用户分为企业用户、个人用户等,或者根据区域性质划分为华南地区、华东地区等等,这种细分就比较简单、直观,数据采集也比较容易,我们把这称为按照外在属性的划分。
通常消费者调研中,我们都会收集消费者的背景统计资料,诸如性别、年龄、学历、收入、婚姻状况等,这则属于按照内在属性分类,通过各种背景属性分类的分析,我们就可以把用户划分为多种类型,为策略的制定提供更精准的建议。
当然,不少行业(如通信、医药)的研究往往还要深入考虑分析消费者的行为,比如话费量、流量开支、比如药品的用量、使用行为习惯等;通过对这些变量的分类进行深入分析,往往能够找出用户中的特点为市场营销活动找到对策。
