弹性力学(徐芝纶)课后习题及答案
弹性力学简明教程第三版徐芝纶课后答案与讲解最全版免费

课后答性力学简明教程第三版徐芝纶课后答案详尽版弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第三版徐芝纶弹性力学简明教程第
徐芝纶弹性力学第三版习题解答

⎞ ⎟ ⎠P
dxdy
+
式中
⎛ ⎜⎝
∂f ∂x
⎞ ⎟⎠P
,
⎛ ⎜ ⎝
∂f ∂y
⎞ ⎟ ⎠P
等表示在点
(
xP
,
yP
)
处的一阶偏导数。
若设 f (x + dx, y) = σ y (x, y) 并令 dy = 0 ,得
5
σyA
=σy
+
∂σ y ∂x
dx
+
1 2
∂2σ y ∂x2
dx2
+
1 6
∂3σ y ∂x3
=
1 E
⎣⎡σ x
−
μ
σy +σz
⎦⎤
=
1− μ E
2
⎛⎜σ ⎝
x
−
μ 1− μ
σ
y
⎞⎪
⎟ ⎠
⎪⎪
⎬
(c)
εy
=
1 E
⎣⎡σ y
−
μ (σ z
+ σ x )⎤⎦
=
1− μ2 E
⎛ ⎜ ⎝
σ
y
−μ 1− μ
σx
⎞⎪ ⎟⎠⎪⎪
γ xy
=
1 G
τ
xy
,
γ
zx
=
1 G
τ
zx
=
0, γ
yz
=
1 G
τ
yz
=
0
⎪ ⎪⎭
解:设薄层的厚度为 δ ,由于 z 方向不受力,即 σ z = τ zx = τ zy = 0
若薄层足够小,则可认为在其厚度 δ 范围内上述三应力保持与表
面一致,考虑上述近似,则有
弹性力学(徐芝纶)前四章习题答案

著应力,对远处影响忽略不计。
3.解:平衡微分方程组为:
3
其中
fx
V x
V , f y y .
x x
yx y
fx
0
y
y
xy x
fy
0
取该方程组的一组特解: x V , y V , xy 0
齐次方程组
x x y
y
yx y
xy x
0
的通解为
0
所以微分平衡方程组的解为
界条件。
(4)位移单值条件为:令应力分量表达式中可能留有的待定函数或待定常数通过积分产生
的多值项为 0。
1
2.解:
1
F X
Y 图a
F
X
Y 图b
h Z
Y 图c
(1) 在图 b 中,我们由剪力平衡方程和弯矩平衡方程得到:
1
F Q 0 ,即 Q F
M Fx 0 ,即 M Fx
在图 a 中,有:
4
4
x(3h 2 A hB C) 0 即 3h 2 A hB C 0
4
4
以上四式联立得:
A
2 g h2
,
B
0, C
3 g 2h
,
D
g 2
代入(a),并注意 E F G 0 得:
x
6 g h2
x2 y+
4 g h2
y3
6Hy
2K
y
2 g h2
y3
3 g 2h
y
gy
g 2
xy
x
2 y 2
y
2 x2
xy
2 xy
x
2 y 2
V
y
徐芝纶编《弹性力学简明教程》第四版__全部章节课后答案详解

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
徐芝纶编《弹性力学简明教程》第四版,全部章节课后答案解析详细讲解

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
弹性力学徐芝纶课后习题答案
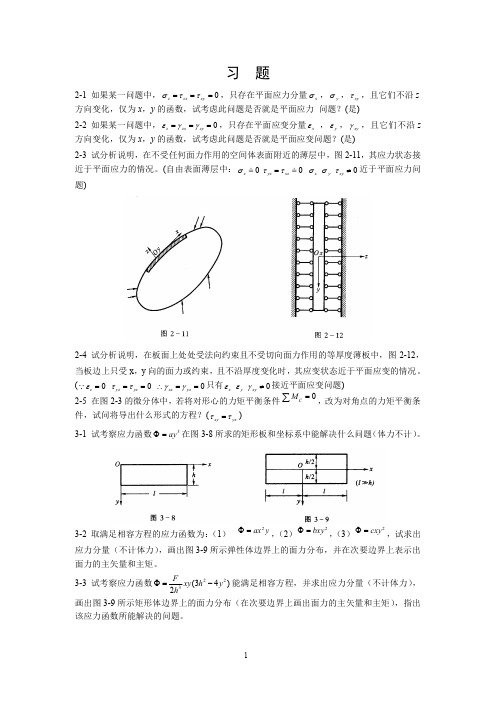
3、边界条件定常数: ( xy ) x 0 0
( xy ) x b q
q A 2 (3 Ab2 2 Bb) q b b q 上端面 0 ( xy ) dx 0 Ab3 Bb2 0 即Ab B 0 y 0 B b
U 2 Fxy 3 3Fxy h3 2h
(1)
U
qx 2 4
4 y 3 3 y qy 2 2 y 3 y 1 3 3 (2) h h h 10 h
应力分 量
x xy
12 Fxy , y 0 h3 2 6 Fy 3F 3 h 2h
2 2 f x 0 x y 2 y 2 f ( x) y 4 0 x 2 y 2 yf ( x ) f1 ( x ) 4 0 y 4
4 d 4 f ( x ) d 4 f1 ( x ) y x 4 dx 4 dx 4
4 0 即 y
d 4 f ( x) 0 dx 4 d 4 f1 ( x ) 0 dx 4
d 4 f ( x ) d 4 f1 ( x ) 0 对 y 的任意值均成立则有: dx 4 dx 4
f ( x ) Ax 3 Bx 2 Cx (略去了与应力无关的常数项 ) f1 ( x ) Ex 3 Fx 2 (略去了与应力无关的常数项及次项 )
0 ( y ) y 0 dy 0 0 ( y ) y 0 xdx 0
则 x 0 y
b
b
3Eb 2 F 0 E F 0 2 Eb F 0
习
题
2-1 如果某一问题中, z zx xy 0 ,只存在平面应力分量 x , y , xy ,且它们不沿 z 方向变化,仅为 x,y 的函数,试考虑此问题是否就是平面应力 问题?(是) 2-2 如果某一问题中, z zx zy 0 ,只存在平面应变分量 x , y , xy ,且它们不沿 z 方向变化,仅为 x,y 的函数,试考虑此问题是否就是平面应变问题? (是) 2-3 试分析说明,在不受任何面力作用的空间体表面附近的薄层中,图 2-11,其应力状态接 近于平面应力的情况。(自由表面薄层中: z 0 yz xz 0 x y xy 0 近于平面应力问 题)
弹性力学(徐芝纶)习题答案

第一章第二章习题答案2-1解:已知 0,0,===-==y x xy y x f f q τσσ1)⎪⎪⎩⎪⎪⎨⎧+∂∂+∂∂+∂∂+∂∂y xy y x yxx f x yf yx τστσ23()()⎩⎨⎧=+=+s xy y s yx x l m m l σστστσ 有:t lq t x -=;代入(*4理、几何方程得:(E x u x ==∂∂ε1(1E y v y ==∂∂ε0==∂∂+∂∂xy yux v γ ()()⇒=+∴0dyy df dx x dg 类似于教材题2-3,可求出 ()()wx v x g wy u y f +=-=00,001;1v wx qy Ev u wy qx Eu ++--=+---=∴υυ从v u ,表达式可见,位移分量是坐标的单值函数,满足位移单值条件。
综合1)~4),。
q xy y x 为问题的正确解答0,=-==τσσ2-2x =σxy τ注意:y x ,代入均满足。
2)验证相容方程:0)(2=+∇y x σσ 亦满足。
3)验证应力边界条件: i) 主要边界:()0,2=±=hy yxy τσ 满足ii) 次要边界:()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧===⎰⎰⎰-=-=-=222222320)1(0h h lx xy h h l x x h h l x x Pdy ydy dy τσσ (1)、(2)满足,(3)式左=⎰-===⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-223332212*41*618218hh P h I P h h I P dy y h I P 右 结论:所列xy y x τσσ,,满足平衡方程、相容方程;在主要边界上严格满足应力边界条件,次要边界近似满足应力边界条件,又为单连体,故在圣维南原理的前提下为问题的正确解。
2-3、证明:1)由,,yVf xV fy x∂∂-=∂∂-=则平衡微分方程为: ()()⎪⎪⎩⎪⎪⎨⎧=∂τ∂+∂-σ∂=∂τ∂+∂-σ∂⇒⎪⎪⎩⎪⎪⎨⎧=∂∂-∂τ∂+∂σ∂=∂∂-∂τ∂+∂σ∂0x y V 0yx V 0y V x y 0x V y x yx y xyx yx y xy x (*) 类似于题2-10的推证过程,(*)式的通解为:y x x V yV 2xy 22y 22x ∂∂ϕ∂-=τ∂ϕ∂=-σ∂ϕ∂=-σ;;即: yx V xV y2xy 22y 22x ∂∂ϕ∂-=τ+∂ϕ∂=σ+∂ϕ∂=σ;;2) 对于平面应力问题,相容方程为:()()⎪⎪⎭⎫⎝⎛∂∂+∂∂+-=+∇y f x f y x y x υσσ12即:2222 2-4、x, y n l σσ2==2l应力主向成∴l()2121σσσ+=n 得证。
弹性-徐志伦-课后练习及答案.doc

弹性-徐志伦-课后练习及答案
弹性——徐志伦——课后练习与回答你也许最终无法环游世界,但你发现自己正在实现自己的梦想。
那就是能为一个目标默默工作,不抱怨,不浮躁,不怕孤独,默默耕耘的自己。
也许你想努力追求的梦想已经在你手中。
我们会感到焦虑,只是因为我们远离想象中的自己,不喜欢现在的自己。
只有通过拼命地寻找改变的方法,只有通过立即行动,因为只有你能做到这一点,只有你能找到出口。
不要害怕改变,真正爱你的人会理解你,会容忍你的缺点,接受你的改变,并祝福你的未来。
那些说你已经改变的人,不要去注意他们,那只是因为你不再遵循他们想要的生活道路。
记住那些和你在一起的人,那些理解你沉默的人,那些说你已经变了并且远离你的人。
事实上,直到有一天你发现你周围所有的支撑点都倒下了,而你也没有倒下,你才会发现自己有多强大。
除了你自己,没有人能打败你。
你必须学会捂住耳朵,不要听喧嚣。
这个世界上没有不痛苦的人,只有你能治愈自己。
总有一天,我们会变得足够强大,没有什么能扰乱我们内心的平静。
欢迎来到我们公司。
下载后可以编辑word文档。
双击以删除页眉和页脚。
谢谢!简单的教科书内容不能满足学生的需要。
教育中常见的问题是教大脑的人不使用手,不使用手的人使用大脑,所以他们什么也做不了。
教育革命的对策是手脑联盟。
因此,双手和大脑的力量都是不可思议的。
单词模型。
弹性力学简明教程(第四版)_课后习题解答(完整资料).doc

【最新整理,下载后即可编辑】弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
弹性力学简明教程(第四版)_课后习题解答

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例解释什么是平均的各向异性体,什么长短平均的各向同性体?【剖析】平均的各项异形体就是知足平均性假定,但不知足各向同性假定;非平均的各向异性体,就是不知足平均性假定,但知足各向同性假定.【解答】平均的各项异形体如:竹材,木材.非平均的各向同性体如:混凝土.【1-2】一般的混凝土构件和钢筋混凝土构件可否作为幻想弹性体?一般的岩质地基和土质地基可否作为幻想弹性体?【剖析】可否作为幻想弹性体,要剖断可否知足四个假定:持续性,完整弹性,平均性,各向同性假定.【解答】一般的混凝土构件和土质地基可以作为幻想弹性体;一般的钢筋混凝土构件和岩质地基不成以作为幻想弹性体.【1-3】五个根本假定在树立弹性力学根本方程时有什么感化?【解答】(1)持续性假定:假定物体是持续的,也就是假定全部物体的体积都被构成这个物体的介质所填满,不留下任何闲暇.引用这一假定后,物体的应力.形变和位移等物理量就可以算作是持续的.是以,树立弹性力学的根本方程时就可以用坐标的持续函数来暗示他们的变更纪律.完整弹性假定:假定物体是完整弹性的,即物体在对应形变的外力被去除后,可以或许完整恢回复复兴型而无任何形变.这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变屈服胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变.平均性假定:假定物体是平均的,即全部物体是由统一材料构成的,引用这一假定后全部物体的所有各部分才具有雷同的弹性,所研讨物体的内部各质点的物理性质都是雷同的,因而物体的弹性常数不随地位坐标而变更.各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个偏向都雷同,引用此假定后,物体的弹性常数不随偏向而变.小变形假定:假定位移和变形是渺小的.亦即,假定物体受力今后全部物体所有各点的位移都远远小于物体本来的尺寸,并且应变和转角都远小于 1.如许在树立物体变形今后的均衡方程时,就可以便利的用变形以前的尺寸来代替变形今后的尺寸.在考核物体的位移与形变的关系时,它们的二次幂或乘积相对于其本身都可以略去不计,使得弹性力学中的微分方程都简化为线性的微分方程.【1-4】应力和面力的符号划定有什么差别?试画出正坐标面和负坐标面上的正的应力和正的面力的偏向.【解答】应力的符号划定是:当感化面的外法线偏向指向坐标轴偏向时(即正面时),这个面上的应力(不管是正应力照样切应力)以沿坐标轴的正偏向为正,沿坐标轴的负偏向为负.当感化面的外法线指向坐标轴的负偏向时(即负面时),该面上的应力以沿坐标轴的负偏向为正,沿坐标轴的正偏向为负.面力的符号划定是:当面力的指向沿坐标轴的正偏向时为正,沿坐标轴的负偏向为负.由下图可以看出,正面上应力分量与面力分量同号,负面上应力分量与面力分量符号相反.正的应力正的面力【1-5】试比较弹性力学和材料力学中关于切应力的符号划定.【解答】材料力学中划定切应力符号以使研讨对象顺时针迁移转变的切应力为正,反之为负.弹性力学中划定,感化于正坐标面上的切应力以沿坐标轴的正偏向为正,感化于负坐标面上的切应力以沿坐标轴负偏向为正,反之为负.【1-6】试举例解释正的应力对应于正的形变.【解答】正的应力包含正的正应力与正的切应力,正的形变包含正的正应变与正的切应变,本题应从两方面解答.正的正应力对应于正的正应变:轴向拉伸情形下,产生轴向拉应力为正的应力,引起轴向伸长变形,为正的应变.正的切应力对应于正的切应变:在如图所示应力状况情形下,切应力均为正的切应力,引起直角减小,故为正的切应变.【1-7】试画出图1-4中矩形薄板的正的体力.面力和应力的偏向.【解答】正的体力.面力正的体力.应力【1-8】试画出图1-5中三角形薄板的正的面力和体力的偏向. 【解答】【1-9】在图1-3的六面体上,y 面上切应力yz τ的合力与z 面上切应力zy τ的合力是否相等?【解答】切应力为单位面上的力,量纲为12L MT --,单位为2/N m .是以,应力的合力应乘以响应的面积,设六面体微元尺寸如dx ×dy ×dz ,则y 面上切应力yz τ的合力为:yz dx dz τ⋅⋅ (a)z 面上切应力zy τ的合力为:zy dx dy τ⋅⋅ (b)由式(a )(b)可见,两个切应力的合力其实不相等.【剖析】感化在两个互相垂直面上并垂直于该两面交线的切应力的合力不相等,但对某点的合力矩相等,才导出切应力互等性.第二章 平面问题的根本理论【2-1】试剖析解释,在不受任何面力感化的空间体概况邻近的薄层中(图2-14)其应力状况接近于平面应力的情形.【解答】在不受任何面力感化的空间概况邻近的薄层中,可以以为在该薄层的高低概况都无面力,且在薄层内所有各点都有0===z xz yz σττ,只消失平面应力分量,,x y xy σστ,且它们不沿z 偏向变更,仅为x,y 的函数.可以以为此问题是平面应力问题.【2-2】试剖析解释,在板面上处处受法向束缚且不受切向面力感化的等厚度薄片中(2-15),当板边上只受x,y 向的面力或束缚,且不沿厚度变更时,其应变状况接近于平面应变的情形.【解答】板上处处受法向束缚时0z ε=,且不受切向面力感化,则0xz yz γγ==(响应0zx zy ττ==)板边上只受x,y 向的面力或束缚,所以仅消失,,x y xy εεγ,且不沿厚度变更,仅为x,y 的函数,故其应变状况接近于平面应变的情形.【2-3】在图2-3的微分体中,若将对形心的力矩平很前提CM0=∑改为对角点的力矩均衡前提,试问将导出什么情势的方程?【解答】将对形心的力矩均衡前提CM0=∑,改为分离对四个角点A.B.D.E 的均衡前提,为盘算便利,在z 偏向的尺寸取为单位1.0AM=∑1()1()11222()1()1110222xy x y x xy y y yx y yx x x dx dy dydx dx dy dx dy dx dy x x dx dy dx dy dx dy dx dy f dxdy f dxdy y y τσσστσστστ∂∂⋅⋅++⋅⋅-+⋅⋅-⋅⋅∂∂∂∂-+⋅⋅++⋅⋅+⋅⋅-⋅⋅=∂∂ (a)0BM=∑()1()1()1221111102222yx y x x yx y xy x y x y dy dxdx dy dy dx dy dy dx x y y dy dx dy dxdy dx dy dx f dxdy f dxdy τσσστστσσ∂∂∂+⋅⋅++⋅⋅++⋅⋅∂∂∂-⋅⋅-⋅⋅-⋅⋅+⋅⋅+⋅⋅= (b)Ozy0DM=∑()1111221()11102222yy xy x yx x x x x y dx dydy dx dy dx dy dx dyy dx dy dy dxdx dx dy f dxdy f dxdy x σστστσσσ∂+⋅⋅-⋅⋅+⋅⋅+⋅⋅∂∂-⋅⋅-+⋅⋅-⋅⋅+⋅⋅=∂ (c)0EM=∑()1111222()1()1110222yy x yx y xy x x xy x y dx dy dxdy dx dy dx dy dx y dy dy dxdx dy dx dy dx f dxdy f dxdy x x σσστστσστ∂-+⋅⋅+⋅⋅+⋅⋅+⋅⋅-∂∂∂+⋅⋅-+⋅⋅-⋅⋅+⋅⋅=∂∂ (d)略去(a).(b).(c).(d)中的三阶小量(亦即令22,d xdy dxd y 都趋于0),并将各式都除今后dxdy 归并同类项,分离得到xy yx ττ=.【剖析】由本题可得出结论:微分体对任一点取力矩均衡得到的成果都是验证了切应力互等定理.【2-4】在图2-3和微分体中,若斟酌每一面上的应力分量不是平均散布的,验证将导出什么情势的均衡微分方程?【解答】微分单元体ABCD 的边长,dx dy 都是微量,是以可以假设在各面上所受的应力如图a 所示,疏忽了二阶以上的高阶微量,而看作是线性散布的,如图(b )所示.为盘算便利,单元体在z 偏向的尺寸取为一个单位.)C)C(a) (b)各点正应力:()=x A x σσ;()=y A y σσ()xx B x dy yσσσ∂=+∂;()y y B y dy yσσσ∂=+∂()∂=+∂xx D x dx xσσσ;()∂=+∂xy D y dx xσσσ ()∂∂=++∂∂∂x xx C x dx y x yσσσσ; ()∂∂=++∂∂∂y y y C y dx y xyσσσσ各点切应力:()xy A xy ττ=;()yx A yx ττ=()∂=+∂xy xy B xy dy yτττ;()∂=+∂yx yx A yx dy yτττ()xy xy D xy dx x τττ∂=+∂;()∂=+∂yx yx D yx dx xτττ()xy xy xy C xy dx dy xyττττ∂∂=++∂∂;()∂∂=++∂∂yx yx yx C yx dx dy xyττττ由微分单元体的均衡前提 0,∑=x F 0,∑=y F 得112211+22x x x x x x x xyx yx yx yx yx yx yx yx dy dy dx dx dy dy y x x y y dx dx dy dx dy x y x y σσσσσσσστττττττ⎧⎧⎫⎫⎡⎤⎡⎤⎛⎫⎛⎫∂∂∂∂⎪⎪⎪⎪⎛⎫-+++++++-⎨⎬⎨⎬⎢⎥⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎪⎪⎣⎦⎣⎦⎪⎪⎭⎭⎩⎩⎧⎫⎡∂⎤⎡∂∂∂⎤⎛⎫⎛⎫⎛⎫⎪⎪++++++⎨⎬⎢⎥⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎪⎣⎦⎣⎦⎪⎭⎩0x dx f dxdy ⎧⎫⎪⎪+=⎨⎬⎪⎪⎭⎩112211+++22y y y y y y y y xy xy xy xy xy xy xy xy dx dx dy dx dy dx x y x y dy dy dx dy dx y x y x σσσσσσσσττττττττ⎧⎧⎫⎫⎡∂⎤⎡∂∂∂⎤⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪-+++++++-⎨⎬⎨⎬⎢⎥⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎪⎪⎣⎦⎣⎦⎪⎪⎭⎭⎩⎩⎧⎫⎡∂⎤⎡∂∂∂⎤⎛⎫⎛⎫⎛⎫⎪⎪++++⎨⎬⎢⎥⎢⎥ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎪⎣⎦⎣⎦⎪⎭⎩0y dy f dxdy ⎧⎫⎪⎪+=⎨⎬⎪⎪⎭⎩以上二式分离睁开并约简,再分离除以dxdy ,就得到平面问题中的均衡微分方程:0;0yxy xy x x y f f x y y xτστσ∂∂∂∂++=++=∂∂∂∂ 【剖析】由本题可以得出结论:弹性力学中的均衡微分方程实用于随意率性的应力散布情势. 【2-5】在导出平面问题的三套根本方程时,分离运用了哪些根本假定?这些方程的实用前提是什么?【解答】(1)在导出平面问题的均衡微分方程和几何方程时运用的根本假设是:物体的持续性和小变形假定,这两个前提同时也是这两套方程的实用前提.(2)在导出平面问题的物理方程时运用的根本假定是:持续性,完整弹性,平均性和各向同性假定,即幻想弹性体假定.同样,幻想弹性体的四个假定也是物理方程的运用前提.【思虑题】平面问题的三套根本方程推导进程中都用到了哪个假定?【2-6】在工地上技巧人员发明,当直径和厚度雷同的情形下,在自重感化下的钢圆环(接近平面应力问题)总比钢圆筒(接近平面应变问题)的变形大.试根据响应的物理方程来解释这种现象.【解答】体力雷同情形下,两类平面问题的均衡微分方程完整雷同,故所求的应力分量雷同.由物理方程可以看出,两类平面问题的物理方程重要的差别在于方程中含弹性常数的系数.因为E 为GPa 级此外量,而泊松比μ取值一般在(0,0.5),故重要掌握参数为含有弹性模量的系数项,比较两类平面问题的系数项,不难看出平面应力问题的系数1/E 要大于平面应变问题的系数()21/-E μ.是以,平面应力问题情形下应变要大,故钢圆环变形大.【2-7】在常体力,全体为应力鸿沟前提和单连体的前提下,对于不合材料的问题和两类平面问题的应力分量x σ,y σ和xy τ均雷同.试问其余的应力,应变和位移是否雷同?【解答】(1)应力分量:两类平面问题的应力分量x σ,y σ和xy τ均雷同,但平面应力问题0z yz xz σττ===,而平面应变问题的()0,xz yz z x y ττσμσσ===+.(2)应变分量:已知应力分量求应变分量须要运用物理方程,而两类平面问题的物理方程不雷同,故应变分量0,xz yz xy γγγ==雷同,而,,x y z εεε不雷同.(3)位移分量:因为位移分量要靠应变分量积分来求解,故位移分量对于两类平面问题也不合. 【2-8】在图2-16中,试导出无面力感化时AB 鸿沟上的xy ,,x y σστ之间的关系式【解答】由题可得:()()()cos ,cos 90sin 0,0x y l m f AB f AB ααα==-===将以上前提代入公式(2-15),得:()()()()()2cos sin 0, sin ()cos 0()tan tan x yx y xy AB AB AB AB x AB yx y ABABσατασαταστασα+=+=⇒=-=x图2-16【2-9】试列出图2-17,图2-18所示问题的全体鸿沟前提.在其端部小鸿沟上,运用圣维南道理列出三个积分的应力鸿沟前提.xM图2-17图2-18【剖析】有束缚的鸿沟上可斟酌采取位移鸿沟前提,若为小鸿沟也可写成圣维南道理的三个积分情势,大鸿沟上应准确知足公式(2-15).【解答】图2-17:上(y =0)左(x =0) 右(x =b )l0 -1 1 m-1() x f s()1g y h ρ+()1g y h ρ-+() yfs1gh ρ代入公式(2-15)得①在重要鸿沟上x=0,x=b 上准确知足应力鸿沟前提:()()100(),0;===-+=x xy x x g y h σρτ ()()1b b (),0;===-+=x xy x x g y h σρτ②在小鸿沟0y =上,能准确知足下列应力鸿沟前提:()(),0yxy y y gh σρτ===-=③在小鸿沟2y h =上,能准确知足下各位移鸿沟前提:()()220,0====y hy h u v这两个位移鸿沟前提可以运用圣维南道理,改用三个积分的应力鸿沟前提来代替,当板厚=1δ时,可求得固定端束缚反力分离为:10,,0s N F F gh b M ρ==-=因为2y h =为正面,故应力分量与面力分量同号,则有:()()()222100000b y y h by y h bxy y h dx gh b xdx dx σρστ===⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩⎰⎰⎰ ⑵图2-18①高低重要鸿沟y=-h/2,y=h/2上,应准确知足公式(2-15)m x y f 2h y =-0 -1 0 q2h y =1-1q-/2()y y h q σ==-,-/2()0yx y h τ==,/2()0y y h σ==,/21()yx y h q τ==-②在x =0的小鸿沟上,运用圣维南道理,列出三个积分的应力鸿沟前提:负面上应力与面力符号相反,有/20/2/20/2/20/2()()()h xy x Sh h x x N h h x x h dx Fdx F ydx M τσσ=-=-=-⎧=-⎪⎪=-⎨⎪⎪=-⎩⎰⎰⎰ ③在x=l 的小鸿沟上,可运用位移鸿沟前提0,0====l x l x v u 这两个位移鸿沟前提也可改用三个积分的应力鸿沟前提来代替.起首,求固定端束缚反力,按面力正偏向假设画反力,如图所示,列均衡方程求反力:110,xN NN N F F F q l F q l F ''=+=⇒=-∑ 0,0yS S S S FF F ql F ql F ''=++=⇒=--∑2211110,'02222A S S q lh ql M M M F l ql q lh M M F l =+++-=⇒=---∑因为x=l 为正面,应力分量与面力分量同号,故/21/22/21/2/2/2()()22()h x x l N Nh h x x l S h h xy x l S Sh dy F q l Fq lh ql ydy M M F l dy F ql Fσστ=-=-=-⎧'==-⎪⎪⎪'==---⎨⎪⎪'==--⎪⎩⎰⎰⎰M '【2-10】试运用圣维南道理,列出图2-19所示的两个问题中OA 边上的三个积分的应力鸿沟前提,并比较两者的面力是否是是静力等效?【解答】因为hl ,OA 为小鸿沟,故其上可用圣维南道理,写出三个积分的应力鸿沟前提:(a)上端面OA 面上面力q bx f f y x ==,0 因为OA 面为负面,故应力主矢.主矩与面力主矢.主矩符号相反,有()()()0000200000022120bb b y y y b b b y y y byx y x qb dx f dx qdx b x b qb xdx f xdx q x dx b dx σστ===⎧=-=-=-⎪⎪⎪⎛⎫=-=-=⎨ ⎪⎝⎭⎪⎪=⎪⎩⎰⎰⎰⎰⎰⎰⎰(对OA 中点取矩) (b)运用圣维南道理,负面上的应力主矢和主矩与面力主矢和主矩符号相反,面力主矢y 向为正,主矩为负,则()()()00200002120by N y by y b xy y qb dx F qb xdx M dx σστ===⎧=-=-⎪⎪⎪=-=⎨⎪⎪=⎪⎩⎰⎰⎰ 综上所述,在小鸿沟OA 上,两个问题的三个积分的应力鸿沟前提雷同,故这两个问题是静力等效的.【2-11】磨练平面问题中的位移分量是否为准确解答的前提是什么? 【解答】(1)在区域内用位移暗示的均衡微分方程式(2-18); (2)在s σ上用位移暗示的应力鸿沟前提式(2-19); (3)在u s 上的位移鸿沟前提式(2-14); 对于平面应变问题,需将E.μ作响应的变换.【剖析】此问题同时也是按位移求解平面应力问题时,位移分量必须知足的前提. 【2-12】磨练平面问题中的应力分量是否为准确解答的前提是什么? 【解答】(1)在区域A 内的均衡微分方程式(2-2);2qb 212qb 图2-19(2)在区域A内用应力暗示的相容方程式(2-21)或(2-22);(3)在鸿沟上的应力鸿沟前提式(2-15),个中假设只求解全体为应力鸿沟前提的问题; (4)对于多连体,还需知足位移单值前提.【剖析】此问题同时也是按应力图解平面问题时,应力分量必须知足的前提.【补题】磨练平面问题中的应变分量是否为准确解答的前提是什么?【解答】用应变暗示的相容方程式(2-20)【2-13】磨练平面问题中的应力函数是否为准确解答的前提是什么?【解答】(1)在区域A内用应力函数暗示的相容方程式(2-25);(2)在鸿沟S上的应力鸿沟前提式(2-15),假设全体为应力鸿沟前提;(3)若为多连体,还需知足位移单值前提.【剖析】此问题同时也是求解应力函数的前提.【2-14】磨练下列应力分量是否是图示问题的解答:图2-20 图2-21(a)图2-20,22xyqb,0==y xyστ.【解答】在单连体中磨练应力分量是否是图示问题的解答,必须知足:(1)均衡微分方程(2-2);(2)用应力暗示的相容方程(2-21);(3)应力鸿沟前提(2-15).(1)将应力分量代入均衡微分方程式,且0==x yf f∂∂+=∂∂yxxx yτσ∂∂+=∂∂y xyy xστ显然知足(2)将应力分量代入用应力暗示的相容方程式(2-21),有等式左=()2222x yx yσσ⎛⎫∂∂++⎪∂∂⎝⎭=22≠qb=右应力分量不知足相容方程.是以,该组应力分量不是图示问题的解答.(b)图2-21,由材料力学公式,=xMyIσ,*=sxyF SbIτ(取梁的厚度b=1),得出所示问题的解答:332=-x x y q lh σ,22233-(4)4=-xy q x h y lh τ.又根据均衡微分方程和鸿沟前提得出:333222=--y q xy xy q xq lh lh lσ.试导出上述公式,并磨练解答的准确性. 【解答】(1)推导公式在散布荷载感化下,梁产生曲折形变,梁横截面是宽度为1,高为h 的矩形,其对中性轴(Z 轴)的惯性矩312=h I ,运用截面法可求出随意率性截面的弯矩方程和剪力方程()23(),62=-=-q qx M x x F x l l.所以截面内随意率性点的正应力和切应力分离为:()332==-x M x x yy q I lhσ()()2222233431.424⎛⎫=-=-- ⎪⎝⎭s xy F x y q x h y bh h lh τ. 根据均衡微分方程第二式(体力不计).0∂∂+=∂∂y xy yxστ得: 333.22=-+y q xy xy q A lh lhσ 根据鸿沟前提()/20==yy h σ得 q .2=-xA l故 333.2.22=--y q xy xy q x q lh lh lσ 将应力分量代入均衡微分方程(2-2) 第一式:22336.60x y x yq q lh lh=-+==左右 知足第二式 天然知足将应力分量代入相容方程(2-23)()22223312.12.0⎛⎫∂∂=++=--≠= ⎪∂∂⎝⎭左右x y xy xyq q x y lh lh σσ应力分量不知足相容方程.故,该分量组分量不是图示问题的解答.【2-15】试证实:在产生最大与最小切应力的面上,正应力的数值都等于两个主应力的平均值. 【解答】(1)肯定最大最小切应力产生地位 随意率性斜面上的切应力为()21nlm τσσ=-,用关系式221l m +=消去m,得)))212121n τσσσσσσ=±-=-=-由上式可见当2102l -=时,即l =,n τ为最大或最小,为 ()12max min 2n σστ-=±.是以,切应力的最大,最小值产生在与x 轴及y 轴(即应力主向)成45°的斜面上.(2)求最大,最小切应力感化面上,正应力n σ的值 任一斜面上的正应力为()2122n l σσσσ=-+最大.最小切应力感化面上2/1±=l ,带入上式,得()()122121122n σσσσσσ=-+=+证毕.【2-16】设已求得一点处的应力分量,试求112,,σσα()100,50,)2000,400;x y xy x y xy a b σστσστ======-,()20001000400; ()1000,1500,500.x y xy x y xy c d σστσστ=-==-=-=-=,,【解答】由公式(2-6)122x y σσσσ+⎫=±⎬⎭及11tan x xy σσατ-=,得11arctan x xy σσατ-= (a)121501005002σσ⎫⎧+=±=⎬⎨⎩⎭13516'α==︒(b)1251220003122σσ⎫⎧+==⎬⎨-⎩⎭ ()1512200arctanarctan 0.783757'400α-==-=-︒-(c) 1210522000100020522σσ⎫⎧-+=±=⎬⎨-⎩⎭ ()110522000arctanarctan 7.388232'400α+==-=-︒-(d) 126911000150018092σσ-⎫⎧--==⎬⎨-⎩⎭ 16911000arctanarctan 0.6183143'500α-+===︒【2-17】设有随意率性外形的等候厚度薄板,体力可以不计,在全体鸿沟上(包含孔口鸿沟上)受有平均压力q .试证-xyq 及0xy τ=能知足均衡微分方程.相容方程和应力鸿沟前提,也能知足位移单值前提,因而就是准确的解答.【解答】(1)将应力分量,0x y xy q σστ==-=,和体力分量0x y f f ==分离带入均衡微分方程.相容方程00xyx x y xy yf xy f yx τσστ∂⎧∂++=⎪∂∂⎪⎨∂∂⎪++=⎪∂∂⎩ (a ) ()20x y σσ∇+= (b )显然知足(a )(b )(2)对于渺小的三角板A,dx,dy 都为正值,斜边上的偏向余弦()()cos ,,cos ,l n x m n y ==,将-,0x y xy q σστ===,代入平面问题的应力鸿沟前提的表达式(2-15),且()()-cos ,,cos ,x y f q n x f q n y ==,则有()()()()cos ,cos ,,cos ,cos ,x y n x q n x n y q n y σσ=-=-所以,x y q q σσ=-=-.对于单连体,上述前提就是肯定应力的全体前提.y(3)对于多连体,应校核位移单值前提是否知足.该题为平面应力情形,起首,将应力分量代入物理方程(2-12),得形变分量,(1)(1),,0x y xy q q E Eμμεεγ---=== (d ) 将(d )式中形变分量代入几何方程(2-8),得=,=,0u v v u q q x y x yμμ∂∂∂∂+=∂∂∂∂(-1)(-1)E E (e ) 前两式积分得到12--=(),=()u qx f y v qy f x μμ++(1)(1)E E(f )个平分()()12,f y f x 离随意率性的待定函数,可以经由过程几何方程的第三式求出,将式(f )代入式(e )的第三式,得12()()df y df x dy dx -=等式左边只是y 的函数,而等式右边只是x 的函数.是以,只可能双方都等于统一个常数ω,于是有12()(),df y df x dy dxωω=-= 积分后得()()1020,f y y u f x x v ωω=-+=+ 代入式(f )得位移分量00(1)(1)u qx y u Ev qy x v Eμωμω-⎧=-+⎪⎪⎨-⎪=++⎪⎩ (g ) 个中00,,u v ω为暗示刚体位移量的常数,需由束缚前提求得从式(g )可见,位移是坐标的单值持续函数,知足位移单值前提.因而,应力分量是准确的解答. 【2-18】设有矩形截面的悬臂梁,在自由端受有分散荷载F (图2-22),体力可以不计.试根据材料力学公式,写出弯应力0y σ=,然后证实这些表达式知足均衡微分方程和相容方程,再解释这些表达式是否就暗示准确的解答.【解答】(1)矩形悬臂梁产生曲折变形,随意率性横截面上的弯矩方程()M x Fx =-,横截面临中性轴的惯性矩为3/12z I h =,根据材料力学公式y弯应力3()12x z M x Fy xy I hσ==-; 该截面上的剪力为()s F x F =-,剪应力为()*2233()/262241/12s xy z F x S F h h y F h y b y y bI h h τ⎛⎫--⎛⎫⎡⎤==⋅-⋅⋅+=-- ⎪ ⎪⎢⎥⨯⎝⎭⎣⎦⎝⎭取挤压应力0y σ=(2)将应力分量代入均衡微分方程磨练 第一式:2312120F Fy y h h=-+==左右 第二式:左=0+0=0=右 该应力分量知足均衡微分方程.(3)将应力分量代入应力暗示的相容方程2()0x y σσ=∇+==左右 知足相容方程(4)考核鸿沟前提①在重要鸿沟/2y h =±上,应准确知足应力鸿沟前提(2-15)lmx fyf2h y =-上0 -1 0 0 2h y =上1代入公式(2-15),得()()()()-/2/2/2/20,0;0,0yxy y yx y h y h y h y h στστ==-======②在次要鸿沟x=0上,列出三个积分的应力鸿沟前提,代入应力分量主矢主矩/20/2/20/22/2/2203/2/2()0()06()()4h x x h h x x h h h xy x h h dy x ydy F h dy y dy F y h σστ=-=-=--⎧⎪==⎪⎪==⎨⎪⎡⎤⎪=--=-=⎢⎥⎪⎣⎦⎩⎰⎰⎰⎰向面力主矢面力主矩向面力主矢知足应力鸿沟前提③在次要鸿沟上,起首求出固定边面力束缚反力,按正偏向假设,即面力的主矢.主矩,0,,N S F F F M Fl ==-=-其次,将应力分量代入应力主矢.主矩表达式,断定是否与面力主矢与主矩等效:/2/23/2/212()0h h x x l Nh h Fdy lydy F h σ=--=-==⎰⎰M/2/223/2/212()h h x x l h h F ydy ly dy Fl Mh σ=--=-=-=⎰⎰2/2/223/2/26()4h h xy x l S h h F h dy y dy F F h τ=--⎛⎫=--=-= ⎪⎝⎭⎰⎰知足应力鸿沟前提,是以,它们是该问题的准确解答.【2-19】试证实,假如体力固然不是常量,但倒是有势的力,即体力分量可以暗示为,x y V Vf f x y∂∂=-=-∂∂,个中V 是势函数,则应力分量亦可用应力函数暗示成为22222=,=,x y xy V V y x x yσστ∂Φ∂Φ∂Φ++=-∂∂∂∂,试导出响应的相容方程.【解答】(1)将,x y f f 带入均衡微分方程(2-2)00 00yx yx x x x y xy y xy yVf x y x y x V f y x yx y ττσσστστ∂∂⎧⎧∂∂∂++=+-=⎪⎪∂∂∂∂∂⎪⎪⇒⎨⎨∂∂∂∂∂⎪⎪++=+-=⎪⎪∂∂∂∂∂⎩⎩ (a ) 将(a )式变换为()0()0yx x xy yV xy V yy τστσ∂⎧∂-+=⎪∂∂⎪⎨∂∂⎪-+=⎪∂∂⎩ (b ) 为了知足式(b ),可以取22222,,x y xy V V y x x yσστ∂Φ∂Φ∂Φ-=-==-∂∂∂∂即22222,,x y xy V V y x x yσστ∂Φ∂Φ∂Φ=+=+=-∂∂∂∂ (2)对体力.应力分量,,,x y x y f f σσ求偏导数,得222222424222222422242422422222, , , y x xx yy f f V Vx x y y V V x x y x y y y V V x x x y x y y σσσσ⎧∂∂∂∂=-=-⎪∂∂∂∂⎪⎪∂∂∂Φ∂∂Φ∂⎪=+=+⎨∂∂∂∂∂∂∂⎪⎪∂∂∂Φ∂∂Φ∂⎪=+=+∂∂∂∂∂∂∂⎪⎩(c ) 将(c )式代入公式(2-21)得平面应力情形下应力函数暗示的相容方程()2(1)y x x y f f x y σσμ∂⎛⎫∂∇+=-++ ⎪∂∂⎝⎭(2-21)4242424222222424222222(1)V V V VV V x y x y y x x x y y x y μ⎛⎫∂Φ∂∂Φ∂∂Φ∂∂Φ∂∂∂+++++++=++ ⎪∂∂∂∂∂∂∂∂∂∂∂∂⎝⎭整顿得:444224224222(1)V V x x y y xy μ⎛⎫∂Φ∂Φ∂Φ∂∂++=--+ ⎪∂∂∂∂∂∂⎝⎭(d ) 即平面应力问题中的相容方程为42(1)V μ∇Φ=--∇将(c )式代入公式(2-22)或将(d )式中的调换为1μμ-,的平面应变情形下的相容方程: 444224224221221V Vx x y y x y μμ⎛⎫∂Φ∂Φ∂Φ-∂∂++=-+ ⎪∂∂∂∂-∂∂⎝⎭(e ) 即 42121V μμ-∇Φ=-∇-. 证毕.第三章 平面问题的直角坐标解答【3-1】为什么在重要鸿沟(大鸿沟)上必须知足准确的应力鸿沟前提式(2-15),而在小鸿沟上可以运用圣维南道理,用三个积分的应力鸿沟前提(即主矢量.主矩的前提)来代替?假如在重要鸿沟上用三个积分的应力鸿沟前提代替式(2-15),将会产生什么问题?【解答】弹性力学问题属于数学物理方程中的边值问题,而要使鸿沟前提完整得到知足,往往比较艰苦.这时,圣维南道理可为简化局部鸿沟上的应力鸿沟前提供给很大的便利.将物体一小部分鸿沟上的面力换成散布不合,但静力等效的面力(主矢.主矩均雷同),只影响近处的应力散布,对远处的应力影响可以疏忽不计.假如在占鸿沟绝大部分的重要鸿沟上用三个积分的应力鸿沟前提来代替准确的应力鸿沟前提(公式2-15),就会影响大部分区域的应力散布,会使问题的解答精度缺少.【3-2】假如在某一应力鸿沟问题中,除了一个小鸿沟前提,均衡微分方程和其它的应力鸿沟前提都已知足,试证:在最后的这个小鸿沟上,三个积分的应力鸿沟前提必定是天然知足的,固而可以不必校核.【解答】区域内的每一渺小单元均知足均衡前提,应力鸿沟前提本质上是鸿沟上微分体的均衡前提,即外力(面力)与内力(应力)的均衡前提.研讨对象整体的外力是知足均衡前提的,其它应力鸿沟前提也都知足,那么在最后的这个次要鸿沟上,三个积分的应力鸿沟前提是天然知足的,因而可以不必校核.【3-3】假如某一应力鸿沟问题中有m 个重要鸿沟和n 个小鸿沟,试问在重要鸿沟和小鸿沟上各应知足什么类型的应力鸿沟前提,各有几个前提?【解答】在m 个重要鸿沟上,每个鸿沟应有2个准确的应力鸿沟前提,公式(2-15),共2m 个;在n 个次要鸿沟上,假如能知足准确应力鸿沟前提,则有2n 个;假如不克不及知足公式(2-15)的准确应力鸿沟前提,则可以用三个静力等效的积分鸿沟前提来代替2个准确应力鸿沟前提,共3n 个.【3-4】试考核应力函数3ay Φ=在图3-8所示的矩形板和坐标系中能解决什么问题(体力不计)?【解答】⑴相容前提:不管系数a 取何值,应力函数3ay Φ=总能知足应力函数暗示的相容方程,式(2-25).⑵求应力分量当体力不计时,将应力函数Φ代入公式(2-24),得6,0,0x y xy yx ay σσττ====⑶考核鸿沟前提高低鸿沟上应力分量均为零,故高低鸿沟上无面力. 阁下鸿沟上;当a>0时,考核x σ散布情形,留意到0xy τ=,故y 向无面力 左端:0()6x x x f ay σ=== ()0y h ≤≤ ()0y xy x f τ===右端:()6x x x l f ay σ=== (0)y h ≤≤ ()0y xy x l f τ=== 应力散布如图所示,当lh 时运用圣维南道理可以将散布的面力,等效为主矢,主矩xf xf主矢的中间在矩下鸿沟地位.即本题情形下,可解决各类偏幸拉伸问题.偏幸距e :因为在A 点的应力为零.设板宽为b,分散荷载p 的偏幸距e :2()0/6/6x A p pee h bh bh σ=-=⇒= 同理可知,当a <0时,可以解决偏幸紧缩问题. 【3-5】取知足相容方程的应力函数为:⑴2,ax y Φ=⑵2,bxy Φ=⑶3,cxy Φ=试求出应力分量(不计体力),画出图3-9所示弹性体鸿沟上的面力散布,并在小鸿沟上暗示出面力的主矢量和主矩.【解答】(1)由应力函数2ax y Φ=,得应力分量表达式0,2,2x y xy yx ay ax σσττ====-考核鸿沟前提,由公式(2-15)()()()()x yx s x y xy s y l m f s m l f s στστ⎧+=⎪⎨+=⎪⎩①重要鸿沟,上鸿沟2hy =-上,面力为()22=-=x hf y ax ()2y h f y ah =-=②重要鸿沟,下鸿沟2hy =,面力为y()2,2x h f y ax ==- ()2y hf y ah ==③次要鸿沟,左鸿沟x=0上,面力的主矢,主矩为 x 向主矢:/20/2()0h x x x h F dy σ=-=-=⎰y 向主矢:/20/2()0h y xy x h F dy τ=-=-=⎰主矩:/20/2()0h x x h M ydy σ=-=-=⎰次要鸿沟,右鸿沟x=l 上,面力的主矢,主矩为 x 向主矢:/2/2()0h x x x l h F dy σ=-'==⎰ y 向主矢:/2/2/2/2()(2)2h h y xy x l h h F dy al dy alh τ=--'==-=-⎰⎰主矩:/2/2()0h x x l h M ydy σ=-==⎰弹性体鸿沟上面力散布及次要鸿沟面上面力的主矢,主矩如图所示 ⑵2bxy Φ=将应力函数代入公式(2-24),得应力分量表达式2x bx σ=,0y σ=,2xy yx by ττ==-考核应力鸿沟前提,重要鸿沟,由公式(2-15)得 在2h y =-重要鸿沟,上鸿沟上,面力为,022x y h h f y bh f y ⎛⎫⎛⎫=-==-= ⎪ ⎪⎝⎭⎝⎭在2h y =,下鸿沟上,面力为,022x y h h f y bh f y ⎛⎫⎛⎫==-== ⎪ ⎪⎝⎭⎝⎭在次要鸿沟上,散布面力可按(2-15)盘算,面里的主矢.主矩可经由过程三个积分鸿沟前提求得:在左鸿沟x=0,面力散布为()()00,02x y f x f x by ==== 面力的主矢.主矩为 x 向主矢:()2020h h x x x F dy σ=-=-=⎰y 向主矢:()()22002220hh h h y xy x x F dy by dy τ==--=-=--=⎰⎰主矩;/20/2()0h x x h M ydy σ=-=-=⎰在右鸿沟x=l 上,面力散布为Oxy()()2,2x y f x l bl f x l by ====-面力的主矢.主矩为 x 向主矢:()/2/2/2/222h h x x x lh h F dy bldy blh σ=--'===⎰⎰y 向主矢:()()/2/2/2/2'20h h y xy x l h h F dy by dy τ=--==-=⎰⎰主矩:()/2/2/2/2'20h h x x l h h M ydy blydy σ=--===⎰⎰弹性体鸿沟上的面力散布及在次要上面力的主矢和主矩如图所示ahxyah(3)3cxy Φ=将应力函数代入公式(2-24),得应力分量表达式26,0,3x y xy yx cxy cy σσττ====-考核应力鸿沟前提,在重要鸿沟上应准确知足式(2-15) ①2h y =-上边界上,面力为23,0242x y h h f y ch f y ⎛⎫⎛⎫=-==-= ⎪ ⎪⎝⎭⎝⎭②hy=2下边界上,面力为 23,0242x y h h f y ch f y ⎛⎫⎛⎫==-== ⎪ ⎪⎝⎭⎝⎭次要鸿沟上,散布面力可按(2-15)盘算,面力的主矢.主矩可经由过程三个积分鸿沟求得:③左鸿沟x=0上,面力散布为。
弹性力学简明教程第四版课后习题解答徐芝纶第一章 绪论1-1试举例说明什么是均匀的各向异性体什么是非

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
弹性力学简明教程(第四版)课后习题解答

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
徐芝纶弹性力学简明教程(第四版)课后习题解答

x x dx y ; x y
( y )C y
y x
dx
y y
y
( xy ) A xy ;
( xy ) B xy xy y
xy x
( yx ) A yx
dy ; ( yx ) A yx yx y dy
y
y
(c)
M
E
0
dx dy dx x dy 1 yx dx 1 dy y dx 1 y 2 2 2 xy dy dy dx ( x x dx)dy 1 ( xy dx)dy 1 dx f x dxdy 1 f y dxdy 1 0 x 2 x 2 2 ( y dy )dx 1
2
正的应力
正的面力
【1-5】试比较弹性力学和材料力学中关于切应力的符号规定。 【解答】 材料力学中规定切应力符号以使研究对象顺时针转动的切应力为正, 反之为负。 弹性力学中规定, 作用于正坐标面上的切应力以沿坐标轴的正方向为正, 作用于负坐标 面上的切应力以沿坐标轴负方向为正,反之为负。 【1-6】试举例说明正的应力对应于正的形变。 【解答】正的应力包括正的正应力与正的切应力,正的形变包 括正的正应变与正的切应变,本题应从两方面解答。 正的正应力对应于正的正应变:轴向拉伸情况下,产生轴向拉 应力为正的应力,引起轴向伸长变形,为正的应变。 正的切应力对应于正的切应变: 在如图所示应力状态情况下, 切应力均为正的切应力, 引起直角减小,故为正的切应变。
y
M
C
0 改为对角点的力矩平衡条件, 试问将导出什么形
式的方程? 【解答】 将对形心的力矩平衡条件
M
C
0, 改为分别
弹性力学第四版徐芝纶课后习题答案全解

【解答】体力相同情况下,两类平面问题的平衡微分方程完全相同,故所求的应力
分量相同。由物理方程可以看出,两类平面问题的物理方程主要的区别在于方程中含弹
性常数的系数。由于 E 为 GPa 级别的量,而泊松比 取值一般在(0,0.5),故主要控
制参数为含有弹性模量的系数项,比较两类平面问题的系数项,不难看出平面应力问题
【1-7】试画出图 1-4 中矩形薄板的正的体力、面力和应力的方向。
【解答】
正的体力、面力
正的体力、应力
【1-8】试画出图 1-5 中三角形薄板的正的面力和体力的方向。【解答】
2
【1-9】在图 1-3 的六面体上,y 面上切应力 yz 的合力与 z 面上切应力 zy 的
合力是否相等?
【解答】切应力为单位面上的力,量纲为 L1MT 2 ,单位为 N / m2 。因此,
【2-2】试分析说明,在板面上处处受法向约束且不受切向面力 作用的等厚度薄片中(2-15),当板边上只受 x,y 向的面力或约束,
且不沿厚度变化时,其应变状态接近于平面应变的情况。 【解答】板上处处受法向约束时 z 0 ,且不受切向面力作用,
则 xz yz 0 (相应 zx zy 0 )板边上只受 x,y 向的面力或约束, 所以仅存在 x , y , xy ,且不沿厚度变化,仅为 x,y 的函数,故其应
(a)
各点正应力:
( x )A x ;
( x )B
x
x y
dy
;
( x )D
x
x x
dx
;
( x )C
x
x x
dx
x y
y
(完整版)弹性力学简明教程第四版课后习题解答徐芝纶第一章绪论1-1试举例说明什么是均匀的各向异性体什

弹性力学简明教程(第四版)课后习题解答徐芝纶第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就连续函数来表示他们的变化规律。
可以用坐标的完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
