3学习情境三
学习情境3纯电动汽车

学习情境三纯电动汽车单元一纯电动汽车结构与工作原理一、告知学习目标了解纯电动汽车的定义及优缺点;重点理解纯电动汽车的关键参数及其计算方法;熟悉纯电动汽车的整体结构;理解纯电动汽车各部件的功能,了解其结构。
二、引入引入问题1:什么是纯电动汽车?引入问题2:纯电动汽车有何优缺点?引入问题3:纯电动汽车的续驶里程?引入问题4:纯电动汽车的整体结构?引入问题5:纯电动汽车的主要组成?三、操练分组观察纯电动汽车,讨论纯电动汽车的结构及工作过程四、深化深化讲解问题1:纯电动汽车的基础知识纯电动汽车(Blade Electric Vehicles,BEV),是一种完全由可充电电池(如铅酸电池、镍镉电池、镍氢电池或锂离子电池)提供动力源的汽车。
以车载电源为动力,通过电池向电机提供电能,驱动电动机运转,从而推动汽车前进,使之符合道路交通、安全法规各项要求的车辆。
根据纯电动汽车当前的发展情况,纯电动汽车必须符合以下几个条件:纯电动车辆研发制造运营必须符合国家各项相关法规。
整车、零部件性能必须满足国家技术标准和各项具体要求。
纯电动车辆是以电为能源,由电动机驱动行驶的,不再产生新的污染,不再产生易燃、易爆之隐患。
纯电动车辆储能用的电池必须是无污染、环保型的。
且具有耐久的寿命,具备超快充电的功能。
车辆根据用途确定一次充电之续行里程,以此装置够用电量的电池组,充分利用公用充电站超快充电以延长续行里程。
电动机组应有高效率的能量转换。
刹车、减速之能量的直接利用和回收,力求车辆之综合能源利用的高效率。
根据车辆用途和行驶场合设定最高车速,且不得超过交通法规的限定值,以合理选择电动机的功率和配置电池组容量。
车辆驾驶操作,控制简单有效、工作可靠,确保行车安全。
机械、电气装置耐用少维修。
车辆运营之费用低廉。
深化讲解问题2:纯电动汽车有哪些优缺点?纯电动汽车的电动机相当于传统汽车的发动机,蓄电池相当于传统的油箱,通常采用高效能的充电电池。
学习情境3:商务谈判的背景调查

2.谈判者自身情况分析 在谈判前的背景调查中,不仅要调查分析客观环境和谈判对手 的情况,还应该正确了解和评估谈判者自身的状况。古人云: “知己知彼,百战不殆。”没有对自身的客观评估,就不会客 观地认定对方的实力。孟子说过:“知人者智,自知者明。” 自我评估首先要看到自身所具备的实力和优势,同时要客观地 分析自己的需要和实现需要缺欠的优势条件。 (1)谈判者自身的实力水平 (2)谈判者自身的人员结构 (3)自我需要的认定 ① 希望借助谈判满足己方哪些需要 ② 各种需要的满足程度 ③ 需要满足的可替代性 ④ 满足对方需要的能力鉴定
3.4实施
3.4.1分工的实施 1.由组长阐明各类工作的内容和任务。 2.采取自愿和协商结合的方式落实各位成员的分工任务。 3.4.2背景调查的实施 1.按照小组决策的背景调查方式、方法和人员任务分配开展 背景调查。 2.落实各位成员任务的完成时间表,进行相互角色检查,整 体进度由组长进行监督。 3.4.3寻求谈判双赢的途径 在背景调查的基础上,在知己知彼之后,设计谈判双赢的方案, 创造谈判价值。 3.4.4撰写背景调查报告 完成规范的背景调查报告,为商务谈判方案和执行计划的制定 打下基础。
3.1资讯
3.1.5 背景调查报告的格式及撰写技巧 调查报告参考格式: 1.题目 题目以简炼、概括、明确的语句反映所要调查的对 象、方向等问题。题目应能概括全篇,引人注目。 2.前言 (1)背景调查目的和意义:阐述调查的必要性和 针对性,初步掌握报告主旨。 (2)背景调查的内容; (3)背景调查的方法:时间、地点、对象、范围 等; (4)有利和不利因素的分析。
3.1资讯
(3)谈判对手资信调查 ① 对客商合法资格的审查 法人应具备三个条件: ◆法人必须有自己场所,组织机构是决定和执行法 人各项事务的主体。 ◆法人必须有自己的财产,这是法人参加经济活动 的物质基础与保证。 ◆法人必须具有权利能力和行为能力。所谓权利能 力是指法人可以享受权利和承担义务,而行为能力 则是法人可以通过自己的行为享有权利和承担义务。 满足了这三方面的条件后,在某个国家进行注册登 记,即成为该国的法人。 ② 对谈判对手资本、信用及履约能力的审查
汽车电气系统与电路调试学习情景3(答案)

学习情境3 起动机不工作一、填空题1.电磁操纵式起动机电磁开关与铁芯的结构形式分整体式和分离式两种。
2.电磁操纵式起动机开关的铁芯断电行程一般设计在:①拨叉与电磁开关铁芯连接处;②拨叉与单向离合器连接处。
3.减速型起动机按齿轮啮合方式可分为内啮合式,外啮合式及行星齿轮啮合式三种,减速比一般为 3~5 。
4.减速型起动机换向器片与转子线圈线头采用银铜硬钎焊,它既能耐高温,又能耐高速。
5.普通起动机电枢铁芯外圆柱表面跳动量不得大于 O.15 mm;换向器片厚度不得小于 2 mm,换向器表面跳动量不得大于 0.05 mm。
6.起动时,普通起动机每次接通时间不得超过 5 s,再次起动,两次间隔时间不得低于 15S 。
7.普通起动机励磁绕组断路多发生在线圈与引线焊接处;电枢绕组断路多发生在线圈与换向片的焊接处。
8.永磁式起动机维修装夹时,只能按设计安装位置装夹。
9.用铰刀铰削起动机铜套时,两手用力应均匀平稳,铰完后应朝顺时针方向旋出铰刀。
10.起动机电磁开关触点闭合后,活动铁芯应能继续移动 1—3 mm附加行程,使开关可靠闭合。
11.起动机行程调节机构常见有偏心螺栓式,调整垫片式和铁芯螺栓式等几种。
12.起动机副开关接通时刻应比主开关接通时刻早。
副开关的作用是在起动时短接点火线圈的附加电阻,增大点火能量。
13.起动机空载试验时,若电流和转速均低于标准值,说明起动机线路中有接触不良故障。
制动试验时,若制动电流小于标准值,电动机空转,表明起动机单向离合器已经打滑。
14.起动机电枢轴的轴向间隙不得过大,应为 0.125~O.500 mm,不合适时,可在转子前后端改变调整垫片厚度进行调整。
二、选择题1.直流串励式起动机中的“串励”是指( B )。
A 吸引线圈和保持线圈串联连接B 励磁绕组和电枢绕组串联连接C 吸引线圈和电枢绕组串联连接2.下列不属于起动机控制装置作用的是( B )。
A 使可动铁心移动,带动拨叉使驱动齿轮和飞轮啮合或脱离B 使可动铁心移动,带动接触盘使起动机的两个主接线柱接触或分开C 产生电磁力,使起动机旋转3.永磁式起动机中用永久磁铁代替常规起动机的( B )。
学习情境3

• 【知识要求】
• 任务1中央门锁控制系统工作不正常故障的 检测与修复
•
任务2汽车防盗系统不起作用故障的检测与 修复
返回
任务1中央门锁控制系统工作 不正常故障的检测与修复
• 一、知识准备
• • 1.中央门锁控制系统的作用 中央门锁控制系统(中控锁)是指通过设在驾驶(副驾驶)侧车门上的 开关,同时控制全车车门的锁止与开启,或通过遥控设备开关车门锁 的一种控制装置。如图3-1所示为中央集控门锁控制按钮的布置,中 央门锁控制系统主要具有以下5项功能。
• • •
上一页 下一页
返回
任务1中央门锁控制系统工作 不正常故障的检测与修复
• (1)主要输入信号 • 主要输入信号有驾驶员提供的锁定/解锁信号(遥控器、门锁控制开 关、钥匙操纵开关)、满足防盗设定条件的开关信号(钥匙未锁警告开 关、门控灯开关、发动机室罩盖控制开关、行李箱室灯开关、点火开 关、位置开关)以及车速信号。 1)遥控器 遥控器主要由铿电池、按钮开关、高频振荡电路、高频放大电路、 天线组成。无线电波式遥控器发射频率为300-500 MHz,有效范围一 般为5-10 m。当遥控器电量不足时,遥控距离会缩短;当遥控器长期 电量不足时,遥控功能将消失,需要对遥控器进行设定。遥控器有钥 匙分离型和钥匙座型两种。
(4)行李箱门开启器开关
•
•
上一页 下一页
返回
任务1中央门锁控制系统工作 不正常故障的检测与修复
• 如图3-3所示,该开关位于仪表板下面,拉动此开关便能打开行李 箱门。钥匙门靠近行李箱门开启器,推压钥匙门,断开行李箱内主开 关,此时再拉开启器开关也不能打开行李箱门。将钥匙插进钥匙门内 顺时针旋转打开钥匙门,主开关接通,这样便可用行李箱门开启器打 开行李箱。 (5)门控开关 门控开关用来探测车门的开闭情况。车门打开时,门控开关接通; 车门关闭时,门控开关断开。
学习情境 (3)

学习情境三:发动机美容学习情境描述:学习目标要求:知识目标:借助教学指导书了解常用清洗剂的种类及其功能、查阅专用设备使用说明书掌握专用清洗设备基本知识和使用方法技能目标:、学会发动机清洗方法及流程能正确使用清洗常用工具和专用设备对发动机进行清洗清洁技术资讯:一、汽车清洗的作用由于发动机室有与外界完全隔绝,因此外界的泥沙、水分及油污是发动机室最大的污染来源;常见的污染是垫片漏油,另外在添加及使用制动液、机油、冷却液、动力转向油、齿轮油等过程可能有部分油泄出,造成发动机室污染。
如果长期未清除将有可能使水分、灰尘、油污进入发动机体或制动液管路中,严重会导致发动机磨损加剧、制动力下降也有可能造成电路组件短路损坏和发动机冷却效果变差等,在长时间行车过程中由于发动机过热驾驶室内可能经常闻到一股浓的油烟味,严重还可酿成发动机室着火烧车。
因此,发动机清洗对保持车容美观,延长车辆使用寿命有着重要作用。
1、保持发动机外观整洁汽车在行驶中经常置身于各种不同的路况,雨雪天气有时还要在泥泞道路上行驶,发动机外表难免被泥土沾污,影响发动机整体性能,为使发动机表面清洁干净,必须定期对发动机表面进行清洗从而提高发动机的整体性能。
2、防止连接管路老化发动机表面的灰尘和油污如果长期附着在各连接管路表面会造成橡胶管路及其他管路的老化与腐蚀,灰尘同时可能会吸附大气中多种带有腐蚀性的气体等可能对发动机表面产生危害的污染物,为此,车主应定期将发动机进行清洗从而防止管路老化。
二、发动机清洗用品发动机室的污染以油性污染物为主,可以用汽油类的有机溶剂如柴油或煤油或用酸性、碱性清洁剂来处理,一般汽车用品商店可买到高浓度的发动机室清洗剂。
采用发动机室清洗剂即可大大的提高清洗速度,用清洗剂代替溶剂清除油垢,减少了汽油和柴油的消耗从而节约了能源大大降低了清洗费用。
如果采用环保型清洗剂清洗,也可减少对环境的污染。
2、清洗剂种类(1)水性清洗剂(2)有机清洗剂(3)油脂清洗剂(4)溶解清洗剂(5)多功能清洗剂三、发动机清洗工具使用工具:水管或清洗机、长柄毛刷、吹气枪使用材料:塑胶手套、防水保鲜膜、锡箔纸、发动机室清洗剂、塑胶及橡胶光泽剂四、汽车清洗流程1、人工清洗工艺流程1.隔离电子零件:分电盘、蓄电池加水盖及接线柱、熔断丝盒用保鲜膜或锡箔纸包裹好。
学习情境3
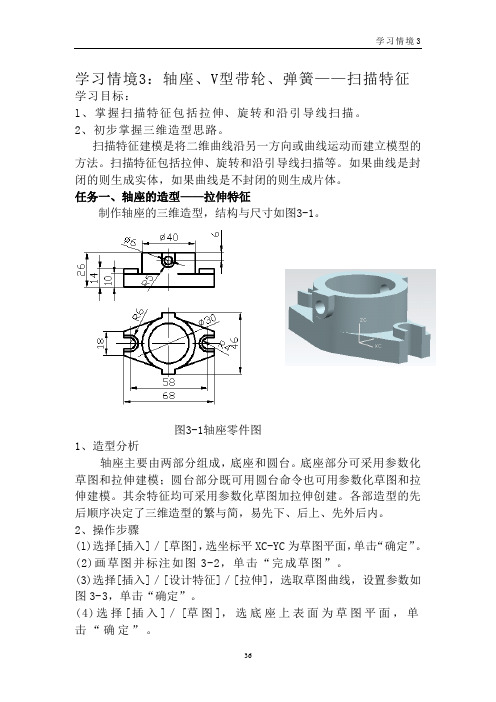
学习情境3:轴座、V型带轮、弹簧——扫描特征学习目标:l、掌握扫描特征包括拉伸、旋转和沿引导线扫描。
2、初步掌握三维造型思路。
扫描特征建模是将二维曲线沿另一方向或曲线运动而建立模型的方法。
扫描特征包括拉伸、旋转和沿引导线扫描等。
如果曲线是封闭的则生成实体,如果曲线是不封闭的则生成片体。
任务一、轴座的造型——拉伸特征制作轴座的三维造型,结构与尺寸如图3-1。
图3-1轴座零件图1、造型分析轴座主要由两部分组成,底座和圆台。
底座部分可采用参数化草图和拉伸建模;圆台部分既可用圆台命令也可用参数化草图和拉伸建模。
其余特征均可采用参数化草图加拉伸创建。
各部造型的先后顺序决定了三维造型的繁与简,易先下、后上、先外后内。
2、操作步骤(l)选择[插入]/[草图],选坐标平XC-YC为草图平面,单击“确定”。
(2)画草图并标注如图3-2,单击“完成草图”。
(3)选择[插入]/[设计特征]/[拉伸],选取草图曲线,设置参数如图3-3,单击“确定”。
(4)选择[插入]/[草图],选底座上表面为草图平面,单击“确定”。
图3-2 草图图3-3设置参数图3-4设置参数(5)画草图(Φ40圆)并标注,单击“完成草图”。
(6)选择[插入]/[设计特征]/[拉伸],选取草图曲线,设置参数如图3-4,单击“确定”。
(7)选择[插入]/[设计特征]/[拉伸],选取R4实体边缘,设置参数如图3-5,单击“确定”。
(8) 选择[插入]/[草图],选坐标平面ZC-XC为草图平面,单击“确定”。
(9)画草图并标注如图3-6,单击“完成草图”。
(10) 选择[插入]/[设计特征]/[拉伸],选取草图曲线,设置参数如图3-7,单击“确定”。
(11)选择[插入]/[草图],选坐标平XC-YC为草图平面,单击“确定”。
图3-6草图图3-5 设置参数图3-7 设置参数(12)画草图(Φ30圆)并标注,单击“完成草图”。
(13)选择[插入]/[设计特征]/[拉伸],选取草图曲线,设置参数距离26、减,单击“确定”。
学习情境三金属材料塑性变形对组织性能的影响

2. 晶粒位向的影响
由于各相邻晶粒位向不同,当一处利于滑移方向晶粒发生滑 移时,必然受到周围位向不同的其他晶粒的约束,使滑移受 到阻碍,从而提高金属塑性变形抗力。
(二) 晶粒大小的影响 晶粒越细,其强度和硬度越高。
细晶强化
晶粒越细晶界越 ,不同位向的晶粒也越 滑 移抗力 强度
晶粒越细晶粒数目越 变形均匀性 应力集 中,裂纹过早产生、扩展 塑性、韧性
一、金属材料变形特性
材料在外力的作用下,变形过程一般可分三个阶段:弹性 变形、塑性变形和断裂。其中对组织和性能影响最大的是 塑性变形阶段。
单晶体的滑移
多晶体
二、单晶体的塑性变形
单晶体塑性变形基本形式:滑移和孪生。
(一)滑移
1、滑移定义
滑移:指晶体在切应力的作用下, 晶体的一部分沿一定的晶面 (滑移面)上的一定方向(滑移方向)相对于另一部分发生滑动。 滑移带:当试样经过塑性变形后,在显微镜下观察,可在表面 看到许多相互平行的线条,称之为滑移带。 若干条滑移线组成一个滑移带。
三、 多晶体的塑性变形
单个晶粒变形与单晶体相似。
而多晶体变形是一个不均匀的塑性变 形过程。
(一)晶界及晶粒位向差的影响
1. 晶界的影响
当位错运动到晶界附近时,由于 晶界处的原子排列紊乱,缺陷和 杂质多,能量高,对位错的滑移
起阻碍作用,位错受到晶界的阻
碍而堆积起来,称位错的塞积。使 位错运动阻力增大,从而使金属 的变形抗力提高。
位错运动使其由冷塑性变形时的 无序状态变为垂直分布,形成亚 晶界,这一过程称多边形化。
回复带来的组织性能变化 (1) 宏观应力基本去除,微观应
力仍然残存;
(2)力学性能,如硬度和强度稍 有降低,塑性稍有提高;
3学习情境三合成氨原料气的净化

学习情境三合成氨工作任务合成氨原料气的脱硫授课地点多媒体教室3-8教学方法讲授法课时 4任务描述及任务目标掌握干法脱硫、氨水催化法脱硫及两生过程的基本原理、主要设备和工艺条件的选择包含章节第三章第三节主要教具、设备、工具多媒体学习重点及难点脱硫方法的选择与对比碱法脱硫的原理及工艺指标的确定学生学习基础已具有无机化学,化工单元操作,物理化学,化工热力学等的学习基础,具有一定的自学能力,接受知识的能力也较强.知识点:第一节原料气的脱硫脱硫方法很多,主要可分为干法脱硫和湿法脱硫。
干法脱硫一般适用于含S量较少的情况。
湿法脱硫一般适用于含S量较大的场合。
一、干法脱硫(一)钴-钼加氢法钴钼加氢法还可将烯烃加氢转变成饱和烷烃,从而减少蒸汽转化工序析碳的可能。
钴钼加氢催化剂以氧化铝为载体,由氧化钴和氧化钼组成。
经硫化后活性组分为MoS2,Co9S8也是活性成份。
主要反应如下:RCH2SH+H2=RCH3 + H2SRCH2-S-CH2R´+2H2=RCH3 + R´CH3 +H2SRCH2S-SCH2R´+3H2=RCH3 + R´CH3 +2H2S操作温度一般在300 ~ 400°C,压力由不同催化剂而定,加氢量一般按照保持反应后气体中有5~10%氢为准。
(二)氧化锌法氧化锌脱除有机硫的能力很强,可使出口硫含量<0.1ppm,当原料气硫含量<50×10-6时,仅用它一步脱硫就行了。
若硫含量较高,可先用湿法,再用此法。
其基本原理如下:ZnO(s)+H2S(g)=ZnS(s)+H2O(g)ZnO(s)+C2H5SH(g)=ZnS(s)+C2H5OH(g)氧化锌脱硫的反应速度主要是内扩散控制,所以氧化锌脱硫剂都做成高孔率的小颗粒。
氧化锌脱硫性能的好坏用硫容量表示。
所谓硫容就是每单位质量氧化锌能脱除S的量。
氧化锌脱硫性能的好坏用硫容量表示。
所谓硫容就是每单位质量氧化锌能脱除S的量二、湿法脱硫湿法脱硫可分为化学吸收法、物理吸收法和化学物理综合吸收法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分层法计算假定:
① 多层多跨框架在一般竖向荷载作用下,侧移小, 作为无侧移框架按力矩分配法进行内力分析 ② 多层框架简化为单层框架,分层作力矩分配计算
③ 假定上下柱的远端为固定,实际仅底层柱为固定, 其它柱端均为弹性支座。修正:除底层柱外,各 层柱线刚度乘以0.9,柱的传递系数为1/3,底层柱 的传递系数取1/2.
分层法的含义
①分层计算的梁端弯矩为最终弯矩 ②上下层所得同一根柱子内力叠加,得到柱得 最终弯矩 ③节点弯矩可能会不平衡,误差不大。如误差较 大,可将节点不平衡弯矩再进行一次分配
力矩分配法应用到分层法中时需注 意什么?
除底层柱外,各层柱线刚度乘以0.9 底层柱的传递系数取1/2. 其它层柱的传递系数为1/3
2.最不利荷载位置法
对于特定截面的最不利内力,采用影响线方法, 直接确定产生此最不利内力的活荷载布置。
3.分层组合法
分层组合法是以分层法为依据的,对活荷载的最不利布置作 如下简化: (1)对于梁,只考虑本层活荷载的不利布置,而不考虑其它 层活荷载的影响。 (2)对于柱端弯矩,只考虑柱相邻上下层的活荷载的影响, 而不考虑其它层活荷载的影响。 (3)对于柱最大力,则必须考虑在该层以上所有 层中与该柱连接的梁的活荷载布置情况。
图3.12 框架在水平荷载作用下的变形
(a) 梁柱弯曲变形;(b) 柱的轴向变形
2 用D值法计算框架的侧移
侧移刚度的物理意义是柱两端产生单位层间侧移 所需的层剪力。当已知框架结构某一层所有柱的侧移 刚度D值和层剪力后,按照侧移刚度的定义,可得第j 层框架的层间相对侧移Δuj应为
u j
即
为了简化计算,作如下假定: (1) 在进行各柱间的剪力分配时,假定梁与柱 的线刚度之比为无穷大,即各柱上下两端的转角为零; (2) 在确定各柱的反弯点位置时,假定除底层 柱以外的各层柱,受力后上下两端将产生相同的转角。
水平荷载下的框架弯矩图和变形
反弯点法的基本内容 (1) 反弯点高度的确定 反弯点高度为反弯点至该层柱下端的距离。 对于上层各柱,根据假定(2),各柱的上下 端转角相等,此时柱上下端弯矩也相等,因而 反弯点在柱中央。 对于底层柱,当柱脚为固定时,柱下端转角 为零,上端弯矩比下端弯矩小,反弯点偏离中 央而向上移动,通常假定y =2h/3。
内力近似计算方法
框架在荷载作用下的内力
分层法 弯矩二次分配法
竖 向 荷 载 作 用 下 的 内 力
计算简图
具体计算步骤:
弯矩二次分配法
(1)根据各杆件的线刚度计算各节点的杆端弯矩分配系数,并计算竖
向荷载作用下各跨梁的固端弯矩。
(2)计算框架各节点的不平衡弯矩,并对所有节点的不平衡弯矩同时 进行第一次分配(其间不进行弯矩传递)。
LOGO
框架在荷载作用下的内力
水 平 荷 载 作 用 下 的 内 力
反弯点法
D值法
反弯点法适用范围:
梁柱刚度之比值ib/ic≥3
反弯点法计算假定:
①框架横梁刚度无穷大——无变形;
②各层柱上下端节点转角相同: 各柱反弯点位于柱中点,
计算简图
底层柱位于距柱底2/3层高处。
内力近似计算方法
框架在荷载作用下的内力
M 图 框架梁柱:均呈线性分布,梁、柱支座 截面分别产生± Mmax 框架梁:各跨内呈均匀分布 框架柱:沿各层高内呈均匀分布
框架柱:截面产生轴向力,部分柱内受拉, 部分柱内受压。“-”为压,“+”为拉
V 图
N 图
框架在荷载作用下的内力 控 制 截 面 及 内 力 组 合
+Mmax:确定梁端底部纵筋
Mj上=Mj下=Vj×hj/2
(4)梁端弯矩的确定
柱端弯矩确定以后,根据节点平衡条件可确 定梁的弯矩。 对于边柱节点有 Mb=Mc1+Mc2
对于中柱节点,有
Mb1=ib1/(ib1+ib2)(Mc1+Mc2) Mb2=ib2/(ib1+ib2)(Mc1+Mc2)
2 D值法
反弯点法是梁柱线刚度比大于3时,假定节 点转角为零的一种近似计算方法。 提出了修正框架柱的侧移刚度和调整反弯 点高度的方法,称为“改进反弯点法”或“D值 法”(D值法的名称是由于修正后的柱侧移刚度 用D表示)。D值法计算简便,精度又比反弯点 法高。
表3.1 α值计算公式
柱的反弯点高度
当横梁线刚度与柱的线刚度之比不很大时, 柱的两端转角相差较大,尤其是最上层和最下 几层,其反弯点并不在柱的中央,它取决于柱 上下两端转角:当上端转角大于下端转角时, 反弯点移向柱上端;反之,则移向柱下端。 各层柱反弯点高度可统一按下式计算: y=yh=(y0+y1+y2+y3)h
(3)将所有杆端的分配弯矩同时向其远端传递(对于刚接框架,传递
系数均取1/2)。 (4)将各节点因传递弯矩而产生的新的不平衡弯矩进行第二次分配,
使各节点处于平衡状态。 至此,整个弯矩分配和传递过程即告结束。
(5)将各杆端的固端弯矩(fixed-end moment)、分配弯矩和传递弯 矩叠加,即得各杆端弯矩。
N 图
框架柱:截面产生轴向压力,“-”表示受压
3.1.2 竖向活载最不利布置
对于活荷载与恒荷载之比不大于3的情况,常采用以下几种方法进 行活荷载布置,以简化计算。 1、逐跨施荷法: 这个方法是将活荷载逐层逐跨单独地作用在结构上, 分别计算出整个结 构的内力, 再组合出任意截面的最不利内力。因此,对于一个多层多跨框 架,共有(跨数×层数)种不同的活荷载布置方式亦即需要计算(跨数 ×层数)次结构的内力,其计算工作量是很大的。但在运用电脑进行内 力组合时,常采用这一方法。
任务二 水平荷载作用下内力的近似计算 【案例引入】 学习情境二的引入案例中已对某框架结构进 行确定计算简图及荷载的计算,试利用其结 论,对此框架结构进行水平荷载作用下的内 力计算,并绘制内力图形。 【任务目标】 1、掌握反弯点法和D值法; 2、熟悉框架结构在水平荷载作用下内力的分 布规律。
内力近似计算方法
框架顶点的总侧移Δ应为各层层间相对侧移之和,
P = D
m
j j
= u j
j=1
侧移限值
在水平荷载作用下框架结构层间相对侧移Δu的 限值要求是: (1)高度不大于150m的框架结构 Δu≤h/550 (2) 高度等于或大于250m的框架结构 Δu≤h/500 (3) 高度在150~250m之间的框架结构 按Δu≤h/550-Δu≤h/500线形插入
混凝土结构与砌体结构
学习情境三 框架结构的内力与侧移计算
LOGO
学习情境三
1
2 3
任务一竖向荷载作用下内力的近似计算
任务二水平荷载作用下内力的近似计算
任务三 水平荷载作用下侧移的近似计算
任务一 竖向荷载作用下内力的近似计算 【案例引入】 学习情境二的引入案例中已对某框架结构进行确定 计算简图及荷载的计算,试利用其结论,对此框 架结构进行竖向荷载作用下的内力计算,并绘制 内力图形。 【任务目标】 1、掌握弯矩二次分配法和分层法; 2、掌握框架结构求剪力和轴力的方法; 3、熟悉框架结构在竖向荷载作用下内力的分布规律。
3.1.1 计算方法
内力近似计算方法
框架在荷载作用下的内力
竖 向 荷 载 作 用 下 的 内 力
分层法
弯矩二次分配法
分层法计算假定:
①框架无侧移; ②每层横梁上荷载对其它层横梁无影响。
计算思路:
可将一个多层框架分解为多个单层 开口框架,使每一框架节点数量大幅度 减少,有效地减少了计算工作量。 计算简图
水 平 荷 载 作 用 下 的 内 力
反弯点法
D值法
D值法适用范围:
梁柱刚度之比值ib/ic<3
反弯点法计算误差:
① 假定ib/ic=∞:横梁无变形,节点无 转角; ②假定各层柱上下端节点转角相同,反 弯点位于柱中点。
D值法——修正反弯点法
修正①:柱的侧移刚度 修正②:调整反弯点高度
1 反弯点法
反弯点法基本假定
框 架 梁
端部支 控制截面 ——结构构件中需要按其内 -Mmax:确定梁端顶部纵筋 座截面 力进行配筋计算的截面。
Vmax:确定箍筋及弯起钢筋 +Mmax:确定梁下部纵筋 跨中 内力组合——寻求结构构件的最不利 截面 内力,作为配筋依据。
-Mmax:确定跨中可能的
顶部纵筋
任务三 水平荷载作用下侧移的近似计算 【案例引入】 框架结构具有在水平荷载作用下侧向刚度小, 水平位移较大的缺点。试计算此学习情境中 框架案例的侧向位移,看其是否满足限值要 求。 【任务目标】 1、掌握框架结构侧移近似计算方法; 2、熟悉框架结构在水平荷载作用下侧移的特 点和限值要求。
设同层各柱剪力为V1、V2、…、Vj、…,根 据层剪力平衡,有 V1+V2+…+Vj+…=∑P 可得: P P = d1 d2 ... d j ... d
于是有
Vj =
dj
P d
(4)柱端弯矩的确定 根据各柱分配的剪力及反弯点位置,可确定 柱端弯矩。 底层柱 上端 Mj上=Vj×hj/3 下端 Mj下=Vj×2hj/3 其它层柱 上下端
4. 满布荷载法
当活荷载的内力远小于恒荷载及水平力所产生的内力时, 可把活荷载同时作用于所有框架梁上,并对梁跨中的弯矩 扩大1.1---1.2倍。
5. 分跨施荷法
当活荷载不是太大时,可将活荷载分跨布置,并求出内力, 然后叠加求出控制截面的不利内力。 这种方法与逐跨施荷法相比,计算工作量大大减少,但此 法求出的内力组合值并非最不利内力。因此,采用此法计 算时可不考虑活荷载的折减。
(1) 标准反弯点高度比y0 标准反弯点高度比y0主要考虑梁柱线刚度比及结构 层数和楼层位置的影响,它可根据梁柱相对线刚度比、 框架总层数m、该柱所在层数n、荷载作用形式由表3.2 查得。 (2) 上下层横梁线刚度不同时的修正值y1 当某层柱的上梁与下梁刚度不同,则柱上下端转角 不同,反弯点位置有变化,修正值为y1。 根据α1和K值由表3.3查得y1 (3) 上下层层高变化时的修正值y2、y3 当柱所在楼层的上下楼层层高有变化时,反弯点也 将偏移标准反弯点位置。 令上层层高h上与本层层高h之比为α2,即α2=h上/h。 由α2和K从表3.4查得修正值y2。
