河南省2019届高三普通高中毕业班高考适应性测试 数学理
河南省2019届普通高中毕业班高考适应性测试理科综合试卷及答案(扫描版)

绝密*肩用蒴2019年河南古拧通莴中毕业班商考适应性测K理科综合能力测试注*寧项:1.答6前,耆生务必将0己的ft名、准考•a号填写在答e旁上。
2.F1答选楫选出每小《答案后.fljffi笔把答题对应姐目的答案标号涂黑,如黑改动,用瘃皮揼f净后.拘选涂K他答案标号e回答曹a择M时.将答案3在答K 卡上,写在本试在上无软a3•名试坊朵后,将木试卷和答HP—并交回。
可能用到的相付肤+质祉:H丨C 12 N 14 0 16 N» 23 Cl 35.5 Fe 56第I卷-、选择H:本邏共13小題.每小題6分,共78分,在毎小8给出的四个迭項+,只有一项是符合题目栗求的...1.下列关于病«的叙述正确的足A.tt筘的蛋b质均在核Ml* h介成B.KNA«S的核肢必須®矜及后淖能蕙制C.T,««体的遠托物顷主要是DNAD.W含有4标记«嘹啶的培搾基诮养RNA阀疳./代病毐一定M朽放射性2.S 5•因姑弟蟎染G•体上的n«*W,在该基W中捕人•个《5对引起rRWtt<(2•的变化』下列相关叙述r.确的是A.该变异4牙致©色体上赛闪的推列顺序发生变化B.在冉倍微镜KnJ若到该基闵序列的改变c.s S因突变后瞟吟谏基和哦啶碱$的比例发生变化D.突变后的基因是S基因的等位基因3.下ra为某家庭的遗传系趙ra.带的个体为未检澜性别的a^u已知A.a g与半乳期Hi症有关的鉍闪,个体丨和个体2不携带改阀的致病缺W,捽制红绽色肓的《因用B和b表示。
下列柑关叙述锘误的是□G)正常B性、ittt ■參半乳糖wrw性、女ftea色性ffcsa®件⑽试《丨贝<共16«)勿内正 C •结膽A.个体丨1的基因帝廷AAX a X l i 4 AaX tf X * B.个体 12的某闵©S AAX B Yt * A H XW C.ffl 中带“?”的个体可能既ffi 红鉍色ft 义患半乳懈崮撖 D. 由个体5、6、10的表现担可确定f .乳糖血症为常染色体險抟逋传铳4. 右图为反射弧W 部纺构示fi 31 .下列相犬叙述锘误的是A. 神妗递构存在于②内,可蚶免»细胞内其他醑系破坏 B .兴&传钎到⑤.使膜紂Nr 通透忭m «.电位变为外 )为过《③及其释放的a ®秣动到④供能 D .堵构④K 屯位的殳化与;RiS 择进H 性密切相X5. 下列与免峻也关的叙述中,正确的是 入.利用效疴T 细抱能检拥氬洧中是否含有相成病#B.病电枝染人体细抱S ,尨C 细抱免疫参与将其消灭 C. 艾滋病患者更容&发生舯®昆因为其汸J 1功能较弱I >.it 滋病ft #无体液免疫戍8^不能产生HIV 的抗体6. 飪关士物学实验呒涉及的仪滟.试刑及技术等的叙述.箱误的技①使用高倍5»铢现寮戏烊沣②负繭体侍ifrrt 由的共st 叶中色索的找取和分 褰④晚察DNA 和RNA 在#«絶t 的分布⑤現察根尖分tBtefc ;細虼的有it 分褽 ⑥鲁*和卡门保充先合作用峰放乳\的衣源AXMd )均笛使用光学《镅镜B .CD _实转始终昆活细胞C 沿X 5)所茁试剂均涉及酒柏D .②⑥均X 使用同位索标记法 7. 物.货的结构.性质和用途之N 有吞非常密切的关系,下列有关物成的性®与用途的因果 对应关系锘误的是S .二环[l .L 0:T 烷单的桥环化合物。
2019年河南省高考数学适应性试题(理科)及答案
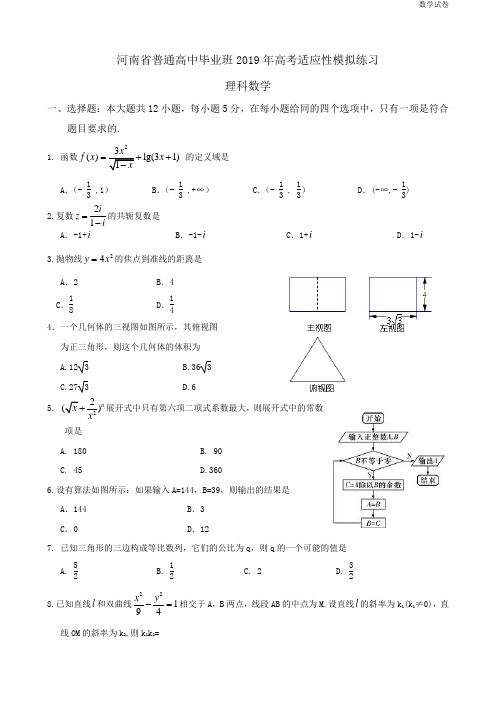
河南省普通高中毕业班2019年高考适应性模拟练习理科数学一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1. 函数2()lg(31)f x x =++ 的定义域是 A .(- 13 ,1)B .(- 13,+∞)C .(- 13 , 13)D .(-∞,- 13)2. A .-1-i C .1+i D .1-i3.抛物线24y x =的焦点到准线的距离是A .2B .4C .18D .144.一个几何体的三视图如图所示,其俯视图 为正三角形,则这个几何体的体积为 A.12 3 B.36 3C.27 3D.65. 22)nx 展开式中只有第六项二项式系数最大,则展开式中的常数项是A. 180B. 90C. 45D.3606.设有算法如图所示:如果输入A=144,B=39,则输出的结果是 A .144 B .3 C .0 D .127. 已知三角形的三边构成等比数列,它们的公比为q ,则q 的一个可能的值是 A. 52 B. 12C. 2D. 328.已知直线l 和双曲线22194x y -=相交于A ,B 两点,线段AB 的中点为M.设直线l 的斜率为k 1(k 1≠0),直线OM 的斜率为k ,则k k =A. 23B. -23C. -49D. 499. 已知命题p:∃,ln 20x R x x ∈+-=,命题q:∀2,2xx R x ∈≥,则下列命题中为真命题的是 A .p ∧q B .⌝p ∧qC .p ∧⌝qD .⌝p ∧⌝q10.对于下列命题:①在∆ABC 中,若cos2A=cos2B, 则∆ABC 为等腰三角形; ②∆ABC 中角A 、B 、C 的对边分别为,,a b c ,若2,5,6a b A π===,则∆ABC 有两组解;③设201420142014sin,cos ,tan ,333a b c πππ=== 则;a b c << ④将函数2sin(3)6y x π=+的图象向左平移π6个单位,得到函数y =2cos(3x +π6)的图象.其中正确命题的个数是 A.0B.1C.2D.311. 四面体ABCD 中,已知AB=CD=29,AC=BD=34,AD=BC=37,则四面体ABCD 的外接球的表面积为A .25πB .45πC .50πD .100π12.设3,0,()(1),0.x x f x f x x -⎧≤=⎨->⎩若()f x x a =+有且仅有三个解,则实数a 的取值范围是A. [1,2]B.(-∞,2)C.[1,+∞)D.(-∞,1) 二.填空题:本大题共4小题,每小题5分.13.2(sin )x x dx π+=⎰.14. 已知实数,x y 满足2268230(3)x y x y x +--+<> ,则z x y =-的取值范围是15. 已知P 为三角形ABC 内部任一点(不包括边界),且满足(→PB -→P A )·(→PB +→P A -2→PC )=0,则∆ABC 的形状一定为___________.16.已知对于任意的自然数n, 抛物线22()(21)1y n n x n x =+-++与x 轴相交于A n ,B n 两点,则|A 1B 1|+|A 2B 2|+|A 3B 3|…+|A 2019B 2019|= 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在锐角∆ABC 中,角A 、B 、C 所对的边分别为,,a b c ,且满足cos 2A-cos 2B=cos(π6-A)cos(π6+A).(Ⅰ)求角B 的值;(Ⅱ)若b=1, 求a c +的取值范围.CBDEA18.(本小题满分12分)某次围棋比赛的决赛阶段实行三番棋决定冠军归属(即三局两胜制,和棋无效,加赛直至分出胜负).打入决赛的两名选手甲、乙平时进行过多次对弈,有记录的30局结果如下表:请根据表中的信息(用样本频率估计概率),回答下列问题:(Ⅰ)如果比赛第一局由掷一枚硬币的方式决定谁先,试求第一局甲获胜的概率; (Ⅱ)若第一局乙先,此后每局负者先, ①求甲以二比一获胜的概率;②该次比赛设冠军奖金为40万元,亚军奖金为10万元,如果冠军“零封”对手(即2:0夺冠)则另加5万元.求甲队员参加此次决赛获得奖金数X 的分布列和数学期望.19.(本小题满分12分)如图,四面体ABCD 中,平面ABC ⊥平面BCD, AC=AB,CB=CD,∠DCB=120°.点E 在BD 上,且DE=13DB=2.(Ⅰ)求证:AB ⊥CE ;(Ⅱ)若AC=CE ,求二面角A-CD-B 的余弦值.20.(本小题满分12分)已知点F 是椭圆C 的右焦点,A ,B 是椭圆短轴的两个端点,且 ABF 是正三角形. (Ⅰ)求椭圆C 的离心率;(Ⅱ)直线l 与以AB 为直径的圆O 相切,并且被椭圆C 截得的弦长的最大值为23,求椭圆C 的标准方EOACFBGD21.(本小题满分12分)已知函数31()ln (),()()(1)6f x x x x ax a R f xg x a x '=--∈=+-. (Ⅰ)当a =2时,求函数()f x 的单调递增区间;(Ⅱ)对于函数F()x 定义域内的两个自变量的值1212121212()(),(),()02F x F x x xx x x x F x x -+'<-=-若,则我们把有序数对12(,)x x 叫作函数F()x 的“零点对”.试问,函数()f x 是否存在这样的“零点对”?如果存在,请你求出其中一个;如果不存在,请说明理由.请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号.22.(本小题满分10分)选修4-1:几何证明选讲如图,在⊙O 的直径AB 的延长线上任取一点C ,过点C 引直线与⊙O 交于点D 、E ,在⊙O 上再取一点F,使⌒AE=⌒AF.(1)求证:E 、D 、G 、O 四点共圆; (2)如果CB=OB ,试求 CBCG 的值.23. (本小题满分10分)选修4—4;坐标系与参数方程在直角坐标系xOy 中,曲线l 的参数方程为1cos (sin x t t y t αα=+⎧⎨=⎩为参数).在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x轴的正半轴为极轴)中,曲线C 的方程为(Ⅰ)判断直线l 与曲线C 公共点个数,并说明理由;(Ⅱ)当4πα=时,求直线l 与曲线C 公共点的坐标.24.(本小题满分10分)选修4—5:不等式选讲(I。
2019年河南省高考适应性考试数学试题(理)及答案

河南省普通高中2019年新课程高考适应性考试(一)数学(理)试题本试题卷分第1卷(选择题)和第Ⅱ卷(必考题和选考题两部分)。
考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试题卷上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共1 2小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U=R ,集合A={1,2,3,4,5},B={|2x x ≥},下图中阴影部分所表示的集合为A .{0,1,2}B .{1,2}C .{1} C .{0,1} 2.复数321iz i i=-+,在复平面上对应的点位于A .第一象限B .第二象限C .第二象限D .第四象限3.若13sin cos ,(0,)αααπ-+=∈,则tan α= A .3 B .3- C .3 D .3-4.已知命题:,p x R ∃∈使得12,x x+<命题2:,10q x R x x ∀∈++>,下列命题为真的是A .p ∧ qB .()p q ⌝∧C .()p q ∧⌝D .()()p q ⌝∧⌝5.某三棱锥的侧视图和俯视图如图所示,则该三棱锥的体积为A .43B .83C .123D .2436.已知△ABC 中,C=45°,则sin 2A=sin 2B 2A .14B .12 C 2D .34 7.如图是计算函数ln(),2,0,23,2,3x x x y x x ⎧-≤-⎪=-<≤⎨⎪>⎩的值的程序框图,在①、②、③处分别应填入的是A .y=ln (一x ),y=0,y=2xB .y=0,y=2x,y=In (一x )C .y=ln (一x ),y=2z,y=0D .y=0,y=ln (一x ),y=2x8.已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足 (a-c )·(b 一c )=0,则|c|的最大值是A .1BC .2D 9.已知A ,B ,C ,D 是同一球面上的四个点,其中△ABC 是正三角形,AD⊥平面ABC ,AD=2AB=6则该球的表面积为A .16πB .24πC .π D .48π103)nx+的展开式中,各项系数之和为M ,各项二项式系数之和为N ,且M+N=72,则展开式中常数项的值为 A .18 B .12 C .9 D .611.已知函数()sin cos (0)f x x x ωωω=+>,如果存在实数x 1,使得对任意的实数x ,都有11()()(2012)f x f x f x ≤≤+成立,则ω的最小值为A .12012 B .2012π C .14024 D .4024π 12.过双曲线22221(0,0)x y a b a b-=>>的右顶点A 作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B ,C ,若A,B ,C 三点的横坐标成等比数列,则双曲线的离心率为 ABCD第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第2l 题为必考题,每个试题考生都必须做答。
〔精品〕2019年河南省普通高中高考数学模拟试卷及解析(理科)(3月份)

2019年河南省普通高中高考数学模拟试卷(理科)(3月份)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A ={0,1,2,3},B ={y|y =x 2+1,x ∈R },P =A ∩B ,则P 的子集个数为()A .4B .6C .8D .162.(5分)已知复数z 满足(1+i )z =(i 为虚数单位),则复数z 在复平面内对应的点所在的象限为()A .第一象限B .第二象限C .第三象限D .第四象限3.(5分)某超市2018年12个月的收入与支出数据的折线图如图所示,根据该折线图,下列说法正确的是()A .该超市2018年的12个月中11月份的收益最高B .该超市2018年的12个月中1月份和3月份的收益最低C .该超市2018年上半年的总收益高于下半年的总收益D .该超市2018年下半年的总收益比上半年的总收益增长了约71.4%4.(5分)下列命题是真命题的是()A .?x 0∈(0,+∞),3<log 3x 0B .若a >b ,则am 2>bm2C .已知A ,B 为△ABC 的两个内角,若A >B ,则sinA >sinBD .函数y =f (1+x )的图象与函数y =f (1﹣x )的图象关于直线x =1对称5.(5分)函数y =的图象大致为()A.B.C.D.6.(5分)已知a=log23?log34,则(ax+)6的展开式中的常数项为()A.15B.60C.120D.2407.(5分)若正方体ABCD﹣A1B1C1D1的棱长为3,E为正方体内任意一点,则AE的长度大于3的概率等于()A.1﹣B.1﹣C.1﹣D.1﹣8.(5分)已知某空间几何体的三视图如图所示,则该几何体的体积为()A.3B.C.D.19.(5分)已知△ABC的三边长分别为a,b,c,面积为S,且a 2+b2﹣c2=4S,c=1,则b﹣a的最大值为()A.B.2C.3D.10.(5分)已知△ABC的顶点A,B在抛物线y 2=2px(p>0)上,顶点C为该抛物线的焦点,则满足条件的正三角形个数为()A.1B.2C.3D.411.(5分)已知奇函数f(x)是定义在R上的增函数,g(x)=sin?f(x),若a=g(﹣log26.1),b=g(20.9),c=g(2),则a,b,c的大小关系为()A.a<b<c B.c<b<a C.b<a<c D.b<c<a12.(5分)已知函数f(x)=3sin(ωx+φ),(ω>0,0<φ<),f(﹣)=0,f()=f(x),且函数f(x)在区间()上单调,则ω的最大值为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。
2019年河南省高考数学适应性试题【理科】及答案

河南省普通高中毕业班2019年高考适应性模拟练习理科数学一、选择题:本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的.1. 函数2()lg(31)f x x =+ 的定义域是A .(- 13 ,1)B .(- 13,+∞)C .(- 13 , 13)D .(-∞,- 13)2. A .-1+i B .-1-i C .1+i D .1-i3.抛物线24y x =的焦点到准线的距离是 A .2 B .4C .18D .144.一个几何体的三视图如图所示,其俯视图 为正三角形,则这个几何体的体积为 A.12 3 B.36 3C.27 3D.65.22)nx 展开式中只有第六项二项式系数最大,则展开式中的常数 项是A. 180B. 90C. 45D.3606.设有算法如图所示:如果输入A=144,B=39,则输出的结果是 A .144 B .3 C .0 D .127. 已知三角形的三边构成等比数列,它们的公比为q ,则q 的一个可能的值是 A. 52 B. 12C. 2D. 328.已知直线l 和双曲线22194x y -=相交于A ,B 两点,线段AB 的中点为M.设直线l 的斜率为k 1(k 1≠0),直线OM 的斜率为k 2,则k 1k 2= A. 23 B. -23C. -49D. 499. 已知 A .p ∧q B .⌝p ∧qC .p ∧⌝qD .⌝p ∧⌝q10.对于下列①在∆ABC 中,若cos2A=cos2B, 则∆ABC 为等腰三角形; ②∆ABC 中角A 、B 、C 的对边分别为,,a b c ,若2,5,6a b A π===,则∆ABC 有两组解;③设201420142014sin,cos ,tan ,333a b c πππ=== 则;a b c << ④将函数2sin(3)6y x π=+的图象向左平移π6个单位,得到函数y =2cos(3x+π6)的图象.其中正确 A.0B.1C.2D.311. 四面体ABCD 中,已知AB=CD=29,AC=BD=34,AD=BC=37,则四面体ABCD 的外接球的表面积为A .25πB .45πC .50πD .100π12.设3,0,()(1),0.x x f x f x x -⎧≤=⎨->⎩若()f x x a =+有且仅有三个解,则实数a 的取值范围是A. [1,2]B.(-∞,2)C.[1,+∞)D.(-∞,1) 二.填空题:本大题共4小题,每小题5分.13.20(sin )x x dx π+=⎰.14. 已知实数,x y 满足2268230(3)x y x y x +--+<> ,则z x y =-的取值范围是15. 已知P 为三角形ABC 内部任一点(不包括边界),且满足(→PB -→PA )·(→PB +→PA -2→PC )=0,则∆ABC 的形状一定为___________.16.已知对于任意的自然数n, 抛物线22()(21)1y n n x n x =+-++与x 轴相交于A n ,B n 两点,则|A 1B 1|+|A 2B 2|+|A 3B 3|…+|A 2018-2019|= 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在锐角∆ABC 中,角A 、B 、C 所对的边分别为,,a b c ,且满足cos 2A-cos 2B=cos(π6-A)cos(π6+A).(Ⅰ)求角B 的值;(Ⅱ)若b=1, 求a c +的取值范围.18.(本小题满分12分)某次围棋比赛的决赛阶段实行三番棋决定冠军归属(即三局两胜制,和棋无效,加赛直至分出胜负).打入决赛的两名选手甲、乙平时进行过多次对弈,有记录的30局结果如下表:请根据表中的信息(用样本频率估计概率),回答下列问题:CDEAEOACFBGD(Ⅰ)如果比赛第一局由掷一枚硬币的方式决定谁先,试求第一局甲获胜的概率; (Ⅱ)若第一局乙先,此后每局负者先, ①求甲以二比一获胜的概率;②该次比赛设冠军奖金为40万元,亚军奖金为10万元,如果冠军“零封”对手(即2:0夺冠)则另加5万元.求甲队员参加此次决赛获得奖金数X 的分布列和数学期望.19.(本小题满分12分)如图,四面体ABCD 中,平面ABC ⊥平面BCD, AC=AB,CB=CD,∠DCB=120°.点E 在BD 上,且DE=13DB=2.(Ⅰ)求证:AB ⊥CE ;(Ⅱ)若AC=CE ,求二面角A-CD-B 的余弦值.20.(本小题满分12分)已知点F 是椭圆C 的右焦点,A ,B 是椭圆短轴的两个端点,且∆ABF 是正三角形. (Ⅰ)求椭圆C 的离心率;(Ⅱ)直线l 与以AB 为直径的圆O 相切,并且被椭圆C 截得的弦长的最大值为23,求椭圆C 的标准方程. 21.(本小题满分12分)已知函数31()ln (),()()(1)6f x x x x ax a R f xg x a x '=--∈=+-. (Ⅰ)当a =2时,求函数()f x 的单调递增区间;(Ⅱ)对于函数F()x 定义域内的两个自变量的值1212121212()(),(),()02F x F x x xx x x x F x x -+'<-=-若,则我们把有序数对12(,)x x 叫作函数F()x 的“零点对”.试问,函数()f x 是否存在这样的“零点对”?如果存在,请你求出其中一个;如果不存在,请说明理由.请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号. 22.(本小题满分10分)选修4-1:几何证明选讲如图,在⊙O 的直径AB 的延长线上任取一点C ,过点C 引直线与⊙O 交于点D 、E ,在⊙O 上再取一点F,使⌒AE =⌒AF.(1)求证:E 、D 、G 、O 四点共圆; (2)如果CB=OB ,试求 CBCG的值.23. (本小题满分10分)选修4—4;坐标系与参数方程在直角坐标系xOy 中,曲线l 的参数方程为1cos (sin x t t y t αα=+⎧⎨=⎩为参数).在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴的正半轴为极轴)中,曲线C 的方程为(Ⅰ)判断直线l 与曲线C 公共点个数,并说明理由;(Ⅱ)当4πα=时,求直线l 与曲线C 公共点的坐标.24.(本小题满分10分)选修4—5:不等式选讲(I (II )如果存在[2,4]x ∈- ,使不等式()(2)f x f x m ++≥成立,求实数m 的取值范围.。
河南2019高三普通高中毕业班高考适应性测试-数学(理)

河南2019高三普通高中毕业班高考适应性测试-数学(理)2018年一般高中毕业班高考适应性测试数 学 试 题〔理〕本试题卷分第I 卷〔选择题〕和第II 卷〔非选择题〕两部分。
考生作答时,将答案答在答题卡上〔答题考前须知见答题卡〕,在本试题卷上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第I 卷【一】选择题:本大题共12小题,每题5分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
1、集合{|3},{1,0,1}x M y R y N =∈==-,那么以下结论正确的选项是〔 〕A 、{0,1}MN =B 、(0,)M N =+∞C 、()(,0)RC M N =-∞D 、(){1,0}R C M N =-2、i 是虚数单位,复数31z i=+的虚部是〔 〕 A 、0B 、-1C 、1D 、-i3、261(1)()x x x x++-的展开式中的常数项为m ,那么函数2y x y mx =-=与的图象所围成的封闭图形的面积为 〔 〕A 、6256B 、2506C 、3756D 、12564、函数(01)||xxa y a x =<<的图象大致形状是〔 〕5、函数(),(0,)mf x x x x=+∈+∞,假设不等式()4f x <的解集是空集,那么 〔 〕A 、4m ≥B 、2m ≥C 、4m ≤D 、2m ≤6、设实数x ,y 满足221x y +≤,那么点(,)x y 不在区域11,11x y x y -≤+≤⎧⎨-≤-≤⎩内的概率是〔 〕A 、14B 、21π-C 、2πD 、187、假设点(cos ,sin )P θθ在直线20x y +=上,那么cos2sin2θθ+=〔 〕A 、15-B 、12- C 、15 D 、128、函数()f x 是定义在R 上的奇函数,且当(],0x ∈-∞时,2()x f x e ex a -=-+,那么函数()f x 在1x =处的切线方程为〔 〕 A 、0x y +=B 、10ex y e -+-=C 、10ex y e +--=D 、0x y -= 9、ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,向量(1,(cos ,sin ),//p q B B p q==且cos cos 2sin ,b C c B a A C +=∠则=〔 〕A 、30︒B 、60︒C 、120︒D 、150︒10、函数()s i n ()(f x M x ωϕω=+>,在区间[a ,b]上是增函数,且(),(),f a M f b M =-=那么函数()cos()g x M x ωϕ=+在[a ,b]上〔 〕 A 、是增函数 B 、是减函数C 、能够取得最大值MD 、能够取得最小值-M11、F 1,F 2分别是双曲线22221(0,0)x y a b a b -=>>的左、右焦点,P 为双曲线上的一点,假设1290F PF ∠=︒,且22F PF ∆的三边长成等差数列,那么双曲线的离心率是〔 〕A 、2B 、3C 、4D 、512、函数731,,1,222()111,[0,],362x x x f x x x ⎧-⎛⎤∈ ⎪⎥⎪+⎝⎦=⎨⎪-+∈⎪⎩函数()sin()22(0)6g x a x a a π=-+>,假设存在12,[0,1]x x ∈,使得12()()f x g x =成立,那么实数a 的取值范围是〔 〕A 、14[,]23B 、10,2⎛⎤ ⎥⎝⎦C 、24[,]33D 、1[,1]2第II 卷本卷包括必考题和选考题两部分。
2019届高三数学下学期适应性考试试题 理(含解析)

2019届高三5月适应性考试理科数学试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则A. B. C. D.【答案】C【解析】分析:利用一元二次不等式的解法化简集合,求出集合的补集,解方程化简集合,利用集合交集的定义进行计算即可.详解:因为或,所以又因为,所以,故选C.点睛:本题主要考查了解一元二次不等式,求集合的补集与交集,属于容易题,在解题过程中要注意在求补集与交集时要考虑端点是否可以取到,这是一个易错点,同时将不等式与集合融合,体现了知识点之间的交汇.2.的值为()A. B. C. D. 1【答案】A【解析】分析:逆用二倍角正弦公式即可得到结果.详解:sin75°cos75°=sin75°cos75°=.故选:A.点睛:本题考查了二倍角正弦公式,属于基础题.3.下列函数中,与函数的定义域、单调性与奇偶性均一致的函数是A. B.C. D.【答案】B【解析】易知原函数的定义域为,单调递增,奇函数,所以A、C、D错误,B正确.故选B.4.的展开式中的系数为()A. B. 84 C. D. 280【答案】C【解析】由题意,根据二项式定理展开式的通项公式,得展开式的通项为,则展开式的通项为,由,得,所以所求的系数为.故选C.点睛:此题主要考查二项式定理的通项公式的应用,以及组合数、整数幂的运算等有关方面的知识与技能,属于中低档题,也是常考知识点.在二项式定理的应用中,注意区分二项式系数与系数,先求出通项公式,再根据所求问题,通过确定未知的次数,求出,将的值代入通项公式进行计算,从而问题可得解.5.设满足约束条件则的最大值为()A. B. 3 C. 9 D. 12【答案】C【解析】【分析】画出可行域,通过平移动直线求最大值.【详解】可行域如图所示:动直线平移到点时,取最大值.故选C.【点睛】一般地,二元一次不等式组条件下的二元一次函数的最值问题,可用线性规划的方法求解.6.已知斜率为3的直线与双曲线交于两点,若点是的中点,则双曲线的离心率等于()A. B. C. 2 D.【答案】A【解析】设,则,所以,,所以,得,所以,所以。
2019年河南省高考数学理科适应性试卷(1)含答案解析

2019年河南省普通高中高考数学适应性试卷(理科)(1)一、选择题(本大题共12道小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的.)1.已知集合A={0,1,2},B={y|y=2x,x∈A},则A∪B中的元素个数为()A.6 B.5 C.4 D.32.如果复数(b∈R,i为虚数单位)的实部与虚部相等,则b的值为()A.1 B.﹣6 C.3 D.﹣93.已知tan(α﹣)=,则的值为()A.B.2 C.2D.﹣24.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣2)2+y2=3相切,则双曲线的离心率为()A.B.C.2 D.25.给出下列四个结论:①已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤2)=0.6,则P(ξ>2)=0.2;②若命题P:∃x0∈[1,+∞),x﹣x0﹣1<0,则¬p:∀x∈(﹣∞,1),x2﹣x﹣1≥0;③已知直线l1:ax+3y﹣1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=﹣3;④设回归直线方程为=2﹣2.5x,当变量x增加一个单位时,y平均增加2个单位.其中正确结论的个数为()A.1 B.2 C.3 D.46.执行如图所示的程序框图,则输出的k的值是()A.10 B.11 C.12 D.137.等差数列{a n}的前n项和为S n,若=,则下列结论中正确的是()A.=2 B.=C.=D.=8.六个人站成一排照相,则甲、乙两人之间恰好站两人的概率为()A.B.C.D.9.已知正数x,y满足x+4y=4,则的最小值为()A.B.24 C.20 D.1810.如图,在边长为1的正方形组成的网格中,画出的是一个几何体的三视图,则该几何体的体积是()A.9 B.C.18 D.2711.已知函数f(x)=ln(2x+)﹣,若f(a)=1,则f(﹣a)=()A.0 B.﹣1 C.﹣2 D.﹣312.已知函数f(x)=|lnx|﹣1,g(x)=﹣x2+2x+3,用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)},则函数h(x)的零点个数为()A.1 B.2 C.3 D.4二、填空题:本大题共4小题,每小题5分.13.已知不等式组表示的平面区域的面积为25,点P(x,y)在所给平面区域内,则z=2x+y的最大值为______.14.(2x+﹣4)9的展开式中,不含x的各项系数之和为______.15.四棱锥P﹣ABCD的五个顶点都在一个球面上,底面ABCD是矩形,其中AB=3,BC=4,又PA⊥平面ABCD,PA=5,则该球的表面积为______.16.已知各项均为正数的数列{a n}满足a n+1=a n+,a1=,S n为数列{a n}的前n项和,若对于任意的n∈N*,不等式≥2n﹣3恒成立,则实数k的取值范围为______.三、解答题:解答应写出文字说明、证明过程或演算步骤17.在△ABC中,角A,B,C的对边分别为a,b,c,已知向量=(cosB,2cos2﹣1),=(c,b﹣2a),且•=0.(Ⅰ)求角C的大小;(Ⅱ)若点D为边AB上一点,且满足=,||=,c=2,求△ABC的面积.18.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5(Ⅰ)根据上表数据,用最小二乘法,求出y关于x的线性回归方程=•x+;(Ⅱ)若周六同一时间段车流量200万辆,试根据(Ⅰ)求出的线性回归方程,预测此时PM2.5的浓度为多少?(参考公式:=,=﹣•;参考数据:x i=540,y i=420)19.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.(Ⅰ)若点P为AA1的中点,求证:平面B1CP⊥平面B1C1P;(Ⅱ)在棱AA1上是否存在一点P,使得二面角B1﹣CP﹣C1的大小为60°?若存在,求出|AP|的值;若不存在,说明理由.20.在平面直角坐标系xOy中,椭圆C: +=1(a>b>0)的离心率为,且过点A(,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.(Ⅰ)求椭圆C的方程;(Ⅱ)若OP⊥OQ,求点Q的纵坐标的值.21.已知函数f(x)=a﹣﹣lnx,其中a为常数.(Ⅰ)若f(x)=0恰有一个解,求a的值;(Ⅱ)(i)若函数g(x)=a﹣﹣﹣f(x)﹣lnp,其中p为常数,试判断函数g(x)的单调性;(ii)若f(x)恰有两个零点x1,x2(x1<x2),求证:x1+x2<3e a﹣1﹣1.四、请考在第22、23、24三题中任选一题作答:注意:只能做所选定的题目:如果多做,则按所做的第一个题目计分.22.如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.(Ⅰ)求证:直线AB是圆O的切线;(Ⅱ)若tan∠CED=,圆O的半径为2,求OA的长.23.在平面直角坐标系xOy中,直线l的参数方程为(t为参数),在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=2sinθ.(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;(Ⅱ)若点P的直角坐标为(1,0),圆C与直线l交于A、B两点,求|PA|+|PB|的值.24.已知函数f(x)=|x﹣2|.(Ⅰ)解不等式f(x)+f(x+5)≥9;(Ⅱ)若|a|<1,|b|<1,求证:f(ab+3)>f(a+b+2).2019年河南省普通高中高考数学适应性试卷(理科)(1)参考答案与试题解析一、选择题(本大题共12道小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的.)1.已知集合A={0,1,2},B={y|y=2x,x∈A},则A∪B中的元素个数为()A.6 B.5 C.4 D.3【考点】并集及其运算.【分析】根据集合的定义与运算法则,进行计算即可.【解答】解:∵集合A={0,1,2},B={y|y=2x,x∈A},∴B={0,2,4};∴A∪B={0,1,2,4};∴A∪B中的元素个数为4.故选:C.2.如果复数(b∈R,i为虚数单位)的实部与虚部相等,则b的值为()A.1 B.﹣6 C.3 D.﹣9【考点】复数代数形式的乘除运算;复数相等的充要条件.【分析】利用复数代数形式的乘除运算化简,然后由实部和虚部相等求得b的值.【解答】解:∵=的实部和虚部相等,∴6﹣b=﹣(2b+3),解得:b=﹣9.故选:D.3.已知tan(α﹣)=,则的值为()A.B.2 C.2D.﹣2【考点】三角函数的化简求值.【分析】由tan(α﹣)=,求出tanα,然后对表达式的分子、分母同除以cosα,然后代入即可求出表达式的值.【解答】解:由tan(α﹣)==,得tanα=3.则=.故选:B.4.双曲线﹣=1(a>0,b>0)的渐近线与圆(x﹣2)2+y2=3相切,则双曲线的离心率为()A.B.C.2 D.2【考点】双曲线的简单性质.【分析】由于双曲线﹣=1(a>0,b>0)的渐近线与(x﹣2)2+y2=3相切,可得圆心(2,0)到渐近线的距离d=r,利用点到直线的距离公式即可得出.【解答】解:取双曲线的渐近线y=x,即bx﹣ay=0.∵双曲线﹣=1(a>0,b>0)的渐近线与(x﹣2)2+y2=1相切,∴圆心(2,0)到渐近线的距离d=r,∴=,化为2b=c,两边平方得3c2=4b2=4(c2﹣a2),化为c2=4a2.∴e==2.故选:C.5.给出下列四个结论:①已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤2)=0.6,则P(ξ>2)=0.2;②若命题P:∃x0∈[1,+∞),x﹣x0﹣1<0,则¬p:∀x∈(﹣∞,1),x2﹣x﹣1≥0;③已知直线l1:ax+3y﹣1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=﹣3;④设回归直线方程为=2﹣2.5x,当变量x增加一个单位时,y平均增加2个单位.其中正确结论的个数为()A.1 B.2 C.3 D.4【考点】命题的真假判断与应用.【分析】①根据正态分布的性质进行判断,②根据含有量词的命题的否定进行判断.③根据直线垂直的等价条件进行判断.④根据回归直线的性质进行判断.【解答】解:①若ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤2)=0.6,则P(ξ>2)===0.2,故①正确,②若命题p:∃x0∈[1,+∞),x﹣x0﹣1<0,则¬p:∀x∈[1,+∞),x2﹣x﹣1≥0;故②错误③当b≠0时,两直线的斜率分别为,,由•()==﹣1,即a=﹣3b,当b=0,a=0时,两直线分别为l1:3y﹣1=0,l2:x+1=0,满足l1⊥l2,故l1⊥l2的充要条件是错误,故③错误,④设回归直线方程为=2﹣2.5x,当变量x增加一个单位时,y平均减少2.5个单位.故④错误,故正确是①,故选:A.6.执行如图所示的程序框图,则输出的k的值是()A.10 B.11 C.12 D.13【考点】绘制结构图.【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量k的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:第1次执行循环体后,S=2,k=2,不满足退出循环的条件,第2次执行循环体后,S=6,k=3,不满足退出循环的条件,第3次执行循环体后,S=14,k=4,不满足退出循环的条件,第4次执行循环体后,S=30,k=5,不满足退出循环的条件,第5次执行循环体后,S=62,k=6,不满足退出循环的条件,第6次执行循环体后,S=126,k=7,不满足退出循环的条件,第7次执行循环体后,S=510,k=8,不满足退出循环的条件,第8次执行循环体后,S=1022,k=9,不满足退出循环的条件,第9次执行循环体后,S=2046,k=10,满足退出循环的条件,故输出的k值为10,故选:A7.等差数列{a n}的前n项和为S n,若=,则下列结论中正确的是()A . =2B . =C . =D . =【考点】等差数列的前n 项和.【分析】由等差数列的求和公式和性质可得=3•=2,解方程可得.【解答】解:∵等差数列{a n }的前n 项和为S n ,且=,∴==2,由等差数列的求和公式和性质可得:===3•=2,∴ =故选:C8.六个人站成一排照相,则甲、乙两人之间恰好站两人的概率为( )A .B .C .D .【考点】列举法计算基本事件数及事件发生的概率.【分析】六个人站成一排照相,先求出基本事件总数,再求出甲、乙两人之间恰好站两人包含基本事件个数,由此能求出甲、乙两人之间恰好站两人的概率.【解答】解:六个人站成一排照相,基本事件总数n==720,甲、乙两人之间恰好站两人包含基本事件个数m==144,∴甲、乙两人之间恰好站两人的概率p===. 故选:B .9.已知正数x ,y 满足x +4y=4,则的最小值为( )A .B .24C .20D .18 【考点】基本不等式.【分析】根据已知可将,化为,利用基本不等式可得≥2=8xy ,从而原式:≥=18.【解答】解:∵x+4y=4,可得:=1,∴====,∵≥2=8xy,∴≥=18.故选:D.10.如图,在边长为1的正方形组成的网格中,画出的是一个几何体的三视图,则该几何体的体积是()A.9 B.C.18 D.27【考点】由三视图求面积、体积.【分析】由三视图和正方体可得该几何体一个三棱锥,由三视图求出几何元素的长度,由锥体的体积公式求出几何体的体积.【解答】解:根据三视图可知几何体是一个三棱锥A﹣BCD,三棱锥的外面是长、宽、高为6、3、3的长方体,∴几何体的体积V==9,故选:A.11.已知函数f(x)=ln(2x+)﹣,若f(a)=1,则f(﹣a)=()A.0 B.﹣1 C.﹣2 D.﹣3【考点】函数的值.【分析】易知f(a)=ln(2a+)﹣=1,化简f(﹣a)=ln(﹣2a+)﹣=ln()﹣,从而求得.【解答】解:由题意知,f(a)=ln(2a+)﹣=1,故f(﹣a)=ln(﹣2a+)﹣=ln()﹣=﹣ln(2a+)﹣2+=﹣(ln(2a+)﹣)﹣2=﹣3,故选:D.12.已知函数f(x)=|lnx|﹣1,g(x)=﹣x2+2x+3,用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)},则函数h(x)的零点个数为()A.1 B.2 C.3 D.4【考点】根的存在性及根的个数判断.【分析】根据min{m,n}的定义,作出两个函数的图象,利用数形结合进行求解即可.【解答】解:作出函数f(x)和g(x)的图象如图,两个图象的下面部分图象,由g(x)=﹣x2+2x+3=0,得x=﹣1,或x=3,由f(x)=|lnx|﹣1=0,得x=e或x=,∵g(e)>0,∴当x>0时,函数h(x)的零点个数为3个,故选:C.二、填空题:本大题共4小题,每小题5分.13.已知不等式组表示的平面区域的面积为25,点P(x,y)在所给平面区域内,则z=2x+y的最大值为17.【考点】简单线性规划.【分析】由约束条件作出可行域,结合可行域的面积求得a值,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得C(4,4),联立,解得A(a,a),联立,解得B(8﹣a,a),∴,即a=﹣1,∴B(9,﹣1),化目标函数z=2x +y 为y=﹣2x +z ,由图可知,当直线y=﹣2x +z 过点B 时,直线在y 轴上的截距最大,z 有最大值为17. 故答案为:17.14.(2x +﹣4)9的展开式中,不含x 的各项系数之和为 ﹣1 .【考点】二项式定理的应用.【分析】先将问题转化为二项展开式的各项系数和问题,再利用赋值法求出各项系数和.【解答】解:(2x +﹣4)9的展开式中,不含x 的各项系数之和,即(﹣4)9的各项系数之和.令y=1,可得(﹣4)9的各项系数之和为(﹣1)9=﹣1,故答案为:﹣1.15.四棱锥P ﹣ABCD 的五个顶点都在一个球面上,底面ABCD 是矩形,其中AB=3,BC=4,又PA ⊥平面ABCD ,PA=5,则该球的表面积为 50π .【考点】球的体积和表面积.【分析】把四棱锥补成长方体,根据长方体的对角线长等于球的直径求得外接球的半径,代入球的表面积公式计算.【解答】解:把四棱锥补成长方体,则四棱锥的外接球是长方体的外接球,∵长方体的对角线长等于球的直径,∴2R==5,∴R=,外接球的表面积S=4πR 2=50π.故答案为:50π.16.已知各项均为正数的数列{a n }满足a n +1=a n +,a 1=,S n 为数列{a n }的前n 项和,若对于任意的n ∈N *,不等式≥2n ﹣3恒成立,则实数k 的取值范围为 . 【考点】数列递推式.【分析】各项均为正数的数列{a n }满足a n +1=a n +,a 1=,变形为:a n +1﹣=(a n ﹣),a 1﹣=3,利用等比数列的通项公式可得:a n =3×+,可得S n .不等式≥2n ﹣3化为:k ≥.再利用数列的单调性即可得出.【解答】解:∵各项均为正数的数列{a n }满足a n +1=a n +,a 1=,∴a n﹣=(a n﹣),a1﹣=3,+1∴数列是等比数列,首项为3,公比为.∴a n﹣=3×,即a n=3×+,∴S n=+=+.不等式≥2n﹣3化为:k≥.令f(n)=,则f(n+1)﹣f(n)=﹣=.则n≤2,a1<a2<a3.n≥3,a3>a4>a5>….∴f(3)最大为.对于任意的n∈N*,不等式≥2n﹣3恒成立,∴k≥.故答案为:.三、解答题:解答应写出文字说明、证明过程或演算步骤17.在△ABC中,角A,B,C的对边分别为a,b,c,已知向量=(cosB,2cos2﹣1),=(c,b﹣2a),且•=0.(Ⅰ)求角C的大小;(Ⅱ)若点D为边AB上一点,且满足=,||=,c=2,求△ABC的面积.【考点】平面向量数量积的运算.【分析】(Ⅰ)利用平面向量的数量积运算法则计算列出关系式,根据二倍角的余弦函数公式,利用两角和与差的正弦函数公式及诱导公式化简,求出cosC的值,(Ⅱ)利用向量的几何意义和向量的模的计算以及余弦定理和三角形的面积公式即可求出.【解答】解:(Ⅰ)∵向量=(cosB,2cos2﹣1),=(c,b﹣2a),且•=0,∴c•cosB+(b﹣2a)cosC=0,由正弦定理可得,sinCcosB+(sinB﹣2sinA)cosC=0,∴sinA﹣2sinAcosC=0,∵sinA ≠0,∴cosC ﹣,∵C ∈(0,π),∴C=,(Ⅱ)=,||=,c=2,∴=﹣,∴2=+,两边平方得4||2=b 2+a 2+2accosC=b 2+a 2+ac=28,(1),∵c 2=b 2+a 2﹣2accosC=b 2+a 2﹣ac=12,(2),由(1),(2)可得ab=8,∴S △ABC =absinC=2.18.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5(Ⅰ)根据上表数据,用最小二乘法,求出y 关于x 的线性回归方程=•x +; (Ⅱ)若周六同一时间段车流量200万辆,试根据(Ⅰ)求出的线性回归方程,预测此时PM2.5的浓度为多少?(参考公式: =, =﹣•;参考数据: x i =540, y i =420)【考点】线性回归方程.【分析】(I )根据回归系数公式计算回归系数,得出回归方程;(II )将x=200代入回归方程计算.【解答】解:(Ⅰ)×=108,(78+80+84+88+90)=84.=(﹣8)×(﹣6)+(﹣6)×(﹣4)+0+6×4+8×6=144,=(﹣8)2+(﹣6)2+0+62+82=200.∴=,=84﹣0.72×108=6.24.∴y关于x的线性回归方程为=0.72x+6.24.(II)当x=200时,=0.72×200+6.24=150.24.∴此时PM2.5的浓度为150.24微克/立方米.19.如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=BC=2AC=4.(Ⅰ)若点P为AA1的中点,求证:平面B1CP⊥平面B1C1P;(Ⅱ)在棱AA1上是否存在一点P,使得二面角B1﹣CP﹣C1的大小为60°?若存在,求出|AP|的值;若不存在,说明理由.【考点】二面角的平面角及求法;平面与平面垂直的判定.【分析】(Ⅰ)推导出B1C1⊥A1C1,B1C1⊥CC1,从而B1C1⊥平面ACC1A1,进而B1C1⊥CP,再求出CP⊥C1P,从而CP⊥平面B1C1P,由此能证明平面B1CP⊥平面B1C1P.(Ⅱ)以C为原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出在棱AA1上存在一点P,使得二面角B1﹣CP﹣C1的大小为60°,且|AP|=2【解答】证明:(Ⅰ)∵∠A1C1B1=∠ACB=90°,∴B1C1⊥A1C1,由直三棱锥性质得B1C1⊥CC1,且A1C1∩CC1=C1,∴B1C1⊥平面ACC1A1,∵CP⊂平面ACC1A1,∴B1C1⊥CP,由A1A=BC=2AC=4,P为A1A中点,知CP=C1P=2,∴=,即CP⊥C1P,B1C1∩C1P=C1,∴CP⊥平面B1C1P,∵CP⊂平面B1CP,∴平面B1CP⊥平面B1C1P.解:(Ⅱ)如图,以C为原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系,设|AP|=a,P(2,0,a),C(0,0,0),B1(0,4,4),B(0,4,0),=(2,0,a),=(0,4,4),设平面B1CP的法向量为=(x,y,z),则,取z=﹣1,得=(),平面C1CP的一个法向量=(0,4,0),∵二面角B1﹣CP﹣C1的大小为60°,∴cos60°===,解得a=2,∴在棱AA1上存在一点P,使得二面角B1﹣CP﹣C1的大小为60°,且|AP|=220.在平面直角坐标系xOy中,椭圆C: +=1(a>b>0)的离心率为,且过点A(,1),点P在椭圆C上,且在第一象限内,直线PQ与圆O:x2+y2=b2相切于点M.(Ⅰ)求椭圆C的方程;(Ⅱ)若OP⊥OQ,求点Q的纵坐标的值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(Ⅰ)由椭圆C: +=1(a>b>0)的离心率为,且过点A(,1),列出方程组,求出a,b,由此能求出椭圆C的方程.(Ⅱ)由圆O的方程为x2+y2=4,设点Q的纵坐标为t,则Q(2,t),当MP⊥x轴时,求出t=﹣2;当PM不垂直于x轴时,设直线OP:y=kx(k>0,x>0),则直线OQ:y=﹣,由|OP|•|OQ|=|PQ|•|OM|,能求出点Q的纵坐标的值.【解答】解:(Ⅰ)∵椭圆C: +=1(a>b>0)的离心率为,且过点A(,1),∴,解得a2=8,b2=4,∴椭圆C的方程为.(Ⅱ)由(Ⅰ)得圆O的方程为x2+y2=4,①设点Q的纵坐标为t,则Q(2,t),当MP⊥x轴时,∵点P在椭圆C上,且在第一象限内,∴P(2,),∵,解得t=﹣2.②当PM不垂直于x轴时,设直线OP:y=kx(k>0,x>0),∴直线OQ:y=﹣,则P(x0,kx0),Q(﹣tx,t),在△OPQ中,|OP|•|OQ|=|PQ|•|OM|,∴=2,即=4[(x0+kt)2+(kx0﹣t)2],,∴,∴,又由,∴,又由,∴,∴,∴=0,∴t2=8,解得t=.∴点Q的纵坐标的值为.21.已知函数f(x)=a﹣﹣lnx,其中a为常数.(Ⅰ)若f(x)=0恰有一个解,求a的值;(Ⅱ)(i)若函数g(x)=a﹣﹣﹣f(x)﹣lnp,其中p为常数,试判断函数g(x)的单调性;(ii)若f(x)恰有两个零点x1,x2(x1<x2),求证:x1+x2<3e a﹣1﹣1.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【分析】(Ⅰ)求出函数的导数,求得单调区间,由单调性,即可判断函数的零点个数;(Ⅱ)(i)求出g(x)的导数,从而判断出g(x)的单调性,(ii)要证x1+x2<3e a﹣1﹣1,可知知,p是h(x)的唯一最大值点,故有,作函数m(x)=lnx﹣﹣lnp,通过导数判断单调性,整理,变形,即可得证.【解答】解:(Ⅰ)f′(x)=,令f′(x)=0,解得:x=1,当0<x<1时,f′(x)>0,f(x)在(0,1)递增,当x>1时,f′(x)<0,f(x)在(1,+∞)递减,f(x)max=f(1)=a﹣1,①当f(x)max=0,解得:a=1,此时最大值点唯一,符合题意,②当f(x)max<0,即a<1时,f(x)<0恒成立,不符合题意,③当f(x)max>0,即a>1时,e a>1,f(e a)=﹣<0,e﹣a<1,∴f(e﹣a)=2a﹣e a≤2a﹣ea<0,(易证e x≥ex),∴f(x)有2个零点,不符合题意,综上:a=1;(Ⅱ)(i)由g(x)=a﹣﹣﹣f(x)﹣lnp,得:g(x)=lnx﹣﹣lnp,函数g(x)的定义域是(0,+∞),且p>0,∵g′(x)=≥0,∴g(x)在(0,+∞)单调递增;(ii)f(x)=0⇔h(x)=ax﹣1﹣xlnx=0,故x1,x2也是h(x)=0的两个零点.由h′(x)=a﹣1﹣ln x=0,得x=e a﹣1(记p=e a﹣1).可知,p是h(x)的唯一最大值点,故有,作函数m(x)=lnx﹣﹣lnp,则m′(x)=≥0,故m(x)单调递增.当x>p时,h(x)>h(p)=0;当0<x<p时,h(x)<0.于是,ax1﹣1=x1ln x1<+x1lnp.整理,得(2+lnp﹣a)x12﹣(2p+ap﹣plnp﹣1)x1+p>0,即x12﹣(3e a﹣1﹣1)x1+e a﹣1>0.同理x22﹣(3e a﹣1﹣1)x2+e a﹣1<0.故x22﹣(3e a﹣1﹣1)x2+e a﹣1<x12﹣(3e a﹣1﹣1)x1+e a﹣1,即(x2+x1)(x2﹣x1)<(3e a﹣1﹣1)(x2﹣x1),于是x1+x2<3e a﹣1﹣1.四、请考在第22、23、24三题中任选一题作答:注意:只能做所选定的题目:如果多做,则按所做的第一个题目计分.22.如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.(Ⅰ)求证:直线AB是圆O的切线;(Ⅱ)若tan∠CED=,圆O的半径为2,求OA的长.【考点】相似三角形的性质.【分析】(I)利用等腰三角形的性质和切线的定义即可证明;(II)利用圆的性质可得=.再利用切线的性质可得△CBD∽△EBC,于是==.设BD=x,BC=3x,利用切割线定理可得BC2=BD•BE,代入解出即可.【解答】(Ⅰ)证明:如图,连接OC,∵OA=OB,CA=CB,∴OC⊥AB,∴AB是⊙O的切线.(Ⅱ)解:∵ED是直径,∴∠ECD=90°,在Rt△BCD中,∵tan∠CED=,∴=.∵AB是⊙O的切线,∴∠BCD=∠E.又∵∠CBD=∠EBC,∴△CBD∽△EBC,∴==.设BD=x,BC=3x,又BC2=BD•BE,∴(3x)2=x•(x+4).解得:x1=0,x2=,∵BD=x>0,∴BD=.∴OA=OB=BD+OD=.23.在平面直角坐标系xOy中,直线l的参数方程为(t为参数),在以原点O为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρ=2sinθ.(Ⅰ)写出直线l的普通方程和圆C的直角坐标方程;(Ⅱ)若点P的直角坐标为(1,0),圆C与直线l交于A、B两点,求|PA|+|PB|的值.【考点】简单曲线的极坐标方程;参数方程化成普通方程.【分析】(Ⅰ)把直线l的参数方程消去参数t可得,它的直角坐标方程;把圆C的极坐标方程依据互化公式转化为直角坐标方程.(Ⅱ)把直线l方程与圆C的方程联立方程组,求得A、B两点的坐标,可得|PA|+|PB|的值.【解答】解:(Ⅰ)∵直线l的参数方程为(t为参数),消去参数t可得3x+y﹣3=0.圆C的方程为ρ=2sinθ,即ρ2=2ρsinθ,即x2+y2=2y,即x2+=3.(Ⅱ)由求得,或,故可得A(,﹣)、B(﹣, +).∵点P(1,0),∴|PA|+|PB|=+=(2﹣)+(2+)=4.24.已知函数f(x)=|x﹣2|.(Ⅰ)解不等式f(x)+f(x+5)≥9;(Ⅱ)若|a|<1,|b|<1,求证:f(ab+3)>f(a+b+2).【考点】绝对值不等式的解法.【分析】(Ⅰ)求出f(x)的复合函数形式,通过讨论x的范围,求出各个阶段上的x的范围,从而求出不等式的解集;(Ⅱ)问题转化为:|ab+1|>|a+b|,通过作差法证明即可.【解答】(Ⅰ)解:f(x)+f(x+5)=|x﹣2|+|x+3|=,当x<﹣3时,由﹣2x﹣1≥9,解得:x<﹣5,当﹣3≤x≤2时,f(x)≥9不成立,当x>2时,由2x+1≥9,解得:x≥4,∴不等式的解集是{x|x≤﹣5或x≥4};(Ⅱ)证明:f(ab+3)>f(a+b+2)即|ab+1|>|a+b|,∵|a|<1,|b|<1,∴(ab+1)2﹣(a+b)2=(a2﹣1)(b2﹣1)>0,∴|ab+1|>|a+b|,故所证不等式成立.2019年10月4日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省2019年普通高中毕业班高考适应性测试数 学 试 题(理)本试题卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
考生作答时,将答案答在答题卡 上(答题注意事项见答题卡),在本试题卷上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.集合{|3},{1,0,1}x M y R y N =∈==-,则下列结论正确的是( )A .{0,1}MN =B .(0,)M N =+∞C .()(,0)R C M N =-∞D .(){1,0}R C M N =-2.i 是虚数单位,复数31z i=+的虚部是 ( )A .0B .-1C .1D .-i3.261(1)()x x x x++-的展开式中的常数项为m ,则函数2y x y mx =-=与的图象所围成的封闭图形的面积为 ( )A .6256 B .2506C .3756D .12564.函数(01)||xxa y a x =<<的图象大致形状是( )5.已知函数(),(0,)mf x x x x=+∈+∞,若不等式()4f x <的解集是空集,则 ( )A .4m ≥B .2m ≥C .4m ≤D .2m ≤6.设实数x ,y 满足221x y +≤,则点(,)x y 不在区域11,11x y x y -≤+≤⎧⎨-≤-≤⎩内的概率是( )A .14B .21π-C .2πD .187.若点(cos ,sin )P θθ在直线20x y +=上,则cos 2sin 2θθ+= ( )A .15-B .12-C .15 D .128.已知函数()f x 是定义在R 上的奇函数,且当(],0x ∈-∞时,2()x f x e ex a -=-+,则函数()f x 在1x =处的切线方程为( )A .0x y +=B .10ex y e -+-=C .10ex y e +--=D .0x y -=9.ABC ∆中,a ,b ,c 分别是角A ,B ,C的对边,向量(1,(cos ,sin ),//p q B B p q ==且cos cos 2sin ,b C c B a A C +=∠则=( )A .30︒B .60︒C .120︒D .150︒10.函数()sin()(0)f x M x ωϕω=+>,在区间[a ,b]上是增函数,且(),(),f a M f b M =-=则函数()cos()g x M x ωϕ=+在[a ,b]上( )A .是增函数B .是减函数C .可以取得最大值MD .可以取得最小值-M11.已知F 1,F 2分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点,P 为双曲线上的一点,若1290F PF ∠=︒,且22F PF ∆的三边长成等差数列,则双曲线的离心率是( )A .2B .3C .4D .512.已知函数731,,1,222()111,[0,],362x x x f x x x ⎧-⎛⎤∈ ⎪⎥⎪+⎝⎦=⎨⎪-+∈⎪⎩函数()s i n ()22(0)6g x a x a a π=-+>,若存在12,[0,1]x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是( )A .14[,]23B .10,2⎛⎤ ⎥⎝⎦C .24[,]33D .1[,1]2第II 卷本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必须做答。
第 22~24题为选考题,考生根据要求做答。
二、填空题:本大题共4小题,每小题5分。
13.命题“存在x R ∈,使得|1||1|3x x --+>”的否定是 。
14.已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm ),可得这个几何体的表面积是cm 2。
15.经过点(0,-1)作圆22:670C x y x +-+=的切线,切点分别为A 和B ,点Q 是圆C 上一点,则ABQ ∆面积的最大值为 。
16.“三角形的三条中线交于一点,且这一点到顶点的距离等于它到对边中点距离的2倍”。
试类比:四面体的四条中线(顶点到对面三角形重心的连线段)交于一点,且这一点到顶点的距离等于它到对面重心距离的 倍。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分) 已知()41x f x x =+,数列{}n a 的首项*111,()()n n a a f a n N +==∈(1)求数列{}n a 的通项公式;(2)设2nn nb a =,数列{}n b 的前n 项和为n S ,求使2012n S >的最小正整数n 。
18.(本小题满分12分)甲、乙两同学进行下棋比赛,约定每局胜者得1分,负者得0分(无平局),比赛进行到有一个人比对方多2分或比满8局时停止,设甲在每局中获胜的概率为1()2p p>,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为58.(I)如右图为统计这次比赛的局数n和甲、乙的总得分S,T的程序框图.其中如果甲获胜,输人a=l.b=0;如果乙获胜,则输人a=0,b=1.请问在①②两个判断框中应分别填写什么条件?(Ⅱ)求p的值;(Ⅲ)设ξ表示比赛停止时已比赛的局数,求随机变量ξ的分布列和.Eξ19.(本小题满分12分)四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA= AB =1,AD =2,点M是PB的中点,点N在BC边上移动.(I)求证:当N是BC边的中点时,MN∥平面PAC;(Ⅱ)证明,无论N点在BC边上何处,都有PN⊥AM;(Ⅲ)当BN等于何值时,PA与平面PDN所成角的大小为45︒.20.(本小题满分12分)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为13,椭圆上的点到右焦点F 的最近距离为2,若椭圆C 与x 轴交于A 、B 两点,M 是椭圆C 上异于A 、B 的任意一点,直线MA 交直线:9l x =于G 点,直线MB 交直线l 于H 点。
(1)求椭圆C 的方程;(2)试探求以GH 为直径的圆是否恒经过x 轴上的定点?若经过,求出定点的坐标;若不经过,请说明理由。
21.(本小题满分12分) 设函数21()ln .2f x x ax bx =-- (1)若x=1是()f x 的极大值点,求a 的取值范围。
(2)当a=0,b=-1时,函数2()()F x f x x λ=-有唯一零点,求正数λ的值。
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。
做答时用2B 铅笔在答题卡上把所选题目的题号涂黑。
22.(本小题满分10分)选修4—1:几何证明选讲 如图,已知ABC ∆中,AB=BC ,以AB 为直径的⊙O 交AC 于点D ,过D 作DE BC ⊥,垂足为E ,连结OE 。
若30CD ACB =∠=︒,分别求AB ,OE 的长。
23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C 1的极坐标方程为4sin ρθ=,曲线C 2的极坐标方程为()6R πθρ=∈,曲线C 1,C 2相交于点M ,N 。
(1)将曲线C 1,C 2的极坐标方程化为直角坐标方程; (2)求线段MN 的长。
24.(本小题满分10分)选修4—5:不等式选讲 设函数()|31| 3.f x x ax =-++ (1)若a=1,解不等式()5f x ≤;(2)若函数()f x 有最小值,求实数a 的取值范围。
参考答案(13)对于任意的x ∈R ,都有113x x --+≤.(14) 32π+ (15)(415+ (16) 3三、解答题 (17)解:(Ⅰ)1()41n n n n a a f a a +==+,1114n n a a +=+,1114n na a +-=.数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项,4为公差的等差数列.………………………………… 3分 114(1)nn a =+-,则数列{}n a 的通项公式为143n a n =-.…………………………6分 (Ⅱ)12325292(43)2.n n S n =+⨯+⨯+⋅⋅⋅+-⋅……………………①2341225292(43)2.n n S n +=+⨯+⨯+⋅⋅⋅+-⋅ ……………………②②-①并化简得1(47)214n n S n +=-⋅+.……………………………………………10分 易见n S 为n 的增函数,2012n S >,即1(47)21998n n +-⋅>.满足此式的最小正整数6n =.…………………………………………………………12分 (18)解:(Ⅰ)程序框图中的①应填2M =,②应填8n =.(注意:答案不唯一.)……………2分 (Ⅱ)依题意得,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止.所以225(1)8p p +-=,解得: 34p =或14p =,因为12p >,所以3.4p =……6分 (Ⅲ)依题意得,ξ的可能值为2,4,6,8.5(2)8P ξ==,5515(4)(1)8864P ξ==-⨯=,55545(6)(1)(1)888512P ξ==--⨯=, 55527(8)(1)(1)(1)1888512P ξ==---⨯=.所以随机变量ξ的分布列为故2468864512512256E ξ=⨯+⨯+⨯+⨯=.…………………………………12分(19)证明:(Ⅰ)取AB 的中点E ,连接EN ,又因为M 是PB 的中点,N 是BC 中点. ME ∴∥PA ,NE ∥AC .ME NE E =,PA AC A =,∴平面MNE ∥平面PAC .又⊂MN 平面MNE ,∴MN ∥平面PAC ………………4分(Ⅱ)1PA AB ==,M 是PB 的中点, PB AM ⊥∴.又⊥PA 平面ABCD ,⊂BC 平面ABCD , BC PA ⊥∴.又AB BC ⊥ , PA AB A =, ⊥∴BC 平面PAB .又⊂AM 平面PAB , BC AM ⊥∴.⊥∴AM 平面PBC .NEA BCDP M又⊂PN 平面PBC , ∴AM PN ⊥.所以无论N 点在BC 边的何处,都有AM PN ⊥.……………………………8分 (Ⅲ)分别以AP AB AD ,,所在的直线为z y x ,,轴,建立空间直角坐标系,设,m BN =则)0,0,0(A ,)0,0,2(D ,(0,1,0)B ,0,1,2(C )0,1,(m N ,)1,0,0(P ,)1,0,2(-=,(,1,1)PN m =-,(0,0,1).PA =-设平面PDN 的法向量为(,,)x y z =n ,则0,PD PN ⎧⋅=⎪⎨⋅=⎪⎩n n 20,0.x z mx y z -=⎧⇔⎨+-=⎩ 令1=x 得m y -=2,2=z , 设PA 与平面PDN 所成的角为θ,sin cos ,PA θ=<>n=22)2(522=-+∴m , 解得32-=m 或32+=m (舍去).2m ∴=……………………………………………………………………………12分(20)解:(Ⅰ)由题意得1,32c a a c ⎧=⎪⎨⎪-=⎩1,3c a =⎧⇒⎨=⎩82=⇒b .椭圆C 的方程为:221.98x y +=……………………………………………………4分 (Ⅱ)记直线MA 、MB 的斜率分别为1k 、2k ,设,,M A B 的坐标分别为00(,)M x y ,)0,3(-A ,)0,3(B ,,3001+=∴x y k 020,3y k x =-2012209y k k x ∴=-. P 在椭圆上,所以)91(818920202020x y y x -=⇒=+,1k 2k ⋅98-=,设),9(1y G ),9(2y H ,则1211y k k AM ==,622yk k MB ==. 722121y y k k =∴,又1k 2k ⋅98-=.1212864729y y y y ∴=-⇒=-.……………………………………………………………8分 因为GH 的中点为)2,9(21y y Q +,12GH y y =-,所以,以GH 为直径的圆的方程为:4)()2()9(2212212y y y y y x -=+-+-.令0=y ,得64)9(212=-=-y y x ,17,1==∴x x ,将两点)0,1(),0,17(代入检验恒成立.所以,以GH 为直径的圆恒过x 轴上的定点(17,0),(1,0).…………………………12分 (21)解:(Ⅰ))(x f 的定义域为(0,)+∞, 1()f x ax b x '=--,由(1)f '=0,得1b a =-.∴1(1)(1)()1ax x f x ax a x x -+-'=-+-=.…………………………………………2分①若a ≥0,由)('x f =0,得x =1.当10<<x 时,()0f x '>,此时)(x f 单调递增; 当1>x 时,()0f x '<,此时)(x f 单调递减.所以x =1是)(x f 的极大值点. …………………………………………………………4分 ②若a <0,由()f x '=0,得x =1,或x =a1-. 因为x =1是)(x f 的极大值点,所以a1->1,解得-1<a <0. 综合①②:a 的取值范围是a >-1. ……………………………………………………6分 (Ⅱ)因为函数()2()F x f x x =-λ有唯一零点,即20x ln x x λ--=有唯一实数解,设2g(x )x ln x x =λ--,则221()x x g'x xλ--=.令0)('=x g ,2210x x λ--=.因为0λ>,所以△=18+λ>0,方程有两异号根设为x 1<0,x 2>0. 因为x >0,所以x 1应舍去. 当),0(2x x ∈时,0)('<x g ,)(x g 在(0,2x )上单调递减; 当),(2+∞∈x x 时,0)('>x g ,)(x g 在(2x ,+∞)单调递增.当2x x =时,)('2x g =0,)(x g 取最小值)(2x g .……………………………………9分因为0)(=x g 有唯一解,所以0)(2=x g ,则⎩⎨⎧==,0)(',0)(22x g x g 即22222220210x ln x x ,x x .⎧λ--=⎪⎨λ--=⎪⎩ 因为0λ>,所以01ln 222=-+x x (*) 设函数1ln 2)(-+=x x x h ,因为当0>x 时,)(x h 是增函数,所以0)(=x h 至多有一解.因为0)1(=h ,所以方程(*)的解为21x =,代入方程组解得1λ=.…………………………………………………………………12分(22)解: BC AB ACB ==∠,30 , 30=∠∴CAB . 又因AB ⊙O 的直径,所以 90=∠ADB , 60=∠ABD . 又因OD OB =,BD OD OB AB 222===∴,3==DC AD .所以2=AB .1===∴BD OD OB ,………………………………………………………………6分 30=∠ACB ,23,60==∠∴DE CDE . OD OA = , 30=∠∴ADO , 90=∠∴ODE ,27143=+=∴OE ……10分 (23)解: (Ⅰ)由θρsin 4=得,θρρsin 42=即曲线1C 的直角坐标方程为0422=-+y y x ,由()6πθρ=∈R 得,x y 33=………………………………………………………5分 (Ⅱ)把x y 33=代入0422=-+y y x 得03343122=-+x x x , 0334342=-x x 解得01=x ,32=x ,所以01=y ,12=y , 213=+=MN ………………………………………………………………………10分(24)解:(Ⅰ)1a =时,()|31|3f x x x =-++. 当13x ≥时,()5f x ≤可化为3135x x -++≤,解之得1334x ≤≤; 当13x <时,()5f x ≤可化为3135x x -+++≤,解之得1123x -<≤. A O B EDC综上可得,原不等式的解集为13{|}.24x x -≤≤……………………………………5分 (Ⅱ)1(3)2,()3()|31|31(3) 4.()3a x x f x x ax a x x ⎧++⎪⎪=-++=⎨⎪-+<⎪⎩≥函数()f x 有最小值的充要条件为30,30,a a +⎧⎨-⎩≥≤即33a -≤≤……………………10分。
