成都市高一上学期期末数学试卷A卷(考试)
高一上学期数学人教A版(2019)期末模拟测试卷B卷(含解析)

高一上学期数学人教A 版(2019)期末模拟测试卷B 卷【满分:150分】一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列命题为假命题的是( )A.若,则B.若,,则C.若,则D.若,,则2.已知函数( )A.是奇函数,且在上单调递增B.是奇函数,且在上单调递减C.是偶函数,且在上单调递增D.是偶函数,且在上单调递减3.已知集合,集合,若,则实数m 的取值范围是( )A. B.C. D.或4.“”是“幂函数在上是减函数”的一个( )条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要5.函数的图像经过点和点,则的单调递增区间是( )A. B.a b >a c b c+>+0a b >>0c d >>a d b c ->-0a b <<22a ab b >>a b >cd >ac bd>()2xf x =()f x (,)-∞+∞(,)-∞+∞(,)-∞+∞(,)-∞+∞{12}A x x =->{10}B x mx =+<|A B A = 103m m ⎧⎫-≤≤⎨⎬⎩⎭113m m ⎧⎫-≤≤⎨⎬⎩⎭{01}m m ≤≤1|03{m m -≤<01}m <≤1n =()()22333nnf x n n x-=-+⋅()0,+∞()()π2tan 02,02f x x ωϕωϕ⎛⎫=+<≤<< ⎪⎝⎭A ⎛ ⎝π,4B ⎛- ⎝()f x ()πππ,π63k k k ⎛⎫-+∈ ⎪⎝⎭Z ()πππ,π36k k k ⎛⎫-+∈ ⎪⎝⎭ZC. D.6.某种药物需要2个小时才能全部注射进患者的血液中.在注射期间,血液中的药物含量以每小时的速度呈直线上升;注射结束后,血液中的药物含量每小时以的衰减率呈指数衰减.若该药物在病人血液中的含量保持在以上时才有疗效,则该药物对病人有疗效的时长大约为( )(参考数据:,,,)A.2小时B.3小时C.4小时D.5小时7.已知函数,若恒成立,则实数a 的取值范围是( )A. B. C. D.8.设函数,若,则的最小值为( )二、选择题:本题共3小题.每小题6分.共18分.在每小题给出的选项中,有多项符合题目要求全部选对的得6分.部分选对的得部分分,有选错的得0分.9.下列四个结论中,正确的结论是( )A.“所有平行四边形都是菱形”是全称量词命题B.已知集合A ,B 均为实数集R 的子集,且,则C.,有,则实数m 的取值范围是D.“”是“”的充分不必要条件10.已知函数,则( )A.函数的值域为B.点是函数的一个对称中心C.函数在区间上是减函数()ππππ,2623k k k ⎛⎫-+∈ ⎪⎝⎭Z ()ππππ,2326k k k ⎛⎫-+∈ ⎪⎝⎭Z 1000mg 20%1000mg 1.80.20.0552≈ 1.90.20.0470≈ 3.10.80.5007≈ 3.20.80.4897≈()cos 2sin 4f x x a x =+-()0f x ≤⎡-⎣[]5,5-[]5,4-[]4,4-()()ln ln f x x x a b x =-+()0f x ≥55a b +B A ⊆()A B =R R ðx ∀∈R 210x mx -+≥[]22-,13x <<04x ≤≤()cos sin f x x x =-()f x ⎡⎣π,04⎛⎫⎪⎝⎭()f x ()f x π5π,44⎡⎤⎢⎥⎣⎦D.若函数在区间11.已知函数A.B.,且,恒有C.函数在上的取值范围为D.,恒有成立的充分不必要条件是三、填空题:本题共3小题,每小题5分,共15分.12.已知函数是定义域为R ,图像恒过点,对于R 上任意,则关于x 的不等式的解集为______.13.已知函数的定义域为,则函数14.已知幂函数,则a 的取值范围是______________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或者演算步骤.15.(13分)已知幂函数是奇函数.(1)求的解析式;(2)若不等式成立,求a 的取值范围.16.(15分)已知函数.(1)当时,求函数的零点;(2)若函数为偶函数,求a 的值;(3)当时,若关于x 的不等式在时恒成立,求的取值范围.17.(15分)已知函数(其中,)的最小正周期是,点()f x [,a a -()f x m =1m =-12,x x ∀∈R 12x x ≠()()()12120x x f x f x -->⎡⎤⎣⎦()f x [2,1)-31,53⎛⎤- ⎥⎝⎦x ∀∈R ()2(21)2f x f ax x -<-6a >()f x ()0,21x x <1>-()2112f x x +<-()f x ()1,3()g x =1 ()f x x ⎛= ⎝()()182f a f a -<-()()2133m f x m m x -=--()f x ()()11233m m a a a ---<-()()33x xf x a a -=⋅-∈R 1a =()f x ()f x 1a =()99140x xf x λ----≤()0,x ∈+∞λ()2tan()f x x ωϕ=+0ω>0πϕ<<2π是函数图象的一个对称中心.(1)求的解析式;(2)求的单调区间;(3)求函数在区间上的取值范围.18.(17分)已知函数.(1)求的定义域及单调区间.(2)求的最大值,并求出取得最大值时x 的值.(3)设函数,若不等式在上恒成立,求实数a 的取值范围.19.(17分)已知函数为奇函数,且(1)求的解析式与单调递减区间;(2)将函数得到函数的图象,当时,求方程的所有根的和.(π,0)P()f x ()f x ()f x ()f x π0,3⎛⎤⎥⎝⎦44()log (1)log (3)f x x x =++-()f x ()f x 4()log [(2)4]g x a x =++()()f x x ≤(0,3)x ∈()2()2sin 1(0,0 )2x f x x ωϕωϕωϕ+⎛⎫=++-><<π ⎪⎝⎭(f x ()f x (f x ()y g x =0,2x ⎡π⎤∈⎢⎥⎣⎦()22()30g x x +-=答案以及解析1.答案:D解析:对于A :若,则,故选项A 正确;对于B :若,,则,所以,故选项B 正确;对于C :将两边同时乘以a 可得:,将两边同时乘以b 可得,所以,故选项C 正确;对于D :取,,,,满足,,但,,不满足,故选项D 不正确;所以选项D 是假命题,故选:D.2.答案:A解析:函数,可得为奇函数,函数和上都单调递增,可得单调递增,故选A 3.答案:B解析:因为,所以或,解得或,即或.因为.当由可得4.答案:A解析:由题意,当时,在上是减函数,故充分性成立;若幂函数在上是减函数,则,解得或,故必要性不成立.因此“”是“幂函数在上是减函数”的一个充分不必要条件.故选:A.2()f x x -=()223()33n nf x n n x-=-+⋅2233130n n n n ⎧-+=⎨-<⎩a b >a c b c +>+0a b >>0c d >>d c ->-a d b c ->-0a b <<2a ab >0a b <<2ab b >22a ab b >>3a =1b =-2c =-3d =-a b >c d >6ac =-3bd =ac bd >()2xf x =-11()2222x xx xf x ---=-=-=12()2x xf x ⎛⎫--=- ⎪⎝⎭()f x 2xy =y =,)-∞+∞()f x |1|2x ->12x ->12x -<-3x >1x <-{3A x x =>∣1}x <-10x +<⇒<B ⊆≤B ⊆131n =(0,)+∞(0,)+∞1n =2n =1n =()223()33n nf x n n x -=-+⋅(0,)+∞5.答案:D解析:依题意,,且因为,得,因为,所以时,得,则.由,所以的单调递增区间是.故选D.7.答案:B解析:依题意,恒成立,即令,设,则恒成立,所以,解得,所以实数a 的取值范围是.故选:B 8.答案:D解析:因为,若,则对任意的,,则当时,,不合乎题意;若时,当时,,,此时,,不合乎题意;若,则当2tan ϕ=π2tan 4ωϕ⎛⎫+=- ⎪⎝⎭ϕ=π4ωϕ⎛⎫+= ⎪⎝⎭0ϕ<<=ππtan 46ω⎛⎫+=⎪⎝⎭ππ()63k k +==-∈Z 42()k k ω=-∈Z 02ω<≤1k =2ω=π()2tan 26f x x ⎛⎫=+ ⎪⎝⎭ππππ2π()262k x k k -<+<+∈Z πππ()326k x k <<+∈Z ()f x ππππ,()2326k k k ⎛⎫-+∈ ⎪⎝⎭Z ()2cos 2sin 412sin sin 4f x x a x x a x =+-=-+-22sin sin 30x a x =-+-≤22sin sin 30x a x -+≥[]sin 1,1t x =∈-()()22311g t t at t =-+-≤≤()0g t ≥()()222113021130a a ⎧⨯--⨯-+≥⎪⎨⨯-⨯+≥⎪⎩55a -≤≤[]5,5-()()()ln ln ln f x x x ab x x a b x =-+=--0a b +≤0x >0x a b -->01x <<()()ln 0f x x a b x =--<01a b <+<1a b x +<<0x a b -->ln 0x <()()ln 0f x x a b x =--<1a b +>时,,,此时,,不合乎题意.所以,,此时,,则,当时,,,此时,;当时,,,此时,.所以,对任意的,,合乎题意,由基本不等式可得时,即当故的最小值为9.答案:ACD解析:对于A ,因为命题中含有量词“所有”,故该命题为全称量词命题,故A 符合题意;对于B ,如图设全集,集合A ,集合B 如图所示,根据运算得,故B 不符合题意;对于C ,,有成立,则,解得,故C 符合题意;对于D ,满足的数一定满足,所以充分性满足,而满足的数不一定满足,所以必要性不满足,即“”是“”的充分不必要条件,故D 符合题意.故选:ACD.10.答案:ABD解析:因为.对于A 选项,函数的值域为,A 对;对于B 选项,,故点是函数的一个对称中心,B 对;,故函数在区间上不单调,C 错;1x a b <<+0x a b --<ln 0x >()()ln 0f x x a b x =--<1a b +=()()1ln f x x x =-()10f =01x <<10x -<ln 0x <()()1ln 0f x x x =->1x >10x ->ln 0x >()()1ln 0f x x x =->0x >()()1ln 0f x x x =-≥55a b +≥==1a b a b =+=a b ==55a b +U =R ()A B ≠R R ðx ∀∈R 210x mx -+≥240m ∆=-≤22m -≤≤13x <<04x ≤≤04x ≤≤13x <<13x <<04x ≤≤()πcos sin 4f x x x x ⎛⎫=-=- ⎪⎝⎭()f x ⎡⎣π004f ⎛⎫== ⎪⎝⎭ π,04⎛⎫⎪⎝⎭()f x x ≤≤ππ4x ≤-≤()f x π5π,44⎡⎤⎢⎥⎣⎦对于D 选项,由题意且函数在上为减函数,当时,,所以,,则ABD.11.答案:ABD解析:函数是奇函数,所以,解得,代入验证可知,所以,故A 正确;在R 上单调递增且,函数上单调递增,所以函数在R 上单调递增,则,且,恒有,故B 正确;因为在上单调递增,在上的取值范围为,故C 错误;若,恒有成立,则,则的解集为R ,当时,,解得时,要使得解集为R ,则有解得,综上,若,恒有成立,则,因此其成立的充分不必要条件可以是,故D 正确.故选ABD.12.答案:0a >()f x [],a a -a x a -≤≤ππ44a x a --≤-≤πππ,444a a ⎡⎤∈---⎢⎥⎣⎦ππππ,,4422a a ⎡⎤⎡⎤---⊆-⎢⎥⎢⎥⎣⎦⎣⎦π4ππ420a a a ⎧--≥⎪⎪⎪-≤⎨⎪>⎪⎪⎩a <≤()f x m =+()f x 2(0)102f m m =+=+=1m =-()f x ()()f x f x =--1m =-()1221222()11121212121xx x x x f x ++-=-+=-+=-+-=+++21x=+1t >y =)+∞()f x 12,x x ∀∈R 12x x ≠()()()12120x x f x f x -->⎡⎤⎣⎦()f x [2,1)-(2)f -=(1)f =()f x [2,1)-31,53⎡⎫-⎪⎢⎣⎭x ∀∈R ()2(21)2f x f ax x -<-2212x ax x -<-2410ax x -+>0a =410x -+>x <0≠20,(4)40,a a >⎧⎨∆=--<⎩4a >x ∀∈R ()2(21)2f x f ax x -<-4a >6a >1,2⎛⎫-∞- ⎪⎝⎭解析:因为,即,即在上单调递增,又,所以.由,即.所以答案为:13.答案:解析:因为的定义域为,所以满足,又函数,所以函数,故答案为:14.答案:解析:由幂函数的定义域为,且是递减函数,因为,可得,解得,即实数a 的取值范围为.故答案为:.15.答案:(1)(2)解析:(1)因为是幂函数,所以,即,所以,解得或.当时,,此时,所以是奇函数,则符合题意;1x x <1>-⇒()()()1212f x f x x x -<--()()1122f x x f x x +<+()()g x f x x =+(),-∞+∞()02f =()()0002g f =+=()2112f x x +<-⇒()()21212f x x +++<()()210g x g +<210x +<⇒x <1,2⎛⎫-∞- ⎪⎝⎭()5,6()f x ()1,3()3f x -13346x x <-<⇒<<()g x =505x ->⇒>()g x =()5,6()5,6(3,4)1101()f x x x ⎛⎫=== ⎪⎝⎭()f x (0,)+∞()()182f a f a -<-18210820a a a a ->-⎧⎪->⎨⎪->⎩34a <<(3,4)(3,4)()3f x x=()(),13,-∞+∞ ()f x 2331m m --=2340m m --=()()410m m -+=4m =1m =-4m =()3f x x =()()3f x x f x -=-=-()f x 4m =当时,,此时,所以是偶函数,则不符合题意.故.(2)由(1)可知,所以不等式,即不等式,因为为增函数,所以,即,所以,解得或,即a 的取值范围是.16.答案:(1)当时,函数的零点为0(2)(3)的取值范围是解析:(1)当时,,令,解得,所以当时,函数的零点为0.(2)因为函数为偶函数,所以,即,所以,又不恒为0,所以,即.(3)当时,,因为关于x 的不等式在时恒成立,所以又因为,当且仅当时等号成立,所以,即的取值范围是.1m =-()2f xx -=()()2f x x f x --==()f x 1m =-()3f x x =4m =()()11233m m a a a ---<-()()33233a a a -<-3y x =233a a a -<-2430a a -+>()()130a a -->3a >1a <()(),13,-∞+∞ 1a =()f x 1a =-λ(],8-∞1a =()33x xf x -=-()330x xf x -=-=0x =1a =()f x ()f x ()()f x f x -=3333x x x x a a --⋅-=⋅-()()1330x xa -+-=33x x --10a +=1a =-0x >()330x xf x -=->()99140x xf x λ----≤()0,x ∈+∞()233169914333333x xx xx x x x x xλ------+++≤==---1633833x x x x---+≥=-33x x--=)3log 2=+8λ≤λ(],8-∞17.答案:(1)(2)增区间是,,无减区间(3)解析:(1)由于的最小正周期为,,即,由于点是函数图象的一个对称中心,,则.由于,所以.(2)由,解得,,所以的增区间是,,无减区间.(3)因为,所以函数在区间上的取值范围为.18.答案:(1)的单调增区间为,单调减区间为(2)的最大值为1,此时x 的值为1(3)解析:(1)根据具体函数定义域的求解方法,根据题意可得解得所以函数的定义域为;1π()2tan 22f x x ⎛⎫=+ ⎪⎝⎭(2π2π,2π)k k -k ∈Z (,-∞-()f x 2π2π=ω=1()2tan 2f x x ϕ⎛⎫=+ ⎪⎝⎭(π,0)P ()f x ϕ+=∈Z π2k ϕ=∈Z 0πϕ<<ϕ=1π()2tan 22f x x ⎛⎫=+ ⎪⎝⎭π1πππ222k x k -<+<∈Z 2π2π2πk x k -<<k ∈Z ()f x (2π2π,2π)k k -k ∈Z π0,3x ⎛∈ ⎝ππ2π,223x ⎛⎤+∈ ⎥⎝⎦()f x π0,3⎛⎤ ⎥⎝⎦(,-∞-()f x ()1,1-()1,3()f x [)2,-+∞1030x x +>⎧⎨->⎩13x -<<()f x ()1,3-令,则函数在单调递增,在上单调递减又函数在定义域上单调递增,根据复合函数单调性“同增异减”的规则函数的单调增区间为,单调减区间为.(2)由(1)中所得单调性可知,时,取得最大值故的最大值为1,此时x 的值为1.(3)根据题意得,在上恒成立,在 上恒成立,即在上恒成立即在上恒成立,令,则,即a 的取值范围为.19.答案:(1),递减区间为,;解析:(1)由题意,的最小正周期为,即可得,又,,又,()()()()2444log 1log 3log 14f x x x x ⎡⎤=++-=--+⎣⎦()()214t x x =--+()t x ()1,1-()1,34log y t =()f x ()1,1-()1,31x =()f x ()()11max f x f ==()f x ()()0f x g x -≤()0,3x ∈1≤()0,3x ∈210x ax ++≤()0,3x ∈1a x x ⎛⎫≥-+ ⎪⎝⎭()0,3x ∈()1(03)h x x x x ⎛⎫=-+<< ⎪⎝⎭()2max h x =-2a ∴≥-[)2,-+∞()2sin 2f x x =3,44k k ππ⎡⎤+π+π⎢⎥⎣⎦k ∈Z 2())2sin 12x f x x ωϕωϕ+⎛⎫=++- ⎪⎝⎭)cos()2sin 6x x x ωϕωϕωϕπ⎛⎫=+-+=+- ⎪⎝⎭ (f x ∴()f x T =π2ω=(f x k =πk ∈Z 0<()2sin 2f x x =函数的递减区间为,(2)将函数的图象,,得到函数的图象,又,则即令时,,画出的图象如图所示:,,关于,,,上有两个不同的根,,,又3222,2k x k k π≤≤+ππ+∈Z 3,4k x k k ππ≤≤+π∈Z ∴()f x 3,44k k ππ⎡⎤+π+π⎢⎥⎣⎦k ∈Z (f x 2sin 23y x π⎛⎫=- ⎪⎝⎭()2sin 43y g x x π⎛⎫==- ⎪⎝⎭()22()30g x x +-=()g x =()g x =sin 43x ⎛⎫-= ⎪⎝⎭π43x ⎛⎫= ⎪⎝⎭π-4z x =0,2⎡π⎤∈⎢⎥⎣⎦54,333z x πππ⎡⎤=-∈-⎢⎥⎣⎦sin y z =sin z =12z z =12z z +=πsin z =3z =44π3z =55π3z =sin 43x π⎛⎫-= ⎪⎝⎭0,2⎤⎥⎦π1x 2x 124433x x ππ-+-=π12x x ∴+=sin 43x ⎛⎫-= ⎪⎝⎭π所以方程在()22()30g x x +-=0,2x π⎡⎤∈⎢⎥⎣⎦。
四川省2021年高一上学期数学期末考试试卷A卷

四川省2021年高一上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)已知集合A={x|x=a+(a2-1)i,a∈R,i是虚数单位},若A R,则a=()A . 0B . 1C . -1D . ±12. (2分) (2019高一上·隆化期中) 函数的定义域是()A .B .C .D .3. (2分) (2016高一上·南昌期中) 已知函数f(x)= ,则f[f(2)]=()A .B .C . 9D .4. (2分)(2020·德州模拟) 函数在区间上大致图象为()A .B .C .D .5. (2分)给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)·g(y),③h(x·y)=h(x)+h(y),④m(x·y)=m(x)·m(y).又给出四个函数的图像,那么正确的匹配方案可以是()甲乙丙丁A . ①甲,②乙,③丙,④丁B . ①乙,②丙,③甲,④丁C . ①丙,②甲,③乙,④丁D . ①丁,②甲,③乙,④丙6. (2分) (2016高一上·绍兴期中) 若函数y=f(x)为奇函数,则它的图象必经过点()A . (0,0)B . (﹣a,﹣f(a))C . (a,f(﹣a))D . (﹣a,﹣f(﹣a))7. (2分) (2019高二下·闵行期末) 若一个直三棱柱的所有棱长都为1,且其顶点都在一个球面上,则该球的表面积为().A .B .C .D .8. (2分)下列命题中:①命题“,使得”,则是假命题.②“若,则互为相反数”的逆命题为假命题.③命题“”,则“”.④命题“若,则”的逆否命题是“若,则”.其中正确命题是()A . ②③B . ①②C . ①④D . ②④9. (2分) (2019高一上·镇海期中) 已知函数,,则以下结论正确的是()A . 任意的,且,都有B . 任意的,且,都有C . 有最小值,无最大值D . 有最小值,无最大值10. (2分) (2017高二下·台州期末) 函数f(x)=(x3﹣3x)sinx的大致图象是()A .B .C .D .11. (2分)(2017·怀化模拟) 某三棱柱的三视图如图所示,该三棱柱的外接球的表面积为()A . 32+8B . 36πC . 18πD . π12. (2分) (2017高二下·福州期末) 函数f(x)=x2ln|x|的图象大致是()A .B .C .D .二、填空题 (共4题;共5分)13. (1分) (2019高一上·永嘉月考) 若,,,则a,b,c的大小关系是________.14. (2分) (2019高一上·杭州期中) 已知幂函数图象经过点,则它的表达式为________;单调递减区间为________.15. (1分)若关于x的不等式x2﹣4x≥m对任意x∈(0,1]恒成立,则m的取值范围是________.16. (1分) (2016高一上·南京期中) 方程x3﹣3x+1=0的一个根在区间(k,k+1)(k∈N )内,则k=________.三、解答题 (共6题;共65分)17. (10分)已知函数f(x)=22x﹣2x+1+1.(1)求f(log218+2log 6);(2)若x∈[﹣1,2],求函数f(x)的值域.18. (10分)(2019高一上·南京月考) 已知全集U=R,集合,.(1)若,求;(2)若,求实数p的取值范围.19. (10分) (2018高一上·湖南月考) 如图,四棱锥中,,平面,, .(1)证明:;(2)若四面体的体积为,求四棱锥的侧面积.20. (15分)已知函数h(x)=2x(x∈R),它的反函数记为h﹣1(x).A、B、C三点在函数h﹣1(x)的图象上,它们的横坐标分别为a,a+4,a+8(a>1),设△ABC的面积为S.(1)求S=f(a)的表达式;(2)求函数f(a)的值域;(3)若S>2,求a的取值范围.21. (10分)求函数的解析式:(1)求一次函数f(x),使f[f(x)]=9x+1;(2)已知f(x﹣2)=x2﹣3x+1,求f(x).22. (10分) (2019高一上·山丹期中) 已知函数.(1)求函数的定义域,并判断函数的奇偶性;(2)对于,恒成立,求实数的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。
四川省成都市蓉城高中联盟2022-2023学年高一上学期期末考试数学试题及答案

高一数学试题一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合522A x x ⎧⎫=∈-<<⎨⎬⎩⎭N ,{}2,1,0,1,2,4B =--,则A B ⋂=() A .{}1,0,1,2-B .{}2,0,4-C .{}0,1,2D .{}0,12.已知命题“x ∀∈R ,2230x ax a +->”为真命题,则实数a 的取值范围是() A .[]3,0-B .()3,0-C .[]12,0-D .()12,0- 3.若m 是方程ln 30x x +-=的根,则下列选项正确的是()A .12m <<B .23m <<C .34m <<D .01m <<4.若函数()y f x =的定义域为[]0,4,则函数()21f x y x =-的定义域为()A .[)(]0,11,2⋃B .[)0,1C .(]1,2D .[)(]0,11,4⋃5.已知131log πa =,0.50.5b =,3log 5c =,则a ,b ,c 的大小关系为() A .a b c >>B .b a c >>C .c b a >>D .c a b >>6.设命题p :()ln 10x -<﹐命题q :2a x a ≤≤+,若p 是q 的充分不必要条件,则实数a 的取值范围是() A .[]0,1B .()0,1C .(][),01,-∞⋃+∞D .()(),01,-∞⋃+∞7.设1a >,函数()()2log 22x x a f x a a =--,则使()0f x >的x 的取值范围是() A .(),0-∞ B .()0,+∞C .(),log 3a -∞D .()log 3,a +∞8.已知函数()513f x x =-+的定义域为[],m n (m ,n 为整数),值域为20,3⎡⎤⎢⎥⎣⎦,则满足条件的整数对(),m n ,共有()对.A .3B .4C .5D .6二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求;全部选对的得5分,选对但不全的得2分,有选错的得0分. 9.下列命题错误的是()A .若0a >,且1a ≠,则0x ∃>,0y >,()log log log a a a x y xy ⋅=B .若0a >,且1a ≠,则0x ∀>,0y >,()log log log a a a x y x y +=+C .函数9ln ln y x x=+的最小值为10 D .若1a b >>,则lg 1lg ab> 10.下列函数是奇函数且在()0,+∞上是增函数的是() A .()13f x x =B .()11f x x =-+C .()()()1010x x f x x x -+<⎧⎪=⎨+≥⎪⎩ D .()22xxf x -=-11.已知函数()()()[)4142,,0,log ,0,1,43,1,,x x f x x x x x x -⎧∈-∞⎪⎪=∈⎨⎪⎪-+-∈+∞⎩若函数()()g x f x m =-恰有两个零点,则实数m 不可能...是() A .-2B .-1C .0D .012.已知函数()26,0,21,0,x x x x f x x -⎧+≤⎪=⎨->⎪⎩若关于x 的方程()()244230f x f x λλ-++=有5个不同的实根,则实数λ可能的取值有() A .43-B .87-C .76-D .32-三、填空题:本题共4小题,每小题5分,共20分. 13.函数22x y a-=+(0a >且1a ≠)的图象恒过定点P ,则点P 的坐标为________.14.函数()()212log 3f x x=-的单调递减区间是________.15.已知函数()()e 0xf x x =<与()()lng x x a =+的图象上存在关于y 轴对称的点,则a 的取值范围是______.16.函数()2521f x x x a =+++,若对于任意1x ,()22,x ∈+∞,当12x x ≠时,都有()()1221210x f x x f x x x ->-,则实数a 的取值范围是________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)化简求值(需要写出计算过程).(1)()129216⎛⎫-⎪⎝⎭;(2)3log 21233lg5log 2lg 2log 3+-⨯⨯.18.(12分)已知集合{}2320A x x x =-+≤,不等式12222x x a +-+>的解集为集合B .(1)当时2a =,求A B ⋂﹔(2)设命题p :x A ∈,命题q :x B ∈,若p 是q 的充分不必要条件,求实数a 的取值范围. 19.(12分)科学实验中,实验员将某种染料倒入装有水的透明水桶,想测试染料的扩散效果,染料在水桶中扩散的速度是先快后慢,1秒后染料扩散的体积是31cm ,2秒后染料扩散的体积是33cm ,染料扩散的体积y 与时间x (单位:秒)的关系有两种函数模型可供选择:①3xy m =,②3log y m x b =+,其中m ,b 均为常数. (1)试判断哪个函数模型更合适,并求出该模型的解析式; (2)若染料扩散的体积达到35cm ,至少需要多少秒. 20.(12分)已知函数()f x 的定义域为()0,+∞,,且满足以下条件:①对任意()0,x ∈+∞,有()0f x >;②对任意m ,()0,n ∈+∞,有()()nf mn f m =⎡⎤⎣⎦;③()11f >.(1)求证:()f x 在()0,+∞上是增函数;(2)若()()2120a f f --<,求a 的取值范围. 21.(12分) 已知()22xxf x b -=-++是定义R 在上的奇函数.(1)求()f x 的解析式;(2)已知0a >,且1a ≠,若对于任意[)2,x ∈+∞,存在[]1,2m ∈,使得()24mf x a x x ≤+-成立,求a 的取值范围. 22.(12分)设函数()()1log 212xa x f x a ⎛⎫=+> ⎪⎝⎭. (1)判断函数的奇偶性; (2)证明函数()f x 在()0,+∞上是增函数;(3)若()()1log 2112xa x g x a ⎛⎫=++> ⎪⎝⎭是否存在常数m ,()0,n ∈+∞,使函数()g x 在[],m n 上的值域为[]1log 2,1log 2a a m n ++,若存在,求出a 的取值范围;若不存在,请说明理由.高一数学参考答案及评分标准一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求;2分,有选错的得0分. 5分,共20分. 13.()2,314.()((⎤⎦也正确)15.(),e -∞16.32a ≤13.解:令20x -=,即2x =,则023y a =+=,∴定点P 为()2,3,故答案为:()2,3.14.解:()()212log 3f x x=-,)230x xx -=>,解得x <<函数23y x =-的开口向下,对称轴是y 轴,12log y x =在()0,+∞上递减,根据复合函数单调性同增异减可知()f x 的单调递减区间是(),故答案为:()或(⎤⎦.15.解:由题意得方程()()0f x g x --=在区间()0,+∞内有解,即()eln 0xx a --+=在区间()0,+∞内有解,即函数e xy -=的图象与()ln y x a =+的图象在区间()0,+∞内有交点,把点()0,1带入()ln y x a =+,得1ln a =,解得e a =,故e a <,故答案为:(),e -∞.16.解:∵对于任意1x ,()22,x ∈+∞当12x x ≠时,都有()()1221210x f xx f x x x ->-,∴()()2121210f x f x x x x x ->-,令()()f x h x x =,则()h x 在()2,+∞上单调递增,又∵()215a h x x x+=++,当210a +≤时,满足题目条件,此时12a ≤-;当210a +>2≤,∴1322a -<≤,故答案为:32a ≤. 三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)解:(1)原式42π13=+-+4π213=+-+1π3=+; (2)原式2lg5lg 23=++=.18.(12分)解:(1)∵A :2320x x -+≤,即12x ≤≤,B :124x x +>-+,∴1x >,∴{}12A B x x ⋂=<≤; (2)∵p 是q 的充分不必要条件,∴AB ,∵{}12A x x =≤≤,213a B x x -⎧⎫=>⎨⎬⎩⎭, ∴2113a -<,∴2a <,∴a 的取值范围是(),2-∞. 19.(12分)解:(1)∵染料扩散的速度是先快后慢, ∴选第二个模型更合适,即3log y m xb =+,由题意33log 11log 23m b m b +=⎧⎨+=⎩,∴23122log 3,log 2b m m =⎧⎪⎛⎫⎨== ⎪⎪⎝⎭⎩也对 ∴232log 3log 1y x =+,(写到这步22log 1y x =+也得6分); (2)∵5y ≥,∴22log 15x +≥,∴22log 4x ≥, ∴2log 2x ≥,∴4x ≥,∴至少需要4秒.20.(12分)解:(1)任取1x ,()20,x ∈+∞且12x x <,()()()()()()1212121111x x f x f x f x f x f f -=⋅-⋅=-⎡⎤⎡⎤⎣⎦⎣⎦,∵()11f >,∴()()12f x f x <,∴()f x 在()0,+∞上是增函数; (2)∵()f x 在()0,+∞上单调递增,∵()()212a f f -<, ∴0212a<-<,∴20log 3a <<,∴a 的取值范围为()20,log 3.21.(12分)解:(1)∵函数在R 上是奇函数,∴()00f =,∴0b =,经检验符合要求,∴()22xxf x -=-+;(2)由题意2224xx m a x x --≤+-,∴224m x x a x -≥-+,令()()2224x x g x x x -=---,∵()g x 在[)2,+∞上单减,∴对[)2,x ∀∈+∞上()max ma g x ≥,∴14ma ≥,又∵存在[]1,2m ∈,使14ma ≥成立,∴当01a <<时,1log 4a m ≤, ∴1log 14a≥,又∵01a <<,∴114a ≤<,当1a >时,1log 4a m ≥, ∴12log 4a≥,∴214a ≥,又∵1a >,∴1a >,综上,a 的范围为()1,11,4⎡⎫⋃+∞⎪⎢⎣⎭. 22.(12分)解:由题意x ∈R ,∵()()21log 22x x f x f x --⎛⎫⎛⎫-=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,∴函数是偶函数,(2)令()122xxu x =+,设1x ∀,()20,x ∈+∞且12x x <, ()()1212121212111122222222x x x x x x x x u x u x -=+--=-+- ()21121212122212222122x x x x x x x x x x ++-⎛⎫=-+=-- ⎪⎝⎭, ∵120x x +>,∴1221x x+>,∴12220xx -<,121102x x +->,∴()()12u x u x <,∴()u x 在()0,+∞上单调递增, 又∵2log y x =在()0,+∞上单增,∴()21log 22xxf x ⎛⎫=+⎪⎝⎭在()0,+∞上是增函数; (3)由第(2)问可得()()1log 2112xa x g x a ⎛⎫=++> ⎪⎝⎭在()0,+∞上是增函数, ∴1log 211log 221log 211log 22m a a m n a a n m n ⎧⎛⎫++=+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪++=+ ⎪⎪⎝⎭⎩,∴1212212122m m m n n n a a ⎧++=⎪⎪⎨⎪++=⎪⎩,即m ,n 是方程12122xxx a ++=的两根, ∴()()212210x x a ---=,当0x >时,令()21x t t =>,则()()211v t a t t =---,若方程()()212210x x a ---=有两个大于零的不等实数根,即方程()2110a t t ---=存在两个大于1的不等实根,∵()010v =-<,1a >,方程()2110a t t ---=是有一个大于0和一个小于0的实根,∴方程()2110a t t ---=不存在两个大于1的不等实根,∴不存在常数m ,n 满足条件.。
四川省成都市2022-2023学年高一上学期期末调研考试语文试题(含答案)

成都市2022-2023学年高一上学期期末调研考试语文本试卷满分150分,考试时间150分钟。
注意事项:1.答卷前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,只将答题卡交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,17分)阅读下面的材料,完成下面1~5小题。
材料一(《乡土中国·礼治秩序》一章的思维导图)材料二乡土社会秩序的维持,有很多方面和现代社会秩序的维持是不相同的,可是所不同的并不是说乡土社会是“无法无天”,或者说“无需规律”。
乡土社会并不是这种社会,我们可以说这是个“无法”的社会,假如我们把法律限于以国家权力所维持的规则;但是“无法”并不影响这社会的秩序,因为乡土社会是“礼治”的社会。
让我先说明,礼治社会并不是指文质彬彬,像《镜花缘》里所描写的君子国一般的社会。
礼并不带有“文明”,或是“慈善”,或是“见了人点个头”、不穷凶极恶的意思。
礼也可以杀人,可以很“野蛮”。
礼是社会公认合式的行为规范。
合于礼的就是说这些行为是做得对的,对是合式的意思。
如果单从行为规范一点说,本和法律无异,法律也是一种行为规范。
礼和法不相同的地方是维持规范的力量。
法律是靠国家的权力条推行的,“国家”是指政治的权力,在现代国家没有形成前,部落也是政治权力,而礼却不需要这有形的权力机构来维持。
维持礼这种规范的是传统。
礼治从表面看去好像是人们行为不受规律拘束而自动形成的秩序。
其实自动的说法是不准确的,只是主动地服于成规罢了,孔子一再地用“克”字,用“约”字来形容礼的养成,可见礼治并不是离开社会,由于本能或天意所构成的秩序了。
(摘编自费孝通《乡土中国·礼治秩序》)材料三古代村民犯错,通常都是请族老主持裁判惩罚,族老根据什么呢,答案是传统。
四川省成都市七中2023-2024学年高一数学第一学期期末调研试题含解析

【详解】 函数的最大值为 5 ,最小值为 1 ,
2
2
A
1 2
5
2
1 2
3 2
,
k
1 2
5 2
1 2
1,
又
函数的周期 T
2
7 12
12
,
2 ,得 w 2 . w
可得函数的表达式为 y 3 sin(2x ) 1, 2
当 x 时,函数有最大值 5 ,
12
2
5 2
3 2
sin
2x
3
1
D.
y
sin
2x
3
1
8.函数
f
x
3cos
2x
6
的一条对称轴是()
A. x 6
B. x 12
C. x 4
D. x 3
9.若幂函数的图象过点
,则它的单调递增区间是( )
A.(0,+∞)
B.[0,+∞)
C.(-∞,+∞)
D.(-∞,0)
10.直线 kx y k 0k R 与圆 x2 y2 2 交点的个数为
故选:B
9、D
【解析】设幂函数为 y=xa,把点(2, 1 )代入,求出 a 的值,从而得到幂函数的方程,再判断幂函数的单调递增区间. 4
【详解】设 y=xa,则 1 =2a,解得 a=-2, 4
∴y=x-2 其单调递增区间为(-∞,0)
故选 D.
【点睛】本题考查了通过待定系数法求幂函数的解析式,以及幂函数的主要性质. 10、A
四川省成都市七中 2023-2024 学年高一数学第一学期期末调研试题
注意事项 1.考生要认真填写考场号和座位序号。 2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑 色字迹的签字笔作答。 3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
2023-2024学年四川省成都市高一上学期期中联考数学质量检测模拟试题(含解析)

19.已知函数()2
41f x x mx =++.
(1)若1m =,求()f x 在43x -≤≤上的最大值和最小值;(2)求()f x 在44x -≤≤上的最小值.
选②,因“x B ∈”是“x A ∈”的必要不充分条件,则A
B ,由(1)知,{|22}B x x =-≤≤,
因此2212a a -≥-⎧⎨+<⎩或2212
a a ->-⎧⎨+≤⎩,解得01a ≤<或01a <≤,即有01a ≤≤,
所以实数a 的取值范围是01a ≤≤.
选③,A B ⋂=∅,由(1)知,{|22}B x x =-≤≤,因此12a +<-或22a ->,解得3a <-或4a >,所以实数a 的取值范围是3a <-或4a >.
18.(1)()22
24,024,0
x x x f x x x x ⎧-+≥=⎨+<⎩(2)图象见解析,函数的单调递减区间为:(),1-∞-,()1,+∞.
【分析】(1)根据奇函数的性质,求解得出0x <时,()f x 的解析式,即可得出答案;(2)根据函数图象,即可得出函数的单调递减区间.【详解】(1)∵函数()f x 是定义在R 上的奇函数,当0x <时,有0x ->,()()2
24f x x x -=---,
∴()()2
24f x f x x x =--=+,
∴()2224,0
24,0x x x f x x x x ⎧-+≥=⎨+<⎩
.
(2)函数的图象为:
由图象可得,函数的单调递减区间为:(),1-∞-,()1,+∞.19.(1)最大值为22,最小值为-3;。
2024-2025学年四川省成都市高一上学期期中考试数学检测试题(含解析)

一、2024-2025学年四川省成都市高一上学期期中考试数学检测试题单选题1. 已知集合A ={1 ,2,3,4,5},{},|15B x x =<<,则A ∩B 的元素个数为( )A. 2B. 3C. 4D. 5【答案】B【解析】【分析】直接根据集合的交集运算求解即可.【详解】因为集合A ={1 ,2,3,4,5},{}|15B x x =<<所以{}2,3,4A B =I ,即A ∩B 的元素个数为3个.故选:B2. 函数221y x mx =++在[2,+∞)单调递增,则实数m 的取值范围是( )A. [2,)-+¥B. [2,+∞)C. (,2)-¥D. (,2]-¥【答案】A【解析】【分析】直接由抛物线对称轴和区间端点比较大小即可.【详解】函数221y x mx =++为开口向上的抛物线,对称轴为x m=-函数221y x mx =++在[2,+∞)单调递增,则2m -£,解得2m ³-.故选:A.3. 若函数的定义域为{}22M x x =-££,值域为{}02N y y =££,则函数的图像可能是()A. B.的C. D.【答案】B【解析】【分析】根据函数的定义域与值域,结合函数的性质判断即可.【详解】对A,该函数的定义域为{}20x x-££,故A错误;对B,该函数的定义域为{}22M x x=-££,值域为{}02N y y=££,故B正确;对C,当()2,2xÎ-时,每一个x值都有两个y值与之对应,故该图像不是函数的图像,故C错误;对D,该函数的值域不是为{}02N y y=££,故D错误.故选:B.4. 已知函数()af x x=,则“1a>”是“()f x在()0,¥+上单调递增”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】【分析】由幂函数的单调性结合充分必要条件的定义判断.【详解】当0a>时,函数()af x x=在()0,¥+上单调递增,则1a>时,一定有()f x在()0,¥+上单调递增;()f x在()0,¥+上单调递增,不一定满足1a>,故“1a>”是“()f x在()0,¥+上单调递增”的充分不必要条件.故选:A.5. 已知0,0x y>>,且121yx+=,则12xy+的最小值为()A. 2B. 4C. 6D. 8【答案】D【解析】【分析】利用不等式的乘“1”法即可求解.【详解】由于0,0x y >>,故11112224448x y x xy y x y xy æöæö+=++=++³+=ç÷ç÷èøèø,当且仅当14,121,xy xy y xì=ïïíï+=ïî即2,14x y =ìïí=ïî时,等号成立,故12x y +的最小值为8.故选:D6. 已知定义域为R 的函数()f x 不是偶函数,则( )A. ()(),0x f x f x "Î-+¹R B. ()(),0x f x f x "Î--¹R C. ()()000,0x f x f x $Î-+¹R D. ()()000,0x f x f x $Î--¹R 【答案】D【解析】【分析】根据偶函数的概念得()(),0x f x f x "Î--=R 是假命题,再写其否定形式即可得答案.【详解】定义域为R 的函数()f x 是偶函数()(),0x f x f x Û"Î--=R ,所以()f x 不是偶函数()()000,0x f x f x Û$Î--¹R .故选:D .7. 若函数()22f x ax bx c=++的部分图象如图所示,则()1f =( ) A. 23- B. 112- C. 16- D. 13-【答案】D【解析】【分析】利用函数图象求得函数定义域,利用函数值可得出其解析式,代入计算即求得函数值.【详解】根据函数图象可知2x =和4x =不在函数()f x的定义域内,因此2x =和4x =是方程20ax bx c ++=的两根,因此可得()()()224f x a x x =--,又易知()31f =,所以可得2a =-;即()()()124f x x x =---,所以()113f =-.故选:D8. 奇函数()f x 在(),0-¥上单调递增,若()10f -=,则不等式()0xf x <的解集是( ).A. ()()101,∪,-¥- B. ()()11,∪,-¥-+¥C. ()()1001,∪,- D. ()()101,∪,-+¥【答案】C【解析】【分析】由()f x 奇偶性,单调性结合题意可得答案.【详解】因奇函数()f x 在(),0¥-上单调递增,()10f -=则()f x 在()0,¥+上单调递增,f (1)=0.得()()()01,01,f x x È¥>ÞÎ-+;()()()0,10,1f x x ¥È<ÞÎ--.则()()000x xf x f x <ì<Þí>î或()()()01,00,10x x f x È>ìÞÎ-í<î.故选:C二、多选题9. 下列关于集合的说法不正确的有( )A. {0}=ÆB. 任何集合都是它自身的真子集C. 若{1,}{2,}a b =(其中,a b ÎR ),则3a b +=D. 集合{}2y y x =∣与{}2(,)x y y x =∣是同一个集合【答案】ABD【解析】【分析】根据集合的定义,真子集的定义,集合相等的定义判断各选项.【详解】{0}中含有一个元素,不是空集,A 错;任何集合都是它自身的子集,不是真子集,B 错;由集合相等的定义得2,1a b ==,3a b +=,C 正确;集合{}2yy x =∣中元素是实数,集合{}2(,)x y y x =∣中元素是有序实数对,不是同一集合,D 错,故选:ABD .10. 已知二次函数()2223y m x mx m =-++-的图象与x 轴有两个交点()()12,0,,0x x ,则下面说法正确的是( )A. 该二次函数的图象一定过定点()1,5--;B. 若该函数图象开口向下,则m 的取值范围为:625m <<;C. 当2m >,且12x ££时,y 的最大值为45m -;D. 当2m >,且该函数图象与x 轴两交点的横坐标12,x x 满足1232,10x x -<<--<<时,m 的取值范围为:21114m <<【答案】ABD【解析】【分析】代入1x =-,解得5y =-,即可求解A ,根据判别式即可求解B ,利用二次函数的单调性即可求解C ,利用二次函数的图象性质即可列不等式求解.【详解】由()2223y m x mx m =-++-可得()22123y m x x =+--,当1x =-时,5y =-,故二次函数的图象一定过定点()1,5--,A 正确,若该函数图象开口向下,且与x 轴有两个不同交点,则()()220Δ44230m m m m -<ìí=--->î,解得:625m <<,故B 正确,当2m >,函数开口向上,对称轴为02m x m =-<-,故函数在12x ££时,单调递增,当2x =时,911y m =-,故y 的最大值为911m -;C 错误,当2m >,则开口向上,又1232,10x x -<<--<<时,则3,4210x y m =-=->,且2,110x y m =-=-<,且1,50x y =-=-<,且0,30x y m ==->,解得21114m <<,m 的取值范围为:21114m <<,D 正确,故选:ABD 11. 已知幂函数()()293m f x m x =-的图象过点1,n m æö-ç÷èø,则( )A. 23m =-B. ()f x 为偶函数C. n =D. 不等式()()13f a f a +>-的解集为(),1-¥【答案】AB【解析】【分析】利用幂函数的定义结合过点1,n m æö-ç÷èø,可求,m n 判断AC ;进而可得函数的奇偶性判断B ;解不等式可求解集判断D.【详解】因为函数()()293m f x m x =-为幂函数,所以2931m -=,解得23m =±,当23m =时,幂函数()23f x x =的图象不可能过点3,2n æö-ç÷èø,故23m ¹,当23m =-,幂函数()23f x x -=的图象过点3,2n æöç÷èø,则2332n -=,解得3232n -æö=±=ç÷èøA 正确,C 错误;()23f x x -=的定义域为{|0}x x ¹,且()2233()()f x x x f x ---=-==,故()f x 为偶函数,故B 正确;函数()23f x x -=在(0,)+¥上单调递减,由()()13f a f a +>-,可得()()13f a f a +>-,所以1310a a a ì+<-ïí+¹ïî,解得1a <且1a ¹-,故D 错误.故选:AB.三、填空题12. 满足关系{2}{2,4,6}A ÍÍ的集合A 有____________个.【答案】4【解析】【分析】由题意可得集合A 为{}2,4,6的子集,且A 中必包含元素2,写出满足条件的集合,即可得答案.【详解】即集合A 为{}2,4,6的子集,且A 中必包含元素2,又因为{2,4,6}的含元素2的子集为:{}2,{}2,4,{}2,6,{2,4,6}共4个.故答案为:4.13. 已知()f x 满足()()()2f x y f x f y +=++,且()22f =,则()3f =______.【答案】4【解析】【分析】令1x y ==得()10f =,再令1x =,2y = 即可求解.【详解】令1x y ==得()()()21122f f f =++=,所以()10f =,令1x =,2y =得()()()31224f f f =++=.故答案为:4.14. 已知函数()()()22223124,,4f x x ax ag x x x a a =-+-=-+-ÎR ,若[]10,1x "Î,[]20,1x $Î,使得不等式()()12f x g x >成立,实数a 的取值范围是__________.【答案】(),6-¥【解析】【分析】由题意将问题转化为()(),min max f x g x >[]0,1x Î,成立,利用二次函数的性质求解即可.【详解】若对任意[]10,1x Î,存在[]20,1x Î,使得不等式()()12f x g x >成立,即只需满足[]min min ()(),0,1f x g x x >Î,()22314g x x x a =-+-,对称轴()1,2x g x =在10,2éö÷êëø递减,在,1,12æùçúèû递增,()2min 18,2g x g a æö==-ç÷èø()[]2224,0,1f x x ax a x =-+-Î,对称轴4a x =,①04a £即0a £时,()f x 在[0,1]递增,()22min min ()04()8f x f a g x a ==->=-恒成立;②014a <<即04a <<时,()f x 在0,4a éö÷êëø递减,在,14a æùçúèû递增,22min min 7()4,()848a f x f a g x a æö==-=-ç÷èø,所以227488a a ->-,故04a <<;③14a ³即4a ³时,()f x 在[0,1]递减,()22min min ()12,()8f x f a a g x a ==--=-,所以2228a a a -->-,解得46a £<,综上(),6a ¥Î-.故答案为:(),6¥-【点睛】方法点睛:本题首先需要读懂题意,进行转化;其次需要分类讨论,结合二次函数的性质最后进行总结,即可求出结果.四、解答题15. 设全集R U =,集合{|23}P x x =-<<,{|31}.Q x a x a =<£+(1)若1a =-,求集合()U P Q I ð;(2)若P Q =ÆI ,求实数a 的取值范围.【答案】(1){|03}x x <<(2)][132,,æö-¥-+¥ç÷èøU 【解析】【分析】(1)先求出U Q ð,再求()U P Q Çð即可;(2)分Q =Æ和Q ¹Æ两种情况求解即可【小问1详解】解:当1a =-时,{|31}{|30}Q x a x a x x =<£+=-<£;{|3U C Q x x =£-或0}x >,又因为{}23P x x =-<<,所以(){|03}.U P Q x x Ç=<<ð【小问2详解】解:由题意知,需分为Q =Æ和Q ¹Æ两种情形进行讨论:当Q =Æ时,即31a a ³+,解得12a ³,此时符合P Q =ÆI ,所以12a ³;当Q ¹Æ时,因为P Q =ÆI ,所以1231a a a +£-ìí<+î或3331a a a ³ìí<+î,解之得3a £-.综上所述, a 的取值范围为][1,3,.2¥¥æö--È+ç÷èø16 已知二次函数()()20f x ax bx c a =++¹满足()()14f x f x x -+=,且()0 1.f =(1)求函数()f x 的解析式;(2)解关于x 的不等式()()2641f x t x t £-+-+.【答案】(1)()2221f x x x =-+(2)答案见解析.【解析】【分析】(1)利用待定系数法计算即可求解析式;(2)根据(1)的结论含参讨论解一元二次不等式即可.【小问1详解】因为()01f =,1c =,所以()21f x ax bx =++,又因为()()14f x f x x -+=,所以()(()22[1)1114a x b x ax bx x ù++++-++=û,所以24ax a b x ++=,所以240a a b =ìí+=î,所以22a b =ìí=-î,即()222 1.f x x x =-+.【小问2详解】由()()2641f x t x t £-+-+,可得不等式()222440x t x t +++£,即()2220x t x t +++£,所以()()20x x t ++£,当2-=-t ,即2t =时,不等式的解集为{|2}x x =-,当2t -<-,即2t >时,不等式的解集为{|2}x t x -££-,当2t ->-,即2t <时,不等式的解集为{|2}x x t -££-,综上所述,当2t =时,不等式的解集为{|2}x x =-,当2t >时,不等式的解集为{|2}x t x -££-,当2t <时,不等式的解集为{|2}.x x t -££-17. 已知函数()221x f x x-=.(1)用单调性的定义证明函数()f x 在()0,¥+上为增函数;(2)是否存在实数l ,使得当()f x 的定义域为11,m n éùêúëû(0m >,0n >)时,函数()f x 的值域为[]2,2m n l l --.若存在.求出l 的取值范围;若不存在说明理由.【答案】(1)证明见详解;(2)存在,()2,+¥.【解析】分析】(1)设()12,0,x x ¥Î+,且12x x <,然后作差、通分、因式分解即可判断()()12f x f x <,得证;(2)根据单调性列不等式组,将问题转化为210x x l -+=存在两个不相等的正根,利用判别式和韦达定理列不等式组求解可得.【小问1详解】()222111x f x x x-==-,设()12,0,x x ¥Î+,且12x x <,【则()()()()22121212122222222212211212111111x x x x x x f x f x x x x x x x x x -+æö--=---=-==ç÷èø,因为120x x <<,所以221212120,0,0x x x x x x <-+>>,所以()()120f x f x -<,即()()12f x f x <,所以函数()f x 在(0,+∞)上为增函数.【小问2详解】由(1)可知,()f x 在11,m n éùêúëû上单调递增,若存在l 使得()f x 的值域为[]2,2m n l l --,则22112112f m m m f n n n l l ìæö=-=-ç÷ïïèøíæöï=-=-ç÷ïèøî,即221010m m n n l l ì-+=í-+=î,因为0m >,0n >,所以210x x l -+=存在两个不相等的正根,所以21212Δ40100x x x x l l ì=->ï=>íï+=>î,解得2l >,所以存在()2,l ¥Î+使得()f x 的定义域为11,m n éùêúëû时,值域为[]2,2m n l l --.18. 习总书记指出:“绿水青山就是金山银山”.淮安市一乡镇响应号召,因地制宜的将该镇打造成“生态水果特色小镇”.调研过程中发现:某珍稀水果树的单株产量W (单位:千克)与肥料费10x (单位:元)满足如下关系:()252,02()48,251x x W x x x x ì+££ï=í<£ï+î其它成本投入(如培育管理等人工费)为20x (单位:元).已知这种水果的市场售价大约为10元/千克,且供不应求.记该单株水果树获得的利润为()f x (单位:元).(1)求()f x 函数关系式;(2)当投入的肥料费用为多少时,该单株水果树获得的利润最大?最大利润是多少?的【答案】(1)25030100,02()48030,251x x x f x x x x xì-+££ï=í-<£ï+î; (2)当投入肥料费用为30元时,获得的利润最大,最大利润是270元.【解析】【分析】(1)由单株产量W 乘以售价减去肥料费和其它成本投入可得出的函数关系式;(2)利用二次函数的单调性求出当02x ££时,()f x 的最大值,由基本不等式求出当25x <£时,()f x 的最大值,即可得出答案.【小问1详解】(1)由题意可得()()()1020101030f x W x x x W x x=--=-()22105230,025030100,024804830,251030,2511x x x x x x x x x x x x x x ì´+-££ì-+££ïï==íí-<£´-<£ïï+î+î.故()f x 的函数关系式为25030100,02()48030,251x x x f x x x x xì-+££ï=í-<£ï+î.【小问2详解】(2)由(1)22319150,025030100,02102()48030,251651030(1),2511x x x x x f x x x x x x x x ììæö-+££ï-+££ïç÷ïïèø==íí-<£éùïï-++<£+êúïï+ëûîî,当02x ££时,()f x 在30,10éùêúëû上单调递减,在3,210æùçúèû上单调递增,且(0)100(2)240f f =<=,max ()(2)240f x f \==;当25x <£时,16()51030(1)1f x x x éù=-++êú+ëû,16181x x ++³=+Q 当且仅当1611x x=++时,即3x =时等号成立. max ()510308270f x \=-´=.的因为240270<,所以当3x =时,max ()270f x =.当投入的肥料费用为30元时,该单株水果树获得的利润最大,最大利润是270元.19. 已知集合,A B 中的元素均为正整数,且,A B 满足:①对于任意,i j a a A Î,若i j a a ¹,都有i j a a B Î;②对于任意,m k b b B Î,若m k b b <,都有k mb A b Î.(1)已知集合{}1,2,4A =,求B ;(2)已知集合{}()2,4,8,8A t t =>,求t ;(3)若A 中有4个元素,证明:B 中恰有5个元素.【答案】(1){}2,48B =,(2)16t =(3)证明见解析【解析】【分析】(1)根据①可得2,4,8都是B 中的元素,进而证明B 中除2,4,8外没有其他元素即可求解,(2)根据条件①②,即可求解,(3)根据题意可得41a a ,3324421123,,,,a a a a a a a a a a ,4321a a a a 是A 中的元素,进而根据11a =和12a ³可得{}2341111,,,A a a a a =,进而{}3456711111,,,,a a a a a B Í,接下来假设B 中还有其他元素,且该元素为k ,利用k 与31a 的关系得矛盾求解.【小问1详解】由①可得2,4,8都是B 中的元素.下面证明B 中除2,4,8外没有其他元素:假设B 中还有其他元素,分两种情况:第一种情况,B 中最小的元素为1,显然81不是A 中的元素,不符合题意;第二种情况,B 中最小的元素为2,设B 中除2,4,8外的元素为()2k k b b >,因为2k b 是A 中的元素,所以k b 为4或8,而4,8也是B 中的元素,所以B 中除2,4,8外没有其他元素.综上,{}2,4,8B =.【小问2详解】由①可得,8,16,32,2,4,8t t t 都是B 中的元素.显然84,82,162t t t <<<,由(2)可得,422,,8816t t t 是A 中的元素,即,,248t t t 是A 中的元素.因为842t t t t <<<,所以2,4,8842t t t ===,解得16t =.【小问3详解】证明:设{}12341234,,,,A a a a a a a a a =<<<.由①可得,1224,a a a a 都是B 中的元素.显然1224a a a a <,由②可得,2412a a a a 是A 中的元素,即41a a 是A 中的元素.同理可得3324421123,,,,a a a a a a a a a a ,4321a a a a 是A 中的元素.若11a =,则34344122a a a a a a a a =>,所以3412a a a a 不可能是A 中的元素,不符合题意.若12a ³,则32311a a a a a <<,所以321211,a a a a a a ==,即23213121,a a a a a a ===.又因为44443211a a a a a a a <<<<,所以444123321,,a a a a a a a a a ===,即441a a =,所以{}2341111,,,A a a a a =,此时{}3456711111,,,,a a a a a B Í.假设B 中还有其他元素,且该元素为k ,若31k a <,由(2)可得71a A k Î,而7411a a k>,与{}2341111,,,A a a a a =矛盾.若31k a >,因为31k A a Î,所以131,1,2,3,4i k a i a ==,则31,1,2,3,4i k a i +==,即{}45671111,,,k a a a a Î,所以B 中除3456711111,,,,a a a a a 外,没有其他元素.所以{}3456711111,,,,B a a a a a =,即B 中恰有5个元素.【点睛】方法点睛:对于以集合为背景的新定义问题的求解策略:1、紧扣新定义,首先分析新定义的特点,把心定义所叙述的问题的本质弄清楚,应用到具体的解题过程中;2、用好集合的性质,解题时要善于从试题中发现可以使用的集合的性质的一些因素.3、涉及有交叉集合的元素个数问题往往可采用维恩图法,基于课标要求的,对于集合问题,要熟练基本的概念,数学阅读技能、推理能力,以及数学抽象和逻辑推理能力.。
四川省成都市第七中学2022-2023学年高一上学期期末数学试题(含答案解析)
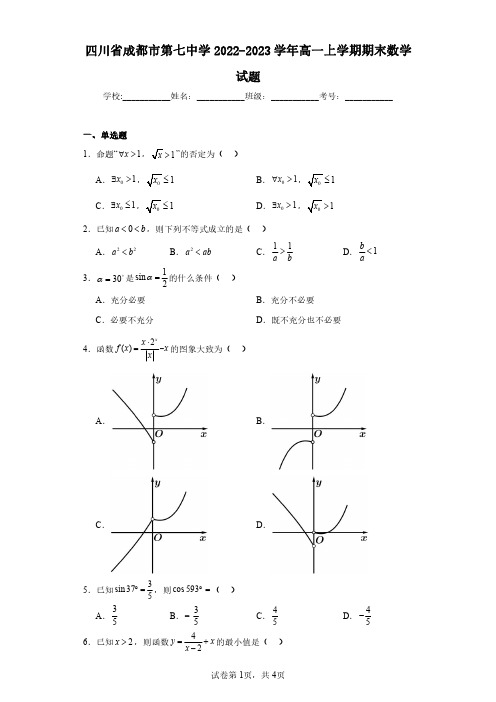
【详解】当
30 时, sin
1 ;当 sin 2
1 时,可能 2
5 6
.
所以
30
是
sin
1 2
的充分不必要条件.
故选:B
【点睛】本小题主要考查充分、必要条件的判断,属于基础题.
4.A
【分析】分类讨论得到分段函数,分析函数的单调性与特值即可得到答案. 答案第 1页,共 11页
【详解】
f
(x)
x 2x x
x
2x x, x 0 2x x, x 0 ,
当 0 x 1时, 2x x 0 ,排除 D 选项;
当 x 0 时, y 2x x 在 , 0 上单调递减,且 f (1) 1 1 0 ,
2 排除 BC,
故选:A
5.B
【分析】根据三角函数的诱导公式结合题干所给条件计算即可.
【详解】 cos 593 cos 720 127 cos 2 360 127 cos 127 cos 127
8 ,得13c
8 ,结合134
85
,
可得出 c 4 ,综合可得出 a 、 b 、 c 的大小关系. 5
【详解】由题意可知 a 、 b 、 c 0,1 ,
a b
log5 3 lg 3 lg 8 1
log8 5 lg 5 lg 5 lg 52
lg 3 lg 82 2
lg 3 lg 82
2 lg 5
则 3 1 的最小值为 ab
.
四、解答题 17.已知函数 f (x) 是二次函数, f (1) 0 , f (3) f (1) 4 .
(1)求 f (x) 的解析式;
(2)解不等式 f (x 1) 4 .
18.已知
四川省成都市2017-2018学年高一上学期期末调研考试数学试题

四川省成都市2017-2018学年高一上学期期末调研考试数学试题2017-2018学年度上期期末高一年级调研考试数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合$P=\{x|<x<2\}$,$Q=\{x|-1<x<1\}$,则$P\capQ=$()A。
$\{x|x<1\}$ B。
$\{x|<x<1\}$ C。
$\{x|-1<x<1\}$ D。
$\{\}$2.已知平面向量$a=(m+1,-2)$,$b=(-3,3)$,若$a//b$,则实数$m$的值为()A。
0 B。
-3 C。
1 D。
-13.函数$y=ax+1-3(a>且a≠1)$的图像一定经过的点是()A。
$(。
-2)$ B。
$(-1.-3)$ C。
$(。
-3)$ D。
$(-1.-2)$4.已知$\frac{\sin\theta+\cos\theta}{1}=\frac{1}{1+2\cos\theta}$,则$\tan\theta$的值为()A。
-4 B。
$-\frac{1}{11}$ C。
$\frac{1}{11}$ D。
45.函数$f(x)=\log_3|x-2|$的大致图像是()A。
B。
C。
D。
6.函数$f(x)=\frac{1}{\pi}\tan(x+\frac{\pi}{4})$的单调递增区间为()A。
$(2k-\frac{3\pi}{4},2k+\frac{\pi}{4}),k∈Z$ B。
$(2k-\frac{3\pi}{4},2k+\frac{\pi}{4}),k∈Z$C。
$(4k-\frac{3\pi}{4},4k+\frac{\pi}{4}),k∈Z$ D。
$(4k-\frac{3\pi}{4},4k+\frac{\pi}{4}),k∈Z$7.函数$f(x)=\ln(-x)-x-2$的零点所在区间为()A。
四川省成都市蓉城名校联盟2023-2024学年高一上学期期末联考数学试题

8.已知函数 f x log2 mx2 4x 3 , m R ,若 f x 在区间1, 上单调递增,则 m
的取值范围为( )
A. , 2
B.2,
C.
5 4
,
2
D. 1, 2
二、多选题 9.下列论述中,正确的有( )
A.集合a,b,c 的非空子集的个数有 7 个
B.第一象限角一定是锐角
C.若 f x 为定义在区间 a,b 上的连续函数,且有零点,则 f a f b 0
D. x 2 是 x 1的充分不必要条件
10.下列函数中,既是奇函数,又在定义域内是增函数的有( )
A. y x 1 x
B. y 2x 2 x
C. y 2x 2x
D. y 2x3 x
11.已知
(1)
64 27
13 31 2 Nhomakorabea6
π 30 ;
(2) 31log32 lg5 log 32 log 23 lg2 .
18.已知
sin 3cos
cos 2sin
1 7
.
(1)求 tan ;
(2)求 2sin2 sin cos 的值.
六、问答题
19.已知函数 f x ax 2 x a (a 0) .
A. f x 的图象关于直线 x= 1 轴对称
B. f x 的图象关于点 2, 0 中心对称
C. f x 4 f x
D. f 1 f 2 f 3 f 17 10
试卷第 2页,共 4页
三、单空题
13.若扇形的弧长为 8,圆心角为 4rad ,则扇形的面积为
.
14.已知 a 0,b 0 ,且 a b 2 ,则 1 2 的最小值为
A. 3
人教版高一数学必修一第一学期期末测试A卷(含答案和解析)

期末测试卷02(本卷满分150分,考试时间120分钟) 测试范围:必修第一册(人教A 版2019)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.设集合}034|{2<+-=x x x A ,}032|{>-=x x B ,则=B A ( )。
A 、)231(,B 、)31(, C 、)323(,D 、)1(∞+,【答案】C【解析】由题意得,}31|{<<=x x A ,}23|{>=x x B ,则)323(,=B A ,故选C 。
2.命题“全等三角形的面积一定都相等”的否定是( )。
A 、全等三角形的面积不一定都相等B 、不全等三角形的面积不一定都相等C 、存在两个不全等三角形的面积相等D 、存在两个全等三角形的面积不相等 【答案】D【解析】命题是省略量词的全称命题,故选D 。
3.已知0>a ,0>b ,且12=+b a ,则ba 11+的最小值为( )。
A 、223+ B 、243+ C 、263+ D 、283+ 【答案】A【解析】∵0>a ,0>b ,∴223221)11)(2(11+≥+++=++=+ab b a b a b a b a , 即最小值为223+,故选A 。
4.已知α为第三象限角,且α=-α2cos 22sin 2,则)42sin(π-α的值为( )。
A 、1027- B 、107- C 、107 D 、1027 【答案】D【解析】由已知得)1(cos 22sin 22-α=-α,则4tan 2=α,由α为第三象限角,得2tan =α,故552sin -=α,55cos -=α,∴1027)2cos 2(sin 22)42sin(=α-α=π-α,故选D 。
5.若函数)2lg()(2a x ax x f +-=的定义域为R ,则实数a 的取值范围为( )。
四川省成都市2020-2021学年高一上学期期末调研考试数学试题 (含答案)

成都市2020~2021学年度上期期末高一年级调研考试数 学 第Ⅰ卷(选择题)一、选择题1.设全集{}1,2,3,4,5U =,集合{}2,3,4M =,{}3,4N =,则()UM N ⋃=( )A .{}2,3,4B .{}1,2,5C .{}3,4D .{}1,52.下列函数中,与函数y x =相等的是( )A.y =B.3y =C.4y =D .2x y x=3.已知角α的顶点与直角坐标系的原点重合,始边与x 轴的非负半轴重合,且45cox α=-. 若角α的终边上有一点(),3P x ,则x 的值为( ) A .4-B .4C .3-D .34.设函数()()222,3,log 1, 3.x e x f x x x ⎧+<⎪=⎨-≥⎪⎩则()()0f f 的值为( ) A .2 B .3C .31e -D .21e -5.已知扇形的圆心角为30°,面积为3π,则扇形的半径为( ) A.B .3C.D .66.函数()ln 29f x x x =+-的零点所在区间是( ) A .()1,2B .()2,3C .()3,4D .()4,57.已知函数()2cos 216f x x π⎛⎫=-- ⎪⎝⎭,则函数()f x 的递减区间是( )A .()7,Z 1212k k k ππππ⎡⎤++∈⎢⎥⎣⎦ B .()5,Z 1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦C .(),Z 63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦D .()5,Z 36k k k ππππ⎡⎤++∈⎢⎥⎣⎦8.函数()233x x f x =-的图象大致为( )A .B .C .D .9.已知函数()2sin 4f x x π⎛⎫=+⎪⎝⎭,先将函数()f x 图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向右平移3π个单位长度,最后得到函数()y g x =的图象,则6g π⎛⎫⎪⎝⎭的值为( )A .1BC .0D .10.已知函数()2112x ax f x +-=在[]1,2上单调递减,则实数a 的取值范围是( )A .[]2,4B .[)2,-+∞C .[]4,2--D .(],4-∞-11.若126a -=,3log 2b =,ln 2c =,则a ,b ,c 的大小关系为( )A .a b c <<B .b c a <<C .c a b <<D .c b a <<12.设函数()21lg 111x x f x x x -=-++-,()()1212g x f x f ⎛⎫=-- ⎪⎝⎭.若()g x 的值不小于0,则x 的取值范围是( )A .3,04⎡⎫-⎪⎢⎣⎭B .3111,,4224⎡⎫⎛⎫--⋃-⎪ ⎪⎢⎣⎭⎝⎭ C .30,4⎛⎤ ⎥⎝⎦D .1130,,224⎛⎫⎛⎤⋃ ⎪⎥⎝⎭⎝⎦第Ⅱ卷(非选择题)二、填空题13.计算tan330︒的值为______. 14.已知函数211x y a-=+(0a >且1a ≠)的图象恒过定点()00,P x y ,则0x 的值为______.15.已知函数()f x 是定义在R 上的偶函数,且对区间(],0-∞上的任意1x ,2x ,当12x x ≠时,都有()()12120f x f x x x -<-.若实数t 满()()213f t f t +≤-,则t 的取值范围是______.16.已知函数()()sin 03f x x πωω⎛⎫=+> ⎪⎝⎭在4,33ππ⎛⎫-⎪⎝⎭上单调,且将函数()f x 的图象向右平移4π个单位长度后与原来的图象重合.当()0,4x π∈时,使得不等式()12f x ≤成立的x 的最大值为______. 三、解答题:17.计算下列各式的值:(Ⅰ)()23232021 1.538-⎛⎫-+⨯ ⎪⎝⎭;(Ⅱ)2log 31lg2100+- 18.已知tan 2θ=-,且,2πθπ⎛⎫∈⎪⎝⎭.(Ⅰ)求sin θ,cos θ的值;(Ⅱ)求()()2sin sin 2cos 2cos 2ππθθππθθ⎛⎫-+- ⎪⎝⎭⎛⎫-++ ⎪⎝⎭的值.19.已知函数()2121x f x =-+. (Ⅰ)用函数单调性的定义证明函数()f x 在R 上是增函数; (Ⅱ)当[]x 1,3∈时,求函数()()3log g x f x =的最值.20.1986年4月26日,一场地震造成乌克兰境内的切尔诺贝利核电站爆炸并引起大火.这一事故导致约8吨的强辐射物严重泄露,事故所在地被严重污染.主要辐射物是锶90,它每年的衰减率为2.47%,经专家模拟估计,辐射物中锶90的剩余量低于原有的8.46%时,事故所在地才能再次成为人类居住的安全区;要完全消除这次核事故对自然环境的影响至少需要800年.设辐射物中原有的锶90有()08a a <<吨.(Ⅰ)设经过()*N t t ∈年后辐射物中锶90的剩余量为()P t 吨,试求()P t 的表达式,并计算经过800年后辐射物中锶90的剩余量;(Ⅱ)事故所在地至少经过多少年才能再次成为人类居住的安全区?(结果保留为整数) 参考数据:ln0.0846 2.47=-,ln0.97530.03=-.21.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的最小值为2-,其图象经过点()0,1-,且图象上相邻的最高点与最低点的横坐标之差的绝对值为2π. (Ⅰ)求函数()f x 的解析式;(Ⅱ)若关于x 的方程()0f x k -=在11,612ππ⎡⎤⎢⎥⎣⎦上有且仅有两个实数根1x ,2x ,求实数k 的取值范围,并求出12x x +的值. 22.已知函数()f x =的定义域为R ,其中a 为实数.(Ⅰ)求a 的取值范围;(Ⅱ)当1a =时,是否存在实数m 满足对任意[]11,1x ∈-,都存在2R x ∈,使得()()1111299331x x x x m f x --++--≥成立?若存在,求实数m 的取值范围;若不存在,请说明理由.2020~2021学年度上期期末高一年级调研考试数学参考答案及评分意见第Ⅰ卷(选择题)一、选择题1.D ;2.B ;3.A ;4.B ;5.D ;6.C ;7.A ;8.C ;9.А;10.В;11.A ;12.D第Ⅱ卷(非选择题)二、填空题13.-14.12; 15.24,3⎡⎤-⎢⎥⎣⎦; 16.113π. 三、解答题17.解:(Ⅰ)原式()()2233274912122894πππ-⎛⎫⎛⎫=+-+⨯=+-+⨯=⎪ ⎪⎝⎭⎝⎭. (Ⅱ)原式21log 32211lg102ln 2322e -=+-=-+-=.18.解:(Ⅰ)由tan 2θ=-,得sin 2cos θθ=-. ∵22sin cos 1θθ+=,∴21cos 5θ=. ∵,2πθπ⎛⎫∈⎪⎝⎭,∴sin 0θ>,cos 0θ<.∴cos θ=,sin θ=.(Ⅱ)原式2sin cos 2tan 1cos sin 1tan θθθθθθ++==-- ∵tan 2θ=-,∴原式41112-+==-+. 19.解:(Ⅰ)任取1x ,2R x ∈,且12x x <.则()()121222112121x x f x f x ⎛⎫-=--- ⎪++⎝⎭()()()1221212222221212121x x x x xx -=-=++++. ∵12x x <,∴1222x x<,即12220x x-<.又∵()()2121210x x ++>,∴()()120f x f x -<,即()()12f x f x <. ∴函数()f x 在R 上单调递增.(Ⅱ)令()t f x =,函数()()3log g x f x =化为()3log h t t =. 由(Ⅰ)知当[]1,3x ∈时,函数()f x 单调递增. ∴当1x =时,函数()f x 有最小值()113f =; 当3x =时,函数()f x 有最大值()739f =.∴17,39t ⎡⎤∈⎢⎥⎣⎦. 又函数()3log h t t =在17,39⎡⎤⎢⎥⎣⎦上单调递增,∴当13t =,即1x =时,函数()h t 有最小值1-,即()g x 有最小值1-; 当79t =,即3x =时,函数()h t 有最大值32log 7-+,即()g x 有最大值32log 7-+. 20.解:(Ⅰ)由题意,得()()1 2.47%tP t a =-,*N t ∈.化简,得()0.9753tP t a =,*N t ∈.∴()8008000.9753P a =.∴经过800年后辐射物中锶90的剩余量为8000.9753a 吨.(Ⅱ)由(Ⅰ),知()0.9753tP t a =,*N t ∈.由题意,得0.97530.0846t a a <,不等式两边同时取对数,得ln 0.9753ln 0.0846t<. 化简,得ln0.9753ln0.0846t <. 由参考数据,得0.03 2.47t -<-.∴2473t >. 又∵24782.33≈,∴事故所在地至少经过83年才能再次成为人类居住的安全区. 21.解:(Ⅰ)由题意,得2A =,122T π=.∴T π=,22Tπω==.∴()()2sin 2f x x ϕ=+. 又函数()f x 的图象经过点()0,1-,则2sin 1ϕ=-.由2πϕ<,得6πϕ=-.∴()2sin 26f x x π⎛⎫=-⎪⎝⎭. (Ⅱ)由题意,关于x 的方程()0f x k -=在11,612ππ⎡⎤⎢⎥⎣⎦上有且仅有两个实数根1x ,2x , 即函数()y f x =与y k =的图象在11,612ππ⎡⎤⎢⎥⎣⎦上有且仅有两个交点. 由(Ⅰ)知()2sin 26f x x π⎛⎫=-⎪⎝⎭.令26t x π=-,则2sin y t =.∵11,612x ππ⎡⎤∈⎢⎥⎣⎦,∴5,63t ππ⎡⎤∈⎢⎥⎣⎦.则[]2,2y ∈-.其函数图象如图所示.由图可知,实数k 的取值范围为([)2,1,2-⋃.①当[)1,2k ∈时,1t ,2t ,关于2t π=对称,则12122266t t x x πππ⎛⎫⎛⎫+=-+-= ⎪ ⎪⎝⎭⎝⎭. 解得1223x x π+=.②当(2,k ∈-时,1t ,2t 关于32t π=对称,则121222366t t x x πππ⎛⎫⎛⎫+=-+-= ⎪ ⎪⎝⎭⎝⎭.解得1253x x π+=.综上,实数k 的取值范围为([)2,1,2-⋃,12x x +的值为23π或53π.22.解:(Ⅰ)由题意,函数()f x =的定义域为R ,则不等式2210ax ax -+≥对任意R x ∈都成立. ①当0a =时,10≥显然成立;②当0a ≠时,欲使不等式2210ax ax -+≥对任意R x ∈都成立,则20440a a a >⎧⎨-≤⎩,解得01a <≤.综上,实数a 的取值范围为[]0,1.(Ⅱ)当1a =时,()f x =∴当R x ∈时,()min 0f x =.令13333xxxxt -⎛⎫=-=- ⎪⎝⎭.显然在[]1,1x ∈-上递增,则88,33t ⎡⎤∈-⎢⎥⎣⎦.∴()2993311x x x x m t mt --++--=++.令()21h t t mt =++,88,33t ⎡⎤∈-⎢⎥⎣⎦.若存在实数m 满足对任意[]11,1x ∈-,都存在2R x ∈,使得()()1111299331xx x x m f x --++--≥成立,则只需()min 0h t ≥.①当823m -≤-即163m ≥时,函数()h t 在88,33⎡⎤-⎢⎥⎣⎦上单调递增. 则()min 864810393h t h m ⎛⎫=-=-+≥ ⎪⎝⎭.解得7324m ≤,与163m ≥矛盾; ②当88323m -<-<即161633m -<<时,函数()h t 在8,32m ⎡⎤--⎢⎥⎣⎦上单调递减, 在8,23m ⎡⎤-⎢⎥⎣⎦上单调递增.则()22min 10242m m m h t h ⎛⎫=-=-+≥ ⎪⎝⎭. 解得22m -≤≤;③当823m -≥即163m ≤-时,函数()h t 在88,33⎡⎤-⎢⎥⎣⎦上单调递减. 则()min 864810393h t h m ⎛⎫==++≥ ⎪⎝⎭.解得7324m ≥-,与163m ≤-矛盾. 综上,存在实数m 满足条件,其取值范围为[]2,2-.。
