一种更简化而高效的粒子群优化算法
粒子群优化算法

粒子群优化算法
粒子群优化算法(PSO)是一种基于群智能的算法,它将仿生学、计算机图形学和优化理论相结合,可以解决复杂的优化问题。
该算法在近年来的应用中受到了广泛关注,并在实际工程中取得了显著的效果,特别是在互联网领域,它能够和其他优化算法一起很好地完成复杂的任务。
粒子群优化算法能够有效地解决多种问题,如:分布式搜索、优化路径规划、模式识别、多优化器混合等等。
该算法利用社会群体同化规律,将算法中的粒子模型作为一种有效的解决优化问题的一种算法,将周期性更新过程中的位置信息和最大值更新来确定粒子的最优位置。
因此,粒子群优化算法在很大程度上可以利用群体行为来最大化和最小化优化目标函数。
此外,粒子群优化算法在互联网领域的应用也得到了很广泛的应用,如入侵检测系统的参数调整、负载均衡的实现以及文本挖掘等技术,都可以利用粒子群优化算法进行优化。
如果把这些参数看做一系列棘手的问题,那么粒子群优化算法就能够有效地帮助解决它们。
作为一种有效的优化算法,粒子群优化技术的发展不断增强,它的应用范围也在快速扩大,特别是在互联网领域,它将能够发挥出更大的作用。
一般来说,粒子群优化算法有较低的时间复杂度,能够尽快找到最优解。
此外,由于粒子群优化可以识别全局最优解,这种技术具有抗噪声能力强、能够适应不断变化的技术参数等特点,值得引起关注。
粒子群优化算法介绍

粒子群优化算法介绍
粒子群优化算法(Particle Swarm Optimization,PSO)是一种
基于群体智能的优化方法,其中包含了一组粒子(代表潜在解决方案)在n维空间中进行搜索,通过找到最优解来优化某个问题。
在PSO的
过程中,每个粒子根据自身当前的搜索位置和速度,在解空间中不断
地寻找最优解。
同时,粒子也会通过与周围粒子交换信息来寻找更好
的解。
这种信息交换模拟了鸟群或鱼群中的信息交流行为,因此PSO
算法也被称为群体智能算法。
由于其并行搜索和对局部最优解的较好处理,PSO算法在多个领
域均得到了广泛应用。
其中最常用的应用之一是在神经网络和其他机
器学习算法中用来寻找最优解。
此外,PSO算法在图像处理、数据挖掘、机器人控制、电力系统优化等领域也有着广泛的应用。
PSO算法的核心是描述每个粒子的一组速度和位置值,通常使用
向量来表示。
在PSO的初始化阶段,每个粒子在解空间中随机生成一
个初始位置和速度,并且将其当前位置作为当前最优解。
然后,每个
粒子在每次迭代(即搜索过程中的每一次)中根据当前速度和位置,
以及粒子群体中的最优解和全局最优解,更新其速度和位置。
PSO算法的重点在于如何更新各个粒子的速度向量,以期望他们能够快速、准
确地达到全局最优解。
总之, PSO算法是一种群体智能算法,目的是通过模拟粒子在解
空间中的移动来优化某个问题。
由于其简单、有效且易于实现,因此PSO算法在多个领域得到了广泛应用。
粒子群优化算法ppt

联合优化
粒子群优化算法可以用于联合优化神经网络的参数和结构,进一步提高神经网络的性能。
粒子群优化算法在神经网络训练中的应用
粒子群优化算法可以用于优化控制系统的控制器参数,以提高控制系统的性能和稳定性。
控制器参数优化
鲁棒性优化
联合优化
粒子群优化算法可以用于提高控制系统的鲁棒性,以应对系统中的不确定性和干扰。
粒子群优化算法可以用于联合优化控制系统的参数和结构,进一步提高控制系统的性能和稳定性。
03
粒子群优化算法在控制系统中的应用
02
01
06
总结与展望
粒子群优化算法是一种高效的全局优化算法,具有速度快、简单易行、易于并行化等优点。它利用群体智慧,通过粒子间的协作与信息共享,可以快速找到全局最优解。
优点
PSO算法的特点包括:简单易懂、易实现、能够处理高维问题、对初始值不敏感、能够处理非线性问题等。
定义与特点
粒子群优化算法的起源与发展
PSO算法的起源可以追溯到1995年,由 Kennedy 和 Eberhart博士提出,受到鸟群觅食行为的启发。
最初的PSO算法主要应用于函数优化问题,后来逐渐发展应用到神经网络训练、模式识别、图像处理、控制等领域。
边界条件的处理
通过对粒子速度进行限制,可以避免粒子在搜索空间中过度震荡,从而更好地逼近最优解。
粒子速度的限制
实例一
针对函数优化问题,通过对粒子速度和位置进行更新时加入随机扰动,可以增加粒子的探索能力,从而寻找到更好的最优解。
实例二
针对多峰函数优化问题,将粒子的个体最佳位置更新策略改为基于聚类的方法,可以使得粒子更好地逼近问题的全局最优解。
粒子的适应度函数用于评估其位置的好坏。
粒子群优化算法概述[1]
![粒子群优化算法概述[1]](https://img.taocdn.com/s3/m/020552f8c1c708a1284a4497.png)
计算机辅助工艺课程作业学生:赵华琳学号: s时间:09年6月粒子群优化算法概述0.前言优化是科学研究、工程技术和经济管理等领域的重要研究工具。
它所研究的问题是讨论在众多的方案中寻找最优方案。
例如,工程设计中怎样选择设计参数,使设计方案既满足设计要求又能降低成本;资源分配中,怎样分配有限资源,使分配方案既能满足各方面的基本要求,又能获得好的经济效益。
在人类活动的各个领域中,诸如此类,不胜枚举。
优化这一技术,正是为这些问题的解决,提供理论基础和求解方法,它是一门应用广泛、实用性很强的科学。
近十余年来,粒子群优化算法作为群体智能算法的一个重要分支得到了广泛深入的研究,在路径规划等许多领域都有应用。
本文主要结合现阶段的研究概况对粒子群优化算法进行初步介绍。
1.粒子群优化算法的基本原理1.1 粒子群优化算法的起源粒子群优化(PSO)算法是由Kennedy和Eberhart于1995年用计算机模拟鸟群觅食这一简单的社会行为时,受到启发,简化之后而提出的[1][2]。
设想这样一个场景:一群鸟随机的分布在一个区域中,在这个区域里只有一块食物。
所有的鸟都不知道食物在哪里。
但是他们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢。
最简单有效的方法就是追寻自己视野中目前离食物最近的鸟。
如果把食物当作最优点,而把鸟离食物的距离当作函数的适应度,那么鸟寻觅食物的过程就可以当作一个函数寻优的过程。
鱼群和鸟群的社会行为一直引起科学家的兴趣。
他们以特殊的方式移动、同步,不会相互碰撞,整体行为看上去非常优美。
生物学家CargiReynolds提出了一个非常有影响的鸟群聚集模型。
在他的模拟模型boids中,每一个个体遵循:避免与邻域个体相冲撞、匹配邻域个体的速度、试图飞向感知到的鸟群中心这三条规则形成简单的非集中控制算法驱动鸟群的聚集,在一系列模拟实验中突现出了非常接近现实鸟群聚集行为的现象。
该结果显示了在空中回旋的鸟组成轮廓清晰的群体,以及遇到障碍物时鸟群的分裂和再度汇合过程。
优化算法-粒子群优化算法

步骤四:对于粒子的每一维,根据式(1)计算得到一个随机点 的位置。
步骤五:根据式(2)计算粒子的新的位置。
步骤六:判断是否满足终止条件。
粒子群优化算法
PSO算法在组合优化问题中的应用
典型的组合优化问题:TSP
粒子群优化算法
量子行为粒子群优化算法的基本模型
群智能中个体的差异是有限的,不是趋向于无穷大的。群体的聚 集性是由相互学习的特点决定的。
个体的学习有以下特点: 追随性:学习群体中最优的知识
记忆性:受自身经验知识的束缚
创造性:使个体远离现有知识
粒子群优化算法
聚集性在力学中,用粒子的束缚态来描述。产生束缚态的原因是 在粒子运动的中心存在某种吸引势场,为此可以建立一个量子化 的吸引势场来束缚粒子(个体)以使群体具有聚集态。
描述为: 给定n 个城市和两两城市之间的距离, 求一条访问各城市
一次且仅一次的最短路线. TSP 是著名的组合优化问题, 是NP难题, 常被用来验证智能启发式算法的有效性。
vid (t 1) wvid (t) c1r1 pid (t) xid (t) c2r2( pgd (t) xid (t))
xid (t 1) xid (t) vid (t 1)
粒子群优化算法
w 惯性权重 可以是正常数,也可以是以时间为变量的线性或非线性
正数。
粒子群优化算法
通常动态权重可以获得比固定值更好的寻优结果,动态权重可以在 pso搜索过程中呈线性变化,也可以根据pso性能的某个测度函数 而动态改变,目前采用的是shi建议的随时间线性递减权值策略。
粒子群优化算法
一种简化粒子群算法及在三维装箱问题中的应用

第3 1 期
2 0 1 3年 1 1 月
科
学
技
术与Βιβλιοθήκη 工程 V0 1 . 1 3 No . 3 1 NO V .2 0 1 3
1 6 7 1 —1 8 1 5 ( 2 0 1 3 ) 3 1 — 9 2 1 4 — 0 6
S c i e nc e Te c hn o l o g y a n d En g i ne e r i n g
算法 、 多约束 F F D算法 j 、 穴度算法_ 4 ] 、 模拟退火
算 法 J 、 禁 忌搜 索算法 _ 6 等。 粒 子群 优 化 ( p a r t i c l e s w a r m o p t i mi z a t i o n ,P S O)
算法是 K e n n e d y 和E b e r h a r t 受人工生命研究结果的
文献标 志码
A
集装 箱装 箱 问题 是一 个 典 型 的组 合 优 化 问题 , 也 是一个 经典 的 N P C 问题 , 分析 和研究 该 问题 对其 他 N P C问题 比如 多处 理 器 任务 调 度 、 资源分配、 板 材 切割 以及 现 实 生 活 中货 物 包 装 布 局 等 等 的研 究
⑥
2 0 1 3 S c i . T e c h . E n g r g .
一
种简化粒子群算法及在三维装 箱 问题 中的应用
孟 非 黄太安 解志斌
( 江苏科技大学 电子信息学院 , 镇江 2 1 2 0 0 3 )
摘
要
在简化粒子群算法 中引入混合蛙跳算法的分组 思想 , 使 得粒子群 算法在进 化后期 能够利用更丰 富的信息 , 有 效避 免
免疫粒子群优化算法

免疫粒子群优化算法一、本文概述随着和计算智能的飞速发展,优化算法在众多领域,如机器学习、数据挖掘、控制工程等,都展现出了巨大的潜力和应用价值。
作为优化算法中的一种重要分支,粒子群优化(Particle Swarm Optimization, PSO)算法因其简单易实现、全局搜索能力强等特点,受到了广泛的关注和研究。
然而,随着问题复杂度的增加和实际应用需求的提升,传统的PSO算法在求解一些高维、多模态或非线性优化问题时,常常陷入局部最优解,难以找到全局最优解。
为了解决这些问题,本文提出了一种免疫粒子群优化算法(Immune Particle Swarm Optimization, IPSO)。
该算法结合了生物免疫系统的自学习、自适应和自组织等特性,通过引入免疫机制来增强PSO算法的全局搜索能力和收敛速度。
免疫粒子群优化算法的核心思想是将免疫算法中的抗体种群与粒子群优化算法中的粒子种群相结合,通过模拟生物免疫系统的多样性和记忆机制,实现粒子种群在搜索过程中的自我更新和优化。
本文首先介绍了粒子群优化算法的基本原理和发展现状,然后详细阐述了免疫粒子群优化算法的基本框架和实现过程。
在此基础上,通过一系列实验验证了免疫粒子群优化算法在求解高维、多模态和非线性优化问题上的有效性和优越性。
本文还对免疫粒子群优化算法的未来发展方向和应用前景进行了展望。
通过本文的研究,旨在为优化算法领域提供一种新颖、高效的算法工具,为解决复杂优化问题提供新的思路和方法。
也希望本文的研究能为相关领域的研究人员和工程师提供有益的参考和借鉴。
二、优化算法概述优化算法是一种寻找问题最优解的数学方法,广泛应用于工程、经济、管理等多个领域。
随着科技的发展,优化算法的种类和复杂性也在不断增加,其中粒子群优化算法(Particle Swarm Optimization, PSO)作为一种群体智能优化算法,因其简洁性和有效性,受到了广泛关注。
然而,传统的粒子群优化算法在面对复杂优化问题时,往往会出现早熟收敛、陷入局部最优等问题,限制了其在实际应用中的性能。
一种改进的粒子群算法

一种改进的粒子群算法摘要:粒子群算法是一种基于群体智能的优化算法,具有全局搜索能力和简单易用的特点,但存在收敛速度慢、易陷入局部最优等问题。
本文针对粒子群算法的不足,提出了一种改进的粒子群算法,主要包括两个方面的改进:自适应惯性权重和差分进化算子。
实验结果表明,改进后的算法在求解复杂函数优化问题时具有更快的收敛速度和更高的搜索精度。
关键词:粒子群算法;自适应惯性权重;差分进化算子;全局搜索1.引言粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,由Kennedy和Eberhart于1995年提出[1]。
PSO算法通过模拟鸟群捕食、觅食等行为,将待优化问题转化为粒子在搜索空间中的移动过程,通过粒子之间的信息交流和个体经验积累,逐步找到全局最优解。
相比其他优化算法,PSO算法具有简单易用、全局搜索能力强等优点,在多个领域都得到了广泛应用[2]。
然而,PSO算法也存在一些不足之处。
首先,PSO算法的收敛速度较慢,需要较长的迭代次数才能找到较优解。
其次,PSO算法容易陷入局部最优解,导致搜索精度不高。
为了解决这些问题,研究者们提出了许多改进的PSO算法,如自适应权重PSO[3]、混沌PSO[4]、改进收缩因子PSO[5]等。
本文针对PSO算法的不足,提出了一种改进的PSO算法,主要包括自适应惯性权重和差分进化算子两个方面的改进。
2.算法描述2.1 基本PSO算法基本PSO算法是由一群粒子组成的集合,每个粒子表示一个解向量。
每个粒子在搜索空间中随机初始化,然后根据自己的经验和全局最优解进行位置更新,直到满足停止条件为止。
具体算法流程如下:(1)初始化粒子群,包括粒子数量、搜索空间范围、速度范围、惯性权重等参数。
(2)对每个粒子,随机初始化位置和速度。
(3)对每个粒子,计算其适应度函数值。
(4)对每个粒子,更新速度和位置。
(5)更新全局最优解。
(6)判断是否满足停止条件,若不满足则返回第(3)步。
粒子群优化算法课件

实验结果对比分析
准确率
01
在多个数据集上,粒子群优化算法的准确率均高于对比算法,
表明其具有较强的全局搜索能力。
收敛速度
02
粒子群优化算法在多数数据集上的收敛速度较快,能够更快地
找到最优解。
鲁棒性
03
在不同参数设置和噪声干扰下,粒子群优化算法的性能表现稳
定,显示出良好的鲁棒性。
结果讨论与改进建议
讨论
其中,V(t+1)表示第t+1次迭代 时粒子的速度,V(t)表示第t次迭 代时粒子的速度,Pbest表示粒 子自身的最优解,Gbest表示全 局最优解,X(t)表示第t次迭代时
粒子的位置,w、c1、c2、 rand()为参数。
算法优缺点分析
优点
简单易实现、参数少、收敛速度快、 能够处理多峰问题等。
03
强化算法的可视化和解释性
发展可视化工具和解释性方法,帮助用户更好地理解粒子群优化算法的
工作原理和结果。
THANKS
感谢观看
粒子群优化算法的改进与扩展
动态调整惯性权重
惯性权重是粒子群优化算法中的一个 重要参数,它决定了粒子的飞行速度 。通过动态调整惯性权重,可以在不 同的搜索阶段采用不同的权重值,从 而更好地平衡全局搜索和局部搜索。
VS
一种常见的动态调整惯性权重的方法 是根据算法的迭代次数或适应度值的 变化来调整权重值。例如,在算法的 初期,为了更好地进行全局搜索,可 以将惯性权重设置得较大;而在算法 的后期,为了更好地进行局部搜索, 可以将惯性权重设置得较小。
并行粒子群优化算法
并行计算技术可以提高粒子群优化算法的计算效率和收敛 速度。通过将粒子群分成多个子群,并在不同的处理器上 同时运行这些子群,可以加快算法的收敛速度。
《粒子群优化算法》课件

CONTENTS
• 粒子群优化算法概述 • 粒子群优化算法的基本原理 • 粒子群优化算法的改进与变种 • 粒子群优化算法的参数选择与
调优 • 粒子群优化算法的实验与分析 • 总结与展望
01
粒子群优化算法概述
定义与原理
定义
粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体智 能的优化算法,通过模拟鸟群、鱼群等生物群体的觅食行为,寻找最优解。
限制粒子的搜索范围,避免无效搜索。
参数选择与调优的方法
网格搜索法
在参数空间中设定网格, 对每个网格点进行测试, 找到最优参数组合。
经验法
根据经验或实验结果,手 动调整参数。
贝叶斯优化法
基于贝叶斯定理,通过不 断迭代和更新参数概率分 布来找到最优参数。
遗传算法
模拟生物进以进一步深化对粒子群优化算法的理 论基础研究,探索其内在机制和本质规律,为算 法设计和改进提供更科学的指导。
为了更好地处理大规模、高维度和复杂问题,未 来研究可以探索更先进的搜索策略和更新机制, 以增强粒子群优化算法的局部搜索能力和全局搜 索能力。
随着人工智能技术的不断发展,粒子群优化算法 的应用领域也将不断扩展,未来研究可以探索其 在机器学习、数据挖掘、智能控制等领域的新应 用和新方法。
04
粒子群优化算法的参数选择与调优
参数对粒子群优化算法性能的影响
粒子数量
惯性权重
粒子数量决定了算法的搜索空间和搜索速 度。过少可能导致算法过早收敛,过多则 可能导致计算量增大。
影响粒子的全局和局部搜索能力,过大可 能导致算法发散,过小则可能使算法过早 收敛。
加速常数
粒子群优化算法

好地求解各类优化问题。
03
多目标优化
多目标优化是未来粒子群优化算法的一个重要研究方向,可以解决实
际优化问题中多个目标之间的权衡和取舍。
THANKS
谢谢您的观看
粒子群优化算法
xx年xx月xx日
目录
• 粒子群优化算法简介 • 粒子群优化算法的基本原理 • 粒子群优化算法的改进 • 粒子群优化算法的应用案例 • 粒子群优化算法的总结与展望
01
粒子群优化算法简介
什么是粒子群优化算法
粒子群优化算法是一种群体智能优化算法,通过模拟鸟群、 鱼群等动物群体的社会行为,利用群体中个体之间的相互作 用和信息共享,寻找问题的最优解。
动态调整约束参数
通过动态调整约束参数,使算法在不同阶段都能保持较好的优化效果。同时 ,可以设置一些参数的自适应调整策略,如根据迭代次数、最优解的位置和 速度等信息来自适应调整。
04
粒子群优化算法的应用案例
函数优化问题
求解函数最大值
粒子群优化算法可以用于求解各类连续或离散函数的最大值,例如非线性函数、 多峰函数等。通过不断迭代寻优,能够找到函数的局部最大值或全局最大值。
03
粒子群优化算法的参数包括粒子群的规模、惯性权重、加速常数和学习因子等 ,这些参数对算法的性能和收敛速度有着重要影响。
粒子群优化算法的应用领域
粒子群优化算法被广泛应用于各种优化问题中,包括函 数优化、路径规划、电力系统优化、机器学习、图像处 理、控制工程、模式识别、人工智能等领域。
具体应用包括:函数优化问题的求解、神经网络训练的 优化、控制系统参数的优化、机器人路径规划、图像处 理中的特征提取和分类等。
空间搜索的改进
引入高斯分布
通过引入高斯分布,使粒子速度更新过程中更侧重于向当前 最优解方向靠拢,提高算法的局部搜索能力。
粒子群优化法-概述说明以及解释

粒子群优化法-概述说明以及解释1.引言1.1 概述粒子群优化法(Particle Swarm Optimization,简称PSO)是一种用于求解优化问题的启发式算法。
它模拟了鸟群或鱼群中的群体协作行为,通过不断更新粒子的位置和速度,逐步逼近最优解。
PSO算法最早由Russell Eberhart和James Kennedy于1995年提出,并在之后的二十多年里得到了广泛应用和研究。
PSO算法是一种简单但高效的优化算法,其灵感源于群体智能中的群体行为。
它通过模拟从鸟群和鱼群等自然界中观察到的协同行为,将搜索空间中的解表示为“粒子”,每个粒子根据自己当前的位置和速度信息动态调整,并通过与其他粒子的互动来引导搜索过程。
在PSO算法中,每个粒子都有自己的位置和速度,并且能够记忆并更新自己及其他粒子的最优解。
通过不断地根据历史最优值和邻域最优值进行位置和速度的更新,粒子能够在搜索空间中逐渐找到最优解。
PSO算法具有计算简单、易于实现、收敛速度较快等优点,能够应用于解决连续优化问题、离散优化问题以及多目标优化问题等多个领域。
总的来说,粒子群优化法是一种基于群体智能的优化算法,通过模拟自然界中群体的协同行为,实现了对复杂优化问题的求解。
在实际应用中,PSO算法已经在函数优化、图像处理、机器学习、工程设计等众多领域展现出了良好的性能和广阔的应用前景。
本文将详细介绍粒子群优化法的原理和应用领域,并探讨其优势和发展前景。
1.2文章结构1.2 文章结构本文将按以下顺序展开对粒子群优化法的深入研究和讨论:1.2.1 粒子群优化法的概述首先,我们将介绍粒子群优化法的概念以及其基本原理。
我们将讨论其运作方式,了解粒子群如何模拟鸟群在搜索问题中寻找全局最优解的行为。
1.2.2 粒子群优化法的应用领域接下来,我们将探讨粒子群优化法在不同领域中的广泛应用。
粒子群优化法已被应用于许多问题领域,包括函数优化、图像处理、数据挖掘等。
粒子群优化算法

1 群体智能概述1.1 群体智能的概念与特点群体智能的概念源于对蜜蜂、蚂蚁、大雁等这类群居生物群体行为的观察和研究,是一种在自然界生物群体所表现出的智能现象启发下提出的人工智能实现模式,是对简单生物群体的智能涌现现象的具体模式研究。
群体智能指的是“简单智能的主体通过合作表现出复杂智能行为的特性”。
该种智能模式需要以相当数目的智能体来实现对某类问题的求解功能。
作为智能个体本身,在没有得到智能群体的总体信息反馈时,它在解空间中的行进方式是没有规律的。
只有受到整个智能群体在解空间中行进效果的影响之后,智能个体在解空间中才能表现出具有合理寻优特征的行进模式。
自然界中动物、昆虫常以集体的力量进行觅食生存,在这些群落中单个个体所表现的行为是简单缺乏智能的,且各个个体之间的行为是遵循相同规则的,但由个体组成的群体则表现出了一种有效的复杂的智能行为。
群体智能可以在适当的进化机制引导下通过个体交互以某种突现形式发挥作用,这是个体的智能难以做到的。
通常,群体智能是指一种人工智能模式,体现的是一种总体的智能特性。
人工智能主要有两种研究范式,即符号主义和联接主义。
符号主义采用知识表达和逻辑符号系统来模拟人类的智能。
联接主义则从大脑和神经系统的生理背景出发来模拟它们的工作机理和学习方式。
符号主义试图对智能进行宏观研究,而联接主义则是一种微观意义上的探索。
20世纪90年代后,计算智能的研究逐渐成为了联接主义人工智能的一个代表性流派。
计算智能系统是在神经网络、模糊系统、进化计算三个分支发展相对成熟的基础上,通过相互之间的有机融合而形成的新的科学方法,也是智能理论和技术发展的崭新阶段。
神经网络反映大脑思维的高层次结构;模糊系统模仿低层次的大脑结构;进化系统则是从生物种群的群体角度研究智能产生和进化过程。
对群居性生物群体行为涌现的群体智能的研究是进化系统的一个新兴研究领域。
群体智能中,最小智能但自治的个体利用个体与个体和个体与环境的交互作用实现完全分布式控制,其具有以下特点:(1)自组织。
粒子群优化算法粒子群优化算法简介
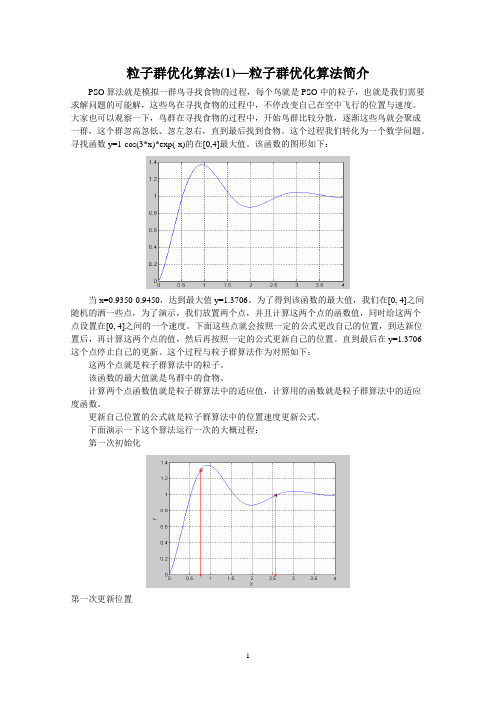
粒子群优化算法(1)—粒子群优化算法简介PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0, 4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0, 4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物。
计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群优化算法(2)—标准粒子群优化算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0, 4]最大值。
并在[0,4]之间放置了两个随机的点,这些点的坐标假设为x1=1.5,x2=2.5;这里的点是一个标量,但是我们经常遇到的问题可能是更一般的情况—x 为一个矢量的情况,比如二维z=2*x1+3*x22的情况。
群体智能优化算法-粒子群优化算法

第二章粒子群优化算法粒子群优化(PSO)是一种基于群体智能的数值优化算法,由社会心理学家James Kennedy和电气工程师Russell Eberhart于1995年提出。
自PSO诞生以来,它在许多方面都得到了改进,这一部分将介绍基本的粒子群优化算法原理和过程。
2.1粒子群优化粒子群优化(PSO)是一种群智能算法,其灵感来自于鸟类的群集或鱼群学习,用于解决许多科学和工程领域中出现的非线性、非凸性或组合优化问题。
图1 Russel Eberhart和James Kennedy2.1.1算法思想许多鸟类都是群居性的,并由各种原因形成不同的鸟群。
鸟群可能大小不同,出现在不同的季节,甚至可能由群体中可以很好合作的不同物种组成。
更多的眼睛和耳朵意味着有更多的及时发现食物和捕食者的机会。
鸟群在许多方面对其成员的生存总是有益的:觅食:社会生物学家E.O. Wilson说,至少在理论上,群体中的个体成员可以从其他成员在寻找食物过程中的发现和先前的经验中获益[1]。
如果一群鸟的食物来源是相同的,那么某些种类的鸟就会以一种非竞争的方式聚集在一起。
这样,更多的鸟类就能利用其他鸟类对食物位置的发现。
抵御捕食者:鸟群在保护自己免受捕食者侵害方面有很多优势。
◆更多的耳朵和眼睛意味着更多的机会发现捕食者或任何其他潜在的危险;◆一群鸟可能会通过围攻或敏捷的飞行来迷惑或压制捕食者;◆在群体中,互相间的警告可以减少任何一只鸟的危险。
空气动力学:当鸟类成群飞行时,它们经常把自己排成特定的形状或队形。
鸟群中鸟的数量不同,每只鸟煽动翅膀时产生不同的气流,这都会导致变化的风型,这些队形会充分利用不同的分型,从而使得飞行中的鸟类能够以最节能的方式利用周围的空气。
粒子群算法的发展需要模拟鸟群的一些优点,然而,为了了解群体智能和粒子群优化的一个重要性质,值得提一下是鸟群的一些缺点。
当鸟类成群结队时,也会给它们带来一些风险。
更多的耳朵和眼睛意味着更多的翅膀和嘴,这导致更多的噪音和运动。
粒子群优化算法的综述

粒子群优化算法的综述
粒子群优化算法(ParticleSwarmOptimization,简称PSO)是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等自然群体的行为方式,通过不断地跟踪当前最优解和群体历史最优解,从而不断地搜索最优解。
PSO算法简单易实现,具有收敛速度快、鲁棒性好、能够避免陷入局部最优等优点,在多个优化问题中表现出较好的效果。
在PSO算法的优化过程中,每个粒子代表一个解,粒子的位置表示解的变量值,粒子的速度表示解的变量值的变化量。
通过不断地更新粒子的位置和速度,逐渐接近最优解。
PSO算法的基本流程包括初始化粒子群、计算适应度函数、更新粒子速度和位置、更新群体历史最优解和个体历史最优解等步骤。
PSO算法的应用领域非常广泛,包括工程设计优化、机器学习、数据挖掘、机器视觉等方面。
在实际应用中,PSO算法可以与其他优化算法相结合,形成混合算法,以提高优化效果。
此外,还可以通过改进PSO算法的参数设置、粒子群模型、适应度函数等方面来提高算法的性能。
总之,PSO算法是一种简单有效的优化算法,具有广泛的应用前景和研究价值,未来还有很大的发展空间。
- 1 -。
粒子群优化算法(详细易懂-很多例子)讲解学习

粒子群算法的构成要素 -停止准则
停止准则一般有如下两种: 最大迭代步数 可接受的满意解
v i k d = w v i k d - 1 c 1 r 1 ( p b e s t i d x i k d 1 ) c 2 r 2 ( g b e s t d x i k d 1 )
粒子速度更新公式包含三部分: 第一部分为粒子先前的速度 第二部分为“认知”部分,表示粒子本身的思考,可理解为 粒子i当前位置与自己最好位置之间的距离。 第三部分为“社会”部分,表示粒子间的信息共享与合作, 可理解为粒子i当前位置与群体最好位置之间的距离。
惯性因子
基本粒子群算法
失去对粒子本身
的速度的记忆
粒子群算法的构成要素-权重因子 权重因子:惯性因子 、学习因子
v i k d = w v i k d - 1 c 1 r 1 ( p b e s t i d x i k d 1 ) c 2 r 2 ( g b e s t d x i k d 1 )
Xik=Xik1+Vik1
V i =V i1,V i2,...,V iN X i= X i1,X i2,...,X iN
算法流程
1. Initial:
初始化粒子群体(群体规模为n),包括随机位置和速度。
2. Evaluation:
根据fitness function ,评价每个粒子的适应度。
3. Find the Pbest:
粒子群优化算法(PS0)
一种速度更快的粒子群优化算法

一种速度更快的粒子群优化算法
何庆元;韩传久;莫建文;张彤
【期刊名称】《桂林电子科技大学学报》
【年(卷),期】2007(027)001
【摘要】由于标准粒子群算法(SPSO)存在后期搜索效率太低的问题,提出了一种速度更快的粒子群优化算法(FPSO).FPSO保留了SPSO前期的全局搜索能力,但改变了SPSO算法后期的搜索策略,使其迭代次数随当前适应度值的变化而自适应改变,从而提高了SPSO算法后期的计算效率.通过实验对FPSO算法中适应度函数的设计进行了讨论,并分析了FPSO算法的应用前景.仿真结果表明,FPSO算法在单峰、多峰和带约束条件的测试函数中都有良好的效果.
【总页数】4页(P10-13)
【作者】何庆元;韩传久;莫建文;张彤
【作者单位】桂林电子科技大学,信息与通信学院,广西,桂林,541004;桂林电子科技大学,信息与通信学院,广西,桂林,541004;桂林电子科技大学,信息与通信学院,广西,桂林,541004;桂林电子科技大学,机电工程学院,广西,桂林,541004
【正文语种】中文
【中图分类】TN911.73
【相关文献】
1.一种速度不完全更新混沌粒子群优化算法 [J], 庞淑萍
2.一种速度改进型粒子群优化算法及应用 [J], 盖锋
3.基于粒子群优化算法的永磁同步电机H∞速度观测器 [J], 朱群;尹忠刚;张延庆;钟彦儒
4.基于迭代方程的无速度粒子群优化算法 [J], 林伟民
5.一种均衡各速度项系数的多目标粒子群优化算法 [J], 耿焕同;赵亚光;陈哲;李辉健
因版权原因,仅展示原文概要,查看原文内容请购买。
粒子群优化算法介绍

粒子群优化算法介绍
粒子群优化算法是一种基于群体智能的优化算法,它模拟了鸟群或鱼群等生物群体的行为,通过不断地迭代寻找最优解。
该算法最初由美国加州大学的Eberhart和Kennedy于1995年提出,目前已经被广泛应用于各种优化问题中。
粒子群优化算法的基本思想是将待优化问题转化为一个多维空间中的搜索问题,将每个解看作空间中的一个粒子,每个粒子的位置表示该解的参数值,速度表示该解的变化方向和速度。
在算法的每一次迭代中,每个粒子都会根据自身的历史最优解和群体最优解来更新自己的速度和位置,以期望找到更优的解。
具体来说,粒子群优化算法的实现过程如下:
1. 初始化粒子群,包括粒子的位置和速度等信息。
2. 计算每个粒子的适应度值,即待优化问题的目标函数值。
3. 更新每个粒子的速度和位置,包括考虑自身历史最优解和群体最优解的影响。
4. 判断是否满足停止条件,如果满足则输出最优解,否则返回第2步。
粒子群优化算法的优点在于其简单易懂、易于实现和收敛速度较快等特点。
同时,该算法还具有较好的全局搜索能力和鲁棒性,能够
应对复杂的非线性优化问题。
然而,粒子群优化算法也存在一些缺点,如易陷入局部最优解、对参数的选择较为敏感等问题。
因此,在实际应用中需要根据具体问题进行调整和优化。
粒子群优化算法是一种有效的优化算法,已经被广泛应用于各种领域,如机器学习、图像处理、控制系统等。
随着人工智能和大数据技术的不断发展,相信粒子群优化算法将会有更广泛的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(School of Computer Science and Engineering, Sichuan University, Chengdu 610065, China)
+ Corresponding author: Phn: +86-28-85466988, E-mail: scuhuwang@,
Hu W, Li ZS. A simpler and more effective particle swarm optimization algorithm. Journal of Software, 2007, 18(4):861−868. /1000-9825/18/861.htm Abstract: The basic particle swarm optimization (bPSO) has some demerits, such as relapsing into local
ISSN 1000-9825, CODEN RUXUEW Journal of Software, Vol.18, No.4, April 2007, pp.861−868 DOI: 10.1360/jos180861 © 2007 by Journal of Software. All rights reserved.
∗
Received 2005-11-23; Accepted 2006-04-03
862
Journal of Software 软件学报 Vol.18, No.4, April 2007
由 Eberhart 和 Kennedy 于 1995 年提出的粒子群优化算法(particle swarm optimization,简称 PSO)[1]是一种 全局优化进化算法,它源于对鸟群和鱼群群体觅食运动行为的模拟.PSO 作为一种并行优化算法,可以用于解决 大量非线性、不可微和多峰值的复杂问题优化 , 并已广泛用于科学和工程领域 ,如函数优化、神经网络训练、 模式分类和模糊系统控制等领域. 与遗传算法类似 , 粒子群优化算法同样基于群体与适应度这两个概念 . 粒子群的个体代表问题的一个可能 解.每个粒子具有位置与速度两个描述量,粒子位置坐标对应的目标函数值即可作为该粒子的适应度,PSO 算法 通过适应度来衡量粒子的优劣 .与遗传算法不同 ,PSO 不是通过遗传算子进化而是通过个体间协作与竞争来寻 找最优解.PSO 在进化初期,收敛速度快,运算简单,易于实现,没有遗传算法的编解码和选择、杂交、变异等复杂 运算.因此,粒子群优化算法一经提出,立刻引起演化计算领域学者们的广泛关注,并出现了大量的研究成果. 但是 , 粒子群优化算法根据全体粒子和自身粒子的搜索经验向着最优解的方向发展 , 在进化后期收敛速度 变慢,同时 ,算法收敛精度不高 ,尤其是对于高维多极值的复杂优化问题 .本文通过简化基本粒子群 (basic particle swarm optimization,简称 bPSO)的进化方程和添加极值扰动算子两个改进策略 ,提出了简化粒子群优化 (simple particle swarm optimization, 简称 sPSO) 算法、带极值扰动的粒子群优化 (extremum disturbed particle swarm optimization, 简称 tPSO) 算法和基于前二者的带极值扰动的简化粒子群优化 (extremum disturbed and simple particle swarm optimization,简称 tsPSO)算法.
1
基本粒子群算法及相关改进
bPSO 算法首先初始化一群随机粒子 , 然后通过迭代找到最优解 . 在每一次迭代中 , 粒子通过跟踪两个 “ 极
值”来更新自己 :个体极值和全局极值.粒子根据上述两个极值更新自己的速度与位置.在 D 维目标搜索空间中, 由种群数为 m 组成粒子群落,其中:第 i 个粒子在第 d 维的位置为 xid,其飞行速度为 vid,该粒子当前搜索到的最 优位置为 Pid,整个粒子群当前的最优位置为 Pgd. Kennedy 和 Eberhart[1]最早提出的 bPSO 算法公式如下:
t +1 t vid = vid + c1r1 ( pid − xid ) + c2 r2 ( p gd − xid )
(1) (2)
x
t +1 id
= x +v
t id
t &,2,…,D;r1 和 r2 是服从 U(0,1)分布的随机数;学习因子 c1 和 c2 为非负常数,通常取 c1=c2=2;
vid∈[−vmax,vmax],vmax 是由用户设定的常数.迭代终止条件为预设的最大迭代次数或(和)预定的最小适应度阈值.
因为 Pgd 为整个粒子群的最优位置,因此,上述算法也被称为全局版 PSO.也可以把第 i 个粒子的部分邻居们 搜索到的最优位置作为 Pgd,则相应算法称为局部版 PSO.全局版 PSO 收敛速度快,但有时会陷入局部最优;局部 版 PSO 收敛速度相对较慢,但相对不易陷入局部最优值. Shi[2]等人通过对式(1)添加动量惯性系数ω来提高跳出局部极值能力.修改后的方程如下:
extremum, slow convergence velocity and low convergence precision in the late evolutionary. Three algorithms, based on the simple evolutionary equations and the extrenum disturbed arithmetic operators, are proposed to overcome the demerits of the bPSO. The simple PSO (sPSO) discards the particle velocity and reduces the bPSO from the second order to the first order difference equation. The evolutionary process is only controlled by the variables of the particles position. The extremum disturbed PSO (tPSO) accelerates the particles to overstep the local extremum. The experiment results of some classic benchmark functions show that the sPSO improves extraordinarily the convergence velocity and precision in the evolutionary optimization, and the tPSO can effectively break away from the local extremum. tsPSO, combined the sPSO and tPSO, can obtain the splendiferous optimization results with smaller population size and evolution generations. The algorithms improve the practicality of the particle swarm optimization. Key words: 摘 要: evolutionary computation; swarm intelligence; particle swarm optimization; disturbed extremum
针对基本粒子群优化(basic particle swarm optimization,简称 bPSO)算法容易陷入局部极值、进化后期
的收敛速度慢和精度低等缺点 , 采用简化粒子群优化方程和添加极值扰动算子两种策略加以改进 , 提出了简化 粒子群优化 (simple particle swarm optimization,简称 sPSO)算法、带极值扰动粒子群优化(extremum disturbed particle swarm optimization,简称 tPSO)算法和基于二者的带极值扰动的简化粒子群优化(extremum disturbed and simple particle swarm optimization,简称 tsPSO)算法.sPSO 去掉了 PSO 进化方程的粒子速度项而使原来的二阶微 分方程简化为一阶微分方程 , 仅由粒子位置控制进化过程 , 避免了由粒子速度项引起的粒子发散而导致后期收 敛变慢和精度低问题 .tPSO 增加极值扰动算子可以加快粒子跳出局部极值点而继续优化 .对几个经典测试函数 进行实验的结果表明 ,sPSO 能够极大地提高收敛速度和精度 ;tPSO 能够有效摆脱局部极值点 ;以上两种策略相 结合,tsPSO 以更小的种群数和进化世代数获得了非常好的优化效果,从而使得 PSO 算法更加实用化. 关键词: 进化计算;群体智能;粒子群优化;极值扰动 文献标识码: A 中图法分类号: TP18
胡旺 等:一种更简化而高效的粒子群优化算法
863
随机变异操作带来的不稳定性.但是,上述研究都是对基本粒子群方程(1)、方程(2)或方程(3)、方程(4)的改进.
t +1 t vid = ωvid + c1r1 ( pid − xid ) + c2 r2 ( p gd − xid )
(3) (4)
Clerc 等人对式(2)添加控制速度的约束因子α:
[3]
t +1 t t +1 xid = xid + αvid
很多学者将式(3)、式(4)视为 bPSO 算法.文献[4]采用模糊规则动态修改 ω值,使算法自适应地调整全局系 数 ,兼顾了搜索效率和搜索精度 .但对许多复杂的非线性优化问题 , 试图通过自适应调整一个全局系数提高搜索 精度的余地是有限的 .Angeline[5]等人借鉴遗传算法思想提出杂交 PSO 算法概念 ,提高了算法的收敛速度和精 度 . 吕振肃 [6] 等人根据粒子群适应度方差作为全局最优化变异条件 ,提出自适应变异的粒子群优化算法 .Van de Bergh[7] 提出了协同 PSO, 使粒子更容易跳出局部极小点 , 达到较高收敛精度 ,但出现了明显的 “启动延迟现象 ”, 在迭代初期减缓了收敛速度.Ratnaweera 等人[8]在自组织算法的基础上给出了一种变异操作随时间变化的自适 应层次 PSO 算法(hierarchical particle swarm optimizer,简称 HPSO),以进一步提高搜索性能,并给出了适合变异 操作的自适应参数选择方式 . 但是 ,HPSO 算法消除了速度公式中的惯性部分 ,其发生变异的条件是微粒速度为 0,使微粒不能快速、有效地逃出局部极小点 .赫然等人 [9]结合生物界中物种发现生存密度过大时会自动分家迁 移的习性 , 给出了一种自适应逃逸微粒群算法 , 通过逃逸运动 , 使微粒能够有效地进行全局和局部搜索 , 减弱了
