差倍问题ppt课件
合集下载
三年级差倍问题 PPT

320+40=360 (本) 360÷120=3
答:。。。。。。。。
得出:如果两个数相同,一个数增加C,另外一个数减少 D,则两数变化之后得差等于C与D得和,也可以表示 为:两数差=C+D。
你学会了吗?
动一动脑筋?加油!
一根铜线长21米,一根铅线长16米,把两根金属 线剪去同样得长,使剩下得铜线长度恰好是铅线 长度得2倍,铜线、铅线各剩下多少米? 解: (1)两数差: 21-16=5(米)
狼得零花钱
我得钱多
羊得零花钱
狼的零花钱是2÷(2-1)=2(元 ) 羊的零花钱是2×2=4(元)
美羊羊蝴蝶结得个数是红太狼平底锅个数 得3倍,锅比蝴蝶结少12个。问美羊羊有多 少个蝴蝶结?
解:红太郎平底锅有12÷(3-1)=6(个)
美羊羊蝴蝶结有6×3=18(个)
商店里有一些足球和篮球, 足球得个数比篮球得3倍多2个,
爸爸得年龄
例5:当爸爸36岁时,懒羊羊8岁,今年爸爸得年龄是 懒羊羊得年龄得3倍,他俩今年各多少岁? 解: 随着爸爸年龄得增长,懒羊羊得年龄同时也在 增长,并且年龄差保持不变。 (1)年龄差:36-8=32(岁) (2)今年懒羊羊得年龄:32 ÷(3-1)=16(岁) (3)今年爸爸得年龄:16 ×3=48(岁) 验算:48÷16=3 答:。。。。。。。。。
大家有疑问的,可以询问和交流
12
学会举一反三!
例4:甲乙两筐得梨得数量相同,如果从甲筐取出10个梨,而 乙筐再放入5个梨,那么乙筐得梨得数量是甲筐得4倍,求甲 乙两筐原来各有多少梨?
假设甲乙原来得数量用“∆”表示
甲现在得数量: ∆-10
乙现在得数量: ∆+5
现在两数差( ∆+5)- (∆-10 )= ∆+5- ∆+10=5+10 =15
差倍问题 ppt课件

孰能生巧
1、商店里有数量相等的英语本和算术本,如果英语本再 添160本,那么英语本的本数就是算术本的本数的3倍。两 种本子原来各有多少本?
2、 小红和小明铅笔的支数相等,如果奶奶再给小红16支 铅笔,那么小红铅笔的支数就是小明的3倍。原来小红和 小明各有铅笔多少支?
பைடு நூலகம்
强化练习
1、小明、小红两人集邮,小明的邮票比小红多15张,小明的张数是小红 的4倍,小明集邮多少张,小红集邮多少张?
两个书架所存书的本书相等,如果从第一个书架里取出200本
书,那么第二个书架书的本数是第一个书架书的本书的3倍。问两
个书架原来各存书多少本? 找到“差”与“倍数”
取出200本
第一书架:
第二书架:
200本
差倍问题数量关系
差÷(倍数-1)=少数 少数×倍数=多数
小试牛刀
1、 两个仓库所存粮食的质量相等,如果从第一个仓库 里取出2400千克粮食,那么第二个仓库粮食的质量是第一 个仓库的7倍。问两个仓库原来各存粮食多少千克?
复习
① 10 ÷ 2 = 5 ↓ 除↓数 商↓
被除数
③
除2数 ×商 5 =被除1数0 ↓ ↓↓
② 10 ÷ 5 = 2
被↓除数 ↓商 ↓除数
① 被除数÷除数=商
10 ÷ 2 = 5 10是2的5倍!
10 ÷ 5 = 2 10是5的2倍!
题型3
被除数比除数大252,商是7,被除数、除数各 是多少?
1倍
梨:
?
18个
苹果:
?
从线段图上可以看出,苹果的个数比梨多了3-1=2倍,梨的2倍就
是18个,所以1倍就是18÷2=9个,也就是梨的个数。
那你会求苹果的个数吗?
趣味数学差倍问题PPT课件
分析:
原长 第一根
12米
1倍
14米
第二根
3倍
第9页/共12页
例六:有两根同样长的绳子,第一根截去12米,第二根接上14 米,这时第二根长度是第一根长度的3倍,两根绳子原来各长多 少米?
答:两根绳子原来各长25米。
第10页/共12页
谢谢大家
第11页/共12页
感谢您的观看!
第12页/共12页
分析: 剩下 300千克
1500千克
剩下
1800千克
3倍
第7页/共12页
例五:菜站运来的西红柿是黄瓜的3倍,卖出西红柿1800千克,黄瓜 30千克后,剩下的两种蔬菜的重量相等,菜站运来的西红柿和黄瓜是 多少千克?
答:菜站运来西红柿2250千克,黄瓜750千克。
第8页/共12页
例六:有两根同样长的绳子,第一根截去12米,第二根接上14 米,这时第二根长度是第一根长度的3倍,两根绳子原来各长多 少米?
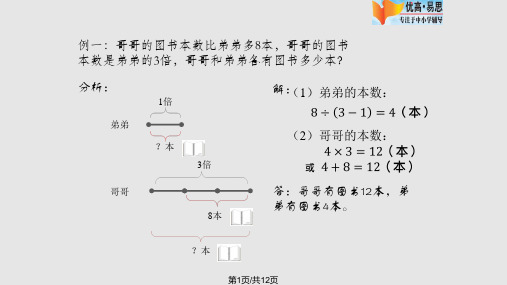
例一:哥哥的图书本数比弟弟多8本,哥哥的图书 本数是弟弟的3倍,哥哥和弟弟各有图书多少本?
分析:
1倍
解:(1)弟弟的本数:
弟弟
?本 3倍
(2)哥哥的本数:
哥哥
答:哥哥有图书12本,弟
弟有图书4本。
8本
?本
第1页/共12页
差倍问题的特点是:已知两个数的差及它们之间 的倍数关系,求这两个数。 解答差倍问题的基本方法是:
例三:有父子二人,父亲48岁,儿子20岁,问几年以后, 父亲的年龄正好是儿子的2倍?
第4页/共12页
例四:甲、乙两校教师的人数相等,由于工作需要,从甲校调30人到乙 校去,这时乙校教师人数正好是甲校教师人数的3倍,求甲、乙两校原 有教师各多少?
原长 第一根
12米
1倍
14米
第二根
3倍
第9页/共12页
例六:有两根同样长的绳子,第一根截去12米,第二根接上14 米,这时第二根长度是第一根长度的3倍,两根绳子原来各长多 少米?
答:两根绳子原来各长25米。
第10页/共12页
谢谢大家
第11页/共12页
感谢您的观看!
第12页/共12页
分析: 剩下 300千克
1500千克
剩下
1800千克
3倍
第7页/共12页
例五:菜站运来的西红柿是黄瓜的3倍,卖出西红柿1800千克,黄瓜 30千克后,剩下的两种蔬菜的重量相等,菜站运来的西红柿和黄瓜是 多少千克?
答:菜站运来西红柿2250千克,黄瓜750千克。
第8页/共12页
例六:有两根同样长的绳子,第一根截去12米,第二根接上14 米,这时第二根长度是第一根长度的3倍,两根绳子原来各长多 少米?
例一:哥哥的图书本数比弟弟多8本,哥哥的图书 本数是弟弟的3倍,哥哥和弟弟各有图书多少本?
分析:
1倍
解:(1)弟弟的本数:
弟弟
?本 3倍
(2)哥哥的本数:
哥哥
答:哥哥有图书12本,弟
弟有图书4本。
8本
?本
第1页/共12页
差倍问题的特点是:已知两个数的差及它们之间 的倍数关系,求这两个数。 解答差倍问题的基本方法是:
例三:有父子二人,父亲48岁,儿子20岁,问几年以后, 父亲的年龄正好是儿子的2倍?
第4页/共12页
例四:甲、乙两校教师的人数相等,由于工作需要,从甲校调30人到乙 校去,这时乙校教师人数正好是甲校教师人数的3倍,求甲、乙两校原 有教师各多少?
苏教版四年级数学下册差倍问题课件

【例题2】小红比小强多做 180 个零件,小红做的是小强的 4 倍多 9 个, 两人各做多少个零件?
差:180-9=171(个) 小强:171÷(4-1)=57(个) 小红:57+180=237(个)
答:小强做了57个,小红做了237个。
【练习2】学校买来的足球比篮球多 18 个,足球的个数比篮球的 2 倍少 4 个,学校买来篮球和足球多少个?
【例题5】兄弟两人各有存款若干元,若哥哥给弟弟 45 元,二人的钱数就 同样多;若弟弟给哥哥 45 元,则哥哥的钱正好是弟弟的 2 倍。兄弟两人 各有存款多少元?
差:45×2+45×2=180(元) 弟弟:180÷(2-1)=180(元)
哥哥:180×2=360(元) 弟弟:180+45=225(元) 哥哥:360-45=315(元)
玉米:63÷(8-1)=9(公顷) 花生:8×9=72(公顷)
答:花生种72公顷,玉米种9公顷。
【练习1】学校合唱组的女同学人数是男同学的4倍,女同学比男同学多42 人,合唱组各有男、女同学多少人?
男同学:42÷(4-1)=14(人) 女同学:14+42=56(人)
答:合唱组有男同学14人,女同学56人。
【练习4】商店运来一批白糖和红糖,红糖的重量是白糖的3倍,卖出红糖 380千克,白糖110千克后,红糖和白糖重量相等,商店原有白糖和红糖各 多少千克?
差:380-110=270(千克) 白糖:270÷(3-1)=135(千克)
红糖:135×3=405(千克)
答:商店原有白糖135千克,红糖405千克。
【例题4】甲、乙两个仓库存的水泥同样多,从甲仓运出 65 吨,从乙仓运 出 9 吨水泥后,乙仓的水泥是甲仓的 3 倍。两仓本来共存水泥多少吨?
三年级 7、差倍问题.ppt

梨:18÷(3-1)=9(个) 苹果:9×3=27(个)
2、妈妈的年龄比小刚大24岁,今年妈妈的年龄正好是小刚的3倍,妈妈和小刚 今年各多少岁?
小刚:24÷(3-1)=12(岁) 妈妈:12×3=36(岁)
例2 被除数比除数大252,商是7,被除数、除数各是多少? 我们可以根据题意画出线段图,分 析数量关系。
1、甲、乙两水桶,如果向甲桶中倒入12千克水,则两桶中的水就一样多;如 果向乙桶中倒入8千克水,则乙桶中的水就是甲桶的5倍。问:甲、乙两桶中原 来各有多少千克水?
甲:(12+8)÷(5-1)=5(千克) 乙:5×5-8=17(千克)
2、甲、乙两个数,如果甲数加上50,就等于乙数;如果乙数加上350就等于 甲数的3倍。甲、乙两数各是多少?
例3 菜场运来的萝卜比青菜多1200千克,萝卜的重量比青菜的3倍多 200千克。萝卜、青菜各有多少千克?
列式计算如下:
青菜有多少千克?
萝卜有多少千克?
(1200-200)÷(3-1)=500千克 500+1200=1700(千克)
或 500×3+200=1700(千克)
答:萝卜有1700千克,青菜有500千克。
(46-19)÷(4-1)=9(米) 9+46=55(米)
2、两筐质量相等的梨,甲筐取出18千克,乙筐取出6千克,这时乙筐的质量 恰好是甲筐质量的3倍。问:两筐原来各有梨多少千克?
(18-6)÷(3-1)=6(千克) 6+18=24(千克)
思维拓展
例7 甲的钱数是乙的钱数的3倍,甲买一套180元的《科技书》,乙买一 套30元的《故事大王》后,两个人余下的钱一样多。甲原来有多少钱?
(180-30)÷(3-1)=75(元) 75×3=225(元)
2、妈妈的年龄比小刚大24岁,今年妈妈的年龄正好是小刚的3倍,妈妈和小刚 今年各多少岁?
小刚:24÷(3-1)=12(岁) 妈妈:12×3=36(岁)
例2 被除数比除数大252,商是7,被除数、除数各是多少? 我们可以根据题意画出线段图,分 析数量关系。
1、甲、乙两水桶,如果向甲桶中倒入12千克水,则两桶中的水就一样多;如 果向乙桶中倒入8千克水,则乙桶中的水就是甲桶的5倍。问:甲、乙两桶中原 来各有多少千克水?
甲:(12+8)÷(5-1)=5(千克) 乙:5×5-8=17(千克)
2、甲、乙两个数,如果甲数加上50,就等于乙数;如果乙数加上350就等于 甲数的3倍。甲、乙两数各是多少?
例3 菜场运来的萝卜比青菜多1200千克,萝卜的重量比青菜的3倍多 200千克。萝卜、青菜各有多少千克?
列式计算如下:
青菜有多少千克?
萝卜有多少千克?
(1200-200)÷(3-1)=500千克 500+1200=1700(千克)
或 500×3+200=1700(千克)
答:萝卜有1700千克,青菜有500千克。
(46-19)÷(4-1)=9(米) 9+46=55(米)
2、两筐质量相等的梨,甲筐取出18千克,乙筐取出6千克,这时乙筐的质量 恰好是甲筐质量的3倍。问:两筐原来各有梨多少千克?
(18-6)÷(3-1)=6(千克) 6+18=24(千克)
思维拓展
例7 甲的钱数是乙的钱数的3倍,甲买一套180元的《科技书》,乙买一 套30元的《故事大王》后,两个人余下的钱一样多。甲原来有多少钱?
(180-30)÷(3-1)=75(元) 75×3=225(元)
三年级差倍问题(共10张PPT)

答:小丽有科技书8本,故事书24本。
练习1 某养鸡专业户养的母鸡比公鸡多246只,
养的母鸡是公鸡的3倍。这个专业户养 的公鸡和母鸡各有多少只?
小结: 差倍问题求法
这样问题,该怎么求呢?
步骤: 同学们参加课外兴趣小组,参加书法组的同学比参加计算机组的少26人,计算机组的人数比书法组的3倍少14人。
〔1〕找出两个数的差值;
已知:两个数的差,两个数的倍数关系,求这两个数?
〔2〕倍数差:3-1=2倍
这样的问题,该怎么求呢?
去年和今年各植树多少棵?
例题2
差值是多少呢?
• 同学们参加课外兴趣小组,参加书法 组的同学比参加计算机组的少26人, 计算机组的人数比书法组的3倍少14人。 参加这两个兴趣小组的人各有多少人?
同学们参加课外兴趣小组,参加书法组的同学比参加计算机组的少26人,计算机组的人数比书法组的3倍少14人。 这样的问题,该怎么求呢? 去年和今年各植树多少棵? 参加这两个兴趣小组的人各有多少人?
解:〔1〕找差值:16本
〔2〕倍数差:3-1=2倍
〔3〕科技书: 16÷2=8〔本〕
〔4〕故事书:8×3=24〔本〕
练习2
• 今年比去年多植树560棵,今年植树 的棵数比去年的3倍少40棵。去年和 今年各植树多少棵?
•
试一试吧!
例题3
调整后,甲比乙多多少呢?
• 甲、乙两人各存款假设干元,甲的存款 是乙的3倍,如果甲取出240元,乙取出 40元,甲、乙两人的存款正好相等。甲、 乙两人原来各存款多少元?
练习3
• 甲、乙两个仓库各存粮食假设干吨, 甲仓库是乙仓库的3倍,如果从甲仓 库取出100吨,从乙仓库取出20吨, 甲、乙剩下的粮食就一样多。甲、乙 原来各存粮多少吨?
练习1 某养鸡专业户养的母鸡比公鸡多246只,
养的母鸡是公鸡的3倍。这个专业户养 的公鸡和母鸡各有多少只?
小结: 差倍问题求法
这样问题,该怎么求呢?
步骤: 同学们参加课外兴趣小组,参加书法组的同学比参加计算机组的少26人,计算机组的人数比书法组的3倍少14人。
〔1〕找出两个数的差值;
已知:两个数的差,两个数的倍数关系,求这两个数?
〔2〕倍数差:3-1=2倍
这样的问题,该怎么求呢?
去年和今年各植树多少棵?
例题2
差值是多少呢?
• 同学们参加课外兴趣小组,参加书法 组的同学比参加计算机组的少26人, 计算机组的人数比书法组的3倍少14人。 参加这两个兴趣小组的人各有多少人?
同学们参加课外兴趣小组,参加书法组的同学比参加计算机组的少26人,计算机组的人数比书法组的3倍少14人。 这样的问题,该怎么求呢? 去年和今年各植树多少棵? 参加这两个兴趣小组的人各有多少人?
解:〔1〕找差值:16本
〔2〕倍数差:3-1=2倍
〔3〕科技书: 16÷2=8〔本〕
〔4〕故事书:8×3=24〔本〕
练习2
• 今年比去年多植树560棵,今年植树 的棵数比去年的3倍少40棵。去年和 今年各植树多少棵?
•
试一试吧!
例题3
调整后,甲比乙多多少呢?
• 甲、乙两人各存款假设干元,甲的存款 是乙的3倍,如果甲取出240元,乙取出 40元,甲、乙两人的存款正好相等。甲、 乙两人原来各存款多少元?
练习3
• 甲、乙两个仓库各存粮食假设干吨, 甲仓库是乙仓库的3倍,如果从甲仓 库取出100吨,从乙仓库取出20吨, 甲、乙剩下的粮食就一样多。甲、乙 原来各存粮多少吨?
人教版数学六年级上册3.7分数除法之和倍、差倍问题课件(28张PPT)

上半场得分+下半场得分=全场得分
下半场看成“1” 解:设下半场得x分,则上半场得2x分。
2x+x=42
看一看和
书上的方
法一样吗?
3x=42
知道下半场得分,
可以表示出上半场得分。
x=14
下半场:42-14=28(分)
答:上半场得28分,下半场得14分。
养成检验的好习惯
第四步 我的收获
这节课你有什么收获?
( 7x )元,列方程为(
)+(
当堂检测
2.按要求解决数是男生人数的
,
5
男生和女生各有多少人?
(1)写出等量关系式:
( 男生人数 )+( 女生人数 )= ( 总人数
)
当堂检测
(2)根据上面的关系式列方程解答:
解:设男生有
3
x x 1600
5
x
3
x 人。
上半场得分=下半场得分×2
因上下半场
得分都是未
知数,可以
使用方程解
答。
上半场得分+下半场得分=全场得分
上半场看成“1” 解:设上半场得了x分,则下半场
知道上半场得分,
得了 x分。
可以表示出下半场得分。
x+ x=42
x=42
下半场: 28× =14(分)
x=28
答:上半场得28分,下半场得14分。
有两个量都是未知的,先把谁看作单位“1”
都可以,设其中一个量为未知数x,用这个量表示
另一个量,然后找出等量关系,列方程解答出一
个量,再解答第二个量。
第五步 小试牛刀
某电视机厂去年全年生产电视机108万台,其中上半年产量是下半年
《和倍和差倍问题》ppt课件

掌握和倍和差倍问题 的基本解题思路和方 法。
提高数学逻辑思维能 力和分析问题能力。
学会运用代数、几何 等知识解决实际问题。
02
CHAPTER
和倍问题
问题定义
总结词
和倍问题是指已知两个数的和以及它们的倍数关系,求这两个数分别是多少的 问题。
详细描述
这类问题通常涉及到两个未知数,它们的和以及它们的倍数关系已知。例如, 已知两个数的和是10,其中一个数是另一个数的2倍,求这两个数是多少。
解题方法
总结词
解题方法包括利用代数方程求解和利用算术方法求解两种。
详细描述
代数方程求解是通过设立代数方程来求解未知数。例如,设两个未知数分别为x和y,根据题目条件建立方程组, 然后解方程组得到未知数的值。算术方法求解则是通过逻辑推理和计算来求解未知数。例如,利用已知的倍数关 系和和的关系,通过计算得出未知数的值。
总结混合问题的常见解题技巧,如先分别 设立和倍和差倍的方程,再联立求解等, 帮助学生提高解题效率。
06
CHAPTER
总结与回顾
本课重点回顾
定义和倍、差倍问题的概念
和倍问题是指两个数的和与它们的倍数之间的关系问题, 差倍问题是指两个数的差与它们的倍数之间的关系问题。
解题思路和方法
解决和倍问题需要先求出两个数的和,再根据倍数关系求 出未知数;解决差倍问题需要先求出两个数的差,再根据 倍数关系求出未知数。
解法二:算术法
根据题目条件,两个 数的差是10,和是50, 可以列出方程:(x - y) = 10 和 (x + y) = 50。 解方程得到 x = 30, y = 20。
04
CHAPTER
混合问题
问题定义
问题定义
提高数学逻辑思维能 力和分析问题能力。
学会运用代数、几何 等知识解决实际问题。
02
CHAPTER
和倍问题
问题定义
总结词
和倍问题是指已知两个数的和以及它们的倍数关系,求这两个数分别是多少的 问题。
详细描述
这类问题通常涉及到两个未知数,它们的和以及它们的倍数关系已知。例如, 已知两个数的和是10,其中一个数是另一个数的2倍,求这两个数是多少。
解题方法
总结词
解题方法包括利用代数方程求解和利用算术方法求解两种。
详细描述
代数方程求解是通过设立代数方程来求解未知数。例如,设两个未知数分别为x和y,根据题目条件建立方程组, 然后解方程组得到未知数的值。算术方法求解则是通过逻辑推理和计算来求解未知数。例如,利用已知的倍数关 系和和的关系,通过计算得出未知数的值。
总结混合问题的常见解题技巧,如先分别 设立和倍和差倍的方程,再联立求解等, 帮助学生提高解题效率。
06
CHAPTER
总结与回顾
本课重点回顾
定义和倍、差倍问题的概念
和倍问题是指两个数的和与它们的倍数之间的关系问题, 差倍问题是指两个数的差与它们的倍数之间的关系问题。
解题思路和方法
解决和倍问题需要先求出两个数的和,再根据倍数关系求 出未知数;解决差倍问题需要先求出两个数的差,再根据 倍数关系求出未知数。
解法二:算术法
根据题目条件,两个 数的差是10,和是50, 可以列出方程:(x - y) = 10 和 (x + y) = 50。 解方程得到 x = 30, y = 20。
04
CHAPTER
混合问题
问题定义
问题定义
差 倍 问 题PPT课件

.
6
学校里白粉笔的盒数是彩色粉笔的4倍,如果 白粉笔和彩色粉笔各购进12盒,那么白粉笔的 盒数是彩色粉笔的3倍。原来白粉笔和彩色粉 笔各多少盒?
.
7
练习:
1、学校今年参加科技兴趣小组的人数比去年多41人, 今年的人数比去年的3倍少35人。今年有多少人参加?
2、三个小朋友们折纸飞机,小晶比小亮多折12架,小 强比小亮少折8架,小晶折的是小强的3倍。三个人各 折纸飞机多少架?
.
4
育红小学买了一些足球、排球和篮球,已知足 球比排球多7个,排球比篮球多11个,足球的 个数是篮球的3倍。足球、排球和篮球各买了 桶中倒入8千 克,则两桶色拉油就一样重;如果向乙桶中倒 入12千克,则乙桶的色拉油就是甲桶的5倍。 求甲、乙两桶原来各有色拉油多少千克?
.
8
3、小明的铅笔支数是小华的3倍,如果小明给小华5支, 小明还比小华多2支。两人原来各有多少支铅笔?
4、三(1)班同学参加英语比赛,如果男生少去1人, 男女参赛人数相等;如果女生少去1人,男生参赛人 数是女生的2倍。问三(1)班参加英语比赛的男、女 生各多少人?
.
9
差倍问题
.
1
已知两个数的差与它们之间的倍数关系,求这 两个数各是多少的应用题,叫做差倍问题。
.
2
仓库里存放着大米和面粉两种粮食,面粉比大 米多3900千克,面粉的千克数比大米的2倍还 多100千克。仓库大米和面粉各有多少千克?
差÷(倍数-1)=小数
.
3
有大小两个书架,大书架上书的本数是小书架 上的4倍。如果从大书架上取出140本放到小 书架上,那么大书架上的书还比小书架上的书 多20本。大、小书架原来各有多少本书?
列一元一次方程解决和差倍分问题PPT课件

方法归纳
(1)和差关系:通过关键词语“多、少、和、差、不 足、剩余……”来体现. (2)倍、分关系:通过关键词语“是几倍,增加几倍, 增加到几倍,增加百分之几,增长率……”来体现. (3)比例问题: 全部数量=各种成分的数量之和, 此类题目通常把一份设为x. 解题的关键是弄清“倍、分”关系及“和、差”关系.
练一练
某足球比赛的计分规则为胜一场得3分,平一场得1分, 负一场得0分.一个队踢了14场球,负了5场,共得19分, 问这个队胜了几场? [解析] 本题的等量关系:胜场得分+平场得分=19. 若设这个队胜了x场,则依题意可用x表示出打平的场 数,这样就可以列出一元一次方程. 解:设这个队胜了x场,则平了(14-5-x)场,即(9-x)场, 依题意,得3x+1×(9-x)=19,
x+(2x+1)=19. 其中大拖拉机耕地的面积比小拖拉机耕地面积的2倍还多1公顷,这两台拖拉机一天各耕地多少公顷?
(1)和差关系:通过关键词语“多、少、和、差、不足、剩余……”来体现.
解得 若设这个队胜了x场,则依题意可用x表示出打平的场数,这样就可以列出一元一次方程.
解方程,得 x=5.
A.5(x-2)+3x=14
分析:本问题中涉及的等量关系有: 椅子数+凳子数=16, 椅子腿数+凳子腿数=60.
解:设有x 张椅子,则有(16-x)条凳子. 根据题意,得4x+ 3(16-x)=60 . 解得 x = 12 . 凳子数为16-12=4(条). 答:有12张椅子,4条凳子.
归纳
找到两个总量,揭示等量关系,设其中一个为未知量, 用一个等量关系转换另一个未知量,利用余下的等量关 系列方程.
各分量之和=总量.
例3 甲、乙、丙三队合修一条公路,计划出280人,如
最新02四年级数学思维---差倍问题ppt课件

热下注,壅遏膀胱,气化失司,气机不畅,亦可促发本病。
肾气亏虚 老年肾虚体弱,或病程较久,反复发作,加重肾虚,进一步耗伤肾阴,阴
肾,又使肾气受损,二者互为影响,互为因果。
病因病机
病机 膀胱湿热 膀胱系州都之官,气化则能出。湿热毒邪,客于膀胱,热邪下注,膀胱气
化不利,气化失司,水道不利,遂发为淋。
湿热中阻 饮食不节,辛热伤胃,胃伤及脾,脾气不足,水湿运化失司,湿热之邪
滞于中焦,湿热下注膀胱,诸症由此而生。
肝胆湿热 肝气失于疏泄,气郁化火,气火郁于下焦,肝脉绕阴器,过少腹,肝胆湿
临床表现复杂多样,症状繁多。
临床表现
无症状型尿路感染
尿路感染可无临床症状,仅表现为无症状性菌尿,这在有原发病(尤其是 糖尿病和脑血管病),泌尿生殖道生理或结构异常及留置导尿的病人特别 多见。
西医诊断标准
尿路感染的诊断: ①正规清洁中段尿(要求尿停留在膀胱中4~6小时以上)细菌定
量培养,菌落数≥105/ml,2天内应重复培养1次。 ②参考清洁离心中段尿沉渣检查,白细胞>10/HP.或有尿路感染
02四年级数学思维---差倍问 题
差倍问题
差倍问题就是已知两个数的差和它们的倍数关系, 求这两个数。
解答差倍问题的关键是找出两个数的差,以及与差
相对应助的倍自数己差,分从析而题示出目一的倍数数,量再求关出系其。它的数。
【方法】:解题时,我们一般也是先借助线段图帮助 自己分析题目的数量关系。
差倍问题
病因病机
病因 感受湿热 感受湿热疫毒之气是本病的主要原因,外阴不洁,秽浊之邪乘虚而入,湿
热毒邪客于膀胱,湿热熏蒸而发病。
饮食不节 过食辛辣肥甘之品,或嗜酒太过,脾胃运化功能失常,湿浊内生,蕴久化热,
肾气亏虚 老年肾虚体弱,或病程较久,反复发作,加重肾虚,进一步耗伤肾阴,阴
肾,又使肾气受损,二者互为影响,互为因果。
病因病机
病机 膀胱湿热 膀胱系州都之官,气化则能出。湿热毒邪,客于膀胱,热邪下注,膀胱气
化不利,气化失司,水道不利,遂发为淋。
湿热中阻 饮食不节,辛热伤胃,胃伤及脾,脾气不足,水湿运化失司,湿热之邪
滞于中焦,湿热下注膀胱,诸症由此而生。
肝胆湿热 肝气失于疏泄,气郁化火,气火郁于下焦,肝脉绕阴器,过少腹,肝胆湿
临床表现复杂多样,症状繁多。
临床表现
无症状型尿路感染
尿路感染可无临床症状,仅表现为无症状性菌尿,这在有原发病(尤其是 糖尿病和脑血管病),泌尿生殖道生理或结构异常及留置导尿的病人特别 多见。
西医诊断标准
尿路感染的诊断: ①正规清洁中段尿(要求尿停留在膀胱中4~6小时以上)细菌定
量培养,菌落数≥105/ml,2天内应重复培养1次。 ②参考清洁离心中段尿沉渣检查,白细胞>10/HP.或有尿路感染
02四年级数学思维---差倍问 题
差倍问题
差倍问题就是已知两个数的差和它们的倍数关系, 求这两个数。
解答差倍问题的关键是找出两个数的差,以及与差
相对应助的倍自数己差,分从析而题示出目一的倍数数,量再求关出系其。它的数。
【方法】:解题时,我们一般也是先借助线段图帮助 自己分析题目的数量关系。
差倍问题
病因病机
病因 感受湿热 感受湿热疫毒之气是本病的主要原因,外阴不洁,秽浊之邪乘虚而入,湿
热毒邪客于膀胱,湿热熏蒸而发病。
饮食不节 过食辛辣肥甘之品,或嗜酒太过,脾胃运化功能失常,湿浊内生,蕴久化热,
四年级下册数学课件-和差 和倍 差倍问题 全国通用(共47 张ppt)

两数的差没有直接告诉。关键 是通过线段图找出两数之差, 第一筐
问题就迎刃而解了。 解:根据题意画出线段图
第二筐
7千克
7千克
80千克
(1)原来两筐相差质量: 7×2+2=16(千克)
(2)第一筐西瓜质量: (80+16)÷2=48(千克)
(3)第二筐西瓜的质量: 80-48=32(千克)
(4)综合算式: (80+7×2+2) ÷2=48(千克)(第一筐) 80-48=32(千克)
举一反三
张宁做加法,把一个加数的个位数字“0”漏掉了,结果得数比 正确答案少了45。这个加数应该是多少?
45÷(10-1)=5 5×10=50
答:这个加数是50。
举一反三
甲桶里装的油重量是乙桶里油的5倍,如果从甲桶倒12千克油 到乙桶,两桶就一样重了。那么甲、乙两桶原来分别有多少 千克油?
(12+12)÷(5-1)=6(千克) 6×5=30(千克)
解:甲筐:(140+10×2)÷2=80个
乙筐:140-80=60个
解决和差问题的思路
已知大小两个数的和及他们的差,求这两个数各是多少,这类问题我们叫做 “和差问题”。掌握了和差问题的特征和规律,我们解答起来就很方便了。
解答和差问题就是求一大一小两个数,通常用假设法,同时结合线段图进 行分析。可以假设小数增加到与大数同样多,先求大数,再求小数;也可以假 设大数减少到与小数同样多,先求小数再求大数。
3、商店有铅笔、钢笔、圆珠笔共560支,圆珠笔的 支数是钢笔的三倍,铅笔的支数是圆珠笔的支数同 样多。铅笔、钢笔、圆珠笔各有多少支?
例题3
三个筑路队共筑路1360米,甲筑队的路程是乙筑队的2倍,乙队比丙 队多筑了240米。三个队各筑了多少米?
三年级下册数学人教版奥数差倍问题(课件)

差:252差对应的倍数:7-1
7-1=6除数:252÷6=42被除数:42X7=294答:被除数是294,除数是42
课堂练习
3、被除数比商大144,除数是7,被除数和商各是多少?
例4:两筐苹果重量相等,甲筐卖出去7千克,乙筐卖出去19千克后,甲筐剩下的苹果重量是乙筐的3倍。两筐苹果各是多少千克?
例8:两块同样长的布,第一块用去31米,第二块用去19米,结果所余米数第二块是第一块的4倍,两块布本来各长______米?
第一块:
第二块:
31
19
31-19=12对应的倍数:4-1=3(一倍数):12÷3=4米甲:4+31=45米答:甲乙本来各长45米
3倍
8、两筐千克数相同的苹果,乙筐卖出7千克,甲筐卖出19千克后,乙筐剩余的苹果是甲筐的3倍。两筐苹果本来各有多少千克?
课堂练习
例10:两个书架所存书的本数相等,如果从第一个书架取出200本数,而第二个书架再放入40本书,那么第二个书架的本数是第一个书架的3倍。问两个书架本来各存书多少本?
第一个:
第二个:
200
40
200+40=240本对应的倍数:3-1=2(一倍数):240÷2=120本第一个书架:120+200=320本答:两个书架本来各存书320本
乙筐:
甲框:
60+60
60
60
差:60+60=120差对应的倍数:3-1=2
3-1=260+60=120乙筐:120÷2=60(千克)甲筐:60X3=180(千克)答:甲筐苹果180千克,乙筐苹果60千克
解答差倍问题与解答和倍问题类似,要先找出差所对应的倍数,求出1倍数。
用关系式可以这样表示:两数差÷(倍数-1)=1倍数
差倍问题 ppt课件

差倍问题
想一想:兰花比月季多几倍? 兰花比月季多的12朵就是月季的几倍?
差倍问题
从例1可以发现,解答差倍问题的关键是 ,运用线段图帮助我们分析,找出两个 数的差以及与它相对应的倍数数,从而 先求出 1倍数,再求出其他数。 差倍问题的基本数量关系式是: 两数差÷(倍数-1)=1倍数(小数) 1倍数×倍数=几倍数(大数) 从上面可以看出,要解答差倍问题必须 要知道两个数的“差”及它们之间的“倍数
差倍问题
差倍问题
精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
• 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭
• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
• “太阳当空照,花儿对我笑,小鸟说早早早……”
例2、光明小学有学生760人,其中男生比女生的3倍 少40人,男、女生各有多少人?
例3、果园里有桃树、梨树、苹果树共552棵.桃树比 梨树的2倍多苹果树各有多少棵?
差倍问题
已知大小两个数的差,还知道大数是小 数的几倍,求大小两个数各是多少的应 用题,叫做差倍问题。差倍问题也是一 种典型的应用题。解答差倍问题与解答 和倍问题的方法类似,我们仍然用画线 段图的方法来帮助分析、思考。我们可 以通过分析数量关系,发现条件和问题 之间的内在联系,找出解题的规律,正 确列式解答。
3、舞蹈队里女生人数是男生人数的3倍。女 生比男生多18人,舞蹈队有男生和女生各 多少人?
例2、甲、乙两个粮仓各存粮若干吨,甲仓存粮的吨 数是乙的3倍。如果甲仓中取出260吨,乙仓中取 出60吨,则甲、乙两个粮仓存粮的吨数相等。甲、 乙两个粮仓各存粮多少吨?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
练习
甲仓存粮吨数是乙仓的3倍,如果甲仓中取出80 吨,乙仓中运进80吨,甲、乙两个粮仓存粮吨 数正好相等。甲、乙两个粮仓各存粮多少吨?
1多3筐。水果店运来的苹果和香蕉 各多少筐?
想一想:如果苹果减少3筐,那么苹果比香蕉多多少筐? 苹果的筐数比香蕉多多少倍? (1)如果苹果减少3筐,那么苹果比香蕉多多少筐? (2)此时苹果的筐数比香蕉多多少倍? (3)运来香蕉多少筐? (4)运来苹果多少筐?
3、舞蹈队里女生人数是男生人数的3倍。女 生比男生多18人,舞蹈队有男生和女生各 多少人?
8
例2、甲、乙两个粮仓各存粮若干吨,甲仓存粮的吨 数是乙的3倍。如果甲仓中取出260吨,乙仓中取 出60吨,则甲、乙两个粮仓存粮的吨数相等。甲、 乙两个粮仓各存粮多少吨?
想一想:甲仓存粮的吨数比乙仓多多 少吨?甲仓存粮的吨数比乙仓多多少 倍? (1)甲仓比乙仓多存粮多少吨? (2)甲仓比乙仓多存粮多少倍? (3)乙仓存粮多少吨? (4)甲仓存粮多少吨?
5
例1、小红买的兰花比月季多12朵,已知兰花的 朵数是月季的3倍。小红买了兰花和月季各多少
朵?
想一想:兰花比月季多几倍? 兰花比月季多的12朵就是月季的几倍?
6
总结
从例1可以发现,解答差倍问题的关键是, 运用线段图帮助我们分析,找出两个数 的差以及与它相对应的倍数数,从而先 求出 1倍数,再求出其他数。 差倍问题的基本数量关系式是: 两数差÷(倍数-1)=1倍数(小数) 1倍数×倍数=几倍数(大数) 从上面可以看出,要解答差倍问题必须 要知道两个数的“差”及它们之间的 7
4
知识点
已知大小两个数的差,还知道大数是小 数的几倍,求大小两个数各是多少的应 用题,叫做差倍问题。差倍问题也是一 种典型的应用题。解答差倍问题与解答 和倍问题的方法类似,我们仍然用画线 段图的方法来帮助分析、思考。我们可 以通过分析数量关系,发现条件和问题 之间的内在联系,找出解题的规律,正 确列式解答。
差倍问题
1
例1 甲班和乙班共有图书160本.甲班的图书本数是乙 班的3倍,甲班和乙班各有图书多少本?
2
例2、光明小学有学生760人,其中男生比女生的3倍 少40人,男、女生各有多少人?
3
例3、果园里有桃树、梨树、苹果树共552棵.桃树比 梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、 梨树和苹果树各有多少棵?
11
练习
甲仓存粮吨数是乙仓的3倍,如果甲仓中取出80 吨,乙仓中运进80吨,甲、乙两个粮仓存粮吨 数正好相等。甲、乙两个粮仓各存粮多少吨?
1多3筐。水果店运来的苹果和香蕉 各多少筐?
想一想:如果苹果减少3筐,那么苹果比香蕉多多少筐? 苹果的筐数比香蕉多多少倍? (1)如果苹果减少3筐,那么苹果比香蕉多多少筐? (2)此时苹果的筐数比香蕉多多少倍? (3)运来香蕉多少筐? (4)运来苹果多少筐?
3、舞蹈队里女生人数是男生人数的3倍。女 生比男生多18人,舞蹈队有男生和女生各 多少人?
8
例2、甲、乙两个粮仓各存粮若干吨,甲仓存粮的吨 数是乙的3倍。如果甲仓中取出260吨,乙仓中取 出60吨,则甲、乙两个粮仓存粮的吨数相等。甲、 乙两个粮仓各存粮多少吨?
想一想:甲仓存粮的吨数比乙仓多多 少吨?甲仓存粮的吨数比乙仓多多少 倍? (1)甲仓比乙仓多存粮多少吨? (2)甲仓比乙仓多存粮多少倍? (3)乙仓存粮多少吨? (4)甲仓存粮多少吨?
5
例1、小红买的兰花比月季多12朵,已知兰花的 朵数是月季的3倍。小红买了兰花和月季各多少
朵?
想一想:兰花比月季多几倍? 兰花比月季多的12朵就是月季的几倍?
6
总结
从例1可以发现,解答差倍问题的关键是, 运用线段图帮助我们分析,找出两个数 的差以及与它相对应的倍数数,从而先 求出 1倍数,再求出其他数。 差倍问题的基本数量关系式是: 两数差÷(倍数-1)=1倍数(小数) 1倍数×倍数=几倍数(大数) 从上面可以看出,要解答差倍问题必须 要知道两个数的“差”及它们之间的 7
4
知识点
已知大小两个数的差,还知道大数是小 数的几倍,求大小两个数各是多少的应 用题,叫做差倍问题。差倍问题也是一 种典型的应用题。解答差倍问题与解答 和倍问题的方法类似,我们仍然用画线 段图的方法来帮助分析、思考。我们可 以通过分析数量关系,发现条件和问题 之间的内在联系,找出解题的规律,正 确列式解答。
差倍问题
1
例1 甲班和乙班共有图书160本.甲班的图书本数是乙 班的3倍,甲班和乙班各有图书多少本?
2
例2、光明小学有学生760人,其中男生比女生的3倍 少40人,男、女生各有多少人?
3
例3、果园里有桃树、梨树、苹果树共552棵.桃树比 梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、 梨树和苹果树各有多少棵?
11
