运筹学-最短路问题[课件参考]
合集下载
第2讲最短路问题PPT教案

2 0
1 3 3,
3 0 5
2 4 1 3 5 0
插入点 v1,得: di(jk ) min{di(jk1) , di(kk 1) dk(jk 1)},
0 1 2
1
0
4 3
1 2 3 4 5 6
1
2
3
4
5
1
D (1)
4
0 2
2 0
3
1 3,
1
R (1)
1
2 2
第2页/共37页
二、Dijkstra算法
算法思想: 按距离u0由近及远为顺序,依次求得 u0到G的各顶点的最短路和距离,直至 所有顶点,算法结束。
第3页/共37页
Dijkstra算法: 求G中从顶点u0到其余顶点的最短路.
1) 置l(u0) 0,对v u0 ,l(v) ,S0 {u0} i 0 且 2) 对每. 个 v Si ,用 min{l(v),l(ui ) w(ui,v)}
于是,D( ) (di(j )) 中元素di(j )就是从vi到v j 的路径中间可 插入任何顶点的路径中最短路的长度,即D( )就是所求距离矩阵.
第19页/共37页
(II)求路径矩阵的方法.
在建立距离矩阵的同时可建立路径矩阵R.
设 R(k) (ri(jk) ) ,这里ri(jk)的含义是从vi到v j 的最短
第2讲最短路问题
会计学
1
定义 1) 若H是赋权图G的一个子图,则称H的各
边的权和 w(H ) w(e) 为H的权. 类似地,若
eE(H )
若P(u,v)是赋权图G中从u到v的路,称 w(P) w(e)
称为路P的权.
eE ( P )
2) 在赋权图G中,从顶点u到顶点v的具有最小权 的路P*(u,v),称为u到v的最短路.
《最短路问题》课件

3 最短路问题的历史
渊源
最短路问题最早由荷兰 数学家 Edsger Dijkstra 在 1956 年提出。
最短路问题的定义
图论中的最短路问 题指什么?
在无向连通图或有向连通图 中,从某一起点到其余各顶 点的最短路径。
什么是路径长度?
路径长度是指路径上边或弧 的权值之和。
什么是无环图?
无环图指不存在环的图,可 以用拓扑排序求解最短路。
《最短路问题》PPT课件
欢迎来到最短路问题的世界。在本课件中,我们将介绍四种最短路算法及其 应用,并分析它们的优缺点。
问题背景
1 什么是最短路问题? 2 为什么需要解决最
短路问题?
最短路问题是计算从源 节点到目标节点的最短 路径的问题。它是图论 中的一个经典算法问题。
很多实际问题都涉及到 最短路径的计算,比如 电网、交通、通信等领 域。
Floyd-Warshall算法解决的是所有点对之间 的最短路径问题,可以处理有向图或负边权 图。
Bellman-Ford算法
Bellman-Ford算法解决的是有向图中含有负 权边的单源最短路径问题。
A*算法
A*算法综合了贪心和广度优先搜索,在启发 函数的帮助下,可以高效解决带权图上的单 源最短路径问题。
算法示例
1
Step 1
假设我们要求从 A 点到其他各点的最
Step 2
2
短路径。
首先初始化 A 点到其他各点的距离为
无穷大,A 点到自身的距离为 0。
3
Step 3
找到 A 点的直接邻居,更新其距离值。
Step 4
4
重复 Step 3,直到所有节点的距离值 都已经更新。
总结
运筹学课件 最短路、最大流、邮路

第i年 价格 ai 使用寿命 费用 bi 1 11 0-1 b1 5 2 11 1-2 b2 6 3 12 2-3 b3 8 4 12 3-4 b4 11 5 13 4-5 b5 18
最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧,弧(i , j)表示在 第 i 年买进的设备一直使用到第 j 年年初(第 j -1年年末)。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧(i , j)的权数为第i年的购置费ai+从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费:b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
(使用寿命为j-i年) 具体权数计算结果如下:
5 41 30 23 17 6 59 41 31 23 18
如:(2-4)权数为:a2+b1+b2=11+5+6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 :
2 16 30 22 41 4 23
最大流问题
两个重要结论: 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *,网络中有一个截集( V1*,V1*), 使v( f *)=C(V1*,V1 *),则f *必是最大流,而( V1*, V1 *)必是所有截集中容量最小的一个,即最小截集。
定理:可行流f *是最大流,当且仅当不存在关于f *的增广链。 于是有如下结论:最大流量最小截量定理:任一个网络中,从vs 到vt的最大流量等于分离vs,vt的最小截集的容量。
最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧,弧(i , j)表示在 第 i 年买进的设备一直使用到第 j 年年初(第 j -1年年末)。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧(i , j)的权数为第i年的购置费ai+从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费:b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
(使用寿命为j-i年) 具体权数计算结果如下:
5 41 30 23 17 6 59 41 31 23 18
如:(2-4)权数为:a2+b1+b2=11+5+6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 :
2 16 30 22 41 4 23
最大流问题
两个重要结论: 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *,网络中有一个截集( V1*,V1*), 使v( f *)=C(V1*,V1 *),则f *必是最大流,而( V1*, V1 *)必是所有截集中容量最小的一个,即最小截集。
定理:可行流f *是最大流,当且仅当不存在关于f *的增广链。 于是有如下结论:最大流量最小截量定理:任一个网络中,从vs 到vt的最大流量等于分离vs,vt的最小截集的容量。
第三节 最短路问题PPT课件

定义: 给定一个赋权有向图,即给了一个有向图
G=(V,A,W) ,对每一个弧aij =(vi,vj)∈A , 相应地有权w(aij ) =wij ∈V1 ,又给定 G中的 两个顶点vs ,vt 。设 P是G 中从vs 到 vt的一条路,
定义路 P的权是 P中所有弧的权之和,记为W(P)
。最短路问题就是要在所有从vs 到vt 的路中,求 一条权最小的路,即求一条从vs 到vt 的路P* ,
Thank You
在别人的演说中思考,在自己的故事里成长
Thinking In Other People‘S Speeches,Growing Up In Your Own Story
讲师:XXXXXX XX年XX月XX日
则resent= vk,
, 。 Sk Sk1 vk
Tk Tk1 vk
若k=n,则结束,否则转第二步。
6
例 用Dijkstra算法求前面例子中从v1到各点的最短路。
v2 1
6 2
v5
2
v9
6
3
v1
3 v3 6
3 4 10
1
2
v4
10
4
v6 2 v7
v8
7
图上标号法:
v2 v1,6 1
v5
v1, ∞ 2
转步骤二。
29
用逐次逼近算法求从V1到V6的最短路
v2
5
4
v1
-3
5
7
v3
v6 v4 6
2
v5
30
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
运筹学——.图与网络分析-最短路课件

运筹学——.图与网络分析-最短路
v2 (4) 5 v4
9
v6
4
1
v1 (0)
4
75
5
v8
① ②
64
v 3(6)
7 v 5 (8) 6
1
v7
③
④
4)接着往下考察,有四条路可走:(v2,v4), (v2,v5).
可选择的最短路为
(v3,v4), (v3,v5).
m k 2 , ik 4 2 n ,k 5 3 ,{ k 4 3 } 5m 9 ,8 , i 1 , n 1 } 0 { 3 8
(v5,v6), (v5,v7 ).
m k 2 ,i k 4 3 n ,k 4 5 ,k { 6 5 } 7 m 9 ,1 i ,1 n ,1 0 } 3 { 4 9
① 给(v2,v4) 划成粗线。
② 给 v 4 标号(9)。
③ 划第5个弧。
运筹学——.图与网络分析-最短路
v 2 ( 4 ) 5 v 4(9 ) 9 v 6 (13 )
运筹学——.图与网络分析-最短路
引言
随着科学技术的进步,特别是电子计算机 技术的发展,图论的理论获得了更进一步的发展, 应用更加广泛。如果将复杂的工程系统和管理问 题用图的理论加以描述,可以解决许多工程项目 和管理决策的最优问题。因此,图论越来越受到 工程技术人员和经营管理人员的重视。
运筹学——.图与网络分析-最短路
树图的各条边称为树枝假定各边均有权重一般图g2含有多个部分树其中树枝总长最小的部分树称为该图的最小部分树也称最小支撑树?定理1图中任一个点i若j是与i相邻点中距离最近的则边ij一定必含在该图的最小部分树内
第6章 图与网络分析
本章内容重点 图的基本概念与基本定理 树和最小支撑树 最短路问题 网络最大流
运筹学-14最短路

9
[1,v1]
[9,v5] [12,v5] [10,v5]
v1 v3 v2 v5 v8 12
v1 v9Leabharlann • 有向图的最短路问 题我会了,可是无
向图的最短路问题 怎样求?
最短路问题
• 一个旅行者从城市V1出发到V10,各城市之间的 距离如图所示,问如何确定旅行路线,才能使
总旅程最短?
2. X,X ’= 3. v9标号[]
求从v 1到各点的最短路(3)
v1 v3 v2
5
v1 v3
3
[5,v3]
[6,v2]
[]
v1 v4
1
v1 v3 v2 v5
6
v1 v3 v2 v5 v6
v1 v3 v2 v5 v7
[0,0]
[3,v1]
10
一旦找到v的最短路就把顶点v割是一个弧集每一条弧计算kijij最小到不了该点标号法dijkstrs算法到各点的最短路11v标号00002minxxminvmin06321105到各点的最短路200min6463661101091211min6466110941012111310vmin66941213到各点的最短路300有向图的最短路问题我会了可是无向图的最短路问题怎样求
(1, V1)
标号法
(10, V4)
[0,0]
(9,V7) (5, V8)
(8, V6)
(3,V1)
(11, V8)
V3:(10,V4) X=V1,V2,V8,V6,V7,V4,V3, X’=V5,V9,V10
(X,X’)={(V8,V9)(V7,V9)(V7,V10)(V3,V10)(V4,V5)(V7,V5)(V3,V5)}
最短路应用问题课件 15页PPT文档
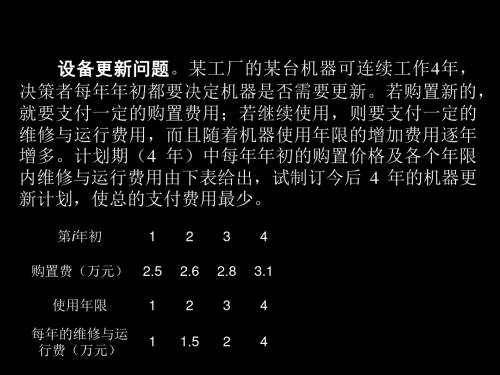
按照最短路算法可得最短路 {v1, v2, v3, v5},即计划 期内机器更新最优计划为第 1 年、第 3 年初各购进 一台新机器,4 年总的支付费用为 6.8万元。
选址问题。选址问题是指为一个或几个服
务设施在一定区域内选定它的位置,使某一指 标达到最优值。选址问题的数学模型依赖于设 施可能的区域和评判位置优劣的标准,有许多 不同类型的选址问题。比较简单的两类选址问 题是中心问题和重心问题。
某生产厂家年初要制定生产策略,已预知其产品在年初 的需求量为a=6万单位,并以b=1万单位/月速度递增。若生 产产品过剩,则需付单位产品单位时间(月)的库存保管 费C2=0.2元;若产品短缺,则单位产品单位时间的短期损 失费C3=0.4元。假定生产率每调整一次带有固定的调整费 C1=1万元,试问工厂如何制定当年的生产策略,使工厂的 总损失最小?
S(vi)m 1ja{dxij},i = 1, 2, …, v 有:S(v1) = 10,S(v2) = 7,S(v3) = 6,S(v4) = 8.5, S(v5) = 7,S(v6) = 7,S(v7) = 8.5。
(3) 求出顶点 vk,使 S(vk)m 1i{iSn(vi)},则 vk 就是要求的建立消防站的地点。因为 S(v3) = 6 最小,故应将消防站设在 v3 处。此点称为图的 中心点。
25
20 10
0
55
10
25
25 55
0
实验作业
生产策略问题:现代化生产过程中,生产部门面临的突出 问题之一,便是如何选取合理的生产率。生产率过高,导致 产品大量积压,使流动资金不能及时回笼;生产率过低,产 品不能满足市场需要,使生产部门失去获利的机会。可见, 生产部门在生产过程中必须时刻注意市场需求的变化,以便 适时调整生产率,获取最大收益。
选址问题。选址问题是指为一个或几个服
务设施在一定区域内选定它的位置,使某一指 标达到最优值。选址问题的数学模型依赖于设 施可能的区域和评判位置优劣的标准,有许多 不同类型的选址问题。比较简单的两类选址问 题是中心问题和重心问题。
某生产厂家年初要制定生产策略,已预知其产品在年初 的需求量为a=6万单位,并以b=1万单位/月速度递增。若生 产产品过剩,则需付单位产品单位时间(月)的库存保管 费C2=0.2元;若产品短缺,则单位产品单位时间的短期损 失费C3=0.4元。假定生产率每调整一次带有固定的调整费 C1=1万元,试问工厂如何制定当年的生产策略,使工厂的 总损失最小?
S(vi)m 1ja{dxij},i = 1, 2, …, v 有:S(v1) = 10,S(v2) = 7,S(v3) = 6,S(v4) = 8.5, S(v5) = 7,S(v6) = 7,S(v7) = 8.5。
(3) 求出顶点 vk,使 S(vk)m 1i{iSn(vi)},则 vk 就是要求的建立消防站的地点。因为 S(v3) = 6 最小,故应将消防站设在 v3 处。此点称为图的 中心点。
25
20 10
0
55
10
25
25 55
0
实验作业
生产策略问题:现代化生产过程中,生产部门面临的突出 问题之一,便是如何选取合理的生产率。生产率过高,导致 产品大量积压,使流动资金不能及时回笼;生产率过低,产 品不能满足市场需要,使生产部门失去获利的机会。可见, 生产部门在生产过程中必须时刻注意市场需求的变化,以便 适时调整生产率,获取最大收益。
运筹学-最短路问题

v1
V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法: 最短路算法:
1. D氏标号法(Dijkstra) 氏标号法(Dijkstra) (1)求解思路 求解思路——从始点出发,逐步顺序 从始点出发, 从始点出发 逐步顺序 地向外探寻,每向外延伸一步都要求是最 地向外探寻,每向外延伸一步都要求是最 短的。 短的。 (2)使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负, 非负,即 wij ≥ 0 。
(4) 计算步骤及例:
第三步:若网络图中已无T标号点 标号点, 第三步:若网络图中已无 标号点,停止 计算。否则 令 计算。否则,令 二步。 二步。 此时,要注意将第二步中的 此时,
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ,转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号) 号( 表P标号) 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2,…,v7} , {v3,…,v7} , {v4,…,v7} , {v5,v6,v7} {v5,v7} {v7}
2
5 2+2 4
V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法: 最短路算法:
1. D氏标号法(Dijkstra) 氏标号法(Dijkstra) (1)求解思路 求解思路——从始点出发,逐步顺序 从始点出发, 从始点出发 逐步顺序 地向外探寻,每向外延伸一步都要求是最 地向外探寻,每向外延伸一步都要求是最 短的。 短的。 (2)使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负, 非负,即 wij ≥ 0 。
(4) 计算步骤及例:
第三步:若网络图中已无T标号点 标号点, 第三步:若网络图中已无 标号点,停止 计算。否则 令 计算。否则,令 二步。 二步。 此时,要注意将第二步中的 此时,
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ,转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号) 号( 表P标号) 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2,…,v7} , {v3,…,v7} , {v4,…,v7} , {v5,v6,v7} {v5,v7} {v7}
2
5 2+2 4
运筹学 PPT课件 第五章 图与网络分析-最短路

Dijkstra最短路算法的特点和适应范围
一种隐阶段的动态规划方法 每次迭代只有一个节点获得永久标记,若有两个或两个以上节点的 临时标记同时最小,可任选一个永久标记;总是从一个新的永久标 记开始新一轮的临时标记,是一种深探法 被框住的永久标记 Tj 表示 vs 到 vj 的最短路,因此 要求 dij0,第 k 次迭代得到的永久标记,其最短路中最多有 k 条边,因此最多有
d
(0) 65
}
min{0 ,2 9,6 3, , 0, 1}
9 取自第3列
v1 v2 v3 v4 v5 v6
0 2 6
2
0
3
8
9
D(0) L 6 3 0 5 3
8
5
0
3
9 3 0 1
3
1
0
d (1) 16
mkin{d1(k0)
d
} (0)
k6
(第1行+第6列)
8
5
0
3
9 3 0 1
3
1
0
d (1) 15
mkin{d1(k0)
d
(0) k5
}
(第1行+第5列)
min{d1(10)
d (0) 15
,
d (0) 12
d (0) 25
,
d (0) 13
d (0) 35
,
d (0) 14
d
(0) 45
,
d (0) 15
d (0) 55
,
d (0) 16
min{d1(10)
d (0) 16
,
d (0) 12
d
(0) 26
,
d (0) 13
最短路算法上课ppt

优点
缺点
优点
优点
效率低,需要遍历所有点(特别是有时候不需要最优解)、运算中占用空间大
缺点
算法简明易懂、并且一定能得到最优解
优点
Dijkstra算法可能不是最优先使用的方法,因为算法的运算速度效率,往往要比精确度更加重要
实际运用
但似乎在实际运行时效果并不理想! 这样利用Dijkstra算法设计一个属于我们自己的导航系统啦。
最佳优先搜索简介
这个算法的运算流程跟Dijkstra的流程类似,只不过它考察的是选取点到终点的距离,并且这个距离的权值是评估出来的,这也就是启发式的思想。举例说明,如果说目标的终点在北面,那么越靠近北面的点权值就越小,那么算法在搜索过程中,所加入点集的点就会倾向于北面,因此不用搜索全图东南西北,更多的是搜索北面的点,速度来说会优于Dijkstra算法很多。
01
A*算法能够解决有固定障碍物的路径规划问题,并且能很快地给出解,但是当障碍物是移动的时候,我们又应该如何对算法进行改从而给出解呢?
02
一个典型问题:AGV小车线路规划!
智能码头:AGV
AGV中文名:自动导引小车
是自动化码头水平运输系统中用于搬运集装箱的搬运设备。
其主要职责:就是在规定的时间窗口范围内完成堆场和岸桥之间实现集装箱的传送。
一
算法的描述上看去相当复杂,我们给出下面例子来具体说明整个算法的运行流程!
首先我们要有如下概念:
假设P:v→km是从顶点v到km的一条最短路径,那对这条路径上任意其他一点ki,都有 P上关于v→ ki的子路径为v到点ki的最短路径。
即最短路径的子路径仍然是最短路径,最短路算法本质上上基于这种思想展开的。
最短路问题及相关算法介绍
运筹学最短路邮递员问题PPT课件

从一点到任意点的最短路
• 木器厂有六个车间,办事员经常 要到各个车间了解生产进度。从 办公室到各车间的路线由图1给出。
找出点1(办公室)到其它各点 (车间)的最短路
11
27
2
2
1 5 3 5 55 7
3
1
4
3
1
6
7
5
12
2
权wij(dij)
2
距离、价格 2
15
3
点(vi)
边eij或记为(vi,vj) 13
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
41
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
42
6 v5
3
5
3
v2
3
6
3
v6
2.5
0
v1
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
43
6 v5
3
5
3
v2
3
6
3
v6
2.5
最短路问题不仅可以求解交通图中两点之间的最短距离,实际 中很多问题也可变为最短路问题加以求解。例如设备更新问题,厂 区合理布局问题等。兹举一例:
例1(设备更新问题)某企业使用一台设备,在每年年底,企业 都要决策下年度是购买一台新设备呢?还是继续使用这台设备。若 购买新的,就要支付一笔购置费;如果使用旧设备,只要支付维修 费,而维修费随着设备的使用年限延长而增加。现根据以往统计资 料已经估算出设备在各年初的价格和不同使用年限的修理费用,分 别如表1、表2所示。
运筹学-最短路问题[课件参考]
![运筹学-最短路问题[课件参考]](https://img.taocdn.com/s3/m/199eaa4c5727a5e9846a6140.png)
Page 10
1、最短路算法基于以下原理:
一个最优策略的任一子策略也是最优策略.
若P是从vs到vt间的最短路, vi是P中的一个点,则vs到vi的最
短路就是从vs 沿P到vi的那条路。 v2
v4
v1
v3
v5
v1 →v2 →v3一定是v1 →v3的最短路,
v2 →v3 →v4也一定是v2 →v4的最短路。
2.设节点 vi 为刚得到P标号的点,考虑点vj,其中 (vi , v j ) E ,且vj为T标号。对vj的T标号进行如下修改:
T (v j ) min[T (v j ) , P(vi ) wi j ]
3.比较与vi相邻的所有具有T标号的节点,把最小者改为P 标号,即: P(vk ) min[T (vi )]
精选课件
Chapter8 图与网络优化
本章主要内容:
§8.1 图的基本概念 §8.2 树 §8.3 最短路问题 §8.4 网络最大流问题 §8.5 最小费用最大流问题 §8.6 中国邮递员问题
精选课件
Page 3
§8.3 最短路问题
The Shortest-Path Problem
精选课件
§8.3 最短路问题
Page 17
解 :(1)首先给v1以P标号,给其余所有点T 标号。
P(v1) 0,T (vi ) (i 2, 3, , 8),(v1) 0;
(2) T (v2 ) min{T (v2 ), P(v1 ) w12 } min{ , 0 3} 3
T (v4 ) min{T (v4 ), P(v1 ) w14 } min{ , 0 7} 7
精选课件
§8.3 最短路问题
最短路问题(课堂PPT)

5
5
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
6
(4)找出所有与v1,v2,v3相邻的未标记的点v4,v5,v6,求出
从v1直接到这些点的距离(v1->v4:7)以及经过v2到这些点 的距离(v1->v2->v4:11;v1->v2->v5:10;v1->v2->v6:8)以及 经过v3到这些点的距离(v1->v3->v4:6;v1->v3->v5:12)找出 这些距离中最短的路径为v1->v3->v4,最短距离为L14=6, 将v4标记为6
3 2 4 1
时间
2 3 3 2
25
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
(2)找出同v1相邻的未标号的点有v2,v3,v4,求出从
v1到其所有相邻点的距离(v1->v2:5;v1->v3:4;v1>v4:7),距离最短路径为v1->v3,最短距离为L13=4, 将v3标记为4
0
5
V2
3
6 5 5 V6
5
0
5
V2
3
6 6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
7
(5)找出所有与v1,v2,v3,v4相邻的未标记的点v5,v6,求出
5
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
6
(4)找出所有与v1,v2,v3相邻的未标记的点v4,v5,v6,求出
从v1直接到这些点的距离(v1->v4:7)以及经过v2到这些点 的距离(v1->v2->v4:11;v1->v2->v5:10;v1->v2->v6:8)以及 经过v3到这些点的距离(v1->v3->v4:6;v1->v3->v5:12)找出 这些距离中最短的路径为v1->v3->v4,最短距离为L14=6, 将v4标记为6
3 2 4 1
时间
2 3 3 2
25
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
(2)找出同v1相邻的未标号的点有v2,v3,v4,求出从
v1到其所有相邻点的距离(v1->v2:5;v1->v3:4;v1>v4:7),距离最短路径为v1->v3,最短距离为L13=4, 将v3标记为4
0
5
V2
3
6 5 5 V6
5
0
5
V2
3
6 6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
7
(5)找出所有与v1,v2,v3,v4相邻的未标记的点v5,v6,求出
运筹学最短路邮递员问题PPT课件

•
新的T(vj)=min{老的T(vj),p(vi)+ ωij }
• 若T(vj)= p(vi)+ ωij ,则记k(vj )=vi(前点标记);
• 3°找出具有最小T标号的点,将其标号改为p标号。若vt 已获得p
标号,则已找到最短路,由k(vt)反向追踪,就可找出vs 到vt 的最
短路径,p(vt)就是vs 到vt 的最短距离。否则,转2°。
p(v2)
=3 3
p(v1) v1
p(v=30)
=4
6
v2
51 1
v4
7 4
v5
v3 3 2
5
v7
26 v6 9 15
v8
T(v4)=min{6,4+1}=5, k(v4 )=v3
T(v6)=min{7,4+2}=6, k(v6 )=v3
目前,点v4 具有最小T标号,将其标号改为p标号: p(v4)=5;
向继续前进,则最先到达终点vt 的流所走过的路径一定是最短的。
为了实现这一想法,对假想流依次到达的点,依次给予p标号,表
示vs到这些点的最短距离。对于假想流尚未到达的点给予T标号,
表示vs到这些点的最短距离的估计值。具体作法如下:
• 1°标p(vs)=0,其余点标T(vi)=+∞;
• 2°由刚刚获得p标号的vi 点出发,改善它的相邻点vj 的T标号,即
对于点v2 :d(v2)=min{16+31,22+23,30+18,41}=41, v对2→于v点6 v;1 :d(v1)=min{16+41,22+31,30+23,41+18,59}
试确定一个五年内的设备更新计划,使五年内总支出最小。
运筹学05_图与网络分析2_最短路演示课件.ppt

5
精选课件
(3,7)
(1,2)
2
2
0
1
2
5
(2,4)
3
7
5
(6,8)
55
7
1
3
3
1
4
6
7
(1,3)
5
精选课件
(3,7)
(1,2)
2
2
0
15
1 3
4
(1,3)
2
(2,4)
3
5
7 (6,8)
5 55
3
1
6
7
精选课件
(3,7)
(5,13)
7
(1,2)
2
2
0
15
1 3
4
(1,3)
2
(2,4)
3
5
7 (6,8)
5 55
3
1
6
7
精选课件
(3,7)
(5,13)
7
对有向图同样可以用标号算法: 例2 如图,有一批货物要从v1运 到v9,弧旁数字表示该段路长, 求最短运输路线。
精选课件
3 0 v1
4
v5
3
5
v2
3
2
v6
2.5
3
1
2
v3 3
v7 2
v4
v9
4 v8
精选课件
v5
3
5
1,3
3 0 v1
v2
3
2
v6
2.5
一个连通图能一笔画的条件是: 它没有奇点;或者它恰好有一个奇点。
精选课件
一个图有5个点,8条边。这个图一定是 A.连通图 B.树 C.完全图 D.不连通图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、Floyd-Warshall算法
Floyd-Warshall算法是解决任意两点间的最短路径的 一种算法,可以正确处理有向图或负权的最短路径问题。
精选课件
§8.3 最短路问题
Page 9
8.3.2 狄克斯特拉算法 (Dijkstra algorithm,也称双标号法)
1959年, Dijkstra发现了在赋权图中求最短路的算法。 迪杰斯特拉(1930-2002,荷兰人),早年钻研物理及数学, 转为计算学。1972年获图灵奖(计算机界的诺贝尔奖)。
没有边,则令 dij = ,若两点之间是有向边,则 dji = ; 令 dii = 0,s 表示始点,t 表示终点
精选课件
§8.3 最短路问题
Page 15
(3)算法步骤:
1.给始点vs以P标号 P(vs ) 0 ,这表示从vs到 vs的最短距离 为0,其余节点均给T标号,P(vi ) (i 2,3, ,n) 。
A
P
B
C
精选课件
§8.3 最短路问题
Page 6
8.3.1 最短路问题
最短路问题: 就是从给定的网络图中找出一点到各点或任意两点之间
距离最短的一条路 .
有些问题,如选址、管道铺设时的选线、设备更新、投 资、某些整数规划和动态规划的问题,也可以归结为求最短 路的问题。因此这类问题在生产实际中得到广泛应用。
精选课件
§8.3 最短路问题
Page 7
定义权设值连的通意图义D是=(广V,A泛),的每。一可弧以a表= (示vi,距vj)离,,有可一以个表非示负交权通运 费,可以表示网络w(流a)=量w,ij (在wij朋≥0友) 关系图甚至可以表示友谊深 如度果。P但是都D可中以从抽vs象到为vt的距一离条。路,称P中所有弧的权之和为路P 的权,记为w(P)。
2.设节点 vi 为刚得到P标号的点,考虑点vj,其中 (vi , v j ) E ,且vj为T标号。对vj的T标号进行如下修改:
若λ(v)=M,表示D中不含从vs到v的路;
若λ(v)=0表示v=vs。
精选课件
§8.3 最短路问题
Page 13
v2
1
v5
6
2
2
v9
6
v1
3 v3 6
4
10 3
3
1
2
v8
4
2 v7
s=1。d(v1,v1)=0。v1是具Pv标4 号的点1。0
v6
现考查从v1发出的三条弧,(v1,v2),(v1,vv1,,v1)+ω12,d(v1,v1)+w13,d(v1,v1)+w14=d(v1,v1)+w14=1
这样就可使v4变成具P标号的点。 精所选以课从件v1出发到v4所需的最小费用必定是1单位,
Page 14
(2)标号含义: 令 dij 表示 vi 到 vj 的直接距离(两点之间有边),若两点之间
常见的最短路算法
1、Dijkstra算法 注意该算法要求不存在负权边 Dijkstra算法是典型的单源最短路径算法,用于计算一
个节点到其他所有节点的最短路径。主要特点是以起始点为 中心向外层层扩展,直到扩展到终点为止。Dijkstra算法在 很多专业课程如数据结构,图论,运筹学等中都作为基本内 容有详细的介绍,。
精选课件
§8.3 最短路问题
Page 12
(2)标号含义:
P(v) ,T(v)分别表示点v的P标号和T标号, Si表示第i步时具P标号点的集合。 为了在求出从vs到各点的距离的同时,也求出从vs到各点的最
短路,给每个点v以一个λ值。算法终止时,
若λ(v)=m,表示在从vs到v的最短路上,v的前一个点是vm;
Page 10
1、最短路算法基于以下原理:
一个最优策略的任一子策略也是最优策略.
若P是从vs到vt间的最短路, vi是P中的一个点,则vs到vi的最
短路就是从vs 沿P到vi的那条路。 v2
v4
v1
v3
v5
v1 →v2 →v3一定是v1 →v3的最短路,
v2 →v3 →v4也一定是v2 →v4的最短路。
定义 设D为有向赋权图,vs与vt是D中两点,在连接vs与vt的 所有路中,权最小的路P0称为从vs到vt的最短路。即
(
P0
)
min P
(
P
)
最小的路P0的权称为从vs到vt的距离,记为d(vs , vt )
d(vs ,vt )和d(vt ,vs )不一定相等。
精选课件
§8.3 最短路问题
Page 8
精选课件
§8.3 最短路问题
Page 4
• 如何用最短的线路将三部电话连起来?
• 此问题可抽象为设△ABC为等边三角形,,连接三顶点的 路线(称为网络)。这种网络有许多个,其中最短路线者 显然是二边之和(如AB∪AC)。
A
B
C
精选课件
§8.3 最短路问题
Page 5
但若增加一个周转站(新点P),连接4点的新网络的最短路 线为PA+PB+PC。最短新路径之长N比原来只连三点的最 短路径要短。这样得到的网络不仅比原来节省材料,而且稳 定性也更好。
1.提出“goto有害论”; 2 .提出信号量和PV原语; 3.解决了“哲学家聚餐”问题6;. THE操作系统的设计者和开发者;
4.最短路径算法和银行家算法的创造者;
5.第一个Algol 60编译器的设计者和实现者;
与D. E. Knuth并称为这个时代最伟大的计算机科学家的人。
精选课件
§8.3 最短路问题
运筹学
( Operations Research )
精选课件
Chapter8 图与网络优化
本章主要内容:
§8.1 图的基本概念 §8.2 树 §8.3 最短路问题 §8.4 网络最大流问题 §8.5 最小费用最大流问题 §8.6 中国邮递员问题
精选课件
Page 3
§8.3 最短路问题
The Shortest-Path Problem
精选课件
§8.3 最短路问题
Page 11
2、Dijkstra算法
(1)基本思想: 从vs出发,给网络中的每个点对应记录一个数(称为这 个点vi的标号),它或者表示从vs到该点vi的最短路的权(称 为P标号,此为永久标号),或者是从vs到该点vi的最短路的 权的上界(称为T标号,此为临时标号),
方法的每一步是去修改T标号,并且把某一个具T标号 的点改变为具P标号的点,从而使D中具P标号的顶点数多 一个,这样至多经过p−1步,当终点vt得到P标号时,就可 以求出从vs到各点的最短路。
Floyd-Warshall算法是解决任意两点间的最短路径的 一种算法,可以正确处理有向图或负权的最短路径问题。
精选课件
§8.3 最短路问题
Page 9
8.3.2 狄克斯特拉算法 (Dijkstra algorithm,也称双标号法)
1959年, Dijkstra发现了在赋权图中求最短路的算法。 迪杰斯特拉(1930-2002,荷兰人),早年钻研物理及数学, 转为计算学。1972年获图灵奖(计算机界的诺贝尔奖)。
没有边,则令 dij = ,若两点之间是有向边,则 dji = ; 令 dii = 0,s 表示始点,t 表示终点
精选课件
§8.3 最短路问题
Page 15
(3)算法步骤:
1.给始点vs以P标号 P(vs ) 0 ,这表示从vs到 vs的最短距离 为0,其余节点均给T标号,P(vi ) (i 2,3, ,n) 。
A
P
B
C
精选课件
§8.3 最短路问题
Page 6
8.3.1 最短路问题
最短路问题: 就是从给定的网络图中找出一点到各点或任意两点之间
距离最短的一条路 .
有些问题,如选址、管道铺设时的选线、设备更新、投 资、某些整数规划和动态规划的问题,也可以归结为求最短 路的问题。因此这类问题在生产实际中得到广泛应用。
精选课件
§8.3 最短路问题
Page 7
定义权设值连的通意图义D是=(广V,A泛),的每。一可弧以a表= (示vi,距vj)离,,有可一以个表非示负交权通运 费,可以表示网络w(流a)=量w,ij (在wij朋≥0友) 关系图甚至可以表示友谊深 如度果。P但是都D可中以从抽vs象到为vt的距一离条。路,称P中所有弧的权之和为路P 的权,记为w(P)。
2.设节点 vi 为刚得到P标号的点,考虑点vj,其中 (vi , v j ) E ,且vj为T标号。对vj的T标号进行如下修改:
若λ(v)=M,表示D中不含从vs到v的路;
若λ(v)=0表示v=vs。
精选课件
§8.3 最短路问题
Page 13
v2
1
v5
6
2
2
v9
6
v1
3 v3 6
4
10 3
3
1
2
v8
4
2 v7
s=1。d(v1,v1)=0。v1是具Pv标4 号的点1。0
v6
现考查从v1发出的三条弧,(v1,v2),(v1,vv1,,v1)+ω12,d(v1,v1)+w13,d(v1,v1)+w14=d(v1,v1)+w14=1
这样就可使v4变成具P标号的点。 精所选以课从件v1出发到v4所需的最小费用必定是1单位,
Page 14
(2)标号含义: 令 dij 表示 vi 到 vj 的直接距离(两点之间有边),若两点之间
常见的最短路算法
1、Dijkstra算法 注意该算法要求不存在负权边 Dijkstra算法是典型的单源最短路径算法,用于计算一
个节点到其他所有节点的最短路径。主要特点是以起始点为 中心向外层层扩展,直到扩展到终点为止。Dijkstra算法在 很多专业课程如数据结构,图论,运筹学等中都作为基本内 容有详细的介绍,。
精选课件
§8.3 最短路问题
Page 12
(2)标号含义:
P(v) ,T(v)分别表示点v的P标号和T标号, Si表示第i步时具P标号点的集合。 为了在求出从vs到各点的距离的同时,也求出从vs到各点的最
短路,给每个点v以一个λ值。算法终止时,
若λ(v)=m,表示在从vs到v的最短路上,v的前一个点是vm;
Page 10
1、最短路算法基于以下原理:
一个最优策略的任一子策略也是最优策略.
若P是从vs到vt间的最短路, vi是P中的一个点,则vs到vi的最
短路就是从vs 沿P到vi的那条路。 v2
v4
v1
v3
v5
v1 →v2 →v3一定是v1 →v3的最短路,
v2 →v3 →v4也一定是v2 →v4的最短路。
定义 设D为有向赋权图,vs与vt是D中两点,在连接vs与vt的 所有路中,权最小的路P0称为从vs到vt的最短路。即
(
P0
)
min P
(
P
)
最小的路P0的权称为从vs到vt的距离,记为d(vs , vt )
d(vs ,vt )和d(vt ,vs )不一定相等。
精选课件
§8.3 最短路问题
Page 8
精选课件
§8.3 最短路问题
Page 4
• 如何用最短的线路将三部电话连起来?
• 此问题可抽象为设△ABC为等边三角形,,连接三顶点的 路线(称为网络)。这种网络有许多个,其中最短路线者 显然是二边之和(如AB∪AC)。
A
B
C
精选课件
§8.3 最短路问题
Page 5
但若增加一个周转站(新点P),连接4点的新网络的最短路 线为PA+PB+PC。最短新路径之长N比原来只连三点的最 短路径要短。这样得到的网络不仅比原来节省材料,而且稳 定性也更好。
1.提出“goto有害论”; 2 .提出信号量和PV原语; 3.解决了“哲学家聚餐”问题6;. THE操作系统的设计者和开发者;
4.最短路径算法和银行家算法的创造者;
5.第一个Algol 60编译器的设计者和实现者;
与D. E. Knuth并称为这个时代最伟大的计算机科学家的人。
精选课件
§8.3 最短路问题
运筹学
( Operations Research )
精选课件
Chapter8 图与网络优化
本章主要内容:
§8.1 图的基本概念 §8.2 树 §8.3 最短路问题 §8.4 网络最大流问题 §8.5 最小费用最大流问题 §8.6 中国邮递员问题
精选课件
Page 3
§8.3 最短路问题
The Shortest-Path Problem
精选课件
§8.3 最短路问题
Page 11
2、Dijkstra算法
(1)基本思想: 从vs出发,给网络中的每个点对应记录一个数(称为这 个点vi的标号),它或者表示从vs到该点vi的最短路的权(称 为P标号,此为永久标号),或者是从vs到该点vi的最短路的 权的上界(称为T标号,此为临时标号),
方法的每一步是去修改T标号,并且把某一个具T标号 的点改变为具P标号的点,从而使D中具P标号的顶点数多 一个,这样至多经过p−1步,当终点vt得到P标号时,就可 以求出从vs到各点的最短路。
